Социальный проект “Краткий справочный материал по математике для студентов 1 курса колледжа (теория и практика)” | Проект по алгебре (11 класс) по теме:
Департамент образования города Москвы
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Педагогический колледж №18 «Митино»
Социальный проект
Краткий справочный материал
по математике
для студентов 1 курса
( теория и практика )
Руководитель и автор проекта: Юнанова Ю.В.
Москва, 2012
Паспорт проектной работы
1. Название проекта: Краткий справочный материал по математике для студентов 1 курса ( теория и практика)
2. Руководитель проекта: Юнанова Ю.В., ГБОУ СПО ПК №18 «Митино»
3. Консультанты проекта: Шевченко А.Е., заслуженный учитель РФ, доцент
4. Учебный предмет, в рамках которого проводится работа по проекту: математика.
5. Учебные дисциплины, близкие к теме проекта : математика.
6. Возраст студентов, на который рассчитан проект: 15-21 лет
7. Состав проектной группы :
№ п\п | ФИО студента | № группы | Предполагаемая роль |
1 | Петрова Мария | 11 | Представление проекта |
2 | Ким Анжела | 11 | Составление краткого справочного материала |
3 | Анисимова Тамара | 11 | Презентация |
4 | Прянишникова Ксения | 11 | Составление краткого справочного материала |
5 | Рагузина Ирина | 11 | Презентация |
6 | Соколова Анастасия | 11 | Представление проекта |
7 | Куракина Евгения | 11 | Составление краткого справочного материала |
8 | Погорелова Екатерина | 11 | Составление краткого справочного материала |
8. Тип проекта: практико-ориентированный, информационный, творческий .
Тип проекта: практико-ориентированный, информационный, творческий .
9. Заказчик проекта: ГБОУ СПО Педагогический колледж №18 «Митино»
10. Проблема проекта: программа по математике 1 курса очень насыщенная: изучаются разделы алгебры, геометрии, начала математического анализа, комбинаторики, статистики и теории вероятности. На изучение некоторых тем отводится небольшой объем часов. Для слабоуспевающих студентов, для студентов, пропустивших занятия, нет кратного изложения теоретического материала с примерами решения типовых заданий, который помог бы им овладеть необходимыми знаниями , умениями и навыками по математике.
11. Цель проекта: улучшение качества формирования математической компетенции – знаний, умений и навыков с использованием краткого теоретического материала по математике 1 курса с примерами решения типовых заданий.
12. Задачи проекта:
– оказание помощи студентам при изучении курса математики 1 курса,
– поддержка и создание психолого-педагогических условий и среды для развития и реализации творческого потенциала студентов,
– организация совместной коллективно – творческой деятельности студентов.
13. Вопросы проекта:
– какие ключевые темы изучаются к каждом разделе;
– что должны знать и уметь студенты в результате изучения ключевых тем;
– какой краткий теоретический материал выделить по каждой выбранной теме;
– какие привести примеры типовых заданий с решениями по каждой выбранной теме;
– какие задания подобрать по каждой теме для самостоятельной работы студентов;
– как скомпоновать и оформить материалы проектной деятельности.
14. Необходимое оборудование:
– Учебные издания : 1. Алимов Ш.А. Алгебра и начала анализа. 10-11 кл.- М., 2010
2. Башмаков М.И.Алгебра и начала математического анализа(базовый уровень). 10 кл. М. 2010
3. Погорелов А.В. Геометрия 10-11 “Базовый уровень” – М. 2011
4. Тюрин Ю.Н. Теория вероятностей и статистика- М. 2010
– ПК;
– Принтер.
15. Аннотация:
Настоящий проект предназначен для студентов 1 курса и может быть также использован в работе преподавателей математики. Он поможет систематизировать имеющиеся знания по математике и ликвидировать пробелы в них, если такие окажутся. Особенно он может быть полезным при подготовке к контрольным работам и экзамену. Проект включает краткий теоретический материал по основным темам математики 1 курса; примеры решения типовых заданий с подробными комментариями ; упражнения для самостоятельной работы.
Он поможет систематизировать имеющиеся знания по математике и ликвидировать пробелы в них, если такие окажутся. Особенно он может быть полезным при подготовке к контрольным работам и экзамену. Проект включает краткий теоретический материал по основным темам математики 1 курса; примеры решения типовых заданий с подробными комментариями ; упражнения для самостоятельной работы.
В состав проектной группы входят студенты, хорошо успевающие по дисциплине. Работа над проектом поможет студенту – будущему преподавателю и в общении, и в профессиональной деятельности. В связи с этим творческое развитие становится явной необходимостью.
Новизна проекта заключается в том, что нами предпринята попытка кратко изложить теоретический и практический материал по математике 1 курса, привлекая для работы над проектом студентов 1 курса. Основная идея нашей работы – использование творческого потенциала студентов, раскрытие их талантов, предоставление возможности поделиться своими знаниями и опытом друг с другом, развитие интереса к математике, нахождение занятий, приносящих удовлетворение.
16. Предполагаемый продукт проекта:
– Планируется создать краткий справочный материал-«шпаргалку» для студентов по основным темам математики 1 курса.
17. Этапы работы над проектом:
Название этапа | Содержание работы | Сроки реализации |
Организационный | Определение темы проекта, постановка цели и задач | Сентябрь – ноябрь 2012 г. |
Основной | Сбор и оформление информации по темам проекта: | |
1. «Корни» | Ноябрь 2012 г. | |
2. «Степени» | Ноябрь 2012 г. | |
3. «Логарифмы» | Ноябрь 2012 г. | |
4. «Элементы комбинаторики» | Ноябрь 2012 г. | |
5. «Координаты и векторы» | Декабрь 2012 г. | |
6. | Декабрь 2012 г. – январь 2013 г. | |
7. «Функции, их свойства (четность/нечетность)» | Февраль – март 2013 г. | |
8. «Преобразование графиков функции» | Март 2013 г. | |
9. «Иррациональные уравнения» | Апрель 2013 г. | |
10. «Рациональные уравнения» | Май 2013 г. | |
11. «Решение простейших тригонометрических уравнений» | Май 2013 г. | |
Продукт проекта Краткий справочный материал – «шпаргалки» по математике для студентов 1 курса |
ПРЕЗЕНТАЦИЯ ПРОЕКТА |
Достижения участников проекта:
- Приняли активное участие в конкурсе проектов МПК №18 «Митино», были награждены Дипломом 2-ой степени;
- Приняли участие в Межрегиональной научно-практической конференции преподавателей и студентов «Пространство детства: современность и будущее» – подготовили стенд-доклад.

№п/п | Тема урока | |
Диагностическая контрольная работа | ||
Диагностическая контрольная работа | ||
Математика в науке, технике, экономике, информационных технологиях и практической деятельности. | ||
Цели и задачи изучения математики в учреждениях начального и среднего профессионального образования. | ||
Раздел 1. Алгебра | ||
Тема 1.1. Действительные числа | ||
Целые числа. | ||
Рациональные числа. | ||
Перевод из обыкновенной дроби в бесконечную десятичную периодической дробь. | ||
Перевод из бесконечной десятичной периодической дроби в обыкновенную дробь и обратно. Решение задач. | ||
Иррациональные числа. | ||
Действительные числа. | ||
Упрощение выражений с действительными числами. | ||
Приближенные числа. Абсолютная и относительная погрешности. Решение задач. | ||
Бесконечно убывающая геометрическая прогрессия. | ||
Разбор примеров перевода бесконечной десятичной дроби в обыкновенную дробь с помощью формулы суммы бесконечной геометрической прогрессии. | ||
Решение задач на нахождение членов и суммы бесконечно убывающей геометрической прогрессии | ||
Перевод бесконечной десятичной дроби в обыкновенную дробь с помощью формулы суммы бесконечной геометрической прогрессии. | ||
Матрицы и определители. | ||
Операции над матрицами | ||
Вычисление определителя матрицы. | ||
Операции над матрицами. Решение задач. | ||
Тема 1.2. Корни, степени, логарифмы | ||
Корни натуральной степени из числа и их свойства. | ||
Разбор заданий на упрощение выражений, содержащих корни натуральной степени. | ||
Упрощение выражений, содержащих корни натуральной степени. Решение задач. | ||
Упрощение выражений, с использовынием свойств корней натуральной степени. Решение задач. | ||
Степени с рациональным показателем и их свойства. | ||
Разбор заданий на упрощение выражений, содержащих степени с рациональным показателем. | ||
Применение свойств степени с рациональным показателем. | ||
Упрощение выражений, с испольвованием свойств степени с рациональным показателем. Решение задач. | ||
Степени с действительными показателями. Свойства степени с действительным показателем. | ||
Разбор заданий на упрощение выражений, содержащих степени с действительным покажателем. | ||
Применение свойств степени с действительным показателем. | ||
Упрощение выражений, с использованием свойств степени с действительным показателем. Решение задач. | ||
Логарифм числа. Основное логарифмическое тождество. | ||
Переход к новому основанию.Правила действий с логарифмами. | ||
Вычисление логарифма числа.Упрощение выражений с помощью основного логарифмического тождества. | ||
Приведение логарифмов к новому основанию. Решение задач. | ||
Разбор примеров применения свойств логарифмов. | ||
Преобразование логарифмических выражений с использованием свойств логарифмов. | ||
Действия с логарифмами. Решение задач. | ||
Упрощение логарифмических выражений с помощью правил действий с логарифмами. | ||
Преобразование рациональных и иррациональных выражений. | ||
Преобразование показательных и логарифмических выражений. | ||
Упрощение рациональных, иррациональных, показательных и логарифмических выражений. | ||
Контрольная работа №1 | ||
Тема 1. | ||
Синус, косинус, тангенс и котангенс числа в треугольнике. | ||
Синус, косинус, тангенс и котангенс числа в тригонометрической окружности. Радианная мера угла. | ||
Практическая работа. Вычисление синуса, тангенса, косинуса, котангенса в треугольнике. | ||
Практическая работа. Построение тригонометрической окружности. | ||
Применение окружности к вычислению тригонометрических функций. | ||
Перевод градусной меры угла в радианную. | ||
Основные тригонометрические тождества. | ||
Основные тригонометрические тождества. Зависимость между синусом и сотангенсом, зависимость между тангенсом и косинусом. | ||
Упрощение тригонометрических выражений с помощью основных тригонометрических тождеств. | ||
Доказательство тождеств. Решение задач. | ||
Формулы приведения. | ||
Упрощение выражение с помощью формул приведения. Решение задач. | ||
“Тригонометрия на ладоне” | ||
Вычисление тригонометрических функций противоположных углов. | ||
Формулы двойного угла. Формулы половинного угла. | ||
Формулы суммы и разности. Формулы сложения и вычитания. | ||
Упрощение выражение с помощью формул двойного угла. Решение задач. | ||
Упрощение выражение с помощью формул половинного угла. Решение задач. | ||
Упрощение выражение с помощью формул суммы и разности тригонометрических функций. Решение задач. | ||
Упрощение выражение с помощью формул сложения и вычитания. Решение задач. | ||
Простейшие тригонометрические уравнения. | ||
Простейшие тригонометрические неравенства. | ||
Решение простейших тригонометрических уравнений sinx=a, cosx=a. | ||
Решение тригонометрических уравнений sinx=a, cosx=a. | ||
Разбор уравнений, решаемых с помощью замены переменных. | ||
Решение тригонометрических уравнений методом замены переменных. | ||
Разбор решения тригонометрических неравенств. | ||
Решение простейших тригонометрических неравенств. | ||
Арксинус, арккосинус, арктангенс числа. | ||
Упрощение выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом. | ||
Преобразование тригонометрических выражений. Решение задач. | ||
Контрольная работа № 2. | ||
Тема 1.4. Функции, их свойства, графики. Степенные, показательные, логарифмические и тригонометрические функции. | ||
Функции. Способы задания функции. | ||
Область определения и множество значений функции. График функции. | ||
Нахождение множества значений функции. | ||
Нахождение области определения функции. | ||
График функции, построение графиков функции, заданных различными способами. | ||
Построение графиков функций. | ||
Анализ функции. | ||
Преобразование графиков функций. | ||
Свойства функции: монотонность, четность, нечетность, ограниченность, периодичность. | ||
Промежутки возрастания и убывания. Наибольшее и наименьшее значение функции. Точки экстремума.Область определения и область значений обратной функции. | ||
Анализ функции и построение графиков функции. | ||
Нахождение наибольшего и наименьшего значения, точек экстремума функции. | ||
Практическая работа. Анализ графика функции. | ||
Контрольная работа № 3. | ||
Тема 1.5. Уравнения и неравенства | ||
Основные приемы решения уравнений и неравенств. | ||
Разбор решения рациональных уравнений, неравенств и их систем. | ||
Решение рациональных уравнений. | ||
Метод интервалов.Решение рациональных неравенств методом интервалов. | ||
Разбор решения иррациональные уравнения, неравенства и их системы. | ||
Решение иррациональных уравнений. | ||
Решение иррациональных неравенств. | ||
Решение систем иррациональных уравнений и неравенств. | ||
Разбор решения показательных уравнений, неравенств и их систем. | ||
Решение показательных уравнений. | ||
Решение показательных неравенств. | ||
Решение систем показательных уравнений и неравенств. | ||
Разбор логарифмических уравнений и их систем. | ||
Разбор решения логарифмических неравенств и их систем. | ||
Решение логарифмических уравнений. | ||
Решение систем логарифмических неравенств. | ||
Разбор решения тригонометрических уравнений. | ||
Разбор решения тригонометрических неравенств. | ||
Решение тригонометрических уравнений. | ||
Решение тригонометрических неравенств. | ||
Решение рациональных, иррациональных, показательных, тригонометрических уравнений и неравенств. | ||
Контрольная работа №4. | ||
Раздел 2. Начало математического анализа | ||
Тема 2.1. Последовательности. | ||
Последовательности. Способы задания числовых последовательностей. | ||
Понятие о пределе последовательности. | ||
Разбор примеров на вычисление предела последовательности. | ||
Вычисление предела последовательности. Решение задач. | ||
Тема 2.2. Производная и ее геометрический смысл | ||
Производная. Понятие о производной. | ||
Правила дифференцирования. | ||
Нахождение производной степенной функции. | ||
Нахождение производных тригонометрических функций функций. Решение задач. | ||
Нахождение производных суммы и разности с помощью правил дифференцирования. | ||
Нахождение производных произведения и частного с помощью правил дифференцирования. | ||
Нахождение производных сложной функции с помощью правил дифференцирования. | ||
Вычисление производных. | ||
Геометрический смысл производной. Уравнение касательной. | ||
Применение производной к исследованию функций и построению графиков. | ||
Нахождение точек экстремума функции. | ||
Нахождение наибольшего и наименьшего значения. | ||
Исследование функций с помощью производной. | ||
Нахождение уравнения касательной | ||
Тема 2.3. Интеграл | ||
Первообразная. Правила нахождения первообразных. Площадь криволинейной трапеции и интеграл. | ||
Вычисление первообразных с помощью формул. | ||
Вычисление неопределенных интегралов. | ||
Вычисление определенных интегралов. | ||
Вычисление площадей с помощью интегралов. | ||
Применение производной и интеграла к решению практических задач. | ||
Вычисление площади криволинейной трапеции. | ||
Контрольная работа №5. | ||
Раздел 3. Элементы теории вероятностей и математической статистики. | ||
Тема 3.1. Комбинаторика. | ||
Понятие комбинаторики. Формулы комбинаторики: сочетания, размещения, перестановки | ||
140. | Правила комбинаторики. Схема решения кобинаторных задач. | |
141. | Разбор комбинаторных задач. | |
142. | Применение формур комбинаторники к решению задач. | |
143. | Решение комбинаторных задач с помощью формул комбинаторики. | |
144. | Решение комбинаторных задач с помощью правил комбинаторики. | |
Тема 3.2. Теория вероятностей. | ||
145. | Простейшие вероятностные задачи. | |
146. | Классическая, геометрическая и статистическая вероятность. | |
147. | Разбор простейших вероятностных задач. | |
148. | Решение простейших вероятностных задач. | |
149. | Вычисление классической вероятности. | |
150. | Вычисление геометрической и ститистической вероятности. | |
151. | Случайные события и их вероятность. | |
152. | Вычисление вероятности случайных событий. | |
153. | Решение комбинаторных и вероятностных задач. | |
154. | Контрольная работа №6. | |
Раздел 3. Геометрия | ||
155 | Диагностическая работа | |
156 | Диагностическая работа | |
Тема 3.1. Прямые и плоскости в пространстве. | ||
157 | Взаимное расположение двух прямых в пространстве. | |
158 | Параллельность прямой и плоскости. Параллельность плоскостей. Тетраэдр и параллелепипед. Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная. | |
159 | Параллельность прямой и плоскости. | |
160 | Параллельность плоскостей. | |
161 | Угол между прямой и плоскостью. Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей. | |
162 | Перпендикулярность прямой и плоскости. | |
163 | Перпендикуляр и наклонная. | |
164 | Контрольная работа № 6 | |
Тема 3.2. Многогранники | ||
165 | Выпуклые многогранники. Призма. | |
166 | Пирамида. | |
167 | Решение задач: Параллелепипед. | |
168 | Решение задач: куб. | |
169 | Решение задач: Призма. | |
170 | Решение задач: Пирамида. | |
171 | Представление о правильных многогранниках. | |
172 | Практическая работа. Развертки. | |
173 | Углы в многограннике. | |
174 | Контрольная работа №7 | |
Тема 3.3. Тела и поверхности вращения | ||
175 | Цилиндр. | |
176 | Конус. | |
177 | Решение задач: Цилиндр. | |
178 | Решение задач: Конус. | |
179 | Сфера, шар и их сечения. Касательная плоскость к сфере. | |
180 | Решение задач: Сфера, шар и их сечения. | |
181 | Решение задач: Касательная плоскость к сфере. | |
182 | Решение задач: Тела вращения. | |
183 | Вписанные и описанные многогранники. | |
184 | Решение задач по теме: Вписанные и описанные многогранники. | |
Тема 3.4. Измерения в геометрии. | ||
185 | Объемы геометрических тел. Объем прямой призмы, цилиндра, конуса и шара. | |
186 | Вычисление площади поверхности призмы. | |
187 | Вычисление площади поверхности пирамиды. | |
188 | Вычисление площади поверхности цилиндра. | |
189 | Вычисление площади поверхности конуса. | |
190 | Вычисление площади поверхности сферы. | |
191 | Вычисление объема призмы. | |
192 | Вычисление объема пирамиды. | |
193 | Вычисление объема цилиндра. | |
194 | Вычисление объема конуса. | |
195 | Вычисление объема сферы. | |
196 | Контрольная работа № 7 | |
Тема 3.5. Координаты и вектора | ||
197 | Понятие вектора. Сложение и вычитание векторов. Сумма нескольких векторов. | |
198 | Умножение вектора на число. Компланарные вектора. Правило параллелепипеда. | |
199 | Сложение и вычитание векторов. Решение задач. | |
200 | Сумма нескольких векторов. Решение задач. | |
201 | Умножение вектора на число. Компланарные вектора. Решение задач. | |
202 | Правило параллелепипеда. Решение задач. | |
203 | Прямоугольная система векторов в пространстве. Связь между координатами вектора и координатами точек. | |
204 | Простейшие задачи в координатах. | |
205 | Угол между векторами. Скалярное произведение векторов. | |
206 | Решение простейших задач в координатах. | |
207 | Решение простейших задач в координатах. | |
208 | Контрольная работа № 8 по теме: «Координаты и векторы». | |
Повторение | ||
209-234 | Решение задач на повторение. Подготовка к экзамену. | |
Тесты по математике 1 курс колледжа
Вариант 1
Часть первая
Задания1-12 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и запишите букву ответа на бланке в соответствующей графе.
1. Тест Стороны прямоугольника равны . Найдите площадь прямоугольника, и результат запишите в стандартном виде:
|
А) |
Б) |
В) |
Г) |
|
Ответ: |
|||
|
2. Дана окружность диаметром 10 см с центром в точке O. Диаметр AB образует с хордой BC угол 30º. Выберите правильное утверждение. |
|||
|
А) |
Б) |
В) DABC — правильный. |
Г) Периметр треугольника AOC |
|
Ответ: |
3. Выполните : .
|
А) |
Б) |
В) |
Г) |
|
Ответ: |
4. Выполните деление:
|
А) |
Б) |
|
Г) |
|
Ответ: |
5. Найдите значение выражения при .
|
А) |
Б) |
В) 2,5 |
Г) |
|
Ответ: |
6. Функция задана формулой . Выберите правильное утверждение.
|
А) Область определения данной функции – все действительные числа |
Б) График заданной функции — гипербола, расположенная в первой |
В) График заданной функции имеет вид: |
Г) При X > 0 значения заданной функции всегда отрицательные. |
|
Ответ: |
7. При каких значениях A и B равенство является тождеством?
|
А) |
Б) |
В) |
Г) |
|
Ответ: |
8.Тест Найдите корни уравнения .
|
А) |
Б) ; |
В) |
Г) |
|
|||
|
Ответ: |
|
||||||
|
|
9. Дан прямоугольник ABCD, в котором О — точка пересечения диагоналей, a = 25°. Выберите правильное утверждение.
|
|
10. Дан треугольник KLM. Сторона KL Разделена на четыре равные части точками С1, С2, С3 . Через точки С1, С2, С3 проведены прямые, параллельные стороне
|
||||||
|
11. В прямоугольном треугольнике АВС катет
Ответ: |
12. Дан прямоугольный треугольник ABC; ÐACB = 90°, CF — высота. Известно, что AF = 9 см,
F
|
А) Треугольники ABC и ACF равны. |
Б) Треугольники AFC и CFB равны. |
В) |
Г) CF= 15 см. |
|
Ответ: |
Вариант 2
Часть первая
Задания1-12 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и запишите на бланке букву ответа в соответствующей графе.
1. Тест. Стороны прямоугольника равны . Найдите площадь прямоугольника, и результат запишите в стандартном виде:
|
А) |
Б) |
В) |
Г) |
|
Ответ: |
|||
|
2. Дана окружность с центром в точке O. Диаметр AB равен 12 см и образует с радиусом OC угол 90º. Выберите правильное утверждение. |
|||
|
А) |
Б) |
В) BC = 6 см. |
Г) AC = AB. |
|
Ответ: |
3. Выполните вычитание: .
|
А) |
Б) |
В) |
Г) |
|
Ответ: |
4. Выполните деление: .
|
А) |
Б) |
В) |
Г) |
|
Ответ: |
5. Найдите значение выражения при X = 3.
|
А) |
Б) |
В) 16 |
Г) |
|
Ответ: |
6. Функция задана формулой . Выберите правильное утверждение.
|
А) Область определения данной функции – все действительные числа |
Б) График заданной функции — гипербола, расположенная в первой и третьей четвертях |
В) График заданной функции имеет вид: |
Г) При X < 0 значения заданной функции всегда положительные. |
|
Ответ: |
7. При каких значениях A И B равенство является тождеством?
|
А) |
Б) |
|
Г) |
|
Ответ: |
Тест 8. Найдите корни уравнения .
|
А) |
Б) ; |
В) |
Г) |
|
|
Ответ: |
||||
|
9. Дан квадрат KLMN. Выберите правильное утверждение. А) a + b = 45°. Б) g = 2a. В) b + g = 120°. Г) b < 45°. Ответ: |
|
10. В прямоугольнике ABCD точки E и F — середины сторон AB и BC соответственно, EF = 3 дм. Выберите правильное утверждение. А) Отрезок EF параллелен AC. Б) AC = 8 дм. в) AC = 3EF. Г) AC < 2EF. Ответ: |
|
|
11. В прямоугольном треугольнике АВС катет AC = 9 м, гипотенуза АВ = 15 м. Выберите правильное утверждение. А) AC2 = АВ2 + ВС2 Б) Катет ВС > 15 м в) Катет ВС = 12 м Г) ВС = AC Ответ: |
12. Дан прямоугольный треугольник ABC; ÐACB = 90°, CF — высота, проведённая к гипотенузе. Известно, что AF = 16 см, FB = 25 см. Выберите правильное утверждение.
|
А) Треугольники ABC и ACF подобны. |
Б) Треугольники AFC и CFB равны. |
В) |
Г) CF< 15 см. |
|
Ответ: |
характеристики педагогов и практики преподавания математики – тема научной статьи по наукам об образовании читайте бесплатно текст научно-исследовательской работы в электронной библиотеке КиберЛенинка
Различия общего образования в колледжах и старших классах школ:
характеристики педагогов и практики преподавания математики
Ю. Н. Корешникова, А. Б. Захаров, Ф. Ф. Дудырев
Статья поступила в редакцию в декабре 2017 г.
Статья подготовлена в ходе работы по Программе фундаментальных исследований Национального исследовательского университета «Высшая школа экономики» и с использованием средств субсидии в рамках государственной поддержки ведущих университетов Российской Федерации «5-100».
Корешникова Юлия Николаевна
аналитик Института образования Национального исследовательского университета «Высшая школа экономики». E-mail: [email protected] Захаров Андрей Борисович кандидат педагогических наук, заведующий Международной лабораторией анализа образовательной политики Института образования Национального исследовательского университета «Высшая школа экономики». E-mail: [email protected] Дудырев Федор Феликсович кандидат исторических наук, директор Центра исследования среднего профессионального образования Института образования Национального исследовательского университета «Высшая школа экономики». E-mail: [email protected]
Адрес: 101000, Москва,ул. Мясницкая, 20.
Аннотация. Доля учащихся, продолжающих по окончании 9-го класса обучение в системе среднего профессионального образования (СПО), увеличивается с каждым годом. Как правило, в колледжи переходят академически менее успешные учащиеся из семей с меньшим экономиче-
ским и культурным капиталом. Тем не менее система СПО должна предоставить возможность получить качественное общее образование всем выбравшим эту траекторию после 9-го класса. В статье на данных лон-гитюда «Траектории в образовании и профессии» сравниваются важные условия получения общего математического образования: профессиональные и демографические характеристики преподавателей колледжей и школьных учителей, а также используемые ими практики преподавания. В ходе сравнения показано неравенство доступа учащихся к образовательным ресурсам, его зависимость от выбранной ими траектории. Выявленные различия связаны с институциональными особенностями сравниваемых траекторий и позволяют говорить о реализации в их рамках разного общего образования. Ключевые слова: образовательное неравенство, качество образования, профессиональное образование, старшие классы школы, преподавание математики, квалификация учителей, практики преподавания.
DOI: 10.17323/1814-9545-2018-2-228-253
Среднее образование в России можно получить в двух типах организаций: общеобразовательных (10-11-й классы школы) и профессиональных образовательных (колледж или училище). Во втором случае общеобразовательная программа совмещается (в несколько измененном виде) с профессиональным обучением.
За последние 15 лет произошло перераспределение потоков учащихся, выбирающих между этими двумя образовательными траекториями после 9-го класса. С 2000 по 2015 г. прием в старшие классы школ сократился с 1422,4 тыс. человек (66,8% общей численности учащихся, получивших аттестат об основном общем образовании) до 638,3 тыс. человек (54,9%). В сельской местности отток из старших классов начался раньше и происходил быстрее. В 2015/2016 учебном году лишь 45,2% сельских школьников продолжили обучение в старшей школе [НИУ ВШЭ, 2010; 2012; 2014;2016].
Колледжи и техникумы соответственно год от года увеличивали прием студентов на базе основного общего образования: 2000 г.— 263,8 тыс. человек, 2005 г.— 313,2 тыс., 2016 г.— 474,4 тыс. В результате доля девятиклассников в числе поступивших на программы среднего профессионального образования за 12 лет выросла с 38,6 до 65,9%. Доля системы СПО среди институтов среднего общего образования увеличилась с 35,9% учащихся в 1990 г. до 49,2% в 2016 г. [Там же]. Численность студентов, получающих среднее образование в профессиональных образовательных организациях, фактически сравнялась с числом старшеклассников в общеобразовательных школах.
Чтобы оценить последствия такого перераспределения учащихся между образовательными траекториями, необходимо сопоставить результаты общего образования, получаемого в общеобразовательной школе и в системе СПО. Стандартизированное тестирование в СПО не проводится, поэтому единственную, пожалуй, возможность для такого сопоставления сегодня предоставляют данные PISA1. Результаты этого международного сравнительного исследования, полученные в 2015 г., позволяют судить о значительных различиях в математической грамотности между 15-летними учащимися 10-11-х классов (526 баллов) и их ровесниками — студентами профессиональных образовательных организаций (478 баллов)2. Разрыв в баллах примерно соответствует 1,6 года обученияз.
1 http://www.oecd.org/pisa/
2 Выводы относительно грамотности учащихся колледжей и старших классов школ на основании данных PISA нужно делать с некоторой осторожностью ввиду особенностей выборки. Репрезентируются именно 15-летние учащиеся, а не студенты СПО или старшеклассники. Соответственно в 2015 г. в России в выборку попали 5268 девятиклассников
Эти различия имеют в том числе и экономические последствия. Люди, не получившие в старшей школе необходимого набора знаний и общих компетенций, скорее всего, будут вынуждены выбирать среди низкоквалифицированных и низкооплачиваемых профессий, что делает их крайне уязвимыми в условиях быстрых социально-экономических и технологических изменений. Отсутствие социальных и когнитивных навыков, необходимых для жизни в современном обществе, в значительной мере дисквалифицирует их как работников, сужает возможности профессионального и карьерного роста [Cedefop, 2016a; 2016b]. В ситуации постоянного роста доли лиц с высшим образованием положение на рынке труда тех, кто не сумел получить качественного общего среднего образования, будет постоянно ухудшаться, и это еще один фактор, обостряющий социальное неравенство [Любимов, 2008].
Выявленный в PISA разрыв в уровне математической грамотности во многом обусловлен различиями между группами учащихся, поступающих после окончания 9-го класса в старшие классы школы и в профессиональные образовательные организации. Результаты российских исследований показывают, что девятиклассники, выбирающие академическую и профессиональную траектории, различаются между собой по уровню учебных достижений и социально-экономическому статусу семей, что является свидетельством неравенства образовательных возможностей [Александров, Тенишева, Савельева, 2015; Бессуднов, Малик, 2016; Константиновский, 2010]. В колледжи и училища поступают учащиеся со средним уровнем учебных достижений. Социально-профессиональный статус их родителей — между квалифицированными рабочими и высококвалифицированными профессионалами. Родители и ученики из этой социальной группы рассматривают программы СПО как относительно безопасный способ повысить статус семьи: после окончания колледжей часть выпускников поступает в высшие учебные заведения [Александров, Тенишева, Савельева, 2015; Бессуднов, Малик, 2016]. В этих же исследованиях показано, что в школе остаются наиболее подготовленные и социально благополучные учащиеся.
(87% выборки), 581 учащийся 10-11-х классов (9%) и 187 студентов колледжей (4%). Понимая указанные ограничения, мы все же предполагаем, что приведенные данные в целом должны соответствовать общей тенденции более низких результатов по общеобразовательным дисциплинам в колледжах.
3 Разница в один учебный год обычно определяется как соответствующая 1/3-1/4 стандартного отклонения, что примерно равно 30 баллам [Woessmann, 2016].
Однако характеристики учащихся и их семей — далеко не единственный фактор, определяющий уровень образовательных достижений. В ходе многочисленных исследований установлено, что значимое влияние на образовательные результаты школьников оказывает качество педагогов. В частности, более высокие результаты показывают дети, обучающиеся у учителей, имеющих определенный, но небольшой профессиональный стаж [Rockoff, 2004; Rivkin, Hanushek, Kain, 2005; Clotfelter, Ladd, Vigdor, 2006] и высшее образование (магистерскую степень) [Goldhaber, Brewer, 2000; Kukla-Acevedo, 2009]. Эффективными преподавателями являются специалисты с высшим образованием в той или иной предметной области (математик, а не учитель математики) [Darling-Hammond, 2000], а также получившие сертификаты, подтверждающие профессиональную квалификацию [Goldhaber, Brewer, 1996; Cavalluzzo, 2004; Clotfelter, Ladd, Vigdor, 2006; Harris, Sass, 2011; Goe, 2007].
Ряд исследований свидетельствует о связи образовательных результатов учащихся с практиками преподавания в классе, например, с применением учителями приемов активного обучения: выполнение проектов и последующее устное или письменное представление результатов, объяснение школьниками способов решения задач перед классом [Frome, Lasater, Cooney, 2005], с работой учащихся в группах с последующим обсуждением ее результатов [Blatchford et al., 2003]. Учащиеся добиваются более высоких результатов в математике, если педагог показывает связь математических понятий с явлениями повседневной жизни [Schoenfeld, Sloane, 2016; Marcoulides, Heck, Papanastasiou, 2005; Wenglinsky, 2000; 2002]. Впрочем, есть данные, свидетельствующие, что эта связь не столь однозначна [Carnoy et al., 2016]. Успешность формирования математического мышления положительно коррелирует с частотой выполнения домашних заданий по математике [Cooper, 1989; Kannapel et al., 2005; Marcoulides, Heck, Papanastasiou, 2005], и в частности с частотой использования в домашней работе заданий выпускного экзамена [Zakharov, Carnoy, Loyalka, 2014].
Все упомянутые исследования касаются обучения в школе. Данных, которые позволяли ли бы судить о том, насколько общее образование, получаемое в системе СПО в России, отличается от общего образования в старших классах школы, в исследовательской литературе нет. Мало известно и про то, как преподаются общие дисциплины в колледжах и училищах. Остается открытым вопрос, усугубляется ли социальное неравенство, наблюдаемое при разветвлении образовательных траекторий после 9-го класса, различиями в доступе к образовательным ресурсам в рамках этих траекторий.
Целью данного исследования было описать различия в обучении математике в колледжах и старших классах школ. В фо-
кусе нашего анализа находятся демографические и профессиональные характеристики преподавателей математики, используемые ими образовательные практики и неравенство доступа к образовательным ресурсам (в виде квалификации педагогов) у учащихся, избравших разные образовательные траектории — 10-11-й класс в школе или учреждение СПО.
Статья выстроена следующим образом. В первом разделе описаны использованные данные и методы анализа. Во втором разделе представлены результаты исследования: основные характеристики педагогов системы СПО в сравнении со школьными учителями; образовательные практики, которые на своих занятиях применяют учителя 10-11-х классов и преподаватели колледжей; анализ доступа учащихся к образовательным ресурсам в школе и в учреждениях СПО. В заключении сформулированы выводы и обсуждаются полученные результаты.
1. Данные и стратегия анализа
1.1. Использованные данные
Эмпирической основой исследования послужили данные лон-гитюдного исследования «Траектории в образовании и профессии»4, организованного НИУ ВШЭ. Это уникальный для России многолетний проект. Началом лонгитюда стал этап международного мониторинга качества образования TIMSS, проведенный весной 2011 г. Выборка репрезентировала учащихся 8-х классов российских школ5. Весной 2012 г. те же школьники (9-й класс) участвовали в международном мониторинге PISA6. После окончания 9-го класса обучение в учреждениях СПО продолжили 32% учащихся (табл. 1). Информация об обучении детей в 1011-м классах и в учреждениях СПО собиралась в ходе последующих волн лонгитюда — осенью 2013 г. и весной 2014 г
Помимо тестирования и опроса учащихся был проведен опрос учителей математики (здесь и далее мы приводим информацию по учителям алгебры7) образовательных организа-ций8.атрПпд
6 Это было дополнение к национальной выборке Р1ЭА-2012.
7 В большинстве школ алгебру и геометрию преподавал один и тот же учитель.
8 Опрос преподавателей школ и колледжей организован Международной лабораторией анализа образовательной политики НИУ ВШЭ (https:// ioe.hse.ru/lepa/) в дополнение к сбору данных в рамках лонгитюда «Траектории в образовании и профессии».
Таблица 1. Движение учащихся—участников лонгитюда «Траектории в образовании и профессии»
Весна 2011 Весна 2012 Весна 2014
Образовательная траектория 8-й класс школы 9-й класс школы 1-й курс колледжей и училищ 11-й класс школы
Число опрошенных учащихся 4893 4399 1348 2731
обучались не менее двух участников лонгитюда. В итоге были опрошены 294 учителя, которые преподавали у 2347 (86% опрошенных) одиннадцатиклассников, и 441 учитель, который преподавал у 741 (55%) студента колледжей и училищ. Учитывая небольшое число опрошенных (60 человек), обучавшихся на программах подготовки квалифицированных рабочих и служащих, педагоги которых также попали в выборку, в ходе анализа сопоставлялись только данные учащихся и преподавателей 11-х классов школ и программ подготовки специалистов среднего звена — колледжей.
В фокусе нашего внимания были доступные показатели профес- 1.2. Переменные сионального опыта педагогов: стаж, квалификационная категория, наличие/отсутствие профессиональных наград и призовых мест в специализированных конкурсах. Также сопоставлялись демографические характеристики преподавателей (пол и возраст) и объем культурного капитала (количество книг дома9). Наконец, сравнивалась интенсивность самообразования педагогов (частота чтения книг по теории преподаваемой дисциплины и методике ее преподавания).
С целью выявить особенности образовательного процесса в школах и колледжах мы прежде всего оценивали, как часто педагоги показывают связь изучаемого материала с другими учебными предметами и с реальной жизнью и деятельностью человека. Педагогов спрашивали, как часто учащиеся описывают математическим языком события повседневной жизни и как часто решают стандартные задания. Кроме того, преподаватели отвечали на вопросы об использовании практик, призван-
9 Согласно концепции П. Бурдье, книги, как и другие культурные товары, представляют объективированное состояние культурного капитала [Бурдье, 2002]. Использование других показателей малопродуктивно. Например, уровень образования (операнд институционализированного состояния культурного капитала) является плохим дифференциатором, так как почти все педагоги окончили вуз.
ных повысить учебную активность детей: с какой частотой учащиеся получают задания в виде длительных (не менее недели) проектов, в результате осуществления которых они должны найти ответ на исследовательский вопрос; как часто они работают в малых группах, чтобы сообща найти решение задачи или проблемы. Также у преподавателей выясняли, как часто они прибегают к дифференцированию заданий для учащихся с разным уровнем подготовки. Наконец, часть вопросов касалась распространенных в школе практик обучения: как часто учащиеся получают домашние задания, как часто при работе в классе используются задания ЕГЭ.
В ходе анализа учитывались характеристики учащихся школ и колледжей. В качестве показателей культурного и экономического капитала семей использовались наличие/отсутствие у матери оконченного высшего образования и индекс материального благосостояния семьиЧ Обе переменные взяты из данных опроса учащихся в TIMSS-2011. Помимо этого, учитывались пол учащихся и баллы PISA по математике.
1.3. Методы анализа В соответствии с исследовательскими вопросами анализ проводился в три этапа. На первом этапе сопоставлялись демографические, культурные и профессиональные характеристики педагогов, преподающих математику учащимся в старших классах школы и в колледжах. Для этого мы использовали описательную статистику. Значимость различий оценивалась с помощью параметрических и непараметрических критериев: f-теста Стьюден-та, критерия Манна—Уитни и Краскела — Уоллиса.
На втором этапе оценивалась значимость различий в образовательных практиках на уроках математики у одиннадцатиклассников и учащихся колледжей. Для этого мы использовали серию порядковых логистических регрессий. Зависимой переменной была частота соответствующих преподавательских практик. Основным предиктором выступало место обучения (школа/колледж). В ходе анализа контролировались характеристики учащихся и педагогов.
На третьем этапе мы сравнивали доступ к образовательным ресурсам у учащихся 11-го класса школы и студентов колледжа. Для анализа использовали описательную статистику и порядковую логистическую регрессию. Зависимой переменной была квалификационная категория педагога. В качестве предикторов использовались социальные характеристики се-
10 Индекс материального благосостояния рассчитан на основе ответов учащихся на вопросы анкеты “ПМЭЭ о наличии в семье тех или иных предметов домашнего обихода и перекодирован нами в порядковую шкалу (низкий, средний и высокий уровни — 30, 40 и 30% наблюдений в каждом уровне соответственно).
мей, пол учащихся и образовательные результаты в конце 8-го и 9-го класса.
При интерпретации полученных результатов нужно учитывать два ограничения. Во-первых, в соответствии с задачами исследования на каждом из этапов анализ носил описательный характер и не претендовал на оценку причинно-следственных связей. Во-вторых, учитывая особенности использованных данных, следует делать выводы не о работе колледжей в сравнении со старшими классами школы (данные не репрезентируют педагогов), но скорее об особенностях образовательных траекторий учащихся. Речь идет о том, в какие образовательные условия попали учащиеся, окончившие 9-й класс в 2012 г.
Независимо от выбранной траектории — колледж или 11-й класс школы — большинство учащихся обучались математике у педагогов-женщин: 92 и 95% соответственно. Различия между группами очень небольшие и статистически не значимы (критерий Манна — Уитни). Средний возраст математиков, преподающих в выпускном классе школ и в колледжах, в нашей выборке составил 55 и 50 лет соответственно. При этом по сравнению с колледжами больше одиннадцатиклассников (на 23%) занимались у учителей в возрасте от 41 до 60 лет (рис. 1). В то же время студенты колледжей чаще (на 20%) обучались математике у более молодых преподавателей (от 25 лет до 41 года). Эти различия статистически значимы (р < 0,05, ¿-критерий Стьюдента).
На рис. 2 и 3 сопоставляются показатели профессионального опыта педагогов. Значительно меньше одиннадцатиклассников, чем студентов колледжей, занимались у педагогов со стажем преподавания до 15 лет (11 и 63% соответственно). Максимальные различия между двумя траекториями наблюдаются в числе обучавшихся у преподавателей, только вошедших в профессию, — со стажем до 5 лет (1 и 35%) (рис. 2). Это соответствует описанному выше распределению учащихся по возрасту преподавателей, стаж которых линейно связан с возрастом. По сравнению с одиннадцатиклассниками среди студентов колледжей было на 20% больше тех, кто обучался у педагогов с самой низкой (второй) квалификационной категорией или у не аттестованных на категорию (рис. 3). Обычно это молодые преподаватели с наименьшим стажем (в среднем 13 лет). В сравнении с учащимися программ СПО в школах на 21% выше доля учащихся, которым преподавали обладатели профессиональных наград и отличий (75,5 и 54,5% соответственно), и на 15%—доля тех, кому преподавали призеры профессиональных конкурсов (27,9 и 13%). У учителей, имеющих награды и отличия, как правило, более продолжительный профессиональный стаж. Различия в распределении учащихся 11-х классов школ и колледжей
2. Результаты исследования
2.1. Демографические, культурные и профессиональные характеристики преподавателей математики
2.2. Образовательные практики, используемые на уроках математики в учреждениях СПО и в школах 2.2.1. Связь математики с повседневной жизнью и другими учебными предметами
по всем показателям опыта педагогов статистически значимы (на уровне р < 0,0511).
На рис. 4-6 сопоставляются уровень культурного капитала (количество книг дома), а также интенсивность самообразования (частота чтения книг по теории преподаваемой дисциплины и методике преподавания) у педагогов в 11-х классах школ и колледжах. Одиннадцатиклассникам чаще преподавали учителя с более высоким культурным капиталом: 54% из них обучались у преподавателей, у которых дома более 200 книг В колледжах доля таких студентов составила только 36%. При этом 22% студентов колледжей занимались у преподавателей математики с минимальным (до 50) количеством книг дома. В школах таких учащихся было всего 6% (рис. 4). Эти различия статистически значимы (на уровне р < 0,05, критерий Крас-кела—Уоллиса).
Школьные учителя чаще, чем преподаватели колледжей, читали специализированную литературу (рис. 5, 6). Наиболее часто (один раз в неделю и чаще) к книгам по математической теории обращались преподаватели у 61% школьников и лишь у 38% студентов колледжей. Наблюдаемые различия статистически значимы (на уровне р < 0,05, критерий Краскела—Уоллиса). Частота чтения книг по методике преподавания математики различается не столь сильно. Такую литературу школьные учителя читали также несколько чаще, однако эти различия не значимы.
Многие преподаватели колледжей ранее работали в школе. Согласно данным опроса, такие педагоги в среднем на 2 года старше своих коллег, не имевших опыта работы в школе. Их педагогический стаж в среднем на 5 лет больше. У преподавателей математики, ранее работавших в школе, занимались 72,1% учащихся колледжей12.
Чтобы оценить, как часто изучаемый на уроках математики материал соотносится с повседневной жизнью детей и содержанием
11 f-критерий Стьюдента для сравнения возраста и стажа педагогов, критерий Краскела — Уоллиса для сравнения квалификационных категорий, критерий Манна — Уитни для сравнения численности обладателей наград и отличий.
12 Этот показатель представляется очень высоким, учитывая, что 35% студентов колледжей обучались у преподавателей математики, педагогический стаж которых составил 5 лет и менее (см. рис. 2). Иными словами, почти все преподаватели со стажем больше 3 лет, согласно этим данным, должны иметь хотя бы минимальный опыт работы в школе. Такой высокий показатель может объясняться и перемещением педагогов внутри системы образования (подробнее об этом в выводах), и субъективным восприятием респондентами опыта работы, к которому они могут относить, например, прохождение практики во время обучения в вузе.
Рис. 1. Возраст
преподавателей математики
25
26
10
18
13
I 1.1…………
Рис. 2. Стаж
преподавателей математики
% 35
123
1 “
Возраст, лет
24
17
19
4″
СТаЖ’ .ЛеТ
Рис. 3. Квалификационная категория преподавателей
математики
%
Рис.
Количество книг
%
9
3
%
Рис. 5. Частота чтения книг по теории математики
Рис. 6. Частота чтения книг по методике преподавания математики
9,
Частота
Никогда 1-2 раза 1-2 раза 1-2 раза или почти в год в месяц в неделю никогда
45 3
Частота
1-2 раза 1-2 раза 1-2 раза в год в месяц в неделю
%
%
Рис. 7. Как часто на уроках преподаватель показывает связь математики с другими учебными предметами
Рис. 8. Как часто на уроках математики учитель показывает связь нового материала с повседневной жизнью
%
%
Студенты колледжей Ученики 11-го класса
% уроков
% уроков
других учебных предметов, мы анализировали ответы учителей на вопросы об их активности на уроках и частоту, с которой учащиеся выполняли на занятиях те или иные виды заданий.
На программах СПО преподаватели чаще показывали связь математики с другими учебными предметами (рис. 7). Более чем на 40% занятий такие объяснения получали 73% студентов колледжей и 60% одиннадцатиклассников. Однако дальнейший анализ показал, что, если учитывать профессиональный опыт и культурный капитал преподавателей, а также характеристики детей (главным образом уровень образования матери), то различия в частоте использования такой практики в школах и колледжах окажутся статистически незначимыми (приложение 1, табл. 1). Иными словами, наблюдаемые различия объясняются не типом учреждения, а характеристиками самих педагогов и учащихся, с которыми они работают.
В колледжах преподаватели математики также несколько чаще демонстрировали, как новый материал связан с повседневным жизненным опытом учащихся (рис. 8). Эти различия в преподавании выражены несильно: более чем на 40% занятий такую информацию получали 68% одиннадцатиклассников и 60% студентов колледжей. Как и в предыдущем случае, они связаны с характеристиками учащихся и становятся статистически незначимыми, если контролировать успеваемость в 9-м классе (балл PISA по математике), уровень материального благосостояния семьи и наличие у матери высшего образования (приложение 1, табл.
………………………………………………….
% уроков
% уроков
Студенты колледжей Ученики 11-го класса
колледжей (рис. 9). Если сравнить учащихся с одинаковой успеваемостью в конце 9-го класса и одинаковыми социально-демографическими характеристиками, занимавшихся у преподавателей математики, в равной степени опытных, то в школе у учащихся шансы часто решать такие задачи в 1,5 раза выше, чем в колледже (приложение 1, табл. 1). А студенты колледжа чаще, чем одиннадцатиклассники, решали на занятиях стандартные задачи (рис. 10). На 61% занятий или чаще в колледжах такие задания выполняли 73%, а в 11-х классах школ — 52% учащихся. Даже при контроле характеристик преподавателей и учеников шансы чаще выполнять традиционные задания у студентов колледжа в 1,7 раза выше, чем у школьников (приложение 1, табл. 1).
Домашние задания чаще задают в школе: 64% одиннадцати- 2.2.2. Организация классников получали их практически на каждом занятии (81-100% работы учащихся уроков). В колледжах с такой же частотой домашние задания получали только 24% студентов (рис. 11). Эти различия сохраняют статистическую значимость при контроле характеристик детей и педагогов: у одиннадцатиклассников шансы чаще получать домашние задания почти в 4 раза выше (приложение 1, табл. 1).
Что касается практик, призванных повысить учебную активность детей, то здесь различия наблюдаются не всегда. Частота работы в малых группах практически одинакова в обеих образовательных программах (рис. 12; приложение 1, табл. 1). При этом в колледжах студенты чаще получали задания, трудность которых различалась в зависимости от уровня их подготовленности (рис. 13). Более чем на 60% занятий дифференцированные задания выполняли 68% студентов программ СПО и 59% одиннадцатиклассников. Наконец, практически все студенты колледжей (96,9%) получали задания по математике в виде
Рис. 11. Как часто на уроках преподаватель задает домашнее задание
Рис. 12. Как часто на уроках учащиеся работают в малых группах
%
Студенты колледжей Ученики 11-го класса
I
% уроков
м ™
………..
% уроков
%
Рис. 13. Как часто на уроках преподаватель дает учащимся разные задания в зависимости от их уровня подготовки
%
% уроков
С^ ^ цэ СО
о
С^ ^ СП
длительных (не менее недели) проектов, в результате выполнения которых должен быть найден ответ на исследовательский вопрос. В школах эта практика в последние годы очень широко применяется, но на момент проведения опроса она не стала повсеместной, в нашей выборке над проектами работали 80,9% одиннадцатиклассников. В целом, если сравнить учащихся с одинаковыми контекстными характеристиками, занимавшихся у преподавателей с одинаковым опытом и культурным капиталом, то в колледжах шансы часто выполнять задания, более соответствующие уровню подготовки учащегося, и участвовать в исследовательско-проектной работе значительно выше (приложение 1, табл. 1).
Несмотря на то что в большинство вузов выпускники программ СПО принимаются без сдачи Единого государственного экзамена (в случае совпадения направлений подготовки), пре-
Рис. 14. Доля времени, отводимая на занятиях на задания части «В» ЕГЭ
Рис. 15. Доля времени, отводимая на занятиях на задания части «С» ЕГЭ
<° к
% времени
% сч
ю ™ сч!
СО
. ю со
подаватели колледжей пользуются заданиями ЕГЭ на занятиях. Однако в 11-х классах, для выпускников которых ЕГЭ обязателен, этим заданиям уделяется больше внимания. Более чем на половине занятий задания части «В» в школах выполняли 34,8% учащихся, задания части «С» — 26,4% учащихся, в колледжах соответственно 8,1 и 10,6%. (рис. 14, 15). Если учитывать характеристики детей и преподавателей, то, например, шансы решать на занятиях задачи части «С», у школьников в 4 раза выше, чем у студентов колледжа13 (приложение 1, табл. 1).
Как показывают проведенные ранее исследования, после 9-го класса в профессиональные образовательные организации чаще уходят школьники, у которых учебные достижения значительно ниже, чем у продолжающих обучение в 10-11-м классе, а при равных учебных достижениях ниже культурный капитал родителей [Александров, Тенишева, Савельева, 2015; Бессуд-нов, Малик, 2016, Константиновский, 2010]. Несмотря на такое распределение, контингент учащихся в общеобразовательной и профессиональной траекториях все же остается неоднородным с точки зрения достигнутых академических результатов и социальных характеристик семей. В нашем исследовании мы проанализировали, равным ли является в этих траекториях доступ учащихся с одинаковыми характеристиками семей к образовательным ресурсам, например в виде профессионального опыта преподавателей.
2.3. Доступ к образовательным ресурсам у учащихся старших классов школ и учреждений СПО
13 Большая разница в шансах выполнять задания части «B» при контроле характеристик детей и педагогов может объясняться корреляцией этих характеристик как с частотой заданий, так и с выбором траектории (школа — колледж).
%
Рис. 16. Распределение учащихся по преподавателям разных квалификационных категорий в зависимости от наличия у матери оконченного высшего образования
Высшая Первая
Категория
Вторая и без категории
Высшее образование у матерей
студентов колледжей
□ Есть Нет
учеников 11-го класса
□ Есть Нет
Рис. 17. Распределение учащихся по преподавателям разных квалификационных категорий в зависимости от уровня материального благосостояния семей
Категория
Высшая
Первая
Вторая
и без категории
Уровень
благосостояния семей студентов колледжей
□ низкий
□ средний высокий
учеников 11-го класса
□ низкий
□ средний
Учащиеся, различающиеся уровнем семейного культурного капитала и материального благосостояния, неравномерно распределяются на обучение к педагогам с разным уровнем квалификации и в школах, и в колледжах (рис. 16). В обеих траекториях преобладает принцип, который условно можно назвать «поддержкой сильного». Учащиеся из семей с более высоким уровнем культурного капитала и материального благосостояния, независимо от выбранной траектории, чаще занимаются у более квалифицированных педагогов (рис. 17). Однако дальнейший анализ показывает, что в школах эта дифференциация более ярко выражена и связана главным образом с материальным достатком родителей. На программах СПО наблюдаемые различия статистически не значимы, а в 11-х классах школ шан-
сы учащихся из семей с низким уровнем материального благосостояния заниматься у учителя математики с высокой квалификационной категорией значимо ниже, чем у детей из семей с высоким достатком, даже при условии равных образовательных достижений в конце 8-го или 9-го класса. Помимо этого, в рамках обеих траекторий шансы попасть к более квалифицированному педагогу выше у учащихся, показавших более высокие образовательные результаты по математике в конце основной школы (приложение 1, табл. 2).
Различия в доступе к качественному образованию в значитель- 3. Выводы ной степени институционально обусловлены. При этом условия и дискуссия обучения в школах и профессиональных образовательных организациях сильно различаются не только в административно-управленческом отношении, но и с точки зрения характеристик образовательной среды. От того, какую траекторию выберет учащийся после 9-го класса, зависит его дальнейший доступ к образовательным ресурсам: насколько квалифицированный педагог будет ему преподавать, какие практики обучения он будет использовать. В связи с этим возникают два вопроса. Чем обусловлены различия между образовательными траекториями? И что выигрывают, а в чем проигрывают учащиеся, выбирая ту или иную траекторию?
Участников лонгитюда, поступивших после 9-го класса в колледж, гораздо чаще, чем их сверстников, оставшихся в школе, встречали более молодые преподаватели математики с относительно меньшим культурным капиталом и небольшим педагогическим стажем, не имеющие высокой квалификационной категории и знаков профессионального признания. Такая ситуация отчасти может быть связана с различиями в оплате труда педагогов школ и колледжей. Так называемые майские указы обязывали довести заработную плату педагогов до среднего в регионе уровня. Эта установка касалась как школ, так и колледжей, однако темпы роста заработной платы в них существенно различались. Если у школьных учителей размер оплаты труда достиг соответствующего уровня уже к 2014 г., то в среднем профессиональном образовании значения, установленные президентским указом, должны быть достигнуты лишь в 2018 г.м В итоге в рассматриваемый период заработная плата преподавателей математики в школах и колледжах при условии равной нагрузки могла различаться на 15-25% [Кузьминов, Попова, Якобсон, 2017], что не могло не сказаться на движении кадров. Молодые
14 Указ Президента РФ от 7 мая 2012 г. № 597 «О мероприятиях по реализации государственной социальной политики». http://legalacts.ru/doc/ ukaz-prezidenta-rf-ot-07052012-n-597/
специалисты, как правило, обладают меньшим опытом и профессиональными навыками, а также менее включены в профессиональные сети, которые могут обеспечить при трудоустройстве доступ к более оплачиваемым рабочим местам [Рощин, 2006]. В итоге выпускникам педагогических вузов было проще начать карьеру в учреждениях среднего профессионального образования.
С другой стороны, в последние годы происходило сокращение учительских ставок в школах и их рост в колледжах в силу перераспределения потоков учащихся. В условиях «демографической ямы» и проведенной в 2000-е годы реструктуризации сети школ число подростков, поступающих в 10-й класс, снизилось за полтора десятилетия на 55,2% (с 1422,4 тыс. человек в 2000 г. до 638,3 тыс. человек в 2015 г.). Колледжи и техникумы, наоборот, постоянно увеличивали прием студентов на базе основного общего образования (2005 г.— 313,2 тыс. человек, 2016 г.— 474,4 тыс. человек) [НИУ ВШЭ, 2010; 2012; 2014; 2016]. В результате не только увеличилось предложение мест для молодых педагогов в учреждениях среднего профессионального образования, но и произошел зафиксированный в нашем исследовании отток учителей из школ в колледжи.
Выбрав ту или иную образовательную траекторию, учащиеся тем самым определяют для себя не только характеристики педагогического состава учебного заведения, но и определенные практики обучения. Студенты колледжей сравнительно реже выполняют задания, предполагающие описание математическим языком событий и явлений повседневной жизни, и чаще имеют дело со стандартными математическими задачами. С другой стороны, в колледжах студенты сравнительно чаще получают на занятиях задания, трудность которых различается в зависимости от уровня их подготовленности, и чаще работают над длительными (не менее недели) исследовательскими проектами. Одиннадцатиклассники чаще, чем студенты колледжей, получают работу на дом и выполняют на уроках задания ЕГЭ.
Некоторые различия, например в частоте использования дифференцированных заданий, объяснить сложно. Другие, на наш взгляд, во многом обусловлены институциональными особенностями сопоставляемых траекторий (содержанием образования и способами оценки качества), а также уровнем подготовленности учащихся к концу 9-го класса. В частности, заданиям ЕГЭ в 11-м классе уделяют гораздо больше внимания, чем в колледжах, поскольку все выпускники школы проходит через государственную итоговую аттестацию в форме ЕГЭ, что не является обязательным для выпускников колледжей.. В итоге сегодня проектная работа является обязательным компонентом содержания образования в колледжах. В то же время на занятиях связи изучаемого материала с повседневной жизнью и с другими учебными предметами устанавливаются скорее формально — в рассказах преподавателей. В нашем исследовании учащимся колледжей и 11-х классов школ о связи изучаемого на уроках математики материала с другими учебными предметами и повседневной жизнью рассказывали на занятиях с одинаковой частотой. О том, что ориентированность обучения математике на практику в колледжах является формальной, свидетельствует и то, что одиннадцатиклассники чаще, чем студенты колледжей, сталкиваются с заданиями, требующими описать явления повседневной жизни математическим языком.
Наблюдаемые различия в практико-ориентированном обучении могут быть связаны с уровнем математической подготовленности детей. После 9-го класса в колледжи приходят, как правило, подростки с более низкими образовательными результатами по математике [Бессуднов, Малик, 2016]. Для большинства из них изучение этого предмета сопряжено со значительными трудностями, а применение математических зависимостей при решении практических задач требует достаточно высокого уровня знания математической теории [Тюменева, Вальдман, Карной, 2014]. Преподавателям колледжей, чтобы обеспечить усвоение каждой темы хотя бы на базовом уровне, приходится отводить гораздо больше учебного времени на объяснение ос-
15 Рекомендации по реализации образовательной программы среднего (полного) общего образования в образовательных учреждениях начального профессионального и среднего профессионального образования в соответствии с федеральным базисным учебным планом и примерными учебными планами для образовательных учреждений Российской Федерации, реализующих программы общего образования. Письмо Министерства образования и науки РФ от 29 мая 2007 г. № 03-1180. http://www.garant.ru/products/ipo/prime/doc/6232537/
новных математических понятий и на решение стандартных задач. Вероятно, в таких условиях обучение учащихся применению математических знаний для решения повседневных практических задач более сложно и требует больше времени.
С уровнем подготовленности учащихся и системой внешней оценки, возможно, связаны и различия в интенсивности самообразования педагогов. Не имея жесткого пресса в виде ЕГЭ и работая с академически более слабыми учащимися, преподаватели колледжей в меньшей степени испытывают потребность постоянно обращаться к литературе по теории математики.
Второй вопрос, связанный с выбором траектории после 9-го класса, касается последствий наблюдаемого неравенства в доступе к образовательным ресурсам. Насколько выигрывают или проигрывают учащиеся в результатах общего образования, выбирая учреждение СПО или старшие классы школы? К сожалению, непосредственно сопоставить образовательные результаты учащихся по завершении обучения в 11-м классе и в колледже невозможно. Стандартизированный экзамен, проверяющий освоение программы общего образования, является обязательным только для выпускников школ. Некоторые предположения можно сделать на основе предыдущих исследований. Например, известно, что учителя с некоторым (но не очень большим) стажем преподавания эффективнее своих коллег, не имеющих опыта, при этом основной прирост эффективности происходит в первые годы работы [Хэтти, 2017. С. 166-167]. Другие авторы показали, что для повышения баллов PISA учащимся с низкой успеваемостью по математике важно заниматься у учителя, аттестованного на категорию, тогда как для хорошо успевающих учеников категория учителя не столь важна [Carnoy et al., 2016]. В колледжи чаще поступают подростки с невысокими баллами по математике, и им чаще преподают молодые учителя с минимальным опытом и без категории. Можно ожидать, что такие учащиеся будут проигрывать от выбора профессиональной траектории.
Социальное неравенство в распределении образовательных ресурсов (в виде квалификации преподавателей) и тем самым, возможно, в шансах на более высокие образовательные результаты проявляется двояко. Когда учащиеся — часто из семей с невысоким культурным капиталом [Бессуднов, Малик, 2016] — выбирают профессиональную траекторию, сам факт этого выбора для них уже означает снижение шансов на доступ к ресурсам. Однако для учащихся, выбравших старшие классы школы, выбор этой траектории не означает автоматически лучшего доступа к образовательным ресурсам. Дальнейшее распределение учащихся на обучение к учителям той или иной квалификационной категории в школах связано с материальным благосостоянием семей старшеклассников.
Выбирая образовательную траекторию по окончании 9-го класса, учащийся выбирает свое будущее. И школы, и профессиональные образовательные организации должны обеспечивать доступ к качественному среднему общему образованию, что вряд ли возможно в условиях неравенства доступа к образовательным ресурсам, накладывающегося на социальное неравенство при выборе самих траекторий.
1. Александров Д. А., Тенишева К. А., Савельева С. С. (2015) Мобиль- Литература ность без рисков: образовательный путь «в университет через колледж» // Вопросы образования / Educational Studies Moscow. № 3.
С. 66-91. DOI: 10.17323/1814-9545-2015-3-66-91.
2. Бессуднов А. Р., Малик В. М. (2016) Социально-экономическое и тендерное неравенство при выборе образовательной траектории после окончания 9-го класса средней школы // Вопросы образования / Educational Studies Moscow. № 1. С. 135-167. DOI: 10.17323/1814-95452016-1-135-167.
3. Бурдье П. (2002) Формы капитала // Экономическая социология. Т. 3. № 5. С. 60-74.
4. Константиновский Д. Л., Вознесенская Е. Д., Чередниченко Г. А., Хо-хлушкина Ф. А. (2010) Жизненные траектории молодежи: «10 лет спустя». Социологическое исследование. М.: Институт социологии РАН.
5. Кузьминов Я. И., Попова С. А., Л. И. Якобсон Л. И. (ред.) (2017) Эффективный контракт для профессионалов социальной сферы: тренды, потенциал, решения. Экспертный доклад. М.: Изд. дом ВШЭ.
6. Любимов Л. Л. (2008) Комментарии к докладу Общественной палаты Российской Федерации «Образование и общество: готова ли Россия инвестировать в свое будущее?» // Вопросы образования / Educational Studies Moscow. № 1. С. 5-31.
7. НИУ ВШЭ (2010) Образование в Российской Федерации: 2010: стат. сб. М.: Изд. дом ВШЭ.
8. НИУ ВШЭ (2012) Образование в Российской Федерации: 2012: стат. сб. М.: Изд. дом ВШЭ.
9. НИУ ВШЭ (2014) Образование в Российской Федерации: 2014: стат. сб. М.: Изд. дом ВШЭ.
10. НИУ ВШЭ (2016) Образование в цифрах: 2014: стат. сб. М.: Изд. дом ВШЭ.
11. Рощин С. Ю. (2006) Переход «учеба — работа»: омут или брод? Препринт WP3/2006/10. Сер. WP3 «Проблемы рынка труда». М.: Изд. дом ГУ ВШЭ.
12. Тюменева Ю. А., Вальдман А. И., Карной М. (2014) Что дают предметные знания для умения применять их в новом контексте? Первые результаты сравнительного анализа TIMSS-2011 и PISA-2012 // Вопросы образования / Educational Studies Moscow. № 1. С. 8-24.
13. Хэтти Дж. (2017) Видимое обучение. Синтез результатов более 50 000 исследований с охватом более 80 миллионов школьников. М.: Национальное образование.
14. Blatchford P., Kutnick P., Baines E., Galton M. (2003) Toward a Social Pedagogy of Classroom Group Work // International Journal of Educational Research. Vol. 39. No 1-2. P. 153-172.
15. Carnoy M., Khavenson T., Loyalka P., Schmidt W., Zakharov A. (2016) Revisiting the Relationship between International Assessment Outcomes and
Educational Production: Evidence from a Longitudinal PISA-TIMSS Sample // American Educational Research Journal. Vol. 53. No 4. P. 1054-1085.
16. Cavalluzzo L. C. (2004) Is National Board Certification an Effective Signal of Teacher Quality? Alexandria, Virginia: CNA Corporation. https://files. eric.ed.gov/fulltext/ED485515.pdf
17. Cedefop (2016a) Leaving Education Early: Putting Vocational Education and Training Centre Stage. Vol. I: Investigating Causes and Extent. Cedefop Research Paper No 57. Luxembourg: Publications Office of the European Union. http://dx.doi.org/10.2801/893397
18. Cedefop (2016b) Leaving Education Early: Putting Vocational Education and Training Centre Stage. Vol. II: Evaluating Policy Impact. Cedefop Research Paper No 58. Luxembourg: Publications Office of the European Union. http://dx.doi.org/10.2801/967263
19. Clotfelter C. T., Ladd H. F., Vigdor J. L. (2007) Teacher Credentials and Student Achievement: Longitudinal Analysis with Student Fixed Effects // Economics of Education Review. Vol. 26. No 6. P. 673-682.
20. Clotfelter C. T., Ladd H. F., Vigdor J. L. (2006) Teacher-Student Matching and the Assessment of Teacher Effectiveness // Journal of Human Resources. Vol. 41. No 4. P. 778-820.
21. Cooper H. (1989) Homework. White Plains. New York: Longman.
22. Darling-Hammond L. (2000) Teacher Quality and Student Achievement // Education Policy Analysis Archives. Vol. 8. No 1. P. 1-40.
23. Frome P., Lasater B., Cooney S. (2005) Well-Qualified Teachers and High Quality Teaching: Are They the Same? (Research Brief). Atlanta, GA: Southern Regional Education Board.
24. Goe L. (2007) The Link between Teacher Quality and Student Outcomes: A Research Synthesis. Washington, DC: National Comprehensive Center for Teacher Quality. http://www.niusileadscape.org/docs/FINAL_PRO-DUCTS/LearningCarousel/LinkBetweenTQandStudentOutcomes.pdf
25. Goldhaber D. D., Brewer D. J. (2000) Does Teacher Certification Matter? High School Teacher Certification Status and Student Achievement // Educational Evaluation and Policy Analysis. Vol. 22. No 2. P. 129-145.
26. Goldhaber D. D., Brewer D. J. (1996) Evaluating the Effect of Teacher Degree Level on Educational Performance // W. Fowler (ed.) Developments in School Finance. Washington, DC: NCES. Google Scholar. P. 197-210.
27. Harris D. N., Sass T. R. (2011) Teacher Training, Teacher Quality and Student Achievement // Journal of Public Economics. Vol. 95. No 7. P. 798812.
28. Kannapel P. J., Clements S. K., Taylor D., Hibpshman T. (2005) Inside the Black Box of High-Performing High-Poverty Schools. Lexington, Kentucky: Prichard Committee for Academic Excellence. http://prichardcommittee. org/wp-content/uploads/2013/02/Inside-the-Black-Box.pdf
29. Kukla-Acevedo S. (2009) Do Teacher Characteristics Matter? New Results on the Effects of Teacher Preparation on Student Achievement // Economics of Education Review. Vol. 28. No 1. P. 49-57.
30. Marcoulides G. A., Heck R. H., Papanastasiou C. (2005) Student Perceptions of School Culture and Achievement: Testing the Invariance of a Model // International Journal of Educational Management. Vol. 19. No 2. P. 140-152.
31. Rivkin S. G., Hanushek E. A., Kain J. F. (2005) Teachers, Schools, and Academic Achievement // Econometrica. Vol. 73. No 2. P. 417-458.
32. Rockoff J. E. (2004) The Impact of Individual Teachers on Student Achievement: Evidence from Panel Data // The American Economic Review. Vol. 94. No 2. P. 247-252.
33. Schoenfeld A. H., Sloane A. H. (eds) (2016) Mathematical Thinking and Problem Solving. Routledge.
34. Wenglinsky H. (2000) How Teaching Matters: Bringing the Classroom Back into Discussions of Teacher Quality. Princeton, NJ: Millikan Family Foundation and Educational Testing Service. https://files.eric.ed.gov/ fulltext/ED447128.pdf
35. Wenglinsky H. (2002) How Schools Matter: The Link between Teacher Classroom Practices and Student Academic Performance // Education Policy Analysis Archives. Vol. 10. No 12.
36. Woessmann L. (2016) The Importance of School Systems: Evidence from International Differences in Student Achievement // Journal of Economic Perspectives. Vol. 30. No 3. P. 3-32.
37. Zakharov A., Carnoy M., Loyalka P. (2014) Which Teaching Practices Improve Student Performance on Highstakes Exams? Evidence from Russia // International Journal of Educational Development. Vol. 36. May. P. 13-21.
Таблица 1. Как различается образовательный процесс Приложение
в 11-м классе школы и колледже
Зависимая переменная Модель 1 Модель 2 Модель 3
Как часто преподаватель показывает связь математики с другими предметами 0,56*** (0,11) 0,54** (0,14) 0,46 (0,23)
Как часто преподаватель показывает связь нового материала с повседневной жизнью 0,67** (0,13) 0,78 (0,23) 0,63 (0,29)
Как часто на уроках учащиеся описывают математическим языком события повседневной жизни 1,90*** (0,41) 1,86*** (0,05) 1,50*** (0,11)
Как часто на уроках учащиеся тренируются решать стандартные задания 0,39*** (0,09) 0,53*** (0,02) 0,59*** (0,02)
Как часто преподаватель задает домашнее задание 3,69*** (0,86) 3,43*** (0,14) 3,97*** (0,43)
Как часто на уроках учащиеся работают в малых группах 1,07 (0,24) 1,15 (0,21) 1,05 (0,26)
Как часто на уроках преподаватель дает учащимся разные задания в зависимости от их уровня подготовленности 0,43*** (0,09) 0,35*** (0,02) 0,37*** (0,02)
Давал ли преподаватель задания в виде проектов 0,12*** (0,86) 0,11*** (0,14) 0,13*** (0,43)
Какую долю времени на уроках преподаватель затрачивает на задания части «В» ЕГЭ 5,82*** (1,35) 8,64*** (2,56) 10,78*** (1,11)
Какую долю времени на уроках преподаватель затрачивает на задания части «С» ЕГЭ 7,68*** (2,40) 5,38*** (0,20) 4,22*** (0,40)
Примечание. В строках таблицы приводятся результаты анализа связи зависимой переменной, указанной в столбце 1, и типа образовательной организации (0 = колледж, 1 = школа). Так как зависимые переменные имели порядковую шкалу (1 = 0-20% уроков; 2 = 21-40% уроков; 3 = 41-60% уроков; 4 = 61-80% уроков; 5 = 81-100% уроков), для оценки связи использовалась порядковая логистическая регрессия. В случае с заданиями в виде проектов применялась логистическая регрессия (бинарный выбор). В столбцах 2-4 приведены отношения шансов учащихся школ и колледжей
на более частое выполнение соответствующих заданий. В модели 1 не использовались ковариаты. В модели 2 анализ выполнен с контролем характеристик учащихся: пол, социально-экономический статус, балл PISA, наличие высшего образования у матери. В модели 3 помимо характеристик учащихся контролировались характеристики учителей: квалификационная категория, частота чтения книг по методике преподавания предмета, количество книг дома. *** p < 0,01; ** p < 0,05; * p < 0,1.
Таблица 2. Как различаются шансы учащихся из семей с низким уровнем материального благосостояния заниматься у преподавателя математики высокой профессиональной категории в школах и колледжах
Переменные Колледжи 11-й класс школы
(1) (2) (3) (4) (5) (6)
Низкий уровень материального благосостояния семьи 1,09 (0,20) 1,09 (0,21) 1,30 (0,27) 0,74** (0,10) 0,77* (0,11) 0,76** (0,10)
Средний уровень материального благосостояния семьи 1,00 (0,22) 1,02 (0,23) 1,17 (0,29) 0,89 (0,10) 0,87 (0,10) 0,87 (0,10)
У матери есть оконченное высшее образование 1,25 (0,25) 1,19 (0,24) 1,23 (0,28) 1,16 (0,17) 0,99 (0,13) 1,02 (0,13)
Образование матери не известно 1,36 (0,27) 1,39* (0,27) 1,36 (0,27) 0,91 (0,15) 0,93 (0,16) 0,94 (0,16)
Пол учащегося (женский) 1,03 (0,20) 1,04 (0,21) 0,99 (0,20) 0,92 (0,09) 1,00 (0,10) 0,98 (0,11)
Балл PISA (стандартизированный) 1,24** (0,13) 1,57*** (0,16)
Балл TIMSS (стандартизированный) 1,40*** (0,16) 1,41*** (0,15)
Примечание. Зависимая переменная — квалификационная категория учителя. Для оценки связи использовалась порядковая логистическая регрессия. Для индекса материального благосостояния семьи референтная группа — «высокий уровень». Для уровня образования матери референтная группа — «нет высшего образования». В столбцах (1) и (4) не контролировались предыдущие образовательные результаты учащихся. В столбцах (2) и (5) контролировались результаты PISA (9-й класс). В столбцах (3) и (6) контролировались результаты TIMSS (8-й класс). *** p < 0,01; ** p < 0,05; * p < 0,1.
Differences in General Education in Vocational and High Schools: Characteristics of Teachers and Teaching Practices in Mathematics
Yulia Koreshnikova Authors
Analyst, Institute of Education, National Research University Higher School of Economics. E-mail: [email protected]
Andrey Zakharov
Candidate of Sciences in Pedagogics, Associate Professor, Laboratory Head, International Laboratory for Educational Policy Research, Institute of Education, National Research University Higher School of Economics. E-mail: [email protected]
Fedor Dudyrev
Candidate of Sciences in History, Director, Centre for the Studies of the Secondary Vocational Education, Institute of Education, National Research University Higher School of Economics. E-mail: [email protected]
Address: 20 Myasnitskaya Str., 101000 Moscow, Russian Federation.
More and more middle school graduates opt for vocational schools every year. Abstract They are normally less academically successful students from lower economic and cultural backgrounds. Still, the vocational education system must provide the chance to have a quality general education to anyone who follows this trajectory after the ninth grade. The article uses findings of the Trajectories in Education and Careers longitudinal study to compare the important conditions of obtaining a general mathematical education, i. e. the professional and demographic characteristics of vocational and high school teachers and their teaching practices. The comparison reveals an inequality in students’ access to educational resources depending on the chosen trajectory. The differences revealed are related to the institutional characteristics of the two trajectories and make it possible to say that the latter embrace different types of general education.
educational inequality, education quality, vocational education, high school, Keywords teaching mathematics, teachers, teaching practices.
Alexandrov D., Tenisheva K., Savelyeva S. (2015) Mobilnost bez riskov: obrazo- References vatelnyy put “v universitet cherez kolledzh” [No-Risk Mobility: Through College to University]. Voprosy obrazovaniya / Educational Studies Moscow, no 3, pp. 66-91. DOI: 10.17323/1814-9545-2015-3-66-91. Bessudnov A., Malik V. (2016) Sotsialno-ekonomicheskoe i gendernoe nera-venstvo pri vybore obrazovatelnoy traektorii posle okonchaniya 9-go klas-sa sredney shkoly [Socio-Economic and Gender Inequalities in Educational Trajectories upon Completion of Lower Secondary Education in Russia]. Voprosy obrazovaniya / Educational Studies Moscow, no 1, pp. 135-167. DOI: 10.17323/1814-9545-2016-1-135-167. Blatchford P., Kutnick P., Baines E., Galton M. (2003) Toward a Social Pedagogy of Classroom Group Work. International Journal of Educational Research, vol. 39, no 1-2, pp. 153-172. Bourdieu P. (2002) Formy kapitala [The Forms of Capital]. Ekonomicheskaya
sotsiologiya, vol. 3, no 5, pp. 60-74. Carnoy M., Khavenson T., Loyalka P., Schmidt W., Zakharov A. (2016) Revisiting the Relationship between International Assessment Outcomes and Ed-
ucational Production: Evidence from a Longitudinal PISA-TIMSS Sample. American Educational Research Journal, vol. 53, no 4, pp. 1054-1085.
Cavalluzzo L. C. (2004) Is National Board Certification an Effective Signal of Teacher Quality? Alexandria, Virginia: CNA Corporation. Available at: https://files.eric.ed.gov/fulltext/ED485515.pdf (accessed 30 April 2018).
Cedefop (2016a) Leaving Education Early: Putting Vocational Education and Training Centre Stage. Vol. I: Investigating Causes and Extent. Cedefop Research Paper No 57. Luxembourg: Publications Office of the European Union. http://dx.doi.org/10.2801/893397
Cedefop (2016b) Leaving Education Early: Putting Vocational Education and Training Centre Stage. Vol. II: Evaluating Policy Impact. Cedefop Research Paper No 58. Luxembourg: Publications Office of the European Union. http://dx.doi.org/10.2801/967263
Clotfelter C. T., Ladd H. F., Vigdor J. L. (2007) Teacher Credentials and Student Achievement: Longitudinal Analysis with Student Fixed Effects. Economics of Education Review, vol. 26, no 6, pp. 673-682.
Clotfelter C. T., Ladd H. F., Vigdor J. L. (2006) Teacher-Student Matching and the Assessment of Teacher Effectiveness. Journal of Human Resources, vol. 41, no 4, pp. 778-820.
Cooper H. (1989) Homework. White Plains. New York: Longman.
Darling-Hammond L. (2000) Teacher Quality and Student Achievement. Education Policy Analysis Archives, vol. 8, no 1, pp. 1-40.
Frome P., Lasater B., Cooney S. (2005) Well-Qualified Teachers and High Quality Teaching: Are They the Same? (Research Brief). Atlanta, GA: Southern Regional Education Board.
Goe L. (2007) The Link between Teacher Quality and Student Outcomes: A Research Synthesis. Washington, DC: National Comprehensive Center for Teacher Quality. Available at: http://www.niusileadscape.org/docs/FINAL_ PRODUCTS/LearningCarousel/LinkBetweenTQandStudentOutcomes.pdf (accessed 30 April 2018).
Goldhaber D. D., Brewer D. J. (2000) Does Teacher Certification Matter? High School Teacher Certification Status and Student Achievement. Educational Evaluation and Policy Analysis, vol. 22, no 2, pp. 129-145.
Goldhaber D. D., Brewer D. J. (1996) Evaluating the Effect of Teacher Degree Level on Educational Performance. Developments in School Finance (ed. W. Fowler) Washington, DC: NCES. Google Scholar, pp. 197-210.
Harris D. N., Sass T. R. (2011) Teacher Training, Teacher Quality and Student Achievement. Journal of Public Economics, vol. 95, no 7, pp. 798-812.
Hattie J. (2017) Vidimoe obuchenie. Sintez rezultatov bole 50000 issledovaniy s okhvatom bolee 80 millionov shkolnikov [Visible Learning: A Synthesis of Over 800 Meta-Analyses Relating to Achievemen]. Moscow: Natsionalnoe obrazovanie.
Kannapel P. J., Clements S. K., Taylor D., Hibpshman T. (2005) Inside the Black Box of High-Performing High-Poverty Schools. Lexington, Kentucky: Prich-ard Committee for Academic Excellence. Available at: http://prichardcom-mittee.org/wp-content/uploads/2013/02/Inside-the-Black-Box.pdf (accessed 30 April 2018).
Konstantinovskiy D., Voznesenskaya E., Cherednichenko G., Khokhlushkina F. (2010) Zhiznennye traektorii molodezhi: Desyat let spustya. Sotsiologich-eskoe issledovanie [Youth Life Trajectories: 10 Years Later. Sociological Study]. Moscow: Institute of Sociology, Russian Academy of Sciences.
Kukla-Acevedo S. (2009) Do Teacher Characteristics Matter? New Results on the Effects of Teacher Preparation on Student Achievement. Economics of Education Review, vol. 28, no 1, pp. 49-57.
Kuzminov Y., Popova S., Yakobson L. (eds) (2017) Effektivny kontrakt dlya pro-fessionalov sotsialnoy sfery: trendy, potentsial, resheniya. Ekspertny doklad [Performance-Based Contracting for Specialists in Social Sphere: Trends, Prospects, Solutions. Expert Report]. Moscow: HSE.
Lyubimov L. (2008) Kommentarii k dokladu Obshchestvennoy palaty Rossiyskoy Federatsii “Obrazovanie i obshchestvo: gotova li Rossiya investirovat v svoe budushchee?” [Comments on the Public Chamber’s report Society and Education: Is Russia Ready to Invest in its Future?]. Voprosy obrazovaniya / Educational Studies Moscow, no 1, pp. 5-31.
Marcoulides G. A., Heck R. H., Papanastasiou C. (2005) Student Perceptions of School Culture and Achievement: Testing the Invariance of a Model. International Journal of Educational Management, vol. 19, no 2, pp. 140-152.
National Research University Higher School of Economics (2010) Obrazovanie v Rossiyskoy Federatsii: 2010 (Statisticheskiy sbornik) [Education in Russian Federation: 2010 (Data Book)]. Moscow: HSE.
National Research University Higher School of Economics (2012) Obrazovanie v Rossiyskoy Federatsii: 2012 (Statisticheskiy sbornik) [Education in Russian Federation: 2012 (Data Book)]. Moscow: HSE.
National Research University Higher School of Economics (2014) Obrazovanie v Rossiyskoy Federatsii: 2014 (Statisticheskiy sbornik) [Education in Russian Federation: 2014 (Data Book)]. Moscow: HSE.
National Research University Higher School of Economics (2016) Obrazovanie v tsifrakh: 2014 (Statisticheskiy sbornik) [Education in Figures: 2014 (Data Book)]. Moscow: HSE.
Rivkin S. G., Hanushek E. A., Kain J. F. (2005) Teachers, Schools, and Academic Achievement. Econometrica, vol. 73, no 2, pp. 417-458.
Rockoff J. E. (2004) The Impact of Individual Teachers on Student Achievement: Evidence from Panel Data. The American Economic Review, vol. 94, no 2, pp. 247-252.
Roshchin S. (2006) Perekhod “ucheba-rabota”: omut ili brod? [Study-to-Work Transition: A Vortex or Shallow Waters?]. Working Paper WP3/2006/10 (WP3 Labor Market Issues). Moscow: HSE.
Schoenfeld A.H., Sloane A. H. (eds) (2016) Mathematical Thinking and Problem Solving. Routledge.
Tyumeneva Y., Valdman A., Carnoy M. (2014) Chto dayut predmetnye znaniya dlya umeniya primenyat ikh v novom kontekste. Pervye rezultaty sravnitel-nogo analiza TIMSS-2011 i PISA-2012 [What Does Subject Knowledge Give for Its Applying in New Context. The First Results from Studies TIMSS-2011 and PISA-2012]. Voprosy obrazovaniya/ Educational Studies Moscow, no 1, pp. 8-24.
Wenglinsky H. (2000) How Teaching Matters: Bringing the Classroom Back into Discussions of Teacher Quality. Princeton, NJ: Millikan Family Foundation and Educational Testing Service. Available at: https://files.eric.ed.gov/full-text/ED447128.pdf (accessed 30 April 2018).
Wenglinsky H. (2002) How Schools Matter: The Link between Teacher Classroom Practices and Student Academic Performance. Education Policy Analysis Archives, vol. 10, no 12.
Woessmann, L. (2016) The Importance of School Systems: Evidence from International Differences in Student Achievement. Journal of Economic Perspectives, vol. 30, no 3, pp. 3-32.
Zakharov A., Carnoy M., Loyalka P. (2014) Which Teaching Practices Improve Student Performance on Highstakes Exams? Evidence from Russia. International Journal of Educational Development, vol. 36, May, pp. 13-21.
Олимпиада по математике и алгоритмике для школьников и студентов колледжей
| | |
Уважаемые участники Олимпиады по математике и алгоритмике для школьников и студентов колледжей!
Дорогие победители и призеры очного этапа Олимпиады по математике и алгоритмике для школьников и студентов колледжей!
Ваши дипломы 1,2,3 степени можно забрать в Колледже информатики и программирования Финуниверситета (адрес: г. Москва, Кронштадтский бульвар, д. 37б; м. Водный стадион), обратившись в каб.201 к педагогу-организатору Ходыковой Ноган Валериевне (8-495-454-2521).
С уважением, искренней признательностью за участие и пожеланиями дальнейших успехов, Организационный комитет Олимпиады.
Уважаемые победители и призеры заочного этапа Олимпиады по математике и алгоритмике для школьников и студентов колледжей!
Колледж информатики и программирования Финансового университета при Правительстве Российской Федерации (адрес: г. Москва, Кронштадтский бульвар, д. 37б, м. Водный стадион) приглашает вас в субботу, 25 января 2020 г., с 11-00 в ауд. 309А, принять участие в очном этапе Олимпиады.
Желаем успехов!
С уважением, Организационный комитет Олимпиады по математике и алгоритмике»
Колледж информатики и программирования Финансового университета при Правительстве Российской Федерации приглашает вас принять участие в Олимпиаде по математике и алгоритмике для школьников и студентов колледжей.
Участники этапов Олимпиады могут претендовать на получение баллов в качестве индивидуальных достижений, в соответствии с правилами приема в Финансовый Университет.
Для того, чтобы принять участие в олимпиаде необходимо с 01 ноября по 01 декабря 2019 г. пройти электронную регистрацию на сайте Финансового университета ССЫЛКА.
Участники заключительного (очного) этапа должны представить следующие документы:
- паспорт
- справку из образовательного учреждения, подтверждающую статус участника и выданную не ранее 15 января 2020 года.
Участие в Олимпиаде бесплатное.
Регистрация открыта с 01 ноября по 01 декабря 2019 г.
Олимпиада проводится в два этапа:
Отборочный (заочный) этап – с 02 декабря по 27 декабря 2019 года (проводится в виде online тестирования).
Заключительный (очный) этап – с 23 января по 26 января 2020 года (проводится в виде письменного тестирования в Финансовом университете).
Результаты отборочного (заочного) этапа размещаются на официальной странице олимпиады после 14 января 2020 года.
Информация о победителях и призерах заключительного (очного) этапа размещается на официальной странице олимпиады не позднее 07 февраля 2020 года.
Контактная информация: +7(495)454-25-21, Ходыкова Ноган Валериевна ([email protected])
Приказ о проведении Олимпиады:
Положение о проведении Олимпиады:
Регламент проведения: Регламент:
Состав организационного комитета:
Состав методического комитета:
Календарный план проведения:
Список победителей, призеров и вне призеров заключительного (очного) этапа Олимпиады по математике и алгоритмике 1 возрастной группы (1-2 курсы)
1 кандидатура из числа участников в качестве победителя заключительного (очного) этапа Олимпиады, набравшая следующее количество баллов (1-е место):
| № | ФИО | Кол-во баллов |
| 1 | Корнеева Анастасия Николаевна (школа №1502 при МЭИ) | 50 |
1 кандидатура из числа участников в качестве призеров заключительного (очного) этапа Олимпиады, набравшая следующее количество баллов (2-е место):
№ | ФИО | Кол-во баллов |
| 1 | Степанова Анна Андреевна (Московский финансовый колледж) | 29 |
2 кандидатуры из числа участников в качестве призеров заключительного (очного) этапа Олимпиады (3-е место):
| № | ФИО | Кол-во баллов |
| 1 | Никитенко Дмитрий Константинович (КИПФИН) | 20 |
| 2 | Латыпова Индира Рустамовна (Уфимский филиал Финуниверситета, СПО) | 20 |
6 кандидатур из числа участников в качестве вне призеров заключительного (очного) этапа Олимпиады:
| № | ФИО | Кол-во баллов |
| 1 | Джигеров Суфьян Замирович (Московский финансовый колледж) | 19 |
| 2 | Квашилава Илья Романович (КИПФИН) | 19 |
| 3 | Кудряшова Ирина Викторовна (Московский финансовый колледж) | 10 |
| 4 | Гильмутдинова Гульназ Рафисовна (Уфимский филиал Финуниверситета, СПО) | 9 |
| 5 | Косачев Никита Олегович (КИПФИН) | 9 |
| 6 | Черногорова Елизавета Ярославовна (Московский финансовый колледж) | 0 |
Список победителей, призеров и вне призеров заключительного (очного) этапа Олимпиады 2 возрастной группы (3-4 курсы):
2 кандидатуры из числа участников в качестве победителей заключительного (очного) этапа Олимпиады, набравшие следующее количество баллов (1-е место):
| № | ФИО | Кол-во баллов |
| 1 | Мамукашвили Илия Роинович (КИПФИН) | 16 |
| 2 | Самарина Анастасия Павловна (Уфимский филиал Финуниверситета, СПО) | 16 |
1 кандидатура из числа участников в качестве призеров заключительного (очного) этапа Олимпиады, набравший следующее количество баллов (2-е место):
| № | ФИО | Кол-во баллов |
| 1 | Красавин Михаил Андреевич (КИПФИН) | 16 |
2 кандидатуры из числа участников в качестве вне призера заключительного (очного) этапа Олимпиады, набравшие следующее количество баллов (3-е место):
| № | ФИО | Кол-во баллов |
| 1 | Гибадуллина Нелли Римовна (Уфимский филиал Финуниверситета, СПО) | 12 |
| 2 | Кривцов Александр Александрович (Бюджетное профессиональное образовательное учреждение Республики Калмыкия «Элистинский политехнический колледж») | 14-2=12 |
1 кандидатура из числа участников в качестве вне призеров заключительного (очного) этапа Олимпиады, набравший следующее количество баллов:
| № | ФИО | Кол-во баллов |
| 1 | Водяхин Арсений Андреевич (КИПФИН) | 2 |
Ключевые дисциплины — Образовательная программа «Прикладная математика» — Национальный исследовательский университет «Высшая школа экономики»
Обучение на программах бакалавриата в Высшей школе экономики строится из 5 основных элементов:
1. Общий цикл дисциплин, включающий для бакалаврской программы «Прикладная математика»:
- Историю – 1 курс
- Право – 1 курс
- БЖД – начало первого курса
- Физическую культуру – все четыре года
2. Профессиональный цикл дисциплин, или «Major». Этот цикл составляет основу бакалаврской программы, на него приходится две трети всех зачетных единиц. Часть дисциплин цикла являются базовыми (обязательными), часть выбираются самим студентом. Обязательными предметами для студента бакалаврской программы «Прикладная математика» являются:
1 курс
- Математический анализ
- Линейная алгебра и аналитическая геометрия
- Физика
- Алгоритмизация и программирование
2 курс
- Математический анализ
- Дискретная математика
- Алгоритмизация и программирование
- Дифференциальные уравнения
- Теория вероятностей и математическая статистика
- Теория функций комплексного переменного
- Алгебра
- Теоретическая механика
- Функциональный анализ
В конце 2-го курса каждый студент выбирает “специализацию”, по которой он будет проходить обучение на 3-4 курсе. Каждая специализация состоит из набора обязательных дисциплин и научно-исследовательского семинара. Подробнее…
3. Дополнительный профиль, или «Minor». Дисциплины этого профиля позволяют студентам получить знания и компетенции в других, отличных от их основного направления подготовки, областях. Minor для себя выбирает сам студент в конце первого курса, причем его специализация может быть любой, ничто не мешает студенту-философу выбрать майнор по программированию и наоборот. Студенты изучают дисциплины майноров в специально выделенные дни на втором и третьем курсах. Список майноров, доступных студентам прошлых лет, доступен по ссылке.
4. Проектная и исследовательская работа включает в себя подготовку курсовых и выпускных работ, компьютерные практикумы, производственную практику, выполнение проектов (учебных, научных), а также участие студентов в проектных и научно-исследовательских семинарах.
На 1-2 курсах в учебный план включены Компьютерные практикумы, профориентационный семинар, проектный семинар.
Основные задачи компьютерных практикумов
- научить использовать программные средства (MatLab, Mathematica) для решения поставленных математических задач и визуализации полученных результатов;
- выработать навыки проектирования и программирования компьютерных приложений, которые будут использоваться при выполнении различных заданий и работ по дисциплинам, изучаемым на последующих курсах;
- формирование практических навыков низкоуровнего программирования на языке ассемблер;
- формирование практических навыков использования базовых принципов объектно-ориентированного программирования, применяемых при разработке и реализации алгоритмов, создании и отладке компьютерных программ.
Основные задачи профориентационного семинара:
- формирование у студентов представления о новых современных концепциях и технологиях в области прикладной математики;
- выбор учащимся профиля (специализации) обучения, определение профессиональной склонности и пути дальнейшего развития в выбранной профессии.
Основные задачи проектных семинаров:
- формирование практических навыков применения студентами знаний в области прикладной математики и компьютерных технологий, необходимых для реализации научно-исследовательских проектов.
На 3 курсе студенты реализуют учебный проект в рамках проектного семинара «Международные научно-технические проекты» с обязательной защитой его на английском языке; выполняют междисциплинарную курсовую работу и проходят обязательную производственную практику.
На 4 курсе планируется выполнение еще одного учебно-исследовательского проекта, а также научно-исследовательский семинар в рамках каждой из специализаций.
Проектами, курсовыми и выпускными работами наших студентов руководят преподаватели МИЭМ, сотрудники лабораторий: Космических исследований в области технологий, систем и процессов, Математических метод естествознания, Имитационного моделирования, сотрудники базовой кафедры «Прикладные информационно-коммуникационные средства и системы» ВЦ РАН, научные сотрудники из внешних организаций-работодателей: НЦ РАН в Черноголовке, Института Прикладной математики им. Келдыша РАН, Института спектроскопии РАН, Института космических исследований РАН, НПО им. Лавочкина, StatSoft, ЗАО «Программирование и новые информационные технологии», ИТ-подразделений предприятий, банков.
5. Государственная итоговая аттестация включает государственный экзамен и защиту выпускной квалификационной работы. Каталог выпускных квалификационных работ студентов прошлых лет доступен по ссылке.
Дополнительно студенту бакалавриата предоставляется возможность бесплатно изучать английский язык. Общий объём — 14 зачетных единиц: на первом курсе 8 з.е., на втором – 6 з.е. После первого курса студенты сдают обязательный внутренний экзамен, после второго курса все студенты ВШЭ проходят внешний независимый экзамен по английскому языку.
На 2 курсе в индивидуальный план студента обязательно включается курс на английском языке, изучаемый дистанционно .
На третьем курсе некоторые дисциплины в бакалавриате преподаются на английском языке. Например, такие: Численные методы, Экономика фирмы, Базы данных.
На четвертом – студентам предложат двухкредитный курс «Академическое письмо на английском языке», по окончании изучения которого студенты создадут проект текста своей выпускной квалификационной работы на английском языке.
что такое сессия, практика в колледже, сколько длится пара
При поступлении в колледж многих будущих студентов интересует вопрос: как там вообще проходит учеба, и чего ждать? Ответим на него в этой статье. Кстати, сейчас, в связи с карантином, учебные заведения переходят на режим дистанционного обучения. Мы уже написали для вас статью о том, как эффективно учиться на удаленке и не терять время попусту.
Присоединяйтесь к нам в телеграме, чтобы быть в курсе актуальных новостей, а также получать приятные бонусы и скидки.
Учеба в колледже: общие сведения
Колледж – учреждение среднего профессионального образования.
Колледжи, техникумы и профессиональные училища можно объединить под общим названием ССУЗ (среднее специальное учебное заведение).
Сколько лет длится учеба в колледже? В зависимости от выбранной программы и специальности, в колледж можно поступать после 9 или 11 класса. Обучение длится от 2 лет и 10 месяцев до 4 лет и 10 месяцев.
Доступные формы обучения в колледже:
- очная;
- заочная;
- дистанционная.
По окончании колледжа выпускнику выдаётся диплом о среднем специальном образовании, дающий право работать по полученной специальности. После колледжа также можно поступить в вуз на бюджет и даже учиться там по ускоренной программе.
Кстати, при поступлении в колледж не требуется сдавать ЕГЭ, а на многие специальности зачисление ведется вообще без вступительных экзаменов.Подборка колледжей по специальностям
Если вы задумываетесь о поступлении в колледж, но не можете определиться, полезно будет узнать о плюсах и минусах этих учебных заведений в сравнении со школой. Также советуем ознакомиться с нашей подборкой колледжей по специальностям:
Учеба вЧто такое пара в колледже
Если в школе все привыкли ходить на уроки, то в колледже добро пожаловать на пары. Пара – занятие в колледже, которое длится два академических часа с перерывом. По сути, это двойной урок.
Академический час равен 45 минутам.Сколько пар в день в колледже? Нагрузка будет больше, чем в школе. Например, на первом курсе в колледже ставят три, максимум четыре пары в день. В субботу пар обычно меньше, зато на старших курсах к парам добавится практика.
Что такое практика в колледже
Практика – обязательная внеурочная часть учебного процесса в вузах и училищах.
Практика дает студентам возможность закрепить полученные теоретические знания и научиться применять их в «боевых» условиях.
Как проходит практика в колледже? В зависимости от курса и специальности, существуют следующие виды практики в колледже:
- Учебная. Учебную практику обычно проходят группой под руководством куратора.
- Производственная. Для прохождения производственной практики студент отправляется на реальное предприятие, знакомится с его особенностями и пробует себя в роли работника.
- Преддипломная. В ходе преддипломной практики учащиеся собирают и анализируют информацию, которая будет в дальнейшем использоваться в дипломном исследовании.
Многих интересует, платят ли за практику в колледже. Отвечаем: нет. В колледже платят только стипендию, да и то лишь студентам бюджетной формы обучения. А вот если при прохождении производственной практики вы убедите руководство предприятия официально принять вас на работу, тогда требуйте зарплату.
Что такое сессия в колледже
Сессия волнует многих, особенно, если это сессия в колледже на первом курсе. Сразу проспойлерим: бояться там нечего.
Сессия – период сдачи экзаменов.
Как проходит сессия в колледже? В это время даже самые злостные прогульщики берутся за учебу и начинают зубрить. Обычно экзаменов бывает 4 или 5, максимум 7.
Сколько сессий в году в колледже? Всего две, зимняя и летняя. Однако это не повод «забивать» на учебу в перерывах между сессиями. Следует помнить, что кроме экзаменов придется сдать несколько зачетов, а на старших курсах еще и курсовую работу.
Как пережить сессию – вопрос, который задают себе все поколения студентов. Если станет совсем невмоготу, вспомните, что профессиональный сервис для учащихся всегда придет на выручку и поможет решить возникающие проблемы с учебой.
Автор: Иван
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Информация для первокурсников – математика и статистика – Carleton College
И математика, и статистика воплощают в себе дух гуманитарных наук. Математика – это искусство, чистая наука, язык и аналитический инструмент для естественных и социальных наук. Статистика – это наука о придании значения данным в контексте неопределенности. Учебные программы первого года обучения математике и статистике намеренно гибкие. Наша цель – предоставить подходящие отправные точки независимо от уровня подготовки учащегося.
Примите участие
Чтобы получать больше информации о событиях и мероприятиях в нашем отделе, подпишитесь на наши списки рассылки и информационный бюллетень, используя эту форму.
Могу ли я специализироваться на этом?
Наш факультет предлагает специальности математики и статистики, а также второстепенную математику.
Как начать заниматься математикой
Большинство студентов-первокурсников, изучающих математический курс, начинают с математической последовательности. Проконсультируйтесь с Таблицей решения о размещении по расчету или посетите страницу о размещении по расчету / статистике, чтобы определить, какой курс по расчету выбрать в первую очередь.
- Математика 101: Исчисление с решением задач. Этот курс знакомит с двумя фундаментальными понятиями исчисления: производной и интегралом. Формат встреч пять дней в неделю позволяет при необходимости рассматривать темы, предшествующие расчету. Допуск к математике 101 осуществляется только после сдачи экзамена №1 Карлтона. После завершения курса «Математика 101» студенты могут пройти курс «Математика 120».
- Математика 111: исчисление 1. Первое введение в исчисление, в котором вычисляются производная и интеграл.Предназначен для студентов, мало или совсем не знакомых с исчислением. После успешного завершения курса математики 111 студенты могут пройти курс математики 120.
- математика 120: исчисление 2. Обратные функции, интегрирование по частям, моделирование с помощью дифференциальных уравнений, векторов, исчисление функций двух независимых переменных, включая производные по направлениям и двойные интегралы , Множители Лагранжа. После успешного завершения по математике 120 студенты могут сдавать математику 210. (Не доступно для студентов, которые уже получили баллы по математике 210, или для студентов, получивших 4 или 5 баллов на экзамене AP Calculus BC.)
- Math 210: Calculus 3. Векторы, кривые, исчисление функций трех независимых переменных, включая производные по направлениям и тройные интегралы, цилиндрические и сферические координаты, линейные интегралы, теорему Грина, несобственные интегралы, последовательности и ряды, степенные ряды , Серия Тейлора. (Не доступно для студентов, которые уже получили зачет по математике 211.)
- Математика 211: многомерное исчисление. Это отправная точка для студентов, получивших на экзамене AP BC 4 или 5 баллов.Он развивает исчисление в двух или более измерениях. После успешного завершения математики 211 студенты могут пройти математику 232.
Если вы выполнили последовательность вычислений, рассмотрите следующие курсы
:- Математика 232: линейная алгебра. Темы включают линейные пространства и линейные преобразования, собственные значения, собственные векторы и определители.
- Math 236: Математические структуры. Введение в методы доказательства (индукция, доказательство от противоречия), а также в другие основополагающие аспекты математики (отношения эквивалентности, количество элементов и т. Д.)).
- Математика 240: Вероятность. (ранее – Math 265) Введение в дискретную и непрерывную вероятность, кульминацией которой являются Центральная предельная теорема и закон больших чисел.
Полное описание см. В каталоге курсов.
Как начать работу в статистике
Есть несколько вариантов для первокурсников, интересующихся статистикой.
- Stat 120: Введение в статистику. Если вам интересна статистика или вы планируете изучать естественные науки, экологию, экономику, политологию или социологию / антропологию, вам следует взять Stat 120 .Хотя Stat 120 не является обязательным курсом для специалиста по статистике, вы все равно можете пройти этот курс и специальность по статистике. Некоторые отделы принимают кредит AP Statistics за свою специальность. Проконсультируйтесь с отдельными отделами.
- Math 240, Stat 250: Вероятность и введение в статистический вывод. (ранее – Math 265, Math 275) Если вы выполнили математический анализ по математике 120 или 211, мы рекомендуем вам рассмотреть эту последовательность (вместо Stat 120 ). Эти два курса необходимы, если вы планируете специализироваться на статистике.
- Stat 230: Прикладной регрессионный анализ. (ранее Math 245) Если вы получили 4 или 5 на экзамене по статистике AP, рассмотрите возможность применения прикладного регрессионного анализа. Завершение этого курса с C- или выше принесет вам 6 кредитов для Stat 120.
Полное описание см. В каталоге курса.
вопросов
Если у вас есть вопросы по размещению на курсах математики, обращайтесь к консультанту по размещению по математике. Если у вас есть вопросы о том, какой курс статистики выбрать, обратитесь к консультанту по размещению статов statplacement @ carleton.edu.
Двухлетний математический журнал колледжа по JSTOR
Журнал по математике двухгодичного колледжа
Охват: 1970-1983 (Том 1, № 1 – Том 14, № 5)
Moving Wall: 3 года (Что такое движущаяся стена?) “Движущаяся стена” представляет собой промежуток времени между последними выпусками
имеется в JSTOR и в последнем опубликованном номере журнала.Подвижные стены обычно обозначаются годами. В редких случаях
издатель решил создать “нулевую” подвижную стену, поэтому их текущая
выпуски доступны в JSTOR вскоре после публикации.
Примечание. При расчете подвижной стены текущий год не учитывается.
Например, если текущий год – 2008, а журнал имеет пятилетний
движущаяся стена, доступны статьи 2002 года выпуска.
- Термины, относящиеся к подвижной стене
- Неподвижные стены: Журналы, в архив которых не добавляются новые тома.
- Поглощено: журналов, объединенных под другим названием.
- Завершено: Журналы, которые больше не публикуются или в сочетании с другим названием.
ISSN: 00494925
Тем: Математика, Наука и математика
Коллекции: Коллекция искусств и наук II, Архивный журнал JSTOR и собрание первичных источников, Основная коллекция JSTOR, Сборник математики и статистики
× Закрыть оверлейЖурнал математики колледжа на JSTOR
Математический журнал колледжа
Описание:The College Mathematics Journal подчеркивает первые два года обучения в колледже.Журнал содержит богатый материал для учителей и студентов. Широкий спектр тем будет держать вас в курсе, вдохновлять и развлекать.
Охват: 1984-2017 (Том 15, № 1 – Том 48, № 5)
Moving Wall: 3 года (Что такое движущаяся стена?) “Движущаяся стена” представляет собой промежуток времени между последними выпусками
имеется в JSTOR и в последнем опубликованном номере журнала.Подвижные стены обычно обозначаются годами. В редких случаях
издатель решил создать “нулевую” подвижную стену, поэтому их текущая
выпуски доступны в JSTOR вскоре после публикации.
Примечание. При расчете подвижной стены текущий год не учитывается.
Например, если текущий год – 2008, а журнал имеет пятилетний
движущаяся стена, доступны статьи 2002 года выпуска.
- Термины, относящиеся к подвижной стене
- Неподвижные стены: Журналы, в архив которых не добавляются новые тома.
- Поглощено: журналов, объединенных под другим названием.
- Завершено: Журналы, которые больше не публикуются или в сочетании с другим названием.
ISSN: 07468342
EISSN: 19311346
Тем: Математика, Наука и математика
Коллекции: Коллекция искусств и наук II, Архивный журнал JSTOR и собрание первичных источников, Основная коллекция JSTOR, Сборник математики и статистики
× Закрыть оверлейКаждый пятый студент колледжа посещает курсы математики, которые повторяют то, что они уже знают
Хотя учеба в колледже обещает привлечение новых идей и обучение новым навыкам, когда дело доходит до математики, опыт иногда может напоминать среднюю школу снова и снова.
В новом исследовании с участием более 5000 студентов двух- и четырехлетних колледжей по всей стране я обнаружил, что примерно каждый пятый прошел курс математики, который, по их оценкам в старших классах, им не нужен, – и тот, который им не нужен. уже закончил среднюю школу. Я называю это избыточной математикой.
Я проверил оценки учащихся на национальном тесте по математике в старших классах школы, а также курсы математики, которые они прошли в первый год обучения в колледже. Я обнаружил, что многие, вероятно, могли бы пройти курс математики более высокого уровня в колледже, если бы они его взяли.Я основываю этот вывод на других учащихся в выборке, которые имели аналогичные результаты тестов и прошли более углубленные курсы математики. Вместо этого – по причинам, не сразу очевидным – эти ученики прошли курс более низкого уровня, который они уже закончили в старшей школе. Это поднимает вопрос о том, является ли математика, которую эти студенты изучают в колледже, пустой тратой времени и денег.
Я изучаю эти вопросы как бывший учитель математики в средней школе и как исследователь, специализирующийся на изучении высшего образования.Моя цель – найти наилучшие способы помочь большему количеству студентов поступить в колледж и завершить его вовремя и эффективно.
Удержание студентов
Важно понимать, когда учащиеся изучают избыточную математику, потому что слишком большое количество математических курсов в колледже может стать камнем преткновения. Например, исследование студентов местных колледжей показало, что чем больше времени студенты проводят на курсах коррекционной или «развивающей» математики, тем меньше у них шансов остаться в школе и получить степень.
Мы с коллегой также обнаружили, что требование к студентам прохождения только одного дополнительного семестра по математике значительно снизилось – примерно на 13 процентных пунктов – независимо от того, приходили ли студенты общественных колледжей в следующий семестр.
Конечно, коррекционные или развивающие математические курсы могут дать студентам возможность укрепить математические навыки, привыкнуть к суровым условиям работы в колледже и подготовиться к работе. Однако стоят ли эти преимущества времени и денег, если учащиеся посещают уроки математики, которые могут быть ненужными и могут привести к тому, что они не закончат школу?
Исправительное или повторяющееся?
Вот почему так важно называть различные математические курсы тем, чем они являются. Например, говорят, что многие студенты проходят «лечебные» или «развивающие» курсы математики в национальных колледжах и университетах.Но я обнаружил, что примерно 40% студентов, которые поступают в колледж с коррекционного курса математики, на самом деле проходили избыточный курс: то есть курс, который они прошли и прошли раньше в старшей школе, и, судя по результатам их тестов по математике, эти студенты мог бы пройти курс математики более высокого уровня в колледже.
Лечебные курсы – не единственные классы, где вы обнаруживаете, что студенты излишне занимаются математикой. Я также обнаружил, что 37% студентов, изучающих математику в колледже на уровне, предшествующем исчислению, то есть более продвинутой математике, на самом деле тоже проходили избыточные математические курсы.
Кто занимается лишней математикой?
Проблема избыточной математики в колледжах не ограничивалась двухгодичными колледжами, где 25% студентов посещали избыточные математические курсы. В четырехлетних колледжах это было 18%. В совокупности это примерно каждый пятый студент колледжа. Избыточная математика также была более вероятной у студентов, посещающих государственные колледжи и университеты (22%), чем у студентов частных колледжей (16%). Кроме того, это было более распространено среди тех, кто посещал менее избирательные колледжи (24%), чем среди тех, кто посещал более избирательные учреждения (14%).
Федерик Нго, автор предоставилДанные также свидетельствуют о том, что студентки и студентки из малообеспеченных семей чаще участвовали в излишней математике в колледжах. Это поднимает вопросы о несправедливых возможностях и опыте учебы в колледже для этих студентов.
Но почему вообще есть студенты, изучающие избыточную математику? С одной стороны, избыточность существует потому, что средние школы и колледжи иногда работают в соответствии с разными определениями и стандартами «готовности к колледжу».”
Например, в похожем исследовании мы с другим коллегой обнаружили, что почти две трети старшеклассников в одном школьном округе Калифорнии были переведены на коррекционные курсы при поступлении в общественный колледж, даже если они достигли высоких результатов по стандартизированной математике штата. тесты и – на основании этих оценок – были признаны готовыми к четырехлетнему обучению в колледже. Эти студенты вообще избежали бы коррекционных курсов, если бы они учились в четырехлетнем колледже, но в конечном итоге попали на коррекционные курсы, потому что тестирование в местных колледжах, которые они посещали, показало, что они не готовы.
Проблема в том, что тесты не всегда точны. Например, исследование 2012 года показало, что примерно каждый четвертый студент колледжа, который действительно был готов к курсам математики на уровне колледжа, был ошибочно помещен на коррекционные курсы. Следовательно, более половины местных колледжей по всей стране реформировали свои подходы к развивающему образованию, отказавшись от единственной зависимости от тестирования по месту жительства.
Тревога по математике
Тем не менее, тестирование– не единственная причина избыточного прохождения курса математики.Некоторые учащиеся из-за беспокойства по поводу математики, неуверенности в себе или проблем с мотивацией могут самостоятельно изучать математику более низкого уровня. Или некоторые могут проходить самый простой курс математики, чтобы удовлетворить любые математические требования, с которыми они могут столкнуться.
По этой причине для консультантов как на уровне средней школы, так и на уровне колледжа может быть полезно спросить учащихся о причинах, по которым они выбирают один вид математики вместо другого, и обсудить потенциальные последствия этих решений.
На карту поставлено многое, в том числе время, деньги и ресурсы.Если проблему избыточной математики в колледже удастся решить, тогда колледж станет немного дешевле, быстрее и справедливее для студентов. Но проблему нельзя решить, не назвав ее сначала тем, чем она является.
[ Подпишитесь на информационный бюллетень The Conversation, чтобы получать ежедневную информацию ]
Учебная программа по математике | Колледж Дикинсона
Major
11 курсов
170, 171, 211, 262, 270, 351, 361
Один курс математики с обязательным условием 351 или 361
Один дополнительный курс математики с номером 301 или выше
Два дополнительных курса по математике с номером 201 или выше.Один из этих курсов может быть заменен на COMP 132 или ECON 398 или, по предварительному согласованию с кафедрой, интенсивным курсом по математике другого факультета.
Незначительный
Пять курсов
171 и 211, один из трех курсов 325, 351 или 361 и два других курса с номерами 201 или выше.
Возможные пути:
Путь 1: 170, 171, 211, 262, 270, 361;
Track 2: 170, 171, 211, 262, 351, факультатив;
Треки 1 и 2 посвящены теоретической математике.
Дорожка 3: 170, 171, 211, 225, 270, 325.Трек 3 посвящен статистике.
Предлагаемый план учебных программ по специальности
Есть много возможных путей прохождения курса по математике. Какой путь выбрать, зависит от предыдущей работы студента и его размещения. Здесь мы представляем четыре модели. При тщательном планировании все четыре модели позволяют студентам провести семестр или год за границей.
Модель 1 – MATH 151 как точка входа (для студентов, которые поступают в 151)
Первый год: 151, 170
Второй год обучения: 171, 211, 270, 262
Младшие и старшие классы: 351 , 361, МАТЕМАТИЧЕСКИЙ факультатив
Модель 2 – MATH 170 в качестве отправной точки (для студентов с соответствующей подготовкой к исчислению)
Первый год: 170, 171
Второй год обучения: 211, 262, 270
Младшие и старшие классы: 351 , 361, МАТЕМАТИЧЕСКИЙ факультатив
Модель 3 – MATH 171 в качестве отправной точки (для студентов с 170 кредитами)
Первый год: 171, 270
Второй год обучения: 211, 262
Младшие и старшие классы: 351, 361, факультативы MATH
Модель 4 – MATH 171 в качестве начальной точки (для студентов со 170 и 270 кредитами)
Первый год [Вариант 1]: 171, 211
Первый год [Вариант 2]: 211, 262
Второй год [Вариант 1]: 262, МАТЕМАТИЧЕСКИЙ факультатив
Второй год обучения [Вариант 2]: 171, МАТЕМАТИЧЕСКИЙ факультатив
Младший и старший классы: 351, 361, МАТЕМАТИЧЕСКИЙ факультатив
Студенты, интересующиеся прикладной математикой, должны рассмотреть факультативы 225, 241, 325 и 331 на третьем и четвертом курсах.
Примечание. Математика и информатика – это один факультет, но для облегчения доступа они сгруппированы по отдельности и в алфавитном порядке.
ОСНОВНЫЕ СОВЕТНИКИ
Студент, желающий заявить о своей специальности, должен принести руководителю факультета соответствующий бланк декларации об основной деятельности, доступный на странице регистратора. На основании предпочтений и интересов студента, а также текущей нагрузки преподавателей, кафедра назначит одного из преподавателей кафедры в качестве главного консультанта.Студентам рекомендуется встречаться со своим главным консультантом не реже одного раза в семестр перед выбором курса, чтобы обсудить направления обучения и их соответствие будущим целям и планам.
Почести
Почести департамента – это высшая награда, которую Департамент может присудить майору. Специальности, удостоенные ведомственных наград, будут те, кто продемонстрирует широкое владение дисциплиной, а также способность выполнять и представлять высококачественные исследования. Хорошее владение дисциплиной демонстрирует средний балл 3.40 и выше на всех курсах, связанных с основной. Способность проводить высококачественные исследования демонстрируется завершением исследовательского проекта, рассчитанного на год. Этот проект будет характеризоваться независимым и глубоким изучением продвинутой темы, включая поиск литературы, чтение первоисточников и новую формулировку результатов. Наконец, способность представить такие исследования демонстрируется подготовкой дипломной работы, публичной презентацией и успешной защитой работы перед профессорско-преподавательским составом кафедры.Подробные инструкции можно найти на веб-странице департамента.
Курсы
121 Элементарная статистика
Введение в науку о сборе, систематизации, анализе и интерпретации данных. Основное внимание уделяется представлению данных и статистическому обоснованию, основанному на анализе наборов данных. Темы включают изучение методов выборки, наблюдательные и экспериментальные исследования, графические и числовые сводки данных, вероятности, выборочные распределения, проверку значимости, оценку и простую линейную регрессию.Не засчитывается в основные или второстепенные по математике.
Студенты не могут проходить этот курс одновременно с 225. Студенты, получившие оценку 225, не могут пройти этот курс для получения кредита. Предлагается каждый семестр.
Атрибуты: ARCH Area A по выбору, ARCH Area B по выбору, подходит для первого года обучения, ENST Foundations (ESFN), LPPM Empirical Social Analysis, Quantitative Reasoning
151 Introduction to Calculus
Введение в лимиты и производные вместе с обзором полиномиальных, рациональных, тригонометрических, экспоненциальных и логарифмических функций.
Три часа аудиторных и полтора часа лабораторных занятий в неделю. Обязательное условие: ведомственное размещение. Предлагается каждый семестр.
Атрибуты: подходят для первого года обучения, основ ENST (ESFN), количественного мышления
170 Исчисление одной переменной
Изучение функций с действительными значениями, включая трансцендентные функции, пределы, производные и их приложения, определение интеграла Римана , и основная теорема исчисления.
Три часа аудиторных и полтора часа лабораторных занятий в неделю.Обязательное условие: 151 или ведомственное размещение. Предлагается каждый семестр.
Атрибуты: подходят для первого года обучения, основ ENST (ESFN), количественного мышления
171 Многопараметрическое исчисление
Многопараметрическое исчисление, включая параметрические и полярные уравнения, векторы, трехмерную аналитическую геометрию, векторнозначные функции, функции нескольких переменных, частные производные и кратные интегралы. Дополнительные темы, если позволяет время.
Три часа аудиторных и полтора часа лабораторных занятий в неделю.Обязательное условие: 170 или ведомственное размещение. Предлагается каждый семестр.
Атрибуты: Подходит для первого года обучения, Основы ENST (ESFN), Количественное мышление
201 Специальные темы
Темы будут объявлены по мере их предложения.
Условие: разрешение инструктора. Кредит на половину или один курс.
202 Особые темы
Темы будут объявлены при их предложении.
Условие: разрешение инструктора. Кредит на половину или один курс.
211 Основы высшей математики
Введение в фундаментальные математические концепции, используемые в математике и информатике, с упором на написание математических аргументов. В курсе представлены принципы математической логики, множества, функции и методы доказательства.
Предпосылка: 170 или COMP 130 или размещение в отделе. Предлагается каждый семестр.
Атрибуты: Подходит для первого года обучения, Основы ENST (ESFN), Написание в дисциплине
225 Вероятность и статистика I
Введение в основные темы вероятности и статистики.Темы включают дискретные и непрерывные случайные величины, совместное распределение, математическое ожидание, дисперсию, случайную выборку из совокупностей, проверку гипотез и доверительные интервалы.
Необходимое условие: 171. Предлагается каждую осень.
Атрибуты: ARCH Area A Elective, ARCH Area B Elective, ENST Foundations (ESFN)
241 Вычислительная математика
Введение в широкий спектр численных методов для решения математических задач, возникающих в науке и технике.Основное внимание уделяется развитию базового понимания численных алгоритмов, их применимости и ограничений. Темы обычно включают представление чисел с плавающей запятой, источники ошибок, согласование и численную стабильность, поиск корня, решения как линейных, так и нелинейных систем, метод наименьших квадратов, сплайны и полиномиальную интерполяцию, оптимизацию и численное дифференцирование и интегрирование. Также подчеркивается реализация и проверка алгоритмов посредством компьютерного программирования.Предварительный опыт программирования не требуется.
Предпосылка: Завершение двух из следующих курсов: 170, 171, 211 и 270. Этот курс внесен в список COMP 241. Предлагается в четных весенних семестрах.
Атрибуты: Основы ENST (ESFN)
262 Линейная алгебра
Введение в матричную алгебру и абстрактные векторные пространства с упором на написание математических аргументов. Темы включают линейные системы и матрицы, векторные пространства, линейную независимость, собственные значения и собственные векторы.
Необходимое условие: 211 или разрешение инструктора. Предлагается каждый семестр.
Атрибуты: ENST Foundations (ESFN)
270 Интеграция и бесконечные серии
Изучение методов интегрирования, приложений интегральных, элементарных дифференциальных уравнений, а также бесконечных последовательностей и рядов.
Пререквизиты: 171 или ведомственное размещение. Предлагается каждую весну.
Атрибуты: подходят для первого года обучения, основы ENST (ESFN)
271 Дифференциальные уравнения
Элементарные методы решения выбранных типов дифференциальных уравнений; решения систем линейных дифференциальных уравнений с постоянными коэффициентами; и краткое введение в численные методы и нелинейные системы.Особое внимание уделяется приложениям.
Пререквизиты: 171 и 270. Предлагаются в осенних семестрах с нечетными номерами.
Атрибуты: ENST Foundations (ESFN)
301 Special Topics
Темы будут объявлены при их предложении.
Предварительное условие зависит от темы. Кредит на половину или один курс.
302 Особые темы
Темы будут объявлены при их предложении.
Предварительное условие зависит от темы. Кредит на половину или один курс.
311 Прикладная комбинаторика
Продвинутый курс дискретной математики, знакомящий с основными инструментами комбинаторики и их приложениями.В курсе будут рассмотрены три основные проблемы комбинаторики: счет, существование и оптимизация.
Пререквизиты: 211. Предлагаются четные весенние семестры.
314 Вычислимость и сложность
Введение в теорию вычислений, посвященное фундаментальному вопросу о том, какие проблемы могут быть решены с помощью компьютеров, как в принципе, так и с учетом эффективности. Темы могут включать: конечные автоматы, неразрешимые проблемы (такие как проблема остановки), машины Тьюринга, регулярные языки, контекстно-свободные грамматики, универсальные вычисления, классы элементарной сложности, NP-полнота и проблема P vs NP.
Необходимые условия: COMP 132 и MATH 211. Этот курс указан в перекрестном списке как COMP 314. Предлагается каждую весну.
325 Вероятность и статистика II
Продолжение Введение в вероятность и статистику I. Темы включают дополнительные дискретные и непрерывные распределения, условные распределения, дополнительные проверки гипотез, простую линейную регрессию и корреляцию, множественную линейную регрессию, дисперсионный анализ и добротность тестов на пригодность. Специальные темы могут включать непараметрические тесты, нелинейную регрессию и анализ временных рядов.
Предпосылки: 171 и 225. Предлагается каждую весну.
Атрибуты: Основы ENST (ESFN), Quantitative Econ Elective
331 Исследование операций
Введение в детерминированное исследование операций, включая линейное программирование, анализ чувствительности и двойственность. Специальные темы могут включать проблемы транспортировки и назначения, сетевые модели, целочисленное программирование и теорию игр.
Пререквизиты: 262. Этот курс указан в перекрестном списке как COMP 331. Предлагаются осенние семестры с нечетными номерами.
Атрибуты: ENST Foundations (ESFN)
351 Абстрактная алгебра
Введение в аксиоматический формализм с использованием алгебраических структур в качестве парадигм. Темы выбираются из групп, колец и полей.
Необходимое условие: 262. Предлагается каждую весну.
361 Реальный анализ
Теоретическое развитие основных идей и концепций реального анализа. Темы включают изучение действительных чисел, последовательностей, пределов и непрерывности, дифференциации и интеграции. Дополнительные темы включают бесконечные серии, последовательности и серии функций, а также введение в топологию точек.
Необходимые условия: 171, 262 и 270. Предлагается каждую осень.
Атрибуты: Количественный Econ Elective
401 Специальные темы
Темы будут объявлены при их предложении.
Предварительное условие зависит от темы. Кредит на половину или один курс.
402 Особые темы
Темы будут объявлены при их предложении.
Предварительное условие зависит от темы. Кредит на половину или один курс.
472 Комплексный анализ
Вводное изучение функций в комплексной плоскости.Темы включают: комплексные числа и функции, теорию дифференцирования и интегрирования сложных функций; Интегральная теорема Коши; Теорема об остатке.
Пререквизиты: 361 и завершение или одновременная регистрация в 351. Предлагается в весенних семестрах с нечетными номерами.
481 Топология
Элементарное исследование топологических пространств. Темы включают открытые и замкнутые множества, свойство Хаусдорфа, компактность, связность, непрерывность, гомеоморфизмы, пространства произведений, идентификационные пространства, эйлерову характеристику, классификацию пространств и введение в фундаментальную группу.
Пререквизиты: 361 и завершение или одновременная регистрация в 351. Предлагается в четных весенних семестрах.
Первокурсников математики и статистики | Кафедра математики и статистики | Колледж естественных наук и математики
Департамент математики и статистики предлагает курсы математики и статистики первого года обучения, которые соответствуют общеобразовательным и основным требованиям для всех дисциплин бакалавриата в штате Райт.Ниже вы найдете общую информацию об этих курсах. Проконсультируйтесь со своим научным руководителем по поводу конкретных требований к математике и статистике вашей программы на получение степени.
Важные примечания:
- Перед тем, как записаться на их первый курс математики или статистики в штате Райт, вам необходимо будет подтвердить свой уровень размещения.
- Все предварительные требования должны быть выполнены перед регистрацией на любой математический или статистический класс. Вопросов? Электронная почта mathstatprerequisites @ wright.edu.
- Уроки развивающей математики (DEV) предлагаются через Foundation Studies. С любыми вопросами о DEV 0970 Intermediate Algebra обращайтесь к своему научному руководителю. Курсы бизнес-статистики MS 2040 и 2050 преподаются Бизнес-колледжем Радж Соин.
- Список ресурсов кампуса для помощи с курсами математики и статистики можно найти на странице справки по математике.
Общие курсы первого года обучения MTH / STT
MTH 1280 Колледж Алгебра
Основная цель этого курса – подготовить студентов к аналитической геометрии и тригонометрии MTH 1350, прикладному исчислению MTH 2240 или бизнес-расчету MTH 2280.
- Учебник: MTH 1280/1350 College Algebra & Trigonometry with Enhanced Web Assign Access, 4-е издание , Stewart, Cengage (Custom), ISBN: 9781305719781
- Syllabus: Ведомственный (PDF)
MTH 1350 Аналитическая геометрия и тригонометрия
Основная цель этого курса – подготовить студентов к обычной последовательности вычислений MTH 2300/2310/2320.
- Учебник: MTH 1280/1350 College Algebra & Trigonometry with Enhanced Web Assign Access, 4-е издание , Stewart, Cengage (Custom), ISBN: 9781305719781
- Syllabus: Ведомственный (PDF)
MTH 1440 Математика и современный мир с алгеброй Обзор
Это общеобразовательный курс, необходимый для многих нетехнических программ, в основном гуманитарных или исполнительских искусств.Охваченный материал включает в себя все, что есть в MTH 1450, с добавлением обзора элементарных навыков алгебры.
- Описание курса: Обзор начальных навыков алгебры с последующим изучением применения математики для моделирования реальных проблем из поведенческих, вычислительных, управленческих и социальных наук. Включает такие темы, как теория графов, линейное программирование, вероятность, описательная и логическая статистика, системы голосования, теория игр, рост населения, компьютерные алгоритмы, а также коды и хранение данных.
- Учебник: определяет инструктор
- Syllabus: от преподавателя
MTH 1450 Математика и современный мир
Это общеобразовательный курс, необходимый для многих нетехнических программ, в основном гуманитарных или исполнительских искусств.
- Описание курса: Применение математики для моделирования реальных проблем из поведенческих, вычислительных, управленческих и социальных наук.Включает такие темы, как теория графов, линейное программирование, вероятность, описательная и логическая статистика, системы голосования, теория игр, рост населения, компьютерные алгоритмы, а также коды и хранение данных.
- Учебник: определяет преподаватель.
- Syllabus: от преподавателя
MTH 2240 Прикладное исчисление
Этот курс предназначен для студентов, обучающихся по программам естественных наук, от которых не требуется проходить обычные курсы математического анализа.Завершение этого курса не переводит студентов на обычный курс математического анализа автоматически. Он не дает кредитов студентам, уже имеющим кредит на какие-либо регулярные курсы по математике.
- Описание курса: Функции, скорости изменения, пределы, производные алгебраических функций, приложения, включая максимумы и минимумы, экспоненциальные и логарифмические функции, а также неопределенные и определенные интегралы с приложениями.
- Учебник: Расчет для бизнеса, экономики и социальных наук или наук о жизни , 11-е издание, краткая версия, Хоффманн и Брэдли.Макгроу-Хилл, ISBN 9780073532387
- Syllabus: Ведомственный (PDF)
MTH 2280 Бизнес-расчет
Этот курс предназначен для студентов, обучающихся по программам экономики / бизнеса, которым не требуется проходить обычные курсы математического анализа. Завершение этого курса не переводит студентов на обычный курс математического анализа автоматически. Он не дает кредитов студентам, уже имеющим кредит на какие-либо регулярные курсы по математике.
- Описание курса: Функции, скорости изменения, пределы, производные алгебраических функций, приложения, включая максимумы и минимумы, экспоненциальные и логарифмические функции, а также неопределенные и определенные интегралы с приложениями.
- Учебник: Прикладное исчисление , 6-е издание, Хьюз-Халлетт, Глисон, Лок, Флат, и др. , Wiley and Sons, ISBN 9780073532387
- Syllabus: от преподавателя
MTH 2300 Исчисление I
Это первый курс последовательности вычислений для людей, изучающих естественные науки, математику, статистику и инженерные программы.
- Описание курса: Изучает пределы, производную, дифференцирование, приложения производной, первообразные, суммы Римана, определенный интеграл и основную теорему исчисления.
- Учебники: Calculus Volume 1 , OpenStax, Печатное издание: OpenStax ISBN 9781938168024 или XanEdu ISBN 9781506698069, Цифровое издание ISBN 9781947172135
- Syllabus: Ведомственный (PDF)
MTH 2415 Основные понятия по математике для учителей 1
Это первый курс из двух курсов по основам математики, необходимых для учащихся начальных и средних школ педагогических программ в Педагогическом и кадровом колледже.Другой курс – 2435 MTH.
- Описание курса: Обзор математических тем с точки зрения учителей дошкольного и среднего образования. Системы счисления, такие как целые числа, дроби, рациональные числа и десятичные дроби. Поместите значение и основы. Смысл и алгоритмы операций сложения, вычитания, умножения и деления. Введение в геометрию.
- Учебники: Математика для учителей начальной школы с упражнениями , 5-е издание, Бекманн.Высшее образование Пирсона, ISBN 9780134423319
- Syllabus: от преподавателя
MTH 2570 Дискретная математика для вычислений
Это курс, необходимый для программ CS / CEG.
- Описание курса : Дискретная математика, полезная в вычислениях. Упор на математическую индукцию, рекуррентные соотношения, асимптотическое поведение функций и анализ алгоритмов.
- Учебник: Математические структуры для информатики – современный подход к дискретной математике , 7-е издание, Дж.Герстинг, MPS, ISBN: 9781429215107
- Syllabus: от преподавателя
STT 1600 Статистические концепции
Это обзорный курс по основным статистическим концепциям и методам, который в основном требуется для программ по сестринскому делу и психологии. Его нельзя использовать в качестве предварительного условия для других курсов MTH / STT.
- Описание курса: Введение в фундаментальные идеи статистики. Темы включают описательную статистику, вероятность, доверительные интервалы и проверку гипотез, а также основы тестов хи-квадрат, регрессию и корреляцию, а также дисперсионный анализ.
- Учебник: Элементарная статистика с использованием Excel , 5-е издание, Триола, Высшее образование Пирсона, ISBN 9780321851680
- Syllabus: Ведомственный (PDF)
STT 2640 Элементарная статистика
Этот курс охватывает элементарные вероятностные и статистические концепции и методы, которые требуются для многих программ в области естественных наук.
- Описание курса: Численные и графические методы поиска и обобщения важных характеристик данных.Принципы построения экспериментов для сбора данных. Введение в вероятность. Использование пакета статистических вычислений для применения методов и иллюстрации концепций. Доверительные интервалы и введение в проверку гипотез. Приложения для средних, пропорций, двухвыборочных сравнений, таблиц сопряженности, линейной регрессии и дисперсионного анализа. Использование пакета статистических вычислений для применения методов к наборам данных.
- Учебники: Статистика , 13-е издание, McClave, Sincich and Mendenhall, Pearson Higher Education, ISBN 9780134080611
- Syllabus: Ведомственный (PDF)
Математический журнал колледжа | Математическая ассоциация Америки
Впервые опубликовано в 1970 году. The College Mathematics Journal разработан для улучшения обучения в классе и стимулирования мышления относительно математики в бакалавриате.
Он публикует статьи, короткие учебные капсулы, проблемы, решения, обзоры средств массовой информации и другие материалы в пяти выпусках ежегодно. Все они нацелены на учебную программу по математике в колледже с упором на темы, преподаваемые в первые два года обучения.
Доминик Клив, редактор
[email protected]
Для членов и подписчиков MAA: прочитать последние выпуски в Интернете, войдя на портал для участников: Нажмите «Войти» в правом верхнем углу.Не участник? Присоединяйтесь к MAA сегодня!
Лауреаты премии Джорджа Полиа от журнала The College Mathematics Journal с 1977 года.
О математическом журнале колледжа | Отправка на CMJ | Тематический указатель | Указатель проблем и решений | Разместить объявление в CMJ | История CMJ | Редакторы CMJ | Отпечатки | Форма запроса персональных данных GDPR | Контакты
Около
The College Mathematics JournalThe College Mathematics Journal – это международный рецензируемый журнал, публикующий высококачественные материалы по математическим темам, связанным с учебной программой бакалавриата.Мы приветствуем увлекательные работы по новой математике или новые взгляды на известную математику и поощряем исторические перспективы, педагогические заметки и открытые вопросы, где это возможно. Кроме того, The College Mathematics Journal традиционно выпускает ежегодный выпуск, посвященный развлекательной математике.
The College Mathematics Journal принимает следующие типы материалов: статьи, учебные капсулы, доказательства без слов, задачи, решения опубликованных задач и обзор средств массовой информации.Также приветствуются письма в редакцию по любой теме и всевозможные комментарии, критические замечания и предложения, которые помогут сделать CMJ более живым, интересным и информативным.
CMJ Статьи имеют длину не более 12 страниц (включая фотографии и биографии авторов) со средней длиной страницы 6. Дополнительные материалы, такие как компьютерный код, решения для упражнений и длинные доказательства, могут быть доступны на веб-сайте журнала. См. Ниже детали стиля и структуры.
Классная капсула – это небольшая статья (1–3 страницы), которая содержит новое понимание темы, изучаемой на курсах математики на бакалавриате, предпочтительно то, что может быть непосредственно представлено в классе колледжа в качестве эффективной стратегии или инструмента обучения.
Доказательства без слов обеспечивают визуальное понимание математического результата максимум на одной странице.
Задачи и решения направлены на то, чтобы бросить вызов студентам и учителям университетской математики. Они могут обратиться к любой части учебной программы бакалавриата. По возможности, предложенная проблема должна сопровождаться решением, соответствующими ссылками и любыми другими материалами, которые могут быть полезны редакторам. Предлагаемые проблемы следует отправлять на [email protected]. Решения опубликованных задач следует присылать на CMJsolutions @ maa.орг.
Media Highlights – это короткие обзоры (до половины страницы), предназначенные помочь читателям CMJ отслеживать широкий спектр публикаций, веб-материалов, профессиональной деятельности и учебных ресурсов. Читателям предлагается присылать материалы, которые будут интересны коллегам из математического сообщества. Обзоры для СМИ следует присылать по адресу [email protected].
Файлы стилей LaTeX и файлы шаблонов доступны здесь.
Отправка в
CMJПодача статей и капсул для занятий требуется через систему редакционного менеджера CMJ ‘ s.Имя (имена) автора (ов) не должно появляться в файле. Первоначальные заявки в формате pdf или LaTeX можно отправить редактору по адресу www.editorialmanager.com/collmathj/. Отправляя статью в CMJ , автор утверждает, что она ранее не публиковалась и в настоящее время не рассматривается для публикации в другом журнале.
Система редакционного менеджера сообщит автору всю необходимую информацию, касающуюся статьи. Вопросы по оформлению статей можно адресовать редактору по адресу cmj @ maa.орг. Авторам, использующим LaTeX, настоятельно рекомендуется использовать стиль статьи CMJ (доступен здесь) и стандартные среды LaTeX без специального форматирования.
Статьи о проблемах и решениях и основные моменты в СМИ должны быть отправлены редактору соответствующего раздела по адресу, указанному внутри журнала. Приглашаются письма в редакцию по любой теме. Комментарии, критика и предложения по тому, как сделать CMJ более живым, интересным и информативным, приветствуются и должны быть отправлены редактору по адресу cmj @ maa.орг.
«Индекс классификации математических предметов (MSC)» доступен на http://www.ams.org/msc/msc2010.html или в формате pdf на http://www.mathem.pub.ro/dept/MSC -2010.pdf. При отправке рукописи укажите хотя бы одну и не более двух 5-значных классификаций MSC, которые лучше всего описывают вашу статью.
Тематический указатель к
The College Mathematics Journal , 1970–2020Индекс с возможностью поиска (pdf) по названию, автору и связанным предметам учебной программы всех статей, капсул и обзоров книг, опубликованных в The College Mathematics Journal с 1970 года.Поддержкой является Дональд Э. Хули, Университет Блаффтона, Блаффтон, Огайо.
Указатель проблем и решений, 1973–2016 гг.
Список (pdf) в порядке публикации всех задач, напечатанных в The College Mathematics Journal вместе с их решениями (по названию и выпуску). Поддержкой занимается Чарльз К. Кук, Самтер, Южная Каролина.
Отпечатки
Официальным членам MAA предоставляется общее разрешение на некоммерческое воспроизведение в ограниченном количестве отдельных статей (полностью или частично) при условии полной ссылки на источник.Разрешение на перепечатку следует запрашивать у Тейлора и Фрэнсиса. Пожалуйста, воспользуйтесь формой ниже.
Rights & permissions
Контакт
Изменение адреса, запросы на отсутствующие проблемы и другую корреспонденцию по подписке следует направлять по адресу:
Taylor & Francis
Изменение адреса: subscriptions@tandf.

 «Основы тригонометрии»
«Основы тригонометрии»
 05.2012 № 413 «Об утверждении федерального государственного образовательного стандарта среднего (полного) общего образования» (Зарегистрировано в Минюсте России 07.06.2012 № 24480)
05.2012 № 413 «Об утверждении федерального государственного образовательного стандарта среднего (полного) общего образования» (Зарегистрировано в Минюсте России 07.06.2012 № 24480)

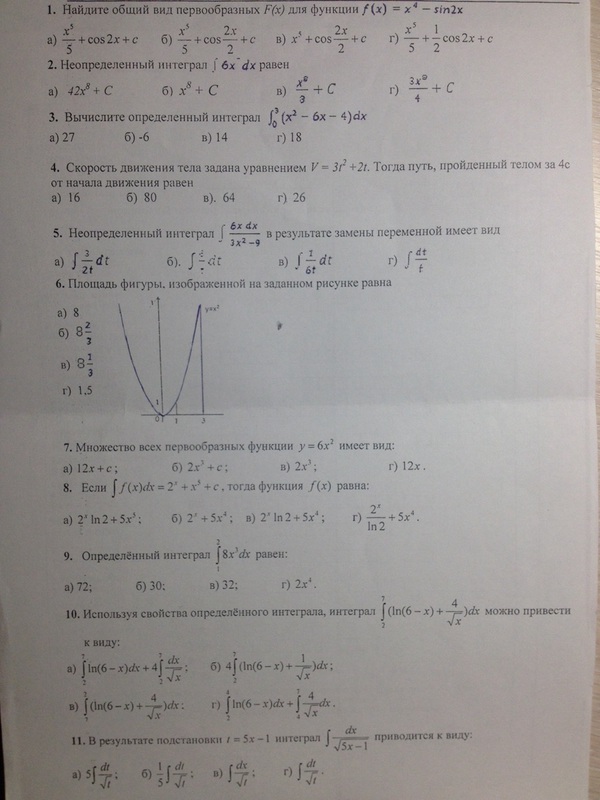
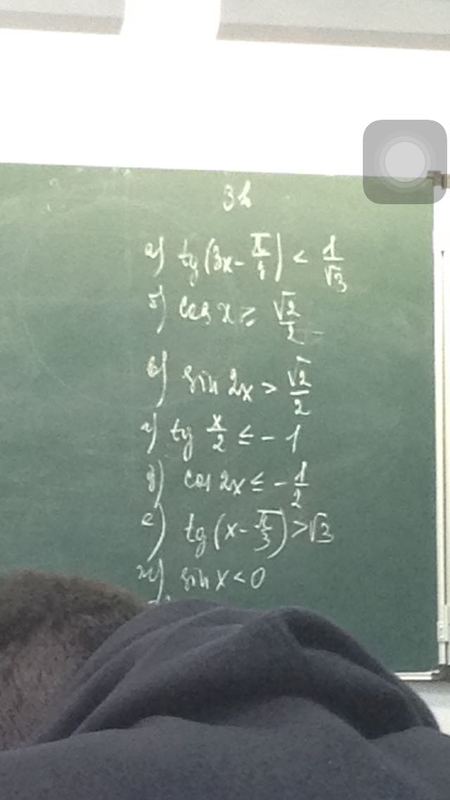





 3. Основы тригонометрии
3. Основы тригонометрии  Зависимость между синусом и косинусом, зависимость между тангенсом и котангенсом.
Зависимость между синусом и косинусом, зависимость между тангенсом и котангенсом.

 Область определения и область значений обратной функции.
Область определения и область значений обратной функции.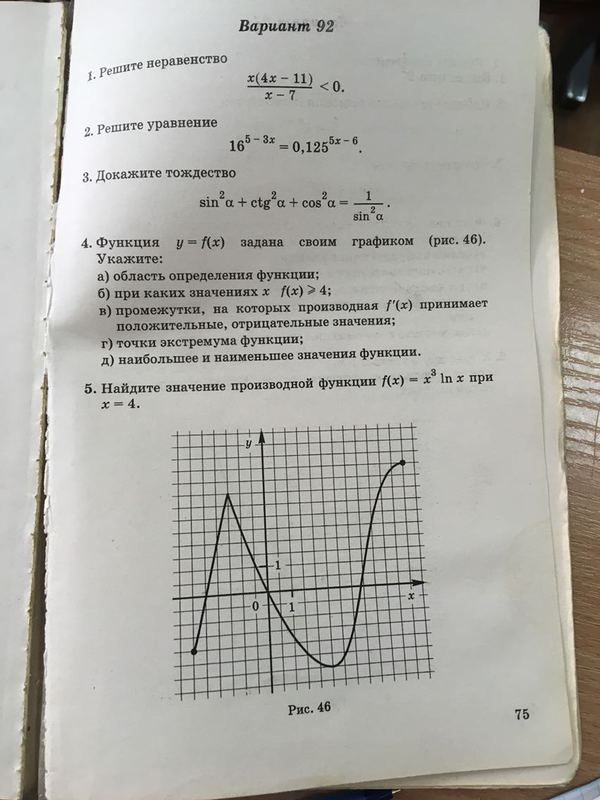
 График обратной функции.
График обратной функции.