Глава 61. Понятие дифференциала функции
Пусть функция дифференцируема в точке , тогда согласно (5.1.4) Лекции 14 приращение В этой точке может быть представлено в виде
. | (5.13.1) |
Первое слагаемое правой части приведенной формулы является бесконечно малой первого порядка, а второе слагаемое – бесконечно малой более высокого порядка, иными словами, величина является главной частью приращения , обусловленного приращением аргумента .
Определение
Дифференциалом функции в точке называется Главная линейная часть Приращения функции в этой точке: .
Поскольку , то эту формулу можно переписать в виде
. | (5.13.2) |
Таким образом, дифференциалом независимой переменной будем называть приращение этой переменной , т. е. соотношение (5.13.
2) принимает вид
. | (5.13.3) |
Из равенства (5.13.3) производную в любой точке можно вычислить как отношение дифференциала к дифференциалу независимой переменной :
. | (5.13.4) |
Тогда равенство (5.13.1) можно переписать в виде
, | (5.13.5) |
Что полностью соответствует определению дифференциала функции.
Пример
Найти приращение и дифференциал функции в точке и .
Решение
Приращение функции есть
Дифференциал функции – . При имеем 3,72 и . Различие между ними составляет всего 0,02 или 0,5%.
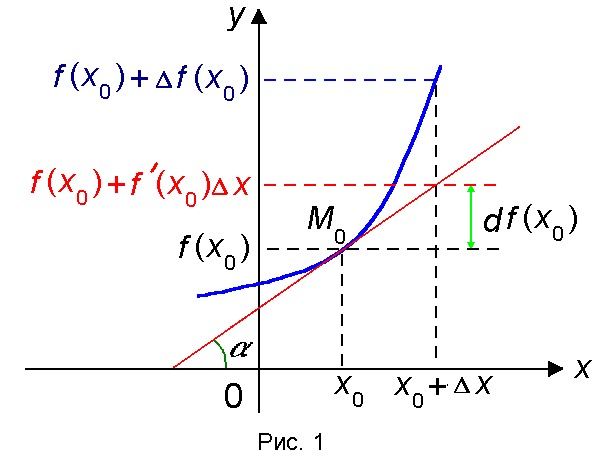
Дифференциал функции имеет четкий Геометрический смысл (рис 5.13.1).
Пусть точка на графике функции соответствует значению аргумента , точка – значению аргумента , – касательная к кривой в точке , – угол между касательной и осью .
Тогда – приращение аргумента, – соответствующее приращение функции. Рассматривая треугольник , получаем , т. е. это главная по порядку величины и линейная относительно нее часть приращения функции . Второе слагаемое в уравнении (5.13.5) более высокого порядка малости соответствует отрезку .
Рис. 5.13.1
Свойства дифференциала
Свойства дифференциала в основном аналогичны свойствам производной.
1. .
2. .
3. .
4. .
5. .
Докажем инвариантность формы первого дифференциала, т. е. универсальность и применимость этой формулы в том случае, когда аргумент сам является функцией другой переменной .
Пусть функция дифференцируема в точке , а сам аргумент является дифференцируемой функцией аргумента , т. е. . Тогда сложная функция аргумента . В силу теоремы о производной сложной функции . Поскольку является независимой переменной, то по форме (5.13.3) записи дифференциала для функции получаем
(5. |
13.6)Аналогично для дифференциала функции имеем . Подставляя это выражение в формулу (5.13.6) получаем , что и требовалось доказать.
61.1. Упражнения
Найти производные функций, пользуясь непосредственно определением производной:
1. | 2. | ||
3. | 4. | ||
5. | 6. |
Определить тангенсы углов наклона касательных к кривым:
7. | 8. | ||
9. | 10. |
Найти производные функций:
11. | 12. | ||
13. | 14. | ||
15. | 16. | ||
17. | 18. | ||
19. | 20. | ||
21. | 22. | ||
23. | 24. | ||
25. | 26. | ||
27. | 28. | ||
29. | 30. | ||
31. | 32. | ||
33. | 34. | ||
35. | 36. | ||
37. | 38. | ||
39. | 40. | ||
41. | 42. | ||
43. | 44. | ||
45. | 46. | ||
47. | 48. | ||
49. | 50. | ||
51. | 52. | ||
53. | 54. | ||
55. | 56. | ||
57. | 58. | ||
59. | 60. | ||
61. | 62. | ||
63. | 64. | ||
65. | 66. | ||
67. | 68. | ||
69. | 70. | ||
71. | 72. | ||
73. | 74. | ||
75. | 76. | ||
77. | 78. | ||
79. | 80. | ||
81. | 82. | ||
83. | 84. | ||
85. | 86. | ||
87. | 88. | ||
89. | 90. | ||
91. | 92. | ||
93. | 94. | ||
95. | 96. | ||
97. | 98. | ||
99. | 100. | ||
101. | 102. | ||
103. | 104. | ||
105. | 106. | ||
107. | 108. | ||
109. | 110. |
Найти производные функций, предварительно логарифмируя эти функции:
111. | |||
113. | 114. |
Дифференцирование неявных функций
Найти dy/dx,
115. | 116. | ||
117. | 118. | ||
119. | 120. | ||
121. | 122. | ||
123. | 124. |
Вычислить следующие пределы:
125. | 126. | ||
127. | 128. |
Найти экстремумы функций:
129. | 130. | ||
131. | 132. |
Найти асимптоты следующих кривых:
133. | 134. | ||
135. | 136. |
| < Предыдущая | Следующая > |
|---|
Производная как смысл жизни или что такое дифференциал(d) / Хабр
Пролог:
Эта одна из статей серии “Производная как смысл жизни”, сначала я хотел сделать одну огромную статью про почти все темы по дифференцированию, но я передумал и сделаю несколько статей, возможно так даже будет легче для людей которые пытаются найти конкретную для себя тему.
Начало
Для начала лучше ознакомиться со статьей о самой прозводной(скоро будет). Ну если вы ознакомились, или уже были ознакомлены то идем дальше.
Как мы уже знаем формула записи производной выглядит так:
-напоминаю, что Δx – приращение аргумента, Δy – приращение функции.
Мы должны понимать, что если мы уберем предел, то к f'(x) прибавиться коофициент, я ее называю “неточность”.
Так же вполне логично, что при Δx->0, β->0, так как чем меньше мы делаем разницу между x и x₀, тем меньше значение “неточности”(в статье о производной об этом подробнее рассказано).
Теперь выразим из этого равенства приращение функции(Δy):
И на этом следует пока остановиться и рассмотреть график.
Смотрим дифференциалу в лицо
Расмотрим такой график:
Как мы знаем производная в точке равняется значению тангенса угла в этой точке, то есть f'(x)=tg(α). Так что давайте обозначим производную, ну и приращения которыми она ограничена.
Как мы видим приращение функции(Δy) как бы разделено на две части: BC и CD.
И ведь по-сути нам ведь интересна именно та часть, которая показывает на сколько изменился у относительно касательной – то есть BC, а CD – это лишь та “погрешность” которая нам не особо интересна, поэтому введем понятие дифференциала:
Дифференциал(d) – это линейная часть приращения функции.
Дифференциал функции(dy) – это главная линейная часть приращения функции.
Зная это введем обозначение на графике:
Вернемся к равенству
BD = Δy и мы знаем, что BD = BC + CD, а значит Δy = BC + CD, где BC мы назвали главной линейной частью приращения функции(dy), следовательно Δy = dy + βΔx.
Из формулы мы понимаем, что dy=f'(x)Δx.
Хорошо, мы определили чему равен дифференциал функции, а что же тогда является дифференциалом независимой пременной функции(аргумента).
Графически мы видим, что Δx никак не разделена касательной, то есть Δx это полное приращение функции, а значит dx = Δx.
Так же мы можем найти по формуле: dx = (x)’Δx = 1*Δx = Δx
И зная, что dy = f'(x)dx, мы можем выразить производную: f'(x)=dy/dx.
Немного пределов
Добавим с левой части и с правой предел
Тогда:
В самом начале мы сказали, что если β->0, то Δx->0 и наборот, а значит:
Зная, что f'(x)Δx = dy, мы делаем вывод, что:
Тогда так же мы можем сказать, что дифференциал функции – это приращения функции у которой приращение аргумента стремиться к нулю, ну и это следуется из того же графика.
В свою очередь dx по прежнему Δx
исчисление – Почему дифференциальные уравнения называются дифференциальными уравнениями?
спросил
Изменено 4 года, 7 месяцев назад
Просмотрено 2к раз
$\begingroup$
Почему дифференциальные уравнения называются дифференциальными уравнениями?
- исчисление
- терминология
- обыкновенные дифференциальные уравнения
$\endgroup$
$\begingroup$
Потому что это уравнения (где переменная является функцией, а не числом), которые включают функцию и ее производные (функции, полученные путем ее дифференцирования).
$\endgroup$
$\begingroup$
Почему дифференциальное уравнение называют дифференциальным уравнением?
Вот ответ в концептуальной форме.
Вы привыкли видеть кривую, описываемую непосредственно как функцию y=f(x).
Но каждая точка на кривой также имеет линейный наклон. если ты
зная наклон в каждой точке кривой (и в начальной точке), вы можете
воспроизвести кривую. Представьте, что все линейные склоны образуют
конверт. Теперь, если вы знаете наклон кривой в каждой точке, то вы
можно составить уравнение, связывающее дельту x в точке с дельтой y в точке
точка, дельта y = наклон (x) * дельта x. Дельта x и дельта y
являются дифференциалами, и, таким образом, у вас есть уравнение, связывающее
дифференциал по x в точке к дифференциалу по y в точке –
то есть дифференциальное уравнение! Обычно это уравнение
переставляется как дельта y / дельта x = наклон (x), или в пределе,
dy/dx = наклон(x) или dy/dx = f(x), где f(x) — наклон.
Теперь решая дифференциальное уравнение
означает нахождение исходной кривой с заданным наклоном
в каждой точке. Это делается путем интеграции. В конечном приближении
с начальной точкой нуля, это будет, например,
f (x) = дельта x * наклон (x1) + дельта x * наклон (x2) + дельта x * наклон (x3)…
и уменьшение дельты x до нуля дает лучшее приближение.
Но эта формула — просто интегрирование.
Интегрирование находит площадь под кривой, но площадь
под кривой по своей сути является решением
дифференциальное уравнение. Интеграция по своей сути решает некоторые
дифференциальное уравнение.
$\endgroup$
0
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
9{2}$. Производная, обычно обозначаемая как $f'(x)$ или $\mathrm{d}f/\mathrm{d}x$, представляет собой функцию, описывающую градиент функции $f$. Чтобы пояснить, мы говорим, что градиент $f$ в точке $x$ — это наклон касательной к $f$ в точке $\big(x, f(x)\big)$. Например, производная от $f$ равна
$$
f ‘(x) = \ frac {\ mathrm {d} f} {\ mathrm {d} x} = 2x.
$$
Это говорит нам о том, что в точке $x = 3$ градиент прямой, касательной к $f$ в точке $(3, 9)$, равен $6$, и так далее. Обратите внимание, что аддитивная константа не изменяет градиент касательных линий, она только изменяет, насколько высок или низок график, поэтому имеет смысл, что она не появится в производной. Это имеет смысл, поскольку $\mathrm{d}f$ обозначает небольшое приращение $f$, а $\mathrm{d}x$ обозначает небольшое приращение $x$, так что $\mathrm{d}f /\mathrm{d}x$ можно понимать как отношение того, насколько $f$ увеличивается/уменьшается при небольшом увеличении $x$.
Чем больше число, тем круче изменяется $f$ по отношению к $x$, так что сам график будет крутым. В этом случае мы имеем, что $\mathrm{d}f/\mathrm{d}x = 2x$, так что $\mathrm{d}f = 2x \mathrm{d}x$. Это как раз та функция, которая сообщает нам, насколько функция $f$ изменяется при изменении $x$. 9{2}$, где $P$ — прибыль, полученная от некоторой переменной $x$. Переменная $x$ может представлять количество произведенных единиц продукта. Уравнение, подобное этому, является естественным в данном случае — построив график, мы видим, что если $x$ слишком мало, то прибыль уменьшается, и аналогично, если $x$ слишком велико, прибыль также уменьшается. Другими словами: если производится слишком мало продукта, то предложения недостаточно для удовлетворения спроса, и прибыль не максимизируется; точно так же, если производится слишком много продукта, спрос на продукт недостаточен для того, чтобы сделать его прибыльным. Ясно, что существует некоторое значение $x$, которое соответствует производству именно того количества продукта, которое необходимо для удовлетворения спроса, но не слишком много, и, глядя на график, довольно легко получить приблизительную оценку этого значения.
Дифференциалы становятся полезными для определения значения $x$ без необходимости построения графика функции. В этом примере оптимальное значение соответствует вершине пика графика. Градиент касательной в этой точке явно равен нулю, поэтому мы находим значение $x$, решая $$ \ гидроразрыва {\ mathrm {d} P} {\ mathrm {d} x} = 0. $$ Мы видим, что $$ \ гидроразрыва {\ mathrm {d} P} {\ mathrm {d} x} = 5 – 2x = 0 $$ дает значение $x = 2,5$. Это означает, что при $x = 2,5$ функция $P$ максимальна.
Дифференциалы
не другой способ выражения функции Наличие только производной функции обычно не так полезно, как наличие самой функции (поскольку, если у вас есть функция, обычно легко вычислить ее производную), и именно поэтому важна теория решений дифференциальных уравнений. В физике бывает много ситуаций, когда известно только дифференциальное уравнение, и цель состоит в том, чтобы найти функцию, удовлетворяющую дифференциальному уравнению. В общем случае нельзя записать функцию через ее производную — снова рассмотрим $f(x) = x^{2}$, производная которой равна $f'(x) = 2x$, а дифференциал равен
$$
\mathrm{d}f = 2x \mathrm{d}x.