Формула ускорения вектора – Ускорение — Википедия - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Ускорение

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).

Среднее ускорение

Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

где – вектор ускорения.

Направление вектора ускорения совпадает с направлением изменения скорости Δ = – ₀ (здесь ₀ – это начальная скорость, то есть скорость, с которой тело начало ускоряться).

В момент времени t1 (см. рис 1.8) тело имеет скорость ₀. В момент времени t2 тело имеет скорость . Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = – ₀. Тогда определить ускорение можно так:

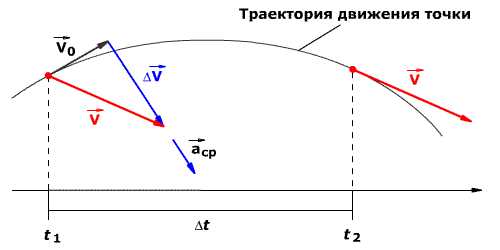
Рис. 1.8. Среднее ускорение.

В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с², то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

Направление ускорения также совпадает с направлением изменения скорости Δ при очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями а_Х, a_Y, a_Z).

При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

v₂ > v₁

а направление вектора ускорения совпадает с вектором скорости ₂.

Если скорость тела по модулю уменьшается, то есть


v₂1

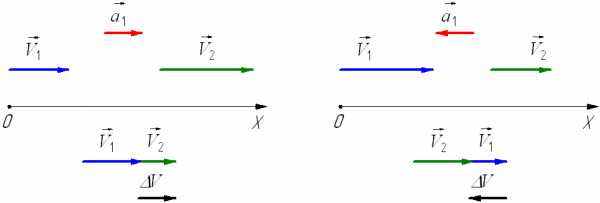
то направление вектора ускорения противоположно направлению вектора скорости ₂. Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а

Рис. 1.9. Мгновенное ускорение.

При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное ускорение

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения _τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой

n. Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов:

 = _τ + _n

www.av-physics.narod.ru

Механическое движение. Виды мех. Движения.

Мех. движение – это изменение с течением времени взаимного расположения тел или их частей. Виды движения: 1). Поступательное – движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. 2). Вращательное – движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. 3). Колебательное – движение характеризующееся некоторой степенью повторяемости во времени.

Система отсчета. Скорость и ускорение как производные радиус-вектора. Нормальная и тангенциальная составляющая вектора ускорения.

Система отсчёта — это совокупность тела отсчёта, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел. 1. Скорость и ускорение материальной точки как производные радиуса-вектора по времени. Положение точки определяется пространственными параметрами: радиус-вектором, декартовыми координатами, дуговой координатой и др. Скорость точки является пространственно – временным параметром. Скоростью точки называется кинематический параметр, характеризующий быстроту изменения положения точки в системе отсчета с течением времени. v=S/t v=v

0+a*t a=(v-v₀)/t Тангенциальное или касательное ускорение (обозначается иногда и т. д., в зависимости от того, какой буквой в конкретном тексте принято обозначать ускорение) направлено по касательной к траектории. Является составляющей вектора ускорения коллинеарной вектору мгновенной скорости. Характеризует изменение скорости по модулю.

Центростремительное или нормальное ускорение (также обозначается иногда и т. д.) возникает (не равно нулю) всегда при движении точки не только по окружности, но и по любой траектории с ненулевой кривизной. Является составляющей вектора ускорения перпендикулярной вектору мгновенной скорости. Характеризует изменение скорости по направлению. Вектор нормального ускорения всегда направлен к мгновенной оси вращения,

а модуль равен

где ω — угловая скорость относительно центра вращения, а r — радиус окружности.

Кроме этих двух компонент, используется также понятие угловое ускорение, показывающее, на сколько изменилась угловая скорость за единицу времени, и, аналогично линейному ускорению, вычисляемое следующим образом:

Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и угловой скорости сонаправлены (или хотя бы их скалярное произведение положительно), значение скорости растёт, и наоборот.

В частном случае равномерного движения по окружности векторы углового ускорения и тангенциального ускорения равны нулю, а центростремительное ускорение постоянно по модулю.

Движение материальной точки по окружности кругово́е движе́ние — это вращательное движение материальной точки или тела, когда ось вращения в выбранной системе отсчёта неподвижна и не проходит через центр тела. В этом случае траектория точки или тела является кругом, круговой орбитой. Оно может быть равномерным (с постоянной угловой скоростью) или неравномерным (с переменной угловой скоростью) Для движения по кругу радиуса R длина окружности будет C = 2π R. Если период вращения есть T, то угловая скорость вращения ω будет равна:

Скорость движения объекта равна

Угол поворота θ за время t равен:

studfiles.net

Теорема о геометрическом сложении векторов ускорений.

3.11. Теорема.Вектор ускорения произвольной точки В плоской фигуры в плоско – параллельном движении равен геометрической сумме вектора ускорения точки А , принятой за полюс, и вектора ускорения , которое точка В приобретает при вращении плоской фигуры относительно полюса А (рис.3.19):

(3.24)

Доказательство: По теореме о сложении векторов скоростей (3.7) вектор скорости произвольной точки плоской фигуры . Продифференцируем последнее равенство по времени и получим:

= + .

Здесь – вектор ускорения точки В. – вектор ускорения полюса А. – вектор ускорения точки В, которое оно приобретает от вращения фигуры (другими словами, отрезка АВ) относительно полюса А. Окончательно, вектор ускорения точки В вычисляется по формуле . Что и требовалось доказать.

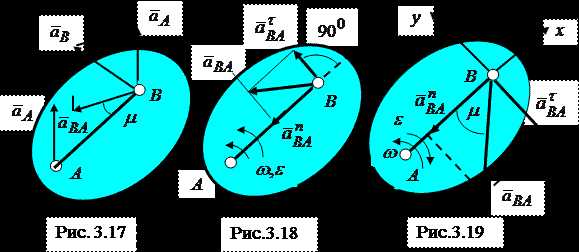
Геометрическая интерпретация формулы (3.24) для одного из возможных вариантов движения фигуры представлена на рис. 3.17.

В общем случае полюс А может двигаться по любой траектории – прямолинейной или криволинейной. Отрезок АВ вращается, поэтому траектория точки В – кривая линия. Следовательно, вектор всегда можно представить в виде суммы его касательной и нормальной составляющих , что бывает удобно в практических расчетах (рис.3.18, рис.3.19). При этом (3.24) принимает вид:

+ (3.25)

Величины векторов вычисляются по формулам теории вращательного движения относительно неподвижной оси :

, , (3.26)

Где – угловая скорость и угловое ускорение плоской фигуры соответственно. С учетом (3.26) имеем:

. (3.27)

Здесь и m – модуль и угол отклонения вектора от отрезка соответственно.

Вектор , независимо от направления вращения фигуры (рис. 3.18, рис. 3.19), направлен от точки В к мгновенной оси вращения, проходящей через точку А. Другими словами, вектор всегда направлен от точки В к точке А, принятой за полюс.

Направление вектора (рис. 3.18, рис. 3.19) соответствует направлению дуговой стрелки углового ускорения и не зависит от направления вращения фигуры, то есть не зависит от направления дуговой стрелки .

Если точка А, которую решено принять за полюс, движется по известной криволинейной траектории, то и вектор можно разложить на касательную и нормальную составляющие , а формула (3.25) примет вид:

(3.28)

И последнее, если и точка В движется по известной криволинейной траектории, то формулу (3.25) можно будет записать в самом общем виде:

(3.29)

Уравнения (3.24) – (3.29) позволяют вычислить вектор ускорения произвольной точки В плоской фигуры. При этом предполагается, что все другие векторы, входящие в эти уравнения, или известны заранее, или могут быть вычислены по исходным данным задачи. Но совершенно очевидно, что эти уравнения справедливы и для случая, когда вектор известен. В этом случае они позволяют найти любой другой один вектор по известным остальным векторам (из одного уравнения можно найти одно неизвестное).

2. Метод проекций для определения ускорений

С методом проекций мы уже сталкивались при обсуждении методов определения скоростей. С математической стороны здесь все делается так же, но применительно к другим механическим уравнениям. Введем на плоскости некоторую прямоугольную систему координат . Начало координат О, и направление осей выбираются произвольно. Спроецировав любое из уравнений (3.24)-(3.29) на эти оси, получают соответствующие уравнения метода проекций. Например, векторное уравнение (3.29) заменится двумя скалярными уравнениями:

, . (3.30)

Все входящие в эти уравнения величины – это проекции соответствующих векторов. Из системы уравнений (3.30) могут быть определены любые две входящие в них величины. Остальные величины должны быть известны заранее. Если, например, из системы (3.30) определены проекции вектора ускорения точки В – , то модуль вектора ускорения находится по формуле:

= . (3.31)

Направление вектора в принятой системе координат можно установить по проекциям . Выбор осей координат не влияет на конечный результат, но может существенно облегчить или затруднить вычисления

Пример 3.11. Стержень движется в плоскости. В данный момент времени точки имеет ускорение , угловая скорость стержня , угловое ускорение . Направление угловой скорости и углового ускорения показаны дуговыми стрелками на рисунке 1 к примеру. Определить величину ускорения точки стержня, если длина его , а модуль вектора ускорения .

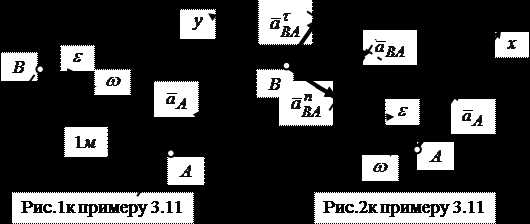
Решение.Стержень в данный момент времени вращается замедленно, так как и имеют противоположные направления. За полюс примем точку , ускорение которой известно. Это единственная причина для выбора полюса в точке . По (3.25) + . Это уравнение позволяет определиться с направлением соответствующих векторов ускорений на плоскости в данный момент времени. Направление вектора дано в условии примера. Направление вектора определено по направлению . Вектор нормального ускорения всегда направлен к выбранному полюсу. Модули двух последних векторов вычисляются по формулам (3.17). , . по условию примера. Далее воспользуемся методом проекций. Введем оси координат, показанные на рисунке 2 к примеру, и спроецируем векторное уравнение (3.25) на эти оси. Получим:

, , (*)

где , = , , , , . Удачный выбор осей координат существенно облегчил нахождение проекций, многие из них равны нулю. Окончательно из (*) получим , , Ответ:

infopedia.su
Векторные формулы для скоростей и ускорений точек тела — Мегаобучалка
Выразим скорость, касательное, нормальное и полное ускорения точки тела в векторной форме. Скорость точки по модулю и направлению можно представить векторным произведением
, (65)
где – радиус-вектор точки , проведенный из произвольной точки оси вращения , например точки (рис. 30). Выражение (65) называется векторной формулой Эйлера. Убедимся в справедливости этой формулы проверкой. Действительно, вектор перпендикулярен плоскости, в которой расположены векторы, входящие в векторное произведение. По направлению он параллелен скорости , направленной по касательной к окружности. Модуль векторного произведения:
,
так как . Таким образом, векторное произведение по модулю и направлению определяет скорость точки. Следует только считать этот вектор приложенным в точке ; он не зависит от точки приложения вектора на оси вращения, а также точки оси, в которой помещено начало вектора . В частности, в качестве радиуса-вектора можно использовать вектор , направив его из точки в точку . Из определения ускорения и векторной формулы Эйлера имеем:
Учитывая, что , , получаем
. (66)
Первое слагаемое в (66) является касательным ускорением, а второе – нормальным, т. е.
, . (67)
В справедливости (67) убеждаемся вычислением их правых частей. Имеем
,
что совпадает с касательным ускорением. Направление вектора параллельно вектору касательного ускорения (рис. 31). Для векторного произведения имеем
,
так как векторы и взаимно перпендикулярны. Направление вектора параллельно вектору нормального ускорения и направлено от точки к оси вращения, поэтому
,
если условиться вектор направлять от оси вращения. Справедливость формул (67) установлена.
Из определения скорости точки известно, что
,
где – радиус-вектор точки, проведенный из любой неподвижной точки, в частности из любой точки на оси вращения тела, вращающегося вокруг неподвижной оси. Но скорость точки при вращательном движении тела определяется по векторной формуле Эйлера
.
Сопоставление двух формул для скорости точки дает формулу для вычисления производной по времени от вектора :

. (68)
В этой формуле вектор имеет постоянный модуль, так как соединяет все время две точки твердого тела. Вектор , являясь угловой скоростью вращения твердого тела вокруг неподвижной оси, выполняет также роль угловой скорости вращения вектора , жестко скрепленного с телом.
Формула (68) остается справедливой также для вектора , начало которого находится в любой точке тела, а не только на оси вращения. По этой формуле вычисляется производная по времени от любого вектора, величина которого постоянна.
megaobuchalka.ru
Будь на волне! Будь с нами!

Полное ускорение и его компоненты. Ускорение тангенциальное и нормальное ускорение. Формулы и пример решения задачи

От DA
13.12.2018 18:31
В кинематике для однозначного определения характеристик движения тела в любой точке траектории необходимо знать его скорость и ускорение. Зависимость от времени этих величин предоставляет всю необходимую информацию для вычисления пройденного телом пути. Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.
В физике
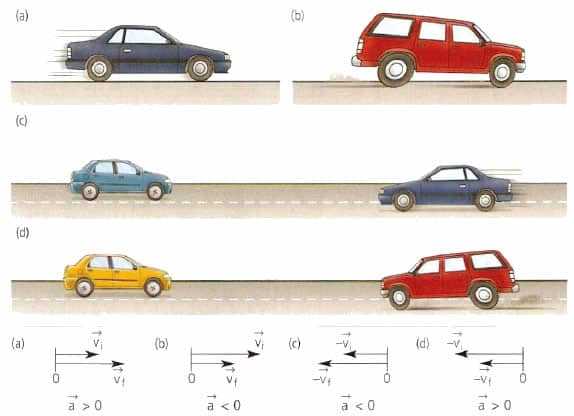
Прежде чем рассматривать для механического движения ускорение нормальное и тангенциальное ускорение, познакомимся с самим физическим понятием. Определение ускорения является достаточно простым. В физике под ним понимают характеристику изменения скорости. Последняя является векторной величиной, определяющей быстроту изменения координат движущегося объекта в пространстве. Скорость измеряется в метрах в секунду (расстояние, пройденное за единицу времени). Если ее обозначить символом v¯, тогда математическое определение ускорения a¯ будет выглядеть так:
a¯ = dv¯/dt
Это равенство определяет так называемое полное мгновенное ускорение. Мгновенным оно называется потому, что характеризует изменение скорости лишь в данный момент времени.
Если движение является равноускоренным, то есть в течение длительного времени ускорение не меняет своего модуля и направления, тогда можно записать следующую формулу для его определения:
a¯ = Δv¯/Δt
Где Δt>>dt. Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.
Ускорение измеряется в системе СИ в метрах в квадратную секунду (м/с2).
Траектория движения и компоненты полного ускорения
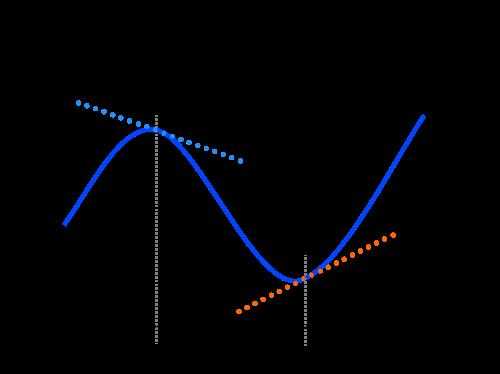
Чаще всего тела в природе движутся по кривым траекториям. Примерами такого перемещения являются: вращение по своим орбитам планет, параболическое падение камня на землю, поворот автомобиля. В случае криволинейной траектории в любой момент времени скорость направлена по касательной к рассматриваемой точке траектории. Как при этом направлено ускорение?
Чтобы ответить на поставленный выше вопрос, запишем скорость тела в следующей форме:
v¯ = v*ut¯
Здесь ut¯ – вектор скорости единичный, индекс t означает, что он направлен по касательной к траектории (тангенциальная компонента). Символом v обозначен модуль скорости v¯.
Теперь, следуя определению ускорения, можно провести дифференцирование скорости по времени, имеем:
a¯ = dv¯/dt = dv/dt*ut¯ + v*d(ut¯)/dt
Таким образом, полное ускорение a¯ представляет собой векторную сумму двух компонент. Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.
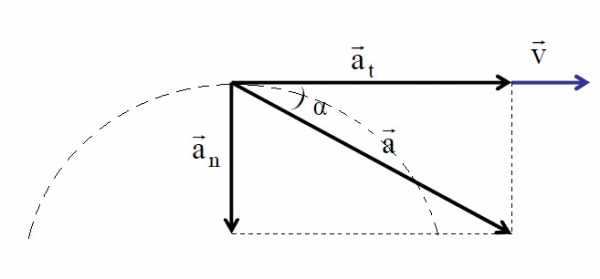
Ускорение тангенциальное
Запишем еще раз формулу для этой компоненты полного ускорения:
at¯ = dv/dt*ut¯
Это выражение позволяет описать свойства величины at¯:
Она направлена точно так же, как и сама скорость или противоположно ей, то есть по касательной к траектории. Об этом свидетельствует элементарный вектор ut¯.
Она характеризует изменение скорости по абсолютной величине, что отражает множитель dv/dt.
Эти свойства позволяют сделать важный вывод: для прямолинейного движения полное и тангенциальное ускорения – это одна и та же величина. В случае криволинейного перемещения полное ускорение всегда больше по модулю, чем тангенциальное. Когда рассматривают физические задачи на прямолинейное равноускоренное движение, то ведут речь именно об этой компоненте ускорения.
Ускорение нормальное
Рассматривая тему скорости, ускорения тангенциального и ускорения нормального, дадим характеристику последней величине. Запишем формулу для нее:
an¯ = v*d(ut¯)/dt = v*d(ut¯)/dL*dL/dt
Чтобы записать явно правую часть равенства, воспользуемся следующими соотношениями:
dL/dt = v;d(ut¯)/dL = 1/r
Здесь dL – это пройденный телом путь за промежуток времени dt, r – радиус кривизны траектории. Первое выражение соответствует определению скорости, второе равенство следует из геометрических соображений. Пользуясь этими формулами, получаем конечное выражение для нормального ускорения:
an¯ = v2/r
То есть величина an¯ не зависит от изменения скорости, как тангенциальная компонента, а определяется исключительно ее модулем. Нормальное ускорение вдоль нормали к данному участку траектории направлено, то есть к центру кривизны. Например, во время движения по окружности вектор an¯ направлен к ее центру, поэтому нормальное ускорение называют часто центростремительным.
Если за изменение абсолютной величины скорости ответственно ускорение тангенциальное, то нормальная компонента ответственна за изменение вектора скорости, то есть она определяет траекторию перемещения тела.
Ускорение полное, нормальное и тангенциальное
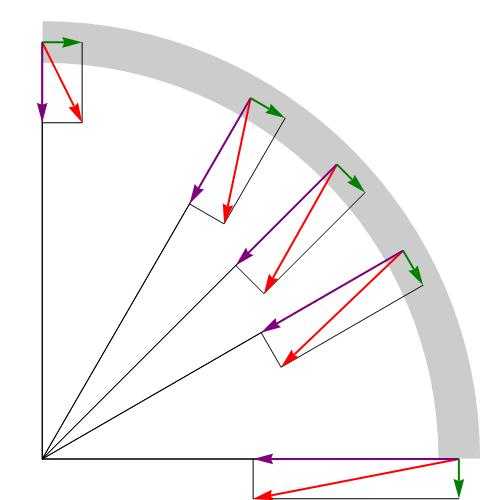
Разобравшись с понятием ускорения и с его компонентами, приведем теперь формулу, которая позволяет определить полное ускорение. Поскольку рассмотренные компоненты направлены под углом 90 o друг к другу, то для определения абсолютной величины их векторной суммы можно использовать теорему Пифагора. Формула для полного ускорения имеет вид:
a = √(at2 + an2)
Направление величины a¯ можно определить по отношению к вектору любой из компонент. Например, угол между a¯ и an¯ вычисляется так:
θ = arctg(at/an)
Учитывая приведенную выше формулу для модуля a¯, можно сделать вывод: при равномерном движении по окружности полное ускорение совпадает с центростремительным.
Решение задачи
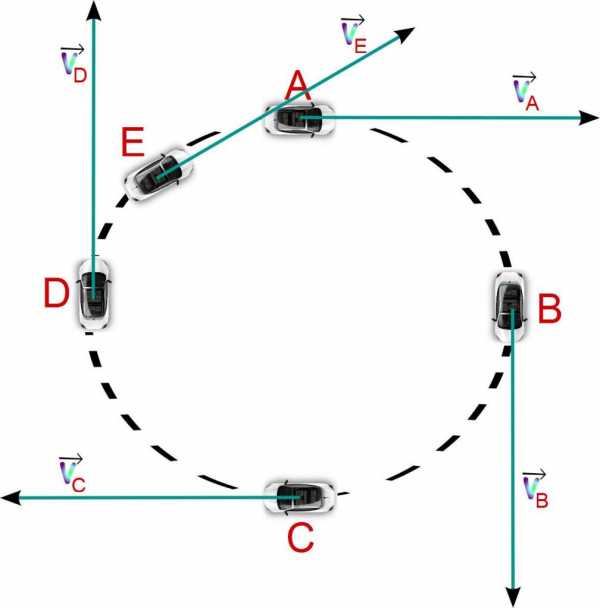
Пусть тело движется по окружности радиусом 1 метр. Известно, что его скорость изменяется по следующему закону:
v = 2*t2 + 3*t
Необходимо определить ускорение тангенциальное и нормальное ускорение в момент t = 4 секунды.
Для тангенциального имеем:
at = dv/dt = 4*t + 3 = 19 м/с2
Для того чтобы найти модуль ускорения нормального, сначала следует вычислить значение скорости в заданный момент времени. Имеем:
v = 2*42 + 3*4 = 44 м/с
Теперь можно воспользоваться формулой для an:
an = v2/r = 442/1 = 1936 м/с2
Таким образом, мы определили все величины, которые требовалось найти для решения задачи.
www.navolne.life
Векторные формулы для скоростей и ускорений точек тела

Скорость точки по модулю и направлению можно определить по формуле Эйлера векторным произведением:

(3.28)

где – радиус-вектор точки М, проведенной из произвольной точки оси вращения Oz, например точки О (рис. 3.10). В справедливости формулы (3.28) можно убедится определив по ней модуль скорости.

Из определения ускорения и векторной формулы Эйлера имеем:
(3.29)
Касательное и нормальное ускорения также можно записать в виде:

где – соответственно ортогональные единичные векторы (см. выше 3.1.2).

Рассмотрим конкретные задачи.

Задача 3.1Ротор мотора в период пуска имеет угловое ускорение e = 2p с^–2. Определить скорость, касательное, нормальное и полное ускорения точки М
(рис. 3.11), лежащей на ободе ротора в момент t = 3 c. Диаметр ротора d = 0,2 м.

Решение

Угловую скорость ротора в момент времени t = 3 c находим, пользуясь формулой (3.25):

w = w_о + e×t

Здесь и далее учитываем, что вращение ротора равноускоренное, начальный угол поворота j_о= 0 и начальная угловая скорость w_о= 0, так как ротор начинает вращаться из состояния покоя. Тогда w = e×t = 2p×3 = 6p с^–2. Для определения положения точки на ободе ротора вычислим также по формуле (3.24) угол поворота По формулам (3.27) определим соответственно скорость, касательное, нормальное и полное ускорение точки М.

Векторы в момент времени t = 3 c изображены на рисунке 3.11.

Задача 3.2В период разгона маховика закон его вращения характеризуется . Определить скорость и ускорение точки, находящейся на расстоянии
R = 0,8 м от оси вращения в тот момент, когда касательное и нормальное ускорения точки равны.

Решение

По формулам (3.21) и (3.22) определяем угловую скорость и угловое ускорение маховика.

Касательное и нормальное ускорения соответственно равны a_t = e×R, a_n = w²R. По условию задачи в момент времени t = t₁a_t = a_n. Поэтому в этот момент e = w² или откуда Подставляя t₁ в выражения для e и w, находим, что в момент времени t₁

Определим скорость и полное ускорение при t = t₁

Задача 3.3Шестерня 1 радиуса r₁ приводится во вращение рукояткой АО₁= l. Эта шестерня сцеплена зубчатым колесом 2 радиуса r₂, которое наглухо насажено на вал диаметра d. На вал намотан нерастяжимый канат, к которому прикреплен груз В. Определить скорость и ускорение груза В, если рукоятка АО₁, вращаясь равноускоренно из состояния покоя совершает 16 оборотов за 2 с после начала движения (рис. 3.12).

Решение
Определяем угловое ускорение из формулы (3.25). По условию задачи j_о = 0,
w_о = 0, . Отсюда

Угловую скорость рукоятки для t = 2 с определяем по формуле (3.25) при
w_о = 0: w = e×t = 16p×2 = 32p c^–1.

Угловая скорость шестерни 1 равна угловой скорости рукоятки, так как они неизменно связаны между собой:

w₁ = w = 32p с^–1

Скорость точки С, которая принадлежит к шестерне 1 и колесу 2, равна

v_C = w₁r₁ = w₂r₂ , откуда

Касательное ускорение а_t^(С) точки С находится по формуле (3.27)
а_t^(С) = e₁r₁= e₂r₂ . Откуда Так как колесо 2 и вал жестко скреплены, имеем:

Поскольку канат нерастяжим и вместе с грузом совершает поступательное движение, можно определить

Сложное движение точки

В ряде случаев приходится рассматривать движение точки по отношению к системе координат O₁x₁y₁z₁, которая в свою очередь движется по отношению системы координат Oxyz, условно принятой в качестве неподвижной. При этом:

1) движение точки относительно системы координат Oxyz называется абсолютным;

2) движение точки относительно подвижной системы осей O₁x₁y₁z₁ называется относительным;

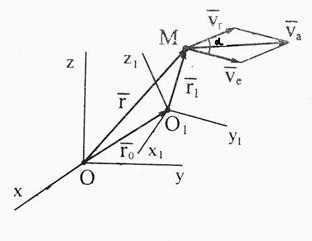
3) движение той точки подвижного пространства, с которой неизменно связана подвижная система отсчета O₁x₁y₁z₁ и с которой в данный момент времени совпадает рассматриваемая точка по отношению к неподвижной системе отсчета Oxyz называется переносным.
Различают также абсолютные, относительные и переносные траектории, скорости и ускорения точки как кинематические характеристики соответствующие указанным выше её движениям.
Разложение сложного (абсолютного) движения точки на относительные, переносные часто дает возможность привести сложное движение к простейшим движениям и этим самым облегчить решение конкретной задачи. Из определения абсолютного движения очевидно (рис. 3.13), что

(3.30)

infopedia.su
Векторные формулы для скоростей и ускорений точек тела

Скорость точки по модулю и направлению можно определить по формуле Эйлера векторным произведением:
(3.28)
где – радиус-вектор точки М, проведенной из произвольной точки оси вращения Oz, например точки О (рис. 3.10). В справедливости формулы (3.28) можно убедится определив по ней модуль скорости.
Из определения ускорения и векторной формулы Эйлера имеем:
(3.29)
Касательное и нормальное ускорения также можно записать в виде:
где – соответственно ортогональные единичные векторы (см. выше 3.1.2).
Рассмотрим конкретные задачи.

Задача 3.1Ротор мотора в период пуска имеет угловое ускорение e = 2p с^–2. Определить скорость, касательное, нормальное и полное ускорения точки М
(рис. 3.11), лежащей на ободе ротора в момент t = 3 c. Диаметр ротора d = 0,2 м.
Решение
Угловую скорость ротора в момент времени t = 3 c находим, пользуясь формулой (3.25):
w = w_о + e×t
Здесь и далее учитываем, что вращение ротора равноускоренное, начальный угол поворота j_о= 0 и начальная угловая скорость w_о= 0, так как ротор начинает вращаться из состояния покоя. Тогда w = e×t = 2p×3 = 6p с^–2. Для определения положения точки на ободе ротора вычислим также по формуле (3.24) угол поворота По формулам (3.27) определим соответственно скорость, касательное, нормальное и полное ускорение точки М.
Векторы в момент времени t = 3 c изображены на рисунке 3.11.
Задача 3.2В период разгона маховика закон его вращения характеризуется . Определить скорость и ускорение точки, находящейся на расстоянии
R = 0,8 м от оси вращения в тот момент, когда касательное и нормальное ускорения точки равны.
Решение
По формулам (3.21) и (3.22) определяем угловую скорость и угловое ускорение маховика.
Касательное и нормальное ускорения соответственно равны a_t = e×R, a_n = w²R. По условию задачи в момент времени t = t₁a_t = a_n. Поэтому в этот момент e = w² или откуда Подставляя t₁ в выражения для e и w, находим, что в момент времени t₁
Определим скорость и полное ускорение при t = t₁

Задача 3.3Шестерня 1 радиуса r₁ приводится во вращение рукояткой АО₁= l. Эта шестерня сцеплена зубчатым колесом 2 радиуса r₂, которое наглухо насажено на вал диаметра d. На вал намотан нерастяжимый канат, к которому прикреплен груз В. Определить скорость и ускорение груза В, если рукоятка АО₁, вращаясь равноускоренно из состояния покоя совершает 16 оборотов за 2 с после начала движения (рис. 3.12).

Решение
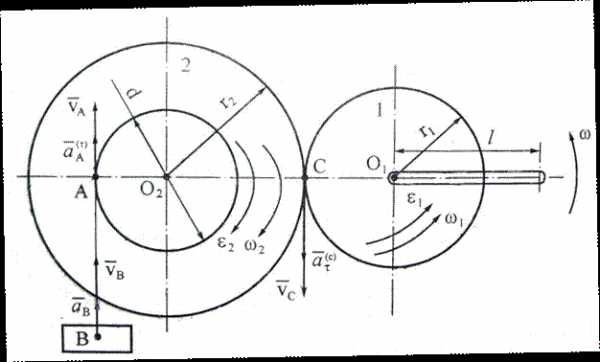
Определяем угловое ускорение из формулы (3.25). По условию задачи j_о = 0,
w_о = 0, . Отсюда
Угловую скорость рукоятки для t = 2 с определяем по формуле (3.25) при
w_о = 0: w = e×t = 16p×2 = 32p c^–1.
Угловая скорость шестерни 1 равна угловой скорости рукоятки, так как они неизменно связаны между собой:
w₁ = w = 32p с^–1
Скорость точки С, которая принадлежит к шестерне 1 и колесу 2, равна
v_C = w₁r₁ = w₂r₂ , откуда
Касательное ускорение а_t^(С) точки С находится по формуле (3.27)
а_t^(С) = e₁r₁= e₂r₂ . Откуда Так как колесо 2 и вал жестко скреплены, имеем:
Поскольку канат нерастяжим и вместе с грузом совершает поступательное движение, можно определить

Сложное движение точки
В ряде случаев приходится рассматривать движение точки по отношению к системе координат O₁x₁y₁z₁, которая в свою очередь движется по отношению системы координат Oxyz, условно принятой в качестве неподвижной. При этом:
1) движение точки относительно системы координат Oxyz называется абсолютным;
2) движение точки относительно подвижной системы осей O₁x₁y₁z₁ называется относительным;
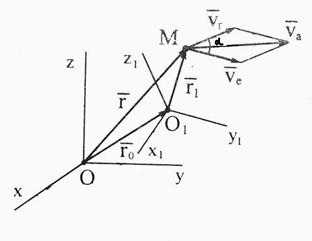
3) движение той точки подвижного пространства, с которой неизменно связана подвижная система отсчета O₁x₁y₁z₁ и с которой в данный момент времени совпадает рассматриваемая точка по отношению к неподвижной системе отсчета Oxyz называется переносным.
Различают также абсолютные, относительные и переносные траектории, скорости и ускорения точки как кинематические характеристики соответствующие указанным выше её движениям.
Разложение сложного (абсолютного) движения точки на относительные, переносные часто дает возможность привести сложное движение к простейшим движениям и этим самым облегчить решение конкретной задачи. Из определения абсолютного движения очевидно (рис. 3.13), что
(3.30)

Рекомендуемые страницы:
lektsia.com