Момент силы | Физика
Моментом силы относительно оси вращения называется физическая величина, равная произведению силы на ее плечо.
Момент силы определяют по формуле:
М – FI , где F — сила, I — плечо силы.
Плечом силы называется кратчайшее расстояние от линии действия силы до оси вращения тела.
На рис. 1.33, а изображено твердое тело, способное вращаться вокруг оси. Ось вращения этого тела перпендикулярна плоскости рисунка и проходит через точку, обозначенную буквой О. Плечом силы F здесь является расстояние 1Хот оси вращения до линии действия силы. Находят его следующим образом. Сначала проводят линию действия силы. Затем из точки О, через которую проходит ось вращения тела, опускают на линию действия силы перпендикуляр. Длина этого перпендикуляра является плечом данной силы.
Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от плеча. Чем больше плечо, тем меньшую силу надо приложить, чтобы получить желаемый результат, т. е. один и тот же момент силы (см. (1.33)). Именно поэтому открыть дверь, толкая ее возле петель, гораздо труднее, чем берясь за ручку, а гайку отвернуть гораздо проще длинным, чем коротким гаечным ключом.
За единицу момента силы в СИ принимается момент силы в 1 Н, плечо которой равно 1м — ньютон-метр (Н • м).
Правило моментов
Твердое тело, способное вращаться вокруг неподвижной оси, находится в равновесии, если момент силы М,, вращающей его по часовой стрелке, равен моменту силы М2, вращающей его против часовой стрелки:
М1 = -М2 или F 1 ll = – F 2 l 2 .
Момент силы принято считать положительным, если тело вращается по часовой стрелке, и отрицательным, если — против.
Правило моментов является следствием одной из теорем механики, сформулированной французским ученым П. Вариньоном в 1687 г.
Пара сил
Если на тело действуют две равные и противоположно направленные силы, не лежащие на одной прямой, то такое тело не находится в равновесии, поскольку результирующий момент этих сил относительно любой оси не равен нулю, т. к. обе силы имеют моменты, направленные в одну сторону. Две такие силы, одновременно действующие на тело, называют парой сил. Если тело закреплено на оси, то под действием пары сил оно будет вращаться. Если пара сил приложена ксвободному телу, то оно будет вращаться вокруг оси, проходящей через центр тяжести тела, рис. 1.33, б.
Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Суммарный момент М пары всегда равен произведению одной из сил F на расстояние I между силами, которое называется плечом пары,независимо от того, на какие отрезки и /2 разделяет положение оси плечо пары:
M = Fll + Fl2=F(l1 + l2) = Fl.
Момент нескольких сил, равнодействующая которых равна нулю, будет одинаковым относительно всех осей, параллельных друг другу, поэтому действие всех этих сил на тело можно заменить действием одной пары сил с тем же моментом.
ibrain.kz
Калькулятор Крутящий момент | Преобразование единиц крутящего момента
Крутящий момент, момент силы – направленность сил на осуществление поворота объекта вокруг оси или точки опоры. В математике крутящий момент определяется как векторное производное расстояния и силы, которой свойственно производить вращение. Проще говоря, крутящий момент — это мера силы вращения объекта, такого как маховик или болт. Как правило, символ — греческая буква Тау (Т) или иногда обозначается буквой «М», от слова «момент». Единицей СИ для крутящего момента является ньютон-метр (Н•м). Единицы фунт-сила-фут, фунт-сила-дюйм и унция-сила-фут также используются для крутящего момента. Для всех этих величин слово «сила» часто выпадает, к примеру, фунт-сила-дюйм сокращается до «фунт-дюйм».
Конвертер крутящего момента
Переводим из
Переводим в
| Основные единицы | |
| Килоньютон на метр | кН·м |
| Ньютон на метр | Н·м |
| Фунт-Сила-Дюйм | lbf∙in |
| Другие единицы | |
| Дина-сантиметр | дин·см |
| Дина-Метр | дин·м |
| Дина-Миллиметр | дин·мм |
| Грамм-Сила-Сантиметр | гс·см |
| Грамм-Сила-Метр | гс·м |
| Грамм-Сила-Миллиметр | гс·мм |
| Килограмм-Сила-Сантиметр | кгс∙см |
| Килограмм-Сила-Метр | кгс∙м |
| Килограмм-Сила-Миллиметр | кгс∙мм |
| Ньютон сантиметр | Н∙cм |
| Ньютон-Миллиметр | Н∙мм |
| Унция-Сила-Дюйм | ozf∙in |
| Основные единицы | |
| Килоньютон на метр | кН·м |
| Ньютон на метр | Н·м |
| Фунт-Сила-Дюйм | lbf∙in |
| Другие единицы | |
| Дина-сантиметр | дин·см |
| Дина-Метр | дин·м |
| Дина-Миллиметр | дин·мм |
| Грамм-Сила-Сантиметр | гс·см |
| Грамм-Сила-Метр | гс·м |
| Грамм-Сила-Миллиметр | гс·мм |
| Килограмм-Сила-Сантиметр | кгс∙см |
| Килограмм-Сила-Метр | кгс∙м |
| Килограмм-Сила-Миллиметр | кгс∙мм |
| Ньютон сантиметр | Н∙cм |
| Ньютон-Миллиметр | Н∙мм |
| Унция-Сила-Дюйм | ozf∙in |
Результат конвертации:
kalkulator.pro
Вращающий момент Википедия
Момент силы, приложенный к гаечному ключу. Направлен
Моме́нт си́лы (синонимы: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент) — векторная физическая величина, равная векторному произведению вектора силы и радиус-вектора, проведённого от оси вращения к точке приложения этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Общие сведения
- M→=[r→×F→],{\displaystyle {\vec {M}}=\left[{\vec {r}}\times {\vec {F}}\right],}
где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — радиус-вектор частицы (в предположении, что ось вращения проходит через начало координат).
Предыстория
Для того чтобы понять, откуда появилось обозначение момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы F→{\displaystyle {\vec {F}}} на рычаг r→{\displaystyle {\vec {r}}}, совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок dl{\displaystyle dl}, которому соответствует бесконечно малый угол dφ{\displaystyle d\varphi }. Обозначим через d→l{\displaystyle {\vec {d}}l} вектор, который направлен вдоль бесконечно малого отрезка dl{\displaystyle dl} и равен ему по модулю. Угол между вектором силы F→{\displaystyle {\vec {F}}} и вектором d→l{\displaystyle {\vec {d}}l} равен β{\displaystyle \beta }, а угол между векторами r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}} — α{\displaystyle \alpha }.
Следовательно, бесконечно малая работа dA{\displaystyle dA}, совершаемая силой F→{\displaystyle {\vec {F}}} на бесконечно малом участке dl{\displaystyle dl}, равна скалярному произведению вектора d→l{\displaystyle {\vec {d}}l} и вектора силы, то есть dA=F→⋅d→l{\displaystyle dA={\vec {F}}\cdot {\vec {d}}l}.
Теперь попытаемся выразить модуль вектора d→l{\displaystyle {\vec {d}}l} через радиус-вектор r→{\displaystyle {\vec {r}}}, а проекцию вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} — через угол α{\displaystyle \alpha }.
Так как для бесконечно малого перемещения рычага dl{\displaystyle dl} можно считать, что траектория перемещения перпендикулярна рычагу r→{\displaystyle {\vec {r}}}, используя соотношения для прямоугольного треугольника, можно записать следующее равенство: dl=rtgdφ{\displaystyle dl=r\mathrm {tg} \,d\varphi }, где в случае малого угла справедливо tgdφ=dφ{\displaystyle \mathrm {tg} \,d\varphi =d\varphi } и, следовательно, |dl→|=|r→|dφ{\displaystyle \left|{\vec {dl}}\right|=\left|{\vec {r}}\right|d\varphi }.
Для проекции вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} видно, что угол β=π2−α{\displaystyle \beta ={\frac {\pi }{2}}-\alpha }, а так как cos(π2−α)=sinα{\displaystyle \cos {\left({\frac {\pi }{2}}-\alpha \right)}=\sin \alpha }, получаем, что |F→|cosβ=|F→|sinα{\displaystyle \left|{\vec {F}}\right|\cos \beta =\left|{\vec {F}}\right|\sin \alpha }.
Теперь запишем бесконечно малую работу через новые равенства: dA=|r→|dφ|F→|sinα{\displaystyle dA=\left|{\vec {r}}\right|d\varphi \left|{\vec {F}}\right|\sin \alpha }, или dA=|r→||F→|sin(α)dφ{\displaystyle dA=\left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin(\alpha )d\varphi }.
Теперь видно, что произведение |r→||F→|sinα{\displaystyle \left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin \alpha } есть не что иное, как модуль векторного произведения векторов r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}}, то есть |r→×F→|{\displaystyle \left|{\vec {r}}\times {\vec {F}}\right|}, которое и было принято обозначить за момент силы M{\displaystyle M}, или модуль вектора момента силы |M→|{\displaystyle \left|{\vec {M}}\right|}.
Теперь полная работа записывается просто: A=∫0φ|r→×F→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {r}}\times {\vec {F}}\right|d\varphi }, или A=∫0φ|M→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {M}}\right|d\varphi }.
Единицы
Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.
Энергия и механическая работа также имеют размерность «сила, умноженная на расстояние» и измеряются в системе СИ в джоулях. Следует заметить, что энергия — это скалярная величина, тогда как момент силы — величина псевдовекторная. Совпадение размерностей этих величин не случайность: момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию 2π{\displaystyle 2\pi } джоуля. Математически:
- E=Mθ,{\displaystyle E=M\theta ,}
где E{\displaystyle E} — энергия, M{\displaystyle M} — вращающий момент, θ{\displaystyle \theta } — угол в радианах.
Специальные случаи
Формула момента рычага
Момент, действующий на рычагОчень интересен особый случай, представляемый как определение момента силы в поле:
- |M→|=|M→1||F→|,{\displaystyle \left|{\vec {M}}\right|=\left|{\vec {M}}_{1}\right|\left|{\vec {F}}\right|,}
где: |M→1|{\displaystyle \left|{\vec {M}}_{1}\right|} — момент рычага, |F→|{\displaystyle \left|{\vec {F}}\right|} — величина действующей силы.
Недостаток такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору r→{\displaystyle {\vec {r}}}, момент рычага будет равен расстоянию от центра до точки приложения силы и момент силы будет максимален:
- |T→|=|r→||F→|.{\displaystyle \left|{\vec {T}}\right|=\left|{\vec {r}}\right|\left|{\vec {F}}\right|.}
Сила под углом
Если сила F→{\displaystyle {\vec {F}}} направлена под углом θ{\displaystyle \theta } к рычагу r, то M=rFsinθ{\displaystyle M=rF\sin \theta }.
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0,ΣV=0{\displaystyle \Sigma H=0,\,\Sigma V=0} и момент силы в третьем измерении ΣM=0{\displaystyle \Sigma M=0}.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
Видеоурок: вращающий момент- M→=dL→dt,{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}},}
где L→{\displaystyle {\vec {L}}} — момент импульса.
Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.
- Lo→=Icω→+[M(ro→−rc→),vc→].{\displaystyle {\vec {L_{o}}}=I_{c}\,{\vec {\omega }}+[M({\vec {r_{o}}}-{\vec {r_{c}}}),{\vec {v_{c}}}].}
Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если I{\displaystyle I} — постоянная величина во времени, то
- M→=Idω→dt=Iα→,{\displaystyle {\vec {M}}=I{\frac {d{\vec {\omega }}}{dt}}=I{\vec {\alpha }},}
где α→{\displaystyle {\vec {\alpha }}} — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с2). Пример: вращается однородный диск.
Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:
- Mc→=Icdω→dt+[w→,Icw→].{\displaystyle {\vec {M_{c}}}=I_{c}{\frac {d{\vec {\omega }}}{dt}}+[{\vec {w}},I_{c}{\vec {w}}].}
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Так же и момент силы, если совершает действие через угловое расстояние, он совершает работу.
- P=M→⋅ω→.{\displaystyle P={\vec {M}}\cdot {\vec {\omega }}.}
В системе СИ мощность P{\displaystyle P} измеряется в ваттах, момент силы — в ньютоно-метрах, а угловая скорость — в радианах в секунду.
Отношение между моментом силы и работой
- A=∫θ1θ2|M→|dθ.{\displaystyle A=\int _{\theta _{1}}^{\theta _{2}}\left|{\vec {M}}\right|\mathrm {d} \theta .}
В случае постоянного момента получаем:
- A=|M→|θ.{\displaystyle A=\left|{\vec {M}}\right|\theta .}
В системе СИ работа A{\displaystyle A} измеряется в джоулях, момент силы — в ньютоно-метрах, а угол — в радианах.
Обычно известна угловая скорость ω{\displaystyle \omega } в радианах в секунду и время действия момента t{\displaystyle t}.
Тогда совершённая моментом силы работа рассчитывается как:
- A=|M→|ωt.{\displaystyle A=\left|{\vec {M}}\right|\omega t.}
Момент силы относительно точки
Если имеется материальная точка OF{\displaystyle O_{F}}, к которой приложена сила F→{\displaystyle {\vec {F}}}, то момент силы относительно точки O{\displaystyle O} равен векторному произведению радиус-вектора r→{\displaystyle {\vec {r}}}, соединяющего точки O{\displaystyle O} и OF{\displaystyle O_{F}}, на вектор силы F→{\displaystyle {\vec {F}}}:
- MO→=[r→×F→].{\displaystyle {\vec {M_{O}}}=\left[{\vec {r}}\times {\vec {F}}\right].}
Момент силы относительно оси
Момент силы относительно оси равен алгебраическому значению проекции момента этой силы на плоскость, перпендикулярную этой оси относительно точки пересечения оси с плоскостью, то есть
- Mz(F)=Mo(F′)=F′h′.{\displaystyle M_{z}(F)=M_{o}(F’)=F’h’.}
Измерение момента силы
Измерение момента силы осуществляется с помощью специальных приборов — торсиометров. Принцип их действия обычно основан на измерении угла закручивания упругого вала, передающего крутящий момент, либо на измерении деформации некоторого упругого рычага. Измерения деформации и угла закручивания производится различными датчиками деформации — тензометрическими, магнитоупругими, а также измерителями малых перемещений — оптическими, ёмкостными, индуктивными, ультразвуковыми, механическими.
Существуют специальные динамометрические ключи для измерения крутящего момента затягивания резьбовых соединений и регулируемые и нерегулируемые ограничители крутящего момента, так называемые «трещотки», применяемые в гаечных ключах, шуруповёртах, винтовых микрометрах и др.
См. также
wikiredia.ru
Момент силы
Возьмем тело произвольной формы и будем вращать его вокруг точки О, действуя на него силой F. Для того, чтобы охарактеризовать внешнее механическое действие на тело, которое приводит к вращению, в статике вводят понятие «момент силы» или «вращающий момент». Обозначается он буквой М.
Векторную величину М, равную векторному произведению силы, на плечо силы, называют моментом силы относительно точки О:
— плечо силы, кратчайшее расстояние от т. О до линии, вдоль которой происходит действие силы, измеряется в системе СИ в метрах.
Для определения плеча достаточно опустить перпендикуляр, из точки вращения на линию, вдоль которой действует сила.
F – сила, приводящая тело во вращение, измеряется в Ньютонах.
Тогда М — момент силы будет измеряться в Ньютонах на метр (H*м).
Можно записать значение вектора момента сил через произведение вектора силы F и радиуса — вектора r, проведенного из точки О в точку приложения силы:
Плечо силы равно:
угол , это угол между векторами F и r.
Так как М векторная величина, определить ее направление можно по направлению приложенной к телу силы F:
- Сила вращает тело по часовой стрелке, имеем дело с отрицательным моментом.
- Сила вращает тело против часовой стрелки, с положительным моментом.
Свойства моментов:
- если линия действия силы проходит через точку вращения, то М=0.
- если перенесем точку приложения силы F в любое место вдоль линии действия этой силы F, момент вектора силы при этом не изменится.
- Приложим к телу несколько сил, выберем точку О — центр вращения, момент вектора силы равен будет равен геометрической сумме моментов сил. Для каждой силы отдельно рассчитываем момент силы.
Рассмотрим случай, когда к телу приложены две силы:
- Первая по часовой стрелке;
- Вторая против часовой стрелки.
Тело находиться в равновесии, значит М1=М2, или 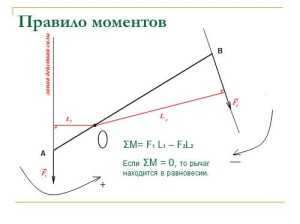 Это так называемое правило моментов и вытекающее из него условие равновесия: тело будет в равновесии, если момент сил, вращающий его по часовой стрелке равен моменту вращающему его против часовой. (частный случай — рычаг)
Это так называемое правило моментов и вытекающее из него условие равновесия: тело будет в равновесии, если момент сил, вращающий его по часовой стрелке равен моменту вращающему его против часовой. (частный случай — рычаг)
Применение правила моментов:
Так как вращающий момент М зависит от приложенной силы и плеча мы это используем в быту и технике. Чтобы нести тяжелый груз в походе было легче, мы используем правило моментов. Берем длинную палку, подвешиваем груз и кладем палку на плечо, выбирая точку вращения таким образом, чтобы плечо с грузом было больше, чем то за которое мы держимся рукой. Закручивая гайки гаечным ключом, берем его в руки как можно дальше от точки вращения. Открывая в доме дверь, толкаем ее как можно дальше от петель.
fizikatyt.ru
Формула момента силы в физике
- Главная
- Справочник
- Формулы по физике
Определение и формула момента силы
ОпределениеВекторное произведение радиус – вектора (), который проведен из точки О (рис.1) в точку к которой приложена сила на сам вектор называют моментом силы ( )по отношению к точке O:
На рис.1 точка О и вектор силы ( )и радиус – вектор находятся в плоскости рисунка. В таком случае вектор момента силы () перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор создают правовинтовую систему. Направление момента сил и углового ускорения совпадают.
Величина вектора равна:
где – угол между направлениями радиус – вектора и вектора силы, – плечо силы относительно точки О.
Момент силы относительно оси
Моментом силы по отношению к оси является физическая величина, равная проекции вектора момента силы относительно точки избранной оси на данную ось. При этом выбор точки значения не имеет.
Главный момент сил
Главным моментом совокупности сил относительно точки О называется вектор (момент силы), который равен сумме моментов всех сил, действующих в системе по отношению к той же точке:
При этом точку О называют центром приведения системы сил.
Если имеются два главных моменты ( и )для одной системы сил для разных двух центров приведение сил (О и О’), то они связаны выражением:
www.webmath.ru
Момент силы – это… Что такое Момент силы?
Момент силы, приложенный к гаечному ключу. Направлен от зрителя
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Общие сведения
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является Ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы.
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искусственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол между вектором и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус-вектор , а проекцию вектора силы на вектор , через угол .
Так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , используя соотношения для прямоугольного треугольника, можно записать следующее равенство: , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть не что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуль вектора момента силы .
Теперь полная работа записывается очень просто: или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является ньютон-метр. Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н·м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н·м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, M— вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычагаОчень интересен особый случай, представляемый как определение момента силы в поле:
- = МОМЕНТ_РЫЧАГА * СИЛА
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ_ДО_ЦЕНТРА * СИЛА
Сила под углом
Если сила F направлена под углом θ к рычагу r, то M = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении ΣM=0.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть, если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ_СИЛЫ * УГЛОВАЯ_СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ_СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ_СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющего точки и , на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM, Lorenz (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
Ссылки
См. также
dic.academic.ru
Момент сил – это… Что такое Момент сил?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
