Метод Гаусса. Схема единственного деления
ЛАБОРАТОРНАЯ РАБОТА №1
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Цель работы: изучить метод Гаусса, используемый наиболее часто для решения систем линейных алгебраических (СЛАУ) уравнений, разработать алгоритм и на его основе написать программу.
ПРОГРАММА РАБОТЫ
Составить программу решения СЛАУ методом Гаусса.
Запустить программу, решив с её помощью одну из линейных систем
уравнений, в соответствии с вариантом задания.
3. Проверить полученное решение.
4. Оформить отчет о лабораторной работе.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РАБОТЕ
Рассмотрим систему из 4-уравнений с четырьмя неизвестными:
(1)
пусть (разрешающий элемент)
Разделив первое уравнение системы (1) на , получим
(2)
где (j=2,3,4,5).
Исключим из второго, третьего и четвертого уравнений системы. Для этого умножим уравнение (2) на , и и вычтем результаты соответственно из второго, третьего и четвертого уравнений системы.
В результате получим систему 3 уравнений:
(3)
где (i=2,3,4; j=2,3,4,5)
Далее первое уравнение системы (3) делим на , в итоге :
, (4)
где (j=3,4,5).
Исключая теперь так же, как исключили , получим систему уравнений
(5)
где (i=3,4; j=3,4,5).
Разделив первое уравнение системы (5) на , получим
,
где (j=4,5).
C помощью этого уравнения исключим из второго уравнения системы (5). Получим уравнение
,
где (j=4,5).
Таким образом, система (1) приводится к эквивалентной схеме с треугольной матрицей:
(6)
откуда последовательно находятся
(7)
Итак, решение системы распадается на два этапа

Рассмотренный метод применим, если все ведущие — разрешающие элементы отличны от нуля. Если же какой-либо из них обращается в ноль, то в соответствующей системе достаточно провести перестановку уравнений, чтобы сделать “ведущий” элемент отличным от нуля. Блок-схема алгоритма (схема единственного деления) приведена на рис.1.
ВАРИАНТЫ ЗАДАНИЙ
А. Решаемые системы уравнений
Решить следующие СЛАУ
1. | 2. |
3. | 4. |
В. Используемые методы
Описанный метод Гаусса (схема единственного деления), с вычислением определителя системы и проверкой на ноль диагонального элемента.
Метод Гаусса с выбором главного элемента.

Метод прямоугольника с расположением разрешающих элементов в любом месте.
Метод квадратных корней с вычислением определителя.
Метод Гаусса для вычисления элементов обратной матрицы.
Рис. 1. Блок-схема алгоритма
ЛАБОРАТОРНАЯ РАБОТА №2
ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
Цель работы: изучить итерационные методы, используемые наиболее часто для решения систем линейных алгебраических уравнений, научиться разрабатывать алгоритмы и писать программы на их основе.
ПРОГРАММА РАБОТЫ
Разработать алгоритмы и составить программы решения СЛАУ методом простой итерации и методом Зейделя.
Запустить поочередно обе программы, решив с их помощью одну из линейных систем уравнений, взятую из соответствующего варианта задания.

Произвести сравнительные оценки сходимостей рассматриваемых методов.
Сравнить полученные результаты решения СЛАУ двумя итерационными методами с решением задачи прямым методом.
Исследовать влияние параметров ЭВМ на скорость сходимости итераций.
Оформить отчет о лабораторной работе.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РАБОТЕ
Системы
линейных уравнений можно решать не
только прямыми, но и итерационными
методами. Итерационные методы применяются,
главным образом, для решения задач
большой размерности, когда использование
прямых методов невозможно из-за
необходимости выполнения чрезмерно
большого числа арифметических операций.
Как правило, большие системы уравнений
являются разреженными. Применение
методов исключения переменных для них
бывает неудобным ввиду того, что при их
использовании большое число нулевых
элементов превращается в ненулевые, и
матрица теряет свойство разреженности,
чего не происходит при использовании
итерационных методов.
Рассмотрим наиболее простые итерационные методы, позволяющие решать достаточно широкий класс систем.
Методы решения СЛАУ. Метод Гаусса
2. Анализ
существующих методов
решения задачи
Прямые методы решения СЛАУ. К прямым (или точным) методам решения СЛАУ относятся алгоритмы, которые в предположении, что вычисления ведутся без округлений, позволяют получить точное решение системы за конечное число арифметических действий. Чаще всего решение задач такими методами осуществляется поэтапно: на первом этапе систему преобразуют к тому или иному простому виду, на втором – решают упрощенную систему и получают значения неизвестных.
Запишем
систему линейных алгебраических уравнений
в развернутом виде:
где x1, x2,. .., xn – неизвестные величины, b1,
b2,…, bn – элементы правой части. Если определитель
системы отличен от нуля, то она имеет
единственное решение. Для удобства дальнейших
преобразований обозначим элементы правой
части
.., xn – неизвестные величины, b1,
b2,…, bn – элементы правой части. Если определитель
системы отличен от нуля, то она имеет
единственное решение. Для удобства дальнейших
преобразований обозначим элементы правой
части
A =
С
этой матрицей можно обращаться так
же, как и с системой – переставлять
строки, прибавлять кратное одной
строки к другой, исключая неизвестные
и приводя матрицу к
Приведем формальное описание схем некоторых прямых методов.
- Метод
Гаусса (схема единственного
деления).
 Алгоритм метода состоит из
двух этапов. Первый этап называется прямым ходом метода и заключается в
последовательном исключении неизвестных
из уравнений, т.е. в приведении матрицы А к верхнему треугольному виду (ниже
главной диагонали все нули). Для этого
на первом шаге разделим первое уравнение
системы на а11 (предположим, что коэффициент а11 ¹ 0, в противном случае
осуществляем перестановку уравнений
системы). Обозначим коэффициенты полученного
Алгоритм метода состоит из
двух этапов. Первый этап называется прямым ходом метода и заключается в
последовательном исключении неизвестных
из уравнений, т.е. в приведении матрицы А к верхнему треугольному виду (ниже
главной диагонали все нули). Для этого
на первом шаге разделим первое уравнение
системы на а11 (предположим, что коэффициент а11 ¹ 0, в противном случае
осуществляем перестановку уравнений
системы). Обозначим коэффициенты полученного  е.
е.
Первое
уравнение в дальнейших преобразования
не участвует. Описанный выше процесс
исключения неизвестных применим к матрице размерами (n-1)
n. После k аналогичных шагов получим k приведенных уравнений с коэффициентами
( 2.4)
и
матрицу размерами (n – k) (n –
k+1), элементы которой вычисляются по
формулам
(2.5)
Элементы , на которые осуществляется деление, называются ведущими элементами метода Гаусса и не должны равняться нулю. Прямой ход метода Гаусса заканчивается после n шагов определением .
Обратный
ход метода Гаусса заключается в последовательном
определении компонент решения, начиная
с хn и заканчивая х1,
по следующим формулам:
(2. 6)
6)
Прямой ход состоит из n – 1 шагов исключения.
1-й шаг. Целью этого шага является исключение неизвестного x1 из уравнений с номерами i = 2, 3, …, n. Предположим, что коэффициент a11¹ 0. Будем называть его главным элементом 1-го шага.
Найдем
величины
qi1 = ai1/a11 (i
= 2, 3, …, n)
называемые множителями 1-го
шага. Вычтем последовательно из второго,
третьего, …, n-го уравнений системы
первое уравнение, умноженное соответственно
на q21,
q31, …, qn1. Это позволит
обратить в нуль коэффициенты при x1 во всех уравнениях, кроме первого. В результате
получим эквивалентную систему
В результате
получим эквивалентную систему
a11x1 + a12x2 + a13x3 + … + a1nxn = b1 ,
a22(1)x2 + a23(1)x3 + … + a2n(1)xn = b2(1) ,
a32(1)x2 + a33(1)x3 + … + a3n(1)xn = b3(1) ,
. . . . . . . . . . . . . . .
an2(1)x2 + an3(1)x3 + …
+ ann(1)xn = bn(1) .
в
которой aij(1) и bij(1) вычисляются по
формулам
aij(1) = aij − qi1a1j , bi(1) = bi −
qi1b1
2-й
шаг. Целью этого шага является исключение
неизвестного x2 из уравнений
с номерами i = 3, 4, …, n. Пусть a22(1) ≠ 0, где a22(1) – коэффициент,
называемый главным (или ведущим) элементом 2-го шага. Вычислим множители
2-го шага
qi2 = ai2(1) / a22(1)
(i = 3, 4, …, n)  10)
10)
и
вычтем последовательно из третьего,
четвертого, …, n-го уравнения системы
второе уравнение, умноженное соответственно
на q32, q42, …, qm2. В результате получим систему
a11x1 + a12x2 + a13x3 + … + a1nxn = b1 ,
a22(1)x2 + a23(1)x3 + … + a2n(1) = b2(1) , (2.11)
a33(2)x3 + … + a3n(2)xn = b3(2) ,
. . . . . .
. . . . .
. . . . .
. . .
. . . . .
. . . . .
. . . . .
. . .
an3(2)x3 + … + ann(2)xn = bn(2) .
Здесь
коэффициенты aij(2) и bij(2) вычисляются
по формулам
aij(2) = aij(1) – qi2a2j(1)
, bi(2) = bi(1) – qi2b2(1).
Аналогично
проводятся остальные шаги. Опишем
очередной k-й шаг.
k-й
шаг. В предположении, что главный (ведущий) элемент
k-го шага akk(k–1) отличен от нуля, вычислим множители
k-го шага
qik = aik(k–1) / akk(k–1)
(i = k + 1, …, n)
и вычтем последовательно из (k + 1)-го, …, n-го уравнений полученной на предыдущем шаге системы k-e уравнение, умноженное соответственно на qk+1,k, qk+2,k, …, qnk.
После
(n – 1)-го шага исключения получим систему
уравнений
a11x1 + a12x2 + a13x3 + … + a1nxn = b1 ,
a22(1)x2 + a23(1)x3 + … + a2n(1)xn = b2(1) ,  14)
14)
a33(2)x3 + … + a3n(2)xn = b3(2) ,
. . . . . . . . . . . . . . . . . . . .
матрица A(n-1) которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Обратный
ход. Из последнего уравнения системы
находим xn. Подставляя найденное значение xn в предпоследнее уравнение,
получим xn–1. Осуществляя
обратную подстановку, далее последовательно
находим xn–1, xn–2,
…, x1. Вычисления неизвестных
здесь проводятся по формулам
Вычисления неизвестных
здесь проводятся по формулам
xn = bn(n–1) / ann(n–1),
xk = (bn(k–1) – ak,k+1(k–1)xk+1 – … – akn(k–1)xn)
/ akk(k–1), (k = n – 1, …, 1).
Необходимость
выбора главных элементов. Заметим,
что вычисление множителей, а также обратная
подстановка требуют деления на главные
элементы akk(k–1).
Поэтому если один из главных элементов
оказывыется равным нулю, то схема единственного
деления не может быть реализована. Здравый
смысл подсказывает, что и в ситуации,
когда все главные элементы отличны от
нуля, но среди них есть близкие к нулю,
возможен неконтролируемый рост погрешности.
Здравый
смысл подсказывает, что и в ситуации,
когда все главные элементы отличны от
нуля, но среди них есть близкие к нулю,
возможен неконтролируемый рост погрешности.
- Метод
Гаусса с выбором главного
элемента. Метод заключается в том,
что при прямом ходе в алгоритме метода
Гаусса на каждом шаге исключения производится
выбор наибольшего по модулю элемента
в качестве ведущего. Этого достигают
перестановкой строк или столбцов матрицы
коэффициентов. Наиболее распространённой
в вычислительной практике является стратегия
выбора главного элемента
столбца – нахождение максимального
по модулю элемента k-го столбца матрицы и использование его в качестве ведущего
элемента на k-м шаге исключения. В
этом случае для невырожденных систем
гарантируется, что ведущие элементы не
равны нулю, и уменьшается погрешность
при делении и последующем вычитании при
преобразованиях.
 Рекомендуется также
масштабировать предварительно каждое
уравнение исходной системы, разделив
на его наибольший по абсолютной величине
коэффициент. Это делает рост элементов
промежуточных матриц ограниченным.
Рекомендуется также
масштабировать предварительно каждое
уравнение исходной системы, разделив
на его наибольший по абсолютной величине
коэффициент. Это делает рост элементов
промежуточных матриц ограниченным.
В
методе Гаусса с выбором главного
элемента по столбцу гарантируется,
что |qik| ≤ 1 для всех k = 1, 2, …, n – 1 и i = k + 1, …, n.
Отличие этого варианта метода Гаусса
от схемы единственного деления заключается
в том, что на k-м шаге исключения в
качестве главного элемента выбирают
максимальный по модулю коэффициент aikk при неизвестной xk в уравнениях с номерами i =
k + 1, …, n. Затем соответствующее
выбранному коэффициенту уравнение с
номером ik меняют местами
с k-м уравнением системы для того,
чтобы главный элемент занял место коэффициента akk(k-1). После этой
перестановки исключение неизвестного xk производят, как в схеме
единственного деления.
После этой
перестановки исключение неизвестного xk производят, как в схеме
единственного деления.
- Метод оптимального исключения. В целях экономии оперативной памяти (примерно в 4 раза) операции прямого и обратного хода метода Гаусса выполняются попеременно. На первом шаге после приведения первого уравнения исключается неизвестное x1 из второго уравнения, а затем с помощью приведенного второго уравнения – неизвестное x2 из первого. После (k-1) таких шагов матрица системы имеет вид
Гауссовский метод исключения – Уроки Византа
Метод решения систем уравнений методом исключения также известен как метод исключения Гаусса
, потому что он приписывается Карлу Фридриху Гауссу как изобретателю метода
.
Исключение или включает в себя манипулирование заданной системой уравнений таким образом, что одна
или более переменных исключается, оставляя уравнение с одной переменной, которое затем может быть легко решено. Оттуда обратная замена используется, чтобы найти другие
Оттуда обратная замена используется, чтобы найти другие
переменных.
Решение систем уравнений методом исключения
При решении систем уравнений с двумя переменными метод исключения включает в себя
манипулирование одним уравнением путем умножения его на константу таким образом, что когда это
уравнение добавляется к другому уравнению в системе, одна переменная удаляется
и все такое. осталось уравнение с одной переменной, которое мы можем легко решить. После того, как
получит решение этой переменной, мы затем подставим это значение в любое из
уравнений, чтобы найти другую переменную.
Учитывая систему уравнений ниже;
Процесс исключения позволяет нам умножить уравнение (1) или (2) так, что
при сложении двух уравнений одна из переменных будет исключена.
Например, если бы мы хотели исключить переменную x , мы бы получили это число
, умножив уравнение (1) или (2) на некоторую константу, которая гарантирует, что
уравнение (1) + уравнение (2) равно уравнению (3), которое имеет только одну переменную
y .
Если мы умножим уравнение (2) на константу -a ⁄ c , мы
получим следующий результат
что упрощается до
Тогда, если бы мы добавили новое уравнение (2n) выше к уравнению (1), мы бы наблюдали
следующее:
будет
Это уравнение с одной переменной для y , и мы можем перейти к решению для
y . После получения значения y мы можем подставить его либо в
уравнение (1), либо в уравнение (2), из которого мы можем вычислить значение x .
Давайте попробуем несколько примеров, чтобы увидеть, как все это работает.
Пример 1
Решите следующую систему уравнений
Шаг 1
Для того, чтобы отслеживать, о каком уравнении идет речь, первым шагом всегда должна быть маркировка уравнений в системе.
Этап 2
Следующим шагом является проверка уравнений, чтобы увидеть, как мы можем манипулировать ими, чтобы получить
избавиться от одной из переменных. Этот пример довольно прост, чтобы избавиться от
переменной y , нам не нужно умножать какое-либо уравнение на какую-либо константу,
мы можем просто сложить два уравнения, и переменная y просто исчезнет.
Это связано с тем, что в обоих уравнениях коэффициент y в уравнении (1) равен
, что противоположно коэффициенту в уравнении (2), т.е. .
Этап 3
Вышеупомянутое уравнение представляет собой уравнение с одной переменной для x , и мы можем легко решить для x
, разделив на 5
Этап 4
Теперь, когда у нас есть решение для x , мы можем заменить x в уравнении (1)
, чтобы получить уравнение с одной переменной, которое мы можем использовать для решения для y .
замена х
Следовательно, мы имеем решение системы уравнений как x = 5 и y = -1 .
Пример 2
Решите следующую систему уравнений
Шаг 1
Первый шаг — пометить уравнения, чтобы мы знали, какое уравнение мы имеем в виду.
Этап 2
Затем мы исследуем систему уравнений, чтобы увидеть, как мы можем эффективно исключить
одну из переменных.
Изучив систему, мы можем заметить, что мы можем умножить уравнение (1) на
-3, так что, сложив два уравнения, мы можем исключить x .
что приводит к
Этап 3
Далее мы продолжаем добавлять новое уравнение к уравнению (2)
Что упрощается до
Этап 4
Значение y было получено как -1 . Мы продолжаем использовать это значение
для решения x , подставляя y в любое из приведенных выше уравнений.
Подставим y в исходное уравнение (1)
Решение системы уравнений: {x,y} = {-1,-1} .
Пример 3
Найдите значения x и y в системе уравнений, приведенной ниже
Шаг 1
Когда вам дана система уравнений в неорганизованном виде, как указано выше,
всегда лучше начать с перестановки уравнений таким образом, чтобы переменные
0003 совпадает. Это облегчит работу с уравнениями. Затем вы можете продолжить
, чтобы пометить уравнения.
Этап 2
При рассмотрении приведенной выше системы не так очевидно, на какую константу умножить
на уравнение (1) или (2), чтобы исключить одну из переменных. Когда возникает такая
ситуация, вы выбираете одну переменную и решаете, что хотите исключить
что, затем вы выбираете одно уравнение и умножаете его на дробь, числитель которой равен
отрицательному значению коэффициентной переменной, которую мы исключаем из другого уравнения,
а знаменатель является коэффициентом переменной для уравнения, которое мы умножаем .
Для этого примера удалим переменную x и сначала поработаем с уравнением (2):
что упрощает как
Этап 3
Добавление вышеуказанного к уравнению (2) приводит к следующим
Шаг 4
Теперь, когда у нас есть значение y , мы можем подставить и найти x
следующим образом;
Решение системы уравнений: {x,y} = { 148 ⁄ 95 , -43 ⁄ 19 }
Решение систем уравнений с тремя переменными методом исключения
Решение систем уравнений с тремя переменными мало чем отличается от решения этих
с двумя переменными. Основная концепция остается той же, только в этом случае мы
Основная концепция остается той же, только в этом случае мы
пойдем немного дальше, чтобы учесть третью переменную.
Подобно тому, как мы решали для двух переменных, когда дело доходит до трех переменных,
мы начинаем с манипулирования двумя из трех уравнений таким образом, что когда они добавляются к другому уравнению, одна из переменных полностью исчезает. Затем мы фокусируемся на этих новых уравнениях с двумя переменными, а также манипулируем ими таким образом, чтобы
0003 остаются с уравнением с одной переменной.
Учитывая систему уравнений ниже
Мы можем найти переменные x , y и z следующим образом:
Сначала мы выбираем уравнение (1) и используем его для исключения переменной x из
других уравнений.
Мы можем добиться этого в уравнении (2), умножив уравнение на константу, такую
, что, когда мы добавляем уравнение (2) к уравнению (1), x переменная исчезает.
Умножение вышеприведенного на константу a ⁄ d
Добавляя вышеуказанное к уравнению (1):
результат:
Выше приведено новое уравнение (2).
Мы также исключаем переменную x из уравнения (3) аналогичным образом:
умножение на константу
Добавляя вышеуказанное к уравнению (1)
что приводит к
Выше приведено новое уравнение (3)
Итак, теперь у нас есть два уравнения с двумя переменными, мы можем решить эти уравнения с двумя переменными
, используя то, что мы узнали в разделе о системах уравнений с двумя переменными выше.
Давайте посмотрим на примере, как работает приведенный выше алгоритм
. Пример 4
Решите следующую систему уравнений
Шаг 1
Мы начнем с того, что пометим наши уравнения, чтобы было легче обращаться к ним
.
Этап 2
Затем мы выбираем переменную уравнения (2) y , мы проверяем это уравнение вместе
с уравнением (1), чтобы найти способ исключить это уравнение.
Этап 3
Из проверки вы можете видеть, что простое добавление уравнения (1) к уравнению (2) вы
эффективно исключите переменную y из уравнения (2)
результаты в
Выше приведено новое уравнение (2)
Этап 4
Делаем то же самое для уравнения (3)
Но обратите внимание, что в этом случае нам повезло, что уравнение (3) уже является уравнением с двумя переменными
в z и x .
Этап 5
Таким образом, мы можем перейти к обработке уравнений (2) и (3) как системы уравнений с двумя переменными
Изучив приведенную выше систему, мы можем выбрать любую переменную для исключения, поскольку
все они будут относительно простыми, но давайте возьмем x .
Шаг 6
Мы можем исключить x, умножив уравнение (3) на -1, а затем добавив результат
к уравнению 2 следующим образом:
что дает
что приводит к
Шаг 7
Выше приведено относительно простое уравнение с одной переменной, из которого мы можем решить для
x , разделив обе части на 3:
Затем, используя обратную замену, мы можем найти x и y , начиная с
x . Чтобы найти x , мы подставляем значение z в уравнение (2)
Чтобы найти x , мы подставляем значение z в уравнение (2)
Шаг 8
Теперь, когда у нас есть значения для x и z , мы можем найти y , подставив
этих значений в уравнение (1)
Решением системы уравнений является {х, у, г} = {1, 2, 3}
Пример 5
Найдите x, y и z из системы уравнений ниже
Шаг 1
Как всегда, мы начинаем с маркировки уравнений, чтобы на них было легче ссылаться.
Этап 2
Далее рассмотрим уравнения (1) и (2) так, чтобы исключить одну из переменных;
в данном случае x
Этап 3
Мы можем видеть, что если мы умножим уравнение (2) на -1 ⁄ 3 ,
, а затем добавим результат к уравнению (1), мы можем получить новое уравнение (2), в котором
будет двумя уравнение переменной в y и z .
что приводит к:
Этап 4
Добавление приведенного выше результата к уравнению (1)
результат:
Приведенное выше становится нашим новым уравнением (2).
Этап 5
Затем мы выполняем ту же процедуру для уравнения (3):
Изучая приведенную выше систему, мы можем видеть, что если мы умножим уравнение (3) на
-1 ⁄ 6
результат:
Шаг 6
Затем мы добавляем вышеуказанное к уравнению (1)
что приводит к:
Приведенный выше результат становится нашим новым уравнением (3)
Шаг 7
Теперь мы получили новую систему уравнений, которая имеет только две переменные:
Шаг 8
Мы можем исключить y из приведенной выше системы, умножив уравнение (3) на
-2 ⁄ 3 , а затем добавив результат к уравнению (2). Результирующее уравнение
Результирующее уравнение
будет уравнением с одной переменной в z , и мы можем решить
для z из этого.
результат:
Шаг 9
Добавляя вышеуказанное к уравнению (2):
что приводит к;
Мы можем решить z из приведенного выше:
Шаг 10
Используя обратную замену, теперь мы можем найти и , затем x .
Сначала мы находим y , подставляя значение z в уравнение (2):
Шаг 11
Получив y , мы можем найти х , подставив y и z
в уравнение (1):
Решение системы уравнений: {x, y, z} = { 1 ⁄ 14 , 4 ⁄ 21 , 8 ⁄ 7 1 1 1 1 7 2} Метод исключения решения системы линейных уравнений алгебраически является наиболее широко используемым методом из всех методов решения линейных уравнений. Метод исключения прост в использовании, потому что здесь мы исключаем одно из условий, упрощающих наши расчеты. В этой статье мы научимся решать системы уравнений методом исключения. Мы будем решать различные примеры, основанные на концепции для лучшего понимания. Метод исключения – определение, этапы, примеры, решение системы уравнений
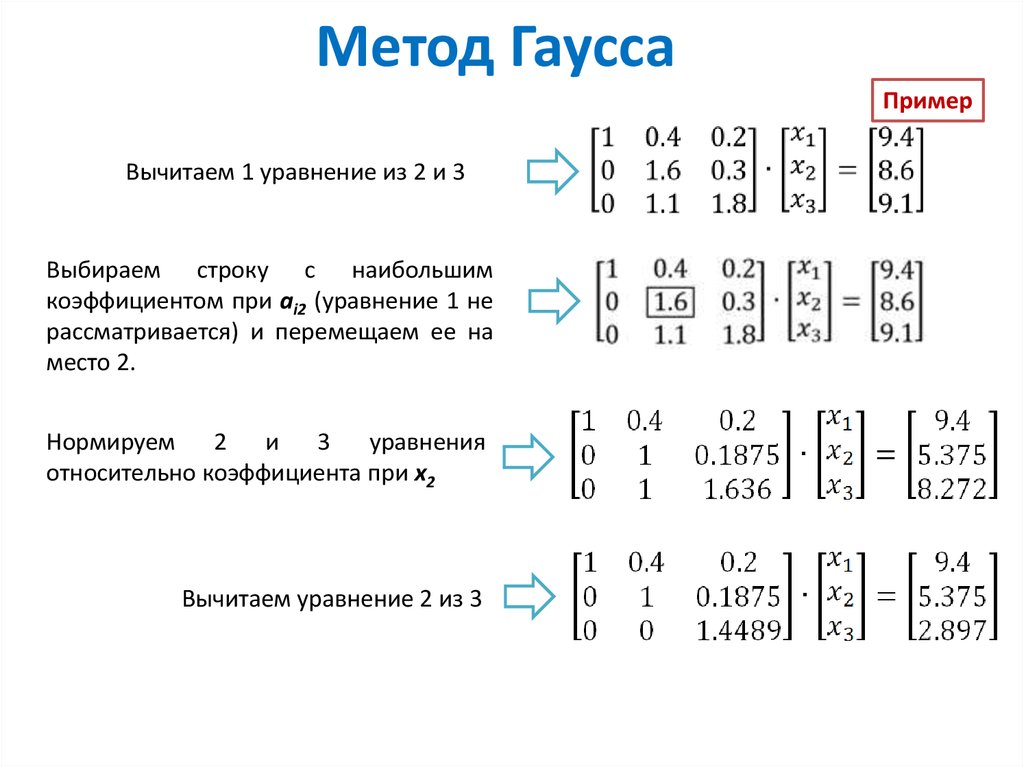 В методе исключения мы исключаем любую из переменных, используя основные арифметические операции, а затем упрощаем уравнение, чтобы найти значение другой переменной. Затем мы можем подставить это значение в любое из уравнений, чтобы найти значение исключаемой переменной.
В методе исключения мы исключаем любую из переменных, используя основные арифметические операции, а затем упрощаем уравнение, чтобы найти значение другой переменной. Затем мы можем подставить это значение в любое из уравнений, чтобы найти значение исключаемой переменной. 1. Что такое метод исключения? 2. Решение систем уравнений методом исключения 3. шагов по использованию метода исключения 4. Система решения 3 уравнений с использованием метода исключения 5. Часто задаваемые вопросы о методе исключения Что такое метод исключения?
Согласно определению метода исключения, речь идет об исключении одного из терминов, содержащих любую из переменных, для упрощения вычислений. Это делается путем умножения или деления числа на уравнение (я) таким образом, чтобы коэффициенты любого из переменных членов стали одинаковыми. Затем мы добавляем или вычитаем оба уравнения, чтобы исключить или удалить этот член из результата. Поэтому метод исключения также называют методом сложения. Например, давайте решим два линейных уравнения, содержащих две переменные, методом исключения.
Это делается путем умножения или деления числа на уравнение (я) таким образом, чтобы коэффициенты любого из переменных членов стали одинаковыми. Затем мы добавляем или вычитаем оба уравнения, чтобы исключить или удалить этот член из результата. Поэтому метод исключения также называют методом сложения. Например, давайте решим два линейных уравнения, содержащих две переменные, методом исключения.
Решение систем уравнений методом исключения
Метод исключения используется для решения систем уравнений путем исключения переменной и определения значения переменной для поиска решения. Ниже приведено изображение, показывающее применение метода исключения для решения системы уравнений с двумя переменными. Рассмотрим два уравнения x – 2y = 8 и 2x + y = 5.
шагов по использованию метода исключения
Метод исключения полезен для решения линейных уравнений, содержащих две или три переменные. Мы также можем решить три уравнения, используя этот метод. Но его можно применить только к двум уравнениям одновременно. Рассмотрим этапы решения системы уравнений методом исключения.
Но его можно применить только к двум уравнениям одновременно. Рассмотрим этапы решения системы уравнений методом исключения.
- Шаг 1: Первый шаг — умножить или разделить оба линейных уравнения на ненулевое число, чтобы получить общий коэффициент любой из переменных в обоих уравнениях.
- Шаг 2: Сложите или вычтите оба уравнения так, чтобы исключить одни и те же члены.
- Шаг 3: Упростите результат, чтобы получить окончательный ответ от пропущенной переменной (скажем, y), чтобы мы получили ответ только в форме y=c, где c — любая константа.
- Шаг 4: Наконец, подставьте это значение в любое из данных уравнений, чтобы найти значение другой заданной переменной.
Это шаги метода исключения для решения одновременных линейных уравнений. Давайте возьмем пример двух линейных уравнений x + y = 8 и 2x-3y = 4, чтобы лучше понять его.
Пусть x + y = 8 → (1) и 2x – 3y = 4 → (2)
Шаг 1: Чтобы сделать коэффициенты при x равными, умножьте уравнение (1) на 2 и уравнение (2) на 1. , Мы получаем,
, Мы получаем,
(x+y=8) × 2 → (1)
(2x-3y=4) × 1 → (2)
Итак, теперь у нас есть два уравнения: 2x + 2y = 16 → (1) и 2x – 3y = 4 → (2).
Шаг 2: Вычтем уравнение 2 из 1, получим y=12/5.
Шаг 3: Подставляем значение y в уравнение 1, получаем x + 12/5 = 8
x = 8 – 12/5
x = 28/5
Следовательно, x = 28/5 и y=12/5.
Но что, если при умножении ненулевой константы мы получим равные коэффициенты обеих переменных? Что, если оба члена были исключены при добавлении или вычитании? Такие случаи мы получаем при решении уравнений параллельных и совпадающих прямых. Уравнения двух пересекающихся прямых будут иметь только два непротиворечивых решения, а уравнения двух параллельных прямых не имеют решений, так как эти прямые никогда не пересекаются друг с другом. И уравнения совпадающих прямых имеют бесконечно много решений, поскольку они лежат друг на друге, поэтому каждая точка является пересечением или общей точкой этих прямых. Рассмотрим подробно каждый из этих двух случаев.
Рассмотрим подробно каждый из этих двух случаев.
Метод исключения: Нет решений
Как известно, уравнения двух параллельных прямых не имеют решений. Итак, если мы решим любые такие уравнения методом исключения, мы получим ответ в виде двух неравных чисел по обе стороны от знака неравно. Например, 0≠8, -2≠0 и т. д. В таких случаях мы не можем исключить только одну переменную. Обе переменные удаляются. Например, решим два уравнения 2x – y = 4 → (1) и 4x – 2y = 7 → (2) методом исключения. Чтобы сделать коэффициенты x равными в обоих уравнениях, мы умножаем уравнение (1) на 2 и уравнение (2) на 1. Таким образом, мы получаем, 4x – 2y = 8 → (3) и 4x – 2y = 7 → (4). Теперь, если мы попытаемся вычесть уравнение 4 из уравнения 3, мы получим 0=1, так как обе переменные исключаются. Другого способа решить эти уравнения нет, так как решения противоречивы. Итак, в методе исключения, когда решения нет, мы получаем результат в таком виде.
Метод исключения: бесконечно много решений
Два уравнения совпадающих прямых имеют бесконечно много возможных решений. Итак, если методом исключения решить систему уравнений совпадающих прямых, то получится непротиворечивая система с бесконечными решениями. В таких случаях мы получаем ответ в виде 0=0, если применяем метод исключения. Например, попробуйте решить уравнения x+y=2 и 2x+2y-4=0. Если вы умножите любую ненулевую константу на оба уравнения, вы обнаружите, что каждый раз, когда члены переменной x и члены переменной y отменяются или исключаются. Итак, в методе исключения, когда возможных решений бесконечно много, мы получаем результат в виде 0=0. Рекомендуется проверить, являются ли заданные линейные уравнения пересекающимися, параллельными или совпадающими прямыми, прежде чем пытаться их решить. Прочтите эту статью, чтобы узнать о решениях линейных уравнений.
Итак, если методом исключения решить систему уравнений совпадающих прямых, то получится непротиворечивая система с бесконечными решениями. В таких случаях мы получаем ответ в виде 0=0, если применяем метод исключения. Например, попробуйте решить уравнения x+y=2 и 2x+2y-4=0. Если вы умножите любую ненулевую константу на оба уравнения, вы обнаружите, что каждый раз, когда члены переменной x и члены переменной y отменяются или исключаются. Итак, в методе исключения, когда возможных решений бесконечно много, мы получаем результат в виде 0=0. Рекомендуется проверить, являются ли заданные линейные уравнения пересекающимися, параллельными или совпадающими прямыми, прежде чем пытаться их решить. Прочтите эту статью, чтобы узнать о решениях линейных уравнений.
Система решения 3 уравнений с использованием метода исключения
Чтобы решить систему трех линейных уравнений методом исключения, сначала убедитесь, что уравнения записаны в стандартной форме Ax+By+C=0 или Ax+By=C без дробного коэффициента. Возьмите любые два уравнения в соответствии с вашим удобством и выберите переменную для исключения. Удалите выбранную переменную. Теперь выберите другую пару уравнений из данных трех уравнений и исключите ту же переменную. Таким образом, вы получите два уравнения только с двумя переменными. Решите их, используя шаги метода исключения, упомянутые выше, и найдите значения этих двух переменных. Подставьте значения в любое из данных уравнений, чтобы найти значение третьей переменной.
Возьмите любые два уравнения в соответствии с вашим удобством и выберите переменную для исключения. Удалите выбранную переменную. Теперь выберите другую пару уравнений из данных трех уравнений и исключите ту же переменную. Таким образом, вы получите два уравнения только с двумя переменными. Решите их, используя шаги метода исключения, упомянутые выше, и найдите значения этих двух переменных. Подставьте значения в любое из данных уравнений, чтобы найти значение третьей переменной.
Давайте решим три уравнения 3x-y+2z=5, 4x+2y-z=6 и 5x-3y+z=1 для лучшего понимания.
Итак, мы нашли, что x=1. Подставляем это значение в уравнение P, получаем 9×(1)-y=7.
9-y=7
y=2
Теперь подставим значения x и y в третье уравнение 5x-3y+z=1, и мы получим z=2. Следовательно, x=1, y=2 и z=2.
Важные замечания по методу исключения
- Метод исключения используется для решения системы уравнений.
- Этот метод прост и упрощает расчеты, поскольку исключает одну переменную и, следовательно, сокращает объем вычислений.

- Мы делаем коэффициент переменной одинаковым, чтобы исключить соответствующую переменную.
Похожие статьи
- Калькулятор метода исключения
- Метод замены
- Решатель системы уравнений
- Метод перекрестного умножения
- Графическое решение пары линейных уравнений
- Решение линейных уравнений
Часто задаваемые вопросы о методе исключения
Что такое метод исключения в математике?
В математике метод исключения используется для решения системы линейных уравнений. Это наиболее широко используемый и простой метод, так как он требует меньше вычислений и шагов. В этом методе мы исключаем одну из двух переменных и пытаемся решить уравнения с одной переменной. Найденное здесь значение можно подставить в любое из приведенных уравнений, чтобы найти также значение другой переменной.
Как решать линейные уравнения методом исключения?
Одновременные линейные уравнения могут быть решены методом исключения. Прежде всего убедитесь, что уравнения записаны в стандартной форме либо Ax+By=C, либо Ax+By+C=0. В этом методе мы умножаем оба уравнения на ненулевое число, чтобы сделать коэффициенты любой одной переменной равными. Затем мы добавляем или вычитаем уравнения, чтобы исключить одну из переменных и найти значение другой переменной. Вот как мы решаем линейные уравнения методом исключения.
Прежде всего убедитесь, что уравнения записаны в стандартной форме либо Ax+By=C, либо Ax+By+C=0. В этом методе мы умножаем оба уравнения на ненулевое число, чтобы сделать коэффициенты любой одной переменной равными. Затем мы добавляем или вычитаем уравнения, чтобы исключить одну из переменных и найти значение другой переменной. Вот как мы решаем линейные уравнения методом исключения.
Какие этапы метода ликвидации?
Шаги метода исключения приведены ниже:
- Выберите любую переменную для исключения. Умножьте или разделите оба уравнения с ненулевой константой, чтобы сделать коэффициенты этой переменной равными.
- Сложите или вычтите полученные уравнения так, чтобы исключить выбранную переменную.
- Упростите и найдите значение другой переменной.
- Подставьте это значение в любое из приведенных уравнений, чтобы найти значение исключаемой переменной.
Можно ли использовать метод исключения для решения системы уравнений с тремя переменными?
Да, метод исключения можно использовать для решения линейных уравнений с тремя переменными. С тремя уравнениями мы берем любые два уравнения и выбираем переменную, которую нужно исключить. Затем мы повторяем тот же процесс, беря другую пару уравнений и исключая ту же переменную. Таким образом, у нас останутся два уравнения только с двумя переменными, которые можно решить методом исключения. Наконец, мы помещаем значения этих двух переменных в любое из данных уравнений, чтобы найти значение третьей переменной.
С тремя уравнениями мы берем любые два уравнения и выбираем переменную, которую нужно исключить. Затем мы повторяем тот же процесс, беря другую пару уравнений и исключая ту же переменную. Таким образом, у нас останутся два уравнения только с двумя переменными, которые можно решить методом исключения. Наконец, мы помещаем значения этих двух переменных в любое из данных уравнений, чтобы найти значение третьей переменной.
Когда следует использовать метод исключения?
Метод исключения лучше использовать, когда коэффициенты какой-либо одной переменной в уравнениях одинаковы. Например, 3x+7y+2=0 и 3x-4y+5=0. Другими методами решения линейных уравнений являются метод подстановки, метод перекрестного умножения, графический метод и матричный метод.
В чем разница между методом исключения и методом замены?
Разница между методом замены и методом исключения заключается в том, что в методе замены мы находим значение одной переменной через другую переменную. Затем мы подставляем это значение во второе уравнение, чтобы найти значение другой переменной.



 Алгоритм метода состоит из
двух этапов. Первый этап называется прямым ходом метода и заключается в
последовательном исключении неизвестных
из уравнений, т.е. в приведении матрицы А к верхнему треугольному виду (ниже
главной диагонали все нули). Для этого
на первом шаге разделим первое уравнение
системы на а11 (предположим, что коэффициент а11 ¹ 0, в противном случае
осуществляем перестановку уравнений
системы). Обозначим коэффициенты полученного
Алгоритм метода состоит из
двух этапов. Первый этап называется прямым ходом метода и заключается в
последовательном исключении неизвестных
из уравнений, т.е. в приведении матрицы А к верхнему треугольному виду (ниже
главной диагонали все нули). Для этого
на первом шаге разделим первое уравнение
системы на а11 (предположим, что коэффициент а11 ¹ 0, в противном случае
осуществляем перестановку уравнений
системы). Обозначим коэффициенты полученного  е.
е. Рекомендуется также
масштабировать предварительно каждое
уравнение исходной системы, разделив
на его наибольший по абсолютной величине
коэффициент. Это делает рост элементов
промежуточных матриц ограниченным.
Рекомендуется также
масштабировать предварительно каждое
уравнение исходной системы, разделив
на его наибольший по абсолютной величине
коэффициент. Это делает рост элементов
промежуточных матриц ограниченным.