Физика. Конспект. Мощность | 7 класс Онлайн
Конспект по физике для 7 класса «Мощность». ВЫ УЗНАЕТЕ: Что такое мощность. Как рассчитать мощность. Единицы мощности. ВСПОМНИТЕ: Что такое механическая работа? Как рассчитать механическую работу?
Конспекты по физике Учебник физики Тесты по физике
Слово «мощность» всем нам хорошо знакомо и употребляется достаточно часто. Мы говорим, что один автомобиль мощнее другого, и, как нам кажется, хорошо понимаем, что означают эти слова.
ОПРЕДЕЛЕНИЕ МОЩНОСТИ
В физике существует физическая величина «мощность», которая напрямую связана с понятием работы.
Нам всем хорошо известно, что одна и та же работа может быть совершена за разное время. Например, лошадь, везущая груженые сани, может в одном случае двигаться медленно и перевезти их на определённое расстояние за полчаса. В другом случае та же лошадь, двигаясь быстрее, перевезёт эти же сани на то же самое расстояние за меньшее время. В этом примере одна и та же механическая работа совершается за разное время.
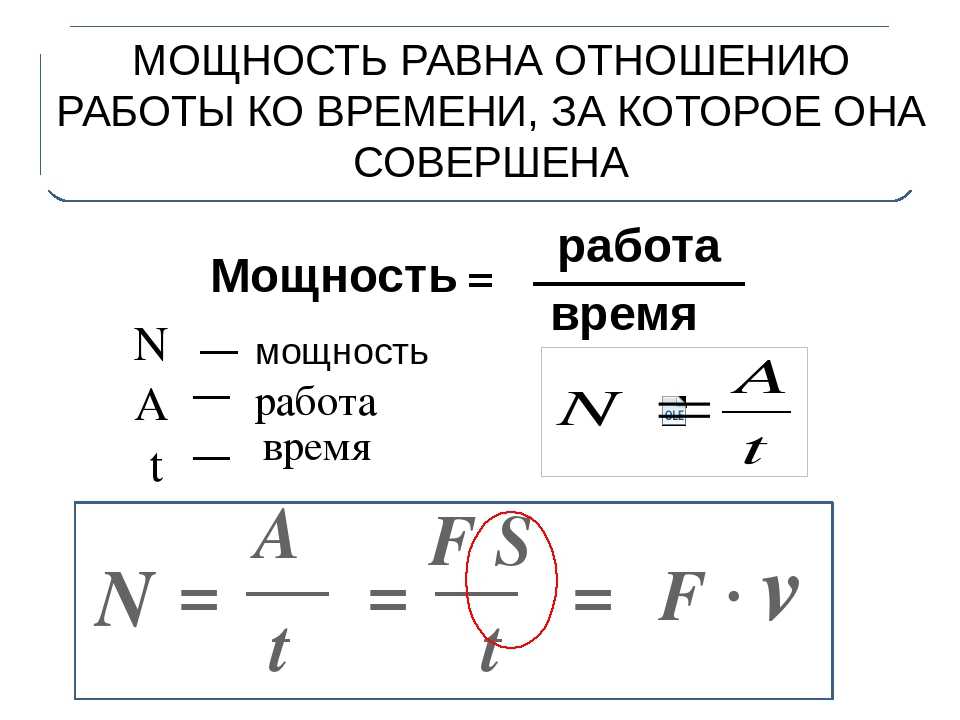
Физическую величину, характеризующую быстроту выполнения работы, называют мощностью. Мощность показывает, какая работа совершается за единицу времени. Таким образом, чтобы найти мощность, надо механическую работу разделить на время, за которое она совершена.
Мощность равна отношению работы ко времени, за которое она была совершена.
ЕДИНИЦЫ МОЩНОСТИ
За единицу мощности принимают такую мощность, при которой за 1 с совершается работа в 1 Дж. Эту единицу называют ваттом (Вт) в честь английского учёного Джеймса Уатта.
1 Вт = 1 Дж/с.В технике широко используют более крупные единицы мощности — киловатт (кВт) и мегаватт (МВт), а также более мелкую единицу милливатт (мВт): 1 МВт = 1000 000 Вт, 1 кВт = 1000 Вт, 1 мВт = 0,001 Вт. Также применяется внесистемная единица мощности лошадиная сила (1л.с.): 1 л.с. = 735,5 Вт.
Джеймс Уатт — английский изобретатель, первым построивший паровую машину, в качестве единицы мощности использовал лошадиную силу. С её помощью он сравнивал работоспособность лошади и своей паровой машины. Эту единицу часто используют и в наши дни для характеристики мощности двигателей автомобиля. Однако мощность, равная одной «лошадиной силе» (735,5 Вт) на самом деле значительно больше той, которую средняя лошадь способна развивать сколько-нибудь долгое время.
С её помощью он сравнивал работоспособность лошади и своей паровой машины. Эту единицу часто используют и в наши дни для характеристики мощности двигателей автомобиля. Однако мощность, равная одной «лошадиной силе» (735,5 Вт) на самом деле значительно больше той, которую средняя лошадь способна развивать сколько-нибудь долгое время.
РЕШЕНИЕ ЗАДАЧ
Рассчитаем мощность двигателя подъёмной машины, если она может поднять кирпичи массой 500 кг на высоту 10 м за 10 с. Сравним полученную мощность с мощностью, которую развил бы рабочий, поднимая эти же кирпичи на ту же высоту, если ему потребуется для этого 1 ч. Запишем условие задачи и решим её.
Ответ: N1 = 5 кВт, N2 = 14 Вт.
Мощность является важной характеристикой любого двигателя. Различные двигатели имеют мощности от сотых и десятых долей киловатта (двигатель электрической бритвы, швейной машины) до миллионов киловатт (двигатели ракет носителей космических кораблей). Например, мощность двигателя автомобиля «Жигули» равна 75 кВт, мощность электрической плиты — 8 кBт, а мощность двигателя космического корабля составляет 20 000 000 кВт. Можно также оценить мощность человека при ходьбе, она в среднем равна 60 Вт. А мощность бегущего гепарда достигает 1 кВт.
Можно также оценить мощность человека при ходьбе, она в среднем равна 60 Вт. А мощность бегущего гепарда достигает 1 кВт.
ДЛЯ СПРАВКИ:
Джеймс Уатт (1736—1819). Английский изобретатель, создатель универсальной паровой машины, член Лондонского королевского общества.
Вы смотрели Конспект по физике для 7 класса «Мощность»: Что такое мощность. Как рассчитать мощность. Единицы мощности.
Вернуться к Списку конспектов по физике (В оглавление).
Пройти онлайн-тест «»
Работа и мощность тока – материалы для подготовки к ЕГЭ по Физике
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа электрического тока, закон Джоуля–Ленца, мощность электрического тока.Электрический ток снабжает нас энергией. Сейчас мы будем учиться эту энергию вычислять.
Откуда вообще берётся эта энергия? Она возникает за счёт работы электрического поля по передвижению свободных зарядов в проводнике. Поэтому нахождение работы поля — наша первая задача.
Поэтому нахождение работы поля — наша первая задача.
Работа тока
Рассмотрим участок цепи, по которому течёт ток . Напряжение на участке обозначим , сопротивление участка равно (рис. 1).
Рис. 1. Участок цепи
За время по нашему участку проходит заряд . Заряд перемещается стационарным электрическим полем, которое совершает при этом работу:
(1)
За счёт работы (1) на рассматриваемом участке может выделяться тепловая энергия или совершаться механическая работа; могут также протекать химические реакции. Короче говоря, данная работа идёт на увеличение энергии нашего участка цепи.
Работа (1) называется работой тока. Термин крайне неудачный — ведь работу совершает не ток, а электрическое поле. Но с укоренившейся терминологией, увы, ничего не поделаешь.
Если участок цепи является однородным, т.е. не содержит источника тока, то для этого участка справедлив закон Ома: . Подставляя это в формулу (1), получим:
Подставляя это в формулу (1), получим:
(2)
Теперь подставим в (1) вместо тока его выражение из закона Ома :
(3)
Подчеркнём ещё раз: формула (1) получена из самых общих соображений, она является основной и годится для любого участка цепи; формулы (2) и (3) получены из основной формулы с дополнительным привлечением закона Ома и потому годятся только для однородного участка.
Мощность тока
Как вы помните, мощностью называется отношение работы ко времени её совершения. В частности, мощность тока — это отношение работы тока ко времени, за которое эта работа совершена:
Из формул (1)–(3) немедленно получаем соответствующие формулы для мощности тока:
(4)
(5)
(6)
Закон Джоуля–Ленца
Предположим, что на рассматриваемом участке цепи не совершается механическая работа и не протекают химические реакции.
Таким образом, для количества теплоты, выделяющегося на данном участке цепи, мы получаем формулы:
(7)
(8)
(9)
Но часто бывает так, что не вся работа тока превращается в тепло. Например, за счёт работы тока может совершать механическую работу электродвигатель или заряжаться аккумулятор. Тепло, разумеется, будет выделяться и в этих случаях, но только на сей раз получится, что (на величину механической работы, совершённой двигателем, или химической энергии, запасённой аккумулятором).
Оказывается, что в подобных случаях остаётся справедливой формула (8): . Это — экспериментально установленный закон Джоуля-Ленца.
Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Работа и мощность тока» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Информация на странице «Работа и мощность тока» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена: 07.02.2023
Калькулятор работы и мощности
Создано Bogna Szyk
Отзыв Стивена Вудинга
Последнее обновление: 23 декабря 2022 г. и калькулятор мощности
Этот калькулятор работы и мощности поможет вам определить механическую мощность конкретного устройства. Вы также можете использовать его, чтобы узнать, какую работу будет выполнять машина данной мощности за определенный промежуток времени.
Если вы хотите рассчитать электрическую мощность, попробуйте наш калькулятор закона Ома.
Определение работы
В физике работа, совершаемая объектом, понимается как количество энергии, которое необходимо приложить для перемещения на определенное расстояние. Например, это может быть энергия, необходимая для подъема по лестнице тяжелых сумок, или кинетическая энергия, приводящая к движению тела (как описано в калькуляторе кинетической энергии).
Как правило, рассчитывается как сила, умноженная на смещение объект перемещается. Точнее говоря, это скалярное произведение этих двух величин. Измеряется в джоулях (Дж), выражается как кг·м²/с² в единицах СИ или киловатт-часах (кВтч).
Определение мощности
Мощность – это скорость изменения работы или количество работы, выполненной за определенный промежуток времени. Чем выше мощность устройства, тем больше работы оно может выполнить за заданный период времени. Измеряется в ваттах (Вт), что эквивалентно кг·м²/с³ в единицах СИ.
Как рассчитать мощность с помощью калькулятора работы и мощности
- Определить значение работы. Вы можете либо напрямую ввести это значение в наш калькулятор, либо использовать расширенный режим
Вт = 9000 Дж. - Определите время , в которое будет выполнена работа. Здесь мы можем взять
t = 60 с. - Мощность равна работе, деленной на время
P = 9000 Дж/60 с = 150 Вт. - Вы также можете использовать наш калькулятор мощности для поиска работы – просто введите значения мощности и времени .
Чтобы узнать о некоторых реальных применениях энергии, воспользуйтесь калькулятором циклической мощности!
FAQ
Как вы считаете время от питания и работы?
Так как мощность равна работе в единицу времени , продолжительность работы можно вычислить как деля работа, совершаемая силой.
Какие единицы используются для расчета работы и мощности?
Единицей работы является джоулей (Дж) , что составляет кг·м²/с² в единицах СИ. Другой стандартной единицей работы является кВтч .
Единицей мощности является ватт (Вт) , что равно числу джоулей работы, выполняемой в секунду . Однако существуют и другие единицы — их можно найти в преобразователе мощности.
Сколько джоулей в кДж?
1000 джоулей в кДж (килоджоуль). Всякий раз, когда вы видите букву k перед единицей, это означает, что единица умножается на 1000.
Сколько джоулей в 1 лошадиной силе?
Одна лошадиная сила равна 735,5 ватт или джоулей в секунду. Итак, если в течение 1 секунды совершается работа в одну лошадиную силу, это равно 735,5 джоулей . Умножьте на продолжительность работы в секундах, чтобы найти полную энергию в джоулях.
Что такое джоули в секунду?
Джоулей в секунду — это скорость работы выполненных работ, более известная как мощность . Единицей мощности является ватт (Вт) , единицами измерения которой являются Дж/с.
Bogna Szyk
Ознакомьтесь с 9 похожими значениями энергии, работы и мощности ⚡
Упругая потенциальная энергияЭнергия удараКинетическая энергия… Еще 6
7.4 Мощность – Общая физика с использованием исчисления I
7 Работа и кинетическая энергия К концу этого раздела вы сможете: Понятие работы включает в себя силу и перемещение; теорема о работе-энергии связывает чистую работу, совершаемую над телом, с разницей его кинетической энергии, вычисленной между двумя точками на его траектории. Цели обучения

[латекс] {P} _ {\ text {ave}} = \ frac {\ Delta W} {\ Delta t}. [/latex]
Затем мы можем определить мгновенную мощность (часто называемую просто мощностью ).
Мощность
Мощность определяется как скорость выполнения работы или предел средней мощности для интервалов времени, приближающихся к нулю,
[latex]P=\frac{dW}{dt}.
Если мощность постоянна в течение временного интервала, средняя мощность для этого интервала равна мгновенной мощности, а работа, выполненная агентом, поставляющим мощность, равна [latex]W=P\Delta t[/latex]. Если мощность в течение интервала меняется со временем, то выполненная работа есть интеграл мощности по времени,
[латекс]W=\int Pdt.[/латекс]
Теорема о работе-энергии описывает, как работа может быть преобразована в кинетическую энергию. Поскольку существуют и другие формы энергии, как мы обсудим в следующей главе, мы также можем определить мощность как скорость передачи энергии. Работа и энергия измеряются в джоулях, поэтому мощность измеряется в джоулях в секунду, которой в системе СИ присвоено название ватт, аббревиатура Вт: [латекс]1\,\текст{Дж/с}=1\, \text{W}[/латекс]. Другой распространенной единицей измерения мощности повседневных устройств является мощность в лошадиных силах: [latex]1\,\text{hp}=746\,\text{W}[/latex].
Пример
Мощность подтягивания
Военнослужащий массой 80 кг делает 10 подтягиваний за 10 с (рисунок). Какую среднюю мощность развивают мышцы тренирующегося при перемещении его тела? ( Подсказка: Сделайте разумные оценки для любых необходимых количеств.)
Какую среднюю мощность развивают мышцы тренирующегося при перемещении его тела? ( Подсказка: Сделайте разумные оценки для любых необходимых количеств.)
Стратегия
Работа, совершаемая против силы тяжести при движении вверх или вниз на расстояние [латекс]\Delta y[/latex], равна [latex]mg\Delta y[/latex] (если вы поднимаете и опускаете себя с постоянной скоростью , сила, которую вы прикладываете, компенсирует гравитацию на протяжении всего цикла подтягивания.) Таким образом, работа, выполняемая мышцами тренирующегося (движущими, но не ускоряющими свое тело) за полное повторение (вверх и вниз), составляет [латекс]2 мг\ Delta y.[/latex] Предположим, что [латекс]\Delta y=2\text{ft}\примерно 60\,\text{см}\text{.}[/latex] Также предположим, что длина ветвей составляет 10 % от массы тела и не входят в подвижную массу. При этих предположениях мы можем рассчитать работу, проделанную за 10 подтягиваний, и разделить на 10 с, чтобы получить среднюю мощность. 9{2})(0,6\,\text{m})}{10\,\text{s}}=850\,\text{W}\text{.}[/latex]
9{2})(0,6\,\text{m})}{10\,\text{s}}=850\,\text{W}\text{.}[/latex]
Значимость
Это типично для расхода энергии при напряженных упражнениях; в бытовых единицах это несколько больше одной лошадиной силы [латекс](1\,\text{hp}=746\,\text{W}).[/latex]
Проверьте свои знания
Оцените мощность, затрачиваемую тяжелоатлетом, поднимающим штангу массой 150 кг на 2 м за 3 с.
Show Solution980 Вт
Сила, необходимая для перемещения тела, также может быть выражена через действующие на него силы. Если сила [латекс]\mathbf{\overset{\to }{F}}[/latex] действует на тело, которое смещается [латекс]d\mathbf{\overset{\to }{r}}[/latex ] за время
[латекс] P = \ frac {dW} {dt} = \ frac {\ mathbf {\ overset {\ to {F}} \ cdot d \ mathbf {\ overset {\ to} {r}}} {dt } = \ mathbf {\ overset {\ to} {F}} \ cdot (\ frac {d \ mathbf {\ overset {\ to {r}}} {dt}) = \ mathbf {\ overset {\ to} {F}}\cdot\mathbf{\overset{\to}}{v}},[/латекс]
, где [латекс]\mathbf{\overset{\to }{v}}[/латекс] — скорость тела.
Пример
Мощность автомобиля Движение вверх по склону
Сколько мощности должен затратить автомобильный двигатель, чтобы поднять автомобиль массой 1200 кг на подъем с уклоном 15% со скоростью 90 км/ч (рисунок)? Предположим, что 25% этой мощности рассеивается на преодоление сопротивления воздуха и трения.
Рисунок 7.15 Мы хотим рассчитать мощность, необходимую для движения автомобиля в гору с постоянной скоростью.Стратегия
При постоянной скорости кинетическая энергия не изменяется, поэтому чистая работа, совершаемая для перемещения автомобиля, равна нулю. Следовательно, мощность двигателя, необходимая для движения автомобиля, равна мощности, затрачиваемой на преодоление силы тяжести и сопротивления воздуха. По предположению, 75% мощности передается против силы тяжести, что равно ,\text{sin}\,\theta ,[/latex], где [latex]\theta[/latex] — угол наклона.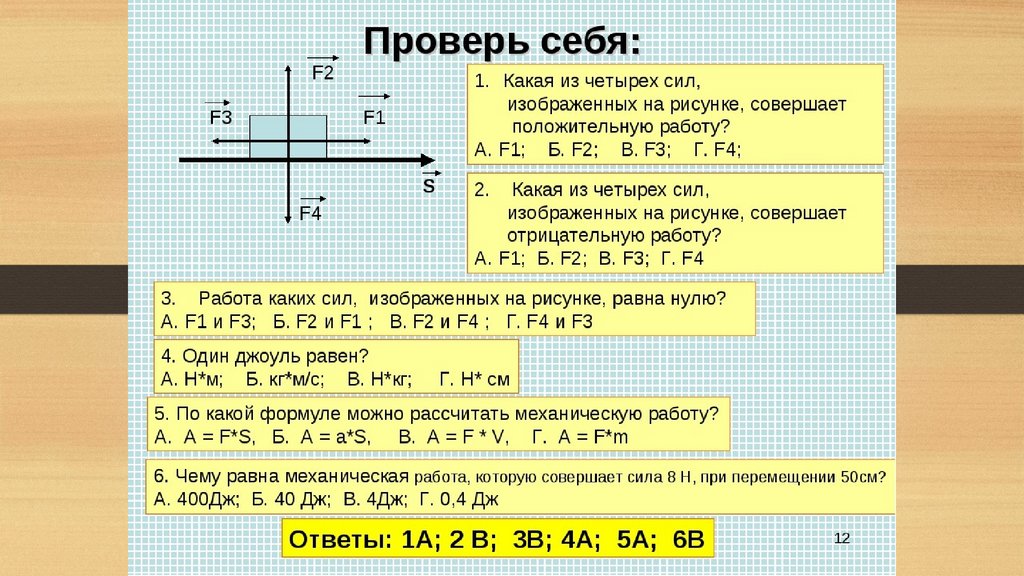 Оценка 15% означает [латекс]\текст{тангенс}\,\тета = 0,15.[/латекс] Это рассуждение позволяет нам определить требуемую мощность. 9\circ)}{0,75}=58\,\text{кВт,}[/latex]
Оценка 15% означает [латекс]\текст{тангенс}\,\тета = 0,15.[/латекс] Это рассуждение позволяет нам определить требуемую мощность. 9\circ)}{0,75}=58\,\text{кВт,}[/latex]
или около 78 л.с. (Вы должны указать шаги, используемые для преобразования единиц.)
Значимость
Это разумное количество мощности для двигателя автомобиля малого и среднего размера, чтобы обеспечить [латекс](1\,\text{л.с.}= 0,746\,\text{кВт}\text{).}[/latex] Обратите внимание, что это только мощность, затраченная на движение автомобиля. Большая часть мощности двигателя уходит куда-то еще, например, на отработанное тепло. Вот почему автомобилям нужны радиаторы. Любая оставшаяся мощность может быть использована для ускорения или для управления аксессуарами автомобиля.
Резюме
- Мощность – это скорость выполнения работы; то есть производная работы по времени.
- В качестве альтернативы, работа, выполненная за интервал времени, является интегралом мощности, подаваемой за интервал времени.
- Мощность, передаваемая силой, действующей на движущуюся частицу, является скалярным произведением силы и скорости частицы.
Ключевые уравнения
| Работа силы над бесконечно малым перемещением | [латекс] dW = \ mathbf {\ overset {\ to {F}} \ cdot d \ mathbf {\ overset {\ to {r}} = | \ mathbf {\ overset {\ to {F}} ||d\mathbf{\overset{\to}}{r}}|\text{cos}\,\theta[/latex] |
| Работа силы, действующей на пути от А до В | [латекс] {W} _ {AB} = \ underset {\ text {path} AB} {\ int} \ mathbf {\ overset {\ to {F}} \ cdot d \ mathbf {\ overset {\ to {r}}[/латекс] |
| Работа, совершаемая постоянной силой кинетического трения | [латекс]{W}_{\text{fr}}=\text{−}{f}_{k}|{l}_{AB}|[/latex] 9{2}}{2 м}[/латекс] |
| Теорема о работе-энергии | [латекс] {W} _ {\ text {net}} = {K} _ {B} – {K} _ {A} [/ латекс] |
| Мощность как скорость выполнения работы | [латекс]P=\frac{dW}{dt}[/латекс] |
| Мощность как скалярное произведение силы и скорости | [латекс] P = \ mathbf {\ overset {\ to {F}} \ cdot \ mathbf {\ overset {\ to {v}} [/latex] |
Концептуальные вопросы
Мощность большинства электроприборов измеряется в ваттах. Зависит ли этот рейтинг от того, как долго прибор включен? (В выключенном состоянии это устройство с нулевой мощностью.) Объясните с точки зрения определения мощности.
Зависит ли этот рейтинг от того, как долго прибор включен? (В выключенном состоянии это устройство с нулевой мощностью.) Объясните с точки зрения определения мощности.
Приборы оцениваются по потребляемой энергии за относительно небольшой интервал времени. Не имеет значения, как долго прибор включен, важна лишь скорость изменения энергии в единицу времени.
Объясните с точки зрения определения мощности, почему потребление энергии иногда указывается в киловатт-часах, а не в джоулях. Какова связь между этими двумя энергетическими единицами?
Искра статического электричества, которую можно получить от дверной ручки в холодный сухой день, может иметь мощность в несколько сотен ватт. Объясните, почему вы не ранены такой искрой.
Показать решениеИскра возникает в течение относительно короткого промежутка времени, поэтому вашему телу передается очень небольшое количество энергии.
Зависит ли работа, совершаемая при подъеме предмета, от скорости его подъема? Зависит ли затрачиваемая мощность от того, как быстро он поднимается?
Может ли мощность, затрачиваемая силой, быть отрицательной?
Показать решение Если сила антипараллельна или направлена в направлении, противоположном скорости, затрачиваемая мощность может быть отрицательной.
Как 50-ваттная лампочка может потреблять больше энергии, чем 1000-ваттная духовка?
Проблемы
Человек в хорошей физической форме может выдавать 100 Вт полезной мощности в течение нескольких часов подряд, например, крутя педали механизма, который приводит в действие электрогенератор. Пренебрегая любыми проблемами эффективности генератора и практическими соображениями, такими как время отдыха: (a) Сколько людей потребуется, чтобы запустить электрическую сушилку для белья мощностью 4,00 кВт? б) Сколько человек потребуется, чтобы заменить крупную электростанцию мощностью 800 МВт?
Показать раствора. 40; б. 8 миллионов
Какова стоимость эксплуатации электрических часов мощностью 3,00 Вт в течение года, если стоимость электроэнергии составляет 💲0,0900 за [латекс]\текст{кВт}\cdot \text{ч}[/латекс]?
Большой бытовой кондиционер может потреблять 15,0 кВт электроэнергии. Какова стоимость эксплуатации этого кондиционера 3,00 часа в день за 30,0 дня, если стоимость электроэнергии составляет 💲0,110 за [латекс]\текст{кВт}\cdot \text{ч}[/латекс]?
Показать решение💲149
(a) Какова средняя потребляемая мощность в ваттах устройства, потребляющего 5,00 [латекс]\текст{кВт}\cdot \текст{ч}[/латекс] энергии в день? б) Сколько джоулей энергии потребляет этот прибор в год? 9{6}\,\text{J}[/latex] полезной работы за 8 часов? б) За какое время при такой скорости этот человек поднимет 2000 кг кирпичей на высоту 1,50 м? (Работа, проделанная для подъема его тела, может быть опущена, поскольку здесь она не считается полезной. )
)
a. 208 Вт; б. 141 с
Драгстер массой 500 кг разгоняется из состояния покоя до конечной скорости 110 м/с на расстоянии 400 м (около четверти мили) и сталкивается со средней силой трения 1200 Н. Какова его средняя выходная мощность в ваттах и лошадиных силах, если это занимает 7,30 с?
(a) За какое время автомобиль массой 850 кг с полезной выходной мощностью 40,0 л.с. (1 л.с. равен 746 Вт) достигнет скорости 15,0 м/с без учета трения? б) Сколько времени займет это ускорение, если при этом автомобиль поднимется на холм высотой 3,00 м?
Показать раствора. 3,20 с; б. 4,04 с
а) Найдите полезную мощность двигателя лифта, который поднимает груз массой 2500 кг на высоту 35,0 м за 12,0 с, если он также увеличивает скорость из состояния покоя до 4,00 м/с. Обратите внимание, что общая масса уравновешенной системы составляет 10 000 кг, так что в высоту поднимается только 2 500 кг, но ускоряются полные 10 000 кг. (b) Сколько это стоит, если электричество стоит 💲0,09{5}\text{-kg}[/latex] самолет с двигателями мощностью 100 МВт, способный развивать скорость 250 м/с и высоту 12,0 км, если бы сопротивление воздуха было пренебрежимо малым? (b) Если это действительно занимает 900 с, какова мощность? в) Какова средняя сила сопротивления воздуха при этой мощности, если самолету потребуется 1200 с? ( Подсказка: Вы должны найти расстояние, которое самолет проходит за 1200 с при постоянном ускорении. \circ[/латекс] с той же скоростью. Предположим, что тормозящая сила трения в обоих случаях одинакова.
\circ[/латекс] с той же скоростью. Предположим, что тормозящая сила трения в обоих случаях одинакова.
1,7 кВт
Дополнительные задачи
Тележку тянут на расстояние D по плоской горизонтальной поверхности под действием постоянной силы F , действующей под углом [латекс]\тета[/латекс] к горизонтальному направлению. Другими силами, воздействующими на объект в это время, являются сила тяжести ([латекс]{F}_{w}[/латекс]), нормальные силы ([латекс]{F}_{N1}[/латекс]) и ([латекс ]{F}_{N2}[/latex]), и трения качения [латекс]{F}_{r1}[/латекс] и [латекс]{F}_{r2}[/латекс], как показано ниже. . Какую работу совершает каждая сила?
Рассмотрим частицу, на которую действует несколько сил, одна из которых, как известно, постоянна во времени: [латекс]{\mathbf{\overset{\to}{F}}}_{1}=(3\ ,\text{N})\mathbf{\hat{i}}+(4\,\text{N})\mathbf{\hat{j}}.[/latex] В результате частица движется по x -ось от [латекс]х=0[/латекс] до [латекс]х=5\,\текст{м}[/латекс] за некоторый интервал времени.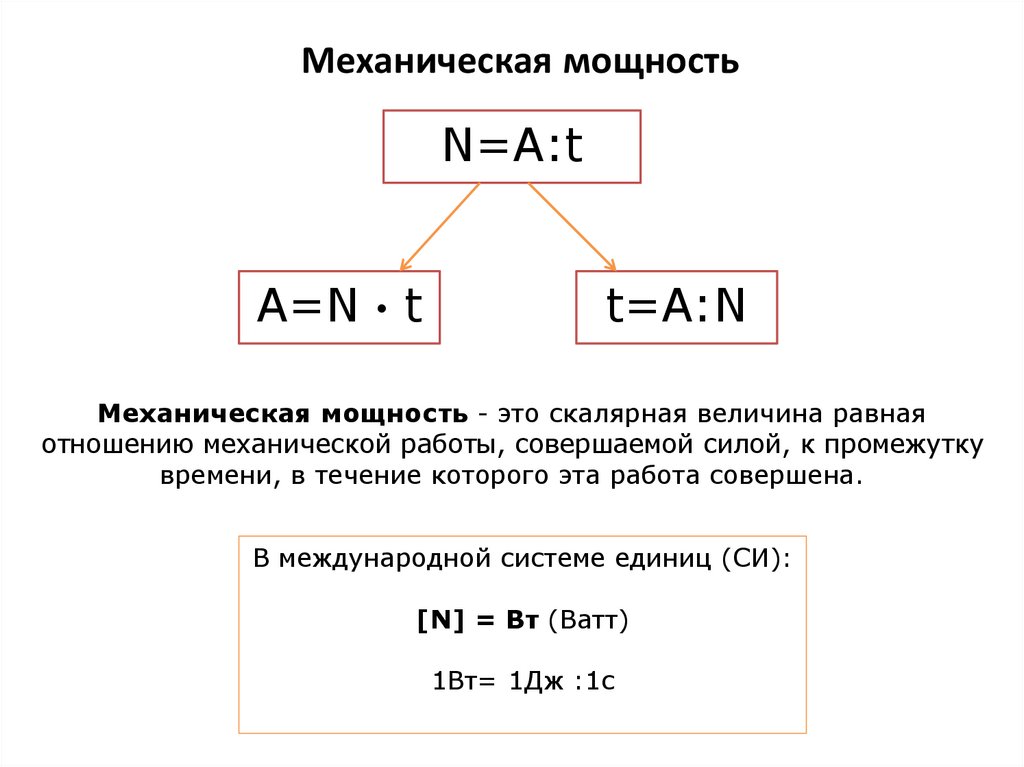 Какую работу выполняет [латекс]{\mathbf{\overset{\to}}{F}}}_{1}[/латекс]?
Какую работу выполняет [латекс]{\mathbf{\overset{\to}}{F}}}_{1}[/латекс]?
[латекс]15\,\текст{N}\cdot \текст{м}[/латекс]
Рассмотрим частицу, на которую действует несколько сил, одна из которых, как известно, постоянна во времени: [латекс]{\mathbf{\overset{\to }{F}}}_{1}=(3\,\ text{N})\mathbf{\hat{i}}+(4\,\text{N})\mathbf{\hat{j}}.[/latex] В результате частица движется сначала по x -ось от [latex]x=0[/latex] до [latex]x=5\,\text{m}[/latex] и затем параллельно y -ось от [latex]y=0 [/latex] to [latex]y=6\,\text{m}\text{.}[/latex] Какую работу выполняет [latex]{\mathbf{\overset{\to} }{F}} }_{1}[/латекс]?
Рассмотрим частицу, на которую действует несколько сил, одна из которых, как известно, постоянна во времени: [латекс]{\mathbf{\overset{\to }{F}}}_{1}=(3\,\ text{N})\mathbf{\hat{i}}+(4\,\text{N})\mathbf{\hat{j}}.[/latex] В результате частица движется по прямому пути от декартовой координаты (0 м, 0 м) до (5 м, 6 м). Какую работу выполняет [латекс]{\mathbf{\overset{\to}}{F}}}_{1}[/латекс]?
Показать решение[latex]39\,\text{N}\cdot \text{m}[/latex]
Рассмотрим частицу, на которую действует сила, зависящая от положения частицы. Эта сила определяется как [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {1} = (2y) \ mathbf {\ hat {i}} + (3x) \ mathbf {\ hat { j}}.[/latex] Найдите работу, совершаемую этой силой при перемещении частицы из начала координат в точку, расположенную на 5 метров вправо на 9\circ[/latex] над горизонталью на том же расстоянии?
Эта сила определяется как [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {1} = (2y) \ mathbf {\ hat {i}} + (3x) \ mathbf {\ hat { j}}.[/latex] Найдите работу, совершаемую этой силой при перемещении частицы из начала координат в точку, расположенную на 5 метров вправо на 9\circ[/latex] над горизонталью на том же расстоянии?
а. [латекс]208\,\текст{N}\cdot \текст{м}[/латекс]; б. [латекс] 240\,\текст{N}\cdot \текст{м}[/латекс]
Вынести ящик массой 200 кг с площадки 1 этажа в квартиру 3 этажа. Рабочие знают, что они могут либо сначала воспользоваться лифтом, а затем переместить его по третьему этажу в квартиру, либо сначала передвинуть ящик в другое место, отмеченное буквой C ниже, а затем подняться на лифте на третий этаж и сдвинуть его на третий. пол меньшее расстояние. Беда в том, что третий этаж очень неровный по сравнению с первым этажом. Учитывая, что коэффициент кинетического трения между ящиком и поверхностью пола равен 0,100, а между ящиком и поверхностью третьего этажа равен 0,300, найдите работу, которую затрачивают рабочие на каждом пути, показанном на рисунке 9. 0175 А до Е . Предположим, что силы, которую должны приложить рабочие, достаточно, чтобы сдвинуть ящик с постоянной скоростью (нулевое ускорение). Примечание: Работа лифта против силы тяжести не выполняется рабочими.
0175 А до Е . Предположим, что силы, которую должны приложить рабочие, достаточно, чтобы сдвинуть ящик с постоянной скоростью (нулевое ускорение). Примечание: Работа лифта против силы тяжести не выполняется рабочими.
Хоккейная шайба массой 0,17 кг брошена по шероховатому полу с разной шероховатостью в разных местах, что можно описать зависящим от положения коэффициентом кинетического трения. Для шайбы, движущейся по x -ось, коэффициент кинетического трения является следующей функцией x , где x выражено в метрах: [латекс]\mu (x)=0,1+0,05x.[/latex] Найдите выполненную работу кинетической силой трения хоккейной шайбы, когда она перемещается (a) из [латекс]x=0[/латекс] в [латекс]x=2\,\text{m}[/латекс] и (б) из [латекс]x=2\,\text{m}[/латекс] в [латекс]x=4\,\текст{м}[/латекс].
Показать раствора. [латекс]\текст{−}0,9\,\текст{N}\cdot \text{м}[/латекс]; б. [латекс]-0,83\,\текст{N}\cdot \текст{м}[/латекс]
Требуется горизонтальная сила 20 Н, чтобы удержать ящик массой 5,0 кг, движущийся с постоянной скоростью вверх по наклонной поверхности без трения при изменении высоты по вертикали на 3,0 м. а) Какова работа силы тяжести при этом изменении высоты? б) Какую работу совершает нормальная сила? в) Какую работу совершает горизонтальная сила?
а) Какова работа силы тяжести при этом изменении высоты? б) Какую работу совершает нормальная сила? в) Какую работу совершает горизонтальная сила?
Коробка массой 7,0 кг скользит по горизонтальному полу без трения со скоростью 1,7 м/с и сталкивается с относительно невесомой пружиной, которая сжимается на 23 см до того, как коробка останавливается. а) Какой кинетической энергией обладает ящик до столкновения с пружиной? б) Вычислите работу, совершенную пружиной. в) Определите жесткость пружины.
Показать раствора. 10. Дж; б. 10. Дж; в. 380 Н/м
Вы едете на автомобиле по прямой дороге с коэффициентом трения между шинами и дорогой 0,55. Большой кусок обломков падает прямо перед вашим взором, и вы тут же нажимаете на тормоза, оставляя след длиной 30,5 м (100 футов) перед остановкой. Полицейский видит, что ваша машина остановилась на дороге, смотрит на след заноса и выписывает вам штраф за превышение скорости 13,4 м/с (30 миль/ч). Стоит ли оспаривать штраф за превышение скорости в суде?
По неровной поверхности пола толкают ящик. Если к ящику не приложено никакой силы, ящик замедлится и остановится. Если ящик массой 50 кг, движущийся со скоростью 8 м/с, останавливается через 10 с, с какой скоростью сила трения, действующая на ящик, отбирает энергию у ящика?
Если к ящику не приложено никакой силы, ящик замедлится и остановится. Если ящик массой 50 кг, движущийся со скоростью 8 м/с, останавливается через 10 с, с какой скоростью сила трения, действующая на ящик, отбирает энергию у ящика?
160 Дж/с
Предположим, что для поддержания скорости 8 м/с ящика массой 50 кг требуется горизонтальная сила 20 Н. а) Какова мощность этой силы? (b) Обратите внимание, что ускорение ящика равно нулю, несмотря на то, что сила 20 Н действует на ящик горизонтально. Что происходит с энергией, переданной ящику в результате работы этой силы в 20 Н? 9\circ[/latex] наклон горизонтальной силой [латекс]\mathbf{\overset{\to }{F}}.[/latex] Коэффициент кинетического трения между ящиком и наклоном равен [латекс]{\mu }_{k}=0,40.[/latex] Рассчитайте работу, совершаемую (а) приложенной силой, (б) силой трения, (в) силой тяжести и (г) результирующей силой.
Показать решение Если ящик поднимается: a. 3,46 кДж; б. −1,89 кДж; в. −1,57 кДж; д. 0; Если ящик опускается: a. −0,39 кДж; б. −1,18 кДж; в. 1,57 кДж; д. 0
0; Если ящик опускается: a. −0,39 кДж; б. −1,18 кДж; в. 1,57 кДж; д. 0
Поверхность предыдущей задачи изменена так, что коэффициент кинетического трения уменьшен. К ящику приложена такая же горизонтальная сила, и после того, как его толкнули на 8,0 м, его скорость составила 5,0 м/с. Какую работу теперь совершает сила трения? Предположим, что ящик находится в состоянии покоя.
Сила F ( x ) зависит от положения, как показано ниже. Найдите работу, совершаемую этой силой над частицей при ее перемещении из [латекс]x=1,0\,\text{m}[/latex] в [латекс]x=5,0\,\text{m}\text{.} [/latex]
Показать решение8,0 Дж
Найдите работу, совершаемую той же силой на рисунке, между теми же точками [латекс]A=(0,0)\,\text{и}\,B =(2\,\text{m},2\,\text{m})[/latex], по дуге окружности радиусом 2 м с центром в точке (0, 2 м). Оцените интеграл пути с помощью декартовых координат. ( Подсказка: Возможно, вам понадобится обратиться к таблице интегралов.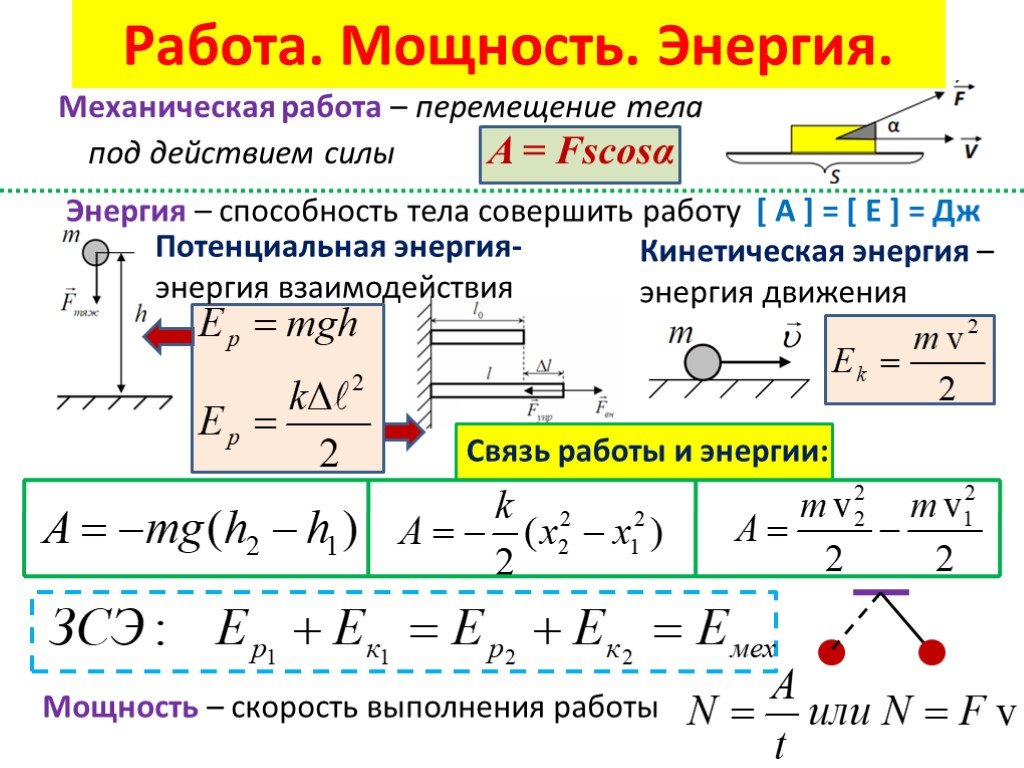 )
)
Ответьте на предыдущую задачу, используя полярные координаты.
Показать раствор35,7 Дж
Найдите работу, совершаемую той же силой на рисунке, между теми же точками [латекс]A=(0,0)\,\text{и}\,B=(2\,\text{m},2\ ,\text{m})[/latex], по дуге окружности радиусом 2 м с центром в точке (2 м, 0). Оцените интеграл пути с помощью декартовых координат. ( Подсказка: Возможно, вам понадобится обратиться к таблице интегралов.) 9{3\text{/}2}.[/latex]
Предположим, что сопротивление воздуха, с которым сталкивается автомобиль, не зависит от его скорости. Когда автомобиль движется со скоростью 15 м/с, его двигатель передает на колеса мощность 20 л.с. а) Какая мощность передается на колеса, если автомобиль движется со скоростью 30 м/с? б) Сколько энергии затрачивает автомобиль, чтобы проехать 10 км со скоростью 15 м/с? При 30 м/с? Предположим, что двигатель имеет КПД 25%. в) Ответьте на те же вопросы, если сила сопротивления воздуха пропорциональна скорости автомобиля.