Физика работа формулы: Механическая работа — урок. Физика, 9 класс.

Работа и мощность электрического тока 10 класс онлайн-подготовка на Ростелеком Лицей

Работа тока

 

Электрический ток, конечно же, не стал бы так широко использоваться, если бы не одно обстоятельство. Работу тока или же электроэнергию легко преобразовывать в любую нужную нам энергию или работу: тепловую, механическую, магнитную…

 

Для практического применения тока прежде всего хочется знать, какую работу можно обратить в свою пользу. Выведем формулу для определения работы тока: 

Формула для работы электрического поля по перемещению заряда нам уже известна:

Или же 

Узнать, какой заряд переместился полем за промежуток времени t можно из определения силы тока: 

Отсюда: 

Так как все величины, входящие в формулу, можно измерить соответствующими приборами (амперметр, вольтметр, часы), формула является универсальной.

Формулу можно также записать в несколько ином виде, используя закон Ома:

Если в исходную формулу для работы тока подставить силу тока, записанную таким образом, то получим:

Если же из закона Ома выразить напряжение, то тогда:

Использование этих формул удобно, когда в цепи присутствует какое-то одно соединение: параллельное для первого случая и последовательное для второго.

 

Закон Джоуля-Ленца

 

 

Особое внимание следует уделить тепловому действию тока. При прохождении тока через проводник, проводник нагревается. Почему это происходит? Мы уже затрагивали молекулярное строение проводников в теме о сопротивлении и отмечали, что при протекании тока свободные электроны сталкиваются с узлами кристаллической решетки. При этих столкновениях электроны постоянно придают некоторую скорость узлам решетки (рис. 1).

 

Рис. 1. Взаимодействие электронов с узлами кристаллической решетки

Так как температура – мера теплового движения, в процессе «расталкивания» температура проводника повышается. В какой-то момент наступает равновесие, когда количество энергии, получаемое проводником вследствие прохождения тока, равно количеству энергии, которое он отдает в окружающую среду.

В том случае, когда работа тока не преобразуется в механическую или же ток не имеет химического действия, работа тока эквивалентна количеству теплоты, высвобождающегося в окружающую среду.

Формулу просчета этого количества теплоты впервые независимо друг от друга открыли двое ученых: русский Эмиль Ленц (рис. 3) и англичанин Джеймс Джоуль (рис. 2).

Закон Джоуля-Ленца:

Как видно, правая часть формулы в точности повторяет одну из форм формулы для работы электрического тока.

Всегда следует помнить, что в случае, когда есть какое-либо другое преобразование энергии тока, формула Джоуля-Ленца не выполняется.

Рис. 2. Джеймс Джоуль (Источник)	Рис. 3. Эмиль Ленц (Источник)

 

Мощность тока

 

 

Наряду с работой тока очень важно отметить мощность тока, так как эта характеристика является ключевой в бытовом использовании электроэнергии (на всех бытовых приборах указано приемлемое напряжение его мощность).

 

Определение. Мощность – это работа, выполненная за единицу времени (скорость выполнения током работы):

Единица измерения мощности – ватт:

И теперь, используя наши знания о работе тока, мы без труда найдем формулу для мощности тока:

Или же, если использовать другие виды формулы для работы:

На следующем уроке мы разберем тему «Электродвижущая сила».

 

Список литературы

1. Тихомирова С. А., Яворский Б. М. Физика (базовый уровень) – М.: Мнемозина, 2012.
2. Генденштейн Л. Э., Дик Ю. И. Физика 10 класс. – М.: Илекса, 2005.
3. Мякишев Г. Я., Синяков А. З., Слободсков Б. А. Физика. Электродинамика. – М.: 2010.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «physics.ru» (Источник)
2. Интернет-портал «constant-current.narod.ru» (Источник)
3. Интернет-портал «mugo.narod.ru» (Источник)

 

Домашнее задание

1. Стр. 105: № 802–805. Физика. Задачник. 10-11 классы. Рымкевич А. П. – М.: Дрофа, 2013. (Источник)
2. Как зависит количество теплоты, которое выделяется в проводнике, в случае параллельного соединения проводников?
3. На фонарике написано «4 В; 1 Вт», а на светильнике – «220 В; 40 Вт». В какой лампе больше сила тока? Сопротивление какой лампы больше и во сколько раз?
4. * Стальной и медный провода одинаковых размеров присоединили к источнику тока сначала параллельно, а потом последовательно. В каком из проводов в каждом случае выделялось большее количество теплоты?

 

“Механическая работа. Мощность”

Сагынбаева Салтанат Какимжановна

ОШ имени Бекқұл баба

Г. АКТОБЕ

УЧИТЕЛЬ ФИЗИКИ

СТАЖ РАБОТЫ: 15 ЛЕТ

Тема урока: Механическая работа и мощность.

Цели обучения, достигаемые на этом уроке (Ссылка на учебный план): 7.2.3.8. применять формулы механической работы и мощности при решении задач

Цель урока : Все учащиеся знают формулы механической работы и мощности.

Большинство учащихся смогут

правильно применять формулы механической работы и мощности при решении задач.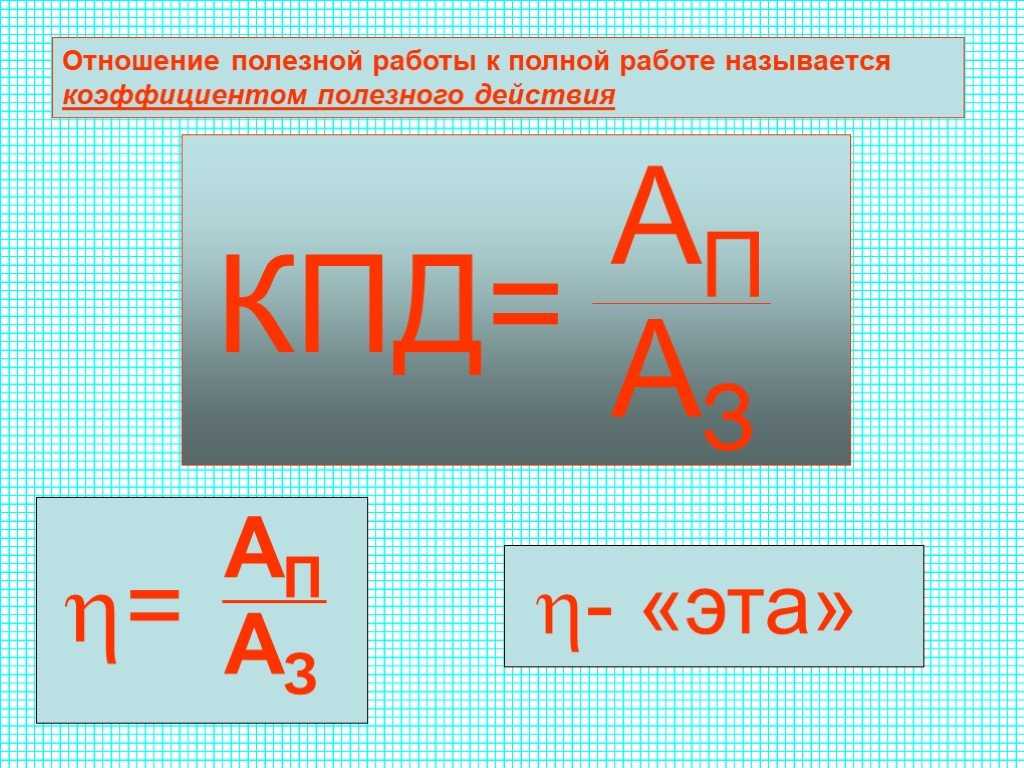

Некоторые учащиеся смогут

решать задачи с преобразованием основной формулы в вспомогательную.

Критерии оценивания: Умеют переводить единицы измерения механической работы и мощности в системе СИ.

Знают формулы механической работы и мощности

Применяют формулы механической работы и мощности

Решают задачи.

Языковые задачи: Используют термины и определения механической работы и мощности.

Ключевые слова и фразы:

Мощность – это

Механическая работа – это

Воспитание ценностей

Межпредметные связи

Общество Всеобщего Труда

Математика

Активные методы обучения

Групповая работа, при решении разно уровневых задач

Фронтальный опрос в начале урока, опрос по пройденной теме, стратегия «Бросание мяча»

Индивидуальная работа, при выполнении теста

Дифференциация

По заданиям

По уровню

По темпу

(Применяются «тонкие» и «толстые» вопросы)

(Группам даются на решение разно уровневые задачи)

(Закрепление знаний с помощью теста)

Цель урока

Научить решать учащихся задачи по теме механическая работа и мощность.

Решение в группах разноуровневых задач

А. Определите работу, совершенную при равномерном подъеме тела весом 40 Н на высоту 120 см.

В. Паровой копер поднимает на высоту 0,5 м свайный молот 15 раз минуту. Вычислите мощность, затрачиваемую на выполнение этой работы, если вес ударника 9 кН.

С. Каждую секунду насос подает 20 литров воды в водонапорную башню на высоту 10 метров. Какая работа совершается за 1 час против сил тяжести.

Этап урока

Дифференциация

От простого к сложному (3 уровня: А, В, С)

Дескриптор:

1 .Краткая запись условия задачи.

2. Определить и записать вопрос задачи.

3. Перевод единиц измерения в системе СИ.

4. Правильно записать формулу для решения задач.

5. Сделать математический расчет.

6 Записать ответ задачи.

Критериальное оценивание

Оценочный лист

№

Задача 1

1

Задача 2

 

2

 

 

3

Задача 3

 

 

 

 

 

 

Критериальное оценивание

Рефлексия

Вызов

Осмысление

Активный метод «Бросание мяча»

Эллективный тест (с использованием ИКТ)

Стратегия «Светофор»

Стратегия взаимооценивания Оценочный лист на каждую команду

Название команды___________

За правильный ответ дается жетон

№

1

З.

1

2

З.2

 

З. 3

3

 

 

 

 

 

 

 

 

Спасибо за внимание!!!

7.2 Кинетическая энергия и теорема о работе-энергии

Чистая работа и теорема о работе-энергии

Мы знаем из изучения законов Ньютона в книге «Динамика: сила» и «Законы движения Ньютона», что результирующая сила вызывает ускорение. В этом разделе мы увидим, что работа, совершаемая результирующей силой, дает системе энергию движения, и в процессе мы также найдем выражение для энергии движения.

Давайте начнем с рассмотрения общей или чистой работы, выполненной в системе. Чистая работа определяется как сумма работы, выполненной всеми внешними силами, то есть чистая работа — это работа, выполненная чистой внешней силой FnetFnet size 12{F rSub { size 8{“net”} } } {}. В форме уравнения это Wnet=FnetdcosθWnet=Fnetdcosθ size 12{W rSub { size 8{“net”} } =F rSub { size 8{“net”} } d”cos”θ} {}, где θθ size 12{ θ} {} — угол между вектором силы и вектором смещения.

На рис. 7.3(a) показан график зависимости силы от смещения для составляющей силы в направлении смещения, то есть FcosθFcosθ размера 12{F”cos”θ} {} в зависимости от dd размера 12{d} {} график. В этом случае размер FcosθFcosθ 12{F”cos”θ} {} является постоянным. Вы можете видеть, что площадь под графиком равна FdcosθFdcosθ size 12{F”cos”θ} {}, или проделанной работе. На рис. 7.3(b) показан более общий процесс, когда сила изменяется. Площадь под кривой разбита на полосы, каждая из которых имеет среднюю силу пр” \) } } } {}. Проделанная работа равна (Fcosθ)i(ave)di(Fcosθ)i(ave)di size 12{ \( F”cos”θ \) rSub { size 8{i \(“ave” \) } } d rSub { size 8{i} } } {} для каждой полосы, а общая проделанная работа представляет собой сумму WiWi size 12{W rSub { size 8{i} } } {}. Таким образом, общая проделанная работа представляет собой общую площадь под кривой, полезное свойство, к которому мы обратимся позже.

Рисунок 7.3 (a) График зависимости FcosθFcosθ от размера dd 12{d} {}, когда размер FcosθFcosθ 12{F”cos”θ} {} является постоянным. Площадь под кривой представляет собой работу силы. (b) График зависимости FcosθFcosθ размера 12{F”cos”q} {} от размера dd 12{d} {}, в котором сила изменяется. Работа, выполненная для каждого интервала, равна площади каждой полосы; таким образом, общая площадь под кривой равна общей проделанной работе.

Связи с реальным миром: работа и направление

Подумайте о вождении автомобиля. Во время движения у вас есть поступательная скорость и, следовательно, кинетическая энергия. Когда вы нажимаете на тормоза, тормоза создают силу, противоположную направлению вашего движения (действующую через колеса). Тормоза работают на вашем автомобиле и уменьшают кинетическую энергию. Точно так же, когда вы ускоряетесь, двигатель (действующий через колеса) оказывает усилие в направлении движения. Двигатель работает на вашем автомобиле и увеличивает кинетическую энергию. Наконец, если вы проходите поворот с постоянной скоростью, у вас одинаковая кинетическая энергия как до поворота, так и после него.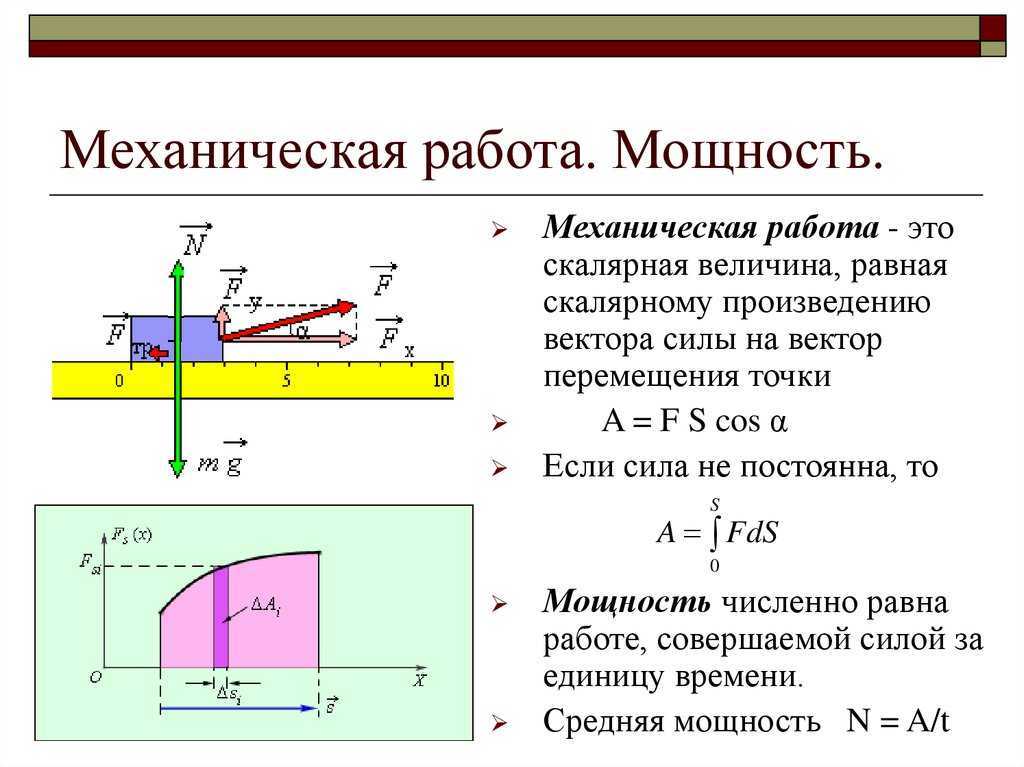 Сила, прилагаемая двигателем, была перпендикулярна направлению движения, поэтому не совершала работы и не изменяла кинетическую энергию.

Сетевую работу будет проще исследовать, если мы рассмотрим одномерную ситуацию, когда сила используется для ускорения объекта в направлении, параллельном его начальной скорости. Такая ситуация возникает для упаковки на роликовой конвейерной системе, показанной на рис. 7.4.

Рис. 7.4 Пакет на роликовой ленте толкают горизонтально на расстояние dd.

Сила тяжести и нормальная сила, действующие на упаковку, перпендикулярны смещению и не совершают работы. Кроме того, они также равны по величине и противоположны по направлению, поэтому они сокращаются при расчете результирующей силы. Чистая сила возникает исключительно из горизонтальной приложенной силы FappFapp и горизонтальной силы трения ff. Таким образом, как и ожидалось, чистая сила параллельна смещению, так что θ=0ºθ=0º и cosθ=1cosθ=1 размер 12{“cos”q=1} {}, а чистая работа определяется как

7. 7 Wnet=Fnetd.Wnet=Fnetd. size 12{W rSub { size 8{“net”} } =F rSub { size 8{“net”} } d} {}

Эффект чистой силы FnetFnet size 12{F rSub { size 8{“net”} } } {} заключается в ускорении пакета с v0v0 size 12{v rSub { size 8{0} } } {} до vv size 12 {т} {}. Кинетическая энергия упаковки увеличивается, указывая на то, что чистая работа, совершаемая над системой, положительна (см. пример 7.2). Применяя второй закон Ньютона и занимаясь алгеброй, мы можем прийти к интересному выводу. Подстановка Fnet=maFnet=ma size 12{F rSub { size 8{“net”} } = ital “ma”} {} из второго закона Ньютона дает

7.8 Wnet=безумие.Wnet=безумие. size 12{W rSub { size 8{“net”} } = ital “безумный”} {}

Чтобы получить соотношение между чистой работой и скоростью, придаваемой системе действующей на нее чистой силой, мы берем d=x−x0d=x−x0 size 12{d=x – x rSub { size 8{0} } } {} и использовать уравнение, изученное в Уравнениях движения для постоянного ускорения в одном измерении, для изменения скорости на расстоянии dd, если ускорение имеет постоянное значение aa; а именно, v2=v02+2adv2=v02+2ad. Обратите внимание, что в выражении для сети появляется aa. Решение для ускорения дает a=v2-v022da=v2-v022d. Когда aa подставляется в предыдущее выражение для WnetWnet, мы получаем

7.9 Wnet=mv2-v022dd.Wnet=mv2-v022dd.

Размер dd 12{d} {} отменяется, и мы переставляем это, чтобы получить

7.10 Wnet=12mv2−12mv0 2.Wnet=12mv2−12mv0 2. size 12{w”” lSub { size 8{ ital “net”} } = {{1} over {2} } ital “mv” rSup { size 8{2} } – { {1} over {2} } ital “mv””” lSub { size 8{0} } “” lSup { size 8{2} } “.” } {}

Это выражение называется теоремой работы-энергии, и оно фактически применимо вообще — даже для сил, которые изменяются по направлению и величине — хотя мы вывели его для частного случая постоянной силы, параллельной перемещению. Из теоремы следует, что чистая работа над системой равна изменению величины 12mv212mv2 size 12{ { {1} над {2} } ital “mv” rSup { size 8{2} } } {}. Эта величина является нашим первым примером формы энергии.

Теорема о работе-энергии

Чистая работа системы равна изменению количества 12mv212mv2 size 12{ { { size 8{1} } over { size 8{2} } } ital “mv” rSup { size 8{ 2} } } {}.

7.11 Wnet=12mv2−12mv0 2.Wnet=12mv2−12mv0 2. size 12{w”” lSub { size 8{ ital “net”} } = {{1} over {2} } ital “mv” rSup { размер 8{2} } – { {1} более {2} } ital “mv””” lSub { размер 8{0} } “” lSup { размер 8{2} } “.” } {}

Количество 12mv212mv2 size 12{ { {1} over {2} } ital “mv” rSup { size 8{2} } } {} в теореме о работе-энергии определяется как поступательная кинетическая энергия (KE) масса мм размер 12{m} {} движется со скоростью vv размер 12{v} {}. Поступательная кинетическая энергия отличается от вращательной кинетической энергии, которая рассматривается позже. В форме уравнения поступательная кинетическая энергия,

7.12 KE=12mv2,KE=12mv2, размер 12{“KE”= {{1} больше {2} } ital “mv” rSup {размер 8{2} } ,} {}

— это энергия, связанная с поступательным движением. Кинетическая энергия — это форма энергии, связанная с движением частицы, отдельного тела или системы объектов, которые движутся вместе.

Мы понимаем, что требуется энергия, чтобы разогнать объект, такой как автомобиль или пакет на рис. 7.4, до нужной скорости; однако может показаться немного удивительным, что кинетическая энергия пропорциональна квадрату скорости. Эта пропорциональность означает, например, что автомобиль, движущийся со скоростью 100 км/ч, имеет в четыре раза больше кинетической энергии, чем на скорости 50 км/ч, что помогает объяснить, почему столкновения на высокой скорости настолько разрушительны. Теперь мы рассмотрим ряд примеров, иллюстрирующих различные аспекты работы и энергии.

Применение научных методов: машинки на холме

Соберите пандус, подходящий для катания игрушечных машинок вверх и вниз. Затем запланируйте серию экспериментов, чтобы определить, как направление силы относительно скорости объекта изменяет кинетическую энергию объекта.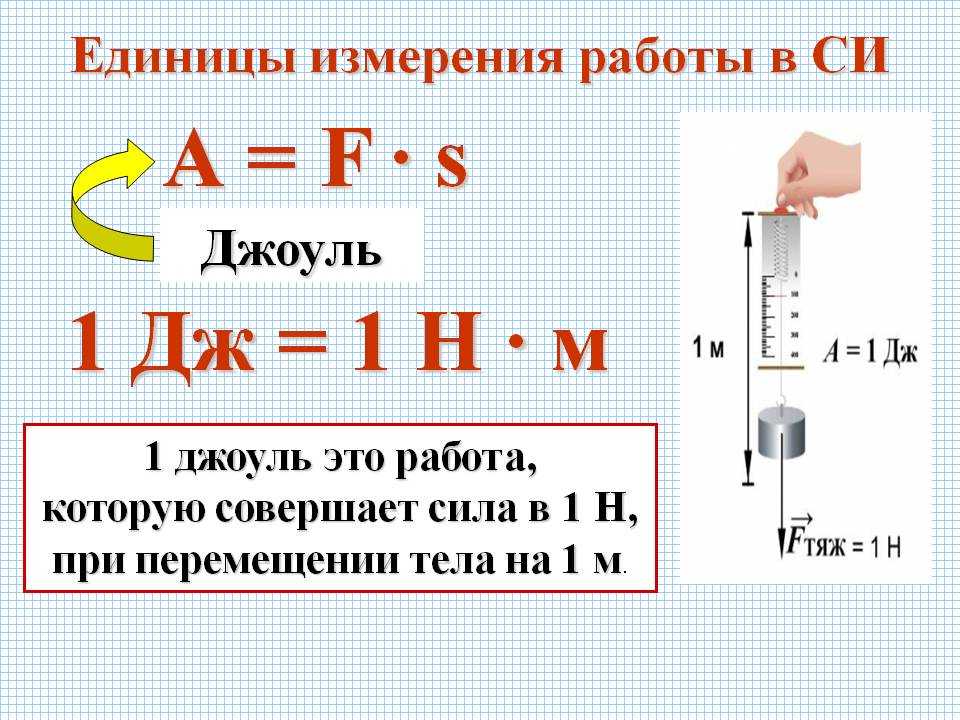 Обратите внимание, что гравитация во всех случаях будет направлена ​​вниз. Что будет, если завести машину сверху? Как насчет дна, с возрастающей начальной скоростью? Если ваша рампа достаточно широкая, что произойдет, если вы отправите игрушечную машинку прямо через нее? Влияет ли изменение поверхности рампы на ваши результаты?

Пример ответа: Когда игрушечная машинка спускается по пандусу с компонентом силы тяжести в том же направлении, кинетическая энергия увеличивается. Отправка автомобиля вверх по пандусу уменьшает кинетическую энергию, поскольку гравитация препятствует движению. Отправка автомобиля боком не должна привести к каким-либо изменениям. Если у вас есть поверхность, которая создает большее трение, чем гладкая поверхность, например ковер, обратите внимание, что трение всегда препятствует движению и, следовательно, уменьшает кинетическую энергию.

Пример 7.2 Расчет кинетической энергии упаковки

Предположим, что пакет массой 30,0 кг на роликовом ленточном конвейере на рис. 7.4 движется со скоростью 0,500 м/с. Какова его кинетическая энергия?

Стратегия

Поскольку масса mm и скорость vv заданы, кинетическая энергия может быть рассчитана по ее определению, приведенному в уравнении KE=12mv2KE=12mv2 size 12{“KE”= { {1} over {2 } } ital “mv” rSup {размер 8{2} } } {}.

Решение

Кинетическая энергия определяется выражением

7,13 KE=12mv2.KE=12mv2. size 12{“KE”= { {1} over {2} } ital “mv” rSup { size 8{2} } “.” } {}

Ввод известных значений дает

7,14 KE=0,5(30,0 кг)(0,500 м/с)2,KE=0,5(30,0 кг)(0,500 м/с)2, размер 12{“KE”=0 “.” 5 \( “30” “.” 0″ кг” \) \( 0 “.” “500”” м/с” \) rSup { размер 8{2} } ,} {}

что дает

7.15 KE=3,75 кг⋅м2/с2=3,75 Дж.KE=3,75 кг⋅м2/с2=3,75 Дж. размер 12{“KE”=3 “.” “75”‘”kg” cdot m rSup { размер 8{2} } “/s” rSup { размер 8{2} } =3 “.” “75” Дж “.” } {}

Обсуждение

Обратите внимание, что единицей кинетической энергии является джоуль, такая же, как единица работы, как упоминалось при первом определении работы. Интересно и то, что, хотя это достаточно массивный пакет, его кинетическая энергия невелика при такой относительно небольшой скорости. Этот факт согласуется с наблюдением, что люди могут перемещать такие пакеты, не утомляя себя.

Связи в реальном мире: центр масс

Предположим, у нас есть две экспериментальные тележки одинаковой массы, закрепленные вместе на гусенице со сжатой пружиной между ними. Когда защелка отпущена, пружина совершает над тележками работу 10 Дж. Мы увидим, как через пару разделов. Тележки перемещаются относительно пружины, являющейся центром масс системы. Однако центр масс остается неподвижным. Как можно учесть кинетическую энергию этой системы?

По теореме о работе-энергии работа, совершаемая пружиной над тележками, должна превращаться в кинетическую энергию. Итак, эта система имеет 10 Дж кинетической энергии. Полная кинетическая энергия системы равна кинетической энергии центра масс системы относительно фиксированного начала координат плюс кинетическая энергия каждой тележки относительно центра масс. Мы знаем, что центр масс относительно неподвижного начала координат не перемещается, и поэтому вся кинетическая энергия должна распределяться между тележками относительно центра масс. Поскольку тележки имеют одинаковую массу, каждая из них получает одинаковое количество кинетической энергии, поэтому каждая тележка имеет 5,0 Дж кинетической энергии.

В нашем примере силы между пружиной и каждой тележкой являются внутренними по отношению к системе. Согласно третьему закону Ньютона, эти внутренние силы будут сокращаться, так как они равны и противоположны по направлению. Однако это не означает, что эти внутренние силы не будут совершать работу. Таким образом, изменение кинетической энергии системы вызвано работой силы пружины и приводит к движению двух тележек относительно центра масс.

Пример 7.3 Определение работы по ускорению пакета

Предположим, что вы толкаете груз массой 30,0 кг, показанный на рис. 7.4, с постоянной силой 120 Н на расстояние 0,800 м, а средняя сила противодействующего трения составляет 5,00 Н.

(a) Рассчитайте чистую работу, выполненную на пакет. (б) Решите ту же задачу, что и в части (а), на этот раз найдя работу, совершаемую каждой силой, которая вносит вклад в результирующую силу.

Стратегия и концепция для (а)

Это движение в одномерной задаче. Сила, направленная вниз (от веса упаковки) и нормальная сила имеют одинаковую величину и противоположное направление, поэтому при расчете результирующей силы они компенсируются, в то время как приложенная сила, трение и перемещение горизонтальны (см. рис. 7.4). Как и ожидалось, чистая работа равна чистой силе, умноженной на расстояние.

Решение для (a)

Чистая сила представляет собой толкающую силу за вычетом силы трения, или Fnet = 120 Н – 5,00 Н = 115 NFnet = 120 Н – 5,00 Н = 115 Н размер 12{F rSub { размер 8{ “net”} } “= 120 Н – 5” “.” “00 Н = 115 Н”} {}. Таким образом, чистая работа равна

7,16 Wnet=Fnetd=115 N0,800 м=92,0 N⋅m=92,0 J.Wnet=Fnetd=115 N0,800 м=92,0 N⋅m=92,0 J. alignl { stack { размер 12 {W rSub { size 8{“net”} } =F rSub { size 8{“net”} } d= слева (“115” N справа) слева (0 “.” “800” справа)} { } # ” “=”92” “.” 0’N cdot m=”92″ “.” 0’J “.” {} } } {}

Обсуждение для (a)

Это значение представляет собой чистую работу, проделанную над упаковкой. Трение совершает отрицательную работу и удаляет часть энергии, затраченной человеком, и преобразует ее в тепловую энергию Чистая работа равна сумме работы, выполненной каждой отдельной силой

Стратегия и концепция (b)

К силам, действующим на упаковку, относятся сила тяжести, нормальная сила, сила трения и приложенная сила. Нормальная сила и сила тяжести перпендикулярны перемещению и, следовательно, не совершают работы.0005

Решение для (b)

Приложенная сила работает.

7.17 Wapp=Fappdcos0º=Fappd=120 N0.800 m= 96.0 J.Wapp=Fappdcos0º=Fappd=120 N0.800 m= 96.0 J.alignl { stack { size 12{W rSub { size 8{“app”} } =F rSub { size 8{“app”} } d”cos” влево (0° вправо)=F rSub { size 8{“app”} } d} {} # ” “= влево (“120 N” вправо ) влево (0 “. ” “800”” м” вправо ) {} # ” “=” 96″ “.” “0 Дж” “.” {} } } {}

Сила трения и перемещение направлены в противоположные стороны, так что θ=180ºθ=180º размер 12{θ=”180″°} {}, а работа, совершаемая трением, равна

7.18 Wfr=Ffrdcos180°=-Ffrd=-5.00 N0.800 м=-4.00 J.Wfr=Ffrdcos180°=-Ffrd=-5.00 N0.800 м=-4.00 J.alignl { stack { size 12{W rSub { size 8{“fr”} } =F rSub { size 8{“fr”} } d”cos” left (“180″° right )= – F rSub { size 8{“fr”} } d} {} # ” “= – левый (5 “.” “00 N” правый ) левый (0 “.” “800”” м” правый ) {} # ital ” “= – 4 “.” “00”Дж”.”. {} } } {}

Таким образом, количество работы, выполненной силой тяжести, нормальной силой, приложенной силой и трением, составляет соответственно

7,19 Wgr=0,WN=0,Wapp=96,0 Дж, Wfr = -4,00 J.Wgr = 0, WN = 0, Wapp = 96,0 Дж, Wfr = -4,00 J.alignl { stack { size 12 {W rSub { size 8 {“gr”}} = 0,} {} # W rSub { size 8{N} } =0, {} # W rSub { size 8{“app”} } =”96″ “.” 0″ J,” {} # W rSub { size 8{“fr”} } = – 4 “.” “00” “Дж” “.” {} } } {}

Тогда общая работа, выполненная как сумма работы, выполненной каждой силой, будет равна

7,20 Wtotal=Wgr+WN+Wapp+Wfr=92,0 J. Wtotal=Wgr+WN+Wapp +Wfr=92,0 Дж. размер 12{W rSub {размер 8{“всего”}} =W rSub {размер 8{“gr”}} +W rSub {размер 8{N}} +W rSub {размер 8{” приложение”} } +W rSub {размер 8{“fr”} } =”92″ “.”0″ J”} {}

Обсуждение для (b)

Рассчитанная общая работа WtotalWtotal size 12{W rSub { size 8{“total”} } } {} как сумма работа каждой силы согласуется с работой, как и ожидалось, WnetWnet size 12{W rSub { size 8{“net”} } } {}, совершаемой суммарной силой. Работа, совершаемая совокупностью сил, действующих на объект, может быть рассчитано с использованием любого подхода

Пример 7.4 Определение скорости по работе и энергии

Найдите скорость пакета на рисунке 7.4 в конце толчка, используя понятия работы и энергии

Стратегия

Здесь можно использовать теорему о работе-энергии, поскольку мы только что рассчитали чистую работу, WnetWnet size 12{W rSub { size 8{“net”} } } {} и начальную кинетическую энергию, 12mv0212mv02 размер 12{ { {1} более {2} } ital “mv” rSub { размер 8{0} rSup { размер 8{2} } } } {}. Эти вычисления позволяют нам найти конечную кинетическую энергию, 12mv212mv2 размер 12{ { {1} над {2} } ital “mv” rSup { размер 8{2} } } {}, и, таким образом, конечную скорость vv размер 12{v } {}.

Решение

Теорема о работе-энергии в виде уравнения:

7.21 Wnet=12mv2−12mv02.Wnet=12mv2−12mv02. size 12{W rSub { size 8{“net”} } = {{1} over {2} } ital “mv” rSup { size 8{2} } – {{1} over {2} } ital “mv” rSub { размер 8{0} rSup { размер 8{2} } } “.” } {}

Решение для 12mv212mv2 размером 12{ { {1} over {2} } ital “mv” rSup { size 8{2} } } {} дает

7.22 12mv2=Wnet+12mv02.12mv2=Wnet+12mv02 . size 12{ { {1} over {2} } ital “mv””” lSup { size 8{2} } =w rSub { size 8{ ital “net”} } + { {1} over {2} } ital “mv””” lSub { размер 8{0} } “” lSup { размер 8{2} } “.” } {}

Таким образом,

7,23 12mv2=92,0 Дж+3,75 Дж=95,75 Дж.12mv2=92,0 Дж+3,75 Дж=95,75 Дж. размер 12{ { {1} над {2} } ital “mv” rSup { размер 8{ 2} } =”92″ “.” 0’J+3 “. ” “75”‘J=”95″ “.” “75”‘J} {}

Решение конечной скорости по запросу и ввод известных значений дает

7,24 v=2(95,75 Дж)m=191,5 кг⋅м2/с230,0 кг=2,53 м/с.v=2 (95,75 Дж)м=191,5 кг⋅м2/с230,0 кг=2,53 м/с.

Обсуждение

Используя работу и энергию, мы не только приходим к ответу, но и видим, что конечная кинетическая энергия является суммой начальной кинетической энергии плюс чистая работа, выполненная на упаковке. Это означает, что работа действительно добавляет энергии упаковке.

Пример 7.5. Работа и энергия также могут показать расстояние

Как далеко уйдет пакет на рис. 7.4 после толчка, если предположить, что трение остается постоянным? Используйте соображения работы и энергии.

Стратегия

Мы знаем, что как только человек перестанет толкать, трение остановит упаковку. С точки зрения энергии трение совершает отрицательную работу до тех пор, пока оно не уберет всю кинетическую энергию упаковки. Работа, совершаемая трением, равна произведению силы трения на пройденное расстояние, умноженному на косинус угла между силой трения и перемещением; следовательно, это дает нам способ найти расстояние, пройденное после того, как человек перестанет толкать.

Решение

Нормальная сила и сила тяжести сокращаются при расчете результирующей силы. Тогда сила горизонтального трения является чистой силой, и она действует противоположно смещению, поэтому θ=180ºθ=180º. Чтобы уменьшить кинетическую энергию пакета до нуля, работа трения WfrWfr должна быть равна минус кинетическая энергия, с которой пакет стартовал, плюс то, что пакет накопил за счет толкания. Таким образом, Wfr=-95,75 JWfr=-95,75 Дж. Кроме того, Wfr=fd’cosθ= -fd’Wfr=fd’cosθ= -fd’, где d’d’ — расстояние, необходимое для остановки. Таким образом,

7,25 d′=−Wfrf=−−95,75 J5,00 N,d′=−Wfrf=−−95,75 J5,00 N, размер 12{ { {d}} sup { ‘ }= – { {W rSub { size 8{“fr”} } } over {f} } = – { { – “95” “.” “75”‘J} более {5 “. ” “00 N”} } } {}

и т. д.

7,26 d′=19,2 м.d′=19,2 м. размер 12{ { {d}} суп { ‘ }=”19″ “.” 2″ м”} {}

Обсуждение

Это решение представляет собой разумное расстояние для перемещения упаковки на конвейерной системе с относительно низким трением. Обратите внимание, что работа, совершаемая трением, отрицательна — сила действует в направлении, противоположном движению, — поэтому она удаляет кинетическую энергию.

Некоторые примеры в этом разделе можно решить без учета энергии, но за счет упущенной возможности получить представление о том, какую работу и энергию выполняют в этой ситуации. В целом решения, связанные с энергией, обычно короче и проще, чем решения, использующие только кинематику и динамику.

6.4: Теорема Работа-Энергия – Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Код страницы

14469

• Безграничный
• Безграничный

Теорема о кинетической энергии и работе-энергии

Теорема о работе-энергии утверждает, что работа всех сил, действующих на частицу, равна изменению кинетической энергии частицы.

цели обучения

• Опишите вывод теоремы работа-энергия

Теорема о работе и энергии

Принцип работы и кинетической энергии (также известный как теорема о работе и энергии) утверждает, что работа, совершаемая суммой всех сил, действующих на частицу, равна изменению кинетической энергии частица. Это определение можно распространить на твердые тела, определив работу крутящего момента и кинетической энергии вращения.

92}\]

где v _i и v _f — скорости частицы до и после приложения силы, а m — масса частицы.

Вывод

Для простоты рассмотрим случай, когда результирующая сила F постоянна как по величине, так и по направлению и параллельна скорости частицы. Частица движется с постоянным ускорением a по прямой. Связь между чистой силой и ускорением определяется уравнением 92}\).

Теорему о работе и энергии можно вывести из второго закона Ньютона.

Работа переносит энергию из одного места в другое или из одной формы в другую. В более общих системах, чем упомянутая здесь система частиц, работа может изменить потенциальную энергию механического устройства, тепловую энергию в тепловой системе или электрическую энергию в электрическом устройстве.

Ключевые термины

• крутящий момент : вращательное или скручивающее действие силы; (Единица СИ ньютон-метр или Нм; имперская единица фут-фунт или фут-фунт)

ЛИЦЕНЗИИ И ОТНОШЕНИЯ

CC ЛИЦЕНЗИОННЫЙ КОНТЕНТ, РАСПРОСТРАНЕННЫЙ РАНЕЕ

• Курирование и доработка. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike

CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ​​КОНКРЕТНОЕ АВТОРСТВО

• Теорема о работе и энергии. Предоставлено : Википедия. Расположен по адресу : en. Wikipedia.org/wiki/Work_energy_theorem%23Work-energy_principle . Лицензия : CC BY-SA: Attribution-ShareAlike
• крутящий момент. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/torque . Лицензия : CC BY-SA: Attribution-ShareAlike
• Сунил Кумар Сингх, Работа – Теорема о кинетической энергии. 2 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m14095/latest/ . Лицензия : CC BY: Attribution

---

Эта страница под названием 6.4: Теорема о работе и энергии распространяется по незаявленной лицензии и была создана, изменена и/или курирована Boundless.