Формулы работа: Механическая работа — урок. Физика, 9 класс.

что это такое, формулы, примеры задач

В этой статье я объясню, что такое работа электрического тока, какие единицы измерения для нее используются и какие важные формулы необходимо знать.

Что такое работа электрического тока?

Давайте рассмотрим обычную батарейку. По сути, батарейка преобразует химическую энергию в электрическую энергию электронов. Если теперь подключить её в электрическую цепь, то электроны могут совершать работу, используя свою электрическую энергию, например, зажигать лампочку.

Если вы хотите узнать, сколько электрической энергии было преобразовано в другой вид энергии, то вам нужно рассчитать работу электрического тока.

Определение понятия «электрическая работа» и её единицы измерения.

Работа электрического тока [A] позволяет определить, сколько электрической энергии было или может быть преобразовано в другие виды энергии.

Когда вы рассчитываете работу электрического тока, вы знаете, сколько электрической энергии было преобразовано в другие формы энергии. А уже какие другие формы энергии могут быть — это зависит от ситуации (несколько примеров в списке ниже):

• Ваш тостер преобразует электрическую энергию в тепловую;
• Когда вы включаете лампочку, электрическая энергия преобразуется в световую;
• Электродвигатель преобразует электрическую энергию в механическую.

Единицей измерения работы электрического тока в СИ является Джоуль [Дж], также часто используется в качестве единицы измерения Ватт-секунда [Вт·с]. Один джоуль всегда соответствует одной ватт-секунде. То есть 1 Дж = 1 Вт·с .

Другой важной единицей измерения является киловатт-час [кВт·ч]. Один киловатт-час равен 3 600 000 ватт-секунд или джоулей.

1 кВт·ч = 1 * 10³ Вт·ч = 1 * 10³ * 3600 Вт·с = 3,6 * 10⁶ Вт·с = 3,6 * 10⁶ Дж.

Полезный факт: а вы знали, что именно электрическую работу измеряют электросчётчики установленные в наших домах и квартирах! Электросчётчики измеряют работу электрического тока в кВт·ч.

По какой формуле вычисляется работа электрического тока?

Если вы на каком-либо участке электрической цепи под действием электрического напряжения U привели в движение заряд q, то вы можете рассчитать электрическую работу A как напряжение U, приложенное на концах этого участка цепи, умноженное на электрический заряд q, который прошёл по нему, то есть: A = U * q .

Зная, что электрический заряд, прошедший по участку цепи, можно определить, измерив силу тока и время его прохождения: q = I * t. Тогда электрическую работу A [Дж] можно определить как напряжение U [В], умноженное на силу тока I [А] и умноженное на время t [с], то есть: A = U * I * q .

Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.

Чуть ниже в статье мы разберем два практических примера, которые покажут применение данных формул. Однако перед этим мы кратко рассмотрим еще несколько важных формул.

Примечание: Вы обязательно должны запомнить первые две формулы. Следующие ниже формулы менее важны, но могут быть полезны для вас при решении тех или иных задач.

Другие формулы для определения работы электрического тока.

Закон Ома для участка цепи связывает напряжение U и ток I. Это позволяет нам рассчитать электрическую работу A другим способом.

Итак, согласно закона Ома, U = I * R или I = U / R , где R — это электрическое сопротивление.

Тогда вы можете подставить эти формулы в A = U * I * t. В итоге получатся другие формулы для нахождения работы электрического тока:

• A = I² * R * t ;
• A = (U² * t ) / R .

Примеры задач

Пример 1.

У вас есть батарея, подающая постоянное напряжение 12 В и ток 2,3 А. Вы используете эту батарею для освещения лампочки в течение 1 часа. Теперь вы хотите знать, какая работа электрического тока была произведена.

Мы знаем формулу для определения работы электрического тока: A = U * I * q, тогда получаем:

A = 12 В * 2,3 А * 1 ч = 27,6 Вт·ч .

Чтобы дать вам представление о единицах измерения, давайте переведем результат в ватт-секунды и джоули

27,6 Вт·ч = 27,6 * 3600 Вт·с = 99360 Вт·с = 99360 Дж.

Пример 2.

У вас есть батарейка с напряжением 5 В. Эта батарейка совершает электрическую работу в 10*10^-2 Вт·с. Нам нужно рассчитать рассчитать количество электрического заряда q, перемещенного между полюсами батареи.

Мы знаем формулу для определения работы электрического тока: A = U * q, тогда q = A / U. Подставляя значения в формулу получаем:

q = 10*10^-2 Вт·с / 5 В = 0,02 Кл.

Работа в Excel с формулами и таблицами для чайников

Формула предписывает программе Excel порядок действий с числами, значениями в ячейке или группе ячеек. Без формул электронные таблицы не нужны в принципе. 2= (знак равенства)РавноМеньше>БольшеМеньше или равно>=Больше или равноНе равно

Символ «*» используется обязательно при умножении. Опускать его, как принято во время письменных арифметических вычислений, недопустимо. То есть запись (2+3)5 Excel не поймет.

Программу Excel можно использовать как калькулятор. То есть вводить в формулу числа и операторы математических вычислений и сразу получать результат.

Но чаще вводятся адреса ячеек. То есть пользователь вводит ссылку на ячейку, со значением которой будет оперировать формула.

При изменении значений в ячейках формула автоматически пересчитывает результат.

Ссылки можно комбинировать в рамках одной формулы с простыми числами.

Оператор умножил значение ячейки В2 на 0,5. Чтобы ввести в формулу ссылку на ячейку, достаточно щелкнуть по этой ячейке. ;

*, /;

+, -.

Поменять последовательность можно посредством круглых скобок: Excel в первую очередь вычисляет значение выражения в скобках.



Как в формуле Excel обозначить постоянную ячейку

Различают два вида ссылок на ячейки: относительные и абсолютные. При копировании формулы эти ссылки ведут себя по-разному: относительные изменяются, абсолютные остаются постоянными.

Все ссылки на ячейки программа считает относительными, если пользователем не задано другое условие. С помощью относительных ссылок можно размножить одну и ту же формулу на несколько строк или столбцов.

1. Вручную заполним первые графы учебной таблицы. У нас – такой вариант:
2. Вспомним из математики: чтобы найти стоимость нескольких единиц товара, нужно цену за 1 единицу умножить на количество. Для вычисления стоимости введем формулу в ячейку D2: = цена за единицу * количество. Константы формулы – ссылки на ячейки с соответствующими значениями.
3. Нажимаем ВВОД – программа отображает значение умножения. Те же манипуляции необходимо произвести для всех ячеек. Как в Excel задать формулу для столбца: копируем формулу из первой ячейки в другие строки. Относительные ссылки – в помощь.

Находим в правом нижнем углу первой ячейки столбца маркер автозаполнения. Нажимаем на эту точку левой кнопкой мыши, держим ее и «тащим» вниз по столбцу.

Отпускаем кнопку мыши – формула скопируется в выбранные ячейки с относительными ссылками. То есть в каждой ячейке будет своя формула со своими аргументами.

Ссылки в ячейке соотнесены со строкой.

Формула с абсолютной ссылкой ссылается на одну и ту же ячейку. То есть при автозаполнении или копировании константа остается неизменной (или постоянной).

Чтобы указать Excel на абсолютную ссылку, пользователю необходимо поставить знак доллара ($). Проще всего это сделать с помощью клавиши F4.

1. Создадим строку «Итого». Найдем общую стоимость всех товаров. Выделяем числовые значения столбца «Стоимость» плюс еще одну ячейку. Это диапазон D2:D9
2. Воспользуемся функцией автозаполнения. Кнопка находится на вкладке «Главная» в группе инструментов «Редактирование».
3. После нажатия на значок «Сумма» (или комбинации клавиш ALT+«=») слаживаются выделенные числа и отображается результат в пустой ячейке.

Сделаем еще один столбец, где рассчитаем долю каждого товара в общей стоимости. Для этого нужно:

1. Разделить стоимость одного товара на стоимость всех товаров и результат умножить на 100. Ссылка на ячейку со значением общей стоимости должна быть абсолютной, чтобы при копировании она оставалась неизменной.
2. Чтобы получить проценты в Excel, не обязательно умножать частное на 100. Выделяем ячейку с результатом и нажимаем «Процентный формат». Или нажимаем комбинацию горячих клавиш: CTRL+SHIFT+5
3. Копируем формулу на весь столбец: меняется только первое значение в формуле (относительная ссылка). Второе (абсолютная ссылка) остается прежним. Проверим правильность вычислений – найдем итог. 100%. Все правильно.

При создании формул используются следующие форматы абсолютных ссылок:

• $В$2 – при копировании остаются постоянными столбец и строка;
• B$2 – при копировании неизменна строка;
• $B2 – столбец не изменяется.

Как составить таблицу в Excel с формулами

Чтобы сэкономить время при введении однотипных формул в ячейки таблицы, применяются маркеры автозаполнения. Если нужно закрепить ссылку, делаем ее абсолютной. Для изменения значений при копировании относительной ссылки.

Простейшие формулы заполнения таблиц в Excel:

1. Перед наименованиями товаров вставим еще один столбец. Выделяем любую ячейку в первой графе, щелкаем правой кнопкой мыши. Нажимаем «Вставить». Или жмем сначала комбинацию клавиш: CTRL+ПРОБЕЛ, чтобы выделить весь столбец листа. А потом комбинация: CTRL+SHIFT+”=”, чтобы вставить столбец.
2. Назовем новую графу «№ п/п». Вводим в первую ячейку «1», во вторую – «2». Выделяем первые две ячейки – «цепляем» левой кнопкой мыши маркер автозаполнения – тянем вниз.
3. По такому же принципу можно заполнить, например, даты. Если промежутки между ними одинаковые – день, месяц, год. Введем в первую ячейку «окт.15», во вторую – «ноя.15». Выделим первые две ячейки и «протянем» за маркер вниз.
4. Найдем среднюю цену товаров. Выделяем столбец с ценами + еще одну ячейку. Открываем меню кнопки «Сумма» – выбираем формулу для автоматического расчета среднего значения.

Чтобы проверить правильность вставленной формулы, дважды щелкните по ячейке с результатом.

Формула работы: вывод, виды работ, решаемые примеры

• Автор Анум
• Последнее изменение 03.10.2023

Формула работы: Представьте, что вы целый день сидите на стуле в одной и той же позе и безостановочно учитесь. Представьте, что кто-то подходит к вам и говорит: «Эй, ты не работал весь день!» Какой была бы ваша реакция? Вы, без сомнения, будете в ярости. Но что, если я скажу вам, что физика утверждает, что вы вообще не совершали никакой работы? Но почему это так? Это связано с тем, что работа предполагает движение.

Давайте узнаем больше о проделанной работе, ее формуле и способах ее расчета.

Работа – это внешняя энергия, передаваемая от объекта или к объекту путем приложения силы в направлении смещения объекта. Говорят, что работа совершается, когда тело перемещается из своего начального положения под действием внешней силы. Сила и перемещение являются важными компонентами для расчета выполненной работы. Таким образом, важно понимать, что никакая работа не будет выполнена, если тело не сместится. Таким образом, вы можете использовать всю свою энергию для толкания стены; если стена не сдвинется, ваша проделанная работа будет равна нулю.

Здесь важно помнить, что работа, совершаемая над телом, совершается не только перемещением тела как целого, но может быть достигнута и, скажем, сжатием газа или вращением вала, и даже вызывая невидимые движения частиц внутри тела под действием внешней магнитной силы.

Какова формула выполненной работы?

Работа считается выполненной, когда приложенная сила смещает объект с его положения. Работа, совершаемая телом, равна точечному произведению силы на вектор смещения. Проще говоря, выполненная работа равна произведению силы, действующей на объект в направлении смещения, и смещения объекта. Таким образом, формула выполненной работы может быть представлена ​​в виде:
\(W = \overrightarrow F .\overrightarrow s \)
\(W = \left( {F\,\cos \,\theta } \right)s\)

Где \(W\) – работа done
\(F\) – сила, действующая на объект.
\(с\) – водоизмещение.
\(\theta \) — угол между векторами силы и смещения.
Как мы видим выше, формула выполненной работы включает скалярное произведение силы и перемещения. Сила и перемещение являются векторными величинами, но мы знаем, что скалярное произведение двух векторных величин дает скалярную величину. Таким образом, выполненная работа является скалярной величиной. 92} = 2\overrightarrow a .\overrightarrow d \)
Подставляя это в уравнение (i), получаем:
\(W = \frac{1}{2}m \times 2\overrightarrow a . \overrightarrow d \ )
\(W = m\overrightarrow a .\overrightarrow d \)

Из второго закона Ньютона мы знаем, что сила, действующая на объект, движущийся с постоянным ускорением, может быть представлена ​​как \(\overrightarrow F = m \overrightarrow a .\)
Таким образом, выражение для проделанной работы принимает вид
\(W = \overrightarrow F .\overrightarrow d \)
Работа, совершаемая постоянной силой, равна произведению силы на перемещение объекта в направлении действия силы или скалярному произведению вектора силы на вектор смещения, т. е. \(W = \overrightarrow F .\overrightarrow d .\)

Формула работы Размер и единица измерения

Выполненная работа зависит от скалярного произведения между векторами силы и смещения. Единицей силы в СИ является ньютон \(\left( \rm{N} \right),\), а единицей перемещения в SI является метр \(\left( \rm{m} \right).\). Таким образом, Единица работы СИ может быть рассчитана как: 9{ – 2}}} \right]\)

Виды работ

Говорят, что над объектом совершается работа, когда он подвергается смещению. {\rm{o}}} \le \theta < {9{\rm{o}}}.\) Например, когда мяч свободно падает вниз, сила тяжести будет действовать вниз вместе с движением мяча. Таким образом, работа силы тяжести над шаром будет положительной.

б. Отрицательная работа: Когда сила (или составляющая силы), приложенная к объекту и смещенная в противоположном направлении, то работа, совершаемая силой над телом, называется отрицательной. Таким образом, для совершения отрицательной работы угол \(\left( \theta \right)\) между векторами силы и смещения должен быть \({\rm{9{\rm{o}}}.\) Например, когда вы бросаете мяч вертикально вверх, сила тяжести действует вниз, противоположно смещению мяча. Таким образом, работа силы тяжести будет отрицательной.

в. Нулевая работа: Когда сила, приложенная к объекту, не вызывает смещения объекта, говорят, что работа, выполненная над объектом, равна нулю. Кроме того, над объектом не совершается никакой работы, когда сила действует перпендикулярно перемещению.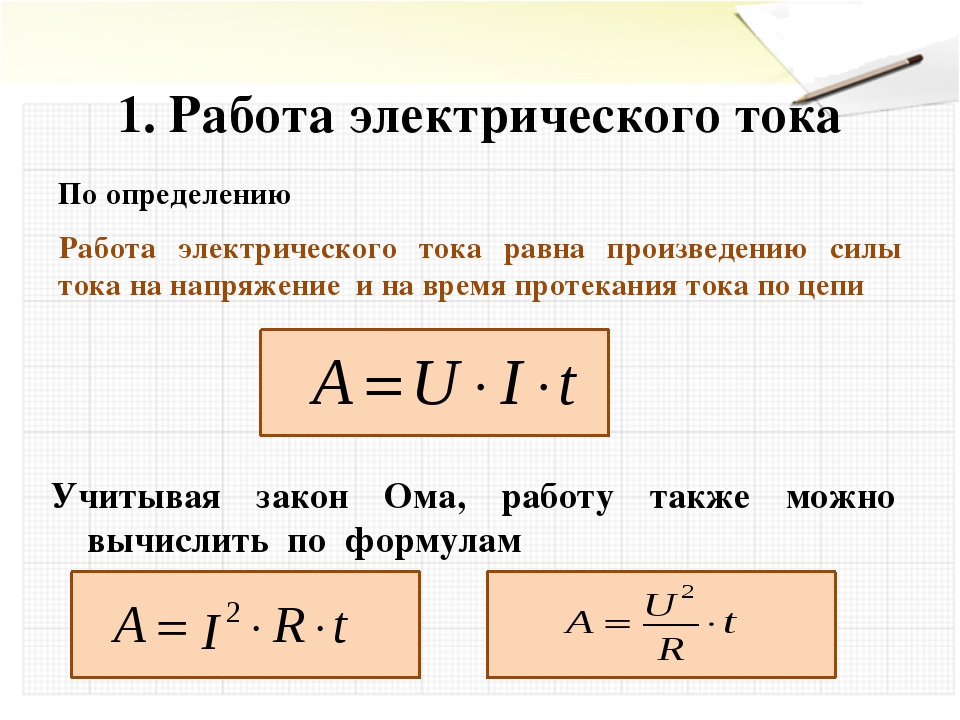 В этом случае угол между векторами силы и смещения равен \({9{\rm{o}}}.\) Например, если вы часами держите в руке тяжелый мяч. Поскольку шарик не смещается, работа, выполняемая вашей рукой, будет равна нулю, даже если ваша рука со временем устанет.

Площадь под графиком силы-перемещения

Сила, действующая на объект, может быть представлена ​​как функция смещения графически. Работу, совершаемую силой, можно рассчитать с помощью графика зависимости силы от смещения. Общая проделанная работа будет равна площади под кривой зависимости силы от смещения; здесь имейте в виду, что области над осью положения представляют собой положительную работу, а области под осью представляют отрицательную работу.

Примеры решения формул работы

Q.1. К телу приложена сила \(20\,\rm{N}\), которая смещает его на \(2\,\rm{m}\) вдоль его направления. Вычислите работу, выполненную с помощью формулы работы.
Решение: Дано: Сила \(\left( F \right) = 10\,\rm{N}\)
Перемещение \(\left( d \right) = 2\,{\rm{m }}\)
Использование формулы для работы, \(W = F. d\)
\(W = \left( {20\,\rm{N}} \right).\left( {2\,{\rm{ m}}} \right)\)
\(W = 40\,\rm{J}.\)

Q.2. Кули на вокзале несет на голове сумку весом \(200\,\rm{N}\) на некоторое расстояние. Вычислите работу силы, приложенной кули, чтобы поддержать это \(200\,\rm{N}\).

Решение: Дано: Вес мешка \( = 200\,\rm{N}\)
В этом случае вес мешка будет действовать в вертикальном направлении, а поддерживающая сила кули находится вертикально вверх. Кроме того, он движется в горизонтальном направлении. Следовательно, перемещение мешка в направлении действия силы (поддерживающей силы) равно нулю.
Используя формулу Для работы, \(W = F.d\)
\(W = \left( {200\,\rm{N}} \right).0\)
\(= 0\,\rm{J} \)
Таким образом, работа поддерживающей силы, приложенной кули к мешку, равна нулю.

Q.3. Вычислите работу, совершаемую силой \(300\,\rm{N}\) при перемещении объекта на расстояние \(14\,\rm{m}\), если объект перетаскивается горизонтально этой силой по всей поверхности.
Решение: Нам дано:
Сила \( = 300\,\rm{N}\) 9{\rm{o}}}\)
\(W = 4200\,\rm{J}.\)

Резюме

Работа определяется как энергия, передаваемая к объекту или от объекта путем приложения силы вдоль смещения в таких областях, как физика. Его часто выражают как произведение силы на перемещение в его простейшей форме. Когда сила приложена к объекту, говорят, что она производит положительную работу, если она имеет составляющую в направлении смещения места приложения. Когда у силы есть составляющая, противоположная направлению смещения в точке приложения, она вызывает отрицательную работу.

Мы можем сказать, например, что когда мяч удерживается над землей, а затем падает, работа силы тяжести, совершаемая над мячом при его падении, равна весу мяча. Смещение определяется как сила, умноженная на расстояние до земли.

Работа – это внешняя энергия, передаваемая от объекта или к объекту путем приложения силы в направлении смещения объекта. Говорят, что работа совершается, когда тело перемещается из своего начального положения под действием внешней силы. Формулу выполненной работы можно записать так:

\(W = \overrightarrow F .\overrightarrow s \) или \(W = \left( {F\,\cos \,\theta } \right)s.\)

Более того, мы узнали, что SI единица работы – Джоуль \(\left( \rm{J} \right).\) Кроме того, в зависимости от направления силы и перемещения работа может быть положительной, отрицательной или нулевой.

Часто задаваемые вопросы (FAQ) по формуле работы

Q.1. Какая работа сделана?
Ответ: Говорят, что работа совершается, когда приложенная сила заставляет тело перемещаться в его направлении.

Q.2. По какой формуле рассчитать работу?
Ответ: Формула для расчета проделанной работы: \(W = \left( {F\,\cos \,\theta } \right)s\)

Q.3. Запишите связь между выполненной работой и кинетической энергией .
Ответ: Совершенная работа равна изменению кинетической энергии тела.

Q.4. Что такое единица выполненной работы в СИ?
Ответ: Единицей выполненной работы в системе СИ является Джоуль.

Q.5. Может ли работа внешней силы быть равна нулю? Если да, приведите пример.
Ответ: Да, работа, совершаемая внешней силой, будет равна нулю, если сила не смещает объект с его положения. Например, когда мы пытаемся толкнуть кирпичную стену, она не двигается, хотя через некоторое время мы чувствуем себя опустошенными. Здесь работа, проделанная нами на стене, равна нулю.

Формула работы — объяснение, примеры, уравнения и часто задаваемые вопросы

В физике работа — это энергия, передаваемая объекту или от него посредством приложения сил вместе со смещением. Другими словами, формула работы есть произведение силы на перемещение. Работа может быть как положительной, так и отрицательной. Работа называется положительной, если и перемещение, и сила направлены в одном направлении. Работа называется отрицательной, если и перемещение, и сила направлены в противоположные стороны. Работа является скалярной величиной, поскольку она имеет только величину и не имеет направления. Единицей работы в системе СИ является Джоуль. Объяснение формулы работы будет охватывать концепции работы, выполняемой объектом, а также формулу выполненной работы и формулу работы по физике.

Что такое работа по физике?

Работа в физике — это мера передачи энергии, которая происходит, когда объект перемещается на расстояние под действием внешней силы, по крайней мере частично, в направлении перемещения. Если приложенная сила постоянна, работу можно рассчитать, умножив длину пути на составляющую силы, действующую вдоль пути. Чтобы математически выразить формулу работы, работа (W) равна силе (f), умноженной на расстояние.

Вт = Сила × Расстояние

Если сила приложена под углом θ к перемещению, то проделанная работа будет рассчитана как:

W = F d Cos θ

Примеры работы

В повседневной жизни есть много примеров работы. Давайте обсудим некоторые из них: мальчик, тянущий продуктовую тележку по коридору продуктового магазина, лошадь, тянущая плуг по полю, студентка, таскающая на плече свою сумку с книгами и т. д. В общем, чтобы работа происходила на объект должна действовать сила, заставляющая его двигаться. Человек, прижимающийся к стене, не считается работой, потому что стена не двигается. Но падение детской игрушки со стола и удар о землю считается работой, потому что сила, действующая на игрушку, заставляет ее смещаться вниз.

Уравнения работы

Уравнения работы или формулы работы сформулированы следующим образом:

W = F d Cos θ

В приведенном выше уравнении работы

W = количество работы.

F = Вектор силы.

D = Величина смещения.

θ = угол между вектором силы и вектором смещения

Единицей работы в системе СИ является джоуль, а его размерность — кг. м²/с².

Выполненная работа

Выполненная работа — это количество переданной энергии. Другими словами, говорят, что работа совершается при приложении силы. Если эта сила постоянна, то формула для работы, совершаемой силой, представляет собой скалярное произведение смещения.

\[W = \overrightarrow{F} . \overrightarrow{D}\]

Чистая работа, выполненная над объектом, равна энергии, добавленной к объекту. Это причина того, что единицей работы являются джоули, Дж. треугольник K Cos \theta\]

Это означает, что для совершения работы объект должен изменить свое положение на величину \[\triangle \overrightarrow{k}\], а сила \[\overrightarrow{F} \] действует на него так, что в направлении силы есть ненулевые компоненты. Отсюда формула выполненной работы:

\[W  = F \triangle K Cos \theta\]

W = проделанная работа (Джоули)

F = Величина силы, для которой работа рассчитывается в Ньютонах

\[\triangle K\] = Величина смещения в метрах

θ = угол между силой и направлением смещения.

Следует отметить, что F Cos θ является величиной составляющей \[\overrightarrow{F}\] в направлении \[\треугольника \overrightarrow{k}\]. если значение θ больше 90° (> 90°), то компонент считается параллельным в направлении смещения, но указывает на противоположное направление, и сила противодействует движению.

Примеры рабочих формул с решениями:

1. Школьный автобус едет по прямой горизонтальной дороге. В направлении движения автобуса действует сила 700 Н. С увеличением скорости автобус проезжает расстояние 10 м. Вычислите работу, совершенную автомобилем.

Решение:

• Величина приложенной силы, F = 700 Н.

• Общее расстояние, пройденное автобусом \[(\треугольник K)\] = 20 метров.

• Приложенная сила и расстояние, пройденное автобусом, имеют одинаковое направление.