Контрольная работа комплексные числа: Контрольная работа “Комплексные числа”

Контрольная работа № 3. Комплексные числа.

Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления

⇐ ПредыдущаяСтр 3 из 12Следующая ⇒   3.1. Даны комплексные числа и . Вычислить . 3.2. Даны числа: , . Изобразить числа на комплексной плоскости, найти модуль и аргумент, записать в тригонометрической и показательной форме. 3.3. Даны числа . Вычислить . 3.4. Решить уравнение .   Краткие теоретические сведения для выполнения контрольной работы № 3 и решение типовых задач   Действия над комплексными числами В алгебраической форме   Выражение вида (1) где х и у – произвольные действительные числа, i – мнимая единица, удовлетворяющая условию , называется алгебраической формой записи комплексного числа. Число х называется действительной частью комплексного числа z и обозначается , число у называется мнимой частью комплексного числа z и обозначается . При число совпадает с вещественным числом х, если число называется чисто мнимым. Два комплексных числа называются равными, если у них равны соответственно действительные и мнимые части: . Комплексные числа называются сопряженными, если у них равны действительные части, а мнимые противоположны по знаку; сопряженные числа обозначают . Определим основные действия над комплексными числами и , заданными в алгебраической форме. Суммой двух комплексных чисел называется комплексное число , т.е. при сложении комплексных чисел складываются действительные и мнимые части соответственно. Разностьюкомплексных чисел называется комплексное число , которое удовлетворяет равенству . Очевидно: . При нахождении разности из действительной и мнимой частей уменьшаемого z1 вычитаются соответственно действительная и мнимая части вычитаемого z2. Произведением комплексных чисел называется комплексное число . Комплексные числа перемножаются как двучлены, при этом учитывается, что . Частным от деления называется такое комплексное число z, которое удовлетворяет уравнению . Для частного имеет место формула: Чтобы разделить число z1 на z2 , следует числитель и знаменатель дроби умножить на число , сопряженное знаменателю. Возведение комплексного числа z в степень n – это нахождение произведения n сомножителей, каждый из которых равен z, т.е. . При возведении в степень n используется правило возведения в степень двучлена , в общем случае применяется формула бинома Ньютона.   Пример Даны комплексные числа . Вычислить . Решение , , , , , Тригонометрическая и показательная формы комплексного числа   Комплексное число изображается на плоскости Оху точкой М с координатами (х;у), либо вектором, начало которого находится в точке О(0;0), а конец – в точке (рис. 1).   у=Im z   М(х,у) r j 0 х=Re z Рис. 1   Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, ось Ох – действительной осью, ось Оу – мнимой осью. Число r – длина радиус-вектора точки (расстояние точки М от начала координат) называется модулем комплексного числа . ( 2 ) Угол j, который образован вектором с осью Ох и отсчитываемый от положительного направления оси Ох, называется аргументомкомплексного числа и обозначается Arg z. Аргумент комплексного числа определен с точностью до слагаемого, кратного : где – главное значение аргумента, определяемое условием . Аргумент числа неопределен. Если вектор расположен в верхней полуплоскости, то угол j отсчитывается от положительного направления оси Ох против часовой стрелки до направления вектора , в данном случае . Если вектор расположен в нижней полуплоскости, то угол j отсчитывается от положительного направления оси Ох по ходу часовой стрелки до направления вектора , в данном случае . Если , то будем считать, что . Существует несколько подходов к определению аргумента. Один из них состоит в следующем. Если , то аргумент , где . Учитывая, что , получим – ( 3 ) тригонометрической форма записи комплексного числа.   Используя формулу Эйлера , получим показательную форму комплексного числа: , ( 4 ) где – модуль, – аргумент комплексного числа. Пример Даны комплексные числа: , . Изобразить числа на комплексной плоскости, найти модуль и аргумент, записать в тригонометрической и показательной форме.   Решение (рис. 2) у     7 z5 5,5 z3 z6 2 z2z1 -7 -5,5 -3,5 0 2 6 12,1 х -2 z8 -6 z4     z7 -12,1   Рис. 2.   1. Найдем модуль и аргумент для комплексного числа . Подставляя модуль и аргумент в формулы (3) и (4), получим . 2. Для имеем: Следовательно: .   3. Для имеем:   Следовательно: . 4. Для имеем:   Следовательно: . 5. Для имеем: Следовательно: . 6. Для имеем: Следовательно: .   7. Для имеем: , Следовательно: . 8. Для имеем: . Следовательно: .   ⇐ Предыдущая12345678910Следующая ⇒ Читайте также:  Формы дистанционного обучения Передача мяча двумя руками снизу Значение правильной осанки для жизнедеятельности человека Основные ошибки при выполнении передач мяча на месте 

Последнее изменение этой страницы: 2016-04-21; просмотров: 648; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.019 с.)

Контрольная работа по теме “Комплексные числа” 11 класс. профильный уровень

Главная / Старшие классы / Алгебра

Скачать

16.24 КБ, 1317891.docx Автор: Голикова Виктория Андреевна, 6 Дек 2015

Контрльная работа по теме “комплексные числа” для профильного 11 класса.

Автор: Голикова Виктория Андреевна

Похожие материалы

Тип	Название материала	Автор	Опубликован
документ	Контрольная работа по теме “Комплексные числа” 11 класс.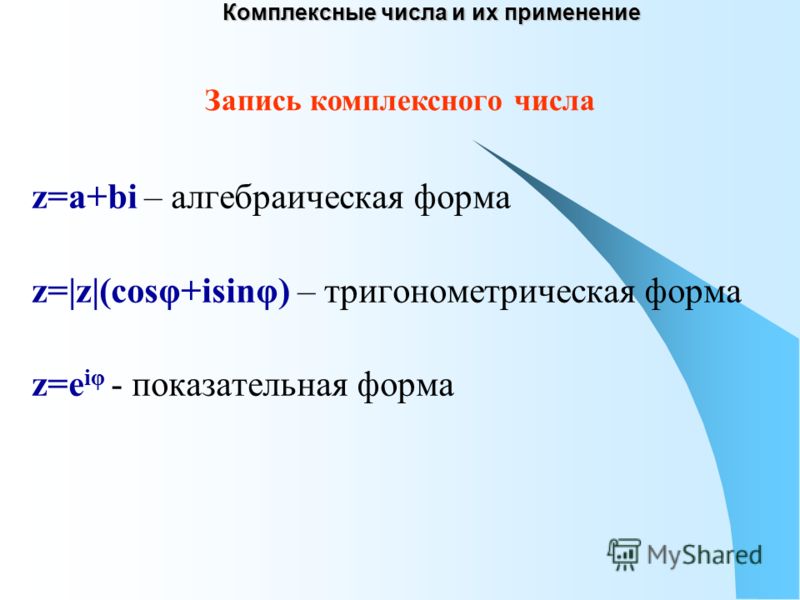 профильный уровень	Голикова Виктория Андреевна	6 Дек 2015
документ	Контрольная работа по теме “Углеводороды”, 10 класс, профильный уровень	Заборская Елена Андреевна	20 Мар 2015
документ	контрольная работа №1 по теме “Углеводороды” (профильный уровень) 10 класс	Хаттунен Галина Алексеевна	20 Мар 2015
документ	контрольная работа”Логические уравнения” 11 класс (профильный уровень)	Шевченко Ольга Викторовна	21 Мар 2015
документ	Контрольная работа 11 класс Теория вероятностей Профильный уровень	Голикова Виктория Андреевна	6 Дек 2015
документ	Контрольная работа по теме “Химические реакции”. 11 класс. Базовый уровень. О.С.Габриелян	Кириллова Ольга Петровна	17 Янв 2016
документ	Рабочая программа 10-11 класс по физике Профильный уровень 5часов/неделя КОНТРОЛЬНАЯ РАБОТА «МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ»	Горбачева Дарья Семеновна	7 Апр 2016
	Контрольная работа по экономике (профильный уровень) 11 класс “Рыночные структуры”	Еремин Евгений Викторович	31 Окт 2016
разное	Тестирование по теме “Наследственное право” (право, профильный уровень, 11 класс)	Диденко Светлана Николаевна	7 Авг 2015
разное	Тестирование по теме “Гражданское право” (профильный уровень, 11 класс)	Диденко Светлана Николаевна	7 Авг 2015
документ	Итоговый тест по теме “Трудовое право” 11 класс (профильный уровень)	Еремин Евгений Викторович	16 Дек 2015
документ	Итоговая контрольная работа по экономике 10 класс (профильный уровень).	Марченко Елена Сергеевна	21 Мар 2015
документ	Рубежная контрольная работа по обществознанию, 10 класс/ профильный уровень	Гашин Виталий Владимирович	7 Дек 2015
документ	Проверочная работа по теме: “Углеводороды”, 10 класс (профильный уровень)	Кокорина Светлана Евгеньевна	20 Мар 2015
документ	Тестовая работа по органической химии 11 класс (профильный уровень)	Демидова Галина Григорьевна	20 Мар 2015
документ	Входная диагностическая работа по алгебре 11 класс( профильный уровень)	Смольникова Виктория Валентиновна	16 Окт 2015
документ	Контрольная работа по алгебре по теме “Комплексные числа”	Петрова Наталья Альбертовна	21 Апр 2015
документ	Конспект урока по обществознанию в 11 классе по теме ” Социальная структура и социальные отношения” (профильный уровень)	Бондарев сергей Михайлович	20 Мар 2015
документ	Календарно-тематическое планирование по предмету “Литература” 11 класс (профильный уровень)	Яценко Ольга Юрьевна	8 Апр 2015
документ	Рабочая учебная программа по физике “Подготовка к ЕГЭ” 11 класс (профильный уровень)	Запорожцева Ольга Ивановна	20 Ноя 2015
презентация	Презентация по экономике 11 класс (профильный уровень). “Фискальная политика государства”	Попова Елена Викторовна	4 Ноя 2015
документ	Контрольная работа по теме “Интеграл”, 11 класс	Чехлова Ольга Юрьевна	21 Мар 2015
разное	Контрольная работа по теме “Производная” 11 класс	Хожулина Елена Валентиновна	1 Апр 2015
разное	онлайн решебник по алгебре 10 класс мордкович профильный уровень	tronarukeh2980	11 Мая 2015
разное	задачник по алгебре 10 класс мордкович профильный уровень решебник	ropipinla1979	11 Мая 2015
разное	решебник по алгебре 10 класс мордкович профильный уровень гдз	tronarukeh2980	11 Мая 2015
разное	онлайн решебник по химии 10 класс габриелян профильный уровень	moukhfeduking1973	11 Мая 2015
разное	решебник по математике за 10 класс мордкович профильный уровень	dregigoxis1972	11 Мая 2015
документ	КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ: «КОМПЛЕКСНЫЕ ЧИСЛА» в 11 классе	БУРМИСТРОВА ЕЛЕНА ЮРЬЕВНА	4 Апр 2015
документ	Контрольная работа по теме “Биогеоценотический уровень жизни”	Якушина Людмила Геннадьевна	31 Мар 2015
документ	Методическая разработка урока по обществознанию 10 класс (профильный уровень) по теме “Сущность человека как проблема философии”	Гончарова Ольга Александровна	7 Дек 2015
документ	Итоговая контрольная работа по органической химии 10 класс (профильный уровень)	Киселёва Наталья Геннадьевна	20 Ноя 2015
документ	контрольная работа №1 по теме “Углеводороды” (базовый уровень) 10 класс	Хаттунен Галина Алексеевна	20 Мар 2015
документ	Контрольная работа по теме “Первоначальные химические понятия”. 8 класс. УМК Рудзитиса. Базовый уровень.	Гостищев Игорь Александрович	20 Мар 2015
документ	Контрольная работа по теме “Популяционно-видовой уровень жизни” 10 класс	Якушина Людмила Геннадьевна	12 Апр 2015
документ	Контрольная работа по теме “Растворы. Вода”. 8 класс. УМК Рудзитиса. Базовый уровень	Гостищев Игорь Александрович	7 Июн 2015
документ	Контрольная работа по теме “Молекулярный уровень” (9 класс)	Гилазтдинова Миляуша Тимергазеевна	16 Ноя 2015
документ	Контрольная работа по теме “Углеводороды”. 10 класс. Базовый уровень. О.С.Габриелян	Кириллова Ольга Петровна	17 Янв 2016
разное	Тестирование по теме “Источники права” (право, профильный уровень, 10 класс)	Диденко Светлана Николаевна	7 Авг 2015
документ	Контрольная работа по теме “Класс Млекопитающие”	Садовская Дина Ивановна	11 Мар 2016

Тригонометрическая форма комплексного числа

Определение 1

Выражение вида $z=a+bi$ , где $a$ и $b$ – вещественные числа, а $i$ – «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=\sqrt{-1}$ или $i^2=-1$ .

Рассмотрим некоторую точку $M(a,b)$ комплексной плоскости. Введем полярную систему координат следующим образом:

• полюс полярной системы координат будет совпадать с началом координат комплексной плоскости, т.е. точкой $O(0;0)$;
• полярная ось будет совпадать с положительным направлением оси $Ox$ .

Обозначим полярные координаты рассматриваемой точки М через $r$ и $\varphi$,

где $r \ge 0$ (рис. 1).

Рис. 1

Связь координат двух систем задается следующими равенствами:

$a=r \cos \varphi $, $b=r \sin \varphi $

Подставим приведенные выше равенства в запись заданного комплексного числа в виде $z=a+bi$ и получим

$$z=r \cos \varphi + i \cdot r \sin \varphi$$

или

$$z=r(\cos \varphi + i \cdot \sin \varphi)$$

Определение 2

Запись некоторого комплексного числа $z$ в виде $z=r(\cos \varphi + i \cdot \sin \varphi)$ называется тригонометрической формой записи, при этом число $r$ – модуль данного комплексного числа $z$ , $\varphi$ – аргумент данного комплексного числа $z$ . 2}} \end{cases} \end{equation*}$$

Примечание 1

Аргумент вещественных чисел равен соответственно:

• 0 для положительного числа;
• $\pi$ для отрицательного числа.

Примечание 2

Аргумент чисто мнимых чисел равен соответственно:

$ \frac {\pi}{2} $ с положительной мнимой частью;

$ \frac {3\pi}{2} $ с отрицательной мнимой частью.

Примечание 3

Аргумент некоторого комплексного числа $z$ считается:

положительным $( \varphi >0)$ при отсчете против часовой стрелки от положительного направления оси $Ox$;

отрицательным $( \varphi

Примечание 4

Аргумент некоторого комплексного числа $z$ определяется не однозначно, а с точностью до слагаемого $2 \pi k$, где $k \in Z$.

Пример 1

Представить в тригонометрической форме заданные комплексные числа, для которых: 1) $r=0, \varphi=5 \pi$ ; 2) $r=10, \varphi= \frac {\pi}{2}$ ; 3) $r= \sqrt {2}, \varphi =- \frac {\pi} {3}$ ; 4) $r=3, \varphi = 0$.

Решение:

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos \varphi + i \cdot sin \varphi)$.

Для $r=0, \varphi=5 \pi$ получаем комплексное число $z=0 \cdot (cos5 \pi + i \cdot sin 5 \pi)$.

Для $r=10, \varphi = \frac {\pi}{2}$ получаем комплексное число $z=10 \cdot (cos \frac {\pi}{2} + i \cdot sin \frac {\pi} {2}$.

Для $r= \sqrt {2}, \varphi=- \frac {\pi}{3}$ получаем комплексное число $z= \sqrt {2} \cdot (cos (- \frac {\pi}{3}) + i \cdot (- \frac {\pi}{3}))$.

Для $r=3, \varphi=0$ получаем комплексное число $z=3 \cdot (cos0+i \cdot sin0)$.

Определение 3

Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:

• $a$ – вещественная (действительная) часть, обозначение Re$z=a$;
• $b$ – мнимая часть, обозначение Im $z=b$.

Алгоритм 1

Чтобы комплексное число $z$, записанное в алгебраической форме, привести к тригонометрической форме записи, необходимо выполнить следующее:

• вычислить модуль и аргумент;
• подставить полученные значения в выражение $z=r(cos \varphi + i \cdot sin \varphi)$. {\pi \cdot i}$.

  Решение:

  Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos \varphi + i \cdot sin \varphi)$.

  1) Определим значения модуля и аргумента: $r=3, \varphi = \frac {\pi}{3}$.

  Запись числа в тригонометрической форме имеет вид: $z=3 \cdot (cos \frac {\pi}{3} + i sin \frac {\pi}{3})$.

  2) Определим значения модуля и аргумента: $r=6, \varphi = \pi$.

  Запись числа в тригонометрической форме имеет вид: $z=6 \cdot (cos \pi + i sin \pi)$.

  Вывод

  Таким образом, можно сделать вывод о том, что в каком бы виде не было записано комплексное число $z$, его всегда можно представить в тригонометрической форме записи $z=r \cdot (cos \varphi + i sin \varphi)$.

  Мнимые числа и сложные функции

  Все предметные тесты GRE: математические ресурсы

  2 диагностических теста 148 практических тестов Вопрос дня Карточки Learn by Concept

  ← Предыдущая 1 2 3 4 5 6 Следующая →

  GRE Subject Test: Math Help » Алгебра » Классификация алгебраических функций » Мнимые числа и комплексные функции

  Оценка:

  Возможные ответы:

  Правильный ответ:

  Объяснение:

  Мы можем установить в кубе биномиальной картины:

  Ошибка

  Упростите следующий продукт:

  .

  Правильный ответ:

  Объяснение:

  Умножьте эти комплексные числа обычным способом:

  и вспомните это по определению. Затем, группируя похожие термины, мы получаем

  , что и является нашим окончательным ответом.

  Сообщить об ошибке

  Упрощение:

  Возможные ответы:

  Правильный ответ:

  Объяснение:

  Начните с использования FOIL. Это означает умножение первых членов вместе, затем внешних членов, за которыми следуют внутренние члены и, наконец, последние члены.

  Запомни это, так что.

  заменить на

  Отчет о ошибке

  Упрощайте:

  Возможные ответы:

  Правильный ответ:

  Объяснение:

  Начните с использования FOIL. Это означает умножение первых членов вместе, затем внешних членов, за которыми следуют внутренние члены и, наконец, последние члены.

  Запомни это, так что.

  заменить на

  Отчет о ошибке

  Упрощайте:

  Возможные ответы:

  Правильный ответ:

  Объяснение:

  Начните с использования FOIL. Это означает умножение первых членов вместе, затем внешних членов, за которыми следуют внутренние члены и, наконец, последние члены.

  Запомни это, так что.

  Замените

  Сообщить об ошибке

  Решите для  и : 

  Возможные ответы:

  Правильный ответ:

  6 Объяснение:

  Помните, что

  Итак, степени цикличны.   Это означает, что когда мы пытаемся вычислить значение показателя степени , мы можем игнорировать все степени, кратные  , потому что они заканчиваются умножением конечного результата на , и, следовательно, ничего не делают.

  Это означает, что

  Теперь, помня отношения показателей степени , мы можем упростить это до:

  Поскольку элементы слева и справа должны соответствовать (без смешивания и сопоставления!), мы получаем отношения: 

  Независимо от того, как вы ее решаете, вы получаете значения , .

  Сообщить об ошибке

  Упрощение: 

  Возможные ответы:

  Ничего из перечисленного

  Правильный ответ:

  Объяснение:

  Шаг 1: Разделите  на .

  Шаг 2. Вспомните это , поэтому давайте заменим его.

  Теперь у нас есть: .

  Шаг 3. Упростите . Для этого смотрим на номер с внутренней стороны.

  .

  Шаг 4. Выполните факторизацию  и удалите любые пары чисел. Для любой пары чисел, которые мы находим, мы берем только числа.

  У нас есть пара , поэтому a  не входит в радикал.
  У нас есть еще пара  , поэтому вне корня ставится еще одна тройка.

  Нам нужно умножить все, что мы выносим наружу:

  Шаг 5: Идет с 9…

  Шаг 6: Последнее после выбрасывания пар возвращается в квадратный корень и записывается сразу после

  Это будет выглядеть примерно так: 

  Сообщить об ошибке

  Возможные ответы:

  Правильный ответ:

  Explanation:

  There are two ways to simplify this problem: 

  Method 1: 

  Method 2: 

   

   

  Report a Ошибка

   

  Возможные ответы:

  Правильный ответ:

  Объяснение:

  Отчет о ошибке

  Возможные ответы:

  Правильный ответ:

  Объяснение:

  Отчет о ошибке

  ← Предыдущий 1 2 3 4 5 6 Следующая →

  Уведомление об авторском праве

  Все предметные тесты GRE: математические ресурсы

  2 диагностических теста 148 практических тестов Вопрос дня Карточки Learn by Concept

  Комплексные числа — Подготовка к оценке TSI

  Упрощение комплексных чисел

  В разделе радикалов мы отметили, что мы не получим действительное число из квадратного корня из отрицательного числа. Например, √ – 9 не является реальным числом, поскольку не существует реального числа, которое мы можем возвести в квадрат и получить ОТРИЦАТЕЛЬНУЮ 9..

  Теперь мы также увидели, что если a и b оба положительны, то √ ab = √ a · √ b . На секунду забудем об этом ограничении и сделаем следующее.

  √ – 9 = √ (9)(– 1) = √ 9 · √ – 1 = 3√ – 1

  Итак, √– 1 не является реальным числом, но если подумать, мы можем сделать это для любой квадратный корень из отрицательного числа. Например,

  √– 100 = √ 100 · √– 1 = 10 √– 1

  √– 5 = √ 5 · √– 1

  √– 290 = √ 290 · √– 1

  Таким образом, даже если число не является полным квадратом, мы всегда можем уменьшить квадратный корень из отрицательного числа до квадратного корня из положительного числа (что мы или калькулятор может работать с) раз √– 1.

  Если бы у нас был способ работать с √– 1, мы могли бы иметь дело с квадратными корнями из отрицательных чисел. Что ж, реальность такова, что на этом уровне просто нет никакого способа справиться с √– 1. Поэтому вместо того, чтобы иметь с ним дело, мы, так сказать, «заставим его уйти», используя следующее определение.

  i = √ – 1

  Обратите внимание, что если мы возведем в квадрат обе стороны, мы получим

  i ² = – 1

  Это будет важно помнить позже. Это показывает, что в некотором роде i — единственное «число», которое мы можем возвести в квадрат и получить отрицательное значение.

  Используя это определение, все приведенные выше квадратные корни равны:0005

  √– 290 = √ 290 i

  Это все примеры комплексных чисел .

  В этот момент возникает естественный вопрос: зачем нам это? Ответ заключается в том, что иногда мы будем сталкиваться с квадратными корнями из отрицательных чисел, и нам понадобится способ с ними справиться. Итак, чтобы разобраться с ними, нам нужно будет обсудить комплексные числа.

  Итак, давайте начнем с некоторых основных определений и терминологии комплексных чисел. стандартная форма комплексного числа:

  a + bi

  , где a и b – действительные числа, и они могут быть любыми, положительными, отрицательными, нулем, целыми числами, дробями, десятичными знаками, это не так. не важно. Когда в стандартной форме a называется действительной частью комплексного числа, а b называется мнимой частью комплексного числа.

  Например, в комплексном номере

  3 + 2 i

  a — то есть 3 в примере — действительная часть.

  б – то есть 2 в примере это мнимая часть.

  Вот несколько примеров комплексных чисел.

  3 + 2 i √ 6 – 10 i ########## ОТСУТСТВУЕТ УРАВНЕНИЕ ##############+ i 16 i 113

  Последние два, вероятно, нуждаются в небольшом пояснении. Вполне возможно, что а или б может быть нулем, поэтому в 16 i действительная часть равна нулю. Когда действительная часть равна нулю, мы часто будем называть комплексное число чисто мнимым числом . В последнем примере (113) мнимая часть равна нулю, а на самом деле мы имеем действительное число. Итак, думая о числах в этом свете, мы можем видеть, что действительные числа — это просто подмножество комплексных чисел.

  Сопряжение комплексного числа, a + bi , является комплексным числом, a – bi . Другими словами, это исходное комплексное число с измененным знаком мнимой части. Вот несколько примеров комплексных чисел и их сопряженных.

  3 + я	3 – и
  12 – 5 и	12 + 5 и
  1 – и	1 + я
  45 и	– 45 и
  101	101

  Обратите внимание, что сопряженное вещественное число представляет собой само себя без изменений.

  Сложение и вычитание комплексных чисел

  Коммутативные, ассоциативные и дистрибутивные свойства действительных чисел применимы и к комплексным числам. Сложение, вычитание, умножение и деление комплексных чисел очень похоже на сложение, вычитание, умножение и деление двучленов. При сложении или вычитании мы складываем действительные части и добавляем мнимые части.

  Самый простой способ думать о сложении и/или вычитании комплексных чисел — думать о каждом комплексном числе как о многочлене и выполнять сложение и вычитание так же, как мы складываем или вычитаем многочлены.

  Пример 1. Выполните указанную операцию и запишите ответ в стандартной форме. (4 + 12 i ) – (3 – 15 i )

  Решение.

  (4 + 12 и ) – (3 – 15 и )

  = 4 + 12 i – 3 + 15 i

  = 1 + 27 i

  Умножение комплексных чисел

  Далее рассмотрим умножение. Опять же, с одним небольшим отличием, вероятно, проще просто думать о комплексных числах как о полиномах и перемножать их, как если бы вы умножали многочлены. Единственное отличие появится на последнем шаге.

  Пример 2. Умножьте следующие числа и запишите ответ в стандартной форме.

  (4 + i )(2 + 3 i )

  Решение.

  (4 + I ) (2 + 3 I )

  = 8 + 12 I + 2 I + 3 I ²

  = 8 + 14 I + 3. (–1)

  = 5 + 14 i

  Деление комплексных чисел

  Произведение комплексно-сопряженных чисел показывает, что при умножении двух комплексно-сопряженных чисел получается действительное число. Это хорошая общая формула, которая будет удобно, когда дело доходит до деления комплексных чисел.

  ( A + BI ) ( A – BI )

  = A ² – ABI + ABI – B ² I ²

  = A ² B. ²

  Итак, когда мы умножаем комплексное число на его сопряженное, мы получаем действительное число, заданное как,

  ( a + bi )( a – bi ) = a ² + b ²

  Теперь мы привели эту формулу с замечанием, что она будет удобна при делении комплексных чисел.

  Пример 3. Запишите следующее в стандартной форме.

  Раствор.

  Стандартная форма не позволяет i быть в знаменателе. Итак, нам нужно получить i из знаменателя.

  На самом деле это довольно просто, если вспомнить, что комплексное число, умноженное на его сопряженное, является действительным числом. Итак, если мы умножим числитель и знаменатель на сопряженную часть знаменателя, мы сможем исключить и из знаменателя.

  Теперь, когда мы выяснили, как это сделать, давайте приступим к решению задач.

  Обратите внимание, что для официального представления ответа в стандартной форме мы разбили дробь на действительную и мнимую части.

  Оценка: я ²¹

  а. 1

  б. -1

  с. я

  д. -я

  Перепишите в терминах i, возведенных в другую степень. Напомним, что я = я, я ² = -1, я ³ = -i, и I ⁴ = 1.

  I ²¹

  = (I ²⁰ ) (I)

  = (I ⁴ ) ⁵ (I ⁴ ) ⁵ (I ⁴ ) =(1) ⁵ (i)

  =(1)(i)

  =i
  Правильный ответ: c

  Умножить (6-4i)(2+4i)

  а. 12-16i ²

  б. 28+16i

  с. 8

  д. -4+16i

  Умножение с использованием свойства распределения.

  (6-4и)(2+4и)

  =(6)(2)+(6)(4i)+(-4i)(2)+(-4i)(4i)

  =12+24i-8i-16i ²

  =12+16i -16i ²

  Помните i ² = -1,

  =12+16i-16(-1)

  =12+16i+16

  =28+16i
  Правильный ответ0:

  Добавить: (3+2i) + (4+5i)

  0 из 0 верно.

  3.1 Комплексные числа. Предварительное исчисление 2e

  Цели обучения

  В этом разделе вы:

  • Выразите квадратные корни из отрицательных чисел кратными   ii.
  • Нанесение комплексных чисел на комплексную плоскость.
  • Сложение и вычитание комплексных чисел.
  • Умножать и делить комплексные числа.

  Изучение математики постоянно саморазвивается. Отрицательные целые числа, например, заполняют пустоту, оставленную набором положительных целых чисел. Множество рациональных чисел, в свою очередь, заполняет пустоту, оставленную множеством целых чисел. Множество действительных чисел заполняет пустоту, оставленную множеством рациональных чисел. Неудивительно, что множество действительных чисел также имеет пустоты. Например, у нас до сих пор нет решения таких уравнений, как

  x2+4=0x2+4=0

  Наши лучшие предположения могут быть +2 или –2. Но если мы проверим +2 в этом уравнении, это не сработает. Если мы проверим -2, это не сработает. Если мы хотим получить решение этого уравнения, нам придется пойти дальше, чем мы до сих пор. В конце концов, до сих пор мы описывали квадратный корень из отрицательного числа как неопределенный. К счастью, есть другая система чисел, которая обеспечивает решение подобных проблем. В этом разделе мы рассмотрим эту систему счисления и то, как в ней работать.

  Выражение квадратных корней из отрицательных чисел как кратных

  i

  Мы знаем, как найти квадратный корень из любого положительного действительного числа. Аналогичным образом мы можем найти квадратный корень из отрицательного числа. Отличие в том, что рут не настоящий. Если значение подкоренной черты отрицательное, корень называется мнимым числом . Мнимое число ii определяется как квадратный корень из минус 1.

  −1=i−1=i

  Итак, используя свойства радикалов,

  i2=(−1)2=−1i2=(−1)2=−1

  Квадратный корень любого отрицательного числа можно записать как кратное i. i. Возьмем квадратный корень из –25.

  −25=25⋅(−1)         =25−1         =5i−25=25⋅(−1)         =25−1         =5i

  Мы используем 5i5i, а не −5i−5i потому что главный корень числа 2525 является положительным корнем.

  Комплексное число представляет собой сумму действительного числа и мнимого числа. Комплексное число выражается в стандартной форме: a+bia+bi, где aa — действительная часть, а bibi — мнимая часть. Например, 5+2i5+2i — комплексное число. Так же и 3+43i.3+43i.

  Мнимые числа отличаются от действительных чисел, потому что возведение в квадрат мнимого числа дает отрицательное действительное число. Вспомните, когда возводится в квадрат положительное действительное число, результатом является положительное действительное число, а когда возводится в квадрат отрицательное действительное число, снова получается положительное действительное число. Комплексные числа представляют собой комбинацию действительных и мнимых чисел.

  Мнимые и комплексные числа

  Комплексное число — это число вида a+bia+bi, где

  • аа — действительная часть комплексного номера.
  • биби — мнимая часть комплексного числа.

  Если b=0,b=0, то a+bia+bi — действительное число. Если a=0a=0 и bb не равно 0, комплексное число называется мнимым числом . Мнимое число – это четный корень из отрицательного числа.

  Как

  Дано мнимое число, представить его в стандартной форме.

  1. Запишите -a-a как a-1.a-1.
  2. Экспресс -1-1 как i.i.
  3. Запишите a⋅ia⋅i в простейшей форме.

  Пример 1

  Выражение мнимого числа в стандартной форме

  Выражение −9−9 в стандартной форме.

  Решение

  −9=9−1=3i−9=9−1=3i

  В стандартной форме это 0+3i.0+3i.

  Попытайся #1

  Express −24−24 в стандартной форме.

  Нанесение комплексного числа на комплексную плоскость

  Мы не можем нанести на числовую прямую комплексные числа, как настоящие числа. Однако мы все еще можем представить их графически. Чтобы представить комплексное число, нам нужно обратиться к двум компонентам числа. Мы используем комплексную плоскость, которая представляет собой систему координат, в которой горизонтальная ось представляет действительную составляющую, а вертикальная ось представляет мнимую составляющую. Комплексные числа — это точки на плоскости, выраженные в виде упорядоченных пар (a,b),(a,b), где aa представляет собой координату по горизонтальной оси, а bb представляет собой координату по вертикальной оси.

  Рассмотрим число −2+3i.−2+3i. Действительная часть комплексного числа равна −2−2, а мнимая часть равна 3i.3i. Мы наносим упорядоченную пару (−2,3)(−2,3) для представления комплексного числа −2+3i−2+3i, как показано на рисунке 1 .

  Рисунок 1

  Сложный самолет

  В комплексной плоскости горизонтальная ось является действительной осью, а вертикальная ось — мнимой осью, как показано на рисунке 2 .

  Рисунок 2

  Как

  Для заданного комплексного числа представить его компоненты на комплексной плоскости.

  1. Определите действительную и мнимую части комплексного числа.
  2. Перемещайтесь по горизонтальной оси, чтобы показать действительную часть числа.
  3. Перемещение параллельно вертикальной оси для отображения мнимой части числа.
  4. Нарисуйте точку.

  Пример 2

  Нанесение комплексного числа на комплексную плоскость

  Нанесите комплексное число 3−4i3−4i на комплексную плоскость.

  Решение

  Действительная часть комплексного числа равна 3,3, а мнимая часть равна −4i.−4i. Наносим упорядоченную пару (3,−4)(3,−4), как показано на рисунке 3.

  Рисунок 3

  Попытайся #2

  Нанесите комплексное число −4−i−4−i на комплексную плоскость.

  Сложение и вычитание комплексных чисел

  Как и с вещественными числами, мы можем выполнять арифметические операции над комплексными числами. Чтобы сложить или вычесть комплексные числа, мы объединяем действительные части и объединяем мнимые части.

  Комплексные числа: сложение и вычитание

  Сложение комплексных чисел:

  (a+bi)+(c+di)=(a+c)+(b+d)i(a+bi)+(c+di)=(a+c)+ (b+d)i

  Вычитание комплексных чисел:

  (a+bi)−(c+di)=(a−c)+(b−d)i(a+bi)−(c+di)= (а-в)+(б-г)i

  Как

  Даны два комплексных числа, найдите их сумму или разность.

  1. Определите действительную и мнимую части каждого числа.
  2. Добавьте или вычтите действительные части.
  3. Сложите или вычтите мнимые части.

  Пример 3

  Добавление комплексных чисел

  Добавьте 3-4i3-4i и 2+5i. 2+5i.

  Решение

  Складываем действительные части и складываем мнимые части.

  (a+bi)+(c+di)=(a+c)+(b+d)i(3−4i)+(2+5i)=(3+2)+(−4+5) i                            =5+i(a+bi)+(c+di)=(a+c)+(b+d)i(3−4i)+(2+5i)=(3+2)+(−4 +5)i                            =5+i

  Попытайся #3

  Вычесть 2+5i2+5i из 3–4i.3–4i.

  Умножение комплексных чисел

  Умножение комплексных чисел очень похоже на умножение биномов. Основное отличие состоит в том, что мы работаем с реальной и мнимой частями отдельно.

  Умножение комплексного числа на вещественное число

  Начнем с умножения комплексного числа на действительное число. Мы распределяем действительное число так же, как и биномиальное. Так, например,

  Как

  Даны комплексное число и действительное число, умножьте их, чтобы найти произведение.

  1. Используйте свойство дистрибутива.
  2. Упростить.

  Пример 4

  Умножение комплексного числа на действительное число

  Найдите произведение 4(2+5i).4(2+5i).

  Решение

  Распределить 4.

  4(2+5i)=(4⋅2)+(4⋅5i)=8+20i4(2+5i)=(4⋅2)+(4⋅5i)=8+20i

  Попытайся #4

  Найдите произведение −4(2+6i).−4(2+6i).

  Умножение комплексных чисел

  Теперь давайте перемножим два комплексных числа. Мы можем использовать либо распределительное свойство, либо метод FOIL. Напомним, что FOIL — это аббревиатура для умножения первого, внешнего, внутреннего и последнего членов вместе. Используя либо распределительное свойство, либо метод FOIL, мы получаем

  (a+bi)(c+di)=ac+adi+bci+bdi2(a+bi)(c+di)=ac+adi+bci+bdi2

  Поскольку i2=−1,i2=−1, у нас

  (a+bi)(c+di)=ac+adi+bci−bd(a+bi)(c+di)=ac+adi+bci−bd

  Для упрощения объединим действительные части, и мы соединить воображаемые части.

  (a+bi)(c+di)=(ac−bd)+(ad+bc)i(a+bi)(c+di)=(ac−bd)+(ad+bc)i

  Как

  Даны два комплексных числа, умножьте их, чтобы найти произведение.

  1. Используйте свойство распределения или метод FOIL.
  2. Упростить.

  Пример 5

  Умножение комплексного числа на комплексное число

  Умножение (4+3i)(2−5i).(4+3i)(2−5i).

  Решение

  Использование (a+bi)(c+di)=(ac−bd)+(ad+bc)i(a+bi)(c+di)=(ac−bd)+(ad+bc)i

  (4+3i)(2−5i)=(4⋅2−3⋅(−5))+(4⋅(−5)+3⋅2)i                              = (8+15)+(−20+6) i                       =23−14i(4+3i)(2−5i)=(4⋅2−3⋅(−5))+(4⋅(−5)+3⋅2)i                                  = (8+15)+( −20+6)i                        =23−14i

  Попытайся #5

  Умножить (3−4i)(2+3i).(3−4i)(2+3i).

  Деление комплексных чисел

  Деление двух комплексных чисел более сложно, чем сложение, вычитание и умножение, потому что мы не можем делить на мнимое число, а это означает, что у любой дроби должен быть действительный знаменатель. Нам нужно найти член, на который мы можем умножить числитель и знаменатель, который исключит мнимую часть знаменателя, чтобы мы получили действительное число в качестве знаменателя. Этот член называется комплексно-сопряженным знаменателем, который находится при изменении знака мнимой части комплексного числа. Другими словами, комплексное сопряжение a+bia+bi есть a−bi.a−bi.

  Обратите внимание, что комплексно-сопряженные числа имеют обратную связь: комплексно-сопряженное число a+bia+bi равно a-bi,a-bi, а комплексно-сопряженное число a-bia-bi равно a+bi.a+bi. Кроме того, когда квадратное уравнение с действительными коэффициентами имеет комплексные решения, решения всегда комплексно сопряжены друг другу.

  Предположим, мы хотим разделить c+dic+di на a+bi,a+bi, где ни aa, ни bb не равны нулю. Сначала запишем деление в виде дроби, затем найдем комплексно-сопряженную часть знаменателя и умножим.

  c+dia+bi где a≠0 и b≠0c+dia+bi где a≠0 и b≠0

  Умножить числитель и знаменатель на комплексно-сопряженное число знаменателя.

  (c+di)(a+bi)⋅(a−bi)(a−bi)=(c+di)(a−bi)(a+bi)(a−bi)(c+di)(a +bi)⋅(a−bi)(a−bi)=(c+di)(a−bi)(a+bi)(a−bi)

  Применить распределительное свойство.

  =ca-cbi+adi-bdi2a2-abi+abi-b2i2=ca-cbi+adi-bdi2a2-abi+abi-b2i2

  Упростите, помня, что i2=-1.i2=-1.

  =ca-cbi+adi-bd(-1)a2-abi+abi-b2(-1)=(ca+bd)+(ad-cb)ia2+b2=ca-cbi+adi-bd(- 1)a2-abi+abi-b2(-1)=(ca+bd)+(ad-cb)ia2+b2

  Комплексное сопряжение

  Комплексное сопряжение комплексного числа a+bia+bi равно a−bi.a−bi. Его находят изменением знака мнимой части комплексного числа. Действительная часть числа остается неизменной.

  • Когда комплексное число умножается на его комплексно-сопряженное, результатом является действительное число.
  • Когда комплексное число добавляется к его комплексно-сопряженному, результатом является действительное число.

  Пример 6

  Нахождение комплексно-сопряженных чисел

  Нахождение комплексно-сопряженных чисел каждого числа.

  1. ⓐ 2+i52+i5
  2. ⓑ −12i−12i

  Решение

  1. ⓐ Номер уже имеет форму a+bi.a+bi. Комплексно-сопряженным является a−bi,a−bi или 2−i5.2−i5.
  2. ⓑ Мы можем переписать это число в виде a+bia+bi как 0−12i.0−12i. Комплексно-сопряженное число равно a−bi,a−bi или 0+12i.0+12i. Это можно записать просто как 12i.12i.

  Анализ

  Хотя мы видели, что мы можем найти комплексное сопряжение мнимого числа, на практике мы обычно находим комплексно-сопряженные только комплексные числа с вещественной и мнимой компонентами. Чтобы получить действительное число из мнимого числа, мы можем просто умножить на i.i.

  Как

  Даны два комплексных числа, разделить одно на другое.

  1. Запишите задачу деления в виде дроби.
  2. Определите комплексное сопряжение знаменателя.
  3. Умножьте числитель и знаменатель дроби на комплексно-сопряженную часть знаменателя.
  4. Упростить.

  Пример 7

  Деление комплексных чисел

  Разделить (2+5i)(2+5i) на (4−i).(4−i).

  Решение

  Начнем с того, что запишем задачу в виде дроби.

  (2+5i)(4−i)(2+5i)(4−i)

  Затем умножаем числитель и знаменатель на комплексное сопряжение знаменателя.

  (2+5i)(4−i)⋅(4+i)(4+i)(2+5i)(4−i)⋅(4+i)(4+i)

  Чтобы умножить два сложных чисел, мы расширяем произведение так же, как и с многочленами (процесс, обычно называемый FOIL).

  (2+5i)(4−i)⋅(4+i)(4+i)=8+2i+20i+5i216+4i−4i−i2                                       =8+2i+20i+5(−1)16 +4i−4i−(−1)Becausei2=−1                          =3+22i17                          =317+2217iРазделите действительную и мнимую части. 2i+20i+5i216+4i – 4i – I2 = 8+2i+20i+5 (−1) 16+4i – 4i – ( – 1), потому что 2 = −1 = 3+22i17 = 317+2217Iseparate реальные и воображаемые части.

  Обратите внимание, что это выражает частное в стандартной форме.

  Пример 8

  Подстановка комплексного числа в полиномиальную функцию

  Пусть f(x)=x2−5x+2.f(x)=x2−5x+2. Вычислите f(3+i).f(3+i).

  Решение

  Подставить x=3+ix=3+i в функцию f(x)=x2−5x+2f(x)=x2−5x+2 и упростить.

  Анализ

  Мы пишем f(3+i)=−5+i.f(3+i)=−5+i. Обратите внимание, что на входе 3+i3+i, а на выходе -5+i.-5+i.

  Попытайся #6

  Пусть f(x)=2×2−3x.f(x)=2×2−3x. Вычислите f(8−i).f(8−i).

  Пример 9

  Замена мнимого числа в рациональной функции

  Пусть f(x)=2+xx+3.f(x)=2+xx+3. Вычислите f(10i).f(10i).

  Решение

  Подставьте x=10ix=10i и упростите.

  2+10i10i+3Подставить 10i на x.2+10i3+10iПереписать знаменатель в стандартной форме. 2+10i3+10i⋅3–10i3–10iПодготовиться к умножению числителя и знаменателя i на комплексно-сопряженное число 9–1i0+30–20 знаменателя.6–30i+30i–100i2Умножьте, используя свойство распределения или метод FOIL.6–20i+30i–100(–1)9–30i+30i–100(–1)Замените –1 на i2.106+10i109Упростите.106109+10109iРазделите действительную и мнимую части.2+10i10i+3Подставить 10i вместо x.2+10i3+10iПереписать знаменатель в стандартной форме.2+10i3+10i⋅3–10i3–10iПодготовиться к умножению числителя и знаменателя на комплексно-сопряженное число знаменателя.6–20i 30i–100i29–30i+30i–100i2Умножьте, используя распределительное свойство или метод FOIL.6–20i+30i–100(–1)9–30i+30i–100(–1)Замените–1 на i2.106+10i109Упростите.106109+10109iРазделите действительную и мнимую части.

  Попытайся #7

  Пусть f(x)=x+1x−4.f(x)=x+1x−4. Вычислите f(−i).f(−i).

  Упрощающие степени

  i

  Степени ii цикличны. Давайте посмотрим, что произойдет, если мы возведем ii в возрастающую степень.

  i1=ii2=-1i3=i2⋅i=-1⋅i=-ii4=i3⋅i=-i⋅i=-i2=-(-1)=1i5=i4⋅i=1⋅i=ii1= ii2=-1i3=i2⋅i=-1⋅i=-ii4=i3⋅i=-i⋅i=-i2=-(-1)=1i5=i4⋅i=1⋅i=i

  Мы можем видим, что когда мы добираемся до пятой степени i,i, оно равно первой степени. Продолжая умножать ii само на себя для увеличения степени, мы увидим цикл 4. Давайте рассмотрим следующие 4 степени i.i.

  i6=i5⋅i=i⋅i=i2=−1i7=i6⋅i=i2⋅i=i3=−ii8=i7⋅i=i3⋅i=i4=1i9=i8⋅i=i4⋅i= i5=ii6=i5⋅i=i⋅i=i2=−1i7=i6⋅i=i2⋅i=i3=−ii8=i7⋅i=i3⋅i=i4=1i9=i8⋅i=i4⋅i= i5=i

  Пример 10

  Упрощение полномочий II

  Оценка i35.i35.

  Решение

  Так как i4=1,i4=1, мы можем упростить задачу, выделив как можно больше множителей i4i4. Для этого сначала определите, сколько раз 4 входит в число 35: 35=4⋅8+3,35=4⋅8+3.

  i35=i4⋅8+3=i4⋅8⋅i3=(i4)8⋅i3=18⋅i3=i3=−ii35=i4⋅8+3=i4⋅8⋅i3=(i4)8⋅i3 =18⋅i3=i3=−i

  вопросы и ответы

  Можем ли мы написать i35i35 другими полезными способами?

  Как мы видели в примере 10, мы уменьшили i35i35 до i3i3, разделив показатель степени на 4 и используя остаток, чтобы найти упрощенную форму. Но, возможно, другая факторизация i35i35 может оказаться более полезной. В таблице 1 показаны некоторые другие возможные факторизации.

  Факторизация i35i35	i34⋅ii34⋅i	i33⋅i2i33⋅i2	i31⋅i4i31⋅i4	i19⋅i16i19⋅i16
  Уменьшенная форма	(i2) 17⋅i(i2)17⋅i	i33⋅(−1)i33⋅(−1)	i31⋅1i31⋅1	i19⋅(i4)4i19⋅(i4)4
  Упрощенная форма	(-1)17⋅я(-1)17⋅я	−i33−i33	и31и31	и19и19

  Стол 1

  Каждый из них в конечном итоге приведет к ответу, который мы получили выше, но может потребоваться несколько больше шагов, чем в нашем предыдущем методе.

  3.1 Секционные упражнения

  Вербальный

  1.

  Объясните, как складывать комплексные числа.

  2.

  Каков основной принцип умножения комплексных чисел?

  3.

  Приведите пример, показывающий, что произведение двух мнимых чисел не всегда мнимое.

  4.

  Что является характеристикой графика действительного числа в комплексной плоскости?

  Алгебраический

  В следующих упражнениях оцените алгебраические выражения.

  5.

  Iff(x)=x2+x−4,Iff(x)=x2+x−4, вычислить f(2i).f(2i).

  6.

  Iff(x)=x3−2,Iff(x)=x3−2, вычислить f(i).f(i).

  7.

  Iff(x)=x2+3x+5,Iff(x)=x2+3x+5, оценить f(2+i). f(2+i).

  8.

  Iff(x)=2×2+x−3,Iff(x)=2×2+x−3, вычислить f(2−3i).f(2−3i).

  9.

  Iff(x)=x+12−x,Iff(x)=x+12−x, вычислить f(5i).f(5i).

  10.

  Iff(x)=1+2xx+3,Iff(x)=1+2xx+3, вычислить f(4i).f(4i).

  Графический

  В следующих упражнениях определите количество действительных и недействительных решений для каждой показанной квадратичной функции.

  11.

  12.

  Для следующих упражнений нанесите комплексные числа на комплексную плоскость.

  13.

  1-2i1-2i

  14.

  −2+3i−2+3i

  15.

  II

  16.

  −3−4i−3−4i

  Цифровой

  Для следующих упражнений выполните указанную операцию и выразите результат в виде упрощенного комплексного числа.

  17.

  (3+2i)+(5−3i)(3+2i)+(5−3i)

  18.

  (−2−4i)+(1+6i)(−2−4i)+(1+6i)

  19.

  (−5+3i)−(6−i)(−5+3i)−(6−i)

  20.

  (2−3i)−(3+2i)(2−3i)−(3+2i)

  21.

  (-4+4i)-(-6+9i)(-4+4i)-(-6+9i)

  22.

  (2+3i)(4i)(2+3i)(4i)

  23.

  (5−2i)(3i)(5−2i)(3i)

  24.

  (6−2i)(5)(6−2i)(5)

  25.

  (−2+4i)(8)(−2+4i)(8)

  26.

  (2+3i)(4−i)(2+3i)(4−i)

  27.

  (-1+2i)(-2+3i)(-1+2i)(-2+3i)

  28.

  (4−2i)(4+2i)(4−2i)(4+2i)

  29.

  (3+4i)(3−4i)(3+4i)(3−4i)

  30.

  3+4i23+4i2

  31.

  6-2i36-2i3

  32.

  −5+3i2i−5+3i2i

  33.

  6+4ii6+4ii

  34.

  2−3i4+3i2−3i4+3i

  35.

  3+4i2-i3+4i2-i

  36.

  2+3i2−3i2+3i2−3i

  37.

  −9+3−16−9+3−16

  38.

  −−4−4−25−4−4−25

  39.

  2+-1222+-122

  40.

  4+-2024+-202

  41.

  i8i8

  42.

  i15i15

  43.

  i22i22

  Технология

  В следующих упражнениях используйте калькулятор, чтобы ответить на вопросы.

  44.

  Вычислить (1+i)k(1+i)k для k=4, 8 и 12.k=4, 8 и 12. Предсказать значение, если k=16.k=16.

  45.

  Вычислить (1−i)k(1−i)k для k=2, 6 и 10.k=2, 6 и 10. Предсказать значение, если k=14.k=14.

  46.

  Вычислить (1+i)k−(1−i)k(1+i)k−(1−i)k для k=4, 8 и 12k=4, 8 и 12. Предсказать значение для к=16.к=16.

  47.

  Покажите, что решение x6+1=0x6+1=0 равно 32+12i.32+12i.

  48.

  Покажите, что решение x8−1=0x8−1=0 равно 22+22i.22+22i.

  Расширения

  В следующих упражнениях оцените выражения, записав результат в виде упрощенного комплексного числа.

  49.

  1i+4i31i+4i3

  50.

  1i11−1i211i11−1i21

  51.