Контрольная работа матрицы и определители: Контрольная работа « Матрицы и определители» для студентов 1 курса

Контрольная работа « Матрицы и определители» для студентов 1 курса

Контрольная работа

«Матрицы и определители»

1). Дано: A,B. Найти:

1

а) 3A+B

б) AB

в)A ^-1

г)A ^-1A

2).Найти def A: а) методом треугольников;

б) приведением к каноническому виду

1). Дано: A,B. Найти:

2

а) -2A-B

б) BA

в)B ^-1

г) B ^-1B

2).Найти def A: а) приведением к каноническому виду;

б) методом треугольников;

1).

Дано: A,B. Найти:

3

а) 3B+A

б) BA

в)B ^-1

г)BB ^-1

2).Найти∆B: а) методом треугольников;

б) приведением к треугольному виду

1). Дано: A,B. Найти:

4

а) 3A+B

б) AB

в)A ^-1

г)A ^-1A

2).Найти def B: а) методом треугольников;

б) приведением к каноническому виду

1). Дано: A,B. Найти:

5

а) 2A+B

б) AB

в)B ^-1

г) BB ^-1

2). Найти def A: а) методом треугольников;

б) приведением к треугольному виду;

Контрольная работа № 1

1). Дано: A,B. Найти:

6

а) 3B-A

б) AB

в)A ^-1

г) AA ^-1

2).Найти ∆B: а) методом треугольников;

б) приведением к треугольному виду

1). Дано: A,B. Найти:

7

а) 2B+3A

б) BA

в)A ^-1

г)A ^-1A

2).Найти∆B: а) методом треугольников;

б) приведением к треугольному виду

1). Дано: A,B. Найти:

8

а) 3B-A

б) AB

в)A ^-1

г)A ^-1A

2). Найти def B: а) методом треугольников;

б) приведением к треугольному виду

1). Дано: A,B. Найти:

9

а) 3B-A

б) AB

в)B ^-1

г) B

-1B

2).Найти ∆ A: а) методом треугольников;

б) приведением к треугольному виду;

1). Дано: A,B. Найти:

10

а) 2B+2A

б) BA

в)A ^-1

г) AA ^-1

2).Найти ∆A: а) методом треугольников;

б) приведением к треугольному виду

Контрольная работа № 1

1). Дано: A,B. Найти:

11

а) 2B-A

б) BA

в)B ^-1

г)B ^-1B

2).Найти def B: а) методом треугольников;

б) приведением к каноническому виду

1). Дано: A,B. Найти:

12

а) 2B+A

б) AB

в)A ^-1

г)A ^-1A

2).Найти ∆ B: а) приведением к треугольному виду;

б) методом треугольников;

1). Дано: A,B. Найти:

13

а) 3A+B

б) AB

в)A ^-1

г) A ^-1A

2). Найти def B: а) методом треугольников;

б) приведением к треугольному виду

1). Дано: A,B. Найти:

14

а) 2B+3A

б) BA

в)B ^-1

г)B ^-1B

2).Найти ∆A: а) методом треугольников;

б) приведением к треугольному виду

1). Дано: A,B. Найти:

15

а) 3A+B

б) BA

в)B ^-1

г)B ^-1B

2).Найти │A│: а) методом треугольников;

б) приведением к каноническому виду

Контрольная работа № 1

1). Дано: A,B. Найти:

16

а) 2A+B

б) AB

в)A ^-1

г) AA ^-1

2). Найти def A: а) методом треугольников;

б) приведением к треугольному виду;

1). Дано: A,B. Найти:

17

а) 3A-B

б) AB

в)B ^-1

г) BB ^-1

2).Найти ∆A: а) методом треугольников;

б) приведением к треугольному виду

1). Дано: A,B. Найти:

18

а) A+2B

б) AB

в)B ^-1

г) B ^-1B

2).Найти def A: а) методом треугольников;

б) приведением к треугольному виду;

1). Дано: A,B. Найти:

19

а) B+3A

б) AB

в)B ^-1

г) BB ^-1

2). Найти def B: а) методом треугольников;

б) приведением к каноническому виду

1). Дано: A,B. Найти:

20

а) 2A-B

б) AB

в)A ^-1

г) A ^-1A

2).Найти def A: а) методом треугольников;

б) приведением к треугольному виду;

Контрольная работа № 1

Контрольная работа № 1 по теме: «Матрицы и определители»

УРОК 9

Контрольная работа № 1

по теме: « Матрицы и определители »

ЦЕЛЬ:

Применение полученных знаний и умений, приобретенных во время лекций и практических занятий на уроках, в процессе выполнения контрольной работы по теме: «Матрицы и определители».

Вариант № 1

1. Найти значение матричного многочлена f (A) :

A =

f (x) = – х³ + 2x² – x + 3

-1 0

3 2

-2 0 8 1

3 -1 7 2

-8 2 -6 -3

2. Найти ранг матрицы методом окаймляющих миноров.

А =

3. Вычислить определитель с помощью «правила треугольников»

-2 3 5

7 -1 4

9 -8 -6

Δ =

-2 3 5

7 -1 4

9 -8 -6

4

А =

. Найти обратную матрицу для матрицы

5. Найти матрицу Х , удовлетворяющую уравнению. Сделать проверку.

3 -1

2 4

1 -2

-3 4

Х =

Вариант № 2

1. Найти значение матричного многочлена f (A) :

f (x) = х³ + 3x² + 2x – 1

0 3

-1 -2

A =

2. Найти ранг матрицы методом окаймляющих миноров.

-2 3 -1 1

3 -1 7 4

8 -3 2 0

А =

3. Вычислить определитель с помощью «правила треугольников»

Δ =

-1 9 5

-4 6 2

3 7 8

4. Найти обратную матрицу для матрицы

-1 9 5

-4 6 2

3 7 8

А =

5. Найти матрицу Х , удовлетворяющую уравнению. Сделать проверку.

4 -2

3 1

3 0

4 2

Х

=

Решение контрольной работы по вариантам

Вариант № 1

1. Найти значение матричного многочлена f (A) :

f (x) = – х³ + 2x² – x + 3

A =

-1 0

3 2

f (А) = – А³ + 2А² – А + 3Е, где Е – единичная матрица

A² = А^. А =

-1 0

3 2

-1 0

3 2

1+0 0+0

-3+6 0+4

=

=

1 0

3 4

.

1 0

3 4

-1 0

3 2

-1+0 0+0

-3+12 0+8

-1 0

9 8

A³ = А ^{2 .} А =

=

=

Е =

1 0

0 1

1 0

3 4

A =

-1 0

9 8

1 0

3 4

-1 0

3 2

1 0

0 1

f (А) = –

+ 2

–

+ 3

=

=

+

–

+

1 0

-9 -8

2 0

6 8

-1 0

3 2

3 0

0 3

=

1+2+1+3 0+0-0+0

-9+6-3+0 -8+8-2+3

7 0

-6 1

=

=

f (А) =

7 0

-6 1

Ответ:

2. Найти ранг матрицы методом окаймляющих миноров.

А =

-2 0 8 1

3 -1 7 2

-8 2 -6 -3

3 _х 4

Решение

ШАГ 1. Рассмотрим миноры 1-го порядка матрицы А

М₁¹ = 8 = 8 ( условие выполнено )

ШАГ 2. Рассмотрим миноры 2-го порядка матрицы А

-2 0

3 -1

М

= 2 – 0 = 2

₂¹ =

( условие выполнено )

ШАГ 3. Рассмотрим миноры 3-го порядка матрицы А

-2 0 8

3 -1 7

-8 2 -6

М₃¹ = = -12 +0 +48 – 64 +28 – 0 = 0

( условие не выполнено )

-2 0 1

3 -1 2

-8 2 -3

М₃² = = – 6 + 0 +6 – 8 + 8 + 0 = 0

( условие не выполнено )

-2 8 1

3 7 2

-8 -6 -3

М₃³ = = – 56 +24 – 72 – 42 + 18 + 128 = 0

( условие не выполнено )

0 8 1

-1 7 2

2 -6 -3

М₃⁴ = = 0 + 6 +32 – 14 – 0 – 24 = 0

( условие не выполнено )

Ответ: rang ( A ) = 2

3. Вычислить определитель с помощью «правила треугольников»

-2 3 5

7 -1 4

9 -8 -6

Δ =

= – 12 – 280 + 108 + 45 – 64 + 126 = – 77

О

-2 3 5

7 -1 4

9 -8 -6

твет: Δ = – 77

А =

4. Найти обратную матрицу Α^-1 для матрицы

ШАГ 1. Найти определитель матрицы А

Δ = – 77 ( см. решение – задание 3)

( условие выполнено )

А – невырожденная матрица, значит, А^-1 существует и определяется по формуле А^-1 = А^*/Δ, где А^* – союзная матрица

А₁₁ А₂₁ А₃₁

А₁₂ А₂₂ А₃₂

А₁₃ А₂₃ А₃₃

А^* =

ШАГ 2. Найти алгебраические дополнения для всех элементов матрицы А

-1 4

-8 -6

А₁₁ = + = 6+32=38

7 4

9 -6

А_{12 = – = – ( – 42 – 36) = 78}

А

7 -1

9 -8

₁₃ = + = – 56 + 9 = – 47

3 5

-8 -6

А

-2 5

9 -6

₂₁ = – = – ( – 18 + 40 ) = -22

А

-2 3

9 -8

₂₂ = + = 12 – 45 = – 33

А

3 5

-1 4

₂₃ = – = – (16 – 27) = 11

А₃₁ = + = 12 + 5 = 17

-2 5

7 4

А

-2 3

7 -1

₃₂ = – = – ( -8 – 35) = 43

А₃₃ = + = 2 – 21= – 19

ШАГ 3. Полученные значения подставить в основную формулу и найдём А^-1

А₁₁ А₂₁ А₃₁

А₁₂ А₂₂ А₃₂

А₁₃ А₂₃ А₃₃

38 -22 17

78_{-33 43}

-47 11 -19

1

Δ

А^-1 =

1

77

= –

-38 22 -17

-78_{33 -43}

47 -11₁₉

1

77

Ответ: А^-1 =

5. Найти матрицу Х , удовлетворяющую уравнению

3 -1

2 4

1 -2

-3 4

Х =

Запишем матричное уравнение в виде АХ = В Х = А^-1 В

Найдём определитель матрицы А

3 -1

2 4

detA = = 12 + 2 = 14 ( условие выполнено )

А – невырожденная матрица, значит, А^-1 существует и определяется по формуле А^-1 = А^*/Δ, где А^* – союзная матрица

Н

4 1

-2 3

1

14

Α^-1 =

айдём обратную матрицу А^-1

4 1

-2 3

1

14

Х = А^-1В =

1 -2

-3 4

Найдём матрицу 

1

14

4-3 -8+4 -2-9 4+12

1 -4

-11 16

1

14

Х =

=

Проверка

3 -1

2 4

1 -4

-11 16

1

14

1

14

3+11 -12-16

2-44 -8+64

1

14

14 -28

-42 72

=

=

=

= В

1 -2

-3 4

А

Х

Ответ: Х =

1 -4

-11 16

1

14

Вариант № 2

1. Найти значение матричного многочлена f (A) :

f (x) = х³ + 3x² + 2x – 1

0 3

-1 -2

A =

f (А) = А³ + 3А² +2А – 1Е, где Е – единичная матрица

A² = А^. А =

0 3

-1 -2

0-3 0-6

0+2 -3+4

=

=

A³ = А ^{2 .} А =

=

=

6 3

-1 4

Е =

1 0

0 1

A =

-3 -6

2 1

-3 -6

2 1

0 3

-1 -2

0+6 -9+12

0-1 6-2

0 3

-1 -2

0 3

-1 -2

f (А) =

+ 3

+ 2

– 1

1 0

0 1

=

=

+

–

–

-9 -18

6 3

0 6

-2 -4

1 0

0 1

=

=

6-9-0-1 3-18-6-0

-1+6+4-0 4+3+4-1

=

-4 -21

9 10

6 3

-1 4

-3 -6

2 1

0 3

-1 -2

6 3

-1 4

f (А) =

-4 -21

9 10

Ответ:

2.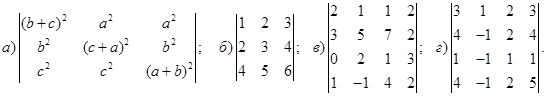 Найти ранг матрицы методом окаймляющих миноров.

А =

-2 3 -1 1

3 -1 7 4

8 -3 2 0

ШАГ 1. Рассмотрим миноры 1-го порядка матрицы А

М₁¹ = 8 = 8 ( условие выполнено )

ШАГ 2. Рассмотрим миноры 2-го порядка матрицы А

-2 3

3 -1

М

= 2 – 9 = -7

₂¹ =

( условие выполнено )

ШАГ 3. Рассмотрим миноры 3-го порядка матрицы А

-2 3 -1

3 -1 7

8 -3 2

М₃¹ = = 4 + 168 + 9 – 8 – 42 – 18 = 113

( условие выполнено )

Ответ: rang ( A ) = 3

3. Вычислить определитель с помощью «правила треугольников»

Δ =

-1 9 5

-4 6 2

3 7 8

= – 48 – 140 + 54 – 90 + 14 + 288 = 78

Ответ: Δ = 78

А =

-1 9 5

-4 6 2

3 7 8

4. Найти обратную матрицу Α^-1 для матрицы

ШАГ 1. Найти определитель матрицы А

Δ = 78 ( см. решение – задание 3)

( условие выполнено )

А – невырожденная матрица, значит, А^-1 существует и определяется по формуле А^-1 = А^*/Δ, где А^* – союзная матрица

А₁₁ А₂₁ А₃₁

А₁₂ А₂₂ А₃₂

А₁₃ А₂₃ А₃₃

А^* =

6 2

7 8

А₁₁ = + = 48-14 = 34

-4 2

3 8

А_{12 = – = – ( – 32 – 6) = 38}

-4 6

3 7

А₁₃ = + = – 28 – 18 = – 46

9 5

7 8

А₂₁ = – = – ( 72-35 ) = – 37

-1 5

3 8

А₂₂ = + = -8 – 15 = – 23

-1 9

3 7

А₂₃ = – = – (-7 – 27) = 34

9 5

6 2

А₃₁ = + = 18 – 30 = – 12

-1 5

-4 2

А₃₂ = – = – ( -2 + 20) = – 18

А

-1 9

-4 6

₃₃ = + = – 6 + 36 = 30

ШАГ 3. Полученные значения подставить в основную формулу и найдём А^-1

А₁₁ А₂₁ А₃₁

А₁₂ А₂₂ А₃₂

А₁₃ А₂₃ А₃₃

1

Δ

А^-1 =

1

78

=

34 –37 12

38_{-23– 18}

–46 34 30

1

78

34 –37 12

38_-23-18

–46 34 30

Ответ: А^-1 =

5. Найти матрицу Х , удовлетворяющую уравнению

4 -2

3 1

3 0

4 2

Х

=

Запишем матричное уравнение в виде ХА = В Х = ВА^-1

Найдём определитель матрицы А

4 -2

3 1

detA = = 4 + 6 = 10 ( условие выполнено )

А – невырожденная матрица, значит, А^-1 существует и определяется по формуле А^-1 = А^*/Δ, где А^* – союзная матрица

Н

1 2

-3 4

1

10

Α^-1 =

айдём обратную матрицу А^-1

1

10

Х = ВА^-1 =

1 2

-3 4

3 0

4 2

Найдём матрицу Х

Х =

1

10

3+0 6+0 4-6 8+8

=

3 6

-2 16

1

10

Проверка

1

10

=

1

10

12+18 – 6+6

-8+48 4+16

=

В

3 0

4 2

А

Х

3 6

-2 16

4 -2

3 1

Ответ: Х =

3 6

-2 16

1

10

Критерий выставления оценок:

Контрольная работа № 1

«Матрицы и определители»

№ задания

1

2

3

4

5

БАЛЫ

5

4

2

4

5

∑

20 балов, что составляет 100%

В работе максимальное количество балов – 20 , что составляет – 100%

от всей выполненной работы

« 5 » – не менее 85% от максимального бала

« 4 » – не менее 70% от максимального бала

« 3 » – не менее 50% от максимального бала

Матрицы и определители (2) (Реферат)

Дисциплина: Высшая математика

Тема: Матрицы и определители

Понятие матрицы.

При изучении вопросов, связанных с действием над векторами, а также при изучении систем линейных уравнений приходится иметь дело с таблицами из чисел, которые называются матрицами.

Определение. Матрицей называется прямоугольная таблица из чисел, содержащая строк и столбцов.

Числа и называются порядками матрицы. Если , то матрица называется квадратной. Для обозначения матрицы пользуются либо вертикальными двойными черточками, либо круглыми скобками:

или .

Для краткого обозначения матрицы может быть использована и одна буква, например, . Кроме того, вместо всей таблицы может быть написано:

, где ; .

Числа называются элементами матрицы, – номер строки, – номер столбца.

Для квадратной матрицы вводится понятие главной и побочной диагонали: главная диагональ идет из верхнего левого угла в нижний правый; побочная – из верхнего правого в нижний левый.

Ранг матрицы. Эквивалентные матрицы.

Дана прямоугольная матрица:

Выделим в этой матрице k произвольных строк и k произвольных столбцов (k Ј m, k Ј n).

Определение. Определитель k-го порядка, составленный из элементов матрицы A, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы A. Матрица A имеет C ^k_m*C ^k_n миноров k-го порядка.

Определение. Рассмотрим всевозможные миноры матрицы A, отличные от нуля. Рангом матрицы A называется наибольший порядок отличных от нуля миноров этой матрицы. Если все элементы матрицы равны нулю, то ранг этой матрицы принимают равным нулю.

Определение. Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.

Ранг матрицы A будем обозначать через r (A). Если r (A) = r (B), то матрицы A и B называются эквивалентными.

Полезно иметь ввиду, что ранг матрицы не изменяется от элементарных преобразований. Под элементарными преобразованиями понимаются:

1) замена строк столбцами, а столбцов соответствующими строками;

2) перестановка строк матрицы;

3) вычеркивание строки, все элементы которой равны нулю;

4) умножение какой-либо строки на число, отличное от нуля;

5) прибавление к элементам одной строки соответствующих элементов другой строки.

Действия над матрицами.

Определение. Две матрица называются равными, если они имеют одинаковые порядки и все их соответствующие элементы совпадают.

Определение. Суммой двух матриц () и () одинаковых порядков называется матрица () того же порядка, элементы которой равны .

На письме это действие может быть записано так: . Операция сложения обладает, очевидно, обычными свойствами: перестановочным ; сочетательным .

Определение. Произведением матрицы на число называется матрица , элементы которой равны .

Умножение матрицы на число может быть записано: или .

Эта операция обладает следующими свойствами: сочетательным относительно числового множителя ; распределительным относительно суммы матриц ; распределительным относительно суммы чисел .

После первых двух действий необходимо отметить, что вычитание матриц производится аналогично сложению, а деление матрицы на число может быть определено как умножение на обратное число.

Определение. Произведением матрицы (), имеющей порядок , на матрицу (), имеющую порядок , называется матрица (), имеющая порядок , элементы которой равны , где .

Записывается это действие так . Из сказанного выше следует, что для нахождения элемента , в произведении необходимо попарно перемножить все соответствующие элементы -ой строки матрицы на элементы -го столбца матрицы , а затем все это сложить. Из определения также следует, что для умножения двух матриц необходимо, чтобы число столбцов матрицы было равно числу строк матрицы . Отсюда следует, что одновременно произведение и существует только лишь в том случае, когда число столбцов равно числу строк , а число столбцов равно числу строк . В этом случае и будут квадратными матрицами, но разных порядков. Чтобы оба произведения были одинакового порядка, необходимо, чтобы и были квадратными матрицами одинакового порядка.

Произведение матриц имеет свойства: сочетательное ; распределительное . Перестановочным свойством в общем случае произведение матриц не обладает. Оно выполняется лишь в некоторых случаях.

Среди квадратных матриц необходимо выделить важный класс диагональных матриц.

Определение. Диагональной называется квадратная матрица, все элементы которой, расположенные вне главной диагонали, равны 0:

.

В том случае, если , то для любой квадратной матрицы порядка справедливо . Действительно, для получаем . Для – . Отсюда, .

Среди диагональных матриц с равными друг другу элементами особое место занимают две матрицы: единичная и нулевая. У единичной матрицы , обозначается она – , у нулевой , обозначается она – .

Как было показано , . Перемножив эти матрицы, можно убедиться, что ; . Таким образом, матрицы и выполняют ту же роль, что и 1 и 0 среди чисел. Вообще нулевой называют любую матрицу, элементы которой равны нулю.

Понятие определителя.

Выше было показано, что матрица – это прямоугольная таблица, составленная из чисел. Особое место среди матриц занимают квадратные матрицы. Рассмотрим произвольную квадратную матрицу порядка или просто :

(3.1.1)

Оказывается, что с такой матрицей всегда можно связать вполне определенную численную характеристику.

Определение. Численная характеристика квадратной матрицы называется ее определителем.

Рассмотрим матрицу первого порядка .

Определение. Численной характеристикой матрицы первого порядка, то есть определителем первого порядка, называется величина ее элемента .

Обозначается определитель одним из символов .

Рассмотрим матрицу второго порядка

.

Определение. Определителем второго порядка, соответствующим матрице второго порядка, называется число, равное .

Обозначается определитель одним из символов

(3.1.2)

Очевидно, что для составления определителя второго порядка, необходимо найти разность произведения элементов, стоящих на главной диагонали матрицы, и произведения элементов, стоящих на побочной диагонали этой матрицы.

Поскольку одна из форм обозначения определителя и обозначения матрицы имеют много общего (записывается таблица из чисел), то так же, как и у матрицы, говорят о столбцах, строках и элементах определителя.

После того как рассмотрены определители 1-го и 2-го порядков, можно перейти к понятию определителя любого порядка. Но перед этим введем понятие минора.

Определение. Минором любого элемента квадратной матрицы порядка называется определитель порядка , соответствующий той матрице, которая получается из первоначальной в результате вычеркивания -ой строки и -го столбца, на пересечении которых стоит элемент .

Обычно минор элемента обозначается .

Определение. Определителем порядка , соответствующим матрице порядка , называется число, равное

.

Обозначается определитель одним из символов

(3.1 3)

Приведенное выражение представляет собой правило вычисления определителя -го порядка по элементам первой строки соответствующей ему матрицы и по минорам элементов этой строки, которые являются определителями порядка . Для это правило дает:

.

В приведенном правиле вычисления определителя фигурирует лишь первая строка. Возникает вопрос, а нельзя ли вычислить определитель, используя элементы других строк?

Теорема. Каков бы ни был номер строки (), для определителя -го порядка справедлива формула

,

называемая разложением этого определителя по -ой строке.

Нетрудно заметить, что в этой формулировке степень при (-1) равна сумме номеров строки и столбца, на пересечении которых стоит элемент .

Докажем эту теорему для . В этом случае может быть равно только 2, так как входит в основное определение величины определителя. Итак:

.

Полученное выражение совпадает с тем, которое было дано в определении, следовательно, для определителя 2-го порядка теорема доказана.

Для произвольного данная теорема доказывается методом математической индукции.

Итак, показано, что определитель может быть разложен по любой строке. Возникает вопрос, а нельзя ли сделать то же самое, использовав произвольный столбец.

Теорема. Каков бы ни был номер столбца (), для определителя -го порядка справедлива формула , называемая разложением этого определителя по -му столбцу.

Докажем теорему для :

.

Данное выражение равно величине определителя, введенной по определению.

Итак, на основании теорем можно сказать, что для вычисления определителя -го порядка необходимо его разложить по произвольной строке или столбцу.

В заключение введем еще одно определение.

Определение. Алгебраическим дополнением данного элемента определителя -го порядка называется число, равное , которое обозначается .

Значит, алгебраическое дополнение отличается от соответствующего минора только лишь знаком. Теперь величину определителя можно вычислить с помощью формул:

.

Литература

1. Лобоцкая Н.Л. Основы высшей математики. Минск, “Высшая школа”, 1973.

2. Минорский В.П. Сборник задач по высшей математики.

3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М., “Наука”, 1986.

4. Гмурман В.Е. Теория вероятностей и математическая статистика. М., “Высшая школа” изд. 5, 1977.

5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., “Высшая школа” изд.2.

6. Баврин И.И. Высшая математика – 1980 г.3

7. Дж. Голуб, Ч. Ван Лоун Матричные вычисления. – М.: Мир, 1999.

8. Беллман Р. Введение в теорию матриц. – М.: Мир, 1969.

9. Гантмахер Ф.Р. Теория матриц (2-е издание). – М.: Наука, 1966.

10. Ланкастер П. Теория матриц. – М.: Наука, 1973.

11. Соколов Н.П. Пространственные матрицы и их приложения. – М.: ГИФМЛ, 1960.

Теория Матриц и Определителей курсовая по математике

F0 B9Средняя школа 45. Город Москва. Ученик 10 класса “Б” Горохов Евгений Курсовая работа (черновик). Введение в теорию матриц и определителей. 1996 год. Оглавление. 1 1. Матрицы……………………………………………………………………………. 3 1.1 1.1 Понятие матрицы…………………………………………………………….. 3 1.2 1.2 Основные операции над матрицами………………………………….. 3 2 2. Определители…………………………………………………………………… 5 2.1 2.1 Понятие определителя…………………………………………………….. 5 2.2 2.2 Вычисление определителей……………………………………………… 5 2.3 2.3 Основные свойства определителей. …………………………………. 6 3 3. Системы линейных уравнений……………………………………………. 8 3.1 3.1 Основные определения…………………………………………………….. 8 3.2 3.2 Условие совместности систем линейных уравнений…………… 8 3.3 3.3 Решение систем линейных уравнений методом Крамера……. 8 3.4 3.4 Решение систем линейных уравнений методом Гаусса………. 9 4 4. Обратная матрица……………………………………………………………… 9 4.1 4.1 Понятие обратной матрицы………………………………………………. 9 4.2 4.2 Вычисление обратной матрицы………………………………………… 9 5 Список литературы……………………………………………………………….. 9 произведений двух квадратных матриц одинакового порядка не обладает, вообще говоря, перестановочным свойством. В самом деле, если положить A = , B = , то AB = , а BA = Те же матрицы, для произведения которых справедливо перестанавочное свойство, принято называть коммутирующими. Среди квадратных матриц выделим класс так называемых диагональных матриц, у каждой из которых элементы, расположенные вне главной диагонали, равны нулю. Среди всех диагональных матриц с совпадающими элементами на главной диагонали особо важную роль играют две матрицы. Первая из этих матриц получается, когда все элементы главной диагонали равны единице, называется единичной матрицей n- ого порядка и обозначается символом E . Вторая матрица получается при всех элементах равных нулю и называется нулевой матрицей n-ого порядка и обозначается символом O. Допустим, что существует произвольная матрица A, тогда AE = EA = A, AO = OA = O. Первая из формул характеризует особую роль единичной матрицы Е, аналогичную то роли, которую играет число 1 при перемножении вещественных чисел. Что же касается особой роли нулевой матрицы О, то ее выявляет не только вторая из формул, но и элементарно проверяемое равенство : A + O = O + A = A. Понятие нулевой матрицы можно вводить и не для квадратных матриц. 2. Определители. 2.1 Понятие определителя. Прежде всего необходимо запомнить, что определители существуют только для матриц квадратного вида, ибо для матриц другого типа не существует определителей. В теории систем линейных уравнений и в некоторых других вопросах удобно использовать понятие определителя, или детерминанта. 2.2 Вычисление определителей. Рассмотрим какую-либо четверку чисел, записанных в виде матрицы по два в строках и по два столбцах, Определителем или детерминантом, составленным из чисел этой таблицы, называется число ad—bc, обозначаемое так:.Такой определитель называется определителем второго порядка, поскольку для его составления взята таблица из двух строк и двух столбцов. Числа, из которых составлен определитель, называются его элементами; при этом говорят, что элементы a и d составляют главную диагональ определителя, а элементы b и c его побочную диагональ. Видно, что определитель равен разности произведений пар элементов, стоящих на его главной и побочной диагоналях . Определитель третьего и любого другого порядка находится примерно также, а именно: Допустим, что у нас есть квадратная матрица . Определителем следующей матрицы является такое выражение : a11a22a33 + a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a22a31.. Как вы видите он просчитывается довольно легко, если запомнить определенную последовательность. С положительным знаком идут главная диагональ и образующиеся из элементов треугольники, имеющие параллельную главной диагонали сторону, в данном случае это треугольники a12a23a31, a13a21a32. С отрицательным знаком идут побочная диагональ и треугольники ей параллельные, т.е. a11a23a32 , a12a21a33. Таким образом находятся определители любого порядка. Но бывают случаи, когда и этот метод становится довольно сложным, например, когда элементов в матрице очень много, и для того, чтобы сосчитать определитель нужно затратить уйму времени и внимания. Существует более легкий способ вычисления определителя n- ого порядка, где n2. Договоримся называть минором любого элемента Aij матрицы n-ого порядка определитель, соответствующий той матрице, которая получается из матрицы в результате вычеркивания i-й строки и j-ого столбца ( той строки и того столбца, на пересечении которых стоит элемент Aij ). Минор элемента Aij будем обозначать символом . В этом обозначении верхний индекс обозначает номер строки, нижний – номер столбца, ф черта над M означает, что указанные строка и столбец вычеркиваются. Определителем порядка n, соответствующим матрице, назовем число, равное и обозначаемое символом . Теорема 1.1 Каков бы ни был номер строки i ( i =1, 2 …, n ), для определителя n-ого порядка справедлива формула = det A = называемая разложением этого определителя по i-й строке. Подчеркнем, что в этой формуле показатель степени, в которую возводится число (-1), равен сумме номеров строки и столбца, на пересечении которых стоит элемент Aij. Теорема 1.2 Каков бы ни был номер столбца j ( j =1, 2 …, n ), для определителя n-го порядка справедлива формула = det A = называемая разложением этого определителя по j-ому столбцу. 2.3 Основные свойства определителей. У определителей также есть свойства, с помощью которых задача их вычисления становится более легкой. Итак, ниже устанавливается ряд свойств, которыми обладает произвольный определитель n-го порядка. 1. Свойство равноправности строк и столбцов. Транспонированием любой матрицы или определителя называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате транспонирования матрицы A получается матрица, называется матрица, называемая транспонированной по отношению к матрице A и обозначается символом A . Первое свойство определителя формулируется так : при транспонировании величина определителя сохраняется, т. е. = . 2. Свойство антисимметрии при перестановке двух строк ( или двух столбцов ). При перестановке местами двух строк ( или двух столбцов ) определитель сохраняет свою абсолютную величину, но меняет знак на противоположный. Для определителя второго порядка это свойство проверяется элементарно ( из формулы вычисления определителя второго порядка сразу вытекает, что определители отличаются лишь знаком ). 3. Линейное свойство определителя. Будем говорить, что некоторая строка (a) является линейной комбинацией двух других строк ( b и c ) с коэффициентами и . Линейное свойство можно сформулировать так : если в определителе n-го порядка некоторая i-я строка является линейной комбинацией двух строк с коэффициентами и , то = + , где – определитель, у которого i-я строка равна одной из двух строк линейной комбинации, а все остальные строки те же, что и у , а – определитель, у которого i-я строка равна второй из двух строк, а все остальные строки те же, что и у . Эти три свойства являются основными свойствами определителя, вскрывающими его природу. Следующие пять свойств являются логическими следствиями трех основных свойств. Следствие 1. Определитель с двумя одинаковыми строками ( или столбцами ) равен нулю. Следствие 2. Умножение всех элементов некоторой строки ( или некоторого столбца ) определителя на число a равносильно умножению определителя на это число a. Иными словами , общий множитель всех элементов некоторой строки ( или некоторого столбца ) определителя можно вынести за знак этого определителя. Следствие 3. Если все элементы некоторой строки ( или некоторого столбца ) равны нулю, то и сам определитель равен нулю. Следствие 4. Если элементы двух строк ( или двух столбцов ) определителя пропорциональны, то определитель равен нулю. Следствие 5. Если к элементам некоторой строки ( или некоторого столбца ) определителя прибавить соответствующие элементы другой строки ( другого столбца ), умножение на произвольный множитель , то величина определителя не изменяется. Следствие 5, как и линейное свойство, допускает более общую формулировку, которую я приведу для строк : если к элементам некоторой строки определителя прибавить соответствующие элементы строки, являющейся линейной комбинацией нескольких других строк

Контрольная работа 1 Матрицы. Определители. Системы

Контрольная работа 1
Матрицы. Определители. Системы линейных
алгебраических уравнений
З.С. Акманова
29 октября 2012 г.
1
Вычислить определитель 4-го порядка (любым способом):
1.
2.
3.
4.
5.
6.
7.
1 −2 −3 0 7 0
5
1 0 2
3 −4
5 −2 −5 −1
1 2 3 4
−2 1 −4 3
3 4 −1 2
4 3 −2 1
1 1
2
3 3 −1 −1 −2
2 3 −1 −1
1 2
3 −1
1 2 −3 4
4 −3 2 1
0 1 −1 2
1 −1 1 1
1 3 2 −1
1 9 2 3 1 3 4 1 2 −9 0 −3
3 0 2 4
2 2 1 0
0 −2 1 3
1 1 1 5
3 1 2 1 4 3 0 −1
1 1 3 6 2 9 0 7 8. 
9.
10.
11.
12.
13.
14.
1 1 7 0 3 2 1 5 0 −1 3 4 1 4 0 −2
3 1 1 1
1 3 1 1
1 1 3 1
1 1 1 3
1 1 1 1 1 2 3 4 1 3 6 10
1 4 10 20
1 2 3 4
2 3 4 1
3 4 1 2
4 1 2 3
1
2
3
4 −2 1 −4 3 3 −4 −1 2 4
3 −2 −1
1 2 3 4
2 1 2 3
3 2 1 2
4 3 2 1
1
2
3
0 −4 −3 −7 1 2 −1 3 −1
0 −9 −5 −1
1
15.
16.
17.
18.
19.
20.
21.
2 −1 3 5 0 7 4 −3
2 6 7 −3
1 0 1 2 −1 0 5
8 2 3 −1 −4
1 3 4
5 2 1 1
0
2
1 −1 −4
1 −1 3
3 0
1
−2
−3
−2 −1 0
5
2 2 1 3
1 2 2 2
3 2 2 3
2 1 1 2
0 1 −3 4 1 0 −2 3 3 2 0 −5
4 3 −5 0 1 2 3 0
0 1 2 3
3 0 1 2
2 3 0 1
1 −4 2
0 2 −3 −1 −4
3 −7 2 −6
0 1 −1 −1
−1 1 −2 0
−2 3
1 8
22. −3 2 −1 3
4 −1 2 1
3 5
1 −7
2 −3 4
5 23. 5
3 5 2
1 2 −1 0 2
−1 −2
3
2
24. −2
−1
1
2
2
1
−1 3
25. 2 −1
0
1
−3
1
−4
3
2
1
−2
−1
1 −1
2 0
0 2 −3
5
Найти матрицу X:

1. X
2. X
3. X
4. X
5. X
6. X
7. X
8. X
9. X
10. X



2 1 −2
1 0
−1 1 −2
= 2C−AB T , если A=1 3 −3, B=
, C=−3 2.
1 −2 1
3 2 −1
1 1




2 2 2
1 −3
1
−2
3
= AT −CB, если A=−1 3 −1, B=
, C=−1 0 .
2 1 −3
1 5 1
−2 2




1 −2
1 2 −1
0
−3
2
, C=1 2 .
= AC−3B T , если A= 0 2 7 , B=
1 −2 3
0 −1
−1 4 1




3 −1
−1 2 −1
2
−1
0
2 −2, B=
, C=−2 1 . 
= 2B T +AC, если A= 3
2 −2 −1
1 −2
1 −1 1




2 0 −1
1 2
1 −1 3
= 2AT + CB, если A=1 2 −2, B=
, C=2 −1.
1 0 2
0 1 2
0 1




2 1
1 2 0
1 3 −2
, C= 3 0.
= 5B T − AC, если A=1 3 2, B=
2 −1 3
2 1 3
−1 3




2 −1 1
2 1
1
2
−1
= AB T −3C, если A= 2 −3 0 , B=
, C=−1 3.
−2 1 −3
−1 1 −2
0 2




−1 2 −1
1
2
−1
2
−3
= CB−2AT , если A= 2 −5 5 , B=
, C=−2 1 .
0 1 −2
1
3
0
1 −2




1 0
2
2 1
2 −1 1
= 5A − CB, если A=1 −1 2 , B=
, C=0 −3.
1 −2 0
2 1 −3
3 2




2 −1 1
3
1
2 1 −1
= A(C+2B T ), если A=−2 2 −3, B=
, C=−2 1 .
3 −2 1
1 −1 1
1 −1
2

11. X
12. X
13. X
14. X
15. X
16. X
17. X
18. X
19. X
20. X
21. X
22. X
23. X



2 0 −1
1 −2
1 −1 2
= 4AT − CB, если A=2 1 −1, B=
, C=1 −3.
0 −1 3
0 1 1
0 1




2 1 0
3 0
1 3 −2
= 3CB+2A, если A= 1 5 2, B=
, C= 1 2.
1 −2 1
−1 1 3
−1 3




−1 2 −2
0 1
−2 1 1
= A(2B T +C), если A= 1 6 −1, B=
, C=2 1 .
1 −2 2
−1 2 1
1 −1




1 2 3
1
0
1
3
−2
= CB−2AT , если A=2 −5 1, B=
, C= 3 −1.
1 −2 3
4 −1 2
−1 2




1 2 0
1 2
1
−2
1
= 3C−AB T , если A= 2 5 1, B=
, C= 3 0. 
2 0 −1
−1 3 2
−1 2




1 0 −2
1 −2
1 −2 0
= AT +5CB, если A=1 2 −1, B=
, C=3 −2.
−1 1 3
1 −1 0
1 2




1
−2 1
0 −1
, B= 1 3 2 , C=1 2 .
= C−2AB T , если A=271 −3
−2 3 −1
1
−2 −1
3 −1




1 −3
2 −1 3
1
−5
0
1 .
, C= 2
= AB T −3C, если A=2 −5 1, B=
2 −1 3
−3 2
4 −1 2




1 1 2
1
0
0
2
−2
= 3C−AT B T , если A=2 −3 3, B=
, C= 4 −1.
−1 1 2
1 2 0
−2 2




1 −3
2 0 1
2
−1
1
= 3C+AB T , если A=1 −6 1, B=
, C=−2 3 .
−2 3 0
3 −1 1
1
2




1 −2
1 0 −2
1 −2 0
= AT +5CB, если A=1 2 −1, B=
, C=3 −2.
−1 1 3
1 −1 0
1 2




1 2 2
2
3
0 1 −2
= AC−2B T , если A=−2 5 1 , B=
, C=−1 3 .
−1 2 1
1 2 −1
0 −2




2 1 0
2 1
0
−4
2
, C=0 3 .
= 2A + CB, если A=1 −2 6, B=
−2 1 4
1 −1 3
2 −1
3




1 3
2
2
1
2 3 −1
24. X = 2AT −CB, если A=2 −3 1 , B=
, C=−1 0 .
2 −1 3
0 2 −1
1 −2




1 2 1
2 1
5 −3 0
25. X = CB + 4A, если A=1 3 5, B=
, C=−1 0.
−1 2 1
2 1 0
2 3
3
Решить систему линейных уравнений тремя
способами: а) методом Гаусса; б) по формулам Крамера; в) матричным методом. 
7.
1.





 5x1 + 2x2 + x3 = 4
2x1 − 2x2 − 3x3 = −3


x1 + 4x2 + 4x3 = 5
x1 − 2x2 + 3x3 = 6
2x1 + 3x2 − 4x3 = 20


3x1 − 2x2 − 5x3 = 6
8.
2.


 4x1 + x2 + 4x3 = −2
x1 + x2 + 2x3 = −1


2x1 − x2 + 2x3 = −4


 3x1 − x2 − 3x3 = −1
x1 − 3x2 − 2x3 = 1


3x1 + 2x2 − 4x3 = −4
9.



3.


 5x1 − 4x2 + 6x3 = 5
2x1 + x2 + 3x3 = 4


x1 − 5x2 + 2x3 = −4


10.
4.


 2x1 − 2x2 − 5x3 = 4
x1 + 3x2 + 2x3 = 1


3x1 + 2x2 + x3 = −1
2x1 − 4x2 − 3x3 = −11
4x1 − 2x2 + 3x3 = 11
x1 + x2 − 2x3 = −4


 8x1 + 3x2 − 6x3 = 2
x1 + x2 − x3 = 1


4x1 + x2 − 3x3 = 3
11.


 3x1 + 4x2 + 2x3 = 8
2x1 − x2 − 3x3 = −4


x1 + 5x2 + x3 = 0
5.
12.


 3x1 − 2x2 − 5x3 = −5
4x1 + 2x2 − 2x3 = −2


x1 + 3x2 + x3 = 3


 x1 + 9x2 − 4x3 = 9
4x1 − 3x2 + 2x3 = 9


2x1 + 5x2 − 3x3 = 4
13.
6.


 3x1 + 2x2 + x3 = 5
2x1 + x2 + 3x3 = 11


2x1 + 3x2 + x3 = 1





4
3x1 + x2 + x3 = 5
x1 − 4x2 − 2x3 = −3
3x1 − 5x2 − 6x3 = −9
14.
21.


 2x1 + x2 − x3 = −2
x1 − 2x2 + x3 = 6


3x1 + 2x2 − x3 = −2
15.





16.
17.
18.





x1 + x2 + 2x3 = 2
3x1 − 2x2 + 5x3 = −5
2x1 + 4x2 − x3 = 3
3x1 − x2 + x3 = 2
x1 + 3x2 + x3 = 2
22.
4x1 + 2x2 + 3x3 = 1





 2x1 + 5x2 − 8x3 = 8
4x1 + 3x2 − 9x3 = 9


2x1 + 3x2 − 5x3 = 7


3x1 − 5x2 + 3x3 = 1
x1 + 2x2 + x3 = 4
−x1 + 7x2 + 2x3 = 8
23.


 x1 + 3x2 − 2x3 = 2
3x1 + 4x2 + 2x3 = 1


x1 + x2 + 3x3 = 2


 3x1 + 2x2 − x3 = 3
4x1 + 3x2 + x3 = 6


x1 − x2 − 2x3 = 1



2x1 − x2 + 2x3 = 2


4x1 − 5x − 2 + x3 = 1
x1 + 2x2 + 3x3 = 4
24.


 3x1 + 3x2 − 5x3 = 1
2x1 − x2 + 7x3 = 8


x1 + 3x2 + 2x3 = 6
19.


 2x1 − 3x2 − 2x3 = 1
x1 − x2 + x3 = −1


3x1 + 4x2 + 5x3 = 2
25.
20.


 4x1 + 2x2 + x3 = 3
2x1 − x2 − 2x3 = −2


x1 − 2x2 − x3 = 2
4


 2x1 + 2x − 2 + x3 = 1
5x1 + 3x2 + x3 = −3


x1 − 2x2 + 5x3 = −1
Решить системы уравнений методом Гаусса.
В неопределенных системах найти общее и
частное решения и сделать проверку.
1.


 2x1 + 7x2 + 3x3 + x4 = 6
a) 3x1 + 5x2 + 2x3 + 2x4 = 4


x1 − 2x2 − x3 + x4 = −2

x1 − x2 − x4 = 2


x1 + x3 − 2x4 = 1
b)


2x1 − x2 + x3 − 3x4 = 1
5


 3x + 7y + 3z = 0
x−y−z =0
c)


x + 4y + 2z = 0
2.
a)
b)








2x1 + 3x2 − x3 = 0


4x1 + 7x2 − 7x − 3 = 9
x1 + 2x2 − 3x3 = 4
3x1 − 2x2 + x3 − x4 + 3x5 = 1
2x1 + x2 − x3 + 2x4 − x5 = 3

−3x1 + 2x2 + 3x3 − x4 + 2x5 = 1



2x1 + x2 + 3x3 + 4x5 = 1


 2x + y − z = 0
c) 5x + 4y − z = 0


x + 2y + z = 0
3.


 3x1 + 2x2 + 2x3 + 2x4 = 2
a) 2x1 + 3x2 + 2x3 + 5x4 = 3


2x1 + 2x2 + 3x3 + 4x4 = 5


 2x − 3y + 5z = 3
x + 2y − 3z = 1
b)


4x + y − z = 4

x1 − 7x2 + 2x3 + 4x4 = 0




2x1 + 3x2 − x3 + x4 = 0
c)

 3x1 − 4x2 + 2x3 + 5x4 = 0


4x1 − 11x2 + 3x3 + 5x4 = 0
4.
a)



2x1 − x2 + x3 + 2x4 + 3x5 = 2
6x1 − 3x2 + 2x3 + 4x4 + 5x5 = 3


4x1 − 2x2 + x3 + x4 + 2x5 = 1


 3x − yy + 2z = 2
b) 4x + 2y − 5z = 1


2x − 4y + 9z = 5

6x1 − x2 + x3 + 2x4 = 0




x1 + 2x2 − x3 + x4 = 0
c)

5x
1 − 3x2 + 2x3 + 3x4 = 0



4x1 + x2 + 3x3 = 0
6
5.


 6x1 + 4x2 + 5x3 + 2x4 + 3x5 = 1
3x1 + 2x2 + 4x3 + x4 + 2x5 = 3
a)


9x1 + 6x2 + x3 + 2x4 + 2x5 = 2


 2x + 5y − z = 1
3x − 2y + 5z = 4
b)


3x + 11y − 8z = 1


 3x − 2y + z = 0
c) x + 2y − 3z = 0


7x − 2y − z = 0
6.
a)



x1 + 2x2 + 3x3 − 2x4 + x5 = 4
3x1 + 7x2 + 5x3 − 4x4 + 3x5 = 5


2x1 + 4x2 + 2x3 − 3x4 + 3x5 = 6


 x − 2y + 4z = 2
3x + y − 2z = 1
b)


x + 5y − 10z = 3

x1 − 5x2 + 3x3 − x4 = 0



 3x + 2x − x + 3x = 0
1
2
3
4
c)

2x
+
7x
−
4x
+
x
1
2
3
4 =0



x1 + 12x2 − x3 + 5x4 = 0
7.


 6x1 + 2x2 + 2x3 + 3x4 + 4x5 = 5
4x1 + 2x2 + x3 + 2x4 + 3x5 = 4
a)


2x1 + x − 2 + 7x3 + 3x4 + 2x5 = 1


 5x − 2y + 3z = 1
2x + y − 2z = 2
b)


x − 4y + 7z = 3


 4x − y + 3z = 0
c) 3x + 3y + 2z = 0


x − 4y + z = 0
8.
a)





x1 + 2x2 + 3x3 + x4 = 3
x1 + 4x2 + 5x3 + 2x4 = 2
3x1 + 7x2 + 7x3 + 2x4 = 12


 3x − 2y + z = 1
b) 5x + 2y − 3z = 2


4x − 8y + 6z = 3
7

2x1 − x2 + 3x3 + x4



 3x + 2x − x + x
1
2
3
4
c)

x1 + 3x2 − 4x3 − x4



7x1 + 6x3 + 3x4
9.
10.
=0
=0
=0
=0


 3x1 + 2x2 + 5x3 + 4x3 = 3
a) x1 − 6x2 − 9x3 − 20x4 = −11


4x1 + x2 + 4x3 + x4 = 2


 x − 3y − z = 1
b) 2x + 4y + 3z = 2


4x − 2y + z = 1


 x + 2y − 3z = 0
c) 5x − 3y + 2z = 0


3x − 7y + 8z = 0


 2x1 + 5x2 + x3 + 3x4 = 2
a) 4x1 + 6x2 + 3x3 + 5x4 = 4


2x1 − 3x2 + 3x3 + 2x4 = 7


 4x − 2y + 3z = 2
5x + y − 2z = 1
b)


2x − 8y + 13z = 1

x1 + x2 − 4x3 + 2x4 = 0



 5x − x + x − 4x = 0
1
2
3
4
c)

3x
+
x
9x
−
8x
1
2
3
4 =0



4x1 − 2x2 + 6x3 − 6x4 = 0
11.
a)





3x1 + 2x2 − x3 − x4 = 1
6x1 + 4x2 + x3 + 2x4 = 2
3x1 + 2x2 + 2x3 + 3x4 = 1

2x − 3y = 1




x + 2z = 3
b)

−y + z = 1



3x − 4y + 3z = 2


 x − 4y + z = 0
2x − y + 3z = 0
c)


3x − 5y + 4z = 0
8
12.
13.
14.

3x1 + 3x2 + 13x3 + 8x4 = −1




x1 + x2 + 5x3 + 2x4 = 1
a)

x1 + x2 + 3x3 + 4x4 = −3



2x1 + x2 + 3x3 + 2x4 = −3


 5x + 2y − z = 3
b) 2x − y + 2z = 1


x + 7y − 8z = 1

3x1 − 2x2 + x3 − x4 = 0



 2x + 3x − 4x + x = 0
1
2
3
4
c)

x1 − 5x2 + 6x3 − 2x4 = 0



−x1 − 8x2 + 9x3 − 3x4 = 0

13x1 + x2 − 3x4 = −13



 x − 2x + 3x + 6x = 5
1
2
3
4
a)
 14x1 − x2 + 3x3 + 3x4 = −8



6x1 − 3x2 + 5x3 + 9x4 = 4

x − 3y + z = 3


4x + 2y − 5z = 1
b)


3x + 19y − 15z = 5


 3x − 6y + 5z = 0
4x − y + 2z = 0
c)


x + 5y − 3z = 0

10x1 − 9x2 + 7x3 + 6x4 = 3



 −15x − 3x − 11x + 2x = 1
1
2
3
4
a)

3x1 − 6x2 + 2x3 + 4x4 = 2



7x1 − 3x2 + 5x3 + 2x4 = 1


 3x + 7y − 2z = 3
2x − y + z = 1
b)


x − 9y + 4z = 1

2x1 + 3x2 − x3 + 2x4 = 0



 4x − 2x + x − x = 0
1
2
3
4
c)

2x
−
5x
+
x
−
3x
2
3
4 =0
 1


−8x2 + 3x3 + x4 = 0
15.
a)





x1 + 3x2 − 2x3 + 5x4 = 3
x1 + 5x2 + 8x3 − 9x4 = 1

4x1 + 13x2 − 3x3 + 13x4 = 11



5x1 + 16x2 − 5x3 + 18x4 = 14
9


 6x − y + 2z = 3
3x + 2y − z = 2
b)


3x + 7y − 5z = 4


 3x + 2y − z = 0
c) 4x − y + 3z = 0


x − 5y + 4z = 0
16.

x1 + 3x2 + 2x3 + 5x4 = 2



 3x + 5x + 4x + 6x = 4
1
2
3
4
a)

x
+
7x
+
4x
+
14x
1
2
3
4 =4



3x1 + x2 + 2x3 − 3x4 = 2


 7x + 3y − z = 3
b) 2x + 2y + 3z = 1


x − 3y − 10z = 2

3x1 + 2x2 − 5x3 + x − 4 = 0




x1 − x2 + 2x3 − x4 = 0
c)

4x1 + 2x2 − 3x3 = 0



x1 + 4x2 − 9x3 + 2x4 = 0
17.
a)





18.
2x1 + 7x2 − x3 + 3x4 = 5
2x1 − 7x2 + 3x3 − 6x4 = −2
−6x1 + 7x2 − 5x3 + 9x4 = 38


 4x − y + 3z = 3
2x + 3y − z = 1
b)


2x − 11y + 9z = 2


 x + 2y − z = 0
5x − y + 2z = 0
c)


3x − 7y + 4z = 0


 2x1 − 3x2 + 5x3 + 7x4 = 1
4x1 − 6x2 + 2x3 + 3x4 = 2
a)


6x1 − 9x2 + 7x3 + 10x4 = 3


 x − 5y + 3z = 1
3x + 2y − z = 3
b)


x − 22y + 15z = 5

4x1 − x2 + x3 + 2x4 = 0



 x + x − 3x + x = 0
1
2
3
4
c)

3x
−
2x
+
x
+
x
1
2
3
4 =0



2x1 − 2x2 + 7x3 = 0
10
19.


 x1 + 3x2 + 2x3 + 4x4 = 3
a) 2x1 + 6x2 + 5x3 + 7x4 = 7


x1 + 3x2 + 3x3 + 3x4 = 4

2x1 + x2 − x3 + 2x4 = −1


3x1 − x2 + x3 − 3x4 = 2
b)


2x1 + 6x2 − 6x3 + 14x4 = 1

x − 6y + 5z = 0


5x − 2y + 3z = 0
c)


2x + 16y − 12z = 0
20.


 2x1 + 5x2 − 8x3 = 8
4x1 + 3x2 − 9x3 = 9
a)


6x1 + 8x2 − 17x3 = 17
b)



x1 − 3x2 + 5x3 + x4 − x5 = 1
2x1 + x2 − 3x3 + 2x4 + 3x5 = 2


3x1 − 2x2 + 2x3 + 3x4 + 2x5 = 1

x1 + x2 − 3x3 + x4 = 0



 2x − 3x + x − 2x = 0
1
2
3
4
c)

x1 − 4x2 + 4x3 + x4 = 0



2x2 + 7x3 − 4x4 = 0
21.
a)



3x1 − x2 + 3x3 = −8


2x1 − 6x2 + 10x3 = −11
x1 + 5x2 − 7x3 = 3


 5x1 − x2 + 3x3 + 4x4
3x1 + 2x2 − x3 + x4
b)


x1 + 5x2 − 5x3 − 2x4

2x1 − x2 + 3x3 + 2x4



 3x + 2x − x + x
1
2
3
4
c)

x
+
3x
−
4x
+
x
1
2
3
4



7x1 + 4x3 + 5x4
22.
=2
=8
=3
=0
=0
=0
=0


 2x1 − 3x2 + x3 = 3
5x1 + 2x2 − x3 = 1
a)


3x1 + 5x2 − 2x3 = −2


 2x1 + x2 − 3x3 + 5x4 = 3
5x1 − 2x2 + x3 − 2x4 = 1
b)


x1 − 3x2 + 7x3 − 12x4 = 2
11

5x1 − 2x2 + 3x3 + x4



 2x + x − 2x + 2x
1
2
3
4
c)

x1 − 4x2 + 2x3 − 3x4



3x1 − 3x2 + 5x3 + x4
23.
=0
=0
=0
=0


 4x1 − 2x2 + x3 = 0
3x1 + x2 − x3 = 4
a)


x1 − 3x2 + 2x3 = −4


 x1 + 2x2 − 3x3 + x4 = 6
3x1 − x2 + 5x3 − 2x4 = 1
b)


x1 − 5x2 + 11x3 − 4x4 = 3


 x + 5y + 2z = 0
3x − 2y + z = 0
c)


4x + 3y + 3z = 0
24.


 4x1 + 2x2 − 3x3 + x4 = 1
a) 3x1 − x2 + 2x3 − 2x4 = 3


x1 + 3x2 − 5x3 + 3x4 = −2

x+y−z =4



 2y + 2z = 1
b)

2x − 2z = 1



x+y+z =2


 4x + 5y − 8z = 0
2x − y + 2z = 0
c)


x + 3y − 5z = 0
25.
a)



2x1 − x2 + 3x3 + x4 − 2x5 = 1


3x1 + 3x2 − 4x3 + 3x4 + 3x5 = 2

x − 2y + 3z = 1



 2x − y + z = 2
b)

5x + 2y − 2z = 3



8x − y + 2z = 1


 5x + 7y − z = 0
c) x + 4y − 3z = 0


3x − y + 5z = 0
5x1 + 2x2 − x3 + 4x4 + x5 = 3
12

Тест «Определители и матрицы»

«Математика – это наука о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями»

Юджин Вигнер, американский физик и математик (1902-1995)

Часть I. Выберите один правильный ответ.

1.      Раздел математики, изучающий определители и матрицы называется:

а)      алгеброй

б)      линейной алгеброй

в)      высшей математикой

г)       линейным программированием

2.      Определитель – это:

а)      число

б)      матрица

в)      таблица чисел

г)       вектор

3.      Чему не может быть равен определитель:

а)      нулю

б)      отрицательному значению

в)      дробному значению

г)       бесконечности

4.      Порядок определителя – это:

а)      диапазон значений его элементов

б)      значение определителя

в)      число его строк и столбцов

г)       сумма индексов последнего элемента последней строки

5.      Минор определителя – это:

а)      сумма элементов главной диагонали

б)      произведение элементов главной диагонали

в)      другой определитель, полученный из данного вычеркиванием строки и столбца 

г)       алгебраическое дополнение элемента определителя

6.      Алгебраическое дополнение каждого элемента равно:

а)      минору этого элемента, взятому с противоположным знаком

б)      минору этого элемента, взятому со своим знаком

в)      минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых стоит данный элемент, нечетно, и с обратным знаком, если – четно

г)       минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых стоит данный элемент, четно, и с обратным знаком, если – нечетно

7.      Разложением определителя по элементам строки называется:

а)      нахождение определителя как суммы произведений элементов строки на их алгебраические дополнения

б)      нахождение определителя как суммы произведений элементов столбца на их алгебраические дополнения

в)      нахождение определителя как суммы произведений элементов строки на миноры этих элементов

г)       нахождение определителя как суммы произведений элементов столбца на миноры этих элементов

8.      Матрица – это:

а)      прямоугольная таблица чисел

б)      определитель

в)      отличный от нуля минор

г)       неопределяемое понятие

9.      Порядок может быть только у матрицы следующего вида:

а)      прямоугольной

б)      квадратной

в)      матрицы-строки

г)       любой

10.  Диагональной называется матрица, у которой:

а)      все элементы вне главной диагонали равны нулю

б)      все элементы главной диагонали равны нулю

в)      все элементы главной диагонали равны единице

г)       все элементы на главной и побочной диагоналях равны нулю

11.  Присоединённой матрицей к квадратной матрице может являться:

а)      матрица того же порядка

б)      матрица, определитель которой равен определителю данной матрицы

в)      матрица порядка на один меньше, чем у данной матрицы

г)       такая матрица, что произведение их определителей равно единице

12.  Чтобы вычислить произведение матрицы на число, нужно:

а)      умножить элементы главной диагонали на это число

б)      умножить элементы первой строки на это число

в)      умножить элементы первого столбца на это число

г)       умножить каждый элемент на это число

13.  При умножении матрицы на единичную матрицу будет получена:

а)      исходная матрица

б)      транспортированная матрица

в)      обратная матрица

г)       единичная матрица

14.  Операция умножения матриц не обладает свойством:

а)      ассоциативности

б)      коммутативности

в)      дистрибутивности

15.  Система линейных уравнений называется совместной, если она:

а)      имеет единственное решение

б)      не имеет решений

в)      имеет бесконечное множество решений

г)       имеет хотя бы одно решение

16.  При решении систем уравнений методом Гаусса нельзя:

а)      удалять равные или пропорциональные строки кроме одной

б)      любую строку умножать или делить на некоторое число

в)      переставлять местами строки

г)       умножать любой столбец на некоторое число

17.  Если при решении системы уравнений методом Крамера все определители равны нулю, то:

а)      система имеет единственное решение

б)      система имеет ненулевые решения

в)      система имеет бесконечное множество решений

г)       система не имеет решений

18.  Методом обратной матрицы может быть решена:

а)      любая система линейных уравнений

б)      система линейных уравнений, имеющая квадратную матрицу

в)      система линейных уравнений, имеющая квадратную невырожденную матрицу

г)       система как линейных, так и нелинейных уравнений

19.  Для решения систем линейных уравнений методом Крамера в MS Excel  ее главный и вспомогательные определители вычисляют с использованием функции:

а)      МОБР

б)      МОПРЕД

в)      МУЛЬТИНОМ

г)       МУМНОЖ

20.  В MathCAD для нахождения определителя используют оператор Determinant на панели инструментов:

а)      Calculator

б)      Calculus

в)      Matrix 

г)       Evaluation

Часть II. Выберите несколько правильных ответов.

1.  Свойства определителей:

а)      определитель транспонированной матрицы равен определителю исходной матрицы

б)      определитель обратной матрицы равен определителю исходной матрицы

в)      умножение всех элементов строки или столбца определителя на некоторое число равносильно умножению определителя на это же число

г)       если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный

д)      если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю

е)      если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен единице

ж)   если две строки (столбца) матрицы пропорциональны друг другу, то определитель этой матрицы равен нулю

з)       определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали

и)      если все элементы k-ой строки (столбца) определителя представлены в виде сумм  ak j + bk j, то определитель можно представить в виде произведения двух определителей

к)      определитель не изменится, если к элементам любой его строки (или столбца) прибавить соответствующие элементы другой строки (или соответствующего столбца), умноженные на одно и то же число

л)      определитель произведения двух квадратных матриц равен произведению определителей этих матриц 

2.  К элементарным преобразованиям матриц относятся:

а)      перестановка строк

б)      умножение любой строки на число, отличное от нуля

в)      прибавление к одной из строк любой другой строки, умноженной на любое число

г)       приписывание к данной матрице единичной матрицы

д)      умножение любой строки матрицы на другую строку

е)      замена строк матрицы ее столбцами

3.  К арифметическим действиям над матрицами относятся:

а)      нахождение обратной матрицы

б)      нахождение транспортированной матрицы

в)      сумма матриц

г)       произведение матрицы на число

д)      произведение матриц

е)      деление матриц

Часть III. Каждому элементу первого столбца поставьте в соответствие один или несколько элементов второго столбца.

1.  Виды матриц.

Виды матриц:	Характеристики:
1. обратная	А. число строк матрицы совпадает с числом столбцов
2. вырожденная	Б. матрица, составленная из алгебраических дополнений элементов данной матрицы, разделенных на величину определителя исходной матрицы
3. квадратная	В. получена из данной матрицы заменой строк столбцами с соответствующим номером
4. диагональная	Г. определитель матрицы равен нулю
5. единичная	Д. не имеет обратной матрицы
6. транспортированная	Е. равна произведению исходной и обратной матриц
	Ж. на главной диагонали стоят некоторые числа, а остальные элементы – нули
	З. на главной диагонали стоят единицы, а остальные элементы – нули
	И. является частным случаем диагональной матрицы
	К. имеет определитель

2.  Методы решения систем линейных уравнений.

Методы:	Характеристики:
1. метод Гаусса	А. матрица-столбец неизвестных вычисляется как произведении обратной матрицы на матрицу-столбец свободных членов
2. метод Крамера	Б. метод последовательного исключения неизвестных, приведение матрицы системы к ступенчатому виду
3. матричный метод	В. неизвестные вычисляются как отношение определителей, полученных из определителя системы заменой соответствующих столбцов на столбец свободных членов, к определителю системы уравнений
	Г. подходит для произвольной системы линейных уравнений
	Д. подходит только для систем линейных уравнений, у которых число уравнений равно числу неизвестных
	Е. матрица системы должна быть невырожденной

 

 Тест в интерактивной форме:

С выбором 1 ответа

Пазл “Классификация матриц”

Контрольная работа №1 системы линейных уравнений тема 1 системы линейных уравнений

ТЕМА 1. Системы линейных уравнений.

Решение типового варианта контрольной работы.

Задача 1. Вычислить определитель .

Решение. Для вычисления определителя третьего порядка будем использовать известную формулу Саррюса (правило треугольников), которое может быть записано следующей формулой:

Ответ: 0.

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Решим систему матричным способом, для этого вычислим обратную матрицу , где – алгебраические дополнения к элементам матрицы.

– матрица невырожденная.

Решим систему методом Крамера. Главный определитель системы:

. Разложим определитель по элементам первой строки, пользуясь формулой .

Запишем и вычислим вспомогательные определители

Тогда

Ответ:

Решим систему методом Гаусса, для этого составим расширенную матрицу системы и упростим ее приведением к треугольному виду.

  

Таким образом, система равносильна системе

Находим

Ответ: , ,

При решении всеми методами одной и той же системы, мы получим один ответ.

Задача 3. Выполнить действия:

Решение. Выполним решение по действиям.

=

.

.

Ответ: .

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Если , , то произведением матрицы называется матрица , такая, что , где .

Пример:

Произведение не определено, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2).

Произведение определено.

Контрольная работа №1.

Вариант 1

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 2

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 3

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 4

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 5

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 6

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 7

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 8

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 9

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 10

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 11

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 12

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 13

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 14

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 15

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 16

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 17

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 18

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 19

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 20

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 21

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 22

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 23

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 24

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 25

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 26

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 27

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 28

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 29

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера

Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 30

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера

Задача 3. Выполнить действия:

детерминантов – предметный тест GRE: математика

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

РЕШЕНИЕ: 7.01 Викторина по матрицам и детерминантам

Прочтите следующие инструкции, чтобы завершить это обсуждение, и просмотрите пример того, как выполнить математику, необходимую для этого задания: На страницах 345, 346 и 353 книги «Элементарная и промежуточная алгебра» есть много проблем с факторизацией.Вы найдете свое задание в следующей таблице. Если ваш присвоенный номер: Фактор, если это возможно. Если многочлен простой, скажите так. Разложите на множители полностью. Если многочлен простой, так и скажите. Разложите на множители с помощью метода AC. Если многочлен простой, скажем так. 1y2 + 6y + 5p. 345 # 822×2 + 11x + 52w2 + 6w + 8p. 345 # 842h3 + 7h + 33b2 + 7b + 12p. 345 # 863т2 + 8т + 54–9м + м2 + 14п. 346 # 883×2 – х – 25a2 + 5a – 6p. 346 # 9021×2 + 2x – 36×2 – x – 12p. 346 # 923a2 – 14a + 157a2 – 5a – 50p. 346 # 947y2 + 16y – 158×2 + 8x + 15p.346 # 964×2 + 17x – 159a2 + 6a – 40p. 346 # 988×2 – 10x – 310м2 – 17м + 16п. 346 # 1009т2 + 5т – 411м2 + 6м – 16п. 346 # 10215×2 – 7x – 212м2 – 10м + 25шт. 346 # 10410×2 + 17xy + 3y213x2 + 3x + 3p. 346 # 1063a2 + 2ab – 21b214y2 + 3y – 10p. 353 # 243м2 – 13мн + 12н215у2 – 6л – 8п. 353 # 267b2 + 8b + 116×2 – 25x + 150p. 353 # 2815y2 + 8y + 117w2 + 8w + 16p. 353 # 303y2 + 10y + 718m2 + 20 + 21mp. 353 # 326z2 + 13z + 519×2 – 5x – 3p. 353 # 7615х2 + 13х – 220х3 + 5х – 36п. 353 # 788×2 – 22x + 521м2 + 23м + 24п. 353 # 8015×2 + 31x + 222t2 – 10т – 24п.353 # 883×2 + 11x + 1023t2 – 12т – 28п. 353 # 903×2 – 17x + 1024200 + 30t + t2p. 353 # 928×2 – 2xy – y225b2 – 7b + 8p. 345 # 8210a2 – 27ab + 5b226z2 + 18z + 45p. 345 # 842×2 – x – 1527×2 – 2x – 15p. 345 # 864×2 – 19x – 528×2 – 14x + 45p. 346 # 884b2 – 16b + 1529b2 + 11b + 30p. 346 # 908y2 – 14y – 1530w2 – 2w – 24p. 346 # 926z2 – 13z – 531b2 – 9b – 22p. 346 # 9410b2 + 7ab + a232t2 + 14t + 24p. 346 # 96y2 + yt – 12t233y2 – 4y – 32p. 346 # 98×2 – 5xs – 24s234b2 – 10b + 21p. 346 # 1001 – ху – 20х2у235м2 – 7м – 7п.346 # 10212м2н2 – 8мн + 136м2 – 6м – 16п. 346 # 1048a2 + 10a – 337r2 – 7r – 60p. 346 # 1062×2 + 7x + 638×2 – 4x – 4p. 353 # 2415×2 + 17x + 439b2 – 15b + 26p. 353 # 263т2 + 16т – 1240б2 + 4п. 353 # 289×2 – 9x + 241– 2a + a2 – 35p. 353 # 302×2 + 5x – 342×2 + 13x + 40p. 353 # 326w2 – 5w – 643b2 – 8b + 15p. 353 # 763a2 + a – 244v2 – 22v – 75p. 353 # 789t2 – 5t – 445w2 + 30w + 81p. 353 # 802×2 + 5x – 3 Для первых двух задач разложите многочлены на множители, используя любую подходящую стратегию. Укажите, какие методы вы будете использовать, а затем продемонстрируйте методы решения ваших проблем, объясняя процесс по ходу дела.[Если у вас есть четырехчленный многочлен для разложения, вам нужно будет использовать разложение по группировке. Два примера этого процесса показаны на стр. 331 Элементарной и Промежуточной алгебры.] Для третьей задачи убедитесь, что вы используете «метод переменного тока» для разложения на множители. Вот видео, демонстрирующее этот процесс: https: //ashford.mediaspace.kaltura.com/media/MAT221+AC+Method/0_j143fdqs (Ссылки на внешний сайт.) Ссылки на внешний сайт .. Покажите шаги этого в своей работе, аналогично тому, как это показано в книге на примерах.Включите в обсуждение следующие пять слов из математического словаря. Используйте полужирный шрифт, чтобы выделить слова в вашем письме (не пишите определения для слов; используйте их соответствующим образом в предложениях, описывающих вашу математическую работу.): FactorGCF Prime факторыPerfect squareGrouping Ваш начальный пост должен быть длиной 150–250 слов. Ответьте хотя бы на два сообщения одноклассников до 7-го дня хотя бы в одном абзаце. Вы согласны с тем, как они использовали лексику? Имеют ли смысл их ответы?

Практический тест – Матрицы и детерминанты

Сообщение от Анджали Каур на 11 сен.2021

Практический тест – матрицы и детерминанты Но сначала присоединитесь к моему каналу на YouTube, группе Facebook для студентов прикладных математиков, подпишитесь на этот веб-сайт и получите ежемесячную сопроводительную рассылку.

Вы можете скачать PDF-файл с вопросом в конце. Используйте его для себя или для своих учеников.

Решение: (б) установка Maxtrix

Решение:

(d) Ничего из этого.

Решение:

(а) В

Решение: (a)

Как показано в предыдущем вопросе.

Решение: (c) A + B

Решение:

(a) AB неособое число

Решение: (c)

Решение: (a)

Решение: (c)

Решение: (c) 10

11.Множество решений уравнения | x + 1 | <3 ______________

Решение: -3

-4

= {x: x принадлежит Z и лежит между -4

= (-4, 2)

12.

Решение: x + 3 ≤ -10 или x + 3 ≥ 10

x ≤ -13 или x ≥ 7

x принадлежит (-∞, 13] U [7, ∞)

13. Решение линейного неравенства по переменной x представлено числовой прямой, как показано на рис.6.36. Решение также можно описать как

Решение. Как видно из числовой прямой, на 9/2 есть открытый интервал, продолженный до бесконечности. Итак, ответ – вариант (а) x принадлежит (9/2, бесконечность)

14. Заштрихованная часть числовой прямой на рис. 6.37 также может быть представлена ​​как

.

Решение: Вариант (d) x принадлежит (5, бесконечность)

15.

Решение: В этом случае существует открытый интервал на 1 и 2.Итак, правильный вариант, который имеет место, – это (а), потому что x может принадлежать -infinity, 1 или 2 и бесконечности.

Решение:

17.

Решение:

Вы можете проверить следующие посты по прикладной математике:

1. Логические рассуждения – основы
2. Что такое функции?
3. Что такое вероятность?
4. Взаимосвязи и функции
5. Наборы и диаграмма Венна
6. Какие бывают типы наборов?
7. Теория множеств

Удачного обучения!

Раскрытие информации: некоторые ссылки на веб-сайте являются рекламными, что означает, что без дополнительных затрат для вас я буду получать комиссию, если вы перейдете по ссылке или сделаете покупку.Пожалуйста, поддержите меня, чтобы я мог продолжать писать для вас отличный контент.

Фото Чарльза Делувио на Unsplash

Поделитесь этим постом с друзьями

Банк вопросов для основных и продвинутых детерминантов и матриц JEE – Матрицы

question_answer 1)

Пусть A и B – две матрицы \ [2 \ times 2 \]. {2}} \]

Тогда

A)

(i) и (ii) неверны, (iii) верно выполнено прозрачный

B)

(ii) и (iii) являются ложными, (i) верно выполнено прозрачный

C)

(i) неверно, (ii) и (iii) верны выполнено прозрачный

D)

(i) и (iii) неверны, (ii) верно выполнено прозрачный

Просмотреть решение play_arrow

question_answer 2)

Если A и B – две матрицы, такие что \ [AB = B \] и \ [BA = A, \], то

A)

\ [{{({{A} ^ {5}} – {{B} ^ {5}})} ^ {3}} = A-B \] готово прозрачный

B)

\ [{{({{A} ^ {5}} – {{B} ^ {5}})} ^ {3}} = {{A} ^ {3}} – {{ B} ^ {3}} \] выполнено прозрачный

C)

\ [A-B \] идемпотентно выполнено прозрачный

D)

\ [A-B \] является нильпотентным выполнено прозрачный

Просмотреть решение play_arrow

question_answer 3)

Если A – квадратная матрица такая, что \ [{{A} ^ {2}} = A \], то \ [{{(I + A)} ^ {3}} – 7A \] –

A)

3I сделано прозрачный

B)

0 выполнено прозрачный

C)

I готово прозрачный

D)

2I готово прозрачный

Просмотреть решение play_arrow

question_answer 4)

A – это непроизвольная матрица, заданная тогда, обратная A / 2 будет

A)

2A сделано прозрачный

B)

\ [\ frac {{{A} ^ {- 1}}} {2} \] выполнено прозрачный

C)

\ [\ frac {A} {2} \] выполнено прозрачный

D)

\ [{{A} ^ {2}} \] выполнено прозрачный

Просмотреть решение play_arrow

question_answer 5)

Если и \ [A- \ frac {1} {2} I \], и \ [A + \ frac {1} {2} I \] являются ортогональными матрицами, то

A)

A ортогонально сделано прозрачный

B)

A кососимметричный четного порядка выполнено прозрачный

C)

\ [{{A} ^ {2}} = \ frac {3} {4} I \] выполнено прозрачный

D)

ни один из этих не выполнено прозрачный

Просмотреть решение play_arrow

question_answer 6)

Если \ [A = \ left [\ begin {matrix} a & b \\ 0 & a \\ \ end {matrix} \ right] \] является корнем n-й степени из \ [{{I} _ {2}} \], затем выберите правильные утверждения:

(i) если n нечетное, \ [a = 1, \ text {} b = 0 \]

(ii) в n нечетно, \ [a = -1, \ text {} b = 0 \]

(iii) если n четное, \ [a = 1, \ text {} b = 0 \]

(iv) если n четное, \ [a = -1, \ text {} b = 0 \]

A)

i, ii, iii выполнено прозрачный

B)

ii, iii, iv выполнено прозрачный

C)

i, ii, iii, iv выполнено прозрачный

D)

i, iii, iv выполнено прозрачный

Просмотреть решение play_arrow

question_answer 7)

Пусть A – квадратная матрица n-го порядка, а B – ее сопряженная, тогда \ [\ left | AB + K {{I} _ {n}} \ right | \] равно (где K – скалярная величина)

A)

\ [{{(\ left | A \ right | + K)} ^ {n-2}} \] выполнено прозрачный

B)

\ [{{(\ left | A \ right | + K)} ^ {n}} \] выполнено прозрачный

C)

\ [{{(\ left | A \ right | + K)} ^ {n-1}} \] выполнено прозрачный

D)

ни один из этих не выполнено прозрачный

Просмотреть решение play_arrow

question_answer 8)

Если и если A обратимая, то что из следующего неверно?

A)

\ [\ left | A \ right | = \ left | B \ right | \] выполнено прозрачный

B)

\ [\ left | A \ right | = – \ left | B \ right | \] выполнено прозрачный

C)

\ [\ left | adj \, A \ right | = \ left | adj \, B \ right | \] готово прозрачный

D)

A обратимо тогда и только тогда, когда B обратимо выполнено прозрачный

Просмотреть решение play_arrow

question_answer 9)

Если A и B – две невырожденные матрицы одного порядка, такие что B? = I, для некоторого положительного целого числа r> 1, то \ [{{A} ^ {- 1}} { {B} ^ {\, r-1}} A – {{A} ^ {- 1}} {{B} ^ {- 1}} A \] =

A)

I готово прозрачный

B)

2I выполнено прозрачный

C)

O готово прозрачный

D)

-I выполнено прозрачный

Просмотреть решение play_arrow

question_answer 10)

Если \ [A = \ left [\ begin {matrix} 1 & \ tan x \\ – \ tan x & 1 \\ \ end {matrix} \ right] \], то \ [{{A} ^ {T}} {{A} ^ {- 1}} \] –

A)

\ [\ left [\ begin {matrix} – \ cos 2x & \ sin 2x \\ – \ sin 2x & \ cos 2x \\ \ end {matrix} \ right] \] выполнено прозрачный

B)

\ [\ left [\ begin {matrix} \ cos 2x & – \ sin 2x \\ \ sin 2x & \ cos 2x \\ \ end {matrix} \ right] \] выполнено прозрачный

C)

\ [\ left [\ begin {matrix} \ cos 2x & \ cos 2x \\ \ sin 2x & \ sin 2x \\ \ end {matrix} \ right] \] выполнено прозрачный

D)

ни один из этих не выполнено прозрачный

Просмотреть решение play_arrow

question_answer 11)

Если тогда \ [A {{(\ alpha, \ beta)} ^ {- 1}} \] равно

A)

\ [A (- \ alpha, – \ beta) \] выполнено прозрачный

B)

\ [A (- \ alpha, \ beta) \] выполнено прозрачный

C)

\ [A (\ alpha, – \ beta) \] выполнено прозрачный

D)

\ [A (\ alpha, \ beta) \] выполнено прозрачный

Просмотреть решение play_arrow

question_answer 12)

Если \ [{{A} ^ {3}} = 0 \], то I = A + \ [{{A} ^ {2}} \] равно

A)

\ [I-A \] готово прозрачный

B)

\ [{{(I + {{A} ^ {1}})} ^ {- 1}} \] выполнено прозрачный

C)

\ [{{(I-A)} ^ {- 1}} \] готово прозрачный

D)

ни один из этих не выполнено прозрачный

Просмотреть решение play_arrow

question_answer 13)

Если A и B квадратные матрицы одного порядка и A невырожденна, то для положительного целого числа n \ [{({{A} ^ {- 1}} BA)} ^ {n}} \] равно

A)

\ [{{A} ^ {- n}} {{B} ^ {n}} {{A} ^ {n}} \] выполнено прозрачный

B)

\ [{{A} ^ {n}} {{B} ^ {n}} {{A} ^ {- n}} \] выполнено прозрачный

C)

\ [{{A} ^ {- 1}} {{B} ^ {n}} A \] выполнено прозрачный

D)

\ [n ({{A} ^ {- 1}} BA) \] выполнено прозрачный

Просмотреть решение play_arrow

question_answer 14)

\ [{{(- A)} ^ {- 1}} \] всегда равно (где A – квадратная матрица n-го порядка)

A)

\ [{{(- 1)} ^ {n}} {{A} ^ {- 1}} \] выполнено прозрачный

B)

\ [- {{A} ^ {- 1}} \] выполнено прозрачный

C)

\ [{{(- 1)} ^ {n-1}} {{A} ^ {- 1}} \] выполнено прозрачный

D)

ни один из этих не выполнено прозрачный

Просмотреть решение play_arrow

question_answer 15)

Если \ [\ left [\ begin {matrix} 2 & 1 \\ 3 & 2 \\ \ end {matrix} \ right] A \ left [\ begin {matrix} -3 & 2 \\ 5 & -3 \\ \ end {matrix} \ right] = \ left [\ begin {matrix} 1 & 0 \\ 0 & 1 \\ \ end {matrix} \ right] \], тогда A =

A)

\ [\ left [\ begin {matrix} 1 & 1 \\ 1 & 0 \\ \ end {matrix} \ right] \] выполнено прозрачный

B)

\ [\ left [\ begin {matrix} 1 & 1 \\ 0 & 1 \\ \ end {matrix} \ right] \] выполнено прозрачный

C)

\ [\ left [\ begin {matrix} 1 & 0 \\ 1 & 1 \\ \ end {matrix} \ right] \] выполнено прозрачный

D)

\ [- \ left [\ begin {matrix} 1 & 1 \\ 1 & 0 \\ \ end {matrix} \ right] \] выполнено прозрачный

Просмотреть решение play_arrow

question_answer 16)

Если A является симметричной, а также кососимметричной матрицей, то A равно

A)

диагональ матрицы сделано прозрачный

B)

нулевая матрица выполнено прозрачный

C)

треугольная матрица готовая прозрачный

D)

ни один из этих не выполнено прозрачный

Просмотреть решение play_arrow

question_answer 17)

Количество решений матричного уравнения \ [{{X} ^ {2}} = \ left [\ begin {matrix} 1 & 1 \\ 2 & 3 \\ \ end { матрица} \ right] \] равно

A)

более 2 выполнено прозрачный

B)

2 выполнено прозрачный

C)

0 выполнено прозрачный

D)

1 выполнено прозрачный

Просмотреть решение play_arrow

question_answer 18)

Учитывая эту матрицу. {50}} – 50A = \ left [\ begin {matrix} a & b \\ c & d \\ \ end {matrix} \ right] \].{2004}} \] _______.

Просмотреть решение play_arrow

question_answer 23)

Если \ [A = {{[{{a} _ {i \, j}}]} _ {4 \, \ times \, 4}}, \] такое, что \ [ {{a} _ {ij}} = \ left \ {\ begin {matrix} 2, \, \, когда \, \, \, i = j \\ 0, \, \, когда \, \, \, i \ ne j \\ \ end {matrix} \ right. \], то \ [\ left \ {\ frac {\ det (adj (adj \, A))} {7} \ right \} \] равно (где {.{-1}} \] равно KI. Тогда значение k равно _______.

Просмотреть решение play_arrow

question_answer 25)

Пусть и. Если B является обратным к A, то \ [\ alpha \] равно _____.

Просмотреть решение play_arrow

Матрицы и детерминанты для JEE Main – Горячие подсказки

Матрицы и детерминанты: Когда дело доходит до экзаменов JEE, глава «Матрицы и детерминанты» является очень важной темой в математике.Хотя многие темы в Maths for JEE включают решение уравнений, эта глава знакомит студентов с инструментом, известным как Матрица или Матрицы, который помогает решать несколько уравнений одновременно. Кроме того, глава «Детерминанты» знакомит студентов с тем, как детерминанты используются для представления функций, связанных с матрицами. Поскольку главы «Матрицы» и «Детерминанты» (главы 3 и 4 в Учебнике для класса 12) очень взаимосвязаны, их часто вместе называют «матрицами» и «детерминантами».

Каждый год из этой главы на основных экзаменах JEE каждый год появляется как минимум несколько вопросов. В этой статье студенты смогут понять, почему эта глава важна, узнать важные подтемы для изучения, изучить несколько основных свойств матриц и детерминант, лучшие книги для изучения тем, а также ссылки на практические занятия для главы. онлайн. Прочтите статью, чтобы узнать больше:

Основная математика JEE – матрицы и детерминанты: определения

Прежде чем углубляться во все подробности и ресурсы о Матрицах и Детерминантах, давайте вкратце разберемся, что они собой представляют:

Что такое матрицы?

Набор чисел, объектов или символов, представленный в виде прямоугольного массива, называется матрицей.Порядок матрицы определяется количеством строк и количеством столбцов, присутствующих в прямоугольном массиве представления. Как показано на следующем изображении, существуют две разные матрицы с одинаковыми номерами, но с другой структурой.

Что такое детерминанты матриц?

Каждой квадратной матрице A = [aij] порядка n мы можем связать число (действительное или комплексное), называемое определителем квадратной матрицы A, где aij = (i, j) -й элемент A. Крайне важно понимать Матрицы, чтобы понять детерминанты и то, как они используются для выполнения вычислений с матрицами.Кроме того, знание определителей очень полезно почти для всех тем математики, особенно в векторах, координатной геометрии и исчислении.

Важные темы в матрицах и детерминантах

Поскольку концепции матриц и определителей полезны в последующих главах, связанных с алгеброй, важно полностью охватить эту главу для всех студентов. Однако есть некоторые подтемы, которые вы определенно не должны пропускать при изучении главы.Вот некоторые из важных тем в Матрицах и детерминантах:

1. Матрица и работа с матрицами
2. Типы матриц
3. Транспонирование матрицы, симметричной и кососимметричной матрицы
4. Сопряжение матрицы, эрмитовой и косоэрмитовой матрицы
5. Определитель матрицы
6. Минор и кофактор элемента матрицы / определителя
7. Сопряжение и обратная матрица
8. Элементарные операции со строками и их использование при нахождении обратной матрицы
9. Система линейных уравнений и правило Крамера
10. Система однородных линейных уравнений

Лучшие книги для изучения Матрицы и детерминанты

Изучив основы матриц и детерминантов, вы можете сослаться на несколько книг, которые предлагают вам расширенные знания по теме и помогут вам овладеть ими.Вот одни из лучших книг для изучения матриц и детерминантов:

Алгебра С.К. Гойал [Арихант]

Комплексная математика TMH для JEE Advanced

Высшая алгебра Холла и Найта [Арихант]

Важные формулы в матрицах и детерминантах 910 для JEE

• Любая матрица A и ее транспонированная матрица имеют одинаковые собственные значения.
• След матрицы равен сумме собственных значений матрицы.
• Определитель матрицы A равен произведению собственных значений A.
• Если λ ₁ , λ ₂ ,… .., λ _n являются n-собственными значениями матрицы A, то

• Пусть A будет матрицей n x n и пусть

• Матрица экспонента для квадратной матрицы A,

Практические вопросы по матрицам и определителям

Чтобы получить хорошие отметки по математике JEE, учащимся важно изучить эту главу во время подготовки к IIT JEE.Соответственно, учащимся необходимо постоянно практиковаться, чтобы они могли решать всевозможные проблемы и вопросы, связанные с матрицами и детерминантами. Система Embibe с искусственным интеллектом содержит множество вопросов по всем темам для экзамена JEE. Соответственно, учащиеся могут попробовать различные тесты по главам для матриц и детерминант, а также могут пройти полные пробные тесты JEE, когда учащиеся пройдут полную программу.

Понятия, относящиеся к матрицам и детерминантам

Часто задаваемые вопросы о матрицах и детерминантах

Вопрос: Что подразумевается под определителем? Ответ: Определитель определяется как скалярное значение, которое связано с квадратной матрицей.Если X – матрица, то определитель матрицы представлен как | X | или det (X).

Вопрос: Почему мы используем детерминанты? Ответ: Определители используются для решения системы линейных уравнений, а также для нахождения обратной матрицы.

Вопрос: Что такое матрица? Ответ: Матрица определяется как прямоугольный массив чисел. Набор чисел организован в ряды и столбцы.

Вопрос: Важны ли матрицы для JEE? Ответ: Матрицы и детерминанты – самая легкая часть вступительных экзаменов, но в то же время они играют важную роль в JEE Main и JEE Advanced.

Мы надеемся, что эта подробная статья о детерминантах и ​​матрицах окажется полезной. Если у вас есть какие-либо вопросы относительно этой статьи, напишите нам через поле для комментариев ниже, и мы свяжемся с вами как можно скорее.

849 Просмотры

Матрицы и детерминанты – Вопросы и ответы Aptitude

Матрицы и детерминанты – Вопросы и ответы о Aptitude

Почему матрицы и детерминанты – Вопросы и ответы о Aptitude Основные матрицы и детерминанты – Вопросы и ответы о Aptitude?

В этом разделе вы можете изучить и практиковать основные матрицы и детерминанты – вопросы и ответы о способностях с ответами, чтобы улучшить свои навыки для прохождения собеседования, конкурсных экзаменов и различных вступительных испытаний (NET SET, CAT, GATE, GRE, MAT, Bank Exam , Тест на право учителя, железнодорожный экзамен и т. Д.) с полной уверенностью.

Где я могу получить матрицы и детерминанты – Вопросы и ответы о Aptitude Основные матрицы и детерминанты – Вопросы и ответы о Aptitude, вопросы и ответы с пояснениями?

Gkindiaonline предоставляет вам множество полностью решенных Матриц и определителей – Вопросы и ответы о способностях (Основные матрицы и определяющие факторы – Вопросы и ответы о способностях), вопросы и ответы с пояснениями. Решенные примеры с подробным описанием ответов, даны пояснения, которые легко понять.Все студенты и первокурсники могут загрузить основные матрицы и детерминанты «Общие знания» – вопросы викторины «Вопросы и ответы о способностях» с ответами в виде файлов PDF и электронных книг.

Где я могу получить матрицы и детерминанты – вопросы и ответы о способностях Основные матрицы и детерминанты – вопросы и ответы о способностях Вопросы и ответы на собеседовании (тип цели, множественный выбор)?

Здесь вы можете найти матрицы и детерминанты объективного типа – Вопросы и ответы о способностях Базовые матрицы и детерминанты – Вопросы и ответы о способностях, вопросы и ответы для собеседований и вступительных экзаменов.Также предусмотрены вопросы с множественным выбором и вопросы истинного или ложного типа.

Как решать матрицы и детерминанты – вопросы и ответы о Aptitude Основные матрицы и детерминанты – проблемы с вопросами и ответами о Aptitude?

Вы можете легко решать все виды матриц и детерминант – вопросы о способностях и ответы на них, основанные на базовых матрицах и детерминантах – вопросы и ответы о способностях, выполняя упражнения типа цели, приведенные ниже, а также получите быстрые методы для решения матриц и детерминант – вопросы о способностях и Ответы на основные матрицы и детерминанты – вопросы о способностях и ответы на них.

Онлайн-тест для глав 7-Матрицы и детерминанты класса 12 по математике

Онлайн-тест для главы 7-Матрицы и определители класса 12 по математике

Найдите онлайн-тест на главу 7-Матрицы и детерминанты класса 12 по математике, подготовленный специалистами Entrancei. Все вопросы в онлайн-тесте главы 7-Матрицы и детерминанты основаны на MCQ с одним правильным выбором.Эти тесты для главы 7 «Матрицы и детерминанты» подготовлены к экзаменам JEE, NEET и Board. Задаваемые вопросы образуют целую главу «7-матриц и детерминантов», охватывающую числовые, теоретические и концептуальные основы для проверки знаний соискателя. Ознакомьтесь с решениями NCERT для класса 12 по математике, подготовленными Entrancei.

Входной онлайн-тест для главы 7-Матрицы и детерминанты 12-го класса по математике

Количество онлайн-тестов по главе 7-Матрицы и определители математики 12-го класса = 08

Количество вопросов MCQ для главы 7-Матрицы и детерминанты математики 12-го класса = 160

Инструкция по онлайн-тестированию главы 7-Матрицы и определители класс 12 по математике

1.Если вы являетесь зарегистрированным студентом Entrancei, просто войдите в свою учетную запись и начните онлайн-тест на предмет

главы 7-Матрицы и детерминанты 12-го класса.

2. Если вы не зарегистрированы, то создайте свой профиль на вкладке «Зарегистрироваться сейчас» в строке меню. Это бесплатно.

3. Все онлайн-тесты по главе 7 «Матрицы и детерминанты математики 12 класса» бесплатны для всех соискателей.

4. Каждый онлайн-тест по главе 7-Матрицы и детерминанты математики 12-го класса состоит из минимум 10 вопросов MCQ, за каждый правильный ответ вы получите +4 балла за каждый неправильный ответ, вы получите -1 балл.

5. Вы можете пропустить вопросы из 7-матриц и детерминантов, которых вы не знаете, и перейти к следующему вопросу.

6. После того, как вы завершите онлайн-тест по 7-матрицам и детерминантам 12-го класса, проведите онлайн-тест, и ваш результат будет показан после этого вместе с вашим рангом.

.