Контрольная работа по алгебре 7 класс мерзляк номер 1 2 3 4 5 6 7 с ответами
Скачиваем контрольные работы по алгебре в седьмом классе по стандарту ФГОС
2019 – 2020 год + ОТВЕТЫ
7 контрольных (проверочных ) работ по предмету АЛГЕБРА в 7 классе по темам включая ответы
- Контрольная № 1 по теме – Линейное уравнение с одной переменной
- Контрольная № 2 по теме – Степень с натуральным показателем. Одночлены. Многочлены
- Контрольная № 3 по теме – Умножение одночлена на многочлен. Умножение многочлена на одночлен. Разложение многочленов на множители
- Контрольная № 4 по теме – Формулы сокращенного умножения
- Контрольная № 5 по теме – Сумма и разность кубов двух выражений. Применение способов разложения многочленов на множите
- Контрольная № 6 – Функции
- Контрольная № 7 по теме – Системы линейных уравнений с двумя переменными
Все контрольные по алгебре 7 класс под авторством Мерзляка Полонского и Якира представленны на данной страгице исключитнльно в ознакомительных целях для постоянного пользования даннвми работами их необходимо купить
Бильбао – самый большой город Страны Басков на севере Испании, на Бискайском заливе. Населен более 350 000 жителей. Город развивается очень динамично во всех отношениях. Это важный культурный, но также промышленный и экономический центр.
Населен более 350 000 жителей. Город развивается очень динамично во всех отношениях. Это важный культурный, но также промышленный и экономический центр.
История
Бильбао был основан в 1300 году магнатом Диего Лопес де Аро, на другой стороне реки напротив рыбацкой деревни. Первоначально он состоял из трех улиц: Somera, Artekale и Tendera, но постепенно развивался. Начало было трудным. Три наводнения и сильный пожар уничтожили город. Несмотря на это, Бильбао был очень важным портовым центром Испании, особенно во времена империи. В 1602 году он стал столицей региона Бискайя. Обмен товарами с другими портами стал чрезвычайно важным. Город рос в силе и богатстве. К сожалению, в конце XVI века его развитие несколько замедлилось. Девятнадцатый век оказался новаторским для Бильбао. С началом промышленной революции город возродился. Судостроение, металлургия и горное дело стали новым источником дохода. С приходом начала 20-го века Бильбао стал самым богатым городом Испании.
Достопримечательности
Самые старые здания в Бильбао включают Базилику де Бегона. Ее строительство началось в 15 веке и не было завершено до 1620 года. Во время вооруженных конфликтов она сильно пострадал и была восстановлена в девятнадцатом веке. Две другие церкви – церковь св. Николаса, жемчужина архитектуры барокко Испании и Катедраль-де-Сантьяго, построенная в начале четырнадцатого века, представляет собой своеобразную смесь архитектурных стилей с преобладанием готики. Помимо церквей заслуживает внимания крепость Кастильо-де-Бутрон, расположенная в 20 километрах от центра города, в окружении зеленых зон, с мощными оборонительными башнями и Кастильо-де-Мунатонес, чуть более поврежденным средневековым зданием. Также заслуживает внимания Киоско де Ареналь – это своеобразный концертный зал под открытым небом, а также Бискайский мост, внесенный в список памятников ЮНЕСКО.
Ее строительство началось в 15 веке и не было завершено до 1620 года. Во время вооруженных конфликтов она сильно пострадал и была восстановлена в девятнадцатом веке. Две другие церкви – церковь св. Николаса, жемчужина архитектуры барокко Испании и Катедраль-де-Сантьяго, построенная в начале четырнадцатого века, представляет собой своеобразную смесь архитектурных стилей с преобладанием готики. Помимо церквей заслуживает внимания крепость Кастильо-де-Бутрон, расположенная в 20 километрах от центра города, в окружении зеленых зон, с мощными оборонительными башнями и Кастильо-де-Мунатонес, чуть более поврежденным средневековым зданием. Также заслуживает внимания Киоско де Ареналь – это своеобразный концертный зал под открытым небом, а также Бискайский мост, внесенный в список памятников ЮНЕСКО.
Современная архитектура
Наиболее интересным и, вероятно, наиболее характерным для Бильбао является знаменитый музей Гуггенхайма. Привлекателен он, однако, не из-за экспонатов, собранных там, но из-за самого здания, которое считается самым красивым в мире. Конечно, красота – вещь относительная, но факт остается фактом: здание, спроектированное всемирно известным архитектором Фрэнком Гери, является единственным в своем роде.
Конечно, красота – вещь относительная, но факт остается фактом: здание, спроектированное всемирно известным архитектором Фрэнком Гери, является единственным в своем роде.
Контрольные работы по алгебре 7 класс по учебнику авторов: Ю.Н. Макарычев, Н. Г. Миндюк. – Оценка знаний учащихся – Математика, алгебра, геометрия
Автор: Ткачева Ирина Алексеевна,
учитель математики
МОУ «Алексеевская СОШ»
Любинского района
Омской области
Контрольные работы по алгебре 7 класс по учебнику Ю.Н. Макарычев, Н. Г. Миндюк
За основу взяты контрольные работы под редакцией В.И. Жохова.
Контрольные работы в двух вариантах, содержат 5 заданий, выделены задания на выполнение обязательного стандарта математического образования, одно из заданий контрольных работ представлено в виде теста.
КОНТРОЛЬНАЯ РАБОТА №1
ВАРИАНТ 1
1. Найдите значение числового выражения:
(2/7 + 3/14)(7,5 – 13,5)
1) -4 2) -3 3) 4 4) 3
2. Упростите выражение:
Упростите выражение:
а) 5а – 3b – 8а + 12 b
б) 16с + (3с – 2) – (5с + 7)
3. Сравните значения выражений 0,5х – 4 и 0,6х – 3 при х = 5
4. Упростите выражение 6,3х – 4 – 3(7,2х + 0,3) и найдите его значение при х = ⅔
5. В прямоугольном листе жести со сторонами х см и y см вырезали квадратное отверстие со стороной 5 см. Найдите площадь оставшейся части. Решите задачу при х = 13, y = 22.
КОНТРОЛЬНАЯ РАБОТА №1
ВАРИАНТ 2
2. Найдите значение числового выражения:
(2/7 + 3/14)( – 7,5 + 13,5)
1) -4 2) -3 3) 4 4) 3
2. Упростите выражение:
а) 3а + 7b – 6а – 4 b
б) 8с + (5 – с) – (7 + 11с)
в) 4 – 5(3y + 8)
3. Сравните значения выражений 3 – 0,2а и 5 – 0,3а при а = 16
4. Упростите выражение 3,2 а – 7 – 7(2,1а – 0,3) и найдите его значение при а = 3/5

КОНТРОЛЬНАЯ РАБОТА №2
ВАРИАНТ 1
1. Решите уравнение:
2х + 1 = 3х – 4
1) -5 2) 1 3) 5 4) свой ответ
2. Решите уравнение:
а) ⅔ х = -6 б) 1,6(5х – 1) = 1,8х – 4,7
3. Турист проехал в 7 раз большее расстояние, чем прошел пешком. Весь путь туриста составил 24 км. Какое расстояние турист проехал?
4. При каком значении переменной значение выражения 3 – 2с на 4 меньше значения выражения 5с + 1 ?
КОНТРОЛЬНАЯ РАБОТА №2
ВАРИАНТ 2
1. Решите уравнение:
– 2х + 1 = – х – 6
1) – 7 2) 5 3) 7 4) свой ответ
2. Решите уравнение:
а) – ⅜ х = 24 б) 2(0,6х + 1,85) = 1,3х + 0,7
3. На одной полке на 15 книг большее, чем другой. Всего на двух полках 53 книги. Сколько книг на каждой полке?
4. При каком значении переменной значение выражения 4а + 8 на 3 больше значения выражения 3 – 2а ?
5. Ширина прямоугольника в 2 раза меньше длины.
КОНТРОЛЬНАЯ РАБОТА №3
ВАРИАНТ 1
1. Функция задана формулой у = ½х – 7. Найдите:
а) значение функции, соответствующее значению аргумента, равному 4;
б) значение аргумента, при котором значение функции равно -8.
2. а) Постройте график функции у= 3х – 4.
б) С помощью графика функции найдите значение функции, соответствующее значению аргумента 2,5.
3. В одной системе координат постройте графики функций у = – 0,5х и у = 2.
4. Проходит ли график функции у = – 5х + 11 через точку М(6; -41)?
5. Каково взаимное расположение графиков функции у = 15х – 51 и у = – 15х + 39 ?
КОНТРОЛЬНАЯ РАБОТА №3
ВАРИАНТ 2
1. Функция задана формулой у = 5 – ⅓х. Найдите:
а) значение функции, соответствующее значению аргумента, равному -6;
б) значение аргумента, при котором значение функции равно -1.
2. а) Постройте график функции у= -2х + 5.
б) С помощью графика функции найдите значение функции, соответствующее значению аргумента -0,5.
3. В одной системе координат постройте графики функций у = 0,5х и у = -5.
4. Проходит ли график функции у = – 7х – 3 через точку М(4; -25)?
5. Каково взаимное расположение графиков функции у = -21х – 15 и у = 21х + 69 ?
КОНТРОЛЬНАЯ РАБОТА №4
ВАРИАНТ 1
1. Выполните действия:
а) х5 х11 б) х15: х3
1) х-6 2) х16 3) х55 1) х18 2) х5 3) х12
2. Выполните действия:
а) (х4)7 б) (3х6)3
3. Упростите выражение:
а) 4а2с (- 2,5ас4) б) ( -2 х10 у6)4
4. Постройте график функции у = х2
С помощью графика определите:
а) значение функции при х = -1,5;
б) значение переменной х при у(х) = 3.
5. Найдите значение выражения:
а) 311 93 б) 3х3 – 1 при х = -⅓
275
6. Упростите выражение (- 1 ½ х5у13)3 0,08 х7у
КОНТРОЛЬНАЯ РАБОТА №4
ВАРИАНТ 2
1. Выполните действия:
а) х9 х13 б) х18: х6
2.
 Выполните действия:
Выполните действия:а) (х7)4 б) (2х3)5
3. Упростите выражение:
а) -7а5с3 1,5ас б) ( -3 х4 у13)3
4. Постройте график функции у = х2
С помощью графика определите:
а) значение функции при х = 2,5;
б) значение переменной х при у(х) = 5.
5. Найдите значение выражения:
а) 83 24 б) 2 – 7х2 при х = -½
45
6. Упростите выражение (- 2½ х15у4)2 0,04 ху7
КОНТРОЛЬНАЯ РАБОТА №5
ВАРИАНТ 1
1. Упростите выражение -12х + 3ху – 2( х +3ху)
а) 10х – 3ху б) -14х + 9ху в) -10х + 9ху г) -14х – 3ху
2. Решите уравнение:
3. Вынесите общий множитель за скобки:
а) 7ха – 7хb б) 16ху2 + 12х2у
4. По плану тракторная бригада должна была вспахать поле за 14 дней. Бригада вспахивала ежедневно на 5 га больше, чем намечалось по плану. И потому закончила пахоту за 12 дней. Сколько гектаров было вспахано?
5. Решите уравнение:
а) 4х + 5 3х – 2 2х – 5
6 4 3
б) х2 + ⅛ х = 0
КОНТРОЛЬНАЯ РАБОТА №5
ВАРИАНТ 2
1. Упростите выражение -12х + 3ху – 2( х +3ху)
Упростите выражение -12х + 3ху – 2( х +3ху)
а) 10х – 3ху б) -14х + 9ху в) -10х + 9ху г) -14х – 3ху
2. Решите уравнение:
10х – 5 = 6(8х + 3) – 5х
3. Вынесите общий множитель за скобки:
а) 8ха + 4хb б) 18ху3 + 12х2у
4. Заказ по выпуску машин должен быть выполнен по плану за 20 дней. Но завод выпускал ежедневно по 2 машины сверх плана и поэтому выполнил заказ за 18 дней. Сколько машин должен был выпускать завод ежедневно по плану ?
5. Решите уравнение:
а) 7х – 4 8 – 2х 3х + 3
9 6 4
б) 2х2 – х = 0
КОНТРОЛЬНАЯ РАБОТА №6
ВАРИАНТ 1
1. Представьте в виде многочлена:
а) ( у – 4)(у – 5) б) (х – 3)(х2 + 2х – 6)
в) (3а + 2b)(5а – b)
2. Разложите на множители:
а) b(b + 1) – 3(b + 1) б) са – сb + 2а – 2b
3. Упростите выражение:
(а2 – b2)(2а + b) – аb( а + b)
а ) 2а3 +в3 – 3ав2 б) 2а3 – в3 – 3ав2 в) 2а3 – в3 + 3ав2
4. Докажите тождество: ( х – 3)( х + 4) = х( х + 1) – 12.
5. Ширина прямоугольника вдвое меньше его длины. Если ширину увеличить на 3 см, а длину – на 2 см, то площадь прямоугольника увеличится на 78 см2. Найдите длину и ширину прямоугольника.
Ширина прямоугольника вдвое меньше его длины. Если ширину увеличить на 3 см, а длину – на 2 см, то площадь прямоугольника увеличится на 78 см2. Найдите длину и ширину прямоугольника.
КОНТРОЛЬНАЯ РАБОТА №6
ВАРИАНТ 2
1. Представьте в виде многочлена:
а) ( у + 7)(у – 2) б) (х + 5)(х2 – 3х + 8)
в) (4а – b)(6а + 3b)
2. Разложите на множители:
а) у(а – b) – 2(b + а) б) 3х – 3у + ах – ау
3. Упростите выражение:
(а2 – b2)(2а + b) – аb( а + b)
а ) 2а3 +в3 – 3ав2 б) 2а3 – в3 – 3ав2 в) 2а3 – в3 + 3ав2
4. Докажите тождество: а( а – 2) – 8 = ( а + 2)(а – 4).
5. Длина прямоугольника на 12 см больше его ширины. Если длину увеличить на 3 см, а ширину – на 2 см, то площадь прямоугольника увеличится на 80 см2. Найдите длину и ширину прямоугольника.
КОНТРОЛЬНАЯ РАБОТА №7
ВАРИАНТ 1
1. Преобразуйте в многочлен:
1) (а – 3)2 2) (2у + 5)2
3) (4а – b)( 4а + b) 4) (х2 + 1)( х2 – 1)
2. Разложите на множители:
1) с2 – 0,25 2) х2 – 8х + 16
3. Найдите значение выражения: (х + 4)2 – (х – 2)(х + 2) при х = 0,125
Найдите значение выражения: (х + 4)2 – (х – 2)(х + 2) при х = 0,125
а) – 21 б) 12 с) 21 д) – 12
4. Выполните действия:
а) 2(3х – 2у)(3х + 2у) б) (а – 5)2 – (а + 5)2
в) ( а3 + b2)2
5. Решите уравнение:
9у2 – 25 = 0
КОНТРОЛЬНАЯ РАБОТА №7
ВАРИАНТ 2
1. Преобразуйте в многочлен:
1) (а + 4)2 2) (3у – с)2
3) (2а – 5)( 2а + 5) 4) (х2 + у)( х2 – у)
2. Разложите на множители:
1) 0,36 – с2 2) а2 + 10а + 25
3. Найдите значение выражения: (а – 2 b)2 + 4 b( а – b) при х = 0,12
а) 144 б) – 0,144 с) 0,0144 д) 0,24
4. Выполните действия:
а) 3(1 + 2ху)( 1 – 2ху) б) (а + b)2 – (а – b)2
в) ( х2 – у3)2
5. Решите уравнение:
16у2 – 49 = 0
КОНТРОЛЬНАЯ РАБОТА №8
ВАРИАНТ 1
1. Преобразуйте в многочлен:
а) (а – 2)( а + 2) – 2а(5 – а)
б) (у – 9)2 – 3у(у + 1)
в) 3(х – 4) 2 – 3х2
2. Разложите на множители:
а) 25х – х3 б) 2х2 – 20х + 50
3. Найдите значение выражения а2 – 4bс, если а = 6, b = -11, с = -10
а) 452 б) -202 в) -404 г) 476
4. Упростите выражение:
Упростите выражение:
(с2 – b)2 – (с2 – 1)(с2 + 1) + 2bс2
5. Докажите тождество:
(а + b)2 – (а – b)2 = 4аb
КОНТРОЛЬНАЯ РАБОТА №8
ВАРИАНТ 2
1. Преобразуйте в многочлен:
а) 4х(2х – 1) – (х – 3)(х + 3)
б) (х + 3)(х – 11) + (х + 6)2
в) 7(а + b) 2 – 14аb
2. Разложите на множители:
а) у3 – 49у б) -3а2 – 6аb – 3b2
3. Найдите значение выражения а2 – 4bс, если а = 6, b = -11, с = -10
а) 452 б) -202 в) -404 г) 476
4. Упростите выражение:
(а – 1)2 (а + 1) + (а + 1)( а – 1)
5. Докажите тождество:
(х – у)2 + (х + у)2 = 2(х2 + у2)
КОНТРОЛЬНАЯ РАБОТА ЗА КУРС 7 КЛАССА
ВАРИАНТ 1
1. Найдите значение выражения:
¼ х3 + 3у2 при х = -2 и у = -1
1) 5 2) -1 3) 1 4) -5
2. Решите систему уравнений:
х + 2у = 11,
5х – 3у = 3
1) (4 ; 3) 2) (3 ; 4) 3) (- 4 ; 3) 4) (-4 ; -3)
3. Решите уравнение:
-0,4(1,5х – 2) = 1 – 0,5(2х + 1)
1) – ¾ 2) ¾ 3) 1⅓ 4) – 1⅓
4. Пешеход рассчитал, что, двигаясь с определенной скоростью, намеченный путь он пройдет за 2,5 часа. Но он шел со скоростью, превышающей намеченную на 1 км/ч, поэтому прошел путь за 2 часа. Найдите длину пути.
Пешеход рассчитал, что, двигаясь с определенной скоростью, намеченный путь он пройдет за 2,5 часа. Но он шел со скоростью, превышающей намеченную на 1 км/ч, поэтому прошел путь за 2 часа. Найдите длину пути.
5. а) Постройте график функции у = 3 – 2х
б) Принадлежит ли графику функции точка М (8; -19)?
КОНТРОЛЬНАЯ РАБОТА ЗА КУРС 7 КЛАССА
ВАРИАНТ 2
1. Найдите значение выражения:
¼ х3 + 3у2 при х = -2 и у = -1
1) 5 2) -1 3) 1 4) -5
2. Решите систему уравнений:
х + 2у = 11,
5х – 3у = 3
1) (4 ; 3) 2) (3 ; 4) 3) (- 4 ; 3) 4) (-4 ; -3)
3. Решите уравнение:
-0,4(1,5х – 2) = 1 – 0,5(2х + 1)
1) – ¾ 2) ¾ 3) 1⅓ 4) – 1⅓
4. Велосипедист должен был проехать весь путь с определенной скоростью за 2 часа. Но он ехал со скоростью, превышающей намеченную на 3 км/ч, поэтому на весь путь затратил 1⅔ часа. Найдите длину пути.
5. а) Постройте график функции у = 2 – 3х
б) Принадлежит ли графику функции точка М (9; -25)?
Всего приводится девять вариантов контрольных работ к учебнику Макарычева за 7 класс.
Полный текст материала Контрольные работы по алгебре 7 класс по учебнику авторов: Ю.Н. Макарычев, Н. Г. Миндюк. смотрите в скачиваемом файле.
На странице приведен фрагмент.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Есть мнение?
Оставьте комментарий
ГДЗ контрольные работы по алгебре 7 класс Дудницын, Тульчинская
Ответы на задания по алгебре за седьмой класс к рабочей тетради Дудницын Ю.П., Тульчинская Е.Е.
Пособие “Контрольные работы” 2006 года:Контрольная работа №1:
Вариант 1:123456
Вариант 2:123456
Вариант 3:123456
Вариант 4:123456
Контрольная работа №2:
Вариант 1:123456
Вариант 2:123456
Вариант 3:123456
Вариант 4:123456
Контрольная работа №3:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
Контрольная работа №4:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
Контрольная работа №5:
Вариант 1:1234
Вариант 2:1234
Вариант 3:1234
Вариант 4:1234
Контрольная работа №6:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
Контрольная работа №7:
Вариант 1:123456
Вариант 2:123456
Вариант 3:123456
Вариант 4:123456
Контрольная работа №8:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
Контрольная работа №9:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
Контрольная работа №10:
Вариант 1:123456
Вариант 2:123456
Вариант 3:123456
Вариант 4:123456
Пособие 2000 года:
Контрольная работа №1:Вариант 1:123456
Вариант 2:123456
Вариант 3:123456
Вариант 4:123456
Контрольная работа №2:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
Контрольная работа №3:
Вариант 1:1234
Вариант 2:1234
Вариант 3:1234
Вариант 4:1234
Контрольная работа №4:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
Контрольная работа №5:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
Контрольная работа №6:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
Контрольная работа №7:
Вариант 1:1234567
Вариант 2:1234567
Вариант 3:1234567
Вариант 4:1234567
Контрольная работа №8:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
Контрольная работа №9:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
Контрольная работа №10:
Вариант 1:123456
Вариант 2:123456
Вариант 3:123456
Вариант 4:123456
Поделись ответами с друзьями в социальных сетях:
Контрольные работы по алгебре 10 класс (базовый уровень)
КОНТРОЛЬНЫЕ РАБОТА
Тема: «Входная контрольная работа»
(коды КЭС: 1. 3.4, 2.4.3, 2.5.1, 2.3.2, 3.1.3, 3.1.5, 3.1.4, 3.2.5, 2.3.4)
3.4, 2.4.3, 2.5.1, 2.3.2, 3.1.3, 3.1.5, 3.1.4, 3.2.5, 2.3.4)
План работы:
План Входной контрольной работы по алгебре для учащихся 10 класса «А»
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 1. 2.4 2.5 | 1.3.4 2.4.3 2.5.1 2.3.2 | Арифметические действия с рациональными числами. Рациональные выражения и их преобразования. Свойства квадратных корней. Формулы сокращенного умножения. | РО | Б | 5 | 1 |
2 | 3.1 | 3.1.3 | Квадратное уравнение. Формула корней квадратного уравнения. | РО | Б | 9 | 3 |
3 | 3. | 3.1.5 | Решение уравнений высших степеней. | РО | П | 8 | 2 |
4 | 3.2 | 3.1.4 | Решение рациональных уравнений. | РО | Б | 8 | 2 |
5 | 3.2 | 3.2.5 | Квадратные неравенства. | РО | Б | 7 | 2 |
6 | 3 | 2. | Текстовые задачи | РО | П | 8 | 2 |
Пояснение
Типы заданий:
ВО – с выбором ответа – ;
КО – с кратким ответом;
РО – с развернутым ответом
Уровень сложности:
Б – базовый;
П – повышенный
Текст контрольной работы
Вариант 1
1. Найдите значение выражения (1 балл)
–
2. Решите уравнение (1 балл за каждое уравнение)
А) 6×2-3x=0
Б) 25×2+2x-1=0
В) 25×2=1
3. Решите биквадратное уравнение (2 балла)
x4 -13×2+36=0
4. Решите неравенство (2 балла)
x2+4x+3≥0
5. (2 балла) Разность корней квадратного уравнения
(2 балла) Разность корней квадратного уравнения
x2-12x+q=0 равна 2. Найдите q.
Вариант 2
1. Найдите значение выражения (1 балл)
–
2. Решите уравнение (1 балл за каждое уравнение)
А) 5×2+20x=0
Б) x2-4x+1=0
В) 49×2=1
3. Решите биквадратное уравнение (2 балла)
x4 -29×2+100=0
4. Решите неравенство (2 балла)
x2-4x-5≥0
5. (2 балла) Разность корней квадратного уравнения
x2+x+с=0 равна 6. Найдите с.
Система оценивания
9-10 баллов (90-100%) – оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 1 Тема: «« Степень с действительным показателем»
(коды КЭС: 1.1.5, 1.1.6, 1.1.7 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 1.3 | 1.1.5 1.1.6 1.1.7 | РО | Б | 5 | 2 | |
2 | 1.3 | 1.1.5 1.1.6 1.1.7 | РО | Б | 5 | 2 | |
3 | 1.3 | 1. 1.1.6 1.1.7 | РО | П | 10 | 2 | |
4 | 1.3 | 1.1.5 1.1.6 1.1.7 | РО | П | 10 | 2 | |
5 | 1.3 | 1.1.5 1.1.6 1.1.7 | РО | П | 10 | 2 |
Пояснение
Типы заданий:
1) ВО – с выбором ответа – ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Контрольная работа №1
Тема « Степень с действительным показателем»
В – 1 В – 2
1. Вычислить:
Вычислить:
1) 1)
2) 2)
2. Упростить выражение при
1) 1)
2) 2)
3. Сократить дробь 3. Сократить дробь
4. Сравнить числа: 4. Сравните числа
1) 1)
2) и 1. 2) и 1.
5. Найти сумму бесконечно убывающей
геометрической прогрессии,
если
Система оценивания
9-10 баллов (90-100%) – оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
5. Найти второй член бесконечно убывающей геометрической прогрессии, если сумма её членов равна , а знаменатель равен
Найти второй член бесконечно убывающей геометрической прогрессии, если сумма её членов равна , а знаменатель равен
№ 2 Тема: «« Степенная функция»
(коды КЭС: 2.1.3, 2.1.7., 3.1.4, 3.3.4 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 3.1 | 2.1.3 2.1.7. | РО | Б | 5 | 2 | |
2 | 3.1 | 2.1.3 2.1.7. | РО | Б | 5 | 2 | |
3 | 3.1 | 3.1.4 3. | РО | П | 10 | 2 | |
4 | 3.1 | 3.1.4 3.3.4 | РО | П | 10 | 2 | |
5 | 3.1 | 2.1.3 2.1.7. 3.1.4 3.3.4 | РО | П | 10 | 2 |
Пояснение
Типы заданий:
1) ВО – с выбором ответа – ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Контрольная работа №2
Тема «Степенная функция»
Вариант 1
1. Найти область определения функции .
Найти область определения функции .
2. Изобразить эскиз графика функции у = х7 и перечислить её основные свойства. Пользуясь свойствами этой функции:
1) сравнить с единицей (0,95)7; 2) сравнить и .
3. Решить уравнение:
1) 2) ; 3)
4. Установить, равносильны ли неравенства и <0.
5. Найти функцию, обратную к функции . Указать её область определения и множество значений. Является ли эта функция ограниченной?
Вариант 2
1. Найти область определения функции .
2. Изобразить эскиз графика функции у = х6 и перечислить её основные свойства. Пользуясь свойствами этой функции:
1) сравнить с единицей (1,001)6; 2) сравнить и .
3. Решить уравнение: 1) 2) .
3)
4. Установить, равносильны ли неравенства и .
5. Найти функцию, обратную к функции . Указать её область определения и множество значений. Является ли эта функция ограниченной?
Система оценивания
9-10 баллов (90-100%) – оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 3 Тема: «« Показательная функция»
(коды КЭС: 2. 1.5, 2.3.3., 3.3.6 )
1.5, 2.3.3., 3.3.6 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 3. | 2.1.5 2.2.3 3.3.6 | РО | Б | 5 | 1 | |
2 | 3.1 | 2.1.5 2.2.3 3.3.6 | РО | Б | 5 | 2 | |
3 | 3.1 | 2.1.5 2.2.3 3.3.6 | РО | П | 5 | 1 | |
4 | 3. | 2.1.5 2.2.3 3.3.6 | РО | П | 6 | 2 | |
5 | 3.1 | 2.1.5 2.2.3 3.3.6 | РО | П | 7 | 2 | |
6 | 3.1 | 2.1.5 2.2.3 3.3.6 | РО | П | 7 | 2 |
Пояснение
Типы заданий:
1) ВО – с выбором ответа – ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Тема 3 «Показательная функция»
Вариант 1
1. Сравнить числа: 1) и ; 2) и .
Сравнить числа: 1) и ; 2) и .
2. Решить уравнение: 1) ; 2)
3. Решить неравенство >
4. Решить неравенство: 1) ; 2)
5. Решить систему уравнений
6. (Дополнительно) Решить уравнение
Вариант 2
1. Сравнить числа: 1) и ; 2) и .
2. Решить уравнение: 1) ; 2)
3. Решить неравенство .
4. Решить неравенство: 1) ; 2)
5. Решить систему уравнений
6. (Дополнительно) Решить уравнение
Система оценивания
9-10 баллов (90-100%) – оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 4 Тема: «Логарифмическая функция»
(коды КЭС: 1.3, 1.4.5, 2.1.6, 2.2.4, 3.3.7 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 2.1 2.3 3.1 1.3 | 1.3 | РО | Б | 5 | 1 | |
2 | 2.1 2.3 3.1 1.3 | 1.4.5 3.3.7 | РО | Б | 5 | 1 | |
3 | 3. 1.3 | 2.2.4 | РО | Б | 5 | 1 | |
4 | 2.1 2.3 | 2.1.6 | РО | Б | 6 | 2 | |
5 | 3.1 1.3 | 2.2.4 | РО | П | 7 | 2 | |
6 | 2. 2.3 | 2.1.6 | РО | П | 7 | 3 |
Пояснение
Типы заданий:
1) ВО – с выбором ответа – ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Тема 4 «Логарифмическая функция»
Вариант 1
1. Вычислите:
2. Сравните числа и
3. Решите уравнение
4. Решите неравенство
5. Решите уравнение
6. Решите неравенство:
Вариант 2
1. Вычислите:
Вычислите:
2. Сравните числа и
3. Решите уравнение
4. Решите неравенство
5. Решите уравнение
6. Решите неравенство:
Система оценивания
9-10 баллов (90-100%) – оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 5 Тема: «Тригонометрические формулы»
(коды КЭС: 1.2.3, 1.2.4, 1.2.5, 1.2.6, 1.2.7 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 1.3 | 1.2.3 1.2.4 | РО | Б | 6 | 3 | |
2 | 1.3 | 1.2.5 1.2.6 | РО | Б | 4 | 1 | |
3 | 1.3 | 1.2.7 | РО | Б | 10 | 2 | |
4 | 1. | 1.2.5 1.2.6 | РО | Б | 10 | 2 | |
5 | 1.3 | 1.2.5 1.2.6 | РО | П | 10 | 2 |
Пояснение
Типы заданий:
1) ВО – с выбором ответа – ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Тема №5 «Тригонометрические формулы»
Вариант 1
1. Найти значение выражения: 1) 2) 3)
Найти значение выражения: 1) 2) 3)
2. Вычислить:
3. Упростить выражение:
4. Доказать тождество:
5. Решить уравнение
Вариант 2
1. Найти значение выражения: 1) 2) 3)
2. Вычислить:
3. Упростить выражение:
4. Доказать тождество:
5. Решить уравнение
Система оценивания
9-10 баллов (90-100%) – оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 6 Тема: «Тригонометрические уравнения»
(коды КЭС: 2.1.4)
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 2.1 | 2.1.4 | РО | Б | 10 | 2 | |
2 | 2.1 | 2.1.4 | РО | Б | 10 | 2 | |
3 | 2.1 | 2.1.4 | РО | Б | 10 | 3 | |
4 | 2. | 2.1.4 | РО | Б | 10 | 3 | |
Пояснение
Типы заданий:
1) ВО – с выбором ответа – ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Тема 6 «Тригонометрические уравнения»
Вариант 1
1. Решите уравнение:
2. Найдите решение уравнения на отрезке .
3. Решите уравнение:
; в)
4. Решите уравнение:
а)
Вариант 2
1. Решите уравнение:
а)
2. Найдите решение уравнения на отрезке .
3. Решите уравнение:
в)
4. Решите уравнение:
а)
Система оценивания
9-10 баллов (90-100%) – оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
Тема: «Итоговая контрольная работа»
(коды КЭС: 1.4.4.. 2.1.4, 2.2.3, 2.2.4, 3.1, 3.2, 3.3)
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 1.3 | 1.4.4. 2.1.4 | РО | Б | 5 | 2 | |
2 | 2.1 | 2.2.3 | РО | Б | 5 | 2 | |
3 | 2.2 | 2.2.4 | РО | Б | 10 | 2 | |
4 | 2. | 3.1 | РО | Б | 10 | 2 | |
5 | 3.1 | 3.2 3.3 | РО | Б | 10 | 2 |
Пояснение
Типы заданий:
1) ВО – с выбором ответа – ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Итоговая контрольная работа по алгебре и началам анализа.
Вариант 1
Базовый уровень
Вычислить:
а) ; в) ;
б) ; г) .
Вычислить:
.
Решите уравнение:
а) ; в) ;
б); г) .
Решите неравенство:
а) ; б).
Упростите выражения:
а); б).
Повышенный уровень
Решите уравнение:
.
Решите уравнение:
.
Решите уравнение:
.
а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие отрезку .
Вариант 2
Базовый уровень
Вычислить:
а) ; в) ;
б) ; г) .
Вычислить:
.
Решите уравнение:
а) ; в) ;
б); г) .
Решите неравенство:
а) ; б).
Упростите выражения:
а); б).
Повышенный уровень
Решите уравнение:
.
Решите уравнение:
.
Решите уравнение:
.
а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие отрезку .
Система оценивания
9-10 баллов (90-100%) – оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
Тестовые контрольные работы по алгебре и началам анализа, 10–11-е классы
Проблемой первостепенной важности в процессе реформирования системы образования становится унификация требований к уровню знаний учащихся. Возможно, поэтому важнейшими критериями при введении ЕГЭ были:
- Необходимость унификации требований к уровню знаний учащихся;
- Возможность последующего использования результатов ЕГЭ в качестве основного критерия при приёме абитуриентов в ВУЗ.
Однако ЕГЭ позволяет установить
субъективность оценки уровня знаний учеников
лишь на конечном этапе его обучения. Для текущего
контроля представляется актуальным создание
единой согласованной системы тематических
контрольных работ, соответствующей минимальным
требованиям к содержанию образования,
федеральному компоненту государственного
стандарта математики.
В пределах соответствующего уровня изложения материала тематические контрольные работы должны быть приспособлены для работы с любым учебником, входящим в Федеральный перечень.
Контрольная работа традиционно ассоциируется с
- Огромной подготовительной работой учителя, скурпулёзно отбирающего разноуровневый, многовариантный тематический материал;
- Значительным стрессом учащихся, которым предстоит не только продемонстрировать достаточный уровень усвоения текущего материала, но и быть уверенным в объективности итоговой отметки.
Наличие ряда программ, учебников по математике, неизбежная субъективность требований учителей, связанная с различием уровня предварительной подготовленности школьников, в конечном итоге приводит к значительной неоднородности уровня подготовки выпускника и его оценки в пределах региона.
Для заблаговременной адаптации школьников к
режиму проведения и требованиям ЕГЭ структура
контрольных работ должна быть сходной со
структурой ЕГЭ. Мы в своей школе группой учителей
составили контрольные работы по всем темам 10 и 11
классов в 4-х – 6-и вариантах. Уровень тестов и
задач соответствует Федеральному компоненту
Государственного стандарта, а также уровням А и В
единого государственного экзамена по
математике.
Мы в своей школе группой учителей
составили контрольные работы по всем темам 10 и 11
классов в 4-х – 6-и вариантах. Уровень тестов и
задач соответствует Федеральному компоненту
Государственного стандарта, а также уровням А и В
единого государственного экзамена по
математике.
Тесты по темам “Тригонометрические функции” и “Свойства функций” включают в себя 10 заданий уровней А и В, все они содержат 4 ответа, один из которых верный. Это первые контрольные работы в 10 классе в форме ЕГЭ, поэтому задания уровня С каждый учитель добавляет сам в зависимости от состава класса и изученного материала.
Тест по теме “Тригонометрические уравнения и неравенства” тоже содержат 10 заданий, но уже 8 заданий с выбором ответа и 2 задания более сложные.
Для ознакомления со структурой ЕГЭ
подготовлена годовая контрольная работа в 10
классе, состоящая из трёх частей: 10 заданий части
А, 6 заданий части В, 4 задания части С.
Аналогично составлены контрольные работы по темам:
- “Тригонометрические функции”
- “Свойства функции”
- “Тригонометрические уравнения и неравенства”
- “Производная. Применение производной”
- “Применение непрерывности и производной”
- Итоговая работа в 10 классе
- “Первообразная и интеграл”
- “Обобщение понятия степени”
- “Показательная функция. Показательные уравнения и неравенства”
- “Логарифмическая функция. Логарифмические уравнения и неравенства”
- “Производная и первообразная показательной и логарифмической функций”
- Контрольная работа за полугодие в 11 классе.
В апреле проводится пробный экзамен для одиннадцатиклассников, задания для него готовит администрация школы.
При проведении работ оговаривается с ребятами
заранее количество баллов за каждое задание и
соответствующая оценка за работу.
Со временем видна положительная динамика усвоения ребятами курса, они привыкают к жёсткому временному контролю тестирования.
Контрольные работы могут быть использованы при работе с любым учебником, соответствующим Федеральному компоненту. Они способствуют улучшению контроля уровня усвоения материала курса “Алгебра и начала анализа” учащимися, являются рациональной тематической имитацией ЕГЭ.
Аналогичная структура контрольных и ЕГЭ, а также принципиальное организационное разделение времени на ответы на сравнительно простые тесты и на решение традиционных задач, должны помочь учащимся в подготовке к ЕГЭ.
Мы предлагаем для коллег тексты всех контрольных работ (См. приложение).
ГДЗ Алгебра 7 класс Кузнецова
- Алгебра 7 класс
- Тип пособия: Контрольные работы
- Авторы: Кузнецова
- Издательство: «Просвещение»
Похожие ГДЗ Алгебра 7 класс
Стр.
 7- 14. Контрольная работа № 1: Вариант 1
7- 14. Контрольная работа № 1: Вариант 1Предыдущее
Следующее
Предыдущее
Следующее
Контрольные работы по алгебре – это пособие, предназначенное для проверки знаний и навыков учеников. Оно является логическим дополнением к учебнику одноименного автора. Тетрадь позволяет подготовиться к предстоящим ОГЭ и ЕГЭ по дисциплине, так как структура заданий соответствует экзаменационным требованиям. Это отличное дополнение к теоретическому материалу, изложенному в учебнике. Автор удачно подобрал задания и разделил их на 4 уровня: начальный, средний, достаточный и высокий.
Преимущества сборника
Контрольные работы по алгебре – это хорошая подборка заданий. Ее отличает:
- Обучающий характер;
- Разные уровни сложности;
- Наличие олимпиадных заданий.
Особого внимания заслуживает последний пункт. Педагоги часто используют пособие для подготовки учебников к школьным и городским олимпиадам. Здесь содержатся нестандартные номера, которые решаются другими способами и требуют наличия логического мышления и смекалки.
Здесь содержатся нестандартные номера, которые решаются другими способами и требуют наличия логического мышления и смекалки.
Что такое ГДЗ
ГДЗ – это готовые домашние задания, книга с решением и ответами ко всем номерам. Пособие позволяет научиться правильно записывать условие и оформлять решение. Вы сможете проверить правильность выполнения номеров и оформить работу в соответствии с требованиями ФГОС. Это очень важно для успешной сдачи экзамена в конце 9 класса и для участия в олимпиадах. Так как ответы, записанные неправильно, не засчитываются. Решебник восполнит пробелы в знаниях, если вы пропустили несколько уроков алгебры в школы. Вы сможете провести самоанализ, выполнив, а затем проверив ответы.
Наше предложение
Наш сайт предлагает воспользоваться онлайн-версией ГДЗ с помощью мобильного телефона или компьютера. В любое удобное для вас время выберите необходимый раздел, вариант и номер упражнения. Перед вами откроется изображение с записанным условием, решением и ответом. Все задания решены лучшими математиками, можете не сомневаться в их правильности.
Перед вами откроется изображение с записанным условием, решением и ответом. Все задания решены лучшими математиками, можете не сомневаться в их правильности.
Учитесь с нами! Повышайте баллы по алгебре!
Algebra 1 Часто задаваемые вопросы о регентах: все, что вам нужно знать
У вас скоро экзамен Риджентс по Алгебре 1? Тогда мы уверены, что у вас есть вопросы, и у нас есть ответы.
Прочтите следующие исчерпывающие ответы на часто задаваемые вопросы, касающиеся экзамена Regents по алгебре 1, чтобы начать подготовку к большому экзамену.
Экзамен Риджентс по алгебре 1 сложный?
Экзамен Риджентс по алгебре 1 сложен в том контексте, что этот предмет может быть сложным для любого студента.Тем не менее, это не очень сложный тест, основанный на том, как он изогнут. Тенденция к снижению кривой вызвала разногласия среди педагогов, считающих, что проходной балл не отражает истинного мастерства в алгебре, и цифры подтверждают это мнение.
Как и в недавнем тесте Риджентс по алгебре 1 в январе 2020 года, учащимся нужно было набрать только 27 необработанных баллов, чтобы получить проходной уровень 3. На январском экзамене 2016 года учащимся нужно было набрать 30 баллов, чтобы получить такой же балл 3.
Эта нисходящая тенденция, по-видимому, предполагает, что Алгебра 1 Регенты становится проще, а не сложнее, как тест.Поскольку экзамен оценивается по 86 баллам, учащимся нужно набрать только 31 % по сравнению с 34 % в 2016 году.
Преподаватели, которые считают, что тест становится легче, говорят об этом из-за того, как сырые баллы преобразуются в баллы по шкале. Например, в верхней части диаграммы преобразования за январь 2020 года 80/86 масштабируется до 93% процентов, что имеет смысл, поскольку это необработанная доля. Однако по мере продвижения вниз по диаграмме, например, до минимального исходного проходного балла 27, это переводится в масштабированный балл 65, когда 27/86 составляет 31%.
Подробнее об этой теме строгости Риджентс Алгебры 1 можно прочитать здесь и здесь.
Рассчитаны ли экзамены Regents по алгебре 1 по времени? Если да, то как долго они?
Экзамен Риджентс по алгебре 1 длится три часа. Студенты часто не используют все время, отведенное на администрацию экзамена, для завершения теста; однако учащиеся не могут покинуть место тестирования до истечения трех часов.
Подробнее о том, как проводятся экзамены Regents по алгебре 1, см. в руководстве по тестированию, предоставленном Управлением образования штата Нью-Йорк, здесь.
Как оцениваются экзамены Риджентс по Алгебре 1?
Что касается оценки экзаменов Regents по Алгебре 1, то тест состоит из четырех компонентов:
В Части I есть 24 вопроса, каждый из которых оценивается в два кредита. Это означает, что общее количество возможных кредитов в Части I равно 48 (24 x 2).
В Части II восемь вопросов по 2 кредита каждый. Это создает общий возможный пул кредитов 16.
Это создает общий возможный пул кредитов 16.
В Части III Алгебры 1 Регенты есть четыре вопроса, оцениваемые в 4 балла, всего 16 кредитов.
Наконец, в Части IV есть один вопрос на шесть баллов.
В совокупности это означает, что за экзамен можно набрать 86 возможных баллов (которые формируют ваш исходный балл). На основе вашей исходной оценки оценщики экзаменов затем ссылаются на официальные таблицы преобразования, выпущенные штатом, чтобы перевести вашу оценку в итоговую оценку за экзамен (известную как оценка по шкале).
Пороговым значением для прохождения теста Риджентс по алгебре 1 является уровень успеваемости 3.
Со ссылкой на экзамены в январе 2019 и 2020 гг. пороговые значения остались относительно стабильными:
Исходный результат | Оценка по шкале | Уровень производительности |
68 | 85 | 5 |
51-52 | 80 | 4 |
27 | 65 | 3 |
19 | 55 | 2 |
Как проходят экзамены Риджентс по Алгебре 1?
Чтобы получить высшее образование, студенты штата Нью-Йорк сдают серию экзаменов Риджентс, одним из которых является экзамен Риджентс по алгебре 1. Студенты сдают трехчасовой экзамен, отвечая на 37 вопросов.
Студенты сдают трехчасовой экзамен, отвечая на 37 вопросов.
После окончания теста оценки за экзамены выставляются лицензированными и обученными учителями Нью-Йорка. Эта оценка обычно начинается для каждого теста Риджентс через два дня после сдачи экзамена. Экзамен Риджентс не оценивается учителем из той же школы, что и учащийся.
Результаты обычно публикуются через несколько недель после даты экзамена. Когда результаты готовы, они публикуются в стенограмме учащегося средней школы, а также в его учетной записи NYC Schools.Средние школы могут отображать все баллы учащегося по программе Риджентс или только высшую оценку, полученную им по каждому экзаменационному предмету.
ЭкзаменыRegents очень важны, поскольку они не только важны для учащихся, чтобы они соответствовали требованиям к выпускным экзаменам, но также используются для оценки школ и преподавателей.
Сколько экзаменов Риджентс нужно сдать, чтобы закончить среднюю школу?
В Нью-Йорке учащиеся старших классов могут получить диплом Риджентс, продвинутый диплом Риджентс или местный диплом. Разница между дипломом Риджентс и продвинутым дипломом Риджентс заключается в количестве экзаменов Риджентс, на которых вы набираете 3 балла или выше.
Разница между дипломом Риджентс и продвинутым дипломом Риджентс заключается в количестве экзаменов Риджентс, на которых вы набираете 3 балла или выше.
Если учащийся включает экзамен Риджентс по алгебре 1, чтобы выполнить требования экзамена по математике для получения диплома Риджентс, он должен набрать 65 баллов или выше. Таким образом, студентам нужно сдать только один экзамен по математике. Другими способами выполнить это требование являются экзамены Regents Geometry или Regents Algebra II/Trigonometry. Подробнее об экзамене Regents по алгебре 2 можно узнать здесь, а об экзамене Regents по геометрии — здесь.
Для получения диплома Риджентс продвинутого уровня учащимся необходимо сдать три экзамена по математике с результатом 65 или выше — это означает, что алгебра 1 составляет всего 33% от необходимого для получения этого диплома.
Если вы хотите получить звание вместе с дипломом (т. е. с отличием), вы должны набрать в среднем 90 баллов на всех обязательных экзаменах Риджентс.
Для местных дипломов требования различаются и не так прямо связаны с вашими результатами по алгебре Regents 1. Проконсультируйтесь с вашим школьным консультантом для получения дополнительной информации о вашем местном дипломе.
Этот рабочий лист для получения диплома может оказаться полезным для определения того, насколько ваш тест Regents Algebra 1 соответствует вашим выпускным требованиям.
Что произойдет, если вы провалите экзамен Риджентс?
Пожалуйста, не волнуйтесь, если вы провалите экзамен Regents по алгебре 1!
Как правило, у вас будет еще один шанс пересдать экзамен. Каждый год экзамен Algebra 1 Regents проводится в течение трех месяцев: августа, января и июня. Это дает вам достаточно времени, чтобы просмотреть концепции, которые вы, возможно, не полностью освоили в первый раз, и лучше подготовиться к следующему разу.
Если вы надеетесь сделать Алгебру 1 своим требованием к получению диплома Риджентс, вам придется продолжать сдавать экзамен до тех пор, пока вы не наберете по крайней мере 65 баллов по шкале (что соответствует уровню успеваемости 3).
В зависимости от вашей школы, если вы не сдадите экзамен Риджентс по алгебре 1, вам может потребоваться пойти в летнюю школу или пройти восстановление кредита. Узнайте у школьного консультанта о правилах вашей школы.
Какова цель экзамена Риджентс по алгебре 1?
Экзамен Regents по алгебре 1 предназначен для оценки беглости учащихся в решении типичных задач, таких как аналитическая геометрия линий, удобство работы с полиномами, преобразование выражений и разбиение на фрагменты в алгебраических вычислениях.
Тест «Алгебра 1 Риджентс» включает в себя пять основных модулей:
- Модуль 1: Отношения между величинами и рассуждения с помощью уравнений и их графиков
- Модуль 2: Описательная статистика
- Модуль 3: линейные и экспоненциальные функции
- Модуль 4: Полиномиальные и квадратичные выражения, уравнения и функции
- Модуль 5: Синтез моделирования с помощью уравнений и функций
В своем обзоре учебной программы Департамент образования штата Нью-Йорк перечисляет цели математической практики для учащихся, основанные на улучшении их способности рассуждать абстрактно и количественно, а также моделировать с помощью математики.
Учащиеся используют знания, полученные в восьмом классе (например, решение линейных уравнений с одной переменной), чтобы овладеть более широкими приложениями, такими как статистика и вероятность. Это виды реальных навыков, которые позволяют учащимся извлекать смысл из чисел.
Когда вы обычно сдаете Алгебру 1 Риджентс?
Департамент образования штата Нью-Йорк разработал трехлетнюю программу обучения математике в средней школе. Алгебра – это первый год этой трехлетней учебной программы.
Это означает, что большинство учащихся сдают Алгебру 1 в 9-м или 10-м классе. В зависимости от школы Алгебра 1 может быть разделена на двухлетнюю последовательность, когда учащиеся начинают с Алгебры 1А, а затем заканчивают Алгебру 1В в следующем году.
После того, как учащиеся завершат алгебру 1, они переходят к экзамену Риджентс по геометрии.
Когда Регентская неделя? Каковы типичные даты начала?
Неделя Регентов обычно приходится на предпоследнюю неделю января, третью и четвертую недели июня и вторую неделю августа. Экзамены Риджентс проводятся три раза в год.
Экзамены Риджентс проводятся три раза в год.
В 2020 году экзамены запланированы на 21-24 января, 17-25 июня и 13-14 августа. Ссылаясь на сайт Департамента образования штата, даты последовательно устанавливаются в декабре или январе в пресс-релизе за два года до начала (то есть в декабре 2018 года были объявлены даты экзаменов Regents 2020 года).
Algebra 1 Regents обычно является более ранним экзаменом в общем графике тестирования. Подробнее о том, когда обычно проводится экзамен по Алгебре 1 Риджентс, мы расскажем в нашем руководстве «Как сдать Алгебра 1 Риджентс ».
В каких штатах проводятся экзамены Риджентс по алгебре 1?
Хотя в других штатах могут быть свои собственные тесты по алгебре 1, тест Риджентс по алгебре 1 уникален для Нью-Йорка. Официальные экзамены Regents проводятся только в штате Нью-Йорк Департаментом образования штата.
Нужна помощь в подготовке к экзамену Риджентс по алгебре 1?
У Альберта есть несколько практических тестов Regents по Алгебре 1, с которыми вы можете попрактиковаться!
Начните подготовку к экзамену Риджентс здесь
У нас также есть ряд очень полезных бесплатных ресурсов для вас:
ALEKS Оценка успеваемости по математике | Кафедра математики
Оценка уровня знаний по математике поможет вам и вашему консультанту выбрать правильный курс математики для вас.
Оценка займет около 90 минут. После оценки вам будет доступен целевой модуль подготовки и обучения, где вы сможете просмотреть и изучить материал, а также улучшить зачисление и конечные результаты курса.
Всем учащимся настоятельно рекомендуется провести несколько часов, используя модуль подготовки и обучения ALEKS. Даже если вы получили место на желаемом курсе, время, проведенное в ALEKS, лучше подготовит вас к предстоящему курсу и, в конечном итоге, приведет к более высоким оценкам.
Прежде всего, РАССЛАБЬТЕСЬ. Это «ОЦЕНКА», а НЕ ТЕСТ. Разница в том, что оценка предназначена для определения того, что вы знаете. По окончании теста ALEKS Placement Assessment у вас будет гораздо лучшее представление о ваших сильных и слабых сторонах в математике. Тогда у вас будет возможность поработать над этими слабостями. Там действительно нет штрафа за неправильный ответ на вопрос об оценке. Самое главное, что вы серьезно относитесь к оценке и прикладываете к ней честные усилия, чтобы оценка действительно отражала ваш уровень знаний и подготовленности к математике.
Честно говорите о своем уровне мастерства. Нет никакой выгоды в мошенничестве при оценке размещения — вашей единственной наградой будет то, что вы попали в математический класс, для которого у вас еще нет навыков, чтобы преуспеть. Поэтому, пока вы проходите оценку, не обращайтесь за помощью к каким-либо другим источникам (друзьям, семье, поиску в Интернете и т. д.). Цель оценки размещения — дать точную оценку ваших текущих математических навыков, чтобы вы были успешными на курсах математики.
Как начать использовать ALEKS?
Войдите на портал my.pitt.edu.
Найдите ALEKS в окне поиска.
Новые студенты, поступающие в университет в главном кампусе, участвуют в программе Main Campus Math Placement 2020-2021, Fall-Spring-Summer 2020 Class Cohort
Как мне получить балл за размещение в системе ALEKS?
После прохождения теста вам будет представлена круговая диаграмма, показывающая ваши сильные и слабые стороны. Ваша общая оценка отображается в верхней части страницы. Если вы проходили тест более одного раза, баллы по предыдущим тестам отображаются под круговой диаграммой. В этом случае ваш наивысший балл оценки используется для целей размещения.
Ваша общая оценка отображается в верхней части страницы. Если вы проходили тест более одного раза, баллы по предыдущим тестам отображаются под круговой диаграммой. В этом случае ваш наивысший балл оценки используется для целей размещения.
Если вы забыли свой оценочный балл, вы можете снова войти в ALEKS, чтобы просмотреть свои баллы.
Если у вас возникли трудности с просмотром результатов, обратитесь к менеджеру по академическим операциям на факультете математики.
Как пересдать оценку места
После истечения двенадцатимесячного периода доступа Если срок действия вашего доступа к ALEKS истек после вашего начального 12-месячного окна и вы хотите пересдать оценку размещения , вы можете войти в ALEKS и ввести код класса, чтобы зарегистрироваться в когорте Main Campus Math Placement – дополнительный доступ, продолжается 2020
Вам нужно будет снова заплатить взнос в размере 25 долларов США, что даст вам 3 попытки размещения и 12-месячный доступ к учебному модулю ALEKS.
1. Войдите на портал my.pitt.edu, чтобы получить доступ к ALEKS.
2. В ALEKS нажмите «Новый класс» или «Добавить класс».
3. Введите код курса .
4. Следуйте инструкциям, чтобы оплатить и завершить регистрацию
Часто задаваемые вопросы
Кто должен сдавать ALEKS Placement Assessment?
Всем желающим пройти следующие курсы:
Математика 0120
Математика 0125
Математика 0200
Математика 0220
Математика 0400
должен пройти тест ALEKS Placement Assessment перед регистрацией на эти курсы.
Есть ли исключения?
Применяются следующие исключения:
- Вы хотите пройти один из следующих курсов:
Математика 0120
Математика 0125
Математика 0200
Математика 0400
и выполнить хотя бы одно из следующих условий:- получили степень C или выше по математике 0031 в Университете Питтсбурга или на переводном курсе, эквивалентном математике 0031
- у вас есть зачет по математике 0120, или математике 0200, или курсу математики более высокого уровня, или их эквивалентам.

- Вы хотите сдать Math 0220 и выполнить хотя бы одно из следующих условий:
- набрали 4 или 5 баллов по математике AB или Math BC Advanced Placement Exam
- получили оценку C или выше по математике 0200
- получили C или выше по переводному курсу, эквивалентному математике 0200
- у вас есть зачет по математическому анализу 1 или по математическому курсу более высокого уровня и вы хотите повторить исчисление 1.
Что, если я пройду тест ALEKS Placement Assessment в CHS?
Если вы сдавали ALEKS Placement Assessment в колледже в старшей школе, вы можете использовать его баллы.
Какие темы рассматриваются при оценке размещения?
Тест Placement Assessment охватывает только темы, предшествующие математическому анализу. В частности
- Целые числа, дроби и десятичные дроби
- Проценты, пропорции и геометрия
- Числа со знаком, линейные уравнения и неравенства
- Линии и системы линейных уравнений
- Отношения и функции
- Целочисленные показатели степени и факторизация
- Квадратичные и полиномиальные функции
- Рациональные выражения и функции
- Радикалы и рациональные показатели
- Экспоненты и логарифмы
- Тригонометрия (здесь учащиеся могут заработать 0 баллов и по-прежнему соответствовать требованиям по математике 0120)
Взимается ли плата за использование ALEKS?
Да. Существует комиссия в размере 25 долларов США (возможны изменения), выплачиваемая непосредственно ALEKS.
Существует комиссия в размере 25 долларов США (возможны изменения), выплачиваемая непосредственно ALEKS.
Могу ли я пересдать ALEKS Placement Assessment?
Да, вы можете сдать до 3 тестов для определения места (первоначальная оценка плюс до двух дополнительных попыток) в течение двенадцати месяцев после вашей первой оценки. Однако, чтобы сделать каждую попытку стоящей, важно, чтобы вы уделяли время работе с модулем ALEKS Prep and Learning Module между оценками размещения, чтобы вы могли улучшить свои навыки.
Могу ли я немедленно пересдать ALEKS Placement Assessment?
Вы должны подождать 24 часа между оценками размещения.Как правило, повторная сдача экзамена сразу после завершения предыдущей попытки не имеет смысла. В отличие от SAT или ACT, вы не можете улучшить свои результаты, просто пересдав экзамен, не тратя время на модуль «Подготовка и обучение», чтобы обновить материал, который вы, возможно, забыли, или изучить новый материал.
Должен ли я работать над модулем ALEKS Prep and Learning Module между экзаменами по зачислению?
Да, после завершения экзамена вы должны провести не менее 5 часов в модуле «Подготовка и обучение», прежде чем повторять экзамен.
Рассчитаны ли оценки размещения по времени?
Да, у вас есть 24 часа, чтобы пройти оценку размещения после ее начала.
Сколько времени займет оценка размещения?
Вступительные экзамены занимают около 90 минут, но это время зависит от учащегося. Будет максимум 30 вопросов.
Что произойдет, если я не пройду оценку размещения в отведенные 24 часа?
Вам придется перезапустить оценку.
Могу ли я использовать калькулятор во время использования ALEKS?
ALEKS предоставит калькулятор на экране, если он вам нужен для решения конкретной задачи. В противном случае вы не можете использовать калькулятор.
Могу ли я использовать какие-либо другие ресурсы во время оценки размещения?
Вы можете использовать только ручку или карандаш, бумагу и ресурсы, предоставленные ALEKS. Вы не можете получать помощь от друзей, семьи, других веб-сайтов, учебников или любых других ресурсов, не предоставленных ALEKS. Использование внешних ресурсов может привести к неправильному размещению и, в конечном итоге, к провалу курса.
Использование внешних ресурсов может привести к неправильному размещению и, в конечном итоге, к провалу курса.
Каков результат моего размещения?
Результат вашего размещения будет выражен в процентах. Для зачисления на любой курс математики начального уровня выше алгебры колледжа (математика 0031) требуется минимальный балл, как показано ниже.
| Курс | Минимальный балл за место |
| Математика 0120 – Деловые расчеты | 61 |
| Математика 0200 – Предварительное исчисление | 61 |
| Математика 0220 – Расчет 1 | 76 |
| Математика 0400 – Дискретная математика | 61 |
Я только что прошел тест ALEKS, но не могу записаться на курс, который я выбрал.Что я должен делать?
Будьте терпеливы! Оценки ALEKS загружаются в информационную систему студентов в одночасье. Завтра вы сможете записаться на курс.
Завтра вы сможете записаться на курс.
Могу ли я попрактиковаться в использовании ALEKS перед тем, как начать размещение?
ALEKS начнет с краткого руководства, прежде чем начнется ваше размещение.
Как долго у меня есть доступ к моему модулю подготовки и обучения и оценке размещения?
У вас будет доступ в течение двенадцати месяцев с момента первоначальной оценки.
Можно ли повторить оценку места размещения по истечении 12 месяцев доступа?
Да. Выполните шаги, описанные выше в разделе «Как пересдать ALEKS Placement Assessment».
Что такое оценки прогресса ALEKS?
Во время работы в модуле «Подготовка и обучение» вы будете периодически проходить оценки прогресса, чтобы закрепить свои знания.
Засчитывается ли прогресс в модуле подготовки и обучения ALEKS при размещении?
Нет, вы должны пройти новую оценку размещения, чтобы изменить результат вашего размещения.Нажмите на вкладку размещения в правом верхнем углу страницы в ALEKS. Только результаты вашей оценки размещения будут использоваться для размещения на курсе.
Только результаты вашей оценки размещения будут использоваться для размещения на курсе.
Что, если я не попаду на желаемый курс?
Вы можете использовать модуль «Подготовка и обучение» для просмотра и обучения, а также можете пройти еще одну оценку размещения, чтобы улучшить свой результат размещения. Вы можете сдать экзамен на размещение до трех раз (первоначальный экзамен плюс до двух дополнительных попыток). Если вы по-прежнему не набираете требуемый балл для зачисления на выбранный вами курс, вам придется пройти обязательный класс и получить минимальный балл C в этом классе.Предпосылки следующие.
| Курс | Необходимое условие |
| Математика 0120 – Деловые расчеты | Математика 0031 |
| Математика 0200 – Предварительное исчисление | Математика 0031 |
| Математика 0220 – Расчет 1 | Математика 0200 |
| Математика 0400 – Дискретная математика | Математика 0031 |
Я не попал в нужный класс.
 Могу ли я взять его в любом случае?
Могу ли я взять его в любом случае?Нет. Чтобы пройти любой из перечисленных выше курсов начального уровня, вы должны либо набрать требуемый минимальный балл для размещения, либо пройти предварительный курс.
Могу ли я выполнить предварительное условие для курса математики начального уровня с переводным кредитом?
Да. Если у вас есть переводной кредит для обязательного курса, вам не нужно будет сдавать оценку для размещения.
Что, если меня переведут в нужный класс?
Поздравляем! Продолжайте использовать модуль «Подготовка и обучение», чтобы повысить свои шансы на успех.Приведенный выше результат размещения — это минимальная подготовка, необходимая для вашего курса! Воспользуйтесь преимуществами целевого обзора и функций обучения в ALEKS, чтобы получить более высокую оценку в своем классе.
Где я могу получить помощь с ALEKS?
https://mhedu.force.com/aleks/s/
http://support.aleks.com/
Базовая алгебра: правила, уравнения и примеры — видео и стенограмма урока
Добавление или вычитание одинаковых терминов
Чтобы складывать или вычитать любые термины в алгебре, ваши термины должны быть подобны терминам , которые имеют одну и ту же переменную и возводятся в одну и ту же степень. Если у вас есть одинаковые термины, вы добавляете или вычитаете числа, прикрепленные к переменной, называемые коэффициентами . Сама переменная остается неизменной. Рассмотрим пример:
Если у вас есть одинаковые термины, вы добавляете или вычитаете числа, прикрепленные к переменной, называемые коэффициентами . Сама переменная остается неизменной. Рассмотрим пример:
На первом этапе, как видите, мы перегруппировали наши термины, чтобы сгруппировать их по похожим терминам. После этого мы переписали подобные термины так, чтобы в скобках были только коэффициенты, а снаружи — переменная. Это не обязательно, но помогает продемонстрировать математику, которую мы выполнили на последнем шаге, чтобы получить ответ 2 x + y .
Этот тип математики называется упрощением выражений. Когда вы смотрите на такое алгебраическое выражение, важно думать о знаках + и – как о присоединенных к термину. Рассмотрим следующее:
Каждый раз, когда мы вычитаем одно число из другого, мы можем изменить его порядок, как мы только что сделали. Вычитаемое число становится отрицательным числом, а число, из которого мы вычитаем, прибавляется к отрицательному числу.Пока вы держите знаки привязанными к своим терминам, вы не меняете значение вашего уравнения.
Вычитаемое число становится отрицательным числом, а число, из которого мы вычитаем, прибавляется к отрицательному числу.Пока вы держите знаки привязанными к своим терминам, вы не меняете значение вашего уравнения.
Рассмотрим еще один пример:
Посмотрите внимательно на этот пример. У нас есть три разные переменные для размышления: n , x и n x . Мы не можем объединить ни один из этих трех элементов вместе, поэтому в конце у нас остается три термина. Вы видите, как мы применили те же шаги, что и раньше, чтобы прийти к этому ответу?
Умножение и деление терминов
Чтобы умножить или разделить термины, вам не обязательно иметь одинаковые термины.Это отличается от сложения и вычитания, так что будьте осторожны! Взгляните на следующий пример базового умножения с переменной:
Мы должны умножить каждую часть уравнения в круглых скобках на 2, и этот пример показывает, что это происходит на втором шаге, где оно ушло от ( x + 5) * 2 к (2 * x ) + (2*5). После умножения наш окончательный ответ будет простым: 2 x + 10.
После умножения наш окончательный ответ будет простым: 2 x + 10.
Теперь, когда мы можем разобраться с основами, давайте немного усложним задачу и включим еще одну переменную:
Несмотря на наличие двух переменных на этот раз, наша процедура такая же, как и в первом примере, в котором ( x + 3) * y превращается в ( y * x ) + ( и *3).Другими словами, мы должны умножить все в скобках на нашу переменную y , что дает нам ответ xy + 3 y . Мы не можем объединить наши xy с y , так что это упрощенное выражение.
Противоположностью умножения является деление. Существует несколько основных способов выражения деления. Тот, который, вероятно, вам знаком, использует символ, похожий на этот «÷», и вы помещаете его между двумя числами. Например: 4 ÷ 2 = 2.Однако мы можем выразить это без символа, создав дробь, представляющую то же самое.
Когда мы делим на число, это то же самое, что и умножение на его обратную величину (или на число, которое мы могли бы получить, если бы «перевернули» дробь). Это означает, что умножение и деление являются операциями, обратными друг другу. В приведенном выше примере мы делим на 2. Обратная величина 2 равна 1 больше 2, или половине, поэтому можно сказать, что мы умножаем на 1/2.
Вы, возможно, помните из предыдущего изучения дробей, что если у вас есть одно и то же число в верхней и нижней части дроби, все это равно 1. Это может помочь вам упростить алгебраические выражения с помощью деления. Если у вас есть переменная сверху и снизу дроби, они исключают друг друга из вашего выражения.
Как вы можете видеть в нашем примере выше, 2 x разделить на 2 равно x , а 2 x разделить на x равно 2. Просто, верно? Вы можете применить эту же идею к терминам со многими переменными. Давайте рассмотрим еще два примера, на этот раз немного посложнее:
Просто, верно? Вы можете применить эту же идею к терминам со многими переменными. Давайте рассмотрим еще два примера, на этот раз немного посложнее:
Нахождение переменной
Хотя алгебра является широкой областью, общая цель состоит в том, чтобы найти переменную или найти значение неизвестного. Мы одинаково манипулируем алгебраическими выражениями по обе стороны от знака равенства, чтобы иметь возможность перемещать элементы до тех пор, пока мы не сможем найти нашу переменную, изолируя ее с одной стороны.Используя все, что мы узнали, мы можем понять, что если 3 умножить на x минус 10 равно 11, то x равно 7.
В этом примере мы добавляем 10 к обеим сторонам, чтобы изолировать x слева. Затем мы делим обе части уравнения на 3, чтобы получить простое x . Если внимательно рассмотреть, то можно увидеть, что мы отменяем (или делаем наоборот) все, что было сделано для разрешения 90 537 x 90 538, чтобы мы могли получить его самостоятельно. Давайте попробуем один последний вызов!
Давайте попробуем один последний вызов!
В этом задании у нас есть:
… и это в конечном итоге показывает нам, что x равно 10. Просто!
Резюме урока
Давайте повторим…
Базовая алгебра — это язык, на котором математика говорит об абстрактном мире чисел. Это область математики, которая на один шаг более абстрактна, чем арифметика. Арифметика фокусируется только на действительных, определенных числах, а алгебра фокусируется на том, как числа работают как группа, и позволяет вам говорить о неизвестных величинах.Ваша основная задача в алгебре — манипулировать выражениями и уравнениями, используя свойства алгебры и обратные операции для упрощения или решения неизвестной величины.
Если вы добавляете или вычитаете какие-либо термины, ваши термины должны быть как термины , которые имеют ту же переменную и возводятся в ту же степень. И если у вас есть одинаковые члены, вы добавляете или вычитаете числа, прикрепленные к переменной, которые называются коэффициентами . Как только вы поймете этот принцип, вы сможете начать делить или умножать алгебраические термины, и вы будете готовы столкнуться с любым уравнением!
Как только вы поймете этот принцип, вы сможете начать делить или умножать алгебраические термины, и вы будете готовы столкнуться с любым уравнением!
Объяснения ответов к ранее выпущенному тесту ACT по математике 2021-22 гг. — Piqosity
Ниже приведены пояснения ответов к полному тесту по математике ранее выпущенного теста ACT 2021–2022 гг. «Подготовка к тесту ACT» (форма 2176CPRE) бесплатное учебное пособие доступно здесь для бесплатной загрузки в формате PDF.
Описанный ниже тест ACT Math начинается на 22-й странице руководства (24 в PDF-файле). Другие объяснения ответов в этой серии статей:
Когда вы закончите изучение этого официального тренировочного теста ACT, начните тренироваться с нашими собственными 10 полноценными тренировочными тестами ACT.
ACT Практический тест по математике Объяснения ответов 2021-2022Вопрос 1 «бумага в банке» ответ E
Этот вопрос проверяет ваше понимание вероятности.
- В банке 15 листов бумаги. Восемь из этих частей меньше 9.
- Вероятность вытягивания нужных фигур равна .
- Таким образом, вероятность равна .
Вопрос 2 «» ответ J
Этот вопрос проверяет ваше понимание работы с алгебраическими выражениями.
- Сначала добавим одинаковые термины () и ()
- В результате мы получаем . Это правильный ответ.
Вопрос 3 «10 + 3(12 ÷ (3x)) » ответ 16
Этот вопрос проверяет ваше понимание упрощения выражения с помощью PEMDAS.
- Первый шаг — подставить x = 2.
- Это упростит уравнение до 10 + 3(12 ÷(3⋅2))
- Упрощая изнутри скобок, мы получили бы 10 + 3 (12 ÷ (6))
- Что будет равно 10+3(2) = 10+6 = 16.
Вопрос 4 «⎪6 − 4⎪ − ⎪3 − 8⎪» ответ G
Этот вопрос проверяет ваше понимание упрощения выражений абсолютного значения.
- Прямые скобы | используются для указания абсолютного значения выражения между двумя скобками.

- Первым шагом будет упрощение двух выражений внутри прямых скобок. Это упростило бы уравнение до |2| – |-5|.
- Следующим шагом является вычисление абсолютного значения каждого члена. Это упростило бы выражение до 2 – 5.
- Наконец, выполнение окончательного вычитания даст ответ -3.
Вопрос 5 «(4c-3d)(3c+d)» ответ C
Этот вопрос проверяет, что мы понимаем свойство распределения.
- Для расчета мы начнем с умножения всех членов во второй скобке на член 4c. Это даст 4c(3c) + 4c(d). Это упростит до +4cd.
- Следующим шагом будет умножение всех членов во второй скобке на член (-3d). Это даст -3d(3c) – 3d(d). Это упростит до .
- Объединяем члены из первого и второго шагов, получаем . Затем, комбинируя подобные термины, мы получаем выражение . Это окончательный ответ.
Вопрос 6 «Оценки учащихся» ответ F
Этот вопрос проверяет ваше понимание применения пропорций в постановке текстовых задач.
- Мы знаем, что в школе 180 учащихся, поэтому, если учащиеся получили пятерку, это будет означать, что 45 учащихся получили пятерку.
- Мы также знаем, что учащиеся получили оценку B, значит, из 180 учащихся 60 получили оценку B.
- Следовательно, мы можем подсчитать количество студентов, получивших оценку C, вычитая из общего числа учащихся, получивших оценку A или B.Это можно рассчитать следующим образом: 180-45-60 = 75, .
- Таким образом, число студентов, получивших оценку C за курс, равно 75.
Вопрос 7 «Шкиперский пруд» ответ B
Этот вопрос проверяет ваше понимание применения пропорций в постановке текстовых задач.
- Нам сказали, что уравнение для представления количества рыбы в пруду имеет вид .
- Следовательно, в 2006 году значение x равно 2006 – 2000 = 6.
- Подстановка этого значения x в уравнение оставит уравнение .Это означает, что на начало 2006 года в пруду было 192 рыбы.

Вопрос 8 «Скорость» ответ H
Этот вопрос проверяет ваше понимание скорости и расстояния.
- Поскольку мы знаем, что Маниш находился в 510 км от Батон-Руж в 8:00 и в 105 км от Батон-Руж в 13:00, мы можем сделать вывод, что Маниш преодолел за это время 510–105 км. Это 405 км.
- Время, затраченное на преодоление 405 км, составляет 5 часов, что является разницей между 13:00 и 13:00.м., и 8:00 утра
- Основываясь на этом, мы могли бы рассчитать скорость, разделив 405 км на 5 часов, что дало бы скорость 81 км в час.
Вопрос 9 «треугольник с параллельными прямыми» ответ D
Этот вопрос проверяет ваше понимание подобных треугольников и параллельных прямых.
- Поскольку мы знаем, что это константа, а что параллельно, мы можем сказать, что ADE похож на ABC.
- Отсюда можно сделать вывод, что отношения сторон подобны.
- В частности, отношение равно отношению .
- Значение составляет упрощение .

- Мы знаем, что = = . Решая для получаем, что = 42.
Вопрос 10 «Катерина» ответ G
Этот вопрос проверяет ваше понимание скорости и того, как она рассчитывается.
- Катерина Среднее время пробега одной мили в минутах можно рассчитать, разделив общее количество минут на общее количество пройденных миль.
- Общее количество минут требует, чтобы мы преобразовали часов в минуты, умножив их на 60.Выполняя этот шаг, мы получаем, что количество пройденных минут составляет 150 минут.
- Общее количество миль равно 15.
- Среднее количество минут на милю можно рассчитать, разделив 150 на 15. Это даст 10 минут на милю.
Вопрос 11 «шарики» ответ B
Этот вопрос проверяет ваше понимание вероятности и алгебраических манипуляций.
- В настоящее время есть 8 красных шариков из 24 шариков.Если мы добавим x новых красных шариков, новое количество красных шариков будет 8 + x, а общее количество шариков будет 24 + x.

- Вероятность вытащить красный шарик равна . Мы знаем, что это равно .
- Приравняв два уравнения друг к другу, мы можем упростить до уравнения 3 (24+x) = 5 (8 + x).
- Находя x, мы получаем 16, то есть количество дополнительных красных шариков, которые нужно добавить в мешок.
Вопрос 12 «средняя точка» ответ G
Этот вопрос проверяет ваше понимание вероятности и алгебраических манипуляций.
- Мы знаем, что середина равна (2,1).
- Из точки C (6,8) проходим 4 единицы влево и 7 единиц вниз, чтобы попасть в среднюю точку.
- Следовательно, чтобы попасть в точку D, нам нужно пройти такое же расстояние от средней точки.
- Таким образом, точка D будет представлена точкой (2-4, 1-7). Это равно (-2,-6).
Вопрос 13 «сверхурочные» ответ D
Этот вопрос проверяет ваше понимание текстовых задач и алгебраических манипуляций.
- Мы знаем, что за первые 40 часов Томас получает 15 долларов.

- После первых 40 часов Томас получает 15 долларов x 1,5 = 22,5 доллара.
- Поскольку Томас проработал 46 часов, его общая заработная плата до вычетов составляет 40 x 15 $ + 6 x 22,5 $ = 600 $ + 135 $ = 735 $.
- Поскольку 117 долларов вычитаются из суммы вычетов, сумма денег, которая остается у Томаса, составляет 735-117 долларов = 618 долларов.
Вопрос 14 «Свежие сладости» ответ J
Этот вопрос проверяет ваше понимание денежных выражений.
- За 2 поездки Жанель купила 3 сумки по 3 доллара за сумку и 4 сумки по 2,80 доллара за сумку.
- Сумма, которую она потратила, составила 9 долларов в понедельник и 11,20 доллара в среду, всего 20,20 доллара.
- Если бы она купила сразу 7 мешков, то заплатила бы 2,60 доллара за мешок, что в сумме составило бы 18,20 доллара.
- Она бы сэкономила 2 доллара.
Вопрос 15 «3% от 4,14 x » ответ A
Этот вопрос проверяет ваше понимание упрощения выражений с процентами.
- 3% от 4,14 х = 0,03 х 4,14 х = 3 х 4,14 х 100 = 12,42 х 100 = 1242.
Вопрос 16 «значение x» ответ K
Этот вопрос проверяет ваше понимание решения алгебраических уравнений.
- Чтобы найти значение x, удовлетворяющее уравнению -3 (4x – 5) = 2 (1 – 5x), мы начнем с распределения значений в обеих скобках.
- В итоге мы получаем уравнение -12x + 15 = 2 – 10x. Комбинируя подобные члены, мы получаем 13 = 2x.
- х = .
Вопрос 17 «прямоугольный треугольник» ответ D
Этот вопрос проверяет ваше понимание синуса угла в треугольнике.
- Sin A = .
- Sin A =
Вопрос 18 « » ответ J
Этот вопрос проверяет ваше понимание упрощающих показателей.
- Начнем с извлечения кубического корня из дроби, чтобы исключить 3 из показателя степени.Делая это, мы получаем термин: .
- Чтобы устранить отрицательный знак в показателе степени, возьмем обратную дробь.
 Мы заканчиваем с термином .
Мы заканчиваем с термином . - Возведя в квадрат числитель и знаменатель, мы получим значение: .
Вопрос 19 «Прогулка Лото» ответ А
Этот вопрос проверяет ваше понимание теоремы Пифагора.
- Суммируя количество ярдов, которые Лото прошел на восток и север отдельно, мы получаем 20 ярдов на восток и 11 ярдов на север.
- Чтобы найти расстояние, которое прошел бы Лото, если бы он мог идти прямо, мы применяем теорему Пифагора, чтобы получить уравнение:
- Находя x, получаем x = 22,83.
- Общая разница в расстоянии, которое Лото сэкономил бы, составляет 20 + 11 – 22,83 = 8,17 ярда, что составляет примерно 8 ярдов.
Вопрос 20 «стандартная оценка» ответ F
Этот вопрос проверяет ваше понимание решения алгебраических уравнений.
- Мы знаем, что z = 2 = .
- Решая x, мы получаем x = 90.
Вопрос 21 «круг» ответ E
Этот вопрос проверяет ваше понимание треугольников в окружении круга.
- Приближаясь к этому, мы можем начать с рассмотрения вариантов ответа и посмотреть, существуют ли они в круге с центром в точке O.
- Треугольник АВО остроугольный. Поскольку это радиус, а также радиус, мы знаем, что A = B. Поскольку мы знаем, что AOB равен 60 градусам, мы можем сделать вывод, что A и B оба равны 60 градусам.
- Следовательно, АОВ также является равносторонним треугольником.
- Поскольку мы знаем, что и оба радиуса окружности, мы можем заключить, что DOC является равнобедренным треугольником. DOC также является прямоугольным треугольником, поскольку угол DOC равен 90 градусам.
- Таким образом, единственный треугольник, который не показан на рисунке, — это разносторонний треугольник.
Вопрос 22 «наклон» ответ G.
Этот вопрос проверяет ваше понимание параллельных линий и уклонов.
- Если линия параллельна x + 5y = 9, мы можем заключить, что они имеют одинаковый наклон.
- Решая уравнение относительно y получаем, y = .
 Итак, наклон есть.
Итак, наклон есть.
Вопрос 23 «y = » ответ E
Этот вопрос проверяет ваше понимание решения уравнений.
- Поскольку мы знаем, что x > 1, мы знаем, что y не может быть отрицательным или равным 0. Следовательно, единственными возможными вариантами ответов являются 0,9 и 1,9
- Заглушка 0.9 для у; мы получаем x = – 9. Поскольку x должен быть больше 1, мы можем сделать вывод, что для y работает только 1,9.
- Подставляя 1.9 вместо y, мы получаем x = 2,111. Поскольку x больше 1, мы можем сделать вывод, что это правильный ответ.
Вопрос 24 «все положительные целые числа» ответ H.
Этот вопрос проверяет ваше понимание простых множителей.
- Чтобы число делилось на 15 и 35, оно должно быть кратно обоим делителям числа.
- 15 имеет простые делители 5 и 3. 35 имеет простые делители 5 и 7.
- Наименьшее общее кратное 5 x 3 x 7. Это 105.
Вопрос 25 «треугольник ABC» ответ D
Этот вопрос проверяет ваше понимание углов.
- Если = , то B = C. Поскольку угол A равен 58 градусам, мы можем вычислить сумму B и C, вычитая 58 из 180.
- 180 – 58 = 122 градуса. Поскольку B равно C, оба угла равны 61 градусу.
Вопрос 26 «Поверхность Земли» ответ G
Этот вопрос проверяет ваше понимание вероятности.
- Чтобы найти вероятность приземления на воду, мы должны найти площадь, покрытую водой, и разделить это значение на общую площадь на поверхности Земли.
- Искомое уравнение должно быть P = . Вынесение на множители и деление числителя и знаменателя на дает уравнение
- Р =
Вопрос 27 «статистические тесты» ответ E
Этот вопрос проверяет ваше понимание среднего значения, медианы и формы ряда чисел.
- До 8-го теста среднее, медиана и мода Джамала были 79, 80 и 80 соответственно.
- После того, как Джамал набрал 90 баллов в 8-м тесте, средний результат Джамала составил 80,13. Его медиана по-прежнему была 80, а его мода по-прежнему была 80.
 Следовательно, единственное значение, которое изменилось, было его средним значением, которое было больше.
Следовательно, единственное значение, которое изменилось, было его средним значением, которое было больше.
Вопрос 28 «сплошная прямоугольная призма» ответ H
Этот вопрос проверяет ваше понимание трехмерных фигур.
- Сплошная прямоугольная призма имеет стороны длиной 5, 6 и 7 единиц.Следовательно, всего 210 кубов.
- Так как черные кубики и белые кубики чередуются одинаково, мы можем сделать вывод, что половина кубиков черные, а половина белые.
- Половина от 210 равна 105.
Вопрос 29 «квадрат ABCD» ответ C
Этот вопрос проверяет вашу способность вычислять площади квадратов и прямоугольников.
- Если одна сторона квадрата ABCD имеет длину 12 метров, то площадь квадрата равна 144 .
- Поскольку мы знаем, что ширина прямоугольника равна 8 метрам, разделив 144 на 8 метров, мы получим длину 18 метров.
Вопрос 30 «средний» ответ H
Этот вопрос проверяет ваше понимание средних значений ряда чисел.
- Мы знаем, что среднее чисел w, x, y и z равно 92,0. Следовательно, сумма w, x, y и z может быть представлена уравнением. ш + х + у + г = 4 х 92 = 368.
- Мы знаем, что z равно 40, поэтому сумма w, x и y равна 368 – 40 = 328.
- Мы также знаем, что 4-е число нового списка равно 48, поэтому сумма чисел нового списка равна выражению w + x + y + 48. Подставим 328 вместо суммы w, x и y дает выражение 328 + 48 = 376,
- Разделив 376 на 4, мы получим среднее значение 94,0.
Вопрос 31 «вектор» ответ B
Этот вопрос проверяет ваше понимание скорости и векторов.
- Поскольку вектор j представляет 1 милю в час на север, -j будет представлять 1 милю в час на юг.
- Скорость Марии составляет 12 миль в час к югу, что соответствует -12j.
Вопрос 32 « очки» ответ К.
Этот вопрос проверяет ваше понимание сложения дробей.
- Для начала добавим объем воды в каждый из стаканов.

- Чтобы равномерно распределить эту воду по 4 стаканам, мы разделим ее на 4. В результате каждый стакан будет полным.
Вопрос 33 «ковровая плитка» ответ D
Этот вопрос проверяет ваше понимание площади поверхности.
- Для начала мы конвертируем длину и ширину пола его гостиной в дюймы. футы = 100 дюймов. Аналогично, 10 футов = 120 дюймов.
- Следовательно, площадь пола гостиной в квадратных дюймах составляет 100 дюймов x 120 дюймов = 12 000
- Каждая ковровая плитка имеет площадь 20 дюймов x 20 дюймов = 400 . Разделив площадь пола гостиной на 400 каждой ковровой плитки, мы получим 30 ковровых плиток, необходимых для покрытия этой площади.
Вопрос 34 «координатная плоскость» ответ F
Этот вопрос проверяет ваше понимание уравнения окружности.
- Окружность с центром в () и радиусом r должна быть нанесена на карту уравнением .
- Подставив соответствующие () = (8,5) и r = 9 в уравнение, мы получим ответ .

Вопрос 35 «общая стоимость» ответ E
Этот вопрос проверяет ваше понимание применения алгебры к текстовым задачам.
- Поскольку каждый тест Yq стоит 2500 долларов, а было проведено 1000 тестов, стоимость теста Yq составила 2 500 000 долларов.
- Аналогичным образом, каждый тест Sam77 стоит 50 груш, и было проведено 1000 тестов, общая стоимость теста Sam77 составила 50 000 долларов.
- Сложение этих двух чисел дает общую стоимость 2 550 000 долларов США.
Вопрос 36 «процент добровольцев» ответ J
Этот вопрос проверяет ваше понимание процентов.
- Число людей, являющихся носителями гена Yq77, можно рассчитать, сложив всех людей, у которых был положительный тест на Yq.Это равно 590 + 25 = 615.
- Так как всего было протестировано 1000 человек, или 61,5% носителей гена Yq77.
Вопрос 37 «сколько добровольцев» ответ C
Этот вопрос проверяет ваше понимание таблиц.
- Чтобы подсчитать, сколько добровольцев дали неправильный результат теста Sam77, мы должны сложить людей, у которых был отрицательный результат теста Sam77, но положительный тест Yq, и людей, у которых был положительный тест Sam77, но отрицательный тест Yq.
- Эти два числа равны 25 и 10 соответственно, поэтому общее количество добровольцев, получивших неправильный результат теста Sam77, равно 25 + 10 = 35.
Вопрос 38 «НЕ обладает Yq77» ответ F
Этот вопрос проверяет ваше понимание вероятности.
- Количество добровольцев с положительным результатом теста Sam77 составило 590 + 10 = 600.
- Из этих добровольцев только у 10 не было гена Yq77.
- Следовательно, вероятность .
Вопрос 39 «матрицы» ответ B
Этот вопрос проверяет ваше понимание матричных манипуляций.
- Чтобы вычислить произведение X и Y, мы должны перемножить матрицы.
- Это можно сделать следующим образом .

Вопрос 40 «симметрия» ответ F
Этот вопрос проверяет ваше понимание линий симметрии.
- Разносторонний треугольник — это треугольник, у которого все три стороны имеют разную длину.Это не будет иметь вертикальной линии симметрии.
- Линия будет иметь вертикальную линию симметрии. Квадрат будет иметь вертикальную линию симметрии. Пятиугольник будет иметь вертикальную линию симметрии. Параллелограмм будет иметь вертикальную линию симметрии.
Вопрос 41 «» ответ A.
Этот вопрос проверяет ваше понимание решения квадратного уравнения.
- Чтобы решить это уравнение, мы можем начать с вычитания 15 из обеих частей.Получаем уравнение.
- Мы можем факторизовать это, чтобы получить (6x+5)(4x-3) = 0. Полагая 6x+5 = 0 и 4x -3 = 0, мы получаем два решения для этого уравнения как и .
- Большее из этих двух решений равно .
Вопрос 42 «» ответ J
Этот вопрос проверяет ваше понимание синуса и косинуса обычных углов.
- Чтобы решить эту проблему, мы должны знать, что . Следовательно, мы можем использовать это, чтобы заменить на .
- Точно так же мы можем заменить из второго члена на .
- Следовательно, исходное уравнение упрощается до = 1.
- Из вариантов ответа единственным, значение которого = 1, является .
Вопрос 43 «площадь круга» ответ D
Этот вопрос проверяет ваше понимание длины окружности и площади круга.
- Мы знаем, что длина окружности = . Решая относительно r, получаем r = 6, .
- Площадь круга . Подставляя r = 6, мы получаем площадь как .
Вопрос 44 «смесь растворителей» ответ G.
Этот вопрос проверяет ваше понимание процентов и смесей.
- Мы знаем, что из 25 литров 40% растворителя и 60% воды. Отсюда можно сделать вывод, что 0,40 х 25 литров растворителя = 10 литров.
- Таким образом, если добавить x литров растворителя, количество растворителя будет равно 10 + x.
 Кроме того, новая смесь будет иметь объем 25 + х.
Кроме того, новая смесь будет иметь объем 25 + х. - Таким образом, процент растворителя в новой смеси будет равен .
- Так как мы знаем, что это 50% или 0.50 мы можем положить эти два значения равными друг другу и найти x.
- Упрощая, получаем 10 + x = (25 + x )(0,5). Дальнейшее упрощение показывает нам, что 0,5x = 2,5, поэтому x = 5, .
Вопрос 45 «» ответ E
Этот вопрос проверяет ваше понимание упрощения выражений с помощью дробей.
- Чтобы упростить это уравнение, мы находим общее кратное двух знаменателей, которое будет .
- Следовательно, нам пришлось бы умножать числитель первого члена на (x-y), а числитель второго члена на (x+y).
- Новое выражение после объединения двух терминов будет .
- Разлагая на множители числитель и знаменатель, получаем .
Вопрос 46 «Реклама на странице» ответ F.
Этот вопрос проверяет ваше понимание решения текстовых задач по алгебре.
- Если Карлос продал c рекламных объявлений, Мэри продала 2c рекламных объявлений, а Джеймс продал 6c рекламных объявлений.
- Всего было продано c + 2c + 6c = 9c рекламных объявлений.
- Следовательно, Карлос продал все объявления.
Вопрос 47 «цветочный магазин» ответ D
Этот вопрос проверяет ваше понимание перестановок.
- Для первого места у Эмили есть 6 растений на выбор.
- После посадки первого растения у Эмили остается только 5 растений на выбор для второго места.
- Наконец, после посадки первых двух растений у Эмили остается только 4 растения на выбор для третьего места.
- Умножая эти варианты, мы получаем 6 х 5 х 4 = 120 различных вариантов расположения растений.
Вопрос 48 «квадратичная функция f » ответ G
Этот вопрос проверяет ваше понимание площади треугольника.
- Для вычисления площади начнем с использования формулы площади треугольника = .

- Исходя из этого, основанием треугольника является расстояние между точкой М и точкой Р, равное 6а-2а = 4а.
- Высота треугольника — это расстояние от точки Q до отрезка MP, равное 5b.
- Следовательно, площадь равна .
Вопрос 49 «Точка М» ответ D
Этот вопрос проверяет ваше понимание наклона линии на координатной плоскости.
- Наклон может быть представлен уравнением .
- Мы знаем, что числитель отрицательный, потому что точка Q имеет меньшее значение y, чем точка M.
- По мере перемещения точки Q вправо разница увеличивается.
- Следовательно, наклон будет отрицательным, но будет увеличиваться по мере увеличения значения Q.
Вопрос 50 «f(5a)» ответ K
Этот вопрос проверяет ваше понимание функции, построенной на координатной плоскости.
- Чтобы найти значение f(5a) , мы смотрим на квадратичную функцию и находим, где она пересекает линию x = 5 a.

- Глядя на кривую, мы видим, что это происходит на 8b, что является правильным ответом.
Вопрос 51 «Присяжные заседатели» ответ D
Этот вопрос проверяет ваше понимание дробей и десятичных знаков.
- Мы знаем, что если мы пригласим x человек, то появится только 0,4x людей.
- Из них одна треть освобождена, так что две трети остаются. В частности, из первоначально приглашенных x человек остаются.
- Мы знаем, что это выражение должно равняться 60 человекам для состава жюри. Отсюда получаем уравнение.
- Находя x, получаем x = 225 человек, которых нужно призвать.
Вопрос 52 «275-я цифра» ответ К
Этот вопрос проверяет ваше понимание повторяющихся цифр в десятичных дробях.
- Поскольку мы знаем, что десятичное число 0,6295 повторяется каждые 4 цифры, мы должны разделить 275 на 4.
- Разделив 275 на 4, мы получим 68 с остатком 3.
- Это будет означать, что 272-я цифра будет 5.
 Тогда следующие три цифры будут 6, 2 и 9 в этом порядке.
Тогда следующие три цифры будут 6, 2 и 9 в этом порядке. - Исходя из этого, 275-я цифра будет 9.
Вопрос 53 « » ответ A
Этот вопрос проверяет ваше понимание факторизации квадратичной функции.
- Поскольку мы знаем, что , мы знаем, что решение f(x) можно найти, вынеся f(x). f (х) = (х + 2) (х-2).
- Следовательно, два решения для f(x) равны x = 2 и x = -2.
- Поскольку мы знаем, что эти два решения x делают f(x) равным 0, мы можем приравнять g(x) к этим значениям.
- Таким образом, мы получаем два уравнения для g(x). х +3 = 2 и х + 3 = -2.
- Решив оба уравнения относительно x, мы получим x = -1 и -5.
Вопрос 54 “p и n” ответ G
Этот вопрос проверяет ваше понимание целых чисел и абсолютных значений.
- Поскольку мы знаем, что p — положительное число, n — отрицательное число и |p| > |n|, мы можем присвоить значения как p, так и n, которые удовлетворяют этим условиям.

- В частности, мы можем назначить p = 5 и n = -3. Тогда мы сможем решить все уравнения;
- ;
- ;
- Из этих вариантов ответа наибольшее выражение
Вопрос 55 « » ответ B
Этот вопрос проверяет ваше понимание мнимых чисел и вычислений с использованием i .
- Начиная с , , затем , и .
- Подставив эти значения в уравнение, мы получим
- . Упрощая это уравнение, мы имеем, что равно -1.
Вопрос 56 «координатная плоскость» ответ К
Этот вопрос проверяет ваше понимание наклонов и линий на координатной плоскости.
- Первое уравнение имеет вид x + 2y ≤ 6. Преобразовав это уравнение для решения для y, мы получим y ≤ -0,5x + 3. Это будет означать, что наклон линии отрицателен, а заштрихованная область должна быть ниже этой линии.
- Из всех вариантов ответа только F и K имеют линию с отрицательным наклоном и заштрихованную область под линией.

- Второе уравнение . Преобразовав это уравнение и разделив на 3, мы получим уравнение .
- Чтобы выбрать между F и K, мы можем найти два отрезка окружности по оси y, и если они лежат под прямой y ≤ -0,5x + 3, мы знаем, что ответ равен K.
- Две точки пересечения y окружности можно вычислить, установив x = 0 в уравнении окружности.
- В итоге мы получаем уравнение , поэтому y = 2 или y = -2 .
- Подставляя положительное пересечение оси y (x,y) = (0,2) в уравнение прямой, мы получаем 2 ≤ -0,5(0) + 3. Упрощая, получаем 2 ≤ 3, что равно верно, поэтому правильный ответ К.
Вопрос 57 «действительные числа» ответ D
Этот вопрос проверяет ваше понимание вашего понимания умножения и деления на 0.
- Поскольку , мы можем заключить, что d = 0.
- Поскольку abc = d, мы знаем, что abc = 0.
- Поскольку ac = 1, мы знаем, что b(1) = 0. Итак, b = 0.
Вопрос 58 « функция косинуса» ответ K
Этот вопрос проверяет ваше понимание функции и функций косинуса.
- Мы знаем, что точка пересечения по оси y равна 3, поэтому это означает, что если x = 0, y должно быть равно 3. Поскольку cos(0) = 1, мы знаем, что константа, умножающая косинус, должна быть равна 3.
- Мы также знаем, что , основаны на графике.Подставляя все значения x, мы получаем y = 3 cos(2x) в качестве решения, которое дает y равное -3.
Вопрос 59 «летающий змей» ответ B
Этот вопрос проверяет ваше понимание треугольников, их сторон и углов.
- В показанном треугольнике недостающий угол равен 60 градусам.
- Тогда мы могли бы составить такое уравнение, что . Решив это для длины строки, мы получим = длина строки.Подставляя значения и , мы можем упростить до .
Вопрос 60 “издатель” ответ F
Этот вопрос проверяет ваше понимание использования алгебры для решения текстовых задач.
- Мы знаем, что издатель берет 15 долларов за первую книгу и 12 долларов за каждую дополнительную копию.

- Если заказано y книг, издатель взимает 15 долларов за первую книгу и 12 долларов за y-1 книг.
- Уравнение стоимости книг принимает вид $15 + $12(y-1).Упрощая это, мы получаем стоимость = 15-12 + 12y = 12y + 3.
Алгебраическое мышление – Элементарная математика
Развитие алгебраических идей и языка
Фокусы с числами — развлечение для детей. Веселье само по себе ценно, но это не математика. Но понимание того, как работает этот трюк, — это хорошее математическое, часто алгебраическое обучение. А понимание трюка достаточно хорошо позволяет детям придумывать свои собственные трюки.
Трюки «Угадай число»
Эти трюки бывают двух типов:
- Задумайте число (но не говорите мне), произведите некоторые арифметические действия с этим числом, и я смогу предсказать ваш результат.
- Задумайте число, выполните некоторые арифметические действия, сообщите мне ваш результат, и я сразу же скажу, с какого числа вы начали.

Четвероклассники обожают эти фокусы! Большинство из них (и даже некоторые младшие дети) также готовы понять, как они работают, и даже научиться придумывать свои собственные трюки! Без нотной записи средней школы то, что они изучают, является началом алгебры!
Трюк
Пример предсказания ответа:
- Задумайте число.
- Добавить 3.
- В два раза больше.
- Вычесть 4.
- Разрежьте его пополам.
- Вычтите исходное число.
- Ваш результат 1!
Как это работает
Я говорю Задумайте число. Я не знаю, о каком числе вы думаете, поэтому я просто представляю мешок с таким количеством шариков или конфет.
Мешок закрыт и завязан, поэтому я не могу заглянуть внутрь, но это не имеет значения. Ваш номер там.
Я знаю, что если я попрошу вас добавить 3, я могу представить эту сумку и еще троих так:
Когда я говорю вам удвоить это, я удваиваю количество на моей картинке следующим образом:
Затем, когда я говорю вычесть 4, я мысленно стираю 4 лишнего:
Судя по самой картинке, я могу быть уверен, что вы можете сократить это пополам , и я представляю это:
Последняя инструкция, вычтите исходное число , избавьтесь от мешка!
Вот почему я могу предсказать ваш результат, не зная, какое число вы придумали. Ваш ответ должен быть 1.
Ваш ответ должен быть 1.
Мы можем обобщить это в таблице.
Изобретение собственных трюков
Вы можете придумывать трюки самостоятельно, если ваши правила[1] позволяют:
- рисовать картинки,
- используйте целые мешки и целые шарики (нечестно резать мешки пополам!), а
- вычесть только видимые шарики. (Нечестно вынимать шарики из мешка. Мешок мог быть пуст!)
Дрю, 9 лет, постоянно просил новых трюков, а затем начал придумывать свои собственные. Вот два для практики. Нарисуйте картинки сами, чтобы понять, какой «волшебник» должен предсказать результат. Тогда придумывайте свои собственные трюки.
| Трюк 1: слова для каждого шага——— | Уловка 1: Картинки |
|---|---|
| Задумайте число. | |
| Удвойте. | |
| Добавить 10 | |
| Разделить на 2. | |
Вычтите исходное число. | |
| Утроить результат. | |
| Ага! | Ваш результат… |
| Трюк 2: слова для каждого шага——— | Уловка 2: Картинки |
|---|---|
| Задумайте число. | |
| Добавьте два. | |
| Умножить на 3. | |
| Добавить 2. | |
| Вычтите исходное число. | |
| Разделить на 2. | |
| Вычтите исходное число еще раз. | |
| Ага! | Ваш результат… |
Изобретения Дрю
Вот три трюка, которые изобрел Дрю. Нарисуй картинки, чтобы понять, как он может легко вычислить твой стартовый номер!
| Трюк Дрю: слова для каждого шага——— | Уловка 1: Картинки |
|---|---|
| Задумайте число. | |
Добавить 20. | |
| В четыре раза больше! | |
| Разделить на 2. | |
| Вычтите исходное число. | |
| Скажи мне свой результат… | |
| Ага! | Вы начали с… |
| Второй трюк Дрю: слова для каждого шага——— | Уловка 2: Картинки |
|---|---|
| Задумайте число. | |
| Добавить 2. | |
| В два раза больше! | |
| Вычесть 4. | |
| Вычтите исходное число. | |
| Ага! | Ваш ответ – это ваш исходный номер! |
| Третий трюк Дрю: слова для каждого шага——— | Уловка 3: Картинки |
|---|---|
| Задумайте число. | |
| Добавить 5. | |
| В два раза больше! | |
Вычтите исходное число. | |
| Вычесть 1. | |
| Вычтите исходное число. | |
| Ага! | Ваш ответ 9! |
- Безусловно, трюки можно придумывать и без ограничений, указанных здесь, но они не подходят для большинства учащихся начальной школы. Алгебра не сложнее, но картинки и арифметика могут быть сложнее.
Двузначное умножение в уме
Трюк
Вы можете научиться умножать определенные пары чисел, такие как 87×93, 52×48, 65×65 или 34×36, мгновенно в уме.
Как это работает
Щелкните здесь, чтобы узнать, как выполнить этот трюк, и понять, как он работает.
GED Math Practice Test (обновлено в 2022 г.)
GED расшифровывается как General Education Development или General Education Diploma. GED является дополнительным вариантом для лиц, которые не закончили среднюю школу и не получили аттестат о среднем образовании.GED, признаваемый во всех 50 штатах, служит документом, эквивалентным средней школе. Имея это удостоверение, выпускники могут подавать заявки на поступление в колледжи и на должности начального уровня. Математический раздел этой оценки проверяет способность учащихся решать алгебраические и количественные задачи.
Имея это удостоверение, выпускники могут подавать заявки на поступление в колледжи и на должности начального уровня. Математический раздел этой оценки проверяет способность учащихся решать алгебраические и количественные задачи.
Кто имеет право сдавать тест GED по математике?
Вы имеете право сдавать тест GED по математике, если соответствуете следующим требованиям:
- Вам не менее 16 лет
- Вы не учитесь в средней школе
- Вы не закончили среднюю школу
- Вы соответствуете все дополнительные требования вашего штата (напр.время, прошедшее после окончания школы)
Сколько стоит тест GED по математике?
В большинстве штатов тест GED по математике стоит 30 долларов или меньше. Студентам рекомендуется посетить веб-сайт GED, чтобы узнать цены своего штата.
Какой тип математики входит в тест GED?
Раздел математического мышления теста GED состоит из двух типов задач: решение количественных задач и решение алгебраических задач. Некоторые из множества темы включают в себя:
Некоторые из множества темы включают в себя:
- Среднее и средняя площадь
- площадь поверхности
- наклон линии
- по периметру
- по периметру
- окружность
- простой интерес
- Pythagorean Theorem
- квадратичная формула
- Общая стоимость
Как долго это тест GED по математике?
Математический тест GED длится 115 минут (1 час и 55 минут).
Можно ли использовать калькулятор на экзамене GED по математике?
Тест GED по математике состоит из двух разделов. В первом разделе, состоящем из 5 вопросов, нельзя пользоваться калькулятором. Для второго раздела, который включает 41 вопрос, вы можете использовать калькулятор. Обратите внимание, что вы должны принести свой собственный калькулятор TI-30XS.
Сколько вопросов вы можете пропустить в тесте GED по математике?
Система оценки GED сложна, поэтому один вопрос не всегда равен одному баллу.Некоторые вопросы заполняются пустым полем или множественным выбором, где вы должны выбрать несколько ответов, что означает несколько баллов. Математическая секция GED состоит из 46 вопросов и имеет проходной балл 145–164. Нет точного количества вопросов, которые вы можете пропустить и все равно пройти, но, согласно Службе тестирования GED, вам нужно примерно 60%-65% ваших баллов, чтобы пройти.
Математическая секция GED состоит из 46 вопросов и имеет проходной балл 145–164. Нет точного количества вопросов, которые вы можете пропустить и все равно пройти, но, согласно Службе тестирования GED, вам нужно примерно 60%-65% ваших баллов, чтобы пройти.
Сколько раз можно пересдавать тест GED по математике?
Количество повторных сдач GED Math Test не ограничено.Как правило, вы можете сдать GED 3 раза, а после 3-й попытки вам придется подождать 60 дней. Аналогичные правила применяются к учащимся, сдающим тест на разных языках. Например, если студент сдает тест 3 раза на испанском языке, после 3-й попытки есть 60-дневный период ожидания, чтобы сдать его на английском языке. В некоторых штатах действуют индивидуальные правила пересдачи. Например, в округе Колумбия (округ Колумбия) после первой попытки есть 30-дневный период ожидания, прежде чем вы сможете пересдать тест. Студентам рекомендуется ознакомиться с политикой повторного тестирования своего штата.
Что нужно набрать, чтобы пройти тест GED по математике?
Чтобы пройти тест GED по математике, вы должны набрать не менее 145 баллов. Самый высокий балл — 164, а все, что ниже 145, считается проваленным.
Самый высокий балл — 164, а все, что ниже 145, считается проваленным.
Сколько вопросов в тесте GED по математике?
Математический тест GED состоит из 46 вопросов. Некоторые из многих типов вопросов включают множественный выбор, перетаскивание, горячую точку и заполнение пробела.
GED Math Practice Test
Чего ожидать в день экзамена
Правила и процедуры дня экзамена различаются в зависимости от центра тестирования.Ниже вы найдете несколько общих советов, которые помогут вам в день экзамена.
- Прибудьте на место тестирования как минимум на 15 минут раньше. В некоторых местах тестирования вам не разрешат пройти тест, если вы опоздаете более чем на 15 минут.
- Принесите удостоверение личности с фотографией, срок действия которого не истек, например, водительские права, удостоверение личности государственного образца, военный билет или паспорт.
- Вы сможете сделать перерыв, если запланировали более одного предмета на один и тот же день.

- Вы не сможете ни есть, ни пить в зоне тестирования.
- Сотовые телефоны и другая электроника не допускаются в зону тестирования.
- Вы должны принести свой собственный калькулятор TI-30XS.
- Вы получите справочный лист и лист математических формул
- Любые дополнительные предметы, такие как рюкзаки и сумки, помещаются на хранение, если они доступны.
Онлайн-курс подготовки к GED Test
Если вы хотите полностью подготовиться, Mometrix предлагает онлайн-курс подготовки к GED. Курс предназначен для предоставления вам любых ресурсов, которые могут вам понадобиться во время обучения.Курс ГЭД включает в себя:
- 118 Уроки, охватывающие все темы
- Более 1000 GED Практические вопросы
- 300+ видеоуправления
- более 400 электронных карточек
- гарантия возврата денег
- Easy Mobile Access
- и многое другое!
Подготовительный курс GED предназначен для того, чтобы помочь любому учащемуся получить все необходимое для подготовки к экзамену GED; нажмите ниже, чтобы проверить это.
Как подготовиться к экзамену GED по математике
Нервничаете ли вы от мысли о сдаче теста GED по математике? Не волнуйтесь – вы находитесь в правильном месте! Наши эксперты по тестированию тщательно изучили GED, чтобы создать учебное пособие Mometrix GED.Это подробное учебное пособие охватывает не только основные темы теста GED по математике, такие как переменные и построение линейных графиков, но также включает практические вопросы теста. С нашими простыми для чтения объяснениями вы обязательно справитесь с практическим тестом, а также с официальным! Учебное пособие Mometrix GED Study Guide охватывает все четыре раздела (социальные науки, естественные науки, рассуждения с помощью языковых искусств и математические рассуждения) теста GED.
Повторение — одна из наиболее проверенных стратегий обучения, поэтому наши эксперты также разработали флэш-карты GED Mometrix.Флэш-карты Mometrix GED делают процесс обучения увлекательным и эффективным. Они идеально подходят для проведения опросов и изучения на ходу! Эти универсальные карточки охватывают все основные темы всех четырех разделов теста GED. Вы также можете рассчитывать на изучение эффективных стратегий сдачи теста, которые будут иметь большое значение в день экзамена!
Вы также можете рассчитывать на изучение эффективных стратегий сдачи теста, которые будут иметь большое значение в день экзамена!
Поздравляем вас с первыми шагами к получению диплома GED. Мы с нетерпением ждем возможности помочь вам пройти тест!
Усовершенствуйте свое обучение с помощью нашего учебного пособия и карточек GED:
Учебное пособие GED
Карточки GED
Онлайн-курс GED Тест GED — домашняя страница
Раскрытие информации о партнерах: Как партнер Amazon, мы можем получать комиссионные за соответствующие покупки на Amazon.ком.
У ребенка проблемы с математикой? 12 признаков и 7 способов помочь
У многих родителей во всем мире, как и у вас, есть ребенок , которому трудно с математикой . Без надлежащих ресурсов или надежной системы поддержки эта реальность может быть пугающей.
Но не волнуйтесь, вы не одиноки! Дети, которые не любят математику, чаще всего жалуются на то, что она слишком сложная или что они недостаточно умны. К сожалению, это убеждение может серьезно повлиять на успехи любого ребенка в математике.
К сожалению, это убеждение может серьезно повлиять на успехи любого ребенка в математике.
Родители часто отмечают, что причины и симптомы могут различаться у разных детей, поэтому мы опишем и поможем вам понять:
- Что вызывает трудности у детей с математикой
- Общие признаки у детей, у которых проблемы с математикой
- Как родители и учителя могут помочь ребенку, у которого проблемы с математикой
Давайте начнем помогать вашему ребенку добиться успеха, а не бороться с математикой. 👇
3 Основные причины проблем с математикой у ребенка
Математика может быть трудной, потому что это кумулятивный предмет — он год за годом строит сам себя.Вот почему так много родителей беспокоятся, когда их дети, кажется, отстраняются от математики или отстраняются от нее.
Родителям важно знать, что это не обязательно означает, что их ребенку не хватает интеллекта или целеустремленности. Хотите верьте, хотите нет, но дети, у которых проблемы с пониманием математики, часто прилагают огромные усилия — умственные и физические.
Итак, что именно заставляет ребенка бороться с математикой? Исследования сузили ответ до трех вещей:
Отсутствие строительных блоков
Как упоминалось ранее, математика накапливается, поэтому изучение и понимание основ является обязательным.Если ребенок отстает в одной области из-за непонимания, переход к более сложным темам останется проблемой.
Например, если ребенок еще не усвоил основы сложения, ему будет очень трудно понять принцип умножения.
В 2015 году Университет Акрона опубликовал исследование под названием «Важность сильной математической основы». Исследователи протестировали 39 девяти- и десятиклассников на дроби, соотношения и пропорции.Участники должны были ответить на вопросы от третьего до седьмого класса.
Оценку смогли пройти только семь участников. Увидев эти результаты, автор исследования Жасмин Ристон написала:
[Учащихся] просто обучали математическим понятиям, соответствующим их текущему уровню обучения, а не основанным на текущих математических знаниях, которые они принесли в класс.Из-за этого учащиеся не осваивали каждый стандарт уровня класса, прежде чем перейти к обучению более высокого уровня.Это отсутствие мастерства создает огромные пробелы в понимании учащимися, мешая учащимся устанавливать необходимые содержательные связи и получать концептуальное понимание.
Беспокойство по математике
Посреди трудностей легко почувствовать, что мы единственные, кто сталкивается с определенной проблемой. Для родителей ребенка, борющегося с математикой, это ничем не отличается. И хотя нас это тревожит, мы надеемся, что родители во всем мире найдут утешение в том, что их ребенок не единственный, кто может испытывать беспокойство, когда дело доходит до математики.
Чувство напряжения и беспокойства, которое мешает работе с числами и решению математических задач в самых разных жизненных и академических ситуациях.
На самом деле, в нашем руководстве по преодолению математической тревожности подчеркивается, что около 93% из взрослых американцев испытывают математическую тревожность в той или иной степени, в то время как 17% американцев в целом страдают от высокого уровня математической тревожности.
Симптомы математики могут включать в себя:
- Убежание
- Отсутствие ответа
- Низкий ответ
- Низкое достижение
- Отрицательный самообслуживание
- Чувство постоянства
- Интенсивные эмоциональные реакции
- Физиологические эффекты, такие как нервозность, клейкие руки, увеличение сердца скорость, расстройство желудка и головокружение
И по этой причине дети могут испытывать трудности с математикой с детства и во взрослую жизнь.
Трудности в обучении
Существует множество нарушений обучаемости математике, в том числе одна из наиболее распространенных: дискалькулия . Другие названия для него включают математика или цифровая дислексия .
Согласно д-ру Даниэлю Ансари, профессору развивающей когнитивной неврологии Западного университета Канады, дети с дискалькулией:
- Часто испытывают трудности с рабочей памятью
- Имеют проблемы с запоминанием математических фактов
- Могут понимать логику математических фактов, но не знает, как и когда применять свои знания для решения задач
- Может не понимать величин или понятий, таких как наибольшее и наименьшее, или разницу между словом пять и числительным 5
Исследователи не совсем уверены, что вызывает дискалькулию но подозреваю, что это связано со структурой и функциями мозга. Поскольку могут быть задействованы различные факторы, такие как развитие, окружающая среда, генетический состав или травма, то, как проявляются симптомы, вероятно, будет различаться, поскольку нет двух одинаковых детей.
Поскольку могут быть задействованы различные факторы, такие как развитие, окружающая среда, генетический состав или травма, то, как проявляются симптомы, вероятно, будет различаться, поскольку нет двух одинаковых детей.
12 Признаки того, что у детей проблемы с математикой
1. Отрицательно отзывается о математике
Заметить, что у ребенка проблемы с математикой, бывает непросто. Один из наиболее заметных признаков заключается в том, что они говорят о предмете.
Когда ваш ребенок говорит что-то вроде «Я ненавижу математику» или «У меня плохо с математикой» и пытается избегать занятий, связанных с математикой, обычно это признак того, что у него проблемы с предметом.
2. Волнуется по поводу математики
Будь то урок, контрольная работа или выполнение домашнего задания, ваш ребенок становится все более беспокойным, когда приходит время заниматься математикой.
Несмотря на то, что они могут понимать концепции, математическая тревога приводит к тому, что они забывают, что они узнали, или как их применять, когда придет время.
3. Более низкие оценки по математике, но более высокие по другим предметам
Слышите ли вы это от учителя или видите в его табеле успеваемости, ваш ребенок хорошо успевает по всем предметам, кроме математики.
Более низкие оценки по математике могут заставить их сосредоточиться на предметах, в которых они уже преуспевают, и тратить мало времени на практику или изучение математики.
4. Проблемы с соединением математических семей
По мере того, как учащиеся узнают больше математических фактов, они должны начать видеть взаимосвязь между определенными числами и уравнениями.
У вашего ребенка могут быть проблемы с математикой, если он не видит связи, например, между 2+3=5 и 5-3=2 .
5. Трудности с управлением временем
Многим людям, в том числе взрослым, трудно управлять временем, поэтому этот признак может показаться несколько расплывчатым. Обратите внимание, есть ли у вашего ребенка проблемы с оценкой времени, соблюдением установленного расписания или чтением часов — аналоговых или цифровых.
6. Проблемы с применением математических понятий к реальным задачам
Ваш ребенок может понимать математические понятия, но с трудом понимает, как они применимы к вещам за пределами класса. Например:
- Выяснение того, сколько дней осталось до дня рождения
- Вычисление стоимости чего-либо и того, сколько сдачи они должны вернуть
- Определение количества определенного ингредиента, которое нужно использовать, помогая вам готовить еду
7 .Умственные математические трудности
Хотя это может быть полезно в раннем возрасте, решение математических задач с помощью пальцев для счета может быть признаком того, что у вашего ребенка проблемы с математикой.
Это связано с тем, что по мере взросления дети будут сталкиваться с большими числами и более сложными уравнениями, требующими умственной арифметики — чего-то, что может препятствовать счету на пальцах.
8. Не пытается найти альтернативные подходы к решению задач
В тот момент, когда возникает препятствие при решении математической задачи, ваш ребенок может разочароваться и двигаться дальше, прежде чем подумать или попробовать другое потенциальное решение.
9. Проблемы с базовыми математическими понятиями и запоминанием фактов
Память может оказать значительное влияние на мышление с помощью чисел. Несмотря на то, что в прошлом его учили фундаментальным математическим понятиям и фактам, ваш ребенок с трудом запоминает и правильно их применяет.
10. Проблемы с усвоением сложных математических понятий и фактов
Из-за кумулятивного характера математики ключевым моментом является установление связи между предыдущими и новыми уроками.
Если у ребенка возникнут трудности с опорой на более ранние математические понятия, это ограничит способность ребенка закреплять новые математические навыки осмысленным и долгосрочным образом.
11. Трудности с концентрацией внимания
Каждый ребенок учится по-своему — некоторые могут сесть за парту и выполнять определенные задания, в то время как другие выигрывают от более активной практической работы.
Если ваш ребенок нервничает, теряет место в задаче или кажется умственно уставшим при выполнении математических действий, возможно, у него возникают проблемы с математикой (особый способ выполнения).
12. Недостижение контрольных точек
Как правило, дети достигают определенных математических целей примерно в одном возрасте, но иногда у них возникают проблемы с развитием этих навыков с одинаковой скоростью, и они отстают.
Учащиеся 1-го и 2-го классов, например, могут с трудом переходить от счета единицами к двойкам, пятеркам и десяткам, в то время как другие учатся с легкостью.
Ознакомьтесь с инфографикой ниже, в которой описаны этапы математики и то, что вы можете ожидать в разном возрасте!
Нажмите, чтобы развернутьКак помочь ребенку, у которого проблемы с математикой (7 способов)
Одной из ваших главных целей как родителя является помочь вашему ребенку добиться успеха. Однако важно помнить, что первым шагом к решению проблемы является ее идентификация.
Знакомство с указанными выше признаками поможет вам выявить проблемы, с которыми ваш ребенок может столкнуться в математике.
И чтобы сделать еще один шаг вперед, мы выделили семь советов, которые вы можете использовать дома, чтобы превратить математику в предмет, который ваш ребенок любит, а не боится!
Превратите математику в развлечение
Некоторым детям достаточно изменить точку зрения, чтобы превратить математику из чего-то, чего они боятся, в то, что они любят. Традиционный подход с ручкой и бумагой не всегда работает, и именно тогда вам нужно проявить творческий подход.
Традиционный подход с ручкой и бумагой не всегда работает, и именно тогда вам нужно проявить творческий подход.
Совет: Подумайте о том, чтобы заново познакомить вашего ребенка с математикой через призму игры. Это может принимать различные формы, такие как текстовые задачи, математические книги, математические приложения и многое другое.
Или попробуйте Prodigy Math Game — увлекательное математическое приложение, адаптированное к учебной программе, которым пользуются более 100 миллионов учащихся и учителей. Весь внутриигровой образовательный контент бесплатен и доступен дома или в классе.
🌟 Кроме того, доступны планы Премиум-членство , которые помогут максимально эффективно использовать математику и помогут вам с легкостью поддержать учебный процесс вашего ребенка.Став участником, вы откроете дополнительные внутриигровые награды для вашего ребенка , а даст вам доступ к новым родительским функциям, таким как цели и награды, области практики и листы практики.
Поиск ежедневных приложений
Математика окружает нас повсюду и присутствует в нашей повседневной жизни, но знают ли об этом ваши дети? Включение математики в свою повседневную жизнь может помочь им понять и оценить ее актуальность.
Так чего же ты ждешь? Начните учиться, делая!
Совет: Вовлекайте своего ребенка в такие занятия, как походы по магазинам, приготовление пищи или работа в саду! Каждое из этих реальных приложений включает в себя числа, факты и концепции, которые могут помочь укрепить знания и понимание, а также удовольствие от математики.
Занимайтесь с ребенком ежедневно
На первый взгляд этот совет может показаться таким же простым, как сидеть рядом с ребенком, пока он делает домашнее задание, и следить за его выполнением. Но участие в образовании вашего ребенка имеет много преимуществ.
По словам автора и психолога по развитию Ребекки Фрейзер-Тилл, участие родителей способствует успеваемости, улучшает социальные навыки и может повысить самооценку.
Совет: Выделяйте время для занятий математикой хотя бы 10 минут каждый вечер.Это поможет закрепить то, что они изучают в классе, и держать в поле зрения основные концепции, когда учителя знакомят их с более сложными концепциями в классе. Даже если у вашего ребенка нет домашнего задания по математике, попробуйте наши бесплатные, красочные рабочие листы, которые можно распечатать:
Определение проблемных областей
Если вы можете определить их самостоятельно, замечательно! Если нет, свяжитесь с учителем вашего ребенка, чтобы получить более подробное и точное представление о том, как вы можете помочь повысить способность вашего ребенка к успеху.
Совет: Работая с учителем вашего ребенка, разработайте план действий дома. Это также отличная возможность поделиться способами обучения, которые лучше всего подходят для вашего ребенка дома — то, о чем их учитель может не знать.
Примите положительное отношение
Хотя у детей может быть негативное отношение к математике, ваше отношение к предмету может сначала измениться. Исследование, проведенное в 2017 году в рамках School Science and Mathematics , показало, что отношение родителей к математике может значительно предсказать отношение учащихся к математике.
Исследование, проведенное в 2017 году в рамках School Science and Mathematics , показало, что отношение родителей к математике может значительно предсказать отношение учащихся к математике.
В большинстве случаев негативное отношение возникает просто потому, что ученики говорят себе, что не могут заниматься математикой; они все равно никогда не будут его использовать; и так далее. Школьные факторы усугубляются, когда они подкрепляются дома, например, негативное отношение родителей к математике.
Совет: Даже если вы презираете математику, старайтесь изо всех сил поддерживать позитивное отношение к ней рядом с ребенком. Не стоит просто восклицать, что вы никогда не были хороши в математике, или отмахиваться от проблемы и просить их обратиться к своему учителю.Вместо этого поощряйте своего ребенка, когда он застревает, и попытайтесь решить проблему вместе, пока вы не найдете решение! Практикуя это, родители могут оказать положительное влияние на отношение своего ребенка к математике. В результате это может повысить общую успеваемость детей и их интерес к математике во взрослой жизни.
В результате это может повысить общую успеваемость детей и их интерес к математике во взрослой жизни.
Наймите репетитора
Некоторые родители давно не ходят в школу и не знакомы с некоторыми стратегиями обучения. Другим просто неудобно быть «учителем» дома.Вот почему некоторые родители рассматривают вариант онлайн-репетиторства.
Совет: Math Geek Mama расскажет, как найти репетитора по математике для вашего ребенка!
- Слово из уст у друзей или семьи
- Проверьте библиотеку или сообщество Центр бюллетенейных досок
- Спросите вашего ребенка учитель или школьный консультант
- Найти местный или онлайн-репетитор с использованием веб-сайтов
Prodigy также предлагает онлайн-репетиторство по математике один на один! Каждый ребенок учится по-разному.Репетиторы Prodigy Math — это сертифицированные учителя, которые адаптируют свой стиль и уроки, чтобы обучать вашего ребенка так, как он учится лучше всего.
Рассмотрите потенциальные нарушения обучаемости
Если у вашего ребенка действительно нарушения обучаемости, чем раньше вы обратитесь за помощью, тем лучше!
Это может быть непростой задачей, но в долгосрочной перспективе своевременная и надлежащая поддержка может помочь обеспечить наилучший образовательный путь для вашего ребенка.
Совет: Если с вами еще не связались, свяжитесь с учителем вашего ребенка или администратором (ами) школы, чтобы обсудить, как они могут помочь. Поскольку нарушения обучаемости, как правило, выявляются в школе, они могут использовать процесс, называемый реакцией на вмешательство, чтобы помочь точно определить, есть ли у ребенка нарушения обучаемости.
Заключительные мысли: Ваш ребенок испытывает трудности с математикой?
Проблемы с математикой могут заставить детей чувствовать, что они не умны, и повлиять на их самооценку.Однако это обычная борьба.
Более того, как видите, есть практические способы помочь! Одна из величайших вещей, которую вы можете сделать сегодня, , — это дать им понять, что все борются, даже вы, и что у всех есть сильные стороны!
Поделитесь личным примером того, как вы боролись с математикой, и, если возможно, как вы это преодолели. Затем попробуйте включить некоторые из полезных советов, перечисленных выше.
Математика может быть трудной, но совместное путешествие поможет повысить уверенность вашего ребенка и мотивировать его продолжать попытки!
Вы хотите, чтобы ваш ребенок преуспел в математике.Мы можем помочь.
Да, Математическая игра Prodigy — это основанная на школьной программе платформа, вдохновленная фэнтези, которую используют многие дети. Но он также поставляется с невероятно ценными инструментами и функциями для таких родителей, как вы. Посмотрите минутное видео ниже:
Готовы мотивировать и помогать поддерживать их на этом пути?
Создайте бесплатную родительскую учетную запись сегодня! .

 1
1 1
1 3.4
3.4
 1.5
1.5
 3.4
3.4 1
1 1
1
 1
1 1
1
 3
3
 1
1
 3
3





 Мы заканчиваем с термином .
Мы заканчиваем с термином . Итак, наклон есть.
Итак, наклон есть.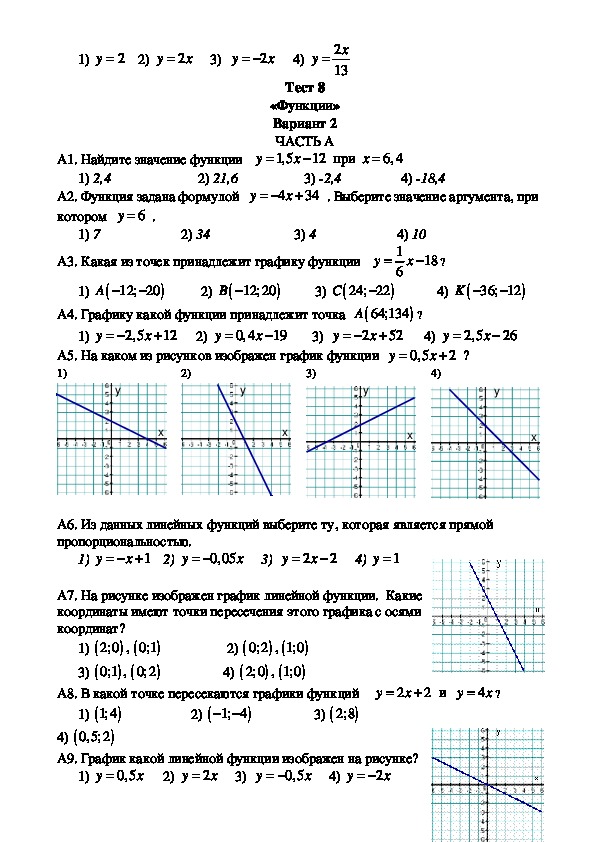 Следовательно, единственное значение, которое изменилось, было его средним значением, которое было больше.
Следовательно, единственное значение, которое изменилось, было его средним значением, которое было больше.

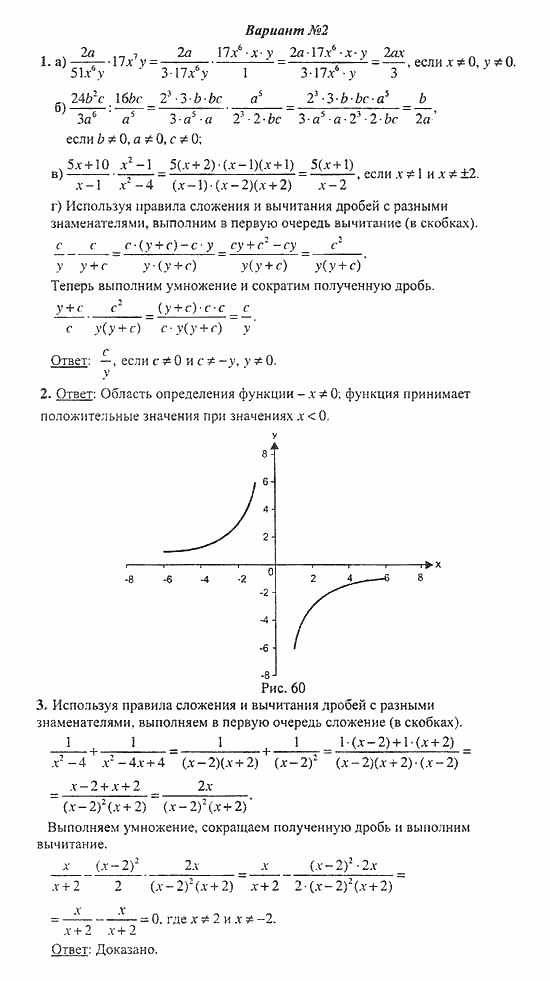
 Кроме того, новая смесь будет иметь объем 25 + х.
Кроме того, новая смесь будет иметь объем 25 + х.

 Тогда следующие три цифры будут 6, 2 и 9 в этом порядке.
Тогда следующие три цифры будут 6, 2 и 9 в этом порядке.




 Из-за этого учащиеся не осваивали каждый стандарт уровня класса, прежде чем перейти к обучению более высокого уровня.Это отсутствие мастерства создает огромные пробелы в понимании учащимися, мешая учащимся устанавливать необходимые содержательные связи и получать концептуальное понимание.
Из-за этого учащиеся не осваивали каждый стандарт уровня класса, прежде чем перейти к обучению более высокого уровня.Это отсутствие мастерства создает огромные пробелы в понимании учащимися, мешая учащимся устанавливать необходимые содержательные связи и получать концептуальное понимание.