Контрольная работа по «Математической логике и теории алгоритмов»
Контрольная работа по «Математической логике и теории алгоритмов»
- Логика и исчисление высказываний
- Записать высказывания в виде формул логики высказываний.
1.5. Иванов сдал экзамен и получил 5 неравнозначно тому, что Иванов сдал экзамен и получил 5
Решение. Выделяем простые высказывания:
X – «Иванов сдал экзамен»;
Y – «Иванов получил 5».
Так как связка «И» в логике означает конъюнкцию (обозн. «⋅»), а инверсия равнозначности –сложение по модулю 2 (обозн. «⊕»), то данное сложное высказывание: «Иванов сдал экзамен и получил 5 неравнозначно тому, что Иванов сдал экзамен и получил 5» в виде формулы логики высказываний запишем следующим образом:
[pic 1]
Ответ: [pic 2].
- Построить таблицы истинности для формул
2.1. [pic 3]
Решение. В данную формулу входят две переменные, следовательно, таблица истинности будет состоять из 22 = 4 строк.
A | B | [pic 9] | [pic 10] | [pic 11] | [pic 12] |
0 | 0 | 1 | 0 | 1 | 1 |
0 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 0 | 0 | 0 | 0 |
1 | 1 | 1 | 1 | 1 | 1 |
2.3. [pic 13]
Решение. В данную формулу входят две переменные, следовательно, таблица истинности будет состоять из 22 = 4 строк. В первые два столбца таблицы запишем все возможные комбинации из 0 и 1 для двух переменных. Остальные столбцы будут соответствовать подформулам: [pic 14], [pic 15] и самой формуле [pic 16], согласно приоритету выполнения логических операций и значениям истинности штриха Шеффера. Получаем следующую таблицу истинности формулы [pic 17]:
В данную формулу входят две переменные, следовательно, таблица истинности будет состоять из 22 = 4 строк. В первые два столбца таблицы запишем все возможные комбинации из 0 и 1 для двух переменных. Остальные столбцы будут соответствовать подформулам: [pic 14], [pic 15] и самой формуле [pic 16], согласно приоритету выполнения логических операций и значениям истинности штриха Шеффера. Получаем следующую таблицу истинности формулы [pic 17]:
A | B | [pic 18] | [pic 19] | [pic 20] |
0 | 0 | 1 | 1 | 0 |
0 | 1 | 1 | 0 | 1 |
1 | 0 | 0 | 1 | 1 |
1 | 1 | 0 | 0 | 1 |
- Доказать, что формулы являются тавтологиями
3. 5. [pic 21]
5. [pic 21]
Решение. Формула является тавтологией, если она принимает значение 1 для любых значений входящих в неё переменных. Построим таблицу истинности для данной формулы. В данную формулу входят две переменные, следовательно, таблица истинности будет состоять из 22 = 4 строк. В первые два столбца таблицы запишем все возможные комбинации из 0 и 1 для двух переменных. Остальные столбцы будут соответствовать подформулам: [pic 22], [pic 23], [pic 24], [pic 25] и самой формуле [pic 26], согласно приоритету выполнения логических операций и значениям истинности отрицания и импликации. Получаем следующую таблицу истинности формулы [pic 27]:
Контрольная работа: «Математическая логика»
Контрольная работа: «Математическая логика» Пробный вариант I. 1. (32.) Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. | C | D | E | F | |||
A | 4 | ||||||
B | 4 | 6 | 3 | 6 | |||
C | 4 | ||||||
D | 3 | 2 | |||||
E | 6 | 4 | 2 | 5 | |||
F | 5 | ||||||
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
1) 9
2) 13
3) 14
4) 15
2. (22.) В таблице приведена стоимость перевозки пассажиров между соседними населенными пунктами. Укажите схему, соответствующую таблице.
B
C
D
E
A
5
3
B
5
4
2
C
3
4
3
D
2
E
3
3. (48.) Дан фрагмент таблицы истинности выражения F.
x1x2
x3
x4
x5
x6
x7
1
1
0
1
1
1
1
1
1
0
1
0
1
1
0
0
0
1
0
1
1
0
1
0
Какое выражение соответствует F?
1) x1 ¬x2
2) x1 ¬x2 x3 ¬x4 x5 x6 ¬x7
3) x1 x2 ¬x3 x4 x5 x6 x7
4) ¬x1 x2 ¬x3 x4
4. (9.) Для какого из значений числа Y высказывание
(9.) Для какого из значений числа Y высказывание
(Y < 5) ((Y > 1) → (Y > 5)) будет истинным?
1) 1 2) 2 3) 3 4) 4
5. (17.) Для какого названия животного ложно высказывание:
Заканчивается на согласную
1) Верблюд 2) Страус 3) Кенгуру 4) Леопард
6. (36.) Для какого слова истинно высказывание:
(Вторая буква согласная Последняя буква гласная) → Первая буква гласная?
1) ГОРЕ 2) ПРИВЕТ 3) КРЕСЛО 4) ЗАКОН
7. (4.) Каково наименьшее целое положительное число X, при котором высказывание: (4 > -(4 + X)·X) → (30 > X·X) будет ложным.
8. (13.) Укажите значения переменных K, L, M, N, при которых логическое выражение (K → M) (L K) ¬N ложно.
Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.
9. (2.) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З?
10. (26.) На одной улице стоят в ряд 4 дома, в которых живут 4 человека: Алексей, Егор, Виктор и Михаил. Известно, что каждый из них владеет ровно одной из следующих профессий: Токарь, Столяр, Хирург и Окулист, но неизвестно, кто какой и неизвестно, кто в каком доме живет. Однако, известно, что:
(1) Столяр живет левее Токаря
(2) Токарь живет рядом с Хирургом и Окулистом
(3) Хирург живет с краю
(4) Окулист живет рядом со Столяром
(5) Алексей живет рядом с Окулистом
(6) Егор не живет рядом с Алексеем
(7) Егор живет рядом с Виктором и Михаилом
(8) Виктор живет рядом со Столяром
Выясните, кто какой профессии, и кто где живет, и дайте ответ в виде заглавных букв имени людей, в порядке слева направо. Например, если бы в домах жили (слева направо) Константин, Николай, Роман и Олег, ответ был бы: КНРО.
Например, если бы в домах жили (слева направо) Константин, Николай, Роман и Олег, ответ был бы: КНРО.
Контрольная работа: «Математическая логика»
Пробный вариант II.
1. (33.) Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
AB
C
D
E
F
A
3
B
9
4
C
3
9
3
8
D
3
2
E
4
8
2
7
F
7
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
1) 11
2) 13
3) 15
4) 17
2. (22.) В таблице приведена стоимость перевозки пассажиров между соседними населенными пунктами. Укажите схему, соответствующую таблице.
B
C
D
E
A
5
3
B
5
4
2
C
3
4
3
D
2
E
3
3. (49.) Дан фрагмент таблицы истинности выражения F.
x1x2
x3
x4
x5
x6
x7
F
1
1
0
1
1
1
1
0
1
0
1
0
1
1
0
1
0
1
0
1
1
0
1
0
Какое выражение соответствует F?
1) x1 ¬x2 x3 ¬x4 x5 x6 ¬x7
2) x1 ¬x2 x3 ¬x4 ¬x5 x6 ¬x7
3) ¬x1 x2 ¬x3 x4 ¬x5 ¬x6 x7
4) ¬x1 x2 ¬x3 x4 x5 ¬x6 x7
4. (21.) Для какого числа X истинно высказывание
(21.) Для какого числа X истинно высказывание
(X(X-16) > -64) →(X > 8)
1) 5 2) 6 3) 7 4) 8
5. (18.) Для какого названия животного ложно высказывание:
В слове 4 гласных буквы ¬ (Пятая буква гласная) В слове 5 согласных букв?
1) Шиншилла 2) Кенгуру 3) Антилопа 4) Крокодил
6. (37.) Для какого имени истинно высказывание:
Первая буква согласная (¬ Вторая буква согласная → Четвертая буква гласная)?
1) ИВАН 2) ПЕТР 3) ПАВЕЛ 4) ЕЛЕНА
7. (5.) Каково наибольшее целое положительное число X, при котором истинно высказывание: ((X – 1) < X) → (40 > X·X)
8. (8.) Укажите значения логических переменных Р, Q, S, Т, при которых логическое выражение (Р ¬Q) (Q → (S Т)) ложно.
Ответ запишите в виде строки из четырех символов: значений переменных Р, Q, S, T (в указанном порядке).
9. (3.) На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З?
10. (27.) На одной улице стоят в ряд 4 дома, в которых живут 4 человека: Алексей, Егор, Виктор и Михаил. Известно, что каждый из них владеет ровно одной из следующих профессий: Токарь, Столяр, Хирург и Окулист, но неизвестно, кто какой и неизвестно, кто в каком доме живет. Однако, известно, что:
(1) Хирург живет рядом с Окулистом
(2) Окулист живет правее Столяра
(3) Токарь живет рядом с Хирургом и Столяром
(4) Алексей живет рядом с Токарем
(5) Егор не живет рядом с Хирургом
(6) Михаил живет левее Алексея
Выясните, кто какой профессии, и кто где живет, и дайте ответ в виде заглавных букв имени людей, в порядке слева направо. Например, если бы в домах жили (слева направо) Константин, Николай, Роман и Олег, ответ был бы: КНРО.
Например, если бы в домах жили (слева направо) Константин, Николай, Роман и Олег, ответ был бы: КНРО.
«5» – 9-10 баллов
«4» – 7-8 баллов
«3» – 5-6 баллов
«5» – 9-10 баллов
«4» – 7-8 баллов
«3» – 5-6 баллов
Контрольная работа по 📝 логике на заказ
Контрольные работы по логике отличаются разным подходом к составлению и содержанию заданий в зависимости от профиля учебного заведения. Как правило, контрольная работа по логике состоит из теоретической части, в которой необходимо продемонстрировать знания законов логики, раскрыть такие понятия, как софизмы, силлогизмы и их основные виды. В практической части студент должен показать свои умения в решении задач, построении логических цепочек и многого другого.
Общепринятое понятие «логика» очень сильно отличается от «логики» научной, поэтому решить задачи, надеясь на «логическое» мышление, практически невозможно. Если вы сомневаетесь в своих знаниях, а времени на подготовку осталось критически мало, доверьте специалистам решение контрольной работы по логике на заказ, и вы будете приятно удивлены высокой оценкой и похвалой преподавателя.
Если вы сомневаетесь в своих знаниях, а времени на подготовку осталось критически мало, доверьте специалистам решение контрольной работы по логике на заказ, и вы будете приятно удивлены высокой оценкой и похвалой преподавателя.
Логика – достаточно сложная дисциплина. Ее основы нельзя просто заучить, их необходимо понять и наработать опыт решения логических задач. Именно по этой причине все специалисты, предлагающие услуги по выполнению контрольных работ на заказ, имеют профильное образование по тем предметам, с которыми работают.
Портал «Все сдал!» отличается от других сайтов, предоставляющих услуги по написанию контрольных и лабораторных работ, курсовых и дипломных проектов, рефератов и эссе, серьезным подходом к проверке исполнителей. Помимо портфолио, каждый исполнитель представляет документы, подтверждающие его образование и квалификацию, и допускается к работе с заказчиками только после положительных результатов проверки.
Несмотря на строгий отбор, на сайте «Все сдал!» заказчик общается напрямую с исполнителем, не тратя время на переговоры с менеджерами. Это экономит деньги заказчика, так как нет необходимости оплачивать услуги посредника, а так же позволяет быстро и оперативно решать любые вопросы, возникающие в ходе работы над заданием. Исполнители, получив задание, заинтересованы выполнить его быстро, качественно и в срок, зарекомендовав себя для дальнейшей работы.
Это экономит деньги заказчика, так как нет необходимости оплачивать услуги посредника, а так же позволяет быстро и оперативно решать любые вопросы, возникающие в ходе работы над заданием. Исполнители, получив задание, заинтересованы выполнить его быстро, качественно и в срок, зарекомендовав себя для дальнейшей работы.
Воспользоваться услугой «контрольные работы по логике на заказ» достаточно просто. Достаточно зарегистрироваться на сайте «Все сдал!», разместить свое задание, ознакомиться с портфолио исполнителей и сделать выбор. Не забудьте оговорить особенности задания, сроки выполнения и размер вознаграждения. Все расчеты на сайте производятся через абсолютно безопасные системы онлайн платежей, в случае невыполнения задания сумма вознаграждения в полном объеме возвращается заказчику.
Учиться на «отлично» стало просто, комфортно и недорого. На портале «Все сдал!» вы сможете не только выполнить контрольную работу по логике на заказ, но и получить онлайн помощь во время контрольной или лабораторной работы, подготовить ответы к экзамену, заказать написание эссе, курсовой или диплома и даже диссертации.
Страница не найдена « Лицей №159
В предновогодние дни как-то по особенному верится в то, что наш мир должен стать лучше, добрее, что счастье и успех непременно придут в каждый дом и в каждую семью. Уверены, что в наших силах подарить своим близким и родным самое дорогое — это тепло, понимание и любовь! Пусть Новый Год поможет в исполнении […]
Полувековая педагогическая деятельность Каменевой Галины Ивановны – это история школы № 159. О славном пути от учителя начальных классов до директора-новатора, ищущего возможность реализации комплексного подхода к организации деятельности учащихся, внедряющего наработки педагогов-единомышленников по повышению эффективности обучения детей, рассказывает книга талантливого воспитателя, руководителя, методиста Каменевой Г.И. «Творческое лицо школы № 159 г. Новосибирска».
[…]
17 ноября 2021 года на базе МАОУ Вторая Новосибирская гимназия состоялся единый городской методический день для учителей начальных классов по теме «Процесс обучения, воспитания и развития в начальной школе». На семинаре, в присутствии 60 учителей начальных классов школ города Новосибирска, с педагогическим опытом по теме: «Воспитание детей в условиях современной реальности» выступила Банникова […]
На семинаре, в присутствии 60 учителей начальных классов школ города Новосибирска, с педагогическим опытом по теме: «Воспитание детей в условиях современной реальности» выступила Банникова […]
16,17 ноября 2021 года в лицее были проведены тематические классные часы под девизом: «Помним, чтобы жить», «Свечи в память зажигаем» в рамках Всемирного дня памяти жертв дорожно-транспортных происшествий, в которых приняли участие учащиеся 4-8 классов.
Это международное событие призвано привлечь внимание всех людей планеты к печальному факту: во всем мире в результате дорожно-транспортных происшествий […]
9 ноября 2021 года в г. Сочи прошёл XIII Международный конкурс научно-исследовательских и творческих работ учащихся. Лицей №159 представляла команда 10 «Б» специализированного класса инженерно-технологического направления. По результатам конкурса у нашей команды только первые и вторые места! Фирстова Анастасия заняла 2 место со своей работой по теме «Численные методы вычисления площадей фигур сложной […]
В нашем лицее начал работу пресс-центр «Перо, карандаш и ручка». Теперь вы сможете найти много увлекательной информации в Инстаграм-аккаунте @lyc159.nios и на электронных стендах школы, а также поприсутствовать там, где вас не было вместе с нашими журналистами! Любой из вас может стать частичкой нашей команды. Здесь рады всем! По всем вопросам обращаться к Полине Николаевне […]
Теперь вы сможете найти много увлекательной информации в Инстаграм-аккаунте @lyc159.nios и на электронных стендах школы, а также поприсутствовать там, где вас не было вместе с нашими журналистами! Любой из вас может стать частичкой нашей команды. Здесь рады всем! По всем вопросам обращаться к Полине Николаевне […]
С 11 октября по 10 декабря начался осенний этап скрининга зрения учащихся. Обследование будет проводиться дистанционно, на компьютерах в кабинете информатики, согласно установленному графику. Все желающие обследоваться могут получить согласия и заполнить (получить образец согласия классный руководитель может у психолога и социального педагога)!
Приказ
Памятка для родителей
22 октября 2021 года в МБОУ «Лицей №159» прошла математическая игра «Умники и умницы» на параллели 5 классов. Участвовало всего 10 команд: 5 «А» класс- 2 команды, 5 «Б» класс- 3 команды, 5 «В» класс- 1 команда, 5 «Г» класс- 1 команда, 5 «М» класс- 3 команды.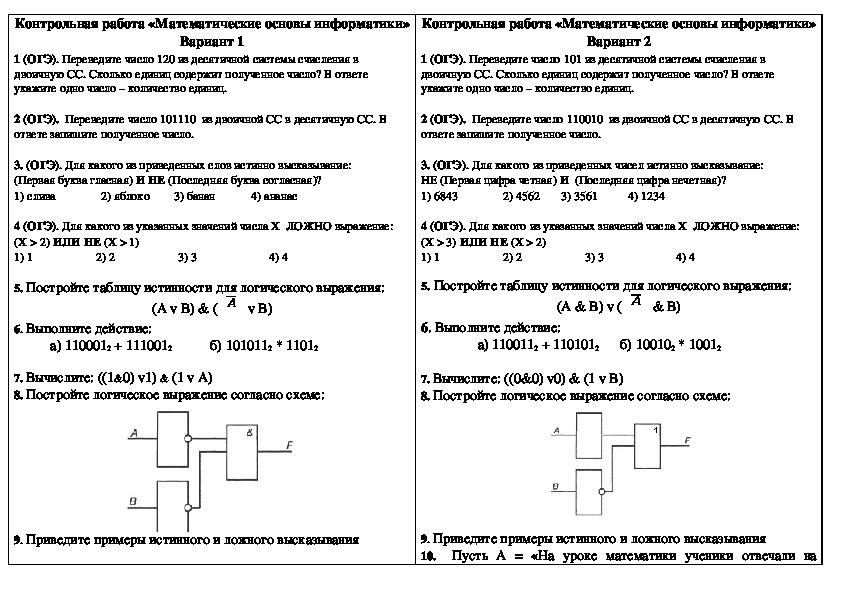 Дети отвечали на сложные логические вопросы, […]
Дети отвечали на сложные логические вопросы, […]
В общественной приёмной Губернатора области 28.10.2021 с 10.00 до 12.00 по бесплатному тел. 8-800-700-84-73 будет проведена «прямая телефонная линия» по теме: «О проведении обязательной вакцинации против новой коронавирусной инфекции COVID-19 отдельным категориям граждан по эпидемическим показаниям». В «прямой телефонной линии» примут участие специалисты министерства здравоохранения Новосибирской области и Управления Федеральной службы по надзору […]
С 2017 года лицей активно сотрудничает с кафедрой электронных приборов НГТУ. В рамках сотрудничества с данной кафедрой МТБ лицея пополнилась стендами «Аналоговой и реальной схемотехники», преподаватели вуза Юпашевский Антон Витальевич, Берг Яна Александровна неоднократно проводили мастер-классы для учителей лицея по обучению работы со стендами, а также проводят спецкурсы для учащихся 7 класса «Основы […]
Контрольная работа по теме “Математические основы компьютера.
 Алгебра логики”
Алгебра логики”Контрольная работа «Элементы алгебры логики» Вариант 1.
1. Какие предложения являются высказываниями:
а) Как пройти в библиотеку? б) Числа 3 является делителем числа 9.
в) Решение задачи – информационный процесс.
г) Ух ты! д) Некоторые птицы улетают на юг.
2. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет. Какое количество страниц будет найдено по запросу Малина&Клубника? Решение задачи оформите с помощью кругов Эйлера-Венна.
|
Запрос |
Найдено страниц |
|
Малина |
2900 |
|
Клубника |
1700 |
|
Малина|Клубника |
3000 |
3. Вычислите (1Λ0) Λ (0Λа) Λ (1v0)
Вычислите (1Λ0) Λ (0Λа) Λ (1v0)
4. Определите истинность высказывания (X>2)v(X<5)&(X>10) при Х=12
5. Напишите наименьшее число x, для которого истинно высказывание: (x > 16) И НЕ (x нечётное)
6. Из предложенных вариантов слов, выберите то, для которого истинно высказывание: (Первая буква слова согласная ИЛИ Вторая буква слова гласная) И Последняя буква гласная
а) ирис б) палка в) словарь
7. Постройте таблицу истинности для высказывания . Постройте логическую схему для данной формулы.
8. Решите задачу с объяснением: Андрей, Аня и Маша решили пойти в кино. Каждый из них высказал свои пожелания по поводу выбора фильма. Андрей сказал: «Я хочу посмотреть французский боевик». Маша сказала: «Я не хочу смотреть французскую комедию». Аня сказала: «Я хочу посмотреть американскую мелодраму». Каждый из них слукавил в одном из двух пожеланий. На какой фильм пошли ребята?
Андрей сказал: «Я хочу посмотреть французский боевик». Маша сказала: «Я не хочу смотреть французскую комедию». Аня сказала: «Я хочу посмотреть американскую мелодраму». Каждый из них слукавил в одном из двух пожеланий. На какой фильм пошли ребята?
9. Определите значение логического сигнала на выходе логической схемы.
Контрольная работа «Элементы алгебры логики» Вариант 2.
1. Какие предложения являются высказываниями:
а) Яблоки растут на яблони. б) Вода – жидкость.
в) В какое море впадает река Волга?
г) 2 + х > 6 д) Пусть сильнее грянет буря!
2. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет. Какое количество страниц будет найдено по запросу Солнце? Решение задачи оформите с помощью кругов Эйлера-Венна.
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет. Какое количество страниц будет найдено по запросу Солнце? Решение задачи оформите с помощью кругов Эйлера-Венна.
|
Запрос |
Найдено страниц |
|
Мороз&Солнце |
1100 |
|
Мороз |
1654 |
|
Мороз|Солнце |
2870 |
3. Вычислите (1v0) & (0vа) v (1v0)
Вычислите (1v0) & (0vа) v (1v0)
4. Определите истинность высказывания (X>2)v(X<5)&(X>10) при Х=1
5. Напишите наименьшее число x, для которого истинно высказывание: (x > 35) И НЕ (x не делится на 7)
6. Постройте таблицу истинности для высказывания . Постройте логическую схему для данной формулы.
7. Из предложенных вариантов слов, выберите то, для которого истинно высказывание: НЕ (Последняя буква гласная ИЛИ Третья буква согласная) И Вторая буква согласная
а) страна б) осада в) оракул
8. Решите задачу с объяснением: Виновник ночного дорожно-транспортного происшествия скрылся с места аварии. Первый из опрошенных свидетелей сказал работникам ГАИ, что это были “Жигули”, первая цифра номера машины — единица. Второй свидетель сказал, что машина была марки “Москвич”, а номер начинался с семёрки. Третий свидетель заявил, что машина была иностранная, номер начинался не с единицы. При дальнейшем расследовании выяснилось, что каждый из свидетелей правильно указал либо только марку машины, либо только первую цифру номера. Какой марки была машина и с какой цифры начинался номер?
Первый из опрошенных свидетелей сказал работникам ГАИ, что это были “Жигули”, первая цифра номера машины — единица. Второй свидетель сказал, что машина была марки “Москвич”, а номер начинался с семёрки. Третий свидетель заявил, что машина была иностранная, номер начинался не с единицы. При дальнейшем расследовании выяснилось, что каждый из свидетелей правильно указал либо только марку машины, либо только первую цифру номера. Какой марки была машина и с какой цифры начинался номер?
9. Определите значение логического сигнала на выходе логической схемы.
Научно-образовательный портал ТУСУР | Дискретная математика: Учебное пособие / Смыслова З. А. — 2000. 116 с.
1. Теория множеств
1.1. Множества и операции над ними
1.1.1. Понятие множества
1.1.2. Способы задания множеств
1.1.3. Основные определения
1.1.4. Диаграммы Эйлера – Венна
1. 1.5. Операции над множествами
1.5. Операции над множествами
1.1.6. Системы множеств
1.1.7. Законы алгебры множеств
1.1.8. Решение задач 1-3 контрольной работы № 1.
1.1.9. Контрольные вопросы и упражнения
1.2. Бинарные отношения
1.2.1. Декартово произведение множеств
1.2.2. Определение бинарного отношения
1.2.3. Способы задания бинарного отношения
1.2.4. Свойства бинарных отношений
1.2.5. Отношения эквивалентности
1.2.6. Отношения порядка
1.2.7. Решение задачи 4 контрольной работы № 1.
1.2.8. Контрольные вопросы и упражнения
1.3. Реляционная алгебра
1.3.1. Применение отношений для обработки данных
1.3.2. Теоретико-множественные операции реляционной алгебры
1.3.3. Специальные операции реляционной алгебры
1.3.4. Решение задачи 5 контрольной работы № 1.
1.3.5. Контрольные вопросы и упражнения
1.4. Конечные и бесконечные множества
1.4.1. Биекция
1.4.2. Равномощные множества
1.4.3. Классы равномощных множеств
1.4.4. Сравнение множеств по мощности
1.4.5. Определение конечного множества
1.4.6. Свойства конечных множеств
1.4.7. Определение счетного множества
1.4.8. Свойства счетных множеств
1.4.9. Несчетные множества
1.4.10. Выводы
1.4.11. Решение задачи 6 контрольной работы № 1.
1.4.12. Контрольные вопросы и упражнения
1.5. Комбинаторика
1.5.1. Задачи комбинаторики
1.5.2. Типы выборок
1.5.3. Основные правила комбинаторики
1.5.4. Размещения с повторениями
1.5.5. Размещения без повторений
1. 5.6. Перестановки без повторений
5.6. Перестановки без повторений
1.5.7. Перестановки с повторениями
1.5.8. Сочетания
1.5.9. Сочетания с повторениями
1.5.10. Решение задач 7,8 контрольной работы № 1.
1.5.11. Бином Ньютона
1.5.12. Свойства биноминальных коэффициентов
1.5.13. Контрольные вопросы и упражнения
2. Элементы математической логики
2.1. Логика высказываний
2.1.1. История математической логики
2.1.2. Понятие высказывания
2.1.3. Операции над высказываниями
2.1.4. Таблицы истинности
2.1.5. Формулы логики высказываний
2.1.6. Равносильные преобразования формул
2.1.7. Решение задач контрольной работы № 2.
2.1.8. Контрольные вопросы и упражнения
2.2. Логические рассуждения
2.2.1. Определение логически правильного рассуждения
2. 2.2. Проверка правильности логического рассуждения
2.2. Проверка правильности логического рассуждения
2.2.3. Прямые и косвенные методы доказательств
2.2.4. Решение задачи контрольной работы № 2.
2.2.5. Контрольные вопросы и упражнения
2.3. Логика предикатов
2.3.1. Понятие предиката
2.3.2. Кванторы
2.3.3. Формулы логики предикатов
2.3.4. Равносильные преобразования формул
2.3.5. Рассуждения в логике предикатов
2.3.6. Решение задачи контрольной работы № 2.
2.3.7. Контрольные вопросы и упражнения
3. Основы теории графов
3.1. Ориентированные графы
3.1.1. Основные понятия
3.1.2. Орграфы и бинарные отношения
3.1.3. Матрицы орграфа
3.1.4. Решение задачи 5 контрольной работы № 2.
3.1.5. Контрольные вопросы и упражнения
3. 2. Неориентированные графы
2. Неориентированные графы
3.2.1. Основные термины
3.2.2. Матрицы графа
3.2.3. Решение задачи 6 контрольной работы № 2.
3.2.4. Контрольные вопросы и упражнения
3.3. Планарные графы
3.3.1. Изоморфизм графов
3.3.2. Планарность
3.3.3. Критерий планарности
3.3.4. Решение задачи 7 контрольной работы № 2.
3.3.5. Контрольные вопросы и упражнения
3.4. Связность графов
3.4.1. Маршруты
3.4.2. Компоненты связности
3.4.3. Эйлеровы цепи и циклы
3.4.4. Цикломатическое число
3.4.5. Решение задачи 8 контрольной работы № 2.
3.4.6. Контрольные вопросы и упражнения
3.5. Графы без циклов
3.5.1. Дерево и лес
3.5.2. Свойства деревьев
3.5.3. Каркасы графа
3. 5.4. Обход графа “в ширину”
5.4. Обход графа “в ширину”
3.5.5. Обход графа “в глубину”
3.5.6. Решение задачи 9 контрольной работы № 2.
3.5.7. Контрольные вопросы и упражнения
Приложение 1. Контрольная работа № 1.
Приложение 2. Контрольная работа № 2.
Контрольная работа по “Математической логике и теории алгоритмов”
Первый вариант
1. Отношение задано на множестве целых чисел {53, 43, 54, 42, 44, 60, 50, 20} . Для каждого из следующих отношений:
1.1 проверить, является ли отношение рефлексивным, симметричным,
антисимметричным (строгим, нестрогим), транзитивным;
1.2. построить матрицы и графы этих отношений;
1.3. определить являются ли эти отношения отношениями эквивалентности,
частичного порядка, линейного порядка;
1.4.. для отношений эквивалентности построить классы эквивалентности;
1.5. для отношений частичного порядка применить алгоритм топологической
сортировки и получить отношение строго порядка;
1. 6. построить транзитивные замыкания
всех отношений.
6. построить транзитивные замыкания
всех отношений.
- xRy ó x и y имеют одинаковые остатки при делении на 3;
- xQy ó в наборе имеется элемент, больший x , но меньший y ;
Решение.
Рассмотрим отношение
xRy ó x и y имеют одинаковые остатки при делении на 3.
Для построения матрицы составим таблицу:
X | 53 | 43 | 54 | 42 | 44 | 60 | 50 | 20 | |
Y | остаток | 2 | 1 | 0 | 0 | 2 | 0 | 2 | 2 |
53 | 2 | 1 | 1 | 1 | 1 | ||||
43 | 1 | 1 | |||||||
54 | 0 | 1 | 1 | 1 | |||||
42 | 0 | 1 | 1 | 1 | |||||
44 | 2 | 1 | 1 | 1 | 1 | ||||
60 | 0 | 1 | 1 | 1 | |||||
50 | 2 | 1 | 1 | 1 | 1 | ||||
20 | 2 | 1 | 1 | 1 | 1 |
1
Данное отношение обладает
свойством рефлексивности, так как
на главной диагонали все единицы.
Данное отношение симметрично, так как наблюдается симметрия матрицы относительно главной диагонали.
Данное отношение не антисимметрично, так как существует симметричные элементы, не лежащие на главной диагонали, то есть выполнение отношений xRy, yRx не влечет за собой отношения x=y.
Данное отношение транзитивно, потому что выполнение отношений xRy и yRz влечет выполнение отношение xRz (если x, y имеют одинаковые остатки при делении на 3 и y, z имеют одинаковые остатки при делении на 3, то x, z также имеют одинаковые остатки при делении на 3).
Данное отношение является отношением эквивалентности, поскольку оно обладает свойствами рефлексивности, симметричности, транзитивности.
Данное отношение не является отношением частичного порядка, поскольку оно не антисимметрично.
Данное отношение не является отношением линейного порядка, поскольку элементы не образуют цепь.
Граф отношения:
Классы эквивалентности: [43],
{53, 44, 20, 50], [60, 42, 54].
Транзитивное замыкание
X | Y |
53 | 53 |
53 | 50 |
53 | 20 |
53 | 44 |
50 | 50 |
50 | 53 |
50 | 20 |
50 | 44 |
44 | 44 |
44 | 43 |
44 | 50 |
44 | 20 |
20 | 20 |
20 | 44 |
20 | 53 |
20 | 50 |
43 | 43 |
54 | 54 |
54 | 60 |
54 | 42 |
42 | 42 |
42 | 54 |
42 | 60 |
60 | 60 |
60 | 54 |
60 | 42 |
Рассмотрим отношение
xQy ó в наборе имеется элемент, больший x , но меньший y
Для построения матрицы составим таблицу:
X/Y | 53 | 43 | 54 | 42 | 44 | 60 | 50 | 20 |
53 | 1 | |||||||
43 | 1 | 1 | 1 | 1 | ||||
54 | ||||||||
42 | 1 | 1 | 1 | 1 | 1 | |||
44 | 1 | 1 | 1 | |||||
60 | ||||||||
50 | 1 | 1 | ||||||
20 | 1 | 1 | 1 | 1 | 1 | 1 |
1
Данное отношение не обладает свойством рефлексивности,
так как на главной диагонали все нули.
Данное отношение не симметрично, не наблюдается симметрия матрицы относительно главной диагонали.
Данное отношение не асимметрично. Нет симметричных элементов, одновременное выполнение отношений xQy, yQx ytdjpvj;yj/
Данное отношение транзитивно, потому что выполнение отношений xRy и yRz влечет выполнение отношение xRz (если есть элементы больше x и меньше y, а также есть элементы больше y и меньше z, то имеются элементф больше x и меньше z.
Данное отношение не является отношением эквивалентности, поскольку оно не обладает свойствами рефлексивности, и симметричности.
Данное отношение не является отношением частичного порядка, поскольку оно не рефлексивно.
Данное отношение является отношением линейного порядка, поскольку для любых двух элементов a, b имеет место a<=b или b<=a.
Данное отношение является отношением строгого порядка.
Граф отношения:
Транзитивное замыкание
X | Y |
20 | 43 |
20 | 44 |
20 | 50 |
20 | 43 |
20 | 54 |
20 | 60 |
42 | 44 |
42 | 50 |
42 | 53 |
42 | 54 |
42 | 60 |
43 | 50 |
43 | 53 |
43 | 54 |
43 | 60 |
44 | 53 |
44 | 54 |
44 | 60 |
50 | 54 |
50 | 60 |
53 | 60 |
2. Будет ли логичным следующее рассуждение:
Если губернатор не имеет
Будет ли логичным следующее рассуждение:
Если губернатор не имеет
соответствующего авторитета или если он не желает принимать на себя
ответственность, то порядок не будет восстановлен и волнения не прекратятся до
тех пор, пока участникам волнений это не надоест, и власти не начнут
примирительные действия. Следовательно, если губернатор не желает взять на себя
ответственность и участникам волнений это не надоест, то волнения не прекратятся.
Решение
Запишем высказывание символами формальной логики. Введем обозначения:
A – волнения прекратятся
X – губернатор имеет авторитет
Y – он желает принимать на себя ответственность
P – участникам это надоест
Q – власти начнут примирительные действия
Подставим значения , , выполним преобразования
То есть в приведенном рассуждении есть ошибка. Правильным будет следующее рассуждение:
Если губернатор не имеет соответствующего авторитета или если он не желает принимать на себя ответственность, то порядок не будет восстановлен и волнения не прекратятся до
тех пор, пока участникам волнений это
не надоест, и власти не начнут примирительные
действия. Следовательно, если губернатор
не желает взять на себя ответственность
и участникам волнений это не надоест,
то волнения не прекратятся, пока власти
не начнут примирительные действия.
Следовательно, если губернатор
не желает взять на себя ответственность
и участникам волнений это не надоест,
то волнения не прекратятся, пока власти
не начнут примирительные действия.
3. Провести исследование булевой функции
a) построить таблицу функции; ответ записать в виде набора значений,
упорядоченного в соответствии с лексикографическим порядком набора
аргументов;
b) построить СДНФ этой функции; ответ записать, упорядочив элементарные
конъюнкции в лексикографическом порядке;
c) упростить полученное выражение с помощью метода минимизирующих карт,
ответ записать в виде минимальной ДНФ;
d) построить многочлен Жегалкина исходной функции;
e) построить таблицу двойственной функции; ответ записать в виде упорядоченного
набора значений;
f) построить СКНФ двойственной функции; ответ записать, упорядочив
элементарные дизъюнкции в лексикографическом порядке;
g) проверить исходную функцию на принадлежность основным классам
замкнутости T0 ,T1 , L, M, S;
h) Можно ли через эту функцию выразить
все остальные булевы функции.
Решение
Составим таблицу истинности:
x | y | z | F(x,y,z) |
0 | 0 | 0 | 0 |
1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 |
1 | 1 | 0 | 1 |
0 | 0 | 1 | 0 |
1 | 0 | 1 | 0 |
0 | 1 | 1 | 0 |
1 | 1 | 1 | 0 |
Построим СДНФ :
F(x,y,z)=
ДНФ:
F(x,y,z)=x˄y˄¬z
Построим многочлен Жегалкина:
F(x,y,z)=x˄y˄(z1)= x˄y˄z x˄y
Двойственная функция:
(F(x,y,z))*=¬( ¬x˄¬y˄z)
Составим таблицу истинности двойственной функции:
x | y | z | (F(x,y,z))* |
0 | 0 | 0 | 1 |
1 | 0 | 0 | 1 |
0 | 1 | 0 | 1 |
1 | 1 | 0 | 1 |
0 | 0 | 1 | 0 |
1 | 0 | 1 | 1 |
0 | 1 | 1 | 1 |
1 | 1 | 1 | 1 |
СКНФ двойственной функции
(F(x,y,z))*= +++++=
==
Проверим функцию на принадлежность к классам замкнутости:
Функция принадлежит к классу Т0, поскольку F(0,0,0)=0
Функция не принадлежит к классу Т1, поскольку F(1,1,1)=0
Функция не принадлежит к классу S, поскольку
Функция не принадлежит к классу М (монотонных функций), поскольку не ыфполняется условие неубывания функции при возрастании значений аргументов
Функция не
принадлежит к классу L линейных
функций, поскольку не представляется
в виде суперпозиции произведений аргументов
на коэффициенты.
Для того, чтобы система булевых функций была полной, необходимо и достаточно, чтобы для каждого из классов Т0, Т1, S, L, M нашлась функция fi из этой системы не принадлежащая этому классу. В данном случае все функции принадлежат классу Т0, поэтому система функций не является полной, не все булевы функции могут быть выражены в этой системе.
4. Машина Тьюринга имеет алфавит из трех символов {2,1,*} (символ ∗ означает
отсутствие символа на ленте), два состояния {q0, q2}, из которых q0–начальное состояние,
q2 – конечное. Символ R означает сдвиг читающей головки вправо по ленте, L – влево,
E – головка остается на месте. В начальный момент головка указывает на крайний левый
символ записи. Команды машины задаются набором: q02 –> q01 R; q01 –> q01 L; q0* –>
q21 E. Какой результат даст машина на наборе 22122?
Решение
Печатающая
головка будет перемещаться  Дойдя до пустой
ячейки, головка напечатает цифру 1 и остановится.
В итоге получится последовательность
111122.
Дойдя до пустой
ячейки, головка напечатает цифру 1 и остановится.
В итоге получится последовательность
111122.
5, Построить порождающую грамматику для языка
Решение
Язык L = {anbncn | n > 0} порождается грамматикой с правилами
S ® aSBC | S ® aBC | CB ® BC | |
| aB ® ab | bB ® bb | |
bC ® bc | cC ® cc |
Второй вариант
1. Отношение задано на множестве целых чисел {53, 43, 54, 42, 44, 60, 50, 20) . Для каждого из следующих отношений:
1.1 проверить, является ли отношение рефлексивным, симметричным,
антисимметричным (строгим, нестрогим), транзитивным;
1.2. построить матрицы и графы этих отношений;
1. 3. определить являются ли эти
отношения отношениями эквивалентности,
3. определить являются ли эти
отношения отношениями эквивалентности,
Логическая математика IQ Вопросы с ответами
4-й вопрос, ка ответь btao
Есть ссылка на страницу ответа на этот вопрос. В любом случае ответ на 4-й «вопрос IQ по логической математике» слева направо и сверху вниз:
3,5, 4,5
9,5, 3,5
Ответ на 4-й вопрос:
3,5 + 4,5
9,5-3,5
3 вопроса ka ans batoa plz
Ответы на все эти головоломки приведены в конце поста.
В любом случае ответ на третью загадку – 7 и 7.
4
20.12.2018 = 448
первый квартал – 718
745 – это ответ на первую проблему
745 не удовлетворяет первому условию. Однако вы очень близки к решению этой проблемы с кодом.
Скажите, пожалуйста, 5-й ответ

Ссылка для ответа на эти головоломки обновлена в конце поста. Пожалуйста, ознакомьтесь с ответами вместе с подробным объяснением каждого из этих вопросов логической математики iq в виде видео-головоломки, ссылка на которую приведена в конце.
Дайте мне знать, если что-то неясно с ответами на эти головоломки?
Мой вопрос: есть числа от 1 до 9, поэтому при добавлении 3 + 3 цифр должно получиться 3 цифры, но в ответе и вопросе должно быть повторение.
Не могли бы вы подробнее рассказать о своем вопросе. О какой загадке вы здесь говорите?
Сэр головоломка 4 ka решение отправить kr dijiye plzz
 ..
..Ссылка на ответ в конце сообщения, чтобы прочитать решение и ответы на каждую головоломку здесь.
Пожалуйста, сэр 4-й, но не даровал.
Пожалуйста, ознакомьтесь с моими предыдущими комментариями. Я уже дал ответ на 4-ю # головоломку. В любом случае проводка снова, как показано ниже
Слева направо и сверху вниз, как показано ниже
3,5, 4,5
9.5, 3,5
5. кеситон = 10
5-й вопрос, ответ: 11
 .
. 3-я головоломка, ответ
Объяснять
3-й puzzzzl ответ, пожалуйста
3-й вопрос ответ
Пожалуйста, объясните, как OS 7 и 7
3,5 + 4,5
9,5–3,5
Верхняя 7 и нижняя 7
Используемая логика выглядит так, как показано ниже.
Возведите в квадрат нижнее число и вычтите верхнее число, чтобы получить число в следующем столбце, записанное сверху вниз.
Их нет..
Muje samaj nahi aai
На 4-й вопрос по логической математике IQ ответ следующий:
A = 3,5, B = 4,5, C = 9,5 и D = 3,5. Пожалуйста, дайте мне знать, если у вас все еще есть сомнения?
2-й вопрос ка ответ
Дан ответ на все вопросы-головоломки. Пожалуйста, проверьте ссылку для ответа в конце головоломок в вышеуказанном сообщении. Пожалуйста, дайте мне знать, если есть сомнения?
 ..
..1 вопрос ответ
1 = 718
Да, я согласен. Ответ 718
результат не должен включать “5”.
Ответы для тех:
(1) 718
(2) 75 кг
(3) 6 и 15
(4) A = D = 3,5, B = 4,5, C = 9,5
(5)
Ответы на все эти головоломки можно найти на сайте
https://www.youtube.com/watch?v=U9QocGKV-1E&feature=youtu.be.
 ..
.. Можете ли вы объяснить ответ: 3-го qustn …. Я не вижу здесь ссылки, пожалуйста,
Как вы получили 7 и 7, пожалуйста, объясните
Ссылка для ответа на эти головоломки находится после 5-го изображения головоломки. Пожалуйста, дайте мне знать, если у вас возникнут проблемы с доступом к этой ссылке для ответов на эту головоломку?
2 вопроса ответьте пожалуйста
Ссылка для ответа на эти логические математические головоломки IQ дана в посте. Пожалуйста, проверьте ответы на все головоломки по этой ссылке.
 ..
.. Вопрос №3плззз как с детальностью?
Математический тест боковой логики
Следующие ниже вопросы проверят вашу способность мыслить нестандартно и математически.Если вы получаете более 50% из них правильно, вы, безусловно, сильны в своих навыках числового и латерального мышления.
Вопросы начинаются легко и становятся все сложнее.
- На вопрос, сколько ей лет, Бет ответила: «Через два года я буду вдвое старше, чем была пять лет назад». Сколько ей лет?
- Что весит больше? Фунт железа или фунт меди?
- Если у вас есть две монеты на общую сумму 11 пенсов, и одна из них не является пенни, что это за две монеты?
- Разделите 40 пополам и прибавьте десять.Какой ответ?
- С точностью до кубического сантиметра сколько почвы находится в яме размером 3 x 2 x 2 м?
- У фермера 15 коров, все, кроме 8, умирают.
 Сколько у него осталось?
Сколько у него осталось? - Возраст матери и ее сына-выпускника в сумме составляет 66 лет. Возраст матери – это возраст сына наоборот. Сколько им лет?
- Если полтора человека могут съесть полторы хот-дога за полторы минуты, сколько времени потребуется шести мужчинам, чтобы съесть шесть хот-догов?
- Ним зашел в супермаркет, чтобы купить фруктов.
По спецпредложению было три упаковки:
1) Десять виноградин и пять ягод клубники: 70 пенсов (сэкономьте 10 пенсов)
2) Десять клубники и десять абрикосов: 2 фунта стерлингов (экономия 40 пенсов)
3) Тридцать ягод винограда: 100 пенсов (сэкономьте 20 пенсов)
Какова будет полная стоимость одного винограда, одной клубники и одного абрикоса по нормальной цене (без специальных предложений)? - Количество воды, поступающей в резервуар, удваивается каждую минуту. Бак наполняется за час.Когда бак наполовину заполнен?
В озере есть столб.
 Половина шеста погружена в ил на дне пруда, другая треть покрыта водой, и 7 футов находится вне воды. Какова общая длина шеста?
Половина шеста погружена в ил на дне пруда, другая треть покрыта водой, и 7 футов находится вне воды. Какова общая длина шеста?- Если часовая стрелка перемещается на 1/60 градуса каждую минуту, на сколько градусов она переместится за час?
- Я трачу треть своих денег на гитару, половину на микрофон и четверть того, что у меня потом осталось на казу.Какая часть моих первоначальных денег осталась у меня?
- Как вы можете взять 1 из 19 и оставить 20?
- Вот список месяцев и код для каждого
- Январь: 7110
- Февраль: 826
- марта: 5313
- Апрель: 541
- Май: 3513
- июнь: 4610
- июль: 4710
- В банке 60 конфет.
 Первый человек взял одну конфету, и каждый следующий человек съел больше конфет, чем предыдущий, пока банка не опустела.
Первый человек взял одну конфету, и каждый следующий человек съел больше конфет, чем предыдущий, пока банка не опустела.
Какое наибольшее количество людей могло есть сладости из банки? - В Университете Кента 36 студентов посетили лекцию ЗАКОН, 39 слушали лекцию ART и 37 слушали лекцию DRAMA. Сколько человек посетили лекцию FILM?
- Если у вас пицца с толщиной корки «a» и радиусом «z», каков ее объем?
- Мужчина зашел в магазин, чтобы купить товар.Спросил у ассистента:
“Сколько стоит один?”
Помощник ответил 2 фунта, сэр “
“. “А сколько за 10?”
Помощник ответил “4 фунта стерлингов”
“Сколько за 100?”
Он получил ответ «6 фунтов стерлингов»
Что покупал мужчина? - В турнире на выбывание участвуют 23 футбольные команды. Какое наименьшее количество матчей им нужно сыграть, чтобы определить победителя?
- Сколько градусов между стрелками часов в 3.
 15?
15? - У вас 8 пакетов сахара, 7 весит столько же, один весит меньше. У вас также есть весы баланса. Найдите тот, который весит меньше, менее чем за 3 шага.
- Есть три коробки: в одной только яблоки, в одной только апельсины, а в третьей яблоки и апельсины. Ящики были помечены неправильно, так что никакая этикетка не идентифицирует фактическое содержимое ящика, который он маркирует. Открывая всего одну коробку, вы, не заглядывая в нее, вынимаете один фрукт.Глядя на фрукты, как сразу правильно промаркировать все коробки?
- 1/2 из 2/3 из 3/4 из 4/5 из 5/6 из 6/7 из 7/8 из 8/9 из 9/10 из 1000 =?
- Сколько раз стрелки часов перекрываются за 24 часа?
Какой код на август месяц?
ответов
- 12
- Они оба весят ровно фунт!
- 10p и 1p – другая монета может быть копейкой!
- 90.
 Деление на половину аналогично умножению на 2.
Деление на половину аналогично умножению на 2. - Нет – это дыра!
- Восемь
- 42 года и 24 года. (Один читатель указал, что это также может быть 51 и 15 лет, хотя другой указал, что 15 лет – это немного молодо для выпускника!)
- Полторы минуты
- Тридцать сортов винограда по нормальной цене стоят 1,20 фунта стерлингов, таким образом, виноград стоит 4 пенни за каждый.Десять виноградин и 5 ягод клубники стоят 80 пенсов по нормальной цене, виноград должен стоить 40 пенсов, поэтому клубника стоит 8 пенсов каждая. Десять клубники и десять абрикосов стоят 2,40 фунта по обычной цене, клубника – 80 пенсов, абрикосы – 16 пенсов за штуку. Таким образом, один абрикос + одна клубника и один виноград стоили 28 пенсов, всего .
- Через 59 минут
- Половина шеста в грязи
Треть покрыта водой
Следовательно, доля полюса в грязи и воде = 1/2 + 1/3 = 3/6 + 2/6 = 5/6
Следовательно, доля полюса вне воды = 1 – 5/6 = 1/6
Итак, одна шестая полюса составляет 7 футов.
Таким образом, общая длина шеста = 42 фута. - Одна степень
- После того, как я потратил треть своих денег на гитару, у меня осталось две трети. Я трачу половину этого на микрофон, так что это снова треть. После этого у меня остается одна треть моих первоначальных денег. Четверть этого я трачу на казу. Четверть одной трети – одна двенадцатая. Таким образом, у меня осталось три четверти одной трети моих денег.Три четверти одной трети – это , одна четверть моих денег осталась . (1/3 = 4/12. 4/12 – 1/12 = 3/12. 3/12 = 1/4)
- Если числа представлены римскими цифрами, возьмите I из XIX (19 римскими цифрами), у вас останется XX – 20 римскими цифрами.
- 681. Первая цифра – это количество букв, вторая – позиция месяца в календаре, а последняя цифра – это позиция первой буквы слова в алфавите.
- Первый человек берет 1 конфету, второй – две, третий – три и т.
 Д. 1+ 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45, поэтому первые девять человек берут 45 конфет на двоих. 10-й человек берет 15 конфет. Он или она не может взять меньше 9 и оставить меньше 11, иначе банка не будет пустой, но следующего человека не хватит, чтобы следовать правилу, изложенному в вопросе (что каждый человек берет больше чем предыдущий.Так что ответ: 10 человек .Спасибо Сэму Паркеру за подробное объяснение этого ответа
Д. 1+ 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45, поэтому первые девять человек берут 45 конфет на двоих. 10-й человек берет 15 конфет. Он или она не может взять меньше 9 и оставить меньше 11, иначе банка не будет пустой, но следующего человека не хватит, чтобы следовать правилу, изложенному в вопросе (что каждый человек берет больше чем предыдущий.Так что ответ: 10 человек .Спасибо Сэму Паркеру за подробное объяснение этого ответа - 40 студентов. Буква A = 1, B = 2, C = 3 и т. Д., Поэтому FILM = 6 + 9 + 12 + 13 = 40
- пи * з * з * а (!)
- Номера домов
- В соревнованиях на выбывание каждая команда, кроме победителя, проигрывает только один раз, поэтому количество матчей на единицу меньше количества команд в данном случае 23-1 = 22.
- Ответ – не ноль градусов, как может показаться на первый взгляд. Минутная стрелка будет на 15 минутах (90 градусов по часовой стрелке от вертикали), а часовая стрелка переместится на четверть расстояния между 15 и 16 часами.

Каждый час представляет 30 градусов (360/12), поэтому одна четверть часа равна 7,5 градусам, поэтому минутная стрелка будет на 97,5 градусах: разница между стрелками 7,5 градуса. - Отложить 2 пакета в сторону.Вес 3 оставшихся мешков против остальных 3 мешков. Если они весят одинаково, взвесьте 2 отложенных мешка, чтобы определить, какая из них тяжелее. Если, однако, один из комплектов из 3 мешков был тяжелее, отложите один из мешков из более тяжелого. Взвесьте оставшиеся два мешка из набора, чтобы определить, какой из них тяжелее. Если они равны, то вы знаете, что это 1 мешок, который вы откладываете.
- Откройте коробку с надписью «Яблоки и апельсины».
Вы знаете, что, поскольку ни одна из этикеток не является правильной, в коробке должны быть либо только яблоки, либо только апельсины.
Предположим, вы достали яблоко из этого ящика. Следовательно, это поле должно быть полем «Только яблоки».
Одно из двух оставшихся ящиков должно быть ящиком «Только апельсины». Однако один помечен «Только яблоки», а другой – «Только апельсины». Следовательно, ящик с надписью «Только яблоки» – это ящик, содержащий только апельсины, а ящик с надписью «Только апельсины» – это ящик, содержащий оба вида фруктов. - 100
- 22: минутная стрелка обойдет циферблат 24 раза, но часовая стрелка также совершит два оборота.24 минус 2 равно 22 .
Оценка
- 17 и больше: отлично – ты и счетный, и боковой!
- 10-16: хорошо
- Ниже 10: требуется немного больше практики в этих типах тестов!
См. Также
- Другие головоломки с числами см. Здесь
Если ваша математика немного ржавая , отличное место, чтобы освежить свои навыки, – это веб-сайт BBC Skillswise www. bbc.co.uk/skillswise
bbc.co.uk/skillswise
Отличный сайт для дальнейших математических головоломок – www.mathsisfun.com
Мок-тест по математической логике (математика) MHT CET 2021
0 из 25 вопросов завершено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
Информация
Вы уже проходили викторину раньше.Следовательно, вы не можете запустить его снова.
Вы должны войти или зарегистрироваться, чтобы начать викторину.
Сначала необходимо заполнить следующее:
Викторина завершена. Результаты записываются.
0 из 25 вопросов ответил правильно
Ваше время:
Истекло время
Вы набрали 0 из 0 баллов, (0)
Заработанные баллы: 0 из 0, (0)
0 Незавершенные эссе (Возможные баллы: 0)
| Средний балл | |
| Ваш результат |
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
1.
 1 Логические операции
1 Логические операцииМатематика обычно включает сочетание истинных (или гипотетически истинных) утверждения различными способами для создания (или доказательства) новых истинных утверждений. Начнем с разъяснения некоторых из этих фундаментальных идей.
Под предложением мы подразумеваем утверждение, имеющее определенное значение истинности , истина (T) или ложь (F) – например,
«В 1492 году Колумб плавал по синему океану». (T)
«Наполеон выиграл битву при Ватерлоо». (F)
В более общем смысле, формула означает утверждение, возможно, с участием некоторых переменных, которое либо истинно, либо false всякий раз, когда мы присваиваем определенные значения каждой из переменных.2 + y = 12 $ ”, то $ P (2,8) $ и $ P (3,3) $ равны истина, а $ P (1,4) $ и $ P (0,6) $ – ложь. Если $ Q (x, y, z) $ равно “$ x + y
Верно ли предложение или ложно, обычно зависит от того, что мы
говорят – одно и то же предложение может быть верным или ложным в зависимости от
по контексту; например, формула $ x | y $ означает `$ x $ делит
$ y $ ‘. То есть $ x | y $, если есть некоторый $ z $, так что $ y = x \ cdot z $. В настоящее время,
правда ли, что $ 3 | 2 $? Это зависит: если мы говорим о целых числах,
ответ – нет; если мы говорим о рациональных числах, ответ
да, потому что $ 2 = 3 \ cdot (2/3) $.(Конечно, если $ x \ not = 0 $ и $ y $ равны любых рациональных чисел, тогда $ x | y $, так что это не очень
полезное понятие. При нормальном использовании вид формулы
“$ x | y $” означает , что $ x $ и $ y $ являются целыми числами.)
То есть $ x | y $, если есть некоторый $ z $, так что $ y = x \ cdot z $. В настоящее время,
правда ли, что $ 3 | 2 $? Это зависит: если мы говорим о целых числах,
ответ – нет; если мы говорим о рациональных числах, ответ
да, потому что $ 2 = 3 \ cdot (2/3) $.(Конечно, если $ x \ not = 0 $ и $ y $ равны любых рациональных чисел, тогда $ x | y $, так что это не очень
полезное понятие. При нормальном использовании вид формулы
“$ x | y $” означает , что $ x $ и $ y $ являются целыми числами.)
Вселенная дискурса для определенного раздела математики – это набор, который содержит все интересное по этой теме. Когда мы изучение математических формул типа `$ x $ делит $ y $ ‘на переменные предполагается, что они принимают значения в любой вселенной дискурса подходит для конкретной темы.Вселенная дискурса обычно это ясно из обсуждения, но иногда нам нужно определите это явно для ясности. Универсум дискурса обычно обозначается $ U $.
Сложные предложения и формулы складываются из более простых,
используя небольшое количество логических операций . Просто горстка
этих операций позволят нам сказать все, что нам нужно сказать в
математика.
Просто горстка
этих операций позволят нам сказать все, что нам нужно сказать в
математика.
Если $ P $ – формула, то “not $ P $” – другое формула, которую мы символически записываем как $ \ lnot P $.Конечно, $ \ lnot P $ ложно, если $ P $ истинно, и наоборот – например,
«6 – не простое число» или «Неверно, что 6 – это простое число». премьер ” или “$ \ lnot (\ hbox {6 простое число}) $ ” (T)
«Рональд Рейган не был президентом». (F)
Предположим, что $ P $ и $ Q $ – формулы. потом «$ P $ и $ Q $» – это формула, записанная символически. как $ P \ land Q $, называемое соединением $ P $ и $ Q $. Для $ P \ land Q $ верны и $ P $, и $ Q $ должно быть истинным, в противном случае – ложным, например,
«5 долларов = 6 долларов и 7 долларов = 8 долларов.” (F)
«Сиэтл находится в Вашингтоне, а Бойсе – в Айдахо». (T)
«Толстой был русским, а Диккенс – Французский ”. (F)
Если $ P $ и $ Q $ являются формулами, то формула «$ P $ или $ Q $» символически записывается как $ P \ lor Q $, называемая дизъюнкция $ P $ и $ Q $. это
важно отметить, что это включительно или, то есть “либо
или оба”. Итак, если $ P $, $ Q $ или и $ P $, и $ Q $ верны,
так и $ P \ lor Q $. Единственный способ, которым $ P \ lor Q $ может быть ложным, – это если оба $ P $
и $ Q $ ложны – например,
это
важно отметить, что это включительно или, то есть “либо
или оба”. Итак, если $ P $, $ Q $ или и $ P $, и $ Q $ верны,
так и $ P \ lor Q $. Единственный способ, которым $ P \ lor Q $ может быть ложным, – это если оба $ P $
и $ Q $ ложны – например,
«Вашингтон находится в Канаде, а Лондон – в Англии.” (T)
“$ 5
«Ленин был испанцем или Ганди был итальянцем». (F)
Если $ P $ и $ Q $ – формулы, то «если $ P $, то $ Q $»
или написано “$ P $ подразумевает $ Q $”
$ P \ подразумевает Q $, используя условный символ ,
$ \ подразумевает $. Не очевидно (по крайней мере, для большинства людей), при каких условиях
обстоятельства $ P \ подразумевают, что Q $ должно быть истинным. Отчасти это потому, что
«if… then» используется более чем одним способом в обычном английском языке, однако
нам нужно исправить правило, которое позволит нам точно знать, когда $ P \ подразумевает
Q $ верно.Конечно, если $ P $ истинно, а $ Q $ ложно, $ P $ не может
следует $ Q $, поэтому $ P \ означает, что Q $ в этом случае неверно. Чтобы помочь нам с
в остальных случаях рассмотрим следующее утверждение:
Чтобы помочь нам с
в остальных случаях рассмотрим следующее утверждение:
«Если $ x $ меньше 2, тогда $ x $ меньше 4.»
Это утверждение должно быть верным независимо от значения $ x $. (при условии, что вселенная дискурса является чем-то знакомым, например целые числа). Если $ x $ равен 1, он оценивается как $ \ rm T \ implies T $, если $ x $ равно 3, оно становится $ \ rm F \ Impies T $, а если $ x $ равно 5, оно становится $ \ rm F \ влечет F $.Получается, что $ P \ подразумевает, что Q $ истинно, если $ P $ истинно, а $ Q $ ложно. Это правило, которое мы принимаем.
Наконец, с двумя условными обозначениями , записываемыми как $ \ Leftrightarrow $, соответствует фраза “тогда и только тогда” или “если и только если” коротко. Итак, $ P \ Leftrightarrow Q $ истинно, когда и $ P $, и $ Q $ имеют то же значение истинности, в противном случае – ложь.
Пример 1.1.2. Предположим, что $ P (x, y) $ – это «$ x + y = 2 $», а $ Q (x, y) $
равно «$ xy> 1 $». Тогда, когда $ x = 1 $ и $ y = 1 $,
$ \ lnot P (x, y) $, $ P (x, y) \ land Q (x, y) $, $ P (x, y) \ lor Q (x, y) $,
$ P (x, y) \ влечет Q (x, y) $ и $ P (x, y) \ Leftrightarrow Q (x, y) $
имеют истинностные значения F, F, T, F, F, соответственно, и когда
$ x = 2 $ и $ y = 3 $ имеют значения истинности
T, F, T, T, F соответственно.$ \ квадрат $
Тогда, когда $ x = 1 $ и $ y = 1 $,
$ \ lnot P (x, y) $, $ P (x, y) \ land Q (x, y) $, $ P (x, y) \ lor Q (x, y) $,
$ P (x, y) \ влечет Q (x, y) $ и $ P (x, y) \ Leftrightarrow Q (x, y) $
имеют истинностные значения F, F, T, F, F, соответственно, и когда
$ x = 2 $ и $ y = 3 $ имеют значения истинности
T, F, T, T, F соответственно.$ \ квадрат $
Используя операции $ \ lnot $, $ \ land $, $ \ lor $, $ \ implies $,
$ \ Leftrightarrow $, мы можем построить составных выражений, таких как
$$
(P \ land (\ lnot Q)) \ подразумевает ((\ lnot R) \ lor ((\ lnot P) \ land Q)).
$$
Как показывает этот пример, иногда необходимо
включать много круглых скобок, чтобы термины были сгруппированы
в формуле ясно. Как и в алгебре, где
умножение имеет приоритет перед сложением, мы можем
убрать скобки
согласование определенного порядка, в котором логические
операции выполняются.Мы
будет применять операции в этом порядке, начиная с
от начала до конца: $ \ lnot $, $ \ land $, $ \ lor $, $ \ подразумевает $
и $ \ Leftrightarrow $. Так
$$ A \ подразумевает B \ lor C \ land \ lnot D
$$
это сокращение от
$$ A \ подразумевает (B \ lor (C \ land (\ lnot D))).
$$
Как и в алгебре, часто имеет смысл включить
несколько дополнительных круглых скобок, чтобы убедиться, что предполагаемое значение ясно.
Большая часть информации, которую мы обсудили, может быть обобщена в таблицах истинности . Например, таблица истинности для
$ \ lnot P $ – это:
Так
$$ A \ подразумевает B \ lor C \ land \ lnot D
$$
это сокращение от
$$ A \ подразумевает (B \ lor (C \ land (\ lnot D))).
$$
Как и в алгебре, часто имеет смысл включить
несколько дополнительных круглых скобок, чтобы убедиться, что предполагаемое значение ясно.
Большая часть информации, которую мы обсудили, может быть обобщена в таблицах истинности . Например, таблица истинности для
$ \ lnot P $ – это:
В этой таблице две строки, потому что есть только две возможности для истинное значение $ P $.В других логических операциях используются две переменные, поэтому им требуется 4 строки в своих таблицах истинности.
| $ P $ | $ Q $ | $ P \ land Q $ | $ P \ lor Q $ | $ P \ Rightarrow Q $ | $ P \ Leftrightarrow Q $ |
|---|---|---|---|---|---|
| T | T | T | T | T | T |
| F | T | F | T | T | F |
| T | F | F | T | F | F |
| F | F | F | F | T | T |
У любого составного выражения есть таблица истинности. n $
строк в таблице, потому что есть много разных способов назначить
Команды “T” и “F” для простых формул $ n $ в составном выражении.
Таблица истинности для $ (P \ land Q) \ lor \ lnot R $:
n $
строк в таблице, потому что есть много разных способов назначить
Команды “T” и “F” для простых формул $ n $ в составном выражении.
Таблица истинности для $ (P \ land Q) \ lor \ lnot R $:
| $ P $ | $ Q $ | $ | $ P \ land Q $ | $ \ lnot R $ | $ (P \ land Q) \ lor \ lnot R $ |
|---|---|---|---|---|---|
| T | T | T | T | F | T |
| F | T | T | F | F | F |
| T | F | T | F | F | F |
| F | F | T | F | F | F |
| T | T | F | T | T | T |
| F | T | F | F | T | T |
| T | F | F | F | T | T |
| F | F | F | F | T | T |
Обратите внимание на то, как включение промежуточных шагов упрощает отображение таблицы. рассчитывать и читать.
рассчитывать и читать.
Тавтология – это логическое выражение, которое всегда оценивается как T, то есть последний столбец своей таблицы истинности состоит только из Т. Иногда говорят, что тавтология – это действительное ; хотя «действительный» используется в других контекстах как что ж, это не должно вызывать путаницы. Например, $ (P \ land Q) \ lor P \ Leftrightarrow P $ является тавтологией, поскольку ее таблица истинности:
| $ P $ | $ Q $ | $ P \ land Q $ | $ (P \ land Q) \ lor P $ | $ (P \ land Q) \ lor P \ Leftrightarrow P $ |
|---|---|---|---|---|
| T | T | T | T | T |
| F | T | F | F | T |
| T | F | F | T | T |
| F | F | F | F | T |
Мы перечислим несколько важных тавтологий в следующей теореме.
Теорема 1.1.3 Справедливы следующие утверждения.
а) $ P \ Leftrightarrow \ lnot \ lnot P $
б) $ P \ lor Q \ Leftrightarrow Q \ lor P $
c) $ P \ land Q \ Leftrightarrow Q \ land P $
d) $ (P \ land Q) \ land R \ Leftrightarrow P \ land (Q \ land R) $
e) $ (P \ lor Q) \ lor R \ Leftrightarrow P \ lor (Q \ lor R) $
f) $ P \ land (Q \ lor R) \ Leftrightarrow (P \ земля Q) \ lor (P \ земля R) $
г) $ P \ lor (Q \ land R) \ Leftrightarrow (P \ lor Q) \ land (P \ lor R) $
ч) $ (P \ подразумевает Q) \ Leftrightarrow (\ lnot P \ lor Q) $
i) $ P \ подразумевает (P \ lor Q) $
j) $ P \ land Q \ подразумевает Q $
k) $ (P \ Leftrightarrow Q) \ Leftrightarrow ((P \ подразумевает Q) \ land (Q \ влечет P)) $
l) $ (P \ подразумевает Q) \ Leftrightarrow (\ lnot Q \ подразумевает \ lnot P) $
Доказательство. Доказательства оставлены как упражнения. $ \ qed $
$ \ qed $
Заметим, что (b) и (c) – коммутативные законы, (d) и (e) – ассоциативные законы и (f) и (g) говорят, что $ \ land $ и $ \ lor $ распределяются друг над другом. Это говорит о том, что существует форма алгебры для логических выражений, аналогичных алгебре для числовых выражений. Этот предмет называется Boolean Algebra и имеет множество применений, особенно в информатике.
Если две формулы всегда принимают одно и то же значение истинности, несмотря ни на что
элементы из вселенной дискурса мы заменяем различными
переменных, то мы говорим, что они равны эквивалентно .Стоимость эквивалента
формулы в том, что они говорят одно и то же. Это всегда правильный шаг
в доказательстве заменить некоторую формулу на эквивалентную. Кроме того,
многие тавтологии содержат важные идеи для построения доказательств. За
Например, (k) говорит, что если вы хотите показать, что $ P \ Leftrightarrow Q $, это
возможно (и часто желательно) разбить доказательство на два
частей, одна из которых доказывает импликацию $ P \ влечет Q $, а вторая
доказывая , обратное , $ Q \ влечет P $.
Читая теорему 1.1.3 у вас может быть заметил, что $ \ land $ и $ \ lor $ удовлетворяют многим аналогичным свойствам. Эти понятия называются «двойственными» – для любого свойства один, есть почти идентичное свойство, которому удовлетворяет другой, при этом экземпляры двух операций поменялись местами. Это часто означает, что когда мы доказываем результат, включающий одно понятие, мы получаем соответствующий результат для его дуала без дополнительной работы.
Джордж Буль. логический
(1815–1864) имел только общее школьное образование, хотя учился
Греческий и латинский сами по себе.Он начал свою карьеру элементарным
школьный учитель, но решил, что ему нужно больше узнать о
математике, поэтому он начал изучать математику, а также
языки, необходимые для чтения современной литературы на
математика. В 1847 году он опубликовал небольшую книгу The Mathematical
Анализ логики , который справедливо можно сказать, положил начало исследованию
математической логики. Ключевой вклад работы был в
новое определение “математики”, чтобы не означать просто “изучение чисел и
величина », но изучение символов и манипуляции с ними в соответствии с
к определенным правилам.Важность этого уровня абстракции для
будущее математики трудно переоценить. Наверное, на
Благодаря этой работе он перешел на работу в Куинс-колледж в Корке.
Ключевой вклад работы был в
новое определение “математики”, чтобы не означать просто “изучение чисел и
величина », но изучение символов и манипуляции с ними в соответствии с
к определенным правилам.Важность этого уровня абстракции для
будущее математики трудно переоценить. Наверное, на
Благодаря этой работе он перешел на работу в Куинс-колледж в Корке.
В «Исследование законов мысли» , опубликованном в 1854 г.,
Буль установил настоящую формальную логику, развивая то, что сегодня называется
Булева алгебра, или иногда алгебра множеств . Он использовал символы для
сложение и умножение как операторы, но полностью абстрактно
смысл.Сегодня эти символы все еще иногда используются в логических
алгебры, хотя символы `$ \ land $ ‘и` $ \ lor $’, `$ \ cap $ ‘и
Также используются `$ \ cup $ ‘. Буль применил алгебраические манипуляции к
процесс рассуждения. Вот простой пример такого рода
манипуляции, которые он совершил: уравнение $ xy = x $ (которое сегодня можно было бы записать
$ x \ land y = x $ или $ x \ cap y = x $) означает, что `все, что удовлетворяет
$ x $ удовлетворяет $ y $, или, в наших терминах, $ x \ влечет y $. Если также $ yz = y $ (что
есть, $ y \ подразумевает z $), то замена $ y = yz $ на $ xy = x $ дает
$ x (yz) = x $ или $ (xy) z = x $.2 + bD + c = 0 $, лечение
$ D $ в виде числа предоставляет информацию о решениях для
дифференциальное уравнение.
Если также $ yz = y $ (что
есть, $ y \ подразумевает z $), то замена $ y = yz $ на $ xy = x $ дает
$ x (yz) = x $ или $ (xy) z = x $.2 + bD + c = 0 $, лечение
$ D $ в виде числа предоставляет информацию о решениях для
дифференциальное уравнение.
Информация здесь взята из A History of Mathematics, by Карл Б. Бойер, Нью-Йорк: Джон Вили и сыновья, 1968. Подробнее информацию см. Лекции о десяти британских математиках , автор Александр Макфарлейн, Нью-Йорк: John Wiley & Sons, 1916.
Упражнения 1.1
Пример 1.1.1 Постройте таблицы истинности для следующих логических выражений:
а) $ (P \ land Q) \ lor \ lnot P $
б) $ P \ подразумевает (Q \ land P) $
c) $ (P \ land Q) \ Leftrightarrow (P \ lor \ lnot R) $
г) $ \ lnot P \ подразумевает \ lnot (Q \ lor R) $
Пр. 1.1,2 Проверьте тавтологии теоремы 1.1.3.
Пример 1.1.3 Предположим, что $ P (x, y) $ – это формула «$ x + y = 4 $», а $ Q (x, y) $ – это формула “$ x
$ P (x, y) \ land Q (x, y) $, $ \ lnot P (x, y) \ lor Q (x, y) $,
$ P (x, y) \ влечет \ lnot Q (x, y) $, $ \ lnot (P (x, y) \ Leftrightarrow Q (x, y)) $,
, используя значения:
| a) $ x = 1, y = 3 $ | c) $ x = 1, y = 2 $ |
| b) $ x = 3, y = 1 | d) $ x = 2, y = 1 $ |
Пр. 1.1,4
1.1,4
а) Найдите таблицы истинности для $$ P \ land (\ lnot Q) \ land R, \ quad \ quad (\ lnot P) \ land Q \ land (\ lnot R) $$
б) Используйте их, чтобы найти таблицу истинности для $$ (П \ земля (\ lnot Q) \ земля R) \ lor ((\ lnot P) \ земля Q \ земля (\ lnot R)) $$
c) Используйте метод, предложенный в частях (a) и (b) найти формулу со следующей таблицей истинности.
| $ P $ | $ Q $ | $ | ??? |
|---|---|---|---|
| T | T | T | T |
| F | T | T | F |
| T | F | T | F |
| F | F | T | F |
| T | T | F | T |
| F | T | F | T |
| T | F | F | F |
| F | F | F | F |
г)
Используйте метод, предложенный частями (a) – (c), чтобы
объясните, почему любой список из $ 2 ^ n $ T и F является
последний столбец таблицы истинности для некоторой формулы с $ n $ буквами.
Пример 1.1.5 Если $ P_1, P_2, \ ldots, P_n $ – список формул $ n $, максимальное количество составных формул, использующих этот список, нет двух из которых эквивалентны?
MCQ по математической логике [Free PDF] – Ответ на объективный вопрос для викторины по математической логике
Предложение (P ⇒ Q) ∧ (Q ⇒ P) является
- тавтология
- противоречие
- случайность
- абсурд
(подробное решение ниже)
Вариант 3: непредвиденные обстоятельства
Концепция:
- Составное суждение, которое всегда верно для всех возможных значений истинности предложений, называется тавтологией.
- Сложное суждение, которое всегда ложно, называется противоречием.
- Предложение, которое не является ни тавтологией, ни противоречием, называется случайностью.
Формула:
a ⇒ b = ¬ a ∨ b
Расчет
(P ⇒ Q) ∧ (Q ⇒ P)
(¬ P ∨ Q) ∧ (¬ Q ∨ P)
заменить ¬ на НЕ (̅), ∨ на ИЛИ (+) и ∧ на И (.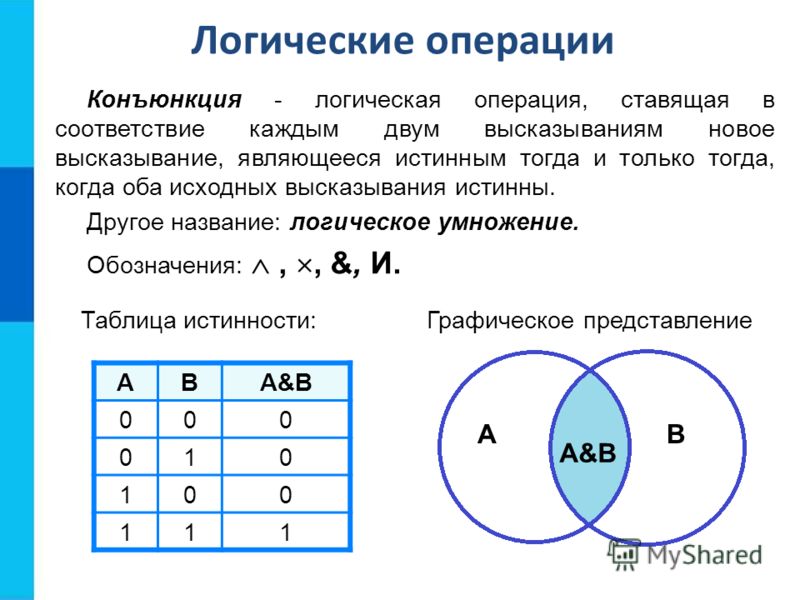 )
)
(P̅ + Q). (Q̅ + P)
P.Q̅ + P̅.P + Q.Q̅ + QP
P̅.Q̅ + QP
P ⊙ Q
Таблица истинности:
Вход P | Ввод Q | Выход Y = P ⊙ Q |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Предложение (P ⇒ Q) ∧ (Q ⇒ P) является случайностью
Советы и рекомендации
(P ⇒ Q) ∧ (Q ⇒ P) = P ⇔ Q (Это всегда случайность)
Отношение площади вписанного круга к площади описанного круга равностороннего треугольника составляет _____
- \ (\ frac {1} {8} \)
- \ (\ frac {1} {6} \)
- \ (\ frac {1} {2} \)
- \ (\ frac {1 } {4} \)
(подробное решение ниже)
Вариант 4: \ (\ frac {1} {4} \)
Пояснение:
Пусть радиус описанной окружности равен R, а радиус вписанной окружности равен r. 2} \)
2} \)
\ (= \ frac {1} {4} \)
Платформа обучения №1 в Индии
Начать полную подготовку к экзамену
Ежедневные живые мастер-классы
Банк практических вопросов
Пробные тесты и викторины
Нам доверяют 2,38,35,014+ студентовКакое из следующих утверждений логически эквивалентно утверждению (¬ p) ⇒ (¬ q)?
- p ⇒ q
- q ⇒ p.
- (¬q) ∨ с.
- (¬p) ∨ в
- только I
- только II и IV
- только II
- только II и III
(подробное решение ниже)
Вариант 4: только II и III
Формула :
p ⇒ q ≡ ¬ p ∨ q
Деривация:
(¬ p) ⇒ (¬ q)
≡ ¬ (¬ p) ∨ (¬ q)
п ∨ (¬ q)
Заявление I,
p ⇒ q
≡ (¬ p) ∨ q,
Заявление II,
q ⇒ p
≡ (¬ q) ∨ п.
п ∨ (¬ q)
Заявление III,
(¬q) ∨ п.
п ∨ (¬ q)
Заявление IV,
(¬p) ∨ в
Только варианты II и III соответствуют заданному значению.
Альтернативный метод:
Используя таблицу истинности:
П | q | ¬ п | ¬ q | (¬ p) ⇒ .(¬ q) | p ⇒ q | q ⇒ p . | (¬q) ∨ p | (¬p) ∨ в |
Истинно | Истинно | Ложь | Ложь | Истинно | Истинно | Истинно | Истинно | Правда |
Истинно | Ложь | Ложь | Истинно | Истинно | Ложь | Истинно | Истинно | Ложь |
Ложь | Истинно | Истинно | Ложь | Ложь | Истинно | Ложь | Ложь | Правда |
Ложь | Ложь | Истинно | Истинно | Истинно | Истинно | Истинно | Истинно | Правда |

Платформа обучения №1 в Индии
Начать полную подготовку к экзамену
Ежедневные живые мастер-классы
Банк практических вопросов
Пробные тесты и викторины
Нам доверяют 2,38,35,014+ студентовПусть p, q, r, s представляют следующие предложения.
p: x ∈ {8, 9, 10, 11, 12}
q: x – составное число
r: x – идеальный квадрат
s: x – простое число
Целое число x ≥ 2, удовлетворяющее ¬ ((p ⇒ q) ∧ (¬ r ∨ ¬ s)), равно __________
Ответ (подробное решение ниже) 11
Данные:
p: x ∈ {8, 9, 10, 11, 12}
q: x – составное число
r: x – идеальный квадрат
s: x – простое число
Пояснение:
p ⇒ q означает p̅ + q
As, q – составное число Итак, p ⇒ приводит к {8, 9, 10, 12}
Поскольку, r: x представляет собой полный квадрат, ¬ r дает все числа, не являющиеся полными квадратами
Итак, ¬ r: {8, 10, 11, 12}
¬с: {8, 9, 10, 12}
¬ r ∨ ¬ s = {8, 9, 10, 11, 12}
Теперь (p ⇒ q) ∧ (¬ r ∨ ¬ s) = {8, 9, 10, 12}
¬ ((p ⇒ q) ∧ (¬ r ∨ ¬ s)) дает число, которого нет в ((p ⇒ q) ∧ (¬ r ∨ ¬ s))
¬ ((p ⇒ q) ∧ (¬ r ∨ ¬s)) даст {11}.
Платформа обучения №1 в Индии
Начать полную подготовку к экзамену
Ежедневные живые мастер-классы
Банк практических вопросов
Пробные тесты и викторины
Нам доверяют 2,38,35,014+ студентов- (¬ p ∧ r) ∧ (¬ r → (p ∧ q))
- (¬ p ∧ r) ∧ ((p ∧ q) → ¬ r)
- (¬ p ∧ r) ∨ ((p ∧ q) → ¬ r)
- (¬ p ∧ r) ∨ (r → (p ∧ q))
(подробное решение ниже)
Вариант 1: (¬ p ∧ r) ∧ (¬ r → (p ∧ q))
Концепция:
И оператор –
Только если означает: q Только если означает, что p является необходимым условием для q, обозначается как: q → p
Пояснение:
p = идет дождь
q = холодно
r = нравится
¬ p = дождя нет
Теперь, «’ Дождь не идет, и приятно »= ¬ p ʌ r
«это неприятно, только если идет дождь и холодно», обозначаемое как = ¬ r → (p ʌ q)
Итак, общее выражение для выражения «Дождь не идет, и это приятно, и это не приятно, только если идет дождь и холодно» будет:
(¬ p ʌ r) ʌ (¬ r → (p ʌ q))
Вариант 1) верен.
Платформа обучения №1 в Индии
Начать полную подготовку к экзамену
Ежедневные живые мастер-классы
Банк практических вопросов
Пробные тесты и викторины
Нам доверяют 2,38,35,014+ студентовКакие из следующих пар предложений не являются логически эквивалентными?
- ((p → r) ∧ (q → r)) и ((p ∨ q) → r)
- p ↔ q и (¬ p ↔ ¬ q)
- (p → q) ∧ (q → p ) и p ↔ q
- ((p ∧ q) → r) и ((p → r) ∧ (q → r))
(подробное решение ниже)
Вариант 4: ((p ∧ q) → r) и ((p → r) ∧ (q → r))
Правильный ответ – вариант 4.
Ключевые точки
Вариант A: ((p → r) ∧ (q → r)) и ((p ∨ q) → r)
Оба равны, и это дает одну и ту же таблицу истинности. Следовательно, это логически эквивалентно.
Вариант B: p ↔ q и (¬ p ↔ ¬ q)
(p → q) (q → p) и (¬ p → q) (¬ q → p)
(p + q̅) (q + p̅) и (p + q̅) (q + p̅)
Оба равны, и это дает одну и ту же таблицу истинности. Следовательно, это логически эквивалентно.
Следовательно, это логически эквивалентно.
Вариант C: (p → q) ∧ (q → p) и p ↔ q
Обе таблицы дают равные значения.Следовательно, это логически эквивалентно.
Вариант D: ((p ∧ q) → r) и ((p → r) ∧ (q → r))
| п. | Q | R | ¬P | ¬Q | P⇒ | рупий.Q⇒ | рупий(P⇒R) ∧ (Q⇒R) | P ∧ Q | P ∧ Q⇒R |
| Т | Т | Т | F | F | Т | Т | Т | Т | Т |
| Т | Т | F | F | F | F | F | F | Т | F |
| Т | F | Т | F | Т | Т | Т | Т | F | Т |
| Т | F | F | F | Т | F | Т | F | F | Т |
| Ф | Т | Т | Т | F | Т | Т | Т | F | Т |
| Ф | Т | F | Т | F | Т | F | F | F | Т |
| Ф | F | Т | Т | Т | Т | Т | Т | F | Т |
| Ф | F | F | Т | Т | Т | Т | Т | F | Т |
Приведенная выше таблица истинности не эквивалентна. Следовательно, приведенное выше утверждение – Истинно, логически не эквивалентно.
Следовательно, приведенное выше утверждение – Истинно, логически не эквивалентно.
∴ Следовательно, правильный ответ: ((p ∧ q) → r) и ((p → r) ∧ (q → r)).
Платформа обучения №1 в Индии
Начать полную подготовку к экзамену
Ежедневные живые мастер-классы
Банк практических вопросов
Пробные тесты и викторины
Нам доверяют 2,38,35,014+ студентовРассмотрим следующие два утверждения.
S1: Если известно, что кандидат коррумпирован, он не будет избран
S2: Если кандидат добрый, он будет избран
Какое из следующих утверждений следует из S1 и S2 согласно логическим правилам логического вывода?- Если известно, что человек коррумпирован, он добрый
- Если известно, что человек коррумпирован, он не добрый
- Если человек добрый, о нем не известно, что он коррумпирован
- Если человек не добрый, коррумпированный не известен
(подробное решение ниже)
Вариант 3. Если человек добрый, о нем не известно, что он коррумпирован
Если человек добрый, о нем не известно, что он коррумпирован
Концепция:
Гипотетический силлогизм,
Если p → q и q → r, то p → r
Формула:
p → q ≡ ¬ q → ¬ p ≡ ¬ p ∨ q
Пояснение:
C (x): x, как известно, поврежден
E (x): x будет избран
K (x): x вид
Заявление S1 можно записать как:
\ ({\ rm {S}} 1 \ Equiv {\ rm {C}} \ left ({\ rm {x}} \ right) {\ rm {\;}} \ to \ neg {\ rm {E }} \ left ({\ rm {x}} \ right) \)
S2 можно записать как:
\ ({\ rm {S}} 2 \ Equiv {\ rm {K}} \ left ({\ rm {x}} \ right) \ to {\ rm {E}} \ left ({\ rm {x }} \ right) \ Equiv \ neg {\ rm {E}} \ left ({\ rm {x}} \ right) \ to \ neg {\ rm {K}} \ left ({\ rm {x}} \ справа) \)
Используя гипотетический силлогизм,
Из S1 и S2 вывод
\ ({\ rm {C}} \ left ({\ rm {x}} \ right) \ to {\ rm {\;}} \ neg {\ rm {\; K}} \ left ({\ rm {x}} \ right) \ Equiv {\ rm {K}} \ left ({\ rm {x}} \ right) \ to \ neg {\ rm {C \;}} \ left ({\ rm {x }} \ right) \)
Если человек добрый, то он не известен своей испорченностью.
Платформа обучения №1 в Индии
Начать полную подготовку к экзамену
Ежедневные живые мастер-классы
Банк практических вопросов
Пробные тесты и викторины
Нам доверяют 2,38,35,014+ студентовРассмотрим следующие выражения:
(i) ложь
(ii)
кв.(iii) верно
(iv) P ∨ Q
(v) ¬ Q ∨ P
Количество приведенных выше выражений, которые логически подразумеваются P ∧ (P ⇒ Q), равно ________Ответ (подробное решение ниже) 4
Концепция:
P ⇒ Q означает P̅ ∨ Q
Пояснение:
P ∧ (P ⇒ Q) = P ∧ (P̅ ∨ Q) = P ∧ Q
Рассмотрим П.Q как A.
Мы должны найти, какое из данного выражения подразумевается A, то есть (A =>)
Построить таблицу истинности для каждого варианта отдельно
Пусть A ≡ P ∧ (P ⇒ Q)
-П | квартал | P ⇒ Q . | А |
Правда | Правда | Правда | Правда |
Правда | Ложь | Ложь | Ложь |
Ложь | Правда | Правда | Ложь |
Ложь | Ложь | Правда | Ложь |
Рассмотрим все варианты по порядку:
(i) Неверно
-П | квартал | А | A ⇒ Ложь |
Правда | Правда | Правда | Ложь |
Правда | Ложь | Ложь | Правда |
Ложь | Правда | Ложь | Правда |
Ложь | Ложь | Ложь | Правда |
Здесь все не так. Значит, этот вариант неверен.
Значит, этот вариант неверен.
(ii)
кв.-П | квартал | А | А ⇒ Q |
Правда | Правда | Правда | Правда |
Правда | Ложь | Ложь | Правда |
Ложь | Правда | Ложь | Правда |
Ложь | Ложь | Ложь | Правда |
Эта опция подразумевается P ∧ (P ⇒ Q).
iii) Верно
-П | квартал | А | А ⇒ Истинно |
Правда | Правда | Правда | Правда |
Правда | Ложь | Ложь | Правда |
Ложь | Правда | Ложь | Правда |
Ложь | Ложь | Ложь | Правда |
iv) P ∨ Q
-П | квартал | А | A ⇒ P ∨ Q |
Правда | Правда | Правда | Правда |
Правда | Ложь | Ложь | Правда |
Ложь | Правда | Ложь | Правда |
Ложь | Ложь | Ложь | Правда |
Это тавтология. Итак, вариант правильный.
Итак, вариант правильный.
v) –Q ∨ P
-П | квартал | A ≡ P ∧ (P ⇒ Q) | A ⇒ –Q ∨ P |
Правда | Правда | Правда | Правда |
Правда | Ложь | Ложь | Правда |
Ложь | Правда | Ложь | Правда |
Ложь | Ложь | Ложь | Правда |
Это тоже тавтология.
Итак, данное выражение подразумевает всего 4.Платформа обучения №1 в Индии
Начать полную подготовку к экзамену
Ежедневные живые мастер-классы
Банк практических вопросов
Пробные тесты и викторины
Нам доверяют 2,38,35,014+ студентов- | x | + | y | = 2
- | x + y | = 2
- | y | = x 2 + sin x
- | x | 2 – х
(подробное решение ниже)
Вариант 4: | x | 2 – х
Концепция:
Функция: Уравнение называется функцией, если для каждого возможного входного значения существует ровно одно выходное значение.
Пояснение:
Здесь уравнение может быть f (x) или f (y), поэтому уравнение, которое удовлетворяет указанным выше критериям, можно назвать функцией.
Уравнение 1) | x | + | y | = 2
- Это уравнение не может быть функцией x или y, поскольку модуль всегда дает два значения для x или y.
Уравнение 2) | x + y | = 2
- Это уравнение не может быть функцией, поскольку открытие скобки модуля дает два значения как x, так и y.
Уравнение 3) | y | = x2 + грех x
- Это уравнение не может быть функцией, поскольку из-за | y | отрицательная часть правой стороны будет отражаться от оси Y и, наконец, даст несколько y для того же x
Уравнение 4) | x | 2 – x
- Если принять уравнение как y = | x | 2 – x, оно становится функцией x.
- Для каждого x существует только одно значение y.

Следовательно, искомое уравнение, которое можно назвать функцией, это | x | 2 – x.
Платформа обучения №1 в Индии
Начать полную подготовку к экзамену
Ежедневные живые мастер-классы
Банк практических вопросов
Пробные тесты и викторины
Нам доверяют 2,38,35,014+ студентовКакое из следующих логических выражений НЕ является тавтологией?
- \ (((a → b) ∧ (b → c)) → (a → c) \)
- \ ((a↔c) → (∼b → (a∧c)) \)
- \ ((a∧b∧c) → (c∨a) \)
- \ (a → (b → a) \)
(подробное решение ниже)
Вариант 2: \ ((a↔c) → (∼b → (a∧c)) \)
(i) Тавтология: импликация транзитивна.
(ii). Непредвиденные обстоятельства: истинное значение этой формулы зависит от значений a, b и c.
(iii). Тавтология: Следующее ясно следует из антецедента.
(iv). Тавтология: a-> b ложно, только когда a истинно, а b ложно.
Платформа обучения №1 в Индии
Начать полную подготовку к экзамену
Ежедневные живые мастер-классы
Банк практических вопросов
Пробные тесты и викторины
Нам доверяют 2,38,35,014+ студентов- ∀𝑥 ∃𝑦 (𝑥,) ↔ ∃𝑦 ∀𝑥 𝑅 (𝑥, 𝑦)
- (∀𝑥 [∃𝑦 (𝑥,) → 𝑆 (𝑥, 𝑦)]) → ∀𝑥∃𝑦 𝑆 (𝑥 , 𝑦)
- [∀𝑥 ∃𝑦 (𝑃 (𝑥, 𝑦) → 𝑅 (𝑥, 𝑦)] ↔ [∀𝑥 ∃𝑦 (¬ (𝑥, 𝑦) ∨ 𝑅 (𝑥, 𝑦)]
- ∀ 𝑥 ∀𝑦 (𝑥,) → ∀𝑥 ∀𝑦 𝑃 (𝑦, 𝑥)
(подробное решение ниже)
Вариант 3: [∀𝑥 ∃𝑦 (𝑃 (𝑥, 𝑦) → 𝑅 (𝑥, 𝑦)] ↔ [∀𝑥 ∃𝑦 (¬ (𝑥, 𝑦) ∨ 𝑅 (𝑥 , 𝑦)]
Вариант 1 : ∀ x ∃y R (x, y) ↔ ∃y ∀ x R (x, y)
∀ x ∃y R (x, y) не эквивалентно ∃y ∀ x R (x, y).
Пусть R (x, y) представляет x> x для набора чисел как вселенной
Пример:
∀ x ∃y R (x, y) означает, что для каждого числа x существует число y, которое меньше x, что является истинным.
В то время как ∃y ∀ x R (x, y) означает, что существует число, которое меньше любого числа. Что ложно
Вариант 2: (∀ x (∃y R (x, y) → S (x, y)]) → ∀ x ∃y S (x, y)
Этот вариант не тавтология. Это ложное выражение, потому что два предиката не могут быть эквивалентны одному предикату справа.
Вариант 4: ∀ x ∀ y P (x, y) → ∀ x ∀ y P (y, x)
Рассмотрим P (x, y) как x , то ∀ x ∀ y P (x, y) представляет для каждого числа x все y больше x. ∀ x ∀ y P (y, x), это означает, что для каждого числа y существует каждый x, который больше y. Эти два утверждения одновременно не эквивалентны. Так что это не тавтология. Вариант 3: [∀x ∃y (P (x, y) → R (x, y)] ↔ [∀ x ∃y (¬ P (x, y) ∨ R (x, y)] As, мы знаем, что P → R = ¬ P + R Здесь то же самое, что и импликационное, так что это тавтология. Платформа обучения №1 в Индии Начать полную подготовку к экзамену Ежедневные живые мастер-классы Банк практических вопросов Пробные тесты и викторины Вариант 4: 64 Пояснение: У нас, \ (\ sqrt {1 + \ frac {x} {{225}}} = \ frac {{17}} {{15}} \) Квадрат с обеих сторон получаем, \ ({1 + \ frac {x} {{225}}} = \ frac {{289}} {{225}} \) \ ({\ frac {x} {{225}}} = \ frac {{289 ~ – ~ 225}} {{225}} \) \ ({\ frac {x} {{225}}} = \ frac {{64}} {{225}} \) х = 64 Следовательно, искомое значение x = 64. Платформа обучения №1 в Индии Начать полную подготовку к экзамену Ежедневные живые мастер-классы Банк практических вопросов Пробные тесты и викторины Вариант 1: 4 Концепция: log x n yz = (1 / n) × logx yz, также журнал a a = 1 Расчет: Здесь мы можем переписать указанный выше термин как \ ({4 ^ {2 {{\ log} _9} 3}} \) \ ({4 ^ {2 {{\ log} _9} 3}} \) = \ ({4 ^ {2 {{\ log} _ {{3 ^ 2}}} 3}} \) \ ({4 ^ {2 {{\ log} _9} 3}} \) = \ ({4 ^ {\ left ({2 \; \ times \; \ frac {1} {2} \; \ times \; {{\ log} _3} 3} \ right)}} \) \ ({4 ^ {2 {{\ log} _9} 3}} \) = 4 Следовательно, значение \ ({4 ^ {2 {{\ log} _9} 3}} \) равно 4. Платформа обучения №1 в Индии Начать полную подготовку к экзамену Ежедневные живые мастер-классы Банк практических вопросов Пробные тесты и викторины Рассмотрим логическое предложение первого порядка F: ∀x (∃ y R (x, y)). Предполагая, что логические домены непустые, какое из предложений ниже подразумевается F? Вариант 2: только I и IV Концепция: Истинно Ложь ∀ x Все По крайней мере одна ложная ∃ x По крайней мере, правда Для всех x, если P (x) ложно, если мы принимаем предикат как P (x) Один из способов ответить на этот вопрос – рассмотреть x и y как домены с помощью некоторых операторов. Предположим, что x для девочки, а y для мальчика. Учитывая, что F – это ∀x (∃ y R (x, y)), в случае английского языка это означает F: Все девочки любят мальчиков Теперь проверьте все варианты по очереди. Из этого утверждения ясно, что это подмножество данного оператора. ИСТИНА Заместитель: ¬ ∃x (∀y ¬ R (x, y)) ≡ ∀x (¬ ∀y (¬ R (x, y))) ≡ ∀x (∃x R (x, y)) Платформа обучения №1 в Индии Начать полную подготовку к экзамену Ежедневные живые мастер-классы Банк практических вопросов Пробные тесты и викторины Если T (x) означает тригонометрическую функцию, P (x) означает, что x является периодической функцией, а C (x) означает, что x является непрерывной функцией, то утверждение «Это не тот случай, когда некоторые тригонометрические функции не являются периодическими» можно логически представить как Вариант 1: ¬ ∃x [T (x) ∧ ¬ P (x)] Заявление: «Некоторые тригонометрические функции не являются периодическими» “некоторые тригонометрические функции не периодические” означает Существуют тригонометрические функции, которые также не являются периодическими. ∃x [T (x) ∧ ¬ P (x)] Отрицание этого. «Некоторые тригонометрические функции не являются периодическими» ¬ ∃x [T (x) ∧ ¬ P (x)] Платформа обучения №1 в Индии Начать полную подготовку к экзамену Ежедневные живые мастер-классы Банк практических вопросов Пробные тесты и викторины Вариант 3: 14 Пояснение: У нас есть \ (x = 7-4 \ sqrt 3 \) Помещая это значение x в \ (x + \ frac {1} {x} \), получаем \ (x + \ frac {1} {x} \) = \ (7-4 \ sqrt 3 + \ frac {1} {{7-4 \ sqrt 3}} \) Обоснование знаменателя 2-го члена \ (x + \ frac {1} {x} \) = \ (7-4 \ sqrt 3 \; + \; 7 + 4 \ sqrt 3 \) \ (x + \ frac {1} {x} \) = 14 Следовательно, значение \ (x + \ frac {1} {x} \) для данного значения x равно 14. Платформа обучения №1 в Индии Начать полную подготовку к экзамену Ежедневные живые мастер-классы Банк практических вопросов Пробные тесты и викторины Вариант 4: Всегда ИСТИНА, если q ИСТИНА (p → q) → r – противоречие, которое возможно только тогда, когда r ложно и (p → q) истинно. Отсюда мы можем ясно сказать, что вариант 4 верен, поскольку (r → p) → q означает ¬ (r → p) ∨ q. Поскольку r ложно, (r → p) истинно, а ¬ (r → p) становится ложным. Итак, это становится (false ∨ q). Теперь это полностью зависит от q. Когда q истинно, это значение всегда будет истинным. Альтернативный метод: Пусть X ≡ p → q, Y ≡ (p → q) → r ≡ X → r, Z ≡ r → p и W ≡ (r → p) → q ≡ Z → p Использование таблицы истинности п. q r Х Я Z Вт 0 0 0 1 0 1 0 0 0 1 1 1 0 1 0 1 0 1 0 1 1 0 1 1 1 1 0 1 1 0 0 0 1 1 0 1 0 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 1 Платформа обучения №1 в Индии Начать полную подготовку к экзамену Ежедневные живые мастер-классы Банк практических вопросов Пробные тесты и викторины Какой из следующих вариантов: ИСПРАВИТЬ с тремя положительными целыми числами x, y и z и предикатом P (x) = – (x = 1) ∧ ∀ y (∃z (x = y * z) ⇒ (y = x) ∨ (y = 1)) Вариант 1: P (x) истинно означает, что x является простым числом Правильный ответ – вариант 1. Ключевые точки P (x) = – (x = 1) ∧ ∀ y (∃z (x = y * z) ⇒ (y = x) ∨ (y = 1)) Если x – простое число, то (x ≠ 1 и единственными делителями x являются x и 1) ∴P (x) истинно означает, что x – простое число. Следовательно, правильный ответ: P (x) истинное значение означает, что x является простым числом . Платформа обучения №1 в Индии Начать полную подготовку к экзамену Ежедневные живые мастер-классы Банк практических вопросов Пробные тесты и викторины Вариант 2: ∃ x (f (x) ∧ ¬ p (x)) Правильный ответ – вариант 2. Ключевые точки f (x) = x мой друг ∴ Следовательно, правильный ответ: ∃x (f (x) ∧ ¬ p (x)). Платформа обучения №1 в Индии Начать полную подготовку к экзамену Ежедневные живые мастер-классы Банк практических вопросов Пробные тесты и викторины Рассмотрим утверждение ниже. Радикал (R) избирается (E), если он / она консерватор (C), но в остальном не избирается. Ниже приводится несколько возможных логических утверждений вышеприведенного предложения. (A) \ (\ left ({R \ wedge E} \ right) \ Longleftrightarrow C \) (B) \ (R \; \ Rightarrow \ left ({E \ Leftrightarrow C} \ right) \) (C) \ (R \ Rightarrow \ left ({\ left ({C \ Rightarrow E} \ right) V \; \ neg \; E} \ right) \) (D) \ (\ left ({\ neg \; R \ vee \ neg \; E \ vee C} \ right) \ wedge \ left ({\ neg \; R \ vee \ neg \; C \ vee E } \ right) \; \; \) Какие из приведенных выше логических утверждений верны? Выберите правильный ответ из представленных ниже вариантов: Вариант 4: только (B) и (D) Правильный ответ – вариант 4 Пояснение: 1) (R ∧ E) ⟺ C говорит, что все (и только) консерваторы радикальны и избираемы. 2) R ⇒ (E ⇔ C) говорит то же самое, что и данное утверждение. Это правильное утверждение. 3) R ⇒ ((C ⇒ E) V ¬E) = ¬R∨ (¬C∨E∨ ¬E), что верно для всех интерпретаций. Это неверное утверждение. 4) (¬ RV ¬ EVC) ∧ (¬ RV ¬ CVE) = (¬ RV (E⇒ C)) ∧ (¬ RV (C ⇒ E)) = R ⇒ (E ⇔ C), что эквивалентно утверждению B Это тоже правда. Платформа обучения №1 в Индии Начать полную подготовку к экзамену Ежедневные живые мастер-классы Банк практических вопросов Пробные тесты и викторины И не забывайте о Билле Гейтсе , который изобрел ОС Windows, операционную систему, на которой работает 90 процентов всех персональных компьютеров в мире. Какая самая важная черта объединяла этих блестящих людей? Все эти люди, которые повлияли почти на весь мир, – все люди с высоким уровнем логического интеллекта. Логический математический интеллект : это способность логически анализировать ситуации или проблемы, находить решения, проводить научные исследования и легко решать логические / математические операции.Это один из восьми множественных типов интеллекта, предложенных Говардом Гарднером. Люди с высоким уровнем числового интеллекта анализируют свои данные, используя логику и исследуя причинно-следственные связи. Вы уверены в своих навыках? Тест множественного интеллекта поможет вам раскрыть свои навыки и убедиться, что вы на правильном пути.Это самый простой способ определить свои особые интересы и навыки. Быстрые и мгновенные результаты! Здесь: Пройдите тест множественного интеллекта прямо сейчас! 📊 Хотя широко распространено мнение, что те, кто хочет улучшить свой логический интеллект, должны хорошо разбираться в математике, это не всегда так. Развить логический интеллект не так сложно, как вы думаете. Людей с высоким уровнем логического интеллекта часто называют «логичными», что означает, что они могут легко определять формы и устанавливать связи между абстрактными понятиями. ВАЖНО : Поддержка развития логического математического интеллекта раскроет потенциал вашего ребенка и повысит его уверенность в себе. Нет никаких препятствий для тех, кто хочет повысить свой логический математический уровень интеллекта и полностью реализовать свой потенциал. Ваш ребенок может использовать множество методов, но упражнения для мозга – одни из лучших. Вместе с миллионами других пользователей ваш ребенок может использовать приложение MentalUP для улучшения своей памяти, логического математического интеллекта, а также внимания, визуальных и словесных навыков. Нажмите здесь, чтобы начать У нас хорошие новости для тех, кто не знает, как улучшить свой логический математический интеллект! Вот подробный ответ на вопрос «Как развить логический математический интеллект?» С помощью очень простых методов и упражнений: Быстро и эффективно проверьте умственные способности вашего ребенка, чтобы узнать его текущий логический математический уровень интеллекта. Затем ваш ребенок может начать совершенствовать свои навыки с помощью ряда логических вопросов математического интеллекта, логических головоломок и интеллектуальных игр. MentalUP, одна из лучших игр в магазине приложений для детей от 4 до 13 лет, была разработана учеными и содержит множество забавных и научных головоломок.Кроме того, нет необходимости искать какие-либо другие приложения для развития нескольких областей интеллекта. Ваш ребенок может получить доступ ко всем из них в одном месте с помощью MentalUP. √ 150+ обучающих игр и математических игр √ Развлекательный и научный контент √ Подходит для всех детей независимо от возраста. √ Легко отслеживайте умственное развитие вашего ребенка с помощью наших многофункциональных модулей отчетности! Играть бесплатно Практически всем нравятся интеллектуальные вопросы, загадки и головоломки. По сути, эти упражнения представляют собой просто логические головоломки в разных формах. Решение логических головоломок, развивающих логическое мышление вашего ребенка, не займет много времени и может быть чрезвычайно увлекательным занятием. ❱❱ Вот вам математическое задание, полное головоломок: Math Puzzles. Настольные игры – отличный способ развить навыки стратегического мышления и логического математического интеллекта. «Все, чему стоит научить, можно представить разными способами. Эти множественные способы могут использовать наш множественный интеллект ». – Ховард Гарднер Вы можете улучшить свой логический интеллект с помощью сложных загадок с ответами или сложных вопросов с ответами, весело проводя время. Они очень полезны для улучшения нашей умственной подготовки и большой логико-математической деятельности интеллекта. Наброски – одно из величайших логических занятий математического интеллекта. С помощью этого задания ваши дети могут поработать над своими письменными навыками, а также над своим логическим математическим интеллектом. Просто попросите их составить схему рассказа, включая время, прошедшее между каждой записью, и убедитесь, что для каждой записи есть как минимум два предложения. Логико-математический стиль обучения включает учеников, которые обладают методичностью и думают в линейном порядке.Логико-математический стиль обучения относится к способности анализировать причинно-следственные связи, рассуждать, решать проблемы, учиться, используя числа и абстрактную визуальную информацию. Вот несколько советов для изучающих логику : Существует множество различных способов помочь вашему ребенку повысить уровень логического интеллекта – игры на логику и эмоциональный интеллект, а также математические игры для детского сада являются одними из самых увлекательных и эффективных. Ваш ребенок может начать развивать свой логический математический интеллект, потенциал и другие области множественного интеллекта с помощью приведенных ниже игровых упражнений. 👇️🎉️ Чтобы закончить эту игру, вам понадобится высокий математический интеллект! Давайте проверим и улучшим ваш логический математический потенциал в увлекательной игре. Этот волшебный шар пытается спрятаться от зорких глаз! Можете ли вы найти это, используя свой логический интеллект? С помощью игр математического интеллекта дети могут развивать логическое мышление и математические навыки. Когда вы смотрите на мир науки, искусства и технологий, довольно легко встретить известных личностей с высоким логическим математическим интеллектом. Уникальное сочетание их интеллекта, сильных и слабых сторон сделало их невероятно успешными людьми.Вот несколько примеров логического математического интеллекта. Мы знаем Эйнштейна, великого деятеля современной науки, по его «Теории относительности». Эйнштейн был физиком-теоретиком, широко признанным одним из величайших физиков всех времен. Он также был озорным ученым, обладавшим высоким уровнем множественного интеллекта, а также логическим математическим интеллектом. Интересно, что Эйнштейн испытывал трудности в обучении в школе, поэтому никогда не следует отчаиваться слишком рано в учебе. Британский физик Хокинг, которого мы знаем по его исследованиям времени и пространства, является одним из ярких примеров людей с высоким логическим математическим интеллектом. Одна из самых интересных подробностей о Хокинге – его болезнь. Он передвигался в инвалидном кресле, не мог говорить и был вынужден общаться через компьютер, но никогда не терял надежды. Знаменитая «Теория большого взрыва» – это работа Хокинга. Эдисон, изобретатель лампочки, также является широко известной фигурой с высоким логическим математическим интеллектом.Эдисон был отцом многих изобретений, несмотря на то, что он был слабослышащим и страдающим дислексией. Кеплер, немецкий астроном и математический гений, живший в 17 веке, является известной фигурой с высоким интеллектом. Гейтс, основатель наиболее широко используемых операционных систем, Windows и Microsoft, страдает дислексией и высоким интеллектом. Гейтс также является одним из самых богатых людей в мире. Цукерберг – основатель Facebook, которым пользуются почти все в мире хотя бы раз в день. Он – еще один пример человека с высоким логическим математическим интеллектом. Вот самые подходящие профессии для детей с высоким уровнем логико-математического интеллекта. Кстати, не забывайте, что некоторые возможности карьерного роста требуют высокого математического интеллекта, а также других способностей. Поскольку данные и аналитика играют в нашей жизни все большую роль, людей с высоким математическим интеллектом можно ожидать светлого будущего.Помните, что во всех сферах жизни будут нужны люди с высоким логическим математическим интеллектом. Те, кто развиваются в этой области, могут легко добиться успеха во многих областях. Инструктор: Генри Тауснер Электронный адрес: hpt at math.ucla.edu Ассистент преподавателя: Шервуд Хахтман Щелкните здесь, чтобы загрузить раздаточный материал курса. Предыдущие промежуточные экзамены: 1 2 Предыдущие вторые промежуточные результаты: 1 2 1.Чистая логика: логика предложений и логика первого порядка, достигающая высшей точки в
доказательство полноты Гёделя
Теорема (не путать с неполнотой Гёделя.
Теоремы). 2. Основная теория моделей: приложения теоремы о полноте.
включая теоремы Лёвенгейма-Сколема, теорему компактности;
и обсуждение элементарной эквивалентности. Поместите следующую информацию в верхний правый угол
первая страница: Ваше имя На каждой дополнительной странице указывайте свое имя в верхнем правом углу.
угол. СКОБЯЙТЕ любое домашнее задание объемом более одной страницы.
Перед отправкой удалите всю перфорацию. Пишите разборчиво. Домашнее задание, которое не соответствует вышеперечисленному
требования будут помечены как “неприемлемые” и возвращены непрочитанными. Все оценки и итоговые оценки будут доступны в журнале успеваемости MyUCLA.
Ответ (подробное решение ниже)
Ответ (подробное решение ниже)

Ответ (подробное решение ниже)

Ответ (подробное решение ниже)

Ответ (подробное решение ниже)
Ответ (подробное решение ниже)
Итак, из таблицы истинности также ясно, что (r → p) → q всегда истинно, когда q истинно, а Y ложно.
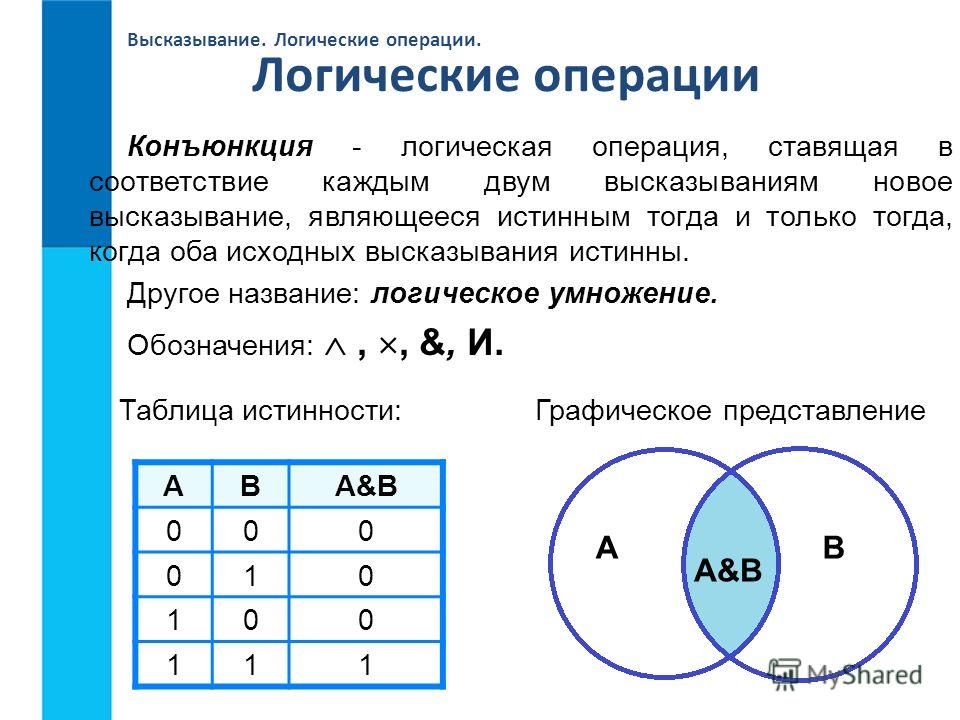
Ответ (подробное решение ниже)
Приоритет логических операторов операторов приоритет ¬ НЕ 1 ∧ И 2 ∨ ИЛИ 3 ⇒ условно 4 ⇔ двухусловный 5
Данный предикат,
Ответ (подробное решение ниже)
P (x) = x идеально
Итак, они спрашивают о НЕКОТОРЫХ. Наконец, самые внешние круглые скобки получат НЕКОТОРЫЕ ∃x.
Им даны условия вроде НЕ идеальные. Итак, получаем ¬ p (x).
Окончательное условие: ∃x (f (x) ∧ ¬ p (x)) только
Ответ (подробное решение ниже)
 Итак, это утверждение не соответствует действительности.
Итак, это утверждение не соответствует действительности. Логико-математический интеллект: примеры, деятельность и карьера

Что такое логический математический интеллект?
 Они часто не работают с субъективной информацией – вместо этого они ценят ясные факты и достоверные данные. Способность делать выводы и наблюдения также является важной характеристикой людей с математическим интеллектом. Хотя иногда у них создается впечатление, что они сбиты с толку, их разум работает как компьютер в фоновом режиме.
Они часто не работают с субъективной информацией – вместо этого они ценят ясные факты и достоверные данные. Способность делать выводы и наблюдения также является важной характеристикой людей с математическим интеллектом. Хотя иногда у них создается впечатление, что они сбиты с толку, их разум работает как компьютер в фоновом режиме. 5 мероприятий по улучшению логико-математического интеллекта
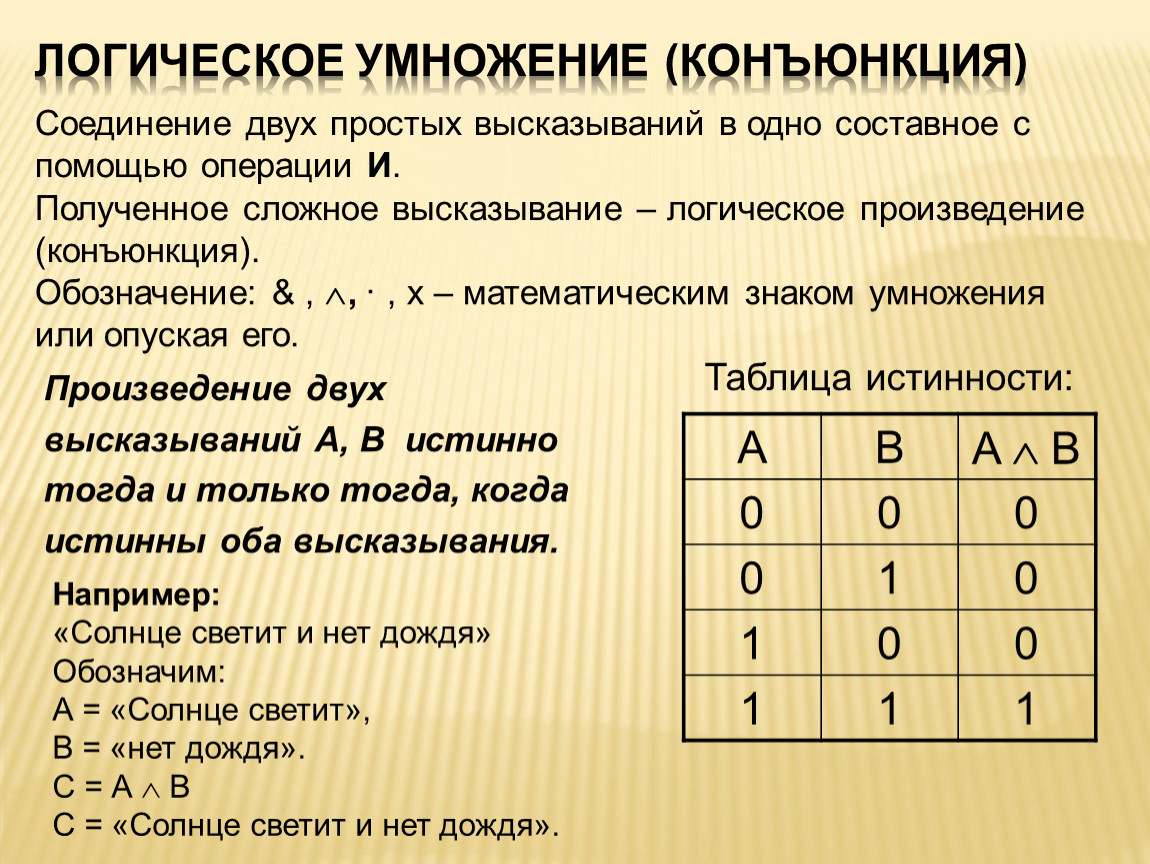 . Все, что вам нужно, это преданность делу.
. Все, что вам нужно, это преданность делу. 1.
 MentalUP
MentalUP 2.Решайте головоломки для мозга
3. Играть в настольные игры
4. Решайте загадки и каверзные вопросы
5. Пишите истории
Учебные советы по стилю обучения логической математике
Веселые логические вопросы и игры для математического интеллекта
6 примеров людей с высоким логическим математическим интеллектом
Альберт Эйнштейн
Стивен Хокинг
Томас Эдисон
Иоганн Кеплер
Билл Гейтс
Марк Цукерберг
Карьера в области логико-математического интеллекта
Math 114L: математическая логика
Math 114L: математическая логика
Время и место: MWF 10-10: 50, MS 7608 Math 114L: математическая логика
Кабинет: Здание математических наук 5634
Рабочий телефон: (310) 825-2697
Часы работы: Понедельник 12: 30-1: 30, четверг 11: 00-1: 00 Заключительный экзамен
Решение 5b, 5c
Каждую неделю будет назначаться набор задач. В
проблемы будут
варьируются по сложности от рутинной до более сложной. Завершенный
решения должны быть переданы в начале урока на
срок, указанный в соответствующем наборе домашних заданий. Домашние работы с опозданием не принимаются.Вам предлагается работать вместе над упражнениями, но любая оценка
задание должно представлять вашу собственную работу.
Math 114L, номер домашнего задания. Будет два
Промежуточные экзамены в классе. Будет заключительный экзамен на вынос. Экзамены по макияжу проводиться не будут.
.

 (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
(Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.) Сколько у него осталось?
Сколько у него осталось? Половина шеста погружена в ил на дне пруда, другая треть покрыта водой, и 7 футов находится вне воды. Какова общая длина шеста?
Половина шеста погружена в ил на дне пруда, другая треть покрыта водой, и 7 футов находится вне воды. Какова общая длина шеста? Первый человек взял одну конфету, и каждый следующий человек съел больше конфет, чем предыдущий, пока банка не опустела.
Первый человек взял одну конфету, и каждый следующий человек съел больше конфет, чем предыдущий, пока банка не опустела.  15?
15? Деление на половину аналогично умножению на 2.
Деление на половину аналогично умножению на 2.
 Д. 1+ 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45, поэтому первые девять человек берут 45 конфет на двоих. 10-й человек берет 15 конфет. Он или она не может взять меньше 9 и оставить меньше 11, иначе банка не будет пустой, но следующего человека не хватит, чтобы следовать правилу, изложенному в вопросе (что каждый человек берет больше чем предыдущий.Так что ответ: 10 человек .Спасибо Сэму Паркеру за подробное объяснение этого ответа
Д. 1+ 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45, поэтому первые девять человек берут 45 конфет на двоих. 10-й человек берет 15 конфет. Он или она не может взять меньше 9 и оставить меньше 11, иначе банка не будет пустой, но следующего человека не хватит, чтобы следовать правилу, изложенному в вопросе (что каждый человек берет больше чем предыдущий.Так что ответ: 10 человек .Спасибо Сэму Паркеру за подробное объяснение этого ответа

