Механическая работа энергия: Работа. Мех. энергия | От урока до экзамена - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Механическая работа. Мощность. Коэффициент полезного действия. Кинетическая и потенциальная энергия. Закон сохранения энергии в механических процессах.

Работа есть мера изменения и превращения энергии.

Механической работой называют скалярную физическую величину, численно равную произведению модулей силы и перемещения на косинус угла а между векторами и :

Поскольку величина А является скалярной, она может приобретать положительные и отрицательные значения. В SI ее измеряют в джоулях (Дж):

Если вектор силы перпендикулярен вектору перемещения, то и работа силы также равняется нулю.
При упругой деформации пружины работа выполняется под действием сменной силы. Изменяется эта сила от 0 до F, поэтому среднее значение силы , работа имеет вид: .
Во время равномерного поднятия тела массой
т на высоту h будет выполняться работа против силы тяготения:
Сила трения будет препятствовать выполнению работы, т.е. ее вектор направлен противоположно перемещению:

Работа сил тяготения и упругости:

Работа же силы трения зависит от формы траектории и по замкнутой траектории не равна нулю.

Мощность – скалярная физическая величина, характеризующая работу в единицу времени.

Мощность измеряют отношением работы к промежутку времени, на протяжении которого эта работа выполнялась: .

Единица мощности — ватт

(Вт):

Ватт — мощность, при которой за 1 с совершается работа в 1 Дж.

Мощность при постоянной силе равна:

N = Fv.

Иногда еще используется единица мощности 1 л. с. (лошадиная сила):

1л. с. = 736 Вт.

A = Nt,

откуда единица работы в технике — 1 кВт ^. ч.

1кВт ^.ч = 3,6 ^.10⁶ Дж.

Отношение полезной работы к полной работе называется коэффициентом полезного действия (КПД) простого механизма (η).

Коэффициент полезного действия (η) определяется по формулам:

или , где η < 1 (η < 100%).

Энергия — это единая мера различных форм движения материи.

Энергия — одно из характерных свойств материи. На практике механическое движение частично или полностью превращается в другие формы движения — тепловое, электромагнитное.

Энергия характеризует движение системы, а также взаимодействие тел или частиц в системе с учетом возможности перехода из одной формы движения в другую.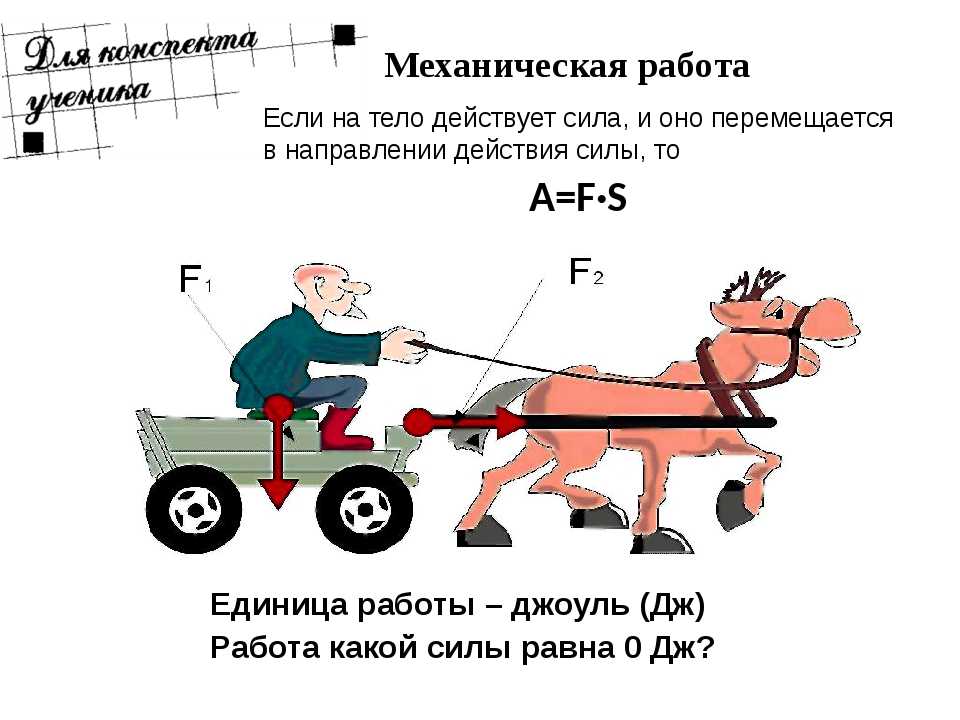

Энергия — функция состояния системы, а работа — функция процесса перехода системы из одного состояния в другое.

Закон сохранения энергии: энергия не возникает и не исчезает, она только превращается из одного вида в другой и передается от одного тела к другому в равных, количествах.

Виды энергии:

Механическая энергия тела (потенциальная и кинетическая).
Внутренняя.
Электромагнитная (электрическая + магнитная).
Химическая.
Световая.
Ядерная, или атомная.

Полная энергия тела:

Энергия покоя тела (внутренняя энергия): .

Кинетическая и потенциальная энергия составляют механическую энергию. Она характеризует механическое движение.

Кинетическая энергия

— это энергия движущегося тела.

Кинетическая энергия в классической механике:

Так как скорость тела является величиной относительной, т.е. зависит от выбора системы отсчета, то и кинетическая энергия относительна. Кинетическая энергия всегда положительна.

Кинетическая энергия в релятивистской механике:

Е_к=Е-Е₀=(т-т₀)с².

Потенциальная энергия – это энергия, обусловленная взаимодействием тел или частиц тела. В механике различают:

потенциальную энергию тела, поднятого над Землей, где

h — высота над уровнем, на котором потенциальная энергия системы «Земля — тело» принимается за нуль (нулевой уровень потенциальной энергии):

Е_п = mgh;

потенциальную энергию упругодеформированного тела: ;

потенциальную энергию гравитационного взаимодействия двух материальных точек с массами т₁ и т₂, находящихся на расстоянии r друг от друга: .

Потенциальная энергия положительна, если она обусловлена силами отталкивания, и отрицательна, если обусловлена силами притяжения.

Закон сохранения механической энергии: полная механическая энергия системы тел, в которой действуют только консервативные силы (потенциальные), есть величина постоянная.

Консервативные силы — это силы тяжести, упругости, кулоновские силы.

Консервативная сила — сила, работа которой при перемещении тела зависит только от начального и конечного положений тела в пространстве. Например, работа силы тяжести:

А₁=А₂=А₃

Работа консервативных сил в любом замкнутом контуре равна нулю:

Потенциальное поле – поле консервативных сил.

Кинетическая и потенциальная энергии — функции состояния системы, т. е. могут быть точно определены, если заданы координаты и скорости всех тел системы, а также система отсчета.

Работа равнодействующей силы равна изменению кинетической энергии –

теорема о кинетической энергии:

Работа консервативных сил равна изменению потенциальной энергии с противоположным знаком:

Механическая работа и энергия – презентация онлайн

Похожие презентации:

Механическая работа и энергия

Механическая работа и энергия. Тема 4

Работа и энергия. Механическая работа. Мощность

Законы сохранения. Работа и энергия. (Тема 3)

Работа и энергия

Кинетическая энергия механической системы

Механическая и кинетическая энергии

Закон сохранения энергии. Работа и кинетическая энергия

Работа и энергия. Закон сохранения энергии в механике

Силовое поле. Работа. Энергия. Мощность

МЕХАНИЧЕСКАЯ РАБОТА И ЭНЕРГИЯ
МЕХАНИЧЕСКАЯ РАБОТА
Работа – физическая величина, характеризующая процесс
превращения одной формы движения в другую.
dA F dr
r2
A12 F d r
r1
[A] 1Н м 1Дж
Элементарная работа dA , совершаемая силой, равна скалярному
произведению силы F на элементарное перемещение точки
приложения силы
dr
dr
dt
d r dt
dA F dr F dt
r2
t2
A12 F d r F dt
r1
t1
dA F dr F dr cos FS dr
FS F cos
A12 Fs dS
S12
Если F const и
движение прямолинейное,
то: A12 Fs dS Fs S12
S12
Графическое представление работы

1. Fs const A12 Fs S12
2. Fs const A12 Fs dS
S12
Быстроту совершения работы характеризует мощность:
Мощность равна работе, совершаемой за единицу
времени.
A
N
Средняя мощность:
t
Мгновенная мощность:
1Дж
[ N]
1Вт
1с
dA
N
dt
dA F d r
N
F
dt
dt
КОНСЕРВАТИВНЫЕ И НЕКОНСЕРВАТИВНЫЕ СИЛЫ
1. КОНСЕРВАТИВНЫЕ СИЛЫ (на примере силы тяжести)
Силы, работа которых не зависит
от формы пути, по которому
материальная точка переходит из
некоторого начального положения в
конечное,
называются
консервативными.

2
A1a 2 mg d r
1
(a )
2
mg d r mg r
1
(a )
2
A1b 2
mg d r
1
(b)
2
mg d r mg r
1
(b)
A1a 2 A1b 2
2. НЕКОНСЕРВАТИВНЫЕ СИЛЫ (на примере силы тяги)
Сила
называется
неконсервативной, если
совершаемая ею работа зависит от
формы
пути,
по
которому
материальная точка переходит из
начального положения в конечное.
F dr
2
A1a 2
1
(a )
2
2
1
(a )
1
(a )
F dr F dS F S1a 2
F dr
2
A1b 2
1
(b)
2
2
1
(b)
1
(b)
F dr F dS F S1b 2
S1a 2 S1b 2 A1a 2 A1b 2
ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
Энергия – мера различных форм движения материи и типов
взаимодействия материальных объектов, являющаяся
однозначной, непрерывной, конечной, дифференцируемой
функцией состояния объекта (измеряется в Джоулях).
Функция состояния – это физическая характеристика
объекта, изменение которой при переходе объекта из одного
состояния в другое не зависит от траектории перехода, а
определяется параметрами начального и конечного
состояний.

Полная механическая энергия объекта является функцией
его скорости и координат :
E Eк Eп
РАБОТА И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ПРИ
ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
Найдем работу силы F , под действием которой тело массой
m изменило свою скорость от 1 до 2 за время t.
d
dA F d r ; F m a; a
dt
d d r
dA m
m d m d
dt
2
2 2
A dA m d m
2
1
1
m 22 m 12
2
2
m 2
Eк
кинетическая энергия
2
A E к 2 E к1 E к
Функция механического состояния, которая зависит от
массы материальной точки и квадрата её скорости и
приращение которой равно работе всех действующих на
точку сил, называется кинетической энергией точки
РАБОТА И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ПРИ
ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
Представим твердое тело, имеющее ось вращения
Z, как систему материальных точек.
Для i-й точки (элемента): E к ,i
m R
i i i
2
2
E к ,i
n
Для тела:
E к E к ,i
i 1
2
mi i2 mi ( i R i ) 2
2
2
r r
1
2
1
2
2
1 2 n
I
m i R i2
2 i 1
2
I 2
Eк
2
.

.. n
r
n
Элементарная работа силы, действующей на твердое
тело при вращении его вокруг неподвижной оси равна
произведению момента этой силы относительно оси вращения
на элементарное угловое перемещение тела.
dA M
внешн.
d
При повороте на конечный угол:
2
.
A M внешн
d
1
M z внеш. I ε z
d
εz
dt
dω
dA I
d I ω dω
dt
2
Jω 22 Jω12
A J ω dω
2
2
1
Это следует и из выражения: А =
Качение тела.
Движение может быть представлено в виде суммы двух
движений: поступательного движения центра масс и
вращательного вокруг оси, проходящей через центр масс и
сохраняющей неизменную ориентацию в пространстве, тогда
кинетическая энергия такого движения равна сумме энергий
поступательного и вращательного движений:
m 2 I 2
Полная кинетическая энергия: E к
2
2
СВОЙСТВА КИНЕТИЧЕСКОЙ ЭНЕРГИИ:
1. Это однозначная, конечная, непрерывная, дифференцируемая функция механического состояния объекта.

2. Она не может быть отрицательной.
3. Кинетическая энергия системы равна сумме кинетических
энергий отдельных тел.
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
A mg r
A mg r cos
A mg (h2 h 2 ) mgh 1 mgh 2
E п mgh
A E п1 Е п 2 E п
Аналогично для силы упругости: A E п1 Е п 2 E п
k x
Eп
2
Функция механического состояния взаимодействующих тел
или их частей, зависящая от их координат, убыль которой равна
работе
консервативных
сил,
называется
взаимной
потенциальной энергией этих тел или их частей.
2
СВОЙСТВА ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ:
1. Это однозначная, конечная, непрерывная, дифференцируемая функция механического состояния объекта.
2. Она может быть как положительной, так и отрицательной.
3. Потенциальная энергия характеризует оба взаимодействующих тела.
4. Числовое значение потенциальной энергии определяется с точностью до произвольной постоянной, зависящей от выбора нулевого уровня.
СВЯЗЬ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
С КОНСЕРВАТИВНОЙ СИЛОЙ
Если в каждой точке пространства на материальную точку
действует консервативная сила, то говорят, что точка находится в
потенциальном поле сил.

dA F d r F dr cos Fr dr
A E п1 Е п 2 E п
dA dE п
Fr dr dE п
dE п
Fr
dr
( 2)
(1)
E п
Fx
x
F Fx i Fy j Fz k
Fy
E п
y
E п
Fz
z
E п E п E п
F
i
j
k
y
z
x
E п E п E п
grad E п
i
j
k
x
y
z
Градиент потенциальной энергии – вектор, указывающий
направление быстрейшего возрастания потенциальной энергии и
численно равный приращению энергии, приходящейся на
единицу длины этого направления.
F grad E п
ЗАКОН СОХРАНЕНИЯ
ПОЛНОЙ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Механическая система называется замкнутой или
изолированной, если на нее не действуют внешние силы
(система не обменивается с внешними телами энергией).
Система называется незамкнутой, если на неё действуют
нескомпенсированные внешние силы.
Механическая система называется консервативной, если
на тела системы действуют только консервативные силы.
Рассмотрим механическую систему, тела которой
взаимодействуют как между собой, так и с внешними телами.

.
внешн.
внутр.
внешн.
dE к dAвнутр
dA
dA
dA
к
к
нк
нк
.
внешн.
dAвнутр
dA
dE п
к
к
.
внешн.
dAвнутр
dA
dAнк
нк
нк
dE к dAнк dE п
dE к dE п dAнк
Приращение полной механической
энергии системы: dE dA нк
dE dA
нк
E Aнк
Приращение механической энергии системы материальных
точек равно алгебраической сумме работ всех внутренних и
внешних неконсервативных сил, действующих на точки
системы.
Если Анк = 0, то Е = const
Полная механическая энергия системы сохраняется, если силы,
действующие на тела системы, являются консервативными –
закон сохранения механической энергии.
ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ
Удар называется центральным, если тела до удара движутся
вдоль прямой, проходящей через их центры масс.
1. Абсолютно неупругий удар.
Кинетическая энергия относительного движения тел на
короткое время преобразуется в энергию упругой деформации.

Абсолютно неупругий удар – столкновение тел, в результате
которого тела объединяются, двигаясь дальше как единое
целое.
m1 1 m2 2 m1 m2 u
m
m
2 2
u 1 1
m1 m 2
m1 12 m 2 22 (m1 m 2 ) u
Q
2
2
2
2
Кинетическая энергия переходит в тепловую или другие формы
энергии.
2. Абсолютно упругий удар.
Абсолютно упругий удар – столкновение тел, в результате
которого в обоих взаимодействующих телах не остается
никаких деформаций и вся кинетическая энергия , которой
обладали тела до удара, после удара снова превращается в
кинетическую энергию.
m1 1 m 2 2 m1 u1 m 2 u 2 (1)
m1 12 m 2 22 m1u12 m 2 u 22
( 2)
2
2
2
2
u1,x
2m 2 2,x (m1 m 2 ) 1,x
m1 m 2
u 2,x
2m1 1,x (m 2 m1 ) 2,x
m1 m 2

English Русский Правила

Расчеты механической работы и передачи энергии: демонстрация силовой модели твердого тела восстанавливаемой ноги при ходьбе

. 1992 декабря; 24 (12): 1396-412.

Г. Э. Колдуэлл ¹ , LW Forrester

принадлежность

¹ Кафедра кинезиологии, Мэрилендский университет, Колледж-Парк 20742.

PMID: 1470024

GE Caldwell et al. Медицинские спортивные упражнения. 1992 Декабрь

. 1992 декабря; 24 (12): 1396-412.

Авторы

Г. Э. Колдуэлл ¹ , ДВ Форрестер

принадлежность

¹ Кафедра кинезиологии, Мэрилендский университет, Колледж-Парк 20742.

PMID: 1470024

Абстрактный

Во многих исследованиях, касающихся механической работы и эффективности человеческого движения, использовались модели, основанные на сегментарной энергии. Теоретически было показано, что такие оценки работы могут быть ошибочными из-за смещения компенсаций в источниках питания, лежащих в основе энергетических профилей. Кроме того, передача механической энергии, рассчитанная на основе этих энергетических моделей, была интерпретирована как метаболические механизмы энергосбережения. В этой статье исследуется использование анализа механической мощности для расчета работы и оценки передачи энергии с использованием движения восстанавливающей ноги при ходьбе и беге для одного субъекта в качестве показательного примера. Оценки работы и передачи энергии из обеих моделей энергии и мощности сравниваются и сопоставляются. Энергетическая модель недооценивает работу восстанавливающей ноги как при ходьбе (54% от оценки силовой модели), так и при беге (38%), из-за силы мышц в суставах, противодействующих друг другу в выработке и поглощении энергии. Показано, что передача энергии, рассчитанная с помощью энергетических моделей, сталкивается с той же проблемой компенсации источников энергии. Напротив, силовая модель определяет четыре механизма передачи энергии (маятник, хлыст, сухожилия и совместная передача силы), которые в той или иной степени способствуют изменению энергии в ноге. Для восстановительной ноги наибольшую величину имеют механизмы совместной силы и передачи хлыста, тогда как передачи маятника и сухожилия намного меньше. Эти передачи энергии можно наблюдать на изменяющейся во времени основе во время последовательности движений и иллюстрировать различия в распределении энергии между ходьбой и бегом. Эти основанные на мощности переносы обсуждаются с точки зрения их природы в отношении стоимости метаболической энергии и распределения механической энергии в многосегментной системе. Предполагается, что работа и передача энергии, рассчитанные на основе анализа мощности, являются более точными, чем рассчитанные на основе моделей механической энергии, и более полезны для понимания производительности.

Цитируется

Связанный со скоростью поток энергии и изменение функции сустава при ходьбе человека.
Hu Z, Ren L, Hu D, Gao Y, Wei G, Qian Z, Wang K. Ху Зи и др. Фронт Биоэнг Биотехнолог. 2021 31 мая; 9:666428. doi: 10.3389/fbioe.2021.666428. Электронная коллекция 2021. Фронт Биоэнг Биотехнолог. 2021. PMID: 34136472 Бесплатная статья ЧВК.
Поглощение энергии в суставах нижних конечностей при различных стратегиях контакта стопы при спуске по лестнице.
Чон Х.М., Ли К.К., Ли Дж.И., Шин Дж.Х., ОМ GM. Чон Х.М. и др. Технол Здравоохранение. 2021;29(S1):433-440. DOI: 10.3233/THC-218041. Технол Здравоохранение. 2021. PMID: 33682780 Бесплатная статья ЧВК.
Влияние отталкивания протеза стопы на механическую нагрузку, связанную с остеоартритом коленного сустава, у пациентов с ампутированными конечностями.
Моргенрот Д.С., Сегал А.Д., Зелик К.Е., Чернецкий Дж.М., Клют Г.К., Адамчик П.Г., Орендурф М.С., Хан М.Е., Коллинз С.Х., Куо А.Д. Моргенрот, округ Колумбия, и др. Осанка походки. 2011 окт; 34 (4): 502-7. doi: 10.1016/j.gaitpost.2011.07.001. Epub 2011 30 июля. Осанка походки. 2011. PMID: 21803584 Бесплатная статья ЧВК. Клиническое испытание.
Взаимосвязь между мышечной, внешней, внутренней и суставной механической работой при нормальной ходьбе.
Сасаки К., Нептун Р.Р., Каутц С.А. Сасаки К. и др. J Эксперт Биол. 2009 март; 212 (часть 5): 738-44. doi: 10.1242/jeb.023267. J Эксперт Биол. 2009. PMID: 19218526 Бесплатная статья ЧВК.

Типы публикаций

термины MeSH

Кинетика • Работа, энергия и мощность

Работа

Работа силы F , действующей на тело, можно определить несколькими способами. Работа, совершаемая постоянной силой, действующей параллельно перемещению тела, определяется как ⁴⁴ :

, где Вт ⁴⁵ — работа (Дж), F — величина силы (Н), а d – водоизмещение корпуса (м).

Работа есть произведение силы и перемещения тела по той же линии, по которой действует эта сила.

Чтобы указать работу, выполняемую при действии силы на тело, мы должны знать три элемента информации:

Средняя сила, действующая на тело.
Направление этой силы.
Смещение тела в направлении действия силы за время действия силы на тело.

Рисунок 12 Силы реакции ⁴⁶, действующие на человека во время выполнения жима лежа и центр тяжести движущейся массы. Черные стрелки F _A и F _B обозначают силы реакции, с помощью которых земля воздействует на уступ. Сплошная синяя стрелка F _C представляет результирующую силу реакции. Синяя точка представляет собой центр тяжести системы штанга — руки.

Например, бодибилдер во время выполнения жима лежа воздействует на штангу и свои руки с постоянной силой 2000 Н. Центр тяжести системы штанга — руки смещен по вертикали на 0,6 м (рис. 12) . Какую работу выполняет кузовщик?

Механическая работа также может иметь отрицательное значение. Это так, когда тело смещается против направления действующей силы. Хоккейный вратарь выполняет отрицательную работу, когда ловит шайбу в перчатку, гимнаст, когда делает распятие на кольцах, тяжелоатлет, когда опускает штангу из верхнего положения в нижнее, подушка выполняет ее, когда гимнаст приземляется на нее, трение сила лыж также отрицательна. Разрушающие силы обычно выполняют отрицательную работу.

Положительная работа совершается при перемещении тела по той же линии, по которой действует сила. Метатель копья совершает положительную работу при перемещении копья в направлении метания, тяжелоатлет – при подъеме штанги, поверхность трамплина – в момент отталкивания прыгуна с трамплина.

Мышцы также могут выполнять механическую работу. Когда мышцы сокращаются, они создают тяговые силы, которые воздействуют на места прикрепления мышц. Мышечные сокращения подразделяются на:

Концентрические сокращения – «вырабатываемой силы достаточно для преодоления сопротивления, и мышца укорачивается при сокращении» (Knuttgen a Kraemer, 1987). Затем мышцы выполняют положительную механическую работу, потому что мышечная сила действует вдоль линии прикрепления мышц. Мышца укорачивается.

Эксцентрическое сокращение – «вырабатываемой силы недостаточно для преодоления внешней нагрузки на мышцу, и мышечные волокна удлиняются по мере сокращения» (Knuttgen a Kraemer, 1987). Затем мышцы выполняют отрицательную механическую работу, потому что мышечная сила действует против направления движения прикрепления мышц. Мышца удлиняется.

Изометрическое сокращение – «мышца остается той же длины» (Knuttgen a Kraemer, 1987). Смещение мест прикрепления мышц относительно друг друга отсутствует, поэтому работа не выполняется.

Энергия

В механике энергия определяется как способность тела совершать работу. Нам известны многие виды энергии: акустическая энергия, световая энергия, химическая энергия, ядерная энергия и т. д. В биомеханике нас больше всего интересует механическая энергия, которая может иметь две формы: кинетическую энергию и потенциальную энергию. Энергия обозначается буквой E, а единицей энергии в системе СИ является джоуль (Дж). тело в гравитационном поле Земли.

Кинетическая энергия

Движущееся тело способно совершать работу посредством своего движения. Кинетическая энергия прямо пропорциональна квадрату скорости тела. Кинетическая энергия определяется как:

, где E _k — кинетическая энергия (Дж), m — масса (кг) и v — скорость (м/с).

Как видно из приведенного выше определения, чтобы выразить величину кинетической энергии, мы должны знать массу и скорость данного тела (или человеческого тела).

Какова кинетическая энергия теннисного мяча массой 60 г (0,06 кг) и скоростью 108 км/ч (30 м/с)?

Спецификация кинетической энергии намного проще, чем механическая работа, потому что измерить массу и скорость тела проще, чем измерить силы, действующие на тело.

Потенциальная энергия

Потенциальная энергия – это способность тела выполнять работу благодаря своему положению. Отметим два вида потенциальной энергии: гравитационную потенциальную энергию и упругую потенциальную энергию ⁴⁷ .

Гравитационная потенциальная энергия – это способность тела выполнять работу благодаря его положению в гравитационном поле Земли. Математически потенциальная энергия может быть выражена как:

где E _p — потенциальная энергия (Дж), m — масса (кг), г — ускорение свободного падения (9,81 м/с ² ) и h высота (м).

Какова потенциальная энергия лыжника массой 90 кг в начале скоростного спуска при разнице высот между стартом и финишем 1000 м?

Упругая энергия – это способность тела совершать работу за счет его деформации. Когда, например, шест прыгуна с шестом согнут, упругая энергия накапливается в стекловолокне прыжка. Чем сильнее деформирован стержень, тем больше упругой энергии запасается в стекловолокне. Величина упругой энергии зависит также от жесткости, которая определяется материальными качествами тела.

, где E _p — упругая энергия (Дж), k — жесткость (Н/м) и Δ x — изменение длины тела (м).

Упругая энергия зависит от меры деформации и жесткости тела.

Какая упругая энергия запасается в сухожилии спортсмена при растяжении на 0,009 м, если жесткость сухожилия составляет 10 000 Н/м?

Полная энергия спортсмена представляет собой сумму кинетической, потенциальной и упругой энергии.

⁴⁴ Работу также можно определить как произведение величины проекции силы, действующей на тело, в направлении движения этого тела и расстояния, пройденного этим телом. – от английского work Zpět

⁴⁶ Силами реакции, действующими на опоры, здесь пренебрегают. Техника жима лежа в этом случае требует ненагруженных ног.

Механическая работа энергия: Работа. Мех. энергия | От урока до экзамена

Механическая работа. Мощность. Коэффициент полезного действия. Кинетическая и потенциальная энергия. Закон сохранения энергии в механических процессах.

Механическая работа и энергия – презентация онлайн

Расчеты механической работы и передачи энергии: демонстрация силовой модели твердого тела восстанавливаемой ноги при ходьбе

принадлежность

Авторы

принадлежность

Абстрактный

Похожие статьи

Цитируется

Типы публикаций

термины MeSH

Кинетика • Работа, энергия и мощность

Работа

Энергия

Кинетическая энергия

Потенциальная энергия

Оставить комментарий Отменить ответ