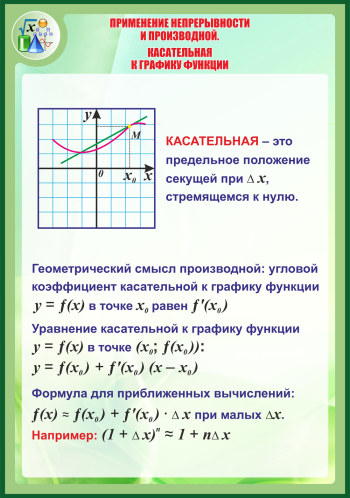
Производная и ее геометрический смысл контрольная работа: Контрольная работа по теме “Производственная и ее геометрический смысл”

“Производная. Механический и геометрический смысл производной”.

Всероссийский дистанционный конкурс для учителей математики «Контрольная работа в формате теста»

11 класс

Алгебра и начала математического анализа

Разработала: учитель математики

ГБОУ РО НШИ с ПЛП М.В. Франк

Контрольная работа в формате теста по теме:

«Производная. Геометрический и механический смысл производной».

КИМ

Инструкция по выполнению работы

Время выполнения работы 40 мин. Задания выполняются в КИМе.

Работа состоит из двух частей и содержит 10 заданий.

Часть I содержит 7 заданий базового уровня.

Задания части I считаются выполненными, если учащийся правильно заполнил пропуски (в заданиях I-II) и записал верный ответ в виде числа или полное решение (в заданиях III – V), а в заданиях VI – VII – верно установил соответствие.

Часть II содержит 3 задания, соответствующих уровню возможностей и доступных учащимся, хорошо успевающим по математике. При выполнении задания VIII надо установить соответствие между элементами четырёх множеств, а в заданиях IX – X записать полное решение и ответ.

При этом реализуется основной принцип итоговой аттестации: успешное выполнение заданий второй части работы не компенсирует отсутствие результата выполнения заданий первой части. Оценивание осуществляется способом «сложения». Система оценивания 5 – балльная.

Оценочная таблица:

№ задания        I       II       III      IV    V       VI     VII      VIII       IX      X     Итого                  Балл                4      4         1       2     1        5      2          5          2       4         30

 Таблица перевода тестовых баллов в оценку:

 Тестовый балл                                                   Оценка

1-10                                                                    «2»

11- 15	«3»
16-21	«4»
22-30	«5»

Советуем для экономии времени пропускать задание, которое не удаётся выполнить сразу, и переходить к следующему.

К выполнению пропущенных заданий можно вернуться, если у вас останется время.

Удачи!

* С данной инструкцией необходимо ознакомить школьников до проведения контрольной работы. Инструкция и текст работы выдаются каждому учащемуся.

Ф. И учащегося 

Класс

Дата

Часть 1.

I. Продолжите утверждения так, чтобы получились верные высказывания:

1) Процесс нахождения производной называется …

2) Значение производной функции в точке х₀показывает …

3) Мгновенной скоростью называется …

4) Геометрический смысл производной состоит в том, что производная функции в точке

есть …

Итого: 4 балла

II. Вставьте пропущенные выражения так, чтобы получились верные правила дифференцирования:

1)   …    =  С f^/(х)

2)   (f(x)+g(x))^/   =  …

3)   …    =  f^/(х)g(x) + f(x)g^/(х)

4) ….

Итого: 4 балла

III. Ма­те­ри­аль­ная точка дви­жет­ся от на­чаль­но­го до ко­неч­но­го по­ло­же­ния. На ри­сун­ке изоб­ражён гра­фик её дви­же­ния. На оси абс­цисс от­кла­ды­ва­ет­ся время в се­кун­дах, на оси ор­ди­нат — рас­сто­я­ние от на­чаль­но­го по­ло­же­ния точки (в мет­рах).    Сред­няя ско­рость дви­же­ния точки в (м/с) равна …

Ответ: 1,6 м/с

Итого: 1 балл

IV. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну x(t) = – t⁴ + 6t³ + 5t + 23, её ско­рость в (м/с) в мо­мент вре­ме­ни t = 1 c, равна:

Решение:

Ответ:

Итого: 2 балла

V.

Укажите, для какой функции:

1) = ; 2) = ;

3) = ; 4) =

функция = является производной.

Ответ:

Итого: 1 балл

VI. Установите соответствие между функцией и её производной: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

f ( x) (функция)	f /( x) (производная функции)
1. 2х2 + 5 х – 47	1.
2. х – 5– 7х	2. – 60(2 – 5 х)11
3. +	3.
4. х5+1/х	4. 4х + 5
5.	5. (х 2+8) + 2х (х-2)
6. (х-2)(х2+8)	6.
7.	7. -5х – 6– 7
8. –	8.
9. (2 – 5 х)12	9.
10. 2х + tgx – lnx	10. 5х4– 1\x2

В таблице под каждой цифрой, соответствующей функции, укажите номер её производной

Ответ:

1	2	3	4	5	6	7	8	9	10

Итого: 5 баллов

VII. Установите соответствия между графиками функций и значениями производных в точке х₀.

Графики функций.

A. B. C.

D.

Значения производных:

1) 0,25;                         2) -1;                      3) 0,5;                          4) – 0,25.

В таблице под каждой буквой, соответствующей графику, укажите номер её значения

Ответ:

A	B	C	D

Итого: 2 балла

Часть 2.

VIII. Установите соответствие между функцией ⇒ графиком функции ⇒ производной ⇒ графиком производной функции.

Функция:    1. у = х³;     2. у = – 3;      3. у = х² – 2;     4. у = – 2х + 5;         5. у = – 1\х

График функции:

1. 2. 3. 4.

5.

Производная функции:   1. у^/ = 2х;          2. у^/ = 3х²;            3. у^/ = 1\х² ;

4. у^/ = 0;          5. у^/ = – 2. 

График производной функции:

1. 23.

4. 5.

В таблице под каждой цифрой, соответствующей функции, укажите номер её графика, затем укажите номер производной этой функции и номер графика, соответствующий графику производной.

Ответ:

1	2	3	4	5

Итого: 5 баллов

IX. Прямая f(x) = – 4х – 11 является касательной к графику функции .     Абсцисса точки касания равна

Решение:

Ответ:

Итого: 2 балла

X. Прямая у = 6х – 5 является касательной к графику функции

f(x) = 9х2 + bх + 76 . Найдите b, учитывая, что абсцисса точки касания меньше 0.

Решение:

Ответ:

Итого: 4 балла

Задания контрольной работы в формате теста предназначены для проверки уровня знаний, умений и навыков по теме: «Производная. Механический и геометрический смысл производной» и соответствуют теории в пределах учебного материала.

Тест позволяют оценить достигнутый уровень усвоения материала учеником и зону его ближайшего развития.

Данная работа может помочь выпускникам и при подготовке к ЕГЭ. Задания по этой теме включены как в КИМы профильного уровня, так и в КИМы базового уровня.

В тесте использованы задания из открытого банк заданий ЕГЭ (базовый и профильный уровень) и сайта “Решу ЕГЭ”.

http://os.fipi.ru/tasks/2/a

Ключи к контрольной работе в формате теста

Часть 1.

I. Продолжите утверждения так, чтобы получились верные высказывания:

1) Процесс нахождения производной называется … дифференцированием

2) Значение производной функции в точке х₀показывает … скорость изменения функции

3) Мгновенной скоростью называется … производная от пути по времени

4) Геометрический смысл производной состоит в том, что производная функции в точке

есть …угловой коэффициент касательной к графику функции в этой точке

II. Вставьте пропущенные выражения так, чтобы получились верные правила дифференцирования:

1) = С f^/(х)

2) (f(x) + g(x))^/ =  f^/ (x)   + g^/(x)

3) (f(x)g(x))^/ = f^/(x)g(x) + f(x)g^/(x)   

4)

III. Ма­те­ри­аль­ная точка дви­жет­ся от на­чаль­но­го до ко­неч­но­го по­ло­же­ния. На ри­сун­ке изоб­ражён гра­фик её дви­же­ния. На оси абс­цисс от­кла­ды­ва­ет­ся время в се­кун­дах, на оси ор­ди­нат — рас­сто­я­ние от на­чаль­но­го по­ло­же­ния точки (в мет­рах). Сред­няя ско­рость дви­же­ния точки в (м/с) равна 1,6 м\с.

Ре­ше­ние.

Чтобы найти сред­нюю ско­рость дви­же­ния точки, не­об­хо­ди­мо прой­ден­ное рас­сто­я­ние по­де­лить на время про­хож­де­ния: 8:5 = 1,6  м/с

 Ответ: 1,6 м\с.

IV. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну

x(t) = – t⁴ + 6t3 + 5t + 23, её ско­рость в (м/с) в мо­мент вре­ме­ни t = 1 c, равна:

Решение: x^/(t) = – 4t³ + 18t² + 5,           x^/(1) = -4 + 18 +5 = 19

Ответ: 19 м/с.

V. Укажите, для какой функции:

1) = ; 2) = ;

3) = ; 4) =

функция = является производной.

Ответ: 4

VI. Установите соответствие между функцией и её производной: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

f ( x) (функция)	f /( x) (производная функции)
1. 2х2 + 5 х – 47	1.
2. х– 5– 7х	2. – 60(2 – 5 х)11
3. +	3.
4. х5+1/х	4. 4х + 5
5.	5. (х2+8) + 2х (х-2)
6. (х-2)(х2+8)	6.
7.	7. -5х – 6– 7
8. –	8.
9. (2 – 5 х)12	9.
10. 2х+ tgx – lnx	10. 5х4– 1\x2

В таблице под каждой цифрой, соответствующей функции, укажите номер её производной

Ответ:

1	2	3	4	5	6	7	8	9	10
4	7	8	10	1	5	3	6	2	9

VII. Установите соответствия между графиками функций и значениями производных в точке х₀.

Графики функций.

A. B. C.

D.

Значения производных:

1) 0,25;         2) -1;        3) 0,5;            4) – 0,25.

В таблице под каждой буквой, соответствующей графику, укажите номер её значения

Ответ:

A	B	C	D
2	1	4	3

Часть 2.

VIII. Установите соответствие между функцией ⇒ графиком функции ⇒ производной ⇒ графиком производной функции.

Функция:  1. у = х³;    2. у = – 3;        3. у = х² – 2;      4. у = – 2х + 5;      5. у = – 1\х 

График функции:

1. 2. 3. 4.

5.

Производная функции:

1. у^/ = 2х;         2. у^/ = 3х²;         3. у^/ =  1\х² ;       4. у^/ = 0;       5. у^/ = – 2

График производной функции:

1.23.

4. 5.

В таблице под каждой цифрой, соответствующей функции, укажите номер её графика, затем укажите номер производной этой функции и номер графика, соответствующий графику производной.

Ответ:

1	2	3	4	5
5	1	3	2	4
2	4	1	5	3
3	5	4	1	2

IX. Прямая f(x) = – 4х – 11 является касательной к графику функции . Абсцисса точки касания равна

Решение: f^/(x) = -4; у^/ = 3х² + 14х +7,     f^/(x)= у^/,

3х² + 14х +7 = – 4, 3х² + 14х +11 = 0, D = 196 – 132 = 64, х₁= – 1, х₂ = –  11\3 .

Ответ: – 1;      – 11\3 .

X. Прямая у = 6х – 5 является касательной к графику функции f(x) = 9х² + bх + 76 . Найдите b, учитывая, что абсцисса точки касания меньше 0.

Решение: f^/(x)= у^/

18х + b = 6,    b = 6 – 18х,

у = f(x),      9х² + х (6 – 18х) + 76 = 6х – 5,   9х² + 6х – 18 х² – 6х + 81 = 0,

– 9х² + 81 = 0,

х² = 9,

х₁ = + 3,   х₂ = -3

Ответ: – 3

Опубликовано 04. 11.20 в 02:23 в группе «УРОК.РФ: группа для участников конкурсов»

Домашняя контрольная работа по алгебре для 11-го класса “Производная и ее геометрический смысл”

Главная / Старшие классы / Алгебра

Скачать

81.67 КБ, 852754.docx Автор: Грук Любовь Владимировна, 1 Апр 2015

Работа ориентирована на учебник под редакцией Ш.Алимова и составлена в четырех вариантах, построенных по одному типу, но варианты немного отличаются по сложности. Данная работа включает задания на нахождение производных элементарных функций, изучаемых в школьном курсе, и задание на составление уравнения касательной. Можно использовать как домашнюю контрольную работу или как проверочную.

Автор: Грук Любовь Владимировна

Похожие материалы

Тип	Название материала	Автор	Опубликован
документ	Домашняя контрольная работа по алгебре для 11-го класса “Производная и ее геометрический смысл”	Грук Любовь Владимировна	1 Апр 2015
документ	Контрольная работа по теме “Производная. Физический и геометрический смысл производной” на 4 варианта. по учебнику Колягина Ю.М.	Шумкова Елена Георгиевна	7 Апр 2015
документ	Контрольная работа №4 по алгебре для 7 класса по теме “Степень и ее свойства. Одночлены”	Баринова Елена Валерьевна	8 Фев 2016
документ	Проверочная работа по теме “Производная. Геометрический и физический смысл производной. Исследование функции по графику производной”.	Демина Елена Максимовна	21 Мар 2015
презентация, документ	конспект урока по алгебре и началам анализа 11 класс “Геометрический смысл производной”	Токарева Тамара Ивановна	1 Апр 2015
презентация	Презентация по алгебре в 11 классе на тему: “Геометрический и физический смысл производной”	Ибрагимова Эльвира Шевкетовна	14 Янв 2016
разное	решебник по алгебре 7 класс домашняя контрольная работа 2	tronarukeh2980	11 Мая 2015
разное	Контрольная работа по обществознанию для 11-го класса по теме “Человек и экономика”	Биктимирова Мария Рафиковна	31 Мар 2015
документ	Открытый урок на тему “Производная, ее геометрический и механический смысл” Наглядные пособия: портреты математиков, высказывания ученых,  программа «Математика 9-11». Раздаточный материал: карточки с заданиями, микроплакаты &n	Калмыкова Татьяна Юрьевна	21 Мар 2015
документ	Контрольная работа по алгебре и началам анализа для 11 класса по теме “Обобщение понятия степени”	Кравченко Николай Анатольевич	21 Мар 2015
документ	Контрольная работа по алгебре и началам анализа для 11 класса по теме ” Комбинаторика”	Аксёнова Светлана Валерьевна	17 Фев 2016
документ	Зачетная работа по алгебре в 10 классе по теме “Производная и ее применение”	Панышева Татьяна Николаевна	1 Апр 2015
документ	Рабочая программа элективного курса по алгебре и началам анализа для учащихся 11-го класса “Практикум по алгебре»	Салбакай Монгушевна Оюн	26 Окт 2015
документ	Рабочая программа элективного курса по алгебре и началам анализа для учащихся 11-го класса “Практикум по алгебре»	Оюн Салбакай Монгушевна	28 Фев 2016
документ	Производная и ее геометрический смысл	Шаршина Юлия Юрьевна	1 Апр 2015
документ	Производная и ее геометрический смысл	Бикмухаметова Ольга Наильевна	20 Ноя 2015
презентация, документ	«Производная и ее геометрический смысл»	Николаева Валентина Васильевна	25 Апр 2015
презентация	Производная и ее геометрический смысл.	Тарасова Ирина Петровна	14 Ноя 2015
разное	Урок в 11 классе, алгебра и начала анализа. Тема: “Производная и её геометрический смысл”.	Тарада Елена Борисовна	31 Мар 2015
документ	Разработка урока по алгебре в 10 классе “Производная и ее применение”	Елена Владимировна Сырыгина	11 Апр 2015
документ	Математическая игротека (урок-зачет) по теме : Производная и ее геометрический смысл.	Салимова Галина Павловна	1 Апр 2015
документ	Открытый урок по теме” Производная и её геометрический смысл”	Шпакова Елена Николаевна	1 Апр 2015
документ	Контрольная работа по алгебре по теме “Производная и первообразная”	Волкова Наталья Евгеньевна	1 Апр 2015
документ	Контрольная работа по алгебре для 11 класса по теме “Комбинаторика”	Аксёнова Светлана Валерьевна	28 Фев 2016
документ	Контрольная работа по алгебре и началам анализа для 10-го класса по материалам ЕГЭ	Грук Любовь Владимировна	6 Апр 2015
разное	Обобщающий урок по алгебре и началам анализа по теме “Производная и ее применение. Повторение в рамках подготовки к ЕГЭ”	Степина Татьяна Петровна	25 Янв 2016
разное	Контрольная работа по теме “Производная” 11 класс	Хожулина Елена Валентиновна	1 Апр 2015
документ	Разработка урока по алгебре в 10 классе “Производная и ее применение”	Сорока Татьяна Алексеевна	5 Апр 2015
документ	Разноуровневая домашняя контрольная работа по геометрии для 8 класса	Горбаченко Валентина Ивановна	21 Мар 2015
документ	Проверочная работа по теме “Производная функции” для 10-го класса.	Дареева Соелма Норбоевна	1 Апр 2015
документ	Электронное пособие по алгебре для учеников 7 класса по теме “Степень и ее свойства”	Тюрина Надежда Игоревна	4 Апр 2015
документ	Самостоятельная работа по алгебра для 11-го класса по теме “Наибольшее и наименьшее значение функции на отрезке”	Грук Любовь Владимировна	1 Апр 2015
документ	Контрольная работа №6 по алгебре для 7 класса по теме “Произведение многочленов”	Баринова Елена Валерьевна	8 Фев 2016
документ	Контрольная работа №5 по алгебре для 7 класса по теме “Многочлены”	Баринова Елена Валерьевна	8 Фев 2016
документ	Контрольная работа №1 по алгебре для 7 класса по теме “Преобразование выражений”	Баринова Елена Валерьевна	8 Фев 2016
документ	Контрольная работа №9 по алгебре для 7 класса по теме “Системы линейных уравнений”	Баринова Елена Валерьевна	8 Фев 2016
документ	Контрольная работа №8 по алгебре для 7 класса по теме “Преобразование целых выражений”	Баринова Елена Валерьевна	8 Фев 2016
документ	Контрольная работа №7 по алгебре для 7 класса по теме “Формулы сокращенного умножения”	Баринова Елена Валерьевна	8 Фев 2016
документ	Контрольная работа для 8 класса по алгебре “Квадратные уравнения”	Северюхина Ксения Николаевна	21 Мар 2015
документ	Домашняя контрольная работа по теме “Цилиндр”	Елена Игоревна Бондарева	21 Мар 2015

Алгебраический и геометрический смысл производной

15 февраля 2010 г. ГБ Исчисление и анализ, Колледж математики

Примечание: Это первая часть серии производных концепций. Вторая часть — «Производная в контексте реальной жизни», а третья — «Производная и проблема максимальной площади».

***

Если мы хотим получить наклон линии, нам нужны две точки. Предположим, точки имеют координаты и , мы узнали, что наклон описывается формулой .

На рисунке 1 у нас есть линия, касательная к функции в точке, где координаты . Проблема, породившая исчисление, заключается в том, чтобы получить наклон этой касательной. Однако есть проблема. Нам нужны две точки для вычисления наклона, но у нас есть только одна точка.

Обратите внимание, что слово касательная в этой задаче отличается от определения касательной к окружности, потому что ясно, что линия будет пересекать график более чем в одной точке.

Рисунок 1 – Прямая l, касающаяся функции f в точке P.

Используя концепцию ограничений, мы можем решить эту проблему. Во-первых, мы создаем точку с единицами координат x справа от координаты x . Затем мы рисуем линию, секанс линию к функции.

Рисунок 2 – Через точку P проведена секущая. касательной, разумно, что мы движемся к фиксированной. Нажмите здесь, чтобы изучить диаграмму выше с помощью GeoGebra.

Из приведенного выше исследования GeoGebra, если мы движемся к , мы наблюдаем следующее:

1.)    Значение подходов .

2.)    Наклон секущей приближается к наклону касательной.

3.)    Наклон секущей приближается к наклону касательной.

4.)    Если точка совпадает с точкой , то наклон секущей и равен наклону касательной.

Если мы допустим наклон секущей и наклон касательной, сосредоточив внимание на наблюдениях 1 и 4, мы можем сказать следующие эквивалентные утверждения:

• Предел наклона секущей при приближении равен .
• Предел наклона секущей при приближении равен .
• Предел по мере приближения равен .

Используя обозначение предела, мы можем сказать, что

Из приведенного выше обсуждения мы можем видеть, что производная функции в конкретной точке равна наклону линии, касательной к этой функции в этой точке. конкретный момент.

В следующем посте мы обсудим значение производной в реальных жизненных ситуациях.

7 комментариев формула производной, дифференциальное исчисление, дифференцирование, первая производная, пределы, секущая, наклон, касательная

Физический или геометрический смысл комплексной производной

Задавать вопрос

спросил 8 лет, 3 месяца назад

Изменено 6 лет, 5 месяцев назад

Просмотрено 5к раз

$\begingroup$

Производная функции с действительным знаком в точке — это наклон функции в этой точке.

Аналогично, каков физический или геометрический смысл производной комплекснозначной функции в точке?

• комплексный анализ
• комплексная геометрия

$\endgroup$

2

$\begingroup$

Вы можете думать о производной как о выражении локального/мгновенного растяжения и вращения.

Например, предположим, что реальная функция $f$ имеет $f'(a)=2$ для некоторого $a$. Мы можем думать об этом как о том, что вблизи $a$ функция (приблизительно) удваивает расстояние, вплоть до добавления константы. Это то, что выражает касательная $2(x-a)+f(a)$. 9{i\theta}$ говорит, что вблизи $a$ мы (приблизительно) растягиваем/сокращаем расстояния на коэффициент $r$, а также поворачиваем на угол $\theta$. Например, $f'(a)=i$ означает, что мы просто вращаемся против часовой стрелки на $\pi/2$ радиан. А $f'(a)=-i/2$ означает, что мы сжимаемся в 2 раза и поворачиваемся против часовой стрелки на $3\pi/2$ радиан.

$\endgroup$

$\begingroup$

Одно четкое физическое значение дает теория гармонических функций. В частности, если $f=u+iv$ комплексно-дифференцируема на открытом множестве, то обе составляющие функции удовлетворяют уравнению Лапласа. Другими словами, их можно рассматривать как возможные функции потенциальной энергии для силового поля, консервативного в домене, или как функции напряжения для электростатического поля в домене.