Работа энергия мощность: Глава 6. Работа, мощность, энергия. Закон сохранения и изменения механической энергии

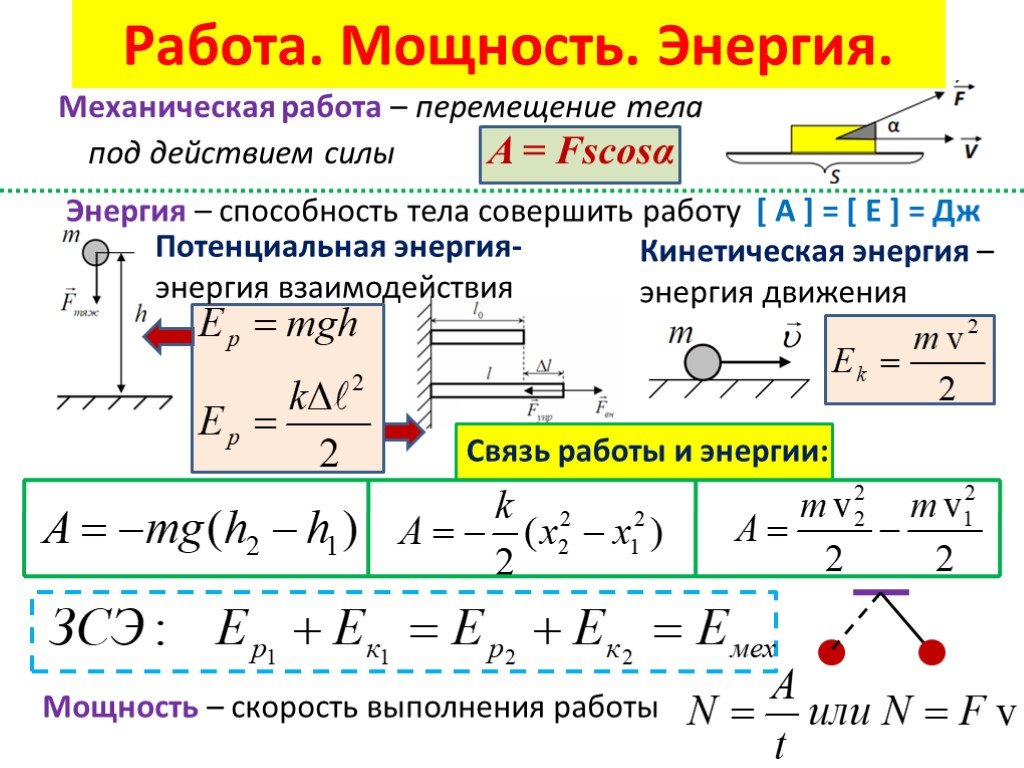
2. Работа силы. Мощность. Энергия.

Пусть тело на которого действует некоторая сила проходит, двигаясь по некоторой траектории, путьS. Действие силы на путиS характеризуется величиной которая называется работой.

при F = const

Работа – Мера передачи действия (механического) от одного тела к другому в процессе взаимодействия

Силы, работа которых не зависит от формы пути, а определяется только наличным и конечным положениями тела в пространстве, называются консервативными или потенциальными.

Силы, работа которых зависит от формы пути называются неконсервативными.

Силы консервативные тогда, когда в системе нет перехода механического движения в другие формы движения материи или наоборот.

Силы, работа которых возрастает по величине, при увеличении пути независимо от того, замкнут путь или нет, называются диссипативными.

В этом случае механическая энергия переходит во внутреннюю, и работа этих сил определяется не однозначно.

Мощность – скалярная физическая величина равная отношению произведенной работы к промежутку времени в течении которого эта работа произошла.

Механическое движение может переходить в другие виды движения материи (в тепловое, в электромагнитное действие и др.). Переходы осуществляются в строго определённых количественных соотношениях. Общей мерой для всех видов движения материи является энергия.

Энергия – Мера количества любых видов движения материи (тела).

Энергия – физическая величина характеризующая способность тела совершать работу. Для характеристики изменения энергии взаимодействующих тел введена специальная физическая величина – работа силы.

Кинетической энергией называется энергия движущегося тела.

Работа равнодействующей сил приложенных к телу, равна изменению кинетической энергии тела.

Если действует ещё сила трения, то A_тр< 0 и кинетическая энергия тела будет уменьшаться.

Потенциальной энергией тела Энергия, обусловленная взаимным расположением тел или частей одного и того же тела и характером их взаимодействия.

Сила направлена всегда в сторону уменьшения потенциальной энергии.

Работа силы тяжести равна изменению потенциальной энергии тела взятому с противоположным знаком

Физическая величина, равная половине произведения жесткости тела (пружины) на квадрат его деформации, называют потенциальной энергией упругодеформированого тела.

Работа силы упругости равна изменению потенциальной энергии упруго деформированного тела взятому с противоположным знаком

Если на частицу в каждой точке пространства действует определённая сила, то эту совокупность сил называют

силовым полем. Если силы поля постоянны по величине, неизменны по направлению и не зависят от времени, то образуемые ими поля называютсяоднородные и постоянные силовые поля.

В однородном постоянном силовом поле:

а) работа по замкнутому пути равна нулю.

б) работа при переносе материальной частицы из одного положения в другое не зависит от формы пути, а определяется положением начальной и конечной точек переноса.

Изолированной, или замкнутой, называют систему тел, взаимодействующих только между собой и не взаимодействующих с телами, не входящими в систему.

Центром масс (центр инерции) – точка, характеризующая распределение масс в механической системе. Радиус вектор центра масс системы состоящей из n точек, равен

где m_i, r_i – масса и радиус вектор i–ой точки. При движении тела системы его центр масс движется как материальная точка с массой, равной массе всего тела, к которой приложены все силы, действующие на тело.

Так как система под действием внешних сил движется, то координаты центра масс со временем меняются

Если система замкнута, т.е.

то

Закон сохранения импульса: полный импульс замкнутой системы сохраняется неизменным, а центр масс движется равномерно и прямолинейно (или покоится).

Векторная сумма импульсов тел, входящих в замкнутую систему, остается неизменной при механическом взаимодействии тел внутри этой системы.

Сумма кинетической и потенциальной энергии тела называется полной механической энергией тела.

Полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения и упругости, остается неизменной.

При любых физических взаимодействиях энергия не возникает не исчезает, а только превращается из одной формы в другую.

Курс физики. Том I. Механика, акустика, молекулярная физика, термодинамика

Курс физики. Том I. Механика, акустика, молекулярная физика, термодинамика

Путилов К.А. Курс физики. Том I. Механика, акустика, молекулярная физика, термодинамика. Москва. Государственное издательство физико-математической литературы, 1963. – 560 с. Данный трёхтомный курс физики предназначается в качестве учебного пособия для высших учебных заведений с расширенной программой физики. В первом томе изложены физические основы механики, акустика, молекулярная физика и термодинамика. Главное внимание уделено достижениям экспериментальной физики, разъяснению основных законов физики и характеристике технических применений физики. Приведены исторические сведения и рассмотрены некоторые философские вопросы физики. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ ЧАСТЬ ПЕРВАЯ. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ И АКУСТИКА § 1. О взаимосвязи явлений и допустимых границах их схематизации в физике § 2. Система ориентировки. Материальная точка и ее перемещение § 3. Элементарное перемещение. Векторы скорости и ускорения § 4. Тангенциальное и центростремительное ускорения § 5. Угловая скорость и угловое ускорение § 6. Абсолютное, переносное и относительное движения § 7. Закон сложения ускорений ГЛАВА II. ЗАКОНЫ НЬЮТОНА § 9. Первый ньютонов закон механики (закон инерции) § 10. О понятиях «покоя» и «равномерности» § 11. Инерциальная система. Принцип относительности § 12. Второй ньютонов закон механики § 13. Различные понимания второго закона механики § 14. Движение под действием постоянной силы § 15. Третий ньютонов закон механики § 16. Статическое и динамическое проявления сил § 17. Силы инерции. Центробежная сила ГЛАВА III. РАБОТА И ЭНЕРГИЯ § 18. Работа, энергия, мощность. Элемент и интеграл работы § 19. Кинетическая энергия и потенциальная энергия § 20. Системы мер и размерность механических величин ГЛАВА IV. ДИНАМИКА СИСТЕМЫ § 21. Механическая система. Внутренние и внешние силы. Центр масс § 22. Закон сохранения количества движения и теорема о движении центра масс § 23. Закон сохранения энергии в консервативных системах. Минимум потенциальной энергии при равновесии § 24. Число степеней свободы и работа сил связи. Принцип возможных перемещений § 25. Принцип Даламбера и релятивистское понимание инерции ГЛАВА V. МЕХАНИЧЕСКАЯ ПЕРЕДАЧА СИЛ И ЭНЕРГИИ (ТРЕНИЕ, УДАР, ТЯГА) § 26. Трение. Тяга § 27. Удар ГЛАВА VI. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ И ЭЛЕМЕНТЫ НЕБЕСНОЙ МЕХАНИКИ § 28. Законы Кеплера § 29. Ньютонов закон тяготения § 30. Зависимость веса и ускорения силы тяжести от высоты и географической широты местности § 31. Вычисление массы Солнца, Земли и планет § 32. Потенциальная энергия и потенциал тяготения § 33. Некоторые теоремы о потенциале тяготения § 34. Потенциальная энергия системы частиц ГЛАВА VII. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДЫХ ТЕЛ § 35. Момент силы § 36. Кинетическая энергия вращательного движения. Момент инерции § 37. Основное уравнение динамики вращательного движения § 38. Закон сохранения момента количества движения § 39. Проявление поворотных (кориолисовых) сил инерции ГЛАВА VIII. ЭЛЕМЕНТЫ ТЕОРИИ УПРУГОСТИ И МЕХАНИЧЕСКИЕ СВОЙСТВА ТЕЛ § 40. Упругие свойства тел § 41. Закон Гуна. Энергия деформированного тела § 42. Модуль объемной упругости. Сжимаемость § 43. Модуль Юнга, коэффициент Пуассона, модуль сдвига и соотношение между ними § 44. Характеристика механических свойств твердого тела по диаграмме растяжения. Явление наклепа § 45. Пластичность § 46. Прочность и твердость § 47. Механические свойства важнейших материалов ГЛАВА IX. ОСНОВЫ ГИДРОДИНАМИКИ И АЭРОДИНАМИКИ § 48. Основные понятия и направления гидродинамики § 49. Уравнение Бернулли § 50. Гидравлическая энергия § 51. Вязкость и течение жидкости при трении § 52. Пограничный слой и вихреобразование. Строение турбулентного потока § 53. Сопротивление движению тел в жидкостях и газах § 54. Числа Рейнольдса. Кинематическая вязкость § 55. Аэродинамические силы. Подъемная сила крыла и тяга самолета ГЛАВА X. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ § 56. Гармоническое колебание § 57. Энергия и собственная частота гармонических колебаний § 58. Сложение колебаний одинаковой частоты и одинакового направления (интерференция колебаний) § 59. Другие случаи сложения колебаний § 60. Затухающие колебания § 61. Вынужденные колебания. Резонанс § 62. Связанные колебания ГЛАВА XI. УЧЕНИЕ О ВОЛНАХ § 63. Волновой процесс. Уравнение волн. Виды волн § 64. Интерференция волн. Стоячие волны § 65. Фазовая и групповая скорости волн ГЛАВА XII. АКУСТИКА § 66. Звук как физическое явление. Распространение звуковых волн § 67. Интенсивность звука § 68. Частота и состав звуков § 69. Явление Допплера § 70. Звук как психофизиологическое явление. Механизм звукового восприятия § 71. Высота и тембр звука § 72. Ультразвуки ЧАСТЬ ВТОРАЯ. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА § 73. Исторические сведения. Картина молекулярного движения § 74. Статистический метод в физике § 75. Термодинамический метод § 76. Термодинамическая характеристика состояния тел и термодинамические процессы § 77. Уравнение Клапейрона § 78. Внутренняя энергия. Теплота и работа. Уравнение первого начала § 79. Изобарная и изотермическая работа газа § 80. Термохимические уравнения ГЛАВА XIV. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ § 81. Схематизация явлений («модели» в молекулярной физике) § 82. Максвеллов закон распределения молекулярных скоростей в газе § 83. Основное уравнение кинетической теории газов § 84. Молекулярно-кинетическое понимание абсолютной температуры § 85. Об уточненном (термодинамическом) понимании абсолютной температуры § 86. Тепловое равновесие и распределение энергии по степеням свободы § 87. Максвеллова теория газовых теплоемкостей § 88. Молекулярно-кинетическое пояснение работы расширения газа § 89. Средний свободный пробег газовых молекул ГЛАВА XV. ТЕПЛОПЕРЕДАЧА, ДИФФУЗИЯ И ВЯЗКОСТЬ. ВАКУУМ § 90. Тепловое излучение (законы Стефана и Ньютона) § 91. Теплопроводность (закон Фурье) § 92. Диффузия (закон Фика) § 93. Молекулярная теория теплопроводности газов § 94. Молекулярная теория вязкости газов § 95. Сопоставление явлений диффузии, теплопроводности и вязкости газов § 96. Вакуум. Манометры § 97. Вакуумные насосы ГЛАВА XVI. ТЕРМОДИНАМИЧЕСКОЕ РАВНОВЕСИЕ И ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ § 98. Термодинамическое равновесие и e-положение Больцмана § 99. Ограничения, налагаемые вторым началом термодинамики на циклические превращения тепла в работу § 100. Уравнение Пуассона. Адиабатная работа газа § 101. Цикл Карно и теорема о сумме приведенных теплот § 102. Энтропия. Основное уравнение термодинамики § 103. Процессы обратимые и необратимые. Теорема о возрастании энтропии § 104. Статистический смысл энтропии § 105. Теоремы о термодинамическом равновесии. Свободная энергия и термодинамический потенциал § 106. О так называемой «тепловой смерти» мира § 107. Уравнения Гиббса — Гельмгольца и Клапейрона—Клаузиуса ГЛАВА XVII. ФИЗИКА РЕАЛЬНЫХ ГАЗОВ И ПАРОВ. УРАВНЕНИЕ ВАН-ДЕР-ВАЛЬСА § 108. Пары насыщенные и перегретые. Диаграмма Эндрюса § 109. Конденсация газов § 110. Уравнение Ван-дер-Вальса § 111. Учение о соответственных состояниях § 112. О качественных превращениях при тепловых процессах ГЛАВА XVIII. ФИЗИКА ЖИДКОСТЕЙ § 113. Механические и термодинамические свойства жидкостей § 114. Поверхностное натяжение § 115. Формула Лапласа. Явления капиллярности и смачивания § 116. Поверхностноактивные вещества § 117. Строение жидкостей § 118. Кинетика испарения. Зависимость давления насыщенного пара от кривизны поверхности жидкости. Формула Томсона — Шиллера § 119. Понижение давления пара над раствором и повышение температуры кипения растворов. Законы Рауля § 120. Осмотическое давление. Закон Вант-Гоффа § 121. Электролитическая диссоциация. Закон Оствальда § 122. Абсорбция. Закон Генри § 123. О столкновении противоположных процессов в молекулярно-тепловых явлениях ГЛАВА XIX. ФИЗИКА ТВЕРДЫХ ТЕЛ § 124. Строение кристаллов § 125. Понятие о кристаллохимии § 126. Форма и рост кристаллов § 127. Теплоемкость твердых тел § 128. Сублимация твердых тел. Тройная точка § 129. Кристаллизация растворов. Диаграмма плавкости § 130. Силы связи в кристаллах § 131. Адсорбция ГЛАВА XX. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ В ДВИГАТЕЛЯХ И СВЕРХЗВУКОВОЕ ДВИЖЕНИЕ § 132. Основное уравнение газодинамики. Адиабатный теплоперепад § 133. Адиабатное течение газа § 134. Ударные волны и скачки уплотнения. Адиабата Гюгонио § 135. Процессы в двигателях внутреннего сгорания § 136. Процессы в паровых машинах и паровых турбинах § 137. Реактивные двигатели

7.8: Работа, энергия и сила у людей

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1525

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Объяснить потребление энергии человеческим телом в состоянии покоя и при выполнении полезной работы.
• Рассчитайте превращение химической энергии пищи в полезную работу.

Преобразование энергии в организме человека

Наши собственные тела, как и все живые организмы, представляют собой машины для преобразования энергии. Сохранение энергии подразумевает, что химическая энергия, хранящаяся в пище, преобразуется в работу, тепловую энергию и/или запасается в виде химической энергии в жировой ткани. (Рисунок 7.09.1.) Доля, входящая в каждую форму, зависит как от того, сколько мы едим, так и от уровня нашей физической активности. Если мы едим больше, чем необходимо для работы и согревания, остаток уходит в жировые отложения.

Рисунок \(\PageIndex{1}\): Энергия, потребляемая человеком, преобразуется в работу, тепловую энергию и накопленный жир. На сегодняшний день самая большая доля приходится на тепловую энергию, хотя эта доля варьируется в зависимости от типа физической активности.

Мощность, потребляемая в состоянии покоя

Скорость, скорость, с которой тело использует энергию пищи для поддержания жизни и выполнения различных действий, называется скоростью метаболизма. Суммарная скорость преобразования энергии человека в покое называется скоростью основного обмена (BMR) и распределяется между различными системами организма, как показано в табл. Самая большая фракция поступает в печень и селезенку, затем следует головной мозг. Конечно, при энергичных физических нагрузках заметно возрастают энергозатраты скелетных мышц и сердца. Около 75% калорий, сожженных за день, идут на эти основные функции. BMR зависит от возраста, пола, общей массы тела и количества мышечной массы (которая сжигает больше калорий, чем жировые отложения). Спортсмены имеют более высокий BMR из-за этого последнего фактора.

Базальный уровень метаболизма (BMR):

Орган	Мощность, потребляемая в состоянии покоя (Вт)	Потребление кислорода (мл/мин)	Процент от BMR
Печень и селезенка	23	67	27
Мозг	16	47	19
Скелетные мышцы	15	45	18
Почки	9	26	10
Сердце	6	17	7
Прочее	16	48	19
Всего	85 Вт	250 мл/мин	100%

Потребление энергии прямо пропорционально потреблению кислорода, поскольку пищеварительный процесс в основном представляет собой процесс окисления пищи. Мы можем измерить энергию, которую люди используют во время различных видов деятельности, измеряя потребление ими кислорода. (См. рис. 7.09.1.) Приблизительно 20 кДж энергии производится на каждый литр потребленного кислорода, независимо от типа пищи. В таблице показаны показатели потребления энергии и кислорода (затрачиваемая мощность) для различных видов деятельности.

Способность выполнять полезную работу

Работа, выполняемая человеком, иногда называется полезной работой, которая представляет собой работу, выполняемую во внешнем мире , такую ​​как поднятие тяжестей. Полезная работа требует силы, воздействующей на внешний мир через расстояние, и поэтому она исключает внутреннюю работу, например, совершаемую сердцем при перекачивании крови. Полезная работа включает в себя подъем по лестнице или ускорение до полного бега, потому что они выполняются за счет приложения сил к внешнему миру. Силы, действующие на тело, неконсервативны, поэтому они могут изменить механическую энергию \((KE + PE)\) системы, на которую воздействуют, и это часто является целью.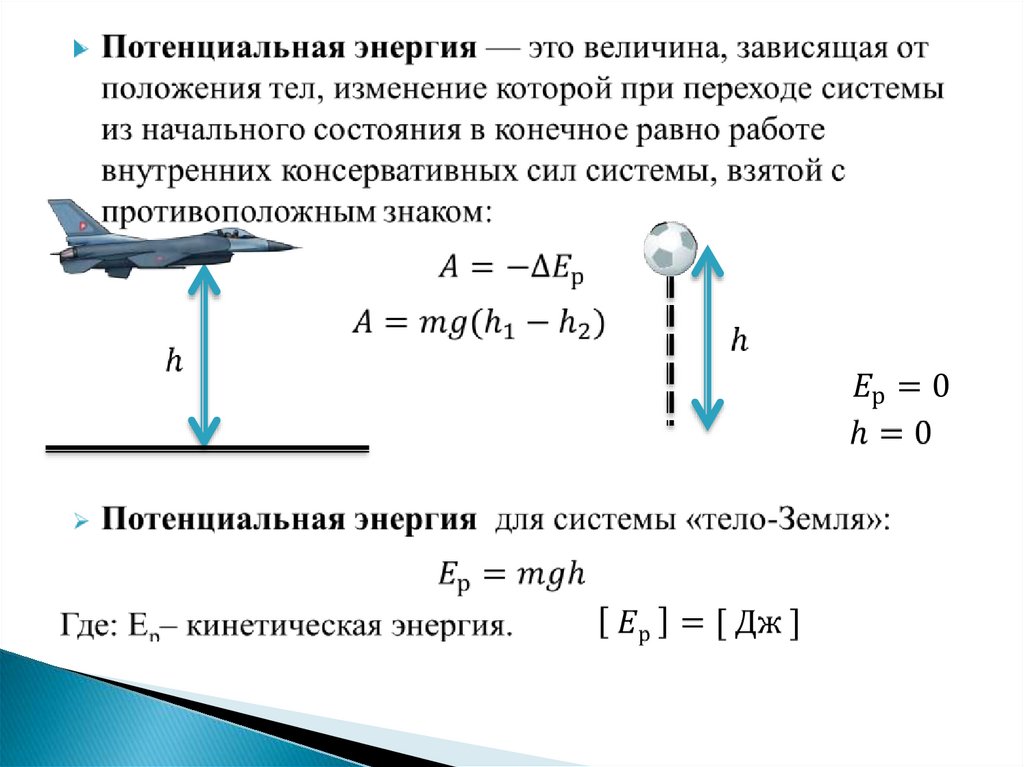 Например, бейсболист, бросающий мяч, увеличивает как кинетическую, так и потенциальную энергию мяча.

Если человеку требуется больше энергии, чем он потребляет, например, при выполнении тяжелой работы, организм должен использовать химическую энергию, хранящуюся в жире. Таким образом, физические упражнения могут помочь в потере жира. Однако, как показывает пример 7.09.1, количество упражнений, необходимых для потери жира или сжигания лишних калорий, потребляемых в этот день, может быть большим.

Пример \(\PageIndex{1}\): расчет потери веса в результате физических упражнений

Если человек, которому обычно требуется в среднем 12 000 кДж (3000 ккал) пищевой энергии в день, потребляет 13 000 кДж в день, он будет постоянно набирать масса. Сколько велосипедов в день требуется, чтобы отработать эти лишние 1000 кДж?

Решение

В таблице указано, что при езде на велосипеде с умеренной скоростью используется мощность 400 Вт. Тогда время, необходимое для отработки 1000 кДж при этой скорости, равно

\[Время = \dfrac{энергия}{\left(\frac{энергия}{время} \right)} = \dfrac{1000 \, кДж}{ 400 \, W} = 2500 \, s = 42 \, min. \]

Обсуждение

Если этот человек использует больше энергии, чем потребляет, его тело будет получать необходимую энергию путем метаболизма жировых отложений. Если человек использует 13 000 кДж, но потребляет только 12 000 кДж, то объем потери жира составит

\[ Жир \, потеря = (1000 \, кДж) \влево ( \фрак{1 \, г \, жир} {30 \, кДж} \вправо) = 26 \, г, \]

при условии энергетическая ценность жира 39 кДж/г.

Рисунок \(\PageIndex{2}\): Пульсоксиметр — это прибор, измеряющий количество кислорода в крови. Информация об уровнях кислорода и углекислого газа указывает на скорость метаболизма человека, то есть на скорость, с которой энергия пищи преобразуется в другую форму. скорость метаболизма человека, то есть скорость, с которой энергия пищи преобразуется в другую форму. Такие измерения могут указывать на уровень спортивной подготовки, а также на определенные медицинские проблемы. (кредит: УусиАйая, Wikimedia Commons)

Нормы потребления энергии и кислорода:

One column lists the activity and the corresponding row in the next column lists the rate of energy consumption in watts. The last column lists the oxygen consumption in liters of oxygen per minute.”>

Деятельность	Энергопотребление в ваттах	Потребление кислорода в литрах O 2 /мин
Спальный	83	0,24
Сидя в состоянии покоя	120	0,34
Стоя расслабленно	125	0,36
Сидя в классе	210	0,60
Ходьба (5 км/ч)	280	0,80
Велоспорт (13–18 км/ч)	400	1,14
Дрожь	425	1,21
Игра в теннис	440	1,26
Плавание брассом	475	1,36
Катание на коньках (14,5 км/ч)	545	1,56
Подъем по лестнице (116/мин)	685	1,96
Велоспорт (21 км/ч)	700	2,00
Бег по пересеченной местности	740	2,12
Игра в баскетбол	800	2,28
Велоспорт, профессиональный гонщик	1855	5,30
Спринт	2415	6,90

Все функции организма, от мышления до поднятия тяжестей, требуют энергии. (См. рис. 7.09.3.) Множество мелких мышечных движений, сопровождающих любую спокойную деятельность, от сна до почесывания головы, в конечном итоге становятся тепловой энергией, как и менее заметные мышечные действия сердца, легких и пищеварительного тракта. Дрожь, по сути, является непроизвольной реакцией на низкую температуру тела, когда мышцы напрягаются друг против друга, чтобы производить тепловую энергию в теле (и не выполнять никакой работы). Почки и печень потребляют удивительное количество энергии, но самым большим сюрпризом является то, что целых 25% всей энергии, потребляемой организмом, используются для поддержания электрических потенциалов во всех живых клетках. (Нервные клетки используют этот электрический потенциал в нервных импульсах.) Эта биоэлектрическая энергия в конечном итоге становится в основном тепловой энергией, но некоторая ее часть используется для питания химических процессов, например, в почках и печени, а также в производстве жира.

Рисунок \(\PageIndex{3}\): МРТ показывает повышенный уровень потребления энергии в зрительном центре головного мозга. Здесь пациента просили распознавать лица. (кредит: NIH через Wikimedia Commons)

Резюме

• Человеческое тело преобразует энергию, хранящуюся в пище, в работу, тепловую энергию и/или химическую энергию, которая запасается в жировой ткани.
• Скорость , с которой организм использует энергию пищи для поддержания жизни и выполнения различных действий, называется скоростью метаболизма, а соответствующая скорость в состоянии покоя называется скоростью основного обмена (BMR)
• Энергия, входящая в состав основного обмена веществ, распределяется между различными системами организма, при этом наибольшая часть направляется в печень и селезенку, а затем в головной мозг.
• Около 75% пищевых калорий расходуются на поддержание основных функций организма, входящих в основной обмен веществ.
• Потребление энергии людьми во время различных видов деятельности можно определить путем измерения потребления ими кислорода, поскольку процесс пищеварения в основном представляет собой процесс окисления пищи.

Глоссарий

скорость метаболизма

скорость, с которой организм использует энергию пищи для поддержания жизни и выполнения различных действий

скорость основного обмена

общий коэффициент преобразования энергии человека в состоянии покоя

полезная работа

работа, выполненная во внешней системе

---

Эта страница под названием 7.8: Работа, энергия и сила в людях распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. скорость основного обмена
   2. скорость метаболизма
   3. источник@https://openstax. org/details/books/college-physics
   4. полезная работа

9.1 Работа, мощность и теорема о работе-энергии

Цели обученияТеорема о работе и энергииРасчеты, связанные с работой и мощностьюЗадания на практику Проверьте свое понимание

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Описывать и применять теорему о работе и энергии
• Описать и рассчитать работу и мощность

Основные термины раздела

энергия	гравитационная потенциальная энергия	джоулей
кинетическая энергия	механическая энергия	потенциальная энергия
мощность	Вт	работа
теорема работа-энергия

Теорема о работе и энергии

В физике термин работа имеет очень конкретное определение. Работа – это приложение силы ff для перемещения объекта на расстояние d , в направлении приложения силы. Работа, W , описывается уравнением

W=fd.W=fd.

Некоторые вещи, которые мы обычно считаем работой, не являются работой в научном смысле этого слова. Рассмотрим несколько примеров. Подумайте, почему каждое из следующих утверждений верно.

• Домашнее задание не является заданием.
• Поднять камень вверх над землей — это работа.
• Перенос камня по прямой траектории через газон с постоянной скоростью это не работа.

Первые два примера довольно просты. Домашняя работа не является работой, потому что объекты не перемещаются на расстояние. Поднять камень над землей — это работа, потому что камень движется в направлении приложения силы. Последний пример менее очевиден. Вспомним из законов движения, что для перемещения объекта с постоянной скоростью требуется , а не сил. Поэтому, хотя может быть приложена некоторая сила, чтобы удерживать камень над землей, результирующая сила не прилагается, чтобы поддерживать движение камня вперед с постоянной скоростью.

Работа и энергия тесно связаны. Когда вы совершаете работу по перемещению объекта, вы изменяете энергию объекта. Вы (или объект) также тратите энергию на выполнение работы. Фактически энергию можно определить как способность совершать работу. Энергия может принимать различные формы, и одна форма энергии может трансформироваться в другую. В этой главе нас будет интересовать механическая энергия, которая существует в двух формах: кинетическая энергия и потенциальная энергия.

• Кинетическая энергия также называется энергией движения. Движущийся объект обладает кинетической энергией.
• Потенциальная энергия, иногда называемая запасенной энергией, бывает нескольких видов. Гравитационная потенциальная энергия — это накопленная энергия, которой обладает объект в результате его положения над поверхностью Земли (или другого объекта в космосе). Автомобиль американских горок на вершине холма обладает гравитационной потенциальной энергией.

Давайте посмотрим, как выполнение работы над объектом изменяет энергию объекта. Если мы приложим силу, чтобы поднять камень с земли, мы увеличим потенциальную энергию камня, PE . Если мы уроним камень, сила гравитации увеличит кинетическую энергию камня по мере его движения вниз, пока он не упадет на землю.

Сила, которую мы прикладываем, чтобы поднять камень, равна его весу, w , что равно его массе, m , умноженной на ускорение свободного падения, g .

f=w=mgf=w=mg

Работа, которую мы совершаем над камнем, равна силе, которую мы прикладываем, умноженной на расстояние, d , на которое мы поднимаем камень. Работа, которую мы совершаем над камнем, также равна выигрышу камня в гравитационной потенциальной энергии, РЕ _и .

W=PEe=fmgW=PEe=fmg

Кинетическая энергия зависит от массы объекта и его скорости, v .

KE=12mv2KE=12mv2

Когда мы бросаем камень, сила тяжести заставляет камень падать, придавая камню кинетическую энергию. Когда работа, совершаемая над объектом, увеличивает только его кинетическую энергию, то чистая работа равна изменению величины величины 12mv212mv2. Это формулировка теоремы работа-энергия, которая математически выражается как

W=ΔKE = 12mv22−12mv12.W=ΔKE = 12mv22−12mv12.

Нижние индексы ₂ и ₁ указывают конечную и начальную скорость соответственно. Эта теорема была предложена и успешно проверена Джеймсом Джоулем (рис. 9.2).

Имя Джоуль звучит знакомо? Джоуль (Дж) является метрической единицей измерения как работы, так и энергии. Измерение работы и энергии в одних и тех же единицах подтверждает идею о том, что работа и энергия связаны и могут быть преобразованы друг в друга. 1,0 Дж = 1,0 Н∙м, единица силы, умноженная на расстояние. 1,0 Н = 1,0 к∙м/с ² , поэтому 1,0 Дж = 1,0 к∙м ² /с ² . Анализ единиц слагаемого (1/2) m v ² даст те же единицы для джоулей.

Рисунок 9.2 Джоуль назван в честь физика Джеймса Джоуля (1818–1889). (C. H. Jeens, Wikimedia Commons)

Смотреть физику

Работа и энергия

В этом видео объясняется теорема о работе и энергии и обсуждается, как работа, выполняемая над объектом, увеличивает КЭ объекта.

Нажмите, чтобы просмотреть содержание

Проверка хватки

Верно или нет — увеличение энергии объекта, на который действует только сила гравитации, равна произведению веса объекта на расстояние, на которое он падает.

1. Правда
2. Ложь

Вычисления, связанные с работой и мощностью

В приложениях, связанных с работой, нас часто интересует, насколько быстро выполняется работа. Например, при проектировании американских горок важным фактором является время, необходимое для подъема автомобиля с американских горок на вершину первого холма. Полчаса подъема наверняка вызовут раздражение у райдеров и снизят продажи билетов. Давайте посмотрим, как рассчитать время, необходимое для выполнения работы.

Вспомните, что ставка может использоваться для описания количества, например работы, за период времени. Мощность – это скорость, с которой совершается работа. В этом случае скорость означает в единицу времени . Мощность рассчитывается путем деления выполненной работы на время, затраченное на эту работу.

P=WtP=Wt

Давайте рассмотрим пример, который поможет проиллюстрировать разницу между работой, силой и мощностью. Предположим, женщина на рис. 9.3, поднимающая телевизор с помощью шкива, поднимает телевизор на четвертый этаж за две минуты, а мужчине, несущему телевизор по лестнице, требуется пять минут, чтобы добраться до того же места. Они проделали одинаковую работу (fd)(fd) на телевидении, потому что они переместили одинаковую массу на одно и то же расстояние по вертикали, что требует такой же величины восходящей силы. Однако женщина, использующая шкив, произвела больше энергии. Это потому, что она выполнила работу за меньшее время, поэтому знаменатель формулы мощности т , меньше. (Для простоты мы пока оставим в стороне тот факт, что человек, поднимающийся по лестнице, также проделал работу над собой.)

Рисунок 9.3 Как бы вы ни перенесли телевизор на четвертый этаж, объем выполненной работы и потенциальный прирост энергии будут одинаковыми.

Мощность может быть выражена в ваттах (Вт). Эта единица может использоваться для измерения мощности, связанной с любой формой энергии или работы. Вы, скорее всего, слышали этот термин, используемый в отношении электрических устройств, особенно лампочек. Умножение мощности на время дает количество энергии. Электричество продается в киловатт-часах, потому что это равно количеству потребляемой электроэнергии.

Единица ватт была названа в честь Джеймса Уатта (1736–1819) (см. рис. 9.4). Он был шотландским инженером и изобретателем, который открыл, как увеличить мощность паровых двигателей.

Рисунок 9.4 Думает ли Джеймс Уатт о ваттах? (Карл Фредерик фон Бреда, Wikimedia Commons)

Watch Physics

Роль Ватта в промышленной революции

В этом видеоролике показано, как ватты, полученные в результате изобретений Ватта, помогли сделать промышленную революцию возможной и позволили Англии вступить в новую историческую эру.

Проверка захвата

Какую форму механической энергии производит паровая машина?

1. Потенциальная энергия
2. Кинетическая энергия
3. Атомная энергия
4. Солнечная энергия

Прежде чем продолжить, убедитесь, что вы понимаете различия между силой, работой, энергией и мощностью. Сила, действующая на объект на расстоянии, работает. Работа может увеличивать энергию, а энергия может выполнять работу. Мощность – это скорость, с которой совершается работа.

Рабочий пример

Применение теоремы о работе-энергии

Фигуристка массой 50 кг скользит по льду со скоростью 8 м/с, когда ее друг подходит сзади и толкает ее, заставляя ее скорость увеличить до 12 м/с. Сколько работы сделал друг на фигуристке?

Стратегия

К задаче можно применить теорему о работе и энергии. Напишите уравнение теоремы и упростите его, если возможно.

W=ΔKE = 12mv22−12mv12W=ΔKE = 12mv22−12mv12

Упростить до W=12m(v22-v12) Упростить до W=12m(v22-v12)

Решение

Определите переменные. м = 50 кг,

9,1v2=12мс, иv1=8мсv2=12мс, иv1=8мс

Замена.

9.2W=1250(122−82)=2000 JW=1250(122−82)=2000 Дж

Обсуждение

Работа над объектом или системой увеличивает ее энергию. В этом случае увеличивается кинетическая энергия фигуриста. Отсюда следует, что прирост энергии должен быть равен разнице КЭ до и после толчка.

Советы по достижению успеха

Эта задача иллюстрирует общий метод решения задач, требующих применения формул: определить неизвестные и известные переменные, выразить неизвестные переменные через известные переменные, а затем ввести все известные значения.

Практические задачи

Какую работу совершает тяжелоатлет, когда поднимает штангу весом 200 Н с пола на высоту 2 м?

1. 0Дж
2. 100Дж
3. 200Дж
4. 400Дж

Определите, какое из следующих действий генерирует больше энергии. Показать свою работу.

• перенос телевизора 100Н на второй этаж в 50с или
• нести арбуз 24N на второй этаж за 10 секунд?

1. При переноске телевизора 100N генерируется больше энергии, чем при переноске арбуза 24N на ту же высоту, потому что мощность определяется как проделанная работа, умноженная на временной интервал.
2. Перенос телевизора 100 Н генерирует больше энергии, чем перенос арбуза 24 Н на ту же высоту, потому что мощность определяется как отношение выполненной работы к интервалу времени.
3. Перенос арбуза 24N генерирует больше энергии, чем перенос телевизора 100N на ту же высоту, потому что мощность определяется как проделанная работа, умноженная на временной интервал.
4. Перенос арбуза 24N генерирует больше энергии, чем перенос телевизора 100N на ту же высоту, потому что мощность определяется как отношение выполненной работы к временному интервалу.

Проверьте свое понимание

Упражнение 1

Укажите два свойства, которые выражаются в джоулях.

1. работа и сила
2. энергия и вес
3. работа и энергия
4. вес и сила

Упражнение 2

Когда кокос падает с дерева, над ним совершается работа W , когда он падает на пляж. Эта работа описывается уравнением

9.5W= Fd = 12mv22−12mv12.W= Fd = 12mv22−12mv12.

Определите количества F , d , m , v ₁ и v ₂ в этом событии.

1. F — сила тяжести, равная весу кокоса, d — расстояние, на которое падает орех, м — масса земли, v ₁ — начальная скорость и v ₂ — скорость, с которой он ударяется о берег.
2. F — сила тяжести, равная весу кокоса, d — расстояние, на которое падает орех, м — масса кокоса, v ₁ — начальная скорость , а v ₂ — скорость, с которой он достигает берега.