Работа формула физика: Механическая работа — урок. Физика, 9 класс.

Механическая работа и мощность

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Другими словами, работа – мера воздействия силы.

Определение механической работы

Определение 1

Работа А, совершаемая постоянной силой F→, – это физическая скалярная величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы F→ и перемещением s→.

Данное определение рассматривается на рисунке 1.

Формула работы записывается как,

A=Fs cos α.

Работа – это скалярная величина. Единица измерения работы по системе СИ – Джоуль (Дж).

Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.

Рисунок 1. Работа силы F→: A=Fs cos α=Fss

При проекции Fs→ силы F→ на направление перемещения s→ сила не остается постоянной, а вычисление работы для малых перемещений Δsiсуммируется и производится по формуле:

A=∑∆Ai=∑Fsi∆si.

Данная сумма работы вычисляется из предела (Δsi→0), после чего переходит в интеграл.

Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком Fs(x)рисунка 2.

Рисунок 2. Графическое определение работы ΔAi=FsiΔsi.

Примером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F→, модуль которой пропорционален удлинению пружины. Это видно на рисунке 3.

Рисунок 3. Растянутая пружина. Направление внешней силы F→ совпадает с направлением перемещения s→. Fs=kx, где k обозначает жесткость пружины.

F→упр=-F→

Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.

Рисунок 4. Зависимость модуля внешней силы от координаты при растяжении пружины.

Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид

A=kx22.

Данная формула применима для выражения работы, совершаемой внешней силой при сжатии пружины. Оба случая показывают, что сила упругости F→упр равняется работе внешней силы F→, но с противоположным знаком.

Определение 2

Если на тело действует несколько сил, то их общая работа равняется сумме всех работ, совершаемых над телом. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.

Мощность

Определение 3

Мощностью называют работу силы, совершаемую в единицу времени.

Запись физической величины мощности, обозначаемой N, принимает вид отношения работы А к промежутку времени t совершаемой работы, то есть:

N=At.

Определение 4

Система СИ использует в качестве единицы мощности ватт (Вт). 1 Ватт – это мощность, которую совершает работу в 1 Дж за время 1 с.

Помимо Ватта, существуют и внесистемные единицы измерения мощности.

Например, 1 лошадиная сила примерна равна 745 Ваттам.  

Автор: Роман Адамчук

Преподаватель физики

Механическая работа и мощность силы

Подробности

Просмотров: 559

«Физика – 10 класс»

Закон сохранения энергии — фундаментальный закон природы, позволяющий описывать большинство происходящих явлений.

Описание движения тел также возможно с помощью таких понятий динамики, как работа и энергия.

Вспомните, что такое работа и мощность в физике.

Совпадают ли эти понятия с бытовыми представлениями о них?

Все наши ежедневные действия сводятся к тому, что мы с помощью мышц либо приводим в движение окружающие тела и поддерживаем это движение, либо же останавливаем движущиеся тела.

Этими телами являются орудия труда (молоток, ручка, пила), в играх — мячи, шайбы, шахматные фигуры. На производстве и в сельском хозяйстве люди также приводят в движение орудия труда.

Применение машин во много раз увеличивает производительность труда благодаря использованию в них двигателей.

Назначение любого двигателя в том, чтобы приводить тела в движение и поддерживать это движение, несмотря на торможение как обычным трением, так и «рабочим» сопротивлением (резец должен не просто скользить по металлу, а, врезаясь в него, снимать стружку; плуг должен взрыхлять землю и т. д.). При этом на движущееся тело должна действовать со стороны двигателя сила.

Работа совершается в природе всегда, когда на какое-либо тело в направлении его движения или против него действует сила (или несколько сил) со стороны другого тела (других тел).

Сила тяготения совершает работу при падении капель дождя или камня с обрыва. Одновременно совершает работу и сила сопротивления, действующая на падающие капли или на камень со стороны воздуха.

Совершает работу и сила упругости, когда распрямляется согнутое ветром дерево.

Определение работы.

Второй закон Ньютона в импульсной форме Δ = Δt позволяет определить, как меняется скорость тела по модулю и направлению, если на него в течение времени Δt действует сила .

Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуются величиной, зависящей как от сил, так и от перемещений тел. Эту величину в механике и называют

работой силы.

Изменение скорости по модулю возможно лишь в том случае, когда проекция силы F_r на направление перемещения тела отлична от нуля. Именно эта проекция определяет действие силы, изменяющей скорость тела по модулю. Она совершает работу. Поэтому работу можно рассматривать как произведение проекции силы F_r на модуль перемещения |Δ| (рис. 5.1):

А = F_r|Δ|.         (5.1)

Если угол между силой и перемещением обозначить через α, то F_r = Fcosα.

Следовательно, работа равна:

А = |Δ|cosα.         (5.2)

Наше бытовое представление о работе отличается от определения работы в физике. Вы держите тяжёлый чемодан, и вам кажется, что вы совершаете работу. Однако с точки зрения изики ваша работа равна нулю.

Работа постоянной силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними.

В общем случае при движении твёрдого тела перемещения его разных точек различны, но при определении работы силы мы под Δ понимаем перемещение её точки приложения. При поступательном движении твёрдого тела перемещение всех его точек совпадает с перемещением точки приложения силы.

Работа, в отличие от силы и перемещения, является не векторной, а скалярной величиной. Она может быть положительной, отрицательной или равной нулю.

Знак работы определяется знаком косинуса угла между силой и перемещением. Если α < 90°, то А > 0, так как косинус острых углов положителен. При α > 90° работа отрицательна, так как косинус тупых углов отрицателен. При α = 90° (сила перпендикулярна перемещению) работа не совершается.

Если на тело действует несколько сил, то проекция равнодействующей силы на перемещение равна сумме проекций отдельных сил:

F_r = F_1r + F_2r + … .

Поэтому для работы равнодействующей силы получаем

А = F_1r|Δ| + F_2r|Δ| + … = А₁ + А₂ + … .         (5.3)

Если на тело действует несколько сил, то полная работа (алгебраическая сумма работ всех сил) равна работе равнодействующей силы.

Совершённую силой работу можно представить графически. Поясним это, изобразив на рисунке зависимость проекции силы от координаты тела при его движении по прямой.

Пусть тело движется вдоль оси ОХ (рис. 5.2), тогда

Fcosα = F_x, |Δ| = Δ_х.

Для работы силы получаем

А = F|Δ|cosα = F_xΔx.

Очевидно, что площадь прямоугольника, заштрихованного на рисунке (5.3, а), численно равна работе при перемещении тела из точки с координатой х1 в точку с координатой х2.

Формула (5.1) справедлива в том случае, когда проекция силы на перемещение постоянна. В случае криволинейной траектории, постоянной или переменной силы мы разделяем траекторию на малые отрезки, которые можно считать прямолинейными, а проекцию силы на малом перемещении Δ — постоянной.

Тогда, вычисляя работу на каждом перемещении Δ а затем суммируя эти работы, мы определяем работу силы на конечном перемещении (рис. 5.3, б).

Единица работы.

Единицу работы можно установить с помощью основной формулы (5.2). Если при перемещении тела на единицу длины на него действует сила, модуль которой равен единице, и направление силы совпадает с направлением перемещения её точки приложения (α = 0), то и работа будет равна единице.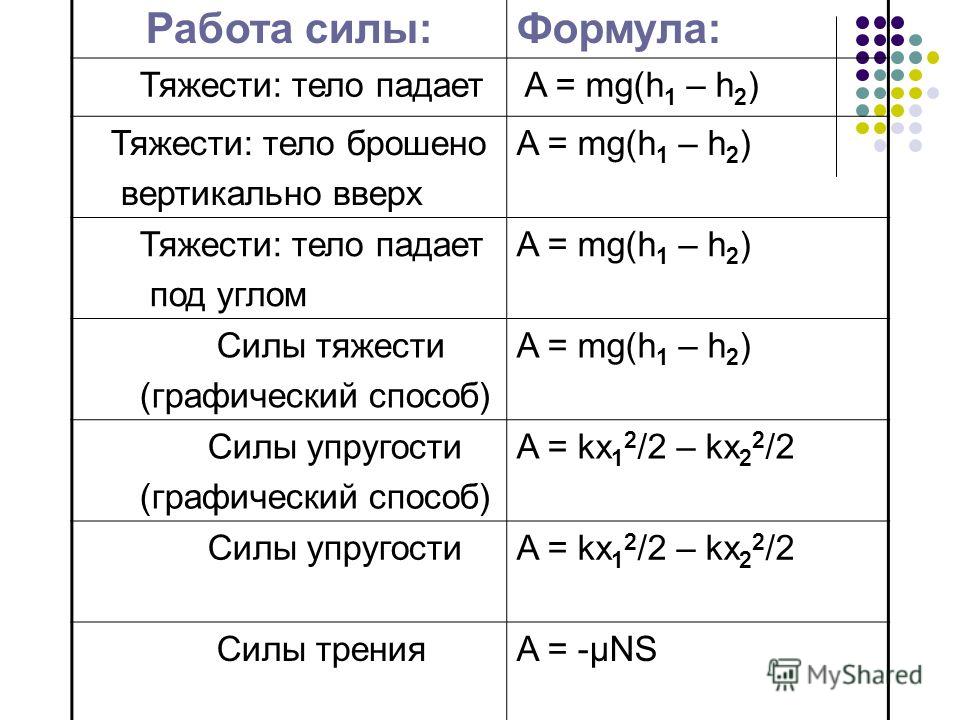 В Международной системе (СИ) единицей работы является джоуль (обозначается Дж):

1 Дж = 1 Н • 1 м = 1 Н • м.

Джоуль — это работа, совершаемая силой 1 Н на перемещении 1 если направления силы и перемещения совпадают.

Часто используют кратные единицы работы — килоджоуль и мега джоуль:

1 кДж = 1000 Дж,
1 МДж = 1000000 Дж.

Мощность.

Работа может быть совершена как за большой промежуток времени, так и за очень малый. На практике, однако, далеко не безразлично, быстро или медленно может быть совершена работа. Временем, в течение которого совершается работа, определяют производительность любого двигателя. Очень большую работу может совершить и крошечный электромоторчик, но для этого понадобится много времени. Потому наряду с работой вводят величину, характеризующую быстроту, с которой она производится, — мощность.

Мощность — это отношение работы А к интервалу времени Δt, за который эта работа совершена, т. е. мощность — это скорость совершения работы:

Подставляя в формулу (5.4) вместо работы А её выражение (5.2), получаем

Таким образом, если сила и скорость тела постоянны, то мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между направлениями этих векторов. Если же эти величины переменные, то по формуле (5.4) можно определить среднюю мощность подобно определению средней скорости движения тела.

Понятие мощности вводится для оценки работы за единицу времени, совершаемой каким-либо механизмом (насосом, подъёмным краном, мотором машины и т. д.). Поэтому в формулах (5.4) и (5.5) под всегда подразумевается сила тяги.

В СИ мощность выражается в ваттах (Вт).

Мощность равна 1 Вт, если работа, равная 1 Дж, совершается за 1 с.

Наряду с ваттом используются более крупные (кратные) единицы мощности:

1 кВт (киловатт) = 1000 Вт,
1 МВт (мегаватт) = 1 000 000 Вт.

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Следующая страница «Энергия. Кинетическая энергия»

Назад в раздел «Физика – 10 класс, учебник Мякишев, Буховцев, Сотский»

Законы сохранения в механике – Физика, учебник для 10 класса – Класс!ная физика

Импульс материальной точки — Закон сохранения импульса — Реактивное движение. Успехи в освоении космоса — Примеры решения задач по теме «Закон сохранения импульса» — Механическая работа и мощность силы — Энергия. Кинетическая энергия — Примеры решения задач по теме «Кинетическая энергия и её изменение» — Работа силы тяжести. Консервативные силы — Работа силы упругости. Консервативные силы — Потенциальная энергия — Закон сохранения энергии в механике — Работа силы тяготения. Потенциальная энергия в поле тяготения — Примеры решения задач по теме «Закон сохранения механической энергии» — Основное уравнение динамики вращательного движения — Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси — Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»

Выполненная работа: определение, уравнения и примеры

После долгих часов выполнения домашнего задания по физике вы можете чувствовать себя довольно усталым, так как проделали много работы. Однако, поскольку вы выполнили домашнее задание, теперь вы знаете, что «работа» — это физическая величина! Вы действительно выполняли работу в физическом смысле?

Определение выполненной работы

Работа равна t количество энергии, переданной объекту внешней силой, когда он перемещается на определенное расстояние под действием этой силы.

работа, выполненная над объектом, представляет собой количество энергии, переданной объекту посредством работы.

Когда вы прикладываете силу к объекту, который заставляет свое положение изменяться в том же направлении, что и сила, y вы выполняете работу над этим объектом. Работа, выполняемая над объектом, состоит из двух основных компонентов: силы : и перемещения объекта. Перемещение объекта должно происходить вдоль линии действия силы, чтобы сила совершила работу над объектом.

Работа имеет единицы измерения энергии, поскольку она определяется как количество (переданной) энергии, поэтому работа обычно имеет единицы измерения \(\mathrm{J}\) (джоули).

Уравнение выполненной работы

Уравнение, описывающее работу \(W\), совершаемую над объектом, который перемещается на расстояние \(s\), когда на него действует сила \(F\) в том же направлении, что и движение объекта задается выражением

\[W=Fs.\]

Проще говоря, имеем

выполненную работу \(=\) силы \(\times\) перемещения вдоль линии действия силы.

Работа измеряется в джоулях, сила измеряется в ньютонах, а перемещение измеряется в метрах. Из этого уравнения мы можем сделать вывод, что

\[1\,\mathrm{Nm}=1\,\mathrm{J}. \]

Это важное преобразование, которое нужно уметь делать!

Это преобразование легко запомнить, если вспомнить уравнение, описывающее работу, проделанную через произведение силы на расстояние.

Сила, приложенная к объекту в направлении, отличном от направления движения, StudySmarter Originals.

Как известно, сила представляет собой вектор, а значит, имеет три составляющие. Мы можем выбрать эти компоненты таким образом, чтобы один из них был точно вдоль направления движения объекта, над которым он работает, а два других компонента были перпендикулярны этому движению. Чтобы проиллюстрировать это, мы обсудим векторы в двух измерениях, так что один компонент будет вдоль направления движения, а другой будет перпендикулярен ему.

Предположим, что движение нашего объекта происходит в направлении \(x\). Глядя на рисунок ниже, мы видим, что горизонтальная составляющая \(F_x\) силы \(F\) вычисляется по формуле:

\[F_x=F\cos\left(\theta\right),\]

где \(\theta \) угол, который сила образует с направлением движения объекта.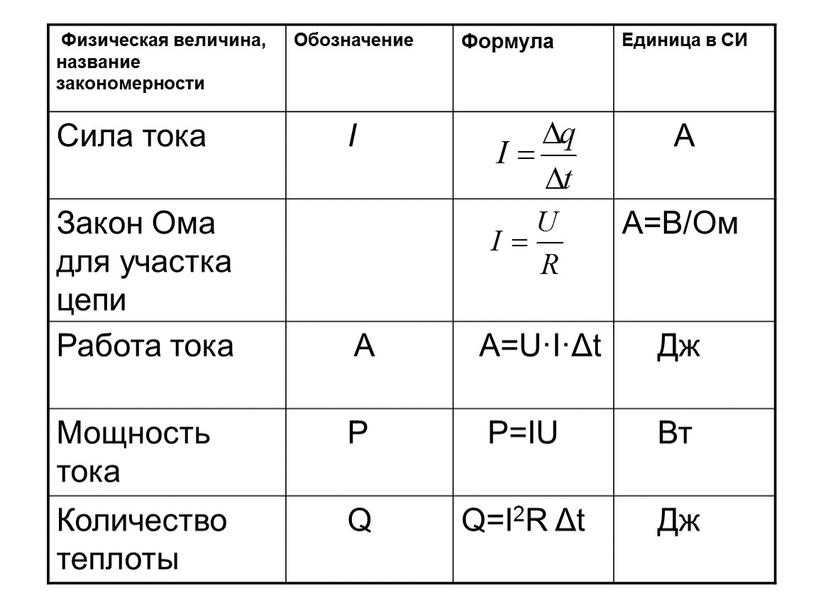 Работа, совершаемая над объектом, совершается только той составляющей силы, которая параллельна направлению движения объекта, поэтому работа \(W\), совершаемая над объектом, перемещающимся на расстояние \(s\), действовала на силу \(F\), которая образует угол \(\theta\) с направлением движения объекта, равным 9\circ\), поэтому работа над этим объектом будет отрицательной. Это логично, потому что мы забираем энергию у объекта, надавливая на него!

Вычисление двух компонентов вектора, поскольку работу выполняет только один из компонентов, StudySmarter Originals.

Примеры выполненной работы

Сила, приложенная к ящику, имеет то же направление, что и направление движения ящика, поэтому работа над ящиком совершается силой, StudySmarter Originals.

Предположим, вы решили сложить все свои книги и журналы в один деревянный ящик. Вы кладете коробку на стол и тянете ее за веревку, прикрепленную к коробке, как показано на рисунке выше. Эта тяга вызывает движение ящика точно в направлении тяги, а именно точно вправо. Это означает, что вы работаете над коробкой! Давайте сделаем пример расчета на этой установке.

Предположим, вы прикладываете постоянную силу \(250\,\mathrm{N}\) и вам удается перетащить коробку на себя на расстояние \(2\,\mathrm{м}\). Работа, которую вы приложили к ящику при этом, равна

\[W=Fs=250\,\mathrm{N}\times2\,\mathrm{m}=500\,\mathrm{Nm}=500\,\mathrm {J}.\]

Это означает, что работа над ящиком равна \(W=500\,\mathrm{J}\).

Теперь предположим, что после этого первого рывка вы устали, а второй рывок вы делаете с половинной силой, и коробка перемещается только на половину расстояния. В этом случае работа, проделанная над ящиком во втором рывке, равна 9.0003

\[W=Fs=125\,\mathrm{N}\times1\,\mathrm{m}=125\,\mathrm{J}.\]

В последней ситуации мы предполагаем, что ящик скользит к вам по льду, и вы пытаетесь остановить его. В конечном итоге вы прикладываете небольшую силу \(F=10\,\mathrm{N}\) к коробке, потому что у вас нет большого сцепления со льдом, и коробка останавливается после \( s=8\,\mathrm{m}\). В этой ситуации важно отметить, что работа, проделанная вами над ящиком, отрицательна, потому что сила, которую вы приложили к ящику, была противоположна направлению движения ящика. Вы сделали

\[W=-10\,\mathrm{N}\times8\,\mathrm{m}=-80\,\mathrm{J}\]

работы над коробкой.

Работа, совершаемая трением и силой тяжести

Работа, совершаемая трением

Вернемся к случаю, когда мы тянем ящик по столу.

Работа трения, StudySmarter Originals.

Поверхность стола будет сопротивляться движению коробки за счет приложения силы, противодействующей направлению движения.

Сила трения всегда будет направлена ​​против движения объекта, поэтому трение всегда совершает над объектами отрицательную работу.

Если мы хотим рассчитать работу силы трения, нам нужно знать, какая сила была приложена к коробке силой трения.

Предположим, что при первом рывке величина силы трения была равна силе, которую вы приложили к ящику. Так как сила и перемещение такие же, как в примере, который мы уже рассмотрели, мы заключаем, что сила трения произвела \(-500\,\mathrm{J}\) работы на ящике. Обратите внимание, что мы включили тот факт, что трение было в направлении, противоположном движению коробки, включив знак минус!

Работа, совершаемая силой тяжести

В нашем примере, когда мы тянем коробку, гравитация не действует, потому что коробка движется горизонтально, а гравитация действует вертикально.

В общем случае гравитационная сила объекта определяется его массой \(m\) и ускорением свободного падения \(g\) через \(-mg\). Здесь знак минус стоит потому, что гравитация действует вниз. Таким образом, работа, которую сила тяжести совершает над объектами, рассчитывается как

\[W=Fs=-mg\Delta h,\]

где \(\Delta h\) — разница высот, которой подвергается объект. Проще говоря, это уравнение равно

проделанной работы \(=-\)массы \(\times\) ускорения свободного падения \(\times\) разности высот.

Вы можете распознать эту величину как разницу в гравитационной потенциальной энергии. Это именно то, что есть: работа, совершаемая гравитацией над объектом, соответствующим образом изменяет его гравитационную потенциальную энергию.

Работа, совершаемая пружиной

Пружина всегда определяется ее жесткостью, которая характеризуется ее 92\)

Эта потенциальная энергия определяет, какую работу пружина может совершить над объектом: без растяжения потенциальная энергия равна \(0\,\mathrm{J}\), поэтому работа, выполненная над объектом, выпущенная пружиной, равна потенциальной энергии пружины непосредственно перед ее отпусканием:

\[W=E_\text{p}.\]

Q: Пружина с жесткостью пружины \(k=6.0\, \mathrm{MN}/\mathrm{m}\) сжимается до тех пор, пока не будет иметь расширение \(2.0\,\mathrm{cm}\). Сколько она действует на объект массой \(m=4,3\,\mathrm{kg}\), если этот объект подбрасывается этой пружиной из заданной его сжатой конфигурации? 92=1200\,\mathrm{J}. \]

Выполненная работа – Основные выводы

• Работа равна t количество энергии, переданной объекту внешней силой, когда он перемещается на определенное расстояние той силой.
• работа, выполненная над объектом, представляет собой количество энергии, переданной объекту посредством работы.
• Уравнение, описывающее работу \(W\), совершаемую над объектом, который перемещается на расстояние \(s\), в то время как на него действует сила \(F\) в том же направлении, что и движение объекта, задается выражением \ (W=Fs\). 92\).

Physics4Kids.com: Движение: Работа

Работа Работа работа. Однажды вы можете отправиться на работу, сесть за компьютер и печатать на клавишах. Это все, что мы делаем здесь. Это работа? Для физика это только части. Работа совершается, когда сила, приложенная к объекту, перемещает этот объект. Работа рассчитывается путем умножения силы на величину перемещения объекта ( Вт = F * d ). Сила в 10 ньютонов , перемещающая тело на 3 метра, совершает работу 30 Нм. А ньютон-метр — это то же самое, что джоуль , поэтому единицы для работы те же, что и для энергии — джоули.

Сидеть и смотреть в экран компьютера не получится. Нажимать на клавиатуру и заставлять клавиши двигаться — это работа. Ваши пальцы прилагают усилие и двигают клавиши. Поездка на работу — это не работа, потому что вы просто сидите, но энергия, которую двигатель вашего автомобиля использует для движения автомобиля, работает. Вы должны приложить силу И переместить что-то, чтобы квалифицироваться как выполнение работы.

Представьте, что вы держите кирпич над землей. Ваша рука вытянута прямо перед собой, и ее довольно сложно удержать. Постепенно ваша рука устает, кирпич становится все тяжелее и тяжелее, и вам, наконец, приходится остановиться, чтобы дать руке отдохнуть. Несмотря на то, что вы приложили много усилий, чтобы удержать кирпич, поработали ли вы над ним? Неа. Кирпич не двигался. Никакая работа не была сделана, если не произошло никакого движения. Если бы вы снова подняли кирпич после того, как ваша рука отдохнула, это было бы работой.

Работа передает энергии от одного объекта к другому. Мы уже говорили о движущихся объектах. Что-то еще? Работа также связана с расширением и сжатием газов. Когда газ пытается расшириться, он воздействует на поверхности контейнера с возрастающей силой и может заставить эти поверхности двигаться. Тогда газ будет совершать работу и передавать энергию контейнеру. Если вы нагреете воздушный шар (осторожно), молекулы воздуха в воздушном шаре приобретут энергию и ударятся о внутренние стенки воздушного шара с большей силой. Поскольку внутренняя поверхность воздушного шара гибкая, эта поверхность движется наружу. Воздух работает и передает энергию воздушному шару. Если вы сжимаете воздушный шар, вы выполняете работу и передаете энергию воздуху внутри воздушного шара.

Когда ученые измеряют работу, проделанную с газами или с их помощью, они смотрят на систему в начале и в конце проекта. Они смотрят на начальное и конечное состояния . Чтобы вычислить общую работу, выполненную газовой системой, они используют формулу W = P (дельта)V . W обозначает работу, P — давление в системе (для газов), дельта V — изменение объема в системе. Вариантом может быть W = V (дельта P), где V — объем, а дельта P — изменение давления. Значения дельты берутся в начале и в конце.

Иногда они могут проводить измерения, пока что-то происходит. Это измерения промежуточных состояний . Затем они могли бы использовать промежуточные измерения для расчета работы, а затем суммировать эти значения работы, чтобы вычислить общую проделанную работу.

Или поищите на сайтах по конкретной теме.