Физика – Работа и Энергия
При действии (приложении силы) происходит смещение точки приложения в направлении силы, известной как работа.
Термин работа впервые был введен французским математиком Гаспаром Гюставом Кориолисом в 1826 году.
Работа, выполняемая силой, действующей на объект, равна величине силы, умноженной на расстояние, пройденное в направлении силы, и рассчитывается как —
Проделанная работа (W) = Сила (F) × Смещение (я)
Работа имеет единственную величину и никакого направления.
Единица работы СИ — джоуль (J) .
Энергия может быть преобразована в форме, но не может быть создана или уничтожена. Например, производство электрической энергии из солнечной энергии и т. Д.
Объект, который выполняет работу, теряет энергию, а объект, над которым выполняется работа, получает энергию.
Кроме того, объект, который обладает энергией, может оказывать силу на другой объект для передачи энергии от прежнего к последующему.
Поэтому энергия, которой обладает объект, измеряется с точки зрения его способности выполнять работу.
Единица энергии СИ — Джоуль (Дж) .
Ниже приведены основные формы энергии —
Потенциальная энергия
Кинетическая энергия
Тепловая энергия
Химическая энергия
Электроэнергия
Энергия света
Давайте обсудим каждого вкратце
Энергия, которой обладает тело в силу его положения относительно других, известна как Потенциальная энергия.
Итак, потенциальная энергия — это запасенная энергия в объекте. Например, гравитационная потенциальная энергия, упругая потенциальная энергия, электрическая потенциальная энергия и т. Д.
Единицей потенциальной энергии СИ является Джоуль (Дж).
Термин потенциальная энергия был введен шотландским инженером и физиком Уильямом Ранкином.
Энергия, которой обладает объект из-за его движения, называется кинетической энергией .
Бегущее / движущееся тело сохраняет свою кинетическую энергию, если только его скорость не изменяется (увеличивается или уменьшается).
Единица СИ кинетической энергии — Джоуль (Дж).
Тепло — это форма энергии, которая спонтанно передается от более горячего тела к более холодному.
Потенциал химического вещества, чтобы испытать преобразование через химическую реакцию и преобразовать другие химические вещества, известен как химическая энергия. Например, разрыв или создание химических связей, батарей и т. Д.
Химическая энергия (химического) вещества может быть преобразована в другие виды энергии посредством химической реакции. Например, зеленые растения преобразуют солнечную энергию в химическую энергию (обычно из кислорода) в процессе фотосинтеза.
Энергия, полученная из электрической потенциальной энергии или кинетической энергии, известна как электрическая энергия.
Электричество обычно производится электромеханическими генераторами на электростанции.
Электромеханические генераторы в основном приводятся в действие тепловыми двигателями, работающими на кинетической энергии текущей воды и ветра.
Электромеханические генераторы также приводятся в действие тепловыми двигателями, работающими на химическом сгорании или ядерном делении.
Свет — это форма электромагнитного излучения.
Энергия света, скорее всего, является единственной формой энергии, которую мы действительно можем увидеть.
Свет передает энергию через пространство естественным образом. Например, солнечная энергия.
Закон сохранения энергии гласит, что энергия не может быть ни создана, ни уничтожена; однако, это может только быть преобразовано от одной формы до другого.
Согласно закону сохранения энергии, полная энергия до и после преобразования остается неизменной.
Закон сохранения энергии остается в силе во всех условиях и местах и для всех видов преобразований.
|
Титульная
Механика Литература |
Все силы, работа которых зависит от формы траектории, называются непотенциальными. Непотенциальными силами являются силы трения, сопротивления. Для системы тел, в которой действуют потенциальные силы взаимодействия, можно ввести понятие потенциальной энергии.
Потенциальная энергия – некоторая
функция, описывающая взаимное расположение тел в системе,
изменение которой взятое с обратным знаком, равно работе
потенциальных сил, действующих между телами ситемы
или же это энергия взаимного действия,
взаимного расположения тел относительно друг друга:
Пример.
Кинетическая энергия – энергия движения.
Работа силы, приложенной к телу при
изменении его V, равна
Закон сохранения энергии.
Энергия может переходить из одного вида в другой, может
переходить от одного тела к другому, но общий запас
механической энергии остаётся неизменным. Докажем закон сохранения энергии в следующем опыте. Стальной шарик, упавший с некоторой высоты на стальную или стеклянную плиту и ударившийся об неё, подскакивает почти на ту же высоту, с которой упал. Во время движения шарика происходит целый ряд превращений энергии. При падении потенциальная энергия переходит в кинетическую энергию шарика. Когда шарик прикоснется к плите, и он и плита начинают деформироваться.
Если рассмотреть кинетическую энергию, то можно сделать
вывод, что она превращается в потенциальную энергию
упругой деформации шарика и плиты, причем этот процесс
продолжается до тех пор, пока шарик не остановится, т.
Поскольку можно считать, что шарик поднялся на ту
же высоту, с которой он начал падать, потенциальная
энергия шарика в начале и в конце описанного
процесса одна и та же. Более, того, в любой момент
времени при всех превращениях энергии сумма
потенциальной энергии тяготения, потенциальной
энергии упругой деформации и кинетической энергии
все время остается одной и той же. Для процесса превращения потенциальной энергии, обусловленной силой тяжести, в кинетическую и обратно при падении и подъеме шарика это было показано простым расчетом. Можно было бы убедиться, что и при превращении кинетической энергии в потенциальную энергию упругой деформации плиты и шарика и затем при обратном процессе превращения этой энергии в кинетическую энергию отскакивающего шарика сумма потенциальной энергии тяготения, энергии упругой деформации и кинетической энергии также остается неизменной, т. е. закон сохранения механической энергии выполнен.
Теперь мы можем объяснить, почему нарушался закон
сохранения работы в простой машине, которая
деформировалась при передаче работы: дело в том, что
работа, затраченная на одном конце машины, частично
или полностью затрачивалась на деформацию самой
простой машины (рычага, веревки и т.
Силы трения и закон сохранения механической
энергии.
Работу против силы сопротивления воздуха
совершает сила тяжести за счет потенциальной,
энергии тела. Хотя при этом и сообщается некоторая
кинетическая энергия окружающему воздуху, но она меньше,
чем убыль потенциальной энергии тела, и, значит,
суммарная механическая энергия убывает.
Работа против сил трения может совершаться и за счет
кинетической энергии. Например, при движении лодки,
которую оттолкнули от берега пруда, потенциальная
энергия лодки остается постоянной, но вследствие
сопротивления воды уменьшается скорость движения лодки,
т. Подобно этому действуют и силы трения между твердыми телами. Например, скорость, которую приобретает груз, соскальзывающий с наклонной плоскости, а, следовательно, и его кинетическая энергия, меньше той, которую он приобрёл бы в отсутствие трения. Можно так подобрать угол наклона плоскости, что груз будет скользить равномерно. При этом его потенциальная энергия будет убывать, а кинетическая – оставаться постоянной, и работа против сил трения будет совершаться за счет потенциальной энергии.
В природе все движения (за исключением движений в
вакууме, например, движений небесных тел) сопровождаются
трением. Поэтому при таких движениях закон сохранения
механической энергии нарушается, и это нарушение
происходит всегда в одну сторону – в сторону уменьшения
полной энергии.
Превращение механической энергии во внутреннюю
энергию.
При движении тел в воздухе с небольшими скоростями,
например, при движении брошенного камня, сопротивление
воздуха невелико, на преодоление сил трения затрачивается
небольшая работа, и камень практически не нагревается.
Но быстро летящая пуля разогревается значительно
сильнее. При больших скоростях реактивных самолетов
приходится уже принимать специальные меры для уменьшения
нагревания обшивки самолета. Мелкие метеориты, влетающие
с огромными скоростями (десятки километров в секунду)
в атмосферу Земли, испытывают такую большую силу
сопротивления среды, что полностью сгорают в
атмосфере. Нагревание в атмосфере искусственного
спутника Земли, возвращающегося на Землю,
так велико, что на нем приходится устанавливать
специальную тепловую защиту. Кроме нагревания, трущиеся тела могут испытывать и другие изменения. Например, они могут измельчаться, растираться в пыль, может происходить плавление, т. е. переход тел из твердого в жидкое состояние: кусок льда может расплавиться в результате трения о другой кусок льда или о какое-либо иное тело.
 Значит, в результате работы по преодолению сил трения
трубки о пластинки трубка с эфиром пришла в новое
состояние, в котором она смогла совершить работу,
требующуюся для выталкивания пробки, т. е. работу
против сил трения, удерживающих пробку в трубке, и
работу, идущую на сообщение пробке кинетической
энергии. В исходном состоянии трубка с эфиром не
могла совершить эту работу.
Значит, в результате работы по преодолению сил трения
трубки о пластинки трубка с эфиром пришла в новое
состояние, в котором она смогла совершить работу,
требующуюся для выталкивания пробки, т. е. работу
против сил трения, удерживающих пробку в трубке, и
работу, идущую на сообщение пробке кинетической
энергии. В исходном состоянии трубка с эфиром не
могла совершить эту работу.
Таким образом, нагревание тел, равно как и другие изменения, их состояния, сопровождается изменением “запаса” способности этих тел совершать работу. Мы видим, что “запас работоспособности” зависит, помимо положения тел относительно Земли, помимо их деформации и их скорости, еще и от состояния тел.
Значит, помимо потенциальной энергии
тяготения и упругости и кинетической энергии тело
обладает и энергией, зависящей, от его состояния.
Будем называть ее внутренней энергией.
Всеобщий характер закона сохранения энергии.
С развитием физики обнаруживались
все новые виды энергии: была обнаружена световая
энергия, энергия электромагнитных волн, химическая
энергия, проявляющаяся при химических реакциях
(в качестве примера достаточно указать хотя бы на
химическую энергию, запасённую во взрывчатых
веществах и превращающуюся в механическую и тепловую
энергию при взрыве), наконец, была открыта ядерная
энергия. Оказалось, что совершаемая над телом работа
равна сумме всех видов энергии тела;
работа же, совершаемая некоторым телом над другими
телами, равна убыли суммарной энергии данного тела. Хотя общее количество энергии остается постоянным, количество полезной для нас энергии может уменьшаться и в действительности постоянно уменьшается. Переход энергии в другую форму может означать переход ее в бесполезную для нас форму. В механике чаще всего это – нагревание окружающей среды, трущихся поверхностей и т. п. Такие потери не только невыгодны, но и вредно отзываются на самих механизмах; так, во избежание перегревания приходится специально охлаждать трущиеся части механизмов. |
Энергия – это… Что такое Энергия?
Эне́ргия (др. -греч. ἐνέργεια — «действие, деятельность, сила, мощь») — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется во времени. Это утверждение носит название закона сохранения энергии. Понятие введено Аристотелем в трактате «Физика».
-греч. ἐνέργεια — «действие, деятельность, сила, мощь») — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется во времени. Это утверждение носит название закона сохранения энергии. Понятие введено Аристотелем в трактате «Физика».
Фундаментальный смысл
С фундаментальной точки зрения энергия представляет собой интеграл движения (то есть сохраняющуюся при движении величину), связанный, согласно теореме Нётер, с однородностью времени. Таким образом, введение понятия энергии как физической величины целесообразно только в том случае, если рассматриваемая физическая система однородна во времени.
Энергия и работа
Энергия является мерой способности физической системы совершить работу, поэтому количественно энергия и работа выражаются в одних единицах.
В специальной теории относительности
Энергия и масса
Согласно специальной теории относительности между массой и энергией существует связь, выражаемая знаменитой формулой Эйнштейна
где E — энергия системы, m — её масса, c — скорость света. Несмотря на то, что исторически предпринимались попытки трактовать это выражение как полную эквивалентность понятия энергии и массы, что, в частности, привело к появлению такого понятия как релятивистская масса, в современной физике принято сужать смысл этого уравнения, понимая под массой массу тела в состоянии покоя (так называемая масса покоя), а под энергией — только внутреннюю энергию, заключённую в системе.
Энергия тела, согласно законам классической механики, зависит от системы отсчета, то есть неодинакова для разных наблюдателей. Если тело движется со скоростью v относительно некоего наблюдателя, то для другого наблюдателя, движущегося с той же скоростью, оно будет казаться неподвижным. Соответственно, для первого наблюдателя кинетическая энергия тела будет равна, , где m — масса тела, а для другого наблюдателя — нулю.
Соответственно, для первого наблюдателя кинетическая энергия тела будет равна, , где m — масса тела, а для другого наблюдателя — нулю.
Эта зависимость энергии от системы отсчета сохраняется также в теории относительности. Для определения преобразований, происходящих с энергией при переходе от одной инерциальной системы отсчета к другой используется сложная математическая конструкция — тензор энергии-импульса.
Зависимость энергии тела от скорости рассматривается уже не так, как в ньютоновской физике, а согласно вышеназванной формуле Эйнштейна:
- ,
где — инвариантная масса. В системе отсчета, связанной с телом, его скорость равна нулю, а энергия, которую называют энергией покоя, выражается формулой:
- .
Это минимальная энергия, которую может иметь массивное тело. Значение формулы Эйнштейна также в том, что до неё энергия определялась с точностью до произвольной постоянной, а формула Эйнштейна находит абсолютное значение этой постоянной.
Энергия и импульс
Специальная теория относительности рассматривает энергию как компоненту 4-импульса (4-вектора энергии-импульса), в который наравне с энергией входят три пространственные компоненты импульса. Таким образом энергия и импульс оказываются связанными и оказывают взаимное влияние друг на друга при переходе из одной системы отсчёта в другую.
В квантовой механике
| В этом разделе не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 12 мая 2011. |
В квантовой механике величина энергии пропорциональна частоте и двойственна времени. В частности, в силу фундаментальных причин принципиально невозможно измерить абсолютно точно энергию системы в каком-либо процессе, время протекания которого конечно. При проведении серии измерения одного и того же процесса значения измеренной энергии будут флуктуировать, однако среднее значение всегда определяется законом сохранения энергии. Это приводит к тому, что иногда говорят, что в квантовой механике сохраняется средняя энергия.
При проведении серии измерения одного и того же процесса значения измеренной энергии будут флуктуировать, однако среднее значение всегда определяется законом сохранения энергии. Это приводит к тому, что иногда говорят, что в квантовой механике сохраняется средняя энергия.
В общей теории относительности
В общей теории относительности время не является однородным, поэтому возникают определённые проблемы при попытке введения понятия энергии. В частности, оказывается невозможным определить энергию гравитационного поля как тензор относительно общих преобразований координат.
Энергия и энтропия
Внутреняя энергия (или энергия хаотического движения молекул) является самым «деградированным» видом энергии — она не может превращаться в другие виды энергии без потерь (см.: энтропия).
Физическая размерность
Энергия E имеет размерность, равную:
В системе величин LMT энергия имеет размерность .
| Единица | Эквивалент | |||
|---|---|---|---|---|
| в Дж | в эрг | в межд.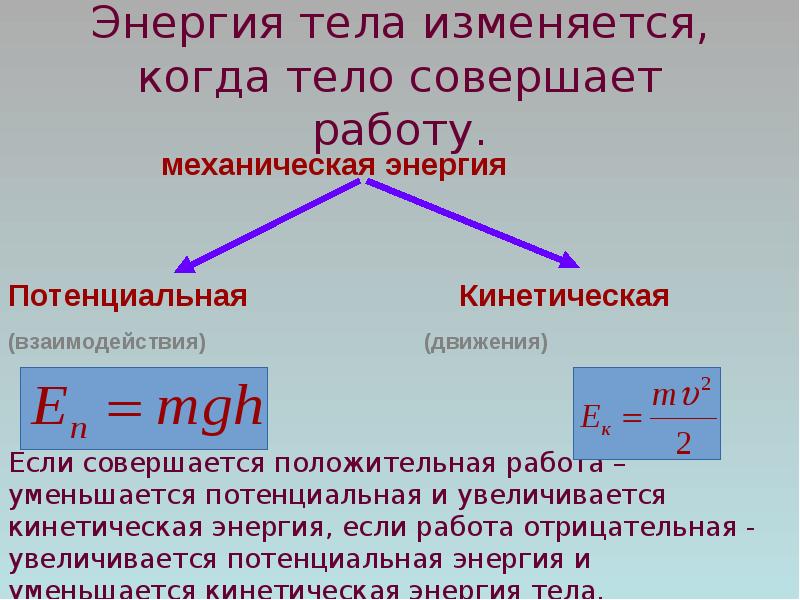 кал кал | в эВ | |
| 1 Дж | 1 | 107 | 0,238846 | 0,624146·1019 |
| 1 эрг | 10−7 | 1 | 2,38846·10−8 | 0,624146·1012 |
| 1 межд. Дж[1] | 1,00020 | 1,00020·107 | 0,238891 | 0,624332·1019 |
| 1 кгс·м | 9,80665 | 9,80665·107 | 2,34227 | 6,12078·1019 |
| 1 кВт·ч | 3,60000·106 | 3,60000·1013 | 8,5985·105 | 2,24693·1025 |
| 1 л·атм | 101,3278 | 1,013278·109 | 24,2017 | 63,24333·1019 |
| 1 межд. кал (calIT) | 4,1868 | 4,1868·107 | 1 | 2,58287·1019 |
| 1 термохим. кал (калТХ) | 4,18400 | 4,18400·107 | 0,99933 | 2,58143·1019 |
| 1 электронвольт (эВ) | 1,60219·10−19 | 1,60219·10−12 | 3,92677·10−20 | 1 |
Виды энергии
Механика различает потенциальную энергию (или, в более общем случае, энергию взаимодействия тел или их частей между собой или с внешними полями) и кинетическую энергию (энергия движения). Их сумма называется полной механической энергией.
Их сумма называется полной механической энергией.
Энергией обладают все виды полей. По этому признаку различают: электромагнитную (разделяемую иногда на электрическую и магнитную энергии), гравитационную и ядерную энергии (также может быть разделена на энергию слабого и сильного взаимодействий).
Термодинамика рассматривает внутреннюю энергию и иные термодинамические потенциалы.
В химии рассматриваются такие величины, как энергия связи и энтальпия, имеющие размерность энергии, отнесённой к количеству вещества. См. также: химический потенциал.
Энергия взрыва иногда измеряется в тротиловом эквиваленте.
Кинетическая
Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Единица измерения в системе СИ — Джоуль. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.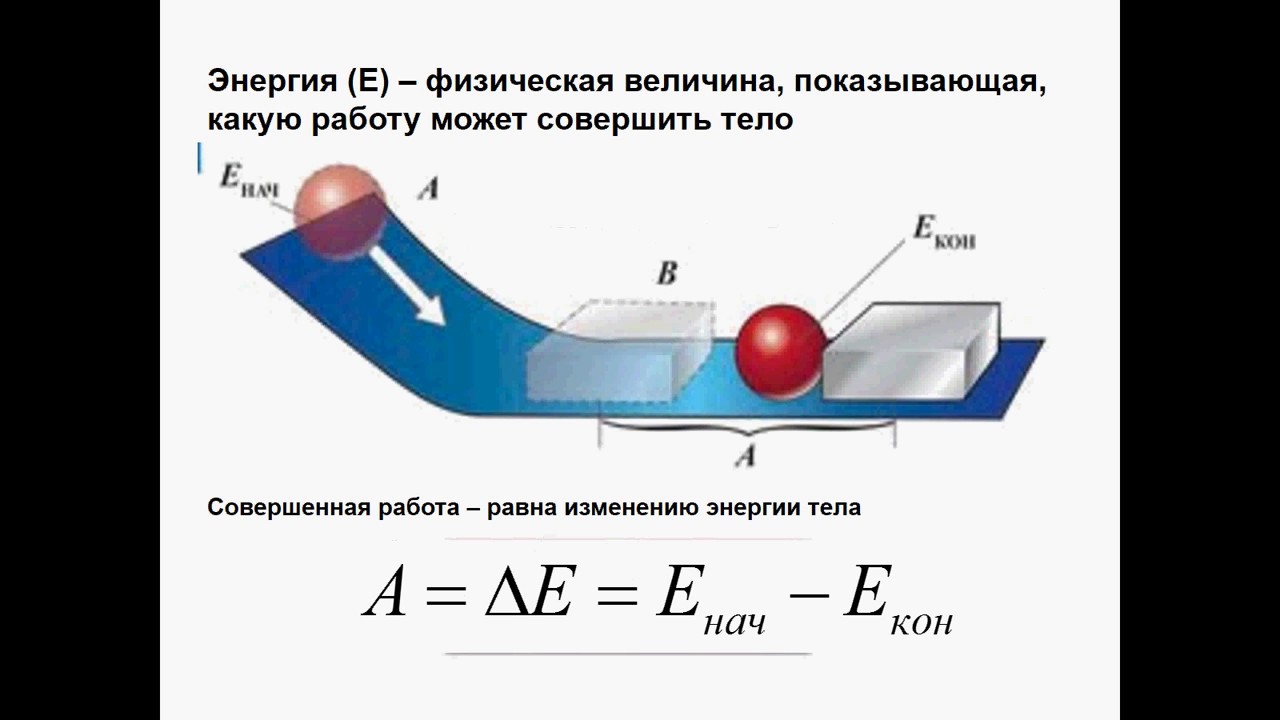
Потенциальная
Потенциальная энергия — скалярная физическая величина, характеризует запас энергии некоего тела (или материальной точки), находящегося в потенциальном силовом поле, который идет на приобретение (изменение) кинетической энергии тела за счет работы сил поля. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы.[2]
Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином. Единицей измерения энергии в СИ является Джоуль. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.
Электромагнитная
Гравитационная
Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным тяготением. Гравитационно-связанная система — система, в которой гравитационная энергия больше суммы всех остальных видов энергий (помимо энергии покоя). Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационную энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии постоянна, для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.
Гравитационно-связанная система — система, в которой гравитационная энергия больше суммы всех остальных видов энергий (помимо энергии покоя). Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационную энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии постоянна, для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.
Ядерная
Ядерная энергия (атомная энергия) — это энергия, содержащаяся в атомных ядрах и выделяемая при ядерных реакциях.
Энергия связи — энергия, которая требуется, чтобы разделить ядро на отдельные нуклоны, называется энергией связи. Энергия связи, приходящаяся на один нуклон, неодинакова для разных химических элементов и, даже, изотопов одного и того же химического элемента.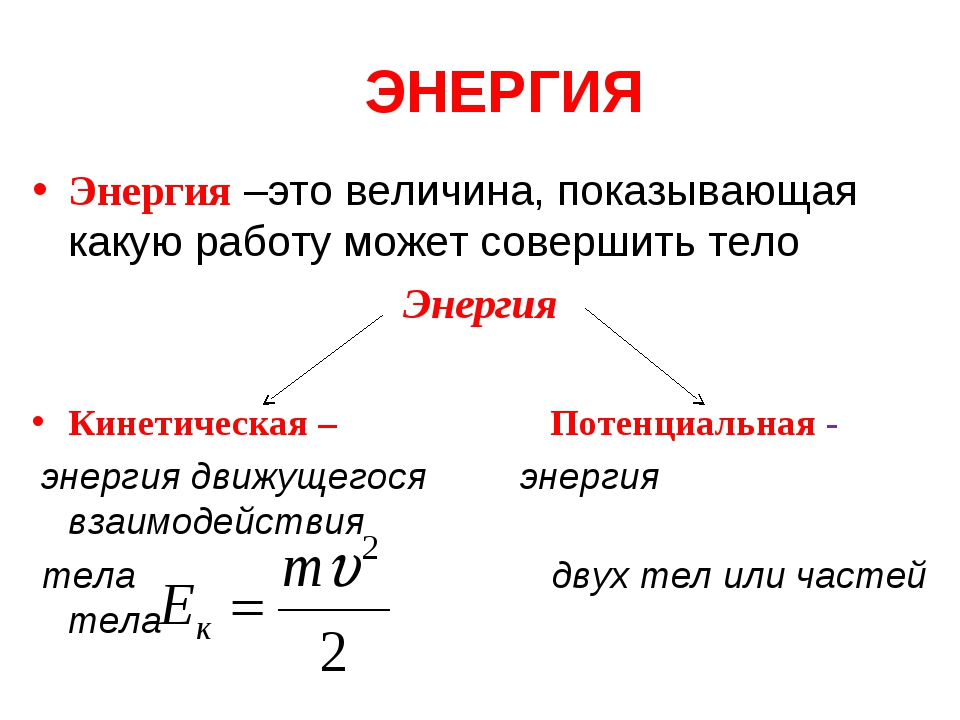
Внутренняя
Внутренняя энергия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутреннюю энергию тела нельзя измерить напрямую. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между её значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Химический потенциал
Химический потенциал — один из термодинамических параметров системы, а именно энергия добавления одной частицы в систему без совершения работы.
Энергия взрыва
Взрыв — физический или/и химический быстропротекающий процесс с выделением значительной энергии в небольшом объёме за короткий промежуток времени, приводящий к ударным, вибрационным и тепловым воздействиям на окружающую среду и высокоскоростному расширению газов.
При химическом взрыве, кроме газов, могут образовываться и твёрдые высокодисперсные частицы, взвесь которых называют продуктами взрыва. Энергию взрыва иногда измеряют в тротиловом эквиваленте — мере энерговыделения высокоэнергетических событий, выраженной в количестве тринитротолуола (ТНТ), выделяющем при взрыве равное количество энергии.
Проблемы энергопотребления
Существует довольно много форм энергии, большинство[3] из которых так или иначе используются в энергетике и различных современных технологиях.
Темпы энергопотребления растут во всем мире, поэтому на современном этапе развития цивилизации наиболее актуальна проблема энергосбережения.
Условно источники энергии можно поделить на два типа: невозобновляемые и постоянные. К первым относятся газ, нефть, уголь, уран и т. д. Технология получения и преобразования энергии из этих источников отработана, но, как правило, неэкологична, и многие из них истощаются. К постоянным источникам можно отнести энергию солнца, энергию, получаемую на ГЭС и т.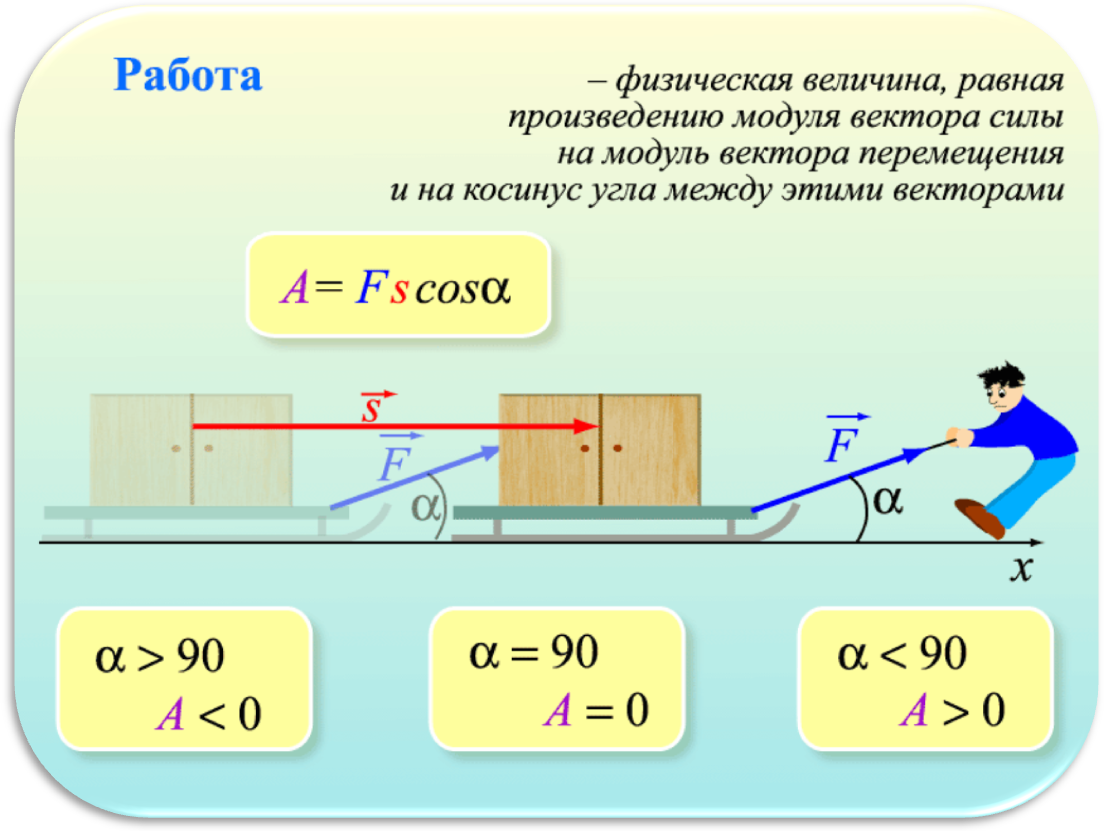 д.
д.
История термина
Термин «энергия» происходит от слова energeia, которое впервые появилось в работах Аристотеля.
Томас Юнг первым использовал понятие «энергия» в современном смысле словаМаркиза Эмили дю Шатле в книге «Уроки физики» (фр. Institutions de Physique, 1740), объединила идею Лейбница с практическими наблюдениями Виллема Гравезанда, чтобы показать: энергия движущегося объекта пропорциональна его массе и квадрату его скорости (не скорости самой по себе как полагал Исаак Ньютон).
В 1807 году Томас Юнг первым использовал термин «энергия» в современном смысле этого слова взамен понятия живая сила.[4]Гаспар-Гюстав Кориолис впервые использовал термин «кинетическая энергия» в 1829 году, а в 1853 году Уильям Ренкин впервые ввёл понятие «потенциальная энергия».
Несколько лет велись споры, является ли энергия субстанцией (теплород) или только физической величиной.
Развитие паровых двигателей требовало от инженеров разработать понятия и формулы, которые позволили бы им описать механический и термический КПД своих систем. Инженеры (Сади Карно), физики (Джеймс Джоуль), математики (Эмиль Клапейрон и Герман Гельмгольц[уточнить]) — все развивали идею, что способность совершать определённые действия, называемая работой, была как-то связана с энергией системы. В 1850-х годах, профессор натурфилософии из Глазго Уильям Томсон и инженер Уильям Ренкин начали работу по замене устаревшего языка механики с такими понятиями как «кинетическая и фактическая (actual) энергии».[4] Уильям Томсон соединил знания об энергии в законы термодинамики, что способствовало стремительному развитию химии. Рудольф Клаузиус, Джозайя Гиббс и Вальтер Нернст объяснили многие химические процессы, используя законы термодинамики. Развитие термодинамики было продолжено Клаузиусом, который ввёл и математически сформулировал понятие энтропии, и Джозефом Стефаном, который ввёл закон излучения абсолютно чёрного тела. В 1853 году Уильям Ренкин ввёл понятие «потенциальная энергия».[4] В 1881 году Уильям Томсон заявил перед слушателями:[5]
Инженеры (Сади Карно), физики (Джеймс Джоуль), математики (Эмиль Клапейрон и Герман Гельмгольц[уточнить]) — все развивали идею, что способность совершать определённые действия, называемая работой, была как-то связана с энергией системы. В 1850-х годах, профессор натурфилософии из Глазго Уильям Томсон и инженер Уильям Ренкин начали работу по замене устаревшего языка механики с такими понятиями как «кинетическая и фактическая (actual) энергии».[4] Уильям Томсон соединил знания об энергии в законы термодинамики, что способствовало стремительному развитию химии. Рудольф Клаузиус, Джозайя Гиббс и Вальтер Нернст объяснили многие химические процессы, используя законы термодинамики. Развитие термодинамики было продолжено Клаузиусом, который ввёл и математически сформулировал понятие энтропии, и Джозефом Стефаном, который ввёл закон излучения абсолютно чёрного тела. В 1853 году Уильям Ренкин ввёл понятие «потенциальная энергия».[4] В 1881 году Уильям Томсон заявил перед слушателями:[5]
|
В течение следующих тридцати лет эта новая наука имела несколько названий, например, «динамическая теория тепла» (англ. dynamical theory of heat) и «энергетика» (англ. energetics). В 1920-х годах общепринятым стало название «термодинамика» — наука о преобразовании энергии.
Особенности преобразования тепла и работы были показаны в первых двух законах термодинамики. Наука об энергии разделилась на множество различных областей, таких как биологическая термодинамика и термоэкономика (англ. thermoeconomics). Параллельно развивались связанные понятия, такие как энтропия, мера потери полезной энергии, мощность, поток энергии за единицу времени, и так далее. В последние два века использование слова энергия в ненаучном смысле широко распространилось в популярной литературе.
Параллельно развивались связанные понятия, такие как энтропия, мера потери полезной энергии, мощность, поток энергии за единицу времени, и так далее. В последние два века использование слова энергия в ненаучном смысле широко распространилось в популярной литературе.
В 1918 году было доказано, что закон сохранения энергии есть математическое следствие трансляционной симметрии времени, величины сопряжённой энергии. То есть энергия сохраняется, потому что законы физики не отличают разные моменты времени (см. Теорема Нётер, изотропия пространства).
В 1961 году выдающийся преподаватель физики и нобелевский лауреат, Ричард Фейнман в лекциях так выразился о концепции энергии:[6]
Существует факт, или, если угодно, закон, управляющей всеми явлениями природы, всем, что было известно до сих пор. Исключений из этого закона не существует; насколько мы знаем, он абсолютно точен. Название его — сохранение энергии. Он утверждает, что существует определённая величина, называемая энергией, которая не меняется ни при каких превращениях, происходящих в природе.
Само это утверждение весьма и весьма отвлечено. Это по существу математический принцип, утверждающий, что существует некоторая численная величина, которая не изменяется ни при каких обстоятельствах. Это отнюдь не описание механизма явления или чего-то конкретного, просто-напросто отмечается то странное обстоятельство, что можно подсчитать какое-то число и затем спокойно следить, как природа будет выкидывать любые свои трюки, а потом опять подсчитать это число — и оно останется прежним.
Оригинальный текст (англ.)
There is a fact, or if you wish, a law, governing natural phenomena that are known to date. There is no known exception to this law—it is exact so far we know. The law is called conservation of energy; it states that there is a certain quantity, which we call energy that does not change in manifold changes which nature undergoes. That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity, which does not change when something happens.
It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number, and when we finish watching nature go through her tricks and calculate the number again, it is the same.
— Фейнмановские лекции по физике[7]
См. также
Примечания
- ↑ Г. Д. Бурдун. Джоуль(единица энергии и работы) // Большая советская энциклопедия.
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теоретическая физика. — 5-е изд. — М.: Физматлит, 2004. — Т. I. Механика. — 224 с. — ISBN 5-9221-0055-6
- ↑ http://profbeckman.narod.ru/InformLekc.files/Inf03.pdf
- ↑ 1 2 3 Смит, Кросби. The science of energy: a cultural history of energy physics in Victorian Britain. — The University of Chicago Press, 1998. — ISBN 0-226-76421-4
- ↑ Томсон, Уильям. Об источниках энергии, доступных человеку для совершения механических эффектов = On the sources of energy available to man for the production of mechanical effect.
 — BAAS Rep, 1881. С. 513
— BAAS Rep, 1881. С. 513 - ↑ Richard Feynman. The Feynman Lectures on Physics. — США: Addison Wesley, 1964. — Vol. 1. — ISBN 0-201-02115-3
- ↑ Фейнман, Ричард. Фейнмановские лекции по физике = The Feynman Lectures on Physics. — Т. 1.
Ссылки
Энергия. Кинетическая энергия – Класс!ная физика
Энергия. Кинетическая энергия
- Подробности
- Просмотров: 364
«Физика – 10 класс»
Вспомните, когда мы можем сказать, что у тела есть энергия.
Какие физические величины определяют механическую энергию тела?
Какие виды механической энергии вы знаете?
Если система тел может совершить работу, то мы говорим, что она обладает энергией.
Энергия характеризует способность тела (или системы тел) совершать работу.
Совершая механическую работу, тело или система тел переходят из одного состояния в другое, в котором их энергия минимальна.
Груз опускается, пружина распрямляется, движущееся тело останавливается.
При совершении работы энергия постепенно расходуется.
Для того чтобы система опять приобрела способность совершать работу, надо изменить её состояние: увеличить скорости тел, поднять тела вверх или деформировать.
Для этого внешние силы должны совершить над системой положительную работу.
Энергия в механике — величина, определяемая состоянием системы — положением тел или частей тела и их скоростями.
Кинетическая энергия — это энергия, которой обладает движущееся тело.
Подсчитаем работу постоянной силы , действующей на материальную точку массой m при его прямолинейном движении.
Пусть направление силы совпадает с направлением скорости материальной точки.
В этом случае направления вектора перемещения Дс и вектора силы совпадают (рис. 5.4).
Поэтому работа силы Δ:
А = F|Δ|.
Выберем координатную ось ОХ так, чтобы векторы , 1, 2 и Δ были направлены в сторону положительного направления этой оси.
Тогда Δrх = Δх, и формулу для работы можно записать так:
А = FΔx. (5.6)
Согласно второму закону Ньютона
F = mа. (5.7)
Так как точка движется с постоянным ускорением, то изменение её координаты Δх при переходе из начального положения в конечное можно найти по известной нам из кинематики формуле
Подставляя формулы (5.7) и (5.8) в формулу (5.6), получаем
Таким образом, работа силы при перемещении точки из начального положения в конечное равна изменению величины называемой кинетической энергией (от греческого слова «кинема» — движение).
Кинетическая энергия материальной точки — это величина, равная половине произведения массы материальной точки на квадрат её скорости:
Энергия выражается в тех же единицах, что и работа.
Учитывая равенство (5.10), уравнение (5.9) можно записать так:
А = Ек2 – Ек1 = ΔЕк.
Равенство (5.11) выражает теорему об изменении кинетической энергии.
Изменение кинетической энергии материальной точки при её перемещении равно работе, совершённой силой, действующей на точку при этом перемещении.
Если на точку действует несколько сил, то изменение её кинетической энергии равно алгебраической сумме работ всех сил, действующих на неё:
ΔЕк = А1 + А2 + … .
Кинетическая энергия тел зависит только от их масс и скоростей.
Изменение кинетической энергии материальной точки зависит от начальной и конечной скоростей точки и не зависит от того, каким образом изменялась её скорость, под действием каких сил происходило это изменение.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы сохранения в механике – Физика, учебник для 10 класса – Класс!ная физика
Импульс материальной точки —
Закон сохранения импульса —
Реактивное движение. Успехи в освоении космоса —
Примеры решения задач по теме «Закон сохранения импульса» —
Механическая работа и мощность силы —
Энергия. Кинетическая энергия —
Примеры решения задач по теме «Кинетическая энергия и её изменение» —
Работа силы тяжести. Консервативные силы —
Работа силы упругости. Консервативные силы —
Потенциальная энергия —
Закон сохранения энергии в механике —
Работа силы тяготения. Потенциальная энергия в поле тяготения —
Примеры решения задач по теме «Закон сохранения механической энергии» —
Основное уравнение динамики вращательного движения —
Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси —
Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
Успехи в освоении космоса —
Примеры решения задач по теме «Закон сохранения импульса» —
Механическая работа и мощность силы —
Энергия. Кинетическая энергия —
Примеры решения задач по теме «Кинетическая энергия и её изменение» —
Работа силы тяжести. Консервативные силы —
Работа силы упругости. Консервативные силы —
Потенциальная энергия —
Закон сохранения энергии в механике —
Работа силы тяготения. Потенциальная энергия в поле тяготения —
Примеры решения задач по теме «Закон сохранения механической энергии» —
Основное уравнение динамики вращательного движения —
Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси —
Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
Энергия. Работа. Мощность. Законы сохранения
1. ФИЗИКА
государственное автономное профессиональное образовательное учреждение Самарской области“Самарский государственный колледж”
ФИЗИКА
Суровость законов в Российской империи смягчается их
неукоснительным неисполнением.

Н.Е. Салтыков-Щедрин
ЭНЕРГИЯ. РАБОТА. МОЩНОСТЬ
ЗАКОНЫ СОХРАНЕНИЯ
2018
«Грош цена вашей физике, если она
застилает для вас все остальное: шорох леса, краски
заката, звон рифмы.
Это какая-то усеченная физика, если хотите –
выхолощенная.
Я, например, в нее не верю… Любая замкнутость,
прежде всего, свидетельствует об ограниченности…
Физик, не воспринимающий поэзии, искусства, –
плохой физик».
Л. Д. Ландау
В этой теме мы познакомимся с простейшими
формулами энергии – потенциальной энергией тела в
силовом поле и кинетической энергией движущегося
тела.
Узнаем, что законы сохранения справедливы для
изолированных систем и в целом обусловлены
фундаментальными свойствами пространства и
времени – изотропностью пространства и
однородностью времени
4. ВОПРОСЫ
Не поискать ли мне тропы иной,Приемов новых,
Сочетаний странных.
В. Шекспир
1.Кинетическая энергия.
 Работа и мощность
Работа и мощность2.Консервативные силы и системы
3.Потенциальная энергия
4.Закон сохранения механической энергии
5.Условие равновесия механической системы
6.Применение законов сохранения
7.Свойства пространства–времени и законы сохранения
8.Контрольные вопросы.
2018
1.Кинетическая энергия. Работа и мощность
Универсальной количественной мерой движения и
взаимодействия всех видов материи является энергия.
Кинетическая энергия Ек – физическая скалярная величина, являющаяся мерой
механического движения тел.
Уравнение движения тела массой т под
действием внешней силы F имеет вид
или, в проекции на
направление
движения
Умножив обе части равенства на υ dt = dr, получим
Левая часть равенства есть полный
дифференциал некоторой функции:
Если полный дифференциал некоторой функции, описывающей
поведение системы, равен нулю, то эта функция может служить
характеристикой состояния данной системы.

Функция состояния системы, определяемая
только скоростью ее движения, называется
кинетической энергией:
Кинетическая энергия системы есть функция состояния движения этой системы.
Кинетическая энергия – величина аддитивная:
где Ек – относительная величина, её значение зависит от выбора системы координат
(так же как и скорость – относительная величина)
Энергия измеряется в СИ в единицах произведения силы на расстояние,
т. е. в ньютонах на метр. 1 Н * м = 1Дж.
Кроме того, в качестве единицы измерения
энергии используется внесистемная единица –
электрон-вольт (эВ).
При решении задач полезна формула,
связывающая кинетическую энергию с
импульсом p.
Связь кинетической энергии с работой и мощностью
Если постоянная сила действует на тело, то оно будет двигаться в направлении
силы. Тогда элементарная работа по перемещению тела из точки 1 в точку 2
будет равна произведению силы F на перемещение dr
Окончательно
получаем:
Следовательно, работа силы, приложенной к телу на пути r,
численно равна изменению кинетической энергии этого тела
Или изменение кинетической энергии dЕк
равно работе внешних сил
А так же как и Е измеряется в Джоулях!!!!
Скорость совершения работы (передачи энергии) называется
мощностью, т.
 е. мощность есть работа, совершаемая в единицу
е. мощность есть работа, совершаемая в единицувремени
Консервативные силы и системы
Кроме контактных взаимодействий, наблюдаются взаимодействия между
телами, удаленными друг от друга. Подобное взаимодействие осуществляется
посредством физических полей (особая форма материи). Каждое тело создает
вокруг себя поле, которое проявляет себя именно воздействием на другие тела.
Силы, работа которых не зависит от пути, по которому двигалось тело, а
зависит от начального и конечного положения тела, называются
консервативными.
Работа
консервативных
сил
по
перемещению тела из точки 1 в точку 2 не
зависит от формы пути, а зависит от
положения начальной и конечной точки
Изменение направления движения на
противоположное вызывает изменение
знака работы консервативных сил.
Отсюда следует, что работа консервативных
сил вдоль замкнутой кривой равна нулю
Интеграл по замкнутому контуру
называется циркуляцией вектора F
СЛЕДОВАТЕЛЬНО
если циркуляция какого-либо вектора силы равна нулю, то эта сила консервативна
Центральные силы являются консервативными независимо от их природы
Сила называется центральной, если она направлена к одной и той же точке
(или от одной и той же точки) и зависит только от расстояния до этой точки,
называемой центром сил.
Консервативные силы:
гравитационные силы тяжести
электростатические силы
силы центрального стационарного поля
и т. д.
Неконсервативные силы:
силы трения,
силы вихревого электрического поля
и т. д.
Консервативная система – такая система , внутренние силы которой
только консервативные, а внешние – консервативны и стационарны
Потенциальная энергия
кинетическая энергия Ек – энергия движения.
Потенциальная энергия Еп – энергия взаимодействия тел или
частиц тела, зависящая от их взаимного расположения.
Можно говорить о потенциальной энергии тела массой т в поле тяжести
Земли, заряда q в электростатическом поле, о потенциальной энергии тела в
поле упругой силы пружины и т. д.
Работа, совершаемая консервативными силами при изменении конфигурации
системы, то есть при изменении положения тел относительно системы отсчета,
не зависит от того, как было осуществлено это изменение. Работа определяется
только начальной и конечной конфигурациями системы.

здесь потенциальная энергия Еп (х, у, z) – функция состояния системы, зависящая только
от координат всех тел системы в поле консервативных сил.
Итак, Ек определяется скоростью движения тел системы, а U – их взаимным
расположением.
следует, что работа консервативных сил равна убыли потенциальной энергии:
dA =-dЕп .
Нет единого выражения для Еп. В разных случаях она определяется по-разному.
Потенциальная энергия при гравитационном взаимодействии
Работа тела при падении A = mgh. Или A = Еп – Еп0.
Условились считать, что на поверхности Земли ( h = 0 ) Еп0 = 0 ,
тогда Еп = А, т. е.
Для случая гравитационного взаимодействия между массами M и m,
находящимися на расстоянии r друг от друга, потенциальную энергию можно
найти по формуле
Диаграмма потенциальной энергии
гравитационного притяжения
масс M и m:
полная энергия E = Ек + Еп
Отсюда кинетическая энергия
Ек =E – Еп
Связь между потенциальной энергией и силой
Пространство, в котором действуют консервативные
силы, называется потенциальным полем.

Каждой точке потенциального поля соответствует некоторое значение силы F ,
действующей на тело, и некоторое значение потенциальной энергии Еп
Значит, между силой F и Еп должна быть связь dA=Fdr , с другой стороны, dA =-dЕп,
следовательно Fdr =-dЕп ,
отсюда
Оператор набла (оператор
Для компонент силы по осям x, y, z
Так как вектор силы
Гамильтона) — векторный
дифференциальный оператор,
компоненты которого являются
частными производными по
координатам.
Обозначается
символом (набла) (∇)
получим
Градиент – это вектор, показывающий направление наибыстрейшего увеличения
функции. Знак «–» показывает, что вектор F направлен в сторону наибыстрейшего
уменьшения Еп.
Следовательно, консервативная сила равна градиенту
потенциальной энергии, взятому со знаком минус:
Закон сохранения механической энергии
Рассмотрим систему, состоящую из N частиц.
Силы взаимодействия между частицами (F внутр) – консервативные.
 Кроме внутренних
Кроме внутреннихсил, на частицы действуют внешние консервативные и неконсервативные силы, т. е.
рассматриваемая система частиц или тел консервативна.
Тогда для этой системы можно найти полную энергию системы
закон сохранения для механической энергии
полная механическая энергия консервативной системы материальных точек
остаётся постоянной.
закон сохранения для механической энергии для замкнутой системы
полная механическая энергия замкнутой системы материальных точек,
между которыми действуют только консервативные силы, остаётся
постоянной
Если в замкнутой системе действуют неконсервативные силы, то полная механическая энергия
системы не сохраняется – частично она переходит в другие виды энергии, неконсервативные.
Система, в которой механическая энергия переходит в другие виды энергии,
называется диссипативной, сам процесс перехода называется диссипацией
энергии.
В диссипативной, изолированной от внешнего воздействия
системе остаётся постоянной сумма всех видов энергии
(механической, тепло-вой и т.
 д.) Здесь действует общий закон
д.) Здесь действует общий законсохранения энергии.
Этот процесс хорошо демонстрирует маятник Максвелла
Роль консервативной внешней силы здесь
играет гравитационное поле. Маятник
прекращает свое движение из-за наличия
внутренних неконсервативных сил (сил
трения, сопротивления воздуха)
Условие равновесия механической системы
Мерой устойчивости тела в положении равновесия является наименьшее
значение работы, совершаемой внешней силой, для того, чтобы переместить
тело в такое положение, откуда после действия силы оно уже не сможет
вернуться в исходное состояние.
Из двух тел более устойчивым является тело, для выведения которого из
положения равновесия требуется совершение большей работы.
Это условие необходимое, но не достаточное, так как система может при этом находиться в
равномерном и прямолинейном движении.
Применение законов сохранения
Абсолютно упругий центральный удар
При абсолютно неупругом ударе закон сохранения механической
энергии не работает.

Применим закон сохранения механической энергии для расчета скорости тел
при абсолютно упругом ударе – ударе, при котором не происходит превращения
механической энергии в другие виды энергии.
Абсолютно неупругий удар
Абсолютно неупругий удар – это столкновение двух тел, в результате которого
тела объединяются и двигаются дальше как единое целое.
Продемонстрировать абсолютно неупругий удар можно с помощью шаров из
пластилина (глины), движущихся навстречу друг другу.
Движение тел с переменной массой
Рассмотрим теперь системы, массы которых изменяются. Такие системы можно
рассматривать как своего рода неупругое столкновение.
Законы сохранения носят фундаментальный характер и тесно связаны с
симметрией пространства и времени:
закон сохранения энергии связан с однородностью времени, т. е.
равнозначностью всех моментов времени;
закон сохранения импульса связан с однородностью пространства, т. е.
равнозначностью всех точек пространства.

Законы сохранения носят общий характер и не зависят от конкретной системы
и ее движения.
Из законов сохранения вытекает, что какие-то процессы заведомо оказываются
невозможными.
Так, в 1775 г. Французская Академия решила не принимать к рассмотрению проекты
вечных двигателей – как противоречащие закону сохранения энергии.
Законы сохранения позволяют рассмотреть общие свойства движения без решения
уравнений и детальной информации о протекании процессов во времени. Поэтому законы
сохранения могут быть использованы даже в тех случаях, когда силы точно не
известны. Так, в частности, обстоит дело в физике элементарных частиц. Даже в тех
случаях, когда силы заданы точно, законы сохранения могут оказать существенную
помощь при решении задач о движении частиц.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем различие между понятиями энергии и работы?
2. Как найти работу переменной силы?
3. Какую работу совершает равнодействующая всех сил,
приложенных к телу, равномерно движущемуся по окружности?
4.
 Что такое мощность? Выведите ее формулу.
Что такое мощность? Выведите ее формулу.5. Дайте определения и выведите формулы для известных видов
механической энергии.
6. Какова связь между силой и потенциальной энергией?
7. Чем обусловлено изменение потенциальной энергии?
8. Необходимо ли условие замкнутости системы для выполнения
закона сохранения механической энергии?
9. В чем заключается закон сохранения механической энергии? Для
каких систем он выполняется?
10.В чем физическая сущность закона сохранения и превращения
энергии? Почему он является фундаментальным законом
природы?
11.Чем отличается абсолютно упругий удар от абсолютно
неупругого?
28 Работа и энергия – СтудИзба
РАБОТА И ЭНЕРГИЯ
Работа силы
Элементарная работа
Предположим, что точка приложения переменной по модулю и направлению силы перемещается по криволинейной траектории. Чтобы вычислить работу силы на этом перемещении, нужно разбить это перемещение на элементарные участки, вычислить работу силы на каждом элементарном участке, как работу постоянной силы, и определить предел суммы элементарных работ при стремлении числа участков к бесконечности и длины каждого из них к нулю.
Элементарная работа силы на участке dl определяется по формуле:
(1),
где – импульс.
Элементарную работу обозначают , а не , так как в общем случае она не является дифференциалом функции. Знак работы определяется только знаком косинуса угла – угла между векторами и . Если < , то работа силы положительна, если > – отрицательна, а если = , то работа силы равна 0.
Полная работа
Рекомендуемые файлы
Полная работа на участке dl равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках и сводится к интегралу
;
(2)
Для вычисления работы нужно:
1. Указать силу, с которой выполняется работа.
2. Определить перемещение, на котором выполняется эта работа, и угол между вектором перемещения и вектором силы.
Единицей измерения работы является джоуль (1 Дж). 1 Дж – работа, совершаемая силой 1 Н на пути 1 м (1 Н = 1 Н×м).
Пример 1.
Точка прошла 1/4 окружности. Найти работу.
Решение.
;
Пример 2.
Посчитать работу гравитационной силы.
;
;
Пример 3.
Посчитать работу силы упругости.
Пример 4.
Посчитать работу силы трения.
тртртр
тр
Мощность силы – изменение работы силы, отнесенное к единице времени.
Если в течение малого промежутка времени dt сила совершает работу , то мощность этой силы
(3)
Таким образом, мощность силы равна скалярному произведению векторов силы и скорости ее точки приложения.
За единицу мощности в системе МКС принимается 1 ватт (Вт) = 1Дж/с.
Все силы, действующие на частицы, можно разбить на две группы: потенциальные и непотенциальные. Силы называются потенциальными, если их работа при изменении положения частиц не зависит от формы пути при перемещении частиц, а определяется начальной и конечной конфигурациями системы. Это силы, зависящие от координат точек системы. Работа, выполняемая этими силами, не зависит от траектории движения, а зависит от начального и конечного положения. На замкнутой траектории работа потенциальных сил равна нулю. Это математическое правило.
Это силы, зависящие от координат точек системы. Работа, выполняемая этими силами, не зависит от траектории движения, а зависит от начального и конечного положения. На замкнутой траектории работа потенциальных сил равна нулю. Это математическое правило.
, где – интеграл по замкнутому контуру.
Чтобы проверить, является ли сила потенциальной, нужно взять интеграл по замкнутому кругу.
Примеры потенциальных сил:
1)
2)
3)
4) Однородное поле сил
5) Центральное поле сил:
Работа непотенциальных сил зависит от формы пути. Примером таких сил является сила трения.
Кинетическая и потенциальная энергии
Кинетическая энергия
Кинетическая энергия механической системы – это энергия механического движения этой системы.
Теорема о кинетической энергии.
(1),
где – кинетическая энергия (энергия движения), она всегда положительная.
Работа, выполняемая в системе любыми силами, равна разности кинетических энергий между конечным и начальным положением.
Потенциальная энергия
Потенциальная энергия – некоторая функция, которая зависит только от координат точек системы, всякое изменения которой, взятое с обратным знаком, равно работе консервативных сил, действующих на точки системы:
U=f(x; y; z).
Потенциальная энергия системы в любом данном ее положении равна сумме работ сил потенциального поля, приложенных к ее точкам на перемещении из данного положения в нулевое.
(2)
(3)
Знак «минус» указывает, что в результате выполнения работы потенциальными силами, энергия уменьшается.
Закон сохранения механической энергии
При движении механической системы под действием сил, имеющих потенциал, изменения кинетической энергии системы определяются зависимостями:
;
(4),
где потенциальные энергии системы в 1 и 2 положениях.
Сумму кинетической и потенциальной энергий системы называют полной механической энергией системы.
По теореме о кинетической энергии:
(5)
Таким образом, в замкнутой системе, в которой действуют только потенциальные силы, полная механическая энергия с течением времени не изменяется при любых процессах, происходящих внутри системы.
Пример.
Тело бросают вертикально вверх с начальной скоростью v0. Найти высоту, на которой кинетическая и потенциальная энергии тела будут равны.
Решение.
Закон сохранения полной энергии
По теореме о кинетической энергии:
В реальных условиях на механическую систему могут действовать не только потенциальные силы, и полная механическая энергия системы может изменяться. Это происходит, когда часть энергии механической системы расходуется на преодоление различных сопротивлений или наблюдается приток энергии от других систем.
Расход механической энергии движущейся механической системы обычно означает превращение ее в теплоту, электричество, звук или свет, а приток механической энергии связан с обратным процессом превращения различных видов энергии в механическую энергию.
Таким образом, энергия не возникает и не исчезает бесследно, происходит только превращение одного вида энергии в другой в разных количествах, поэтому полная энергия системы с течением времени сохраняется при любых взаимодействиях внутри неё.
Работа, выполняемая непотенциальными силами, равна разности полной механической энергии между конечным положением и начальным.
Закон сохранения энергии для системы материальных точек
Предположим, что силы взаимодействия (Fвз) между частичками системы – потенциальные силы.
-для замкнутой системы материальных частиц.
Рассмотрим случай, когда на систему действуют потенциальные силы . Изменение .
(1)
е
явным образом не зависит от времени.
На частички некоторой системы действуют ещё и диссипативные силы, совершающие работу часть будет превращаться в другие виды энергии.
Если умножить на , то диссипативная сила даст
Энергия материальной точки в релятивистском случае и закон сохранения энергии в этом случае.
В релятивистском случае масса частиц зависит от n:
– умножим обе части равенства на v и т.к.
Покажем, что при малых v формула
Безмассовые частицы – частицы у которых и они движутся со скоростью света, например фотоны, для них:
Найдём связь между E и p:
Информация в лекции “63. Культурная адаптация работников” поможет Вам.
– инвариантная величина
Энергия в физике – виды, формулы и определение с примерами
Содержание:
Для работы двигателей, приводящих в движение автомобили, трактора, тепловозы, самолёты, необходимо топливо, являющееся источником энергии. За счёт энергии воды, падающей с высоты, вращаются гидротурбины, соединённые с электрическими машинами, вырабатывающими электрический ток. Человеку для того чтобы существовать и работать, также необходим источник энергии. Говорят, что для того, чтобы выполнять любую работу, необходима энергия. Что же такое энергия?
Опыт 1. Поднимем над Землёй мяч. Пока он находится в состоянии покоя, механическая работа не выполняется. Отпустим его. Под действием силы тяжести мяч падает на Землю с определённой высоты. При падении мяча выполняется механическая работа.
Опыт 2. Сожмём пружину, зафиксируем её нитью и поставим на пружину гирю (рис. 171).
Пережжём нить, пружина распрямится и поднимет гирю на некоторую высоту. Пружина выполнила механическую работу.
Пружина выполнила механическую работу.
Опыт 3. На тележке закрепим стержень с блоком на конце (рис. 172). Через блок перекинем нить, один конец которой намотан на ось тележки, а на втором висит грузик. Отпустим грузик, под действием силы тяжести он будет опускаться вниз и приведёт в движение тележку. Грузик выполнил механическую работу .
Опыт 4. Стальной шарик А, скатившийся по наклонной плоскости (рис. 173), также выполнил механическую работу: он переместил цилиндр В на некоторое расстояние.
Если тело или несколько тел при взаимодействии выполняют механическую работу, то это значит, что они имеют механическую энергию, или энергию.
Мяч, поднятый над Землёй, сжатая пружина, движущийся стальной шарик имеют энергию.
Энергия – физическая величина, характеризующая способность тел выполнять работу.
Энергия (от греческого слова энергия — деятельность) обозначается большой латинской буквой Е. Единицей энергии, а также и работы в СИ является один джоуль (1 Дж). Из приведённых опытов видно, что тело выполняет работу тогда, когда переходит из одного состояния в другое: поднятый над Землёй грузик опускается, сжатая пружина распрямляется, движущийся шарик останавливается. Энергия тела при этом изменяется (уменьшается), а выполненная телом механическая работа равна изменению его механической энергии. Различают два вида механической энергии – потенциальную и кинетическую.
Единицей энергии, а также и работы в СИ является один джоуль (1 Дж). Из приведённых опытов видно, что тело выполняет работу тогда, когда переходит из одного состояния в другое: поднятый над Землёй грузик опускается, сжатая пружина распрямляется, движущийся шарик останавливается. Энергия тела при этом изменяется (уменьшается), а выполненная телом механическая работа равна изменению его механической энергии. Различают два вида механической энергии – потенциальную и кинетическую.
Энергия и механическая работа
Как древние египтяне, строя свои колоссальные пирамиды, поднимали на огромную высоту такие тяжеленные каменные блоки, что их трудно было даже сдвинуть?
Для их подъема использовали, например, рычаги. Рычагами пользовались и древние греки, когда строили огромные храмы.
Опыт:
Убедимся, что с помощью рычага действительно можно получить значительный выигрыш в силе. Положите на короткое плечо рычага тяжелую книгу — и вы сможете поднять ее, надавив на длинное плечо мизинцем (рис. 5.1)!
5.1)!
Однако выигрыш в силе всегда сопровождается проигрышем в перемещении.
Например, если груз, прикрепленный к короткому плечу рычага, поднимают, прикладывая к длинному плечу рычага силу, которая в 10 раз меньше веса этого груза, то длинное плечо рычага надо опустить на расстояние, которое в 10 раз больше высоты, на которую поднимется груз.
Этот и подобный ему опыты показывают, что, используя любые простые механизмы, мы выигрываем в силе как раз во столько раз, во сколько проигрываем в перемещении.
Эта закономерность, обнаруженная еще древними греками, оказалась настолько важной, что со временем ее назвали «золотым правилом механики».
Механическая работа:
Из золотого правила механики следует: если не учитывать трения, произведение силы на перемещение одинаково для каждой из сил, приложенных к плечам рычага. Поэтому ввели физическую величину, которую назвали механической работой. В дальнейшем для простоты мы ограничимся случаем, когда направление силы совпадает с направлением перемещения. В этом случае
В дальнейшем для простоты мы ограничимся случаем, когда направление силы совпадает с направлением перемещения. В этом случае
Механическая работа силы равна произведению силы на перемещение1.
Механическую работу обозначают буквой . Если сила направлена вдоль перемещения, работа силы , где — модуль силы, a — модуль перемещения.
Единицу работы в SI назвали джоуль (Дж) в честь английского физика Джеймса Прескотта Джоуля. Один джоуль — это работа, которую совершает сила в I Н, перемещая тело на I м в направлении действия силы, то есть . Например, поднимая полное ведро воды, вы прикладываете силу, равную примерно 100 Н. Значит, поднимая ведро на высоту 1 м, вы выполняете работу, равную примерно 100 Дж.
Механическую работу часто называют просто работой, однако ее не следует путать с работой в повседневном значении этого слова. Мы еще расскажем об этом в разделе «Хочешь узнать больше?».
Определение энергииМеханическую работу человек давно научился «перекладывать на плечи» машин и механизмов.
Одним из первых таких механизмов была водяная мельница (рис. 5.2): работу здесь выполняет сила, с которой падающая вода давит на лопасти колеса. Современная гидроэлектростанция, заставляющая «работать» огромную реку (рис. 5.3), «выросла» из небольшой водяной мельницы на ручье.
Чтобы мельница работала или электростанция вырабатывала электроэнергию, необходимо создать разность уровней воды. Итак, вода и притягивающая ее Земля образуют систему тел, способную совершить работу.
Способностью совершить работу обладает также движущееся тело. Например, вода, падая, ударяет в подвижные лопасти колеса или турбины, то есть действует на них с некоторой силой. При этом скорость воды уменьшается. Физическую величину, которая характеризует способность тела или системы тел совершать работу вследствие изменения своего состояния, называют энергией.
Физическую величину, которая характеризует способность тела или системы тел совершать работу вследствие изменения своего состояния, называют энергией.
Говорят, что тело (или система тел) обладает энергией, если это тело (или система тел) может совершить работу. Мерой изменения энергии является совершенная работа: когда тело совершает работу, его энергия уменьшается на величину, равную совершенной работе.
Поэтому энергию измеряют в тех же единицах, что и работу: единицей энергии в SI является джоуль. Если тело (система тел) совершает работу в 1 Дж, энергия тела (системы тел) уменьшается на 1 Дж.
Виды энергииТело или система тел может совершать работу вследствие различных изменений своего состояния.
Работа может быть совершена вследствие изменения взаимного положения взаимодействующих тел, а также вследствие изменения скоростей тел. В этих случаях изменяется механическая энергия тела или системы тел.
Часть механической энергии, обусловленную взаимодействием тел, называют потенциальной энергией, а часть механической энергии, обусловленную движением тел, — кинетической энергией.
Например, поднятое над Землей тело и Земля притягивают друг друга, то есть взаимодействуют. Благодаря этому тело при падении может выполнить некоторую работу. Значит, поднятое тело обладает потенциальной энергией. При падении тела его потенциальная энергия уменьшается, зато кинетическая — увеличивается, так как увеличивается скорость тела.
Рассмотрим еще один случай, когда тело может совершить работу. Газ, расширяясь в цилиндре, двигает поршень, совершая при этом работу (на этом основано действие автомобильных двигателей). Но, расширяясь, газ охлаждается, то есть его температура понижается. А при этом, как вы скоро узнаете, замедляется хаотическое1, то есть беспорядочное, движение молекул газа. Значит, расширяясь, газ выполняет работу благодаря уменьшению кинетической энергии хаотического движения молекул.
Энергию, обусловленную хаотическим движением частиц тела и их взаимодействием, называют внутренней энергией.
Когда газ расширяется, он совершает работу, а его внутренняя энергия уменьшается.
Ученые установили, что существуют и другие виды энергии — например, электромагнитная и атомная энергия. О них вы узнаете подробнее из курса физики старших классов.
Энергия является важнейшей физической величиной, поэтому мы и рассказали о ней в начале вашего знакомства с физикой.
Целые эпохи в истории человечества называли «в честь» используемого вида энергии. Так, время паровых двигателей (от второй половины 18-го века до конца 19-го века) называли «веком пара». А 20-й век называли «веком электричества», а также «веком атома».
Закон сохранения энергии
Опыты показывают, что, если можно пренебречь силами трения, механическая энергия взаимодействующих тел, то есть сумма их потенциальной и кинетической энергии, не изменяется. Это — проявление закона сохранения энергии, открытого в 19-м веке.
Закон сохранения энергии: во всех процессах, происходящих в природе, суммарная энергия взаимодействующих тел не изменяется.
Физический смысл закона сохранения энергии состоит в том, что энергия является общей мерой движения и взаимодействия тел и частиц, она никогда не исчезает и не появляется, а лишь преобразуется из одного вида в другой.
Многие происходящие в природе процессы сопровождаются преобразованиями энергии. Например, когда вследствие трения движущееся тело останавливается, его механическая энергия переходит во внутреннюю, потому что вследствие трения тела нагреваются.
Мог ли Архимед сдвинуть землюПравило рычага установил на опыте выдающийся древнегреческий ученый и инженер Архимед, который жил в 3-м веке до нашей эры в Сиракузах, одном из греческих городов-государств на острове Сицилия.
Архимед достиг такого совершенства в сооружении различных механизмов, что заявил как-то царю Сиракуз: «С помощью своих механизмов я один могу поднять любой груз!» Более того, Архимед утверждал, что он мог бы сдвинуть даже Землю, если бы только нашел «точку опоры» — например, другую Землю, на которую можно стать! Царь очень удивился и предложил Архимеду продемонстрировать свое могущество.
Тогда Архимед попросил загрузить корабль, который с трудом вытянули на берег, и посадить на него весь экипаж. Привязав к кораблю крепкий канат, Архимед начал тянуть канат с помощью изобретенного им механизма. И корабль плавно тронулся по песку к Архимеду — будто поплыл по морю! Царь и все присутствующие были поражены могуществом Архимеда — не могуществом его рук, а могуществом его разума.
Однако, утверждая, что он мог бы сдвинуть даже Землю, Архимед очень переоценил свои возможности. Расчеты показывают, что даже если бы Архимеду фантастически «повезло» и он смог бы найти «точку опоры» и огромный рычаг, то не успел бы заметно сдвинуть Землю не только за всю свою жизнь, но и за все время существования Земли.
Может ли человек устать, не совершая механической работыПочему очень устаешь, когда долго держишь, например, полное ведро воды? Ведь механической работы при этом не совершаешь, так как перемещение равно нулю! Чтобы убедиться в том, что держание груза не является работой в физическом значении этого слова, поставьте ведро на пол: пол без устали будет «держать» ведро как угодно долго!
Человек же, держа груз, устает из-за напряжения мышц. Положите тот же груз на колени, и вы почувствуете значительное облегчение. Итак, не следует путать механическую работу как физическую величину с работой в повседневном значении слова, то есть с любой деятельностью, которая вызывает усталость. Ведь устать можно, совсем не выполняя механической работы — например, сочиняя музыку или стихи. А больше всего, как известно, устаешь от безделья!
Положите тот же груз на колени, и вы почувствуете значительное облегчение. Итак, не следует путать механическую работу как физическую величину с работой в повседневном значении слова, то есть с любой деятельностью, которая вызывает усталость. Ведь устать можно, совсем не выполняя механической работы — например, сочиняя музыку или стихи. А больше всего, как известно, устаешь от безделья!
Вы уже узнали, что одной из физических величин, которые обладают свойством сохранения в замкнутой системе, является общий импульс системы. Другой очень важной физической величиной, обладающей свойством сохранения в замкнутой системе, является энергия. Понятие “энергия” часто используется в повседневной жизни (например, энергия является самой обсуждаемой темой на переговорах по международным экономическим вопросам). Вы имеете достаточно информации о различных видах энергии и о ее превращении из одного вида в другой. Самое важное то, что для каждого вида энергии учеными-физиками была определена своя формула. Проведенные с помощью этих формул вычисления каждый раз подтверждают постоянство суммы всех видов энергии замкнутой системы.
Проведенные с помощью этих формул вычисления каждый раз подтверждают постоянство суммы всех видов энергии замкнутой системы.
Как вы знаете, энергия характеризует способность тела совершать работу. С другой стороны, энергия — общая мера движения и взаимодействия тел. Движение тела характеризуется его кинетической энергией, а взаимодействие тел характеризуется потенциальной энергией.
Работа, совершаемая равнодействующей силой, и кинетическая энергия тела при поступательном движении. Если тело под действием равнодействующей силы совершает работу, то модуль его скорости изменяется от до то есть тело получает ускорение. Для простоты предположим, что тело под действием параллельной горизонту постоянной равнодействующей силы совершает положительную работу. В этом случае тело, двигаясь равноускоренно с
ускорением совершает работу:
или
В последней формуле половина произведения массы на квадрат скорости выражает физическую величину, называемую кинетической энергией.
Кинетическая энергия—это энергия, возникающая в результате движения тела:
Кинетическая энергия зависит от массы тела и модуля его скорости (а не от его направления). Если запишем формулу (3.12) с учетом (3.13), то получим выражение, которое называется теоремой о кинетической энергии-.
Работа, совершаемая над телом постоянной равнодействующей силой, равна изменению кинетической энергии тела:
Где и — начальное и конечное значения кинетической энергии тела. Кинетическая энергия – скалярная физическая величина и, в отличие от работы, может иметь только положительные значения или равняться нулю (превращается в другой вид энергии). Из выражения (3.14) видно, что:
a) если работа, совершенная постоянной равнодействующей силой, положительна то изменение кинетической энергии тела больше нуля: — кинетическая энергия увеличивается;
b) если работа, совершенная постоянной равнодействующей силой, отрицательна то изменение кинетической энергии тела меньше нуля: — кинетическая энергия уменьшается;
c) если работа, совершенная постоянной равнодействующей силой, равна нулю то и изменение кинетической энергии равно нулю: – кинетическая энергия не изменяется, то есть остается постоянной
Примечание:
- При доказательстве теоремы о кинетической энергии не было отмечено, какова природа силы, совершающей работу.
 Это значит, что теорема о кинетической энергии справедлива для любых сил (сила тяжести, сила трения, сила упругости или их равнодействующая сила), действующих на тело.
Это значит, что теорема о кинетической энергии справедлива для любых сил (сила тяжести, сила трения, сила упругости или их равнодействующая сила), действующих на тело. - Кинетическая энергия, так же как и скорость движения, зависит от выбора системы отсчета. Например, если скорость пассажира в движущемся вагоне относительно системы отсчета, связанной с вагоном, равна нулю, то и кинетическая энергия пассажира относительно этой системы отсчета равна нулю. Однако кинетическая энергия пассажира относительно системы отсчета, связанной с Землей, отлична от нуля.
Из теоремы о кинетической энергии видно, что единицей измерения кинетической энергии, как и работы, в СИ является джоуль
Так как скорость связана с импульсом, то и кинетическая энергия связана с импульсом:
Если масса тела известна, то его скорость и импульс можно выразить через кинетическую энергию:
Потенциальная энергияРабота силы тяжести и потенциальная энергия:
Предположим, что замкнутая система состоит из Земли и тела, поднятого на определенную высоту над ее поверхностью. Если тело свободно выпустить с этой высоты, то оно начинает движение под действием силы тяжести в направлении поверхности Земли. Сила тяжести, перемещая тело на до определенной высоты от поверхности Земли, совершает положительную работу (при совпадении направлений силы тяжести и перемещения (с):
Если тело свободно выпустить с этой высоты, то оно начинает движение под действием силы тяжести в направлении поверхности Земли. Сила тяжести, перемещая тело на до определенной высоты от поверхности Земли, совершает положительную работу (при совпадении направлений силы тяжести и перемещения (с):
Где модуль перемещения свободно падающего тела с высоты на высоту
Если тело брошено вертикально вверх с высоты то в момент достижения его высоты модуль перемещения будет равен (d). Так как в этом случае
угол между направлением силы тяжести и вектором перемещения равен a то сила тяжести совершит отрицательную работу:
Выражение (3.19) схоже с выражением (3.18), то есть тело, брошенное вертикально вверх, и свободно падающее тело совершают под действием силы тяжести одинаковую работу.
- Работа силы тяжести не зависит от формы траектории движения тела, она зависит от начального и конечного положения центра тяжести тела.

- Силы, под действием которых совершается работа, не зависящая от траектории движения тела, называются консервативными силами. Это значит, что сила тяжести является консервативной силой.
Формулу (3.18) можно записать и так:
или
Это означает, что работа, совершаемая силой тяжести, равна изменению величины взятой с противоположным знаком. Эта величина является энергией взаимодействия тела, находящегося на высоте над поверхностью Земли, с самой Землей.
Энергия, которой обладают взаимодействующие тела (или частицы), называется потенциальной энергией:
Приняв во внимание выражение (3.21) в выражении (3.20), получаем выражение, которое называется теоремой о потенциальной энергии:
Работа, совершаемая силой тяжести, равна изменению потенциальной энергии, взятому с противоположным знаком:
Из теоремы о потенциальной энергии видно, что единицей измерения потенциальной энергии, так же, как и работы, в СИ является джоуль
Потенциальная энергия тела, на которое действует сила тяжести, зависит от выбора нулевого уровня. За нулевой уровень можно принять уровень моря, поверхность стола, пол комнаты и другие. Потенциальная энергия тела, находящегося на какой-либо высоте относительно этих уровней, будет иметь разные значения. Однако разность потенциальных энергий двух, соответственно, разных положений тела не зависит от выбора нулевого положения, и она измеряется работой, совершенной силой тяжести. Из этого получаем физический смысл потенциальной энергии: Потенциальная энергия тела на высоте равна работе, совершаемой силой тяжести в случае падения данного тела с этой высоты на нулевой уровень.
За нулевой уровень можно принять уровень моря, поверхность стола, пол комнаты и другие. Потенциальная энергия тела, находящегося на какой-либо высоте относительно этих уровней, будет иметь разные значения. Однако разность потенциальных энергий двух, соответственно, разных положений тела не зависит от выбора нулевого положения, и она измеряется работой, совершенной силой тяжести. Из этого получаем физический смысл потенциальной энергии: Потенциальная энергия тела на высоте равна работе, совершаемой силой тяжести в случае падения данного тела с этой высоты на нулевой уровень.
В зависимости от выбора нулевого уровня потенциальная энергия может быть, как положительной, так и отрицательной. Так, потенциальная энергия тела, помещенного на определенной высоте от нулевого уровня, положительна, а потенциальная энергия тела, помещенного на определенной глубине от нулевого уровня, отрицательна.
Работа силы упругости и потенциальная энергия:
Еще одной консервативной силой является сила упругости. Поэтому работа, совершенная силой упругости, также должна быть равна изменению потенциальной энергии тела. Исследуем это: прикрепим один конец пружины к опоре, другой же конец прикрепим к телу (шарику), способному двигаться по гладкому стержню. Сдвинув шарик вправо, растянем пружину на Модуль силы упругости, возникшей в пружине, равен Под действием этой силы свободно отпущенный шарик движется влево, например, из положения 1 в положение 2 (е).
Поэтому работа, совершенная силой упругости, также должна быть равна изменению потенциальной энергии тела. Исследуем это: прикрепим один конец пружины к опоре, другой же конец прикрепим к телу (шарику), способному двигаться по гладкому стержню. Сдвинув шарик вправо, растянем пружину на Модуль силы упругости, возникшей в пружине, равен Под действием этой силы свободно отпущенный шарик движется влево, например, из положения 1 в положение 2 (е).
Так как в этом положении деформация пружины равна то модуль перемещения шарика равен разности растяжений пружины: Так как направление перемещения совпадает с направлением действия силы упругости, то работа, совершенная этой силой, положительна, однако должно быть принято во внимание, что модуль силы упругости не постоянен: он изменяется от значения до значения На этом участке среднее значение модуля силы упругости равно среднеарифметическому значению его начального и конечного значений:
Таким образом, упруго деформированная пружина совершает положительную работу:
или
Эту формулу можно записать и так:
Как видно, работа, совершенная силой упругости, зависит от начальной и конечной деформации пружины.
Из сравнения формул (3.20) и (3.23) видно, что работа силы упругости также равна изменению некоторой величины, в этом случае которая тоже является энергией взаимодействия:
Потенциальная энергия упругодеформированного тела равна половине произведения ее жесткости на квадрат растяжения (или сжатия):
Полная механическая энергия и закон сохранения энергииПолная механическая энергия:
Система тел одновременно может обладать как кинетической, так и потенциальной энергией. Например, самолет, летящий на некоторой высоте с определенной скоростью, обладает наряду с кинетической энергией, также и потенциальной энергией вследствие взаимодействия с Землей.
Сумму кинетической и потенциальной энергий системы тел называют полной механической энергией:
Закон сохранения полной механической энергии:
Вы уже знаете, что работа силы тяжести и упругости, являющихся консервативными силами, равна изменению потенциальной энергии системы, взятому с противоположным знаком. С другой стороны, эта работа также равна изменению кинетической энергии системы:
С другой стороны, эта работа также равна изменению кинетической энергии системы:
Таким образом, получается, что:
Сгруппировав соответствующие величины, это выражение можно записать в следующим виде:
Полученное равенство является выражением закона сохранения полной механической энергии.
Полная механическая энергия замкнутой системы тел, взаимодействующих друг с другом консервативными силами, остается неизменной.
Закон сохранения полной механической энергии является результатом однородности времени.
Однородность времени – это симметрия относительно переноса во времени: физические свойства замкнутой системы не зависят от выбора начального момента времени, то есть все моменты времени эквивалентны (равноправны).
Согласно закону сохранения полной механической энергии, увеличение потенциальной энергии системы сопровождается соответствующим уменьшением ее кинетической энергии, и наоборот. Превращение потенциальной энергии в кинетическую или кинетической в потенциальную, т.е. сохранение полной механической энергии является одним из самых важных законов в природе.
Превращение потенциальной энергии в кинетическую или кинетической в потенциальную, т.е. сохранение полной механической энергии является одним из самых важных законов в природе.
Частные случаи:
1. Полная механическая энергия для тела, движущегося под действием силы тяжести:
Где – высота над нулевым уровнем, на котором находится тело в данный момент времени, — скорость его движения. Значение полной механической энергии, оставаясь постоянным, зависит от данных условий. Например:
a) если тело было брошено с нулевого уровня вверх с начальной скоростью то его полная механическая энергия будет равна:
В этом случае, закон сохранения полная механическая энергии в произвольной точке траектории движения записывается так (с):
b) если тело, брошенное вертикально вверх, поднимется на максимальную высоту то его полная механическая энергия будет:
В этом случае закон сохранения полной механической энергии тела, брошенного вертикально вверх, в произвольной точке траектории движения записывается так (d):
2. Если оттянуть и отпустить шарик массой закрепленный к одному из концов невесомой пружины жесткостью и способный двигаться вдоль гладкого стержня (другой конец пружины закреплен к неподвижной опоре), то выражение полной механической энергии колебательного движения системы “шарик-пружина” будет следующим (е):
Если оттянуть и отпустить шарик массой закрепленный к одному из концов невесомой пружины жесткостью и способный двигаться вдоль гладкого стержня (другой конец пружины закреплен к неподвижной опоре), то выражение полной механической энергии колебательного движения системы “шарик-пружина” будет следующим (е):
Известно, что полная механическая энергия свободно падающего тела во всех точках траектории одинакова.
- — Что происходит при падении тела и его остановке на поверхности Земли?
- — Можно ли в этом случае сказать, что “как кинетическая, так и потенциальная энергия тела равны нулю, то есть механическая энергия исчезает и нарушается закон сохранения энергии “?
Механическая энергия тел, составляющих замкнутую систему, не исчезает! Механическая энергия превращается в другой вид энергии – внутреннюю энергию системы: в результате соударения тела с поверхностью Земли система нагревается и ее внутренняя энергия увеличивается.
Можно привести примеры превращения энергии также и в других замкнутых системах. Например, в системе автомобиль-шоссе при торможении движущего автомобиля его кинетическая энергия в результате трения превращается во внутреннюю энергию нагретых покрышек.
Таким образом, говоря о законе сохранения полной энергии, подразумевается сохранение всех видов энергии (механической, внутренней, электромагнитной и другие), превращающихся друг в друга, в замкнутой системе:
Энергия не исчезает и не возникает из ничего, она превращается из одного вида в другой.
гл. 7 Введение в работу, энергию и энергетические ресурсы – College Physics
Энергия играет важную роль как в повседневных событиях, так и в научных явлениях. Вы, без сомнения, можете назвать многие формы энергии, от той, что доставляется нам в пищу, до энергии, которую мы используем для работы наших автомобилей, до солнечного света, который согревает нас на пляже. Вы также можете привести примеры того, что люди называют энергией, которые могут быть ненаучными, например, кто-то с энергичной личностью. Мало того, что энергия имеет много интересных форм, она участвует почти во всех явлениях и является одним из важнейших понятий физики.Что делает его еще более важным, так это то, что общее количество энергии во Вселенной постоянно. Энергия может менять форму, но она не может появиться из ничего или исчезнуть бесследно. Таким образом, энергия является одной из немногих физических величин, которые, как мы говорим, сохраняются .
Мало того, что энергия имеет много интересных форм, она участвует почти во всех явлениях и является одним из важнейших понятий физики.Что делает его еще более важным, так это то, что общее количество энергии во Вселенной постоянно. Энергия может менять форму, но она не может появиться из ничего или исчезнуть бесследно. Таким образом, энергия является одной из немногих физических величин, которые, как мы говорим, сохраняются .
Сохранение энергии (как физики любят называть принцип, согласно которому энергия не может быть ни создана, ни уничтожена) основано на эксперименте. Даже когда ученые открывали новые формы энергии, принцип сохранения энергии всегда находил применение.Возможно, наиболее ярким примером этого является Эйнштейн, когда он предположил, что масса эквивалентна энергии (его знаменитое уравнение E = mc2E = mc2 size 12 {E = “mc” {rSup} {size 8 {2}}} {} ).
С социальной точки зрения энергия является одним из основных строительных блоков современной цивилизации.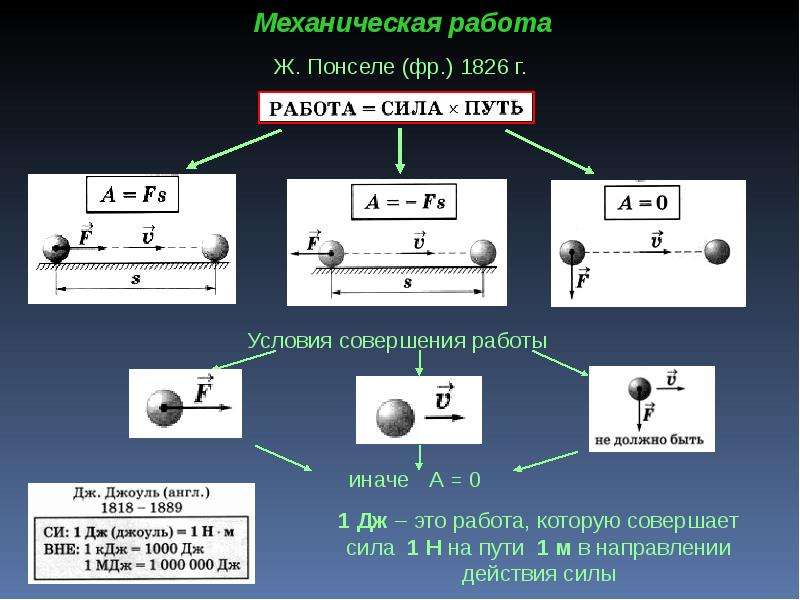 Энергетические ресурсы являются ключевыми ограничивающими факторами экономического роста. Мировое использование энергетических ресурсов, особенно нефти, продолжает расти, что имеет зловещие последствия в экономическом, социальном, политическом и экологическом плане.В конце этой главы мы кратко рассмотрим модели использования энергии в мире.
Энергетические ресурсы являются ключевыми ограничивающими факторами экономического роста. Мировое использование энергетических ресурсов, особенно нефти, продолжает расти, что имеет зловещие последствия в экономическом, социальном, политическом и экологическом плане.В конце этой главы мы кратко рассмотрим модели использования энергии в мире.
Нет простого, но точного научного определения энергии. Энергия характеризуется множеством форм и тем фактом, что она сохраняется. Мы можем в общих чертах определить энергию как способность выполнять работу, допуская, что в некоторых обстоятельствах не вся энергия доступна для выполнения работы. Поскольку энергия связана с работой, мы начинаем главу с обсуждения работы. Работа тесно связана с энергией и тем, как энергия переходит из одной системы в другую или меняет форму.
|
|
Работа – Работа и энергия – WJEC – GCSE Physics (Single Science) Revision – WJEC
Расчет выполненной работы
Вот уравнение, которое относится к выполненной работе, приложенной силе и пройденному расстоянию в направлении силы.
\ [\ text {Work done} = {\ text {Force}} \ times {\ text {Distance}} \]
\ [\ text {W} = {\ text {F}} \ times {\ текст {d}} \]
где
W измеряется в джоулях, J
F измеряется в ньютонах, N
d измеряется в метрах, м
В приведенном выше примере, Применяется 10 Н для перемещения коробки на 2 м.
Работа выполнена = 10 × 2 = 20 Дж
Треугольник выше поможет вам изменить формулу.
Проделанная работа имеет те же единицы, что и энергия – джоули. Это потому, что энергия – это способность выполнять работу. У вас должна быть энергия, чтобы делать работу. Однако вам не нужно выполнять работу, если у вас есть энергия – потенциальная энергия не работает. В частности, в приведенном выше примере человек не мог толкать ящик (и работать) без энергии. Выполненная работа равна переданной энергии, т.е. работа = переданная энергия.
Объект может обладать энергией в результате:
- положения (потенциальная энергия)
- движения (кинетическая энергия)
- деформации (упругой энергии)
Работа, энергия и мощность – AP Physics B
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Работа, Энергия и Мощность – Значение, Определение, Различия и Часто задаваемые вопросы
Работа Энергия и Мощность – это наиболее важные термины, используемые в физике, которые учащиеся изучают в школе на раннем этапе.Работа и энергия – две стороны медали, поскольку они взаимосвязаны друг с другом. Работа называется смещением объекта при приложении к нему силы (толкания или тяги), а энергия – как способность выполнять работу. Он существует в различных формах, таких как потенциальная, кинетическая, химическая, тепловая, ядерная, электрическая энергия и так далее. Мощность – это работа, выполняемая за единицу времени. Изучение мощности энергии работы важно как с точки зрения приобретения знаний, так и с точки зрения получения более высоких оценок на экзамене.
Физика Работа и энергия
Когда объект движется в направлении приложенной силы, работа считается выполненной. Но для того, чтобы работа была сделана, важнее всего энергия, поскольку это способность работать. Когда работа выполняется животными или людьми, они получают энергию из пищи, а когда работа выполняется машинами, они получают энергию из электричества или топлива.
Работа
Работа выполняется, когда сила вызывает какое-то движение. Например, когда человек поднимается на гору, работа выполняется, потому что, поднимаясь на гору, он движется против силы тяжести.Следовательно, работа зависит от двух факторов. Это:
Следовательно, работа измеряется произведением смещения и силы тела вместе с направлением силы. Она называется скалярной величиной, а единица работы в системе СИ – джоуль. Таким образом, уравнение выглядит следующим образом:
[Изображение будет загружено в ближайшее время]
Работа = F * S
Если тело смещается посредством S, в то время как на него действует Сила F, в таком случае
Работа W = FS Cos (угол между смещением и силой)
Здесь следует отметить одну вещь: сила считается действующей, когда она вызывает движение в объекте.Например, человек пытается сдвинуть стену, но стена не движется, следовательно, работа, выполняемая человеком, равна нулю, поскольку никакого смещения не происходит. Но он действительно теряет энергию, потому что при попытке толкнуть стену он растягивает мышцы и, таким образом, чувствует усталость.
Таким образом, это показывает, что работу не нужно выполнять всякий раз, когда к объекту прикладывается сила. Работа выполняется только тогда, когда приложенная сила может изменить направление объекта или сдвинуть его.
Энергия
Способность человека, позволяющая ему выполнять работу, называется энергией.Проще говоря, энергия – это способность работать. Он имеет скалярную величину и имеет только величину и не имеет направления. энергия не может быть ни создана, ни уничтожена, она может только изменить свою форму. Энергию можно найти во многих вещах, поэтому существует множество форм энергии. Наиболее важными видами энергии являются кинетическая энергия и потенциальная энергия.
Кинетическая энергия – это энергия тела, возникающая в результате его движения или движения. Это работа, которая требуется для ускорения тела данной массы, отличаясь от его скорости.Во время ускорения после того, как тело набирает энергию, оно сохраняет кинетическую энергию до тех пор, пока его скорость не изменится. Формула кинетической энергии – 1 / 2mv2
Следовательно, из приведенной выше формулы мы можем заявить:
1. Кинетическая энергия тела удваивается всякий раз, когда его масса удваивается.
2. Если масса тела уменьшается вдвое, кинетическая энергия также уменьшается вдвое.
3. Кинетическая энергия массы увеличивается в четыре раза, когда скорость удваивается.
Power Definition Physics
Рабочая мощность или просто мощность упоминается как физическое понятие, которое включает в себя несколько значений, в зависимости от контекста и доступных деталей.Мощность можно определить как скорость выполнения работы. Мощность – это энергия, потребляемая в единицу времени. Он присутствует в скалярном количестве, так как не имеет направления. Единица мощности в системе СИ – джоули в секунду и называется ватт. Ватт означает мощность, необходимую для выполнения одного Джоуля работы в секунду.
Разница между работой и мощностью
Различия между работой и мощностью указаны в следующей таблице:
Работа | Мощность |
Работа называется процесс энергии, который передается движению объекта за счет приложения силы.Обычно его представляют как произведение смещения и силы. | Мощность – это количество энергии, которое передается за единицу времени. |
Единица работы СИ – Джоуль (Дж) | Единица мощности СИ – Ватт (Вт) |
Формула для расчета силы: Работа = Сила * Смещение. | Формула расчета мощности: Мощность = Работа / Время |
Работа может быть выполнена в различных других единицах измерения, таких как кВтч, МВтч, ГВтч и вольт (эВ) | Энергия может быть измерена в единицах как ГВт, МВт и кВт. |
Работа не зависит от времени. | Мощность зависит от времени. |
Работа, энергия и энергия
РаботаРабота имеет особое определение в физике. Работа выполняется, когда к объекту прилагается сила, и объект перемещается из одного места в другое. Работа – это результат силы, действующей на определенном расстоянии. Это расстояние называется перемещением объекта. Если сила F и смещение d находятся в одном направлении, то работа W определяется формулой
W = Fd
Работа является произведением силы и смещения.В единицах СИ (международная система) единицей силы является Ньютон (Н), а единицей измерения расстояния или смещения является метр (м). Следовательно, единицу работы можно выразить как Ньютон-метр, Н ∙ м. Это также известно как Джоуль, J. Ньютон – составная единица, поэтому Джоуль также равен,
Уравнение W = Fd зависит от силы и смещения в одном направлении. Есть много ситуаций, в которых их направления различаются, например, когда человек толкает ящик близко к земле.Компонент силы, которую прикладывает человек, направлен вниз, несмотря на то, что результирующее направление коробки – вперед. В таком случае только составляющая силы, действующая на пути перемещения коробки, вносит свой вклад в проделанную работу. Если рассматривать силу и смещение как векторы, работу можно найти с помощью скалярного произведения (также известного как скалярное произведение). Работа равна,
В этой формуле θ – это угол между векторами силы и смещения, а F и d – величины векторов.
Энергия
Кинетическая энергия (K) объекта равна количеству работы, которая требуется для ускорения объекта от состояния покоя до определенной скорости v. Это соотношение между кинетической энергией и работой называется работой. -энергетическая теорема. Кинетическая энергия объекта – это скалярная величина, то есть она не зависит от направления, в котором движется объект. Значение кинетической энергии всегда положительно или равно нулю. Единица кинетической энергии такая же, как и единица работы, Джоуль (Дж).
Кинетическая энергия объекта может быть связана с его массой и скоростью с помощью формулы:
Эту формулу для кинетической энергии можно найти из уравнения для работы, если сила направлена в том же направлении, что и смещение объекта. . Эта формула зависит от кинематической формулы:
Изменение положения (x – x 0 ) равно величине смещения d. Формулу можно переставить так, чтобы выделить ускорение, a,
Сила равна массе объекта, умноженной на его ускорение, поэтому сила равна
F = ma
Эта формула силы может подставляется в формулу для работы,
W = Fd
Следовательно, работа, совершаемая силой над объектом, равна изменению кинетической энергии объекта,
W = K 2 – K 1
W = ΔK
В этой формуле греческая заглавная буква Δ («дельта») используется для обозначения «изменения в».
Работа может использоваться для понимания энергии многих объектов, испытывающих силы. Одним из примеров является работа, необходимая для растяжения пружины. Если величина смещения объекта обозначена x, и это представляет смещение от положения равновесия x = 0, то сила, необходимая для прижатия объекта к пружине в положение x, составляет
F = kx
Константа k в этом уравнении – это жесткость пружины, которая различна для каждой пружины.

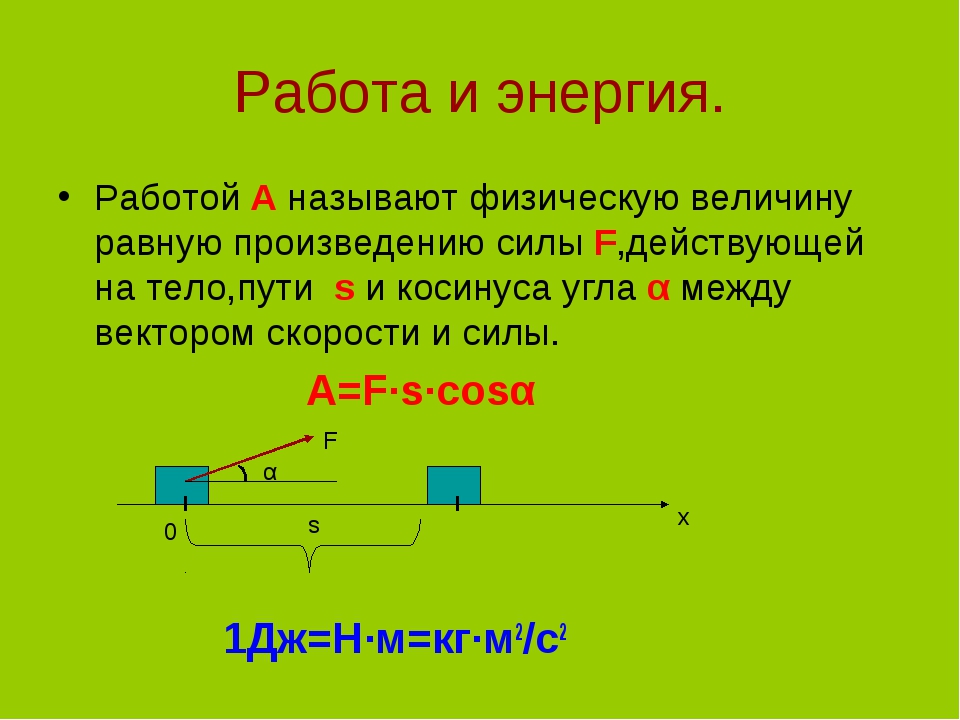



 е.
пока вся его кинетическая энергия не перейдёт в
потенциальную энергию упругой деформации. Затем под
действием сил упругости деформированной плиты шарик
приобретает скорость, направленную вверх: энергия
упругой деформации плиты и шарика превращается в
кинетическую энергию шарика. При дальнейшем движении
вверх скорость шарика под действием силы тяжести
уменьшается, и кинетическая энергия превращается в
потенциальную энергию тяготения. В наивысшей точке
шарик обладает снова только потенциальной энергией тяготения.
е.
пока вся его кинетическая энергия не перейдёт в
потенциальную энергию упругой деформации. Затем под
действием сил упругости деформированной плиты шарик
приобретает скорость, направленную вверх: энергия
упругой деформации плиты и шарика превращается в
кинетическую энергию шарика. При дальнейшем движении
вверх скорость шарика под действием силы тяжести
уменьшается, и кинетическая энергия превращается в
потенциальную энергию тяготения. В наивысшей точке
шарик обладает снова только потенциальной энергией тяготения.

 д.), создавая в
ней некоторую потенциальную энергию деформации, и
лишь остаток работы передавался на другой конец
машины. В сумме же переданная работа вместе с энергией
деформации оказывается равной затраченной работе.
В случае абсолютной жесткости рычага, нерастяжимости
веревки и т. д. простая машина не может накопить в
себе энергию, и вся работа, произведенная на одном ее
конце, полностью передается на другой конец.
д.), создавая в
ней некоторую потенциальную энергию деформации, и
лишь остаток работы передавался на другой конец
машины. В сумме же переданная работа вместе с энергией
деформации оказывается равной затраченной работе.
В случае абсолютной жесткости рычага, нерастяжимости
веревки и т. д. простая машина не может накопить в
себе энергию, и вся работа, произведенная на одном ее
конце, полностью передается на другой конец.
 Вообще, при наличии трения закон
сохранения механической энергии всегда нарушается и
полная энергия тел уменьшается. За счет этой убыли
энергии и совершается работа против сил трения. Например,
при падении тела с большой высоты скорость, вследствие
действия возрастающих сил сопротивления среды, вскоре
становится постоянной; кинетическая энергия тела
перестает меняться, но его потенциальная энергия
уменьшается.
Вообще, при наличии трения закон
сохранения механической энергии всегда нарушается и
полная энергия тел уменьшается. За счет этой убыли
энергии и совершается работа против сил трения. Например,
при падении тела с большой высоты скорость, вследствие
действия возрастающих сил сопротивления среды, вскоре
становится постоянной; кинетическая энергия тела
перестает меняться, но его потенциальная энергия
уменьшается.
 е. ее кинетическая энергия, приращение кинетической
энергии воды, наблюдающееся при этом, меньше, чем убыль
кинетической энергии лодки.
е. ее кинетическая энергия, приращение кинетической
энергии воды, наблюдающееся при этом, меньше, чем убыль
кинетической энергии лодки.

 Например, при торможении поезда тормозные колодки
сильно нагреваются. При спуске корабля со стапелей на
воду для уменьшения трения стапеля обильно смазываются,
и все же нагревание так велико, что смазка дымится, а
иногда даже загорается.
Например, при торможении поезда тормозные колодки
сильно нагреваются. При спуске корабля со стапелей на
воду для уменьшения трения стапеля обильно смазываются,
и все же нагревание так велико, что смазка дымится, а
иногда даже загорается.
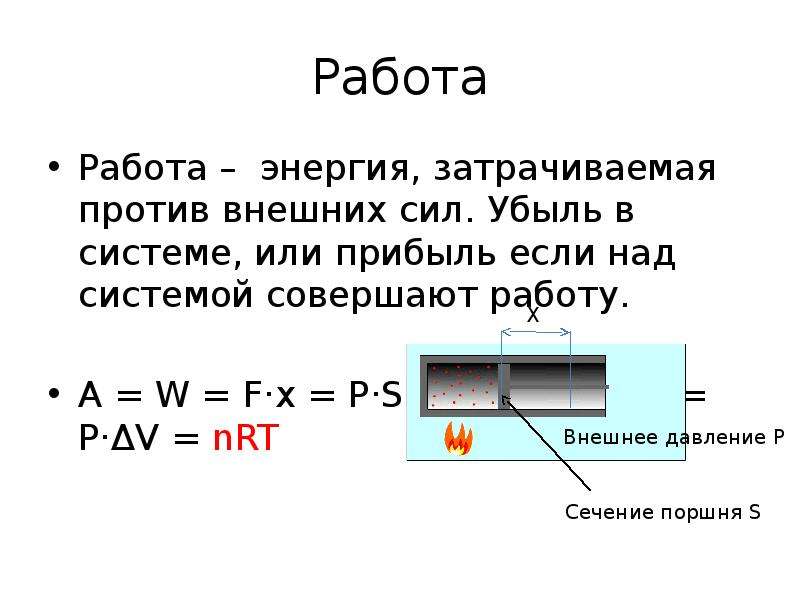
 Внутренняя энергия
тела зависит от его температуры, от того, является
ли тело твердым, жидким или газообразным, как велика
его поверхность, является ли оно сплошным или мелко
раздробленным и т. д. В частности, чем температура
тела выше, тем больше его внутренняя энергия.
Таким образом, хотя при движениях, связанных с
преодолением сил трения, механическая энергия систем
движущихся тел уменьшается, но зато возрастает их
внутренняя энергия. Например, при торможении поезда
уменьшение его кинетической энергии сопровождается
увеличением внутренней энергии тормозных колодок,
бандаж колес, рельсов, окружающего воздуха и
т. д. в результат нагревания этих тел.
Все сказанное относится также и к тем случаям,
когда силы трения возникают внутри тела, например,
при разминании куска воска, при неупругом ударе
свинцовых шаров, при перегибании куска проволоки.
Внутренняя энергия
тела зависит от его температуры, от того, является
ли тело твердым, жидким или газообразным, как велика
его поверхность, является ли оно сплошным или мелко
раздробленным и т. д. В частности, чем температура
тела выше, тем больше его внутренняя энергия.
Таким образом, хотя при движениях, связанных с
преодолением сил трения, механическая энергия систем
движущихся тел уменьшается, но зато возрастает их
внутренняя энергия. Например, при торможении поезда
уменьшение его кинетической энергии сопровождается
увеличением внутренней энергии тормозных колодок,
бандаж колес, рельсов, окружающего воздуха и
т. д. в результат нагревания этих тел.
Все сказанное относится также и к тем случаям,
когда силы трения возникают внутри тела, например,
при разминании куска воска, при неупругом ударе
свинцовых шаров, при перегибании куска проволоки.

 Для всех видов энергии оказалось, что возможен
переход энергии из одного вида в другой,
переход энергии от одного тела к другому, но
что при всех таких переходах общая энергия всех
видов остаётся все время строго постоянной. В
этом заключается всеобщность закона сохранения энергии.
Для всех видов энергии оказалось, что возможен
переход энергии из одного вида в другой,
переход энергии от одного тела к другому, но
что при всех таких переходах общая энергия всех
видов остаётся все время строго постоянной. В
этом заключается всеобщность закона сохранения энергии.
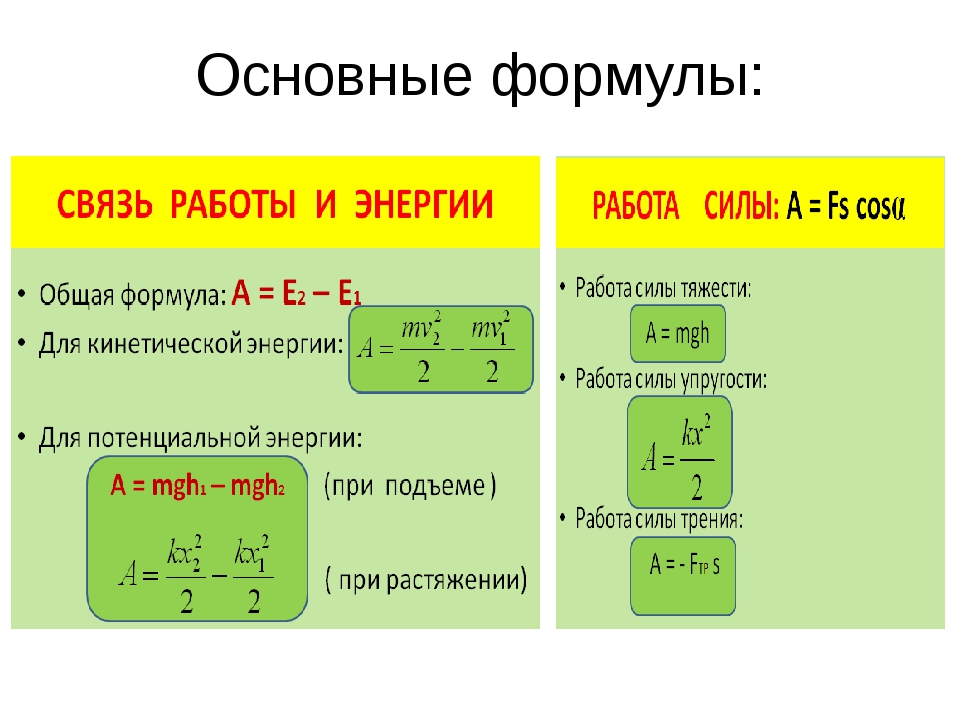
 Само это утверждение весьма и весьма отвлечено. Это по существу математический принцип, утверждающий, что существует некоторая численная величина, которая не изменяется ни при каких обстоятельствах. Это отнюдь не описание механизма явления или чего-то конкретного, просто-напросто отмечается то странное обстоятельство, что можно подсчитать какое-то число и затем спокойно следить, как природа будет выкидывать любые свои трюки, а потом опять подсчитать это число — и оно останется прежним.
Само это утверждение весьма и весьма отвлечено. Это по существу математический принцип, утверждающий, что существует некоторая численная величина, которая не изменяется ни при каких обстоятельствах. Это отнюдь не описание механизма явления или чего-то конкретного, просто-напросто отмечается то странное обстоятельство, что можно подсчитать какое-то число и затем спокойно следить, как природа будет выкидывать любые свои трюки, а потом опять подсчитать это число — и оно останется прежним. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number, and when we finish watching nature go through her tricks and calculate the number again, it is the same.
It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number, and when we finish watching nature go through her tricks and calculate the number again, it is the same. — BAAS Rep, 1881. С. 513
— BAAS Rep, 1881. С. 513 Это значит, что теорема о кинетической энергии справедлива для любых сил (сила тяжести, сила трения, сила упругости или их равнодействующая сила), действующих на тело.
Это значит, что теорема о кинетической энергии справедлива для любых сил (сила тяжести, сила трения, сила упругости или их равнодействующая сила), действующих на тело.
 Работа с объектом не выполняется, если объект не перемещается из-за действия силы. Само по себе применение силы не является работой. Когда сила, действующая на объект, и смещение объекта действуют в разных направлениях, работает только тот компонент силы, который направлен в направлении смещения объекта.Компоненты силы, перпендикулярной смещению, не работают. Если прилагаемая сила горизонтальна, все усилие перемещает объект. Если сила отличается от горизонтальной, только горизонтальная составляющая приложенной силы вызывает смещение и работает. Если в объекте действует много постоянных сил, мы можем найти чистую работу, проделанную первым, найдя чистую силу. Произведение имеет размерность силы, умноженной на длину. В системе СИ работа измеряется единицей измерения ньютон на метр или джоуль.
Работа с объектом не выполняется, если объект не перемещается из-за действия силы. Само по себе применение силы не является работой. Когда сила, действующая на объект, и смещение объекта действуют в разных направлениях, работает только тот компонент силы, который направлен в направлении смещения объекта.Компоненты силы, перпендикулярной смещению, не работают. Если прилагаемая сила горизонтальна, все усилие перемещает объект. Если сила отличается от горизонтальной, только горизонтальная составляющая приложенной силы вызывает смещение и работает. Если в объекте действует много постоянных сил, мы можем найти чистую работу, проделанную первым, найдя чистую силу. Произведение имеет размерность силы, умноженной на длину. В системе СИ работа измеряется единицей измерения ньютон на метр или джоуль.  Если работа, выполняемая над объектом, приводит только к изменению скорости объекта, знак сети на объекте сообщает вам, увеличивается или уменьшается id скорости объекта. Если чистая работа положительна, скорость объекта увеличивается, и чистая сила действует на объект. Если результирующая сила отрицательна, скорость объекта уменьшается, и объект выполняет работу над другим объектом. Энергия:
Если работа, выполняемая над объектом, приводит только к изменению скорости объекта, знак сети на объекте сообщает вам, увеличивается или уменьшается id скорости объекта. Если чистая работа положительна, скорость объекта увеличивается, и чистая сила действует на объект. Если результирующая сила отрицательна, скорость объекта уменьшается, и объект выполняет работу над другим объектом. Энергия:  Скорость объекта уменьшается, если сетка отрицательна, потому что конечная кинетическая энергия меньше начальной кинетической энергии. Теорема позволяет нам подумать, является ли кинетическая энергия работой, которую объект может выполнять в состоянии покоя, или количеством энергии, хранящейся в объекте. Движущийся объект обладает кинетической энергией.
Скорость объекта уменьшается, если сетка отрицательна, потому что конечная кинетическая энергия меньше начальной кинетической энергии. Теорема позволяет нам подумать, является ли кинетическая энергия работой, которую объект может выполнять в состоянии покоя, или количеством энергии, хранящейся в объекте. Движущийся объект обладает кинетической энергией. Это результат положения объекта, поэтому его необходимо измерять относительно некоторого нулевого уровня.Нулевой уровень – это вертикальная координата, при которой гравитационная потенциальная энергия определяется равной нулю.
Это результат положения объекта, поэтому его необходимо измерять относительно некоторого нулевого уровня.Нулевой уровень – это вертикальная координата, при которой гравитационная потенциальная энергия определяется равной нулю.  Это не означает, что количество не может измениться с течением времени, но если мы рассмотрим все формы, которые может принимать количество, мы обнаружим, что у нас всегда одно и то же количество.Масса – привычная законсервированная величина.
Это не означает, что количество не может измениться с течением времени, но если мы рассмотрим все формы, которые может принимать количество, мы обнаружим, что у нас всегда одно и то же количество.Масса – привычная законсервированная величина. Хотя количество механической энергии постоянно, сама механическая энергия может изменять форму. Математическое выражение для сохранения механической энергии зависит от форм потенциальной энергии в данной задаче.Если присутствуют другие силы, кроме трения, мы должны просто добавить соответствующие члены потенциальной энергии, связанные с каждой силой. В ситуациях, когда присутствуют силы трения, принцип сохранения механической энергии больше не действует, потому что кинетическая энергия не просто преобразуется в форму потенциальной энергии.
Хотя количество механической энергии постоянно, сама механическая энергия может изменять форму. Математическое выражение для сохранения механической энергии зависит от форм потенциальной энергии в данной задаче.Если присутствуют другие силы, кроме трения, мы должны просто добавить соответствующие члены потенциальной энергии, связанные с каждой силой. В ситуациях, когда присутствуют силы трения, принцип сохранения механической энергии больше не действует, потому что кинетическая энергия не просто преобразуется в форму потенциальной энергии.  Механическая энергия преобразуется в формы энергии, которые гораздо труднее учесть, и считается, что механическая энергия теряется.
Механическая энергия преобразуется в формы энергии, которые гораздо труднее учесть, и считается, что механическая энергия теряется. Поскольку работа является скалярной величиной, вы можете
используйте знак + для работы, когда энергия системы увеличивается
а – знак на работу, когда энергия системы
уменьшается.
Поскольку работа является скалярной величиной, вы можете
используйте знак + для работы, когда энергия системы увеличивается
а – знак на работу, когда энергия системы
уменьшается. 3b выше:
3b выше:
 Ноль
точка гравитационной потенциальной энергии для двух точек
частицы есть бесконечность.
Ноль
точка гравитационной потенциальной энергии для двух точек
частицы есть бесконечность. 4а, площадь под графиком a в зависимости от t,
изменение скорости = 3,0 м / с 2 (4,0
с) = 12 м / с. Работа, выполняемая за счет чистой силы = изменение кинетики
энергия = 1/2 мВ f 2 – 1/2 мв o 2
4а, площадь под графиком a в зависимости от t,
изменение скорости = 3,0 м / с 2 (4,0
с) = 12 м / с. Работа, выполняемая за счет чистой силы = изменение кинетики
энергия = 1/2 мВ f 2 – 1/2 мв o 2  0 кг) (5 м / с) 2 -1/2 (5,0 кг) (0) 2
0 кг) (5 м / с) 2 -1/2 (5,0 кг) (0) 2  Брать
начальная точка i на вершине склона и
конечная точка f в нижней части склона. Позволять
U f = 0. В начальной точке потенциал
энергия равна mgh, где h – вертикальная высота выше нижней части склона. Объект, являющийся
освобожден от вершины склона означает, что его
начальная скорость v i равна нулю, так что K i = 1/2 мВ i 2 = 0.Из консервации
энергии, U i + K i = U f + K f
Брать
начальная точка i на вершине склона и
конечная точка f в нижней части склона. Позволять
U f = 0. В начальной точке потенциал
энергия равна mgh, где h – вертикальная высота выше нижней части склона. Объект, являющийся
освобожден от вершины склона означает, что его
начальная скорость v i равна нулю, так что K i = 1/2 мВ i 2 = 0.Из консервации
энергии, U i + K i = U f + K f 