Работа магнитного поля не совершается: «Магнитное поле не может совершать работу. Значит, оно не обладает энергией?» — Яндекс Кью

«Магнитное поле не может совершать работу. Значит, оно не обладает энергией?» — Яндекс Кью

Популярное

Сообщества

ФизикаМагнитное поле

Юрий Алымов

9 октября 2021  ·

6,7 K

Ответить1Уточнить

Центр магнитно-резонансных исследований Спинус СПбГУ

66

Мы создаём ЯМР-приборы на заказ, производим ремонт, консультируем, проводим обучающие…  · 28 окт 2021  · magres.ru

Отвечает

Павел Куприянов

С чего вы взяли, что магнитное поле не совершает работу? А как же магнитики притягиваются и отталкиваются, как работают генераторы?

Это однородное магнитное поле не совершает работы, а мы окружены градиентами магнитных полей. В градиентном поле магнитики двигаются в сторону увеличения индукции поля…

1 эксперт согласен

Юрий Алымов

29 октября 2021

Павел Куприянов. Утверждения в вопросе принадлежат не мне. Просто они кочуют из учебника в учебник : магнитное… Читать дальше

Комментировать ответ…Комментировать…

asfarty ganama

35

свидетель настоящего  · 11 окт 2021

Совершать работу может сила, а не поле. Другое дело, что поле может действовать на материальные объекты с некоторой силой. Здесь скорее всего подразумевалась сила Лоренца, с которой магнитное поле действует на движущуюся заряженную частицу. Эта сила действительно не совершает работу, поскольку она в любой точке траектории частицы всегда ей (траектории) перпендикулярна… Читать далее

Комментировать ответ…Комментировать…

Алексей Сивохин

546

Физика, компьютеры, электроника, велосипед, политика, диванный философ, диванный. ..  · 2 дек 2021

Постоянное магнитное поле содержит в себе потенциальную энергию, которая высвобождается, когда магнитное поле исчезает. на этом основана работа радиодетали, называемой дросселем. Он может забирать энергию из электроцепи и запасать её в магнитном поле сердечника (если он есть) или в магнитном поле в окружающем пространстве(если сердечника нет), а потом отдавать эту… Читать далее

Алексей Сивохин

15 мая 2022

Понятие “энергия” очень часто не может быть сопоставлено с одним определённым физическим объектом. Энергией “распол… Читать дальше

Комментировать ответ…Комментировать…

борис калеганов

8

Данные обо мне есть на моей странице ВКонтакте. Калеганов Борис, возраст 75 лет.  · 26 окт 2021

Если рассмотреть магнитное притяжение или отталкивание параллельных проводников с электротоками, то там магнитное поле производит работу, перемещает проводники, а значит тратит энергию. Но тут намного сложнее с об\яснением этого феномена. Давно показано, что так называемое магнитное поле есть всего лишь релятивистское искажение электрического поля движущихся зарядов… Читать далее

Юрий Алымов

3 декабря 2021

Движущиеся заряды в проводниках настолько медленны, что релятивистские искажения электрического поля практически… Читать дальше

Комментировать ответ…Комментировать…

Набочинко Виктор Иванович

4

не имею, не состоял, не участвовал.  · 28 окт 2021

В науке будущего термины электрическое, магнитное и даже электромагнитное будут исключены из научного тезауруса как понятия искажающие физическую действительность. Та теоретическая база, которую за прошедшие столетия наработала наука, совершенно не годится для объяснения, так как она не учитывает присутствие мировой среды. Хотя это понятие и присутствует под маской. .. Читать далее

Комментировать ответ…Комментировать…

Вы знаете ответ на этот вопрос?

Поделитесь своим опытом и знаниями

Войти и ответить на вопрос

Электричество и магнетизм

Познакомимся с опытами, которые проводил Фарадей (рис. 8.3, 8.4).

 

Рис. 8.3. Опыты Фарадея 

 

Рис. 8.4. Опыты Фарадея 

Для более близкого знакомства с явлением электромагнитной индукции, подробно рассмотрим два опыта (рис. 8.5).

Рис. 8.5. ЭДС индукции возникает в катушке, когда:
1 — к нейприближается постоянный магнит; 2 — когда меняется ток в соседней катушке

 

На левом рисунке изображена катушка, подсоединенная к гальванометру G. Если приближать к витку постоянный магнит, стрелка гальванометра отклонится: по катушке пройдет ток. При неподвижном же магните ничего не происходит.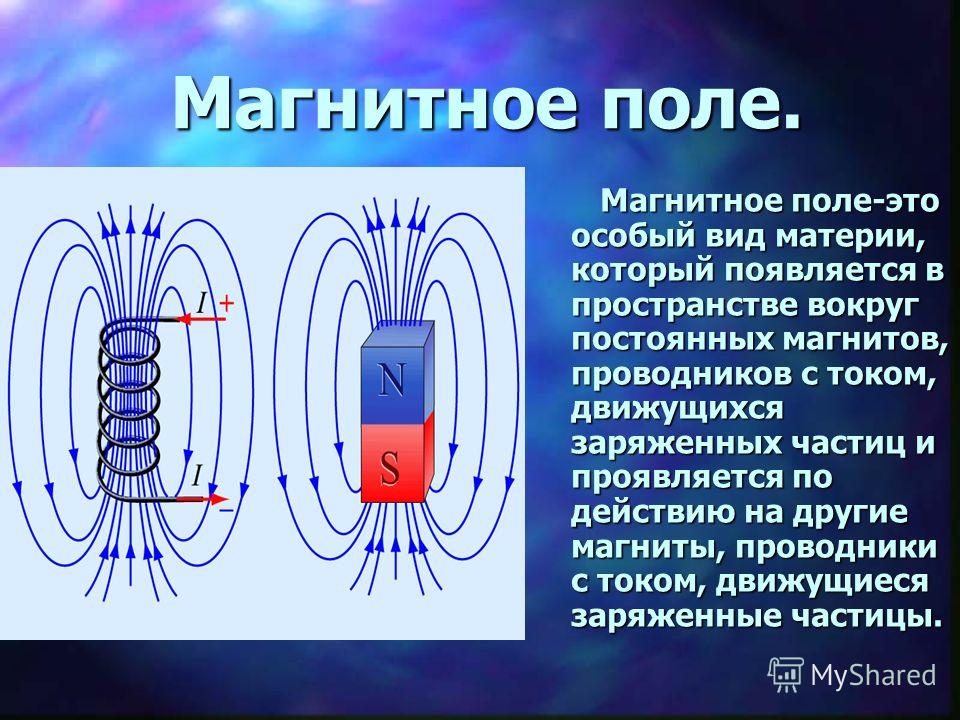 На правом рисунке вблизи такой же катушки с гальванометром помещена другая катушка. Если замкнуть ключ К, то по верхней катушке пойдет электрический ток. В этот момент стрелка гальванометра отклонится, зарегистрировав импульс тока в нижней катушке. То же самое произойдет при размыкании ключа К. 

Видео 8.2. Закон Фарадея: гибкий контур в магнитном поле катушек Гельмгольца.

В обоих случаях виток с гальванометром не был подсоединен к источнику тока. Тем не менее, ток в нем появился, что свидетельствует о возникновении какой-то электродвижущей силы. Ее называют ЭДС электромагнитной индукции. Рассмотренные опыты приводят к выводу, что ЭДС индукции возникает, когда что-то меняетсяв системе проводников. 

Обратимся к одному из возможных вариантов изменений в системе — перемещению одного из ее проводников. Поскольку на проводник с током действует сила, то при перемещении этого проводника будет совершаться работа. Рассмотрим устройство на рис.

8.6. 

 

Рис. 8.6. Работа по перемещению проводника с током в магнитном поле 

Видео 8.3. К рисунку 8.6: возникновение индукционного тока при движении небольшого участка замкнутого проводящего контура в магнитном поле.

Пусть отрезок проводника с током  длиной перемещается из положения 1 в положение 2 под действием силы Ампера в магнитном поле

(8.1)

Работа, совершаемая полем по перемещению проводника на расстояние , равна

(8.2)

Произведение  есть элемент площади, которую пересек отрезок проводника при своем движении из положения 1 в положение 2. Таким образом,

(8.3)

где — изменение потока вектора магнитной индукции через площадь, охватываемую током.

Согласно (8.3) работа, совершаемая магнитным полем при перемещении в нем подвижного проводника с током, равна произведению силы тока I  в проводнике и потока  сквозь поверхность, заметаемую проводником при его движении. 

Полученному результату можно дать несколько иную интерпретацию. Токи, текущие в проводнике, так или иначе замкнуты, образуют контур. Если перемещать или деформировать контур с током во внешнем магнитном поле, то полная работа определится суммированием (интегрированием) элементарных работ

(8.4)

где и — значения потока магнитной индукции в начальном и конечном состоянии контура с током (мы предполагали, что ток в контуре при этом не меняется).

Пример 1. По кольцу радиусом 10 см, сделанному из тонкого гибкого провода, течет ток 100 А. Перпендикулярно плоскости кольца создано внешнее однородное магнитное поле 0,1 Тл. Направление этого поля совпадает с направлением собственного магнитного поля кругового тока на его оси. Определить работу А внешних сил, которую надо затратить, чтобы превратить кольцо в квадрат, не меняя его ориентации относительно внешнего поля. Работой против упругих сил пренебречь. Ток в кольце поддерживается постоянным. Как изменится результат, если внешнее поле будет иметь противоположное направление?

Решение. 1-й способ. Площадь кольца равна , так что поток магнитной индукции через кольцо равен . При деформации кольца в квадрат его периметр не изменится, так что сторона квадрата в четыре раза меньше длины окружности кольца

Его площадь равна

а магнитный поток

Поэтому величина работыбудет равна

Подставляем численные значения и получаем

Работа получилась отрицательной, то есть ее надо совершить против сил поля. Действительно, при правовинтовом (по условию) расположении тока и внешнего поля сила Ампера стремится растянуть кольцо- увеличить его площадь. Превращая кольцо в квадрат, мы уменьшаем площадь, тем самым совершаем работу против сил поля.

Если поле имеет обратный знак, то эту работу совершит сила Ампера, и она будет положительной. При решении задачи в этом случаепотоквнешнего поля отрицателен (внешнее поле изменило своё направление на противоположное, а нормаль к поверхности, ограниченной контуром, осталась прежней, связанной правилом правого винта с направлением тока в контуре). Поэтому

и для работы  получится то же выражение, но с обратным знаком.

Решение. 2-й способ. Как известно, магнитный момент витка с током равен , а его потенциальная энергия в магнитном поле определяется выражением

При правовинтовом расположении тока и магнитного поля угол между векторами Р_m  и В  равен нулю, так что

Разность потенциальных энергий при деформации витка равна

Поскольку , потенциальная энергия при деформации увеличилась, на что надо затратить работу против сил поля. При изменении направления поля угол между ним и магнитным моментом равен  , так что

и

Естественно, мы получили те же результаты, что и при первом способе решения.

Пример 2. Круглый виток с током 20 А свободно установился в однородном магнитном поле с магнитной индукцией 0,016 Тл. Радиус витка равен 5 см. Определить работу, которую надо совершить, чтобы повернуть виток на углы , ,  относительно оси, совпадающей с диаметром витка.

Решение. Раз в начальном положении виток установился свободно, значит его магнитный момент параллелен вектору В. Поток через плоскость витка положителен и равен . При повороте витка на угол  поток станет равным . Совершаемая при этом работабудет равна 

Отсюда находим

При углах поворота  работа отрицательна: контур находится в состоянии устойчивого равновесия, и надо затратить усилия против сил поля, чтобы вывести его из равновесного состояния. Но при  контур уже сам стремится к положению равновесия, так что работа будет совершаться силами поля, и это частично компенсирует затраченную прежде работу. При полном обороте работа сил поля в точности равна работе внешних сил, так что полная работа оказывается равной нулю.

Этот пример также можно решить другим способом — в терминах потенциальной энергии взаимодействия магнитного момента с полем.

Отметим, что использовать для вычисления работы магнитный момент контура с током можно лишь в том случае, если внешнее поле однородно или слабо неоднородно. Последнее означает, что внешнее поле в пределах контура меняется настолько мало, что этим можно пренебречь. Если внешнее поле в пределах контура меняется существенно, то точный результат для работы может быть получен только путем интегрирования работы сила Ампера с учетом величины и направления внешнего поля в точке её приложения. Такой подход и приводит к точной формуле (8.4), полученной выше на примере системы простейшей геометрии, изображенной нa рис.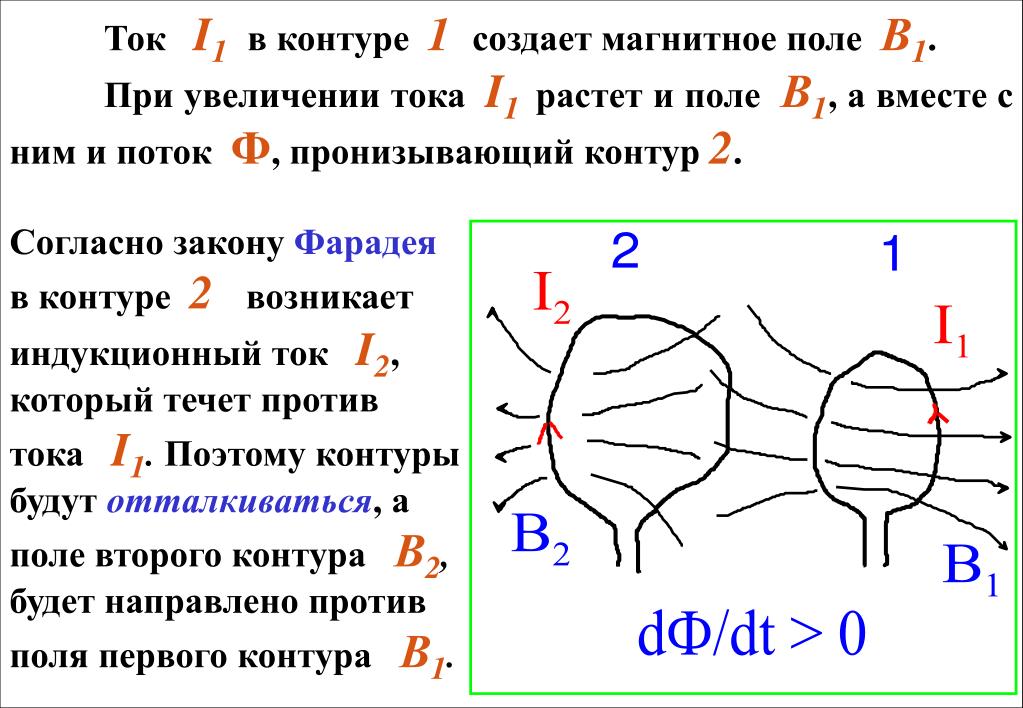 8.2. Таким образом, формула (8.4) точная и общая — для задачи любой геометрии.

 

Дополнительная информация

http://rack1.ul.cs.cmu.edu/is/faraday/  — опыты Фарадея;

http://www.juliantrubin.com/bigten/faradaycageexperiments.html — изобретения и открытия Фарадея.

электромагнетизм – Работа не совершается магнитным полем?

спросил 6 лет, 4 месяца назад

Изменено 1 год, 10 месяцев назад

Просмотрено 9к раз

$\begingroup$

Согласно моему учебнику:

Сила Лоренца F, действующая на заряженную частицу, движущуюся в электромагнитном поле, определяется по формуле:

$$F= qE + q(v\times B)$$

затем говорится, что «следует отметить, что работает только электрическая сила, в то время как магнитная сила не совершает никакой работы. просто отклоняющая сила».

Каким образом это, правда, не будет ли магнитная сила иметь значительную величину, будет ли она теперь сообщать заряду кинетическую энергию? Любые объяснения очень помогут. Пожалуйста, не усложняйте терминологию, спасибо.

• электромагнетизм
• магнитные поля
• электрические поля
• заряд
• работа

$\endgroup$

7

$\begingroup$

Работа выполняется со скоростью $\vec{F} \cdot \vec{v}$. Таким образом, любая составляющая силы, перпендикулярная скорости во все моменты времени , не может классически совершать никакой работы. Кинетическая энергия остается неизменной, потому что для кинетической энергии важна только величина скорости, а не ее направление. Все, что делает магнитная сила, — это изменяет направление скорости, сохраняя постоянную величину скорости, и для этого не требуется никакой работы.

$\endgroup$

7

$\begingroup$

Тот факт, что магнитные силы не действуют, не является следствием малости или большой величины магнитного поля или магнитной силы. Но это связано с направлением магнитной силы относительно направления скорости заряженной частицы.

Магнитное поле $\vec{B}$ действует на заряженную частицу с зарядом $q$ и скоростью $v$ с силой $\vec{F}$ по формуле

$\vec{F}=q(\vec{v}$x$\vec{B})$

Как следует из этой формулы, эта сила всегда будет перпендикулярна скорости частицы и, следовательно, мощность сообщается частице с помощью этой силы, $\vec{F}.\vec{v}$ $=0$, всегда. Таким образом, никакое количество энергии не передается посредством магнитных сил частице, и, таким образом, магнитные силы не изменяют скорость частиц.

$\endgroup$

$\begingroup$

Хотя это утверждение верно, следует подчеркнуть, что магнитная сила не совершает работы В ОТНОШЕНИИ МАГНИТНОГО ПОЛЯ. Если смотреть в другой системе отсчета (часто, когда поле движется относительно вас), это может сработать.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

электромагнетизм – Работа, совершаемая магнитной силой

спросил 5 лет, 9 месяцев назад

Изменено 5 лет, 9 месяцев назад

Просмотрено 1к раз

$\begingroup$

По закону силы Лоренца $F_m$ всегда перпендикулярна скорости заряда $v$. Но $F_m$ не обязательно перпендикулярно смещению заряда, вызванному $F_m$.

Тогда как мы можем говорить, что магнитная сила не работает?

Редактировать:

Необходимо прояснить один момент: совершена ли работа = перемещение непосредственно перед приложением силы с точками силы ИЛИ перемещение сразу после приложения силы с точками силы? Если бы первое было правдой, вы были бы правы. Но если бы последнее было правдой, я не вижу причин, по которым $F_m$ перпендикулярна смещению сразу после приложения силы, поскольку должна быть составляющая смещения в направлении действия силы.

• электромагнетизм
• силы
• магнитные поля
• электроны

$\endgroup$

0

$\begingroup$

Сила магнитного поля определяется магнитной частью уравнения силы Лоренца: $$\mathbf{F} = q \mathbf{v} \times \mathbf{B}. {t_f} \mathbf{F}\cdot \mathbf{v}\, \mathrm{d}t. \end{выравнивание}$$ Подынтегральная функция во второй строке — это один из способов записи мощности (скорости обмена энергией).

Дело в том, что поскольку магнитная сила всегда перпендикулярна скорости, подынтегральная функция всегда равна нулю, поэтому работа тоже равна нулю. Неважно, действует только магнитная сила или нет.

Магнитное поле может накапливать энергию, но эта энергия добавляется к нему и отнимается от него опосредованно через электрическое поле в соответствии с законом Фарадея.

Возьмите уравнение Фарадея-Максвелла и расставьте точки с обеих сторон $\mathbf{B}$: $$\mathbf{B}\cdot \left(\nabla \times \mathbf{E}\right) = – \mathbf{B}\cdot \frac{\partial \mathbf{B}}{\partial t}. $$ Правая часть равна $- \frac{1}{2} \frac{\partial}{\partial t} \left(\mathbf{B}\cdot \mathbf{B}\right) = -\mu_0 \frac{\partial}{\partial t} u_B $, где $u_B$ – плотность энергии в магнитном поле. Таким образом: $$\Delta u_B = -\frac{1}{\mu_0} \int_{t_0}^{t_f} \mathbf{B}\cdot \left(\nabla \times \mathbf{E}\right) \, \ матрм{д} т.