Научно-исследовательская работа “Матрица и её практическое применение” • Наука и образование ONLINE
Главная Работы на конкурс Предметное образование Физико-математические дисциплины Научно-исследовательская работа «Матрица и её практическое применение»
Автор: Рахмет Алеме Мейрамбековне
Место работы/учебы (аффилиация): Назарбаев Интеллектуальная школа химико-биологического направления города Павлодар, Казахстан, 9 класс
Научный руководитель: Сугралинова Бибигуль Алпысбаевна, учитель математики
Матрицы применяются в повседневной жизни и используются во всех отраслях деятельности. При решении различных практических задач в математике, биологии, физике, технике, химии, экономике, маркетинге, психологии и других областях науки используют матрицы. Матрицы внедрились в программные обеспечения, что является актуальным в современном мире.
Цель: Изучить матрицы, применение их в практических задачах, а также и в прикладных задачах, основанных на жизненных решениях проблем.
Задачи:
- изучение понятия матриц;
- определение видов матриц;
- вычисление определителей матриц;
- выполнение действий над матрицами;
- решение задач с применением матриц;
- использование задач из повседневной жизни.
Объект исследования: теория матриц, её применение
Гипотеза: зная свойства матриц и действия над ними, можно решать задачи широкого спектра, а применение её в различных сферах деятельности показывает и доказывает востребованность в познании мира матриц.
Работа состоит из трех частей. В теоретической части раскрыт вопрос о матрицах, видах матриц, действиях над ними и как проводятся вычисления определителей матриц. В практической части приведены решения семи авторских сложных задач на матрицы. В исследовательской части рассмотрены пять практических задач на матричные исчисления в экономике.
Загрузка…
4″>Проект «Перископ»Актуальность. В 2020 году мы отвечали 75 лет Победы в Великой Отечественной войне. По телевизору транслировалось много фильмов посвященных этому событию. Меня привлек момент, как военные наблюдали из окопов за вражескими танками, а из подводной лодк…
Посмотреть работу
Исследовательский проект «Модель гидравлического подъёмника»
Актуальность выбранной темы обусловлена широким применением гидравлических систем в различных областях нашей жизни, достоинством которых является получение больших усилий и мощностей при ограниченных размерах силовых исполнительных двигателей. Сегодн…
Посмотреть работу
Проект «Исследование температурно-влажностного режима в школьном музее»
Доступна к просмотру полнотекстовая версия работы
По всему миру расположены музеи, начиная от больших городов и маленьких деревень. Несмотря на то, что в большом (государственном), деревенском, школьном музеях по-разному расставлены приоритеты, тем ни менее, очевидно, что направления их деятельности…
Несмотря на то, что в большом (государственном), деревенском, школьном музеях по-разному расставлены приоритеты, тем ни менее, очевидно, что направления их деятельности…
Посмотреть работу
Проект «Сила трения — наш «друг» или «враг»?»
В повседневной жизни мы каждый день сталкиваемся с тем, об истинной природе чего практически ничего не знаем. Сила трения – одно из самых распространенных явлений на Земле, без нее не обходится ни одно движение. И, конечно, сила трения играет важную…
Посмотреть работу
Мероприятие завершено
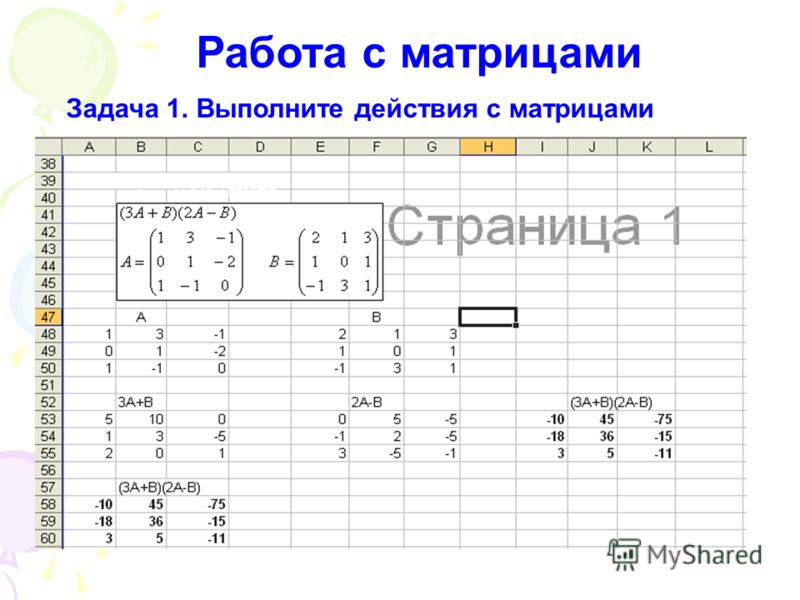
Работа с матрицами. Реферат, курсовая, диплом на компьютере
Работа с матрицами. Реферат, курсовая, диплом на компьютереВикиЧтение
Реферат, курсовая, диплом на компьютере
Баловсяк Надежда Васильевна
Содержание
Работа с матрицами
Для ввода матриц на панели инструментов редактора формул существует специальная палитра шаблонов.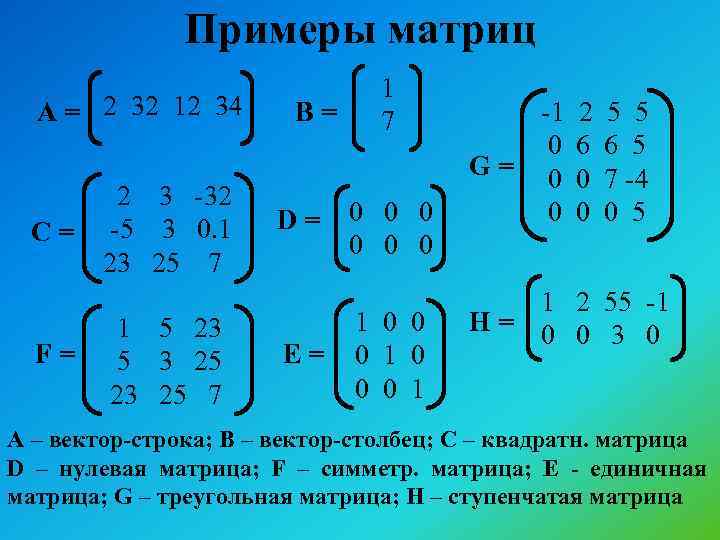 После выбора шаблона в меню Формат становится доступным пункт Матрица. В открывшемся окне можно определить количество строк и столбцов матрицы (не более 31) и задать их выравнивание. Установив флажок Столбцы равной ширины, вы приведете все столбцы матрицы к ширине самого широкого. Аналогичную функцию имеет флажок Строки равной высоты (рис. 3.7).
После выбора шаблона в меню Формат становится доступным пункт Матрица. В открывшемся окне можно определить количество строк и столбцов матрицы (не более 31) и задать их выравнивание. Установив флажок Столбцы равной ширины, вы приведете все столбцы матрицы к ширине самого широкого. Аналогичную функцию имеет флажок Строки равной высоты (рис. 3.7).
Рис. 3.7. В диалоговом окне Матрица можно настроить параметры матрицы
Примечание
При вводе матрицы, состоящей из нескольких строк и столбцов, перемещаться между ее элементами можно с помощью клавиши Tab.
Поместив указатель в просвет между ячейками матрицы, щелчком можно выбрать тип ее разделительной линии. При этом в просвете будут появляться доступные разделительные линии. Чтобы создать линию вдоль края матрицы, щелкните на ее внешней границе. Таким образом можно создавать таблицы, внутри которых вводятся формулы.
Примечание
Чтобы заключить формулу в рамку, создайте в поле матрицы рамку размером 1×1.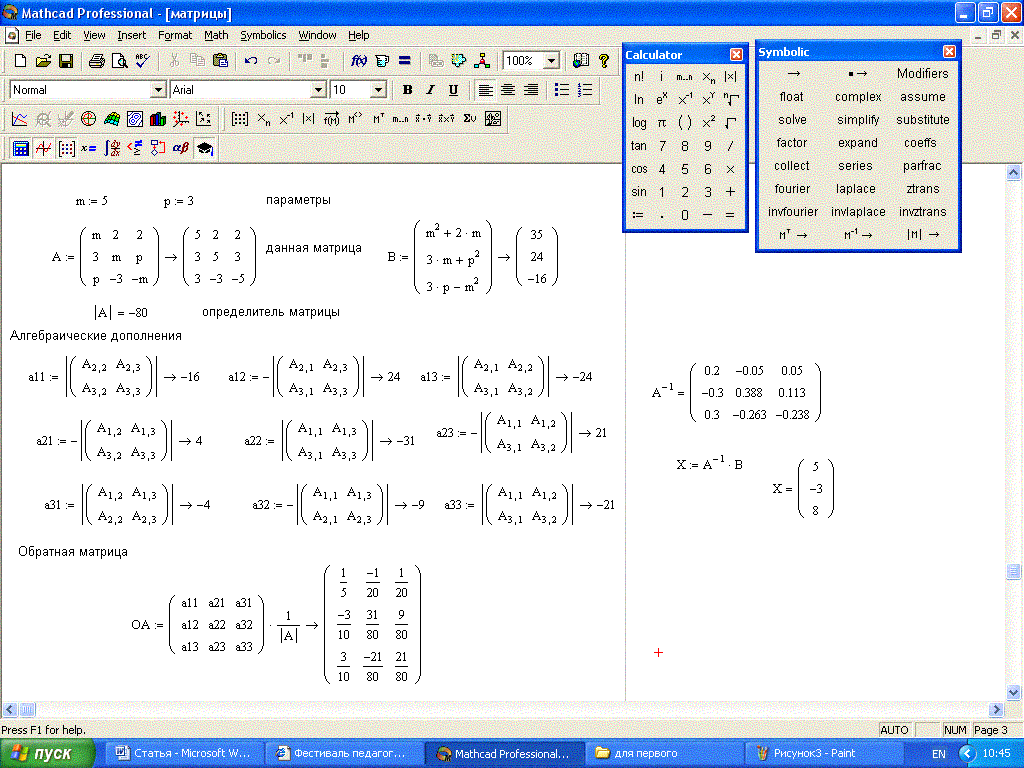 При форматировании матрицы выберите сплошные линии вокруг ячейки, содержащей формулу.
При форматировании матрицы выберите сплошные линии вокруг ячейки, содержащей формулу.
Данный текст является ознакомительным фрагментом.
Работа не волк. Работа – вервольф
1.3.3 Лабораторная работа #3 “Работа с внешними устройствами”
1.3.3 Лабораторная работа #3 “Работа с внешними устройствами”
1. Используя функции XKeysymToString() и XKeycodeToKeysym(), напишите программу, которая реагирует на нажатие клавиш в окне выдачей в него кода символа, состояния модификаторов и символьной расшифровки нажатой клавиши.
Практическая работа 5. Работа с фрагментами текста
Практическая работа 5. Работа с фрагментами текста Задание. Создать текстовый документ и переставить местами его отдельные фрагменты. Вставить в текстовый документ результаты вычислений в Калькуляторе.Последовательность выполнения1. Запустите Блокнот и создайте
Практическая работа 8. Работа с меню Пуск
Практическая работа 8. Работа с меню Пуск Задание. Настроить значки меню Пуск.Последовательность выполнения1. Запустите программу Блокнот с помощью строки поиска в меню Пуск.2. Запустите программу Калькулятор с помощью строки поиска, не пользуясь мышью. Для этого:1)
Практическая работа 12. Работа с окнами папок
Практическая работа 12. Работа с окнами папок
Задание. Изучить работу с окнами папок. Научиться перемещаться по файлам и папкам.Последовательность выполнения1. С помощью меню Пуск откройте папку Компьютер. Ознакомьтесь с содержимым окна, покажите его составляющие.2. С
Изучить работу с окнами папок. Научиться перемещаться по файлам и папкам.Последовательность выполнения1. С помощью меню Пуск откройте папку Компьютер. Ознакомьтесь с содержимым окна, покажите его составляющие.2. С
Практическая работа 14. Работа с файлами и папками
Практическая работа 15. Работа с изображениями в Проводнике
Практическая работа 15. Работа с изображениями в Проводнике
Задание. Просмотреть и отредактировать изображения с помощью встроенных средств Windows Vista.Последовательность выполнения1. Откройте папку, содержащую цифровые изображения.
Практическая работа 16. Работа со сменными носителями
Практическая работа 16. Работа со сменными носителями Задание 1. Скопировать файлы и папки на flash-диск.Последовательность выполнения1. Подключите к компьютеру устройство flash-памяти. При этом обратите внимание на размещение выступов на разъеме и самом устройстве, чтобы
Практическая работа 19. Поиск в Интернете. Работа с папками Избранное и Журнал
Практическая работа 19. Поиск в Интернете. Работа с папками Избранное и Журнал Задание 1. Научиться выполнять поиск в Интернете, настраивать параметры поиска, работать с папками Избранное и Журнал.Последовательность выполнения1. Запустите Internet Explorer.2. Щелкните кнопкой мыши
Практическая работа 24. Работа с программой Dr.
 Web
WebПрактическая работа 24. Работа с программой Dr.Web Задание. Изучить приемы работы с программой Dr.Web.Для выполнения этой работы на компьютере должен быть установлен антивирус Dr.Web. При отсутствии какой-либо антивирусной программы на вашем компьютере вы можете установить Dr.Web
Практическая работа 26. Работа с файловым менеджером
Практическая работа 26. Работа с файловым менеджером Задание 1. Установить и настроить программу Total Commander.Последовательность выполнения1. Загрузите последнюю версию Total Commander с сайта wincmd.ru.2. Запустите загруженный файл и установите программу, ответив на несколько простых
Практическая работа 27. Работа с проигрывателем Windows Media
Практическая работа 27. Работа с проигрывателем Windows Media
Задание 1. Изучить средства управления воспроизведением проигрывателя Windows Media. Последовательность выполнения1. Откройте для воспроизведения с помощью проигрывателя любой музыкальный файл, например из папки
Последовательность выполнения1. Откройте для воспроизведения с помощью проигрывателя любой музыкальный файл, например из папки
Практическая работа 30. Редактирование документа. Работа с фрагментами.
Практическая работа 30. Редактирование документа. Работа с фрагментами. Задание. Отредактировать сохраненный документ.Последовательность выполнения1. Откройте ранее сохраненный документ Урок 1 любым способом.2. Выделите слово, предложение, строку, абзац, весь документ.
Практическая работа 53. Запуск Access. Работа с объектами базы данных
Практическая работа 53. Запуск Access. Работа с объектами базы данных Задание. Ознакомиться с окном программы Access. Запустить и рассмотреть учебную базу данных. ВНИМАНИЕ При выполнении задания помните, что все внесенные в базу данных изменения записываются немедленно и их
Практическая работа 61.
 Работа с оборудованием
Работа с оборудованиемПрактическая работа 61. Работа с оборудованием Задание. Проверить параметры и работу установленного оборудования и выполнить проверку жесткого диска.Последовательность выполнения1. Щелкните правой кнопкой мыши на значке Компьютер и выберите пункт Свойства. В
Глоссарий терминов, используемых в матричной алгебре: (жирный шрифт: наиболее важные для нас)
Глоссарий терминов, используемых в матричной алгебре: (жирный шрифт: наиболее важные для нас)( полужирный: самое важное для нас)
Возврат на главную страницу указателя
Совместимость:
Две матрицы совместимы (для умножения) если количество столбцов в первом равно количеству строк в второй. Это потому, что каждая строка (с j элементов) в первом матрица будет умножаться на каждый столбец (с i элементами) в вторая матрица.Совместимость: “внутренних” терминов ( c1 должен быть равен r2) Размерность результата: “внешние” термины (r1 * с2)Чтобы поэлементный принцип работал, число элементов (столбцов) в первом должно быть равно количеству элементов (строк) В секунду. Эвристика: m x n * o x p приводит к NO GO, если n < > o. Делать они совпадают, где они касаются?
Определитель (Det):
Только квадратные матрицы . Дет А = · aij (-1)i+j Det M ij, где M ij — минор числа A с i-я строка и j-й столбец удалены. (Сумма по j для расширения по столбцам, что является обычным способом сделай это). Для больших матриц вычисление определителя выполняется по строке развязки. Определитель может сказать нам о количестве решений к набору уравнений (уникальных, бесконечных?) и различным другим полезным свойствам матрицы.Собственные значения:
Характеристические корни системы уравнений.Собственный вектор:В матричной форме собственные значения (l) определены так, что Det( A – l I) = 0 [характеристическое уравнение]. Характеристическое уравнение будет многочлен от л степень n , где n — порядок (размер) матрицы. В демографии, доминирующим собственным значением является скорость роста населения, л , в то время как второе собственное значение дает коэффициент затухания (как быстро население вернется к равновесию после возмущения).
Вектор, u , такой, что A*u = l* u. Для матричных моделей правый и левый собственные векторы, соответствующие доминирующим собственным значением являются репродуктивных значения (левый собственный вектор, вектор-строка) и стабильное (st)возрастное распределение (правый собственный вектор, вектор-столбец).Идентификационная матрица:
Матрица обычно записывается как I , с 1 (единицы) на главной диагонали и нули в остальных местах.Обратное:
А -1 * А = I . Обратной матрицей называется та матрица, которая при предварительно умноженный на A , дает единичную матрицу. Обратное существует только когда матрица сингулярна (то есть имеет определитель).Неснижаемый:
Эквивалентно «сильно связанным» на диаграмме теории (см. Кейфиц, стр. 30). Каждая точка на графике (или в матрице) можно добраться из любой другой точки либо напрямую, либо через промежуточные узлы.Матрица Лесли:
Матрица возрастной классификации, используемая в анализе истории жизни. В нем есть элементы только в верхнем ряду (плодовитость) и по поддиагональному (выживаемость). Чтобы получить стабильное возрастное распределение, матрица должна быть несокращаемый (сильно связанный) и примитивный .Умножение:
см. Совместимость. Выполнено ряд за столбцом, элемент за элементом.Примитив :Произведение матрицы r x c * c x s представляет собой матрицу порядок (= размер) r x s (количество строк в первом по количеству столбцы во втором). Итак, совместимость включает в себя два внутренних числа и «порядок» матрицы произведения включает два внешних числа.
Любая матрица, для которой А п (для некоторых произвольных n ) имеет только положительные элементы, называется примитивный. Примитивность неотрицательной неприводимой матрицы является достаточным условие стабильности. Для простой матрицы Лесли это означает, что при должны существовать как минимум две возрастные группы, у которых m i > 0 и которые имеют i относительно простые (например, для шестилетнего срока службы плодовитость только в возрастных классах 3 и 6 будет давать циклы, а не стабильную возрастное распределение).Единственное число :
Матрица, определитель которой равен нулю.
Нижний индекс:
Для матрицы A , a ij означает элемент в i-й строке и j-й столбец.Симметричный:A = {aij}, где {} означает “множество”.
Матрица симметрична, если она равна своей транспонировать. То есть если А + А ‘.След :
Только квадратные матрицы . Сумма элементы главной диагонали.Транспонировать:
Для матрицы А , транспонировать А ‘ = {arc}’ = {acr} (используйте i и j в качестве индексов, если хотите). То есть элементы в строках из первых становятся элементами столбцов транспонирования.ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА: Кейфиц, Н. 1985. С. 27–33 обсуждаются матрицы и графики, используемые в демографии.
Рафгарден, Дж. 1979. Приложение 3, стр. 579-590 In : Теория популяционной генетики. и эволюционная экология: введение. Макмиллан, Нью-Йорк
Серл, С.Р. 1966. Матричная алгебра для биологических наук. Wiley and Sons, NY
Вернуться к началу страницыTranspose, Multiplication, NumPy Примеры массивов
Что такое матрица Python?
Матрица Python — это специализированный двумерный прямоугольный массив данных, хранящихся в строках и столбцах.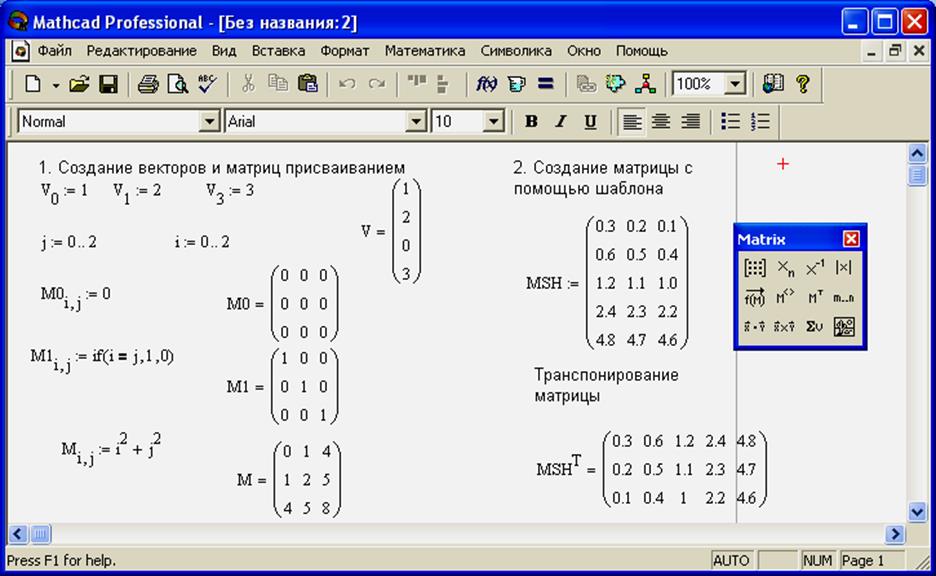 Данные в матрице могут быть числами, строками, выражениями, символами и т. д. Матрица — одна из важных структур данных, которую можно использовать в математических и научных расчетах.
Данные в матрице могут быть числами, строками, выражениями, символами и т. д. Матрица — одна из важных структур данных, которую можно использовать в математических и научных расчетах.
Из этого руководства по Python вы узнаете:
- Что такое матрица Python?
- Как работают матрицы Python?
- Создание матрицы Python с использованием типа данных вложенного списка
- Для чтения данных внутри Python Matrix с помощью списка.
- Пример 2: Чтобы прочитать последний элемент из каждой строки.
- Пример 3: Печать строк в матрице
- Добавление матриц с использованием вложенного списка
- Умножение матриц с использованием вложенного списка
- Создание матрицы Python с использованием массивов из пакета Python Numpy
- Матричная операция с использованием Numpy.Array()
- Доступ к матрице NumPy
Как работают матрицы Python?
Данные внутри двумерного массива в матричном формате выглядят следующим образом:
Шаг 1)
Он показывает матрицу 2×2. Он имеет две строки и 2 столбца. Данные внутри матрицы являются числами. Строка1 имеет значения 2,3, а строка2 имеет значения 4,5. Столбцы, т. е. col1, имеют значения 2,4, а col2 — значения 3,5.
Он имеет две строки и 2 столбца. Данные внутри матрицы являются числами. Строка1 имеет значения 2,3, а строка2 имеет значения 4,5. Столбцы, т. е. col1, имеют значения 2,4, а col2 — значения 3,5.
Шаг 2)
Показывает матрицу 2×3. Он имеет две строки и три столбца. Данные внутри первой строки, т. е. row1, имеют значения 2, 3, 4, а row2 — значения 5, 6, 7. Столбцы col1 имеют значения 2,5, col2 имеют значения 3,6, а col3 имеют значения 4,7.
Точно так же вы можете хранить свои данные внутри матрицы nxn в Python. Многие операции могут быть выполнены с матричным сложением, вычитанием, умножением и т. д.
В Python нет простого способа реализации матричного типа данных.
Матрица Python использует массивы, и то же самое можно реализовать.
- Создание матрицы Python с использованием типа данных вложенного списка
- Создание матрицы Python с использованием массивов из пакета Python Numpy
Создание матрицы Python с использованием типа данных вложенного списка
В Python массивы представляются с использованием типа данных списка. Итак, теперь мы будем использовать список для создания матрицы Python.
Итак, теперь мы будем использовать список для создания матрицы Python.
Мы создадим матрицу 3×3, как показано ниже:
- Матрица состоит из 3 строк и 3 столбцов.
- Первая строка в формате списка будет следующей: [8,14,-6]
- Вторая строка в списке будет: [12,7,4]
- Третья строка в списке будет: [-11,3,21]
Матрица внутри списка со всеми строками и столбцами показана ниже:
Список = [[Row1],
[Ряд 2],
[Строка 3]
...
[РядN]]
Таким образом, в соответствии с приведенной выше матрицей тип списка с матричными данными выглядит следующим образом:
М1 = [[8, 14, -6], [12,7,4], [-11,3,21]]
Для чтения данных внутри Python Matrix с помощью списка.
Мы будем использовать матрицу, определенную выше. Пример будет читать данные, печатать матрицу, отображать последний элемент из каждой строки.
Пример: для печати матрицы
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
#Чтобы распечатать матрицу
печать(M1)
Вывод:
Матрица M1 = [[8, 14, -6], [12, 7, 4], [-11, 3, 21]]
Пример 2: Чтобы прочитать последний элемент из каждой строки.

М1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
длина_матрицы = длина (M1)
#Чтобы прочитать последний элемент из каждой строки.
для i в диапазоне (matrix_length):
печать (M1[i][-1])
Вывод:
-6 4 21
Пример 3: Печать строк в матрице
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
длина_матрицы = длина (M1)
#Чтобы напечатать строки в матрице
для i в диапазоне (matrix_length):
печать (M1 [я])
Вывод:
[8, 14, -6] [12, 7, 4] [-11, 3, 21]
Добавление матриц с помощью вложенного списка
Мы можем легко добавить две заданные матрицы. Матрицы здесь будут в виде списка. Давайте поработаем над примером, который позаботится о добавлении данных матриц.
Матрица 1:
М1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
Матрица 2 :
M2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
Последняя инициализирует матрицу, в которой будет храниться результат M1 + M2.
Матрица 3 :
M3 = [[0,0,0],
[0,0,0],
[0,0,0]]
Пример: добавление матриц
Для добавления матриц будет использоваться цикл for, который будет проходить по обеим заданным матрицам.
М1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
М2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
М3 = [[0,0,0],
[0,0,0],
[0,0,0]]
длина_матрицы = длина (M1)
#Чтобы добавить матрицы M1 и M2
для i в диапазоне (len (M1)):
для k в диапазоне (len (M2)):
M3[i][k] = M1[i][k] + M2[i][k]
#Распечатать матрицу
print("Сумма матриц M1 и M2 = ", M3)
Вывод:
Сумма матриц M1 и M2 = [[11, 30, -12], [21, 14, 0], [-12, 6, 34]]
Умножение матриц с использованием вложенного списка
Чтобы умножить матрицы, мы можем использовать цикл for для обеих матриц, как показано в коде ниже:
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
М2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
М3 = [[0,0,0],
[0,0,0],
[0,0,0]]
длина_матрицы = длина (M1)
#Для умножения матриц M1 и M2
для i в диапазоне (len (M1)):
для k в диапазоне (len (M2)):
M3[i][k] = M1[i][k] * M2[i][k]
#Распечатать матрицу
print("Умножение матриц M1 и M2 = ", M3)
Вывод:
Умножение матриц M1 и M2 = [[24, 224, 36], [108, 49, -16], [11, 9, 273]]
Создание матрицы Python с использованием массивов из пакета Python Numpy
Библиотека Python Numpy помогает работать с массивами. Numpy обрабатывает массив немного быстрее, чем список.
Numpy обрабатывает массив немного быстрее, чем список.
Для работы с Numpy его необходимо сначала установить. Следуйте инструкциям ниже, чтобы установить Numpy.
Шаг 1)
Команда для установки Numpy:
pip install NumPy
Шаг 2)
Чтобы использовать Numpy в своем коде, его необходимо импортировать.
import NumPy
Шаг 3)
Вы также можете импортировать Numpy, используя псевдоним, как показано ниже:
import NumPy as np
матрица питона.
Пример: массив в Numpy для создания матрицы Python
импортировать numpy как np M1 = np.массив([[5, -10, 15], [3, -6, 9], [-4, 8, 12]]) печать(M1)
Вывод:
[[ 5 -10 15] [ 3 -6 9] [-4 8 12]]
Матричная операция с использованием Numpy.Array()
Матричная операция, которую можно выполнить, — это сложение, вычитание, умножение, транспонирование, чтение строк, столбцов матрицы, нарезка матрицы и т. д. Во всех примерах мы собирается использовать метод array().
д. Во всех примерах мы собирается использовать метод array().
Сложение матрицы
Чтобы выполнить сложение матрицы, мы создадим две матрицы с помощью numpy.array() и добавим их с помощью оператора (+).
Пример:
импортировать numpy как np M1 = np.array([[3, 6, 9], [5, -10, 15], [-7, 14, 21]]) M2 = np.array([[9, -18, 27], [11, 22, 33], [13, -26, 39]]) М3 = М1 + М2 печать(M3)
Вывод:
[[ 12 -12 36] [ 16 12 48 ] [ 6 -12 60]]
Вычитание матрицы
Чтобы выполнить вычитание матрицы, мы создадим две матрицы с помощью numpy.array() и вычтем их с помощью оператора (-).
Пример:
импортировать numpy как np M1 = np.array([[3, 6, 9], [5, -10, 15], [-7, 14, 21]]) M2 = np.array([[9, -18, 27], [11, 22, 33], [13, -26, 39]]) М3 = М1 - М2 печать(M3)
Вывод:
[[ -6 24 -18] [-6-32-18] [-20 40 -18]]
Умножение матриц
Сначала создадим две матрицы, используя numpy. arary(). Чтобы умножить их, вы можете использовать метод numpy dot(). Numpy.dot() — это точечный продукт матриц M1 и M2. Numpy.dot() обрабатывает двумерные массивы и выполняет умножение матриц.
arary(). Чтобы умножить их, вы можете использовать метод numpy dot(). Numpy.dot() — это точечный продукт матриц M1 и M2. Numpy.dot() обрабатывает двумерные массивы и выполняет умножение матриц.
Пример:
импортировать numpy как np M1 = np.массив ([[3, 6], [5, -10]]) M2 = np.массив ([[9, -18], [11, 22]]) М3 = М1.точка(М2) печать(M3)
Вывод:
[[ 93 78] [-65-310]]
Транспонирование матрицы
Транспонирование матрицы вычисляется путем преобразования строк в столбцы и столбцов в строки. Функцию transpose() из Numpy можно использовать для вычисления транспонирования матрицы.
Пример:
импортировать numpy как np M1 = np.массив([[3, 6, 9], [5, -10, 15], [4,8,12]]) M2 = M1.транспонировать() печать(М2)
Вывод:
[[ 3 5 4] [ 6 -10 8] [ 9 15 12]]
Нарезка матрицы
Нарезка вернет вам элементы из матрицы на основе заданного начального/конечного индекса.
- Синтаксис для нарезки – [начало:конец]
- Если начальный индекс не указан, он считается равным 0.
 Например, [:5], это означает [0:5].
Например, [:5], это означает [0:5]. - Если конец не передан, он будет считаться длиной массива.
- Если начало/конец имеют отрицательные значения, нарезка будет выполняться с конца массива.
Прежде чем мы приступим к срезу матрицы, давайте сначала разберемся, как применить срез к простому массиву.
импортировать numpy как np массив = np.массив ([2,4,6,8,10,12,14,16]) print(arr[3:6]) # напечатает элементы с 3 по 5 print(arr[:5]) # напечатает элементы от 0 до 4 print(arr[2:]) # напечатает элементы от 2 до длины массива. print(arr[-5:-1]) # будет печатать с конца, т.е. от -5 до -2 print(arr[:-1]) # будет печатать с конца, т.е. от 0 до -2
Вывод:
[8 10 12] [ 2 4 6 8 10 ] [ 6 8 10 12 14 16] [ 8 10 12 14 ] [ 2 4 6 8 10 12 14]
Теперь реализуем нарезку матрицы. Чтобы выполнить нарезку матрицы
, синтаксис будет M1[начало_строки:конец_строки, начало_столбца:конец_столбца]
- Первое начало/конец будет для строки, т.
 е. для выбора строк матрицы.
е. для выбора строк матрицы. - Второе начало/конец будет для столбца, т.е. для выбора столбцов матрицы.
Матрица M1 t, которую мы собираемся использовать, выглядит следующим образом:
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
Всего 4 ряда. Индекс начинается с 0 до 3. Строка 0 th — это [2,4,6,8,10], строка 1 st — это [3,6,9,-12,-15], за которой следуют 2 -й -й и 3-й -й -й.
Матрица M1 имеет 5 столбцов. Индекс начинается от 0 до 4. Столбец 0 th имеет значения [2,3,4,5], столбцы 1 st имеют значения [4,6,8,-10], за которыми следуют 2 -й , 3-й -й , 4-й -й и 5-й -й -й.
Вот пример, показывающий, как получить данные строк и столбцов из матрицы с помощью срезов. В примере мы печатаем строки 1 st и 2 nd , а для столбцов нам нужны первый, второй и третий столбцы. Чтобы получить этот вывод, мы использовали: M1[1:3, 1:4]
Чтобы получить этот вывод, мы использовали: M1[1:3, 1:4]
Пример:
import numpy as np
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[1:3, 1:4]) # Для 1:3 это даст первую и вторую строку.
#Столбцы будут взяты с первого по третий.
Вывод:
[[ 6 9 -12] [ 8 12 16]]
Пример: для печати всех строк и третьих столбцов
импортировать numpy как np
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:,3]) # Это напечатает все строки и данные третьего столбца.
Вывод:
[ 8 -12 16 -20]
Пример: для печати первой строки и всех столбцов
импортировать numpy как np
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:1,]) # Будет напечатана первая строка и все столбцы
Вывод:
[[ 2 4 6 8 10]]
Пример: для печати первых трех строк и первых 2 столбцов
импортировать numpy как np M1 = np.массив([[2, 4, 6, 8, 10], [3, 6, 9, -12, -15], [4, 8, 12, 16, -20], [5, -10, 15, -20, 25]]) печать (M1 [: 3,: 2])
Вывод:
[[2 4] [3 6] [4 8]]
Доступ к матрице NumPy
Мы видели, как работает нарезка. Принимая это во внимание, мы узнаем, как получить строки и столбцы из матрицы.
Для печати строк матрицы
В примере будут напечатаны строки матрицы.
Пример:
импортировать numpy как np M1 = np.массив([[3, 6, 9], [5, -10, 15], [4,8,12]]) print(M1[0]) # первая строка print(M1[1]) # вторая строка print(M1[-1]) # -1 напечатает последнюю строку
Вывод:
[3 6 9] [ 5 -10 15] [ 4 8 12]
Чтобы получить последнюю строку, вы можете использовать индекс или -1. Например, матрица имеет 3 строки:
, поэтому M1[0] даст вам первую строку,
M1[1] даст вам вторую строку
M1[2] или M1[-1] даст вам третий ряд или последний ряд.
Для печати столбцов матрицы
импортировать numpy как np M1 = np.массив([[2, 4, 6, 8, 10], [3, 6, 9, -12, -15], [4, 8, 12, 16, -20], [5, -10, 15, -20, 25]]) print(M1[:,0]) # Будет напечатан первый столбец print(M1[:,3]) # Будет напечатан третий столбец print(M1[:,-1]) # -1 даст вам последний столбец
Вывод:
[2 3 4 5] [ 8 -12 16 -20] [ 10 -15 -20 25]
Резюме:
- Матрица Python представляет собой специализированный двумерный прямоугольный массив данных, хранящихся в строках и столбцах. Данные в матрице могут быть числами, строками, выражениями, символами и т. д. Матрица — одна из важных структур данных, которую можно использовать в математических и научных расчетах.
- В Python нет простого способа реализовать матричный тип данных. Матрица Python может быть создана с использованием типа данных вложенного списка и библиотеки numpy.
- Библиотека Python Numpy помогает работать с массивами. Numpy обрабатывает массив немного быстрее, чем список.
- Матричная операция, которую можно выполнять, — это сложение, вычитание, умножение, транспонирование, чтение строк и столбцов матрицы, разрезание матрицы и т.


 Чтобы поэлементный принцип работал, число
элементов (столбцов) в первом должно быть равно количеству элементов (строк)
В секунду. Эвристика: m x n * o x p приводит к NO GO, если n < > o. Делать
они совпадают, где они касаются?
Чтобы поэлементный принцип работал, число
элементов (столбцов) в первом должно быть равно количеству элементов (строк)
В секунду. Эвристика: m x n * o x p приводит к NO GO, если n < > o. Делать
они совпадают, где они касаются? В матричной форме собственные значения (l)
определены так, что Det( A – l I) =
0 [характеристическое уравнение]. Характеристическое уравнение будет
многочлен от л
степень n , где n — порядок (размер) матрицы. В демографии, доминирующим собственным значением является скорость роста населения, л ,
в то время как второе собственное значение дает коэффициент затухания (как быстро население
вернется к равновесию после возмущения).
В матричной форме собственные значения (l)
определены так, что Det( A – l I) =
0 [характеристическое уравнение]. Характеристическое уравнение будет
многочлен от л
степень n , где n — порядок (размер) матрицы. В демографии, доминирующим собственным значением является скорость роста населения, л ,
в то время как второе собственное значение дает коэффициент затухания (как быстро население
вернется к равновесию после возмущения).
 Произведение матрицы r x c * c x s представляет собой матрицу
порядок (= размер) r x s (количество строк в первом по количеству
столбцы во втором). Итак, совместимость включает в себя два внутренних числа
и «порядок» матрицы произведения включает два внешних числа.
Произведение матрицы r x c * c x s представляет собой матрицу
порядок (= размер) r x s (количество строк в первом по количеству
столбцы во втором). Итак, совместимость включает в себя два внутренних числа
и «порядок» матрицы произведения включает два внешних числа.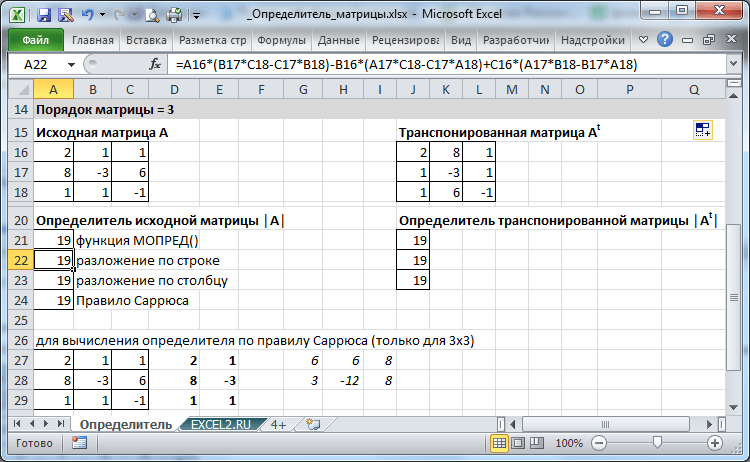 A = {aij}, где {} означает “множество”.
A = {aij}, где {} означает “множество”. Например, [:5], это означает [0:5].
Например, [:5], это означает [0:5]. е. для выбора строк матрицы.
е. для выбора строк матрицы. массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
печать (M1 [: 3,: 2])
массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
печать (M1 [: 3,: 2])
 массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:,0]) # Будет напечатан первый столбец
print(M1[:,3]) # Будет напечатан третий столбец
print(M1[:,-1]) # -1 даст вам последний столбец
массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:,0]) # Будет напечатан первый столбец
print(M1[:,3]) # Будет напечатан третий столбец
print(M1[:,-1]) # -1 даст вам последний столбец