Работа механическая энергия: Работа. Мех. энергия | От урока до экзамена

Работа. Механическая Энергия. Кинетическая и потенциальная энергии. Закон сохранения механической энергии

1. Работа. Механическая Энергия. Кинетическая и потенциальная энергии. Закон сохранения механической энергии

Санкт-Петербургское государственное бюджетное
профессиональное образовательное учреждение “Пожарноспасательный колледж “Санкт-Петербургский центр подготовки
спасателей”
Работу подготовила
студентка 671 группы:
Чекмарева Е.
Работу проверила:
Захарова О. А.

2. Механическая работа

представляет собой процесс движения тела под
действием приложенной к телу силы. За величину работы принимается
произведение силы на путь, пройденый по направлению силы.
A=F*S
Если
направление
силы
совпадает с направлением
движения, то работа является
положительной. Сила в этом
случае будет называться
движущей силой.
Если же направление силы не
совпадает с направлением
движения, то работа будет
являться отрицательной. Сила
в
этом
случае
будет
называться
силой
сопротивления.
Когда
направление
действующей силы на тело
перпендикулярно
направлению движения, то
работа равна нулю.

4. Энергия.

Энергия – величина, характеризующая способность тела или системы
тел совершать работу.
Энергия
Потенциал
ьная
Кинетичес
кая

5. Потенциальная энергия

Энергия, которая определяется взаимным положением тел или частей
одного и того же тела, называется потенциальной энергией.
Если тело P поднято на высоту h, то величина совершаемой при
падении работы A равна произведению веса тела на высоту.
A=Ph
Обозначим потенциальную энергию через Eп. Поскольку Eп=A, то
Eп=A=mgh.

6. Примеры потенциальной энергии

7. Кинетическая энергия

Энергия, которой обладает тело вследствие своего движения, называется

Кинетической энергией.
Если принять кинетическую энергию покоящегося тела равной нулю, то
кинетическая энергия тела будет равна той работе, которая производится
при уменьшении скорости тела до нуля.
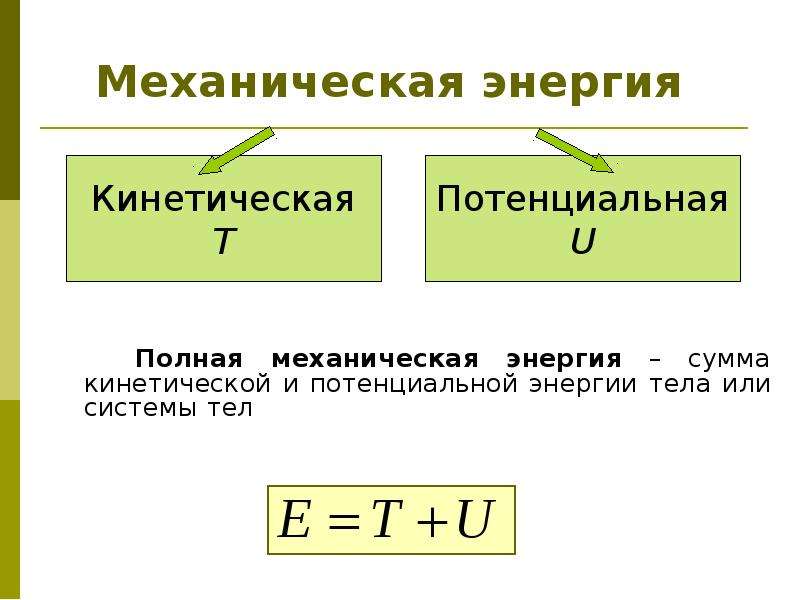
Eк=

8. Пример кинетической энергии

9. Закон сохранения энергии

Энергия не исчезает и не создается. Она лишь превращается из
одного вида в другой.

10. Пример закона сохранения энергии

11. Источники:

•Учебник
1964 г. Курс физики. Часть 1. А.В. Перышкин, В.В. Крауклис

Механическая работа, энергия, мощность | Физика для студентов | Студенту | Статьи и обсуждение вопросов образования в Казахстане | Образовательный сайт Казахстана

Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать это изменение, в механике вводится понятие работы силы. Если F=const, то:

A=F_s•S=F•S•cosα (2.14), где F_s – проекция вектора силы на направление перемещения. «Работа – это скалярная величина». В общем случае сила может изменяться как по модулю, так и по направлению, поэтому:

A=F_s•dS (2.15) [A]=1Дж=1Н•м

Энергия – универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В механике рассматривается кинетическая и потенциальная энергии механической системы.

Кинетическая энергия – это энергия механического движения системы. Сила F, действуя на тело, вызывает его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы.

dA=dT (2.16)

mυdυ=dT; T=mυdυ=mυ²/2 (2.17)

Таким образом, тело массой m, движущееся со скоростью υ, обладает кинетической энергией: T=mυ²/2 (2.18)

Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

Если взаимодействие тел осуществляется посредством силовых полей, характеризующимся тем, что работа сил при перемещении тела не зависит от формы траектории, а зависит только от начального и конечного положений, то такие поля называются потенциальными, а силы, действующие в них, – консервативными.

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа в потенциальном поле сил совершается за счет убыли потенциальной энергии:

dA=-dП (2.19)

Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:

N=dA/dt=F•dr/dt=Fυ (2.20)

N – скалярная величина. Единица измерения мощности – 1Ватт (Вт), 1Вт=1Дж/с

Законы сохранения в механике. Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа.  / / Законы сохранения в механике. Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел Поделиться:    Законы сохранения в механике. Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел Импульс: Второй закон Ньютона в импульсной форме: изменение импульса тела равно импульсу силы: Механическая работа, мощность: Механическая работа постоянной силы F на перемещении s: Работа силы тяжести: Работа силы упругости: Мощность – это работа, совершаемая в единицу времени: Энергия: Энергия – это физическая величина, характеризующая способность тела совершать работу: Кинетическая энергия  – это энергия движущегося тела: Теорема об изменении кинетической энергии:  Изменение кинетической энергии тела за некоторый промежуток времени равно работе, совершенной за это же время силой, действующей на тело: Потенциальная энергия: это энергия взаимодействия тел или частей одного и того же тела: Потенциальная энергия тела на высоте h над землей: Потенциальная энергия упруго деформированного тела: Закон сохранения импульса: Закон сохранения импульса: Независимо от природы сил взаимодействия полный импульс тел, составляющих замкнутую систему, является постоянным: Закон сохранения энергии: Закон сохранения энергии: в замкнутой системе, в которой действуют только консервативные силы, механическая энергия сохраняется: Равновесие твердых тел: Плечо силы d  – это кратчайшее расстояние от оси вращения до прямой, на которой лежит вектор силы F Момент силы F относительно оси вращения:  Первое условие равновесия: Если твердое тело находится в равновесии, то геометрическая сумма внешних сил, приложенных к нему, равна нулю: Второе условие равновесия: При равновесии твердого тела сумма моментов всех внешних сил, приложенных к нему, равна нулю: Поиск в инженерном справочнике DPVA. Введите свой запрос: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Конспект занятия по теме «Работа и энергия.

Закон сохранения механической энергии»

Дисциплина: физика

Занятие №: 1.6

Тема: Работа и энергия. Закон сохранения механической энергии

Цель: усвоение теоретических основ изучаемой темы (работа силы, потенциальная сила, консервативная сила, потенциальная энергия, принцип минимума потенциальной энергии, виды равновесия, кинетическая энергия, теорема о кинетической энергии, мощность, закон сохранения механической энергии).

Задачи:

образовательные (обеспечить усвоение теоретических основ изучаемой темы, продолжить формирование общих учебных умений и навыков на материале данной темы)

Обеспечение занятия: учебник, конспект лекции, задания для проверки дз (приложение 1).

Тип занятия: комбинированный урок (занятие)

Технология обучения: развивающее обучение

Методы обучения: лекция, работа с книгой

Компетенции:

ОК 1. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 2. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК 3. Использовать информационно-коммуникационные технологии в профессиональной деятельности.

ОК 4. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение своей квалификации.

ПК 1. Оформлять документы первичного учета.

Межпредметные связи:

Используемая литература: Федорова В.Н., Фаустов Е.В. Физика: учебник для студентов учреждений сред. проф. образования – литература для студентов

Жданов Л.С., Жданов Г.Л. Физика для средних специальных учебных заведений – литература для преподавателя

Тихомирова С. А. Физика. 10 класс: учеб. для общеобразоват. учреждений (базовый и профильный уровни) – литература для преподавателя

Содержание занятия

1. Организационный момент: 1-2 мин

(отметка отсутствующих, проверка внешнего вида учащихся, санитарного состояния кабинета)

2. Проверка знаний по пройденному материалу: 10-15 мин

Письменное задание и фронтальный опрос

Задания для проверки дз (приложение 1) – выполняются индивидуально вызванным обучающимся у доски или на месте. Уровень выполнения заданий может варьироваться в зависимости от сложности и подготовки обучающихся.

Фронтальный опрос проводится одновременно с выполнением письменного задания

Вопросы:

1. Какую величину называют импульсом тела?

2. В каких единицах измеряется импульс тела?

3. Какая величина названа импульсом силы?

4. Чем абсолютно упругий удар отличается от абсолютно неупругого?

5. Как формулируется закон сохранения импульса?

6. Какое движение называют реактивным?

7. Где встречается реактивное движение в природе и технике?

3. Изложение материала: 44-57 мин

План:

1) Работа силы.

2) Потенциальная энергия. Виды равновесия.

3) Кинетическая энергия.

4) Закон сохранения механической энергии.

4. Закрепление нового материала:15-20 мин

Вопросы для самоконтроля:

Дайте определения работы силы.

При каких условиях работа силы положительна? отрицательна? равна нулю?

Дайте определение потенциальной силы и потенциальной энергии.

Почему сила упругости является потенциальной силой?

Сформулируйте определение кинетической энергии тела.

Сформулируйте теорему о кинетической энергии.

Сформулируйте закон сохранения полной механической энергии?

Задача 3.8-3.9 из учебника

5. Задание на дом: 2 мин

лекция

6. Подведение итогов: 5-7 мин

(выставляются оценки, дается комментарий)

Тезисы лекции теме «Работа и энергия. Закон сохранения механической энергии»

Презентация к занятию “Работа и энергия”
PPT / 2.96 Мб

Вопрос 1

Все наши ежедневные действия сводятся к тому, что мы с помощью мышц либо приводим в движение окружающие тела и поддерживаем это движение, либо же останавливаем движущиеся тела. Этими телами являются орудия труда, в играх — мячи, шайбы, шахматные фигуры. На производстве и в сельском хозяйстве люди также приводят в движение орудия труда. Правда, в настоящее время роль рабочего все больше и больше сводится к управлению механизмами. Но в любой машине можно обнаружить подобие простых орудий ручного труда. В швейной машинке имеется игла, резец токарного станка подобен рубанку, ковш экскаватора заменяет лопату.

Применение машин во много раз увеличивает производительность труда благодаря использованию в них двигателей. Назначение любого двигателя в том, чтобы приводить тела в движение и поддерживать это движение, несмотря на торможение как обычным трением, так и «рабочим» сопротивлением (резец должен не просто скользить по металлу, а, врезаясь в него, снимать стружку; плуг должен взрыхлять землю и т. д.). При этом на движущееся тело должна действовать со стороны двигателя сила, точка приложения которой перемещается вместе с телом.

Когда человек (или какой-либо двигатель) действует с определенной силой на движущееся тело, то мы говорим, что он совершает работу. Это бытовое представление о работе легло в основу формирования одного из важнейших понятий механики — понятия работы силы.

Работа совершается в природе всегда, когда на какое- либо тело в направлении его движения или против него действует сила (или несколько сил) со стороны другого тела (других тел). Так, сила тяготения совершает работу при падении капель дождя или камня с обрыва. Одновременно совершают работу и силы трения, действующие на падающие капли или на камень со стороны воздуха. Совершает работу и сила упругости, когда распрямляется согнутое ветром дерево.

Второй закон Ньютона в форме позволяет определить, как меняется скорость тела по модулю и направлению, если на него в течение времени Δt действует сила F.

Во многих случаях важно уметь вычислять изменение скорости по модулю, если при перемещении тела на Δr на него действует сила F. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуются величиной, зависящей как от сил, так и от перемещений тел. Эту величину в механике и называют работой силы.

Работа — физическая величина, равная произведению проекции силы на ось X на перемещение по этой оси:

(1)

Если угол между силой и перемещением обозначить через а, то .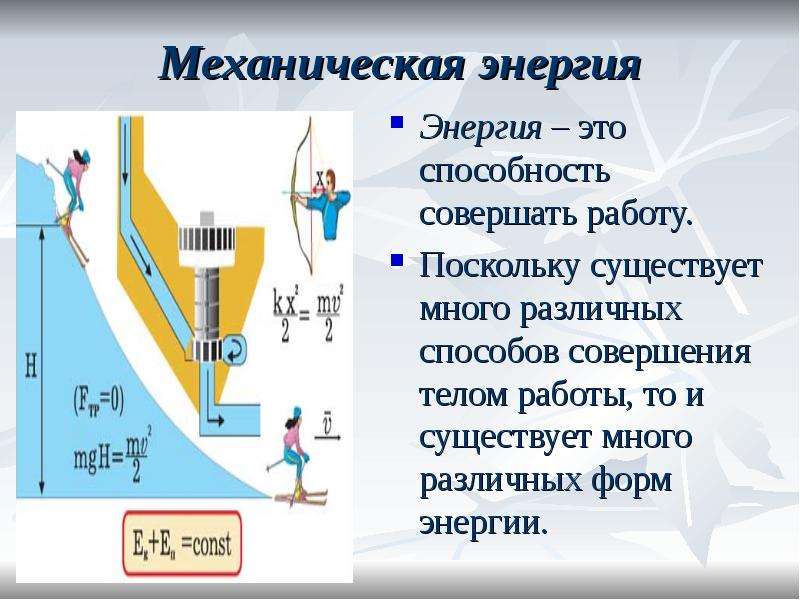 Следовательно, работа равна:

Формула (1) справедлива в том случае, когда сила постоянна и перемещение тела происходит вдоль прямой. В случае криволинейной траектории и переменной силы мы разделяем траекторию на малые отрезки, которые можно считать прямолинейными, а силу на них постоянной.

Работа, в отличие от силы и перемещения, является не векторной, а скалярной величиной. Она может быть положительной, отрицательной или равной нулю.

Знак работы определяется знаком косинуса угла между силой и перемещением.

Если α < 90°, то работа положительна, так как косинус острых углов положителен.

При α > 90° работа отрицательна, так как косинус тупых углов отрицателен.

При α = 90° (сила перпендикулярна перемещению) работа не совершается. Так, сила тяжести не совершает работу при перемещении тела по горизонтальной плоскости. При движении спутника по круговой орбите сила тяготения также не совершает работу.

Если на тело действует несколько сил, то проекция результирующей силы на перемещение равна сумме проекций отдельных сил:

В Международной системе единиц (СИ) работа измеряется в джоулях (обозначается Дж): 1 Дж = 1Н*1м = 1Н*м. Джоуль — это работа, совершаемая силой 1 Н на перемещении 1 м, если направления силы и перемещения совпадают.

Справка: единица работы «джоуль» получила название в честь английского физика Дж. Джоуля (1819-1889), в трудах которого был раскрыт физический смысл понятий работы и энергии.

Вопрос 2

Если система тел может совершить работу, то мы говорим, что она обладает энергией. Для совершения работы необходимо, чтобы на движущееся тело действовала та или иная сила. Рассмотрим простые системы движущихся тел, взаимодействующих между собой посредством сил тяготения и способных в той или иной мере деформироваться. (Пружина или резиновый шнур деформируются значительно, а камень, дерево, металл — столь мало, что их деформациями обычно можно пренебречь) Будем считать, что никаких химических превращений тел не происходит и что в системе нет заряженных тел и электрических токов. Тогда легко обнаружить, что поднятые над землей грузы, а также устройства, имеющие сжатые пружины, способны действовать на движущееся тело и совершать работу лишь в течение определенного промежутка времени. Рано или поздно пружина распрямится, а груз опустится на землю и силы перестанут совершать работу.

Совершение работы не проходит для систем тел бесследно. Рассмотрим, например, часы с пружинным заводом. При заводе часов состояние системы меняется так, что она приобретает способность совершать работу в течение длительного времени. Пружина поддерживает движение всех колес, стрелок и маятника, испытывающих сопротивление движению, вызванное трением. По мере хода часов способность пружины совершать работу постепенно утрачивается. Состояние пружины меняется. Подобным образом при совершении работы меняется состояние сжатого газа и скоростей движущихся тел.

Энергия характеризует способность тела (или системы тел) совершать работу.

Совершая механическую работу, тело или система тел переходят из одного состояния в другое, в котором их энергия минимальна. Груз опускается, пружина распрямляется, движущееся тело останавливается. При совершении работы энергия постепенно расходуется. Для того чтобы система опять приобрела способность совершать работу, надо изменить ее состояние: увеличить скорости тел, поднять тела вверх или деформировать. Для этого внешние силы должны совершить над системой положительную работу.

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ

Рассмотрим движение тела массой m под действием силы тяжести с высоты h2 на высоту h3. Известно, что изменение энергии равно совершенной работе, т.е.

Как известно

Т.о., выражение для работы силы тяжести запишется:

Работа силы тяжести не зависит от формы траектории, а определяется только начальным и конечным положением тела.

Потенциальная сила – сила, работа которой при перемещении материальной точки зависит только от начального и конечного положений точки в пространстве. Сила тяжести является потенциальной силой.

Работа силы тяжести равна разности двух величин, которые называются потенциальной энергией тела в начальном и конечном положениях :

Потенциальная энергия тела в данной точке – скалярная физическая величина, равная работе, совершаемой потенциальной силой при перемещении тела из этой точки в точку, принятую за нуль отсчета потенциальной энергии. Единица потенциальной энергии – джоуль (1 Дж).

Нуль отсчета потенциальной энергии выбирается произвольно. Энергия тела в других положениях отсчитывается относительно нулевого уровня. Вблизи поверхности Земли нуль отсчета выбирают на меньшей высоте.

Как следует из рисунка, , .

Потенциальная энергия в этом случае характеризует энергию гравитационного притяжения материальной точки к Земле.

Потенциальная энергия материальной точки массой m, поднятого на высоту H над нулем отсчета равна:

При этом потенциальная энергия, как и работа, может принимать отрицательное, положительное и нулевое значение.

Отрицательное значение работа силы тяжести принимает при движении тела вверх

Положительное значение принимает при движении вниз

При движении тела по замкнутой траектории работа силы тяжести равна нулю.

Следовательно, равна нулю и работа силы тяжести на всем замкнутом контуре.

Силы, обладающие такими свойствами, называют консервативными.

Работа силы тяжести не зависит от формы траектории тела; она определяется лишь начальным и конечным положениями тела.

Если потенциальная энергия тела в начальном положении больше его потенциальной энергии в конечном положении (Ep0>Ep), то согласно выражению

работа потенциальной энергии положительна. Т.е. сила направлена в сторону убывания потенциальной энергии. Такая закономерность имеет общий характер и справедлива не только для гравитационного, но и для любого фундаментального взаимодействия.

Состояние с меньшей потенциальной энергией является энергетически выгодным.

Принцип минимума потенциальной энергии: любая замкнутая система стремится перейти в такое состояние, в котором ее потенциальная энергия минимальна.

Т.о., состояние с большей потенциальной энергией является энергетически невыгодным. Это подтверждается примерами видов равновесия тела.

Устойчивое равновесие — равновесие, при котором тело, выведенное из положения равновесия, возвращается в первоначальное положение.

При отклонении шара из положения равновесия его потенциальная энергия возрастает. Сила тяжести возвращает его к положению равновесия, в котором его потенциальная энергия минимальна.

Неустойчивое равновесие — равновесие, при котором тело, выведенное из положения равновесия, не возвращается в первоначальное положение.

Безразличное равновесие — равновесие, при котором соседние положения тела также являются равновесными.

Если толкнуть тело в любую сторону, то оно, согласно первому закону Ньютона, будет двигаться прямолинейно и равномерно, удаляясь от начального положения.

Потенциальная энергия упругодеформированной пружины равна работе силы упругости при переходе пружины из деформированного состояния в недеформированное.

Вопрос 3

Определим физическую величину, изменяющуюся при совершении силой работы. Рассмотрим для этого движение тела массой m, скорость которого увеличивается от v0 до v под действием всех приложенных к нему сил.

Работа равнодействующей постоянной силы F, совпадающей по направлению с перемещением Δx, равна

Так как , , т.о.

или (1)

Левая часть формулы (работа) является пространственной характеристикой внешнего воздействия на тело (систему).

Правая часть содержит изменение физической величины, которая характеризует энергию движения тела, или кинетическую энергию.

Кинетическая энергия тела — скалярная физическая величина, равная половине произведения массы тела на квадрат его скорости:

Кинетическая энергия, как и работа, измеряется в джоулях (1 Дж).

Кинетическая энергия в начальный момент времени

Формулу (1) называют теоремой о кинетической энергии.

Теорема о кинетической энергии: изменение кинетической энергии тела равно работе всех сил, действующих на тело:

Ek – Ek0 = А

Кинетическая энергия тел зависит только от их масс и скоростей. Как мы увидим дальше, полная механическая энергия системы зависит от скоростей тел и расстояний между ними.

Очень часто важно знать не только работу, но и время, в течение которого она произведена. Поэтому надо ввести еще одну величину — мощность.

Работа может быть совершена как за большой промежуток времени, так и за очень малый. На практике, однако, далеко не безразлично, быстро или медленно может быть произведена работа. Временем, в течение которого совершается работа, определяют производительность любого двигателя. Очень большую работу может совершить и крошечный электромотор, но для этого понадобится много времени. Потому наряду с работой вводят величину, характеризующую быстроту, с которой она производится, — мощность.

Мощностью называют скалярную величину, равную отношение работы А к интервалу времени Δt, за который эта работа совершена:

(1)

Иными словами, мощность численно равна работе, совершенной в единицу времени.

Подставляя в формулу (1) вместо работы А ее выражение, получим

Таким образом, мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между направлениями этих векторов.

Понятие мощности вводится для оценки работы за единицу времени, совершаемой каким-либо механизмом (насосом, подъемным краном, мотором машины и т. д.). Поэтому в формулах под F всегда подразумевается сила тяги.

В СИ мощность выражается в ваттах (Вт). Мощность равна 1 Вт, если работа 1 Дж совершается за 1 с.

Справка: единица мощность «ватт» названа в честь английского изобретателя Дж. Уатта (1736-1819), который первым создал паровую машину, получившую практическое применение.

Мощность можно повысить как за счет увеличения действующих сил, так и за счет увеличения скорости движения. Подобная закономерность имеет общий характер и справедлива не только для гравитационного, но и для любого фундаментального взаимодействия.

Вопрос 4

В изолированной системе тел положительная работа внутренних сил увеличивает кинетическую энергию и уменьшает потенциальную. Отрицательная работа, напротив, увеличивает потенциальную энергию и уменьшает кинетическую. Именно благодаря этому выполняется закон сохранения энергии.

Снова обратимся к простой системе тел, состоящей из земного шара и поднятого над Землей тела, например камня.

Камень падает под действием силы тяжести. Силу сопротивления воздуха учитывать не будем. Работа, совершаемая силой тяжести при перемещении камня из одной точки в другую, равна изменению (увеличению) кинетической энергии камня:

А = ΔЕk (1)

В то же время эта работа равна уменьшению потенциальной энергии:

А = -ΔЕp (2)

Работа силы всемирного тяготения, действующей со стороны камня на Землю, практически равна нулю. Из-за большой массы Земли ее перемещением и изменением скорости можно пренебречь. Так как в формулах (1) и (2) левые части одинаковы, то равны и правые части:

ΔЕk = -ΔEp (3)

Равенство (3) означает, что увеличение кинетической энергии системы равно убыли ее потенциальной энергии (или наоборот). Отсюда вытекает, что

ΔЕk + ΔЕp = 0,

или

Δ(Еk + Еp) = 0 (4)

Изменение суммы кинетической и потенциальной энергий системы равно нулю.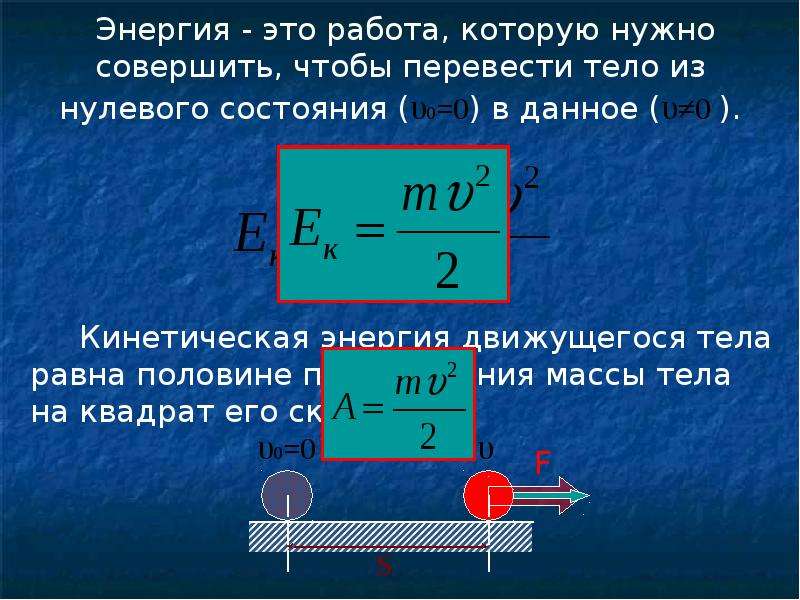

Величину Е, равную сумме кинетической и потенциальной энергий системы, называют механической энергией системы:

Е = Еk + Еp (5)

Так как изменение полной энергии системы в рассматриваемом случае согласно равно нулю, то энергия остается постоянной:

Е = Еk + Ep = const (6)

Таким образом, в изолированной системе, в которой действуют консервативные силы, механическая энергия сохраняется. В этом состоит закон сохранения механической энергии. Энергия не создается и не уничтожается, а только превращается из одной формы в другую: из кинетической в потенциальную и наоборот.

Закон сохранения полной механической энергии предполагает взаимное превращение кинетической энергии в потенциальную и обратно в равных количествах. При этом полная энергия остается неизменной. Закон сохранения энергии проявляется при прыжках с трамплина, при натягивании лука, в игрушке йо-йо.

Приложение 1

1. Мяч массой 500 г летит со скоростью 18 км/ч. Чему равен импульс мяча?

2. Тележка массой 250 г движется равномерно по горизонтальной поверхности стола со скоростью 18 км/ч. Чему равен импульс тележки?

3. Мяч массой 350 г летит со скоростью 36 км/ч. Чему равен импульс мяча?

4. Тележка массой 450 г движется равномерно по горизонтальной поверхности стола со скоростью 36 км/ч. Чему равен импульс тележки?

5. Две тележки массами 3 кг и 10 кг движутся навстречу друг другу. Скорости тележек соответственно равны 18 км/ч и 36 км/ч. Определить модуль скорости тележек после абсолютно неупругого столкновения.

6. Вагон массой 6,5 т, движущийся по горизонтальному пути со скоростью 18 км/ч, автоматически на ходу сцепился с неподвижным вагоном массой 4,5 т. С какой скоростью будут двигаться вагоны после сцепления?

7. По железнодорожному полотну движется платформа с песком массой 20 т со скоростью 1 м/с. Ее догоняет горизонтально летящий со скоростью 800 м/с снаряд массой 50 кг и врезается в песок без взрыва. С какой скоростью будет двигаться платформа с застрявшем в песке снарядом?

8. Две тележки массами 14 кг и 25 кг движутся навстречу друг другу. Скорости тележек соответственно равны 36 км/ч и 72 км/ч. Определить модуль скорости тележек после абсолютно неупругого столкновения.

Механическая работа – это… Что такое Механическая работа?

Механическая работа

Работа силы

Ключевые статьи

См. также: Портал:Физика

Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы^[1].

Определение

В механике можно ввести понятие работы, исходя из довольно простых представлений^[2]

Работа силы (сил) над одной точкой

• Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения^[3]:

Здесь точкой обозначено скалярное произведение^[4],  — вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа.

Если сила не постоянна, то в этом случае она вычисляется как интеграл^[5]:

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат^[6], интеграл определяется^[7] следующим образом:

,

где и  — радиус-векторы начального и конечного положения тела соответственно.

• Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.

Работа силы (сил) над системой или неточечным телом

Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой).

Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.

• Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Кинетическая энергия

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).

Если  — полная работа, совершённая над частицей, определяемая как сумма работ совершенных приложенными к частице силами, то она выражается как:

где называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до величины скорости и выражается как:

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Потенциальная энергия

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая , такая что

Если все силы, действующие на частицу консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:

.

Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы

является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.

Работа в термодинамике

В термодинамике работа, совершенная газом при расширении^[8], рассчитывается как интеграл давления по объёму:

Работа, совершенная над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.

• Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объема, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
• В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет

Видно, что это и есть произведение давления на приращение объема вблизи данной элементарной площадкой. А просуммировав по всем dS получим конечный результат, где будет уже полное приращение объема, как и в главной формуле параграфа.

Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.

Пусть материальная точка движется по непрерывно дифференцируемой кривой , где s — переменная длина дуги, и на неё действует сила , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина , называется элементарной работой силы на участке и принимается за приближенное значение работы, которую производит сила , воздействующая на материальную точку, когда последняя проходит кривую . Сумма всех элементарных работ является интегральной суммой Римана функции .

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма всех элементарных работ, когда мелкость разбиения стремится к нулю, называется работой силы вдоль кривой .

Таким образом, если обозначить эту работу буквой , то, в силу данного определения,

,

следовательно,

(1).

Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути , является непрерывно дифференцируемой функцией, то из формулы (1) получим

Единицей измерения работы в СИ является Джоуль, в СГС — эрг

1 Дж = 1 кг·м²/с² = 1 Н·м

1 эрг = 1 г·см²/с² = 1 дин·см

1 эрг = 10⁻⁷Дж

Ссылки

1. ↑ Концепции современного естествознания
2. ↑ Такие представления можно конкретизировать как систему постулатов, приводящую достаточно однозначно к определению, описанному в основной статье:
   1. работу совершает только компонента силы, совпадающая с направлением перемещения точки, к которой она приложена, или противоположная направлению перемещения точки (в последнем случае работа считается отрицательной),
   2. работа постоянной силы пропорциональна компоненте такой силы, описанной в пункте 1, и длине вектора перемещения,
   3. работа по перемещению точки за несколько последовательных промежутков времени суммируется (работа за всё это время равна сумме работ, совершенных за каждый промежуток),
   4. работа суммы (векторной суммы) сил, приложенных к точке равна сумме работ, совершенных каждой силой в отдельности,
   5. работа, совершенная над системой (телом) равна сумме работ, совершенных над каждой ее частью (в частности — равна сумме работ, совершенных над каждой точкой системы).
3. ↑ Механическая работа. Мощность
4. ↑ Можно считать, что механическая работа может служить в области физики одной из главных иллюстраций для скалярного произведения.
5. ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения , на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях суммируется, что и дает в результате интеграл.
6. ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
7. ↑ По сути через предыдущий, поскольку здесь ; вектор же малого перемещения совпадает с .
8. ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить ее к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

Литература

• Кудрявцев Л. Д. Курс математического анализа. — 5-е, переработанное и дополненное. — М.: Дрофа, 2003. — Т. 1. — С. 640—641. — 703 с.

См. также

Полная механическая энергия — урок. Физика, 8 класс.

Полная механическая энергия тела равна сумме его кинетической и потенциальной энергии.

Полную механическую энергию рассматривают в тех случаях, когда действует закон сохранения энергии и она остаётся постоянной.

Если на движение тела не оказывают влияния внешние силы, например, нет взаимодействия с другими телами, нет силы трения или силы сопротивления движению, тогда полная механическая энергия тела остаётся неизменной во времени.

Eпот&plus;Eкин=const

 

Разумеется, что в повседневной жизни не существует идеальной ситуации, в которой тело полностью сохраняло бы свою энергию, так как любое тело вокруг нас взаимодействует хотя бы с молекулами воздуха и сталкивается с сопротивлением воздуха. Но, если сила сопротивления очень мала и движение рассматривается в относительно коротком промежутке времени, тогда такую ситуацию можно приближённо считать теоретически идеальной.

Закон сохранения полной механической энергии обычно применяют при рассмотрении свободного падения тела, при его вертикальном подбрасывании или в случае колебаний тела.

Пример:

При вертикальном подбрасывании тела его полная механическая энергия не меняется, а кинетическая энергия тела переходит в потенциальную и наоборот.

Преобразование энергии отображено на рисунке и в таблице.

 

 

Точка нахождения тела	Потенциальная энергия	Кинетическая энергия	Полная механическая энергия
3) Самая верхняя  (h = max)	Eпот = m⋅g⋅h (max)	Eкин = 0	Eполная = m⋅g⋅h
2) Средняя  (h = средняя)	Eпот = m⋅g⋅h	Eкин = m⋅v22	Eполная=m⋅v22+m⋅g⋅h
1) Самая нижняя  (h = 0)	Eпот = 0	Eкин = m⋅v22 (max)	Eполная = m⋅v22

 

Исходя из того, что в начале движения величина кинетической энергии тела одинакова с величиной его потенциальной энергии в верхней точке траектории движения, для расчётов могут быть использованы ещё две формулы.

Если известна максимальная высота, на которую поднимается тело, тогда можно определить максимальную скорость движения по формуле:

 

 vmax=2⋅g⋅hmax.

 

Если известна максимальная скорость движения тела, тогда можно определить максимальную высоту, на которую поднимается тело, брошенное вверх, по такой формуле:

 

 hmax=vmax22g.

 

 

Чтобы отобразить преобразование энергии графически, можно использовать имитацию «Энергия в скейт-парке», в которой человек, катающийся на роликовой доске (скейтер) перемещается по рампе. Чтобы изобразить идеальный случай, предполагается, что не происходит потерь энергии в связи с трением. На рисунке показана рампа со скейтером, и далее на графике показана зависимость механической энергии от места положения скейтера на траектории.

 

 

На графике синей пунктирной линией показано изменение потенциальной энергии. В средней точке рампы потенциальная энергия равна \(нулю\). Зелёной пунктирной линией показано изменение кинетической энергии. В верхних точках рампы кинетическая энергия равна \(нулю\). Жёлто-зелёная линия изображает полную механическую энергию — сумму потенциальной и кинетической — в каждый момент движения и в каждой точке траектории. Как видно, она остаётся \(неизменной\) во всё время движения. Частота точек характеризует скорость движения — чем дальше точки расположены друг от друга, тем больше скорость движения.

 

 

На графике видно, что значение потенциальной энергии в начальной точке совпадает со значением кинетической энергии в середине рампы.

В реальной ситуации всегда происходят потери энергии, так как часть энергии выделяется в виде тепла под влиянием сил трения и сопротивления. 

Поэтому для того, чтобы автомобиль двигался с равномерной и неизменной скоростью, необходимо постоянно подводить дополнительную энергию, которая компенсировала бы энергетические потери.

Работа силы тяготения. Потенциальная энергия в поле тяготения

Работа силы тяготения. Потенциальная энергия в поле тяготения

Подробности

Просмотров: 539

«Физика – 10 класс»

В чём выражается гравитационное взаимодействие тел?
Как доказать наличие взаимодействия Земли и, например, учебника физики?

Как известно, сила тяжести — консервативная сила. Теперь найдём выражение для работы силы тяготения и докажем, что работа этой силы не зависит от формы траектории, т. е. что сила тяготения также консервативная сила.

Напомним, что работа консервативной силы по замкнутому контуру равна нулю.

Пусть тело массой m находится в поле тяготения Земли. Очевидно, что размеры этого тела малы по сравнению с размерами Земли, поэтому его можно считать материальной точкой. На тело действует сила тяготения

где G — гравитационная постоянная,
М — масса Земли,
r — расстояние, на котором находится тело от центра Земли.

Пусть тело перемещается из положения А в положение В по разным траекториям: 1) по прямой АВ; 2) по кривой АА’В’В; 3) по кривой АСВ (рис. 5.15)

1. Рассмотрим первый случай. Сила тяготения, действующая на тело, непрерывно уменьшается, поэтому рассмотрим работу этой силы на малом перемещении Δr_i = r_{i + 1} — r_i. Среднее значение силы тяготения равно:

где r²_сpi = r_ir_{i + 1}.

Чем меньше Δri, тем более справедливо написанное выражение r²_сpi = r_ir_{i + 1}.

Тогда работу силы F_сpi, на малом перемещении Δr_i, можно записать в виде

Суммарная работа силы тяготения при перемещении тела из точки А в точку В равна:

2. При движении тела по траектории АА’В’В (см. рис. 5.15) очевидно, что работа силы тяготения на участках АА’ и В’В равна нулю, так как сила тяготения направлена к точке О и перпендикулярна любому малому перемещению по дуге окружности. Следовательно, работа будет также определяться выражением (5.31).

3. Определим работу силы тяготения при движении тела от точки А к точке В по траектории АСВ (см. рис. 5.15). Работа силы тяготения на малом перемещении Δs_i равна ΔА_i = F_срiΔs_icosα_i,..

Из рисунка видно, что Δs_icosα_i = – Δr_i, и суммарная работа опять же будет определяться по формуле (5. 31).

Итак, можно сделать вывод, что А₁ = А₂ = А₃, т. е. что работа силы тяготения не зависит от формы траектории. Очевидно, что работа силы тяготения при перемещении тела по замкнутой траектории АА’В’ВА равна нулю.

Сила тяготения — консервативная сила.

Изменение потенциальной энергии равно работе силы тяготения, взятой с обратным знаком:

Если выбрать нулевой уровень потенциальной энергии на бесконечности, т. е. Е_пВ = 0 при r_В → ∞, то следовательно,

Потенциальная энергия тела массой m, находящегося на расстоянии r от центра Земли, равна:

Закон сохранения энергии для тела массой m, движущегося в поле тяготения, имеет вид

где υ₁ — скорость тела на расстоянии r₁ от центра Земли, υ₂ — скорость тела на расстоянии r₂ от центра Земли.

Определим, какую минимальную скорость надо сообщить телу вблизи поверхности Земли, чтобы оно в отсутствие сопротивления воздуха могло удалиться от неё за пределы сил земного притяжения.

Минимальную скорость, при которой тело в отсутствие сопротивления воздуха может удалиться за пределы сил земного притяжения, называют второй космической скоростью для Земли.

На тело со стороны Земли действует сила тяготения, которая зависит от расстояния центра масс этого тела до центра масс Земли. Поскольку неконсервативных сил нет, полная механическая энергия тела сохраняется. Внутренняя потенциальная энергия тела остаётся постоянной, так как оно не деформируется. Согласно закону сохранения механической энергии

На поверхности Земли тело обладает и кинетической, и потенциальной энергией:

где υ_II — вторая космическая скорость, М₃ и Я₃ — соответственно масса и радиус Земли.

В бесконечно удаленной точке, т. е. при r → ∞, потенциальная энергия тела равна нулю (W_п = 0), а так как нас интересует минимальная скорость, то и кинетическая энергия также должна быть равна нулю: W_к = 0.

Из закона сохранения энергии следует:

отсюда

Эту скорость можно выразить через ускорение свободного падения вблизи поверхности Земли (при расчётах, как правило, этим выражением пользоваться удобнее). Поскольку то GM₃ = gR²₃.

Следовательно, искомая скорость

Точно такую же скорость приобрело бы тело, упавшее на Землю с бесконечно большой высоты, если бы не было сопротивления воздуха. Заметим, что вторая космическая скорость в раза больше, чем первая.

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Законы сохранения в механике – Физика, учебник для 10 класса – Класс!ная физика

Импульс материальной точки — Закон сохранения импульса — Реактивное движение. Успехи в освоении космоса — Примеры решения задач по теме «Закон сохранения импульса» — Механическая работа и мощность силы — Энергия. Кинетическая энергия — Примеры решения задач по теме «Кинетическая энергия и её изменение» — Работа силы тяжести. Консервативные силы — Работа силы упругости. Консервативные силы — Потенциальная энергия — Закон сохранения энергии в механике — Работа силы тяготения. Потенциальная энергия в поле тяготения — Примеры решения задач по теме «Закон сохранения механической энергии» — Основное уравнение динамики вращательного движения — Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси — Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»

Связь между работой и механической энергией, Рон Куртус

SfC Home> Физика> Сила>

Рона Куртуса

Работа – это измерение силы, действующей на объект, которая преодолевает силу сопротивления (например, трение или гравитацию), умноженную на расстояние, на которое перемещается объект. Если нет расстояния, нет работы, какие бы усилия ни прилагались.

В определенных ситуациях существует взаимосвязь между этой работой и механической энергией (в отличие от тепла или лучистой энергии).

Когда вы ускоряете объект, вы выполняете работу против инерции , так что работа равна изменению кинетической энергии объекта.

Изменение KE означает, что вы ускорили объект.

Когда вы ускоряете объект, вы изменяете его скорость и, следовательно, его KE. Ускоряя объект в течение определенного периода времени, вы перемещаете объект на некоторое расстояние, изменяя его скорость. Таким образом, вы работаете против инерции

.

, вы выполняете работу против инерции , так что работа равна изменению кинетической энергии объекта.

Когда вы выполняете работу против непрерывных сил сопротивления , таких как сила тяжести или натяжение пружины, выполненная работа равна изменению потенциальной энергии объекта.

Вопросы, которые могут у вас возникнуть:

• Какое уравнение для работы?
• Как работает изменение кинетической энергии?
• Когда происходит изменение потенциальной энергии на работе?

Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц

---

---

Уравнение для работы

Определение механической работы (в отличие от термодинамической работы) состоит в том, что она равна силе против некоторого сопротивления, умноженной на расстояние, пройденное при приложении этой силы.

Примечание : К сожалению, многие учебники физики небрежно опускают идею о том, что существует сила сопротивления инерции, а также другие возможные сопротивления.

Уравнение работы:

W = Fd

где:

• W – работа в джоулях (Дж или кг-м² / с²)
• F – сила, приложенная к объекту, преодолевая любое сопротивление, в ньютонах (Н или кг-м / с²)
• d – расстояние или смещение, на которое объект перемещается в направлении силы, в метрах (м)
• Fd – F раза d

Таким образом, если вы примените силу F = 3 ньютона (3 Н), чтобы преодолеть инерцию и, возможно, трение, и переместить объект на расстояние d = 5 метров (5 м), проделанная работа будет W = Fd = 15 джоулей.

Работа как изменение кинетической энергии

Когда вы ускоряете объект, вы меняете его скорость.

Когда вы ускоряете объект, вы выполняете работу против инерции плюс любые силы сопротивления, такие как гравитация или трение, на расстоянии, на которое ускоряется объект.

Это означает, что скорость объекта – и, следовательно, его кинетическая энергия – изменяется на пройденном расстоянии.

Кинетическая энергия объекта:

KE = mv ² /2

где

• KE – кинетическая энергия в Дж или кг-м ² / с ²
• м – масса объекта в кг
• v – скорость в м / с

Работа, выполняемая при изменении скорости против некоторого сопротивления, тогда равна изменению кинетической энергии объекта:

ΔKE = mv _f ² /2 – mv _i ² /2

Вт = ΔKE

где

• Δ означает изменение (дельта заглавной греческой буквы)
• v _f – конечная скорость объекта
• v _i – начальная скорость

Таким образом, в определенных ситуациях работа – это изменение кинетической энергии.

( См. Дополнительную информацию в разделе «Доказательство того, что работа может быть изменением кинетической энергии». )

Работа как изменение потенциальной энергии

Некоторые силы сопротивления, такие как сила тяжести и натяжение пружины, непрерывно действуют на объект, так что объект может перемещаться из своего текущего положения. Это называется его потенциальной энергией ( PE ).

Перемещение объекта с одного PE на более высокий требует работы, которую можно измерить по изменению потенциальной энергии ( ΔPE ).

Пример с гравитацией

Например, PE объекта из-за силы тяжести составляет:

PE = mgh _i

где

• м – масса объекта
• g – ускорение свободного падения
• h _i – начальная высота над землей

Если вы подняли объект на другую высоту ( h _f ), новая потенциальная энергия будет:

PE = mgh _f

Объем выполненных работ составит

W = Fd

где

Таким образом:

W = мг (h _f – h _i )

W = mgh _f – mgh _i

W = PE _f – PE _i = ΔPE

Вт = ΔPE

Таким образом, в определенных ситуациях работа – это изменение потенциальной энергии.

Работа как комбинация KE и PE

Если вы проецируете объект вверх, вы выполняете работу как против силы тяжести, так и против инерции. В этой ситуации общий объем выполненных работ составляет:

Вт = ΔPE + ΔKE

Сводка

Когда вы прикладываете достаточно силы к объекту, чтобы преодолеть силу сопротивления , так что вы перемещаете этот объект, вы выполняете работу над этим объектом. Между этой работой и механической энергией существует связь.

Когда вы ускоряете объект, вы выполняете работу против инерции, так что работа равна изменению кинетической энергии объекта.

Когда вы работаете против постоянных сил сопротивления, таких как сила тяжести или натяжение пружины, вы изменяете потенциальную энергию объекта.

---

Правила физики

---

Ресурсы и ссылки

Полномочия Рона Куртуса

Сайтов

Работа: передача механической энергии – Из онлайн-книги по физике Бенджамина Кроуэлла

Определение и математика работы – Физический класс

Работа (физика) – Википедия

Работа, энергия и мощность – HyperPhysics

Физические ресурсы

Книги

(Примечание: Школа чемпионов может получать комиссионные от покупки книг)

Книги по физике труда с самым высоким рейтингом

---

Поделиться страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

---

Студенты и исследователи

Веб-адрес этой страницы:
www. school-for-champions.com/science/
work_energy.htm

Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.

Авторские права © Ограничения

---

Где ты сейчас?

Школа чемпионов

Физические темы

Взаимосвязь между работой и механической энергией

---

Работа – Энергетическое образование

Работа – это передача механической энергии от одного объекта к другому.Поскольку работа – это движение энергии, она измеряется в тех же единицах, что и энергия: джоулях (Дж). Определение работы в контексте физики сильно отличается от того, как оно используется в повседневной жизни человека, и выглядит следующим образом: ^[1]

Работа выполняется при приложении силы к объекту на расстоянии.

Это означает, что когда к объекту на расстоянии применяется сила, это влияет на общую энергию объекта. Объект будет либо ускоряться, либо замедляться, что приведет к изменению его кинетической энергии (см. Рисунок 1), либо у него будет измененная потенциальная энергия, если, например, он был поднят на определенную высоту под действием силы тяжести. ^[1]

Рис. 1. Питчер работает с бейсбольным мячом, чтобы увеличить его кинетическую энергию. Его рука отводится как можно дальше назад, а затем как можно дальше вперед, чтобы максимально увеличить расстояние, на которое была приложена сила. ^[2]

Работа также выходит за рамки того, что человек может видеть физически. Это также может повлиять на микроскопические свойства системы, такие как температура. В 1843 году эту идею начали исследовать ученые, ^[3] , и ее результаты привели к формулировке того, что сейчас известно как термодинамика.Работа с системой может повлиять на ее внутреннюю энергию, как и добавление тепла. Тем не менее, эти два процесса принципиально разные, и их можно изучить на странице тепло и работа.

Все описанные до сих пор случаи того, как работа может влиять на систему, можно суммировать в одном уравнении: ^[1]

[математика] W = \ Delta K + \ Delta U + \ Delta E_ {th} [/ math]

Это уравнение говорит, что работа ([math] W [/ math]) может изменять ([math] \ Delta [/ math]) кинетическую энергию системы ([math] K [/ math]), потенциальную энергию ([math] U [/ math]), тепловая энергия ([math] E_ {th} [/ math]) или любая их комбинация.

Фактически выполненную работу можно рассчитать по следующей формуле: ^[4]

[математика] W = \ vec {F} \ cdot \ vec {d} [/ math]

Где

• [math] W [/ math] – работа или изменение механической энергии, измеряемое в джоулях (Дж)
• [math] F [/ math] – сила, измеряемая в ньютонах (Н)
• [math] d [/ math] – смещение объекта

Стрелки над силой и смещением указывают, что они являются векторами. Это означает, что у них есть связанное с ними направление, которое имеет важное значение для того, сколько работы выполняется с объектом. Если оба направления совпадают, как показано на рисунке 1, энергия системы увеличится, что означает, что была проделана положительная работа. Если направления противоположны, например сила трения и сопротивления воздуха движущемуся автомобилю, энергия системы будет уменьшаться, что приведет к выполнению отрицательной работы.

С точки зрения физики работа никогда не бывает чем-то, что есть у объекта. Это всего лишь то, что один объект делает с другим. Работа изменяет количество механической и внутренней энергии, которой обладают объекты.Когда работа выполняется на системе или объекте, к ней добавляется энергия. Когда работа выполняется на над системой или объектом, она отдает часть своей энергии чему-то другому.

Бросок мяча означает, что рука прикладывает силу, когда рука движется вперед. Приложив силу к мячу на этом расстоянии, рука выполняет работу с мячом, и мяч получает кинетическую энергию. Это то, что придает ему скорость.

Математические отношения между полной работой и полной энергией описываются теоремой работы-энергии и сохранения энергии. Простые машины могут изменять количество силы, необходимой для перемещения объекта, но сила должна прилагаться через большее расстояние; они не меняют объем проделанной работы.

Список литературы

1. ↑ ^{1.0 1.1 1.2} Р. Д. Найт, «Работа и кинетическая энергия» в книге Физика для ученых и инженеров: стратегический подход, 3-е изд. Сан-Франциско, США: Pearson Addison-Wesley, 2008, глава 11, разделы 2 и 3, стр. 278-301.
2. ↑ Wikimedia Commons [Online], Доступно: https: // upload.wikimedia.org/wikipedia/commons/2/25/Baseball_pitching_motion_2004.jpg
3. ↑ Hyperphysics, Механический эквивалент тепла [Online], Доступно: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/heat.html#c3
4. ↑ R. Nave. (2015, 21 июня) Работа Онлайн. Доступно: http://hyperphysics.phy-astr.gsu.edu/hbase/wcon.html

8.3: Механическая энергия и сохранение энергии

Вспомните теорему работы-энергии, которая связывает чистую работу, проделанную над объектом, с его изменением кинетической энергии на пути от точки \ (A \) к точке \ (B \ ): \ [\ begin {align} W ^ {net} = \ Delta K = K_B – K_A \ end {align} \], где \ (K_A \) – начальная кинетическая энергия объекта, а \ (K_B \) – его конечная кинетическая энергия. { NC} = \ Delta U_1 + \ Delta U_2 + \ Delta K \ end {align} \] То есть работа, совершаемая неконсервативными силами, равна сумме изменений потенциальной и кинетической энергии.{NC} = \ Delta U + \ Delta K \]

В частности, обратите внимание, что если нет неконсервативных сил, выполняющих работу на объекте:

\ [\ Delta K + \ Delta U = 0 \ text {если нет неконсервативных сил} \]

\ (- \ Delta U = \ Delta K \)

То есть сумма изменений потенциальной и кинетической энергии объекта всегда равна нулю. Это означает, что если потенциальная энергия объекта увеличивается, то кинетическая энергия объекта должна уменьшаться на ту же величину.

Мы можем представить «механическую энергию», \ (E \), объекта как сумму потенциальной и кинетической энергии объекта:

\ [E = U + K \]

Если объект стартовал в позиции \ (A \), с потенциальной энергией \ (U_A \) и кинетической энергией \ (K_A \), и закончил в позиции \ (B \) с потенциальной энергией \ (U_B \) и кинетической энергией. {NC} = \ Delta U + \ Delta K = \ Delta E \ end {align} \]

, и если неконсервативные силы не работают с объектом, то механическая энергия объекта не изменяется:

\ [\ begin {align} \ Delta E & = 0 \ quad \ text {если нет неконсервативных сил} \\ \ поэтому E & = \ text {constant} \ end {align} \]

Это то, что мы обычно называем «сохранением механической энергии».Если нет неконсервативных сил, выполняющих работу с объектом, его механическая энергия сохраняется (т. Е. Постоянна).

Введение механической энергии дает нам совершенно другой взгляд на механику. Теперь мы можем думать об объекте как об имеющем «энергию» (потенциальную и / или кинетическую), и мы можем думать о силах как об изменении энергии объекта.

Упражнение \ (\ PageIndex {1} \)

Имеет ли значение значение механической энергии объекта или значение имеет только разница в механической энергии?

1. Да, значение механической энергии имеет значение. В любой момент времени объект будет обладать поддающимся количественному измерению количеством механической энергии.
2. Нет, значение не имеет смысла, потому что значение потенциальной энергии произвольно. Имеют значение только различия в механической энергии.
3. Нет, значение не имеет смысла, потому что и потенциальная, и кинетическая энергии произвольны. Их значения будут меняться в зависимости от того, где вы установите нулевое значение энергии.
4. Это зависит от того, какие консервативные силы действуют на объект (и, следовательно, какой «вид» потенциальной энергии имеет объект).{other} + \ Delta U + \ Delta K = 0 \ end {align} \], что мы обычно называем «сохранением энергии». То есть полная энергия в системе, включая кинетическую, потенциальную и любую другую форму (например, тепловую, электрическую и т. Д.), Постоянна, если на систему не действует какой-либо внешний агент.

   Мы всегда можем включить этого внешнего агента в систему, чтобы общая энергия системы была постоянной. Самая большая система, которую мы можем иметь, – это сама Вселенная. Таким образом, общая энергия во Вселенной постоянна и может преобразовываться только из одного типа в другой, но никакая энергия не может быть добавлена ​​или удалена из Вселенной.

   Мысли Оливии

   Вот пример, который может помочь вам понять концепцию внешних агентов и энергосбережения. Скажем, у нас есть масса, которая свисает с пружины, так что масса колеблется вверх и вниз, как йо-йо. Если мы определим нашу систему, чтобы она включала в себя пружину, массу и гравитацию, энергия будет сохранена (энергия преобразуется из потенциальной энергии в кинетическую и обратно).

   А что, если кто-то держит конец пружины и начинает идти так, что вся система ускоряется? Энергия не сохраняется, потому что система получает кинетическую энергию, казалось бы, из ниоткуда.На систему действует внешний агент (человек). Если мы расширим нашу систему так, чтобы она включала в себя пружину, массу, гравитацию и человека , энергия сохраняется. Вместо кинетической энергии, «идущей из ниоткуда», мы можем видеть, что она на самом деле исходит от человека, преобразующего химическую энергию в своем теле, чтобы двигать мускулами.

   Рисунок \ (\ PageIndex {1} \): человек ускоряет массу и пружину при ходьбе. Если система не включает человека, энергия не сохраняется.Если он действительно включает человека, энергия сохраняется.

   Но что, если в нашей новой системе действует внешний агент? Мы можем продолжать «уменьшать масштаб», чтобы включать все больше и больше внешних источников в определение нашей системы. Если вы продолжаете уменьшать масштаб, в конечном итоге вы достигнете точки, когда вся Вселенная будет включена в вашу систему. На этом этапе вы больше не можете уменьшать масштаб. Это означает, что, если Вселенная – это ваша система, энергия всегда должна сохраняться, потому что не может быть никаких внешних агентов, действующих на систему.

   Пример \ (\ PageIndex {1} \)

   Рисунок \ (\ PageIndex {2} \): блок запускается по поверхности без трения, сжимая пружину на расстояние \ (D \). Верхняя панель показывает пружину в состоянии покоя, а нижняя панель показывает пружину, сжатую на расстояние \ (D \) непосредственно перед тем, как освободить блок.

   Блок массой \ (м \) может скользить по горизонтальной поверхности без трения. Горизонтальная пружина с жесткостью пружины \ (k \) прикреплена к стене одним концом, а другой конец может двигаться, как показано на рисунке 8.3.2. Система координат определяется так, что ось \ (x \) горизонтальна, а свободный конец пружины находится в точке \ (x = 0 \), когда пружина находится в состоянии покоя. Блок прижимается к пружине, так что пружина сжимается на расстояние \ (D \). Затем блок снимается. Какая скорость будет у блока, когда он выйдет из пружины?

   Решение :

   Это снова тот же пример, что мы видели в главах 6 и 7. Мы покажем здесь, что эта проблема решается очень легко с помощью сохранения энергии.2} {m}} \ end {align} \], как мы обнаружили ранее.

   Пример \ (\ PageIndex {2} \)

   Рисунок \ (\ PageIndex {3} \): блок скользит вниз по склону, прежде чем скользить по плоской поверхности и остановиться.

   Блок массы \ (m \) покоится на наклоне, который составляет угол \ (\ theta \) по отношению к горизонтали, как показано на рисунке \ (\ PageIndex {3} \). Блок слегка подталкивают, чтобы преодолеть силу статического трения, и блок начинает ускоряться вниз по склону. Внизу уклона блок скользит по горизонтальной поверхности.Коэффициент кинетического трения между блоком и уклоном равен \ (\ mu_ {k1} \), а коэффициент кинетического трения между блоком и горизонтальной поверхностью равен \ (\ mu_ {k2} \). Если предположить, что блок начался в состоянии покоя на расстоянии \ (L \) от нижней части склона, как далеко по горизонтальной поверхности будет проскальзывать блок перед остановкой?

   Решение

   Это та же проблема, которую мы решили в , Пример 6.2.1 . В этом случае мы вычислили ускорение блока, используя Второй закон Ньютона, а затем использовали кинематику, чтобы определить, как далеко ушел блок.Мы можем решить эту проблему намного проще, используя сохранение энергии.

   По-прежнему неплохо подумать о том, какие силы действуют на объект, чтобы определить, действуют ли неконсервативные силы. В этом случае силы на блоке равны:

   1. Нормальная сила, которая не работает, поскольку она всегда перпендикулярна движению.
   2. Вес, который работает при изменении высоты объекта, который мы можем смоделировать с помощью функции потенциальной энергии.
   3. Трение, неконсервативная сила, работу которой мы должны определить.

   Разобьем движение на два сегмента: (1) сегмент вдоль наклона (позиции от \ (A \) до \ (B \) на рисунке \ (\ PageIndex {3} \)), где изменяется гравитационная потенциальная энергия. , и (2) горизонтальный отрезок от позиций \ (B \) до позиции \ (C \) на рисунке. Затем мы можем применить сохранение энергии для каждого сегмента.

   Начиная с первого сегмента, мы можем выбрать нулевую гравитационную потенциальную энергию, когда блок находится внизу склона.Блок начинается на высоте \ (h = L \ sin \ theta \) над нижней частью склона. 2 – mgL \ sin \ theta \ end {align} \]

   Наконец, поскольку у нас есть неконсервативная сила, сила кинетического трения, действующая на первый сегмент, нам нужно вычислить работу, совершаемую этой силой.2 \)) равно отрицательному изменению потенциальной энергии (\ (mgL \ sin \ theta \)) за вычетом работы, совершаемой трением (\ (\ mu_ {k1} mg \ cos \ theta L \)) ». Другими словами, блок обладал потенциальной энергией, которая была преобразована в кинетическую энергию и тепло (работу, совершаемую трением, можно рассматривать как тепловую энергию).

   Аналогичным образом поступим для второго отрезка от позиции \ (B \) к позиции \ (C \). Единственная сила, которая может работать вдоль этого сегмента (длины \ (x \)), – это сила кинетического трения, поскольку и вес, и нормальная сила перпендикулярны смещению.{NC} & = \ Delta E \\ – \ mu_ {k2} mg x & = – mgL \ sin \ theta + \ mu_ {k1} mg \ cos \ theta L \\ \, следовательно, x & = L \ frac {1} { \ mu_ {k2}} \ left (\ sin \ theta – \ mu_ {k1} \ cos \ theta \ right) \ end {align} \]

   , что является тем же результатом, что мы получили в примере 6.2.1 .

   Обсуждение

   Используя закон сохранения энергии, мы смогли смоделировать движение блока вниз по склону способом, который был намного проще, чем то, что было сделано в , Пример 6.2.1 .Более того, хотя мы моделировали трение как неконсервативную силу, выполняющую работу, мы получили некоторое представление о том, что это можно рассматривать как потерю энергии. Что касается энергии, мы бы сказали, что блок изначально имел гравитационную потенциальную энергию, которая затем была преобразована в кинетическую энергию, а также в тепловую энергию (в тепле, генерируемом трением).

   Сноски

   1. Вот почему мы определили потенциальную энергию как отрицательную часть работы; он становится положительным, когда мы перемещаем его в ту же сторону уравнения, что и кинетическая энергия!

   Что это и как работает?

   Механическая энергия повсюду вокруг нас.Будь то ребенок, бьющий футбольный мяч, или массивная ветряная турбина, дающая нам электричество, от этой силы никуда не деться. Но что такое механическая энергия? В этом руководстве мы поможем вам больше узнать о механической энергии, о том, как она работает и производит энергию, и почему она важна для вас (и всех нас).

   Что такое механическая энергия и как она работает?

   Механическая энергия – это предмет физической науки. Это энергия движения или энергия движущегося объекта.Все формы жизни и многие системы используют механическую энергию для своего функционирования, а энергию движения можно увидеть в повседневной жизни. Вот несколько примеров:

   • Ребенок держит мяч в воздухе, просматривая поле, чтобы бросить его. Они прилагают силу (удерживают мяч вверх), но еще не совершили никакого количества работы (сила вызывает смещение объекта).
   • Ребенок бьет по мячу (внешняя сила) – сила действует на него, толкая его вперед.
   • Мяч летит по воздуху (энергия движения), опускается (сила тяжести), отскакивает от земли, чтобы снова подняться в точку (потенциальная энергия гравитации), затем возвращается вниз и катится до остановки.
   • Самолет, мчащийся по взлетно-посадочной полосе, представляет собой энергию движения.
   • Самолет, набирающий скорость, врезается в вертолет, передает кинетическую энергию другому летательному аппарату.
   • Частный самолет замедляется до остановки, когда пилот нажимает на педаль тормоза (сила трения).

   Механическая энергия (кинетическая энергия или потенциальная энергия) – это энергия движущегося объекта или энергия, которая хранится в объектах в зависимости от их положения.

   Механическая энергия также является двигателем возобновляемой энергии.Многие формы возобновляемой энергии полагаются на механическую энергию для адекватного производства или преобразования энергии.

   Двумя примерами возобновляемой энергии, зависящей от механической энергии, являются гидроэнергетика и энергия ветра.

   Механическая энергия – это лишь одна из нескольких форм энергии, к которым также относятся:

   • Свет
   • Тепло
   • Звуковая энергия
   • Химическая энергия
   • Электроэнергия
   • Атомная энергия

   Интересно, что все эти формы энергии взаимозаменяемы – переходят из одного состояния в другое в зависимости от обстоятельств.Это потому, что научный закон сохранения гласит, что энергия никогда не перестает существовать полностью; он может только переходить из одной формы в другую.

   Какие примеры механической энергии?

   Механическая энергия может быть произведена живыми существами, твердыми предметами, газами, водой или воздухом. Примеры механической энергии есть повсюду.

   Потенциальная и кинетическая энергия – это всего лишь два примера, которые мы можем увидеть или испытать.

   Пример потенциальной энергии

   Представьте, что вы пришли домой с местного фермерского рынка и среди вашей корзины органических вкусностей есть жирный, сочный, круглый арбуз.

   Вы кладете арбуз на кухонный стол. Теперь он обладает потенциальной энергией из-за своей высоты над полом кухни и из-за своего веса.

   Затем вы случайно толкаете его локтем, когда вытаскиваете банку для хранения свежих органических кофейных зерен. Вы пытаетесь поймать его, когда дыня начинает катиться к краю прилавка. Это энергия движения.

   Поскольку ваши руки заняты банкой и пакетом кофе, ваша дыня падает на пол (сила тяжести – пример неконсервативной силы), врезаясь в керамическую плитку и взрываясь на миллиард кусков.Теперь «работа» сделана, потому что удар разбил дыню на кусочки сочной кашицы. Пунктирный арбуз также создает звуковую энергию, одну из форм энергии, о которых говорилось ранее.

   Пример кинетической энергии

   источник

   Многим из нас нравится чистая энергия, поскольку она благотворно влияет на изменение климата. Мы можем выбрать план экологически чистой энергии при выборе поставщика электроэнергии или установить солнечные батареи в нашем доме.

   Когда мы выбираем план «зеленой» энергии, эта энергия часто вырабатывается турбинами.Существуют различные типы кинетической энергии, которые заставляют турбины производить электричество.

   • Ветер: Например, ветряная турбина – это тип технологии возобновляемой энергии, которая вырабатывает энергию за счет движения воздуха. Когда дует ветер, он вращает лопасти турбины по кругу, что приводит к вращению приводного вала, вырабатывающего электричество, при его вращении.
     
   • Пар: Точно так же паровые турбины используют давление для перемещения лопастей турбины.Лопасти вращаются по кругу, когда пар дует, используя механическую энергию для вращения вала вращателя. Вал вращателя соединен с генератором, который принимает кинетическую энергию и преобразует ее в электрическую. Этот же процесс используется для работы паровых двигателей.
     
   • Вода: Гидроэнергетика получает механическую энергию движения воды через гидротурбины или гидроаккумуляторы. Подобно ветровым или паровым турбинам, гидротурбины используют кинетическую энергию текущей воды для вращения лопастей.С другой стороны, в гидроаккумулирующих системах используются водохранилища на разных высотах для перемещения воды вперед и назад и выработки гидроэлектроэнергии. Оба метода отражают естественные силы механической энергии рек, ручьев, водопадов, океанов и даже дождя.

   Механическая энергия потенциальная или кинетическая?

   Существует два типа механической энергии – движение (кинетическая энергия) и запасенная (потенциальная энергия). Вы можете узнать больше в нашем руководстве, которое объясняет потенциальную и кинетическую энергию.

   Механическое преобразование зависит от количества потенциальной энергии объекта и от того, сколько кинетической энергии он может произвести.

   Однако, независимо от потенциала, энергия движения является неотъемлемой частью производства энергии, и многие источники энергии не могли бы работать без нее.

   Механическая энергия зависит от положения и движения объекта, а ее мощность складывается из суммы движущейся (кинетической энергии) и запасенной (потенциальной) энергии. Другими словами, когда потенциальная энергия объекта объединяется с его кинетической энергией, он создает механическую энергию.

   Например, американские горки получают наибольшую гравитационную потенциальную энергию, когда они достигают первого пика в начале поездки – это то, что определяет общее количество энергии, доступное для движения автомобилей вперед во время поездки.

   Поднимаясь на вершину одного из холмов или петель, он получает потенциальную энергию – чем выше он поднимается, тем больше потенциальной энергии он получает. Когда он переходит в нисходящее движение, он начинает преобразовывать свою потенциальную энергию в кинетическую.По мере того, как тележка движется вниз по холму, ее кинетическая энергия увеличивается; одновременно его потенциальная энергия уменьшается.

   Некоторые примеры объектов с потенциальной энергией: валун на краю обрыва, вода в заткнутой ванне или шар, ожидающий разрушения. Все они находятся в энергии положения, прежде чем они катятся, текут или раскачиваются.

   Источники кинетической энергии происходят от движения или гравитационных сил, таких как океанские волны, пар, текущая вода или ветер. Это также может быть энергия, проявляемая, когда человек бегает, прыгает, танцует, водит машину, бросает дротик или швыряет шар для боулинга по аллее.

   Когда валун скатывается со скалы или пробка из ванны снимается и вода начинает устремляться в канализацию, эти объекты или источники получают кинетическую энергию.

   По мере накопления кинетической энергии они теряют потенциальную энергию, и вместе они создают уровень силы, скорости или мощности объекта.

   Все другие типы энергии могут быть только кинетической или потенциальной энергией – по одному, но никогда одновременно. Следовательно, механическая энергия – единственная форма энергии, которая может использовать потенциальную и кинетическую энергию и переключаться между ними.

   Как механическая энергия производит энергию?

   Механическая энергия производится путем получения потенциальной и кинетической энергии и превращения ее в энергию. Примерами этого могут быть пар, вода, ветер, газ или жидкое топливо, используемое в турбинах.

   Машины часто используются для выработки других форм энергии путем преобразования перед использованием в качестве энергии. Как только механическая энергия изменится определенным образом, мы сможем использовать ее так, как мы хотим или как нам нужно, чтобы она работала.

   Можно ли сохранить механическую энергию?

   Вы можете сэкономить механическую энергию, что очень важно, потому что при использовании энергия может уйти, а мощность может быть потрачена впустую в процессе преобразования.

   Некоторая потеря энергии неизбежна, когда возникают неконсервативные или останавливающие силы или ситуации, но отклонение или сохранение энергии может помочь достичь максимальной эффективности.

   Неэффективные системы преобразования энергии обходятся дороже и могут повлиять на эффективность энергосистем. Например, если энергия ветра преобразуется в механическую энергию для вращения ветряной турбины, но в процессе преобразования теряется более половины потребляемой энергии, система работает медленно, требует больше времени и тратит энергию.

   Что такое преобразование энергии?

   источник

   Преобразование энергии происходит разными способами. Например, Министерство энергетики США приводит данные об эксплуатации автомобиля.

   Бензин, находящийся в баке автомобиля перед включением, содержит потенциальную химическую энергию. Когда газ сжигается после запуска транспортного средства, он превращается из химической энергии в тепловую энергию, форму тепловой энергии.

   Затем тепловая энергия преобразуется в механическую, с использованием силы и движения (кинетической энергии) для перемещения транспортного средства.

   Когда автомобилю больше не нужно двигаться или он на мгновение останавливается, включаются тормоза, которые создают трение, неконсервативную силу.

   Механическая кинетическая энергия снова преобразуется в тепловое состояние и снова становится тепловой энергией.

   Согласно закону сохранения механической энергии, когда система изолирована или взаимодействует только с консервативными силами, механическая энергия постоянна.

   Другими словами, автомобиль будет постоянно сохранять свою механическую энергию до тех пор, пока либо не закончится бензин и механическая энергия не перестанет вырабатываться, либо пока он не вступит во взаимодействие с неконсервативной силой, такой как трение от торможения или полюса, другого транспортного средства или здания.

   Кроме того, если скорость движущегося объекта или материала изменяется, кинетическая энергия изменяется вместе с ней.

   В случае с автомобилем, если он замедлится, но продолжит движение, а затем врежется в другое транспортное средство со скоростью всего несколько миль в час, удар будет меньше, чем если бы автомобиль разогнался и ударился о другое транспортное средство при движении в качестве так быстро, как машина могла ехать.

   Чем быстрее движется автомобиль, тем больше кинетической энергии он вырабатывает и тем большую мощность он проявляет при ударе.

   Иногда, когда объекты сталкиваются с неконсервативными силами, такими как трение, они также могут терять энергию.

   Количество энергии, потерянной при столкновении, будет зависеть от того, какой тип столкновения произошел, когда это произошло.

   Если столкновение или взаимодействие являются эластичными, например, игрушка Slinky, движущаяся вниз по лестнице, количество энергии останется прежним, а мощность объекта будет сохранена.

   Если столкновение неэластичное, например, сплющенное тесто лепешки, приземлившейся на сковороду, энергия преобразуется в тепловую и не сохраняется.

   Механическая энергия везде

   Энергия движения – это механическая энергия, и ее можно увидеть практически во всем, что мы делаем и испытываем в жизни. Это бейсболист, размахивающий битой, чтобы отбить мяч через поле. Он находится в блендере, когда он крутится, измельчая и измельчая наши фрукты, капусту и лед в зеленый смузи. Это происходит в педалях тормоза велосипеда, поскольку они используют трение, чтобы остановить вращение колес.

   Как энергия, хранящаяся в объекте, она может быстро перейти от потенциальной энергии к кинетической, а затем, возможно, полностью трансформироваться в энергию другого типа, когда вступает в силу закон сохранения.Механическая энергия не так сложна, как кажется. Это часть повседневной жизни.

   Получено от justenergy.com

   Все изображения лицензированы Adobe Stock.
   Рекомендуемое изображение:

   Что нужно знать

   Механическая энергия – это не только то, что вы узнаете в классе физики в средней школе. Это все вокруг нас. Механическую энергию можно найти в грузовике, движущемся по шоссе, или в баскетбольном мяче, когда он находится в воздухе.Он присутствует в повседневной жизни, например, в двигателях, кранах и даже в искусственных озерах. Это одна из движущих сил мира, в котором мы живем.

   Существует два типа механической энергии: потенциальная энергия и кинетическая энергия. Обе они будут обсуждаться далее, чтобы помочь вам лучше понять механическую энергию и то, как она является частью вашей повседневной жизни.

   Что такое механическая энергия?

   Механическая энергия – это энергия, которую тело имеет благодаря своему движению или положению.Хорошим примером может служить энергия, которая высвобождается при падении из определенного положения. Механическая энергия – одна из основ, изучаемых в машиностроении, поскольку она буквально является движущей силой окружающего нас мира, будь то естественный или созданный руками человека. Механическая энергия выражается в джоулях.

   Какие бывают типы механической энергии?

   Существует два типа механической энергии: потенциальная энергия и кинетическая энергия. В совокупности их сумма называется общей механической энергией.Механическая энергия безгранична по своей природе.

   Потенциальная энергия

   Потенциальная энергия – это сила, которую тело могло бы потенциально развить, если бы оно было приведено в движение. Потенциальная энергия – это не энергия движения. Вместо этого это энергия, запасенная в теле из-за его физических свойств, таких как масса или положение объекта.

   Гравитационная потенциальная энергия – лучший пример потенциальной энергии. Представьте, что вы подбрасываете баскетбольный мяч высоко в воздух.Траектория мяча проста: он идет вверх, достигает своей наивысшей точки, остается там на мгновение, а затем начинает падать обратно. В самой высокой точке мяч имеет максимальную потенциальную энергию. В момент времени, когда он не движется (каким бы коротким он ни был), у него нет кинетической энергии. Когда объект подвергается действию силы тяжести, его потенциальная энергия увеличивается.

   Существуют различные формы потенциальной энергии, такие как упругая потенциальная энергия, гравитационная потенциальная энергия, электрическая (электромагнитная) потенциальная энергия и ядерная потенциальная энергия.

   Способ вычисления потенциальной энергии и максимальной кинетической энергии объекта – это формула mgh: PE = mgh, где:

   • PE: потенциальная энергия
   • м: масса объекта
   • г: сила тяжести (9,81 м / с2), принятая как чистая сила (без учета любой другой энергии, которая может воздействовать на тело) и
   • h: высота объекта
     

   Таким образом, механическая энергия объекта пропорциональна массе, высоте объекта или его вертикальному положению.

   Кинетическая энергия

   В отличие от потенциальной энергии, кинетическая энергия – это механическая энергия движения или энергия движения, а не положения. Чем быстрее движение, тем выше кинетическая энергия. Максимальная скорость, которую может развить тело во время движения, – это наивысшая кинетическая энергия этого тела.

   Вернемся к нашему примеру с баскетболом: мяч поднимается, достигает своей наивысшей точки и падает обратно. На первом этапе, когда мяч поднимается вверх, он теряет свою скорость из-за силы тяжести, поэтому его кинетическая энергия уменьшается.При падении вниз он набирает обороты, а с увеличением скорости его кинетическая энергия увеличивается. В тот момент, когда он ударяется о землю, его кинетическая энергия достигает максимума, прежде чем он обращается в ноль (при условии, что он не отскакивает назад).

   Общая механическая энергия

   Полная механическая энергия – это сумма потенциальной энергии и кинетической энергии, которую может иметь тело. В одном случае сумма двух типов механической энергии всегда одинакова. Конечно, потенциальная и кинетическая энергия быстро меняются при движении мяча вверх и вниз, но их сумма всегда одинакова.

   Когда мяч поднимается вверх, он теряет кинетическую энергию. Однако на самом деле энергия не может быть потеряна, и она просто преобразуется в потенциальную энергию – или тепло, которое на самом деле представляет собой беспорядочную смесь кинетической и потенциальной энергии. Когда мяч падает обратно, его кинетическая энергия увеличивается по мере того, как мяч набирает скорость. Эта кинетическая энергия не может появиться из воздуха. Вместо этого это потенциальная энергия, которую шар приобрел при взлете, теперь преобразуется в кинетическую энергию.

   Что делает механическая энергия?

   источник

   Если механическая энергия не может быть потеряна или извлечена из воздуха, почему мяч не может бесконечно подпрыгивать вверх и вниз? Это очень актуальный вопрос, поскольку теоретически при отсутствии других сил он действительно должен отскакивать вечно.Однако, когда он движется по воздуху, часть его кинетической энергии может казаться «потерянной» из-за трения между воздухом и поверхностью мяча. Однако общая энергия системы остается прежней.

   Это похоже на лопасти вентилятора: лопасти теряют часть своей кинетической энергии из-за трения и сопротивления воздуха, но вместо того, чтобы замедляться, лопасти продолжают вращаться, потому что они приводятся в действие двигателем. Кинетическая энергия, передаваемая воздуху, ощущается как ветер, исходящий от вентилятора.Эта кинетическая энергия может быть довольно сильной: просто представьте кинетическую силу, необходимую для удержания вертолета или самолета в воздухе.

   Какие 5 примеров механической энергии?

   Есть много примеров механической энергии как в природе, так и в нашем рукотворном мире:

   1. Гравитационная потенциальная энергия : Когда что-то находится в высоком положении, оно имеет высокую гравитационную потенциальную энергию. Чем выше объект, тем быстрее он будет падать.Подумайте о том, чтобы уронить монету из руки, а не сбросить ее с вершины Эмпайр-стейт-билдинг. Какая монета достигает более высокой скорости? Власть, которую монета получает от своего положения и движения, является примером механической энергии.
   2. Движущиеся объекты : Движущиеся автомобили, грузовики, лодки, самолеты и даже птицы в воздухе обладают определенным количеством кинетической энергии. Чем тяжелее движущийся объект и чем выше его скорость, тем выше его кинетическая энергия. Представьте кинетическую энергию пули, вылетающей из BB-пистолета.А теперь подумайте о кинетической энергии, необходимой для удержания всего самолета на высоте 30 000 футов.
   3. Американские горки : Эти потрясающие аттракционы из вашего детства предлагают удивительные примеры как потенциальной, так и кинетической энергии. Поездка на американских горках начинается с подъема, накопления потенциальной энергии. Как только вы достигли вершины рельса, каретка опускается, и ускорение, которое вы испытываете, становится вашей собственной потенциальной энергией, преобразующейся в кинетическую энергию. Каждый раз, когда вы поднимаетесь вверх, потенциальная энергия увеличивается, а кинетическая энергия уменьшается.Именно эти постоянные колебания между двумя типами энергии делают американские горки такими увлекательными!
   4. Шар для боулинга: Вот пример кинетической энергии. Потенциальная энергия мяча зависит от того, насколько быстро вы можете заставить его катиться к кеглям. Энергия, которая сбивает кегли, когда мяч касается их, и есть кинетическая энергия мяча. Поскольку полная энергия системы всегда одинакова, мяч потерял часть своей кинетической энергии и теперь движется вперед с меньшей скоростью.
   5. Hydro Plants : Они представляют собой пример потенциальной энергии, поскольку вода хранится в искусственно созданных озерах, чтобы высвободиться для производства электричества – используя потенциальную энергию гравитации для зажигания кинетической энергии. Искусственное озеро построено максимально высоко по одной причине: чем выше столб воды, тем выше потенциальная энергия воды. Как только вода высвобождается, потенциальная энергия быстро преобразуется в кинетическую энергию, которая попадает в турбины.Круговое движение турбин генерирует электрическую энергию. В этом случае кинетическая энергия воды преобразуется в электрическую энергию. Чем больше плотина, тем больше потенциальной энергии может хранить вода и тем выше выходная мощность.
      

   Что такое производство механической энергии?

   источник

   Производство механической энергии начинается с основного понятия, что полная механическая энергия равна сумме потенциальной энергии и кинетической энергии.Например, когда вам нужно произвести механическую энергию для движения вашего автомобиля, ваш двигатель преобразует химическую энергию, хранящуюся в газе, в кинетическую энергию для движения вашего двигателя. Также электромобиль преобразует электрическую энергию в механическую. Это снижает его потенциальную энергию и увеличивает кинетическую энергию.

   Что такое возобновляемая механическая энергия?

   Возобновляемая механическая энергия – это любая механическая энергия, произведенная из возобновляемых источников энергии. Например, парусники получают свою механическую энергию от силы ветра.Энергия ветра также используется для производства электроэнергии в ветряных турбинах. Возобновляемая энергия воды преобразуется в механическую энергию как при рафтинге (для перемещения плота), так и на гидроэлектростанциях, для вращения турбин и производства гидроэлектроэнергии. Возобновляемая механическая энергия также доступна в любом электромобиле, если электричество, хранящееся в батареях, поступает из возобновляемых источников, таких как солнечная энергия.

   Зависимость потенциальной энергии от кинетической

   Потенциальная энергия и кинетическая энергия – это разные типы механической энергии.В то время как потенциальная энергия объекта зависит от положения тела, кинетическая энергия – это энергия движения того же тела.

   Потенциальная энергия объекта равна объему работы, которую необходимо выполнить, или объему работы, которую объект может выполнить, чтобы переместить объект в определенное положение. Парашютист, выпрыгивающий из самолета, имеет максимальную потенциальную энергию в момент выпрыгивания из самолета. Эта энергия быстро превращается в кинетическую энергию, когда они начинают падать.

   В то время как кинетическая энергия увеличивается при падении, потенциальная энергия уменьшается. В воображаемом сценарии, когда они не раскрывают парашют, они достигают максимальной кинетической энергии при ударе, в то время как потенциальная энергия будет равна 0. Чтобы этого не произошло, они открывают парашют. Сопротивление воздуха и трение парашюта позволяют мягко приземлиться и предотвратить травмы.

   Откуда берется механическая энергия?

   Механическая энергия зависит от положения тела и скорости его движения.Две энергии также могут быть объединены. Например, когда вы едете на машине со скоростью 60 миль в час, все еще остается много потенциальной энергии, которую можно высвободить, нажав на педаль газа.

   Где найти механическую энергию?

   Механическую энергию можно найти повсюду вокруг нас. Любой движущийся объект обладает некоторой механической энергией. Объект, который не движется, также обладает механической энергией, но имеет тип потенциальной энергии. Подумайте о горах и о том, сколько механической энергии они хранят – любой оползень является доказательством того, сколько энергии они могут высвободить.

   Что такое механическая энергия для детей?

   Механическая энергия – это энергия, которая перемещает объект. Это также энергия падающего тела. Когда игрушка падает, она получает механическую энергию. Чем выше будет игрушка, когда она начнет падать, тем больше механической энергии она получит при падении.

   Что такое механическая энергия в науке?

   Механическая энергия в науке – это любая энергия движущегося объекта. Это макроскопический тип энергии, который остается в системе постоянным.Сама система не должна получать энергию извне, поскольку эта дополнительная энергия может повлиять на работу системы.

   На молекулярном и атомном уровне механическая энергия проявляется в молекулах, которые движутся или колеблются вокруг своего положения покоя. Это иначе известно как тепловая энергия. Чем больше энергии, тем горячее становится тело. Это известно как микроскопическая механическая энергия или тепловая энергия.

   Что такое сохранение механической энергии?

   Теорема сохранения механической энергии – это закон физики или закон сохранения механической энергии.Закон гласит, что в замкнутой системе полная механическая энергия всегда остается неизменной. Это означает, что отсутствуют силы, такие как сопротивление воздуха или силы трения, рассеивающие механическую энергию. Такие рассеивающие силы также известны как неконсервативные силы. В замкнутой системе механическая энергия не может быть разрушена или создана, она просто переключается с потенциальной энергии на кинетическую и наоборот.

   Как не сохраняется механическая энергия?

   Механическая энергия не сохраняется в не полностью закрытых системах.Такие системы могут быть подвержены внешним силам, которые могут увеличивать или уменьшать механическую энергию системы. Такая сила действует таким образом, что ставит под угрозу целостность нашей экспериментальной системы. Кроме того, некоторые рассеивающие среды могут препятствовать сохранению механической энергии.

   Сколько механической энергии теряется при столкновении?

   Во время столкновения полная механическая энергия равна сумме кинетических энергий сталкивающихся тел. Например, это может быть так просто, как наезд автомобиля на каменную стену или наезд двух автомобилей на шоссе.При этом типе столкновения вся кинетическая энергия преобразуется обратно в потенциальную энергию, а другая ее часть преобразуется в силы, разрушающие автомобили. Тот же принцип можно наблюдать при любом другом типе столкновения, будь то разбивающийся шар или удар стекла об пол.

   Механическая энергия – часть нашей повседневной жизни

   Совершенно очевидно, что механическая энергия присутствует повсюду вокруг нас, проникая в наше существование как видимым, так и невидимым образом. Он используется для перемещения предметов, создания удобств и помогает нам достичь того, чего мы не можем сделать с помощью одной лишь человеческой силы.От гидроэнергетики до энергии ветра и машин , которые производят машины , вырабатывающие электричество, механическая энергия не только присутствует, но и является движущей силой.

   Tara Energy обеспечивает электричеством все ваши современные приборы, гаджеты и машины, которые превращают механическую энергию в рабочий мир, который мы видим вокруг. Мы можем не всегда думать об этом, но эта энергия всегда выполняет свою работу, замечаем мы это или нет. Надежная энергия делает механическую энергию надежной частью нашей жизни, позволяя нам делать больше, чем наши предки даже мечтали.

   Получено от taranergy.com

   Все изображения лицензированы Adobe Stock.
   Главное изображение

   9.2 Механическая энергия и сохранение энергии – Физика

   Задачи обучения разделу

   К концу этого раздела вы сможете делать следующее:

   • Объясните закон сохранения энергии в терминах кинетической и потенциальной энергии
   • Выполните расчеты кинетической и потенциальной энергии.Применяем закон сохранения энергии

   Поддержка учителей

   Поддержка учителей

   Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:

   • (6) Научные концепции. Учащийся знает, что в физической системе происходят изменения, и применяет законы сохранения энергии и количества движения. Ожидается, что студент:
     • (B) исследовать примеры кинетической и потенциальной энергии и их преобразований;
     • (D) демонстрируют и применяют законы сохранения энергии и сохранения количества движения в одном измерении.

   Кроме того, в Руководстве по лаборатории физики средней школы рассматривается содержание этого раздела лаборатории под названием «Работа и энергия», а также следующие стандарты:

   • (6) Научные концепции. Учащийся знает, что в физической системе происходят изменения, и применяет законы сохранения энергии и количества движения. Ожидается, что студент:
     • (В) исследовать примеры кинетической и потенциальной энергии и их превращений;
     • (D) продемонстрировать и применить законы сохранения энергии и сохранения количества движения в одном измерении.

   Раздел Основные термины

   Закон сохранения энергии

   Поддержка учителей

   Поддержка учителей

   [BL] [OL] Начните с отделения механической энергии от других форм энергии. Объясните, почему общее определение энергии как способности выполнять работу имеет смысл с точки зрения любой из форм механической энергии. Обсудите закон сохранения энергии и развейте любые заблуждения, связанные с этим законом, такова идея о том, что движущиеся объекты просто естественным образом замедляются.Определите тепло, выделяемое трением, как обычное объяснение явных нарушений закона.

   [AL] Начните обсуждение о том, как другие полезные формы энергии также превращаются в потраченное впустую тепло, например свет, звук и электричество. Постарайтесь научить студентов понимать тепло и температуру на молекулярном уровне. Объясните, что энергия, теряемая на трение, действительно преобразует кинетическую энергию на макроскопическом уровне в кинетическую энергию на атомном уровне.

   Механическая энергия и сохранение энергии

   Ранее мы видели, что механическая энергия может быть потенциальной или кинетической.В этом разделе мы увидим, как энергия преобразуется из одной из этих форм в другую. Мы также увидим, что в замкнутой системе сумма этих форм энергии остается постоянной.

   Немного потенциальной энергии получает автомобиль с американскими горками и его пассажиры, когда они поднимаются на вершину первого холма. Помните, что часть термина с потенциалом означает, что энергия была сохранена и может быть использована в другое время. Вы увидите, что эту накопленную энергию можно использовать для работы или преобразовать в кинетическую энергию.Например, когда объект, обладающий гравитационной потенциальной энергией, падает, его энергия преобразуется в кинетическую энергию. Помните, что и работа, и энергия выражаются в джоулях.

   Вернитесь к Рисунку 9.3. Объем работы, необходимой для подъема телевизора из точки A в точку B, равен количеству потенциальной энергии гравитации, которую телевизор получает от его высоты над землей. Обычно это верно для любого объекта, поднятого над землей. Если вся работа, выполняемая над объектом, используется для поднятия объекта над землей, объем работы равен приросту объекта в потенциальной энергии гравитации.Однако обратите внимание, что из-за работы, выполняемой трением, эти преобразования энергия-работа никогда не бывают идеальными. Трение вызывает потерю некоторой полезной энергии. В следующих обсуждениях мы будем использовать приближение, согласно которому преобразования происходят без трения.

   Теперь посмотрим на американские горки на рис. 9.6. Была проделана работа на американских горках, чтобы добраться до вершины первого подъема; в этот момент американские горки обладают гравитационной потенциальной энергией. Он движется медленно, поэтому обладает небольшой кинетической энергией.Когда автомобиль спускается по первому склону, его PE преобразуется в KE . В нижней точке большая часть оригинального PE была преобразована в KE , а скорость максимальна. По мере того, как автомобиль движется вверх по следующему склону, часть KE превращается обратно в PE , и автомобиль замедляется.

   Рис. 9.6 Во время этой поездки на американских горках происходит преобразование потенциальной энергии в кинетическую.

   Поддержка учителей

   Поддержка учителей

   [OL] [AL] Спросите, имеют ли смысл определения энергии для класса, и постарайтесь выявить любые выражения недоумения или неправильных представлений.Помогите им совершить логический скачок: если энергия – это способность выполнять работу, логично, что она выражается в одной и той же единице измерения. Попросите учащихся назвать все возможные формы энергии. Спросите, помогает ли это им понять природу энергии. Спросите, есть ли у них проблемы с пониманием того, как могут работать некоторые формы энергии, например солнечный свет.

   [BL] [OL] Вы можете ввести понятие контрольной точки как начальной точки движения. Свяжите это с началом координатной сетки.

   [BL] Дайте понять, что энергия – это другое свойство с разными единицами измерения, чем сила или мощность.

   [OL] Помогите учащимся понять, что скорость, с которой доставляется телевизор, не входит в расчет PE . Предполагается, что скорость постоянна. Любой KE из-за увеличения скорости доставки будет потерян при остановке движения.

   [BL] Убедитесь, что есть четкое понимание различия между кинетической и потенциальной энергией, а также между скоростью и ускорением.Объясните, что слово потенциал означает, что энергия доступна, но это не означает, что имеет , которые нужно использовать, или будет использоваться .

   Virtual Physics

   Energy Skate Park Basics

   Это моделирование показывает, как кинетическая и потенциальная энергия связаны между собой в сценарии, аналогичном американским горкам. Наблюдайте за изменениями в KE и PE , щелкая по полям гистограммы. Также попробуйте три скейт-парка разной формы.Перетащите фигуриста на дорожку, чтобы запустить анимацию.

   Проверка захвата

   Это моделирование (http://phet.colorado.edu/en/simulation/energy-skate-park-basics) показывает, как связаны кинетическая и потенциальная энергии, в сценарии, аналогичном американским горкам. Наблюдайте за изменениями в KE и PE, нажимая на поля гистограммы. Также попробуйте три скейт-парка разной формы. Перетащите фигуриста на дорожку, чтобы запустить анимацию. Гистограммы показывают, как KE и PE преобразуются взад и вперед.Какое утверждение лучше всего объясняет, что происходит с механической энергией системы при увеличении скорости?
   1. Механическая энергия системы увеличивается при отсутствии потерь энергии из-за трения. Энергия преобразуется в кинетическую при увеличении скорости.
   2. Механическая энергия системы остается постоянной при условии отсутствия потерь энергии из-за трения. Энергия преобразуется в кинетическую при увеличении скорости.
   3. Механическая энергия системы увеличивается при отсутствии потерь энергии из-за трения. Энергия преобразуется в потенциальную при увеличении скорости.
   4. Механическая энергия системы остается постоянной при условии отсутствия потерь энергии из-за трения. Энергия преобразуется в потенциальную при увеличении скорости.

   Поддержка учителей

   Поддержка учителей

   На этой анимации показаны преобразования между KE и PE , а также изменение скорости в процессе.Позже мы можем вернуться к анимации, чтобы увидеть, как трение преобразует часть механической энергии в тепло и как сохраняется общая энергия.

   На настоящих американских горках бывает много взлетов и падений, и каждый из них сопровождается переходами между кинетической и потенциальной энергией. Предположим, что на трение не теряется энергия. В любой момент поездки общая механическая энергия одинакова и равна энергии, которую автомобиль имел на вершине первого подъема. Это результат закона сохранения энергии, который гласит, что в замкнутой системе сохраняется полная энергия, то есть она постоянна.Используя индексы 1 и 2 для обозначения начальной и конечной энергии, этот закон выражается как

   KE1 + PE1 = KE2 + PE2.KE1 + PE1 = KE2 + PE2.

   Каждая сторона равна общей механической энергии. Фраза в закрытой системе означает, что мы предполагаем, что энергия не теряется в окружающую среду из-за трения и сопротивления воздуха. Если мы проводим расчеты для плотных падающих объектов, это хорошее предположение. Для американских горок это предположение вносит некоторую неточность в расчет.

   Расчеты с использованием механической энергии и сохранения энергии

   Советы для успеха

   При расчете работы или энергии используйте метры для расстояния, ньютоны для силы, килограммы для массы и секунды для времени. Это гарантирует, что результат будет выражен в джоулях.

   Поддержка учителей

   Поддержка учителей

   [BL] [OL] Поразите учащихся значительным объемом работы, необходимой для того, чтобы привести автомобиль-американские горки к вершине первой, самой высокой точки.Сравните это с объемом работы, который потребуется, чтобы подняться на вершину американских горок. Спросите студентов, почему они могут чувствовать усталость, если им пришлось идти или взбираться на вершину американских горок (они должны использовать энергию, чтобы приложить силу, необходимую для перемещения их тела вверх против силы тяжести). Убедитесь, что учащиеся могут правильно предсказать, что отношение массы автомобиля к массе человека будет соотношением проделанной работы и полученной энергии (например, если масса автомобиля в 10 раз больше массы человека, объем работы, необходимый для переместить машину на вершину холма будет в 10 раз больше работы, необходимой для подъема на холм).

   Watch Physics

   Сохранение энергии

   В этом видео обсуждается преобразование PE в KE и сохранение энергии. Сценарий очень похож на американские горки и скейт-парк. Это также хорошее объяснение изменений энергии, изученных в лаборатории моментальных снимков.

   Поддержка учителя

   Поддержка учителя

   Перед показом видео просмотрите все уравнения, касающиеся кинетической и потенциальной энергии и сохранения энергии.Также убедитесь, что учащиеся имеют качественное представление о происходящем преобразовании энергии. Вернитесь в лабораторию моментальных снимков и лабораторию моделирования.

   Проверка захвата

   Смотреть Физика: Сохранение энергии. Это видео знакомит с законом сохранения энергии и объясняет, как потенциальная энергия преобразуется в кинетическую.

   Вы ожидали, что скорость внизу склона будет такой же, как при падении объекта прямо вниз? Какое утверждение лучше всего объясняет, почему это не совсем так в реальных жизненных ситуациях?

   1. Скорость была такой же в сценарии анимации, потому что объект скользил по льду, где есть большое трение.В реальной жизни большая часть механической энергии теряется в виде тепла из-за трения.
   2. Скорость была такой же в сценарии в анимации, потому что объект скользил по льду, где есть небольшое трение. В реальной жизни большая часть механической энергии теряется в виде тепла из-за трения.
   3. Скорость была такой же в сценарии в анимации, потому что объект скользил по льду, где есть большое трение.В реальной жизни механическая энергия не теряется из-за сохранения механической энергии.
   4. Скорость была такой же в сценарии в анимации, потому что объект скользил по льду, где есть небольшое трение. В реальной жизни механическая энергия не теряется из-за сохранения механической энергии.

   Рабочий пример

   Применение закона сохранения энергии

   Камень весом 10 кг падает со скалы высотой 20 м.Какова кинетическая и потенциальная энергия при падении камня на 10 м?

   Стратегия

   Выберите уравнение.

   KE1 + PE1 = KE2 + PE2KE1 + PE1 = KE2 + PE2

   9,4

   КЕ = 12мв2; PE = mghKE = 12мв2; PE = mgh

   9,5

   12mv12 + mgh2 = 12mv22 + mgh312mv12 + mgh2 = 12mv22 + mgh3

   9,6

   Перечислите известные.

   м = 10 кг, v ₁ = 0, г = 9.80

   h ₁ = 20 м, h ₂ = 10 м

   Определите неизвестные.

   KE ₂ и PE ₂

   Подставьте известные значения в уравнение и решите относительно неизвестных переменных.

   Решение

   PE2 = mgh3 = 10 (9,80) 10 = 980 JPE2 = mgh3 = 10 (9,80) 10 = 980 Дж

   9,8

   KE2 = PE2− (KE1 + PE1) = 980 – {[0− [10 (9.80) 20]]} = 980 JKE2 = PE2− (KE1 + PE1) = 980 – {[0− [10 (9.80) 20] ]} = 980 Дж

   9,9

   Обсуждение

   В качестве альтернативы уравнение сохранения энергии может быть решено для v ₂ и KE ₂ может быть вычислено.Обратите внимание, что м также могут быть исключены.

   Советы для успеха

   Обратите внимание, что мы можем решить многие проблемы, связанные с преобразованием между KE и PE , не зная массы рассматриваемого объекта. Это потому, что кинетическая и потенциальная энергия пропорциональны массе объекта. В ситуации, когда KE = PE , мы знаем, что м g h = (1/2) м v ² .

   Разделив обе стороны на м и переставив, получим соотношение

   2 г h = v ² .

   Поддержка учителя

   Поддержка учителя

   Кинетическая и потенциальная энергия пропорциональны массе объекта. В ситуации, когда KE = PE , мы знаем, что м g h = (1/2) м v ² .Разделив обе стороны на м и переставив, получим соотношение 2 g h = v ² .

   Практические задачи

   5.

   Ребенок скатывается с детской горки. Если высота горки 3 м, а вес ребенка 300 Н, сколько потенциальной энергии находится у ребенка в верхней части горки? (Круглый г до 10 м / с 2,10 м / с2.)

   1. 0 Дж
   2. 100 Дж
   3. 300 Дж
   4. 900 Дж
   6.

   Яблоко на яблони весом 0,2 кг имеет потенциальную энергию 10 Дж. Оно падает на землю, превращая весь свой PE в кинетическую энергию. Какова скорость яблока перед тем, как оно упадет на землю?

   1. 0 м / с
   2. 2 м / с
   3. 10 м / с
   4. 50 м / с

   Snap Lab

   Преобразование потенциальной энергии в кинетическую

   В этом упражнении вы рассчитаете потенциальную энергию объекта и спрогнозируете скорость объекта, когда вся эта потенциальная энергия будет преобразована в кинетическую энергию.Затем вы проверите свой прогноз.

   Вы будете сбрасывать предметы с высоты. Обязательно держитесь на безопасном расстоянии от края. Не наклоняйтесь слишком далеко через перила. Убедитесь, что вы не роняете предметы в место, где проезжают люди или автомобили. Убедитесь, что падающие предметы не вызовут повреждений.

   Вам понадобится:

   Материалы для каждой пары учеников:

   • Четыре шарика (или аналогичные маленькие, плотные предметы)
   • Секундомер

   Материалы для класса:

   • Метрическая рулетка достаточной длины для измерения выбранной высоты
   • Масштаб

   Инструкции

   Порядок действий

   1. Работа с партнером.Найдите и запишите массу четырех маленьких плотных объектов в каждой группе.
   2. Выберите место, где предметы можно будет безопасно сбросить с высоты не менее 15 метров. Хорошо подойдет мост через воду с безопасной пешеходной дорожкой.
   3. Измерьте расстояние, на которое упадет объект.
   4. Рассчитайте потенциальную энергию объекта перед тем, как его уронить, используя PE = м г ч = (9.80) мч.
   5. Предскажите кинетическую энергию и скорость объекта, когда он приземлится, используя PE = KE и, следовательно, mgh = mv22; v = 2 (9.80) h = 4.43h.mgh = mv22; v = 2 (9.80) h = 4.43h.
   6. Один партнер роняет предмет, а другой измеряет время, необходимое для его падения.
   7. По очереди будьте капельницей и таймером, пока не сделаете четыре измерения.
   8. Усредните ваше падение, умноженное на, и рассчитайте скорость объекта, когда он приземлился, используя v = a t = g t = (9.80) t .
   9. Сравните ваши результаты с вашим прогнозом.

   Поддержка учителя

   Поддержка учителя

   Перед тем, как учащиеся приступят к лабораторной работе, найдите ближайшее место, где предметы можно безопасно уронить с высоты не менее 15 м.

   По мере того, как учащиеся работают в лаборатории, предложите партнерам по лаборатории обсудить свои наблюдения. Поощряйте их обсуждать различия в результатах между партнерами. Спросите, есть ли какая-то путаница в используемых ими уравнениях и кажутся ли они верными на основании того, что они уже узнали о механической энергии.Попросите их обсудить эффект сопротивления воздуха и то, как плотность связана с этим эффектом.

   Проверка захвата

   Эксперименты Галилея доказали, что, вопреки распространенному мнению, тяжелые предметы не падают быстрее легких. Как уравнения, которые вы использовали, подтверждают этот факт?

   1. Тяжелые объекты не падают быстрее, чем легкие, потому что при сохранении механической энергии системы член массы аннулируется, и скорость не зависит от массы.В реальной жизни изменение скорости различных объектов наблюдается из-за ненулевого сопротивления воздуха.
   2. Тяжелые объекты не падают быстрее легких, потому что при сохранении механической энергии системы массовый член не отменяется, а скорость зависит от массы. В реальной жизни изменение скорости различных объектов наблюдается из-за ненулевого сопротивления воздуха.
   3. Тяжелые объекты не падают быстрее легких, потому что, сохраняя механическую энергию в системе, массовый член аннулируется, и скорость не зависит от массы.В реальной жизни изменение скорости различных объектов наблюдается из-за нулевого сопротивления воздуха.
   4. Тяжелые объекты не падают быстрее легких, потому что при сохранении механической энергии системы массовый член не отменяется, а скорость зависит от массы. В реальной жизни изменение скорости различных объектов наблюдается из-за нулевого сопротивления воздуха.

   Проверьте свое понимание

   7.

   Опишите преобразование между формами механической энергии, которое происходит с падающим парашютистом перед раскрытием ее парашюта.

   1. Кинетическая энергия преобразуется в потенциальную.
   2. Потенциальная энергия преобразуется в кинетическую энергию.
   3. Работа превращается в кинетическую энергию.
   4. Кинетическая энергия превращается в работу.
   8.

   Верно или неверно. Если камень подбросить в воздух, увеличение высоты увеличит кинетическую энергию камня, а затем увеличение скорости при падении на землю увеличит его потенциальную энергию.

   1. Истинно
   2. Ложь
   9.

   Определите эквивалентные термины для накопленной энергии и энергии движения .

   1. Накопленная энергия – это потенциальная энергия, а энергия движения – это кинетическая энергия.
   2. Энергия движения – это потенциальная энергия, а запасенная энергия – это кинетическая энергия.
   3. Накопленная энергия – это потенциальная, а также кинетическая энергия системы.
   4. Энергия движения – это потенциальная, а также кинетическая энергия системы.

   Поддержка учителей

   Поддержка учителей

   Используйте вопросы «Проверьте свое понимание», чтобы оценить достижения учащимися учебных целей раздела. Если учащиеся не справляются с какой-либо конкретной целью, «Проверьте свое понимание» поможет определить, какая из них, и направит учащихся к соответствующему содержанию.

   10 примеров использования механической энергии в повседневной жизни – StudiousGuy

   Механическую энергию можно назвать энергией движения; поскольку он обнаружен в объектах, которые движутся или могут двигаться. В физической науке это сумма потенциальной энергии и кинетической энергии.

   Формула механической энергии:

   Механическая энергия = кинетическая энергия + потенциальная энергия

   Закон сохранения механической энергии

   В нем говорится, что механическая энергия объекта в замкнутой системе остается постоянной, если она не находится под влиянием какой-либо диссипативной силы (например, трения, сопротивления воздуха), за исключением силы тяжести.

   Давайте попробуем более ясно понять концепцию механической энергии, взяв несколько примеров из повседневной жизни.

   1. Разрушающий шар

   Мяч для сноса – это большая круглая конструкция, которая используется для сноса зданий. Когда мяч находится на высоте, он содержит некоторое количество потенциальной энергии (запасенной энергии), и как только он падает, он также получает некоторое количество кинетической энергии. Когда разрушающий шар ударяется о разрушаемое здание, он прикладывает силу (в виде механической энергии), которая заставляет выполнять работу, как в этом случае, снос зданий.

   2. Молоток

   Каждый раз, когда мы используем молоток, чтобы, скажем, забить гвоздь и вбить его в стену, мы просто прикладываем некоторую силу к гвоздю с помощью молотка, что заставляет выполнять некоторую работу. В состоянии покоя молот не содержит кинетической энергии, а содержит лишь некоторое количество потенциальной энергии. Когда мы поднимаем молоток на некоторое расстояние от гвоздя перед тем, как ударить по нему, в игру вступает кинетическая энергия, и комбинация кинетической энергии и потенциальной энергии в молотке, называемая механической энергией, вызовет вбивание гвоздя в стену.Или мы можем сказать, что сила, прилагаемая молотком для работы с гвоздем, представляет собой механическую энергию, которая является суммой потенциальной и кинетической энергии.

   3. Дротик

   Дротик – еще один пример механической энергии, наблюдаемой в повседневной жизни. Дротик работает по принципу упругой потенциальной энергии. Пружина, используемая в дротиках, состоит из накопленной упругой потенциальной энергии. Когда дротик заряжен, пружина сжимается. В этот момент дротик состоит из упругой потенциальной энергии.Благодаря этой энергии пружина может воздействовать на дротик с силой и совершать работу, то есть перемещать дротик.

   4. Ветряная мельница

   Ветряные мельницы – это конструкции, которые преобразуют энергию ветра в электрическую, и эта энергия затем поступает в наши дома. Но откуда эта энергия ветра приходит и вращает большие лопасти ветряной мельницы? Ветряные мельницы работают по принципу механической энергии и работы. Движущийся воздух (ветер) обладает некоторым количеством энергии в виде кинетической энергии (из-за движения).Эта энергия дает воздуху возможность работать с лопастями вентилятора. Движущийся воздух прикладывает силу к лопастям и позволяет выполнять работу, что приводит к их вращению. Таким образом, механическая энергия давала ветру возможность работать с лопастями вентилятора.

   5. Шар для боулинга

   Этот интересный целевой вид спорта иллюстрирует еще один хороший пример механической энергии и работы, совершаемой объектом, обладающим ею. Шар для боулинга состоит из некоторого количества энергии в виде кинетической энергии, как только он начинает катиться к цели.Благодаря этой энергии мяч может работать с кеглями. Когда мяч попадает в эти целевые булавки, он (мяч) прикладывает силу (в виде механической энергии) и смещает их, тем самым вызывая выполнение работы. Следовательно, и здесь мы можем сказать, что механическая энергия дала шару для боулинга способность совершать работу с кеглями, вызывающими их смещение.

   6. Гидроэлектростанция

   На гидроэлектростанциях электричество вырабатывается с помощью проточной воды.Гидроэлектростанции являются прекрасным примером использования механической энергии для выполнения работы. На гидроэлектростанциях мы часто видим воду, бегущую по склону с огромной скоростью. Проточная вода выбрасывается с большой высоты, чтобы получить достаточное количество энергии, которая присутствует в виде потенциальной энергии гравитации (из-за высоты) и кинетической энергии (из-за движения). Вода, падающая со склона, затем ударяется о лопасти турбин, установленных на дне водопада.Механическая энергия воды позволяет ей работать с лопастями; в результате их вращения. Когда лопасти движутся, турбина преобразует механическую энергию воды в электрическую. Следовательно, механическая энергия дает воде возможность работать с лопастями турбины.

   7. Велоспорт

   Человек, едущий на велосипеде, обладает некоторым количеством энергии в виде потенциальной химической энергии. Эта энергия используется велосипедистом для работы с лопастями велосипеда, прикладывая некоторую силу и позволяя велосипеду двигаться вперед.

   8. Луна

   Луна – единственный естественный спутник Земли, и она вращается вокруг Земли так же, как Земля, а остальные семь планет вращаются вокруг Солнца. Луна обладает потенциальной энергией из-за своего положения относительно Земли, а также кинетической энергией, поскольку она вращается вокруг Земли. Следовательно, мы можем сказать, что Луна демонстрирует высокую механическую энергию в виде потенциальной энергии и кинетической энергии из-за своего положения и движения соответственно.Механическая энергия системы Земля-Луна остается постоянной из-за закона сохранения механической энергии. Как объяснялось ранее, этот закон гласит, что механическая энергия замкнутой системы остается постоянной, если к ней не приложена внешняя сила, за исключением силы тяжести. Поскольку в космосе нет трения или сопротивления воздуха, механическая энергия системы Земля-Луна остается постоянной с ритмическим обменом между кинетической и потенциальной энергией в разное время месяца.

   9. Электродвигатель

   Электродвигатели присутствуют в большинстве бытовых устройств, таких как пылесосы, блендеры, стиральные машины, вентиляторы, кондиционеры и т. Д. Электродвигатели преобразуют электрическую энергию в механическую. Например, когда мы включаем вентилятор, электродвигатель начинает преобразовывать электрическую энергию в механическую. Затем механическая энергия дает лопастям вентилятора возможность выполнять работу, и, следовательно, они начинают вращаться.Таким образом, мы можем сказать, что механическая энергия, преобразованная электродвигателем, была ответственна за работу, проделанную с лопастями.

   10. Лук и стрела

   Лук и стрела – еще один повседневный пример механической энергии.