По какой формуле можно рассчитать механическую работу. А полезная формула
Основные теоретические сведения
Механическая работа
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы . Работой, совершаемой постоянной силой F , называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы F и перемещения S :
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.
Если же сила изменяется с течением времени, то для нахождения работы строят график зависимости силы от перемещения и находят площадь фигуры под графиком – это и есть работа:
Примером силы, модуль которой зависит от координаты (перемещения), может служить сила упругости пружины, подчиняющаяся закону Гука (

Мощность
Работа силы, совершаемая в единицу времени, называется мощностью . Мощность P (иногда обозначают буквой N ) – физическая величина, равная отношению работы A к промежутку времени t , в течение которого совершена эта работа:
По этой формуле рассчитывается средняя мощность , т.е. мощность обобщенно характеризующая процесс. Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:
По этой формуле мы можем рассчитать мгновенную мощность (мощность в данный момент времени), если вместо скорости подставим в формулу значение мгновенной скорости. Как узнать, какую мощность считать? Если в задаче спрашивают мощность в момент времени или в какой-то точке пространства, то считается мгновенная. Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.
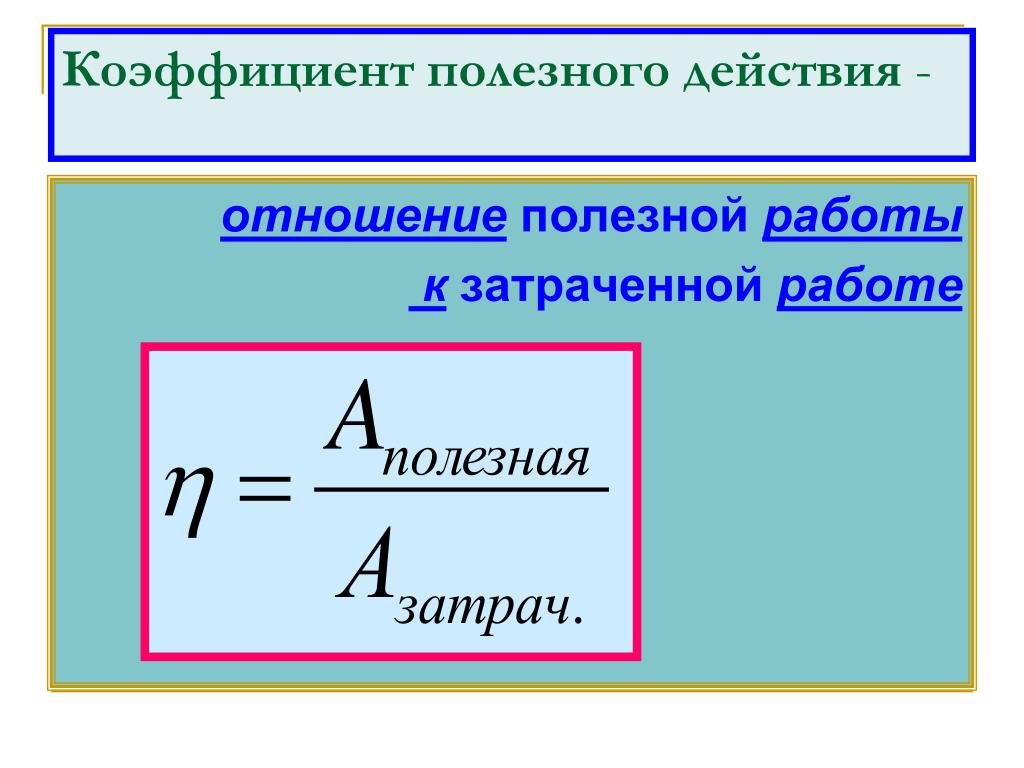
КПД – коэффициент полезного действия , равен отношению полезной работы к затраченной, либо же полезной мощности к затраченной:
Какая работа полезная, а какая затраченная определяется из условия конкретной задачи путем логического рассуждения. К примеру, если подъемный кран совершает работу по подъему груза на некоторую высоту, то полезной будет работа по поднятию груза (так как именно ради нее создан кран), а затраченной – работа, совершенная электродвигателем крана.
Итак, полезная и затраченная мощность не имеют строгого определения, и находятся логическим рассуждением. В каждой задаче мы сами должны определить, что в этой задаче было целью совершения работы (полезная работа или мощность), а что было механизмом или способом совершения всей работы (затраченная мощность или работа).
В общем случае КПД показывает, как эффективно механизм преобразует один вид энергии в другой. Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:
Кинетическая энергия
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела (энергией движения) :
То есть если автомобиль массой 2000 кг движется со скоростью 10 м/с, то он обладает кинетической энергией равной Е к = 100 кДж и способен совершить работу в 100 кДж.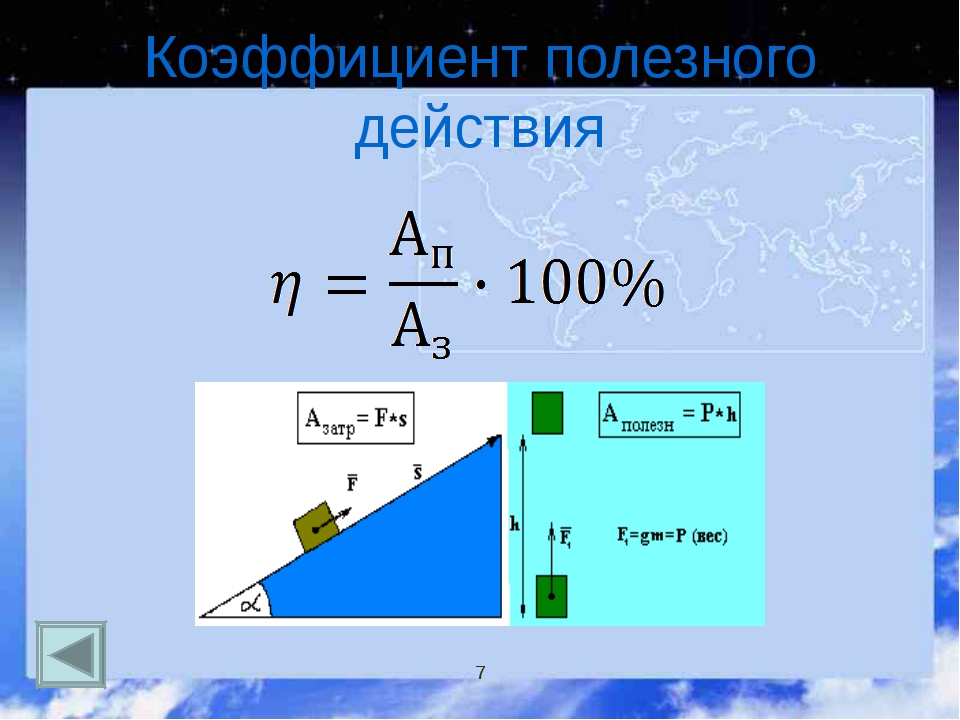 Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.
Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.
Тело обладает энергией, если способно совершить работу. Например, движущееся тело обладает кинетической энергией, т.е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.
Физический смысл кинетической энергии: для того чтобы покоящееся тело массой m стало двигаться со скоростью v необходимо совершить работу равную полученному значению кинетической энергии. Если тело массой

Теорема о кинетической энергии: работа равнодействующей силы равна изменению кинетической энергии тела:
Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Применять данную теорему удобно в задачах на разгон и торможение тела.
Потенциальная энергия
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы ). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:
Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня). Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Часто в задачах на энергию приходится находить работу по поднятию (переворачиванию, доставанию из ямы) тела. Во всех этих случаях нужно рассматривать перемещение не самого тела, а только его центра тяжести.
Потенциальная энергия Ep зависит от выбора нулевого уровня, то есть от выбора начала координат оси OY. В каждой задаче нулевой уровень выбирается из соображения удобства. Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Потенциальная энергия растянутой пружины рассчитывается по формуле:
где: k
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x 1 , тогда при переходе в новое состояние с удлинением x 2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком (так как сила упругости всегда направлена против деформации тела):
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Работа силы трения зависит от пройденного пути (такой вид сил, чья работа зависит от траектории и пройденного пути называется: диссипативные силы ). Понятие потенциальной энергии для силы трения вводить нельзя.
Коэффициент полезного действия
Коэффициент полезного действия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой (формула уже приведена выше).
КПД можно рассчитывать как через работу, так и через мощность. Полезная и затраченная работа (мощность) всегда определяются путем простых логических рассуждений.
В электрических двигателях КПД – отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника. В тепловых двигателях – отношение полезной механической работы к затрачиваемому количеству теплоты. В электрических трансформаторах – отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.
В силу своей общности понятие КПД позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т.д.
Из–за неизбежных потерь энергии на трение, на нагревание окружающих тел и т.п. КПД всегда меньше единицы. Соответственно этому КПД выражается в долях затрачиваемой энергии, то есть в виде правильной дроби или в процентах, и является безразмерной величиной. КПД характеризует как эффективно работает машина или механизм. КПД тепловых электростанций достигает 35–40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением – 40–50%, динамомашин и генераторов большой мощности – 95%, трансформаторов – 98%.
Задачу, в которой нужно найти КПД или он известен, надо начать с логического рассуждения – какая работа является полезной, а какая затраченной.
Закон сохранения механической энергии
Полной механической энергией называется сумма кинетической энергии (т. е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):
е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):
Если механическая энергия не переходит в другие формы, например, во внутреннюю (тепловую) энергию, то сумма кинетической и потенциальной энергии остаётся неизменной. Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему (т.е. такую в которой не действует внешних сил, и их работа соответственно равна нолю) и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной:
Это утверждение выражает закон сохранения энергии (ЗСЭ) в механических процессах . Он является следствием законов Ньютона. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой силами упругости и тяготения. Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.
Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.
Алгоритм решения задач на закон сохранения энергии:
- Найти точки начального и конечного положения тела.
- Записать какой или какими энергиями обладает тело в данных точках.
- Приравнять начальную и конечную энергию тела.
- Добавить другие необходимые уравнения из предыдущих тем по физике.
- Решить полученное уравнение или систему уравнений математическими методами.
Важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими силами действуют силы трения или силы сопротивления среды. Работа силы трения зависит от длины пути.
Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). Таким образом энергия в целом (т.е. не только механическая) в любом случае сохраняется.
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии .
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.
Разные задачи на работу
Если в задаче требуется найти механическую работу, то сначала выберите способ её нахождения:
- Работу можно найти по формуле: A = FS ∙cosα .
 Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения. - Работу внешней силы можно найти, как разность механической энергии в конечной и начальной ситуациях. Механическая энергия равна сумме кинетической и потенциальной энергий тела.
- Работу по подъёму тела с постоянной скоростью можно найти по формуле: A = mgh , где h – высота, на которую поднимается центр тяжести тела .
- Работу можно найти как произведение мощности на время, т.е. по формуле: A = Pt .
- Работу можно найти, как площадь фигуры под графиком зависимости силы от перемещения или мощности от времени.
Закон сохранения энергии и динамика вращательного движения
Задачи этой темы являются достаточно сложными математически, но при знании подхода решаются по совершенно стандартному алгоритму. Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:
Решение будет сводиться к следующей последовательности действий:
- Надо определить интересующую Вас точку (ту точку, в которой необходимо определить скорость тела, силу натяжения нити, вес и так далее).
- Записать в этой точке второй закон Ньютона, учитывая, что тело вращается, то есть у него есть центростремительное ускорение.
- Записать закон сохранения механической энергии так, чтобы в нем присутствовала скорость тела в той самой интересной точке, а также характеристики состояния тела в каком-нибудь состоянии про которое что-то известно.
- В зависимости от условия выразить скорость в квадрате из одного уравнения и подставить в другое.
- Провести остальные необходимые математические операции для получения окончательного результата.
При решении задач надо помнить, что:
- Условие прохождения верхней точки при вращении на нити с минимальной скоростью – сила реакции опоры N в верхней точке равна 0. Такое же условие выполняется при прохождении верхней точки мертвой петли.

- При вращении на стержне условие прохождения всей окружности: минимальная скорость в верхней точке равна 0.
- Условие отрыва тела от поверхности сферы – сила реакции опоры в точке отрыва равна нулю.
Неупругие соударения
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц). В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары .
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Для описания любых ударов Вам нужно записать и закон сохранения импульса, и закон сохранения механической энергии с учетом выделяющейся теплоты (предварительно крайне желательно сделать рисунок).
Абсолютно упругий удар
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения. Центральный удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.
Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
Законы сохранения. Сложные задачи
Несколько тел
В некоторых задачах на закон сохранения энергии тросы с помощью которых перемещаются некие объекты могут иметь массу (т.е. не быть невесомыми, как Вы могли уже привыкнуть). В этом случае работу по перемещению таких тросов (а именно их центров тяжести) также нужно учитывать.
Если два тела, соединённые невесомым стержнем, вращаются в вертикальной плоскости, то:
- выбирают нулевой уровень для расчёта потенциальной энергии, например на уровне оси вращения или на уровне самой нижней точки нахождения одного из грузов и обязательно делают чертёж;
- записывают закон сохранения механической энергии, в котором в левой части записывают сумму кинетической и потенциальной энергии обоих тел в начальной ситуации, а в правой части записывают сумму кинетической и потенциальной энергии обоих тел в конечной ситуации;
- учитывают, что угловые скорости тел одинаковы, тогда линейные скорости тел пропорциональны радиусам вращения;
- при необходимости записывают второй закон Ньютона для каждого из тел в отдельности.

Разрыв снаряда
В случае разрыва снаряда выделяется энергия взрывчатых веществ. Чтобы найти эту энергию надо от суммы механических энергий осколков после взрыва отнять механическую энергию снаряда до взрыва. Также будем использовать закон сохранения импульса, записанный, в виде теоремы косинусов (векторный метод) или в виде проекций на выбранные оси.
Столкновения с тяжёлой плитой
Пусть навстречу тяжёлой плите, которая движется со скоростью v , движется лёгкий шарик массой m со скоростью u н. Так как импульс шарика много меньше импульса плиты, то после удара скорость плиты не изменится, и она будет продолжать движение с той же скоростью и в том же направлении. В результате упругого удара, шарик отлетит от плиты. Здесь важно понять, что не поменяется скорость шарика относительно плиты . В таком случае, для конечной скорости шарика получим:
Таким образом, скорость шарика после удара увеличивается на удвоенную скорость стены. Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
По физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ.
 После этого Вам останется подумать только над самыми сложными задачами.
После этого Вам останется подумать только над самыми сложными задачами. - Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
В повседневной жизни часто приходится встречаться с таким понятием как работа. Что это слово означает в физике и как определить работу силы упругости? Ответы на эти вопросы вы узнаете в статье.
Механическая работа
Работа – это скалярная алгебраическая величина, которая характеризует связь между силой и перемещением. При совпадении направления этих двух переменных она вычисляется по следующей формуле:
- F – модуль вектора силы, которая совершает работу;
- S – модуль вектора перемещения.
Не всегда сила, которая действует на тело, совершает работу. Например, работа силы тяжести равна нулю, если ее направление перпендикулярно перемещению тела.
Если вектор силы образует отличный от нуля угол с вектором перемещения, то для определения работы следует воспользоваться другой формулой:
A=FScosα
α – угол между векторами силы и перемещения.
Значит, механическая работа – это произведение проекции силы на направление перемещения и модуля перемещения, или произведение проекции перемещения на направление силы и модуля этой силы.
Знак механической работы
В зависимости от направления силы относительно перемещения тела работа A может быть:
- положительной (0°≤ α
- отрицательной (90°
- равной нулю (α=90°).
Если A>0, то скорость тела увеличивается. Пример – падение яблока с дерева на землю. При A
Единица измерения работы в СИ (Международной системе единиц) – Джоуль (1Н*1м=Дж). Джоуль – это работа силы, значение которой равно 1 Ньютону, при перемещении тела на 1 метр в направлении действия силы.
Работа силы упругости
Работу силы можно определить и графическим способом. Для этого вычисляется площадь криволинейной фигуры под графиком F s (x).
Так, по графику зависимости силы упругости от удлинения пружины, можно вывести формулу работы силы упругости.
Она равна:
A=kx 2 /2
- k – жесткость;
- x – абсолютное удлинение.
Что мы узнали?
Механическая работа совершается при действии на тело силы, которая приводит к перемещению тела. В зависимости от угла, который возникает между силой и перемещением, работа может быть равна нулю или иметь отрицательный или положительный знак. На примере силы упругости вы узнали о графическом способе определения работы.
Вы знаете, что такое работа? Вне всякого сомнения. Что такое работа, знает каждый человек, при условии, что он рожден и живет на планете Земля. А что такое механическая работа?
Это понятие тоже известно большинству людей на планете, хотя некоторые отдельные личности и имеют довольно смутное представление об этом процессе. Но речь сейчас не о них. Еще меньшее число людей имеют представление, что такое механическая работа с точки зрения физики. В физике механическая работа – это не труд человека ради пропитания, это физическая величина, которая может быть совершенно никак не связана ни с человеком, ни с другим каким-нибудь живым существом.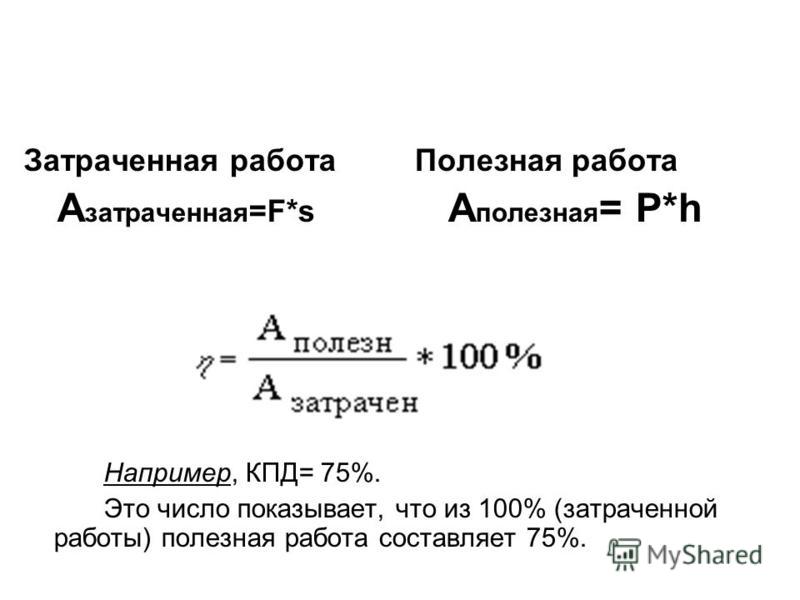 Как так? Сейчас разберемся.
Как так? Сейчас разберемся.
Механическая работа в физике
Приведем два примера. В первом примере воды реки, столкнувшись с пропастью, шумно падают вниз в виде водопада. Второй пример – это человек, который держит на вытянутых руках тяжелый предмет, например, удерживает надломившуюся крышу над крыльцом дачного домика от падения, пока его жена и дети судорожно ищут, чем ее подпереть. В каком случае совершается механическая работа?
Определение механической работы
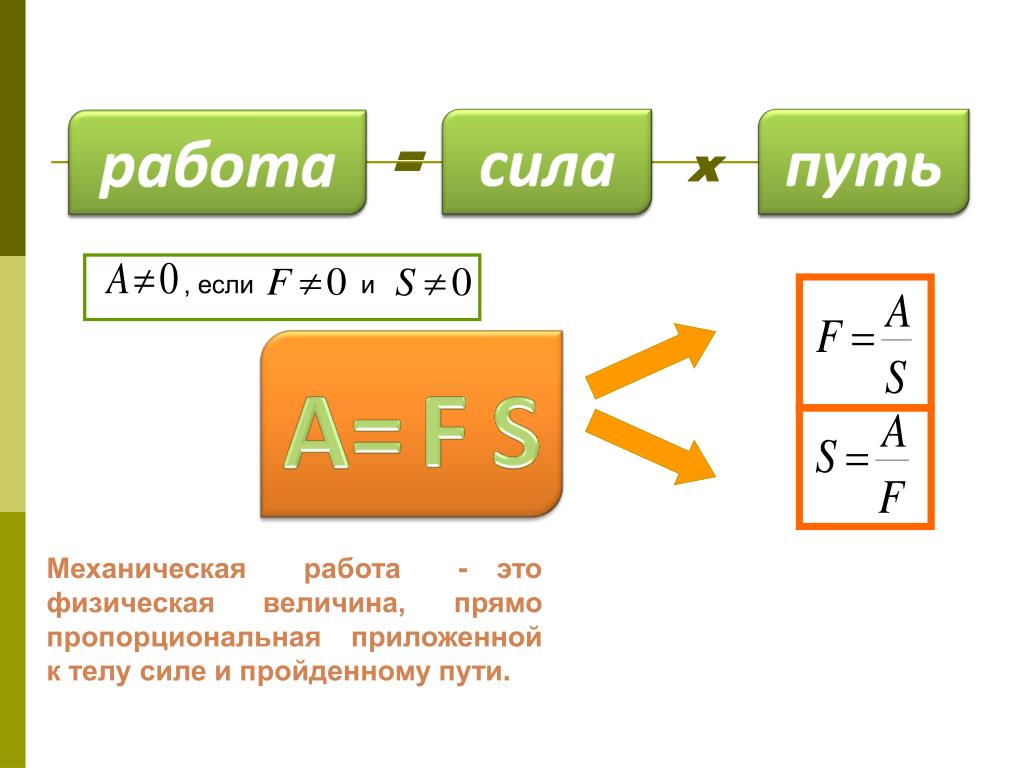
Практически все, не задумываясь, ответят: во втором. И будут неправы. Дело обстоит как раз наоборот. В физике механическая работа описывается следующими определениями: механическая работа совершается тогда, когда на тело действует сила, и оно движется. Механическая работа прямо пропорциональна приложенной силе и пройденному пути.
Формула механической работы
Определяется механическая работа формулой:
где A – работа,
F – сила,
s – пройденный путь.
Так что, несмотря на весь героизм уставшего держателя крыши, проделанная им работа равна нулю, а вот вода, падая под действием силы тяжести с высокого утеса, совершает самую, что ни на есть, механическую работу. То есть, если мы будем толкать тяжелый шкаф безуспешно, то проделанная нами работа с точки зрения физики будет равна нулю, несмотря на то, что мы прикладываем много сил. А вот если мы сдвинем шкаф на некоторое расстояние, то тогда мы проделаем работу, равную произведению приложенной силы на расстояние, на которое мы передвинули тело.
То есть, если мы будем толкать тяжелый шкаф безуспешно, то проделанная нами работа с точки зрения физики будет равна нулю, несмотря на то, что мы прикладываем много сил. А вот если мы сдвинем шкаф на некоторое расстояние, то тогда мы проделаем работу, равную произведению приложенной силы на расстояние, на которое мы передвинули тело.
Единица работы – 1 Дж. Это работа, совершенная силой в 1 ньютон, по передвижению тела на расстояние в 1 м. Если направление приложенной силы совпадает с направлением движения тела, то данная сила совершает положительную работу. Пример – это когда мы толкаем какое-либо тело, и оно двигается. А в случае, когда сила приложена в противоположную движению тела сторону, например, сила трения , то данная сила совершает отрицательную работу. Если же приложенная сила никак не влияет на движение тела, то сила, совершаемая этой работой, равна нулю.
Лошадь тянет телегу с некоторой силой, обозначим её F тяги. Дедушка, сидящий на телеге, давит на неё с некоторой силой. Обозначим её F давл. Телега движется вдоль направления силы тяги лошади (вправо), а в направлении силы давления дедушки (вниз) телега не перемещается. Поэтому в физике говорят, что F тяги совершает работу над телегой, а F давл не совершает работу над телегой.
Обозначим её F давл. Телега движется вдоль направления силы тяги лошади (вправо), а в направлении силы давления дедушки (вниз) телега не перемещается. Поэтому в физике говорят, что F тяги совершает работу над телегой, а F давл не совершает работу над телегой.
Итак, работа силы над телом или механическая работа – физическая величина, модуль которой равен произведению силы на путь, пройденный телом вдоль направления действия этой сил ы:
В честь английского учёного Д.Джоуля единица механической работы получила название 1 джоуль (согласно формуле, 1 Дж = 1 Н·м).
Если на рассматриваемое тело действует некоторая сила, значит, на него действует некоторое тело. Поэтому работа силы над телом и работа тела над телом – полные синонимы. Однако, работа первого тела над вторым и работа второго тела над первым – частичные синонимы, поскольку модули этих работ всегда равны, а их знаки всегда противоположны. Именно поэтому в формуле присутствует знак «±». Обсудим знаки работы более подробно.
Обсудим знаки работы более подробно.
Числовые значения силы и пути – всегда неотрицательные величины. В отличие от них механическая работа может иметь как положительный, так и отрицательный знаки. Если направление силы совпадает с направлением движения тела, то работу силы считают положительной. Если направление силы противоположно направлению движения тела, работу силы считают отрицательной (берём «–» из «±» формулы). Если направление движения тела перпендикулярно направлению действия силы, то такая сила работу не совершает, то есть A = 0.
Рассмотрите три иллюстрации по трём аспектам механической работы.
Совершение силой работы может выглядеть по-разному с точек зрения различных наблюдателей. Рассмотрим пример: девочка едет в лифте вверх. Совершает ли она механическую работу? Девочка может совершать работу только над теми телами, на которые действует силой. Такое тело лишь одно – кабина лифта, так как девочка давит на её пол своим весом. Теперь надо выяснить, проходит ли кабина некоторый путь. Рассмотрим два варианта: с неподвижным и движущимся наблюдателем.
Теперь надо выяснить, проходит ли кабина некоторый путь. Рассмотрим два варианта: с неподвижным и движущимся наблюдателем.
Пусть сначала мальчик-наблюдатель сидит на земле. По отношению к нему кабина лифта движется вверх и проходит некоторый путь. Вес девочки направлен в противоположную сторону – вниз, следовательно, девочка совершает над кабиной отрицательную механическую работу: A дев A дев = 0.
Коэффициент полезного действия показывает отношение полезной работы, которая выполняется механизмом или устройством, к затраченной. Часто за затраченную работу принимают количество энергии, которое потребляет устройство для того, чтобы выполнить работу.
Вам понадобится
- – автомобиль;
- – термометр;
- – калькулятор.
Инструкция
- Для того чтобы рассчитать коэффициент полезного действия (КПД) поделите полезную работу Ап на работу затраченную Аз, а результат умножьте на 100% (КПД=Ап/Аз∙100%). Результат получите в процентах.
 6∙7)∙100%=30%.
6∙7)∙100%=30%. - В общем случае чтобы найти КПД, любой тепловой машины (двигателя внутреннего сгорания, парового двигателя, турбины и т.д.), где работа выполняется газом, имеет коэффициент полезного действия равный разности теплоты отданной нагревателем Q1 и полученной холодильником Q2, найдите разность теплоты нагревателя и холодильника, и поделите на теплоту нагревателя КПД= (Q1-Q2)/Q1. Здесь КПД измеряется в дольных единицах от 0 до 1, чтобы перевести результат в проценты, умножьте его на 100.
- Чтобы получить КПД идеальной тепловой машины (машины Карно), найдите отношение разности температур нагревателя Т1 и холодильника Т2 к температуре нагревателя КПД=(Т1-Т2)/Т1. Это предельно возможный КПД для конкретного типа тепловой машины с заданными температурами нагревателя и холодильника.
- Для электродвигателя найдите затраченную работу как произведение мощности на время ее выполнения. Например, если электродвигатель крана мощностью 3,2 кВт поднимает груз массой 800 кг на высоту 3,6 м за 10 с, то его КПД равен отношению полезной работы Ап=m∙g∙h, где m – масса груза, g≈10 м/с² ускорение свободного падения, h – высота на которую подняли груз, и затраченной работы Аз=Р∙t, где Р – мощность двигателя, t – время его работы.
 Получите формулу для определения КПД=Ап/Аз∙100%=(m∙g∙h)/(Р∙t) ∙100%=%=(800∙10∙3,6)/(3200∙10) ∙100%=90%.
Получите формулу для определения КПД=Ап/Аз∙100%=(m∙g∙h)/(Р∙t) ∙100%=%=(800∙10∙3,6)/(3200∙10) ∙100%=90%.
Какая формула у полезной работы?
Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную или затраченную работу Аз и полезную работу Ап. Если, например, наша цель-поднять груз массой m на высоту Н, то полезная работа – это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:
Ап =FH= mgH
Полезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм.
Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется коэффициентом полезного действия механизма.
Что такое работа в физике определение формула.
 нн
ннПомогите расшифровать формулу по физике
КПД тепловых двигателей.физика (формулы,определения,примеры) напишите! физика (формулы,определения,примеры) напишите!
Чему равна работа тела. А полезная формула
Одно из важнейших понятий механики – работа силы .
Работа силы
Все физические тела в окружающем нас мире приводятся в движение с помощью силы. Если на движущееся тело в попутном или противоположном направлении действует сила или несколько сил со стороны одного или нескольких тел, то говорят, что совершается работа .
То есть, механическая работу совершает действующая на тело сила. Так, сила тяги электровоза приводит в движение весь поезд, тем самым совершая механическую работу. Велосипед приводится в движение мускульной силой ног велосипедиста. Следовательно, эта сила также совершает механическую работу.
В физике работой силы называют физическую величину, равную произведению модуля силы, модуля перемещения точки приложения силы и косинуса угла между векторами силы и перемещения.
A = F · s · cos (F, s) ,
где F модульсилы,
s – модуль перемещения.
Работа совершается всегда, если угол между ветрами силы и перемещения не равен нулю. Если сила действует в направлении, противоположном направлению движения, величина работы имеет отрицательное значение.
Работа не совершается, если на тело не действуют силы, или если угол между приложенной силой и направлением движения равен 90 о (cos 90 o = 0).
Если лошадь тянет телегу, то мускульная сила лошади, или сила тяги, направленная по ходу движения телеги, совершает работу. А сила тяжести, с которой извозчик давит на телегу, работы не совершает, так как она направлена вниз, перпендикулярно направлению перемещения.
Работа силы – величина скалярная.
Единица работы в системе измерений СИ – джоуль. 1 джоуль – это работа, которую совершает сила величиной в 1 ньютон на расстоянии 1 м, если направления силы и перемещения совпадают.
Если на тело или материальную точку действуют несколько сил, то говорят о работе, совершаемой их равнодействующей силой.
В случае, если приложенная сила непостоянна, то её работа вычисляется как интеграл:
Мощность
Сила, приводящая в движение тело, совершает механическую работу. Но как совершается эта работа, быстро или медленно, иногда очень важно знать на практике. Ведь одна и та же работа может быть совершена за разное время. Работу, которую выполняет большой электромотор, может выполнить и маленький моторчик. Но ему для этого понадобится гораздо больше времени.
В механике существует величина, характеризующая быстроту выполнения работы. Эта величина называется мощностью .
Мощность – это отношение работы, выполненной за определённый промежуток времени, к величине этого промежутка.
N = A /∆ t
По определению А = F · s · cos α , а s/∆ t = v , следовательно
N = F · v · cos α = F · v ,
где F – сила, v скорость, α – угол между направлением силы и направление скорости.
То есть мощность – это скалярное произведение вектора силы на вектор скорости движения тела .
В международной системе СИ мощность измеряется в ваттах (Вт).
Мощность в 1 ватт – это работа в 1 джоуль (Дж), совершаемая за 1 секунду (с).
Мощность можно увеличить, если увеличить силу, совершающую работу, или скорость, с которой эта работа совершается.
Коэффициент полезного действия показывает отношение полезной работы, которая выполняется механизмом или устройством, к затраченной. Часто за затраченную работу принимают количество энергии, которое потребляет устройство для того, чтобы выполнить работу.
Вам понадобится
- – автомобиль;
- – термометр;
- – калькулятор.
Инструкция
- Для того чтобы рассчитать коэффициент полезного действия (КПД) поделите полезную работу Ап на работу затраченную Аз, а результат умножьте на 100% (КПД=Ап/Аз∙100%). Результат получите в процентах.
 6∙7)∙100%=30%.
6∙7)∙100%=30%. - В общем случае чтобы найти КПД, любой тепловой машины (двигателя внутреннего сгорания, парового двигателя, турбины и т.д.), где работа выполняется газом, имеет коэффициент полезного действия равный разности теплоты отданной нагревателем Q1 и полученной холодильником Q2, найдите разность теплоты нагревателя и холодильника, и поделите на теплоту нагревателя КПД= (Q1-Q2)/Q1. Здесь КПД измеряется в дольных единицах от 0 до 1, чтобы перевести результат в проценты, умножьте его на 100.
- Чтобы получить КПД идеальной тепловой машины (машины Карно), найдите отношение разности температур нагревателя Т1 и холодильника Т2 к температуре нагревателя КПД=(Т1-Т2)/Т1. Это предельно возможный КПД для конкретного типа тепловой машины с заданными температурами нагревателя и холодильника.
- Для электродвигателя найдите затраченную работу как произведение мощности на время ее выполнения. Например, если электродвигатель крана мощностью 3,2 кВт поднимает груз массой 800 кг на высоту 3,6 м за 10 с, то его КПД равен отношению полезной работы Ап=m∙g∙h, где m – масса груза, g≈10 м/с² ускорение свободного падения, h – высота на которую подняли груз, и затраченной работы Аз=Р∙t, где Р – мощность двигателя, t – время его работы.
 Получите формулу для определения КПД=Ап/Аз∙100%=(m∙g∙h)/(Р∙t) ∙100%=%=(800∙10∙3,6)/(3200∙10) ∙100%=90%.
Получите формулу для определения КПД=Ап/Аз∙100%=(m∙g∙h)/(Р∙t) ∙100%=%=(800∙10∙3,6)/(3200∙10) ∙100%=90%.
Какая формула у полезной работы?
Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную или затраченную работу Аз и полезную работу Ап. Если, например, наша цель-поднять груз массой m на высоту Н, то полезная работа – это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:
Ап =FH= mgH
Что такое работа в физике определение формула. нн
Виктор Чернобровин
В физике “механической работой” называют работу какой-нибудь силы (силы тяжести, упругости, трения и т. д.) над телом, в результате действия которой тело перемещается. Иногда можно встретить выражение ” тело совершило работу”, что в принципе означает “сила, действующая на тело, совершила работу”.
Евгений Макаров
Работа есть физическая величина, численно равная произведению силы на перемещение в направлении действия этой силы и ей же вызванное.
Соответственно формула A = F*s. Если перемещение по направлению не совпадает с направлением действия силы, то появляется косинус угла.
Aysha Allakulova
роман воробьев
Работа – это процесс, требующий приложения умственных или физических усилий, который целью своей ставит получение определенного результата. Именно работа, как правило, определяет социальный статус человека. И является, по сути, главным двигателем прогресса в обществе. Работа, как явление, присуще только живым организмам и прежде всего человеку.
Механик
Механическая работа – это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек), тела или системы .
Помогите понять формулу!!
Сёма
в каждом конкретном случае мы рассматриваем разную полезную энергию, но обычно это работа или теплота, которая нас интересовала (например, работа газа по перемещению поршня) , а затраченная энергия – энергия, которую мы предали, чтобы наше всё заработало (например, энергия, выделившаяся при сгорании дров под цилиндром с поршнем, внутри которого газ, который, расширяясь совершил работу, которую мы рассмотрели как полезную)
ну как-то так должно быть
Возьмем для примера паровоз.
Чтобы паровоз прошел x км нужно затратить y тонн угля. При сгорании угля выделится всего Q1 теплоты, но не вся теплота преобразуется в полезную работу (по законам термодинамики это невозможно) . Полезная работа в данном случае – движение паровоза.
Пусть при движении на паровоз действует сила сопротивления F (она возникает вследствие трения в механизмах и из-за др. факторов) .
Так, пройдя x км, паровоз совершит работу Q2 = x*F
Таким образом,
Q1 – затраченная энергия
Q2 – полезная работа
ДельтаQ = (Q1 – Q2) – энергия, затраченная на преодоление трения, на нагревание окружающего воздуха и т. д.
Техническая Поддержка
КПД – полезная РАБОТА к затраченной.
Например, кпд=60%, на нагревание идет 60 джоулей от сгорания вещества. Это полезная работа.
Нас интересует затраченная, т. е сколько всего тепла выделилось, если на нагревание пошло 60 дж.
Распишем.
КПД=Апол/Азатр
0.6=60/Азатр
Азатр=60/0.6=100дж
Как видим, если сгорает при таком КПД вещество и при сгорании выделяется 100 ДЖ (затраченная работа) , то на нагревание пошло только 60%, то есть 60Дж (полезная работа) . Остальное тепло рассеялось.
Остальное тепло рассеялось.
Прохоров Антон
Надо понимать в прямом смысле: Если речь идет о тепловой энергии, то затраченной считаем ту энергию, которую дает топливо, а полезной считаем ту энергию, которую сумели использовать для достижения своей цели, например, какую энергию получила кастрюля с водой.
Полезная энергия всегда меньше затраченной!
Futynehf
КПД коэффициент полезного действия вырожается в процентах, характеризует процент который пошел на полезную работу от всего затраченного. Проще затраченная энергия это энергия полезная + энергия потерь тепла в системе (если речь идет о тепле и т д) трения. тепло с выхлопными газами если имеется в виду автомобиль
Формула кпд? работа полезная и полная?
Орбитальная группировка
Коэффициент полезного действия
Коэффициент полезного действия
(кпд) , характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии; определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно h = Wполная/Wcyммарная.
В электрических двигателях кпд – отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника; в тепловых двигателях – отношение полезной механической работы к затрачиваемому количеству теплоты; в электрических трансформаторах – отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой. Для вычисления кпд разные виды энергии и механическая работа выражаются в одинаковых единицах на основе механического эквивалента теплоты, и др. аналогичных соотношений. В силу своей общности понятие кпд позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т. д.
http://ru.wikipedia.org/wiki/Работа_силы
Поле́зная нагру́зка – термин, который применяется в очень многих областях науки и техники.
Часто вводится параметр «эффективности» , как отношение «веса» полезной нагрузки к полному «весу» системы. При этом «вес» может измеряться как в килограммах/тоннах, так и битах (при передаче пакетов по сети) , или минутах/часах (при расчёте эффективности процессорного времени) , или в других единицах.
При этом «вес» может измеряться как в килограммах/тоннах, так и битах (при передаче пакетов по сети) , или минутах/часах (при расчёте эффективности процессорного времени) , или в других единицах.
http://ru.wikipedia.org/wiki/Полезная_нагрузка
Что такое полезная работа,а что такое затраченная?
Bладимир Попов
Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную илизатраченную работу Аз и полезную работу Ап. Если, например, наша цель-поднять груз массой ш на высоту Н, то полезная работа – это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:
Если же мы применяем для подъема груза блок или какой- либо другой механизм, то, кроме силы тяжести груза, нам приходится преодолевать еще и силу тяжести частей механизма, а также действующую в механизме силу трения. Например, используя подвижный блок, мы вынуждены будем совершать дополнительную работу по подъему самого блока с тросом и по преодолению силы трения в оси блока. Кроме того, выигрывая в силе, мы всегда проигрываем в пути (об этом подробнее будет рассказано ниже) , что также влияет на работу. Все это приводит к тому, что затраченная нами работа оказывается больше полезной:
Например, используя подвижный блок, мы вынуждены будем совершать дополнительную работу по подъему самого блока с тросом и по преодолению силы трения в оси блока. Кроме того, выигрывая в силе, мы всегда проигрываем в пути (об этом подробнее будет рассказано ниже) , что также влияет на работу. Все это приводит к тому, что затраченная нами работа оказывается больше полезной:
Аз > Ап.
Полезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм.
Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется коэффициентом полезного действия механизма.
Великолепная
Кпд (коэффициент полезного действия) показывает какую долю от всей затраченной работы составляет полезная работа.
Чтобы найти кпд, надо найти отношение полезной работы к затраченной:
Коэффициент полезного действия показывает отношение полезной работы, которая выполняется механизмом или устройством, к затраченной.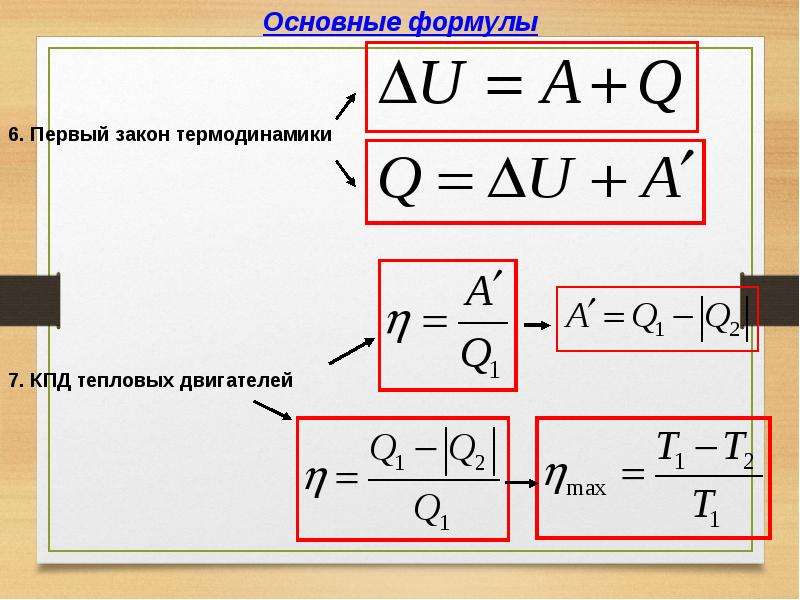 Часто за затраченную работу принимают количество энергии, которое потребляет устройство для того, чтобы выполнить работу.
Часто за затраченную работу принимают количество энергии, которое потребляет устройство для того, чтобы выполнить работу.
Вам понадобится
- – автомобиль;
- – термометр;
- – калькулятор.
Инструкция
- Для того чтобы рассчитать коэффициент полезного действия (КПД) поделите полезную работу Ап на работу затраченную Аз, а результат умножьте на 100% (КПД=Ап/Аз∙100%). Результат получите в процентах.
- При расчете КПД теплового двигателя, полезной работой считайте механическую работу, выполненную механизмом. За затраченную работу берите количество теплоты, выделяемое сгоревшим топливом, которое является источником энергии для двигателя.
- Пример. Средняя сила тяги двигателя автомобиля составляет 882 Н. На 100 км пути он потребляет 7 кг бензина. Определите КПД его двигателя. Сначала найдите полезную работу. Она равна произведению силы F на расстояние S, преодолеваемое телом под ее воздействием Ап=F∙S. Определите количество теплоты, которое выделится при сжигании 7 кг бензина, это и будет затраченная работа Аз=Q=q∙m, где q – удельная теплота сгорания топлива, для бензина она равна 42∙10^6 Дж/кг, а m – масса этого топлива.
 6∙7)∙100%=30%.
6∙7)∙100%=30%. - В общем случае чтобы найти КПД, любой тепловой машины (двигателя внутреннего сгорания, парового двигателя, турбины и т.д.), где работа выполняется газом, имеет коэффициент полезного действия равный разности теплоты отданной нагревателем Q1 и полученной холодильником Q2, найдите разность теплоты нагревателя и холодильника, и поделите на теплоту нагревателя КПД= (Q1-Q2)/Q1. Здесь КПД измеряется в дольных единицах от 0 до 1, чтобы перевести результат в проценты, умножьте его на 100.
- Чтобы получить КПД идеальной тепловой машины (машины Карно), найдите отношение разности температур нагревателя Т1 и холодильника Т2 к температуре нагревателя КПД=(Т1-Т2)/Т1. Это предельно возможный КПД для конкретного типа тепловой машины с заданными температурами нагревателя и холодильника.
- Для электродвигателя найдите затраченную работу как произведение мощности на время ее выполнения. Например, если электродвигатель крана мощностью 3,2 кВт поднимает груз массой 800 кг на высоту 3,6 м за 10 с, то его КПД равен отношению полезной работы Ап=m∙g∙h, где m – масса груза, g≈10 м/с² ускорение свободного падения, h – высота на которую подняли груз, и затраченной работы Аз=Р∙t, где Р – мощность двигателя, t – время его работы.
 Получите формулу для определения КПД=Ап/Аз∙100%=(m∙g∙h)/(Р∙t) ∙100%=%=(800∙10∙3,6)/(3200∙10) ∙100%=90%.
Получите формулу для определения КПД=Ап/Аз∙100%=(m∙g∙h)/(Р∙t) ∙100%=%=(800∙10∙3,6)/(3200∙10) ∙100%=90%.
Какая формула у полезной работы?
Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную или затраченную работу Аз и полезную работу Ап. Если, например, наша цель-поднять груз массой m на высоту Н, то полезная работа – это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:
Ап =FH= mgH
Полезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм.
Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется коэффициентом полезного действия механизма.
Что такое работа в физике определение формула.
 нн
ннПомогите расшифровать формулу по физике
КПД тепловых двигателей.физика (формулы,определения,примеры) напишите! физика (формулы,определения,примеры) напишите!
В повседневной жизни часто приходится встречаться с таким понятием как работа. Что это слово означает в физике и как определить работу силы упругости? Ответы на эти вопросы вы узнаете в статье.
Механическая работа
Работа – это скалярная алгебраическая величина, которая характеризует связь между силой и перемещением. При совпадении направления этих двух переменных она вычисляется по следующей формуле:
- F – модуль вектора силы, которая совершает работу;
- S – модуль вектора перемещения.
Не всегда сила, которая действует на тело, совершает работу. Например, работа силы тяжести равна нулю, если ее направление перпендикулярно перемещению тела.
Если вектор силы образует отличный от нуля угол с вектором перемещения, то для определения работы следует воспользоваться другой формулой:
A=FScosα
α – угол между векторами силы и перемещения.
Значит, механическая работа – это произведение проекции силы на направление перемещения и модуля перемещения, или произведение проекции перемещения на направление силы и модуля этой силы.
Знак механической работы
В зависимости от направления силы относительно перемещения тела работа A может быть:
- положительной (0°≤ α
- отрицательной (90°
- равной нулю (α=90°).
Если A>0, то скорость тела увеличивается. Пример – падение яблока с дерева на землю. При A
Единица измерения работы в СИ (Международной системе единиц) – Джоуль (1Н*1м=Дж). Джоуль – это работа силы, значение которой равно 1 Ньютону, при перемещении тела на 1 метр в направлении действия силы.
Работа силы упругости
Работу силы можно определить и графическим способом. Для этого вычисляется площадь криволинейной фигуры под графиком F s (x).
Так, по графику зависимости силы упругости от удлинения пружины, можно вывести формулу работы силы упругости.
Она равна:
A=kx 2 /2
- k – жесткость;
- x – абсолютное удлинение.
Что мы узнали?
Механическая работа совершается при действии на тело силы, которая приводит к перемещению тела. В зависимости от угла, который возникает между силой и перемещением, работа может быть равна нулю или иметь отрицательный или положительный знак. На примере силы упругости вы узнали о графическом способе определения работы.
Расчёт КПД наклонной плоскости – Физика дома
Задача на расчёт КПД наклонной плоскости. Вопросы подобного типа вполне могут встретиться и на ЕГЭ, и на ГИА. Задачи этого типа — не самые сложные. Но, как и при решении любой задачи, есть некоторые нюансы, которые надо знать.
По наклонному помосту длиной 8 м и высотой 1,6 м втаскивают груз массой 225 кг. Найдите КПД наклонной плоскости, если коэффициент трения равен 0,1.
Как и любую другую задачу на расчёт КПД, эту задачу необходимо начинать решать с записи формулы для определения КПД (коэффициента полезного действия).
Конкретно для решения этой, ещё нужно нарисовать рисунок.
Далее требуется определить, какая работа является полезной, а какая работа затраченная.
Полезная работа — это то, что необходимо выполнить в задаче (здесь — поднять тело на высоту h). Затраченная работа — это работа, при совершении которой часть энергии идёт на работу по преодолению силы трения.
Записываем формулы для определения работы полезной и работы затраченной. И, используя алгоритм для решения задач на законы динамики, вычисляем силы, которые надо приложить для выполнения работы.
Важно! При определении работы полезной и работы затраченной задайте вопрос: что необходимо сделать в задаче и за счёт чего эта задача может быть выполнена. Таким образом можно очень быстро понять, где какую работу (энергию) подставлять в формулу для расчёта КПД.
Таким образом можно очень быстро понять, где какую работу (энергию) подставлять в формулу для расчёта КПД.
И не только наклонной плоскости.
Вы можете оставить комментарий, или поставить трэкбек со своего сайта.
Написать комментарий
Урок 25. тепловые двигатели. кпд тепловых двигателей – Физика – 10 класс
Физика, 10 класс
Урок 25. Тепловые двигатели. КПД тепловых двигателей
Перечень вопросов, рассматриваемых на уроке:
1) Понятие теплового двигателя;
2)Устройство и принцип действия теплового двигателя;
3)КПД теплового двигателя;
4) Цикл Карно.
Глоссарий по теме
Тепловой двигатель – устройство, в котором внутренняя энергия топлива превращается в механическую.
КПД (коэффициент полезного действия) – это отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.
Двигатель внутреннего сгорания – двигатель, в котором топливо сгорает непосредственно в рабочей камере (внутри) двигателя.
Реактивный двигатель – двигатель, создающий необходимую для движения силу тяги посредством преобразования внутренней энергии топлива в кинетическую энергию реактивной струи рабочего тела.
Цикл Карно – это идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов.
Нагреватель – устройство, от которого рабочее тело получает энергию, часть которой идет на совершение работы.
Холодильник – тело, поглощающее часть энергии рабочего тела (окружающая среда или специальные устройства для охлаждения и конденсации отработанного пара, т.е. конденсаторы).
Рабочее тело – тело, которое расширяясь, совершает работу (им является газ или пар)
Основная и дополнительная литература по теме урока:
1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М. : Просвещение, 2017. – С. 269 – 273.
: Просвещение, 2017. – С. 269 – 273.
2. Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.: Дрофа,2014. – С. 87 – 88.
Открытые электронные ресурсы по теме урока
http://kvant.mccme.ru/1973/12/teplovye_mashiny.htm
Теоретический материал для самостоятельного изучения
Сказки и мифы разных народов свидетельствуют о том, что люди всегда мечтали быстро перемещаться из одного места в другое или быстро совершать ту или иную работу. Для достижения этой цели нужны были устройства, которые могли бы совершать работу или перемещаться в пространстве. Наблюдая за окружающим миром, изобретатели пришли к выводу, что для облегчения труда и быстрого передвижения нужно использовать энергию других тел, к примеру, воды, ветра и т.д. Можно ли использовать внутреннюю энергию пороха или другого вида топлива для своих целей? Если мы возьмём пробирку, нальём туда воду, закроем её пробкой и будем нагревать. При нагревании вода закипит, и образовавшие пары воды вытолкнут пробку. Пар расширяясь совершает работу. На этом примере мы видим, что внутренняя энергия топлива превратилась в механическую энергию движущейся пробки. При замене пробки поршнем способным перемещаться внутри трубки, а саму трубку цилиндром, то мы получим простейший тепловой двигатель.
Пар расширяясь совершает работу. На этом примере мы видим, что внутренняя энергия топлива превратилась в механическую энергию движущейся пробки. При замене пробки поршнем способным перемещаться внутри трубки, а саму трубку цилиндром, то мы получим простейший тепловой двигатель.
Тепловой двигатель – тепловым двигателем называется устройство, в котором внутренняя энергия топлива превращается в механическую.
Вспомним строение простейшего двигателя внутреннего сгорания. Двигатель внутреннего сгорания состоит из цилиндра, внутри которого перемещается поршень. Поршень с помощью шатуна соединяется с коленчатым валом. В верхней части каждого цилиндра имеются два клапана. Один из клапанов называют впускным, а другой – выпускным. Для обеспечения плавности хода поршня на коленчатом вале укреплен тяжелый маховик.
Рабочий цикл ДВС состоит из четырех тактов: впуск, сжатие, рабочий ход, выпуск.
Во время первого такта открывается впускной клапан, а выпускной клапан остается закрытым. Движущийся вниз поршень засасывает в цилиндр горючую смесь.
Движущийся вниз поршень засасывает в цилиндр горючую смесь.
Во втором такте оба клапана закрыты. Движущийся вверх поршень сжимает горючую смесь, которая при сжатии нагревается.
В третьем такте, когда поршень оказывается в верхнем положении, смесь поджигается электрической искрой свечи. Воспламенившаяся смесь образует раскаленные газы, давление которых составляет 3 -6 МПа, а температура достигает 1600 -2200 градусов. Сила давления толкает поршень вниз, движение которого передается коленчатому валу с маховиком. Получив сильный толчок маховик будет дальше вращаться по инерции, обеспечивая движение поршня и при последующих тактах. Во время этого такта оба клапана остаются закрытыми.
В четвертом такте открывается выпускной клапан и отработанные газы движущимся поршнем выталкиваются через глушитель (на рисунке не показан) в атмосферу.
Любой тепловой двигатель включает в себя три основных элемента: нагреватель, рабочее тело, холодильник.
Для определения эффективности работы теплового двигателя вводят понятие КПД.
Коэффициентом полезного действия называют отношение полезной работы, совершенной данным двигателем, к количеству теплоты, полученному от нагревателя.
Q1 – количество теплоты полученное от нагревания
Q2 – количество теплоты, отданное холодильнику
– работа, совершаемая двигателем за цикл.
Этот КПД является реальным, т.е. как раз эту формулу и используют для характеристики реальных тепловых двигателей.
Зная мощность N и время работы t двигателя работу, совершаемую за цикл можно найти по формуле
Передача неиспользуемой части энергии холодильнику.
В XIX веке в результате работ по теплотехнике французский инженер Сади Карно предложил другой способ определения КПД (через термодинамическую температуру).
Главное значение этой формулы состоит в том, что любая реальная тепловая машина, работающая с нагревателем, имеющим температуру Т1, и холодильником с температурой Т2, не может иметь КПД, превышающий КПД идеальной тепловой машины. Сади Карно, выясняя при каком замкнутом процессе тепловой двигатель будет иметь максимальный КПД, предложил использовать цикл, состоящий из 2 адиабатных и двух изотермических процессов
Цикл Карно – самый эффективный цикл, имеющий максимальный КПД.
Не существует теплового двигателя, у которого КПД = 100% или 1.
Формула дает теоретический предел для максимального значения КПД тепловых двигателей. Она показывает, что тепловой двигатель тем эффективнее, чем выше температура нагревателя и ниже температура холодильника. Лишь при температуре холодильника, равной абсолютному нулю, η = 1.
Но температура холодильника практически не может быть ниже температуры окружающего воздуха. Повышать температуру нагревателя можно. Однако любой материал (твердое тело) обладает ограниченной теплостойкостью, или жаропрочностью. При нагревании он постепенно утрачивает свои упругие свойства, а при достаточно высокой температуре плавится.
Сейчас основные усилия инженеров направлены на повышение КПД двигателей за счет уменьшения трения их частей, потерь топлива вследствие его неполного сгорания и т. д. Реальные возможности для повышения КПД здесь все еще остаются большими.
д. Реальные возможности для повышения КПД здесь все еще остаются большими.
Повышение КПД тепловых двигателей и приближение его к максимально возможному — важнейшая техническая задача.
Тепловые двигатели – паровые турбины, устанавливают также на всех АЭС для получения пара высокой температуры. На всех основных видах современного транспорта преимущественно используются тепловые двигатели: на автомобильном – поршневые двигатели внутреннего сгорания; на водном – двигатели внутреннего сгорания и паровые турбины; на железнодорожном – тепловозы с дизельными установками; в авиационном – поршневые, турбореактивные и реактивные двигатели.
Сравним эксплуатационные характеристики тепловых двигателей.
КПД:
Паровой двигатель – 8%.
Паровая турбина – 40%.
Газовая турбина – 25-30%.
Двигатель внутреннего сгорания – 18-24%.
Дизельный двигатель – 40– 44%.
Реактивный двигатель – 25%.
Широкое использование тепловых двигателей не проходит бесследно для окружающей среды: постепенно уменьшается количество кислорода и увеличивается количество углекислого газа в атмосфере, воздух загрязняется вредными для здоровья человека химическими соединениями. Возникает угроза изменения климата. Поэтому нахождение путей уменьшения загрязнения окружающей среды является сегодня одной из наиболее актуальных научно-технических проблем.
Возникает угроза изменения климата. Поэтому нахождение путей уменьшения загрязнения окружающей среды является сегодня одной из наиболее актуальных научно-технических проблем.
Примеры и разбор решения заданий
1. Какую среднюю мощность развивает двигатель автомобиля, если при скорости 180 км/ч расход бензина составляет 15 л на 100 км пути, а КПД двигателя 25%?
Дано: v=180км/ч = 50 м/с, V = 15 л = 0,015 м3, s = 100 км = 105 м, ɳ = 25% = 0,25, ρ = 700 кг/м3, q = 46 × 106 Дж/кг.
Найти: N.
Решение:
Запишем формулу для расчёта КПД теплового двигателя:
Работу двигателя, можно найти, зная время работы и среднюю мощность двигателя:
Количество теплоты, выделяющееся при сгорании бензина, находим по формуле:
Учитывая всё это, мы можем записать:
Время работы двигателя можно найти по формуле:
Из формулы КПД выразим среднюю мощность:
.
Подставим числовые значения величин:
После вычислений получаем, что N=60375 Вт.
Ответ: N=60375 Вт.
2. Тепловая машина имеет КПД 25 %. Средняя мощность передачи теплоты холодильнику составляет 4 кВт. Какое количество теплоты рабочее тело получает от нагревателя за 20 с?
Дано: ɳ = 25%, N = 4000 Вт, t = 20 с.
Найти: Q1.
Решение
=
– это количество теплоты, отданное холодильнику
Коэффициент полезного действия механизма. 7 класс
Коэффициент полезного действия механизма. 7 класс
- Подробности
- Просмотров: 331
При перемещении тела с помощью простых механизмов (рычагов, блоков, наклонной плоскости) приложенной силе приходится преодолевать не только вес самого груза.
Например:
Надо поднять груз с помощью подвижного блока на высоту.
Для поднятия груза человек прикладывает к веревке силу (F тяги).
Какую работу он при этом совершает?
Надо поднять непосредственно груз весом Р.
Кроме груза надо поднять еще веревку и блок весом Р бл.
Надо преодолеть трение о воздух и в осях блока, мешающее подьему.
1. Какую работу называют полной?
Полная ( или иначе затраченная) работа – это работа, совершенная приложенной силой, и равная работе по подъему груза и преодолению какого-либо сопротивления подъему.
Полную (затраченную) работу обычно обозначают — А3.
1. Какую работу называют полезной?
Полезная работа – это работа приложенной силы, совершенная для подъема непосредственно груза.
Полезную работу обычно обозначают — Ап.
Совершаемая с помощью механизма полная работа всегда больше полезной работы.
Часть затрачиваемой работы расходуется на преодоление трения в оси механизма и сопротивления воздуха, а также на движение самого механизма.
3. Что такое коэффициент полезного действия механизма?
Что такое коэффициент полезного действия механизма?
Отношение полезной работы к полной работе называется коэффициентом полезного действия.
Сокращенно коэффициент полезного действия обозначается КПД.
КПД обычно выражают числом или в процентах и обозначают греческой буквой, которая читается как «эта».
4. Может ли КПД быть больше единицы?
Полезная работа всегда меньше затраченной работы.
Поэтому КПД любого механизма всегда меньше 100% ( или меньше 1).
Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их вес.
4. Пример решения задачи на расчет КПД.
Задача.
На коротком плече рычага подвешен груз массой 100 кг.
Для его подъема к длинному плечу приложили силу 250 Н.
Груз подняли на высоту h1 = 0,08 м, при этом точка приложения движущей силы опустилась на высоту h2 = 0,4 м.
Найти КПД рычага.
Следующая страница – смотреть
Назад в “Оглавление” – смотреть
| 3. Повторение. | 1. Повторим известный вам
материал.
2. Во время подготовки этих учеников, происходит работа со всем классом.
Подготовившиеся ребята, дают ответы по плану. |
1. Приспособления, служащие для
преобразования силы. 2. Чтобы получать выигрыш в силе. 1. Блок представляет собой колесо с желобом, укрепленное в обойме. Подвижный и неподвижный блок. Выигрыша в работе блок не дает. Применяется для поднятия грузов, при этом подвижный блок дает выигрыш в силе. 2. Рычаг – это твердое тело, которое может вращатся вокруг неподвижной опоры. Рычаг находится в равновесии, когда силы, действующие на него, обратно пропорциональны плечам этих сил. Выигрыша в работе нет. Применяют рычаг в технике (педаль автомобиля, подъемный кран), быту (ножницы, весы), природе. |
5. Какая сила удерживает рычаг в
равновесии? А) Учителем открывается правильный ответ и проверяется ответ ученика. Б) В) Расставьте на доске силы, действующие на
рычаг, отметьте плечи и точку опоры. Г) В тетради расставьте силы, действующие на рычаг, отметьте плечи и точку опоры. Д) Найдите ошибку в рисунке. Е) Запиши формулу в тетради 1. Работа 2. Мощность 3. Правило равновесия рычага 4. Момент силы 5. Выигрыш в силе подвижного блока. После выполненного задания на доске появляются правильные ответы и команда учителя: “Проверь себя”. Ученики ставят себе за каждую формулу баллы. Ж) Сделай правильное соединение. Один ученик на доске выпоняет. А все ученики у себя в тетрадях пишут для физисеской величины ей соответствующую единицу измерения. Выполняющий у доски называет для данных
физических величин единицы измерения, остальные
ученики проверяют и оценивают себя. |
Блок подвижный, поэтому F=P/2=10Н.
Ученик открывает ответ и дает объяснения.
F=P=250H. Два блока, подвижный дает выигрыш в силе в 2 раза, неподвижный не дает выигрыша в силе. Ученик на интерактивной доске расставляет силы, действующие на рычаг, отмечает плечи и точку опоры.
Ученики выполняют в тетрадях, а на интерактивной доске открывается ответ и они проверяют.
Против длинного плеча должна лежать большая сила. |
5. Целеполагание | Понятие полезной и полной работы вы
тоже не знаете, поэтому изучим сначала понятие
полной и полезной работы. Работу, совершенную телом при движении по наклонной плоскости мы вычисляли, но не учитывали, что часть работы совершается против сил трения в механизме и по перемещению его отдельных частей. Рассмотрим наклонную плоскость и поднимем по ней тело. Работа полезная заключается в том, чтобы поднять тело на высоту h. Ребята, какая работа называется полезной? |
1.плоскость 2.плечо 3.Джоуль
Коэффициент полезного действия. |
6. Новая тема | Рассмотрим интерактивные слайды: (приложение 2, слайды 18-21) Или http://files.school-collection.edu.ru/dlrstore/669b526a-e921-11dc-95ff-0800200c9a66/5_12.swf – Идеальный КПД – Наклонная плоскость – Рычаг – Блок Из чего состоит полная работа? Ребята, какая работа больше – полная или полезная? Рассмотрите и по картинке назовите в чем заключается полезная и полная работа при подъеме мальчиком раычага? Итак, еще раз, что такое КПД? Переходим ко второму пункту плана. Как обозначается КПД? |
Отношение полезной работы к полной работе называется КПД механизма. |
6.Физкультминутка
7. Закрепление нового материала
8.Индивидуальная работа
9. Итог урока
10.
11. Оценки.
12. Домашняя работа. |
Эта буква называется “этта”- буква
греческого алфавита. Третий пункт плана. Назовите формулу для определения КПД. Четвертый пункт плана. Единица измерения КПД? КПД определяется в процентах. = 40%. КПД машины= 40%. Что это означает? Пятый пункт плана. Определим КПД наклонной плоскости при поднятии груза. На партах у каждого из вас лежат листочки с лабораторной работой. Выполните её. (Приложение 3) Оцените себя и поставьте балл, если вы получили КПД при выполнении лабораторной работы. Вы устали, отдохнем. Все встаньте. Изобразите рычаг на своем теле так, чтобы
центром являлась голова. Изобразите наклонную плоскость так, что верхняя точка будет палец правой руки, а нижняя – носочек левой ноги. Изобразите блок, силы которого приложены к правой и левой руке. Назовите новые физические термины, с которыми вы познакомились сегодня. КПД= 70%. Что это значит? Рычагом мальчик поднимает груз. Назовите полезную и затраченную работу. Ученики выполняют тестовое задание. (Приложение 4) В результате выполненного теста ученики отмечают у себя в тетрадях набранный балл (от 1 до 3 баллов). Достигли ли цели урока? Посмотрим на план урока и ответим на каждый пункт? 1. Что такое КПД? 2. Как обозначается? 3. Формула. 4. Единицы измерения. 5. Как определить КПД простого мехаизма? Ученики отвечают на каждый пункт плана, который
ставили в начале урока. Ребята выполним еще один небольшой мини-тест: Твой КПД сегодня на уроке 1. 100% 2.больше 100% 3. меньше 100% 4. 0% Поднимите руки, кто поставил 100 % ? Почему? У кого КПД <100% Подсчитаем количество баллов за урок. 17-18 баллов—оценка “5” 15-16———–оценка “4” Меньше 15—-оценка “3” Параграф 61, карточка (приложенние5) (3 механизма – всем, все механизмы – дополнительно). Спасибо за работу, активность и внимание, старание, терпение, а так же понимание! Урок окончен.До свидания. |
Полезная работа – работа, совершенная по подъему грузов или преодолению какого-либо сопротивления.
Полная работа – работа, приложенная,
совершенной силой.
Отношение полезной работы к полной работе называется КПД механизма.
Что машина совершает 40% полезной работы от всех 100%.
КПД, Аполезная, Азатраченная. Это значит, что 70% работы является полезной, а 30% бесполезной.
После каждого отмеченного ответа у себя в
тетрадях ученики проверяют правильный ответ
интерактивно вышедший на доске. |
Глава 15. Работа газа в циклическом процессе. Тепловые двигатели. Цикл Карно
В программу школьного курса физики входит ряд вопросов, связанных с тепловыми двигателями. Школьник должен знать основные принципы работы теплового двигателя, понимать определение коэффициента полезного действия (КПД) циклического процесса, уметь находить эту величину в простейших случаях, знать, что такое цикл Карно и его КПД.
Тепловым двигателем (или тепловой машиной) называется процесс, в результате которого внутренняя энергия какого-то тела превращается в механическую работу. Тело, внутренняя энергия которого превращается двигателем в работу, называется нагревателем двигателя. Механическая работа в тепловых машинах совершается газом, который принято называть рабочим телом (или рабочим веществом) тепловой машины. При расширении рабочее тело и совершает полезную работу.
Для того чтобы сделать процесс работы двигателя циклическим, необходимо еще одно тело, температура которого меньше температуры нагревателя и которое называется холодильником двигателя. Действительно, если при расширении газ совершает положительную (полезную) работу (левый рисунок; работа газа численно равна площади «залитой» фигуры), то при сжатии газа он совершает отрицательную («вредную») работу, которая должна быть по абсолютной величине меньше полезной работы. А для этого сжатие газа необходимо проводить при меньших температурах, чем расширение, и, следовательно, газ перед сжатием необходимо охладить. На среднем рисунком показан процесс сжатия газа 2-1, в котором газ совершает отрицательную работу , абсолютная величина которой показана на среднем рисунке более светлой «заливкой». Чтобы суммарная работа газа за цикл была положительна, площадь под графиком расширения должна быть больше площади под графиком сжатия. А для этого газ перед сжатием следует охладить. Кроме того, из проведенных рассуждений следует, что работа газа за цикл численно равна площади цикла на графике
Действительно, если при расширении газ совершает положительную (полезную) работу (левый рисунок; работа газа численно равна площади «залитой» фигуры), то при сжатии газа он совершает отрицательную («вредную») работу, которая должна быть по абсолютной величине меньше полезной работы. А для этого сжатие газа необходимо проводить при меньших температурах, чем расширение, и, следовательно, газ перед сжатием необходимо охладить. На среднем рисунком показан процесс сжатия газа 2-1, в котором газ совершает отрицательную работу , абсолютная величина которой показана на среднем рисунке более светлой «заливкой». Чтобы суммарная работа газа за цикл была положительна, площадь под графиком расширения должна быть больше площади под графиком сжатия. А для этого газ перед сжатием следует охладить. Кроме того, из проведенных рассуждений следует, что работа газа за цикл численно равна площади цикла на графике
зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» — если против.
Таким образом, двигатель превращает в механическую работу не всю энергию, взятую у нагревателя, а только ее часть; остальная часть этой энергии используется не для совершения работы, а передается холодильнику, т.е. фактически теряется для совершения работы. Поэтому величиной, характеризующей эффективность работы двигателя, является отношение
(15.1) |
где — работа, совершаемая газом в течение цикла, — количество теплоты, полученное газом от нагревателя за цикл. Отношение (15.1) показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу и называется коэффициентом полезного действия (КПД) двигателя.
Если в течение цикла рабочее тело двигателя отдает холодильнику количество теплоты (эта величина по своему смыслу положительна), то для работы газа справедливо соотношение . Поэтому существует ряд других форм записи формулы (15. 1) для КПД двигателя
1) для КПД двигателя
(15.2) |
Французский физик и инженер С. Карно доказал, что максимальным КПД среди всех процессов, использующих некоторое тело с температурой в качестве нагревателя, и некоторое другое тело с температурой ( ) в качестве холодильника, обладает процесс, состоящий из двух изотерм (при температурах нагревателя и холодильника ) и двух адиабат (см. рисунок).
Изотермам на графике отвечают участки графика 1-2 (при температуре нагревателя ) и 3-4 (при температуре холодильника ), адиабатам — участки графика 2-3 и 4-1. Этот процесс называется циклом Карно. КПД цикла Карно равен
(15.3) |
Теперь рассмотрим задачи. В задаче 15.1.1 необходимо использовать то обстоятельство, что работа газа в циклическом процессе численно равна площади цикла на графике зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» — если против. Поэтому во втором цикле работа газа положительна, в третьем отрицательна. Первый цикл состоит из двух циклов, один из которых проходится по, второй — против часовой стрелки, причем, как следует из графика 1, площади этих циклов равны. Поэтому работа газа за цикл в процессе 1 равна нулю (правильный ответ — 2).
Поэтому во втором цикле работа газа положительна, в третьем отрицательна. Первый цикл состоит из двух циклов, один из которых проходится по, второй — против часовой стрелки, причем, как следует из графика 1, площади этих циклов равны. Поэтому работа газа за цикл в процессе 1 равна нулю (правильный ответ — 2).
Поскольку в результате совершения циклического процесса газ возвращается в первоначальное состояние (задача 15.1.2), то изменение внутренней энергии газа в этом процессе равно нулю (ответ 2).
Применяя в задаче 15.1.3 первый закон термодинамики ко всему циклическому процессу и учитывая, что изменение внутренней энергии газа равно нулю (см. предыдущую задачу), заключаем, что (ответ 3).
Поскольку работа газа численно равна площади цикла на диаграмме «давление-объем», то работа газа в процессе в задаче 15.1.4 равна (ответ 1). Аналогично в задаче 15.1.5 газ за цикл совершает работу (ответ 1).
Работа газа в любом процессе равна сумме работ на отдельных участках процесса. Поскольку процесс 2-3 в задаче 15.1.6 — изохорический, то работа газа в этом процессе равна нулю. Поэтому (ответ 3).
По определению КПД показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу (задача 15.1.7 — ответ 4).
Работа двигателя за цикл равна разности количеств теплоты, полученного от нагревателя и отданного холодильнику : . Поэтому КПД цикла есть
(задача 15.1.8 — ответ 3).
По формуле (15.3) находим КПД цикла Карно в задаче 15.1.9
(ответ 2).
Пусть температура нагревателя первоначального цикла Карно равна , температура холодильника (задача 15.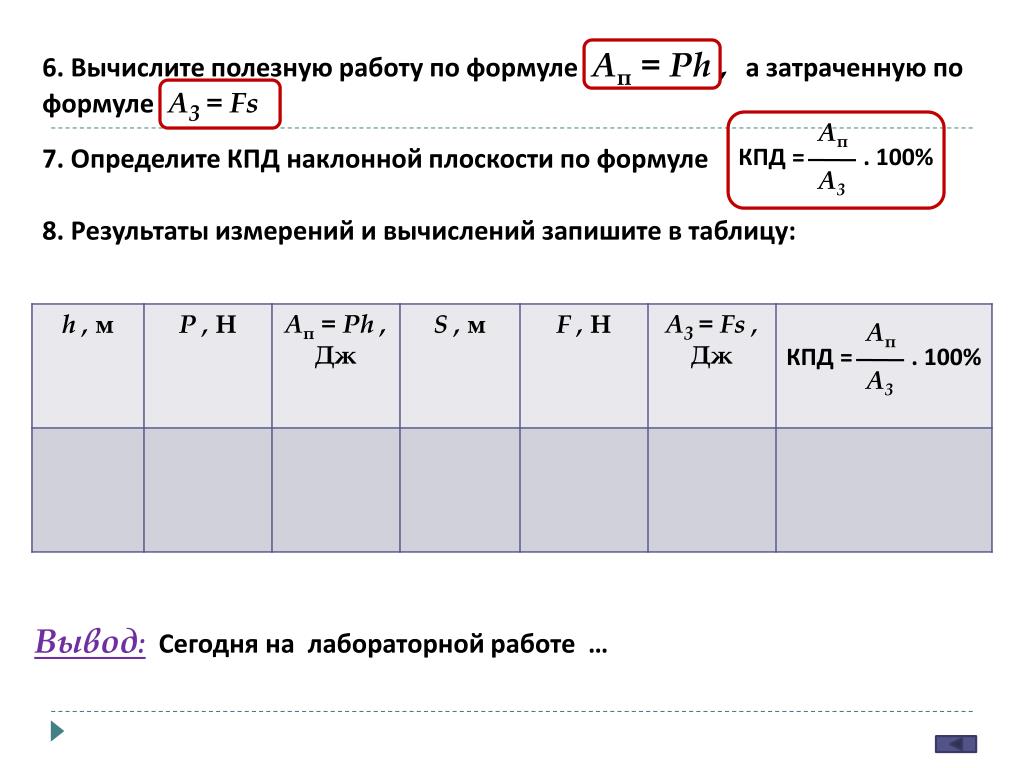 1.10). Тогда по формуле (15.3) для КПД первоначального цикла имеем
1.10). Тогда по формуле (15.3) для КПД первоначального цикла имеем
Отсюда находим . Поэтому для КПД нового цикла Карно получаем
(ответ 2).
В задаче 15.2.1 формулы (2), (3) и (4) представляют собой разные варианты записи определения КПД теплового двигателя (см. формулы (15.1) и (15.2)). Поэтому не определяет КПД двигателя только формула 1. (ответ 1).
Мощностью двигателя называется работа, совершенная двигателем в единицу времени. Поскольку работа двигателя равна разности полученного от нагревателя и отданного холодильнику количеств теплоты, имеем для мощности двигателя в задаче 15.2.2
(ответ 3).
По формуле (15.2) имеем для КПД двигателя в задаче 15. 2.3
2.3
где — количество теплоты, полученное от нагревателя, — количество теплоты, отданное холодильнику (правильный ответ — 2).
Для нахождения КПД теплового двигателя в задаче 15.2.4 удобно использовать последнюю из формул (15.2). Имеем
где — работа газа, — количество теплоты, отданное холодильнику. Поэтому правильный ответ в задаче — 3.
Пусть газ совершает за цикл работу (задача 15.2.5). Поскольку количество теплоты, полученное от нагревателя равно ( — количество теплоты, отданное холодильнику), и работа составляет 20 % от этой величины, то для работы справедливо соотношение = 0,2 ( + 100). Отсюда находим = 25 Дж (ответ 1).
Поскольку работа теплового двигателя в задаче 15.2.6 равна 100 Дж при КПД двигателя 25 %, то двигатель получает от нагревателя количество теплоты 400 Дж. Поэтому он отдает холодильнику 300 Дж теплоты в течение цикла (ответ 4).
Поэтому он отдает холодильнику 300 Дж теплоты в течение цикла (ответ 4).
В задаче 15.2.7 газ получает или отдает теплоту только в процессах 1-2 и 3-1 (процесс 2-3 по условию адиабатический). Поэтому данное в условии задачи количество теплоты является количеством теплоты, полученным от нагревателя в течение цикла, — количеством теплоты, отданном холодильнику. Поэтому работа газа равна (ответ 1). |
Цикл, данный в задаче 15.2.8, состоит из двух изотерм 2-3 и 4-1 и двух изохор 1-2 и 3-4. Работа газа в изохорических процессах равна нулю. Сравним работы газа в изотермических процессах. Для этого удобно построить график зависимости давления от объема в рассматриваемом процессе, поскольку работа газа есть площадь под этим графиком. График зависимости давления от объема для заданного в условии процесса приведен на рисунке. Поскольку изотерме 2-3 соответствует бóльшая температура, чем изотерме 4-1, то она будет расположена выше на графике . |
Для сравнения работ газа на различных участках процесса в задаче 15.2.9 построим график зависимости давления от объема. Этот график представлен на рисунке. Из рисунка следует, что работы газа в процессах 1-2 и 3-4 одинаковы по модулю (этим работам отвечают площади прямоугольников, «залитых» на рисунке светлой и темной «заливкой»). Работе газа на участке 4-1 отвечает площадь под графиком 4-1, которая меньше площади под графиком 1-2. Работе газа на участке 2-3 отвечает площадь под кривой 2-3 на рисунке, которая заведомо больше площади «залитых» прямоугольников. Поэтому в процессе 2-3 газ и совершает наибольшую по абсолютной величине (среди рассматриваемых процессов) работу (ответ 2.).
Согласно определению коэффициент полезного действия представляет отношение работы газа за цикл к количеству теплоты , полученному от нагревателя . Как следует из данного в условии задачи 15.2.10 графика, и в процессе 1-2-4-1 и в процессе 1-2-3-1 газ получает теплоту только на участке 1-2. Поэтому количество теплоты, полученное газом от нагревателя в процессах
1-2-4-1 и 1-2-3-1 одинаково. А вот работа газа в процессе 1-2-4-1 вдвое меньше (так площадь треугольника 1-2-4 как вдвое меньше площади треугольника 1-2-4-1). Поэтому коэффициент полезного действия процесса 1-2-4-1 вдвое меньше коэффициента полезного действия процесса 1-2-3-1 (ответ 1).
Как следует из данного в условии задачи 15.2.10 графика, и в процессе 1-2-4-1 и в процессе 1-2-3-1 газ получает теплоту только на участке 1-2. Поэтому количество теплоты, полученное газом от нагревателя в процессах
1-2-4-1 и 1-2-3-1 одинаково. А вот работа газа в процессе 1-2-4-1 вдвое меньше (так площадь треугольника 1-2-4 как вдвое меньше площади треугольника 1-2-4-1). Поэтому коэффициент полезного действия процесса 1-2-4-1 вдвое меньше коэффициента полезного действия процесса 1-2-3-1 (ответ 1).
Расчет количества работы, выполненной силами
В предыдущей части Урока 1 работа описывалась как происходящая, когда на объект действует сила, вызывающая перемещение. Когда действует сила, вызывающая перемещение объекта, для вычисления работы необходимо знать три величины. Этими тремя величинами являются сила, смещение и угол между силой и смещением. Затем работа рассчитывается как сила • перемещение • косинус (тета), где тета — угол между векторами силы и смещения. В этой части Урока 1 концепции и математика работы будут применяться для анализа различных физических ситуаций.
В этой части Урока 1 концепции и математика работы будут применяться для анализа различных физических ситуаций.
Проверьте свое понимание
Выразите свое понимание концепции и математики работы, ответив на следующие вопросы. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
1. Примените уравнение работы, чтобы определить количество работы, выполненной приложенной силой в каждой из трех ситуаций, описанных ниже.
2. Во многих случаях на объект действует более одной силы. Диаграмма свободного тела — это диаграмма, которая изображает тип и направление всех сил, действующих на объект. Следующие описания и сопровождающие их диаграммы свободного тела показывают силы, действующие на объект. Для каждого случая укажите, какие силы совершают работу над объектом. Затем вычислить работу этих сил.
| Свободное тело Схема | Силы, выполняющие работу на Объект | Объем выполненной работы Каждая сила |
Сила 10 Н толкает брусок по поверхности, свободной от трения, с перемещением 5. 0 м вправо. 0 м вправо. | ||
| Сила трения 10 Н замедляет движущийся блок до полной остановки после перемещения вправо на 5,0 м. | ||
| Сила 10 Н приложена, чтобы толкнуть брусок по поверхности трения с постоянной скоростью для смещения 5.0 м вправо. | ||
| Объект массой около 2 кг скользит с постоянной скоростью по поверхности без трения, перемещаясь вправо на 5 м. | ||
| Объект массой около 2 кг тянет вверх с постоянной скоростью под действием силы 20 Н при вертикальном перемещении 5 м. |
3. Перед началом спуска автомобиль на американских горках всегда поднимается по первому холму на большую начальную высоту. На автомобиле выполняется работа (обычно цепью) для достижения этой начальной высоты. Разработчик каботажных судов рассматривает три различных угла наклона, при которых 2000-килограммовый автопоезд должен тянуться к вершине 60-метрового холма.В каждом случае сила, приложенная к автомобилю, будет приложена параллельно холму. Ее критический вопрос: какой угол потребует наибольшей работы? Проанализируйте данные, определите работу, проделанную в каждом случае, и ответьте на этот важный вопрос.
На автомобиле выполняется работа (обычно цепью) для достижения этой начальной высоты. Разработчик каботажных судов рассматривает три различных угла наклона, при которых 2000-килограммовый автопоезд должен тянуться к вершине 60-метрового холма.В каждом случае сила, приложенная к автомобилю, будет приложена параллельно холму. Ее критический вопрос: какой угол потребует наибольшей работы? Проанализируйте данные, определите работу, проделанную в каждом случае, и ответьте на этот важный вопрос.
| Угол | Сила | Расстояние | Работа (J) | |
а. | 35 градусов | 1,12 x 10 4 Н | 105 м | |
б. | 45 градусов | 1,39 x 10 4 Н | 84,9 м | |
с. | 55 градусов | 1,61 x 10 4 Н | 73,2 м |
4. Бен Травлун несет чемодан с усилием 200 Н на три лестничных пролета (высота 10,0 м), а затем толкает его с горизонтальной силой 50,0 Н с постоянной скоростью 0,5 м/с на расстояние 35 по горизонтали.0 метров. Сколько работы Бен проделывает со своим чемоданом во время всего этого движения ?
5. На брусок действует сила 50 Н под углом, показанным на схеме. Блок перемещается по горизонтали на расстояние 3,0 м. Какую работу совершает приложенная сила?
6. Какую работу совершает приложенная сила, чтобы поднять блок массой 15 ньютонов 3.0 метров по вертикали с постоянной скоростью?
7. Студент массой 80,0 кг преодолевает три лестничных пролета за 12,0 сек.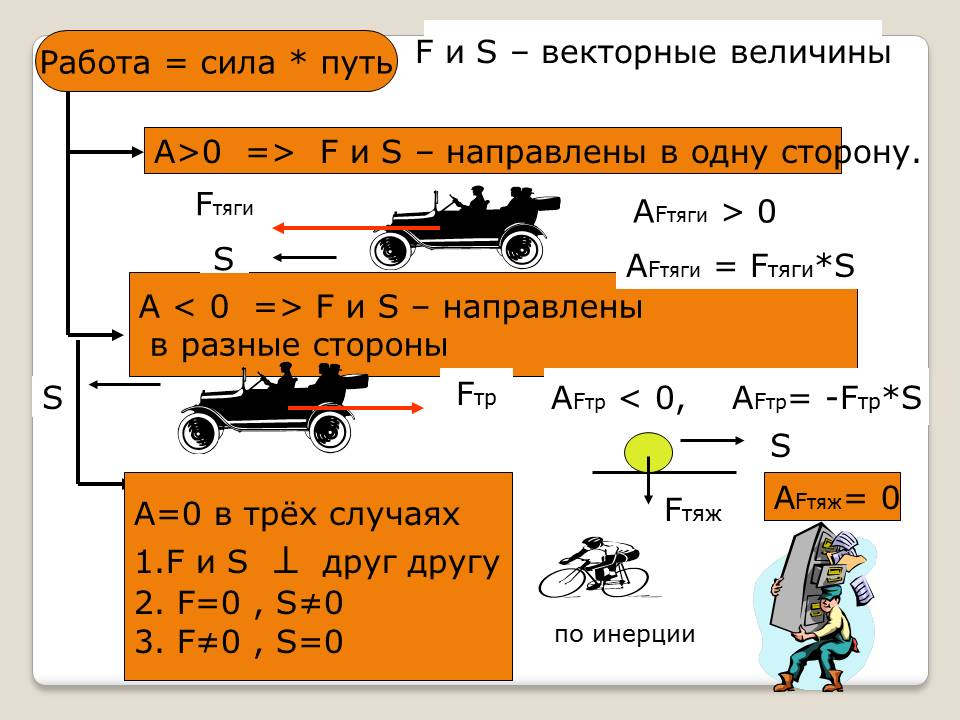 Студент прошел вертикальную дистанцию 8,0 м. Определить работу, которую совершил студент, чтобы поднять свое тело на эту высоту. Предположим, что его скорость постоянна.
Студент прошел вертикальную дистанцию 8,0 м. Определить работу, которую совершил студент, чтобы поднять свое тело на эту высоту. Предположим, что его скорость постоянна.
8.Рассчитайте работу, совершаемую силой 2,0 Н (направленной под углом 30° к вертикали) для перемещения 500-граммовой коробки на расстояние 400 см по горизонтали по шероховатому полу с постоянной скоростью 0,5 м/с. (СОВЕТ: будьте осторожны с юнитами.) |
9. Уставшая белка (масса 1 кг) отжимается, прилагая силу, поднимающую ее центр масс на 5 см.Оцените количество отжиманий, которое должна сделать уставшая белка, чтобы совершить работу примерно в 5,0 Дж.
Мы хотели бы предложить… Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom.
 Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей Интерактивной программы It’s All Uphill Interactive.Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивное приложение It’s All Uphill позволяет учащимся изучить влияние угла наклона на силу и работу, выполняемую при подъеме тележки в гору с постоянной скоростью.
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей Интерактивной программы It’s All Uphill Interactive.Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивное приложение It’s All Uphill позволяет учащимся изучить влияние угла наклона на силу и работу, выполняемую при подъеме тележки в гору с постоянной скоростью.Выполненная работа – определение, формула, примеры и важные часто задаваемые вопросы
Выполненная работа Определение
Выполненная работа разработана таким образом, что она включает как силу, воздействующую на тело, так и полное перемещение тела.
Этому блоку предшествует постоянная сила F. Цель этой силы состоит в том, чтобы переместить тело на определенное расстояние d по прямой траектории в направлении действия силы.
[Изображение скоро будет загружено]
Рассмотрим блок, расположенный на горизонтальной поверхности без трения. На этот брусок действует постоянная сила F. Цель этой силы состоит в том, чтобы переместить тело на определенное расстояние по прямой траектории в направлении действия силы.
На этот брусок действует постоянная сила F. Цель этой силы состоит в том, чтобы переместить тело на определенное расстояние по прямой траектории в направлении действия силы.
Теперь полная работа, выполненная этой силой, равна произведению величины приложенной силы на расстояние, пройденное телом.С научной точки зрения формула выполненной работы будет выглядеть так:
W = F * d:
В этом случае сила, действующая на блок, постоянна, но направление силы и направление смещения, на которое воздействует эта сила, различны. Здесь сила F реагирует под углом θ на перемещение d.
W = (|F| cosθ) |d|
Мы знаем, что выполненная работа определяется как произведение величины смещения d и составляющей силы, направленной в направлении смещения.{2}\] = 2as
W = \[\frac{1}{2}\]m(2as)
W = (m*a)*s
Из второго закона Ньютона известно, что F = ma
W = F * s
Работа, выполненная системой
При описании работы мы подчеркиваем влияние того, что система не воздействует на свое окружение.
Таким образом, мы выражаем работу как положительную, когда система прилагает какое-либо усилие к окружающей среде (т. е. энергия покидает систему). Работа отрицательна, если над системой совершается работа (т.е., добавленная в систему энергия).
[Изображение будет загружено в ближайшее время]
Примеры выполненной работы
Положительная работа: Если сила перемещает объект в его направлении, то выполненная работа является положительной.
Примером такой работы является движение мяча, падающего на землю, при этом смещение мяча происходит в направлении действия силы тяжести.
Отрицательная работа: Когда сила и перемещение направлены в противоположные стороны, работа считается отрицательной.
Например, когда мяч брошен вверх, смещение будет направлено вверх; однако сила гравитации земли будет направлена вниз.
Нулевая работа: если направление силы и перемещение перпендикулярны друг другу, общая работа, выполненная силой над объектом, равна нулю. {2}\]
{2}\]
Где
m = масса объекта, измеренная в килограммах.
Вт = работа, выполненная объектом, измеряемая в джоулях.
vf = конечная скорость объекта, измеренная в м/с.
vi = начальная скорость объекта, измеренная в м/с.
Следовательно, принцип работы-энергии утверждает, что:
Суммарная работа всех сил, действующих на частицу, или работа равнодействующей силы F (в нижнем индексе равнодействующая) эквивалентна изменению кинетической энергии частица.
Что такое формула работы? Примеры
Формула работы используется для расчета работы. Прежде чем мы выучим формулу, давайте вспомним, что означает работа. Говорят, что работа совершается, когда мы прикладываем силу к объекту, и объект испытывает перемещение. Если перемещение в направлении действия силы равно нулю, то совершенная работа равна нулю. Формула работы используется для расчета работы, совершаемой при перемещении объекта. Давайте узнаем больше о формуле для работы вместе с решенными примерами в следующем разделе.
Если перемещение в направлении действия силы равно нулю, то совершенная работа равна нулю. Формула работы используется для расчета работы, совершаемой при перемещении объекта. Давайте узнаем больше о формуле для работы вместе с решенными примерами в следующем разделе.
Что такое формула работы?
Формула работы используется для расчета работы, затрачиваемой на перемещение любого объекта. Работа есть произведение приложенной силы и перемещения в направлении действия силы. Работа есть скалярное произведение двух векторов: силы и перемещения. Таким образом, работа является скалярной величиной. Единицей работы в системе СИ является Джоуль (Дж).
Рабочая формула
Формула для работы может быть выражена как
.Ш = Ф.д
Вт = (Fcos θ)d
Где,
- Вт = выполненная работа
- F = Величина приложенной силы
- d = Величина смещения в направлении действия силы.

- θ = угол между векторами: силы и перемещения
Единицей работы в системе СИ является Джоуль (Дж). Если совершить работу в 1 джоуль, то формула работы будет следующей: 1 Дж = 1 Н·м
.Вывод формулы работы
Рассмотрим блок, помещенный на горизонтальном полу без трения, на который действует постоянная сила F, благодаря которой этот блок перемещается на расстояние d по прямой линии в направлении действия силы.
В общем случае работа силы F равна изменению кинетической энергии
W = (1/2)mv 2 – (1/2) mu 2 = 1/2m(v 2 -u 2 )
Применение v 2 -u 2 = 2as
Вт = (1/2)м(2ас)
Вт =
мас.
Так как F = ma (второй закон Ньютона), то W = Fs.(s=d=смещение)
Теперь, если эффективная составляющая силы вдоль направления перемещения равна Fcosθ и отвечает за перемещение любого объекта в заданном направлении, то работа, совершаемая силой F при перемещении тела на перемещение d, равна W=(|F| cosθ)|d|
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Забронируйте бесплатный пробный урок
Примеры использования формулы для работы
Пример 1: 10 Ньютон Сила, приложенная к телу, перемещает его на 2 метра. Вычислите работу, выполненную по формуле работы.
Решение:
Чтобы найти: Работа выполнена
Дано: Сила (F) = 10 Н
Водоизмещение (d) = 2 м
Использование формулы для работы,
Вт = F. d
d
= (10)(2)
= 20 Нм
Ответ: Работа в 20 Нм совершается, когда сила в 10 Ньютонов перемещает тело на 2 метра.
Пример 2: Кули на вокзале несет сумку массой 100 Н на некоторое расстояние. Вычислите работу, которую совершает кули над сумкой, используя формулу работы.
Решение:
Найти работу, выполненную кули.
Дано: Вес мешка = 100 Н
Кроме того, вес мешка будет действовать в вертикальном направлении, а его движение будет происходить в горизонтальном направлении. Значит, смещение мешка в направлении действия силы (веса) равно нулю.
д = 0
Использование формулы для работы,
Вт = F.d
= (100)(0)
= 0 Дж
Ответ: Работа кули над сумкой равна нулю.
Пример 3: Рассчитайте работу, выполненную силой при перемещении объекта на расстояние 7 м, если объект протаскивается горизонтально по поверхности под действием силы 150 Н, действующей параллельно поверхности.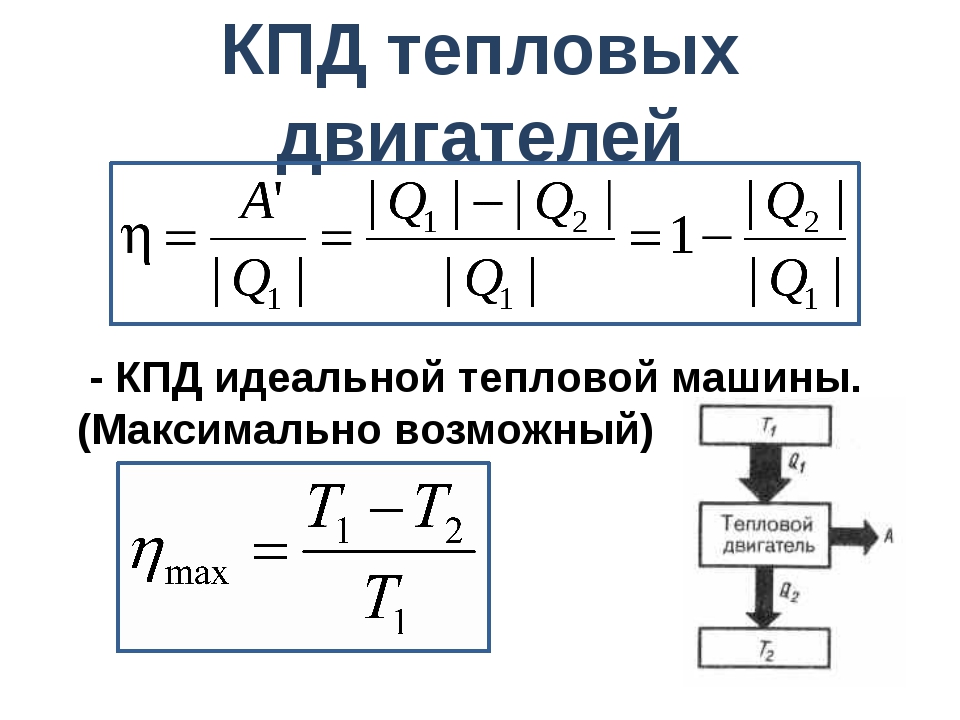
Решение:
Найти: Работа силы при перемещении тела на расстояние 7 м
Дано: F = 150 Н, d = 7 м
Так как F и d находятся в одном направлении,
θ = 0, [θ — угол силы к направлению движения]
Вт = F × Cos θ × d
= 150×7×Cos 0
= 1050 Дж [Поскольку Cos 0 = 1]
Ответ: Работа, совершаемая силой при перемещении тела, равна 800 Дж.
Часто задаваемые вопросы о формуле для работы
Что такое формула работы?
Формула работы определяется как формула для расчета работы, выполненной при перемещении объекта. Совершенная работа равна произведению величины приложенной силы на расстояние, которое тело перемещает из своего начального положения в конечное. Математически проделанная работа Формула задается как W = Fd
.Какие существуют версии формулы работы?
Математически понятие проделанной работы W равно силе f, умноженной на расстояние (d), то есть W = f. d и если сила приложена под углом θ к смещению, то выполненная работа рассчитывается как W = f . д потому что θ.
d и если сила приложена под углом θ к смещению, то выполненная работа рассчитывается как W = f . д потому что θ.
Каковы применения формулы работы?
Формула работы имеет множество применений, например, для вычисления проделанной работы, силы или перемещения в любой задаче.
Что такое d в формуле работы?
В формуле работы W = F. d, d — это смещение, на сколько предмет сместился со своего начального места.
Работайте как интеграл – видео и расшифровка урока
Пример
Начнем с простого диагонального графика:
На этом графике сила равна kx – константа, умноженная на перемещение.2. Это наше уравнение для работы, проделанной в этом процессе. Все, что нам нужно, это наклон графика и конечное смещение, и мы можем вычислить работу.
Практические задачи
Время для практических задач. Задача 1:
Задача 1:
Сила, приложенная к объекту, определяется уравнением F = 3x + 2. Если полное перемещение равно 5 м, какая работа совершается при этом?
Чтобы решить эту задачу, нам сначала нужно найти уравнение для проделанной работы.3 + 2 х . И эти значения x снова становятся общим смещением. Подставляем наше значение 10 метров, и мы получаем, что проделанная работа составляет 353,3 Дж. И это наш ответ.
Итоги урока
Работа — важная величина в физике. Он определяется как энергия, передаваемая от одного типа к другому всякий раз, когда применяется сила, заставляющая объект перемещаться на расстояние. В форме уравнения работа – это сила, умноженная на смещение, перемещаемое в направлении этой силы.Или, другими словами, W = Fx cos (тета). Часть cos (тета) — это фактор, который просто гарантирует, что сила, на которую вы смотрите, направлена в правильном направлении.
Это значение Fx является просто площадью под идеально плоским графиком сила-перемещение. Но что, если ваш график не плоский? А если по диагонали? Или изогнутый?
Но что, если ваш график не плоский? А если по диагонали? Или изогнутый?
В такой ситуации вам нужен расчет. Работа — это не просто сила, умноженная на перемещение; это интеграл силы НА смещение.Или, другими словами, если у вас есть сила как функция смещения и вы интегрируете ее по отношению к этому перемещению, вы получите выражение для работы. Используя эту интегральную форму, вы можете решить любую проблему, которая может возникнуть на вашем пути.
Результаты обучения
После этого урока вы сможете:
- Давать определение работе с точки зрения физики
- Определите уравнение для работы
- Объясните, как использовать интегральную форму для решения рабочих задач по исчислению
7.3 Теорема о работе-энергии – University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Применять теорему о работе-энергии, чтобы найти информацию о движении частицы, учитывая силы, действующие на него
- Используйте теорему о работе-энергии, чтобы найти информацию о силах, действующих на частицу, учитывая информацию о ее движении
Мы обсудили, как найти работу, совершаемую над частицей силами, действующими на нее, но как эта работа проявляется в движении частицы? Согласно второму закону движения Ньютона, сумма всех сил, действующих на частицу, или результирующая сила, определяет скорость изменения импульса частицы или ее движение. Следовательно, мы должны рассмотреть работу, совершаемую всеми силами, действующими на частицу, или общую работу, чтобы увидеть, какое влияние она оказывает на движение частицы.
Следовательно, мы должны рассмотреть работу, совершаемую всеми силами, действующими на частицу, или общую работу, чтобы увидеть, какое влияние она оказывает на движение частицы.
Давайте начнем с рассмотрения чистой работы, совершаемой частицей при ее движении с бесконечно малым смещением, которое является скалярным произведением чистой силы и смещения: dWnet=F→net·dr→.dWnet=F→net·dr →. Второй закон Ньютона говорит нам, что F→net=m(dv→/dt), F→net=m(dv→/dt), поэтому dWnet=m(dv→/dt)·dr→.dWnet=m(dv→ /дт)·др→. Для математических функций, описывающих движение физической частицы, можно переставить дифференциалы dt и т. д., как алгебраические величины в этом выражении, то есть
dWnet=m(dv→dt)·dr→=mdv→·(dr→dt)=mv→·dv→,dWnet=m(dv→dt)·dr→ =mdv→·(dr→dt)=mv→·dv→,, где мы заменили производную смещения по времени на скорость и использовали коммутативное свойство скалярного произведения [уравнение 2.30]. Поскольку производные и интегралы скаляров, вероятно, вам более знакомы, мы выражаем скалярное произведение в терминах декартовых координат, прежде чем интегрировать между любыми двумя точками A и B на траектории частицы. Это дает нам чистую работу, проделанную частицей:
Это дает нам чистую работу, проделанную частицей:
7,8
На среднем этапе мы использовали тот факт, что квадрат скорости есть сумма квадратов его декартовых составляющих, а на последнем этапе мы использовали определение кинетической энергии частицы. Этот важный результат называется теоремой работы-энергии (рис. 7.11).
Теорема о работе-энергии
Чистая работа, совершенная частицей, равна изменению кинетической энергии частицы:
Wnet=КБ-КА.Wnet=КБ-КА.7,9
Фигура 7.11 Конные тяги – обычное дело на государственных ярмарках. Работа, выполняемая лошадьми, тянущими груз, приводит к изменению кинетической энергии груза, что в конечном итоге приводит к его ускорению. (кредит: модификация работы Jassen/Flickr)
Согласно этой теореме, когда объект замедляется, его конечная кинетическая энергия меньше его начальной кинетической энергии, изменение его кинетической энергии отрицательно, как и чистая работа, совершаемая над ним. Если объект ускоряется, чистая работа, совершенная над ним, положительна. При расчете чистой работы необходимо учитывать все силы, действующие на объект. Если вы исключите любые силы, действующие на объект, или добавите любые силы, которые на него не действуют, вы получите неправильный результат.
Если объект ускоряется, чистая работа, совершенная над ним, положительна. При расчете чистой работы необходимо учитывать все силы, действующие на объект. Если вы исключите любые силы, действующие на объект, или добавите любые силы, которые на него не действуют, вы получите неправильный результат.
Важность теоремы о работе-энергии и дальнейших обобщений, к которым она приводит, заключается в том, что она делает некоторые типы вычислений намного проще для выполнения, чем если бы они пытались решить второй закон Ньютона.Например, в законах движения Ньютона мы нашли скорость объекта, скользящего по плоскости без трения, решив второй закон Ньютона для ускорения и используя кинематические уравнения для постоянного ускорения, получив
vf2=vi2+2g(sf−si)sinθ,vf2=vi2+2g(sf−si)sinθ,, где s — смещение вниз по плоскости.
Мы также можем получить этот результат из теоремы работа-энергия в уравнении 7.1. Поскольку на объект действуют только две силы — гравитация и нормальная сила, а нормальная сила не совершает никакой работы, чистая работа — это просто работа, совершаемая силой тяжести. . После скалярного произведения и интегрирования от начального положения yiyi до конечного положения yfyf можно найти чистую работу как
. После скалярного произведения и интегрирования от начального положения yiyi до конечного положения yfyf можно найти чистую работу как
, где и — плюс. Теорема о работе и энергии говорит, что это равно изменению кинетической энергии:
−mg(yf−yi)=12m(vf2−vi2).−mg(yf−yi)=12m(vf2−vi2).Используя прямоугольный треугольник, мы видим, что (yf−yi)=(sf−si)sinθ, (yf−yi)=(sf−si)sinθ, поэтому результат для конечной скорости тот же.
Что достигается с помощью теоремы о работе и энергии? Ответ заключается в том, что для плоской поверхности без трения это не так уж и много.Однако второй закон Ньютона легко решить только для этого частного случая, тогда как теорема о работе-энергии дает конечную скорость для любой поверхности без трения. Для произвольной искривленной поверхности нормальная сила непостоянна, и второй закон Ньютона может быть трудно или невозможно решить аналитически. Постоянная или нет, но при движении по поверхности нормальная сила никогда не совершает никакой работы, потому что она перпендикулярна смещению. Вычисление с использованием теоремы о работе и энергии позволяет избежать этой трудности и применимо к более общим ситуациям.
Вычисление с использованием теоремы о работе и энергии позволяет избежать этой трудности и применимо к более общим ситуациям.
Стратегия решения проблем
Теорема о работе-энергии
- Нарисуйте диаграмму свободного тела для каждой силы, действующей на объект.
- Определите, работает ли каждая сила над перемещением на диаграмме. Обязательно сохраняйте любые положительные или отрицательные признаки в проделанной работе.
- Сложите общую работу, выполненную каждой силой.
- Приравняйте эту общую работу к изменению кинетической энергии и найдите любой неизвестный параметр.
- Проверьте свои ответы.Если объект движется с постоянной скоростью или нулевым ускорением, полная проделанная работа должна быть равна нулю и соответствовать изменению кинетической энергии. Если общая работа положительна, объект должен ускориться или увеличить кинетическую энергию. Если общая работа отрицательна, объект должен замедлиться или уменьшить кинетическую энергию.

Пример 7,9
Петля-петля
Путь без трения для игрушечной машинки включает в себя петлю радиусом R . На какой высоте, измеренной от низа петли, должен находиться автомобиль, чтобы начать движение из состояния покоя на приближающемся участке пути и полностью объехать петлю?Фигура 7.12 В гусенице игрушечной машинки без трения есть петля-петля. С какой высоты должен стартовать автомобиль, чтобы он мог объехать петлю и не упасть?
Стратегия
Диаграмма свободного тела в конечном положении объекта показана на рис. 7.12. Гравитационная работа — это единственная работа, совершаемая над смещением, которое не равно нулю. Поскольку вес направлен в том же направлении, что и чистое вертикальное смещение, полная работа силы тяжести положительна. По теореме о работе-энергии начальная высота определяет скорость автомобиля в верхней части петли. –mg(y2−y1)=12mv22, –mg(y2−y1)=12mv22,, где обозначения показаны на прилагаемом рисунке. В верхней части петли нормальная сила и гравитация направлены вниз, а ускорение является центростремительным, поэтому
В верхней части петли нормальная сила и гравитация направлены вниз, а ускорение является центростремительным, поэтому
Условием сохранения контакта с гусеницей является наличие некоторой нормальной силы, какой бы незначительной она ни была; то есть N>0N>0. Подставляя вместо v22v22 и N , мы можем найти условие для y1y1.
Решение
Реализуйте шаги стратегии для достижения желаемого результата: N=-mg+mv22R=-mgR+2mg(y1-R)R>0 или y1>5R2.N=-mg+mv22R=-mgR+2mg(y1-R)R>0 или y1>5R2.Значение
На поверхности петли нормальная составляющая силы тяжести и нормальная контактная сила должны обеспечивать центростремительное ускорение автомобиля, движущегося по петле. Тангенциальная составляющая силы тяжести замедляет или ускоряет автомобиль. Ребенок выяснил бы, с какой высоты заводить машину, путем проб и ошибок, но теперь, когда вы знаете теорему о работе и энергии, вы можете предсказать минимальную высоту (а также другие более полезные результаты) на основе физических принципов. Используя теорему о работе и энергии, вам не нужно было решать дифференциальное уравнение для определения высоты.
Используя теорему о работе и энергии, вам не нужно было решать дифференциальное уравнение для определения высоты.Проверьте свое понимание 7.7
Предположим, что радиус петли в примере 7.9 равен 15 см, а игрушечная машинка стартует из состояния покоя на высоте 45 см над днищем. Какова его скорость в верхней точке петли?
В ситуациях, когда известно движение объекта, но неизвестны значения одной или нескольких сил, действующих на него, вы можете использовать теорему о работе-энергии, чтобы получить некоторую информацию о силах.Работа зависит от силы и расстояния, на котором она действует, поэтому информация предоставляется через их произведение.
Пример 7.10
Определение останавливающей силы
Пуля имеет массу 40 гран (2,60 г) и начальную скорость 1100 футов/с (335 м/с). Он может пробить восемь 1-дюймовых сосновых досок, каждая толщиной 0,75 дюйма. Какова средняя тормозная сила дерева, как показано на рис. 7.13?
7.13?Фигура 7.13 Доски прикладывают силу, чтобы остановить пулю.В результате доски работают, а пуля теряет кинетическую энергию.
Стратегия
Мы можем предположить, что при указанных общих условиях пуля теряет всю свою кинетическую энергию, пробивая доски, поэтому теорема о работе говорит, что ее начальная кинетическая энергия равна средней тормозной силе, умноженной на пройденное расстояние. Изменение кинетической энергии пули и чистая работа, совершаемая для ее остановки, отрицательны, поэтому, когда вы записываете теорему о работе-энергии с чистой работой, равной средней силе, умноженной на тормозной путь, вот что вы получаете.Общая толщина восьми 1-дюймовых сосновых досок, через которые проходит пуля, составляет 8×34 дюйма = 6 дюймов = 15,2 см. 8×34 дюйма = 6 дюймов = 15,2 см.Решение
Применяя теорему о работе-энергии, получаем Wnet=-FaveΔsstop=-Kinitial,Wnet=-FaveΔsstop=-Kinitial,так
Fave=12мв2Δsстоп=12(2,6×10-3кг)(335м/с)20,152м=960Н. Fave=12мв2Δsстоп=12(2,6×10-3кг)(335м/с)20,152м=960Н.
Fave=12мв2Δsстоп=12(2,6×10-3кг)(335м/с)20,152м=960Н.Значение
В этом примере мы могли бы использовать второй закон Ньютона и кинематику, но теорема о работе и энергии дает ответ и в менее простых ситуациях.Проникновение пули, выпущенной вертикально вверх в деревянный брусок, обсуждается в одном из разделов недавней статьи Асифа Шакура [«Научная видеоголоволомка Bullet-Block». Учитель физики (январь 2015 г.) 53(1): 15-16]. Если пуля выпущена точно по центру блока, она теряет всю свою кинетическую энергию и проникает немного дальше, чем если бы она была выпущена не по центру. Причина в том, что если пуля попадает не в центр, у нее остается небольшая кинетическая энергия после того, как она прекращает проникать, потому что блок вращается.Теорема о работе-энергии подразумевает, что меньшее изменение кинетической энергии приводит к меньшему проникновению. Вы поймете больше о физике в этой интересной статье после того, как закончите читать Angular Momentum.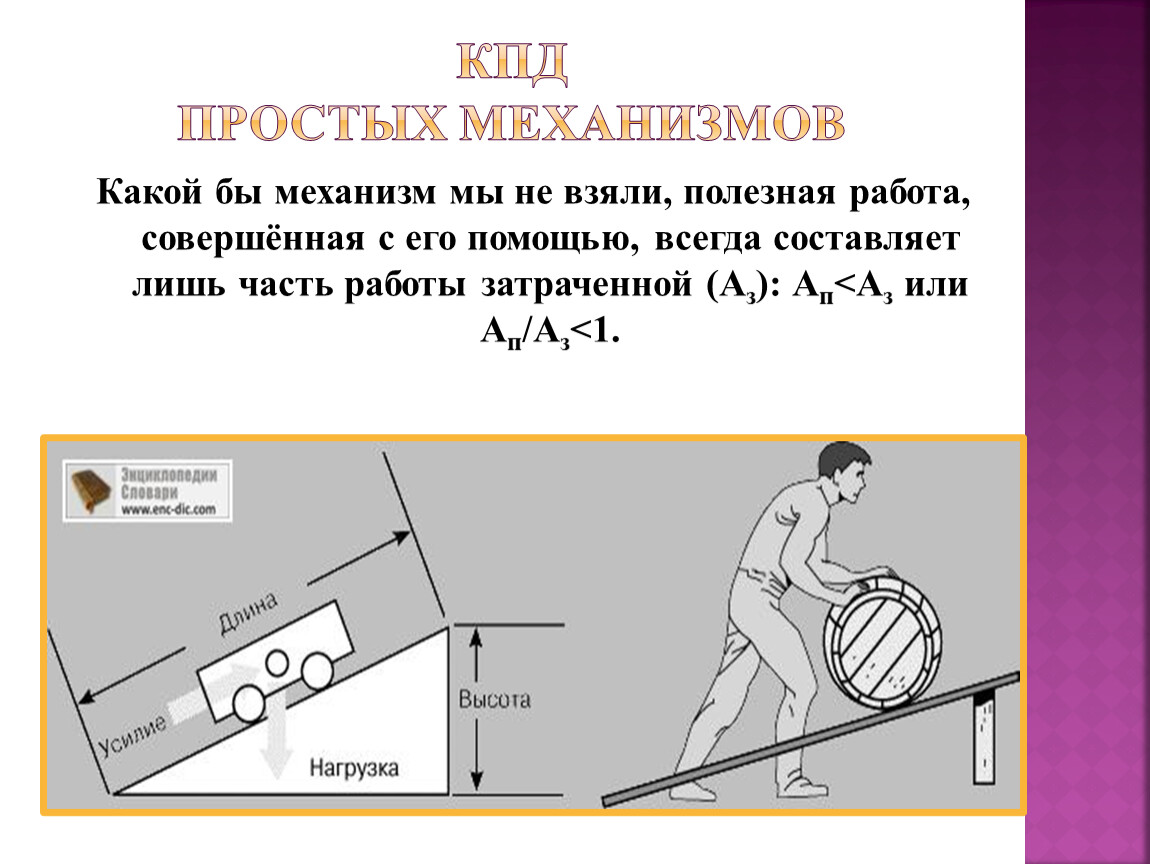
Исчисление I – Работа
Хорошо, в этом случае мы не можем просто определить силовую функцию \(F\left( x \right)\), которая нам подойдет. Итак, нам нужно подойти к этому с другой точки зрения.
Давайте сначала установим \(x = 0\) как нижний конец резервуара/конуса и \(x = 15\) как верхнюю часть резервуара/конуса.*\) любая точка из \(i\) -го -го подинтервала, где \(i = 1,2, \ldots n\). Теперь для каждого подинтервала мы аппроксимируем воду в резервуаре, соответствующую этому интервалу, в виде цилиндра радиуса \({r_i}\) и высоты \(\Delta x\).
Вот краткий набросок танка. Обратите внимание, что эскиз на самом деле не в масштабе, и мы смотрим на резервуар прямо спереди, поэтому мы можем видеть все различные количества, с которыми нам нужно работать.
Красная полоса на рисунке представляет собой «цилиндр» воды в \(i\) -м -м подинтервале.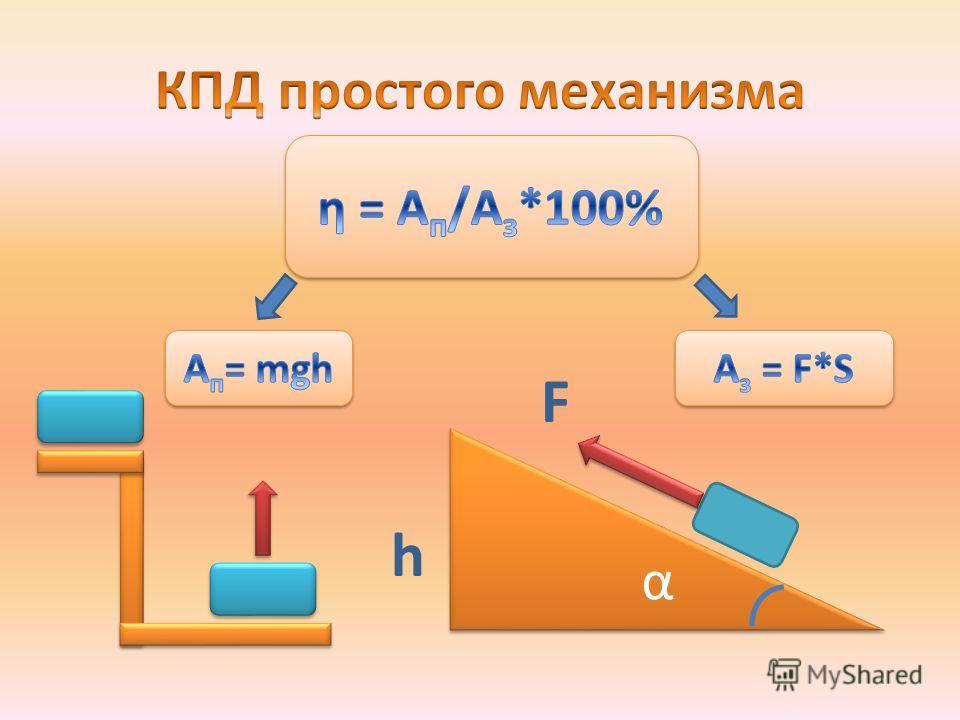 2}\Delta x\]
2}\Delta x\]
Чтобы поднять этот объем воды, нам нужно преодолеть силу тяжести, действующую на объем, то есть \(F = {m_i}g\), где \(g = 9.{12} = 7 566 362,543\,{\mbox{J}}\end{align*}\]
Работа, энергия и простые механизмы
Что такое простая машина?
Простые механизмы облегчают работу за счет умножения, уменьшения или изменения направления силы. Научная формула работы такова: w = f x d, или работа равна силе, умноженной на расстояние.Простые машины не могут изменить объем выполняемой работы, но они могут уменьшить усилие, необходимое для выполнения работы! Для наклонной плоскости и рычага требуется меньшее усилие (сила усилия) для выполнения той же работы, потому что расстояние увеличивается. Используя простые машины, египтяне смогли построить пирамиды.
Наклонные плоскости уменьшают необходимое усилие, но требуют большего расстояния.
Толкая предмет вверх по наклонной поверхности, можно переместить предмет на высоту h с меньшей силой, чем вес предмета. Сила сопротивления Fr =мг, вес объекта. Требуется работа (Fxd = mgh), чтобы преодолеть эту силу сопротивления и поднять объект на высоту h. Совершая над ним работу, мы сообщаем ему гравитационную потенциальную энергию mgh. Прилагая силу (усилие), чтобы подтолкнуть объект вверх по склону, мы выполняем ту же работу в идеальном случае отсутствия трения.Таким образом, установив работу равной FeL = Frh, мы получим идеальное механическое преимущество Fr/Fe = L/h или Din/Dout.
Другой подход к наклону состоит в том, чтобы просто рассчитать величину силы, необходимой для толкания объекта вверх по склону без трения. Если силы решить, как в стандартной задаче наклона, вы обнаружите, что требуемая сила равна Fe=mgsinθ = mgh/L = Fr (h/L) .
Ideal Mechanical Advantage (IMA) представляет сценарий отсутствия трения
Actual Mechanical Advantage учитывает трение
Термины могут сбивать с толку!
Как видно на рисунке справа, ААД рассчитывается путем деления силы сопротивления на силу усилия.В других источниках вы увидите их помеченными как выходная сила и входная сила соответственно. Сила сопротивления – это ВЕС объекта, который необходимо переместить. Это выходная сила простой машины. Входное усилие такое же, как усилие, прилагаемое для перемещения объекта с помощью машины. Эта формула для ААД одинакова для рычага и наклонной плоскости.
Эффективность = работа/работа в x 100
Другой способ расчета эффективности: AMA/IMA x 100
Рычаг облегчает работу, уменьшая усилие, необходимое для перемещения груза, за счет увеличения расстояния.

Рычаг представляет собой простой механизм, состоящий из жесткого стержня, который вращается вокруг фиксированной точки, называемой точкой опоры. Рычаг облегчает работу, уменьшая усилие, необходимое для перемещения объекта. Чтобы уменьшить необходимую силу, необходимо увеличить расстояние, на котором действует сила. Чтобы увеличить это расстояние, груз, который нужно переместить, должен находиться близко к точке опоры, а сила должна быть приложена далеко от точки опоры.
Типичным примером рычага являются качели.Человеческая рука также является рычагом, где локоть является точкой опоры, а мышцы прилагают усилие.
Как и в случае с наклонными плоскостями, термины также могут сбивать с толку в случае с рычагами.
Как показано на рисунке слева, IMA для рычага можно рассчитать, разделив длину плеча рычага от точки опоры до силы (усилия) на длину плеча рычага от точки опоры до нагрузки. Другой способ, которым вы можете увидеть это, — это разница между усилием и сопротивлением.

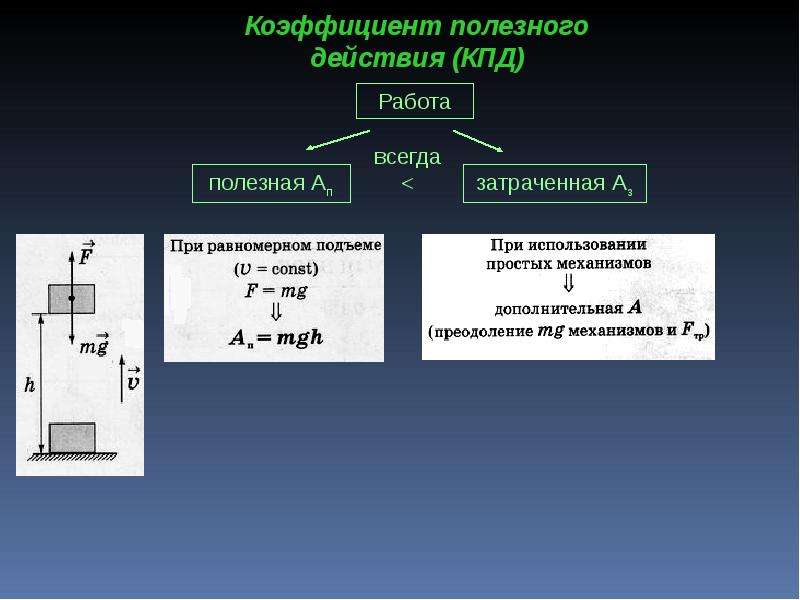
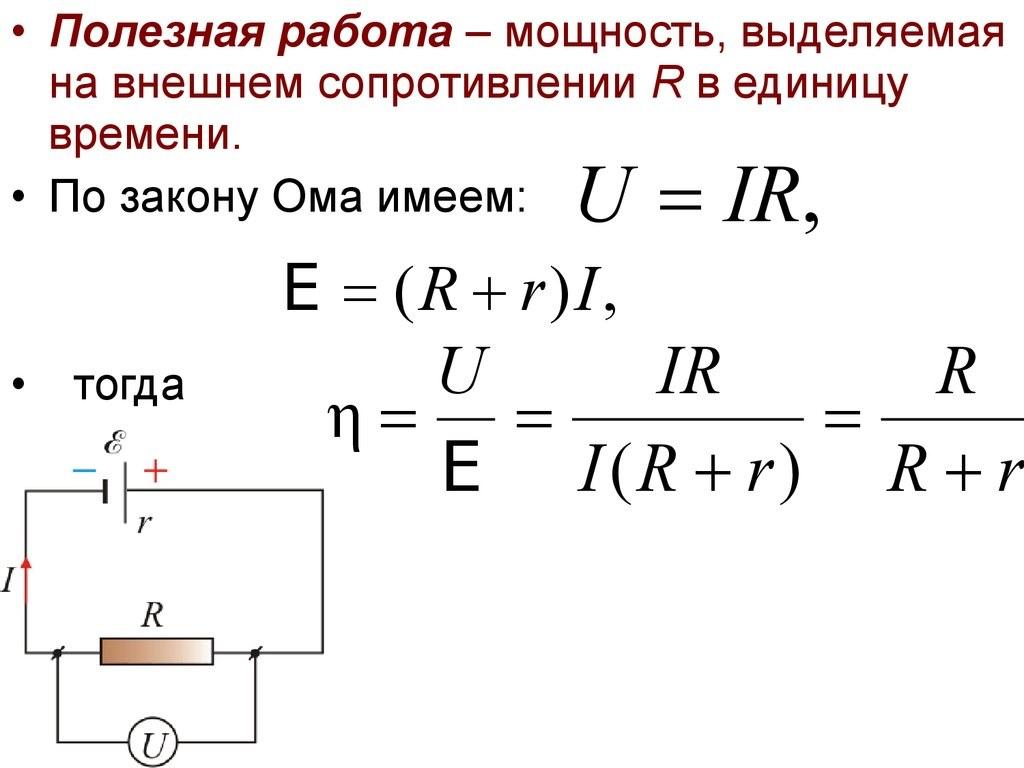

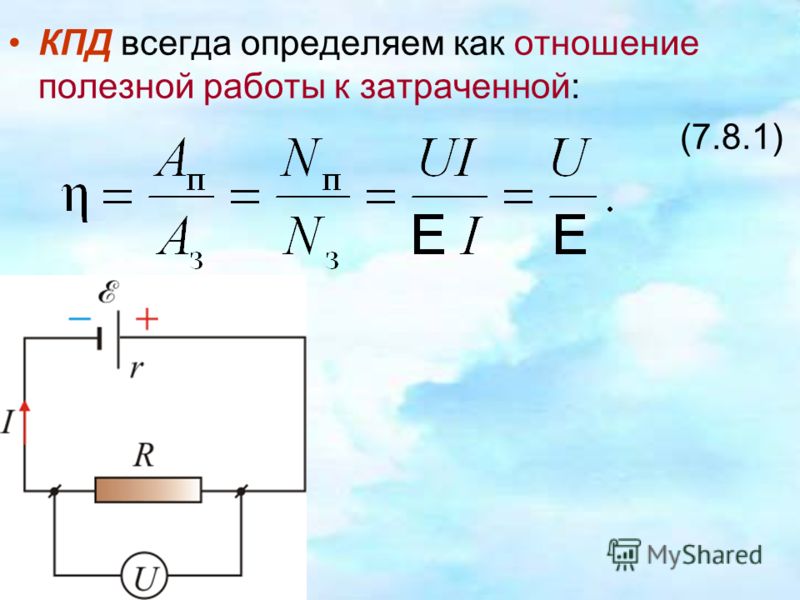 Рефлексия
Рефлексия



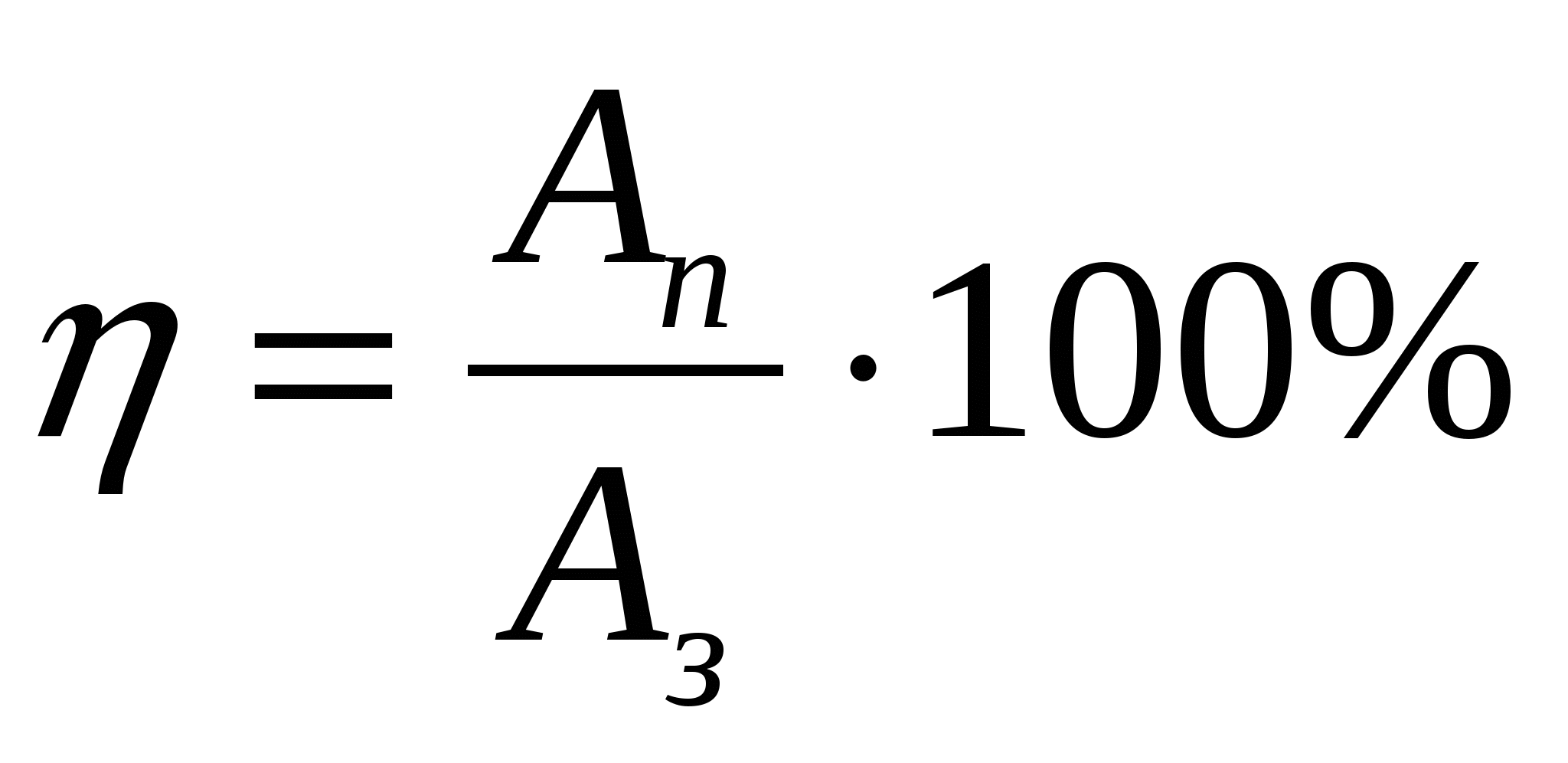 Объем газа в процессе 2-3 увеличивается, в процессе 4-1 уменьшается. Таким образом, график процесса на графике проходится по часовой стрелке, и, следовательно, работа газа за цикл положительна (ответ 1).
Объем газа в процессе 2-3 увеличивается, в процессе 4-1 уменьшается. Таким образом, график процесса на графике проходится по часовой стрелке, и, следовательно, работа газа за цикл положительна (ответ 1).
