Формула КПД (коэффициента полезного действия) в физике
Формула КПД (коэффициента полезного действия) в физикеВ реальной действительности работа, совершаемая при помощи какого – либо устройства, всегда больше полезной работы, так как часть работы выполняется против сил трения, которые действуют внутри механизма и при перемещении его отдельных частей. Так, применяя подвижный блок, совершают дополнительную работу, поднимая сам блок и веревку и, преодолевая силы трения в блоке.
Введем следующие обозначения: полезную работу обозначим $A_p$, полную работу – $A_{poln}$. При этом имеем:
\[A_p Определение и формула КПД
Определение
Коэффициентом полезного действия (КПД) называют отношение полезной работы к полной. Обозначим КПД буквой $\eta $, тогда:
\[\eta =\frac{A_p}{A_{poln}}\ \left(2\right).\]
Чаще всего коэффициент полезного действия выражают в процентах, тогда его определением является формула:
\[\eta =\frac{A_p}{A_{poln}}\cdot 100\%\ \left(2\right). \]
\]
При создании механизмов пытаются увеличить их КПД, но механизмов с коэффициентом полезного действия равным единице (а тем более больше единицы) не существует.
И так, коэффициент полезного действия – это физическая величина, которая показывает долю, которую полезная работа составляет от всей произведенной работы. При помощи КПД оценивают эффективность устройства (механизма, системы), преобразующей или передающей энергию, совершающего работу.
Для увеличения КПД механизмов можно пытаться уменьшать трение в их осях, их массу. Если трением можно пренебречь, масса механизма существенно меньше, чем масса, например, груза, который поднимает механизм, то КПД получается немного меньше единицы. Тогда произведенная работа примерно равна полезной работе:
\[A_p\approx A_{poln}\left(3\right).\]
Золотое правило механики
Необходимо помнить, что выигрыша в работе, используя простой механизм добиться нельзя.
Выразим каждую из работ в формуле (3) как произведение соответствующей силы на путь, пройденный под воздействием этой силы, тогда формулу (3) преобразуем к виду:
\[F_1s_1\approx F_2s_2\left(4\right).
Выражение (4) показывает, что используя простой механизм, мы выигрываем в силе столько же, сколько проигрываем в пути. Данный закон называют «золотым правилом» механики. Это правило сформулировал в древней Греции Герон Александрийский.
Это правило не учитывает работу по преодолению сил трения, поэтому является приближенным.
КПД при передаче энергии
Коэффициент полезного действия можно определить как отношение полезной работы к затраченной на ее выполнение энергии ($Q$):
\[\eta =\frac{A_p}{Q}\cdot 100\%\ \left(5\right).\]
Для вычисления коэффициента полезного действия теплового двигателя применяют следующую формулу:
где $Q_n$ – количество теплоты, полученное от нагревателя; $Q_{ch}$ – количество теплоты переданное холодильнику.
КПД идеальной тепловой машины, которая работает по циклу Карно равно:
\[\eta =\frac{T_n-T_{ch}}{T_n}\left(7\right),\]
где $T_n$ – температура нагревателя; $T_{ch}$ – температура холодильника.
Примеры задач на коэффициент полезного действия
Пример 1
Задание. Двигатель подъемного крана имеет мощность $N$. За отрезок времени равный $\Delta t$ он поднял груз массой $m$ на высоту $h$. Каким является КПД крана?\textit{}
Решение. Полезная работа в рассматриваемой задаче равна работе по подъему тела на высоту $h$ груза массы $m$, это работа по преодолению силы тяжести. Она равна:
\[A_p=mgh\ \left(1.1\right).\]
Полную работу, которая выполняется при поднятии груза, найдем, используя определение мощности:
\[N=\frac{A_{poln}}{\Delta t}\to A_{poln}=N\Delta t\left(1.2\right).\]
Воспользуемся определением коэффициента полезного действия для его нахождения:
\[\eta =\frac{A_p}{A_{poln}}\cdot 100\%\left(1.3\right).\]
 1) и (1.2):
1) и (1.2):\[\eta =\frac{mgh}{N\Delta t}\cdot 100\%.\]
Ответ. $\eta =\frac{mgh}{N\Delta t}\cdot 100\%$
Пример 2
Задание. Идеальный газ выполняет цикл Карно, при этом КПД цикла равно $\eta $. Какова работа в цикле сжатия газа при постоянной температуре? Работа газа при расширении равна $A_0$
Решение. Коэффициент полезного действия цикла определим как:
Рассмотрим цикл Карно, определим, в каких процессах тепло подводят (это будет $Q$).
Так как цикл Карно состоит из двух изотерм и двух адиабат, можно сразу сказать, что в адиабатных процессах (процессы 2-3 и 4-1) теплообмена нет. В изотермическом процессе 1-2 тепло подводят (рис.1 $Q_1$), в изотермическом процессе 3-4 тепло отводят ($Q_2$). Получается, что в выражении (2. 1) $Q=Q_1$. Мы знаем, что количество теплоты (первое начало термодинамики), подводимое системе при изотермическом процессе идет полностью на выполнение газом работы, значит:
1) $Q=Q_1$. Мы знаем, что количество теплоты (первое начало термодинамики), подводимое системе при изотермическом процессе идет полностью на выполнение газом работы, значит:
Газ совершает полезную работу, которую равна:
\[A_p=Q_1-Q_2\left(2.3\right).\]
Количество теплоты, которое отводят в изотермическом процессе 3-4 равно работе сжатия (работа отрицательна) (так как T=const, то $Q_2=-A_{34}$). В результате имеем:
\[A_p=A_{12}+A_{34}\left(2.4\right).\]
Преобразуем формулу (2.1) учитывая результаты (2.2) – (2.4):
\[\eta =\frac{A_{12}+A_{34}}{A_{12}}\to A_{12}\eta =A_{12}+A_{34}\to A_{34}=(\eta -1)A_{12}\left(2.4\right).\]
Так как по условию $A_{12}=A_0,\ $окончательно получаем:
\[A_{34}=\left(\eta -1\right)A_0.\]
Ответ. $A_{34}=\left(\eta -1\right)A_0$
Читать дальше: формула линейной скорости.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Коэффициент полезного действия (КПД) — формулы и расчеты » Kupuk.net
Эффективность и продолжительность работы силового агрегата зависит от коэффициента полезного действия (КПД). При эксплуатации двигатель превращает тепловую энергию, которая образуется в результате сгорания топлива в механическую. Чтобы найти коэффициент, учитываются характеристики мотора. Формула КПД в физике представлена в виде процентного отношения полезной работы к общей.
Трактовка понятия
Электродвигатель и другие механизмы выполняют определённую работу, которая называется полезной. Устройство, функционируя, частично растрачивает энергию. Для определения эффективности работы применяется формула ɳ= А1/А2×100%, где:
- А1 — полезная работу, которую выполняет машина либо мотор;
- А2 — общий цикл работы;
- η — обозначение КПД.

Показатель измеряется в процентах. Для нахождения коэффициента в математике используется следующая формула: η= А/Q, где А — энергия либо полезная работа, а Q — затраченная энергия. Чтобы выразить значение в процентах, КПД умножается на 100%. Действие не несёт содержательного смысла, так как 100% = 1. Для источника тока КПД меньше единицы.
В старших классах ученики решают задачи, в которых нужно найти КПД тепловых двигателей. Понятие трактуется следующим образом: отношение выполненной работы силового агрегата к энергии, полученной от нагревателя. Расчет производится по следующей формуле: η= (Q1-Q2)/Q1, где:
- Q1 — теплота, полученная от нагревательного элемента;
- Q2 — теплота, отданная холодильной установке.
Максимальное значение показателя характерно для циклической машины. Она оперирует при заданных температурах нагревательного элемента (Т1) и холодильника (Т2). Измерение осуществляется по формуле: η= (Т1-Т2)/Т1.
Чтобы узнать КПД котла, который функционирует на органическом топливе, используется низшая теплота сгорания.
Плюс теплового насоса как нагревательного прибора заключается в возможности получать больше энергии, чем он может затратить на функционирование. Показатель трансформации вычисляется путём деления тепла конденсации на работу, затрачиваемую на выполнение данного процесса.
Мощность разных устройств
По статистике, во время работы прибора теряется до 25% энергии. При функционировании двигателя внутреннего сгорания топливо сгорает частично. Небольшой процент вылетает в выхлопную трубу. При запуске бензиновый мотор греет себя и составные элементы. На потерю уходит до 35% от общей мощности.
При движении механизмов происходит трение. Для его ослабления используется смазка. Но она неспособна полностью устранить явление, поэтому затрачивается до 20% энергии. Пример на автомобиле: если расход составляет 10 литров топлива на 100 км, на движение потребуется 2 л, а остаток, равный 8 л — потеря.
Но она неспособна полностью устранить явление, поэтому затрачивается до 20% энергии. Пример на автомобиле: если расход составляет 10 литров топлива на 100 км, на движение потребуется 2 л, а остаток, равный 8 л — потеря.
Если сравнивать КПД бензинового и дизельного моторов, полезная мощность первого механизма равна 25%, а второго — 40%. Агрегаты схожи между собой, но у них разные виды смесеобразования:
Асинхронные механизмы
Расшифровка термина «асинхронность» — несовпадение по времени. Понятие используется во многих современных машинах, которые являются электрическими и способны преобразовывать соответствующую энергию в механическую. Плюсы устройств:
- простое изготовление;
- низкая цена;
- надёжность;
- незначительные эксплуатационные затраты.
Чтобы рассчитать КПД, используется уравнение η = P2 / P1. Для расчёта Р1 и Р2 применяются общие данные потери энергии в обмотках мотора. У большинства агрегатов показатель находится в пределах 80−90%. Для быстрого расчёта используется онлайн-ресурс либо личный калькулятор. Для проверки возможного КПД у мотора внешнего сгорания, который функционирует от разных источников тепла, используется силовой агрегат Стирлинга. Он представлен в виде тепловой машины с рабочим телом в виде жидкости либо газа. Вещество движется по замкнутому объёму.
Принцип его функционирования основан на постепенном нагреве и охлаждении объекта за счёт извлечения энергии из давления. Подобный механизм применяется на косметическом аппарате и современной подводной лодке. Его работоспособность наблюдается при любой температуре. Он не нуждается в дополнительной системе для запуска. Его КПД возможно расширить до 70%, в отличие от стандартного мотора.
Значения показателя
В 1824 году инженер Карно дал определение КПД идеального двигателя, когда коэффициент равен 100%. Для трактовки понятия была создана специальная машина со следующей формулой: η=(T1 — Т2)/ T1. Для расчёта максимального показателя применяется уравнение КПД макс = (T1-T2)/T1x100%. В двух примерах T1 указывает на температуру нагревателя, а T2 — температуру холодильника.
На практике для достижения 100% коэффициента потребуется приравнять температуру охладителя к нулю. Подобное явление невозможно, так как T1 выше температуры воздуха. Процедура повышения КПД источника тока либо силового агрегата считается важной технической задачей. Теоретически проблема решается путём снижения трения элементов двигателя и уменьшения теплопотери. В дизельном моторе подобное достигается турбонаддувом. В таком случае КПД возрастает до 50%.
Подобное явление невозможно, так как T1 выше температуры воздуха. Процедура повышения КПД источника тока либо силового агрегата считается важной технической задачей. Теоретически проблема решается путём снижения трения элементов двигателя и уменьшения теплопотери. В дизельном моторе подобное достигается турбонаддувом. В таком случае КПД возрастает до 50%.
Мощность стандартного двигателя увеличивается следующими способами:
- подключение к системе многоцилиндрового агрегата;
- применение специального топлива;
- замена некоторых деталей;
- перенос места сжигания бензина.
КПД зависит от типа и конструкции мотора. Современные учёные утверждают, что будущее за электродвигателями. На практике работа, которую совершает любое устройство, превышает полезную, так как определённая её часть выполняется против трения. Если используется подвижный блок, совершается дополнительная работа: поднимается блок с верёвкой, преодолеваются силы трения в блоке.
Решение примеров
Задача 1. Поезд на скорости 54 км/ч развивает мощность 720 кВт. Нужно вычислить силу тяги силовых агрегатов. Решение: чтобы найти мощность, используется формула N=F x v. Если перевести скорость в единицу СИ, получится 15 м/с. Подставив данные в уравнение, определяется, что F равно 48 kН.
Задача 2. Масса транспортного средства соответствует 2200 кг. Машина, поднимаясь в гору под уклоном в 0,018, проходит расстояние 100 м. Скорость развивается до 32,4 км/ч, а коэффициент трения соответствует 0,04. Нужно определить среднюю мощность авто при движении. Решение: вычисляется средняя скорость — v/2. Чтобы определить силу тяги мотора, выполняется рисунок, на котором отображаются силы, воздействующие на машину:
- тяжесть — mg;
- реакция опоры — N;
- трение — Ftr;
- тяга — F.

Первая величина вычисляется по второму закону Ньютона: mg+N+Ftr+F=ma. Для ускорения используется уравнение a=v2/2S. Если подставить последние значение и воспользоваться cos, получится средняя мощность. Так как ускорение считается постоянной величиной и равно 9,8 м/с2, поэтому v= 9 м/с. Подставив данные в первую формулу, получится: N= 9,5 kBt.
При решении сложных задач по физике рекомендуется проверить соответствие предоставленных в условиях единиц измерения с международными стандартами. Если они отличаются, необходимости перевести данные с учётом СИ.
определение и расшифровка, полезная работа, формула КПД и применение в физике
Физика — это наука, которая изучает процессы, происходящие в природе. Наука эта очень интересная и любопытная, ведь каждому из нас хочется удовлетворить себя ментально, получив знания и понимание того, как и что в нашем мире устроено. Физика, законы которой выводились не одно столетие и не одним десятком ученных, помогает нам с этой задачей, и мы должны только радоваться и поглощать предоставленные знания.
Физика, законы которой выводились не одно столетие и не одним десятком ученных, помогает нам с этой задачей, и мы должны только радоваться и поглощать предоставленные знания.
Но в то же время физика — наука далеко непростая, как, собственно, и сама природа, но разобраться в ней было бы очень интересно. Сегодня мы будем говорить о коэффициенте полезного действия. Мы узнаем, что такое КПД и зачем он нужен. Рассмотрим все наглядно и интересно.
Содержание:
- Определение и расшифровка КПД
- Полезная работа
- Физическая формула КПД
- Применение в разных сферах физики
- Видео
Определение и расшифровка КПД
Расшифровка аббревиатуры — коэффициент полезного действия. Однако и такое толкование с первого раза может оказаться не особо понятным. Этим коэффициентом характеризуется эффективность системы или какого-либо отдельного тела, а чаще — механизма. Эффективность характеризуется отдачей или преобразованием энергии.
Этот коэффициент применим практически ко всему, что нас окружает, и даже к нам самим, причём в большей степени. Ведь совершаем мы полезную работу все время, только вот как часто и насколько это важно, уже другой вопрос, с ним и используется термин «КПД».
Ведь совершаем мы полезную работу все время, только вот как часто и насколько это важно, уже другой вопрос, с ним и используется термин «КПД».
Важно учесть, что этот коэффициент — величина неограниченная, она, как правило, представляет собой либо математические значения, к примеру, 0 и 1, либо же, как это чаще бывает — в процентах.
В физике этот коэффициент обозначается буквой Ƞ, или, как её привыкли называть, Эта.
Полезная работа
При использовании каких-либо механизмов или устройств мы обязательно совершаем работу. Она, как правило, всегда больше той, что необходима нам для выполнения поставленной задачи. Исходя из этих фактов различается два типа работы: это затраченная, которая обозначается большой буквой, А с маленькой з (Аз), и полезная — А с буквой п (Ап). Для примера, возьмем такой случай: у нас есть задача поднять булыжник определенной массой на определенную высоту. В этом случае работа характеризует только преодоление силы тяжести, которая, в свою очередь, действует на груз.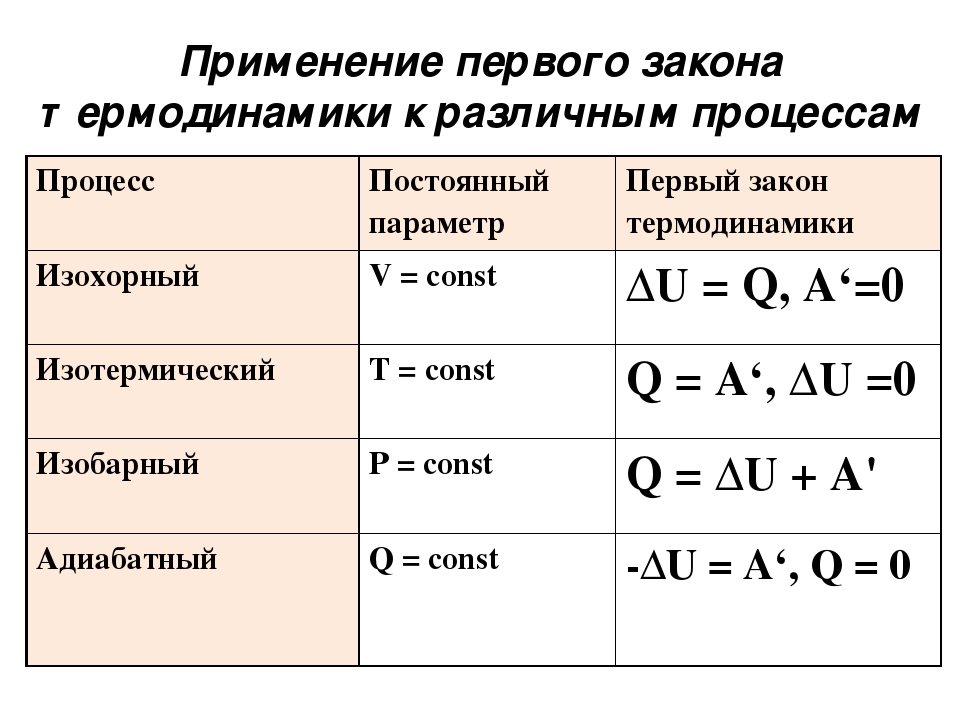
В случае когда для подъема применяется какое-либо устройство, кроме силы тяжести булыжника, важно учесть еще и силу тяжести частей этого устройства
Полезная работа — это часть затрачиваемой, которую мы совершаем, используя механизм. А КПД — это как раз та физическая величина, которая показывает, какую часть составляет полезная работа от всей затраченной.
Итог:
- Затрачиваемая работа Aз всегда больше полезной Ап.
- Чем больше отношение полезной к затрачиваемой, тем выше коэффициент, и наоборот.
- Ап находится произведением массы на ускорение свободного падения и на высоту подъема.

Физическая формула КПД
Существует определенная формула для нахождения КПД. Она звучит следующим образом: чтобы найти КПД в физике, нужно количество энергии разделить на проделанную системой работу. То есть КПД — это отношение затраченной энергии к выполненной работе. Отсюда можно сделать простой вывод, что тем лучше и эффективнее система или тело, чем меньше энергии затрачивается на выполнение работы.
Сама формула выглядит кратко и очень просто Ƞ будет равняться A/Q. То есть Ƞ = A/Q. В этой краткой формулы и фиксируют нужные нам элементы для вычисления. То есть A в этом случае является использованной энергией, которая потребляется системой во время работы, а большая буква Q, в свою очередь, будет являться затраченной A, или опять же затраченной энергией.
В идеале КПД равен единице. Но, как это обычно бывает, он её меньше. Так происходит по причине физики и по причине, конечно же, закона о сохранении энергии.
Все дело в том, что закон сохранения энергии предполагает, что не может быть получено больше А, чем получено энергии. И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.
И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.
Итак, формула КПД:
Ƞ=А/Q, где
- A — полезная работа, которую выполняет система.
- Q — энергия, которую потребляет система.
Применение в разных сферах физики
Примечательно, что КПД не существует как понятие нейтральное, для каждого процесса есть свой КПД, это не сила трения, он не может существовать сам по себе.
Рассмотрим несколько из примеров процессов с наличием КПД.
К примеру, возьмем электрический двигатель. Задача электрического двигателя — преобразовывать электрическую энергию в механическую. В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1.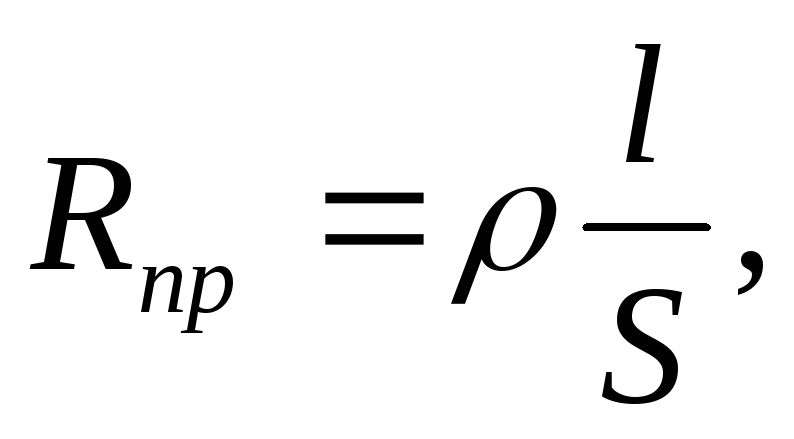 Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.
Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.
Нетрудно догадаться что структура формулы коэффициента всегда сохраняется, меняются в ней лишь данные, которые нужно подставить. Они зависят от конкретного случая, если это двигатель, как в случае выше, то необходимо оперировать затрачиваемой мощностью, если работа, то исходная формула будет другая.
Теперь мы знаем определение КПД и имеем представление об этом физическом понятии, а также об отдельных его элементах и нюансах. Физика — это одна из самых масштабных наук, но её можно разобрать на маленькие кусочки, чтобы понять. Сегодня мы исследовали один из этих кусочков.
Видео
Это видео поможет вам понять, что такое КПД.
Коэффициент полезного действия ?, формула КПД в физике. Как найти КПД⚡
Автор Даниил Леонидович На чтение 7 мин. Просмотров 42.7k. Опубликовано
Обновлено
Просмотров 42.7k. Опубликовано
Обновлено
Содержание
- Что такое КПД
- Примеры расчета КПД
- Единицы измерения
- От чего зависит величина КПД
- Как обозначается
- Символ, обозначающий КПД
- Мощность и КПД
- Формула работы в физике
- Это интересно
Что такое КПД
Коэффициент полезного действия машины или механизма – это важная величина, характеризующая энергоэффективность данного устройства. Понятие используется и в повседневной жизни. Например, когда человек говорит, что КПД его усилий низкий, это значит, что сил затрачено много, а результата почти нет. Величина измеряет отношение полезной работы ко всей совершенной работе.
Согласно формуле, чтобы найти величину, нужно полезную работу разделить на всю совершенную работу. Или полезную энергию разделить на всю израсходованную энергию.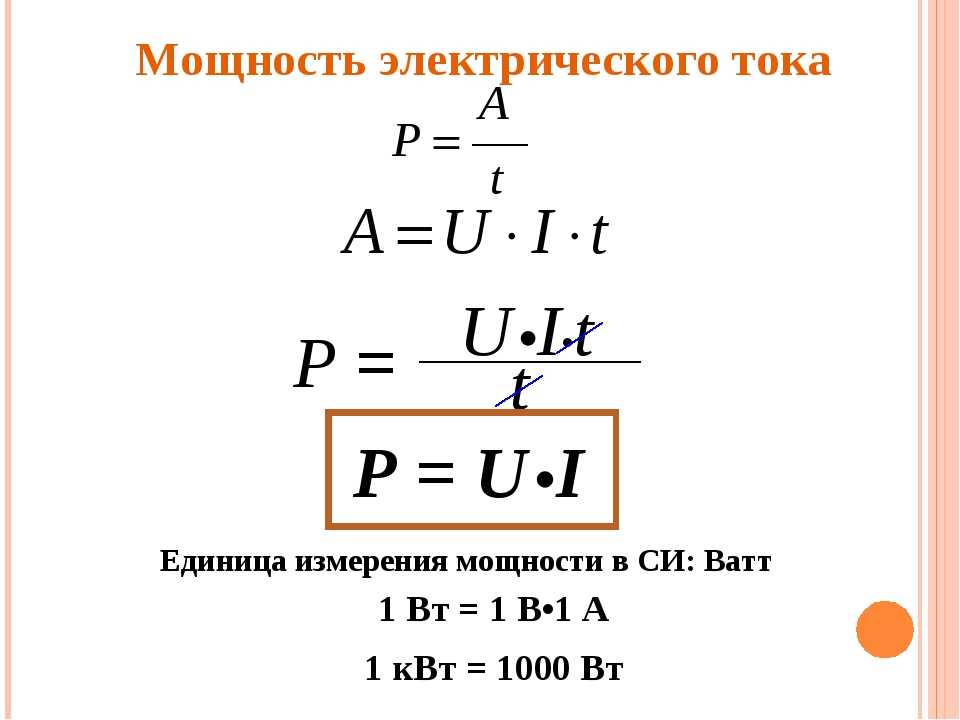 Этот коэффициент всегда меньше единицы. Работа и энергия измеряется в Джоулях. Поделив Джоули на Джоули, получаем безразмерную величину. КПД иногда называют энергоэффективностью устройства.
Этот коэффициент всегда меньше единицы. Работа и энергия измеряется в Джоулях. Поделив Джоули на Джоули, получаем безразмерную величину. КПД иногда называют энергоэффективностью устройства.
Если попытаться объяснить простым языком, то представим, что мы кипятим чайник на плите. При сгорании газа образуется определенное количество теплоты. Часть этой теплоты нагревает саму горелку, плиту и окружающее пространство. Остальная часть идет на нагревание чайника и воды в нем. Чтобы рассчитать энергоэффективность данной плитки, нужно будет разделить количество тепла, требуемое для нагрева воды до температуры кипения на количество тепла, выделившееся при горении газа.
Данная величина всегда ниже единицы. Например, для любой атомной электростанции она не превышает 35%. Причиной является то, что электростанция представляет собой паровую машину, где нагретый за счет ядерной реакции пар вращает турбину. Большая часть энергии идет на нагрев окружающего пространства. Тот факт, что η не может быть равен 100%, следует из второго начала термодинамики.
Примеры расчета КПД
Пример 1. Нужно рассчитать коэффициент для классического камина. Дано: удельная теплота сгорания березовых дров – 107Дж/кг, количество дров – 8 кг. После сгорания дров температура в комнате повысилась на 20 градусов. Удельная теплоемкость кубометра воздуха — 1,3 кДж/ кг*град. Общая кубатура комнаты – 75 кубометров.
Чтобы решить задачу, нужно найти частное или отношение двух величин. В числителе будет количество теплоты, которое получил воздух в комнате (1300Дж*75*20=1950 кДж ). В знаменателе – количество теплоты, выделенное дровами при горении (10000000Дж*8 =8*107 кДж). После подсчетов получаем, что энергоэффективность дровяного камина – около 2,5%. Действительно, современная теория об устройстве печей и каминов говорит, что классическая конструкция не является энергоэффективной. Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу. Для повышения эффективности устраивают дымоход с каналами, где воздух сначала отдает тепло кладке каналов, и лишь потом выходит наружу. Но справедливости ради, нужно отметить, что в процессе горения камина нагревается не только воздух, но и предметы в комнате, а часть тепла выходит наружу через элементы, плохо теплоизолированные — окна, двери и т.д.
Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу. Для повышения эффективности устраивают дымоход с каналами, где воздух сначала отдает тепло кладке каналов, и лишь потом выходит наружу. Но справедливости ради, нужно отметить, что в процессе горения камина нагревается не только воздух, но и предметы в комнате, а часть тепла выходит наружу через элементы, плохо теплоизолированные — окна, двери и т.д.
Пример 2. Автомобиль проделал путь 100 км. Вес машины с пассажирами и багажом – 1400 кг. При этом было затрачено14 литров бензина. Найти: КПД двигателя.
Для решения задачи необходимо отношение работы по перемещению груза к количеству тепла, выделившемуся при сгорании топлива. Количество тепла также измеряется в Джоулях, поэтому не придется приводить к другим единицам. A будет равна произведению силы на путь( A=F*S=m*g*S). Сила равна произведению массы на ускорение свободного падения. Полезная работа = 1400 кг x 9,8м/с2 x 100000м=1,37*108 Дж
Удельная теплота сгорания бензина – 46 МДж/кг=46000 кДж/кг. Восемь литров бензина будем считать примерно равными 8 кг. Тепла выделилось 46*106*14=6.44*108 Дж. В результате получаем η ≈21%.
Восемь литров бензина будем считать примерно равными 8 кг. Тепла выделилось 46*106*14=6.44*108 Дж. В результате получаем η ≈21%.
Единицы измерения
Коэффициент полезного действия – величина безразмерная, то есть не нужно ставить какую-либо единицу измерения. Но эту величину можно выразить и в процентах. Для этого полученное в результате деления по формуле число необходимо умножить на 100%. В школьном курсе математики рассказывали, что процент – этот одна сотая чего-либо. Умножая на 100 процентов, мы показываем, сколько в числе сотых.
От чего зависит величина КПД
Эта величина зависит от того, насколько общая совершенная работа может переходить в полезную. Прежде всего, это зависит от самого устройства механизма или машины. Инженеры всего мира бьются над тем, чтобы повышать КПД машин. Например, для электромобилей коэффициент очень высок – больше 90%.
А вот двигатель внутреннего сгорания, в силу своего устройства, не может иметь η, близкий к 100 процентам. Ведь энергия топлива не действует непосредственно на вращающиеся колеса. Энергия рассеивается на каждом передаточном звене. Слишком много передаточных звеньев, и часть выхлопных газов все равно выходит в выхлопную трубу.
Ведь энергия топлива не действует непосредственно на вращающиеся колеса. Энергия рассеивается на каждом передаточном звене. Слишком много передаточных звеньев, и часть выхлопных газов все равно выходит в выхлопную трубу.
Как обозначается
В русских учебниках обозначается двояко. Либо так и пишется – КПД, либо обозначается греческой буквой η. Эти обозначения равнозначны.
Символ, обозначающий КПД
Символом является греческая буква эта η. Но чаще все же используют выражение КПД.
Мощность и КПД
Мощность механизма или устройства равна работе, совершаемой в единицу времени. Работа(A) измеряется в Джоулях, а время в системе Си – в секундах. Но не стоит путать понятие мощности и номинальной мощности. Если на чайнике написана мощность 1 700 Ватт, это не значит, что он передаст 1 700 Джоулей за одну секунду воде, налитой в него. Это мощность номинальная. Чтобы узнать η электрочайника, нужно узнать количество теплоты(Q), которое должно получить определенное количество воды при нагреве на энное количество градусов. Эту цифру делят на работу электрического тока, выполненную за время нагревания воды.
Эту цифру делят на работу электрического тока, выполненную за время нагревания воды.
Величина A будет равна номинальной мощности, умноженной на время в секундах. Q будет равно объему воды, умноженному на разницу температур на удельную теплоемкость. Потом делим Q на A тока и получаем КПД электрочайника, примерно равное 80 процентам. Прогресс не стоит на месте, и КПД различных устройств повышается, в том числе бытовой техники.
Напрашивается вопрос, почему через мощность нельзя узнать КПД устройства. На упаковке с оборудованием всегда указана номинальная мощность. Она показывает, сколько энергии потребляет устройство из сети. Но в каждом конкретном случае невозможно будет предсказать, сколько конкретно потребуется энергии для нагрева даже одного литра воды.
Например, в холодной комнате часть энергии потратится на обогрев пространства. Это связано с тем, что в результате теплообмена чайник будет охлаждаться. Если, наоборот, в комнате будет жарко, чайник закипит быстрее. То есть КПД в каждом из этих случаев будет разным.
То есть КПД в каждом из этих случаев будет разным.
Формула работы в физике
Для механической работы формула несложна: A = F x S. Если расшифровать, она равна приложенной силе на путь, на протяжении которого эта сила действовала. Например, мы поднимаем груз массой 15 кг на высоту 2 метра. Механическая работа по преодолению силы тяжести будет равна F x S = m x g x S. То есть, 15 x 9,8 x 2 = 294 Дж. Если речь идет о количестве теплоты, то A в этом случае равняется изменению количества теплоты. Например, на плите нагрели воду. Ее внутренняя энергия изменилась, она увеличилась на величину, равную произведению массы воды на удельную теплоемкость на количество градусов, на которое она нагрелась.
Это интересно
Наукой обосновано, что коэффициент полезного действия любого механизма всегда меньше единицы. Это связано со вторым началом термодинамики.
Для сравнения, коэффициенты полезного действия различных устройств:
- гидроэлектростанций 93-95%;
- АЭС – не более 35%;
- тепловых электростанций – 25-40%;
- бензинового двигателя – около 20%;
- дизельного двигателя – около 40%;
- электрочайника – более 95%;
- электромобиля – 88-95%.

Наука и инженерная мысль не стоит на месте. постоянно изобретаются способы, как уменьшить теплопотери, снизить трение между частями агрегата, повысить энергоэффективность техники.
Коэффициент полезного действия (КПД) – формулы и расчеты
Эффективность и продолжительность работы силового агрегата зависит от коэффициента полезного действия (КПД). При эксплуатации двигатель превращает тепловую энергию, которая образуется в результате сгорания топлива в механическую. Чтобы найти коэффициент, учитываются характеристики мотора. Формула КПД в физике представлена в виде процентного отношения полезной работы к общей.
Содержание
- Трактовка понятия
- Мощность разных устройств
- Асинхронные механизмы
- Значения показателя
- Решение примеров
Трактовка понятия
Электродвигатель и другие механизмы выполняют определённую работу, которая называется полезной. Устройство, функционируя, частично растрачивает энергию. Для определения эффективности работы применяется формула ɳ= А1/А2×100%, где:
Устройство, функционируя, частично растрачивает энергию. Для определения эффективности работы применяется формула ɳ= А1/А2×100%, где:
- А1 — полезная работу, которую выполняет машина либо мотор;
- А2 — общий цикл работы;
- η — обозначение КПД.
Показатель измеряется в процентах. Для нахождения коэффициента в математике используется следующая формула: η= А/Q, где А — энергия либо полезная работа, а Q — затраченная энергия. Чтобы выразить значение в процентах, КПД умножается на 100%. Действие не несёт содержательного смысла, так как 100% = 1. Для источника тока КПД меньше единицы.
В старших классах ученики решают задачи, в которых нужно найти КПД тепловых двигателей. Понятие трактуется следующим образом: отношение выполненной работы силового агрегата к энергии, полученной от нагревателя. Расчет производится по следующей формуле: η= (Q1-Q2)/Q1, где:
- Q1 — теплота, полученная от нагревательного элемента;
- Q2 — теплота, отданная холодильной установке.

Максимальное значение показателя характерно для циклической машины. Она оперирует при заданных температурах нагревательного элемента (Т1) и холодильника (Т2). Измерение осуществляется по формуле: η= (Т1-Т2)/Т1. Чтобы узнать КПД котла, который функционирует на органическом топливе, используется низшая теплота сгорания.
Плюс теплового насоса как нагревательного прибора заключается в возможности получать больше энергии, чем он может затратить на функционирование. Показатель трансформации вычисляется путём деления тепла конденсации на работу, затрачиваемую на выполнение данного процесса.
Мощность разных устройств
По статистике, во время работы прибора теряется до 25% энергии. При функционировании двигателя внутреннего сгорания топливо сгорает частично. Небольшой процент вылетает в выхлопную трубу. При запуске бензиновый мотор греет себя и составные элементы. На потерю уходит до 35% от общей мощности.
При запуске бензиновый мотор греет себя и составные элементы. На потерю уходит до 35% от общей мощности.
При движении механизмов происходит трение. Для его ослабления используется смазка. Но она неспособна полностью устранить явление, поэтому затрачивается до 20% энергии. Пример на автомобиле: если расход составляет 10 литров топлива на 100 км, на движение потребуется 2 л, а остаток, равный 8 л — потеря.
Если сравнивать КПД бензинового и дизельного моторов, полезная мощность первого механизма равна 25%, а второго — 40%. Агрегаты схожи между собой, но у них разные виды смесеобразования:
 Если проверить КПД при низком функционировании и большом объёме, результат превысит 50%.
Если проверить КПД при низком функционировании и большом объёме, результат превысит 50%.Асинхронные механизмы
Расшифровка термина «асинхронность» — несовпадение по времени. Понятие используется во многих современных машинах, которые являются электрическими и способны преобразовывать соответствующую энергию в механическую. Плюсы устройств:
- простое изготовление;
- низкая цена;
- надёжность;
- незначительные эксплуатационные затраты.
Чтобы рассчитать КПД, используется уравнение η = P2 / P1. Для расчёта Р1 и Р2 применяются общие данные потери энергии в обмотках мотора. У большинства агрегатов показатель находится в пределах 80−90%. Для быстрого расчёта используется онлайн-ресурс либо личный калькулятор. Для проверки возможного КПД у мотора внешнего сгорания, который функционирует от разных источников тепла, используется силовой агрегат Стирлинга. Он представлен в виде тепловой машины с рабочим телом в виде жидкости либо газа. Вещество движется по замкнутому объёму.
Он представлен в виде тепловой машины с рабочим телом в виде жидкости либо газа. Вещество движется по замкнутому объёму.
Принцип его функционирования основан на постепенном нагреве и охлаждении объекта за счёт извлечения энергии из давления. Подобный механизм применяется на косметическом аппарате и современной подводной лодке. Его работоспособность наблюдается при любой температуре. Он не нуждается в дополнительной системе для запуска. Его КПД возможно расширить до 70%, в отличие от стандартного мотора.
Значения показателя
В 1824 году инженер Карно дал определение КПД идеального двигателя, когда коэффициент равен 100%. Для трактовки понятия была создана специальная машина со следующей формулой: η=(T1 — Т2)/ T1. Для расчёта максимального показателя применяется уравнение КПД макс = (T1-T2)/T1x100%. В двух примерах T1 указывает на температуру нагревателя, а T2 — температуру холодильника.
На практике для достижения 100% коэффициента потребуется приравнять температуру охладителя к нулю. Подобное явление невозможно, так как T1 выше температуры воздуха. Процедура повышения КПД источника тока либо силового агрегата считается важной технической задачей. Теоретически проблема решается путём снижения трения элементов двигателя и уменьшения теплопотери. В дизельном моторе подобное достигается турбонаддувом. В таком случае КПД возрастает до 50%.
Мощность стандартного двигателя увеличивается следующими способами:
- подключение к системе многоцилиндрового агрегата;
- применение специального топлива;
- замена некоторых деталей;
- перенос места сжигания бензина.
КПД зависит от типа и конструкции мотора. Современные учёные утверждают, что будущее за электродвигателями. На практике работа, которую совершает любое устройство, превышает полезную, так как определённая её часть выполняется против трения.
Если используется подвижный блок, совершается дополнительная работа: поднимается блок с верёвкой, преодолеваются силы трения в блоке.
Решение примеров
Задача 1. Поезд на скорости 54 км/ч развивает мощность 720 кВт. Нужно вычислить силу тяги силовых агрегатов. Решение: чтобы найти мощность, используется формула N=F x v. Если перевести скорость в единицу СИ, получится 15 м/с. Подставив данные в уравнение, определяется, что F равно 48 kН.
Задача 2. Масса транспортного средства соответствует 2200 кг. Машина, поднимаясь в гору под уклоном в 0,018, проходит расстояние 100 м. Скорость развивается до 32,4 км/ч, а коэффициент трения соответствует 0,04. Нужно определить среднюю мощность авто при движении. Решение: вычисляется средняя скорость — v/2. Чтобы определить силу тяги мотора, выполняется рисунок, на котором отображаются силы, воздействующие на машину:
- тяжесть — mg;
- реакция опоры — N;
- трение — Ftr;
- тяга — F.

Первая величина вычисляется по второму закону Ньютона: mg+N+Ftr+F=ma. Для ускорения используется уравнение a=v2/2S. Если подставить последние значение и воспользоваться cos, получится средняя мощность. Так как ускорение считается постоянной величиной и равно 9,8 м/с2, поэтому v= 9 м/с. Подставив данные в первую формулу, получится: N= 9,5 kBt.
При решении сложных задач по физике рекомендуется проверить соответствие предоставленных в условиях единиц измерения с международными стандартами. Если они отличаются, необходимости перевести данные с учётом СИ.
Предыдущая
ФизикаФормула давления – примеры и условия расчетов
Следующая
ФизикаАбсолютно упругий и неупругий удар двух тел – формулы и примеры расчетов
Понятие КПД: определение, формула и применение в физике – Справочник
Что такое кпд в физике
Физика — это наука, которая изучает процессы, происходящие в природе. Наука эта очень интересная и любопытная, ведь каждому из нас хочется удовлетворить себя ментально, получив знания и понимание того, как и что в нашем мире устроено. Физика, законы которой выводились не одно столетие и не одним десятком ученных, помогает нам с этой задачей, и мы должны только радоваться и поглощать предоставленные знания.
Наука эта очень интересная и любопытная, ведь каждому из нас хочется удовлетворить себя ментально, получив знания и понимание того, как и что в нашем мире устроено. Физика, законы которой выводились не одно столетие и не одним десятком ученных, помогает нам с этой задачей, и мы должны только радоваться и поглощать предоставленные знания.
Но в то же время физика — наука далеко непростая, как, собственно, и сама природа, но разобраться в ней было бы очень интересно. Сегодня мы будем говорить о коэффициенте полезного действия. Мы узнаем, что такое КПД и зачем он нужен. Рассмотрим все наглядно и интересно.
Определение и расшифровка КПД
Расшифровка аббревиатуры — Коэффициент полезного действия. Однако и такое толкование с первого раза может оказаться не особо понятным. Этим коэффициентом характеризуется эффективность системы или какого-либо отдельного тела, а чаще — механизма. Эффективность характеризуется отдачей или преобразованием энергии.
Этот коэффициент применим практически ко всему, что нас окружает, и даже к нам самим, причём в большей степени. Ведь совершаем мы полезную работу все время, только вот как часто и насколько это важно, уже другой вопрос, с ним и используется термин «КПД».
Ведь совершаем мы полезную работу все время, только вот как часто и насколько это важно, уже другой вопрос, с ним и используется термин «КПД».
Важно учесть, что Этот коэффициент — величина неограниченная, она, как правило, представляет собой либо математические значения, к примеру, 0 и 1, либо же, как это чаще бывает — в процентах.
В физике этот коэффициент обозначается буквой Ƞ, или, как её привыкли называть, Эта.
Полезная работа
При использовании каких-либо механизмов или устройств мы обязательно совершаем работу. Она, как правило, всегда больше той, что необходима нам для выполнения поставленной задачи. Исходя из этих фактов различается два типа работы: это затраченная, которая обозначается большой буквой, А с маленькой з (Аз), и полезная — А с буквой п (Ап). Для примера, возьмем такой случай: у нас есть задача поднять булыжник определенной массой на определенную высоту. В этом случае работа характеризует только преодоление силы тяжести, которая, в свою очередь, действует на груз.
В случае когда для подъема применяется какое-либо устройство, кроме силы тяжести булыжника, важно учесть еще и Силу тяжести частей этого устройства. И кроме всего этого, важно помнить, что, выигрывая в силе, мы всегда будем проигрывать в пути. Все эти факты приводят к одному выводу, что затрачиваемая работа в любом варианте окажется больше полезной, Аз > Ап, вопрос как раз заключается в том, насколько её больше, ведь можно максимально сократить эту разницу и тем самым увеличить КПД, наш или нашего устройства.
Полезная работа — это часть затрачиваемой, которую мы совершаем, используя механизм. А КПД — это как раз та физическая величина, которая показывает, какую часть составляет полезная работа от всей затраченной.
Итог:
- Затрачиваемая работа Aз всегда больше полезной Ап. Чем больше отношение полезной к затрачиваемой, тем выше коэффициент, и наоборот. Ап находится произведением массы на ускорение свободного падения и на высоту подъема.

Физическая формула КПД
Существует определенная формула для нахождения КПД. Она звучит следующим образом: чтобы найти КПД в физике, нужно количество энергии разделить на проделанную системой работу. То есть КПД — это отношение затраченной энергии к выполненной работе. Отсюда можно сделать простой вывод, что тем лучше и эффективнее система или тело, чем меньше энергии затрачивается на выполнение работы.
Сама формула выглядит кратко и очень просто Ƞ будет равняться A/Q. То есть Ƞ = A/Q. В этой краткой формулы и фиксируют нужные нам элементы для вычисления. То есть A в этом случае является использованной энергией, которая потребляется системой во время работы, а большая буква Q, в свою очередь, будет являться затраченной A, или опять же затраченной энергией.
В идеале КПД равен единице. Но, как это обычно бывает, он её меньше. Так происходит по причине физики и по причине, конечно же, закона о сохранении энергии.
Все дело в том, что закон сохранения энергии предполагает, что не может быть получено больше А, чем получено энергии. И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.
И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.
Итак, формула КПД:
Ƞ=А/Q, где
- A — полезная работа, которую выполняет система. Q — энергия, которую потребляет система.
Применение в разных сферах физики
Примечательно, что КПД не существует как понятие нейтральное, для каждого процесса есть свой КПД, это не сила трения, он не может существовать сам по себе.
Рассмотрим несколько из примеров процессов с наличием КПД.
К примеру, Возьмем электрический двигатель. Задача электрического двигателя — преобразовывать электрическую энергию в механическую. В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1. Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.
Нетрудно догадаться что структура формулы коэффициента всегда сохраняется, меняются в ней лишь данные, которые нужно подставить. Они зависят от конкретного случая, если это двигатель, как в случае выше, то необходимо оперировать затрачиваемой мощностью, если работа, то исходная формула будет другая.
Теперь мы знаем определение КПД и имеем представление об этом физическом понятии, а также об отдельных его элементах и нюансах. Физика — это одна из самых масштабных наук, но её можно разобрать на маленькие кусочки, чтобы понять. Сегодня мы исследовали один из этих кусочков.
Физика это наука, которая изучает процессы, происходящие в природе.
Liveposts. ru
11.02.2017 15:21:29
2017-02-11 15:21:29
Источники:
Https://liveposts. ru/articles/education-articles/fizika/ponyatie-kpd-opredelenie-formula-i-primenenie-v-fizike
Коэффициент полезного действия (кпд) — формулы, обозначение, расчет » /> » /> .keyword { color: red; }
Что такое кпд в физике
Любой механизм хочется оценить с точки зрения его пользы. Важно же понять, хорошо он выполняет свою функцию или нет. Для этого нужно такое понятие, как КПД.
Важно же понять, хорошо он выполняет свою функцию или нет. Для этого нужно такое понятие, как КПД.
КПД: понятие коэффициента полезного действия
Представьте, что вы пришли на работу в офис, выпили кофе, поболтали с коллегами, посмотрели в окно, пообедали, еще посмотрели в окно — вот и день прошел. Если вы не сделали ни одного дела по работе, то можно считать, что ваш коэффициент полезного действия равен нулю.
В обратной ситуации, когда вы сделали все запланированное — КПД равен 100%.
По сути, КПД — это процент полезной работы от работы затраченной.
Вычисляется по формуле:
Формула КПД
Η = (Aполезная/Aзатраченная) · 100%
Η — коэффициент полезного действия [%]
Aполезная — полезная работа [Дж]
Aзатраченная — затраченная работа [Дж]
Есть такое философское эссе Альбера Камю «Миф о Сизифе». Оно основано на легенде о неком Сизифе, который был наказан за обман. Его приговорили после смерти вечно таскать огромный булыжник вверх на гору, откуда этот булыжник скатывался, после чего Сизиф тащил его обратно в гору. То есть он делал совершенно бесполезное дело с нулевым КПД. Есть даже выражение «Сизифов труд», которое описывает какое-либо бесполезное действие.
То есть он делал совершенно бесполезное дело с нулевым КПД. Есть даже выражение «Сизифов труд», которое описывает какое-либо бесполезное действие.
Давайте пофантазируем и представим, что Сизифа помиловали и камень с горы не скатился. Тогда, во-первых, Камю бы не написал об этом эссе, потому что никакого бесполезного труда не было. А во-вторых, КПД в таком случае был бы не нулевым.
Полезная работа в этом случае Равна приобретенной булыжником Потенциальной энергии. Потенциальная энергия прямо пропорционально зависит от высоты: чем выше расположено тело, тем больше его потенциальная энергия. То есть, чем выше Сизиф прикатил камень, тем больше потенциальная энергия, а значит и полезная работа.
Потенциальная энергия
Еп = mg
Еп — потенциальная энергия [Дж]
M — масса тела [кг]
G — ускорение свободного падения [м/с 2 ]
На планете Земля g ≃ 9,8 м/с 2
Затраченная работа здесь — Это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
За счет чего происходит процесс?
Ради какого результата?
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы). Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
КПД в механике
Главный секрет заключается в том, что эта формула подойдет для всех видов КПД.
Если КПД получился больше 100 — идем проверять на ошибки. Такое может получиться, если неправильно подставили в формулу или перепутали затраченную и полезную работу.
Η = (Aполезная/Aзатраченная) · 100%
Η — коэффициент полезного действия [%]
Aполезная — полезная работа [Дж]
Aзатраченная — затраченная работа [Дж]
Дальше мы просто заменяем полезную и затраченную работы на те величины, которые ими являются.
Давайте разберемся на примере задачи.
Задача
Чтобы вкатить санки массой 4 кг в горку длиной 12 метров, мальчик приложил силу в 15 Н. Высота горки равна 2 м. Найти КПД этого процесса. Ускорение свободного падения принять равным g ≃9,8 м/с 2
Запишем формулу КПД.
Теперь задаем два главных вопроса:
Ради чего все это затеяли?
Чтобы санки в горку поднять — то есть ради приобретения телом потенциальной энергии. Значит в данном процессе полезная работа равна потенциальной энергии санок.
Потенциальная энергия
Еп = mg
Еп — потенциальная энергия [Дж]
M — масса тела [кг]
G — ускорение свободного падения [м/с 2 ]
На планете Земля g ≃ 9,8 м/с 2
За счет чего процесс происходит?
За счет мальчика, он же тянет санки. Значит затраченная работа равна механической работе
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
Заменим формуле КПД полезную работу на потенциальную энергию, а затраченную — на механическую работу:
Η = Eп/A · 100% = mgh/FS · 100%
Η = 4 · 9,8 · 2/15 · 12 · 100% = 78,4/180 · 100% ≃ 43,6 %
Ответ: КПД процесса приблизительно равен 43,6%
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
КПД в термодинамике
В термодинамике КПД — очень важная величина. Она полностью определяет эффективность такой штуки, как тепловая машина.
Она полностью определяет эффективность такой штуки, как тепловая машина.
- Тепловой двигатель (машина) — это устройство, которое совершает механическую работу циклически за счет энергии, поступающей к нему в ходе теплопередачи.
Схема теплового двигателя выглядит так:
У теплового двигателя обязательно есть нагреватель, который (не может быть!) нагревает рабочее тело, передавая ему количество теплоты Q1 или Qнагревателя (оба варианта верны, это зависит лишь от учебника, в котором вы нашли формулу).
- Рабочее тело — это тело, на котором завязан процесс (чаще всего это газ или топливо). Оно расширяется при подводе к нему теплоты и сжимается при охлаждении. Часть переданного Q1 уходит на механическую работу A. Из-за этого производится движение.
Оставшееся количество теплоты Q2 или Qхолодильника отводится к холодильнику, после чего возвращается к нагревателю и процесс повторяется.
КПД такой тепловой машины будет равен:
КПД тепловой машины
Η = (Aполезная/Qнагревателя) · 100%
Η — коэффициент полезного действия [%]
Aполезная — полезная работа (механическая) [Дж]
Qнагревателя — количество теплоты, полученное от нагревателя[Дж]
Если мы выразим полезную (механическую) работу через Qнагревателя и Qхолодильника, мы получим:
A = Qнагревателя — Qхолодильника.
Подставим в числитель и получим такой вариант формулы.
КПД тепловой машины
Η = Qнагревателя − Qхолодильника/Qнагревателя · 100%
Η — коэффициент полезного действия [%]
Qнагревателя — количество теплоты, полученное от нагревателя [Дж]
Qхолодильника — количество теплоты, отданное холодильнику [Дж]
А возможно ли создать тепловую машину, которая будет работать только за счет охлаждения одного тела?
Точно нет! Если у нас не будет нагревателя, то просто нечего будет передавать на механическую работу. Любой такой процесс — когда энергия не приходит из ниоткуда — означал бы возможность существования вечного двигателя.
Поскольку свидетельств такого процесса в мире не существует, то мы можем сделать вывод: Вечный двигатель невозможен. Это второе начало термодинамики.
Запишем его, чтобы не забыть:
Невозможно создать периодическую тепловую машину за счет охлаждения одного тела без изменений в других телах.
Задача
Найти КПД тепловой машины, если рабочее тело получило от нагревателя 20кДж, а отдало холодильнику 10 кДж.
Решение:
Возьмем формулу для расчета КПД:
Η = Qнагревателя − Qхолодильника/Qнагревателя · 100%
Решать будем в системе СИ, поэтому переведем значения из килоджоулей в джоули и затем подставим в формулу:
Η = 20 000 − 10 000/20 000 · 100% = 50%
Ответ: КПД тепловой машины равен 50%.
Идеальная тепловая машина: цикл Карно
Давайте еще чуть-чуть пофантазируем: какая она — идеальная тепловая машина. Кажется, что это та, у которой КПД равен 100%.
На самом деле понятие «идеальная тепловая машина» уже существует. Это тепловая машина, у которой в качестве рабочего тела взят идеальный газ. Такая тепловая машина работает по Циклу Карно. Зависимость давления от объема в этом цикле выглядит следующим образом
А КПД для цикла Карно можно найти через температуры нагревателя и холодильника.
КПД цикла Карно
Η = Tнагревателя − Tхолодильника / Tнагревателя · 100%
Η — коэффициент полезного действия [%]
Tнагревателя — температура нагревателя [Дж]
Tхолодильника — температура холодильника [Дж]
КПД в электродинамике
Мы каждый день пользуемся различными электронными устройствами: от чайника до смартфона, от компьютера до робота-пылесоса — и у каждого устройства можно определить, насколько оно эффективно выполняет задачу, для которой оно предназначено, просто посчитав КПД.
КПД
Η = (Aполезная/Aзатраченная) · 100%
Η — коэффициент полезного действия [%]
Aполезная — полезная работа [Дж]
Aзатраченная — затраченная работа [Дж]
Для электрических цепей тоже есть нюансы. Давайте разбираться на примере задачи.
Задачка, чтобы разобраться
Найти КПД электрического чайника, если вода в нем приобрела 22176 Дж тепла за 2 минуты, напряжение в сети — 220 В, а сила тока в чайнике 1,4 А.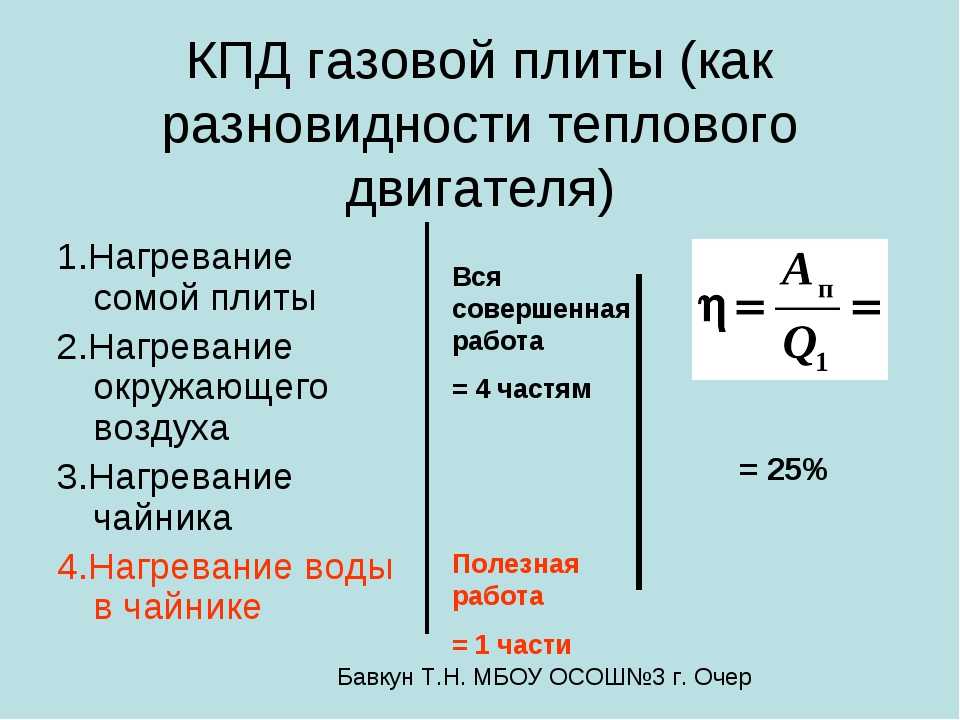
Решение:
Цель электрического чайника — вскипятить воду. То есть его полезная работа — это Количество теплоты, которое пошло на нагревание воды. Оно нам известно, но формулу вспомнить все равно полезно 😉
Количество теплоты, затраченное на нагревание
Q — количество теплоты [Дж]
C — удельная теплоемкость вещества [Дж/кг · ˚C]
Tконечная — конечная температура [˚C]
Tначальная — начальная температура [˚C]
Работает чайник, потому что в розетку подключен. Затраченная работа в данном случае — это Работа электрического тока.
Работа электрического тока
A = (I 2 ) · Rt = (U 2 )/R · t = UIt
A — работа электрического тока [Дж]
U — напряжение [В]
R — сопротивление [Ом]
То есть в данном случае формула КПД будет иметь вид:
Η = Q/A · 100% = Q/UIt · 100%
Переводим минуты в секунды — 2 минуты = 120 секунд. Теперь нам известны все значения, поэтому подставим их:
Η = 22176/220 · 1,4 · 120 · 100% = 60%
Ответ: КПД чайника равен 60%.
Давайте выведем еще одну формулу для КПД, которая часто пригождается для электрических цепей, но применима ко всему. Для этого нужна формула работы через мощность:
Работа электрического тока
A — работа электрического тока [Дж]
Подставим эту формулу в числитель и в знаменатель, учитывая, что мощность разная — полезная и затраченная. Поскольку мы всегда говорим об одном процессе, то есть полезная и затраченная работа ограничены одним и тем же промежутком времени, можно сократить время и получить формулу КПД через мощность.
A работа электрического тока Дж.
Skysmart. ru
17.07.2017 8:18:50
2017-07-17 08:18:50
Источники:
Https://skysmart. ru/articles/physics/koefficient-poleznogo-dejstviya-kpd
Понятие КПД: определение, формула и применение в физике. Как найти кпд в физике. » /> » /> .keyword { color: red; }
Что такое кпд в физике
Чтобы что-то сделать, необходимо затратить определенное количество энергии.
Чтобы ехать на велосипеде, вы тратите мышечную энергию, крутя педали. Для движения автомобиля используется энергия сжигаемого топлива (бензина, нефти или газа).
Что такое коэффициент полезного действия (КПД) и как рассчитать его по формуле
Слово «полезный» в физике — это результат после сопротивления. Типичным примером является сопротивление металла в станке. В случае с кранами это масса объекта. Например, эффективность традиционных ламп накаливания составляет менее 5%, в то время как эффективность светодиодов гораздо выше. Это связано с тем, что большая часть потребляемой энергии расходуется на производство тепла, а не света.
То же самое относится и к электронике, и этот фактор необходимо учитывать при проектировании плат и электрических схем. Здесь важно учитывать проводимость металла и использовать материалы с низким сопротивлением. В этой статье описаны ключевые аспекты эффективности, способы ее расчета, ее влияние и основные возможности для повышения эффективности.
Что такое КПД
Коэффициент эффективности (степень эффективности) — это отношение эффективной энергии Wp Wp/W — общее количество энергии W, полученное системой (двигателем или двигателями) в виде проекта. В реальных системах это всегда имеет место, поскольку потери энергии из-за трения и других неравновесных процессов неизбежны. Исходя из второго принципа термодинамики тепловых двигателей, наилучший КПД (отношение количества Wp, затраченного в цикле, и количества тепла Q, подведенного в этом цикле) имеют нагреватель T1 и охладитель T2, равный = Wp/Q = (T1- T2 / T1 (теорема Карно).
В электродвигателях степень эффективности — это отношение механического КПД к количеству электроэнергии, поставляемой источником питания. В электрических трансформаторах степень эффективности — это отношение электромагнитной энергии вторичной обмотки к энергии первичной обмотки. Понятие эффективности является универсальным и может быть применено к различным системам, таким как генераторы, различные типы двигателей, полупроводниковые устройства и биологические объекты, и поэтому может быть использовано для сравнительной оценки эффективности различных процессов.
Мощность и коэффициент полезного действия электродвигателей
Электродвигатели имеют высокие коэффициенты полезного действия, но они все еще далеки от идеальных показателей, к которым продолжают стремиться производители. Причина этого в том, что во время работы энергоблока один вид энергии преобразуется в другой вид энергии, выделяется тепло и неизбежны потери. Распространение тепловой энергии может быть зарегистрировано в различных компонентах двигателей всех типов. Потери мощности в электродвигателях являются результатом местных потерь в обмотках, стальных компонентах и во время механической работы. Имеется небольшой, но существенный вклад в виде дополнительных потерь.
Магнитные потери.
Магнитные потери возникают в магнитном поле якоря двигателя при перемагничивании. Их величина складывается из суммы потерь на вихревые токи и потерь на перемагничивание и является функцией частоты намагничивания, магнитной индукции арматуры и зубцов арматуры. Толщина используемого металлического листа и качество изоляции также играют важную роль.
Механические и электрические потери
Подобно магнитным потерям, механические потери в электродвигателях постоянны. Они включают в себя потери на трение в подшипниках, потери на трение щеток и потери на вентиляцию двигателя. Минимизация механических потерь возможна благодаря использованию современных материалов с улучшенными с годами характеристиками. Электрические потери, с другой стороны, непостоянны и зависят от уровня нагрузки электродвигателя. В основном они вызваны нагревом кисти, контактом кисти.
Броня и полевые потери снижают эффективность. Механические и электрические потери являются основными факторами, способствующими изменению характеристик двигателя.
Дополнительные потери.
Потери мощности в двигателях складываются из потерь из-за балансирных соединений и потерь из-за неравномерной индукции арматуры при высоких нагрузках. Потери на токовых и полюсных зажимах вносят свой вклад в общие дополнительные потери. Поскольку точно определить все эти величины сложно, обычно считается, что их сумма составляет от 0,5 до 1%.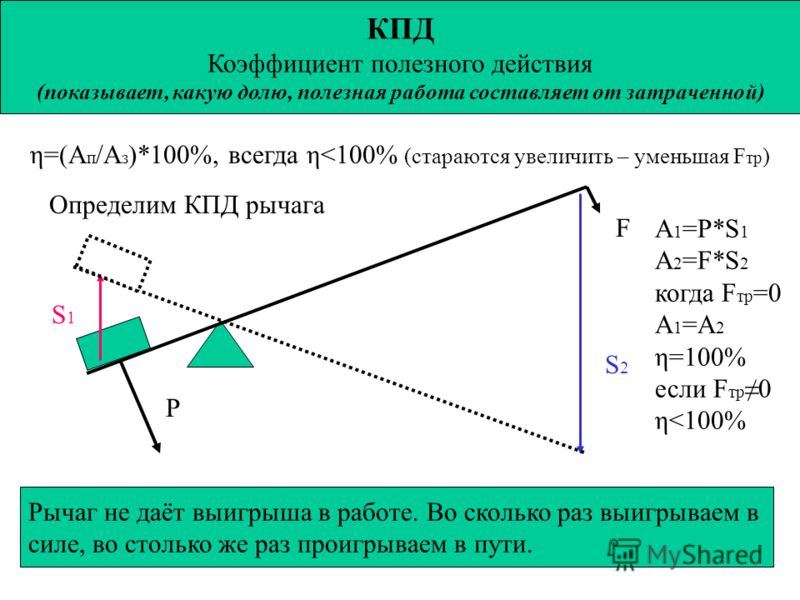 Эти данные используются для расчета общих потерь, чтобы определить эффективность двигателя.
Эти данные используются для расчета общих потерь, чтобы определить эффективность двигателя.
Эффективность и ее зависимость от нагрузки
КПД электродвигателя — это отношение эффективной мощности силового агрегата к потребляемой мощности. Для двигателей мощностью до 100 кВт эти значения составляют от 0,75 до 0,9. Для более мощных двигателей КПД значительно выше: от 0,9 до 0,97. Определив общие потери мощности электродвигателя, можно с достаточной точностью рассчитать КПД любого силового агрегата. Этот метод определения производительности называется косвенным и может применяться к машинам различной мощности.
Инженер по специальности «Вычислительная техника и программное обеспечение автоматизированных систем», МИФИ, 2005-2010 гг.
Чтобы что-то сделать, необходимо затратить определенное количество энергии. Чтобы ехать на велосипеде, вы тратите мышечную энергию, крутя педали. Для движения автомобиля используется энергия сжигаемого топлива (бензина, нефти или газа).
Определение и расшифровка КПД
Аббревиатура для этого термина — «норма прибыли». Это толкование может быть не совсем ясным даже в первый раз. Это фактор производительности системы или отдельного органа, часто механизма. Эффективность — это мера выработки или преобразования энергии.
Этот фактор можно применить практически ко всему, что нас окружает, и даже больше. В конце концов, мы постоянно выполняем полезную работу, но как часто и сколько — это другой вопрос, поэтому используется термин «эффективность».
Важно отметить, что этот коэффициент является неограниченной величиной, обычно это математическое значение, например, 0 и 1, или часто процент.
В физике этот коэффициент обозначается буквой Ƞ, или Eta, как его обычно называют.
Полезная работа
При использовании механизма или устройства вы обязаны выполнять работу. Как правило, это всегда больше, чем требуется для выполнения каждого задания. Исходя из этих данных, можно выделить два типа работы. Это обозначается буквой А и полезной работой с маленькой буквы (AZ) и полезной работой с буквой Р (AP). Например, возьмем следующий случай. Есть задача поднять камень на определенную высоту и с определенной массой. В этом случае проект описывает только преодоление силы тяжести, которая действует на груз.
Это обозначается буквой А и полезной работой с маленькой буквы (AZ) и полезной работой с буквой Р (AP). Например, возьмем следующий случай. Есть задача поднять камень на определенную высоту и с определенной массой. В этом случае проект описывает только преодоление силы тяжести, которая действует на груз.
Помимо тяжести валуна, важно учитывать тяжесть детали, если она используется для подъема устройства. И помимо всего этого, важно помнить, что хотя мы берем власть и побеждаем, мы всегда проигрываем поездку. Все это приводит к выводу, что в любом случае более полезным является проект AZ> AP, поскольку задача состоит в том, чтобы максимально уменьшить эту разницу и тем самым улучшить производительность. или наши устройства.
Полезная работа — это часть затрат, сделанных при использовании механизма. Производительность — это натуральная величина того, насколько полезен полезный проект по сравнению с проектом в целом.
- Входной проект AZ всегда больше, чем выходной проект AP.
 Чем выше отношение полезности к расходам, тем выше коэффициент, и наоборот. ПД умножается на массу за счет силы тяжести и увеличения высоты.
Чем выше отношение полезности к расходам, тем выше коэффициент, и наоборот. ПД умножается на массу за счет силы тяжести и увеличения высоты.Физическая формула КПД
Существуют определенные типы факторов эффективности, которые необходимо найти. Он заключается в следующем. В физике, чтобы найти коэффициент полезного действия, количество энергии нужно разделить на работу, выполненную системой. Другими словами, степень производительности является причиной энергии, затраченной на работу. Отсюда следует простой вывод: если система или организм работает лучше и эффективнее, то для выполнения работы требуется меньше энергии.
Сам тип выглядит коротким и очень простым ƞ равен A/Q. То есть, ƞ = a/q. В этом коротком типе элементы, которые необходимо рассчитать, являются твердыми. Таким образом, в данном случае используется энергия, потребленная системой во время работы, а большая буква Q — это энергия, использованная A или использованная снова.
В идеале коэффициент производительности равен единице. Однако, как это обычно бывает, она меньше. Это объясняется физикой и, конечно же, законом сохранения энергии.
Однако, как это обычно бывает, она меньше. Это объясняется физикой и, конечно же, законом сохранения энергии.
Все дело в том, что закон сохранения энергии означает, что он не может заработать больше, чем получает. И даже не способствует, потому что энергия постоянно расходуется. Кроме того, работа связана с потерями. В случае с двигателями, например, потери заключаются в обильном нагреве.
Максимальные коэффициенты характерны для круглых машин. Они работают при определенных температурах в радиаторах (T1) и холодильниках (T2). Измерение производится по типу: h = (t1-t2)/t1. Экзотермическая мощность используется для определения производительности котлов, работающих на ископаемом топливе.
Мощность разных устройств
По статистике, до 25% энергии теряется во время работы устройства. При работе двигателя внутреннего сгорания происходит частичное сгорание топлива. Небольшой процент улетучивается через выхлопную трубу. Когда бензиновый двигатель закипает, компоненты, входящие в его состав, нагреваются. Теряется до 35% общей мощности.
Теряется до 35% общей мощности.
Трение возникает при движении механизмов. Для уменьшения этого используется смазка. Но это не может полностью устранить явление, поэтому расходуется до 20% энергии. Пример автомобиля: Если расход составляет 10 литров топлива на 100 км, то 2 литра расходуются, а остальные 8 литров теряются.
Если сравнить КПД бензинового и дизельного двигателей, то полезный КПД первого составляет 25%, а второго — 40%. Аппараты похожи друг на друга, но имеют разные типы смешивания:
Асинхронные механизмы
Термин асинхронный интерпретируется как несовпадение по времени. Этот термин используется во многих современных машинах, которые являются электрическими и могут преобразовывать соответствующую энергию в механическую. Преимущества устройств :
- Простая конструкция, 低価格、 信頼性、 низкие эксплуатационные расходы.
Для расчета КПД используется уравнение h = P2/P1. Общие потери энергии в обмотках двигателя используются для расчета P1 и P2. В большинстве подразделений этот показатель составляет 80-90%. Для быстрого расчета можно воспользоваться онлайн-источником или персональным калькулятором. Для проверки потенциальной эффективности двигателя внешнего сгорания, работающего на различных источниках тепла, используется силовая установка Стирлинга. Он имеет форму теплового двигателя с рабочей жидкостью в виде жидкости или газа. Вещество движется в замкнутом объеме.
Для быстрого расчета можно воспользоваться онлайн-источником или персональным калькулятором. Для проверки потенциальной эффективности двигателя внешнего сгорания, работающего на различных источниках тепла, используется силовая установка Стирлинга. Он имеет форму теплового двигателя с рабочей жидкостью в виде жидкости или газа. Вещество движется в замкнутом объеме.
Принцип его работы основан на постепенном нагревании и охлаждении объекта за счет извлечения энергии из давления. Подобный механизм используется в косметических приборах и в современной подводной лодке. Его функциональность наблюдается при любых температурах. Она не требует дополнительной пусковой системы. КПД может быть увеличен до 70%, в отличие от стандартного двигателя.
Значения показателя
В 1824 году инженер Карно определил КПД идеального двигателя, когда коэффициент равен 100%. Для интерпретации концепции была создана специальная машина со следующей формулой: h=(T1 — T2)/T1. Для расчета максимального значения применяется уравнение КПД max = (T1 — T2)/T1x100%. В двух примерах T1 обозначает температуру нагрева, а T2 — температуру охлаждения.
В двух примерах T1 обозначает температуру нагрева, а T2 — температуру охлаждения.
На практике для достижения коэффициента 100% температура радиатора должна быть приравнена к нулю. Такой эффект невозможен, так как Т1 выше температуры воздуха. Процесс повышения эффективности энергоснабжения или электростанции считается важным техническим вопросом. Теоретически, проблема решается за счет снижения трения в компонентах двигателя и уменьшения тепловых потерь. В дизельном двигателе это достигается за счет турбонаддува. В этом случае эффективность повышается до 50%.
Мощность типичного двигателя может быть увеличена следующими способами:
- подключение многоцилиндрового агрегата к системе, использование специального топлива замену определенных компонентов, перенос места сгорания бензина.
Эффективность зависит от типа и конструкции двигателя. Современные ученые утверждают, что будущее за электрическими двигателями. На практике работа, выполняемая каждым устройством, превышает полезную работу, поскольку определенная ее часть выполняется при трении.
При использовании подвижного шкива совершается дополнительная работа: шкив с канатом поднимается и преодолеваются силы трения на шкиве.
Чтобы что-то сделать, необходимо затратить определенное количество энергии. Чтобы ехать на велосипеде, вы тратите мышечную энергию, крутя педали. Для движения автомобиля используется энергия сжигаемого топлива (бензина, нефти или газа).
Чтобы что-то сделать, необходимо затратить определенное количество энергии. Чтобы ехать на велосипеде, вы тратите мышечную энергию, крутя педали. Для движения автомобиля используется энергия сжигаемого топлива (бензина, нефти или газа).
Слово «полезный» в физике — это результат после сопротивления. Типичным примером является сопротивление металла в станке. В случае с кранами это масса объекта. Например, эффективность традиционных ламп накаливания составляет менее 5%, в то время как эффективность светодиодов гораздо выше. Это связано с тем, что большая часть потребляемой энергии расходуется на производство тепла, а не света.
То же самое относится и к электронике, и этот фактор необходимо учитывать при проектировании плат и электрических схем. Здесь важно учитывать проводимость металла и использовать материалы с низким сопротивлением. В этой статье описаны ключевые аспекты эффективности, способы ее расчета, ее влияние и основные возможности для повышения эффективности.
Максимальные коэффициенты характерны для круглых машин. Они работают при определенных температурах в радиаторах (T1) и холодильниках (T2). Измерение производится по типу: h = (t1-t2)/t1. Экзотермическая мощность используется для определения производительности котлов, работающих на ископаемом топливе.
Мощность разных устройств.
Avto-dim. ru
27.09.2018 12:13:23
2018-09-27 12:13:23
Источники:
Https://avto-dim. ru/ponyatie-kpd-opredelenie-formula-i-primenenie-v-fizike-kak-najti-kpd-v-fizike-4562/
Вычисление количества работы, выполненной силами
В предыдущей части Урока 1 работа описывалась как происходящая, когда на объект действует сила, вызывающая перемещение. Когда действует сила, вызывающая перемещение объекта, для вычисления работы необходимо знать три величины. Этими тремя величинами являются сила, смещение и угол между силой и смещением. Впоследствии работа рассчитывается как сила • перемещение • косинус (тета), где тета — угол между векторами силы и смещения. В этой части Урока 1 концепции и математика работы будут применяться для анализа различных физических ситуаций.
Когда действует сила, вызывающая перемещение объекта, для вычисления работы необходимо знать три величины. Этими тремя величинами являются сила, смещение и угол между силой и смещением. Впоследствии работа рассчитывается как сила • перемещение • косинус (тета), где тета — угол между векторами силы и смещения. В этой части Урока 1 концепции и математика работы будут применяться для анализа различных физических ситуаций.
Выразите свое понимание концепции и математики труда, ответив на следующие вопросы. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
1. Примените уравнение работы, чтобы определить количество работы, выполняемой приложенной силой в каждой из трех ситуаций, описанных ниже.
2. Во многих случаях на объект действует более одной силы. Диаграмма свободного тела — это диаграмма, которая изображает тип и направление всех сил, действующих на объект. Следующие описания и сопровождающие их диаграммы свободного тела показывают силы, действующие на объект. Для каждого случая укажите, какие силы совершают работу над объектом. Затем вычислить работу этих сил.
Следующие описания и сопровождающие их диаграммы свободного тела показывают силы, действующие на объект. Для каждого случая укажите, какие силы совершают работу над объектом. Затем вычислить работу этих сил.
Схема | на Объект | Каждая сила |
 | ||
3. Перед началом спуска горка всегда поднимается на первый холм на большую начальную высоту. На автомобиле выполняется работа (обычно цепью) для достижения этой начальной высоты. Разработчик каботажных судов рассматривает три различных угла наклона, при которых 2000-килограммовый автопоезд должен тянуться к вершине 60-метрового холма. В каждом случае сила, приложенная к автомобилю, будет приложена параллельно холму. Ее критический вопрос: какой угол потребует наибольшей работы? Проанализируйте данные, определите работу, проделанную в каждом случае, и ответьте на этот важный вопрос.
В каждом случае сила, приложенная к автомобилю, будет приложена параллельно холму. Ее критический вопрос: какой угол потребует наибольшей работы? Проанализируйте данные, определите работу, проделанную в каждом случае, и ответьте на этот важный вопрос.
а. | ||||
б. | ||||
с. |
4. Бен Травлун несет чемодан с усилием 200 Н на три лестничных пролета (высотой 10,0 м), а затем толкает его с горизонтальной силой 50,0 Н с постоянной скоростью 0,5 м/с в течение горизонтальное расстояние 35,0 метров. Сколько работы проделал Бен со своим чемоданом за эти 9 дней?0149 всего движения ?
5. На брусок действует сила 50 Н под углом, показанным на схеме. Блок перемещается по горизонтали на расстояние 3,0 м. Какую работу совершает приложенная сила?
6. Какую работу совершает приложенная сила, чтобы поднять блок массой 15 ньютонов на 3,0 м по вертикали с постоянной скоростью?
7. Студент массой 80,0 кг преодолевает три лестничных пролета за 12,0 сек. Студент прошел вертикальную дистанцию 8,0 м. Определить работу, которую совершил студент, чтобы поднять свое тело на эту высоту. Предположим, что его скорость постоянна.
Студент прошел вертикальную дистанцию 8,0 м. Определить работу, которую совершил студент, чтобы поднять свое тело на эту высоту. Предположим, что его скорость постоянна.
8. Рассчитайте работу, совершаемую силой 2,0 Н (направленной под углом 30° к вертикали) для перемещения 500-граммового ящика на горизонтальное расстояние 400 см по шероховатому полу с постоянной скоростью 0,5 м/с. (СОВЕТ: будьте осторожны с единицами измерения.) |
9. Усталая белка (масса 1 кг) отжимается, прикладывая силу, чтобы поднять ее центр масс на 5 см. Оцените количество отжиманий, которое должна сделать уставшая белка, чтобы совершить работу примерно в 5,0 Дж.
Мы хотели бы предложить …
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей Интерактивной программы It’s All Uphill Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивное приложение It’s All Uphill позволяет учащимся изучить влияние угла наклона на силу и работу, выполняемую при подъеме тележки в гору с постоянной скоростью.
Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей Интерактивной программы It’s All Uphill Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивное приложение It’s All Uphill позволяет учащимся изучить влияние угла наклона на силу и работу, выполняемую при подъеме тележки в гору с постоянной скоростью.
Посетите: It’s All Uphill Interactive
Следующий раздел:
Перейти к следующему уроку:
Что такое формула работы? Примеры
Формула работы используется для расчета работы. Прежде чем мы выучим формулу, давайте вспомним, что означает работа. Говорят, что работа совершается, когда мы прикладываем силу к объекту, и объект испытывает перемещение. Если перемещение в направлении действия силы равно нулю, то совершенная работа равна нулю. Формула работы используется для расчета работы, совершаемой при перемещении объекта. Давайте узнаем больше о формуле для работы вместе с решенными примерами в следующем разделе.
Формула работы используется для расчета работы, совершаемой при перемещении объекта. Давайте узнаем больше о формуле для работы вместе с решенными примерами в следующем разделе.
Что такое формула работы?
Формула работы используется для расчета работы, затраченной на перемещение любого объекта. Работа есть произведение приложенной силы и перемещения в направлении действия силы. Работа есть скалярное произведение двух векторов: силы и перемещения. Таким образом, работа является скалярной величиной. Единицей работы в системе СИ является Джоуль (Дж).
Формула работы
Формула работы может быть выражена следующим образом:
W = F.d
Вт = (Fcos θ)d
Где,
- Вт = выполненная работа
- F = Величина приложенной силы
- d = Величина смещения в направлении действия силы.

- θ = угол между векторами: силы и перемещения
Единицей работы в системе СИ является Джоуль (Дж). Если совершена работа в 1 джоуль, то формула работы будет следующей: 1 Дж = 1 Н·м
Вывод формулы работы
Рассмотрим блок, помещенный на горизонтальном полу без трения, на который действует постоянная сила F, благодаря которой этот блок перемещается на расстояние d по прямой линии в направлении действия силы.
В общем случае работа силы F равна изменению кинетической энергии
W = (1/2)mv 2 – (1/2) mu 2 -u 2 )
Применение v 2 -u 2 = 2as
W = (1/2)m(2as)
W = maston’s
закон), таким образом, W = Fs. (s=d=перемещение)
(s=d=перемещение)Теперь, если эффективная составляющая силы вдоль направления перемещения Fcosθ отвечает за перемещение любого объекта в заданном направлении, то работа, совершаемая силой F при перемещении тела на перемещение d есть, W=(|F|cosθ)|d|
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Примеры использования формулы для работы
Пример 1: 10 ньютонов силы, приложенной к телу, которое перемещает его на 2 метра. Вычислите работу, выполненную по формуле работы.
Решение:
Найти: Работа выполнена
Дано: Сила (F) = 10 Н
Перемещение (d) = 2 м
Используя формулу для работы,
W = F.d
= (10)(2)
= 20 Нм
9000 Ответ Работа Нм совершается, когда сила в 10 ньютонов перемещает тело на 2 метра.
Пример 2: Кули на вокзале несет сумку массой 100 Н на некоторое расстояние. Вычислите работу, которую совершает кули над сумкой, используя формулу работы.
Решение:
Найти работу, выполненную кули.
Дано: Вес мешка = 100 Н
Кроме того, вес мешка будет действовать в вертикальном направлении, а его движение будет происходить в горизонтальном направлении. Значит, смещение мешка в направлении действия силы (веса) равно нулю.
d = 0
Используя формулу для работы,
W = F.d
= (100)(0)
= 0 Дж
Ответ: Работа, выполненная кули на мешке, равна нулю.
Пример 3: Рассчитайте работу, выполненную силой при перемещении объекта на расстояние 7 м, если объект протаскивается горизонтально по поверхности под действием силы 150 Н, действующей параллельно поверхности.
Решение:
Найти: Работа силы при перемещении тела на расстояние 7 м
Дано: F = 150 Н, d = 7 м
Поскольку F и d направлены в одном направлении,
θ = 0, [θ — угол действия силы к направлению движения]
W = F × Cos θ × d
= 150× 7 × Cos 0
= 1050 Дж [Поскольку Cos 0 = 1]
Ответ: Работа, совершаемая силой при перемещении объекта, равна 800 J.
Часто задаваемые вопросы о формуле работы
Что такое формула работы?
Формула работы определяется как формула для расчета работы, выполненной при перемещении объекта. Совершенная работа равна произведению величины приложенной силы на расстояние, которое тело перемещает из своего начального положения в конечное. Математически проделанная работа Формула задается как W = Fd
Какие существуют версии формулы работы?
Математически концепция выполненной работы W равна силе f, умноженной на расстояние (d), то есть W = f. d и если сила приложена под углом θ к смещению, то выполненная работа рассчитывается как W = f . д потому что θ.
Каковы применения формулы работы?
Формула работы имеет множество применений, например, для вычисления выполненной работы, силы или перемещения в любой задаче.
Что такое d в рабочей формуле?
В рабочей формуле W = F. d, d – это смещение, на сколько объект сместился со своего начального места.
9.1 Работа, мощность и теорема о работе и энергии. Физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать и применять теорему работа-энергия
- Описать и рассчитать работу и мощность
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (6) Научные концепции. Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:
- (А) описывать и применять теорему работа-энергия;
- (С) описать и вычислить работу и мощность.
Кроме того, Руководство по физике для средней школы касается следующих стандартов:
- (6) Научные концепции. Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса.
 Ожидается, что студент:
Ожидается, что студент:- (С) рассчитать механическую энергию, мощность, генерируемую внутри, приложенный к ней импульс и импульс физической системы.
Используйте лабораторную работу под названием «Работа и энергия» в качестве дополнения к материалам этого раздела.
Основные термины раздела
| энергия | гравитационная потенциальная энергия | джоуля | кинетическая энергия | механическая энергия |
| потенциальная энергия | сила | Вт | работа | теорема работа-энергия |
Поддержка учителей
Поддержка учителей
В этом разделе учащиеся узнают, как работа определяет изменения кинетической энергии и что мощность — это скорость выполнения работы.
[BL][OL] Проверьте понимание массы, скорости и ускорения под действием силы тяжести. Дайте общее определение слов потенциал и кинетика .
Дайте общее определение слов потенциал и кинетика .
[AL][AL] Напомните учащимся уравнение W=PEe=fmgW=PEe=fmg . Укажите, что ускорение свободного падения является постоянным, поэтому PE e , являющееся результатом работы силы тяжести, также будет постоянным. Сравните это с ускорением за счет других сил, таких как приложение мышц для подъема камня, которое может быть непостоянным.
Теорема о работе и энергии
В физике термин работа имеет очень конкретное определение. Работа — это приложение силы ff для перемещения объекта на расстояние d в направлении приложения силы. Работа, Вт , описывается уравнением
W=fd.W=fd.
Некоторые вещи, которые мы обычно считаем работой, не являются работой в научном смысле этого слова. Рассмотрим несколько примеров. Подумайте, почему каждое из следующих утверждений верно.
- Домашнее задание не является заданием.
- Поднять камень вверх над землей — это работы.
- Перемещение камня по прямой траектории через газон с постоянной скоростью не является работой.
Первые два примера довольно просты. Домашняя работа не является работой, потому что объекты не перемещаются на расстояние. Поднять камень над землей — это работа, потому что камень движется в направлении приложения силы. Последний пример менее очевиден. Напомним из законов движения, что сила равна , а не требуется для перемещения объекта с постоянной скоростью. Поэтому, хотя может быть приложена некоторая сила, чтобы удерживать камень над землей, результирующая сила не прилагается, чтобы поддерживать движение камня вперед с постоянной скоростью.
Поддержка учителей
Поддержка учителей
[BL][OL] Объясните, что когда эта теорема применяется к объекту, который сначала покоится, а затем ускоряется, член 12mv1212mv12 равен нулю.
[OL][AL] Работа измеряется в джоулях и W=fdW=fd . Сила измеряется в ньютонах, а расстояние в метрах, поэтому джоули эквивалентны ньютон-метрам (Н⋅м)(Н⋅м)
Работа и энергия тесно связаны. Когда вы совершаете работу по перемещению объекта, вы изменяете энергию объекта. Вы (или объект) также тратите энергию на выполнение работы. Фактически энергию можно определить как способность совершать работу. Энергия может принимать различные формы, и одна форма энергии может трансформироваться в другую. В этой главе нас будет интересовать механическая энергия, которая существует в двух формах: кинетическая энергия и потенциальная энергия.
- Кинетическая энергия также называется энергией движения. Движущийся объект обладает кинетической энергией.
- Потенциальная энергия, иногда называемая запасенной энергией, бывает нескольких видов. Гравитационная потенциальная энергия — это накопленная энергия, которой обладает объект в результате его положения над поверхностью Земли (или другого объекта в космосе).
 Автомобиль американских горок на вершине холма обладает гравитационной потенциальной энергией.
Автомобиль американских горок на вершине холма обладает гравитационной потенциальной энергией.
Давайте посмотрим, как выполнение работы над объектом изменяет энергию объекта. Если мы приложим силу, чтобы поднять камень с земли, мы увеличим потенциальную энергию камня, PE . Если мы уроним камень, сила гравитации увеличит кинетическую энергию камня по мере его движения вниз, пока он не упадет на землю.
Сила, которую мы прикладываем, чтобы поднять камень, равна его весу, w , что равно его массе, m , умноженной на ускорение свободного падения, g .
f=w=mgf=w=mg
Работа, которую мы совершаем над камнем, равна силе, которую мы прикладываем, умноженной на расстояние d , на которое мы поднимаем камень. Работа, которую мы совершаем над камнем, также равна выигрышу камня в гравитационной потенциальной энергии, РЕ и .
W=PEe=mgdW=PEe=mgd
Кинетическая энергия зависит от массы объекта и его скорости, v .
KE=12mv2KE=12mv2
Когда мы бросаем камень, сила тяжести заставляет камень падать, придавая камню кинетическую энергию. Когда работа, совершаемая над телом, увеличивает только его кинетическую энергию, то чистая работа равна изменению величины величины 12mv212mv2. Это формулировка теоремы работа-энергия, которая математически выражается как
W=ΔKE = 12mv22−12mv12.W=ΔKE = 12mv22−12mv12.
Нижние индексы 2 и 1 указывают конечную и начальную скорость соответственно. Эта теорема была предложена и успешно проверена Джеймсом Джоулем (рис. 9.2).
Имя Джоуль звучит знакомо? Джоуль (Дж) является метрической единицей измерения как работы, так и энергии. Измерение работы и энергии в одних и тех же единицах подтверждает идею о том, что работа и энергия связаны и могут быть преобразованы друг в друга. 1,0 Дж = 1,0 Н∙м, единица силы, умноженная на расстояние.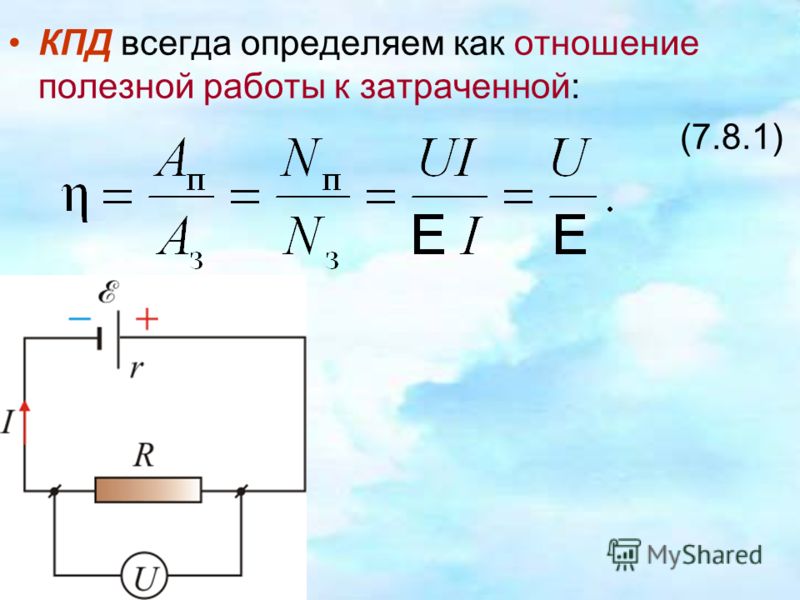 1,0 Н = 1,0 кг∙м/с 2 , поэтому 1,0 Дж = 1,0 кг∙м 2 /с 2 . Анализ единиц слагаемого (1/2) m v 2 даст те же единицы для джоулей.
1,0 Н = 1,0 кг∙м/с 2 , поэтому 1,0 Дж = 1,0 кг∙м 2 /с 2 . Анализ единиц слагаемого (1/2) m v 2 даст те же единицы для джоулей.
Рисунок 9.2 Джоуль назван в честь физика Джеймса Джоуля (1818–1889). (Ч. Х. Джинс, Wikimedia Commons)
Смотреть физику
Работа и энергия
В этом видео объясняется теорема об энергии работы и обсуждается, как работа, выполняемая над объектом, увеличивает КЭ объекта.
Проверка захвата
Верно или неверно — прирост энергии объекта, на который действует только гравитационная сила, равен произведению веса объекта на расстояние, на которое он падает.
- Правда
- Ложь
Поддержка учителей
Поддержка учителей
Повторите информацию о кинетической и потенциальной энергии, обсуждавшуюся ранее в этом разделе. Попросите учащихся различать и понимать два способа увеличения энергии объекта (1) приложение горизонтальной силы для увеличения KE и (2) приложение вертикальной силы для увеличения PE.
Попросите учащихся различать и понимать два способа увеличения энергии объекта (1) приложение горизонтальной силы для увеличения KE и (2) приложение вертикальной силы для увеличения PE.
Расчеты с использованием работы и мощности
В приложениях, связанных с работой, нас часто интересует, насколько быстро выполняется работа. Например, при проектировании американских горок важным фактором является время, необходимое для подъема автомобиля с американских горок на вершину первого холма. Полчаса подъема наверняка вызовут раздражение у райдеров и снизят продажи билетов. Давайте посмотрим, как рассчитать время, необходимое для выполнения работы.
Напомним, что ставка может использоваться для описания количества, например работы, за период времени. Мощность – это скорость, с которой совершается работа. В этом случае скорость означает за единицу времени . Мощность рассчитывается путем деления выполненной работы на время, затраченное на эту работу.
P=WtP=Wt
Давайте рассмотрим пример, который поможет проиллюстрировать разницу между работой, силой и мощностью. Предположим, женщина на рис. 9.3, поднимающая телевизор с помощью шкива, поднимает телевизор на четвертый этаж за две минуты, а мужчине, несущему телевизор по лестнице, требуется пять минут, чтобы добраться до того же места. Они проделали одинаковую работу (fd)(fd) на телевидении, потому что они переместили одинаковую массу на одно и то же расстояние по вертикали, что требует такой же величины восходящей силы. Однако женщина, использующая шкив, произвела больше энергии. Это потому, что она выполнила работу за меньшее время, поэтому знаменатель формулы мощности т , меньше. (Для простоты мы пока оставим в стороне тот факт, что человек, поднимающийся по лестнице, также проделал работу над собой.)
Рисунок
9.3
Как бы вы не перенесли телевизор на четвертый этаж, объем выполняемой работы и потенциальный прирост энергии одинаков.
Мощность может быть выражена в ваттах (Вт). Эта единица может использоваться для измерения мощности, связанной с любой формой энергии или работы. Вы, скорее всего, слышали этот термин, используемый в отношении электрических устройств, особенно лампочек. Умножение мощности на время дает количество энергии. Электричество продается в киловатт-часах, потому что это равно количеству потребляемой электроэнергии.
Единица ватт была названа в честь Джеймса Уатта (1736–1819) (см. рис. 9.4). Он был шотландским инженером и изобретателем, который открыл, как увеличить мощность паровых двигателей.
Рисунок 9.4 Думает ли Джеймс Уатт о ваттах? (Карл Фредерик фон Бреда, Wikimedia Commons)
Поддержка учителей
Поддержка учителей
[BL][OL] Повторите концепцию, согласно которой работа изменяет энергию объекта или системы. Вспомните единицы работы, энергии, силы и расстояния. Используйте уравнения для механической энергии и работы, чтобы показать, что является работой, а что нет. Объясните, почему держать что-то над землей или нести что-то по ровной поверхности — это не работа в научном смысле.
Объясните, почему держать что-то над землей или нести что-то по ровной поверхности — это не работа в научном смысле.
[ПР] Попросите учащихся использовать уравнения механической энергии, чтобы объяснить, почему каждое из них работает или не работает. Попросите их привести больше примеров, пока они не поймут разницу между научным термином работа и задачей, которая просто трудна, но не буквально работает (в научном смысле).
[BL][OL] Подчеркните, что мощность — это скорость, и эта скорость означает «в единицу времени». В метрической системе это обычно секунды. Завершите раздел, устранив любые неверные представления о различиях между силой, работой и мощностью.
[AL] Объясните отношения между единицами силы, работы и мощности. Если W=fdW=fd и работу можно выразить в Дж, то P=Wt=fdtP=Wt=fdt, поэтому мощность можно выразить в единицах N⋅msN⋅ms
Также объясните, что мы покупаем электроэнергию в киловатт-часах, потому что , когда мощность умножается на время, единицы времени сокращаются, остается работа или энергия.
Смотреть физику
Роль Уатта в промышленной революции
Это видео демонстрирует, как ватты, полученные в результате изобретений Уатта, помогли сделать промышленную революцию возможной и позволили Англии вступить в новую историческую эру.
Проверка захвата
Какой вид механической энергии вырабатывает паровая машина?
- Потенциальная энергия
- Кинетическая энергия
- Атомная энергия
- Солнечная энергия
Прежде чем продолжить, убедитесь, что вы понимаете различия между силой, работой, энергией и мощностью. Сила, действующая на объект на расстоянии, работает. Работа может увеличивать энергию, а энергия может выполнять работу. Мощность – это скорость, с которой совершается работа.
Рабочий пример
Применение теоремы о работе и энергии
Фигуристка массой 50 кг скользит по льду со скоростью 8 м/с, когда ее друг подходит сзади и толкает ее, в результате чего ее скорость увеличивается до 12 м/с. Сколько работы сделал друг над фигуристом?
Сколько работы сделал друг над фигуристом?
Стратегия
К задаче можно применить теорему о работе-энергии. Напишите уравнение теоремы и упростите его, если возможно.
W=ΔKE = 12mv22−12mv12W=ΔKE = 12mv22−12mv12
Упростить до W=12m(v22−v12) Упростить до W=12m(v22−v12)
Решение
Определите переменные. м = 50 кг,
v2=12мс, иv1=8мсv2=12мс, иv1=8мс
9,1
Замена.
W=1250(122−82)=2000 JW=1250(122−82)=2000 Дж
9.2
Обсуждение
Работа над объектом или системой увеличивает ее энергию. В этом случае увеличивается кинетическая энергия фигуриста. Отсюда следует, что прирост энергии должен быть равен разнице КЭ до и после толчка.
Советы для успеха
Эта задача иллюстрирует общий метод решения задач, требующих применения формул: определить неизвестные и известные переменные, выразить неизвестные переменные через известные переменные, а затем ввести все известные значения.
Поддержка учителей
Поддержка учителей
Определите три переменные и выберите соответствующее уравнение. Различайте начальную и конечную скорость и обращайте внимание на знак минус.
Определите переменные. м = 50 кг,
v2=12мс, иv1=8мсv2=12мс, иv1=8мс
Замена.
W=1250(122−82)=2000 JW=1250(122−82)=2000 J
Практические задачи
1.
(кредит: модификация работы Pass My Exams, CC BY-SA 4.0)Рисунок 9.6
Тяжелоатлет поднимает с пола штангу массой 200 Н на высоту 2 м. Сколько работы сделано?
0\,\текст{J}
100\,\text{J}
200\,\text{J}
400\,\text{J}
2.
Определите, какое из следующих действий генерирует больше энергии. Показать свою работу.
- перенос телевизора 100\,\text{N} на второй этаж через 50\,\text{s} или
- нести 24\,\text{N} арбуз на второй этаж в 10\,\text{s}?
Перенос телевизора весом 100\,\text{N} генерирует больше энергии, чем перенос арбуза весом 24\,\text{N} на ту же высоту, потому что мощность определяется как проделанная работа, умноженная на временной интервал.
Перенос телевизора весом 100\,\text{N} генерирует больше энергии, чем перенос арбуза весом 24\,\text{N} на ту же высоту, потому что мощность определяется как отношение выполненной работы к интервалу времени.
Перенос 24\,\text{N} арбуза генерирует больше энергии, чем перенос 100\,\text{N} телевизора на ту же высоту, потому что мощность определяется как проделанная работа, умноженная на временной интервал.

Перенос 24\,\text{N} арбуза генерирует больше энергии, чем перенос 100\,\text{N} телевизора на ту же высоту, потому что мощность определяется как отношение выполненной работы к временному интервалу.
Проверьте свое понимание
3.
Укажите два свойства, которые выражаются в джоулях.
работа и сила
энергия и вес
работа и энергия
вес и сила
4.
Когда кокос падает с дерева, над ним совершается работа W , когда он падает на пляж. Эта работа описывается уравнением
W= Fd = 12mv22−12mv12.W= Fd = 12mv22−12mv12.
9.3
Определите количества F , d , m , v 1 и v 2 в этом событии.
- F — сила тяжести, равная весу кокоса, d — расстояние, на которое падает орех, м — масса земли, v 1 — начальная скорость, а 90 590 v 90 004 90 597 2 90 598 — скорость, с которой он достигает берега.
- F — сила тяжести, равная весу кокоса, d — расстояние, на которое падает орех, м — масса кокоса, v 1 — начальная скорость, а v 2 — скорость, с которой он достигает берега.

- F — сила тяжести, равная весу кокоса, d — расстояние, на которое падает орех, м — масса земли, v 1 — скорость с которой он попадает на берег, а v 2 — начальная скорость.
- F — сила тяжести, равная весу кокоса, d — расстояние, на которое падает орех, м — масса кокоса, v 1 — скорость, с которой он падает на пляж, v 2 — начальная скорость.
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверить ваше понимание», чтобы оценить достижение учащимися учебных целей раздела. Если учащиеся испытывают трудности с выполнением определенной задачи, функция «Проверить понимание» поможет определить, какая из них, и направит учащихся к соответствующему содержанию.
Выполненная работа – определение, формула, примеры и важные часто задаваемые вопросы
В нашей повседневной жизни мы наблюдаем различные виды работы, начиная с пробуждения и заканчивая толканием газонного катка и так далее. Вы замечаете что-то во всей работе, которую делаете ежедневно? Кроме того, есть ли что-то, что нам нужно сделать для выполнения какой-либо работы? Что ж, нужна сила. Чтобы определить, если мы толкаем коробку на некоторое расстояние «d», применяя силу «F», мы совершаем некоторую работу, и умножение Силы на «d» — это проделанная работа.
Следовательно, для каждой работы, которую мы делаем, нам нужна сила или работа выполняется, когда сила что-то двигает.
Работа по физике
Когда мы толкаем блок с некоторой силой F, тело движется с некоторым ускорением или, кроме того, его скорость возрастает или падает в зависимости от направления силы. По мере увеличения или уменьшения скорости кинетическая энергия системы изменяется. Мы знаем, что энергия не может быть ни сформирована, ни разрушена, поэтому энергия должна быть преобразована в какую-то другую форму. В этой позиции это называется выполненной работой. Энергия уменьшается, когда завершается отрицательная энергия, и энергия увеличивается, когда завершается положительная работа. Теперь мы поймем, как определить выполненную работу.
Мы знаем, что энергия не может быть ни сформирована, ни разрушена, поэтому энергия должна быть преобразована в какую-то другую форму. В этой позиции это называется выполненной работой. Энергия уменьшается, когда завершается отрицательная энергия, и энергия увеличивается, когда завершается положительная работа. Теперь мы поймем, как определить выполненную работу.
Определение выполненной работы
Произведенная работа определяется таким образом, что она включает в себя как силы, действующие на тело, так и полное перемещение тела.
Этому блоку предшествует постоянная сила F. Цель этой силы состоит в том, чтобы переместить тело на определенное расстояние d по прямой траектории в направлении действия силы.
(Изображение будет загружено в ближайшее время)
Теперь давайте проделаем работу по выводу.
Какая работа совершается для движения блока?
Рассмотрим блок, расположенный на горизонтальной поверхности без трения.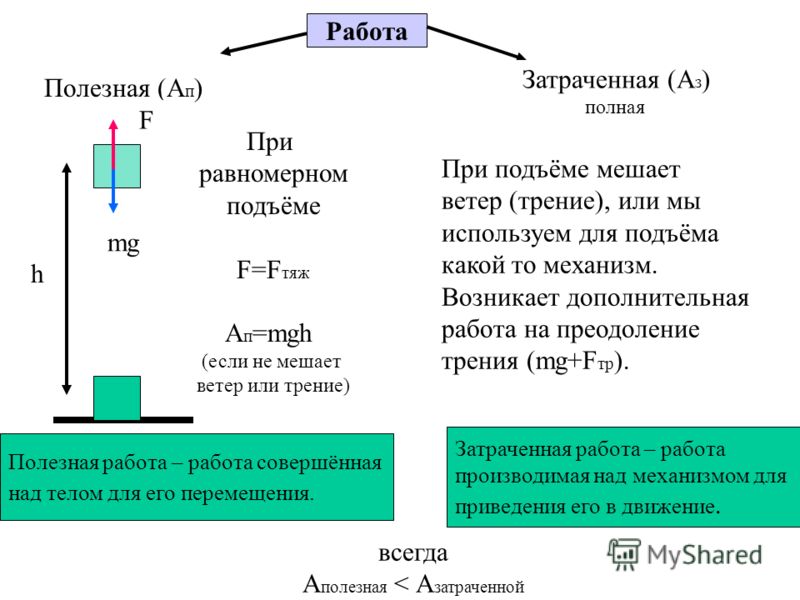 На этот брусок действует постоянная сила F. Цель этой силы состоит в том, чтобы переместить тело на определенное расстояние по прямой траектории в направлении действия силы.
На этот брусок действует постоянная сила F. Цель этой силы состоит в том, чтобы переместить тело на определенное расстояние по прямой траектории в направлении действия силы.
Теперь полная работа, выполненная этой силой, равна произведению величины приложенной силы на расстояние, пройденное телом. С научной точки зрения формула выполненной работы будет выглядеть так:
W = F * d
В этом случае сила, действующая на блок, постоянна, но направление силы и направление смещения, на которое воздействует эта сила, различны. Здесь сила F реагирует под углом θ на перемещение d. 9{2})\] ……..(1)
Мы знаем, что согласно третьему уравнению движения: v2 – u2= 2as …..(2)
Подставляя уравнение (2) в (1), получаем:
\[W=\frac{1}{2}m(2as)\]
\[W=m\times a \times s\]
Из уравнения второго закона Ньютона мы знаем, что F = ma (подставляя теперь о Ф).
\[W=F. s\]
s\]
Так как К.Е. это работа, совершаемая силой F, поэтому W = F.s
Работа, совершаемая системой
При описании работы мы подчеркиваем, что система не воздействует на свое окружение.
Таким образом, мы выражаем работу как положительную, когда система прилагает какое-либо усилие к окружающей среде (т. е. энергия покидает систему). Работа отрицательна, если над системой совершается работа (т. е. энергия, добавленная к системе).
(Изображение будет загружено в ближайшее время)
Виды выполненных работ
Например, когда мяч подбрасывается вверх, смещение будет направлено вверх; однако сила гравитации земли будет направлена вниз.
Например, когда мы сильно упираемся в стену, сила, которую мы прикладываем к стене, не работает, потому что в этом случае смещение стены равно d = 0.
Соотношение выполненной работы и энергии
Чтобы переместить предмет, ему нужно передать энергию. Передача энергии может осуществляться методом силы. Это количество энергии, переданное силой для перемещения объекта, называется выполненной работой. Следовательно, отношение между Работой и Энергией связано напрямую.
Передача энергии может осуществляться методом силы. Это количество энергии, переданное силой для перемещения объекта, называется выполненной работой. Следовательно, отношение между Работой и Энергией связано напрямую.
(Изображение скоро будет загружено)
Мы пришли к выводу, что работа и энергия прямо пропорциональны друг другу. Работа, совершаемая объектом, может быть научно выражена следующим образом:
W = \[\frac{1}{2}\]mvf2 – \[\frac{1}{2}\]mui2
Где
m = масса объекта измеряется в килограммах.
Вт = работа, выполненная объектом, измеряемая в джоулях.
vf = конечная скорость объекта, измеренная в м/с.
vi = начальная скорость объекта, измеренная в м/с.
Следовательно, принцип работы-энергии утверждает, что:
Суммарная работа всех сил, действующих на частицу, или работа равнодействующей силы F (в нижнем индексе равнодействующая) эквивалентна изменению кинетической энергии частицы .
Ньютоновская механика – Почему работа зависит от расстояния?
$\begingroup$
Итак, формула работы $$ \left[\text{work}\right] ~=~ \left[\text{force}\right] \, \times \, \left[\text{расстояние}\right] \,. $$
Я пытаюсь понять, как это представляет энергию.
Если я нахожусь в вакууме и толкаю блок с силой $1 \, \mathrm{N},$, он будет двигаться вперед бесконечно. Так что, пока я жду достаточно долго, расстояние будет увеличиваться. Кажется, это означает, что чем дольше я жду, тем больше работы (энергии) было приложено к блоку.
Должно быть, я что-то упускаю, но не могу точно определить, что именно.
Это действительно имеет смысл только тогда, когда я думаю о противоположном сценарии: при замедлении блока, который (изначально) движется с постоянной скоростью.
- ньютоновская механика
- силы
- работа
- определение
- расстояние
$\endgroup$
7
$\begingroup$
Вы должны положить расстояние, на которое действует сила. Если вы отпустите силу, работа не будет совершена, так как на тело не действует никакая сила.
Если вы отпустите силу, работа не будет совершена, так как на тело не действует никакая сила.
$\endgroup$
$\begingroup$
Часто важно знать, является ли данная формула упрощением более общего уравнения, и, когда вы сталкиваетесь с концептуальной проблемой, проверить общую формулу. В данном случае это упрощение этой формулы: $$W=\int_S F\cdot ds $$ Где $S$ — путь, над которым мы работаем, а $ds$ — бесконечно малый отрезок пути $S$.
Итак, вернемся к вашему вопросу: везде, где $F=0$, подынтегральная функция равна $0$ независимо от длины этого отрезка пути. Таким образом, работа выполнена только в том первом сегменте, где вы применяете 1N. Как только вы прекращаете толкать, расстояние увеличивается, но работа не увеличивается.
$\endgroup$
4
$\begingroup$
Если я нахожусь в вакууме и толкаю блок с силой 1 Н, он будет двигаться вперед бесконечно
и ускорить блок, т. е. изменить скорость блока и, следовательно, изменить кинетическую энергию блока.
е. изменить скорость блока и, следовательно, изменить кинетическую энергию блока.
Чем дольше вы прикладываете силу, тем больше работы совершает сила, что приводит к большему изменению кинетической энергии блока.
$\endgroup$
1
$\begingroup$
Это концептуальный ответ для учащихся, а не строгий ответ.
Как узнать, что вы что-то передвинули?
Итак, мы определяем «работу» как продукт этих двух вещей.
Физики вскоре обнаружили, что это определение действительно полезно для расчета поведения систем. Когда вы работаете над объектом, у вас отнимается такое же количество работы. Таким образом, общий объем работы, которая была выполнена (или может быть выполнена) внутри системы, остается постоянной величиной.
Из этой простой концепции вы можете разработать более строгое определение:
- 905:18 Расстояние имеет смысл только в течение интервала, к которому применяется ваша сила.
- Положительная работа означает «добавление» к движению объекта. Отрицательная работа означает «устранение» движения объекта.
- Сила может быть направлена под углом к расстоянию (введите скалярное произведение).
- Сила может меняться (ввести интеграл по расстоянию).
- Мы можем говорить о работе, которая была сделана в прошлом, и о способности выполнять работу в будущем (энергия). 92$ и др.).
- Мы можем более строго исследовать сохранение энергии.
 Любое продолжающееся движение по инерции не считается вашей работой.
Любое продолжающееся движение по инерции не считается вашей работой.$\endgroup$
$\begingroup$
Работа – это определение, поэтому причина в том, “потому что она так определена”.
Однако мы можем спросить , почему имеет смысл определять его таким образом. Интуитивно вы хотели бы думать о «работе» как о мере того, что вы делаете, когда толкаете, скажем, коробку по пандусу, что заставляет вас уставать.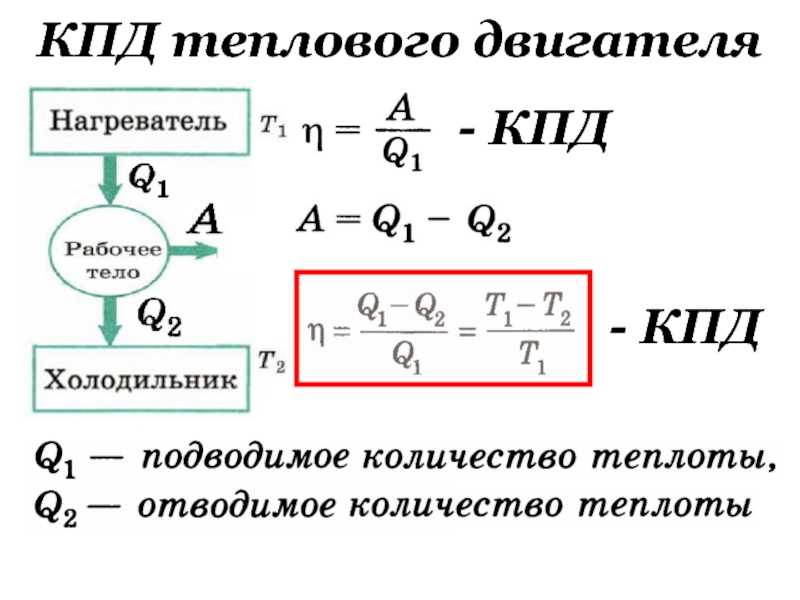 При этом вы прикладываете силу к ящику, а также перемещаетесь на расстояние, и если ящик тяжелее (т.е. вам нужно приложить больше силы) или расстояние, на которое вы должны его толкнуть (длина пандуса), дольше, то вы хотели бы сказать, что работа больше. Если мне придется толкать в два раза сильнее на то же расстояние или мне придется толкать в два раза дольше, «интуитивно» я должен рассчитывать на вдвое большую работу, и, таким образом, мы получаем
При этом вы прикладываете силу к ящику, а также перемещаетесь на расстояние, и если ящик тяжелее (т.е. вам нужно приложить больше силы) или расстояние, на которое вы должны его толкнуть (длина пандуса), дольше, то вы хотели бы сказать, что работа больше. Если мне придется толкать в два раза сильнее на то же расстояние или мне придется толкать в два раза дольше, «интуитивно» я должен рассчитывать на вдвое большую работу, и, таким образом, мы получаем
$$\mathrm{Работа} = \mathrm{Сила} \cdot \mathrm{Расстояние}$$
И эта простая, интуитивная идея, как оказалось, имеет большой физический смысл, когда мы ее используем на самом деле, далеко за пределами какими бы ограничениями ни обладала первоначальная интуиция (например, биологическая неспособность наших собственных тел выполнять «работу»), таким образом, мы сохраняем ее. В частности, это приводит нас к концепции кинетической и потенциальной энергии, и их общая сумма в конечном итоге сохраняется, тем самым показывая, что мы наткнулись на основную физическую концепцию Вселенной. На самом деле нет большего «почему», чем это — это наука. Наука — это применение интуиции или воображения, доказательств и рассуждений вместе, чтобы понять, как устроен мир. Интуиция и воображение генерируют идеи о том, что происходит, из которых мы можем сделать вывод о последствиях, а затем мы используем доказательства, чтобы увидеть, подтверждаются ли эти последствия и, таким образом, связаны ли наши идеи с реальностью.
На самом деле нет большего «почему», чем это — это наука. Наука — это применение интуиции или воображения, доказательств и рассуждений вместе, чтобы понять, как устроен мир. Интуиция и воображение генерируют идеи о том, что происходит, из которых мы можем сделать вывод о последствиях, а затем мы используем доказательства, чтобы увидеть, подтверждаются ли эти последствия и, таким образом, связаны ли наши идеи с реальностью.
$\endgroup$
$\begingroup$
Когда груз стоит на полу, пол действует на вес (и наоборот), но не на расстояние. И должно быть интуитивно понятно, что никакой работы не делается.
Для вашего примера груз в вакууме: если вы толкнете его с силой 1 Н на расстояние 1 м, а затем перестанете толкать, он будет двигаться вечно с постоянной скоростью. Если вы толкнете другой блок с силой 1 Н на расстояние 2 м, он будет двигаться вечно с более высокой постоянной скоростью. Вы проделали с ним больше работы, поэтому у него больше кинетической энергии.
Вы проделали с ним больше работы, поэтому у него больше кинетической энергии.
$\endgroup$
$\begingroup$
Под единицей работы понимается то, что вы делаете, когда поднимаете килограмм на высоту метра. Как сделать 2 единицы работы? Вы поднимаете этот килограмм на 2 метра. 3 единицы? 3 метра. И т. д. Если вы что-то поднимаете, работа, которую вы совершаете, — это сила, которую вы прилагаете, умноженная на пройденное расстояние (поднятую высоту).
В вашем примере с толканием тела в вакууме вы выполняете работу только тогда, когда на самом деле толкаете, и таким образом заставляете его двигаться быстрее. Если вы позволите ему двигаться по инерции, вы не будете выполнять работу, потому что сила в это время равна нулю.
Затрачиваемая вами работа — это изменение энергии объекта. Когда вы поднимаете вес, проделанная вами работа превращается в потенциальную энергию (запасенную энергию). Когда вы толкаете объект в пространстве, ваша работа становится кинетической энергией (энергией движения). Вы можете изменить потенциальную энергию на кинетическую, позволив предмету упасть, и, очевидно, он будет падать быстрее после того, как упадет на большую высоту.
Когда вы толкаете объект в пространстве, ваша работа становится кинетической энергией (энергией движения). Вы можете изменить потенциальную энергию на кинетическую, позволив предмету упасть, и, очевидно, он будет падать быстрее после того, как упадет на большую высоту.
$\endgroup$
2
$\begingroup$
Я вижу несколько ответов, которые, кажется, все объясняют, но для тех, кто пытается понять почему, возможно, лучше ответить просто.
Для меня будет намного больше «работы», чтобы вытолкнуть тяжелый мусорный бак из двери и по подъездной дорожке, чем для меня, чтобы просто вытолкнуть мусорный бак из дома.
$\endgroup$
1
$\begingroup$
Другие ответы касались недоразумений, связанных с уравнением $W=F \cdot d$. Думаю, стоит также отметить, что «пройденное расстояние» — это не форма энергии. В физике фраза «совершать работу» означает преобразование энергии из одной формы в другую, поэтому вам не нужно совершать какую-либо работу, чтобы путешествовать на бесконечное расстояние. Вам нужно только совершить работу в начале, чтобы получить кинетическую энергию. 92}{2} \\
v_f L = v_0 + \frac{F}{m}t
$$
Думаю, стоит также отметить, что «пройденное расстояние» — это не форма энергии. В физике фраза «совершать работу» означает преобразование энергии из одной формы в другую, поэтому вам не нужно совершать какую-либо работу, чтобы путешествовать на бесконечное расстояние. Вам нужно только совершить работу в начале, чтобы получить кинетическую энергию. 92}{2} \\
v_f L = v_0 + \frac{F}{m}t
$$
Играя с этими двумя последними выражениями, мы можем заключить, что:
$$ LF = \Дельта E $$
F: сила, L: расстояние, m: масса, $v_f$: конечная скорость, $v_0$: начальная скорость, t: конечное время.
Еще одно хорошее более дифференцированное объяснение этого: https://physics.stackexchange.com/a/79529/31891
$$ F = \frac{dp}{dt} \\ F = \ frac {d} {dt} (\ sqrt {2 м E}) = \ frac {\ sqrt {2 м}} {2 \ sqrt {E}} \ frac {dE} {dt} = \ frac {m }{p} \frac{dE}{dt}=\frac{1}{v}\frac{dE}{dt}=\frac{dt}{dx}\frac{dE}{dt}=\frac{ dE}{dx} $$
$\endgroup$
$\begingroup$
Сила, по Аристотелю, есть то, что применяется к чему-то, что может измениться, действительно изменяется.
Поскольку изменение — это прежде всего движение, это означает, что движение переходит от естественного движения (т. е. движения по инерции) к насильственному движению, которое происходит при приложении силы (неинерционное или ускоренное движение).
Более того, мы видим, что сила, приложенная к чему-либо и не вызывающая изменения, не является силой. В нашем мире таких сил нет, силы всегда вызывают изменение, даже если это изменение незаметно или находится в равновесии.
Теперь, когда мы прикладываем силу к деревянному блоку, он движется. Если нам нужна мера этого изменения, то есть только две переменные, на которые мы можем обратить внимание: пройденное расстояние и скорость. Из первого мы можем построить работу, а из второго — кинетическую энергию. Получается, что в нашем мире изменение кинетической энергии бруска равно работе, совершаемой над бруском. Теперь в любой изменяющейся ситуации всегда стоит искать то, что не меняется. Это равенство не меняется, это инвариант. Это также предшественник принципа сохранения энергии — одного из основных принципов физики. И это одна из веских причин взглянуть на эти понятия в их традиционном определении.
Это также предшественник принципа сохранения энергии — одного из основных принципов физики. И это одна из веских причин взглянуть на эти понятия в их традиционном определении.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
уравнений в физике: значение и расчет
Какая польза от уравнений в реальном мире? Почему физики описывают физику на языке математических уравнений? Что такого особенного в математике, что мы можем использовать ее в окружающем нас мире? Какие есть примеры физических уравнений, что они нам говорят и как мы их решаем? Узнайте об этом в этой статье!
Определение уравнения в физике
Существует определение уравнения (будь то в физике или нет), но оно очень техническое и совсем не информативное. что мы может сказать об уравнениях физики то, что они делают . Уравнения в физике описывают отношения между физическими величинами. Уравнение всегда содержит знак «равно», =.
В физике есть уравнение, описывающее зависимость между вашей скоростью, продолжительностью вашего путешествия и пройденным расстоянием. Чем больше ваша скорость, тем большее расстояние вы преодолеваете за то же время. Уравнение скажет:. Мы видим, что удвоение времени в пути означает удвоение пройденного расстояния, если скорость остается неизменной, и что удвоение скорости означает удвоение пройденного расстояния, если время в пути остается прежним.
Уравнение скажет:. Мы видим, что удвоение времени в пути означает удвоение пройденного расстояния, если скорость остается неизменной, и что удвоение скорости означает удвоение пройденного расстояния, если время в пути остается прежним.
Уравнение физики, которое мы ввели выше, выглядит немного неясным: букв так много, что отношения (знаки умножения и равенства) отходят на второй план. Однако отношения очень важны в физике. Вот почему люди присваивают символы количествам. Важно объяснить другим людям, что означают ваши символы, и удобно использовать стандартные символы для вещей, которые имеют стандартные символы.
Чтобы уравнение выглядело яснее, мы можем дать названия величинам, участвующим в задаче. Предположим, что пройденное расстояние (для расстояния), наша скорость (для скорости) и продолжительность нашего путешествия (для времени). Уравнение сейчас.
Мы опустили крестик умножения, потому что ясно, что это две разные вещи. Ничего не помещая между двумя величинами, мы умножаем их. Это уравнение выглядит намного яснее, и нетрудно сразу же вспомнить, что означает, например, расстояние. Это хорошо, мы только что записали уравнение физики!
Это уравнение выглядит намного яснее, и нетрудно сразу же вспомнить, что означает, например, расстояние. Это хорошо, мы только что записали уравнение физики!
Уравнение, которое всегда верно (также называемое тавтологией), StudySmarter Originals.
Типы физических уравнений
У вас может сложиться впечатление, что существует много разных типов физических уравнений, потому что все они выглядят по-разному. Хотя верно, что во многих областях физики есть свои собственные уравнения, каждое уравнение в физике имеет одну и ту же цель, а именно описание отношения между величинами. Однако мы можем провести различие между уравнениями, основываясь на том, как представляются величины в уравнении, как показывают следующие примеры.
- Линейное уравнение содержит величины только в первой степени, например уравнение для расстояния,.
- Квадратное уравнение также содержит величины, возведенные в квадрат, например уравнение кинетической энергии,.
У нас также есть дифференциальные уравнения (содержащие производные величин), тензорные уравнения (содержащие величины с несколькими входными данными, как и векторы) и многие другие способы, которыми величины могут появляться в уравнениях.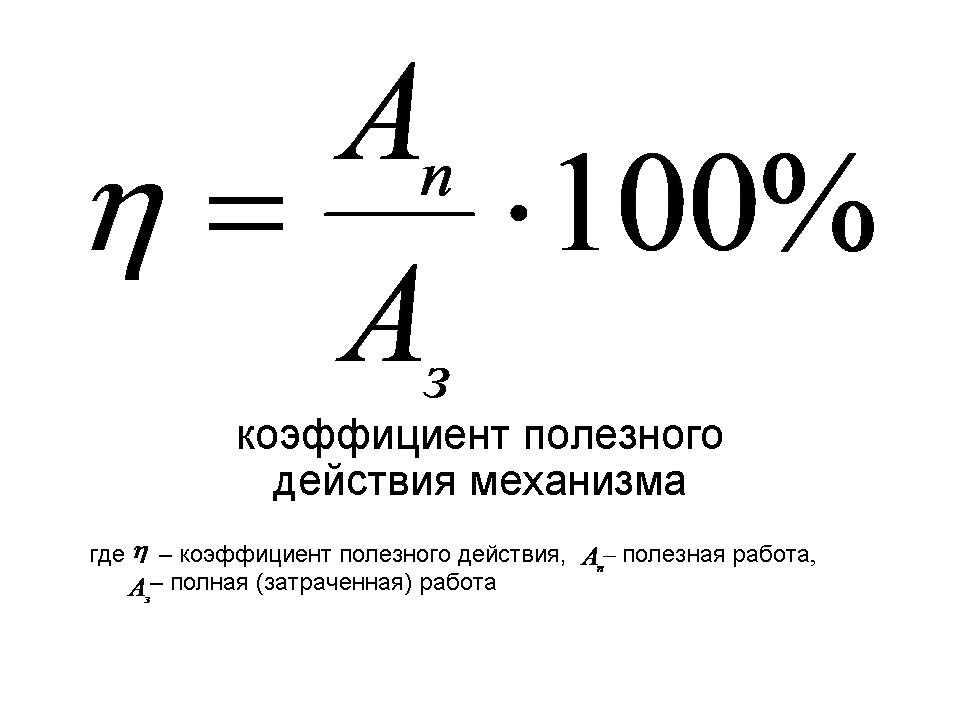
Примеры физических уравнений
Уравнения Эйнштейна о гравитации, StudySmarter Originals.
Соотношение между силой, которую вы прикладываете к объекту, массой объекта и скоростью, с которой объект будет ускоряться (описывается ускорением ) в результате приложения силы, задается уравнением
Это Второй закон Ньютона. Например, мы видим, что нам нужно приложить большую силу, чтобы произошло большее ускорение, или чтобы сдвинуть объект с большей массой с тем же ускорением.
Связь между кинетической энергией объекта, его массой и скоростью определяется уравнением
.
Это говорит нам о том, что удвоение массы объекта приведет к удвоению его кинетической энергии, а удвоение его скорости приведет к четырехкратному увеличению его кинетической энергии. Чтобы убедиться в этом, предположим, что конечная скорость в два раза больше начальной скорости, т. е. Тогда конечная энергия, деленная на начальную энергию, равна
.
Мы видим, что энергия действительно увеличивается в четыре раза, если скорость удваивается. Это основная причина того, почему автомобиль разгоняется медленнее на высоких скоростях, чем на низких: ему нужно добавить больше энергии, чтобы получить ту же скорость из-за квадрата в уравнении выше!
Это основная причина того, почему автомобиль разгоняется медленнее на высоких скоростях, чем на низких: ему нужно добавить больше энергии, чтобы получить ту же скорость из-за квадрата в уравнении выше!
Мы видели большое количество физических уравнений, но теперь пришло время поработать с ними и решить их.
Решение уравнений в физике
Эдвард Виттен пишет уравнения по теории струн на доске, Wikimedia Commons Public Domain.
Решение уравнений в физике очень похоже на решение уравнений в математике, за исключением двух основных отличий.
- В физике всегда есть контекст, поэтому физическое уравнение следует из небольшой истории. Мы должны распаковать историю и преобразовать ее в разрешимое уравнение.
- Мы должны быть осторожны с юнитами. В общем, мы включаем единицы в все расчеты .
Давайте посмотрим, как это работает на примере задачи.
В: Джон всегда ходит со скоростью (миль в час). В прошлое воскресенье он гулял по городу и в итоге покрыл в общей сложности. Сколько времени у него ушло?
В прошлое воскресенье он гулял по городу и в итоге покрыл в общей сложности. Сколько времени у него ушло?
A: Первый шаг — преобразовать эту историю в разрешимое уравнение. Начнем с присвоения имен нужным нам величинам. Мы называем скорость ходьбы Джона, пройденное им расстояние и время, которое ему потребовалось. Тот факт, что это было воскресенье и что он гулял по городу, не имеет значения для вопроса. Из рассказа мы знаем и то, и то. Теперь нам нужно найти уравнение, которое относится к и . К счастью, мы это знаем. Как и в случае с математическими уравнениями, мы изолируем, разделив обе части на , и у нас остается уравнение. Мы знаем и, значит, это разрешимое уравнение, значит, шаг 1 выполнен! Давайте решим ее, соблюдая осторожность с единицами измерения. Заполняем:
.
Теперь давайте обязательно ответим на вопрос полностью. Джону потребовалось 3 часа (чтобы прогуляться по городу в прошлое воскресенье).
В приведенном выше примере у нас не было проблем с единицами измерения, потому что информация, предоставленная нам, была в единицах, которые «хорошо сочетаются друг с другом». Если это не так, нам придется использовать наши знания о преобразованиях единиц измерения, как показано в примере ниже.
Если это не так, нам придется использовать наши знания о преобразованиях единиц измерения, как показано в примере ниже.
В: Анна хочет толкнуть машину, о которой мы можем предположить, что она не имеет трения и не находится ни на каком уклоне. Она толкает с силой, масса автомобиля равна, а масса Анны равна. Каково ускорение автомобиля?
A: Мы называем приложенную силу, массу автомобиля , ускорение автомобиля и массу Анны. Мы это знаем, поэтому изолируем ускорение и получаем уравнение. Мы знаем и, поэтому шаг 1 выполнен.
Решим, заполнив данные (включая единицы!):
Мы видим, что нам понадобилось преобразование между кг и фунтами, именно это, чтобы ответить на вопрос. Ответ заключается в том, что ускорение автомобиля равно .
Надеюсь, эти примеры прояснили, как язык математических уравнений полезен в реальном (физическом) мире.
Резюме: шаг за шагом
- Читая вопрос, дайте названия указанным величинам и запишите их значения (с указанием единиц).

- Определите, какую величину вам нужно знать, чтобы ответить на вопрос, и запишите уравнение физики, связывающее эту величину с записанными вами величинами.
- Решите уравнение (будьте осторожны с единицами измерения) и ответьте на вопрос полным предложением и с правильными единицами измерения.
Уравнения движения в физике
Уравнение Шредингера, описывающее квантовую механику, StudySmarter Originals.
В конце концов, все, к чему стремится физика, — это предсказывать движение объектов. Следовательно, мы можем утверждать, что все уравнения в физике в некотором роде являются уравнениями движения. Однако некоторые уравнения описывают только движение объектов, а не причины движения. Давайте посмотрим на эти уравнения.
Сначала рассмотрим уравнение, описывающее движение с постоянной скоростью. Для начальной точки, скорости и продолжительности движения местоположение объекта задается как
.
Ранее мы знали, что пройденное расстояние равно, поэтому это логично: местоположение объекта равно его начальному местоположению плюс пройденное расстояние.
Объект также может ускоряться. Для постоянного ускорения, начальной скорости, начальной точки и продолжительности движения местоположение объекта определяется как
.
У нас уже есть некоторое интуитивное представление о том, почему он здесь, но давайте рассмотрим остальное. Скорость, полученная через время, равна, поэтому через время скорость нашего объекта равна. Это означает, что средняя скорость нашего объекта равна среднему значению и , т.е. Пройденное расстояние равно
,
, и мы приходим к приведенному выше уравнению! Обратите внимание, что для нулевого ускорения мы снова приходим к уравнению для постоянной скорости, что и ожидаем найти.
Уравнения в физике – основные выводы
- Уравнение в физике описывает отношение между физическими величинами.
- Уравнение всегда содержит знак “равно” =.
- Мы присваиваем значениям символы, чтобы уравнения были читабельными.
- Решение уравнений в физике во многом похоже на решение уравнений в математике, с двумя отличиями:
- Часто нам приходится самим составлять уравнения из рассказа.

- Часто нам приходится самим составлять уравнения из рассказа.


 Чтобы узнать КПД котла, который функционирует на органическом топливе, используется низшая теплота сгорания.
Чтобы узнать КПД котла, который функционирует на органическом топливе, используется низшая теплота сгорания.




 Если используется подвижный блок, совершается дополнительная работа: поднимается блок с верёвкой, преодолеваются силы трения в блоке.
Если используется подвижный блок, совершается дополнительная работа: поднимается блок с верёвкой, преодолеваются силы трения в блоке.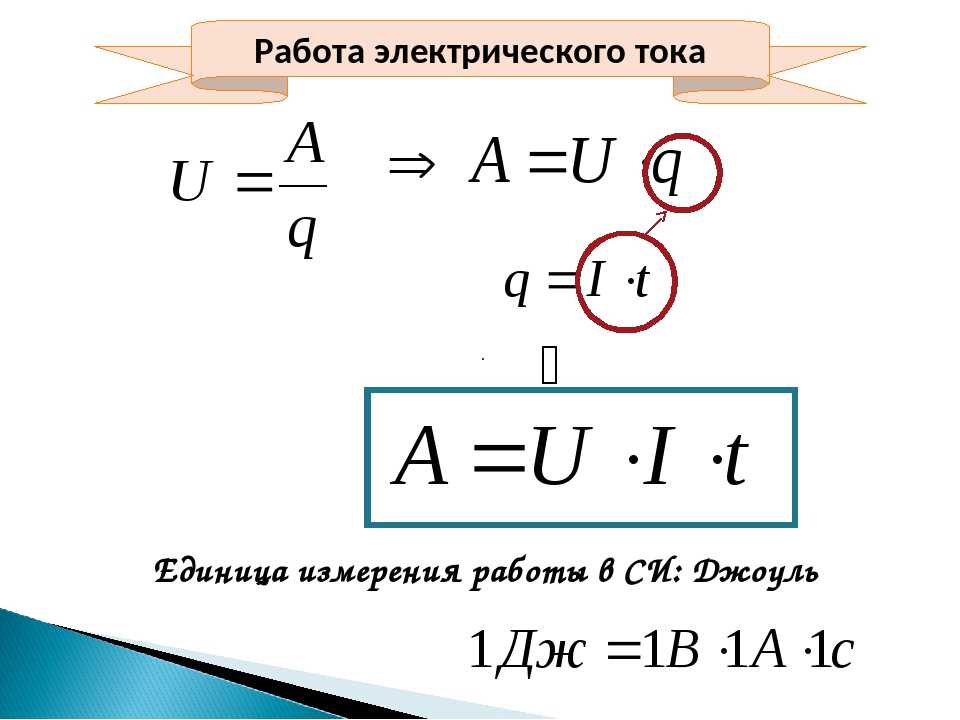
 Чтобы ехать на велосипеде, вы тратите мышечную энергию, крутя педали. Для движения автомобиля используется энергия сжигаемого топлива (бензина, нефти или газа).
Чтобы ехать на велосипеде, вы тратите мышечную энергию, крутя педали. Для движения автомобиля используется энергия сжигаемого топлива (бензина, нефти или газа).
 При использовании подвижного шкива совершается дополнительная работа: шкив с канатом поднимается и преодолеваются силы трения на шкиве.
При использовании подвижного шкива совершается дополнительная работа: шкив с канатом поднимается и преодолеваются силы трения на шкиве.

 Ожидается, что студент:
Ожидается, что студент: Автомобиль американских горок на вершине холма обладает гравитационной потенциальной энергией.
Автомобиль американских горок на вершине холма обладает гравитационной потенциальной энергией.


