Работа с матрицами: Основные операции над матрицами (сложение, умножение, транспонирование) и их свойства.

Функциональное программирование на примере работы с матрицами из теории линейной алгебры / Хабр

Вступление

В основе работы с матрицами (в данной статье мы будем рассматривать только двумерные матрицы) лежит мощная математическая теория из области линейной алгебры. Одно определение или действие следует из другого, одна функция вызывает другую. Поэтому для программной реализации функционала математических операций над матрицами функциональные языки подходят очень хорошо. В рамках данной статьи мы рассмотрим конкретные примеры на языке F# и дадим подробные комментарии, как это работает. Так как F# входит в семейство .NET, то полученный функционал можно без каким либо проблем использовать в других императивный языках, например C#.

Определение матрицы и реализация на F#

Матрицы являются базовой и важнейшей частью линейной алгебры. Матрицы часто используются в программировании, например в 3D-моделировании или гейм-девелопинге. Разумеется, велосипед уже давно изобретен и необходимые фреймворки для работы с матрицами уже готовы, и их можно и нужно использовать. Данная статья не ставит своей целью изобретение нового фреймворка, но показывает реализацию базовых математических операций для работы с матрицами в функциональном стиле с использованием языка программирования F#. По мере рассмотрения материала мы будем обращаться к математической теории матриц и смотреть, как ее можно реализовать в коде.

Для начала вспомним, что такое матрица? Теория говорит нам следующее

Прямоугольная таблица чисел, содержащая m строк и n столбцов, называется матрицей размера m x n

Матрицы, как правило, обозначаются прописными буквами латинского алфавита и записываются в виде

Или коротко

Для работы с матрицами в F# создадим запись, основанную на двумерной таблице, которую в дальнейшем будем расширять полезными методами для того, чтобы совершать необходимые математические операции над ней.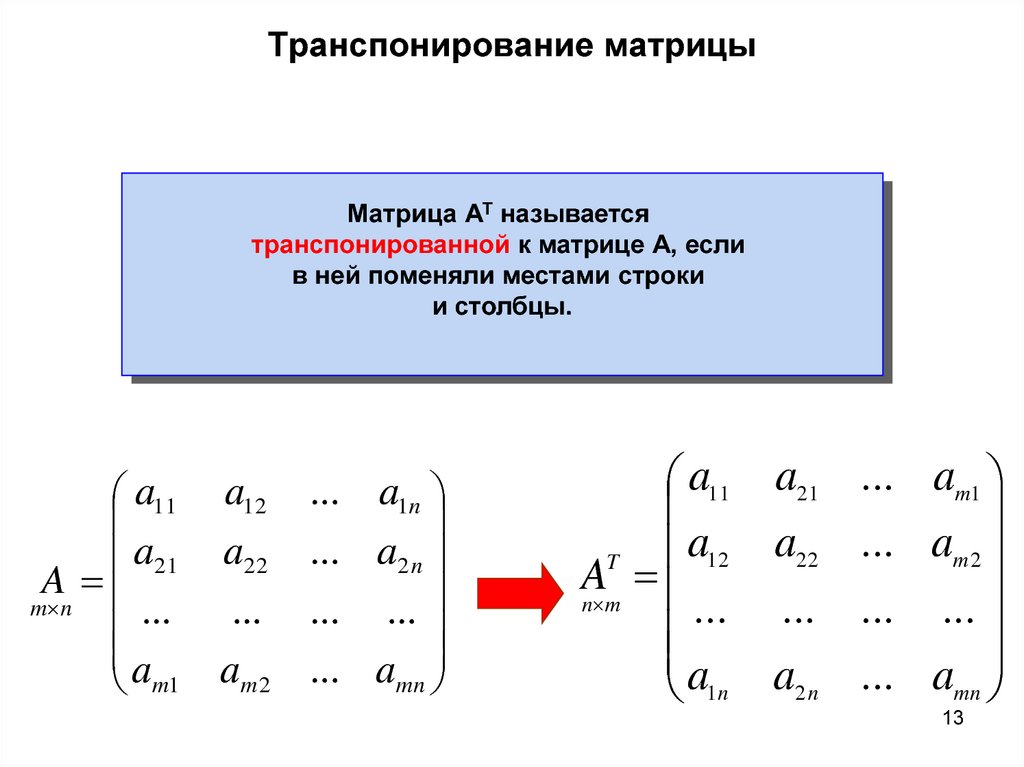

type Matrix = { values: int[,] }
    with
        // здесь будем добавлять методы
    end

Добавим вспомогательный метод для инициализации записи двумерным массивом

static member ofArray2D (values: int [,]) = 
    { values = values }

Входным аргументом функции будет двумерный массив, а на ее выходе — запись типа Matrix. Ниже приведем пример инициализации записи.

let a = array2D [[1;0;2]
                 [3;1;0]]
let A = Matrix.ofArray2D a

Две матрицы A=(aij) и B=(bij) называются равными, если они совпадают поэлементно, т.е. aij=bij для всех i=1,2…,m и j=1,2…n

Для реализации этого правила будем использовать переопределенный оператор == и добавим пару полезных функций, которые также понадобятся нам в дальнейшем.

static member sizes matrix =
    let rows = matrix.  values.[*,0].Length
    let cols = matrix.values.[0,*].Length
    (rows, cols)
static member isEquallySized matrix1 matrix2 =
    let dim1 = Matrix.sizes matrix1
    let dim2 = Matrix.sizes matrix2
    (dim1 = dim2)
static member (==) (matrix1, matrix2) =
    if not (Matrix.isEquallySized matrix1 matrix2) then false
    else
        not (matrix1.values
               |> Array2D.mapi (fun x y v -> if matrix2.values.[x, y] <> v then false else true)
               |> Seq.cast<bool>
               |> Seq.contains false)

Давайте подробнее рассмотрим код выше. Как можно заметить, здесь есть три функции. Первая функция sizes возвращает размерность матрицы в виде кортежа. Так как мы работаем только с прямоугольными матрицами, то для получения количества строк мы берем полный срез первой колонки и возвращаем ее длину.

let rows = matrix.values.[*,0].Length

Аналогичным способом работает определение количества колонок — получаем полный срез первой строки и возвращаем ее длину.

Следующая функция isEquallySized сравнивает размерность двух матриц и возвращает

true если они равны. Для этого она использует уже готовую функцию sizes и просто сравнивает результаты.

Оператор == для поэлементного сравнения двух матриц кажется сложнее, но сейчас вы увидите, что он также простой.

Перед тем, как сравнивать две матрицы, сравним их размерность. Если они не равны, то нет дальше смысла проводить проверку, так как уже понятно, что и матрицы будут не равны.

if not (Matrix.isEquallySized matrix1 matrix2) then false

Далее, на основе исходных матриц matrix1 и matrix2 мы формируем новую матрицу, заполненную true или false, в зависимости от того, совпадают ли соответствующие ячейки обеих матриц.

matrix1.values
|> Array2D.mapi (fun x y v -> if matrix2.values.[x, y] <> v then false else true

Функция Array2D. mapi перебирает все элементы matrix1 и передает в обработчик три параметра
x — индекс строки
y — индекс колонки
v — содержимое ячейки
Содержимое ячейки v мы сравниваем с соответствующей ячейкой matrix2 и если они равны, то пишем true, иначе — false.

Если есть хоть одна ячейка с элементом

false, то это означает, что матрицы не равны между собой.

Так как Array2D не содержит в себе методов для фильтрации или поиска, то реализуем это сами. Для этого разложим матрицу в линейный список

|> Seq.cast<bool>

И найдем хоть одно несовпадение

|> Seq.contains false

Функция Seq.contains вернет true если в разложенном списке будет найдено хоть одно значение false. Поэтому нам нужно инвертировать полученный результат, чтобы оператор == работал так, как мы хотим

else
    not (matrix1.  values
           |> Array2D.mapi (fun x y v -> if matrix2.values.[x, y] <> v then false else true)
           |> Seq.cast<bool>
           |> Seq.contains false)

Матрица O называется нулевой или нуль-матрицей, если все ее элементы равны нулю.

static member O rows cols =
    let array2d = Array2D.zeroCreate rows cols
    { values = array2d }

Пример использования этой функции

let AO = Matrix.O 5 5

Полагаю, что здесь нет ничего сложного, что требует пояснений, поэтому продолжаем.

Матрица, число строк которой равно числу столбцов и равно n, называется квадратной матрицей порядка n

Таким образом, квадратная матрица имеет вид.

В рамках этого правила мы создадим функцию, которая прямоугольную матрицу трансформирует в квадратную путем отсечения всех элементов, которые не попадают в квадрат.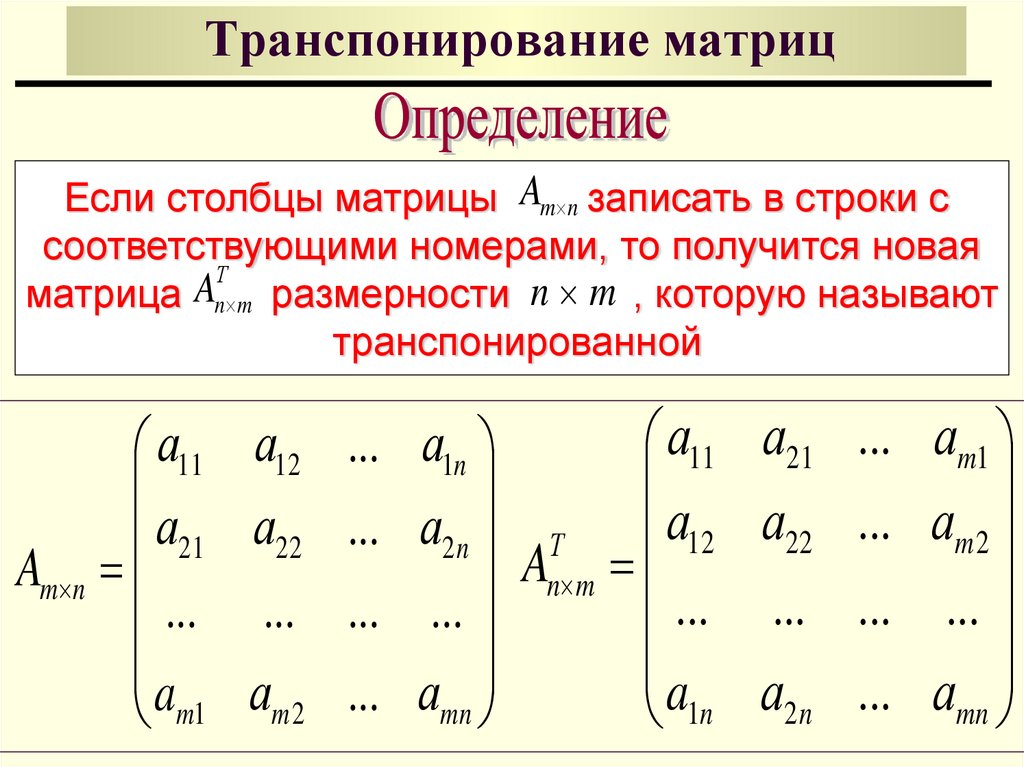

static member toSquare matrix =
    // получаем размерность исходной матрицы
    let dim = Matrix.sizes matrix
    // получаем количество колонок
    let colCount: int = snd dim
    // получаем количество строк
    let rowCount: int = fst dim
    // находим размер минимальной стороны
    let length = System.Math.Min (colCount, rowCount)
    // создаем пустой квадратный массив с размерностью
    // равной наименешей стороне исходной матрицу
    let zero = Array2D.zeroCreate length length
    // копируем исходную матрицу в квадратную
    let square = zero |> Array2D.mapi (fun x y _ -> matrix.values.[x, y])
    // позвращаем полученную матрицу
    { values = square }

Комментариев в исходном коде поясняют принцип работы функции, поэтому продолжим.

Квадратная матрица называется треугольной, если все ее элементы ниже главной диагонали равны нулю, т.е. треугольная матрица имеет вид

Ниже приведен код функции, который преобразует исходную матрицу в треугольную. Но в нашей функции мы будем работать с прямоугольной матрицей, то есть она может быть не квадратной. Читатель легко может модифицировать код функции так, чтобы она возвращала квадратную треугольную матрицу, используя функцию, которую мы рассмотрели ранее.

static member T matrix =
    let values = matrix.values |> Array2D.mapi (fun x y v -> if y < x then 0 else v)
    { values = values }

Функция Array2D.mapi преобразовывает исходный двумерный массив в новый при помощи обработчика, который принимает три параметра

x — номер строки
y — номер колонки
v — содержимое ячейки

if y < x then 0 else v

Здесь мы делаем проверку, находится ли элемент ниже главной диагонали и если да, то заполняем ячейку 0. В противном случае — исходным значение из входной матрицы.

Ниже приведен пример использования этой функции.

let a = array2D [[1;2;3]
                 [4;5;6]
                 [7;8;9]
                 [10;11;12]]
let A = Matrix. ofArray2D a
let R = Matrix.triangular A
printfn "origin = \n %A" A.values
printfn "triangular = \n %A" R.values

Получаем следующий результат

origin = 
 [[1; 2; 3]
 [4; 5; 6]
 [7; 8; 9]
 [10; 11; 12]]
triangular = 
 [[1; 2; 3]
 [0; 5; 6]
 [0; 0; 9]
 [0; 0; 0]]

Квадратная матрица называется диагональной, если все ее элементы, расположенные вне главной диагонали, равны нулю

static member D matrix =
    let diagonal = matrix.values |> Array2D.mapi (fun x y v -> if x <> y then 0 else v)
    { values = diagonal }

Эта функция очень похожа на предыдущую, отличается только условие проверки. Ниже пример использования

let a = array2D [[1;2;3]
                 [4;5;6]
                 [7;8;9]
                 [10;11;12]]
let A = Matrix.ofArray2D a
let R = Matrix.D A
printfn "origin = \n %A" A.values
printfn "diagonal = \n %A" R.values

origin = 
 [[1; 2; 3]
 [4; 5; 6]
 [7; 8; 9]
 [10; 11; 12]]
diagonal = 
 [[1; 0; 0]
 [0; 5; 0]
 [0; 0; 9]
 [0; 0; 0]]

Диагональная матрица является единичной и обозначается E, если все ее элементы, расположенные на главной диагонали, равны единице

Реализация такой матрицы на F# выглядит так

static member E rows cols =
    let array2d = Array2D. init rows cols (fun x y -> if x = y then 1 else 0)
    { values = array2d }

Операции над матрицами при помощи F#

Над матрицами, как и над числами, можно производить ряд действий, причем некоторые из них аналогичны операциям над числами, а некоторые — специфические.

Суммой двух матриц Amn=(aij)и Bmn=(bij)одинаковых размеров называется матрица того же размера A+B=Cmn=(cij), элементы которой равны сумме элементов матриц A и B, расположенных на соответствующих местах

Пример, для заданных матриц A и B находим сумму A+B

Рассмотрим код для сложения двух матриц

static member (+) (matrix1, matrix2) =
    if Matrix.isEquallySized matrix1 matrix2 then
        let array2d = matrix1.values |> Array2D.mapi (fun x y v -> matrix2.values.[x, y] + v)
        { values = array2d }
    else failwith "matrix1 is not equal to matrix2"

Перед тем, как складывать матрицы, нужно убедиться, что их размерность совпадает, в противном случае функция генерирует исключение. Ниже приведем пример использования данной функции

let a = array2D [[2;3]
                 [1;-5]
                 [0;6]]
let A = Matrix.ofArray2D a
let b = array2D [[-3;3]
                 [1;7]
                 [2;0]]
let B = Matrix.ofArray2D b
let R = A+B
printfn "A+B =\n %A" R.values

A+B =
 [[-1; 6]
 [2; 2]
 [2; 6]]

Произведением матрицы A=(aij) на число k называется матрица kA=(kaij) такого же размера, что и матрица A, полученная умножением всех элементов матрицы A на число k

Пример, для заданной матрицы A находим матрицу 3A

static member (*) (value, matrix) = 
    let array2d = matrix.values |> Array2D.mapi (fun _ _ v -> v * value)
    { values = array2d }

Матрицу -A=(-1)*A будем называть противоположной матрице A. Из этого определения плавно переходим к следующему

Разностью матриц A и B одинаковых размеров называется сумма матрицы A и матрицы, противоположной к B

static member (-) (matrix1: Matrix, matrix2: Matrix) = 
    if Matrix. isEquallySized matrix1 matrix2 then
        matrix1 + (-1)*matrix2
    else failwith "matrix1 is not equal to matrix2"

Две матрицы называются согласованными, если число столбцов первой равны числу строк второй

static member isMatched matrix1 matrix2 = 
    let row1Count = matrix1.values.[0,*].Length
    let col2Count = matrix2.values.[*,0].Length
    row1Count = col2Count

Проверка согласованности матриц требуется для их перемножения.

Произведением AB согласованных матриц Amn=(aij) и Bnp=(bjk) называется матрица Cmn=(cik), элемент cik которой вычисляется как сумма произведений элементов i-й строки матрицы A и соответствующих элементов k-го столбца матрицы B

Вычислить произведение матриц

Решение по определению произведения матриц

Рассмотрим код для умножения двух матриц

static member (*) (matrix1, (matrix2: Matrix)) =
    if Matrix. isMatched matrix1 matrix2 then
        let row1Count = matrix1.values.[*,0].Length
        let col2Count = matrix2.values.[0,*].Length
        let values = Array2D.zeroCreate row1Count col2Count
        for r in 0..row1Count-1 do
            for c in 0..col2Count-1 do
                let row = Array.toList matrix1.values.[r,*]
                let col = Array.toList matrix2.values.[*,c]
                let cell = List.fold2 (fun acc val1 val2 -> acc + (val1 * val2)) 0 row col
                values.[r,c] <- cell
        { values = values }
    else failwith "matrix1 is not matched to matrix2"

Давайте разберемся с кодом подробнее.
Перед умножением нужно убедиться, что матрицы являются согласованными

if Matrix.isMatched matrix1 matrix2 then

Итоговая матрица будет иметь размерность, в которой количество строк такое же, как у первой матрицы и количество столбцов такое же, как у второй матрицы

let row1Count = matrix1. values.[*,0].Length
let col2Count = matrix2.values.[0,*].Length
// формируем пустой двумерный массив для сохранения результатов умножения
let values = Array2D.zeroCreate row1Count col2Count

После этого мы последовательно перебираем все строки и все столбцы исходных матриц

for r in 0..row1Count-1 do
    for c in 0..col2Count-1 do
        let row = Array.toList matrix1.values.[r,*]
        let col = Array.toList matrix2.values.[*,c]

Вычисляем итоговое значение каждой ячейки

let cell = List.fold2 (fun acc val1 val2 -> acc + (val1 * val2)) 0 row col

Функция List.fold2 на вход получает два списка (строку и колонку) и передает в обработчик следующие параметры

acc — аккумулятор, содержащий результат предыдущего вычисления
val1 — содержимое ячейки из первого массива. В нашем случае это строка из первой матрицы
val2 — содержимое ячейки из второго массива, то есть колонки второй матрицы

Так как матрицы являются согласованными, то мы уверены, что у нас не произойдет выхода за пределы массивов.

Обработчик добавляет к аккумулятору произведение ячеек из строк и столбца и полученное значение будет передано следующей итерации. Таким образом конечным итогом работы функции List.fold2 будет итоговое значение произведений двух матриц. Остается только заполнить им предварительно созданную пустую матрицу

values.[r,c] <- cell

Которая вернется как результат

{ values = values }

Ниже приведем пример использования данной функции

let a = array2D [[1;0;2]
                 [3;1;0]]
let A = Matrix.ofArray2D a
let b = array2D [[-1;0]
                 [5;1]
                 [-2;0]]
let B = Matrix.ofArray2D b
let R = A*B
printfn "A*B =\n %A" R.values

A1*B1 =
 [[-5; 0]
 [2; 1]]

Если k ∈ N, то k-й степенью квадратной матрицы Aназывается произведение k матриц A

Рассмотрим код на F# для произведения матрицы в степень. Здесь будет использоваться хвостовая рекурсия для того, чтобы не переполнить стек при больших значениях степеней. Хвостовая рекурсия — это такая рекурсия, которая компилятором в итоге преобразуется в цикл. По возможности рекомендуется всегда использовать именно хвостовую рекурсию вместо обычной, но для этого нужно чтобы каждый кадр рекурсии возвращал итоговое вычисленное значение. Это значение обычно называется аккумулятором и передается в следующий кадр рекурсии. То есть, в отличие от обычной рекурсии, которая возвращает вычисленное значение вверх по стеку, хвостовая рекурсия передает вычисленное значение вниз по стеку. Каждый новый кадр рекурсии делает свои вычисления и добавляет их к уже ранее вычисленному значению, которое хранится в аккумуляторе. После того, как последний кадр рекурсии отработал, в аккумуляторе уже есть вычисленное значение, которое просто возвращается как результат.

Таким образом, компилятор может оптимизировать код и преобразовать его в обычный цикл.

// возводим матрицу в степень
// matrix - исходная матрица
// value - значение степени
static member (^^) (matrix, value) =
    // внутренняя функция, которая реализует хвостовую рекурсию
    // m - матрица
    // p = значение степени
    let inRecPow m p =
        // рекурсивная функция
        // acc - накопленный аккумулятор.  имеет тип Matrix
        // p - значение степени для текущего кадра
        // с каждым кадром рекурсии это значение уменьшается на единицу
        let rec recPow acc p =
            // сравниваем текущую степень
            match p with
            | x when x > 0 ->
                // вычисляем новое значение аккумулятора
                // умножаем исходную матрицу на старый аккумулятор, то есть возводим в следующую степень
                let nextAcc = acc*m
                // рекурсивно вызываем функцию и передаем ей уменьшенное на единицу значение степени
                recPow nextAcc (x-1)
            // если степень достигла нуля, то возвращаем вычисленный аккумулятор
            | _ -> acc
        // создаем единичную матрицу, чтобы передать ее в качестве аккумулятор для вычисления степени
        let dim = Matrix.sizes matrix
        let colCount = snd dim
        let rowCount = fst dim
        let u = Matrix.E rowCount colCount
        // вызываем рекурсивную функцию и передаем ей единичную матрицу в качестве аккумулятора
        recPow u p
    // вызываем функцию, реализующую хвостовую рекурсию для получения результата
    let powMatrix = inRecPow matrix value
    // возвращаем итоговую матрицу
    { values = powMatrix. values }

Код содержит подробные комментарии о том, как он работает. Требует небольшого пояснения, зачем используется единичная матрица? Она нужна для первого кадра рекурсии и служит в качестве базового значения аккумулятора, в котором будет накапливаться итоговый результат.
Ниже рассмотрим пример использования нашей функции

Вычислим следующее произведение

Где E — это единичная матрица. Так как мы не можем к матрице прибавить число, то мы должны прибавлять 3E.

// возвращает сумму матрицы и числа
static member (+) (matrix, (value: int)) =
    let dim = Matrix.sizes matrix
    let r = fst dim
    let c = snd dim
    // создаем единичную матрицу
    let unit = Matrix.E r c
    // умножаем единичную матрицу на число и прибавляем к входной матрице
    value*unit + matrix

let a = array2D [[1;0]
                 [2;-1]]
let A = Matrix. 2 + 3 =
 [[1; 0]
 [4; -3]]

Матрица A^T, столбцы которой составлены из строк матрицы A с теми же номерами и тем же порядком следования элементов, называется транспонированной к матрице A

static member transpose matrix =
    let dim = Matrix.sizes matrix
    let rows = fst dim
    let cols = snd dim
    // создаем нулевую матрицу для вычисления результатов
    let tMatrix = Matrix.O cols rows
    // копируем в нее данные из исходной матрицы
    matrix.values |> Array2D.iteri(fun x y v -> tMatrix.values.[y, x] <- v)
    // возвращаем результат
    tMatrix

Пример использования

let a = array2D [[1;2;3]
                 [4;5;6]
                 [7;8;9]
                 [10;11;12]]
let A = Matrix.ofArray2D a
let R6 = Matrix.T A
printfn "origin = \n %A" A.values
printfn "transpose = \n %A" R.values

origin = 
 [[1; 2; 3]
 [4; 5; 6]
 [7; 8; 9]
 [10; 11; 12]]
transpose = 
 [[1; 4; 7; 10]
 [2; 5; 8; 11]
 [3; 6; 9; 12]]

Итоги

В этот статье мы рассмотрели примеры реализации и использования матриц из теории линейной алгебры. А также основных математических операций над ними, с использованием функционального подхода на языке F#. Я надеюсь, что читатель смог оценить ту гибкость, которую дают функциональные языки.

Полный исходный код модуля матриц, фрагменты которого были рассмотрены в рамках статьи, вы сможете найти на гитхабе.

Github Matrix.fs

Математика для ИИ: операции с матрицами

Из операций с матрицами можно выделить транспонирование, псевдоинверсию, преобразование в скаляр, умножение на вектор и умножение на обратную матрицу. Знание этих операций пригодится вам в контексте понимания принципов работы ИИ.

Транспонирование матрицы

После транспонирования мы получим так называемую транспонированную матрицу. Можно сказать, что это будет зеркальным отображением матрицы по главной диагональной линии (начинается в левом верхнем углу и идёт в нижний правый угол).

Представьте, что у нас есть матрица A. Транспонированной будет являться матрица А^т( А^t, А^tr). Вдобавок к этому, такую матрицу мы сможем получить, если запишем ряды матрицы A в виде столбцов матрицы A^т, а столбцы — в виде рядов.

Умножаем единичную матрицу на вектор

Понятие единичной матрицы вам должно быть знакомо. Если умножить такую матрицу на вектор, то значения вектора не изменятся. На картинке ниже элементы главной диагонали единичной матрицы равны 1, остальные — 0:

Следует отметить, что диагональная матрица очень похожа на единичную. Все её элементы, кроме находящихся на главной диагонали, равняются нулю. Однако в отличие от единичной, здесь на главной диагонали матрицы элементы не равны 1. Следовательно, можно сказать, что единичная матрица является видом диагональной матрицы. Такие матрицы весьма полезны при решении ряда алгоритмов.

Умножаем на обратную матрицу

Обратную матрицу определяют так:

Умножив матрицу A на обратную ей матрицу A со степенью -1, мы получим единичную матрицу. Говоря об обратной матрице, можно вспомнить обратное число.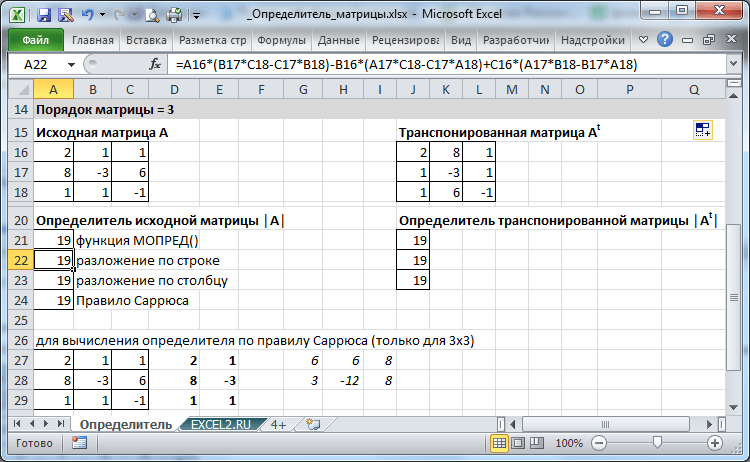 Например, для числа a обратным будет 1/a. Если же обычное число мы умножим на обратное ему, мы получим единицу: a * 1/a = 1. То же самое и с матрицами. Но тут стоит учесть, что данное утверждение справедливо лишь для квадратных матриц.

Псевдоинверсия Мура-Пенроуза

Когда нам нужно выполнить операцию для неквадратных матриц, подойдёт псевдоинверсия Мура-Пенроуза:

Здесь U, D и V — сингулярное разложение нашей матрицы A.

Псевдоинверсия D⁺ матрицы D формируется путём взятия элементов, которые обратны элементам матрицы, а также её дальнейшим транспонированием. Однако следует быть осторожным с концепцией обратной матрицы A^-1, ведь пока она больше применяется в теории, чем на практике. Ситуация обусловлена тем, что вычислительные способности даже самых современных компьютеров дают лишь приблизительный ответ.

Преобразуем матрицу в скаляр

Случается, что необходимо преобразовать матрицу в скаляр, для чего надо найти определитель, обозначаемый det(A) либо |A|. Это преобразование возможно лишь с ними, ниже вы увидите пример с матрицей 2×2:

Тут же следует сказать несколько слов о линейной зависимости. Набор векторов тогда считается линейно зависимым, когда хоть один вектор может быть представлен в виде комбинации других векторов из набора. В обратном случае набор является линейно независимым. Как правило, векторы x и y можно считать линейно независимыми, только когда значения для скаляров a и b, удовлетворяющих ax + by = 0, равняются a = b = 0.

Источник — «Mathematics for Artificial Intelligence – Linear Algebra»

Операции с матрицами (Алгебра 2, Матрицы) – Mathplanet

Матрицы считаются равными, если они имеют одинаковые размеры и если каждый элемент одной матрицы равен соответствующему элементу другой матрицы. Вы можете умножать матрицу на любую константу, это называется скалярным умножением.

---

Пример

$$2\begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}= \begin{bmatrix} {\color{green} 2}\cdot 1 & {\color{ зеленый} 2}\cdot2\\ {\color{green} 2}\cdot3 & {\color{green} 2}\cdot4 \end{bmatrix} = \begin{bmatrix} 2 & 4\\ 6 & 8 \ end {bmatrix}$$

Матрицы одинакового размера можно складывать и вычитать по записи, а матрицы совместимых размеров можно умножать.

---

Пример

Сложите две матрицы A и B:

$$A=\begin{bmatrix} {\color{green} 2} & {\color{green} -1}\\ {\color {зеленый} 1} & {\color{зеленый} 0} \end{bmatrix}B=\begin{bmatrix} {\color{синий} 1} & {\color{синий} 4} \\ {\color{синий } 2} & \,{\color{blue} 3} \end{bmatrix}$$

Это возможно, так как A и B так как обе матрицы имеют две строки и два столбца. Складываем каждый элемент матрицы A с соответствующим элементом матрицы B:

$$A+B=\begin{bmatrix} {\color{green} 2}+{\color{blue} 1} & {\color{green} -1}+{\color{blue} 4} \ \ {\color{green} 1}+{\color{blue} 2} & {\color{green} 0}+\,{\color{blue} 3} \end{bmatrix}=\begin{bmatrix} 3 & 3\\ 3 & 3 \end{bmatrix}$$

Точно так же вычитаются матрицы.

Если умножить матрицу A _p*q и матрицу B _m*n , произведение равно

$$A_{p\times q}+B_{m\times n}=(AB)_{ p\times n}$$

Элемент g-й строки и h-го столбца матрицы AB является суммой произведения соответствующих элементов g-й строки A и h-го столбца матрицы B. Вы можете умножать две матрицы только в том случае, если количество столбцов в первой матрице и количество строк во второй равно.

Рабочие листы

Если вы хотите попрактиковаться в сложении матриц, у нас есть несколько рабочих листов с ответами ниже. Рабочий лист 1 Ответы 1 003

Умножить матрицы A и B:

$$A =\begin{bmatrix} {\color{green} 1} & {\color{green} 3}\\ {\color{green} -1} & {\color{green} 0} \end{bmatrix}B= \begin{bmatrix} {\color{blue} 2} & {\color{blue} 1} & {\color{blue} 1}\\ {\color{blue} -1} & {\color{blue} 2 }&{\color{синий} 4} \end{bmatrix}$$

Это возможно, поскольку первая матрица содержит 2 столбца, а вторая — 2 строки.

$$\\ AB =\begin{bmatrix} {\color{green} 1}\cdot {\color{blue} 2}+{\color{green} 3}\cdot {\color{blue} -1 } & {\ цвет {зеленый} 1} \ cdot {\ цвет {синий} 1} + {\ цвет {зеленый} 3} \ cdot {\ цвет {синий} 2} & {\ цвет {зеленый} 1} \ cdot {\ цвет {синий} 1} + {\ цвет {зеленый} 3} \ cdot {\ цвет {синий} 4} \\ {\ цвет {зеленый} -1} \ cdot {\ цвет {синий} 2} + { \ цвет {зеленый} 0} \ cdot {\ цвет {синий} -1} & {\ цвет {зеленый} -1} \ cdot {\ цвет {синий} 1} + {\ цвет {зеленый} 0} \ cdot { \ цвет {синий} 2} & {\ цвет {зеленый} -1} \ cdot {\ цвет {синий} 1} + {\ цвет {зеленый} 0} \ cdot {\ цвет {синий} 4} \ end {bmatrix }=\\ \\ =\begin{bmatrix} -1 & 7 & 13\\ -2 & -1 & -1 \end{bmatrix}$$

---

Если возможно, выполните указанную операцию:

$$\begin{bmatrix} 2 &0 \\ 1&3 \\ -4&1 \end{bmatrix}\cdot \begin{bmatrix} 6 &2 & 3\\ 0& -2 & 4 \end{bmatrix}$$