Работа сторонних сил формула: Сторонние силы формула. ЭДС. Закон Ома для полной цепи

Закон Ома для полной цепи

1. Источник тока

При прохождении тока в проводнике выделяется некоторое количество теплоты. Согласно закону сохранения энергии при этом в электрическую цепь должна поступать энергия.

Может ли источником этой энергии быть электростатическое поле? Нет, не может, потому что при перемещении заряда вдоль всей цепи, то есть по замкнутой траектории, работа электростатического поля равна кулю.

Следовательно, для существования тока в замкнутой цепи в ней должен быть участок, на котором свободные заряды движутся против сил электростатического поля. Таким участком цепи является источник тока (рис. 59.1).

В источнике тока на свободные заряды действуют силы, которые имеют не электростатическую природу. Их называют сторонними силами. В результате действия сторонних сил происходит разделение зарядов: на одном полюсе источника тока накапливается положительный заряд, а на другом – отрицательный. Вследствие этого возникает электростатическое поле, которое движет свободные заряды в электрической цепи вне источника тока, то есть во внешней цепи.

В химических источниках тока сторонние силы имеют химическую природу. Например, если погрузить цинковый и медный электроды в серную кислоту, то положительные ионы цинка будут чаще покидать электрод, чем положительные ионы меди. В результате между медным и цинковым электродами возникнет разность потенциалов: потенциал медного электрода будет больше, чем цинкового. Медный электрод станет положительным полюсом источника тока, а цинковый – отрицательным.

В генераторах электростанций сторонними силами являются силы, действующие на свободные электроны в металле со стороны вихревого электрического поля, порождаемого переменным магнитным полем. Работа вихревого электрического поля по перемещению заряда вдоль замкнутого контура не равна нулю. Действие генераторов тока мы рассмотрим в курсе физики 11-го класса.

Электродвижущая сила источника тока

В источнике тока сторонние силы, перемещая свободные заряды против действия сил электростатического поля, совершают работу, которую мы обозначим A_стор.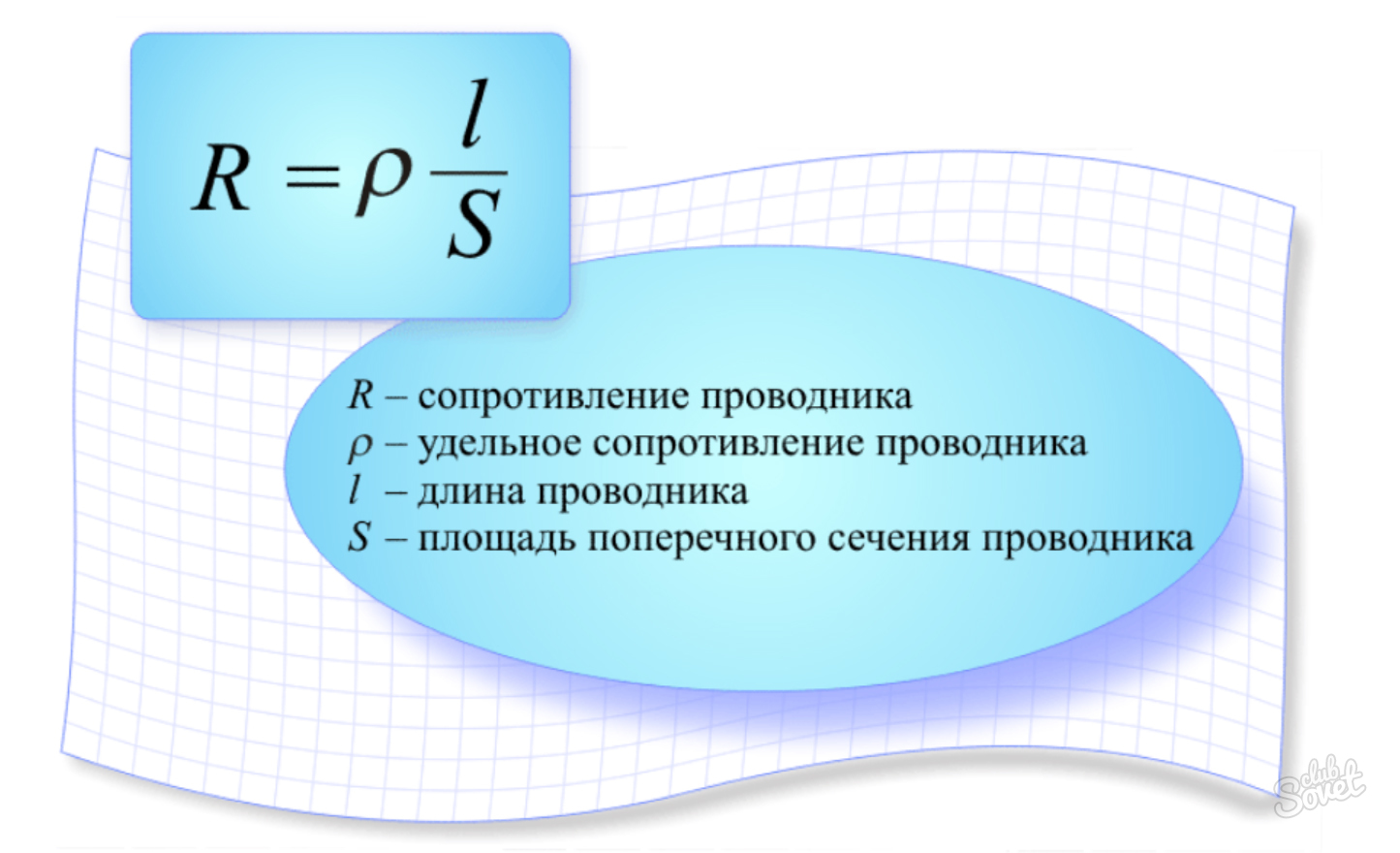

Эта работа пропорциональна заряду q, который перемещается вдоль цепи за данный промежуток времени. Поэтому отношение работы сторонних сил к величине заряда не зависит ни от Aстор, ни от q. Следовательно, оно является характеристикой источника тока. Это отношение называют электродвижущей силой источника (ЭДС) и обозначают ξ:

ξ = A_стор/q.     (1)

(Это название не совсем удачно, потому что ЭДС – не «сила» в механическом смысле, а энергетическая характеристика источника.)

ЭДС, как и напряжение, измеряют в вольтах. Например, ЭДС батарейки составляет несколько вольт.

2. Закон Ома для полной цепи

Если сила тока в цепи равна I, то за время t по цепи проходит заряд q = It. Поэтому формулу (1) можно записать в виде

A_стор = ξIt.     (2)

При этом во внешней цепи сопротивлением R выделяется количество теплоты

Q_внеш = I²Rt,     (3)

а внутри источника тока выделяется количество теплоты

Q_внутр = I²rt,     (4)

где r – сопротивление источника, которое называют его внутренним сопротивлением.

Из закона сохранения энергии следует, что

Q_внеш + Q_внутр = A_стор.     (5)

? 1. Докажите, что из формул (2) – (5) следует:

I = ξ / (R + r).     (6)

Это соотношение называют законом Ома для полной цепи.

Сумму сопротивлений R + r называют полным сопротивлением цепи.

? 2. ЭДС источника тока 12 В, а его внутреннее сопротивление равно 2 Ом.
а) Чему равна сила тока в цепи, если сопротивление внешней цепи равно 4 Ом?

б) Какова максимально возможная сила тока в цепи? При каком сопротивлении внешней цепи это имеет место?

? 3. При внешнем сопротивлении 2 Ом сила тока в цепи равна 1,5 А, а при внешнем сопротивлении 4 Ом сила тока равна 1 А.
а) Чему равно внутреннее сопротивление источника?
б) Чему равна ЭДС источника?

Напряжение на полюсах источника

Закон Ома для полной цепи можно записать в виде

ξ = IR + Ir.     (7)

Первое слагаемое в этой формуле согласно закону Ома для участка цепи равно напряжению U на полюсах источника тока:

IR = U.

Поэтому формулу (7) можно записать в виде

U = ξ – Ir.     (8)

Формула (8) выражает зависимость напряжения U на полюсах источника тока от силы тока I в цепи.

Поставим опыт
Зависимость U(I) можно измерить на опыте, изменяя силу тока в цепи с помощью реостата (рис. 59.2, а, б). Красная пунктирная линия на схеме 59.2, б показывает, как идет ток в реостате. Например, если ползунок реостата, изображенного на рисунке 59,2, а, сдвинуть вправо, то сопротивление реостата увеличится, потому что увеличится длина обмотки, по которой идет ток.

? 4. На рисунке 59.3 изображен график зависимости U(I) для некоторого источника тока.

а) Чему равна ЭДС этого источника тока?
б) Чему равна наибольшая сила тока?

в) Чему равно внутреннее сопротивление источника тока?
г) Чему равно внешнее сопротивление, когда сила тока равна нулю?
д) Чему равно внешнее сопротивление, когда сила тока максимальна?
е) Чему равно внешнее сопротивление при I = 1,5 А?

Максимальное напряжение на полюсах источника равно ξ. Это имеет место при I = 0. Сила тока равна нулю, когда полюса источника разомкнуты (в этом случае внешнее сопротивление цепи является бесконечно большим).

Следовательно, напряжение между разомкнутыми полюсами источника тока равно ЭДС этого источника.

Минимальное же напряжение между полюсами источника равно нулю. Это имеет место при коротком замыкании, когда внешнее сопротивление R = 0. В этом случае сила тока максимальна. Ее называют силой тока короткого замыкания.

? 5. Покажите, что сила тока короткого замыкания выражается формулой

Iка = ξ/r.     (9)

Подсказка. Воспользуйтесь законом Ома для полной цепи.

Из формулы (9) видно, что при очень малом внутреннем сопротивлении источника (как, например, у автомобильного аккумулятора) сила тока короткого замыкания будет очень большой, что может вывести источник тока из строя.

? 6. Сила тока при коротком замыкании батарейки равна 2 А. Когда к батарейке подключили резистор сопротивлением 4 Ом, сила тока стала равной 1 А.

а) Как изменилось полное сопротивление цепи?
б) Чему равно внутреннее сопротивление батарейки?

Измерив напряжение на полюсах источника и силу тока в цепи при двух различных значениях сопротивления внешней цепи, можно найти ЭДС ξ и внутреннее сопротивление r источника тока. Это можно сделать графически и аналитически.

? 7. При силе тока в цепи 2 А напряжение на полюсах источника равно 8 В, а при силе тока 4 А напряжение на полюсах равно 4 В.
а) Постройте систему координат I, U и нанесите две точки графика зависимости U(I) согласно приведенным данным.

б) Проведите прямую через эти точки и отметьте точки пересечения этой прямой с осями координат. Используя этот график, найдите, чему равны ЭДС, сила тока короткого замыкания и внутреннее сопротивление источника тока.
в) Используя уравнение (8), составьте систему двух уравнений с двумя неизвестными ξ и r и решите ее.

3. КПД источника тока

Работу тока во внешней цепи называют полезной работой. Обозначим ее A_пол. Используя формулу для работы тока, получаем:

A_пол = I²Rt.

Поскольку источник обладает внутренним сопротивлением, полезная работа меньше работы сторонних сил, потому что часть работы сторонних сил расходуется на выделение в источнике тока количества теплоты I

2rt. Поскольку

A_стор = I²Rt + I²rt,

получаем для отношения полезной работы к работе сторонних сил:

η = A_пол / A_стор = (I²Rt) / (I²Rt + I²rt) = R / (R + r).

Это отношение, выраженное в процентах, называют КПД источника тока.

? 8. При каком отношении внешнего сопротивления к внутреннему сопротивлению КПД источника тока равен: 50 %; 80 %? Почему случай, когда КПД источника тока равен 100 %, не представляет практического интереса?

Дополнительные вопросы и задания

9. На рисунке 59.4 изображена схема измерения зависимости напряжения U на полюсах источника тока от силы тока I. Амперметр и вольтметр считайте идеальными. Сопротивление всей обмотки реостата 16 Ом. При первом положении ползунка реостата показания приборов 3 А и 8 В, а при втором положении – 2 А и 12 В.

а) Как сдвинули ползунок реостата между первым и вторым измерениями – влево или вправо?
б) Чему равны ЭДС источника тока и его внутреннее сопротивление?
в) Каковы будут показания приборов, если ползунок реостата передвинуть в крайнее левое положение? в крайнее правое?

10. При силе тока 6 А мощность тока во внешней цепи равна 90 Вт, а при силе тока 2 А она равна 60 Вт.
а) Чему равна ЭДС источника тока?
б) Чему равно внутреннее сопротивление источника тока?
в) Чему равно напряжение на полюсах источника в первом и втором случаях?
г) Чему равен КПД источника тока в первом и втором случаях?

§ 13.2 Сторонние силы. Электродвижущая сила и напряжение

Если в проводнике создать электрическое поле и не принять мер для его поддержания, то, как было уже установлено, перемещение носителей заряда приведет очень быстро к тому, что поле внутри проводника исчезнет и, следовательно, ток прекратиться. Для того чтобы поддерживать ток достаточно долго, нужно от конца проводника с меньшим потенциалом (носители тока предполагаются положительными) непрерывно отводить приносимые сюда заряды, а к концу с большим потенциалом непрерывно их подводить. Т.е. необходимо осуществить круговорот зарядов, при котором они двигались бы по замкнутому пути (13.2). Циркуляция вектора напряженности электростатического поля, как известно равна нулю. Поэтому в замкнутой цепи наряду с участками, на которых положительные заряды движутся в сторону убывания потенциала, должны иметься участки, на которых перенос положительных зарядов происходит в направлении возрастания потенциала, т.е. против сил электростатического поля. Перемещение, зарядов на этих участках возможно лишь с помощью сил не электростатического происхождения, называемых сторонними силами.

Таким образом, для поддержания тока необходимы сторонние силы, действующие либо на всем протяжении цепи, либо на отдельных ее участках. Они могут быть обусловлены химическими процессами, диффузией носителей заряда в неоднородной среде или через границу двух разнородных, веществ, электрическими (но не электростатическими) полями, порожденными меняющимися во времени магнитными полями и т.д.

Например, в гальванических элементах и аккумуляторах происхождение сторонних сил – химическое. В генераторах электрического тока сторонние силы – это силы Лоренца, действующие со стороны магнитного поля.

Устройства, обеспечивающие возникновение и действие сторонних сил, называют источниками тока. В этих устройствах происходит разделение разноимённых зарядов. Под действием сторонних сил электрические заряды внутри источника тока движутся в направлении, противоположном действию сил электрического поля. В результате этого на полюсах источника тока поддерживается постоянная разность потенциалов.

Подобно тому, как насос сообщает энергию воде, поднимая её вверх, источник тока сообщает энергию заряженным частицам. Как для работы насоса, поднимающего воду, так и для работы источника тока необходима энергия. В зависимости от типа источника тока, в нём происходит преобразование механической, внутренней или ещё какой-либо энергии в электрическую. В зависимости от вида энергии, которая внутри источника тока преобразуется в электрическую энергию, различают механические, химические, тепловые источники тока.

Сторонние силы совершают работу по перемещению электрических зарядов.

Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (э.д.с.) ε, действующей в цепи.

Сторонняя сила F_ст, действующая на заряд q₀, может быть выражена как

F_ст = E_ст q₀,

где E_ст – напряжённость поля сторонних сил. Работа же сторонних сил по перемещению заряда q₀ на замкнутом участке цепи равна

(13. 6)

Разделив на q₀, получим выражение для э.д.с., действующей в цепи:

(13.7)

т.е. эдс, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряжённости поля сторонних сил. ЭДС, действующая на участке 1-2, равна

На заряд q₀ помимо сторонних сил действует также силы электростатического поля F_э = E q₀. Таким образом, результирующая сила, действующая в цепи на заряд q₀, равна

F =F_ст + F_э = q₀(Е_ст + E_э) (13.8)

Рисунок – 13.3

Работа, совершаемая результирующей силой над зарядом q₀ на участке 1-2, равна

(13.9)

Используя выражения и , можем записать

А₁₂ = q₀ε₁₂ + q₀ (φ₁-φ₂) (13. 10)

Для замкнутой цепи работа электростатических сил равна нулю, поэтому в данном случае А₁₂ = q₀ε₁₂

Напряжением U на участке 1-2 называется физическая величина, определяемая работой, совершаемой суммарным полем кулоновских и сторонних сил при перемещении положительного единичного заряда на данном участке цепи.

U₁₂ = ε₁₂ + (φ₁-φ₂) (13.11)

Полная цепь 🐲 СПАДИЛО.РУ

Полная цепь содержит источник тока — элемент электрической цепи, который поддерживают энергию с заданными параметрами. При этом энергоснабжение цепи не зависит от характеристик элементов, входящих в её состав, в частности, сопротивления.

Определения

В полной цепи действует электродвижущая сила, или ЭДС — скалярная физическая величина, которая характеризует работу сторонних сил, действующих в электрических цепях постоянного и переменного тока.

Сторонние силы — это силы любой природы (кроме электрической), которые разделяют заряды внутри источника тока. Виды сторонний сил:

• механические;
• магнитные;
• химические;
• световые;
• тепловые.

Принято считать, что сторонние силы переносят положительные заряды в направлении от «–» к «+».

Электродвижущая сила обозначается как ε. Единица измерения — Вольт (В). Численно ЭДС равна отношению работы сторонних сил по перемещению заряда к величине этого заряда:

ε=Aстq..

Aст (Дж) — работа сторонних сил по перемещению заряда q (Кл).

Не следует путать напряжение и ЭДС. Напряжение характеризует работу электрического поля, а ЭДС — работу сторонних сил.

Закон Ома для полной цепи

Определение

Сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи:

I=εR+r..

R (Ом) — полное сопротивление внешней цепи, r (Ом) — внутреннее сопротивление источника тока.

Пример №1. Рассчитайте силу тока в замкнутой цепи, состоящей из источника тока, у которого ЭДС равна 10 В, а внутреннее сопротивление равно 1 Ом. Сопротивление резистора равно 4 Ом.

I=εR+r..=101+4..=2 (А)

Напряжение на внешней цепи

Напряжение на внешней цепи — это напряжение на клеммах источника, или падение напряжения на внешней цепи. Оно равно:

U=IR

Выразим сопротивление через ЭДС:

R=εI..−r

Следовательно, напряжение на внешней цепи равно:

U=I(εI..−r)=ε−Ir

КПД источника тока

Не вся работа сторонних сил идет непосредственно на перемещение зарядов. Для выражения доли, которая идет именно на перемещение зарядов, вводится понятие КПД (коэффициента полезного действия).

КПД источника тока равен:

η=Uε..100%=RR+r..100%

Пример №2. Напряжение на внешней цепи равно 6 В, ЭДС источника тока равно 12 В. Определить КПД источника тока.

η=Uε..100%=612..=50%

Короткое замыкание

Рассмотрим простую электрическую цепь:

Она состоит из источника тока (1), ключа (2) и потребителя (3). Теперь поговорим о том, что же произойдет, если цепь замкнуть проводником так, как показано на рисунке ниже.

Соединив точки А и В напрямую, мы заставим течь ток, минуя потребитель тока, поскольку сопротивление проводника АВ много меньше сопротивления потребителя. А ток всегда течет по пути наименьшего сопротивления.

В результате соединения точек А и В сопротивление в электрической цепи резко упадет, что приведет к резкому скачку силы тока. Такое явление называется коротким замыканием.

Определение

Короткое замыкание — соединение концов участка цепи проводником, сопротивление которого очень мало по сравнению с сопротивлением участка цепи.

Если полное сопротивление внешней цепи R стремится к нулю, то сила тока при коротком замыкании равна:

Iк.з.=εr

 

.

Задание EF22543 В цепи, изображённой на рисунке, идеальный амперметр показывает 1 А. Найдите ЭДС источника, если его внутреннее сопротивление 1 Ом.

Ответ:

а) 23 В

б) 25 В

в) 27 В

г) 29 В

Алгоритм решения

1.Записать исходные данные.

2.Записать закон Ома для полной цепи.

3.Выполнить решение в общем виде.

4.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Сила то на первом резисторе: I₁ = 1 А.

• Внутреннее сопротивление источника тока: r = 1 Ом.

• Сопротивление первого резистора: R₁= 3 Ом.

• Сопротивление первого резистора: R₂= 1 Ом.

• Сопротивление первого резистора: R₃= 5 Ом.

Закон Ома для полной цепи:

I=εR+r..

R — полное сопротивление внешней цепи. Цепь состоит из последовательно соединенного третьего резистора с параллельным участком цепи, состоящим из первого и второго резисторов. Вычислим сопротивление параллельного участка цепи:

1R12. .=1R1..+1R2..

R12=R1R2R1+R2..

Полное сопротивление внешней цепи равно:

R=R12+R3=R1R2R1+R2..+R3

Следовательно, ЭДС источника тока равен:

ε=I(R+r)=I(R1R2R1+R2..+R3+r)

Полная сила тока равна силе тока параллельного участка цепи, так как I = I₃ = I₁₂. А сила тока параллельного участка цепи равна сумме силы тока на первом и втором резисторе:

I12=I1+I2=I

Сначала найдем напряжение на первом резисторе, используя закон Ома для участка цепи:

U1=I1R1

Так как это параллельный участок, то:

U1=U2=U12

Следовательно, сила тока на втором резисторе равна:

I2=U2R2..=I1R1R2..

Сила тока на всем участке цепи равна:

I=I12=I1+I1R1R2..=I1(1+R1R2..)

Теперь можем вычислить ЭДС источника тока:

ε=I1(1+R1R2..)(R1R2R1+R2..+R3+r)

ε=1(1+31..)(3·13+1..+5+1)=6,75·4=27 (В)

Ответ: в

---

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17511 Конденсатор ёмкостью С = 2 мкФ присоединён к батарее с ЭДС ε = 10 В и внутренним сопротивлением r = 1 Ом. В начальный момент времени ключ К был замкнут (см. рисунок). Какой станет энергия конденсатора через длительное время (не менее 1 с) после размыкания ключа К, если сопротивление резистора R = 10 Ом? Ответ округлите до сотен.

Ответ:

а) 100 нДж

б) 200 нДж

в) 100 мкДж

г) 200 мкДж

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Записать закон Ома для полной цепи и формулу для нахождения энергии конденсатора.

3.Выполнить решение задачи в общем виде.

4.Подставить исходные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Емкость конденсатора: C = 2 мкФ.

• ЭДС батареи: ε = 10 В.

• Внутреннее сопротивление источника тока: r = 1 Ом.

• Сопротивление резистора: R = 10 Ом.

2 мкФ = 2∙10^–6 Ф

Запишем закон Ома для полной цепи:

I=εR+r..

Энергия конденсатора определяется формулой:

W=CU22. .

Напряжение внешней цепи связано с ЭЛС источника формулой:

U=ε−Ir

Используя закон Ома для полной цепи, получаем:

U=ε−εrR+r..=εR+εr−εrR+r..=εRR+r..

Тогда энергия конденсатора через длительное время станет равной:

W=12..C(εRR+r..)2

Округлим ответ до сотен и получим 100 мкДж.

Ответ: в

---

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17550 Реостат R подключен к источнику тока с ЭДС E и внутренним сопротивлением r (см. рисунок). Зависимость силы тока в цепи от сопротивления реостата представлена на графике. Найдите сопротивление реостата, при котором мощность тока, выделяемая на внутреннем сопротивлении источника, равна 8 Вт.

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу для определения мощности тока, выделяемой на внутреннем сопротивлении источника, и выразить из нее сопротивление.

3.С помощью закона Ома для полной цепи найти неизвестные величины.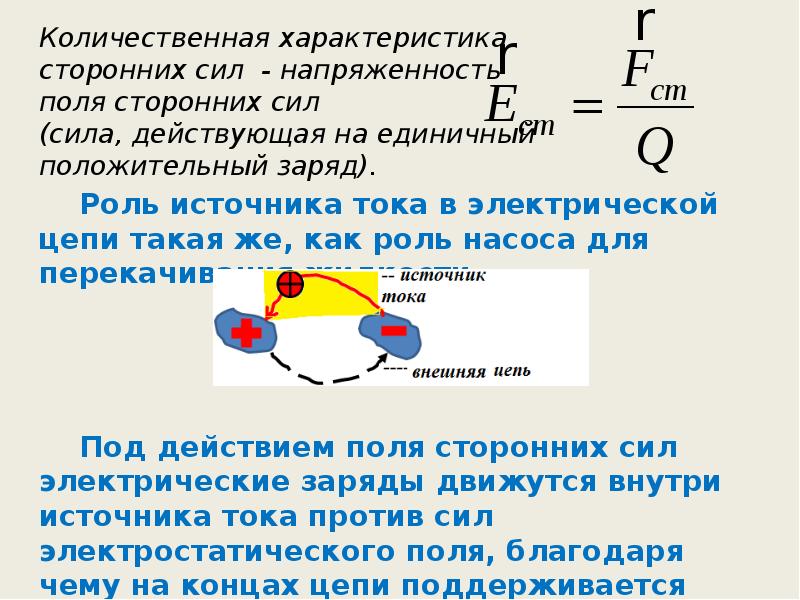

4.Выполнить решение в общем виде.

5.Выполнить вычисления, подставив известные и найденные данные.

Решение

Запишем исходные данные:

• Внутренне сопротивление источника тока: r.

• ЭДС источника тока: ε.

• Мощность тока, выделяемая на внутреннем сопротивлении источника: P_внутр = 8 Вт.

Мощность тока, выделяемая на внутреннем сопротивлении источника, определяется формулой:

Pвнутр=(εR+r..)2r

Выразим отсюда сопротивление реостата:

R=ε√rPвнутр..−r

Запишем закон Ома для полной цепи:

I=εR+r..

Согласно графику, при нулевом сопротивлении реостата, сила тока, равна 6 Амперам. Следовательно:

I(0 Ом)=εr..=6

Но при сопротивлении реостата в 4 Ом сила тока равна 2 Амперам. Следовательно:

I(4 Ом)=ε4+r..=2

Получили систему уравнений:

{.εr..=6..ε4+r..=2.)

ε=6r

6r4+r..=2

6r=8+2r

4r=8

r=2 (Ом)

ε=6·2=12 (В)

Теперь можем вычислить искомое сопротивление:

R=12√28. .−2=4 (Ом)

Ответ: 4

---

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18414 Конденсатор подключён к источнику тока последовательно с резистором R=20 кОм (см. рисунок). В момент времени t=0 ключ замыкают. В этот момент конденсатор полностью разряжен. Результаты измерений силы тока в цепи представлены в таблице.

Внутренним сопротивлением источника и сопротивлением проводов пренебречь. Выберите два верных утверждения о процессах, наблюдаемых в опыте.

Ответ:

а) Ток через резистор в процессе наблюдения увеличивается.

б) Через 6 с после замыкания ключа конденсатор полностью зарядился.

в) ЭДС источника тока составляет 6 В.

г) В момент времени  t = 3 с напряжение на резисторе равно 0,6 В.

д) В момент времени t = 3 с напряжение на конденсаторе равно 5,7 В.

Алгоритм решения

1.Проверить истинность каждого утверждения.

2.Записать в ответе только истинные утверждения.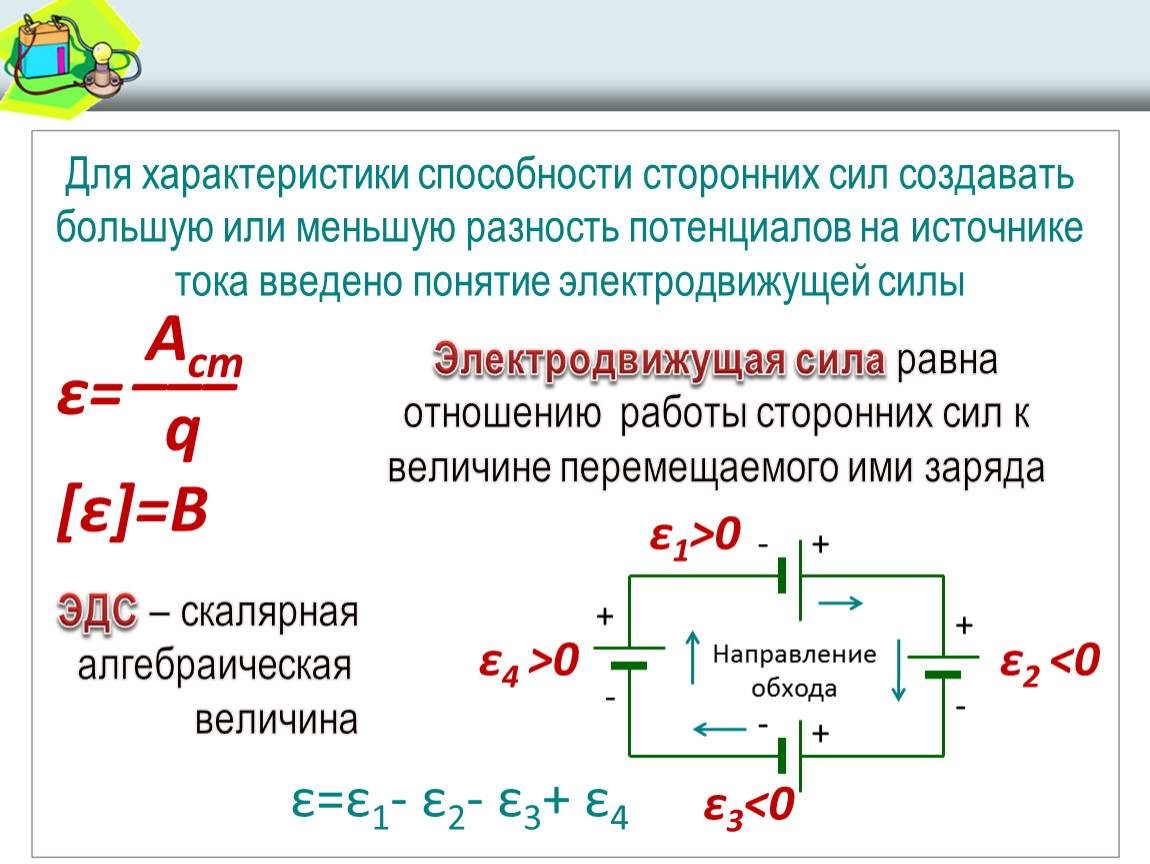

Решение

Согласно утверждению «а», ток через резистор в процессе наблюдения увеличивается. Но это не так, поскольку в таблице с течением времени сила тока уменьшается. Утверждение «а» неверно.

Согласно утверждению «б», через 6 с после замыкания ключа конденсатор полностью зарядился. Если это было бы так, то сила тока была бы равна 0. Но в момент времени t = 6 с она равна 1 мкА. Следовательно, утверждение «б» неверно.

Согласно утверждению «в», ЭДС источника тока составляет 6 В. Напряжение в цепи в начальный момент времени равно ЭДС источника. Следовательно:

ε=U(при t=0 c)=IR=300 мкА ·20 кОм=0,3·10−3А·20·103Ом=6 (В)

Вывод: утверждение «в» верное.

Согласно утверждению «г», в момент времени t = 3 с напряжение на резисторе равно 0,6 В. Чтобы проверить это, нужно умножить соответствующую силу тока на сопротивление резистора:

U=IR=15 мкА ·20 кОм=0,015·10−3А·20·103Ом=0,3 (В)

Вывод: утверждение «г» неверное.

Согласно утверждению «д», в момент времени t = 3 с напряжение на конденсаторе равно 5,7 В. Чтобы проверить это, нужно из ЭДС в этот момент времени вычесть напряжение на внешней цепи. Его мы уже нашли. Оно равно 0,3 В. ЭДС мы тоже нашли. Она равна 6 В. Их разность равна 5,7 В. Следовательно, утверждение «д» верно.

Ответ: вд

---

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18453

На рис. 1 изображена зависимость силы тока через светодиод D от приложенного к нему напряжения, а на рис. 2 – схема его включения. Напряжение на светодиоде практически не зависит от силы тока через него в интервале значений 0,05 А<I<0,2 А. Этот светодиод соединён последовательно с резистором R и подключён к источнику с ЭДС E1=6 В. При этом сила тока в цепи равна 0,1 А. Какова сила тока, текущего через светодиод, при замене источника на другой с ЭДС E2=4,5 В? Внутренним сопротивлением источников пренебречь.

Алгоритм решения

1.Записать исходные данные.

2.С помощью закона Ома для участка и для полной цепи определить сопротивление на светодиоде.

3.Выполнить решение задачи в общем виде.

4.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• ЭДС первого источника тока: ε1=6 В.

• Сила тока, проходящая через светодиод, подключенный к первому источнику тока: I₁ = 0,1 А.

• ЭДС второго источника тока: ε2=4,5 В.

Из рисунка 1 следует, что при силе тока, равной I₁= 0,1 А напряжение на светодиоде равно U_D = 3 В. По закону Ома для участка цепи напряжение на резисторе, будет равно:

U1=I1R

По закону Ома для полной (замкнутой) цепи, имеем:

ε1=U1+UD

Следовательно:

U1=ε1−UD

Тогда сопротивление резистора равно:

R=ε1−UDI1..

Напряжение на светодиоде не зависит от силы тока, проходящего через него в интервале значений (это следует из графика рис. 1), поэтому U2=ε2−UDдля любой силы тока из этого интервала значений, следовательно, сила тока в цепи при изменении ЭДС источника:

I2=U2R. .=ε2−UDR..=I1ε2−UDε1−UD..

I2=0,14,5−36−3..=0,05 (А)

Ответ: 0,05

---

pазбирался: Алиса Никитина | обсудить разбор | оценить

Сторонние силы и эдс – справочник студента

В разгар учебного года многим ученым деятелям требуется эдс формула для разных расчетов. Эксперименты, связанные с гальваническим элементом, так же нуждаются в информации об электродвижущей силе. Но для начинающих не так-то просто понять, что же это такое.

Формула нахождения эдс

Первым делом разберемся с определением. Что означает эта аббревиатура?

Узнай стоимость своей работы

Бесплатная оценка заказа!

ЭДС или электродвижущая сила – это параметр характеризующий работу любых сил не электрической природы, работающих в цепях где сила тока как постоянного, так и переменного одинакова по всей длине. В сцепленном токопроводящем контуре ЭДС приравнивается работе данных сил по перемещению единого плюсового (положительного) заряда вдоль всего контура.

Ниже на рисунке представлена эдс формула.

• Аст – означает работу сторонних сил в джоулях.
• q – это переносимый заряд в кулонах.
• Сторонние силы – это силы которые выполняют разделение зарядов в источнике и в итоге образуют на его полюсах разность потенциалов.

Для этой силы единицей измерения является вольт. Обозначается в формулах она буквой «E».

Только в момент отсутствия тока в батареи, электродвижущая си-а будет равна напряжению на полюсах.

ЭДС индукции:

ЭДС индукции в контуре, имеющем N витков:

Узнай стоимость своей работы

Бесплатная оценка заказа!

При движении:

Электродвижущая сила индукции в контуре, крутящемся в магнитном поле со скоростью w:

Таблица значений

Простое объяснение электродвижущей силы

Предположим, что в нашей деревне имеется водонапорная башня. Она полностью наполнена водой. Будем думать, что это обычная батарейка. Башня — это батарейка!

Вся вода будет оказывать сильное давление на дно нашей башенки. Но сильным оно будет только тогда, когда это строение полностью наполнено h3O.

В итоге чем меньше воды, тем слабее будет давление и напор струи будет меньше. Открыв кран, заметим, что каждую минуту дальность струи будет сокращаться.

В результате этого:

1. Напряжение – это сила с которой вода давит на дно. То есть давление.
2. Нулевое напряжение — это дно башни.

С батареей все аналогично.

Первым делом подключаем источник с энергией в цепь. И соответственно замыкаем ее. Например, вставляем батарею в фонарик и включаем его. Изначально заметим, что устройство горит ярко. Через некоторое время его яркость заметно понизится. То есть электродвижущая сила уменьшилась (вытекла если сравнивать с водой в башне).

Если брать в пример водонапорную башню, то ЭДС это насос качающие воду в башню постоянно. И она там никогда не заканчивается.

Эдс гальванического элемента – формула

Электродвижущую силу батарейки можно вычислить двумя способами:

• Выполнить расчет с применением уравнения Нернста. Нужно будет рассчитать электродные потенциалы каждого электрода, входящего в ГЭ. Затем вычислить ЭДС по формуле .
• Посчитать ЭДС формуле Нернста для суммарной ток образующей реакции, протекающей при работе ГЭ.

Таким образом вооружившись данными формулами рассчитать электродвижущую силу батарейки будет проще.

Где используются разные виды ЭДС?

1. Пьезоэлектрическая применяется при растяжении или сжатии материала. С помощью нее изготавливают кварцевые генераторы энергии и разные датчики.
2. Химическая используется в гальванических элементах и аккумуляторах.
3. Индукционная появляется в момент пересечения проводником магнитного поля.

   Ее свойства применяют в трансформаторах, электрических двигателях, генераторах.

4. Термоэлектрическая образуется в момент нагрева контактов разнотипных металлов. Свое применение она нашла в холодильных установках и термопарах.
5. Фото электрическая используется для продуцирования фотоэлементов.

Batareykaa.ru

Источник: https://batareykaa.ru/eds-formula-i-ee-raschety/

ЭДС: определение и формула, в чём измеряется, работа источника электродвижущей силы

От электростатики к электрокинетике

Между концом XVIII и началом XIX века работы таких учёных, как Кулон, Лагранж и Пуассон, заложили математические основы определения электростатических величин. Прогресс в понимании электричества на этом историческом этапе очевиден. Франклин уже ввёл понятие «количество электрической субстанции», но пока ещё и он, ни его преемники не смогли его измерить.

Следуя за экспериментами Гальвани, Вольта пытался найти подтверждения того, что «гальванические жидкости» животного были одной природы со статическим электричеством.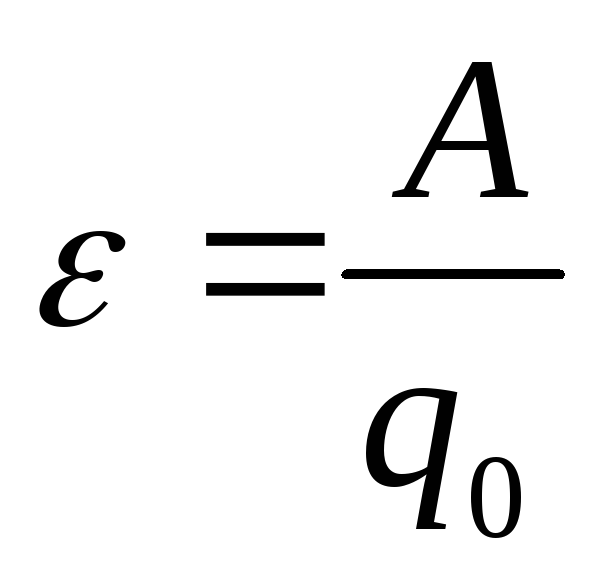

В поисках истины он обнаружил, что когда два электрода из разных металлов контактируют через электролит, оба заряжаются и остаются заряженными несмотря на замыкание контура нагрузкой.

Это явление не соответствовало существующим представлениям об электричестве потому, что электростатические заряды в подобном случае должны были рекомбинировать.

Вольта ввёл новое определение силы, действующей в направлении разделения зарядов и поддержании их в таком состоянии. Он назвал её электродвижущей. Подобное объяснение описания работы батареи не вписывалось в теоретические основы физики того времени. В Кулоновской парадигме первой трети XIX века э. д. с. Вольта определялась способностью одних тел вырабатывать электричество в других.

Важнейший вклад в объяснение работы электрических цепей внёс Ом. Результаты ряда экспериментов привели его к построению теории электропроводности. Он ввёл величину «напряжение» и определил её как разность потенциалов на контактах.

Подобно Фурье, который в своей теории различал количество тепла и температуру в теплопередаче, Ом создал модель по аналогии, связывающую количество перемещаемого заряда, напряжение и электропроводность.

Закон Ома не противоречил накопленным знаниям об электростатическом электричестве.

Затем, благодаря Максвеллу и Фарадею, пояснительные модели тока получили новую теорию поля. Это позволило разработать связанную с полем концепцию энергии как для статических потенциалов, так и для электродвижущей силы. Основные даты эволюции понятия ЭДС:

• 1800 г. — создание Вольтой гальванической батареи;
• 1826 г. — Ом формулирует свой закон для полной цепи;
• 1831 г. — обнаружение электромагнитной индукции Фарадеем.

Определение и физический смысл

В качестве иллюстрации их работы удобно рассматривать замкнутый контур из сопротивления и гальванического источника питания (батареи). Если предположить, что внутри батареи тока нет, то описанная проблема объединения зарядов остаётся неразрешённой. Но в цепи с реальным источником питания электроны перемещаются постоянно. Это происходит благодаря тому, что поток ионов протекает и внутри батареи от отрицательного электрода к положительному. Источник энергии, перемещающий эти заряды в батарее — химические реакции. Такая энергия называется электродвижущей силой.

ЭДС является характеристикой любого источника энергии, способного управлять движением электрических зарядов в цепи. В аналогии с замкнутым гидравлическим контуром работа источника э. д. с. соответствует работе насоса для создания давления воды. Поэтому значок, обозначающий эти устройства, неотличим на гидравлических и электрических схемах.

Несмотря на название, электродвижущая сила на самом деле не является силой и измеряется в вольтах. Её численное значение равно работе по перемещению заряда по замкнутой цепи. ЭДС источника выражается формулой E=A/q, в которой:

• E — электродвижущая сила в вольтах;
• A — работа сторонних сил по перемещению заряда в джоулях;
• q — перемещённый заряд в кулонах.

Из этой формулы ЭДС следует, что электродвижущая сила не является свойством цепи или нагрузки, а есть способность генератора электроэнергии к разделению зарядов.

Сравнение с разностью потенциалов

Электродвижущая сила и разность потенциалов в цепи очень похожие физические величины, так как оба измеряются в вольтах и определяются работой по перемещению заряда. Одно из основных смысловых различий заключается в том, что э. д. с. (E) вызывается путём преобразования какой-либо энергии в электрическую, тогда как разность потенциалов (U) реализует электрическую энергию в другие виды. Другие различия выглядят так:

• E передаёт энергию всей цепи. U является мерой энергии между двумя точками на схеме.
• Е является причиной U, но не наоборот.
• Е индуцируется в электрическом, магнитном и гравитационном поле.
• Концепция э. д. с. применима только к электрическому полю, в то время как разность потенциалов применима к магнитным, гравитационным и электрическим полям.

Напряжение на клеммах источника питания, как правило, отличается от ЭДС источника. Это происходит из-за наличия внутреннего сопротивления источника (электролита и электродов, обмоток генератора). Связывающая разность потенциалов и ЭДС источника тока формула выглядит как U=E-Ir. В этом выражении:

• U — напряжение на клеммах источника;
• r — внутреннее сопротивление источника;
• I — ток в цепи.

Из этой формулы электродвижущей силы следует, что э. д. с. равна напряжению когда ток в цепи не течёт. Идеальный источник ЭДС создаёт разность потенциалов независимо от нагрузки (протекающего тока) и не обладает внутренним сопротивлением.

В природе не может существовать источника с бесконечной мощностью при замыкании на клеммах, как и материала с бесконечной проводимостью. Идеальный источник используется как абстрактная математическая модель.

Источники электродвижущей силы

Суть источника ЭДС заключается в преобразовании других видов энергии в электрическую с помощью сторонних сил. С точки зрения физики обеспечения э. д. с различают следующие два основных вида источников:

• гальванические;
• электромагнитные.

Первые представляют собой электрохимические источники, основанные на вовлечение в химическую реакцию процесса переноса электронов. В обычных условиях химические взаимодействия сопровождаются выделением или поглощением тепла, но существует немало реакций, в результате которых генерируется электрическая энергия.

Электрохимические процессы в большинстве случаев обратимы, поскольку энергия электрического тока может быть использована, чтобы заставить реагировать вещества между собой. Эта возможность позволяет создавать возобновляемые гальванические источники — аккумуляторы.

В генераторах тока э. д. с. создаётся другим способом. Разделение зарядов происходит с помощью явления электромагнитной индукции, которое заключается в том, что изменение величины или направления магнитного поля создаёт ЭДС. Согласно закону Фарадея, нахождение э. д. с. индукции возможно из выражения E=—dФ/dt. В этой формуле:

• Ф — магнитный поток;
• t — время.

Вам это будет интересно  Устройство термопары, ее виды и принцип работы

ЭДС индукции измеряется также в вольтах. В зависимости от того, каким способом вызываются изменения магнитного потока, различают:

• Динамически индуцированную. Когда в стационарном магнитном поле перемещается проводник. Характерен для генераторов.
• Статически индуцированную. Когда изменения потока возникают из-за изменений магнитного поля вокруг неподвижного проводника. Так работают трансформаторы.

Существуют также источники э. д. с, не основанные на электрохимии или магнитной индукции. К таким устройствам можно отнести полупроводниковые фотоэлементы, контактные потенциалы и пьезокристаллы.

Понятие ЭДС имеет практическое применение прежде всего как параметр выбора источников питания для тех или иных целей. Чтобы получить максимальный эффект от работы устройств в цепи, нужно согласовывать их возможности и характеристики.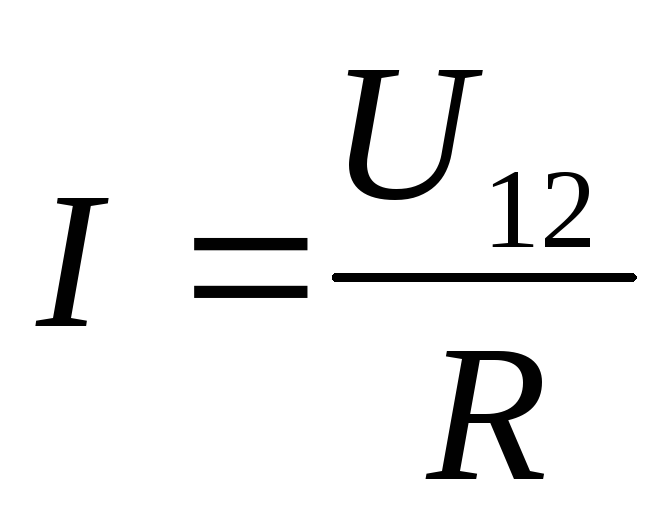

Прежде всего внутреннее сопротивление источника ЭДС силы с характеристиками подключаемой нагрузки.

Источник: https://rusenergetics.ru/praktika/istochniki-eds

Инфофиз — мой мир..

Кратковременный ток в проводнике можно получить, если соединить этим проводником два заряженных проводящих тела, которые имеют различный потенциал. Ток в проводнике исчезнет, когда потенциал тел станет одинаковым. Для существования электрического тока в проводнике необходимо создать в нем и длительное время поддерживать электрическое поле.

Постоянный электрический ток может быть создан только в замкнутой цепи, в которой свободные носители заряда циркулируют по замкнутым траекториям. При перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю.

Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения.

 Поле внутри проводников, составляющих замкнутую цепь должен поддерживать источник  электрической энергии.

Устройства, способные создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. называются источниками постоянного тока.

Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.

Природа сторонних сил может быть различной.

В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле.

Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.

В цепь включают также потребители электрической энергии, в которых ток выполняет полезную работу. Кроме того, в цепь включают соединительные провода и выключатель (рубильник) для замыкания и размыкания цепи. Простая электрическая цепь состоит из источника тока, потребителя, подводящих проводов и выключателя.

Цепь постоянного тока можно разбить на определенные участки. Те участки, на которых не действуют сторонние силы (то есть участки, не содержащие источников тока), называются однородными. Участки, включающие источники тока, называются неоднородными.

На рисунке изображена замкнутая цепь постоянного тока. Участок цепи (cd) является однородным.

Часть цепи, в которой заряды движутся по направлению действия электрических сил (a-d-c-b)называют внешней, а часть цепи, в которой заряды движутся в сторону действия сторонних сил (a-b), называют внутренней.

Те точки, в которых внешняя цепь граничит с внутренней называют полюсами. У одного из полюсов имеется самый большой потенциал, а у другого самый маленький потенциал по сравнению с другими точками цепи. Полюс с наибольшим потенциалом называют положительным и обозначают знаком «+», а полюс с наименьшим потенциалом называют отрицательным и обозначают знаком «-».

При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы.

Для существования постоянного тока необходимо наличие в электрической цепи источника постоянного тока — устройства, способного создавать и поддерживать разности потенциалов на участках цепи.

Возникновение разности потенциалов на полюсах любого источника является результатом разделения в нем положительных и отрицательных зарядов. Это разделение происходит благодаря работе, совершаемой сторонними силами.

 При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.

Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):

• ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда.
• Электродвижущая сила, как и разность потенциалов, измеряется в вольтах [В].
• Чтобы измерить ЭДС источника, надо присоединить к нему вольтметр при разомкнутой цепи.

Источник тока является проводником и всегда имеет некоторое сопротивление, поэтому ток выделяет в нем тепло. Это сопротивление называют внутренним сопротивлением источникаи обозначают r.

1. При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.
2. Работа сторонних сил по перемещению единичного заряда равна по определению электродвижущей силе ε12, действующей на данном участке. Поэтому полная работа по перемещению единичного заряда равна 
3. Величину U12 , равную работе по перемещению единичного заряда, принято называть напряжением на участке цепи 1–2.

Если цепь состоит из внешней части сопротивлением R и внутренней сопротивлением r, то,  согласно закону сохранения энергии, ЭДС источника будет равна сумме напряжений на внешнем и внутреннем участках цепи, т.к. при перемещении по замкнутой цепи заряд возвращается в исходное положение , где IR – напряжение на внешнем участке цепи, а Ir — напряжение на внутреннем участке цепи.

• Таким образом, для участка цепи, содержащего ЭДС:
• Эта формула выражает закон Ома для полной цепи: сила тока в полной цепи прямо пропорциональна электродвижущей силе источника и обратно пропорциональна сумме сопротивлений внешнего и внутреннего участков цепи.
• На рисунке изображена замкнутая цепь постоянного тока.

Продолжение лекции

Источник: http://infofiz.ru/index.php/mirfiziki/fizst/lkf/140-lk35ft

Сторонние силы, электродвижущая сила и напряжение

⇐ ПредыдущаяСтр 3 из 10Следующая ⇒

Если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение носителей (они предполагаются положительными) от точек с большим потенциалом к точкам с меньшим потенциалом. Это приведет к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля.

Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называютсяисточниками тока.

Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называютсясторонними.

Природа сторонних сил может быть различной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе — за счет механической энергии вращения ротора генератора и т. п.

Роль источника тока в электрической цепи, образно говоря, такая же, как роль насоса, который необходим для перекачивания жидкости в гидравлической системе.

Под действием создаваемого поля сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему на концах цепи поддерживается разность потенциалов и в цепи течет постоянный электрический ток.

Сторонние силы совершают работу по перемещению электрических зарядов. Физи­ческая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называетсяэлектродвижущей силой (э.д.с.),действующей в цепи:

Сторонняя сила Fст, действующая на заряд Q, может быть выражена как

где Е — напряженность поля сторонних сил. Работа же сторонних сил по перемещению заряда Q0 на замкнутом участке цепи равна

Разделив (97.2) на Q, получим выражение для э. д. с., действующей в цепи:

т. е. э.д.с., действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил. Э.д.с., действующая на участке 1—2, равна

На заряд Q0 помимо сторонних сил действуют также силы электростатического поля Fe=QE. Таким образом, результирующая сила, действующая в цепи на заряд Q0, равна

Работа, совершаемая результирующей силой над зарядом Q0 на участке 1—2, равна

Используя выражения (97.3) и (84.8), можем записать

Напряжением U на участке 1—2 называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи. Таким образом, согласно (97.4),

Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует Э.д.с., т. е. сторонние силы отсутствуют.

18 Правила Кирхгофа для разветвленных цепей

Первое правило Кирхгофа утверждает, что алгебраическая сумма токов, сходящихся в любом узле цепи равна нулю:

В случае установившегося постоянного тока в цепи ни в одной точке проводника, ни на одном из его участков не должны накапливаться электрические заряды (узел – любой участок цепи, где сходятся более двух проводников (рис. 7.8)).

Рис. 7.8

Токи, сходящиеся к узлу, считаются положительными:

Второе правило Кирхгофаявляется обобщением закона Ома для разветвленной цепи.Для произвольного замкнутого контура с произвольным числом разветвлений (рис. 7.9) можно записать для каждого элемента контура:

Рис. 7.9

Складывая эти уравнения получим второе правило Кирхгофа:

В любом замкнутом контуре электрической цепи алгебраическая сумма произведения тока на сопротивление равна алгебраической сумме ЭДС, действующих в этом же контуре.

Обход контуров осуществляется по часовой стрелке, если направление обхода совпадает с направлением тока, то ток берется со знаком «плюс».

19. мощность в цепи постоянного тока. Работа выхода — разница между минимальной энергией (обычно измеряемой в электрон-вольтах), которую необходимо сообщить электрону для его «непосредственного» удаления из объёма твёрдого тела, и энергией Ферми.

Здесь «непосредственность» означает то, что электрон удаляется из твёрдого тела через данную поверхность и перемещается в точку, которая расположена достаточно далеко от поверхности по атомным масштабам (чтобы электрон прошёл весь двойной слой), но достаточно близко по сравнению с размерами макроскопических граней кристалла.

При этом пренебрегают дополнительной работой, которую необходимо затратить на преодоление внешних полей, возникающих из-за перераспределения поверхностных зарядов. Таким образом, работа выхода для одного и того же вещества для различных кристаллографических ориентаций поверхности оказывается различной.

При удалении электрона на бесконечность его взаимодействие с зарядами, остающимися внутри твёрдого тела приводит к индуцированию макроскопических поверхностных зарядов (при рассмотрении полубесконечного образца в электростатике это называют «изображением заряда»).

При перемещении электрона в поле индуцированного заряда совершается дополнительная работа, которая определяется диэлектрической проницаемостью вещества, геометрией образца и свойствами других поверхностей.

За счет этого полная работа по перемещению электрона из любой точки образца в любую другую точку (в том числе и точку бесконечности) не зависит от пути перемещения, то есть от того, через какую поверхность был удален электрон. Поэтому в физике твёрдого тела эта работа не учитывается и не входит в работу выхода.

20.работа выхода электрона. термоэлектронная эмиссияТермоэлектро́нная эми́ссия (эффект Ричардсона, эффект Эдисона) — явление испускания электронов нагретыми телами.

Концентрация свободных электронов в металлах достаточно высока, поэтому даже при средних температурах вследствие распределения электронов по скоростям (по энергии) некоторые электроны обладают энергией, достаточной для преодоления потенциального барьера на границе металла.

С повышением температуры число электронов, кинетическая энергия теплового движения которых больше работы выхода, растет, и явление термоэлектронной эмиссии становится заметным.

Исследование закономерностей термоэлектронной эмиссии можно провести с помощью простейшей двухэлектродной лампы — вакуумного диода, представляющего собой откачанный баллон, содержащий два электрода: катод К и анод А. В простейшем случае катодом служит нить из тугоплавкого металла (например, вольфрама), накаливаемая электрическим током.

Анод чаще всего имеет форму металлического цилиндра, окружающего катод. Если диод включить в цепь, то при накаливании катода и подаче на анод положительного напряжения (относительно катода) в анодной цепи диода возникает ток. Если поменять полярность батареи, то ток прекращается, как бы сильно катод ни накаливали.

Следовательно, катод испускает отрицательные частицы — электроны. Если поддерживать температуру накаленного катода постоянной и снять зависимость анодного тока от анодного напряжения — вольт-амперную характеристику, то оказывается, что она не является линейной, то есть для вакуумного диода закон Ома не выполняется.

Зависимость термоэлектронного тока от анодного напряжения в области малых положительных значений описывается законом трех вторых (установлен русским физиком С. А. Богуславским (1883— 1923) и американским физиком И. Ленгмюром (1881 — 1957)): , где В — коэффициент, зависящий от формы и размеров электродов, а также их взаимного расположения.

При увеличении анодного напряжения ток возрастает до некоторого максимального значения, называемого током насыщения. Это означает, что почти все электроны, покидающие катод, достигают анода, поэтому дальнейшее увеличение напряженности поля не может привести к увеличению термоэлектронного тока.

Следовательно, плотность тока насыщения характеризует эмиссионную способность материала катода. Плотность тока насыщения определяется формулой Ричардсона — Дешмана, выведенной теоретически на основе квантовой статистики: , где А — работа выхода электронов из катода, Т — термодинамическая температура, С — постоянная, теоретически одинаковая для всех металлов (это не подтверждается экспериментом, что, по-видимому, объясняется поверхностными эффектами). Уменьшение работы выхода приводит к резкому увеличению плотности тока насыщения. Поэтому применяются оксидные катоды (например, никель, покрытый оксидом щелочноземельного металла), работа выхода которых равна 1 −1,5 эВ.

⇐ Предыдущая12345678910Следующая ⇒

Рекомендуемые страницы:

Источник: https://lektsia.com/5x3cdb.html

Электродвижущая сила — Класс!ная физика

«Физика — 10 класс»

Любой источник тока характеризуется электродвижущей силой, или сокращённо ЭДС. Так, на круглой батарейке для карманного фонарика написано: 1,5 В. Что это значит?

Если соединить проводником два разноимённо заряженных шарика, то заряды быстро нейтрализуют друг друга, потенциалы шариков станут одинаковыми, и электрическое поле исчезнет (рис. 15.9, а).

Сторонние силы.

Для того чтобы ток был постоянным, надо поддерживать постоянное напряжение между шариками.

Для этого необходимо устройство (источник тока), которое перемещало бы заряды от одного шарика к другому в направлении, противоположном направлению сил, действующих на эти заряды со стороны электрического поля шариков.

В таком устройстве на заряды, кроме электрических сил, должны действовать силы неэлектростатического происхождения (рис. 15.9, б). Одно лишь электрическое поле заряженных частиц (кулоновское поле) не способно поддерживать постоянный ток в цепи.

Любые силы, действующие на электрически заряженные частицы, за исключением сил электростатического происхождения (т. е. кулоновских), называют сторонними силами.

Вывод о необходимости сторонних сил для поддержания постоянного тока в цепи станет ещё очевиднее, если обратиться к закону сохранения энергии.

Электростатическое поле потенциально. Работа этого поля при перемещении в нём заряженных частиц по замкнутой электрической цепи равна нулю. Прохождение же тока по проводникам сопровождается выделением энергии — проводник нагревается.

Следовательно, в цепи должен быть какой-то источник энергии, поставляющий её в цепь. В нём, помимо кулоновских сил, обязательно должны действовать сторонние, непотенциальные силы.

Работа этих сил вдоль замкнутого контура должна быть отлична от нуля.

Именно в процессе совершения работы этими силами заряженные частицы приобретают внутри источника тока энергию и отдают её затем проводникам электрической цепи.

Сторонние силы приводят в движение заряженные частицы внутри всех источников тока: в генераторах на электростанциях, в гальванических элементах, аккумуляторах и т. д.

При замыкании цепи создаётся электрическое поле во всех проводниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны от положительно заряженного электрода к отрицательному), а во внешней цепи их приводит в движение электрическое поле (см. рис. 15.9, б).

Природа сторонних сил.

Природа сторонних сил может быть разнообразной. В генераторах электростанций сторонние силы — это силы, действующие со стороны магнитного поля на электроны в движущемся проводнике.

В гальваническом элементе, например в элементе Вольта, действуют химические силы.

Элемент Вольта состоит из цинкового и медного электродов, помещённых в раствор серной кислоты. Химические силы вызывают растворение цинка в кислоте.

В раствор переходят положительно заряженные ионы цинка, а сам цинковый электрод при этом заряжается отрицательно. (Медь очень мало растворяется в серной кислоте.

) Между цинковым и медным электродами появляется разность потенциалов, которая и обусловливает ток во внешней электрической цепи.

• Электродвижущая сила.
• Действие сторонних сил характеризуется важной физической величиной, называемой электродвижущей силой (сокращённо ЭДС).
• Электродвижущая сила источника тока равна отношению работы сторонних сил при перемещении заряда по замкнутому контуру к абсолютной величине этого заряда:

Электродвижущую силу, как и напряжение, выражают в вольтах.

Разность потенциалов на клеммах батареи при разомкнутой цепи равна электродвижущей силе. ЭДС одного элемента батареи обычно 1—2 В.

Можно говорить также об электродвижущей силе и на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всём контуре, а только на данном участке.

1. Электродвижущая сила гальванического элемента есть величина, численно равная работе сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому.
2. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории перемещения зарядов.
3. Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Следующая страница «Закон Ома для полной цепи» Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»

Законы постоянного тока — Физика, учебник для 10 класса — Класс!ная физика

Электрический ток. Сила тока — Закон Ома для участка цепи. Сопротивление — Электрические цепи. Последовательное и параллельное соединения проводников — Примеры решения задач по теме «Закон Ома.

Последовательное и параллельное соединения проводников» — Работа и мощность постоянного тока — Электродвижущая сила — Закон Ома для полной цепи — Примеры решения задач по теме «Работа и мощность постоянного тока.

Закон Ома для полной цепи»

Источник: http://class-fizika.ru/10_a164.html

Чем отличается ЭДС от напряжения: простое объяснение на примере

Многие люди (в то числе и некоторые электрики) путают понятие электродвижущей силы (ЭДС) и напряжения. Хотя эти понятия имеют отличия.

Несмотря на то, что они незначительные, не специалисту сложно в них разобраться. Не маловажную роль в этом играет единица измерения. Напряжение и ЭДС измеряются в одних единицах – Вольтах.

На этом отличия не заканчиваются, подробно обо всем мы рассказали в статье!

Что такое электродвижущая сила

Подробно этот вопрос мы рассмотрели в отдельной статье: https://samelectrik.ru/chto-takoe-eds-obyasnenie-prostymi-slovami.html

Под ЭДС понимается физическая величина, характеризующая работу каких-либо сторонних сил, находящихся в источниках питания постоянного или переменного тока.

При этом, если имеется замкнутый контур, то можно сказать, что ЭДС равна работе сил по перемещению положительного заряда к отрицательному по замкнутой цепи.

Или простыми словами, ЭДС источника тока представляет работу, необходимую для перемещения единичного заряда между полюсами.

При этом если источник тока имеющего бесконечную мощность, а внутреннее сопротивление будет отсутствовать (позиция А на рисунке), то ЭДС можно рассчитать по закону Ома для участка цепи, т.к. напряжение и электродвижущая сила в этом случае равны.

I=U/R,

где U – напряжение, а в рассмотренном примере — ЭДС.

Однако, реальный источник питания имеет конечное внутреннее сопротивление. Поэтому такой расчет нельзя применять на практике. В этом случае для определения ЭДС пользуются формулой для полной цепи.

I=E/(R+r),

где E (также обозначается как «ԑ») — ЭДС; R – сопротивление нагрузки, r – внутреннее сопротивление источника электропитания, I – ток в цепи.

Однако, эта формула не учитывает сопротивление проводников цепи. При этом необходимо понимать, что внутри источника постоянного тока и во внешней цепи, ток течет в разных направлениях. Разница заключается в том, что внутри элемента он течет от минуса к плюсу, то во внешней цепи от плюса к минусу.

Это наглядно представлено на ниже приведенном рисунке:

При этом электродвижущая сила измеряется вольтметром, в случае, когда нет нагрузки, т.е. источник питания работает в режиме холостого хода.

Чтобы найти ЭДС через напряжение и сопротивление нагрузки нужно найти внутреннее сопротивление источника питания, для этого измеряют напряжение дважды при разных токах нагрузки, после чего находят внутреннее сопротивление.

Ниже приведен порядок вычисления по формулам, далее R1, R2 — сопротивление нагрузки для первого и второго измерения соответственно, остальные величины аналогично, U1, U2 – напряжения источника на его зажимах под нагрузкой.

• Итак, нам известен ток, тогда он равен:
• I1=E/(R1+r)
• I2=E/(R2+r)
• При этом:
• R1=U1/I1
• R2=U2/I2
• Если подставить в первые уравнения, то:
• I1=E/( (U1/I1)+r)
• I2=E/( (U2/I2)+r)
• Теперь разделим левые и правые части друг на друга:
• (I1/I2)= [E/( (U1/I1)+r)]/[E/( (U2/I2)+r)]
• После вычисления относительно сопротивления источника тока получим:
• r=(U1-U2)/(I1-I2)
• Внутреннее сопротивление r:
• r= (U1+U2)/I,
• где U1, U2 — напряжение на зажимах источника при разном токе нагрузки, I — ток в цепи.
• Тогда ЭДС равно:
• E=I*(R+r) или E=U1+I1*r

Что такое напряжение

Электрическое напряжение (обозначается как U) – это физическая величина, которая отражает количественную характеристику работы электрического поля по переносу заряда из точки А в точку В.

Соответственно напряжение может быть между двумя точками цепи, но в отличии от ЭДС оно может быть между двумя выводами какого-то из элементов цепи.

Напомним, что ЭДС характеризует работу, выполненную сторонними силами, то есть работу самого источника тока или ЭДС по переносу заряда через всю цепь, а не на конкретном элементе.

Это определение можно выразить простым языком. Напряжение источников постоянного тока – это сила, которая перемещает свободные электроны от одного атома к другому в определенном направлении.

Для переменного тока используют следующие понятия:

• мгновенное напряжение — это разность потенциалов между точками в данный промежуток времени;
• амплитудное значение – представляет максимальную величину по модулю мгновенного значения напряжения за промежуток времени;
• среднее значение – постоянная составляющая напряжения;
• среднеквадратичное и средневыпрямленное.

Напряжение участка цепи зависит от материала проводника, сопротивления нагрузки и температуры. Так же как и электродвижущая сила измеряется в Вольтах.

Часто для понимания физического смысла напряжения, его сравнивают с водонапорной башней. Столб воды отождествляют с напряжением, а поток с током.

При этом столб воды в башне постепенно уменьшается, что характеризует понижение напряжения и уменьшения силы тока.

Так в чем же отличие

Для лучшего понимания, в чем состоит разница электродвижущей силы от напряжения, рассмотрим пример. Имеется источник электрической энергии бесконечной мощности, в котором отсутствует внутреннее сопротивление. В электрической цепи смонтирована нагрузка. В этом случае будет справедливо утверждение, что ЭДС и напряжение тождественно равны, т.е между этими понятиями отсутствует разница.

Однако, это идеальные условия, которые в реальной жизни не встречаются. Эти условия используют исключительно при расчетах. В реальной жизни учитывается внутреннее сопротивление источника питания. В этом случае ЭДС и напряжение имеют отличия.

На рисунке представлено, какая разница будет в значениях электродвижущей силы и напряжении в реальных условиях. Вышеприведенная формула закона Ома для полной цепи описывает все процессы. При разомкнутой цепи на клеммах батарейки будет значение 1,5 Вольта. Это значение ЭДС. Подключив нагрузку, в данном случае это лампочка, на ней будет напряжение 1 вольт.

Разница от идеального источника заключается в наличии внутреннего сопротивления источника питания. На этом сопротивлении и происходит падение напряжения. Эти процессы описывает закон Ома для полной цепи.

Если измерительный прибор на зажимах источника электроэнергии показывает значение 1,5 Вольта, это будет электродвижущая сила, но повторим, при условии отсутствия нагрузки.

При подключении нагрузки на клеммах будет заведомо меньшее значение. Это и есть напряжение.

Вывод

Из вышесказанного можно сделать вывод, что основная разница между ЭДС и напряжением состоит:

1. Электродвижущая сила зависит от источника питания, а напряжение зависит от подключенной нагрузки и тока, протекающего по цепи.
2. Электродвижущая сила это физическая величина, характеризующая работу сторонних сил неэлектрического происхождения, происходящих в цепях постоянного и переменного тока.
3. Напряжение и ЭДС имеет единую единицу измерения – Вольт.
4. U -величина физическая, равная работе эффективного электрического поля, производимой при переносе единичного пробного заряда из точки А в точку В.

Таким образом, кратко, если представить U в виде столба воды, то ЭДС можно представить что это насос, поддерживающий уровень воды на постоянном уровне. Надеемся, после прочтения статьи Вам стало понятно основное отличие!

Материалы по теме:

Источник: https://samelectrik.ru/chem-otlichaetsya-eds-ot-napryazheniya-prostoe-obyasnenie-na-primere.html

Сторонние силы. Электродвижущая сила и напряжение

Если в цепи на свободные носители заряда действуют только силы электростатического поля, то происходит перемещение носителей (они предполагаются положительными) от точек с большим потенциалом к точкам с меньшим потенциалом. Это приведет к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля.

Поэтому для существования постоянного тока в цепи необходимо наличие устройства, способного создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками тока.

Силы неэлектростатического происхождения, действующие на заряды внутри источника тока, называются сторонними.

Природа сторонних сил может быть различной.

Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами, в генераторе — за счет механической энергии вращения ротора генератора и т. п.

Роль источника тока в электрической цепи, образно говоря, такая же, как роль насоса, который необходим для перекачивания жидкости в гидравлической системе.

Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему на концах цепи поддерживается разность потенциалов и в цепи течет постоянный электрический ток.

Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС) «Г,

Эта работа производится за счет энергии, затрачиваемой в источнике тока, поэтому величину W можно также называть электродвижущей силой источника тока, включенного в цепь.

Часто, вместо того чтобы сказать: «В цепи действуют сторонние силы», говорят: «В цепи с ЭДС», т.е. термин «электродвижущая сила» употребляется как характеристика сторонних сил.

ЭДС, как и потенциал, выражается в вольтах (см. формулу (4) п. 1.6 и (1)).

На заряд Q0, помимо сторонних сил, действуют также силы электростатического поля. Работа, совершаемая силами электростатического поля при перемещении заряда Q0 из точки 1 в точку 2 (см. (3) п. 8.6), равна:

Работа, совершаемая результирующей силой над зарядом Q0Ha участке 1—2, равна:

Если цепь замкнута, то работа электростатических сил равна нулю, и в данном случае

Напряжение на участке 1—2 — физическая величина, равная работе, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи:

или, учитывая формулу (3), получим

Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует ЭДС, т. е. отсутствуют сторонние силы.

Источник: https://bstudy.net/748089/spravochnik/storonnie_sily_elektrodvizhuschaya_sila_napryazhenie

Работа и мощность электрического тока в цепи

Определение 1

Во время протекания тока по однородному участку цепи электрическое поле совершает работу. За пройденное время Δt по цепи имеется заряд Δq=IΔt.

Электрическое поле выделенного участка выполняет работу, формулу которой мы запишем так: ΔA=(φ1–φ2) Δq=Δφ12IΔt=UIΔt, где U=Δφ12 – напряжение. Такая величина называется работой электрического тока.

Обе части формулы RI=U выражают закон Ома для однородного участка цепи с сопротивлением R, умноженным на IΔt. В итоге получим соотношение RI2Δt=UIΔt=ΔA, выражающее закон сохранения энергии для однородного участка цепи. Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике. ΔQ=ΔA=RI2Δt.

Закон Джоуля-Ленца

Дж. Джоуль и Э. Ленц установили закон преобразования работы тока в тепло.

Определение 2

Формула мощности электрического тока (измеряется в амперах) записывается в виде отношения изменения работы тока ΔA за определенный промежуток времени Δt:

P=∆A∆t=UI=I2R=U2R.

Работа и мощность электрического тока обратно пропорциональны.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

По таблице СИ понятно, в чем измеряется мощность: в ваттах (ВТ), а работа в Джоулях (Дж).

Перейдем к рассмотрению полной цепи постоянного тока, которая состоит из источника с электродвижущей силой ε и внутренним сопротивлением r на участке R. Запись основного закона Ома для полной цепи имеет вид (R + r)I=ε. При умножении обеих частей на Δq=IΔt получаем, что соотношение для выражения сохранения энергии полной цепи постоянного тока запишется: R I2Δt+r I2Δt=ε IΔt=ΔAст. Из левой части видно, что ΔQ=R I2Δt обозначает выделяющееся тепло на внешнем участке за промежуток времени Δt, а ΔQист=rI2Δt – внутри источника за тот же время.

εIΔt – это обозначение работы сторонних сил ΔAст,_{действующих внутри. Если имеется замкнутая цепь, тогда ΔAстпереходит в тепло, которое выделяется во внешней цепи (ΔQ)и внутри источника (ΔQист).}

ΔQ+ΔQист=ΔAст=εIΔt.

Работа сторонних сил

Работа электрического поля не входит в данное соотношение, так как в замкнутой цепи работа не совершается, следовательно, тепло идет только от внутренних сторонних сил. В данном случае электрическое поле перераспределяет тепло по всем участкам цепи.

Внешняя цепь может иметь не только проводник с R сопротивлением, но и механизм, потребляющий мощность. Такой случай говорит о том, что R эквивалентно сопротивлению нагрузки. Энергия, которая выделяется по внешней цепи, преобразуется в тепло и другие виды энергии.

Определение 3

Работа, совершаемая сторонними силами за единицу времени, равняется Pист=εI=ε2R+r. Внешняя цепь характеризуется мощностью P=RI2=εI-rI2=ε2R(R+r)2.

Коэффициентом полезного источника называют отношение η=PPист, записываемое как η=PPист=1-rεI=RR+r.

Рисунок 1.11.1 показывает зависимость Pист, полезной Р, выделяемой во внешней цепи, кпд η от тока I для источника с ЭДС, равной ε, и внутренним сопротивлением r. Изменение тока в цепи происходит в пределах от I=0( при R=∞) до I=Iкз=εr( при R=0).

Рисунок 1.11.1. Зависимость мощности источника Pист, мощности во внешней цепи Р и КПД источника η от силы тока.

Приведенные графики показывают, что максимальная мощность во внешней цепи может быть достигнута при R=r и запишется Pmax=ε24r. Формула тока в цепи будет иметь вид Imax=12Iкз=ε2r, где КПД источника не превышает 50%. При I→0может достигаться максимальное значение КПД, тогда сопротивление R→∞. При коротком замыкании значение мощности Р=0. Тогда она только выделяется внутри источника, что грозит перегревом, причем КПД обращается в ноль.

суть и принцип для начинающих чайников

Что такое ЭДС (электродвижущая сила) в физике? Электрический ток понятен далеко не каждому. Как космическая даль, только под самым носом. Вообще, он и ученым понятен не до конца. Достаточно вспомнить Николу Тесла с его знаменитыми экспериментами, на века опередившими свое время и даже в наши дни остающимися в ореоле тайны. Сегодня мы не разгадываем больших тайн, но пытаемся разобраться в том, что такое ЭДС в физике.

Определение ЭДС в физике

ЭДС – электродвижущая сила.  Обозначается буквой E или маленькой греческой буквой эпсилон.

Электродвижущая сила – скалярная физическая величина, характеризующая работу сторонних сил (сил неэлектрического происхождения), действующих в электрических цепях переменного и постоянного тока.

ЭДС, как и напряжение, измеряется в вольтах. Однако ЭДС и напряжение – явления разные.

Напряжение (между точками А и Б) – физическая величина, равная работе эффективного электрического поля, совершаемой при переносе единичного пробного заряда из одной точки в другую.

Объясняем суть ЭДС  “на пальцах”

Чтобы разобраться в том, что есть что, можно привести пример-аналогию. Представим, что у нас есть водонапорная башня, полностью заполненная водой. Сравним эту башню с батарейкой.

Схема водонапорной башни

Вода оказывает максимальное давление на дно башни, когда башня заполнена полностью. Соответственно,  чем меньше воды в башне, тем слабее давление и напор вытекающей из крана воды. Если открыть кран, вода будет постепенно вытекать сначала под сильным напором, а потом все медленнее, пока напор не ослабнет совсем. Здесь напряжение – это то давление, которое вода оказывает на дно. За уровень нулевого напряжения примем само дно башни.

Водокачка

То же самое и с батарейкой. Сначала мы включаем наш источник тока (батарейку) в цепь, замыкая ее. Пусть это будут часы или фонарик. Пока уровень напряжения достаточный и батарейка не разрядилась, фонарик светит ярко, затем постепенно гаснет, пока не потухнет совсем.

Но как сделать так, чтобы напор не иссякал? Иными словами, как поддерживать в башне постоянный уровень воды, а на полюсах источника тока – постоянную разность потенциалов. По примеру башни ЭДС представляется как бы насосом, который обеспечивает приток в башню новой воды.

Советская батарейка

Природа ЭДС

Причина возникновения ЭДС в разных источниках тока разная. По природе возникновения различают следующие типы:

•  Химическая ЭДС.  Возникает в батарейках и аккумуляторах вследствие  химических реакций.
• Термо ЭДС.  Возникает, когда находящиеся при разных температурах контакты  разнородных проводников соединены.
• ЭДС индукции. Возникает в генераторе при  помещении вращающегося проводника в магнитное поле. ЭДС будет наводиться в проводнике, когда проводник  пересекает силовые линии постоянного магнитного поля или когда магнитное поле изменяется по величине.
• Фотоэлектрическая ЭДС. Возникновению этой ЭДС способствует явление  внешнего или внутреннего фотоэффекта.
• Пьезоэлектрическая ЭДС. ЭДС возникает при растяжении или сдавливании веществ.

Дорогие друзья, сегодня мы рассмотрели тему «ЭДС для чайников». Как видим, ЭДС  –  сила неэлектрического происхождения, которая поддерживает протекание электрического тока в цепи. Если Вы хотите узнать, как решаются задачи с ЭДС, советуем обратиться к нашим авторам – скрупулезно отобранным и проверенным специалистам, которые быстро и доходчиво разъяснят ход решения любой тематической задачи.  И по традиции в конце предлагаем Вам посмотреть обучающее видео. Приятного просмотра и успехов в учебе!

 

Автор: Иван

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Электродвижущая сила (ЭДС)

Невозможно получать в проводнике постоянный электрический ток, если для создания напряжения на его концах имеются только, например, заряженные конденсаторы. Электростатическое поле будет перемещать заряды так, что разности потенциалов будут уменьшаться.

Для того чтобы в цепи проводников непрерывно поддерживался электрический ток необходимо наличие в ней какого – либо устройства, в котором происходило бы разделение электрических зарядов и таким образом поддерживалось напряжение в цепи.

Такое устройство называют источником (генератором) электрического тока.

Определение 1

Силы, которые разделяют заряды в источнике тока, называют сторонними. Сторонние силы – это силы неэлектростатического происхождения, они работают внутри источника тока.

Сторонние силы создают разность потенциалов между концами части цепи. Тогда в рассматриваемой части цепи электрический ток вызывает поле, которое порождает разность потенциалов между концами цепи.

Сторонние силы могут иметь разную природу:

• механическую,
• электромагнитную,
• химическую и другую.

При движении электрического заряда в замкнутой цепи, работа, которую выполняют электростатические силы, равна нулю. Поэтому, результирующая работа сил, которые действуют на заряд при таком движении, будет равна работе сторонних сил.

Определение 2

Электродвижущей силой (ЭДС) генератора тока называют физическую величину, равную:

$Ɛ=\frac{A}{q}\left( 1 \right)$,

где $A$ – работа сторонних сил при перемещении положительного заряда $q$ внутри источника от отрицательного полюса к положительному.

Направлением ЭДС считают направление, в котором внутри источника движутся положительные заряды. Если источник ЭДС в цепи один, то направление ЭДС совпадет с направлением тока в контуре цепи.

Словосочетание «электродвижущая сила» не надо понимать дословно, так как размерность ЭДС отлична от размерности силы или работы.

$[Ɛ]=В.$

B – вольт в Международной системе единиц (СИ).

В качестве меры ЭДС, которую создает генератор, принимают разность потенциалов, создаваемую на его зажимах, когда генератор разомкнут.

Электрическое напряжение и ЭДС

Допустим, у нас имеется электрическое поле. Рассмотрим в нем произвольную кривую (рис.1) $l$, которая соединяет точки $A$ и $B$. Укажем на этой криво положительное направление.

Рисунок 1. Электрическое поле. Автор24 — интернет-биржа студенческих работ

Напряжение по избранной нами кривой равно:

$U=\int\limits_l {\vec{E}d\vec{l}=\int\limits_l {E_{l}dl} \left( 2 \right).} $

Так как напряженность $\vec E$ имеет смысл силы, которая действует на единичный положительный заряд, то интеграл (2) – это работа поля по движению заряда по кривой $l$. Напряжение равно разности потенциалов в начале и конце рассматриваемой кривой:

$U=\varphi_{1}-\varphi_{2}\left( 3 \right)$.

Электрическое напряжение вдоль кривой не зависит от ее формы и полностью определено положением начала и конца линии.

Рассмотрим циркуляцию вектора напряженности по контуру $L$ рис.2.

Рисунок 2. Циркуляция вектора напряженности по контуру. Автор24 — интернет-биржа студенческих работ

Выделим на рассматриваемом контуре две точки $A$ и $B$, которые делят наш контур на два незамкнутых криволинейных отрезка $l_{12}$ и $l_{21}$, учитывая (2) и (3), имеем:

$\oint\limits_L {\vec{E}d\vec{l}=\int\limits_A^B{\vec{E}d\vec{l}+\int\limits_B^A {\vec{E}d\vec{l}=} } } \left( \varphi{1}-\varphi_{2} \right)+\left( \varphi_{2}-\varphi_{1} \right)=0\,\left( 4 \right)$

Мы получили, что циркуляция вектора напряженности по замкнутому контуру равна нулю.

Определение 3

В теории электричества электродвижущей силой контура (ЭДС) называют циркуляцию вектора напряженности по этому контуру.

$Ɛ=\oint\limits_L {\vec{E}d\vec{l}=0\, \left( 5 \right).} $

В электростатическом поле ЭДС любого замкнутого контура равна нулю.

Закон Ома для цепи с ЭДС

Пусть у нас имеется химический источник ЭДС – элемент Вольта. Он состоит из двух электродов:

• медного,
• цинкового,

которые находятся в растворе серной кислоты.

Цинк растворяется в кислоте, при этом теряет положительные ионы и получает относительно раствора до отрицательного потенциала. Медный электрод имеет положительный потенциал. Результирующая сторонняя ЭДС получается примерно равна 1,1 В. Она сосредоточена в тонких слоях контактов цинк – электролит и электролит – медь. При включении элемента в цепь (рис.3), по контуру $L$ будет течь ток $I$. При этом на сопротивлениях внешней (1) и внутренней частей цепи появятся разности потенциала.

Рисунок 3. Цепь. Автор24 — интернет-биржа студенческих работ

Допустим, что сопротивления участков цепи имеют равномерные распределения вдоль контура $L$.

По закону сохранения энергии работа электрического поля ($A_q$) по движению заряда $q$ вдоль внешнего участка цепи $1$ и в электролите ($2$) равна:

$A_{q}=\left( \varphi_{1}-\varphi_{2} \right)q+\left( \varphi_{3}-\varphi_{4} \right)q\left( 6 \right)$.

Суммарную работу сторонних сил запишем как:

$Ɛ_q=A_{st}=\left( \varphi_{3}-\varphi_{2} \right)q+\left( \varphi_{1}-\varphi_{4} \right)q\left( 7 \right)$.

Сравнив правые части выражений (6) и (7) имеем:

$A_{q}=A_{st}\left( 8 \right)$.

Формула (8) означает, что работа электрического поля равна работе сторонних сил источника. Принимая во внимание, что:

$\varphi_{1}-\varphi_{2}=IR\, ;\, \varphi_{3}-\varphi_{4}=Ir\, \left( 9\right)$. получим:

$Ɛ=I\left( R+r \right)\left( 10 \right)$.

Формула (10) называется законом Ома для замкнутой цепи.

Второе правило Кирхгофа

Из закона Ома (10) следует, что ЭДС, которая включена в цепь, равна сумме произведений силы тока на сопротивления, которые имеются в цепи. Утверждение данного рода, относимое к любым замкнутым цепям, называют вторым правилом Кирхгофа.

Сформулируем данное правило так:

Алгебраическая сумма произведений сил токов на сопротивления по любому замкнутому контуру, равна суммарной ЭДС, которые входят в рассматриваемый контур.

Произведение силы тока на сопротивление участка цепи считают большим нуля, если избранное направление обхода контура совпадает с направлением течения тока на этом участке. В противном случае произведение отрицательно.

ЭДС считают положительной, если в результате обхода контура в источнике осуществляется переход от полюса со знаком минус к полюсу со знаком плюс.

При неизвестном направлении токов, их направления принимают произвольно. Если в результате вычислений получают знак минус для рассматриваемого тока, то это значит, что верным направлением тока будет противоположное принятому.N {I_{m}R_{m}\left( 11\right),} $

где $N$ – количество участков избранного контура.

Второе правило Кирхгофа позволяет записать независимые уравнения только для контуров сложной цепи, которые не получены наложением уже описанных.

Количество независимых контуров ($n_2$) можно определить:

$n_2=p-m+1$(12),

где $p$ – количество ветвей в цепи; $m$- количество узлов.

Анализ ситуаций с участием внешних сил

В предыдущей части Урока 2 обсуждалась взаимосвязь между работой и изменением энергии. Всякий раз, когда над объектом воздействует внешняя сила, происходит изменение общей механической энергии объекта. Если только внутренние силы выполняют работу (не работают внешние силы), общая механическая энергия не изменяется; общая механическая энергия составляет сохраненных . Поскольку внешние силы способны изменять общую механическую энергию объекта, их иногда называют неконсервативными силами.Поскольку внутренние силы не изменяют общую механическую энергию объекта, их иногда называют консервативными силами. В этой части Урока 2 мы продолжим исследовать количественную связь между работой и энергией.

Работа с энергией

Количественная связь между работой и механической энергией выражается следующим уравнением:

TME _i + W _доб = TME _f

Уравнение утверждает, что начальное количество полной механической энергии (TME _i ) плюс работа, совершаемая внешними силами (W _ext ), равно конечному количеству полной механической энергии (TME _f ).Следует сделать несколько замечаний по поводу приведенного выше уравнения. Во-первых, механическая энергия может быть либо потенциальной энергией (в этом случае она может быть вызвана пружинами или гравитацией), либо кинетической энергией. Учитывая этот факт, приведенное выше уравнение можно переписать как

KE _i + PE _i + W _ext = KE _f + PE _f

Второе замечание, которое следует сделать в отношении приведенного выше уравнения, заключается в том, что работа, совершаемая внешними силами, может быть положительной или отрицательной.Принимает ли рабочий член положительное или отрицательное значение, зависит от угла между силой и движением. Вспомните из Урока 1, что работа зависит от угла между векторами силы и смещения. Если угол составляет 180 градусов, а иногда бывает, то рабочий срок будет отрицательным. Если угол равен 0 градусов, то рабочий член будет положительным.

Приведенное выше уравнение выражает количественную связь между работой и энергией. Это уравнение будет основой для остальной части этого устройства.Это сформирует основу концептуального аспекта нашего исследования работы и энергии, а также , руководящего force для нашего подхода к решению математических задач. большой срез мира движения можно понять, используя эту взаимосвязь между работой и энергией.

Подъем штанги вертикально

Чтобы начать наше исследование отношения работа-энергия, мы исследуем ситуации, в которых работа выполняется внешними силами (неконсервативными силами).Представьте себе штангиста, который прилагает к штанге направленную вверх силу (скажем, 1000 Н), чтобы переместить ее вверх на заданное расстояние (скажем, 0,25 метра) с постоянной скоростью. Начальная энергия плюс работа, совершаемая внешней силой, равняется конечной энергии. Если штанга начинается с 1500 Джоулей энергии (это просто выдуманное значение), а штангист выполняет 250 Джоулей работы (F • d • косинус угла = 1000 Н • 0,25 м • косинус 0 градусов = 250 Дж), тогда штанга наберет 1750 Джоулей механической энергии. Конечное количество механической энергии (1750 Дж) равно начальному количеству механической энергии (1500 Дж) плюс работа, совершаемая внешними силами (250 Дж).

Ловля бейсбола

Теперь рассмотрим бейсбольного кетчера, который применяет направленную вправо силу (скажем, 6000 Н) к бейсбольному мячу, движущемуся влево, чтобы перевести его с высокой скорости в исходное положение на заданном расстоянии (скажем, 0,10 метра). Начальная энергия плюс работа, совершаемая внешней силой, равняется конечной энергии. Если мяч начинается с 605 Джоулей энергии (это просто еще одно придуманное значение), а ловец выполняет -600 Джоулей работы (F • d • косинус угла = 6000 Н • 0.10 м • косинус 180 градусов = -600 Дж), то мяч закончится с 5 Джоулями механической энергии. Конечная энергия (5 Дж) равна начальной энергии (605 Дж) плюс работа, совершаемая внешними силами (-600 Дж).

Тренажер

Теперь рассмотрим автомобиль, который заносит с высокой скорости на более низкую. Сила трения между шинами и дорогой оказывает левое воздействие (скажем, 8000 Н) на движущийся вправо автомобиль на заданном расстоянии (скажем, 30 м).Начальная энергия плюс работа, совершаемая внешней силой, равняется конечной энергии. Если автомобиль начинается с 320 000 Джоулей энергии (это просто еще одно придуманное значение), а сила трения составляет -240 000 Джоулей работы (F • d • косинус угла = 8000 Н • 30 м • косинус 180 градусов = -240 000 Дж), то машина финиширует с 80 000 Джоулей механической энергии. Конечная энергия (80 000 Дж) равна начальной энергии (320 000 Дж) плюс работа, совершаемая внешними силами (-240 000 Дж).

Вытягивание тележки по наклонной поверхности с постоянной скоростью

В качестве последнего примера рассмотрим тележку, которую студент поднимает по наклонной плоскости с постоянной скоростью во время лабораторной работы по физике.Приложенная к тележке сила (скажем, 18 Н) направлена ​​параллельно уклону, заставляя тележку смещаться параллельно уклону при заданном смещении (скажем, 0,7 м). Начальная энергия плюс работа, совершаемая внешней силой, равняется конечной энергии. Если тележка начинается с 0 Джоулей энергии (это просто еще одно придуманное значение), а ученик выполняет 12,6 Джоулей работы (F • d • косинус угла = 18 Н • 0,7 м • косинус 0 градусов = 12,6 Дж), тогда тележка закончится с 12,6 Джоулями механической энергии.Конечная энергия (12,6 Дж) равна начальной энергии (0 Дж) плюс работа, совершаемая внешними силами (12,6 Дж).

В каждом из этих примеров внешняя сила действует на объект на заданном расстоянии, изменяя общую механическую энергию объекта. Если внешняя сила (или неконсервативная сила) совершает положительную работу, то объект получает механическую энергию. Количество полученной энергии равно работе, проделанной над объектом.Если внешняя сила (или неконсервативная сила) совершает отрицательную работу, то объект теряет механическую энергию. Количество потерянной механической энергии равно работе, проделанной над объектом. В общем, полная механическая энергия объекта в начальном состоянии (до выполнения работы) плюс проделанная работа равняется полной механической энергии в конечном состоянии.

Ваша очередь попробовать

Представленное здесь соотношение работы и энергии можно комбинировать с выражениями для потенциальной и кинетической энергии для решения сложных задач.Как и все сложные задачи, их можно сделать простыми , если сначала проанализировать их с концептуальной точки зрения и разбить на части. Другими словами, избегайте рассматривать проблемы рабочей энергии как простые математические проблемы. Скорее займитесь своим умом и используйте свое понимание физических концепций, чтобы подойти к проблеме. Спросите: «Какие формы энергии присутствуют изначально и в конечном итоге?» и «Основываясь на уравнениях, какое количество каждой формы энергии присутствует изначально и в конечном итоге?» и «Работают ли внешние силы?» Используйте этот подход для решения следующих трех практических задач.После решения нажмите кнопку, чтобы просмотреть ответы.

Хотим предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного интерактивного приложения «Это все в гору» и / или интерактивного интерактивного интерфейса «Тормозной путь».Оба интерактивных элемента можно найти в разделе «Интерактивная физика» на нашем веб-сайте, и они предоставляют интерактивную возможность изучить значение взаимосвязи между работой и энергией.

Практическая задача № 1

Автомобиль массой 1000 кг, движущийся со скоростью 25 м / с, останавливается в салазках. Автомобиль испытывает силу трения 8000 Н. Определите тормозной путь автомобиля.

Практическая задача № 2

В конце поездки на американских горках “Ударная волна” 6000-килограммовый состав вагонов (включая пассажиров) замедляется со скорости 20 м / с до скорости 5 м / с на расстоянии 20 метров.Определите тормозное усилие, необходимое для замедления поезда на эту величину.

Практическая задача № 3

Тележка с продуктами стоит на вершине холма высотой 2,0 м. Тележка начинает катиться, пока не наткнется на пень у подножия холма. При ударе банка персиков массой 0,25 кг вылетает из тележки горизонтально и ударяется о припаркованный автомобиль со средней силой 500 Н.Насколько глубока вмятина в автомобиле (т.е. на каком расстоянии сила 500 Н действует на банку с персиками, прежде чем она остановится)?

Тормозной путь

Все три вышеупомянутые проблемы имеют одну общую черту: существует сила, действующая на расстоянии, чтобы отводить механическую энергию от объекта.2) объекта связана с кинетической энергией, также должна быть прямая связь между тормозным путем и квадратом скорости. Обратите внимание на вывод ниже.

TME _i + W _доб = TME _f

KE _i + W _ext = 0 Дж

0,5 • m • v _i ² + F • d • cos (Theta) = 0 Дж

0,5 • м • v _i ² = F • d

v _i ² d

Вышеприведенное уравнение показывает, что тормозной путь зависит от квадрата скорости .Это означает, что двукратное увеличение скорости приведет к четырехкратному (два в квадрате) увеличению тормозного пути. Трехкратное увеличение скорости приведет к девятикратному (трехкратному) увеличению тормозного пути. А четырехкратное увеличение скорости приведет к шестнадцатикратному (четыре в квадрату) увеличению тормозного пути. Это еще один пример, в котором уравнение становится больше, чем просто алгебраическим рецептом решения проблем. Уравнения также могут быть мощным руководством к размышлениям о том, как две величины связаны друг с другом.В случае действия горизонтальной силы, заставляющей объект останавливаться на некотором горизонтальном расстоянии, тормозной путь объекта связан с квадратом скорости объекта.

Проверьте свое понимание, предсказав значения тормозного пути в таблице ниже (и просмотрите практические задачи в конце этой страницы).

Скорость (м / с)	Остановочный путь (м)
0 м / с	0
5 м / с	4 мес.
10 м / с
15 м / с
20 м / с
25 м / с

Вышеупомянутый принцип – тормозной путь пропорционален квадрату скорости – часто находится в центре внимания популярных физических лабораторий.Автомобиль Hot Wheels катится по наклонной плоскости на этаж ниже. Достигнув пола, он ударяется об ящик компьютерных дискет и останавливается в результате трения между системой автомобиль / ящик и полом. Время фотосъемки используется для определения скорости автомобиля до удара по ящику. Выполняется несколько испытаний, собирается набор данных и наносится на график. По мере увеличения скорости автомобиля тормозной путь увеличивается. Если данные нанесены на график, то видно четкое соотношение мощности.Если для набора данных выполняется степенная регрессия, результаты обычно показывают, что d = k • v ² , где k – константа пропорциональности.

Примеры, упомянутые на этой странице, включают применение отношения работа-энергия к ситуациям, в которых задействованы внешние или неконсервативные силы, выполняющие работу. Совершенно иной исход приводит к ситуациям, в которых не работают внешние силы. Следующая часть Урока 2 включает анализ этих ситуаций.

Кинетическая энергия и теорема работы-энергии

Цели обучения

К концу этого раздела вы сможете:

• Объясните работу как передачу энергии, а чистую работу – как работу, совершаемую чистой силой.
• Объясните и примените теорему работы-энергии.

Работа передает энергию

Что происходит с работой, выполняемой в системе? Энергия передается в систему, но в какой форме? Он останется в системе или продвинется дальше? Ответы зависят от ситуации.Например, если на газонокосилку на Рисунке 1а толкнуть достаточно сильно, чтобы она продолжала работать с постоянной скоростью, тогда энергия, вложенная в газонокосилку человеком, непрерывно удаляется за счет трения и в конечном итоге покидает систему в виде теплопередачи. . Напротив, работа, проделанная с портфелем человеком, несущим его по лестнице на рисунке 1d, хранится в системе портфель-Земля и может быть восстановлена ​​в любое время, как показано на рисунке 1e. Фактически, строительство пирамид в Древнем Египте является примером хранения энергии в системе путем выполнения работы с системой.Некоторая энергия, передаваемая каменным блокам при их подъеме во время строительства пирамид, остается в системе камень-Земля и имеет потенциал для выполнения работы.

Рисунок 1. Примеры работы. (a) Работа, выполняемая силой F на этой газонокосилке, составляет Fd cos θ . Обратите внимание, что F cos θ – это составляющая силы в направлении движения. (б) Человек, держащий портфель, не работает с ним, потому что нет движения.Энергия не передается ни в чемодан, ни из него. (c) Человек, перемещающий портфель в горизонтальном направлении с постоянной скоростью, не работает с ним и не передает ему энергию. (d) Работа с портфелем выполняется путем его подъема по лестнице с постоянной скоростью, поскольку обязательно присутствует составляющая силы F в направлении движения. Энергия передается в портфель и, в свою очередь, может использоваться для работы. e) когда портфель опускается, энергия передается из портфеля в электрический генератор.Здесь работа, выполняемая генератором с портфелем, является отрицательной, что приводит к отведению энергии из портфеля, потому что F и d находятся в противоположных направлениях.

В этом разделе мы начинаем изучение различных видов работы и форм энергии. Мы обнаружим, что некоторые виды работы, например, оставляют энергию системы постоянной, тогда как другие каким-то образом изменяют систему, например заставляют ее двигаться. Мы также разработаем определения важных форм энергии, таких как энергия движения.

Чистая работа и теорема работы-энергии

Мы знаем из изучения законов Ньютона в динамике: сила и законы движения Ньютона, что результирующая сила вызывает ускорение. В этом разделе мы увидим, что работа, совершаемая чистой силой, дает системе энергию движения, и в процессе мы также найдем выражение для энергии движения.

Давайте начнем с рассмотрения общей, или чистой, работы, проделанной в системе. Чистая работа определяется как сумма работы, выполненной всеми внешними силами, то есть чистая работа – это работа, выполненная чистой внешней силой F _чистая .В форме уравнения это W _net = F _net d cos θ , где θ – угол между вектором силы и вектором смещения.

На рис. 2а показан график зависимости силы от смещения для составляющей силы в направлении смещения, то есть график F cos θ против d . В этом случае F cos θ является постоянным. Вы можете видеть, что площадь под графиком равна Fd cos θ , или проделанной работе.На рис. 2b показан более общий процесс изменения силы. Площадь под кривой разделена на полосы, каждая из которых имеет среднюю силу ( F cos θ ) _{i (средн.)} . Выполненная работа составляет ( F cos θ ) _{i (средн.)} d _i для каждой полосы, а общая проделанная работа равна сумме W _i . Таким образом, общая проделанная работа – это общая площадь под кривой, полезное свойство, о котором мы поговорим позже.

Рис. 2. (a) График F cos θ от d , когда F cos θ является постоянным. Площадь под кривой представляет работу, совершаемую силой. (б) График зависимости F cos θ от d , в котором сила изменяется. Работа, проделанная для каждого интервала, – это площадь каждой полосы; таким образом, общая площадь под кривой равна общей проделанной работе.

Чистую работу будет проще исследовать, если мы рассмотрим одномерную ситуацию, когда сила используется для ускорения объекта в направлении, параллельном его начальной скорости.Такая ситуация возникает для упаковки на ленточном роликовом конвейере, показанном на Рисунке 3.

Рис. 3. Пакет на роликовой ленте продвигается горизонтально на расстояние d .

Сила тяжести и нормальная сила, действующая на упаковку, перпендикулярны перемещению и не работают. Более того, они также равны по величине и противоположны по направлению, поэтому они сокращаются при вычислении чистой силы. Чистая сила возникает исключительно из приложенной горизонтальной силы F _app и горизонтальной силы трения f .Таким образом, как и ожидалось, чистая сила параллельна смещению, так что θ = 0º и cos θ = 1, а чистая работа определяется как W _net = F _net д .

Эффект чистой силы F _net заключается в ускорении пакета с v ₀ до v . Кинетическая энергия пакета увеличивается, указывая на то, что чистая работа, выполняемая в системе, является положительной.(См. Пример 1.) Используя второй закон Ньютона и занимаясь алгеброй, мы можем прийти к интересному выводу. Подстановка F _net = ma из второго закона Ньютона дает W _net = mad .

Чтобы получить взаимосвязь между работой сети и скоростью, придаваемой системе действующей на нее чистой силой, возьмем d = x – x ₀ и воспользуемся уравнением, изученным в уравнениях движения для постоянного ускорения. в одном измерении для изменения скорости на расстоянии d , если ускорение имеет постоянное значение a ; а именно, v ² = v ₀ ² + 2 ad (обратите внимание, что a появляется в выражении для чистой работы).2 \\ [/ latex], это энергия, связанная с поступательным движением. Кинетическая энергия – это форма энергии, связанная с движением частицы, отдельного тела или системы объектов, движущихся вместе.

Мы знаем, что требуется энергия, чтобы привести объект, такой как автомобиль или пакет на Рисунке 3, к скорости, но может быть немного удивительно, что кинетическая энергия пропорциональна квадрату скорости. Эта пропорциональность означает, например, что автомобиль, движущийся со скоростью 100 км / ч, имеет в четыре раза большую кинетическую энергию, чем при 50 км / ч, что помогает объяснить, почему столкновения на высокой скорости настолько разрушительны.Теперь мы рассмотрим серию примеров, чтобы проиллюстрировать различные аспекты работы и энергии.

Пример 1. Расчет кинетической энергии упаковки

Предположим, что 30,0-килограммовая упаковка на роликовой ленточной конвейерной системе, показанной на рисунке 3, движется со скоростью 0,500 м / с. Какова его кинетическая энергия?

Стратегия

Поскольку даны масса м и скорость v , кинетическая энергия может быть рассчитана на основе ее определения, приведенного в уравнении [латекс] \ text {KE} = \ frac {1} {2} mv ^ 2 \ \[/латекс].2 \\ [/ латекс].

Ввод известных значений дает KE = 0,5 (30,0 кг) (0,500 м / с) ² , что дает

KE = 3,75 кг м ² / с ² = 3,75 Дж.

Обсуждение

Обратите внимание, что единицей кинетической энергии является джоуль, то же самое, что и единица работы, как упоминалось при первом определении работы. Также интересно то, что, хотя это довольно массивный пакет, его кинетическая энергия невелика при такой относительно низкой скорости. Этот факт согласуется с наблюдением, что люди могут перемещать пакеты таким образом, не изнуряя себя.

Пример 2. Определение работы по ускорению пакета

Предположим, что вы толкаете 30,0-килограммовый пакет, показанный на рис. 3, с постоянной силой 120 Н на расстояние 0,800 м, а сила трения противоположной стороны в среднем составляет 5,00 Н.

1. Рассчитайте чистую работу, проделанную с упаковкой.
2. Решите ту же проблему, что и в части 1, на этот раз определив работу, выполняемую каждой силой, которая вносит вклад в результирующую силу.

Стратегия и концепция части 1

Это движение в задаче одного измерения, потому что направленная вниз сила (от веса упаковки) и нормальная сила имеют равную величину и противоположное направление, так что они компенсируются при вычислении чистой силы, в то время как приложенная сила, трение, и смещения все горизонтальные.(См. Рисунок 3.) Как и ожидалось, чистая работа – это чистая сила, умноженная на расстояние.

Решение для Части 1

Чистая сила равна толкающей силе минус трение, или F _net = 120 Н – 5,00 Н = 115 Н. Таким образом, чистая работа равна

[латекс] \ begin {array} {lll} W _ {\ text {net}} & = & F _ {\ text {net}} d = (115 \ text {N}) (0.800 \ text {m}) \\ \ text {} & = & 9.20 \ text {N} \ cdot {\ text {m}} = 92.0 \ text {J} \ end {array} \\ [/ latex]

Обсуждение части 1

Это значение представляет собой чистую работу, выполненную с пакетом.Человек на самом деле выполняет больше работы, потому что трение препятствует движению. Трение совершает негативную работу и удаляет часть энергии, которую человек тратит, и преобразует ее в тепловую энергию. Чистая работа равна сумме работы, проделанной каждой отдельной силой.

Стратегия и концепция части 2

К силам, действующим на упаковку, относятся сила тяжести, нормальная сила, сила трения и приложенная сила. Нормальная сила и сила тяжести перпендикулярны перемещению и поэтому не работают.{\ circ}) = F _ {\ text {fr}} d \\\ text {} & = & – (5.00 \ text {N}) (0.800 \ text {m}) \\\ text {} & = & -4.00 \ text {J} \ end {array} \\ [/ latex]

Таким образом, количество работы, совершаемой гравитацией, нормальной силой, приложенной силой и трением, составляет, соответственно,

.

[латекс] \ begin {array} {lll} W _ {\ text {gr}} & = & 0, \\ W _ {\ text {N}} & = & 0, \\ W _ {\ text {app}} & = & 96.0 \ text {J}, \\ W _ {\ text {fr}} & = & – 4.00. \ Text {J} \ end {array} \\ [/ latex]

Общая проделанная работа как сумма работы, выполненной каждой силой, тогда составляет Вт _итого = Вт _gr + W _N + W _app + W _фр = 92.0 Дж.

Обсуждение части 2

Расчетная общая работа Вт _итого , поскольку сумма работы каждой силы согласуется, как и ожидалось, с работой Вт _нетто , выполненной чистой силой. Работа, выполняемая совокупностью сил, действующих на объект, может быть рассчитана любым подходом.

Пример 3. Определение скорости работы и энергии

Найдите скорость пакета на Рисунке 3 в конце толчка, используя концепции работы и энергии.2} {30.0 \ text {kg}}} \\\ text {} & = & 2.53 \ text {m / s} \ end {array} \\ [/ latex]

Обсуждение

Используя работу и энергию, мы не только приходим к ответу, мы видим, что конечная кинетическая энергия – это сумма начальной кинетической энергии и чистой работы, проделанной с упаковкой. Это означает, что работа действительно увеличивает энергию упаковки.

Пример 4. Работа и энергия тоже могут определять расстояние

Как далеко паковка на рис. 3 продвигается по инерции после толчка, если трение остается постоянным? Используйте соображения работы и энергии.

Стратегия

Мы знаем, что как только человек перестанет толкать, трение остановит упаковку. Что касается энергии, трение выполняет отрицательную работу до тех пор, пока не убирает всю кинетическую энергию упаковки. Работа, совершаемая трением, – это сила трения, умноженная на пройденное расстояние, умноженное на косинус угла между силой трения и смещением; следовательно, это дает нам способ определить расстояние, пройденное после того, как человек прекратил толкать.

Решение

Нормальная сила и сила тяжести отменяются при вычислении чистой силы.Горизонтальная сила трения тогда представляет собой результирующую силу, и она действует противоположно смещению, поэтому θ = 180º. Чтобы уменьшить кинетическую энергию пакета до нуля, работа за счет трения должна быть минус кинетическая энергия, с которой пакет был запущен, плюс то, что пакет накопил в результате толкания. Таким образом, W _fr = -95,75 Дж. Кроме того, W _fr = f d ′ cos θ = – fd ′, где d ′ – расстояние, необходимое для останавливаться.Таким образом,

[латекс] \ displaystyle {d} \ prime = – \ frac {W _ {\ text {fr}}} {f} = – \ frac {-95,75 \ text {J}} {5,00 \ text {N}} \ \ [/ латекс]

и поэтому d ′ = 19,2 м.

Обсуждение

Это разумное расстояние, на котором упаковка может двигаться по инерционной катушке на конвейерной системе без трения. Обратите внимание, что работа, совершаемая трением, отрицательна (сила направлена ​​в противоположном направлении движения), поэтому она снимает кинетическую энергию.

Некоторые из примеров в этом разделе могут быть решены без учета энергии, но за счет упущения понимания того, какая работа и энергия делают в этой ситуации.2 \\ [/ латекс].

Концептуальные вопросы

1. Человек на Рисунке 4 работает с газонокосилкой. При каких условиях газонокосилка будет набирать энергию? При каких условиях он потеряет энергию?

   Рисунок 4.

2. Человек, толкающий газонокосилку с силой F. Сила представлена ​​вектором, составляющим угол тета ниже горизонтали, а расстояние, пройденное движителем, представлено вектором d. Компонент вектора F вдоль вектора d равен F косинус тета.Работа, проделанная человеком, W равна F d косинус тета.
   Работа, проделанная в системе, вкладывает в нее энергию. Работа, выполняемая системой, лишает ее энергии. Приведите пример для каждого утверждения.
3. При вычислении скорости в примере 3 мы сохранили только положительный корень. Почему?

Задачи и упражнения

1. Сравните кинетическую энергию грузовика массой 20 000 кг, движущегося со скоростью 110 км / ч, с кинетической энергией космонавта весом 80,0 кг на орбите, движущегося со скоростью 27 500 км / ч.
2. (a) Насколько быстро должен двигаться слон весом 3000 кг, чтобы иметь такую ​​же кинетическую энергию, как 65-й слон.Спринтер 0 кг бежит со скоростью 10,0 м / с? (б) Обсудите, как большая энергия, необходимая для передвижения более крупных животных, будет связана со скоростью метаболизма.
3. Какое значение имеет кинетическая энергия авианосца массой 90 000 тонн на скорости 30 узлов? Вам нужно будет найти определение морской мили (1 узел = 1 морская миля / ч).
4. (a) Рассчитайте усилие, необходимое для остановки автомобиля массой 950 кг со скорости 90,0 км / ч на расстоянии 120 м (довольно типичное расстояние для остановки без паники).(b) Предположим, что вместо этого автомобиль на полной скорости врезается в бетонную опору и останавливается через 2,00 м. Вычислите силу, действующую на автомобиль, и сравните ее с силой, указанной в части (а).
5. Бампер автомобиля спроектирован таким образом, чтобы выдерживать столкновение с неподвижным предметом на скорости 4,0 км / ч (1,1 м / с) без повреждения кузова автомобиля. Бампер амортизирует удар, поглощая силу на расстоянии. Вычислите величину средней силы, действующей на бампер, который разрушается на 0,200 м при остановке автомобиля массой 900 кг с начальной скорости, равной 1.1 м / с.
6. Боксерские перчатки имеют мягкую подкладку для уменьшения силы удара. (a) Рассчитайте силу, прилагаемую боксерской перчаткой к лицу соперника, если перчатка и лицо сжимают 7,50 см во время удара, при котором рука и перчатка весом 7,00 кг останавливаются с начальной скорости 10,0 м / с. (b) Рассчитайте силу, оказываемую идентичным ударом в старые кровавые времена, когда не использовались перчатки, а суставы и лицо сжимались только на 2 см. (c) Обсудите величину силы в перчатке. Кажется, что он достаточно высок, чтобы нанести урон, даже если он ниже, чем сила без перчатки?
7. Используя соображения энергии, вычислите среднюю силу a 60.Спринтер весом 0 кг делает движение назад по трассе для ускорения от 2,00 до 8,00 м / с на расстоянии 25,0 м, если он встречает встречный ветер, который оказывает на него среднюю силу 30,0 Н.

Глоссарий

чистая работа: работа, выполненная чистой силой или векторной суммой всех сил, действующих на объект

теорема работы-энергии: результат, основанный на законах Ньютона, что чистая работа, выполненная над объектом, равна его изменению кинетической энергии

кинетическая энергия: энергия, которую объект имеет в результате своего движения, равная [latex] \ frac {1} {2} {\ text {mv}} ^ {2} \\ [/ latex] для поступательного (я.е., без вращения) движение объекта массой м , движущегося со скоростью v

Избранные решения проблем и упражнения

1. [латекс] \ frac {1} {250} \\ [/ latex]

3. 1,1 × 10 ¹⁰

5. 2,8 × 10 ³ N

7. 102 N

7. РАБОЧАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ

7. РАБОЧАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ

---

В этой главе мы познакомимся с понятиями работы и кинетической энергии.Эти инструменты значительно упростят решение некоторых проблем. можно решить.

Рисунок 7.1. Сила F , действующая на тело. Результирующий смещение обозначается вектором d .

Предположим, что на тело действует постоянная сила F, пока объект движется по расстояние d. И сила F, и смещение d являются векторами, которые не являются обязательно указывая в том же направлении (см. рисунок 7.1). Работа проделана сила F, действующая на объект, когда он претерпевает смещение d, определяется как

Работа, совершаемая силой F, равна нулю, если:

* d = 0: смещение равно нулю

* [phi] = 90 градусов: сила, перпендикулярная перемещению

Рис. 7.2. Положительная или отрицательная работа.

Работа, совершаемая силой F, может быть положительной или отрицательной, в зависимости от [фи].Например, предположим, что у нас есть объект, движущийся с постоянной скоростью. В момент времени t = 0 с прикладывается сила F. Если F – единственная сила, действующая на тело, объект будет либо увеличивать, либо уменьшать свою скорость в зависимости от указывают ли скорость v и сила F на одно и то же направление (см. рисунок 7.2). Если ( F * v )> 0, скорость объект будет увеличиваться, и работа, выполняемая силой над объектом, будет положительной. Если ( F * v ) <0, скорость объекта уменьшится и работа, выполняемая силой, воздействующей на объект, отрицательна.Если ( F * v ) = 0 мы имеем дело с центростремительным движением и скорость объекта остается постоянный. Обратите внимание, что для силы трения ( F * v ) <0 (всегда) и скорость объекта всегда снижается!

По определению, работа – это скаляр. Единица работы – Джоуль (J). Из Из определения работы видно, что:

1 Дж = 1 Н · м = 1 кг · м ² / с ²

Рисунок 7.3. Силы, действующие на сейф.

Пример задачи 7-2

Сейф массой m перемещается по плиточному полу с постоянной скоростью в течение расстояние d. Коэффициент трения между дном сейфа и этаж у _к . Определите все силы, действующие на сейф и рассчитать работу, проделанную каждым из них. Какая в целом проделанная работа?

На рис. 7.3 показаны все силы, действующие на сейф. Поскольку сейф движется с постоянной скоростью, его ускорение равно нулю, а результирующая сила действующий на нем равен нулю

Компоненты чистой силы по оси x и по оси y следовательно, также должно быть ноль

Второе уравнение показывает, что N = W = m g.Применяемая сила в сейф теперь можно рассчитать

Работа, проделанная над сейфом каждой из четырех сил, теперь может быть вычислено:

Таким образом, общий объем работы, проделанной с сейфом, составляет

.

чего и следовало ожидать, поскольку чистая сила на сейфе равна нулю.

Пример задачи 1

Обрешетка массой m поднимается по откосу (угол наклона [theta]) с постоянной скоростью. Рассчитайте объем работы, проделанной усилие после того, как ящик переместился на высоту h (см. Рисунок 7.4).

Рисунок 7.4. Пример задачи 1.

Система координат, которая будет использоваться, показана на рисунке 4. Поскольку ящик движется с постоянной скоростью, результирующая сила в осях x и y направление должно быть нулевым.Чистая сила в направлении x равна

.

а сила F, необходимая для перемещения ящика с постоянной скоростью, равна фиксировано:

Эта сила действует на расстоянии d. Значение d фиксируется угол [theta] и высота h:

(см. рисунок 7.4). Работа, проделанная силой на обрешетке, дана по

Работа, проделанная с ящиком под действием силы тяжести, определяется как

.

Работа, совершаемая на обрешетке нормальной силой N, равна нулю, поскольку N равно перпендикулярно d.Делаем вывод, что общая проделанная работа по обрешетке дана по

что ожидалось, поскольку результирующая сила на ящике равна нулю.

Рисунок 7.5. Ящик перемещался в вертикальном направлении.

Если тот же ящик был поднят на высоту h по вертикали направлении (см. рисунок 7.5), сила F, необходимая для создания постоянной скорости будет равно

F = m g

Эта сила действует на расстоянии h, и работа, совершаемая этой силой на объект

W _F = m g h

что равняется работе, совершаемой силой на наклонном склоне.Хотя работа, выполняемая каждой силой, одинакова, сила требуемого сила сильно различается в каждом из двух случаев.

Пример задачи 2

Блок массой 3,57 кг вытягивается с постоянной скоростью 4,06 м по горизонтальному полу с помощью веревка, прикладывающая силу 7,68 Н под углом 15 градусов. выше горизонтали. Вычислите (а) работу, проделанную веревкой на блоке, и (б) коэффициент кинетическое трение между блоком и полом.

Рисунок 7.6. Пример задачи 2.

На массу m действуют четыре силы: гравитационная сила W, нормальная сила N, сила трения f _k и приложенная сила F. Эти четыре силы схематически показаны на рисунке 7.6. Поскольку скорость масса постоянна, его ускорение равно нулю. X и y-компоненты чистой силы, действующей на массу, равны

Поскольку результирующая сила, действующая на массу, должна быть равна нулю, последнее уравнение может использоваться для определения нормальной силы N:

Кинетическая сила трения f _k определяется как

.

Однако, поскольку чистая составляющая силы вдоль оси x должна также равна нулю, кинетическая сила трения f _k также связана с применяет силу следующим образом

Комбинируя эти последние два выражения, мы можем определить коэффициент кинетического трения:

Работу, совершаемую веревкой с массой m, можно рассчитать достаточно легко:

Работа, совершаемая силой трения, определяется по формуле

.

Работа, совершаемая нормальной силой N и весом W, равна нулю, поскольку сила и перемещение перпендикулярны.Общая работа, проделанная с массой, составляет поэтому задано

Это неудивительно, поскольку результирующая сила, действующая на массу, равна нуль.

В предыдущем обсуждении мы предположили, что сила, действующая на объект постоянно (не зависит от положения и / или времени). Однако во многих случаях это неверное предположение. За счет уменьшения размера смещения (например, уменьшив интервал времени), мы можем получить интервал более сила которого почти постоянна.Работа, проделанная за этот небольшой промежуток времени (dW) можно рассчитать

Общая работа, совершаемая силой F, равна сумме всех dW

.

Пример: пружина

Примером переменного усилия является сила пружины. что растягивается или сжимается. Предположим, мы определяем нашу систему координат таким образом что его начало совпадает с концом пружины в расслабленном состоянии (см. рисунок 7.7). Пружина растягивается, если x> 0, и сжимается, если x < 0. Сила, прилагаемая пружиной, будет пытаться вернуть пружину в исходное положение. расслабленное состояние:

, если x <0: F> 0

, если x> 0: F <0

Экспериментально установлено, что для многих пружин сила пропорционально x:

F = – k x

Рисунок 7.7. Расслабленные, растянутые и сжатые пружины.

где k – жесткость пружины (положительная и не зависящая от Икс).Единицы СИ для жесткости пружины – Н / м. Чем больше пружина постоянная, тем жестче пружина. Работа, проделанная пружиной на объекте прикрепленный к его концу, можно вычислить, если мы знаем начальное положение x _i и конечное положение x _f объекта:

Если пружина изначально находится в расслабленном состоянии (x _i = 0) находим, что к весне проделанная работа

Рисунок 7.8. Маятник в плоскости x-y

Рассмотрим маятник, показанный на рисунке 7.8. Маятник перемещается из из положения 1 в положение 2 с помощью постоянной силы F, направленной в горизонтальном направлении. направление (см. рисунок 7.8). Масса маятника m. Что за работа осуществляется суммой приложенной силы и гравитационной силы, чтобы переместить маятник из положения 1 в положение 2?

Метод 1 – сложный

Векторная сумма приложенной силы и гравитационной силы равна показано на рисунке 7.9. Угол между приложенной силой F и векторной суммой F _t – это. На рисунке 7.9 показано, что следующие уравнения связывают F с F _т и F _{г от} до F _т :

Рисунок 7.9. Векторная сумма F _т из F _г и F.

Чтобы рассчитать работу, выполненную общей силой на маятник, нам нужно знать угол между полной силой и направлением движения.Рисунок 7.10 показывает, что если угол между маятником и Ось Y – [тета], угол между общей силой и направлением движение равно [тета] + а. Расстояние dr зависит от d [тета]:

Для очень небольшого расстояния dr угол между dr и F _t не изменится. Работа, проделанная F _t на маятнике, указана в

.

Общая работа, проделанная F _t , может быть получена путем интегрирования уравнение для dW по всем углам между [theta] = 0deg.и [тета] = [theta] _макс. . Максимальный угол легко выразить через r и h:

Рисунок 7.10. Угол между суммарной силой и направлением.

Всего выполнено

работ.

Используя одно из тригонометрических тождеств (Приложение, стр. A15), мы можем перепишите это выражение как

Используя приведенные выше уравнения для F _t cos (a), F _t sin (a), r cos ([theta] _max ) и r sin ([theta] _max ) мы можем перепишем это выражение и получим для W:

Метод 2 – простой

Суммарная работа, совершенная на маятнике приложенной силой F и гравитационная сила F _g могла быть получена намного проще, если бы было использовано соотношение:

Общая работа W – это сумма работы, совершенной приложенной силой F и работа, совершаемая силой тяжести F _g .Эти две величины легко рассчитывается:

А всего работ

что идентично результату, полученному с использованием метода 1.

Наблюдение за движением объекта с определенной скоростью указывает на что когда-то в прошлом над этим, должно быть, велась работа.Предположим, наш объект имеет массу m и движется со скоростью v. Его текущая скорость равна результат действия силы F. Для данной силы F мы можем получить ускорение нашего объект:

Предполагая, что объект находился в состоянии покоя в момент времени t = 0, мы можем получить скорость в любое более позднее время:

Следовательно, время, за которое масса достигает скорости v, может быть вычислено:

Если в это время выключить силу, масса продолжит двигаться с постоянная скорость, равная v.Чтобы рассчитать работу, проделанную силы F на массу, нам нужно знать общее расстояние, на котором эта сила действовал. Это расстояние d легко найти из уравнений движения:

Работа, совершаемая силой F над массой, равна

.

Работа не зависит от силы силы F и зависит только от от массы объекта и его скорости.Поскольку эта работа связана с движение объекта, оно называется его кинетической энергией K :

Если кинетическая энергия частицы изменяется от некоторого начального значения K _i до некоторого окончательного значения K _f объем выполненных работ на частица задается формулой

W = K _f – K _i

Это указывает на то, что изменение кинетической энергии частицы равно равной общей работе, совершенной над этой частицей всеми силами, действующими на Это.

Альтернативная деривация

Рассмотрим частицу с массой m, движущуюся вдоль оси x и на которую действует сеть сила F (x), которая указывает вдоль оси x. Работа, совершаемая силой F на массы m, когда частица перемещается из исходного положения x _i в свое конечная позиция x _f –

Из определения a мы можем заключить

Подставляя это выражение в интеграл, получаем

Пример задачи 3

Объект с массой m находится в состоянии покоя в момент времени t = 0.Подпадает под влияние силы тяжести на расстояние h (см. рисунок 7.11). Что это за скорость в этой точке?

Поскольку объект изначально находится в состоянии покоя, его начальная кинетическая энергия равна нулю:

K _i = 0 Дж

Сила, действующая на объект, – это сила тяжести

F _g = m g

Рисунок 7.11. Падающий объект.

Работа, совершаемая гравитационной силой над объектом, просто равна

W = F _g h = m g h

Кинетическая энергия объекта после падения на расстояние h может быть рассчитано:

W = ^м. г ^. h = K _f – K _i = К _f

а его скорость в этой точке равна

Рисунок 7.12. Движение снаряда.

Пример задачи 4

Бейсбольный мяч подбрасывается в воздух с начальной скоростью v ₀ (см. Рисунок 7.12). Какой наивысшей точки он достигает?

Начальная кинетическая энергия бейсбольного мяча –

.

В самой высокой точке скорость бейсбольного мяча равна нулю, и поэтому его кинетическая энергия равна нулю.Проделанная работа по бейсболу по силе тяжести можно получить:

W = K _f – K _i = – K _i

В этом случае направление перемещения мяча противоположное. к направлению силы тяжести. Предположим, что бейсбол достигает высота h. На этом этапе работа, проделанная с бейсбольным мячом, составляет

W = – m g h

Теперь можно рассчитать максимальную высоту h:

В повседневной жизни объем работы, который может выполнять аппарат, не велик. всегда важно.В общем, важнее знать время в пределах который может быть проделан определенный объем работы. Например: взрывной эффект динамита основан на его способности выделять большое количество энергии в очень короткое время. Такой же объем работы можно было бы проделать с помощью небольшого обогреватель (и если он работает в течение длительного времени), но обогреватель не вызвать взрыва. Интересующая величина – это мощность. Сила говорит нам кое-что о скорости выполнения работы.Если объем работы W равен выполняется во временном интервале [Delta] t, средняя мощность для этого временной интервал

Мгновенную мощность можно записать как

.

Единица измерения мощности в системе СИ – Дж / с или Вт (Ватт). Например, наше использование электричество всегда выражается в киловаттах ^. час. Этот эквивалентно

7.3.1. кВт ^. ч = (10 ³ Вт) (3600 с) = 3.6 х 10 ⁶ Дж = 3,6 МДж

Мы также можем выразить мощность, передаваемую телу, через силу что действует на тело и его скорость. Таким образом, для частицы, движущейся в одном размер получаем

В более общем случае движения в трех измерениях мощность P может быть выражается как

---

Отправляйте комментарии, вопросы и / или предложения по электронной почте на адрес wolfs @ pas.rochester.edu и / или посетите домашнюю страницу Фрэнка Вольфса.

Work – The Physics Hypertextbook

Обсуждение

что такое работа?

Целевая аудитория этой книги – люди с некоторым образованием. Это не детская книга; и под детьми я не имею в виду противоположность взрослых. Я считаю подростков (или подростков, если хотите) прото-взрослыми. Если это относится к вам, значит, у вас было формальное научное образование (хорошее, плохое или уродливое).Где-то по ходу дела вы должны были познакомиться с концепцией энергии. Если нет, то перестаньте читать это и найдите себе образование (или хотя бы какой-то жизненный опыт).

Те из вас, у кого было небольшое формальное образование, вероятно, получили урок энергии в какой-то момент своей жизни. Если так, то велики шансы, что вам дали определение энергии как «способность выполнять работу». Если вы были хорошим учеником или просто хотели доставить удовольствие своему учителю, вы, вероятно, слышали это и сказали себе: «Хорошо, энергия – это способность выполнять работу.«Если бы вы были действительно хорошим учеником с желанием учиться или действительно плохим учеником с желанием указать на интеллектуальные недостатки вашего учителя, тогда вам следовало бы задать следующий логичный вопрос. Что такое работа?

Надеюсь, вам дали правильный ответ, но шансы пятьдесят на пятьдесят, что вы проигнорировали. Не потому, что правильный ответ так сложно узнать, а потому, что правильный ответ так трудно объяснить или, по крайней мере, трудно объяснить так, чтобы его можно было быстро уловить.Я думаю, это в основном связано с тем, что слово «работа» имеет два значения: обычное для повседневной жизни и техническое – для физики.

Технически работа представляет собой произведение силы-смещения (для тех из вас, кто предпочитает алгебру)

W = F ∆ s cos θ

или интеграл по путям сила-смещение (для тех из вас, кто предпочитает исчисление).

Я понимаю, что для многих из вас это бессмысленное определение.Так много слов и так мало сказано, не так ли? На самом деле, как раз наоборот. Это определение настолько компактно, что похоже на поэзию. Он говорит как можно больше, используя как можно меньше слов. Оно настолько компактно, что объяснение его на обычном языке приводит к тому, что полдюжины слов технического определения расширяются до почти сотни слов так называемого «естественного языка». Позвольте мне объяснить, что такое работа, с помощью серии мысленных образов. Каждый раз, когда приводится пример, помните, что работа выполняется всякий раз, когда сила вызывает смещение.

Представьте себе, что учитель физики неподвижно стоит перед классом учеников. Поскольку он не прилагает никаких сил, которые могли бы сместить что-либо за пределами его тела, он не выполняет никакой работы. Очевидно. Но выполнение этого в течение любого промежутка времени, безусловно, истощит его энергию, как если бы он весь день толкал бумаги по своему столу (пример, когда сила приводит к смещению ). Конечно, теперь вы могли бы убедить его, что его определение работы должно быть неправильным. Может быть, под давлением уступит меньший учитель, но не учитель физики.

Безусловно, учитель физики или любой другой человек, стоящий , – это , выполняющий работу, но проделанную работу нелегко увидеть. Внутри тела сердце перекачивает кровь, пищеварительная система переваривает завтрак, рецепторы перемещают молекулы через клеточные мембраны. Мы работаем, даже когда спим. Силы, вызывающие смещения, происходят повсюду у нас под кожей. Человеческое тело – это занятое место.

Если система в целом воздействует на свое окружение и происходит смещение, выполненная работа называется внешней работой .Учитель физики, толкая бумаги через стол, выполняет внешнюю работу. Стоящий неподвижно учитель физики не выполняет значительной внешней работы.

Если часть системы воздействует на другую часть той же системы и происходит смещение, выполненная работа называется внутренней работой . Учитель физики глубоко мыслящий или лежащий в коме выполняет внутреннюю работу. (Дополнительный балл, если вы можете отличить их.) Учитель физики, который что-то делает – или ничего не делает – выполняет внутреннюю работу.Умерший учитель физики не выполняет никакой работы, внутренней или внешней. В механике, когда мы говорим, что работа сделана, мы часто имеем в виду внешнюю работу.

Теперь, когда мы решили, что учитель, стоящий на месте, не выполняет никакой работы, давайте представим, что учитель двигается и спрашивает, была ли работа выполнена. Хм, хорошо, когда руки и ноги начинают двигаться, ситуация умеренно сложная. Это затрудняет определение того, что в движении требует работы, а что нет. Нам нужно еще немного упростить.Дайте учителю книгу (например, учебник физики) и попросите его переместить книгу несколькими простыми способами. Теперь возникает вопрос: «Выполнил ли учитель какую-нибудь работу по книге ?» Это гораздо уже, чем спрашивать, выполнял ли учитель какую-либо работу, а это значит, что на него легче ответить и он лучше подходит для ознакомления с концепцией.

Для учителя, держащего книгу или любую другую систему в этом отношении, работа выполняется всякий раз, когда сила приводит к смещению. Рассмотрим следующие шесть примеров, представленных по три за раз.

Никакая работа не выполняется с учебником, когда он находится в покое. Положительная работа выполняется с учебником, когда он поднимается вертикально с постоянной скоростью. Положительная работа также выполняется с учебником, когда он поднимается по диагонали с постоянной скоростью.

Первый пример имеет очевидный смысл. Если держать книгу, не перемещая ее, работа с книгой не выполняется. Замени учителя на стол или пол. На полу лежит книга. Какую работу выполняет пол? Ничего никуда не денется.Ничего не происходит. Ничего не делается – даже не работает.

Второй и третий примеры тоже имеют смысл. Учитель толкает книгу, и она движется. Сила привела к смещению. Работа была сделана. Это согласуется с нашим повседневным представлением о работе. Все в порядке с миром.

Рассмотрим еще три примера.

Работа с учебником не выполняется, если его переносят горизонтально с постоянной скоростью. Отрицательная работа выполняется с учебником, когда его опускают по диагонали с постоянной скоростью.Отрицательная работа также выполняется над учебником, когда он опускается вертикально с постоянной скоростью.

Первый в этом наборе надоедливый. Это нелогично. По сути, это говорит о том, что не нужно переносить книгу по ровной поверхности. Это настолько очевидно глупо, что должно быть неправильно, верно? Неправильный! Это верно. (Вы должны прочитать этот последний бит как внутренний диалог, чтобы он имел смысл.) Работа над объектом выполняется всякий раз, когда сила вызывает смещение. В этом примере приложенная сила вертикальна, но смещение горизонтально.Как вертикальная сила влияет на горизонтальное движение? Короткий ответ: «Это не так».

Вертикальные силы влияют на вертикальное движение. Горизонтальные силы влияют на горизонтальное движение. Когда движение и сила параллельны, жизнь проста. Когда движение и сила , а не параллельны, жизнь , а не просто. Ангелы уходят, и демоны вступают во владение. Под демонами я подразумеваю векторы – в частности, векторные компоненты. Работа выполняется всякий раз, когда сила или составляющая силы приводит к смещению.Никакая составляющая силы не действует в направлении движения, когда книга перемещается горизонтально с постоянной скоростью. Сила и смещение независимы. Ручная работа над книгой не выполняется.

Взгляните на последние два примера в этом наборе из шести. Здесь мы видим, что ведется негативная работа. Учитывая то, что я сказал о компонентах, это может иметь или не иметь для вас смысла. И снова, когда сила и смещение параллельны, жизнь проста.

Применить силу → Переместить объект → Выполнить работу

Когда сила не совсем параллельна смещению, это похоже на то, что для выполнения работы используется меньшая сила.

Приложите меньшее усилие → Сделайте меньше работы

Это тоже довольно просто. Когда угол между силой и смещением достигает 90 °, составляющая силы, параллельная смещению, уменьшается до нуля.

Не применять силу → Не работать

Хорошо, сначала это было нелогично, но теперь в этом есть смысл.

Чем дальше два вектора удаляются от параллели, тем меньше работы выполняется. Увеличьте угол до 90 °. Сила и смещение начинают двигаться в противоположных направлениях.При 90 ° никаких работ не производилось. Если угол превышает 90 °, работа не должна выполняться. Это отрицательная работа.

Приложите меньшее усилие → Работайте меньше, чем не работайте

Есть еще одна причина принять негативную работу. Знак работы указывает направление изменения. Отрицательный знак указывает на потерю чего-либо. В случае опускания книги это означает снижение ее способности выполнять работу – снижение ее энергии.

Следуйте этой цепочке рассуждений. Чтобы поднять книгу, нужно потрудиться.Поднятие книги повышает ее энергию. Теперь я могу использовать энергию, хранящуюся в книге, для работы – и под «работой» я имею в виду физический труд, а не обучение американской молодежи. Я могу толкать им разные вещи – грецкие орехи, насекомых, квадратные колышки в круглые отверстия. Я делаю эту работу, опуская книгу. Это также снижает его энергию. Он больше не может работать, когда снова лежит на столе. Поднятие книги действительно работает. Его опускание отменяет работу над ним. С точки зрения работы или энергии книга вернулась в исходное состояние.Численно положительная проделанная работа, повышающая его, была аннулирована отрицательной проделанной работой, понижающей его, что привело к нулю выполненной работы в целом по книге . (Ситуация иная для разбитого грецкого ореха, насекомого или квадратного колышка.)

алгебра

Работа выполняется всякий раз, когда сила вызывает смещение. При прочих равных условиях применение большей силы должно приводить к выполнению большего объема работы. Точно так же приложение заданной силы на большем расстоянии должно привести к выполнению большего количества работы.И, как мы обсуждали в дюжине параграфов, предшествующих этому, важна составляющая силы, параллельная смещению. Работа прямо пропорциональна первым двум факторам: силе и перемещению. Направление обрабатывается функцией косинуса. Косинус наибольший, когда угол равен нулю (угол между двумя векторами, указывающими в одном направлении, равен нулю), ноль при девяноста градусах (силы, перпендикулярные смещению, не действуют), и отрицательный для тупых углов (силы, действующие в противоположном направлении смещения, отменяют работу). .

Работа лучше всего определяется уравнением. Вот одна распространенная версия…

W = F ∆ s cos θ

где…

W =	работ выполнено
F =	Среднее приложенное усилие
∆ с =	смещение, вызванное силой
θ =	угол сила-смещение

Это уравнение предполагает, что сила постоянна как по величине, так и по направлению относительно смещения в любое время.Для многих задач это предположение разумно, поэтому оно написано здесь.

исчисление

Для тех случаев, когда изменения в величине или направлении значительны, мы представляем наше знакомое исчисление. При некотором конечном смещении сила может изменяться по величине и направлению. При меньшем смещении он наверняка изменится меньше. Разрежьте смещение на серию небольших смещений, вычислите работу, проделанную на каждом шаге, и сложите результаты вместе. Для достижения наилучших результатов позвольте ступенькам приблизиться к бесконечно малому размеру.

Пока мы занимаемся этим, давайте также заменим функцию косинуса более компактной нотацией скалярного произведения. Есть два способа умножения векторов – скалярное произведение · и кросс-произведение ×. Скалярное произведение – это скалярный продукт, который увеличивается с увеличением сходства направления. Триггерная функция, которая делает это, – косинус. Перекрестное произведение – это векторное произведение, которое увеличивается с увеличением перпендикулярности и выходит за пределы плоскости, содержащей два вектора.Триггерная функция, которая это делает, – синус. Поскольку мы ранее определили косинус как правильную функцию, мы будем использовать скалярное произведение.

В пределе конечное ∆ s становится бесконечно малым d s , а конечное ∑ становится бесконечным ∫. Конечная сумма конечных величин всегда конечна. Бесконечный интеграл бесконечно малых дифференциалов также может быть конечным. Магия исчисления в том, что последнее вообще может быть правдой.

Работа лучше всего определяется уравнением.Вот еще одна распространенная версия…

Это уравнение является примером линейного интеграла (или линейного интеграла ). Когда большинство студентов знакомятся с интеграцией, им говорят, что интеграция – это способ найти площадь под кривой. Это делается путем математического разбиения кривой на бесконечно малые сегменты одинаковой ширины, измерения площади прямоугольной полосы, которая помещается между каждым сегментом кривой и горизонтальной осью, а затем сложения площадей сегментов вместе.Нет ничего плохого в том, что это введение в интеграцию, но иногда студенты зацикливаются на понятии, что интеграция – это просто «поиск области». На самом деле интеграция заключается в соединении частей в единое целое. Это основное значение слова на английском языке и – основное значение слова в исчислении. Интегрирование можно использовать для нахождения площади под кривой (я назову это традиционным интегралом ), но его также можно использовать для определения количества некоторой величины, накопленной на пути (интеграл по пути ), чтобы найти количество некоторой величины, захваченной поверхностью ( интеграл поверхности ), или количество некоторой величины, содержащейся в объеме (интеграл объема ).

Квартир

Единица измерения в системе СИ – джоуль .

[J = Н · м = кг · м ² / с ² ]

Работа и энергия могут быть выражены в одних и тех же единицах. К сожалению, помимо джоуля есть много единиц для энергии. (Это обсуждается в другом разделе этой книги.) Наиболее часто встречающиеся в США в начале 21 века, вероятно, калории (диета и питание), британские тепловые единицы (отопление и охлаждение), киловатт-час (счета за электричество), тепловые ( счета за природный газ), квадроцикл (макроэкономика), тонна тротила (ядерное оружие), эрг (ученые старшего возраста) и фут-фунт (инженеры старшего возраста).Первые два в этом списке, калория и британская тепловая единица, были впервые введены учеными 19 века, изучающими калориметрию. (Французы дали нам калорию, а англичане дали британские тепловые единицы или британские тепловые единицы.) Последний в списке фунт-фут был введен учеными 19 века, изучающими механику. В XIX веке калориметрия и механика были отдельными дисциплинами. Калориметрия – это исследование тепла. Механика – это изучение движения и сил. Образованный джентльмен (а в то время они обычно были мужчинами) мог изучать и то, и другое, но он, вероятно, не связывал их сколько-нибудь значительным образом.То есть, если только его не звали Джоуль.

Джеймс Джоуль (1818–1889) был богатым английским пивоваром, занимавшимся различными аспектами науки и экономики. Иногда эти усилия совпадали. Он изобрел фут-фунт как единицу работы: фут является единицей перемещения, а фунт – единицей силы. Это позволило ему количественно сравнить «экономичность» различных механических систем. В то время паровые двигатели, работающие на угле, были основным источником промышленной мощи, но тогда на горизонте высоких технологий появилась электроэнергия.Джоуль понял, что механическая работа, тепло и электрическая энергия каким-то образом взаимозаменяемы. Тепло может работать. Работа может вызвать тепло. Работа может производить электричество, Электричество может производить работу, Электричество может производить тепло. Тепло может производить электричество. Энергия – актер разносторонний.

Самый известный эксперимент

Джоуля – это, вероятно, определение механического эквивалента тепла (я надеюсь, что он будет обсуждаться более подробно в другом месте этой книги). Теплота измерялась в британских тепловых единицах (по крайней мере, британцами), а работа – в фут-фунтах (что изобрел Джоуль).Джоуль установил, что одна британская тепловая единица тепла эквивалентна примерно 770 фут-фунтам механической работы – очень близко к сегодняшнему значению 778 фут-фунт / британских тепловых единиц. Этот результат был важен для осознания того, что, несмотря на то, что она проявляется во множестве форм, энергия – это одно.

Международная система единиц, которая начала доминировать в научном мире в середине 20 века, имела французское происхождение. Футам-фунтам и британским тепловым единицам не место в этой гораздо более логичной системе.12 дюймов в футе. 16 унций в фунте. 128 унций в галлоне в США и неизвестно сколько в Великобритании. Математика была слишком сложной. Parlez-vous les unités métriques ? СИ был французским по происхождению, но международным по своему характеру. Когда прозвучал призыв назвать единицу энергии, ответ был громким: Джоуль! Отпущение грехов!

Некоторые примечания к агрегатам.

• Джоуль эквивалентен ньютон-метру , но он никогда не должен называться таковым.Эта единица зарезервирована для крутящего момента. Крутящий момент также является произведением силы-смещения, но другого вида. Крутящий момент максимизируется, когда сила и смещение перпендикулярны, что означает, что он использует синус вместо косинуса для согласования направления (или для более продвинутых читателей он использует перекрестное произведение вместо скалярного произведения). Крутящий момент не измеряется в джоулях, и работу никогда не следует измерять в ньютон-метрах.
• Гауссовская единица работы – эрг [эрг = дин см = г см ² / с ² ].10 000 000 эрг = 1 джоуль. Слово эрг происходит от классического греческого слова, обозначающего работу: εργον ( ergon ). ERG также было названием спортивного напитка, появившегося в США в конце 1960-х или начале 1970-х годов. ERG расшифровывалось как «замена электролита глюкозой».
• Англо-американская единица работы – фут-фунт (когда фунт является единицей силы) или фут-фунтал (когда фунт является единицей массы). Первое встречается чаще, чем второе. Путаницы с единицами крутящего момента можно избежать, изменив порядок.Англо-американская единица крутящего момента – фунт-фут или фунт-фут в зависимости от вашего определения фунта. И снова первое встречается чаще, чем второе. Джеймс Джоуль изобрел фут-фунт.

консервативные и неконсервативные силы

текст

Положительная работа выполняется, когда учебник перемещается вправо по поверхности стола уровня с постоянной скоростью. Положительная работа также выполняется, когда учебник перемещается влево по поверхности стола уровня с постоянной скоростью.

текст

Положительная работа выполняется над учебником, когда он поднимается вертикально с постоянной скоростью. Отрицательная работа выполняется над учебником, когда он опускается вертикально с постоянной скоростью.

текст

теорема об энергии работы

текст

W = ∆ E

• работа вызывает изменение энергии
• работа переводит энергию из одной системы в другую

Условные обозначения:

• Когда система работает в своей среде, W <0; то есть полная энергия системы уменьшается.Работа выполняется по системе.
• Когда среда работает в системе, W > 0; то есть полная энергия системы увеличивается. Работа ведется по системе .

Томас Янг (1773–1829) был первым, кто использовал эту формулу. ← Это правда?

Работа

Сила без движения или сила, перпендикулярная движению, не работает

Эти два примера сил, которые не работают, парадоксальны.Вы определенно можете почувствовать усталость, выполняя любое из этих действий, так как же вы можете сказать, что работа не выполняется?

В случае, показанном слева, независимо от того, насколько сильно и как долго вы толкали ящик, если ящик не двигается, значит, вы не работали с ящиком. Он сидит на том же месте! Почему тогда вы чувствуете усталость (а также разочарование и т. Д.). Решение этой дилеммы приходит в том случае, если учесть, что, когда ваши мышцы используются для приложения силы к чему-либо, отдельные мышечные волокна находятся в непрерывном процессе сокращения и высвобождения, чтобы поддерживать общий коллективный результат постоянной силы, воздействующей на внешний объект.Это сокращение и отпускание включает в себя силу и движение и составляет внутреннюю работу в вашем теле. Энергия проявляется в нагревании ваших мышечных тканей, но если ящик не двигается, сетка по-прежнему не работает.

Пример справа – еще один стандартный парадокс в определении работы. Если ящик переносится с постоянной скоростью, то для его движения не требуется никакой чистой силы. Сила, прилагаемая человеком, направлена ​​вверх, равная весу коробки, и эта сила перпендикулярна движению.Если нет движения в направлении силы, то эта сила не совершает никакой работы. Тем не менее, вы определенно чувствуете, что делаете работу, если несете тяжелую коробку. Разрешение парадокса аналогично первому примеру – ваши мышцы должны сохранять дополнительное напряжение, чтобы оставаться в вертикальном положении под нагрузкой. Это требует большего внутреннего сокращения и высвобождения наших мышечных волокон и, следовательно, внутренней работы нашего тела. Но работа, проделанная с коробкой, равна нулю, поскольку при движении по прямой с постоянной скоростью его энергия остается той же самой.

Есть много важных примеров сил, которые не работают, потому что действуют перпендикулярно движению. При круговом движении центростремительная сила всегда действует под прямым углом к ​​движению. Он меняет направление движения, но не воздействует на объект. Это можно применить к любой круговой орбите.

7.2 Кинетическая энергия и теорема работы-энергии

Чистая работа и теорема работы-энергии

Мы знаем из изучения законов Ньютона в динамике: сила и законы движения Ньютона, что результирующая сила вызывает ускорение.В этом разделе мы увидим, что работа, совершаемая чистой силой, дает системе энергию движения, и в процессе мы также найдем выражение для энергии движения.

Давайте начнем с рассмотрения общей, или чистой, работы, проделанной в системе. Сетевая работа определяется как сумма работы, выполненной всеми внешними силами, то есть сетевая работа – это работа, выполняемая чистой внешней силой FnetFnet размером 12 {F rSub {size 8 {“net”}}} {}. В форме уравнения это Wnet = FnetdcosθWnet = Fnetdcosθ size 12 {W rSub {size 8 {“net”}} = F rSub {size 8 {“net”}} d “cos” θ} {}, где θθ size 12 { θ} {} – угол между вектором силы и вектором смещения.

На рис. 7.3 (a) показан график зависимости силы от смещения для составляющей силы в направлении смещения, то есть для FcosθFcosθ размером 12 {F “cos” θ} {} в зависимости от dd размера 12 {d} {} график. В этом случае FcosθFcosθ size 12 {F “cos” θ} {} является постоянным. Вы можете видеть, что область под графиком соответствует FdcosθFdcosθ размером 12 {F “cos” θ} {} или проделанной работе. На рис. 7.3 (b) показан более общий процесс изменения силы. Площадь под кривой разделена на полосы, каждая из которых имеет среднюю силу (Fcosθ) i (ave) (Fcosθ) i (ave) размер 12 {\ (F “cos” θ \) rSub {size 8 {i \ (” пр. “\)}}} {}.Проделанная работа (Fcosθ) i (ave) di (Fcosθ) i (ave) di size 12 {\ (F “cos” θ \) rSub {size 8 {i \ (“ave” \)}} d rSub { размер 8 {i}}} {} для каждой полосы, а общая проделанная работа представляет собой сумму WiWi size 12 {W rSub {size 8 {i}}} {}. Таким образом, общая проделанная работа – это общая площадь под кривой, полезное свойство, о котором мы поговорим позже.

Рисунок 7.3 (a) График зависимости FcosθFcosθ от размера dd 12 {d} {}, когда FcosθFcosθ размером 12 {F “cos” θ} {} является постоянным. Площадь под кривой представляет работу, совершаемую силой.(b) График зависимости FcosθFcosθ размера 12 {F “cos” q} {} от размера dd 12 {d} {}, в котором сила изменяется. Работа, проделанная для каждого интервала, – это площадь каждой полосы; таким образом, общая площадь под кривой равна общей проделанной работе.

Связи в реальном мире: работа и руководство

Рассмотрите возможность вождения в машине. Во время движения у вас есть поступательная скорость и, следовательно, кинетическая энергия. Когда вы нажимаете на тормоз, тормоза создают силу, противоположную направлению вашего движения (действуя через колеса).Тормоза воздействуют на вашу машину и уменьшают кинетическую энергию. Точно так же, когда вы ускоряетесь, двигатель (действующий через колеса) прикладывает силу в направлении движения. Двигатель действительно работает на вашем автомобиле и увеличивает кинетическую энергию. Наконец, если вы завернете за угол с постоянной скоростью, у вас будет одинаковая кинетическая энергия как до поворота, так и после него. Сила, прилагаемая двигателем, была перпендикулярна направлению движения, поэтому не работала и не изменяла кинетическую энергию.

Чистую работу будет проще исследовать, если мы рассмотрим одномерную ситуацию, когда сила используется для ускорения объекта в направлении, параллельном его начальной скорости. Такая ситуация возникает для упаковки на ленточном роликовом конвейере, показанном на Рисунке 7.4.

Рис. 7.4 Пакет на роликовой ленте продвигается горизонтально на расстояние dd.

Сила тяжести и нормальная сила, действующая на упаковку, перпендикулярны перемещению и не работают.Кроме того, они также равны по величине и противоположны по направлению, поэтому они отменяются при вычислении чистой силы. Чистая сила возникает исключительно из приложенной горизонтальной силы FappFapp и горизонтальной силы трения ff. Таким образом, как и ожидалось, чистая сила параллельна смещению, так что θ = 0ºθ = 0º и cosθ = 1cosθ = 1 размер 12 {“cos” q = 1} {}, а чистая работа равна

7.7 Wnet = Fnetd.Wnet = Fnetd. размер 12 {W rSub {размер 8 {“net”}} = F rSub {размер 8 {“net”}} d} {}

Эффект чистой силы FnetFnet размером 12 {F rSub {size 8 {“net”}}} {} заключается в ускорении пакета с v0v0 размера 12 {v rSub {size 8 {0}}} {} до размера vv 12 {v} {}.Кинетическая энергия пакета увеличивается, указывая на то, что чистая работа, выполняемая в системе, положительна (см. Пример 7.2). Используя второй закон Ньютона и занимаясь алгеброй, мы можем прийти к интересному выводу. Подстановка Fnet = maFnet = ma size 12 {F rSub {size 8 {“net”}} = ital “ma”} {} из второго закона Ньютона дает

7.8 Wnet = безумный. Wnet = безумный. размер 12 {W rSub {размер 8 {“net”}} = ital “mad”} {}

Чтобы получить взаимосвязь между чистой работой и скоростью, придаваемой системе действующей на нее чистой силой, мы берем d = x − x0d = x − x0 размер 12 {d = x – x rSub {size 8 {0}} } {} и используйте уравнение, изученное в Уравнениях движения для постоянного ускорения в одном измерении, для изменения скорости на расстоянии dd, если ускорение имеет постоянное значение aa; а именно, v2 = v02 + 2adv2 = v02 + 2ad.Обратите внимание, что aa появляется в выражении для сети. Решение для ускорения дает a = v2 − v022da = v2 − v022d. Когда aa подставляется в предыдущее выражение для WnetWnet, мы получаем

7.9 Wnet = mv2-v022dd.Wnet = mv2-v022dd.

ДД размером 12 {d} {} отменяется, и мы изменяем это так, чтобы получить

7.10 Wnet = 12mv2−12mv0 2.Wnet = 12mv2−12mv0 2. размер 12 {w “” lSub {size 8 {ital “net”}} = {{1} over {2}} ital “mv” rSup {size 8 {2}} – {{1} больше {2}} ital “mv” “” lSub {size 8 {0}} “” lSup {size 8 {2}} “.”} {}

Это выражение называется теоремой работы-энергии, и оно фактически применяет в целом – даже для сил, которые меняются по направлению и величине, – хотя мы вывели его для частного случая постоянной силы, параллельной смещению. Теорема подразумевает, что сетевая работа в системе равна изменению количества 12mv212mv2 размера 12 {{{1} по сравнению с {2}} курсивом “mv” rSup {size 8 {2}}} {}. Эта величина – наш первый пример формы энергии.

Теорема работы-энергии

Чистая работа в системе равна изменению количества 12mv212mv2 размером 12 {{{size 8 {1}} по сравнению с {размером 8 {2}}} ital “mv” rSup {size 8 {2}}} {}.

7.11 Wnet = 12mv2−12mv0 2.Wnet = 12mv2−12mv0 2. размер 12 {w “” lSub {size 8 {ital “net”}} = {{1} over {2}} ital “mv” rSup {size 8 {2}} – {{1} больше {2}} ital “mv” “” lSub {size 8 {0}} “” lSup {size 8 {2}} “.” } {}

Величина 12mv212mv2 размер 12 {{{1} больше {2}} ital “mv” rSup {size 8 {2}}} {} в теореме о работе-энергии определяется как поступательная кинетическая энергия (KE) масса мм размер 12 {м} {} движется со скоростью vv размером 12 {v} {}. Трансляционная кинетическая энергия отличается от вращательной кинетической энергии , которая будет рассмотрена позже.В форме уравнения поступательная кинетическая энергия,

7.12 KE = 12 м2, KE = 12 м2, размер 12 {“KE” = {{1} больше {2}} ital “mv” rSup {size 8 {2}},} {}

– энергия, связанная с поступательным движением. Кинетическая энергия – это форма энергии, связанная с движением частицы, отдельного тела или системы объектов, которые движутся вместе.

Мы знаем, что требуется энергия, чтобы разогнать объект, например автомобиль или пакет на рис. 7.4, до скорости; однако может показаться немного удивительным, что кинетическая энергия пропорциональна квадрату скорости.Эта пропорциональность означает, например, что автомобиль, движущийся со скоростью 100 км / ч, имеет в четыре раза большую кинетическую энергию, чем при 50 км / ч, что помогает объяснить, почему столкновения на высокой скорости настолько разрушительны. Теперь мы рассмотрим серию примеров, чтобы проиллюстрировать различные аспекты работы и энергии.

Применение научных практик: автомобили на холме

Соберите пандус, подходящий для катания игрушечных машинок вверх и вниз. Затем запланируйте серию экспериментов, чтобы определить, как направление силы относительно скорости объекта изменяет кинетическую энергию объекта.Обратите внимание, что сила тяжести во всех случаях будет направлена ​​вниз. Что будет, если завести машину сверху? Как насчет нижней части с увеличивающейся начальной скоростью? Если у вас достаточно широкий пандус, что произойдет, если вы отправите игрушечную машинку прямо через дорогу? Изменяет ли изменение поверхности пандуса ваши результаты?

Пример ответа: Когда игрушечная машинка спускается по рампе, с компонентом силы тяжести в том же направлении, кинетическая энергия увеличивается. Отправка автомобиля по рампе снижает кинетическую энергию, поскольку гравитация противодействует движению.Отправка автомобиля в сторону должна практически не привести к изменениям. Если у вас есть поверхность, которая создает большее трение, чем гладкая поверхность, например ковер, обратите внимание, что трение всегда противодействует движению и, следовательно, уменьшает кинетическую энергию.

Пример 7.2 Расчет кинетической энергии упаковки

Предположим, что 30,0-килограммовая упаковка на роликовой ленточной конвейерной системе, показанной на рис. 7.4, движется со скоростью 0,500 м / с. Какова его кинетическая энергия?

Стратегия

Поскольку даны масса, мм и скорость vv, кинетическая энергия может быть рассчитана на основе ее определения, приведенного в уравнении KE = 12mv2KE = 12mv2 размер 12 {“KE” = {{1} over {2}} ital “mv” rSup {размер 8 {2}}} {}.

Решение

Кинетическая энергия определяется как

. 7.13 KE = 12 мв2. KE = 12 мв2. размер 12 {“KE” = {{1} больше {2}} ital “mv” rSup {size 8 {2}} “.” } {}

Ввод известных значений дает

7.14 KE = 0,5 (30,0 кг) (0,500 м / с) 2, KE = 0,5 (30,0 кг) (0,500 м / с) 2, размер 12 {“KE” = 0 “.” 5 \ (“30” “.” 0 “кг” \) \ (0 “.” “500” “м / с” \) rSup {размер 8 {2}},} {}

, что дает

7,15 KE = 3,75 кг⋅м2 / с2 = 3,75 J.KE = 3,75 кг⋅м2 / с2 = 3,75 J. размер 12 {“KE” = 3 “.” “75” ‘”кг” cdot m rSup {size 8 {2}} “/ s” rSup {size 8 {2}} = 3 “.”” 75 “‘J”. “} {}

Обсуждение

Обратите внимание, что единицей кинетической энергии является джоуль, то же самое, что и единица работы, как упоминалось при первом определении работы. Также интересно то, что, хотя это довольно массивный пакет, его кинетическая энергия невелика при такой относительно низкой скорости. Этот факт согласуется с наблюдением, что люди могут перемещать пакеты таким образом, не изнуряя себя.

Соединения в реальном мире: центр масс

Предположим, у нас есть две экспериментальные тележки одинаковой массы, скрепленные вместе на рельсе с сжатой пружиной между ними.Когда защелка отпущена, пружина работает с тележками на 10 Дж. Мы увидим, как это сделать, в паре разделов. Тележки движутся относительно пружины, которая является центром масс системы. Однако центр масс остается неизменным. Как мы можем учесть кинетическую энергию этой системы?

Согласно теореме работы-энергии, работа, выполняемая пружиной на тележках, должна превратиться в кинетическую энергию. Итак, эта система имеет кинетическую энергию 10 Дж. Полная кинетическая энергия системы – это кинетическая энергия центра масс системы относительно фиксированного начала координат плюс кинетическая энергия каждой тележки относительно центра масс.Мы знаем, что центр масс относительно неподвижного начала координат не перемещается, и поэтому вся кинетическая энергия должна распределяться между тележками относительно центра масс. Поскольку тележки имеют равную массу, каждая из них получает равное количество кинетической энергии, поэтому каждая тележка имеет 5,0 Дж кинетической энергии.

В нашем примере силы между пружиной и каждой тележкой являются внутренними по отношению к системе. Согласно третьему закону Ньютона, эти внутренние силы уравновешиваются, поскольку они равны и противоположны по направлению.Однако это не означает, что эти внутренние силы не работают. Таким образом, изменение кинетической энергии системы вызывается работой, совершаемой силой пружины, и приводит к движению двух тележек относительно центра масс.

Пример 7.3 Определение работы по ускорению пакета

Предположим, что вы толкаете 30,0-килограммовый пакет, показанный на рис. 7.4, с постоянной силой 120 Н на расстояние 0,800 м, а сила трения противоположной стороны в среднем составляет 5.00 Н.

(a) Рассчитайте чистую работу, проделанную с упаковкой. (b) Решите ту же задачу, что и в части (a), на этот раз найдя работу, выполняемую каждой силой, которая вносит вклад в результирующую силу.

Стратегия и концепция (а)

Это задача движения в одном измерении. Сила, направленная вниз (от веса упаковки), и нормальная сила имеют равную величину и противоположное направление, поэтому они взаимно компенсируются при вычислении чистой силы, в то время как приложенная сила, трение и смещение являются горизонтальными (см. Рисунок 7.4). Как и ожидалось, чистая работа – это чистая сила, умноженная на расстояние.

Решение для (а)

Чистая сила – это сила толчка за вычетом трения, или Fnet = 120 Н – 5,00 Н = 115 НFnet = 120 Н – 5,00 Н = 115 Н размер 12 {F rSub {размер 8 {“net”}} “= 120 Н – 5 “”. ” “00 N = 115 N”} {}. Таким образом, чистая работа

7.16 Wnet = Fnetd = 115 N0.800 m = 92.0 N⋅m = 92.0 J.Wnet = Fnetd = 115 N0.800 m = 92.0 N⋅m = 92.0 J.alignl {stack {size 12 {W rSub {size 8 {) “net”}} = F rSub {размер 8 {“net”}} d = left (“115” ‘N справа) left (0 “.”” 800 “прав)} {} #” “=” 92 “”. “0’N cdot m =” 92 “”. “0’J”. “{}}} {}

Обсуждение для (а)

Это значение представляет собой чистую работу, выполненную с пакетом. На самом деле человек выполняет больше работы, потому что трение препятствует движению. Трение совершает негативную работу и удаляет часть энергии, которую человек тратит, и преобразует ее в тепловую энергию. Чистая работа равна сумме работы, проделанной каждой отдельной силой.

Стратегия и концепция (b)

К силам, действующим на упаковку, относятся сила тяжести, нормальная сила, сила трения и приложенная сила.Нормальная сила и сила тяжести перпендикулярны перемещению и поэтому не работают.

Решение для (b)

Приложенная сила работает.

7.17 Wapp = Fappdcos0º = Fappd = 120 N0.800 m = 96.0 J.Wapp = Fappdcos0º = Fappd = 120 N0.800 m = 96.0 J.alignl {stack {size 12 {W rSub {size 8 {“app”}} = F rSub {размер 8 {“app”}} d “cos” влево (0 ° вправо) = F rSub {размер 8 {“app”}} d} {} # “” = left (“120 N” справа) влево (0 “.” “800” “м” вправо) {} # “” = “96” “.”” 0 J “”. “{}}} {}

Сила трения и смещение имеют противоположные направления, так что θ = 180ºθ = 180º, размер 12 {θ = “180” °} {}, а работа, выполняемая трением, равна

7.18 Wfr = Ffrdcos180º = −Ffrd = −5.00 N0.800 m = −4.00 J.Wfr = Ffrdcos180º = −Ffrd = −5.00 N0.800 m = −4.00 J.alignl {stack {size 12 {W rSub {size 8 {) “fr”}} = F rSub {размер 8 {“fr”}} d “cos” влево (“180” ° вправо) = – F rSub {размер 8 {“fr”}} d} {} # “” = – left (5 “.” “00 N” right) left (0 “.” “” 800 “” m “right) {} # ital” “= – 4”. “. “00” J “.”{}}} {}

Таким образом, количество работы, совершаемой гравитацией, нормальной силой, приложенной силой и трением, составляет, соответственно,

. 7,19 Wgr = 0, WN = 0, Wapp = 96,0 Дж, Wfr = −4,00 J.Wgr = 0, WN = 0, Wapp = 96,0 Дж, Wfr = −4,00 J.alignl {stack {size 12 {W rSub {size 8 {“gr”}} = 0,} {} # W rSub {size 8 {N}} = 0, {} # W rSub {size 8 {“app”}} = “96” “.” 0 “J” {} # W rSub {size 8 {“fr”}} = – 4 “.” “00” “J” “.” {}}} {}

Общая проделанная работа как сумма работы, проделанной каждой силой, тогда составляет

. 7.20 Wtotal = Wgr + WN + Wapp + Wfr = 92,0 J.Wtotal = Wgr + WN + Wapp + Wfr = 92,0 J. размер 12 {W rSub {размер 8 {“total”}} = W rSub {размер 8 {“gr “}} + W rSub {размер 8 {N}} + W rSub {размер 8 {” app “}} + W rSub {размер 8 {” fr “}} =” 92 “”. ” 0 “J”} {}

Обсуждение для (б)

Рассчитанная общая работа WtotalWtotal size 12 {W rSub {size 8 {“total”}}} {} как сумма работы каждой силы соответствует работе, как и ожидалось, размер WnetWnet 12 {W rSub {size 8 { “net”}}} {} сделано чистой силой. Работа, выполняемая совокупностью сил, действующих на объект, может быть рассчитана любым подходом.

Пример 7.4 Определение скорости по работе и энергии

Найдите скорость пакета на рис. 7.4 в конце проталкивания, используя концепции работы и энергии.

Стратегия

Здесь можно использовать теорему работы-энергии, потому что мы только что вычислили чистую работу, размер WnetWnet 12 {W rSub {size 8 {“net”}}} {} и начальную кинетическую энергию, 12mv0212mv02 size 12 {{{ 1} больше {2}} ital “mv” rSub {size 8 {0} rSup {size 8 {2}}}} {}.Эти расчеты позволяют нам найти окончательную кинетическую энергию, 12 мв212 мв2 размер 12 {{{1} сверх {2}} ital “mv” rSup {size 8 {2}}} {}, и, таким образом, конечную скорость vv размер 12 {v } {}.

Решение

Теорема работы-энергии в форме уравнения:

7.21 Wnet = 12mv2−12mv02.Wnet = 12mv2−12mv02. размер 12 {W rSub {size 8 {“net”}} = {{1} больше {2}} ital “mv” rSup {size 8 {2}} – {{1} больше {2}} ital “mv” rSub {размер 8 {0} rSup {размер 8 {2}}} “.” } {}

Решение для 12mv212mv2 размера 12 {{{1} больше {2}} ital “mv” rSup {size 8 {2}}} {} дает

7.22 12mv2 = Wnet + 12mv02. 12mv2 = Wnet + 12mv02. размер 12 {{{1} over {2}} ital “mv” “” lSup {size 8 {2}} = w rSub {size 8 {ital “net”}} + {{1} over {2}} ital “mv” “” lSub {size 8 {0}} “” lSup {size 8 {2}} “.” } {}

Таким образом,

7.23 12mv2 = 92.0 J + 3.75 J = 95.75 J.12mv2 = 92.0 J + 3.75 J = 95.75 J. размер 12 {{{1} больше {2}} ital “mv” rSup {size 8 {2}} = “92 “”. ” 0’J + 3 “.” “75” ‘J = “95” “.” “75” ‘J} {}

Определение конечной скорости в соответствии с запросом и ввод известных значений дает

7,24 v = 2 (95.75 Дж) м = 191,5 кг⋅м2 / с 230,0 кг = 2,53 м / с. V = 2 (95,75 Дж) м = 191,5 кг⋅м2 / с 230,0 кг = 2,53 м / с.

Обсуждение

Используя работу и энергию, мы не только приходим к ответу, мы видим, что конечная кинетическая энергия – это сумма начальной кинетической энергии плюс чистая работа, проделанная с упаковкой. Это означает, что работа действительно увеличивает энергию упаковки.

Пример 7.5 Работа и энергия могут выявить слишком большое расстояние

Как далеко паковка на рис. 7.4 уходит по инерции после толчка, если трение остается постоянным? Используйте соображения работы и энергии.

Стратегия

Мы знаем, что как только человек перестанет толкать, трение остановит упаковку. Что касается энергии, трение выполняет отрицательную работу до тех пор, пока не убирает всю кинетическую энергию упаковки. Работа, совершаемая трением, – это сила трения, умноженная на пройденное расстояние, умноженная на косинус угла между силой трения и смещением; следовательно, это дает нам способ определить расстояние, пройденное после того, как человек прекратил толкать.

Решение

Нормальная сила и сила тяжести отменяются при вычислении чистой силы.Горизонтальная сила трения тогда представляет собой результирующую силу, и она действует противоположно смещению, поэтому θ = 180ºθ = 180º. Чтобы уменьшить кинетическую энергию пакета до нуля, работа WfrWfr за счет трения должна быть минус кинетическая энергия, с которой пакет начал, плюс то, что пакет накопил из-за толкания. Таким образом, Wfr = -95,75 JWfr = -95,75 Дж. Кроме того, Wfr = fd′cosθ = –fd′Wfr = fd′cosθ = –fd ′, где d′d ′ – расстояние, необходимое для остановки. Таким образом,

7,25 d ′ = – Wfrf = −− 95,75 J5,00 N, d ′ = – Wfrf = −− 95,75 J5.00 N, размер 12 {{{d}} sup {‘} = – {{W rSub {size 8 {“fr”}}} больше {f}} = – {{- “95” “.” “75” ‘J} больше {5 “.” “00 Н”}}} {}

и так

7,26 d ′ = 19,2 м. D ′ = 19,2 м. размер 12 {{{d}} sup {‘} = “19” “.” 2 “м”} {}

Обсуждение

Это решение представляет собой разумное расстояние, на котором упаковка может двигаться по инерционной системе относительно свободной от трения конвейерной системы. Обратите внимание, что работа, совершаемая трением, отрицательна – сила направлена ​​в противоположном направлении движения – поэтому она снимает кинетическую энергию.

Некоторые из примеров в этом разделе могут быть решены без учета энергии, но за счет упущения понимания того, какая работа и энергия делают в этой ситуации. В целом решения с использованием энергии обычно короче и проще, чем решения, использующие только кинематику и динамику.

домашних заданий и упражнений – Работа, выполняемая с использованием трения и других внешних сил

Блок массой $ 1 $ кг помещается в точку A неровной дорожки, показанной на рисунке.Если слегка сдвинуть вправо, он остановится в точке B пути. Рассчитайте работу, проделанную силой трения на блоке во время перехода от точки A к точке B.

Я подошел к этому, используя закон сохранения энергии.

Допустим, на гусенице нет трения. Затем, если блок выталкивается из точки A, он не остановится в точке B, но будет иметь некоторую скорость, скажем, $ Vb $. Теперь мы можем легко сказать, что по закону сохранения энергии

Начальный P.E $ + Начальный K.2 $ энергии. Но я знаю, что

Начальная общая энергия $ = долларов Конечная общая энергия

Значит, потеря энергии должна быть преобразована в какую-то другую форму. Другой формой может быть тепловая энергия, производимая трением, которая будет равна работе, совершаемой силой трения, скажем, $ Wf $. Таким образом, мы должны добавить эту энергию в сторону Final Total Energy . Таким образом, наше последнее уравнение будет

.

мгH $ = 9000 $ 9 мгH $ + $ Wf $

Таким образом, $ Wf = 9000 $ 9 мг $ ( $ H $ – $ 9 $) $.

Подставляем все значения $ Wf = (1) (9,8) (1-0,8) = 1,96 Дж $. Но ответ был $ -1,96 J $. Скажите, пожалуйста, мою ошибку. Я очень не понимаю, как решать вопросы, связанные с работой, связанной с трением и внешними силами. Если бы вы могли объяснить мне какой-либо другой простой способ, это было бы мне очень полезно.

---

Вы могли бы сказать, что смещение и сила трения противоположны друг другу, и, следовательно, $ Wf $ следовало принять как отрицательное значение, но решение приведенного ниже вопроса аналогичным образом дало мне правильный ответ

Если я снова использую Начальная общая энергия $ = долларов Конечная общая энергия .