Решение задач Расчетно 📝 – графическая работа Сопротивление материалов
1. Сколько стоит помощь?
Цена, как известно, зависит от объёма, сложности и срочности. Особенностью «Всё сдал!» является то, что все заказчики работают со экспертами напрямую (без посредников). Поэтому цены в 2-3 раза ниже.
2. Каковы сроки?
Специалистам под силу выполнить как срочный заказ, так и сложный, требующий существенных временных затрат. Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока.
Выполняете ли вы срочные заказы?Да, у нас большой опыт выполнения срочных заказов.
4. Если потребуется доработка или дополнительная консультация, это бесплатно?
Да, доработки и консультации в рамках заказа бесплатны, и выполняются в максимально короткие сроки.
5. Я разместил заказ. Могу ли я не платить, если меня не устроит стоимость?
Да, конечно – оценка стоимости бесплатна и ни к чему вас не обязывает.
6. Каким способом можно произвести оплату?
Работу можно оплатить множеством способом: картой Visa / MasterCard, с баланса мобильного, в терминале, в салонах Евросеть / Связной, через Сбербанк и т.
д.
На все виды услуг мы даем гарантию. Если эксперт не справится — мы вернём 100% суммы.
8. Какой у вас режим работы?
Мы принимаем заявки 7 дней в неделю, 24 часа в сутки.
РГР на заказ по термеху, сопромату, электротехнике
Расчетно-графическая работа – это весьма специфический вид задания, который характерен для студентов технических направлений обучения. Наиболее частыми являются 
д.
Сама суть работы включает в себя сложные расчеты и отображение результатов этих расчетов в графическом виде с точными и подробными объяснениями всех деталей и нюансов работы.
Сколько стоит написание РГР?
Стоимость РГР в Оренбурге – от 99 ₽
Бесплатные доработки. Прохождение проверки на уникальность. Гарантия выполнения или возврат денег.
Без определенных знаний и навыков выполнения подобных заданий, впервые столкнувшись с необходимостью самостоятельно подготовить материал, студент может растеряться. Так как же поступить, к кому обратиться за помощью? Есть несколько вариантов развития событий. Первый- самостоятельно выполнить все так, как посчитает нужным. Однако в этом случае, полной уверенности в том, что все сделано правильно, быть не может. Второе, не менее опасное решение – можно пойти к студентам-старшекурсникам и взять готовый материал у них.
Третий и самый обдуманный и взвешенный вариант – это обратиться за помощью к специалистам, которые не только имеют богатый опыт выполнения подобных заявок, но и достаточно глубокие знания для того, чтобы сделать работу профессионально, а расчеты произвести максимально точно.
Выполнить расчетно-графическую работу срочно и недорого
РГР на заказ у специалистов – это материал, который будет выполнен с учетом всех требований и методических рекомендаций. Каждое графическое изображение будет подкреплено уточняющими сопроводительными записками, содержащими формулы и все необходимые расчеты. Мы готовы принять к выполнению как простую ргр, содержащую 1-2 графические изображения, так и объемные задания, отнимающие много времени и содержащие сложные расчеты.
Стоимость расчетно-графической работы на заказ вполне доступна для простого студента и напрямую зависит от сложности задания и его объема.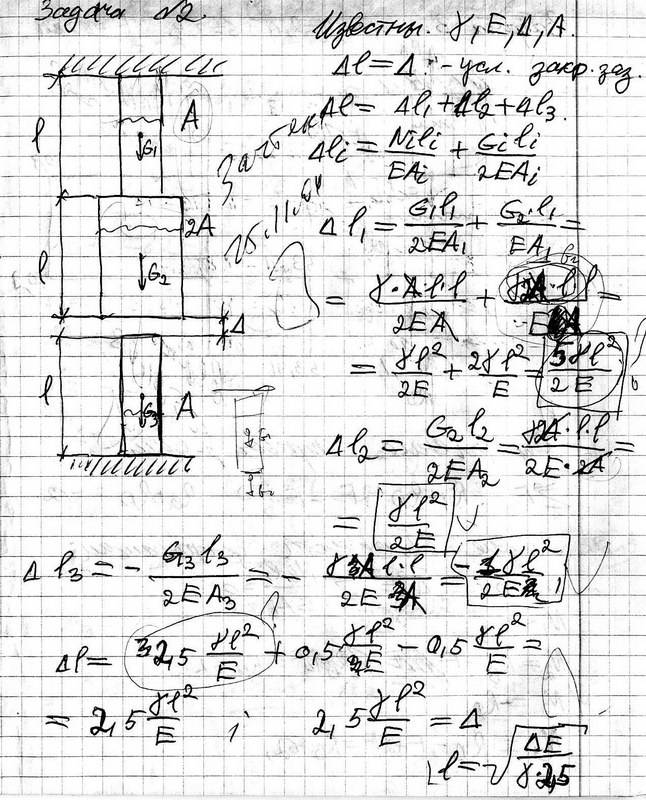
Мы принимаем к выполнению «срочные» заявки, однако стоит понимать, что данное задание не может быть выполнено за несколько часов, да и за срочность необходимо будет заплатить. Поэтому рекомендуем Вам при малейших сомнениях в том, что Вы самостоятельно одолеете данный труд, сразу же обращаться за помощью к нашим сотрудникам, и тогда успех Вам гарантирован.
Методические рекомендации по выполнению расчетно-графических работ по сопротивлению материалов (Реферат)
Министерство образования Российской Федерации
Курский государственный технический университет
Кафедра сопротивления материалов и строительной механики
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
по выполнению расчетно-графических работ
по сопротивлению материалов
Курск 2003
Составители: Л. Ю. Ступишин, А. В. Масалов
УДК 539.3/8
Рецензент
канд. техн. наук.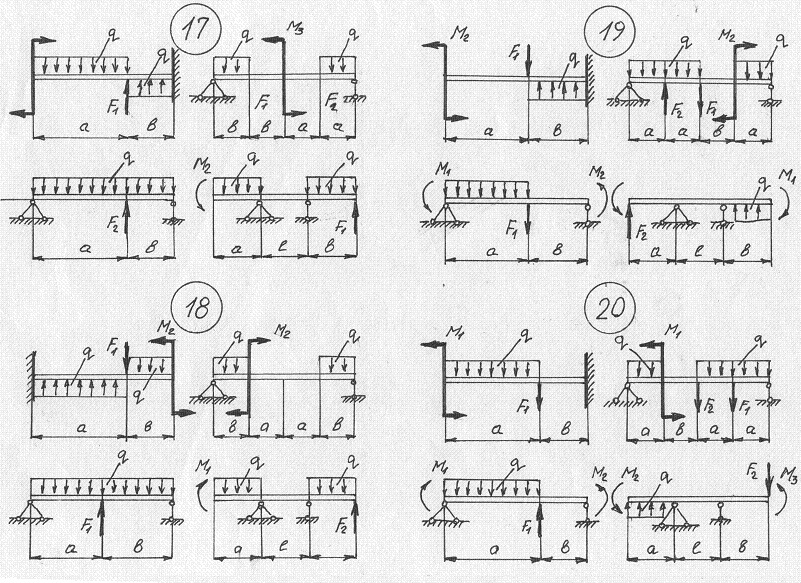
Методические рекомендации по выполнению расчетно-графических работ по сопротивлению материалов/ Курск.гос.техн.ун-т; Сост. Л. Ю. Ступишин, А. В. Масалов. Курск 2003
Излагаются методические рекомендации по выполнению расчетно-графических работ по сопротивлению материалов.
Предназначены для студентов технических специальностей.
Ил. 14. Табл. 1
Редактор Т. Н. Иванова
Подписано в печать 16.11.95. Формат 60 х 84 1/16.
Печать офсетная
Усл.печ.л.3,74 Уч.изд.л. 3,96 Тираж 200 экз.
Заказ 464 .Бесплатно
Курский государственный технический университет.
Издательско-полиграфический УСИТР . Курского государственного технического университета. 305035, Курс, ул. 50 лет Октября, 94.
ВВЕДЕНИЕ
Общие замечания
При изучении дисциплин кафедры
наибольшие трудности у студентов
возникают при решении практических
задач.
Вместе с тем именно решение задач в значительной степени способствует развитию инженерного мышления у студентов, приобретению ими необходимых навыков прочности расчетов элементов инженерных конструкций. В настоящей методической разработке подробно рассмотрены решения типовых задач, а также изложены требования по выполнению и оформлению индивидуальных расчетно-графических работ, предусмотренных программками курсов сопротивления материалов, механики деформируемого твердого тела, прикладной и технической механики для студентов дневного обучения всех специальностей.
Основные требования по выполнению расчетно-графических работ
1.2.1 Оформление титульного листа
Все расчетно-графические работы выполняются из стандартных листах бумаги с размерами 210 х 297 мм, окропленных в тетрадь.
Все
надписи на титульном листе располагаются
в строго определенных местах выполняются
чертежным шрифтом. Разрешается выполнять
титульный лист в компьютерном варианте.Рекомендуется следующие номера шрифта для конкретных надписей:
«Министерство образования РФ» – шрифт №7+; в компьютерном варианте шрифт Times 16пт;
«Курский государственный технический университет» – шрифт №5; в компьютерном варианте шрифт Times 14пт;
«Кафедра сопротивления материалов и строительной механики» – шрифт №5; в компьютерном варианте шрифт Times 14пт;
названию расчетно-графической работы – шрифт №10; в компьютерном варианте Times 18пт;
«расчетно-графическая работа №…» – шрифт №7; в компьютерном варианте Times 14пт;
«Выполнил …», «Проверил …» – шрифт №5; в компьютерном варианте Times 14пт;
год
выполнения работы – шрифт №5; в
компьютерном варианте Times
14пт.
1.2.2. Оформление расчетно-пояснительной записки
Расчетно-пояснительная записка должна быть достаточно краткой, без лишних подробных пояснений и теоретических выводов, имеющихся в учебниках и других учебных пособиях, но не чересчур краткой, содержащей один только формулы и вычисления. В расчетно-пояснительной записке от начала до конца должна четко прослеживаться логическая связь выполняемых операций, а также должны быть отмечены основания для выполнения этих операций. Приведенные в настоящей методической разработке примеры решения отдельных задач могут послужить основой для составления записок.
Формулы, приводимые в записке,
должны быть, как правило, записаны
сначала в общем виде, а затем уже должна
быть произведена подстановка исходных
данных и выполнены необходимые вычисления.
При подстановке исходных данных нужно
внимательно следить за соблюдением
одинаковой размерности. После получения
значения искомой (промежуточной или
окончательной) величины обязательно
проставляется ее размерность.
Все записи в расчетно-пояснительной записке ведутся чернилами на одной стороне листа писчей бумаги четкими разборчивым почерком, с расстоянием между строками в 8/12 мм.
На каждой странице оставляются поля: слева шириной 25 мм – для скрепления листов в тетрадь, и справа – 10мм.
Если у автора расчетно-графической работы неразборчивый почерк, то записку он должен выполнять чертежным шрифтом.
Изложение текстового материал записки следует вести от первого лица множественного числа, например: «…определяем…», «…вычисляем…», «…находим…», и т.д., или в безличной форме: «…можно определить…», и т.п., а не «…я определяю…», «…нахожу…», и т.д. Текст всей записки должен быть выдержан в единой стиле; например, если пояснения ведутся в безличной форме, то эта форма должна сохраняться во всей работе.
В конце записки необходимо
привести перечень литературы,
использованной студентом в процессе
выполнения работы, в той последовательности,
в какой литературные источники отмечены
квадратными скобками в тексте.
В страницы расчетно-графической работы должны быть последовательно пронумерованы в правой верхней части страницы арабскими цифрами с точкой. Нумерация страниц должна быть сквозное от титульного листа до последней страницы, включая чертежи (схемы). На титульном листе, который является первой страницей, номер страницы не ставится, хотя и подразумевается.
1.2.3. Выполнение графической части работы
Графическая часть работы выполняется на бумаге формате А4 (210 х 297 мм) или формата А3 (297 х 480 мм) карандашом или тушью с применением необходимых чертежей инструментов.
В соответствии с заданной схемой
по числовым данным варианта вычерчивается
в масштабе схема сооружения (расчетная
схема, поперечные сечения бруса и т.д.),
на которой проставляются исходные
данные (размеры) как в буквенных
обозначениях, так и в числах, а также
наносится заданная нагрузка. Кроме
того, все размеры, используемые в
расчетах, также должны быть показаны
на чертеже.
Эпюры внутренних усилий
(напряжений, перемещений) должны
вычерчиваться строго под расчетной
схемой бруса (или рядом с ней). На расчетной
схеме должны быть отмечены все сечения,
для которых, определяются внутренние
усилия; на эпюрах обязательно проставляются
значения вычисленных характерных
ординат. Для каждой экстремальной точки
любой эпюры обязательно определяется
ее положение и подсчитывается значение
ордината (max
или min).
Эпюры заштриховываются тонкими линиями
(расстояние между линиями 2+3 мм).
Перпендикулярно оси элемента конструкции.
На заштрихованном поле эпюры проставляется
ее знак «+» или «-».
1.2.4. Защита расчетно-графических работ
Каждым студентом все
расчетно-графические работы должны
выполняться и сдаваться на проверку
преподавателю в сроки, предусмотренные
графиком работы студентов в текущем
семестре. После исправления студентом
всех ошибок, отмечен их преподавателем
при проверке, каждая расчетно-графическая
работа должна быть защищена.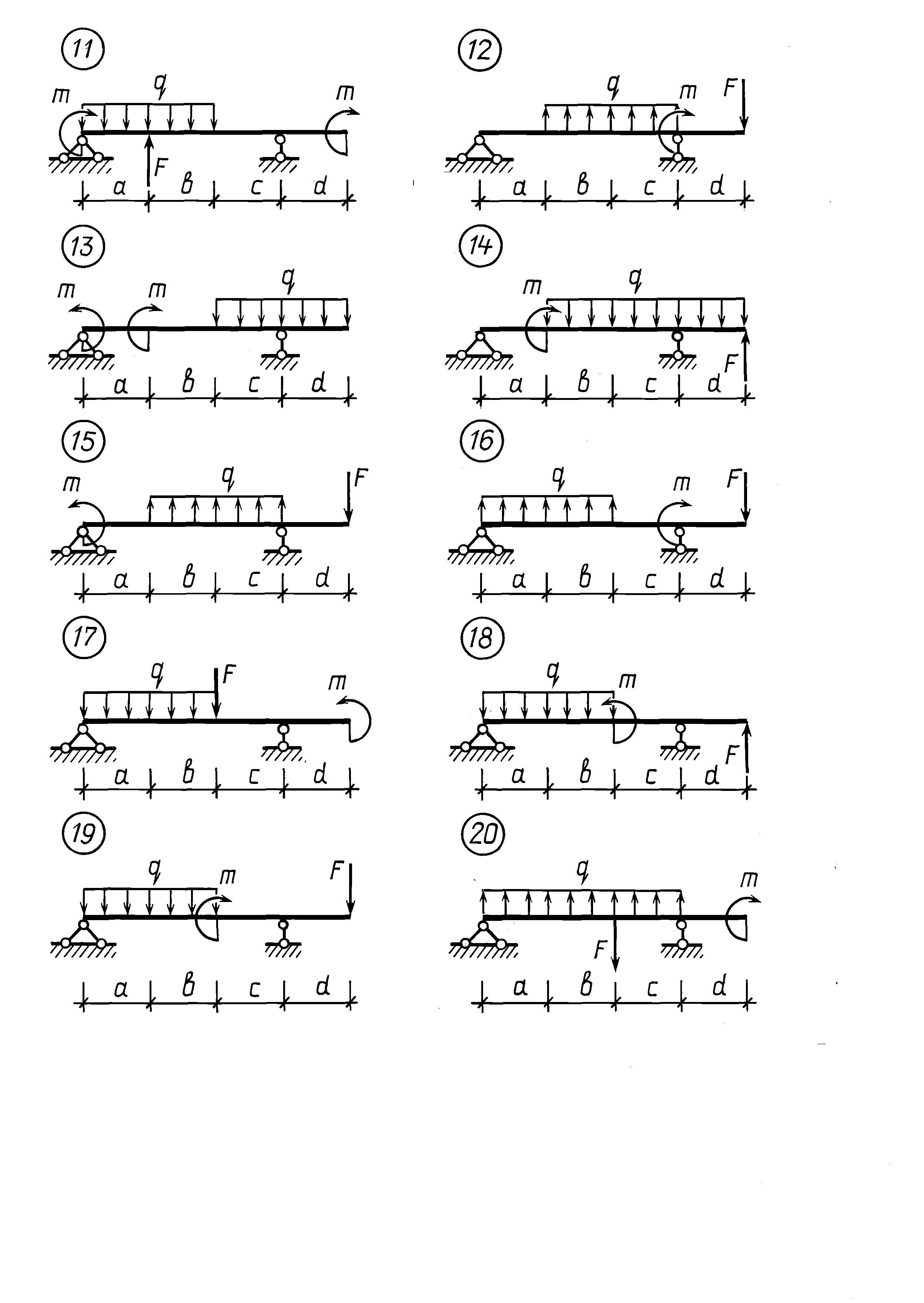
При
исправлении ошибок из проверенной
работы ни в коем случае ничего не
выбрасывается. Исправления аккуратно
записываются студентом на чистых
страницах. На защиту студенты приносят
исправленные работы, сдают их преподавателю,
получают индивидуальные карточки-задания
на решение задачи по соответствующему
разделу курса. На решение задачи отводится
максимум 30+40 мин. Если студент успешно
решил задачу и у преподавателя нет
никаких дополнительных замечаний по
расчетно-графической работе, то защита
считается законченной. После защиты
работа остается у преподавателя. Если
студентом все работы защищены успешно
и в срок, то в конце семестра он
автоматически получает зачет по курсу.
В случае, когда студент при защите не
справляется с решением типовых задач,
то преподавателем назначается
дополнительная защита (не более двух
раз!). Если студентом какие-либо
расчетно-графические работы не защищены
в течении семестра, то их защита и сдача
зачета по курсу производится в зачетное
– экзаменационную сессию.
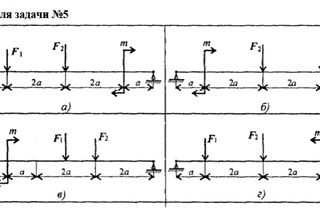
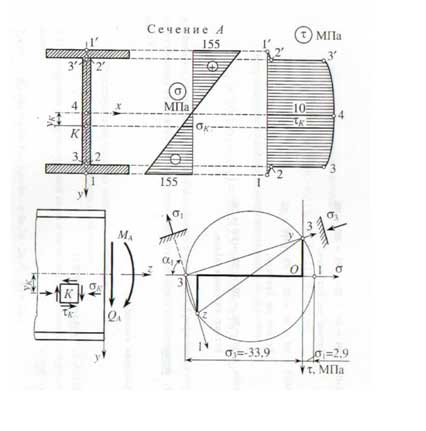
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
ПРИМЕР 1
Для изображенного на рис. 1.1. поперечного сечения требуется:
Определить положение центра тяжести сечения;
Определить положение главных центральных осей инерции;
Сопротивление материалов
(Для студентов механического и строительного направлений)
Скачать учебник А.В. Александров Сопротивление материалов (для строит. спец. ВУЗов, 2003г, 7.5Мб )
Скачать учебник В.И. Феодосьев “Сопротивление материалов”. изд. МГТУ им Баумана, для ВТУЗов 1999г, 8Мб)
Скачать учебник А.В. Дарков Г.С.Шпиро “Сопротивление материалов” ( для ВТУЗов, Москва, 1975г, 15Мб)
Скачать учебник М.Д. Подскребко “Сопротивление материалов” ( для ВТУЗов, Минск, 2007г, 14Мб)
Скачать пособие Б.А. Ободовский Сопротивление материалов в примерах и задачах
( для ВТУЗов, 1982г, 5Мб)
Скачать задачник Н.
М.Беляев Сборник задач по сопромату
( для ВТУЗов, 1968г, 4,3Мб)
Скачать пособие к решению задач. И.Н.Миролюбов, 1967г. ( для механ. спец, 5Мб)
Скачать руководство к решению задач. В.А.Бобрин, 2006г. ( для стр. трансп. спец , 1Мб)
Скачать решение задач по сопротивлению материалов. Э.А.Буланов,
1994г. ( для немашиностр. спец , 17Мб)
Ознакомиться, (скачать – если нужно) мою программу МКЕ для расчёта плоских рам (и балок)
Скачать или открыть документ MS Excel “Геометрические характеристики плоских сечений” (нужно ввести данные и просмотреть результаты). Есть примеры, формулы, инструкция. 250 кб
Скачать или открыть документ MS Excel “Построение эпюр нормальных, касательных и главных напряжений в поперечном (двутавровом) сечении” (нужно ввести данные и просмотреть результаты) 31кб
Скачать или открыть документ MS Excel “Вычисление напряжений в опасных точках при внецентренном сжатии” (нужно ввести данные и просмотреть результаты) 38кб
Рассчитать в on-line (платно) балку, ферму, раму
( перейти на сайт sopromat.
org)
Скачать учебники, методички (в виде RAR-архивов или смотреть в формате PDF)
подготовленные кафедрой СМиСМ
КубГТУ
Содержание
- Основные термины, гипотезы.
- Определение реакций опор.
- Деформации, внутренние силы, внутренние силовые факторы.
- Пример построения эпюр ВСФ для балки.
- Правила контроля эпюр
- Простой способ построения эпюр для балок. New: 21.03.2012
Разделы, предназначенные только для механических специальностей помечены знаком (М), разделы для строителей – знаком (С).
Примеры построения эпюр В.С.Ф. (для строителей)
Примечания к этим примерам:- Размерности не проставлены. Имеется в виду: силы – в кН, моменты – в кНм, распределённые нагрузки – в кН/м.
- Масштаб не соблюдается
- Картинки задач перекрываются, т е на страничке могут быть лишние эпюры (от предыдущей или следующей задачи)
Примеры решения заданий РГР (для механиков)
Методические указания по выполнению расчетно-графической работы №1 по дисциплине ОП.
02 Техническая механика, часть 2 «Сопротивление материалов» для обучающихся специальности 08.02.01. Строительство эксплуатация зданий и сооруженийМинистерство образования и науки РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«КРЫМСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ ИМЕНИ в.И. вЕРНАДСКОГО»
(фгаоу во «кфу им. В.И. ВЕРНАДСКОГО»)
«Бахчисарайский колледж строительства, архитектуры и дизайна»
Утверждаю
Директор Бахчисарайского колледжа строительства, архитектуры и дизайна (филиал) ФГАОУ ВО «КФУ им. В.И. Вернадского»
_____________ Г.П. Пехарь
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению расчетно-графической работы №1 по
дисциплине ОП.02 Техническая механика, часть П «Сопротивление материалов» для обучающихся специальности 08.02.01. «Строительство эксплуатация зданий и сооружений»
На тему: «Построение эпюр продольных сил
и нормальных напряжений при растяжении (сжатии).
Определение перемещений сечений »
Бахчисарай – 2016
Теоретические сведения.
Центральным растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила N, а остальные силовые факторы равны нулю. Явление центрального растяжения (сжатия) возникает только тогда, когда все внешние нагрузки действуют по оси, проходящей через центры тяжести поперечных сечений бруса.
1. Для определения внутренних продольных сил «N» пользуются методом сечений.
Брус рассекают на отдельные участки отбрасывают одну из частей, а ее влияние на оставшуюся часть заменяют неизвестной внутренней силой «N». Из условия равновесия для оставшейся части определяют величину силы «N». Для наглядного представления характера (закона) изменения какого-либо из внутренних силовых факторов по длине бруса строят график изменения этого фактора, который называется эпюрой продольных сил.
2. В поперечных сечениях бруса при центральном растяжении (сжатии) возникают равномерно распределенные нормальные напряжения , равные отношению внутренней продольной силы к площади поперечного сечения.
Нормальные напряжения при растяжении принимаются положительными, а при сжатии отрицательными и определяются по формуле
Если внешняя сила растягивает брус, ее в уравнении записывают со знаком «плюс», а если сжимает – со знаком «минус». Напряжения в поперечных сечениях определяют по формуле (Па; кПа; МПа).
Границами сечений являются точки приложения сил и места изменения площади поперечного сечения бруса. Для наглядного изображения характера изменения интенсивности напряжений в различных сечениях по длине бруса строят эпюры продольных сил и нормальных напряжений, т. е. графики, осью которых являются ось бруса, а ординатами являются значения интенсивности нормальных напряжений и продольных сил.
3. Под действием растягивающихся сил длина стержня увеличивается на ∆, а поперечные размеры его уменьшаются. По закону Гука продольное удлинение стержня определяется по следующей формуле
– абсолютное удлинение стержня;
-первоначальная длина стержня;
А- площадь поперечного сечения стержня;
Е- модуль продольной упругости, это физическая постоянная материала характеризующая его способность сопротивляться упругой деформации;
Е*А- жесткость поперечного сечения при растяжении (сжатии).
Расчетно-графическая работа выполняется на листах формата А-4 писчей бумаги. Задание выполняется по вариантам. Решение задачи и пояснения пишутся чернилами четко и понятно. Условие задачи переписывать обязательно. Выполненая расчетно-графическая работа защищается обучающимся.
Дисциплина «Сопротивление материалов» изучает расчет конструкций на прочность, жесткость и устойчивость при различных видах деформаций для выполнений этих расчетов сначала определяют внутренние силовые факторы, возникающие в поперечных сечениях конструкции под действием внешних сил. Внутренние силы определяют методом сечений, для каждого из которых составляется уравнение равновесия. Растяжение и сжатие характеризуются возникновением в поперечных сечениях внутренних сил «N» и нормальных напряжений , Продольная сила в сечении определяется из уравнений равновесия ; Иначе, продольная сила в сечении равна алгебраической сумме внешних сил. .
Последовательность выполнения работы разберем на примере:
Рассмотрим прямой стальной стержень ступенчатого симметрического поперечного сечения, жестко закрепленный вверху и нагруженный двумя внешними сосредоточенными силами ,,приложенными в точках А и С и направленными вдоль его продольной оси.
Площади поперечных сечений стержня и .Модуль продольной упругости материала стержня
Задача: Построить эпюры продольных сил и нормальных напряжений и определить полное удлинение стержня по данным одного из вариантов таблицы №1.
Решение:
Верхний конец стержня жёстко защемлён, нижний конец свободный. Разобьём стержень на отдельные участки, начиная со свободного конца. Границами участков будут сечения, в которых приложены внешние заданные силы или места изменения площади поперечного сечения бруса. Рассмотрим брус по высоте:
Первый участок АВ, от точки приложения силы F1, т. е. от нижнего конца бруса до сечения, в котором меняется площадь поперечного сечения бруса.
Второй участок ВС- до сечения в котором приложена сила F2. Третий участок СД- от точки приложения силы F2 до опоры. Пользуясь методом сечений определяем значения внутренних продольных сил в сечениях стержня.
Проводим сечение 1-1 в границах первого участка.
Мысленно отбрасываем верхнюю часть стержня от сечения 1-1 и рассмотрим равновесие
нижней, оставшейся части.
Составляем уравнение суммы проекций всех сил на ось у:
Продольная сила N1 положительная, поэтому на участке АВ имеет место растяжение.
Проводим сечение 2 – 2 на участке ВС стержня, мысленно отбрасываем верхнюю часть и рассматриваем равновесие оставшейся части. Составляем уравнение суммы проекций всех сил на ось у: ; ;
Проводим сечение 3 – 3 на участке СД, аналогично предыдущему запишем.
Продольная сила N3 отрицательная, поэтому на участке СД имеет место сжатие. Зная продольную силу на каждом из трёх участков, определяем значение нормальных напряжений, приняв во внимание, что
А1=18см2=0,0018м2; А2=А3=12см2=0,0012м2
По найденным значением N и (строим эпюру продольных сил N и эпюру нормальных
напряжений
Для этого проводим 2 прямые (базовые линии), параллельно оси стержня. Приняв прямые
за нулевую линию, откладываем право или влево от неё найденные значения «N»и
Эпюра интенсивности нормальных напряжений имеет скачки не только в сечениях, в
которых приложены сосредоточенные силы (где имеет скачки эпюра продольных сил), но
и в местах изменения поперечных сечений бруса.
Знаки на эпюрах ставить обязательно. Значения отложенных ординат подписываются.
Эпюры штрихуются линиями перпендикулярными к нейтральной оси. Длина штрихов
определяет в масштабе величину напряжения или продольной силы в соответствующем .
сечении бруса.
Определяем полное удлинение стержня:
Вопросы для самоконтроля:
Задача: построить эпюры продольных сил и нормальных напряжений и определить полное
удлинение стержня по данным одного из вариантов таблицы №1. Модуль продольной упругости материала
Контрольные вопросы
1. Дать определение продольной силы.
2. В чём заключается сущность метода сечений.
3. Как определить знак продольной силы N ?
4. Что представляет собой эпюра продольных сил?
5. По какой формуле вычисляться нормальные напряжения в сечениях балки?
6. Как определить полное или абсолютное удлинение стержня.
7. Записать закон Гука для практических расчетов при растяжении (сжатии).
8.
Что показывает модуль продольной упругости при растяжении и как обозначается.
9. Какая размерность у модуля продольной упругости?
10. Какая размерность у нормальных напряжений в поперечных сечениях стержня.
Литература:
1. Портаев Л.П., Петраков А.А., Портаев В.Л., ” Техническая механика”; М. Стройиздат, 1987.стр 134-145.
2. Улитин Н.С., “сопротивление материалов”, М. Высшая школа. 1975. стр 18-55.
3. Михайлов А.М.” сопротивление материалов” , М. Сройиздат 1989. стр 25-97.
Министерство образования и науки РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«КРЫМСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ ИМЕНИ в.И. вЕРНАДСКОГО»
(фгаоу во «кфу им. В.И. ВЕРНАДСКОГО»)
«Бахчисарайский колледж строительства, архитектуры и дизайна»
Утверждаю
Директор Бахчисарайского колледжа строительства, архитектуры и дизайна (филиал) ФГАОУ ВО «КФУ им. В.И. Вернадского»
_____________ Г.
П. Пехарь
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению расчетно-графической работы № 3 по
дисциплине ОП.02 Техническая механика, часть П «Сопротивление материалов» для обучающихся специальности 08.02.01. «Строительство эксплуатация зданий и сооружений»
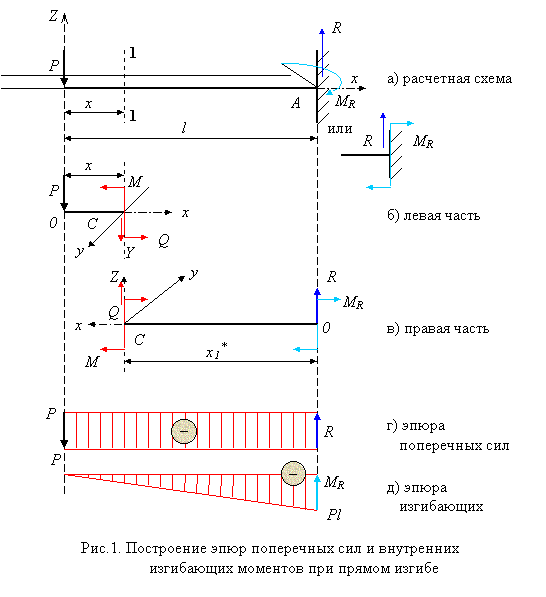
На тему: «Построение эпюр поперечных сил и изгибающих моментов
для балки на двух опорах»
Бахчисарай – 2016
Теоретические сведения.
Для наглядного представления о законах изменения поперечной силы и изгибающего момента по длине балки удобно изображать их в виде графиков, ординаты которых соответствуют значениям поперечных сил или изгибающих моментов в любом ее сечении балки.
Графики, выражающие закон изменения поперечных сил или изгибающих моментов по длине б…
Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта – свяжитесь, пожалуйста, с нами.
Research: Лаборатория перспективной вычислительной механики и материалов: Университет Рочестера
Обзор
Мультимасштабное моделирование наноразмерных металлических многослойных слоев
Мы используем вычислительные методы, чтобы понять фундаментальные механизмы деформации наноразмерных металлических многослойных слоев при малых масштабах времени и длины, а также исследовать влияние таких параметров, как структура интерфейса, химический состав и морфология на эти механизмы.
Мы используем многомасштабные модели атомистического моделирования, методы Монте-Карло, пластичность кристаллов и механику сплошной среды для механизмов деформации многослойных композитов и предоставляем математические модели для определения коллективного поведения этих материалов в различных масштабах длины.
Вычислительное прогнозирование структуры полукогерентных интерфейсов
Твердотельные интерфейсы широко используются в материаловедении: от границ зерен в поликристаллических металлах до гетерофазных интерфейсов в многокомпонентных многофункциональных композитах. По мере того как осознание их далеко идущего влияния на поведение материалов растет, растет и интерес к прогнозированию и контролю их структуры и свойств. В этом проекте мы продвигаем основанную на дислокациях модель для структуры интерфейса, разрабатывая метод определения уникального эталонного состояния, в котором должны быть определены векторы Бюргерса интерфейса.
Нанопористые материалы
Нанопористые (NP) металлы представляют собой трехмерную сеть связанных между собой пор и связок.
Их структура с открытыми ячейками и большая площадь поверхности на единицу объема придают им уникальные электрические, механические и каталитические свойства, а также высокую радиационную стойкость. Деформационное поведение материалов NP часто контролируется их микроструктурой, включая пористость, размер и форму связок. Цель этого проекта – выявить механизмы, контролирующие пластическую деформацию НЧ-металлов, и разработать прогнозные модели / карты для определения их механических свойств, включая пластичность и прочность.
Композитные псевдоупругие нанопроволоки
Статья по теме: Структурное фазовое превращение под действием напряжений увеличивает пластичность в двунепрерывных переплетенных композитах Mo / Cu Металлические нанопроволоки могут восстанавливаться после пластической деформации до 50%, когда их площадь поперечного сечения меньше определенного критического значения значение, которое составляет порядка нескольких нм. Такое поведение называется псевдоупругостью, и ответственный за это механизм – образование частичных дислокаций (двойникование).
В частности, мы исследуем совместное влияние геометрии и когерентного интерфейса на склонность композитных нанопроволок к деформации двойников и проявлению псевдоупругого поведения.Идея сэндвич-нанопроволок может быть использована в случае металлов с низкой двойниковостью для улучшения их пластичности и псевдоупругих свойств в будущем.
Машинное обучение в информатике материалов: последние применения и перспективы
Гопник А. Делаем ИИ более человечным. Sci. Являюсь. 316 , 60–65 (2017).
Артикул Google ученый
Иордания, М.И. и Митчелл, Т. М. Машинное обучение: тенденции, перспективы и перспективы. Наука 349 , 255–260 (2015).
Артикул Google ученый
Шринивасан С. и Ранганатан С. Легендарная индийская сталь Wootz: усовершенствованный материал древнего мира (Национальный институт перспективных исследований, 2004 г.
).
Уорд, Г. В. Р. Энциклопедия материалов и методов в искусстве Гроув (Oxford University Press, 2008).
Хьюм-Розери, У. Теория атома для студентов-металлургов. J. Менее распространенный Met. 3 , 264 (1961).
Артикул Google ученый
Холл, Э. О. Деформация и старение мягкой стали: III обсуждение результатов. Proc. Phys. Soc. B 64 , 747–753 (1951).
Артикул Google ученый
Петч, Н. Дж. Влияние межзеренного карбида и размера зерна на прочность на скалывание и температуру ударного перехода стали. Acta Metall. 34, , 1387–1393 (1986).
Артикул Google ученый
Ван Кревелен, Д. В. и Те Нийенхуис, К. Свойства полимеров: их корреляция с химической структурой; их численная оценка и прогноз на основе вкладов аддитивных групп (Elsevier, 2009).
Мюллер Т., Кусне А.Г. и Рампрасад Р. В обзоре по вычислительной химии , 186–273 (John Wiley & Sons, Inc., 2016).
Уорд, Л. и Волвертон, К. Атомистические расчеты и информатика материалов: обзор. Curr. Opin. Solid State Mater. Sci. 21 , 167–176 (2017).
Артикул Google ученый
Green, M. L. et al. Выполнение обещания инициативы по геному материалов с помощью высокопроизводительных экспериментальных методологий. Заявл. Phys. Сборка 4 , 011105 (2017).
Артикул Google ученый
Хаттрик-Симперс, Дж. Р., Грегуар, Дж. М. и Кусне, А. Г. Перспектива: отображение состава, структуры и свойств в высокопроизводительных экспериментах: превращение данных в знания. APL Mater. 4 , 053211 (2016).
Артикул Google ученый
Бишоп, К. М. Распознавание образов и машинное обучение (Springer, 2006).
Теодоридис С. Машинное обучение: байесовская и оптимизационная точки зрения (Academic Press, 2015).
Хасти Т., Тибширани Р. и Фридман Дж. Элементы статистического обучения: интеллектуальный анализ данных, вывод и прогнозирование (Springer Science & Business Media, 2013).
Санчес Дж., Дукастель Ф. и Гратиас Д. Обобщенное кластерное описание многокомпонентных систем. Phys. A: Стат. Мех. Прил. 128 , 334–350 (1984).
Артикул Google ученый
Фонтейн Д. Кластерный подход к превращениям порядка-беспорядка в сплавах. Физика твердого тела. 47 , 33–176 (1994).
Артикул Google ученый
Зунгер А. Основные принципы статистической механики полупроводниковых сплавов и интерметаллических соединений, Институт перспективных исследований НАТО, Серия B: Physics Vol. 319 (Turchi, P. & Gonis, A. eds), 361419 (Пленум, Нью-Йорк, 1994).
Лакс, Д. Б., Феррейра, Л. Г., Фройен, С. и Зунгер, А. Эффективное расширение кластера для систем замещения. Phys. Ред. B 46 , 12587–12605 (1992).
Артикул Google ученый
ван де Валле, А. и Седер, Г. Автоматизация расчетов фазовых диаграмм из первых принципов. J. Phase Equilib. 23 , 348 (2002).
Артикул Google ученый
Мюллер Т. и Седер Г. Байесовский подход к расширению кластера. Phys. Ред. B 80 , 024103 (2009).
Артикул Google ученый
Кокейн, Э. и ван де Валль, А. Построение эффективных моделей на основе редких, но точных данных: приложение к модели расширения кластеров сплава. Phys. Ред. B 81 , 012104 (2010).
Артикул Google ученый
Секо, А., Кояма, Ю. и Танака, И. Метод кластерного разложения для многокомпонентных систем, основанный на оптимальном выборе структур для расчетов теории функционала плотности. Phys. Ред. B 80 , 165122 (2009).
Артикул Google ученый
Мюллер Т. и Седер Г. Точные выражения для выбора структуры в кластерных расширениях. Phys. Ред. B 82 , 184107 (2010).
Артикул Google ученый
Лэнс, Н. Дж., Харт, Г. Л. У., Чжоу, Ф. и Озолинс, В. Измерение сжатия как парадигма для построения физических моделей.
Phys. Ред. B 87 , 24–32 (2015).
Google ученый
Сандерс, Дж. Н., Андраде, X. и Аспуру-Гузик, А. Компрессионное зондирование для быстрого вычисления матриц: приложение к молекулярным колебаниям. ACS Cent. Sci. 1 , 035125 (2013).
Google ученый
Шмидт, М. и Липсон, Х. Извлечение естественных законов свободной формы из экспериментальных данных. Наука 324 , 81–85 (2009).
Артикул Google ученый
Гирингелли, Л. М., Выбирал, Дж., Левченко, С. В., Драксл, К. и Шеффлер, М. Большие данные материаловедения: критическая роль дескриптора. Phys. Rev. Lett. 114 , 105503 (2015).
Артикул Google ученый
Ghiringhelli, L. M. et al. Изучение физических дескрипторов для материаловедения с помощью сжатого зондирования. Новый. J. Phys. 19 , 023017 (2017).
Артикул Google ученый
Лукман Т., Александр, Ф. Дж. И Раджан, К. Информационные науки для открытия и проектирования материалов (Springer, 2015).
Ким К., Пилания Г. и Рампрасад Р. От организованных высокопроизводительных данных до феноменологической теории с использованием машинного обучения: пример пробоя диэлектрика. Chem. Матер. 28 , 1304–1311 (2016).
Артикул Google ученый
Ким К., Пилания Г. и Рампрасад Р. Машинное обучение помогало прогнозировать внутреннюю диэлектрическую прочность перовскитов ABX3. J. Phys. Chem. C 120 , 14575–14580 (2016).
Артикул Google ученый
Goldsmith, B.R. et al. Выявление взаимосвязей между структурой и свойством материалов путем открытия подгрупп. Новый. J. Phys. 19 , 013031 (2017).
Артикул Google ученый
Биалон, А. Ф., Хаммершмидт, Т. и Драутц, Р. Трехпараметрическое предсказание кристаллической структуры для sp-d-валентных соединений. Chem. Матер. 28 , 2550–2556 (2016).
Артикул Google ученый
Данные кристалла Пирсона. База данных кристаллической структуры неорганических соединений. Choice Rev. Online 45 , 45–3800–45–3800 (2008).
Google ученый
Олийнык А.О. и др. Высокопроизводительный синтез соединений Фулл-Гейслера на основе машинного обучения.
Chem. Матер. 28 , 7324–7331 (2016).
Артикул Google ученый
ASM international материалы информационного общества – ASM international.http://www.asminternational.org/. Дата обращения 23.06.2017.
Dey, P. et al. Информатика и технология запрещенной зоны для солнечных материалов. Comput. Матер. Sci. 83 , 185–195 (2014).
Артикул Google ученый
Уорд, Л., Агравал, А., Чоудхари, А. и Волвертон, К. Универсальная среда машинного обучения для прогнозирования свойств неорганических материалов. NPJ Comput. Матер. 2 , 201628 (2016).
Артикул Google ученый
Ли, Дж., Секо, А., Шитара, К., Накаяма, К. и Танака, И. Модель прогнозирования ширины запрещенной зоны для неорганических соединений путем сочетания расчетов теории функционала плотности и методов машинного обучения.
Phys. Ред. B Конденс. Дело 93 , 115104 (2016).
Артикул Google ученый
Pilania, G. et al. Запрещенные зоны машинного обучения двойных перовскитов. Sci. Реп. 6 , 19375 (2016).
Артикул Google ученый
Пилания, Г., Губернатис, Дж. Э. и Лукман, Т. Модели машинного обучения с множественной точностью для точного прогнозирования запрещенной зоны твердых тел. Comput. Матер. Sci. 129 , 156–163 (2017).
Артикул Google ученый
Faber, F. A., Lindmaa, A., von Lilienfeld, O. A. & Armiento, R. Энергия машинного обучения 2 миллионов кристаллов эльпасолита (ABC 2 D 6 ). Phys. Rev. Lett. 117 , 135502 (2016).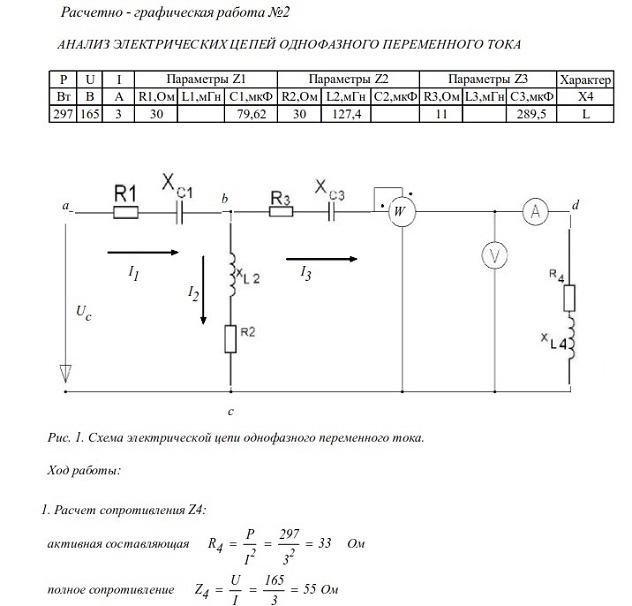
Артикул Google ученый
Meredig, B. et al. Комбинаторный отбор новых материалов в неограниченном композиционном пространстве с помощью машинного обучения. Phys. Ред. B Конденс. Дело 89 , 094104 (2014).
Артикул Google ученый
Демл, А. М., О’Хайр, Р., Волвертон, К. и Стеванович, В. Предсказание полных энергий и энтальпий образования металл-неметаллических соединений по теории функционала плотности с помощью линейной регрессии. Phys. Ред. B Конденс. Дело 93 , 085142 (2016).
Артикул Google ученый
Легрейн, Ф., Каррет, Дж., Ван Рокегем, А., Куртароло, С. и Минго, Н. Как только химический состав может предсказывать колебательные свободные энергии и энтропии твердых тел. Chem. Материал .
29 , 6220–6227 (2017).
Medasani, B. et al. Прогнозирование поведения дефектов в интерметаллидах B2 путем объединения неэмпирического моделирования и машинного обучения. NPJ Comput. Матер. 2 , 1 (2016).
Артикул Google ученый
Секо, А., Маэкава, Т., Цуда, К. и Танака, И. Машинное обучение с систематическими расчетами теории функционала плотности: применение к температурам плавления однокомпонентных и двухкомпонентных твердых тел. Phys. Ред. B Конденс. Дело 89 , 054303 (2014).
Артикул Google ученый
Пилания, Г., Губернатис, Дж. Э. и Лукман, Т. Классификация структуры и прогнозирование температуры плавления октетных твердых тел AB с помощью машинного обучения. Phys. Ред. B Конденс. Дело 91 , 214302 (2015).
Артикул Google ученый
Чаттерджи, С., Муруганант, М.& Бхадешия, Х. К. Д. Х. δ TRIP сталь. Mater. Sci. Technol. 23 , 819–827 (2007).
Артикул Google ученый
De Jong, M. et al. Структура статистического обучения для материаловедения: приложение к модулям упругости k-рых неорганических поликристаллических соединений. Sci. Реп. 6 , 34256 (2016).
Артикул Google ученый
Aryal, S., Sakidja, R., Barsoum, M. W. & Ching, W.-Y. Геномный подход к стабильности, упругим и электронным свойствам MAX-фаз. Phys. Статус Solidi 251 , 1480–1497 (2014).
Артикул Google ученый
Seko, A.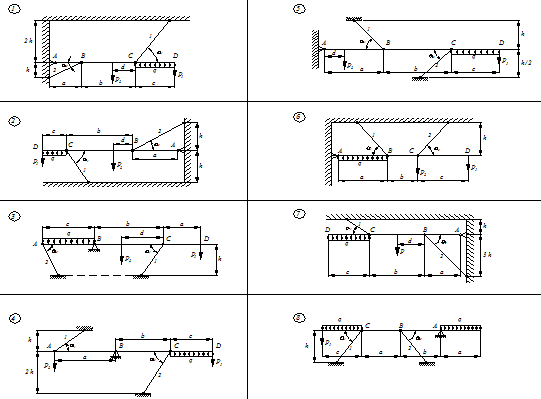
et al. Прогнозирование соединений с низкой теплопроводностью с помощью первопринципных расчетов ангармонической динамики решетки и байесовской оптимизации. Phys. Rev. Lett. 115 , 205901 (2015).
Артикул Google ученый
Li, Z., Ma, X. & Xin, H. Разработка характеристик хемосорбционных моделей с машинным обучением для разработки катализаторов. Catal. Сегодня 280 , 232–238 (2017).
Артикул Google ученый
Хонг, В. Т., Велш, Р. Э. и Шао-Хорн, Ю. Дескрипторы активности выделения кислорода для оксидов: статистическая оценка. J. Phys. Chem. C 120 , 78–86 (2016).
Артикул Google ученый
Pilania, G. et al. Использование машинного обучения для определения факторов, определяющих аморфизацию облученных пирохлоров.
Chem. Матер. 29 , 2574–2583 (2017).
Артикул Google ученый
Xue, D. et al. Ускоренный поиск материалов с заданными свойствами за счет адаптивного дизайна. Nat. Commun. 7 , 11241 (2016).
Артикул Google ученый
Xue, D. et al. Ускоренный поиск пьезоэлектриков на основе BaTiO3 с вертикальной морфотропной фазовой границей с использованием байесовского обучения. Proc. Natl Acad. Sci. США A 113 , 13301–13306 (2016).
Артикул Google ученый
Эштон, М., Хенниг, Р. Г., Бродерик, С. Р., Раджан, К. и Синнотт, С. Б. Вычислительное открытие стабильных фаз M 2 AX. Phys. Ред. Б. Конденс. Дело 94 , 20 (2016).
Артикул Google ученый
Пилания Г., Балачандран П. В., Ким К. и Лукман Т. Поиск новых галогенидов перовскита с помощью машинного обучения. Фронт. Матер. 3 , 19 (2016).
Артикул Google ученый
Фернандес, М., Бойд, П. Г., Дафф, Т. Д., Агаджи, М. З. и Ву, Т. К. Быстрое и точное распознавание машинным обучением высокопроизводительных металлоорганических каркасов для захвата CO 2 . J. Phys. Chem. Lett. 5 , 3056–3060 (2014).
Артикул Google ученый
Эмери А. А., Заал Дж. Э., Кирклин С., Хегде В. И. и Волвертон К. Высокопроизводительный вычислительный скрининг перовскитов для термохимического разделения воды. Chem. Матер. 28 , 5621–5634 (2016).
Артикул Google ученый
Kalidindi, S. R. et al. Роль материаловедения и информатики в ускорении разработки материалов. MRS Bull. 41 , 596–602 (2016).
Артикул Google ученый
Броу, Д. Б., Каннан, А., Хааланд, Б., Бакнелл, Д. Г. и Калидинди, С. Р. Извлечение связей эволюции процесса и структуры из измерений рассеяния рентгеновских лучей с использованием уменьшения размерности и анализа временных рядов. Integr. Матер. Manuf. Иннов. 6 , 147–159 (2017).
Артикул Google ученый
Калидинди, С. Р., Гомберг, Дж. А., Траутт, З. Т. и Беккер, К. А. Применение инструментов науки о данных для количественной оценки и различения структур и моделей в наборах данных молекулярной динамики. Нанотехнологии 26 , 344006 (2015).
Артикул Google ученый
Гупта А., Сесен А., Гоял С., Сингх А. К. и Калидинди С. Р. Взаимосвязи структуры и свойств с использованием подхода науки о данных: применение к композитной системе неметаллические включения / сталь. Acta Mater. 91 , 239–254 (2015).
Артикул Google ученый
Броу, Д. Б., Уиллер, Д., Уоррен, Дж. А. и Калидинди, С. Р. Системы знаний на основе микроструктуры для фиксации взаимосвязей между процессом и эволюцией структуры. Curr. Opin. Solid State Mater. Sci. 21 , 129–140 (2017).
Артикул Google ученый
Панчал, Дж. Х., Калидинди, С. Р. и Макдауэлл, Д. Л. Ключевые вопросы вычислительного моделирования в комплексной инженерии вычислительных материалов. Comput. Помощь Дес.
Прил. 45 , 4–25 (2013).
Артикул Google ученый
Броу Д. Б., Уилер Д. и Калидинди С. Р. Системы знаний о материалах в Python – структура науки о данных для ускоренной разработки иерархических материалов. Integr. Матер. Manuf. Иннов. 6 , 36–53 (2017).
Артикул Google ученый
Калидинди, С. Р. Эффективное с точки зрения вычислений, полностью связанное многомасштабное моделирование явлений в материалах с использованием калиброванных локализационных связей. Уведомления о международных научных исследованиях 2012 , 1–13 (2012).
Адамсон, Г. У. и Буш, Дж. А. Метод связи структуры и свойств химических соединений. Природа 248 , 406–407 (1974).
Артикул Google ученый
Адамсон, Г. У., Буш, Дж. А., МакЛюр, А. Х. У. и Линч, М.F. Оценка системы поиска подструктуры на основе фрагментов с центром в связях. J. Chem. Док. 14 , 44–48 (1974).
Артикул Google ученый
Джадсон, П. Экспертные системы, основанные на знаниях в химии: не считая компьютеров (Королевское химическое общество, 2009).
Huan, T. D. et al. Набор данных по полимерам для ускоренного прогнозирования свойств и проектирования. Sci. Данные 3 , 160012 (2016).
Артикул Google ученый
Mannodi-Kanakkithodi, A. et al. Рациональная совместная разработка полимерных диэлектриков для накопления энергии. Adv. Матер. 28 , 6277–6291 (2016).
Артикул Google ученый
Treich, G. M.и другие. Рациональный совместный подход к созданию новых диэлектрических полимеров с высокой плотностью энергии. IEEE Trans. Dielectr. Электр. Insul. 24 , 732–743 (2017).
Артикул Google ученый
Huan, T. D. et al. Усовершенствованные полимерные диэлектрики для приложений с высокой плотностью энергии. Прог. Матер. Sci. 83 , 236–269 (2016).
Артикул Google ученый
Sharma, V. et al. Рациональная конструкция всех диэлектриков из органических полимеров. Nat. Commun. 5 , 4845 (2014).
Артикул Google ученый
Лоренцини, Р. Г., Клайн, В. М., Ван, К. К., Рампрасад, Р. и Сотцинг, Г. А. Рациональная конструкция полимочевины и полиуретановых диэлектрических материалов.
Полимер 54 , 3529 (2013).
Артикул Google ученый
Liu, C. S., G, P., C, W. & R, R. Насколько критичны ван-дер-ваальсовы взаимодействия в полимерных кристаллах? J. Phys. Chem. А 116 , 9347 (2012).
Артикул Google ученый
Манноди-Канаккитоди, А., Пилания, Г., Хуан, Т. Д., Лукман, Т., Рампрасад, Р. Стратегия машинного обучения для ускоренного проектирования полимерных диэлектриков. Sci. Реп. 6 , 20952 (2016).
Артикул Google ученый
Пилания, Г., Ван, К., Цзян, X., Раджасекаран, С., Рампрасад, Р. Ускорение прогнозирования свойств материалов с помощью машинного обучения. Sci. Реп. 3 , 2810 (2013).
Артикул Google ученый
Хуан, Т. Д., Манноди-Канаккитоди, А. и Рампрасад, Р. Ускоренное прогнозирование свойств материалов и дизайн с использованием отпечатков пальцев на основе мотивов. Phys. Ред. B Конденс. Дело 92 , 014106 (2015).
Манноди-Канаккитоди А., Хуан Т. Д. и Рампрасад Р. Правила проектирования горных материалов на основе данных: пример полимерных диэлектриков.(На рассмотрении). Chem. Мат. 29 , 9001–9010 (2017)
PolymerGenome. http://polymergenome.org.
Hautier, G., Fischer, C.C., Jain, A., Mueller, T. & Ceder, G. Поиск отсутствующих в природе тройных оксидных соединений с использованием машинного обучения и теории функционала плотности. Chem. Матер. 22 , 3762–3767 (2010).
Артикул Google ученый
Белер, Дж. И Парринелло, М.
Обобщенное нейросетевое представление многомерных поверхностей потенциальной энергии. Phys. Rev. Lett. 98 , 146401 (2007).
Артикул Google ученый
Белер, Дж., Мартонак, Р., Донадио, Д. и Парринелло, М. Метадинамическое моделирование фаз высокого давления кремния с использованием многомерного потенциала нейронной сети. Phys. Rev. Lett. 100 , 185501 (2008).
Артикул Google ученый
Белер, Дж. Представление поверхностей потенциальной энергии многомерными потенциалами нейронной сети. J. Phys. Конденс. Дело 26 , 183001 (2014).
Артикул Google ученый
Барток, А. П., Пейн, М. К., Кондор, Р. и Чаньи, Г. Потенциалы гауссовского приближения: точность квантовой механики без учета электронов.
Phys. Rev. Lett. 104 , 136403 (2010).
Артикул Google ученый
Рупп М., Ткаченко А., Мюллер К.-Р. & фон Лилиенфельд, О. А. Быстрое и точное моделирование энергий молекулярной атомизации с помощью машинного обучения. Phys. Rev. Lett. 108 , 058301 (2012).
Артикул Google ученый
Chmiela, S. et al. Машинное обучение точных энергосберегающих молекулярных силовых полей. Sci. Adv. 3 , e1603015 (2017).
Артикул Google ученый
Барток, А. П., Кондор, Р. и Чаньи, Г. О представлении химической среды. Phys. Ред. B Конденс. Дело 87 , 184115 (2013).
Артикул Google ученый
Szlachta, W. J., Bartók, A. P. & Csányi, G. Точность и переносимость моделей потенциала гауссовой аппроксимации для вольфрама. Phys. Ред. Б. Конденс. Дело 90 , 104108 (2014).
Артикул Google ученый
Барток, А. П. и Чаньи, Г. Гауссовские аппроксимационные потенциалы: краткое введение в учебное пособие. Внутр. J. Quantum Chem. 115 , 1051–1057 (2015).
Артикул Google ученый
Дерингер В. Л. и Чаньи Г. Межатомный потенциал аморфного углерода на основе машинного обучения. Phys. Ред. B Конденс. Дело 95 , 094203 (2017).
Артикул Google ученый
Джиндал С., Чирики С. и Булусу С. Дескриптор на основе сферических гармоник для потенциалов нейронной сети: структура и динамика нанокластера Au 147 . J. Chem. Phys. 146 , 204301 (2017).
Артикул Google ученый
Томпсон А., Свайлер Л., Тротт С., Фойлз С. и Такер Г. Метод спектрального анализа соседей для автоматического создания квантово-точных межатомных потенциалов. J. Comput. Phys. 285 , 316–330 (2015).
Артикул Google ученый
Рупп М. Машинное обучение для квантовой механики в двух словах. Внутр. J. Quantum Chem. 115 , 1058–1073 (2015).
Артикул Google ученый
Ли, З., Кермод, Дж. Р. и Де Вита, А. Молекулярная динамика с машинным обучением на лету квантово-механических сил. Phys. Rev. Lett. 114 , 096405 (2015).
Артикул Google ученый
Боту В. и Рампрасад Р. Схема обучения для прогнозирования атомных сил и ускорения моделирования материалов. Phys. Ред. Б. Конденс. Дело 92 , 094306 (2015).
Артикул Google ученый
Глиельмо, А., Соллих, П. и Де Вита, А. Точные межатомные силовые поля с помощью машинного обучения с ковариантными ядрами. Phys. Ред. Б. Конденс. Дело 95 , 214302 (2017).
Артикул Google ученый
Боту В. и Рампрасад Р. Адаптивная среда машинного обучения для ускорения молекулярной динамики ab initio. Внутр. J. Quantum Chem. 115 , 1074–1083 (2015).
Артикул Google ученый
Боту В., Чепмен Дж. И Рампрасад Р. Исследование созревания адатомов на поверхности al (111) с помощью силовых полей машинного обучения. Comput. Матер. Sci. 129 , 332–335 (2017).
Артикул Google ученый
Боту, В., Батра, Р., Чепмен, Дж. И Рампрасад, Р. Силовые поля машинного обучения: построение, проверка и перспективы. J. Phys. Chem. С. 121 , 511–522 (2017).
Артикул Google ученый
Фейнман Р. П. Силы в молекулах. Phys. Сборка 56 , 340–343 (1939).
Артикул Google ученый
Бьянкини, Ф., Кермод, Дж. Р. и Де Вита, А. Моделирование дефектов в Ni – Al с помощью расчетов методом EAM и DFT. Modell. Simul. Матер. Sci. Англ. 24 , 045012 (2016).
Артикул Google ученый
Эрколесси Ф. и Адамс Дж. Б. Межатомные потенциалы на основе расчетов из первых принципов: метод согласования сил. Europhys. Lett. 26 , 583–588 (1994).
Артикул Google ученый
Снайдер, Дж. К., Рупп, М., Хансен, К., Мюллер, К.-Р. И Берк К. Нахождение функционалов плотности с помощью машинного обучения. Phys. Rev. Lett. 108 , 253002 (2012).
Артикул Google ученый
Snyder, J. C. et al. Разрыв безорбитальных связей с помощью машинного обучения. J. Chem. Phys. 139 , 224104 (2013).
Артикул Google ученый
Снайдер, Дж. К., Рупп, М., Мюллер, К.-Р. И Берк, К. Нелинейное градиентное шумоподавление: поиск точных экстремумов из неточных функциональных производных. Внутр. J. Quantum Chem. 115 , 1102–1114 (2015).
Артикул Google ученый
Fancher, C.M. et al. Использование байесовского вывода в уточнении кристаллографической структуры с помощью анализа полного дифракционного профиля. Sci. Реп. 6 , 31625 (2016).
Артикул Google ученый
Kusne, A. G. et al. Машинное обучение на лету для высокопроизводительных экспериментов: поиск постоянных магнитов, не содержащих редкоземельные элементы. Sci. Реп. 4 , 6367 (2014).
Артикул Google ученый
Кусне А.Г., Келлер Д., Андерсон А., Забан А. и Такеучи И. Высокопроизводительное определение структурной фазовой диаграммы и составляющих фаз с помощью GRENDEL. Нанотехнологии 26 , 444002 (2015).
Артикул Google ученый
Хаттрик-Симперс, Дж. Р., Грегуар, Дж. М. и Кусне, А. Г. Перспектива: сопоставление свойств состава и структуры в высокопроизводительных экспериментах: превращение данных в знания. APL Mater. 4 , 053211 (2016).
Артикул Google ученый
Банн, Дж. К., Ху, Дж. И Хаттрик-Симперс, Дж. Р. Полуконтролируемый подход к идентификации фаз по комбинаторным дифрактограммам образца. JOM 68 , 2116–2125 (2016).
Артикул Google ученый
Де, С., Барток, А. П., Чаньи, Г. и Чериотти, М. Сравнение молекул и твердых тел в структурном и алхимическом пространстве. Phys. Chem. Chem. Phys. 18 , 13754–13769 (2016).
Артикул Google ученый
Лукман Т., Балачандран П. В., Сюэ Д., Хогден Дж. И Тайлер Дж. Статистический вывод и адаптивный дизайн для открытия материалов. Curr. Opin. Solid State Mater. Sci. 21 , 121–128 (2017).
Артикул Google ученый
Фельзенштейн, Дж. Уровни достоверности начальной загрузки для филогенетических деревьев. В The Science of Bradley Efron , Springer Series in Statistics (eds Morris, C.N. & Tibshirani, R.) 336–343 (Springer, New York, NY, 2008).
Powell, W. B. et al. Оптимальное обучение . (Wiley, Oxford, 2012).
Забронировать Google ученый
Powell, W. B. et al. Градиент знаний для оптимального обучения. В Энциклопедия исследований операций и науки управления Wiley (John Wiley & Sons, Inc., 2010).
Рыжов, И.О., Пауэлл, В. Б. и Фрейзер, П. I. Алгоритм градиента знаний для общего класса задач онлайн-обучения. Опер. Res. 60 , 180–195 (2012).
Артикул Google ученый
Микчелли, К. А. и Понтил, М. Об обучении векторных функций. Neural Comput. 17 , 177–204 (2005).
Артикул Google ученый
Альварес, М. А., Росаско, Л. и Лоуренс, Н. Д. Ядра для векторно-значных функций: обзор (Now Publishers Incorporated, 2012).
Форрестер, А. И., Собестер, А. и Кин, А. Дж. Оптимизация множественной точности с помощью суррогатного моделирования. Proc. R. Soc. А 463 , 3251–3269 (2007).
Артикул Google ученый
Perdikaris, P., Вентури, Д., Ройсет, Дж. О. и Карниадакис, Г. Е. Моделирование множественной точности с помощью рекурсивного ко-кригинга и гауссовско-марковских случайных полей. Proc. Математика. Phys. Англ. Sci. 471 , 20150018 (2015).
Артикул Google ученый
Дудий, С. В. и Зунгер, А. Поиск конфигураций сплавов с заданными физическими свойствами: дизайн примесей с помощью метода обратной полосовой структуры генетического алгоритма. Phys. Rev. Lett. 97 , 046401 (2006).
Артикул Google ученый
Представление микроструктуры и реконструкция гетерогенных материалов с помощью сети глубокого убеждения для вычислительного проектирования материалов
@article {0e00a0e3f7844a0aaccf6cd247689c4a,
title = “Представление микроструктуры и реконструкция неоднородных материалов с помощью сети глубокого проектирования
000 для проектирования гетерогенных материалов“. = “Интегрированная вычислительная инженерия материалов (ICME) направлена на ускорение оптимального проектирования сложных систем материалов за счет интеграции материаловедения и автоматизации проектирования.Для податливого ICME требуется, чтобы (1) было определено пространство структурных особенностей, чтобы можно было реконструировать новые конструкции, и (2) процесс реконструкции был сохранен. Большинство существующих схем структурного представления полагается на понимание проектировщиком конкретных систем материалов для определения геометрических и статистических характеристик, которые могут быть предвзятыми и недостаточными для реконструкции физически значимых микроструктур сложных систем материалов. В этой статье мы разрабатываем механизм обучения признакам, основанный на сверточной сети глубоких убеждений (CDBN), для автоматизации двустороннего преобразования между микроструктурами и их представлениями низкоразмерных признаков, а также для достижения 1000-кратного уменьшения размерности пространства микроструктур.Предложенная модель применяется к широкому спектру неоднородных систем материалов с отчетливыми микроструктурными особенностями, включая сплав Ti-6Al-4V, сплав Pb63-Sn37, песчаник Фонтенбло и сферические коллоиды, для получения реконструкций материалов, близких к исходным образцам в отношении к двухточечным корреляционным функциям и средней критической прочности разрушения. Эта возможность не достигается существующими методами синтеза, которые основаны на марковском предположении о микроструктурах материалов.”,
author =” Жуйцзинь Цан и Яопэнсяо Сюй, Шаохуа Чен и Юнмин Лю и Ян Цзяо и Рен, {Макс Ии} “,
note =” Авторское право издателя: {\ textcopyright} 2017 by ASME. “,
год = “2017”,
месяц = июл,
день = “1”,
doi = “10.1115 / 1.4036649”,
language = “Английский (США)”,
volume = “139”,
journal = “Journal of Mechanical Design – Transactions of the ASME”,
issn = “1050-0472”,
publisher = “Американское общество инженеров-механиков (ASME)”,
number = “7”,
}
Описание курсов – Архитектурные технологии – Архитектура и управление объектами
ARCH 101 Архитектурная графика
Основа графических методов, используемых для планирования и представления зданий.Жесткая линия
и методы создания эскизов будут использоваться для разработки орфографических, аксонометрических, изобразительных,
и смоделированные изображения зданий. Упор будет сделан на макет чертежа,
графическая коммуникация и визуальное улучшение.
ARCH 102 Архитектурная цифровая графика
Введение в использование цифровых графических носителей в качестве инструментов архитектурного проектирования,
представление и документация.Включает двухмерную документацию и трехмерное моделирование, а также
методы рендеринга.
ARCH 112 Конструкционные материалы, системы и коды
Обзор свойств, характеристик, ограничений, критериев выбора и графики
интерпретация бетона, стали, кирпичной кладки и дерева, используемых в фундаменте, подконструкции,
и системы зданий надстройки. Включает в себя эстетику, производительность, ремонтопригодность,
и аспекты затрат / выгод.Вводит основные строительные нормы и правила, стандарты материалов и отрасли,
и использование каталогов производителя.
ARCH 115 Внутренняя и внешняя отделка и системы
Обзор свойств, характеристик, ограничений, критериев выбора и графики
интерпретация общих материалов и систем внутренней и внешней отделки, используемых в
внешнее закрытие, кровля и внутреннее строительство.Включает в себя эстетику, производительность,
ремонтопригодность и аспекты затрат и выгод.
ARCH 119 Устойчивое развитие в архитектуре: Введение
Обзор истории устойчивого развития с акцентом на искусственную среду.
Темы лекций варьируются от корней экологической мысли до современных проблем.
Архитектурная документация ARCH 203
Введение в графический язык, методы и организационные принципы строительства
документы.Особое внимание уделяется строительным материалам, процессам и сборкам, а также
их графическое изображение в рабочих чертежах. Дополнительный упор сделан на адаптацию
стандартных практик для повышения устойчивости. Студенческие проекты создаются в
цифровая среда в соответствии с общепринятыми принципами архитектурной
профессия.
ARCH 204 Архитектурная детализация
Введение в процесс разработки деталей конструкции и сборки
материалы, отвечающие как функциональным, так и эстетическим требованиям архитектуры.Акцент делается на исследованиях продуктов, оценке производительности, исследованиях затрат / выгод,
и устойчивость. Для общения будут использоваться различные методы презентации.
понимание материальных взаимоотношений и собраний.
ARCH 241 Принципы проектирования
Изучение принципов, лежащих в основе архитектурного дизайна, таких как форма; форма
и космос; узор и фактура; масштаб и пропорции; функция и кровообращение; цвет
и свет; окружающая среда, контекст и значение.Студенты разовьют словарный запас дизайна;
навыки публичного выступления; развитые графические и модельные навыки; и понимание
интеграции архитектурной формы с дополнительными дисциплинами.
ARCH 244 История архитектуры 1
Исследование основных стилей и движений в западной и незападной архитектуре
от доисторического периода до средневековья.Курс будет изучать культурные,
архитектурные и технологические разработки в период становления цивилизаций,
расширение империй и развитие религиозной и правительственной структуры.
ARCH 245 История архитектуры 2
Исследование основных стилей и движений в западной и незападной архитектуре
от эпохи Возрождения до 20 века.В рамках курса будут изучены культурные, архитектурные,
и технологические разработки в периоды модернизации в мировой истории,
включая промышленную и технологическую революции.
ARCH 223 Statics and Structures
Предоставляет информацию о первичных структурных системах, включая дерево, бетон,
и сталь, и соответствующее использование каждого материала.Базовая статика и сила
знакомятся с материальными принципами, и учащиеся знакомятся со ссылками, такими
как справочник AISC Steel и Кодекс ACI.
HVAC 337 Механические и электрические системы для зданий
Информация о системах отопления, вентиляции и кондиционирования, водоснабжения, канализации,
шторм, системы противопожарной защиты, распределение электроэнергии, освещение и акустика
системы для зданий.Акцент делается на системной интеграции, энергетических соображениях и
их влияние на планирование, детализацию и строительство здания. Обсуждает оборудование,
требования к коду и построение приложений.
Архитектурные факультативы
ARCH 242 Принципы архитектурного проектирования (ARCH 241) Введение в принципы архитектурного проектирования и архитектурного проектирования. процесс проектирования.Этот курс основывается на основных принципах проектирования, применяя их к архитектурным решениям. формы. Акцент делается на форме, пространстве, пропорциях, тектонике и материальности как они применяются к архитектурному дизайну, отвечающему основным программным требованиям.
ARCH 250 Оценка стоимости систем (MATH 116 или 120, ARCH 203) Базовая методология оценки стоимости строительства на основе по системному подходу.Проблемы будут включать взлет и подготовку сметы это было бы уместно для использования на стадии проектирования проекта.
ARCH 270 BIM и параметрическое проектирование (ARCH 203) Введение в основы вычислительного и параметрического проектирования в среде BIM. Возможности моделей BIM, управляемых данными, для помощи в архитектуре. процесс проектирования рассматривается с акцентом на самостоятельное изучение передовых параметрические и вычислительные инструменты.Работа в Revit сгенерированных BIM-моделях, генеративная сценарии, вычислительные методы и основные параметрические инструменты используются для разработки архитектурных решения, основанные на экологических данных, критериях производительности, требованиях кодов, и / или другие контекстные факторы. Графические интерфейсы сценариев и их возможности для генерации параметрических и вычислительных форм также вводятся.
COHP 330 Закон OSHA Этот курс разработан для ознакомления с основными концепциями безопасности и гигиены труда. закон.Студенты познакомятся с различными правовыми концепциями, законом OSHA о праве на знание. (Закон о предупреждении), положение об общих обязанностях, использование юридической библиотеки, оценка прецедентного права, Законы OSHA и соблюдение требований до и после проверок. Периодические обсуждения текущих событий, связанных с Законом о безопасности и гигиене труда, играют важную роль участие в понимании и соблюдении OSHA.
CONM 211 Оценка количества строительных работ Элементы, участвующие в подготовке тендерного предложения подрядчика.Количество взлет, численность экипажа, суточная производительность, удельные затраты и организация пакетов предложений на генеральные подрядные и субподрядные работы.
CONM 212 Грунты и фундаменты Введение в механику почвы. Происхождение и инженерные характеристики грунта, системы классификации грунтов, прочность грунтовых масс, контроль конструкционных насыпей, и введение в конструкцию фундаментов.
[PDF] Расчетное моделирование самодействующих деформируемых тел с использованием материала с памятью формы.
ПОКАЗЫВАЕТ 1-10 ИЗ 36 ССЫЛОК
СОРТИРОВАТЬ ПО РелевантностиБольше всего повлияли документыНедавно
Активное оригами с помощью 4D-печати
Последние достижения в технологии трехмерной (3D) печати, которые позволяют печатать несколько материалов на каждом слое, позволяют создавать материалы и компоненты с точно контролируемыми… Развернуть
- Просмотреть 2 выдержки, справочные материалы
Микроструктуры для управления эластичностью в 3D-печати
Эта работа основана на работе в области метаматериалов, с использованием численной оптимизации для проектирования плиточных микроструктур с желаемыми свойствами, но с Ключевое отличие заключается в том, что этот метод создает семейства связанных структур, которые можно интерполировать для плавного изменения свойств материала в широком диапазоне.Развернуть- Просмотреть 1 отрывок, справочная информация
Мультиматериальная 4D-печать с настраиваемыми полимерами с памятью формы
Новый подход к 4D-печати, позволяющий создавать многоматериальные архитектуры полимеров с памятью формы (SMP) с высоким разрешением (до нескольких микрон) на основе высоких технологий. проекционная микростереолитография с разрешением (PμSL) и использует семейство фотоотверждаемых сополимерных сеток на основе метакрилата. Развернуть- Просмотр 1 отрывок, справочная информация
4DMesh: 4D Printing Morphing Non-Developable Mesh Surfaces
Мы представляем 4DMesh, метод комбинирования термопластичных приводов для усадки и гибки с индивидуальными геометрическими алгоритмами для 4D печати и преобразования сантиметров в метр -размерные функциональные без развертывания… Развернуть
- Просмотреть 2 выдержки, справочная информация
Эластичные текстуры для аддитивного изготовления
Мы представляем эластичные текстуры: набор параметрических, плиточных, печатаемых, кубических узоров, обеспечивающих широкий диапазон изотропной эластичности свойства материала: самый мягкий узор более тысячи раз… Развернуть
- Просмотреть 1 отрывок, справочный фон
CurveUps: формирование объектов из плоских пластин с кривизной, вызываемой растяжением
В этой работе представлен вычислительный подход для проектирования CurveUps, изогнутых оболочек эта форма из изначально плоского состояния, основанного на ef эффективная приближенная модель и стратегия локальной оптимизации для трудноразрешимой в противном случае задачи нелинейной оптимизации.Развернуть- Просмотреть 3 выдержки, справочная информация
Среднезападный интегрированный центр вычислительных материалов
В дополнение к недавно финансируемым центрам, основные проекты вычислительных материалов по всему миру включают:
The Materials Project обеспечивает открытый веб-доступ к вычисленной информации об известных и прогнозируемых материалах, а также мощные инструменты анализа для создания новых материалов.
Группа теоретической спектроскопии в Laboratoire des Solides Irradiés разрабатывает фундаментальную теорию конденсированного состояния в тесном контакте с экспериментом и приложениями.Теоретическая основа охватывает статическую и зависящую от времени функциональную теорию плотности и теорию возмущений многих тел.
Междисциплинарный центр современного моделирования материалов (ICAMS) специализируется на разработке и применении нового поколения инструментов моделирования для многомасштабного моделирования материалов с целью сокращения затрат и времени на разработку новых материалов.
Некоторые из проблем, над которыми в настоящее время работает Центр вычислительного моделирования (CCS), – это гидродинамика, аналитика больших данных, моделирование нейронных решеток, молекулярная динамика, модели энергоэффективности, а также квантовая информация и вычисления.
Интегрированный центр проектирования материалов (IMDC) управляет высокопроизводительным вычислительным моделированием материалов в рамках интегрированного процесса открытия и проектирования, работая рука об руку с основными областями прочности в области синтеза, определения характеристик и испытаний материалов.
Центр вычислительного материаловедения (CCMS) был основан в апреле 2006 года. Он поддерживается Министерством науки и технологий в рамках его Инициативы по нанонауке и технологиям.
Основная цель IKST (Индо-корейский научно-технический центр) – укрепить сотрудничество между индийскими и корейскими учеными за счет использования дополнительных сильных сторон и опыта двух стран в области вычислительного материаловедения.
Исследовательский центр вычислительного проектирования передовых функциональных материалов (CD-FMat) при Национальном институте передовых промышленных наук и технологий (AIST) был создан в 2015 году для разработки новых вычислительных методов для выяснения часто противоречивых свойств функциональных материалов и устройств. , и работать над тем, чтобы сделать эти вычислительные методы более крупномасштабными и крупномасштабными.
Центр вычислительного материаловедения (CCMS) в Университете Тохоку специализируется на суперкомпьютерных системах для проектирования материалов.
Пекинский научно-исследовательский центр вычислительной науки (CSRC) проводит исследования в области вычислительной науки в различных областях, включая физику конденсированного состояния, функциональные материалы и материалы с экологически чистой энергией, квантовую оптику и информацию, материаловедение и механику, сложные системы в биологии и активных веществах, прикладную математику, и разработка алгоритмов.
CECAM – Вычислительные сложные механические системы
Последние достижения в области машинного обучения и компьютерной графики предоставляют уникальную возможность для проектирования и анализа сложных механических систем (материалов и конструкций). Машинное обучение (ML) и другие методологии, основанные на данных, подрывают наши давние взгляды на предсказание поведения физических явлений. Параллельно с этим современные экспериментальные методы (например, высокоскоростная фотография, быстрое прототипирование, трехмерное изображение, автоматизация с компьютерным управлением) сформировали новую культуру прецизионных экспериментов, позволив исследовать большие пространства дизайна, которые приносят новые фундаментальные идеи и генерируют беспрецедентные данные в сложные (сильно нелинейные) конструкции.
Однако, в то время как машинное обучение становится повсеместным в нашей повседневной жизни, превращение этих методологий в неотъемлемую часть исследовательского инструментария, доступного для экспериментальной инженерной механики (ЭМ), развивается относительно медленно. В частности, отсутствие последних достижений в использовании современных методов машинного обучения для решения проблем структурной механики контрастирует с другими областями (например, вычислительным материаловедением), где большие наборы данных имеются в большом количестве из-за эффективных вычислительных методов. Мы предполагаем, что у этого есть три причины: во-первых, эксперименты в области механики, как правило, дают наборы данных, которые значительно менее объемны, чем в других областях, основанных на данных, что препятствует применению ML.Во-вторых, сообщество инженеров-механиков имеет давние традиции аналитического моделирования, основанного на дифференциальных уравнениях, и всегда «ломает лед» с помощью методов на основе машинного обучения. Наконец, сложные механические системы имеют тенденцию демонстрировать сильную нелинейность из-за, например, геометрии, продольного изгиба и больших деформаций. Это затрудняет выполнение крупномасштабного моделирования с использованием стандартных методов (например, FEM) и требует помощи новых вычислительных подходов, таких как высокоточные алгоритмы, которые изначально были разработаны в области компьютерной анимации, для создания наборов данных.
В общем, пришло время изучить потенциал для деятельности на стыке экспериментов, компьютерной графики и машинного обучения.
Наша мастерская будет построена на двух центральных опорах. Thrust Я расскажу, как ML / CG может помочь исследовать и распутать экспериментально наблюдаемую сложность структурных систем. Thrust II будет стремиться мотивировать и обучать EM-сообщество генерировать соответствующие наборы данных, которые поддаются современным методологиям машинного обучения.Одной из важных областей является использование гибридов экспериментальных и синтетических данных (например, полученных с помощью GC или других методов моделирования). Еще одна интригующая область, которую следует изучить на семинаре, – это использование последовательного обучения для информирования при разработке новых экспериментов и руководства принятием решений в последовательных экспериментальных кампаниях.
В конечном итоге, наша цель состоит в том, чтобы объединить извлеченный опыт из Направлений I и II, чтобы прийти к инновационным стратегиям, позволяющим прогнозировать сложное поведение механических систем и использовать это понимание как для информирования, так и для управления инженерным проектированием.