С работа с матрицей: Работа с матрицами в C#

Как создать матрицу в Python: инструкция

Матрицы являются одним из основных объектов в математике. Они используются для представления и манипулирования данными в виде таблицы, состоящей из строк и столбцов. Их используют для решения систем линейных уравнений, определения матричных действий, преобразования координат и многого другое.

В этой статье мы опишем несколько способов создать матрицу в Python. И дополнительно рассмотрим некоторые основные операции, такие как сложение, умножение и определение обратной матрицы.

Что такое матрица

Матрица — это таблица из чисел, которая используется в математике и инженерных науках для представления данных. Матрицы имеют форму таблицы, состоящей из строк и столбцов. Каждый элемент имеет свой уникальный индекс, обозначающий строку и столбец, в котором он находится. Например, матрица размером 3×3 будет иметь 3 строки и 3 столбца, и каждый элемент будет иметь индекс вида (i, j), где i — номер строки, а j — номер столбца.

Создание матрицы

В Python существует несколько способов создания матрицы. Ниже приведены некоторые из них:

• С помощью списков. Можно создать матрицу, используя вложенные списки. Каждый вложенный список будет соответствовать одной строке. Так можно создать квадратную матрицу Python:

matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

• С помощью NumPy. NumPy — это библиотека для математических вычислений и обработки данных. В ней есть класс Array, который можно использовать для создания матрицы:

import numpy as np 
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

Если вам нужно производить стандартные математические операции с матрицами, то стоит использовать NumPy. Его проще использовать и все операции уже реализованы в библиотеке. А если вы хотите самостоятельно создавать методы, например, в образовательных целях, или же планируете совершать нестандартные манипуляции, то используйте вложенные списки. 

Теперь рассмотрим матричные операции и поработаем с ними с помощью вложенных списков и NumPy.

Матричные операции

Вот список основных манипуляций:

• Сложение. Две матрицы можно сложить, если их размеры совпадают. Каждый элемент итоговой матрицы будет равен сумме соответствующих элементов исходных матриц.
• Вычитание. Одну матрицу можно вычесть из другой, если их размеры совпадают. Каждый элемент итоговой матрицы будет равен разности соответствующих элементов исходных матриц.
• Умножение на число. Каждый элемент итоговой матрицы будет равен произведению соответствующего элемента исходной матрицы на число.
• Произведение матриц. Матрицы можно перемножить, если число столбцов первой матрицы равно числу строк второй матрицы. В результате получится новая матрица с размером, соответствующим числу строк первой матрицы и числу столбцов второй матрицы. Более подробно эту операцию мы разберем чуть дальше.
• Транспонирование матрицы.  Транспонирование — это операция, в которой строки и столбцы меняются местами. Т.е. первый столбец становится первой строкой, второй столбец — второй строкой и так далее.
• Нахождение обратной матрицы. Матрица B будет являться обратной матрицей для матрицы A, если результатом операции A*B является единичная матрица.

Сложение

Важно не забывать, что при сложении двух матриц их размеры должны совпадать.

Вот пример сложения с помощью вложенных списков и циклов:

matrix1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] 
matrix2 = [[9, 8, 7], [6, 5, 4], [3, 2, 1]] 
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for i in range(len(matrix1)): 
for j in range(len(matrix1[0])): 
                 result[i][j] = matrix1[i][j] + matrix2[i][j] 
print(result)

Результат:

[[10, 10, 10], [10, 10, 10], [10, 10, 10]]

Вот аналогичное сложение с помощью метода add() из библиотеки NumPy:

import numpy as np 
matrix1 = np. array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) 
matrix2 = np.array([[9, 8, 7], [6, 5, 4], [3, 2, 1]]) 
result = np.add(matrix1, matrix2)
print(result)

Результат:

[[10 10 10]
 [10 10 10]
 [10 10 10]]

Вычитание 

В Python можно выполнять вычитание матриц с помощью цикла или метода subtract() из библиотеки NumPy. При вычитании размеры должны совпадать.

Вычитание с помощью цикла:

matrix1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] 
matrix2 = [[9, 8, 7], [6, 5, 4], [3, 2, 1]] 
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]] 
for i in range(len(matrix1)): 
for j in range(len(matrix1[0])): 
                 result[i][j] = matrix1[i][j] - matrix2[i][j] 
print(result)

Результат:

[[-8, -6, -4], [-2, 0, 2], [4, 6, 8]]

Вычитание с помощью метода subtract() из библиотеки NumPy:

import numpy as np 
matrix1 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) 
matrix2 = np. array([[9, 8, 7], [6, 5, 4], [3, 2, 1]]) 
result = np.subtract(matrix1, matrix2) 
print(result)

Результат:

[[-8 -6 -4]
 [-2  0  2]
 [ 4  6  8]]

Умножение на число

В Python умножение матрицы на число можно реализовать с помощью цикла или воспользоваться методом dot() из библиотеки NumPy.

При умножении матрицы на число, каждый элемент умножается на это число.

Умножение с помощью цикла:

matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] 
scalar = 2 
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]] 
for i in range(len(matrix)): 
for j in range(len(matrix[0])): 
                 result[i][j] = matrix[i][j] * scalar 
print(result)

Результат:

[[2, 4, 6], [8, 10, 12], [14, 16, 18]]

Вот пример работы метода dot() из библиотеки NumPy с теми же вводными:

import numpy as np 
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) 
scalar = 2 
result = np. dot(matrix, scalar)
print(result)

Результат:

[[ 2  4  6]
 [ 8 10 12]
[14 16 18]]

Также вместо метода dot() можно использовать знак операции умножения *:

import numpy as np 
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) 
scalar = 2 
result = matrix * scalar 
print(result)

Результат:

[[ 2  4  6]
 [ 8 10 12]
 [14 16 18]]

В большинстве случаев метод dot() работает быстрее вручную реализованных циклов.

Произведение матриц

Произведение — это операция, в результате которой получается новая матрица с числом строк первой матрицы и числом столбцов второй. При матричном умножении, число столбцов первой матрицы должно совпадать с числом строк второй. Каждый элемент новой матрицы — это сумма произведения элементов строки первой матрицы и элементов столбцов второй матрицы, как на картинке ниже:

Как и прежде, реализуем произведение с помощью циклов и NumPy.

Умножение, реализованное на циклах, может иметь такой вид:

matrix1 = [[1, 2], [3, 4]] 
matrix2 = [[5, 6], [7, 8]] 
result = [[0, 0], [0, 0]] 
for i in range(len(matrix1)): 
for j in range(len(matrix2[0])): 
                 for k in range(len(matrix2)): result[i][j] += matrix1[i][k] * matrix2[k][j]
print(result)

Результат: 

[[19, 22], [43, 50]]

В NumPy для матричного умножения используется метода dot():

import numpy as np 
matrix1 = np.array([[1, 2], [3, 4]]) 
matrix2 = np.array([[5, 6], [7, 8]]) 
result = np.dot(matrix1, matrix2) 
print(result)

Результат:

[[19 22]
 [43 50]]

Аналогично методу dot() работает операция @:

import numpy as np 
matrix1 = np.array([[1, 2], [3, 4]]) 
matrix2 = np.array([[5, 6], [7, 8]]) 
result = matrix1 @ matrix2 
print(result)

Результат:

[[19 22]
 [43 50]]

Использование метода dot() или оператора @ даёт более быстрый, по сравнению с использованием вручную реализованных циклов, результат.  

Не забывайте, что произведение является некоммутативной операцией, то есть порядок умножения матриц имеет значение и результат будет разным, если их переставить местами.

Транспонирование

Транспонирование — это операция, в результате которой строки исходной матрицы становятся столбцами новой матрицы, а столбцы — строками.

В Python можно выполнить транспонирование с помощью свойства T или метода transpose() из библиотеки NumPy.

Пример транспонирования с использованием свойства T:

import numpy as np 
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) 
result = matrix.T
print(result)

Результат:

[[1 4 7]
 [2 5 8]
 [3 6 9]]

И пример транспонирования с использованием метода transpose():

import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
result = np.transpose(matrix)
print(result)

Результат:

[[1 4 7]
 [2 5 8]
 [3 6 9]]

В обоих случаях результат одинаковый.

С помощью цикла транспонирование можно реализовать следующим образом:

matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] 
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for i in range(len(matrix)):
for j in range(len(matrix[0])): 
result[j][i] = matrix[i][j] 
print(result)

Результат:

[[1, 4, 7], [2, 5, 8], [3, 6, 9]]

Этот метод может быть медленным и неэффективным для больших матриц, поэтому для более быстрого и эффективного решения рекомендуется использовать NumPy.

Нахождение обратной матрицы

Обратная матрица — это матрица, которая при умножении на исходную матрицу в результате дает единичную матрицу (с единицами на диагонали и нулями в остальных ячейках).

В Python можно найти обратную матрицу с помощью метода inv() из библиотеки NumPy.

import numpy as np 
matrix = np.array([[1, 2], [3, 4]]) 
result = np.linalg.inv(matrix) 
print(result)

Результат:

[[-2.   1. ]
 [ 1. 5 -0.5]]

Если матрица не имеет обратной матрицы, то метод inv() вызовет исключение LinAlgError: Singular matrix.

Чтобы проверить, имеет ли матрица обратную, используйте метод det() из библиотеки NumPy, который возвращает определитель матрицы. Если определитель равен нулю, то матрица вырожденная и она не имеет обратной матрицы:

import numpy as np
matrix = np.array([[1, 2], [3, 4]])
determinant = np.linalg.det(matrix)
if determinant == 0:
print("The matrix does not have an inverse.")
else:
result = np.linalg.inv(matrix)
print(result)

Нахождение обратной матрицы с помощью циклов может быть достаточно сложным и трудоемким процессом, особенно для больших матриц. Поэтому рекомендуем использовать NumPy.

Заключение

Матрицы являются важной концепцией в линейной алгебре и часто используются в различных областях, таких как искусственный интеллект, графика и оптимизация. В Python представлено множество инструментов для работы с матрицами, включая библиотеку NumPy. Понимание матриц и их операций может быть полезным для решения множества практических задач в различных областях.

Матрица Эйзенхауэра: что это такое

Содержание

• Матрица Эйзенхауэра: что такое простыми словами
• Категории матрицы Эйзенхауэра
  • Первая категория (важно/срочно)
  • Вторая категория (важно, несрочно)
  • Третья категория (срочно, неважно)
  • Четвёртая категория (несрочно, неважно)
• Как применять матрицу Эйзенхауэра
• Где собирать матрицу Эйзенхауэра
• Советы по работе с матрицей

Матрица Эйзенхауэра: что такое простыми словами Матрица Эйзенхауэра — модель организации дел, которая помогает определить приоритеты и эффективно распределить время на задачи. Цель — сосредоточиться на важных делах и проектах, не браться за ненужное. Эту модель придумал президент США Дуайт Эйзенхауэр, чтобы оптимизировать процесс принятия решений. Матрица Эйзенхауэра состоит из четырёх полей, категорий. Достаточно распределить все задачи по матрице — найти подходящее поле для каждого дела. […]

Матрица Эйзенхауэра: что такое простыми словами

Матрица Эйзенхауэра — модель организации дел, которая помогает определить приоритеты и эффективно распределить время на задачи. Цель — сосредоточиться на важных делах и проектах, не браться за ненужное. Эту модель придумал президент США Дуайт Эйзенхауэр, чтобы оптимизировать процесс принятия решений.

Матрица Эйзенхауэра состоит из четырёх полей, категорий. Достаточно распределить все задачи по матрице — найти подходящее поле для каждого дела. В итоге получится четыре списка задач. Слева вверху — приоритетные, справа внизу — те, которые можно оставить на потом или не делать.

Хотите освоить сквозную аналитику?

Посетите регулярный мастер-класс по аналитике от Roistat.

Подключиться

Пример: маркетинговый отдел банка обсуждает на встрече все текущие задачи, цель — решить, что нужно делать прямо сейчас, а что может подождать. Рисуем табличку 3×3 и распределяем задачи по полям:

Категория	Срочно	Не срочно
Важно	Запуск кампании для новой кредитной карты	Создание лендинга для вебинара
Не важно	Создание Telegram-канала на замену Instagram*	Запуск собственного медиа

Матрица помогает определить, что в первую очередь нужно работать над новой рекламной кампанией, а запуск собственного медиа можно отложить.

Как настраивать рекламу в рекламной сети Яндекса — рассказали в блоге.

Преимущества матрицы Эйзенхауэра

:

• подходит для любой сферы бизнеса и жизни;
• не требует изучения и специальной подготовки;
• легко составляется — нужно лишь определить список задач и рассортировать их по полям матрицы;
• быстро даёт результат — сразу видно, что задачи из поля «важно/срочно» нужно брать в работу;
• помогает оценивать эффективность текущего плана — увидите, какие дела и проекты отнимают много ресурсов и, возможно, не стоят затрат времени.

Категории матрицы Эйзенхауэра

Не всегда легко определить, какая задача важная, а какая срочная. Универсальной формулы не существует, определять критерии придётся самостоятельно. За основу можно взять определения важности и срочности:

1. Срочные задачи нужно делать прямо сейчас, они неизбежны. Пример — перезвонить крупному клиенту, составить отчёт для сегодняшнего совета директоров.
2. Важные задачи помогают достигать целей, на их выполнение есть время и силы, они мотивируют. Пример — изучить исследования по рынку, внедрить удобную CRM-систему.

Первая категория (важно/срочно)

Самые актуальные дела, отказ от которых угрожает помешать достижению цели. В этот список попадают «горящие» задачи — их нужно сделать как можно быстрее, они имеют наивысший приоритет.

Большое количество дел в этом поле — признак неэффективного распределения задач. Это значит, что человек берёт слишком много проектов и не успевает закрывать их в срок. Задачи копятся, сроки выполнения истекают — человек работает в стрессовой обстановке, пытаясь всё успеть. Обычно такое поведение приводит к выгоранию или срыву дедлайнов. Важных и срочных дел должно быть немного.

Вторая категория (важно, несрочно)

В неё попадают задачи, требующие максимум времени и сил. Однако на выполнение таких задач есть время, они не «горят». Дела из второй категории можно выполнять в комфортном темпе, а значит — с максимальной эффективностью.

Они не отвлекают от основных целей, как задачи из следующей категории. Выполняя важные, но несрочные дела, человек уменьшает уровень стресса. Есть время сделать то, что приносит результат и приближает к достижению целей.

Единственный риск — если слишком затянуть с важными, но не срочными задачами, они перейдут в первую категорию.

Третья категория (срочно, неважно)

Рутинные, повседневные дела, дополнительные проекты. Обычно их выполнения ждут другие люди, однако срочные, но неважные задачи не приближают человека, команду или компанию к достижению целей.

Дела из третьей категории отвлекают от более важных проектов, однако их всё равно нужно делать. Если набрать множество задач, высока вероятность смешать дела из первой и из третьей категории. В этом случае человек будет делать только срочные проекты, оставляя без внимания те задачи, которые нужно выполнить для достижения целей отдела или компании.

Например, менеджер берёт на себя много задач по одному проекту — договаривается с заказчиком, формирует ТЗ для дизайнера, самостоятельно запускает кампанию на первый сегмент аудитории и пишет тексты для креативов. В итоге времени для запуска второй кампании не остаётся. Компания не дополучает прибыль, которую могли принести пользователи из второго сегмента. Решение — делегировать задачи или отказаться от некоторых проектов.

Четвёртая категория (несрочно, неважно)

Ненужные дела, которые больше всего отвлекают от целей и по-настоящему важных проектов. Задачи в четвёртой категории есть всегда. Если их слишком много, высока вероятность не достичь поставленных целей.

Например, интернет-маркетолог вместо запуска новой рекламной кампании решает написать тексты для email-рассылки, которая должна быть отправлена только через месяц. Дела из четвёртой категории могут бесконечно долго отвлекать от цели. В итоге маркетолог не приведёт нужное количество лидов.

Как работать с задачами четвёртой категории:

• следить, сколько времени уходит на каждую такую задачу в течение дня;
• придумать, чем их заменить или как ограничить время на их выполнение.

Как применять матрицу Эйзенхауэра

1. Тайм-менеджмент. Основная сфера применения модели — распределить время так, чтобы успевать сделать важные задачи. Матрица Эйзенхауэра в тайм-менеджменте — удобный инструмент планирования. Её можно использовать для формирования личного расписания или для работы целой команды.
2. Приоритезация задач. Матрица приоритетов Эйзенхауэра помогает разобраться с «горящими» проектами. Помогает понять, что срочные задачи будут сделаны вовремя и какие несрочные задачи можно отложить.
3. Управление проектом. Матрицу используют в бизнес-командах на планировании или ревью, когда оценивают успехи работы и ищут способы повысить эффективность.

Где собирать матрицу Эйзенхауэра

1. В онлайн-сервисах. Существует множество программ и инструментов для организации дел. В большинстве из них можно расставлять приоритеты — делить задачи по блокам матрицы Эйзенхауэра. В Notion создаётся отдельная страница для приоритизации задач. В Trello удобно распределять проекты по системе Канбан — назначать приоритеты карточкам с заданиями, добавлять метки и статусы, указывать дедлайны.
2. В приложениях. На смартфоне удобно заполнять готовые шаблоны — не нужно ничего чертить, достаточно добавить задачи и распределить их по блокам. Полезные приложения: Taskman, Todoist, Focus Matrix.
3. В блокноте или в тетради. Матрицу можно начертить от руки и заполнить категории. Выполненные задачи можно вычёркивать из списка.

Советы по работе с матрицей

1. Установите комфортный лимит для каждого блока. Например, в одной категории не может быть больше 5 задач. Прежде чем добавить новую нужно выполнить одну из текущих.
2. Начните заполнять матрицу с важных, но несрочных задач. Сосредоточьтесь на главных проектах, которые помогают достигнуть цели, а потом заполните оставшиеся поля.
3. Сперва внесите в своё расписание срочные и важные задачи, а потом — важные, но несрочные дела. Если осталось свободное время, добавьте неважные, но срочные проекты.

*Meta и продукты компании — Instagram, Facebook — признаны экстремистскими организациями на территории РФ.

6 основных ключей к успешной работе в матричной организации

По мере того, как организации стремятся делать больше с меньшими ресурсами и лучше использовать скудные знания во всей своей организации, они обнаружили, что традиционная иерархическая структура управления больше не отвечает потребностям бизнес. Предприятия обратились к матричной организационной структуре для увеличения потока информации между отделами и большей гибкости и оперативности.

Но это изменение включает в себя нечто большее, чем просто перестановку имен на организационной схеме. Многочисленные линии подчинения и пересекающиеся обязанности могут привести к хаосу и путанице, если вы не измените свое отношение к своей роли лидера и не разовьете навыки, необходимые для того, чтобы воспользоваться преимуществами, которые предлагает матрица.

 

Что такое матричное управление?

Традиционная модель управления имеет иерархическую структуру. Он создан по образцу военных, а управление бизнесом централизовано. Все, кто работает в бизнесе, следуют цепочке инстанций и знают, какое место они занимают в организационной структуре. Как сотрудник организации такого типа, вы точно знаете, кому подчиняетесь и за управление какой командой отвечаете.

Преимущество этой структуры заключается в том, что стратегические решения можно принимать быстро, а менеджеры имеют большой контроль над решениями в организации. Недостатком является то, что иерархические организации развиваются медленно, препятствуют творчеству и с трудом адаптируются к изменяющимся рыночным условиям.

Матричная структура имеет две цепочки команд. Одна из них — традиционная иерархия, а другая — латеральная власть или влияние. Традиционная иерархия работает по функциональным линиям, в то время как другая больше касается отдельных проектов.

Простой способ визуализировать разницу: традиционную организацию можно представить в виде древовидной диаграммы, где каждый сотрудник связан с руководителями выше и со своей командой ниже и выше.

Матричная организация лучше всего представлена ​​в виде таблицы, представляющей два измерения лидерства в организации, хотя на некоторых предприятиях может быть больше измерений. В матрице нарушена строгая субординация. Сотрудники подчиняются непосредственно двум или более руководителям.

Есть много способов, которыми предприятия определяют матричную структуру. Общие измерения включают продукт и функцию, где одно измерение управления отвечает за конкретный проект или продукт, над которым работает компания, а другое измерение — это отдел компании, такой как продажи, бухгалтерия или обслуживание клиентов.

Другие возможные параметры включают географическое положение и отраслевую специализацию. Многие предприятия имеют гибридную структуру, в которой традиционная иерархическая структура используется для высшего руководства, а матрица используется в других подразделениях организации.

 

Преимущества матричной организации

У матричной организационной структуры есть несколько преимуществ, в том числе:

 

Сотрудничество между отделами

нужные навыки для выполнения текущей задачи.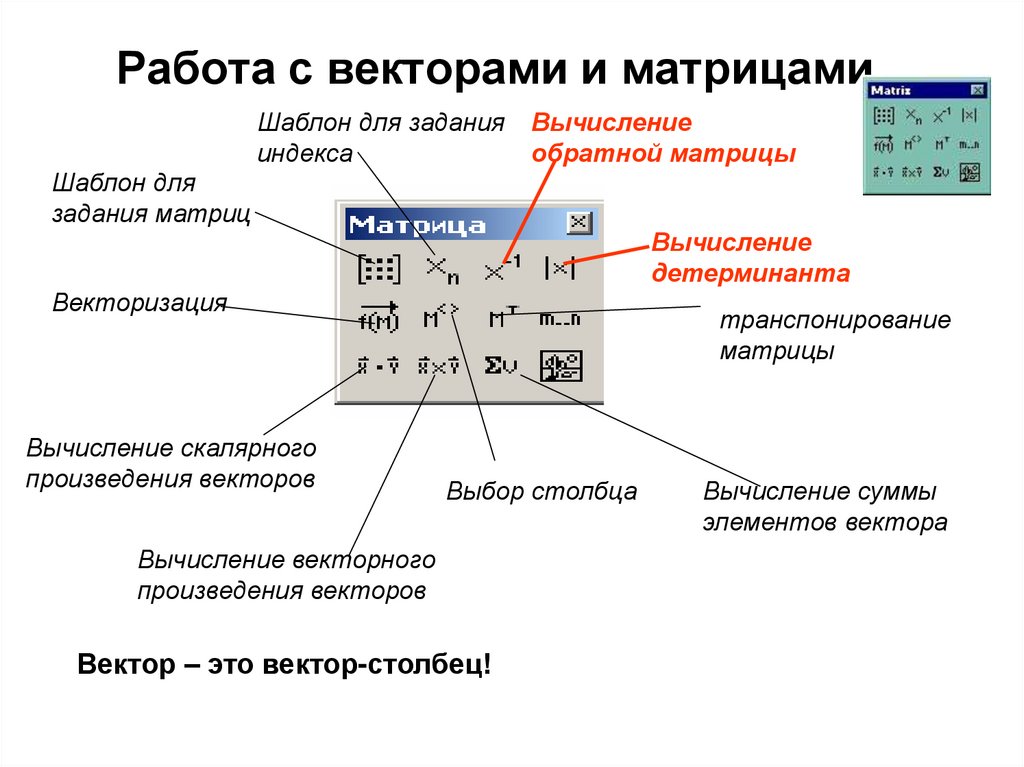 Эксперты в каждой функциональной части компании могут работать вместе для решения проекта, задачи или цели. В матричной структуре проектные задания никогда не бывают постоянными. Это дает сотрудникам возможность делиться своими навыками с более широким кругом коллег.

 

Больше гибкости

Объединяя функциональную направленность и ориентацию на конкретный проект, компании могут лучше соответствовать потребностям рынка. Когда члены команды отчитываются перед несколькими отделами, при принятии решений открывается больше точек зрения. Матричная структура также дает командам больше автономии, устраняет барьеры более формальных процессов и позволяет им быстро достигать своих целей.

 

Улучшение связи между отделами

В иерархической структуре коммуникации идут сверху вниз, и часто эти коммуникации остаются в рамках своего функционального блока. Вице-президент продукта общается с руководителями проектов, которые затем общаются с разработчиками программного обеспечения. Матричная структура позволяет общаться через эти границы, давая руководителям возможность принимать более обоснованные решения.

 

Эффективное использование ресурсов

Поскольку оборудование и сотрудники используются в проектах совместно, матричная структура позволяет использовать ресурсы более эффективно. Матричная структура позволяет руководителям проектов посвящать свое время и таланты конкретным областям, а не заниматься множеством проектов, максимизируя свое влияние.

 

Расширение возможностей для развития новых навыков

В матричной структуре управления сотрудники работают над самыми разными проектами, и им часто требуется обучение или использование новых навыков. Знакомство с новыми должностными обязанностями и обязанностями может ускорить формирование их профессиональных навыков и повысить их ценность для компании.

 

Проблемы матричной организации

Каждая организационная структура сталкивается с проблемами, и матрица не исключение.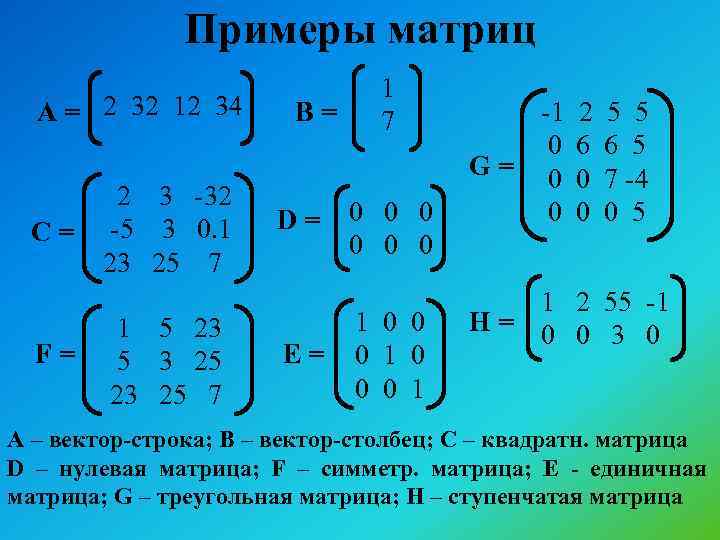 Если вы знаете об этих проблемах, вы будете лучше подготовлены к их решению.

 

Отсутствие ясности в отношении ролей

Матричную структуру может быть труднее усвоить, чем иерархическую. Когда сотрудник отчитывается и перед функциональным менеджером, и перед менеджером проекта, и приоритеты конфликтуют, что делает этот сотрудник? Когда сотруднику требуется дополнительное обучение, какой менеджер отвечает за это?

 

Несоответствие приоритетов влияет на эффективность бизнеса

Всякий раз, когда задействовано более одного менеджера, существует вероятность возникновения конфликтов. Менеджер по продажам может поставить цель роста продаж в следующем квартале, но руководитель проекта может установить для команды другие приоритеты. Это может привести к встречам и обсуждениям, на которых конфликт разрешается, но команда может застрять в подвешенном состоянии, пока не будет принято окончательное решение.

 

Работу сотрудников будет сложнее измерить

Поскольку члены команды в матричной организации подчиняются более чем одному менеджеру и могут выполнять более одной роли, может быть сложно оценить вклад сотрудника в проект. Это может привести к отсутствию мотивации и плохому личному развитию.

 

Ключи к успеху в матричной организации

Нет никаких сомнений в том, что матричная структура может предложить значительное количество преимуществ, включая более эффективное использование ресурсов и стандартизацию процессов/рабочих методов в различных реализациях. Проблема заключается в том, что работа в матричной организации требует новых навыков и компетенций, чтобы гарантировать, что запланированные преимущества матрицы будут реализованы так, как предполагалось. Для эффективной работы менеджером функциональных ресурсов или менеджером проектов в матричной структуре руководителям необходимо:

 

Организационное мышление

Это можно определить как глубокое понимание формальной организации (например, целей, ролей, процессов и т. д.) и неформальной организации (например, политики, неформальных процессов, власти и т. д.) и применяя эти знания для принятия всех решений.
Матрица может дать вам несколько ролей на предприятии, и вы будете подчиняться более чем одному человеку. Знание деталей того, как вы вписываетесь в матрицу, поможет вам воспользоваться возможностями, которые открывает матричная организация.

 

Влияние

Влияние — это способность влиять на характер, развитие или поведение кого-либо или чего-либо. Успешные влиятельные лица реализуют стратегии таким образом, чтобы добиться положительных результатов и построить или укрепить отношения.
В иерархической структуре управления вы можете требовать, чтобы что-то было сделано, и предполагать, что это будет сделано. В матрице вы должны научиться руководить без полномочий, используя социальный интеллект, характер и навыки сотрудничества.

 

Самоуправление

Это можно определить как способность понимать и контролировать/управлять своими эмоциями и реакциями. Самоуправление включает в себя самосознание, саморегуляцию и мотивацию. Чтобы хорошо руководить, вы должны знать себя и понимать свой стиль управления. Вы также должны уметь выявлять пробелы в своей компетенции и работать над развитием навыков, которых вам может не хватать.

 

Сотрудничество

Это способность сотрудничать с другими для достижения общих целей. Сотрудничество предполагает гибкость, умение ставить коллективные потребности группы выше своих собственных и сотрудничество с другими для достижения положительных результатов.
Если вы пришли из иерархического управленческого прошлого, вы должны сопротивляться желанию впасть в старые шаблоны. Выйдите за границы и воспользуйтесь одним из преимуществ матричного управления.

 

Ориентация на клиента

Ориентация на клиента может быть определена как создание клиента и его удовлетворенности в центре всей вашей деятельности.
Речь идет о том, чтобы убедиться, что вы понимаете, что важно для клиента, и работать над тем, чтобы превзойти эти ожидания, чтобы углубить и укрепить отношения. Матричная организация может добавить предприятию гибкости и сотрудничества, которые следует использовать на благо ваших клиентов.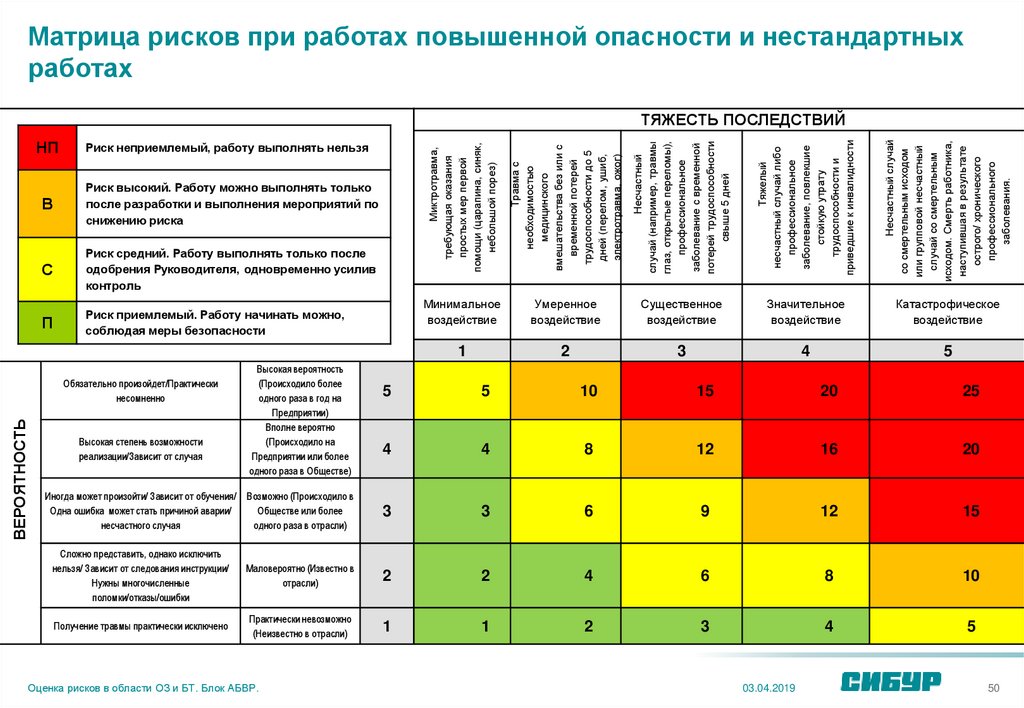

 

Эмпатия

Эмпатия подразумевает способность смотреть на вещи с точки зрения другого человека, даже если вы с ним не согласны.
Эмпатия позволяет лидерам лучше понять точку зрения своей команды и образ мыслей своих клиентов. Когда приоритеты в матрице пересекаются, как это часто бывает, эффективному лидеру необходимо подходить к конфликту с нескольких точек зрения.

 

Матричная модель делает бизнес более гибким, но требует времени

Матричная организационная структура может сделать ваш бизнес более гибким, адаптивным и способным быстро приспосабливаться к изменениям, но для того, чтобы она работала, требуется нечто большее, чем просто создание новой организационной схемы.

Конечно, здесь есть свои трудности, но их можно преодолеть и использовать в своих интересах. Многие организации тратят время на внедрение политик и процедур для поддержки своей матричной среды, но для настоящего успеха им также следует рассмотреть возможность инвестирования в обучение, чтобы сформировать у своих руководителей необходимые навыки и компетенции.

Global Knowledge, авторизованный поставщик услуг по обучению крупнейших имен в области технологий, предлагает обучение лидерству в бизнесе, управлению проектами и управлению ИТ-услугами по всему миру. Смотрите наш каталог обучения лидерству здесь.

Управление работой матрицы | Careersmart

Определение матричной работы – это люди, работающие в матричной организационной структуре.

Матричная организационная структура

Традиционная организационная структура бизнеса носит иерархический характер. Например, сотрудник будет подчиняться менеджеру, который будет подчиняться руководителю группы, который будет подчиняться начальнику отдела, который будет подчиняться главному исполнительному директору. Однако организации могут быть структурированы и по-другому.

Матричная организационная структура сочетает в себе традиционную модель бизнеса со структурой, типичной для проектных команд. Если иерархическая структура понимается как «вертикальная», то матричная структура позволяет организации работать как «горизонтально», так и «вертикально». Сотрудники назначаются на должности в командах, которые относятся к конкретному проекту (или продукту), и подчиняются «горизонтально» руководителю группы этого проекта.

В то же время сотрудники сохраняют свои функциональные должности в своем первоначальном отделе и продолжают подчиняться «вертикально» своему первоначальному руководителю. Полученная организационная диаграмма представляет собой матрицу горизонтальных строк проекта и вертикальных столбцов функций.

Матричная структура может сочетать в себе лучшие элементы обеих структур (иерархической и проектной). Матричные структуры можно разделить на слабые, сбалансированные и сильные.

В слабой матрице руководитель проекта имеет ограниченные полномочия и подчиняется функциональному руководителю. Слабая матрица приобретает некоторые преимущества матричной организационной структуры, но сохраняет многие проблемы иерархической организационной структуры.

В прочной матрице руководитель проекта обладает большими полномочиями и независимостью от функционального руководителя. Функциональный менеджер выполняет вспомогательную, а не управленческую роль. Сильная матрица — это сложная структура, которая опирается на хорошие рабочие отношения и достаточно гибкую рабочую среду.

В сбалансированной матрице полномочия распределяются поровну между менеджером проекта и функциональным менеджером. Хотя эта модель считается идеальной комбинацией, она также является самой сложной в обслуживании.

Матричное управление

Матричные организационные структуры широко распространены, и большинство крупных организаций в той или иной степени используют матричное управление. Матричное управление обычно относится к управлению, которое работает как «вертикально» (в соответствии с функцией), так и «горизонтально» (в соответствии с проектом, продуктом или регионом). Матричное управление подходит для рабочих сред, связанных с проектом или продуктом.

При матричном управлении сотрудники могут подчиняться более чем одному руководителю. Например, они могут отчитываться перед руководителем проекта на ежедневной основе, но отчитываться перед руководителем отдела по своим основным функциям.

Примеры

Примеры матричного управления включают:

• Специалист по продажам, который подчиняется менеджеру по работе с продуктами и региональному менеджеру по работе с клиентами.
• Специалист отдела кадров, который поддерживает и подчиняется децентрализованному филиалу своей компании, но также подчиняется отделу кадров.
• ИТ-специалист, который отчитывается перед центральным отделом, но также отчитывается перед руководителями групп по нескольким ИТ-проектам с ограниченными сроками.

Преимущества и недостатки матричных структур

Как и любая организационная структура, матричная структура имеет свои преимущества и недостатки.

Преимущества матричной организационной структуры включают:

• Больше гибкости
• Повышенная отзывчивость
• Лучшее использование навыков
• Улучшенная связь
• Больше сотрудничества
• Снижение затрат напр. общие ресурсы
• Повышение мотивации
• Общие знания
• Работать более эффективно

К недостаткам матричной организационной структуры относятся:

• Меньшая подотчетность
• Конфликтующая лояльность
• Меньше координации
• Увеличение бюрократии
• Дополнительные расходы, например.