1. Самостоятельная работа матрицы
Самостоятельная работа №3
Системы линейных уравнений
ТЕМА 1. Системы линейных уравнений.
Матрицы и действия с ними.
Определители и их основные свойства.
Методы решения систем линейных уравнений.
СПИСОК ЛИТЕРАТУРЫ
Ильин В. А., Позняк Э. Г. Линейная алгебра: Учеб. для вузов.-5-е изд., стер. – М.: Физматлит, 2002. – 317 с.
Беклемишев Д. В. Курс линейной алгебры и аналитической геометрии: – М.: Физматлит, 2003. – 303 с.
Клетеник Д. В. Сборник задач по аналитической геометрии: Учеб. пособие для втузов / ред. Ефимов Н. В. – 17-е изд., стер. – СПб: Профессия, 2001. – 199 с.
Бугров Я.С., Никольский С.М. Высшая математика: Учеб.для вузов: в 3т.-5-е изд., стер.-М.:Дрофа.- (Высшее образование. Современный учебник). т.1. Элементы линейной алгебры и аналитической геометрии.-2003.-284 с.
Данко П.Е. и др. Высшая математика в упражнениях и задачах (с решениями): в 2 ч./ Данко П.Е., Попов А.Г., Кожевникова Т.Я -6-е изд..-М.: ОНИКС 21 век, ч.1. -2002.-304 с.
Решение типового варианта контрольной работы.
Задача 1. Вычислить
определитель 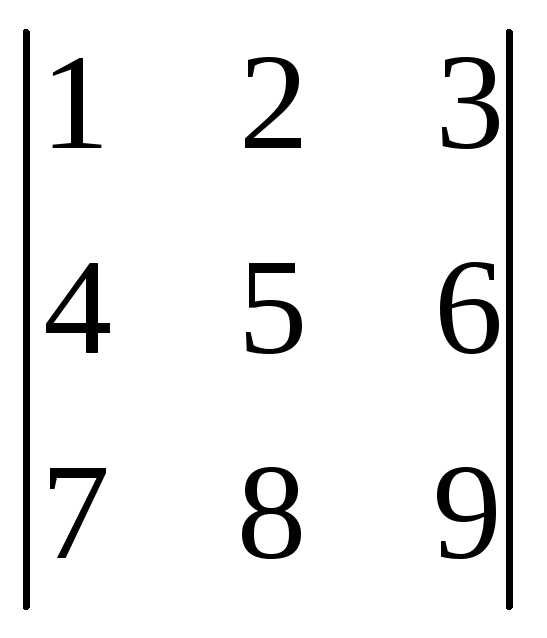 .
.
Ответ: 0.
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
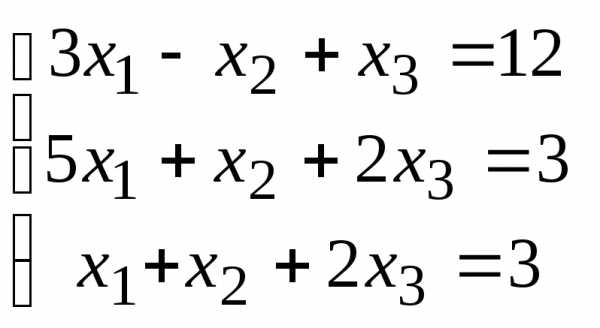
Решение:
Решим систему
матричным способом, для этого вычислим
обратную матрицу 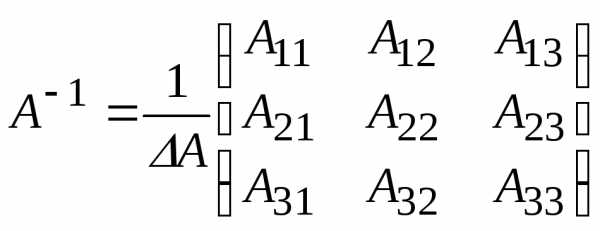 ,
где
,
где – алгебраические дополнения к элементам
матрицы.
– алгебраические дополнения к элементам
матрицы.
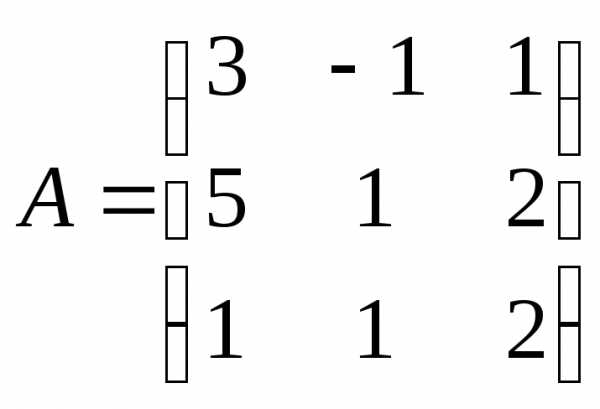
– матрица невырожденная.
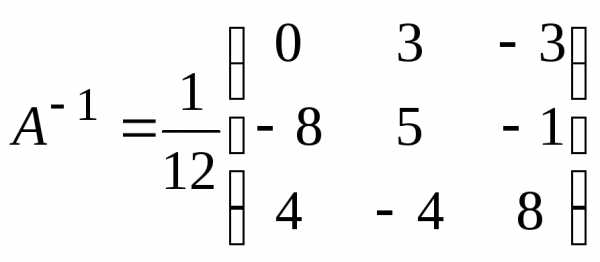
Решим систему методом Крамера. Главный определитель системы:
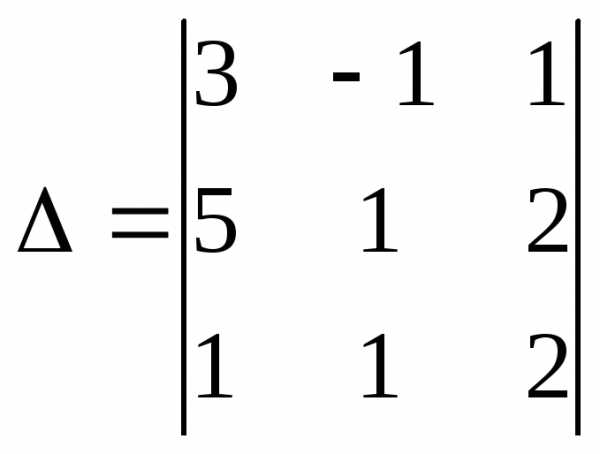 .
Разложим определитель по элементам
первой строки, пользуясь формулой
.
.
Разложим определитель по элементам
первой строки, пользуясь формулой
.
Запишем и вычислим вспомогательные определители
Тогда 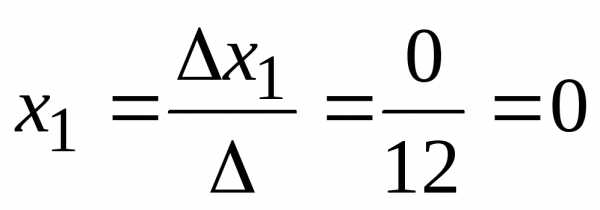
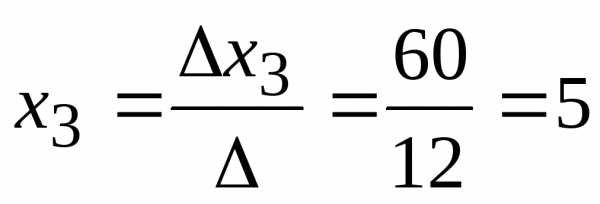
Ответ: 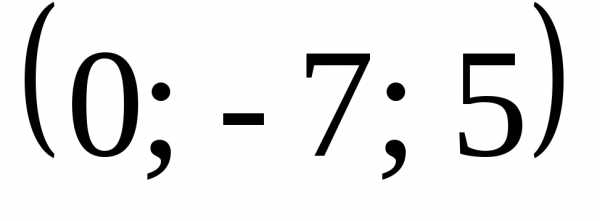
Решим систему методом Гаусса, для этого составим расширенную матрицу системы и упростим ее приведением к треугольному виду.
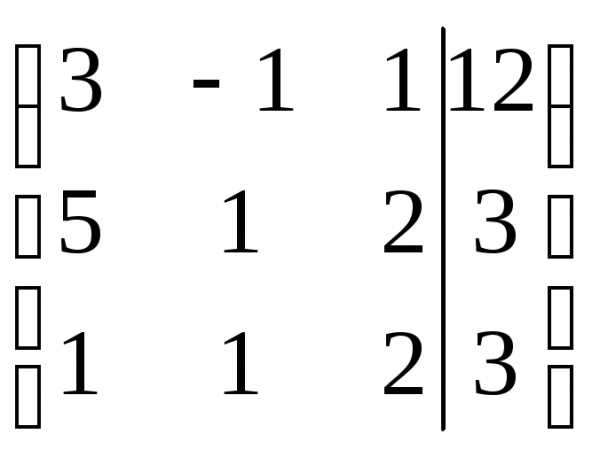
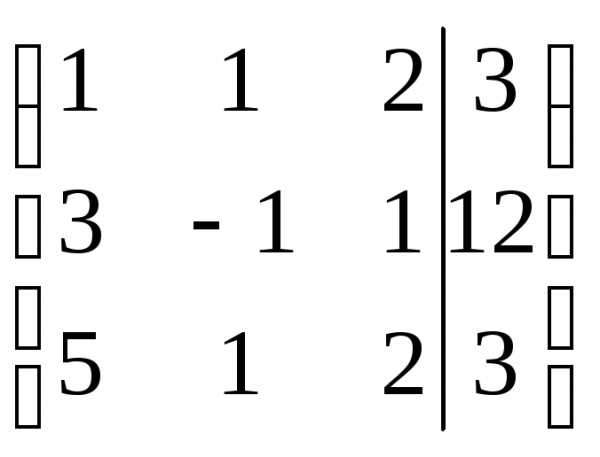
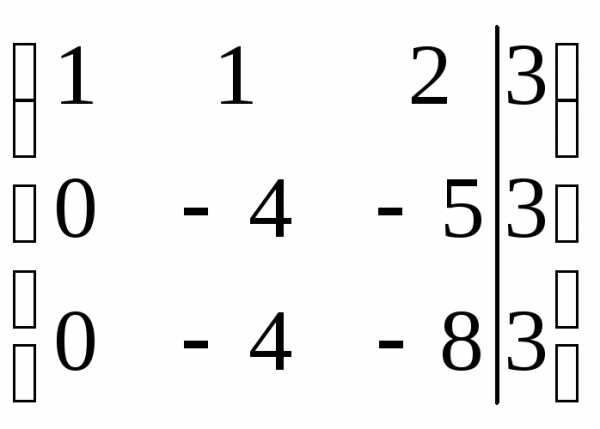
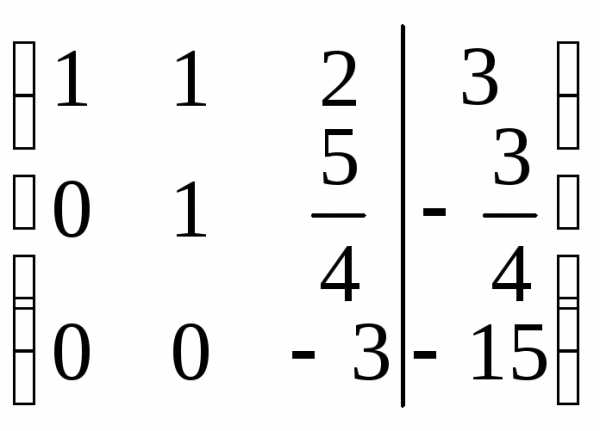
Таким образом, система равносильна системе
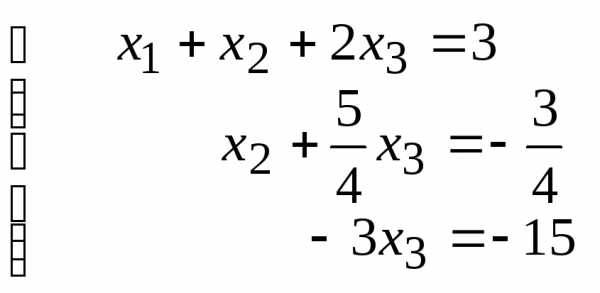
Находим 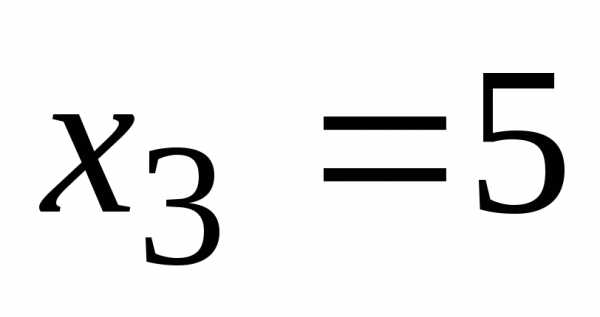
Ответ: 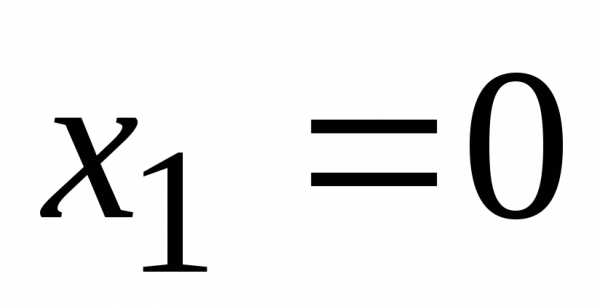 ,
,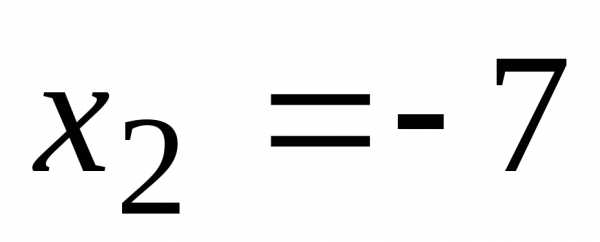 ,
,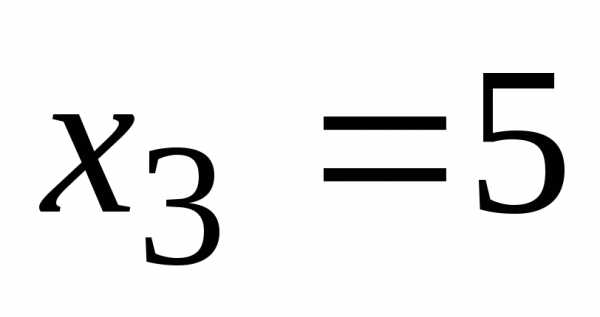
При решении всеми методами одной и той же системы, мы получим один ответ.
Задача 3. Выполнить действия:
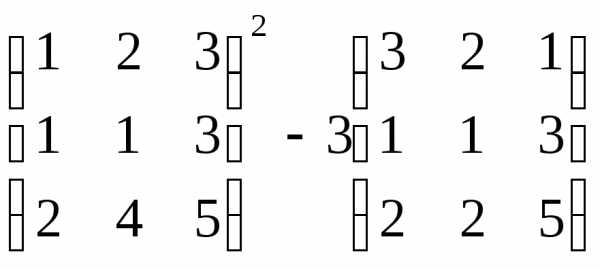
Решение. Выполним решение по действиям.
=
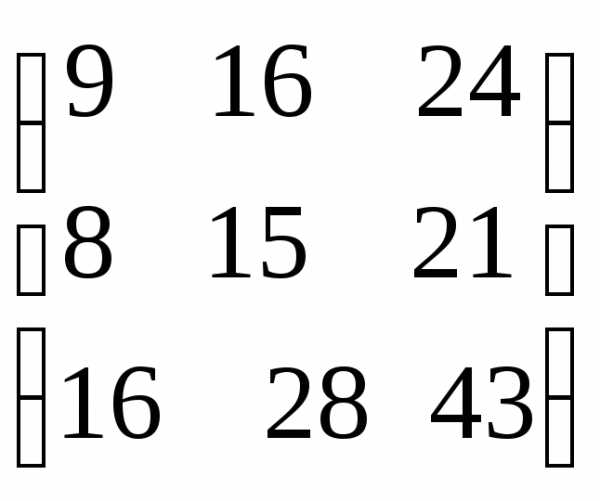 .
.
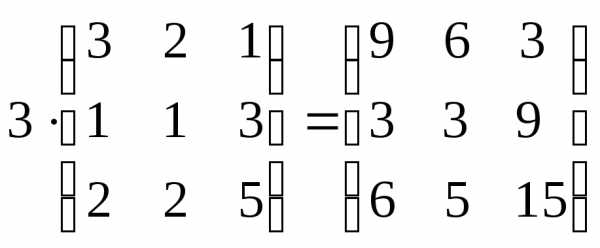 .
.
Ответ: 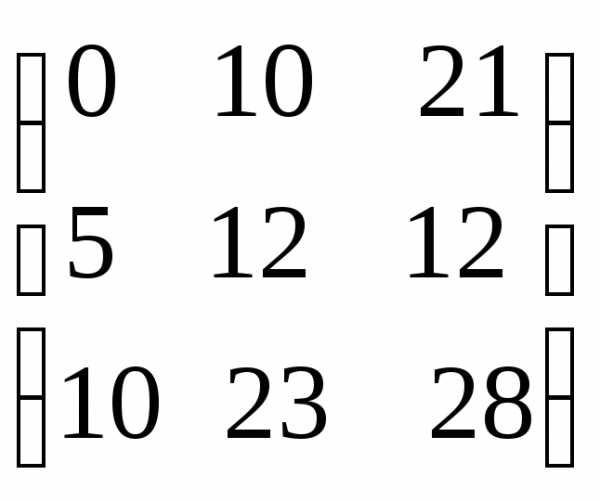 .
.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Если ,, то произведением матрицыназывается матрица, такая, что, где.
Пример: 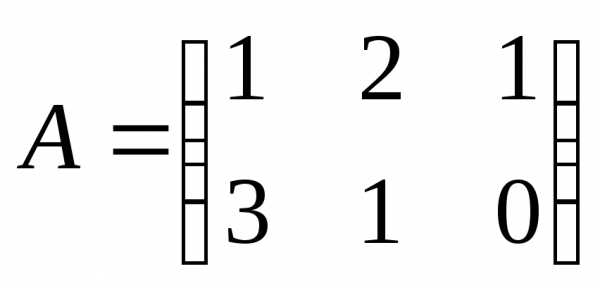
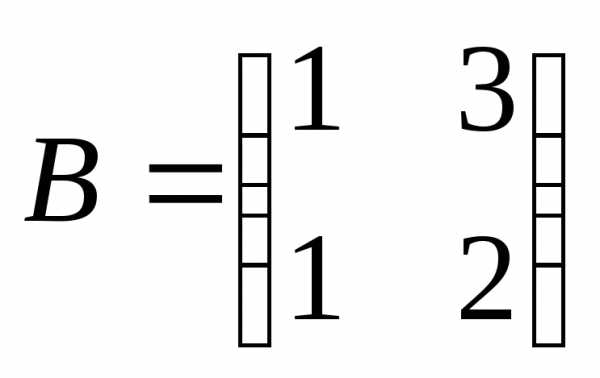
Произведение 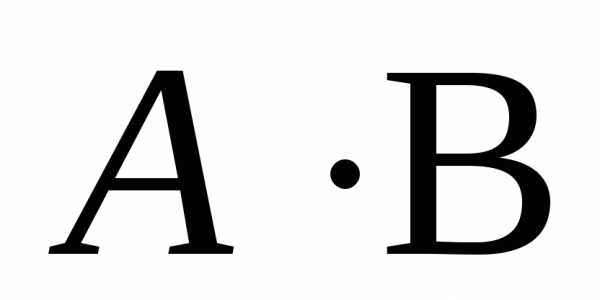 не
определено, так как число столбцов
матрицыА (3) не совпадает с числом строк матрицы В (2).
не
определено, так как число столбцов
матрицыА (3) не совпадает с числом строк матрицы В (2).
Произведение 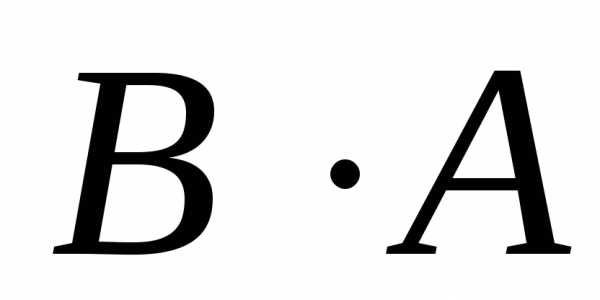 определено.
определено.
Контрольная работа №1.
Вариант 1
Задача 1. Вычислить определитель:
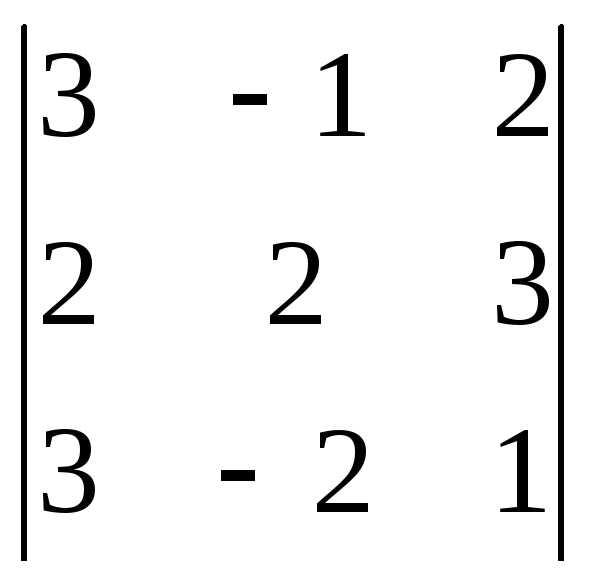
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 2
Задача 1. Вычислить определитель:
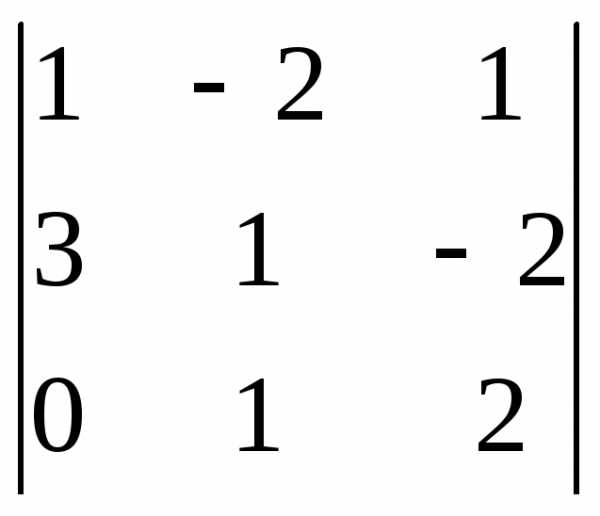
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
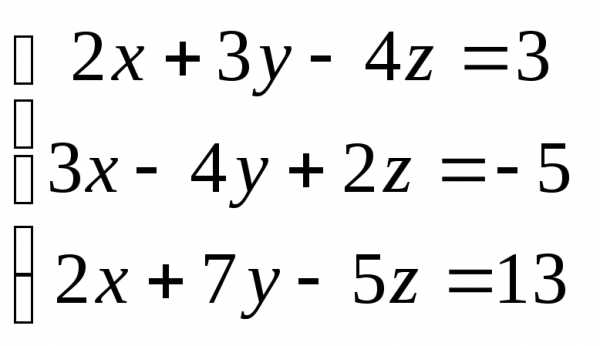
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 3
Задача 1. Вычислить определитель:
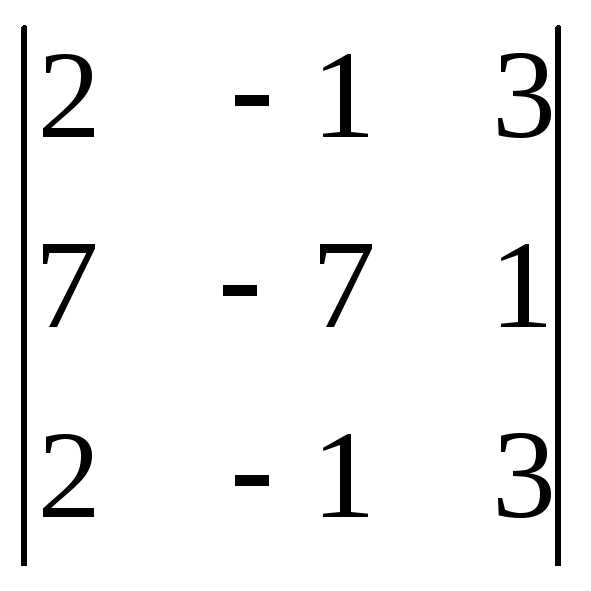
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
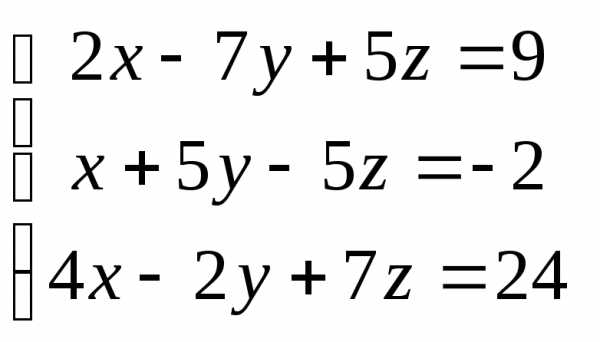
Задача 3. Выполнить действия:
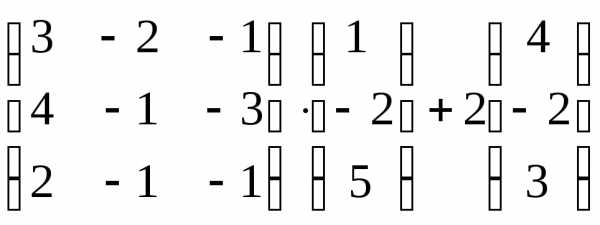
Контрольная работа №1.
Вариант 4
Задача 1. Вычислить определитель:
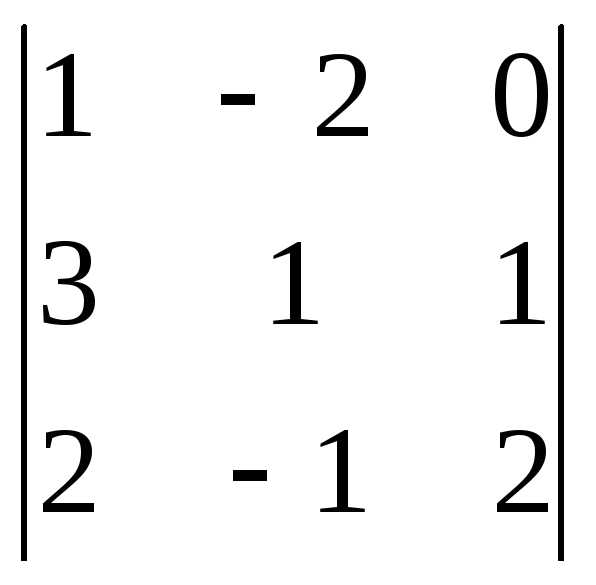
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
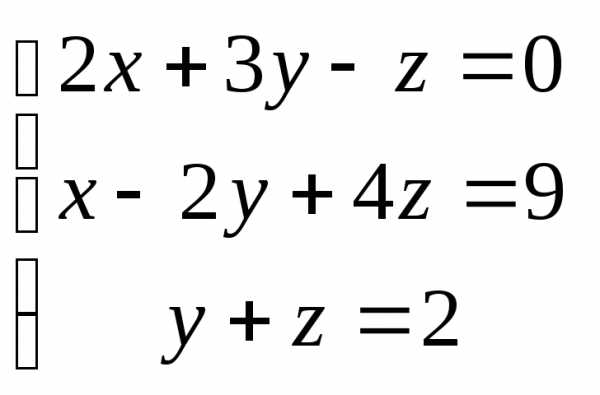
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 5
Задача 1. Вычислить определитель:
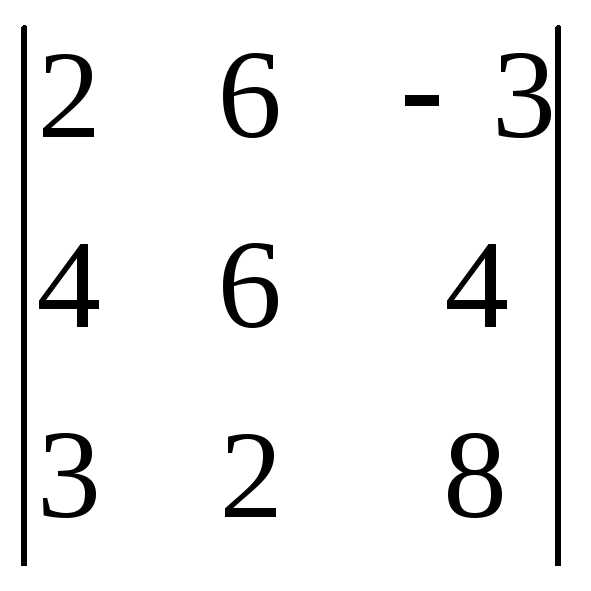
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
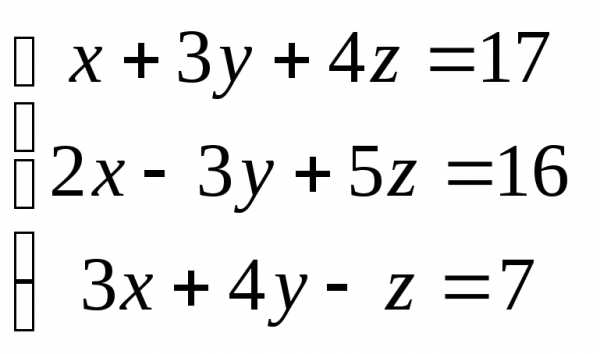
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 6
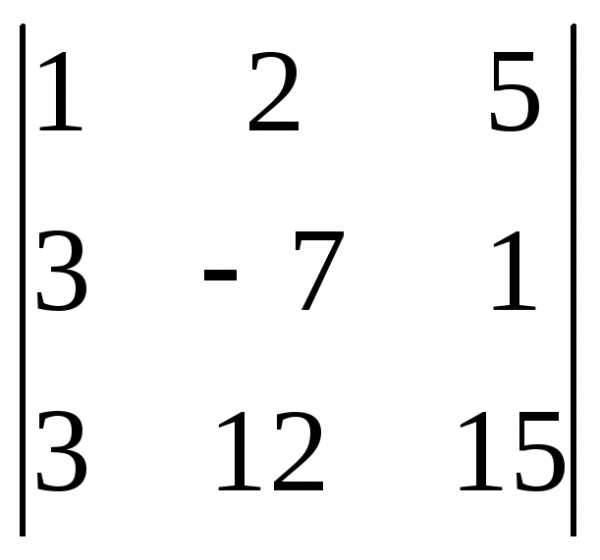
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
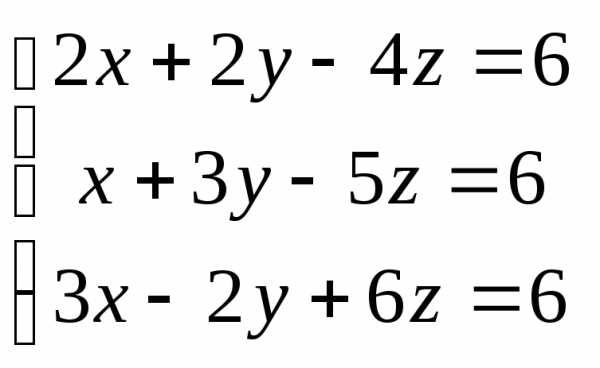
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 7
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
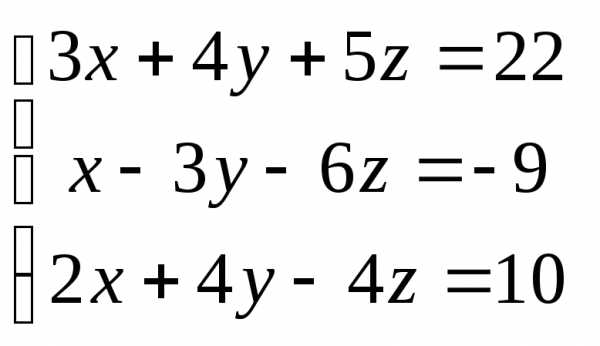
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 8
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
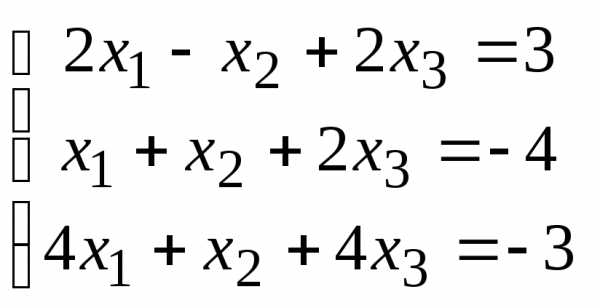
Задача 3. Выполнить действия:
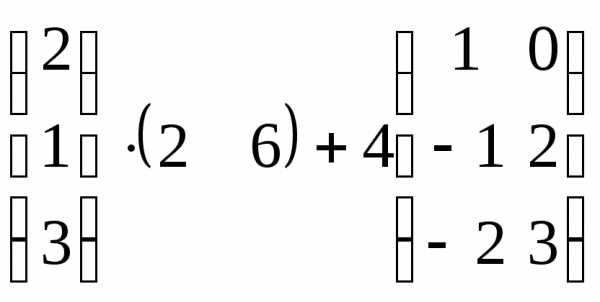
Контрольная работа №1.
Вариант 9
Задача 1. Вычислить определитель:
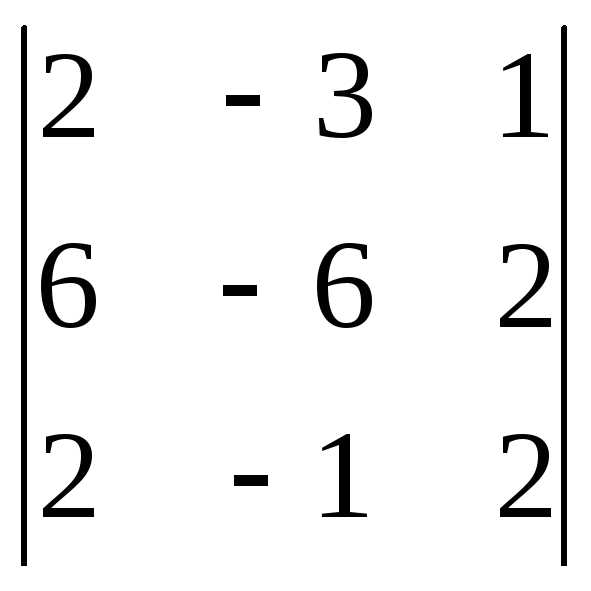
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
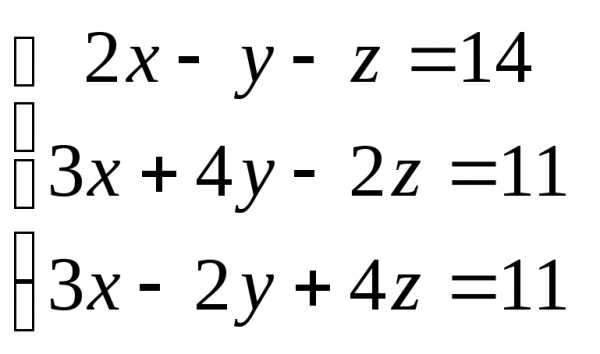
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 10
Задача 1. Вычислить определитель:
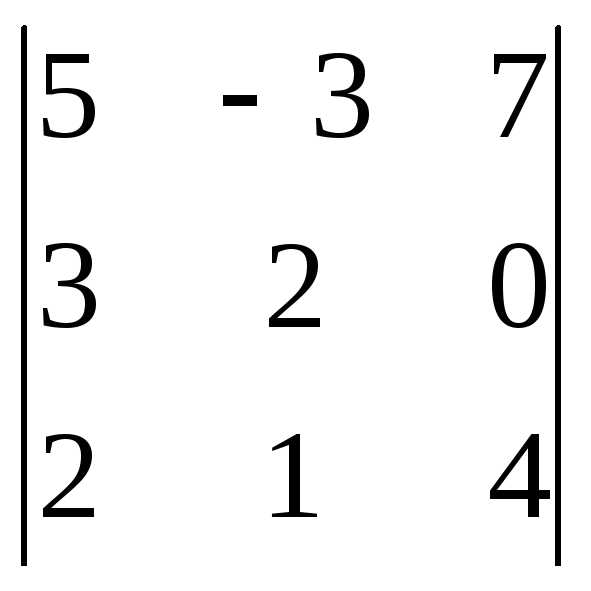
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
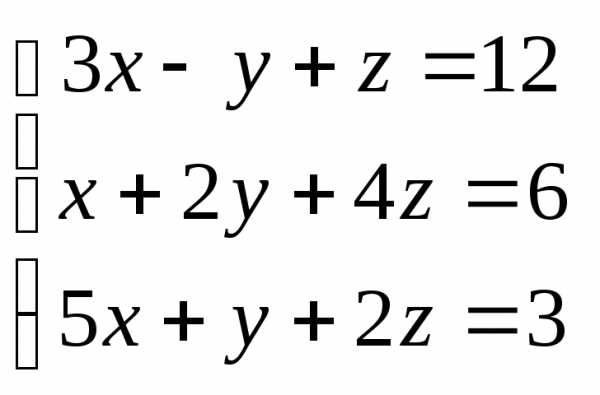
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 11
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
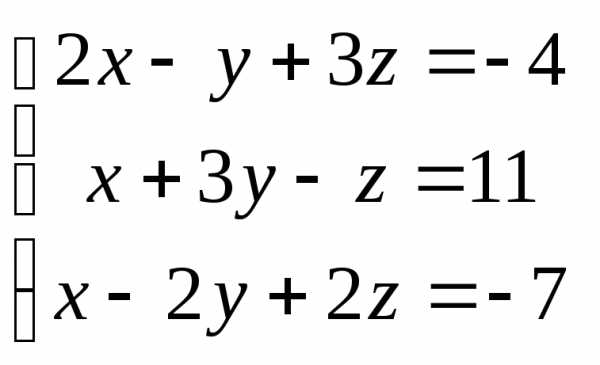
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 12
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
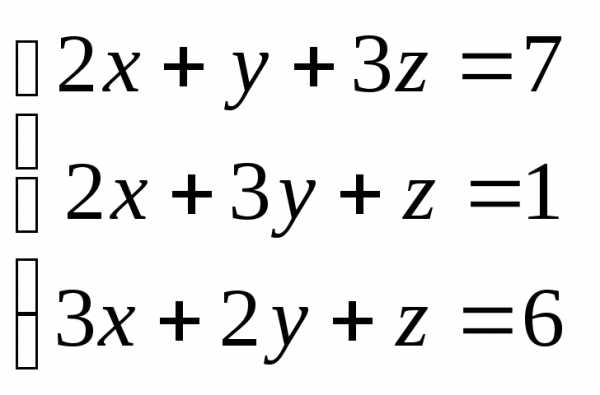
Задача 3. Выполнить действия:
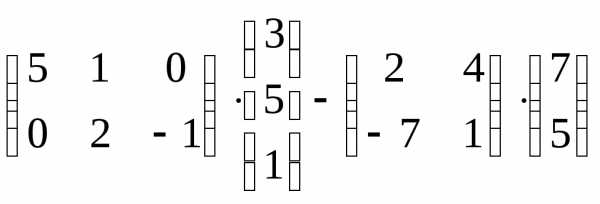
Контрольная работа №1.
Вариант 13
Задача 1. Вычислить определитель:
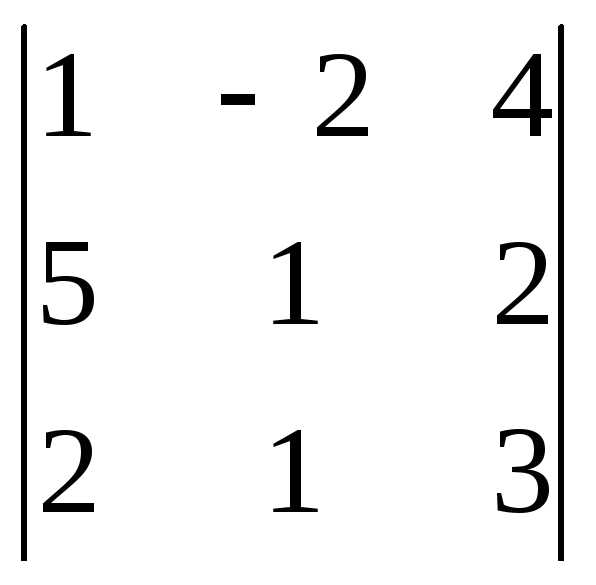
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
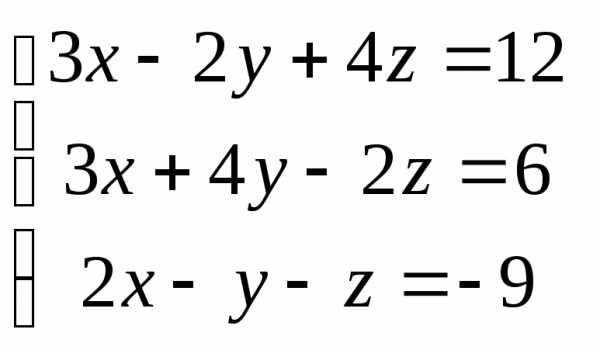
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 14
Задача 1. Вычислить определитель:
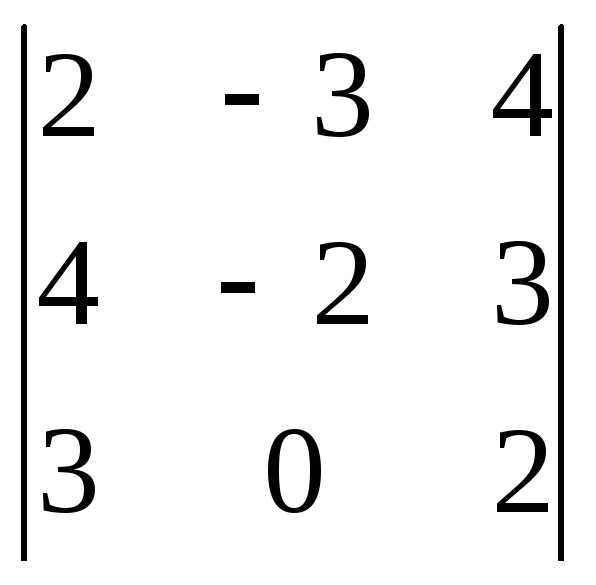
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
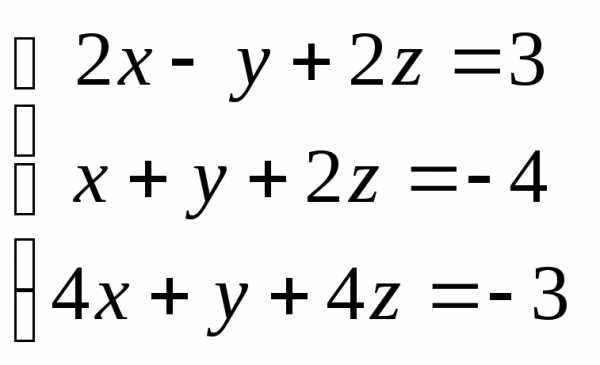
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 15
Задача 1. Вычислить определитель:
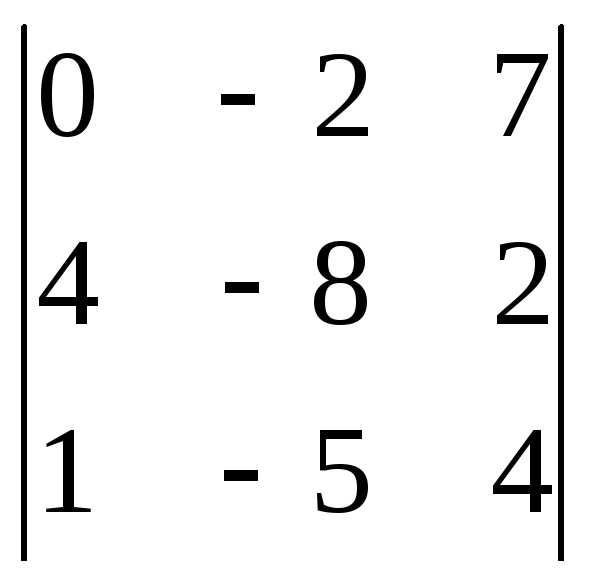
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
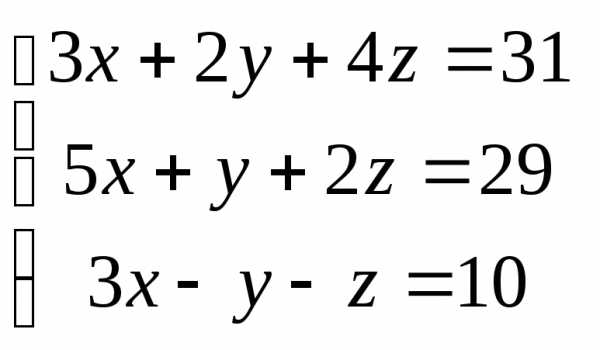
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 16
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
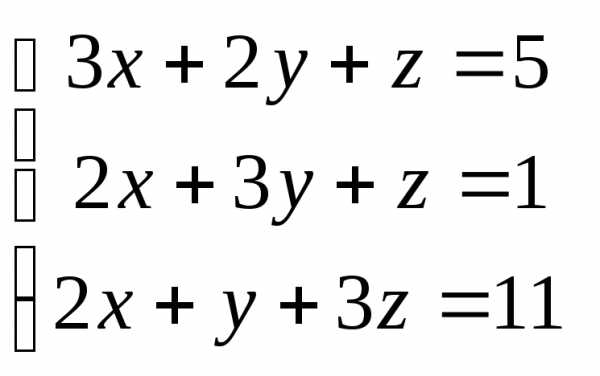
Задача 3. Выполнить действия:
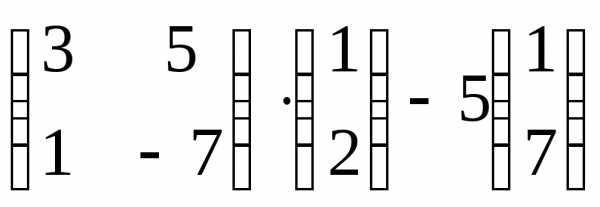
Контрольная работа №1.
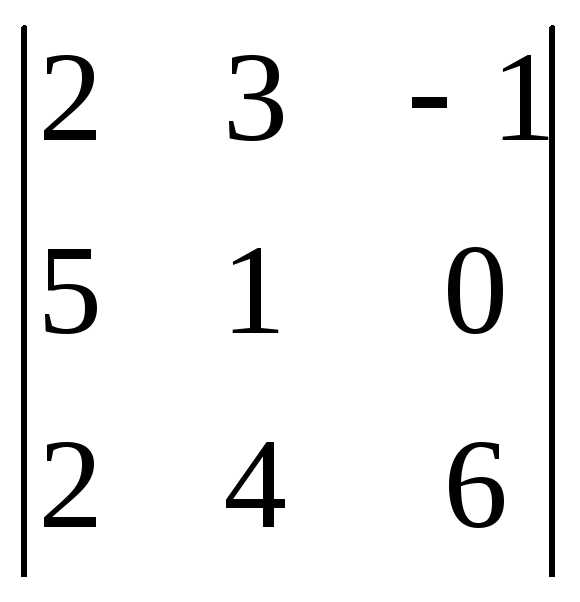
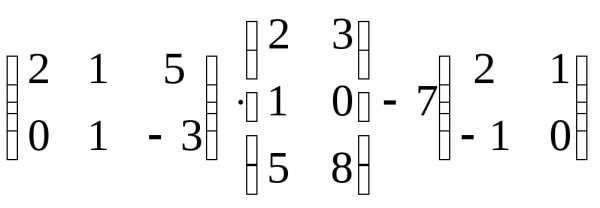
Вариант 17
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
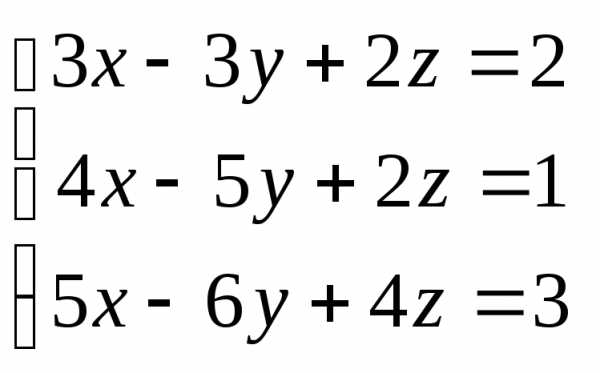
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 18
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
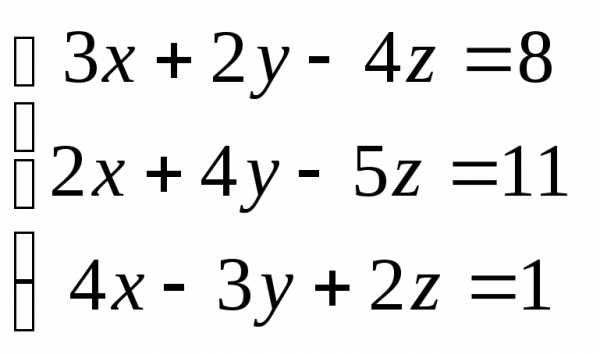
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 19
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:
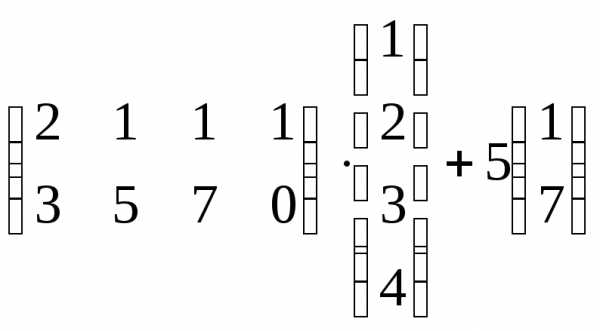
Контрольная работа №1.
Вариант 20
Задача 1. Вычислить определитель:
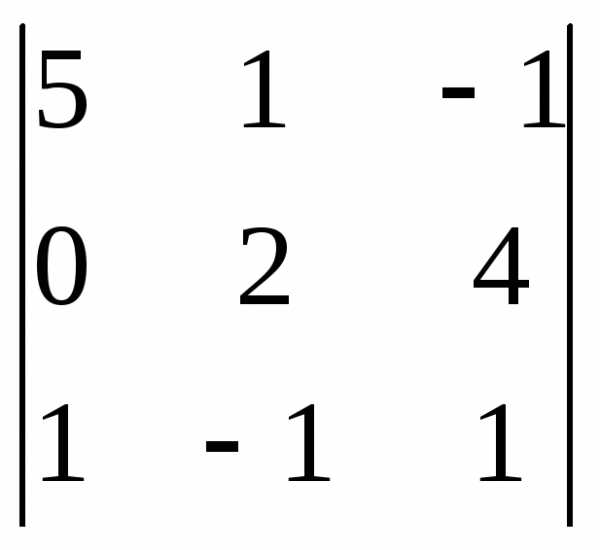
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
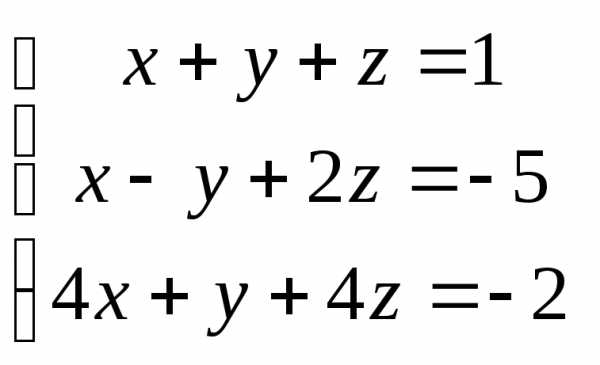
Задача 3. Выполнить действия:
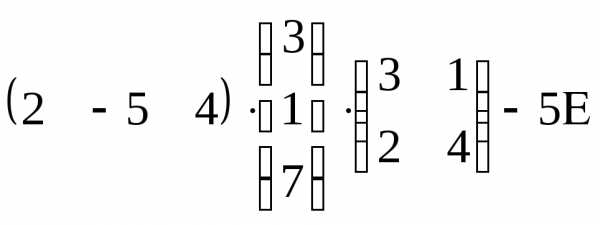
Контрольная работа №1.
Вариант 21
Задача 1. Вычислить определитель:
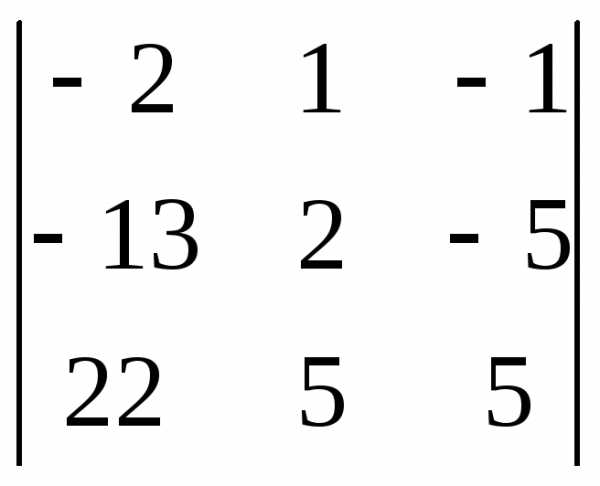
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
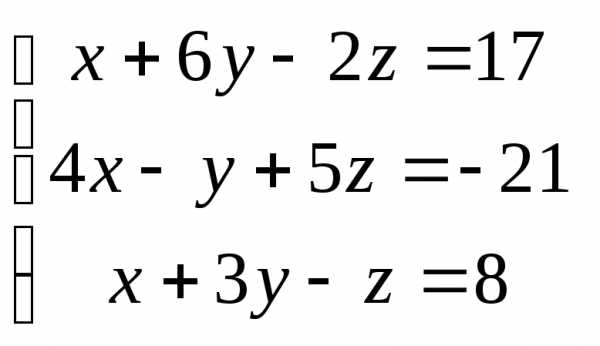
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 22
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
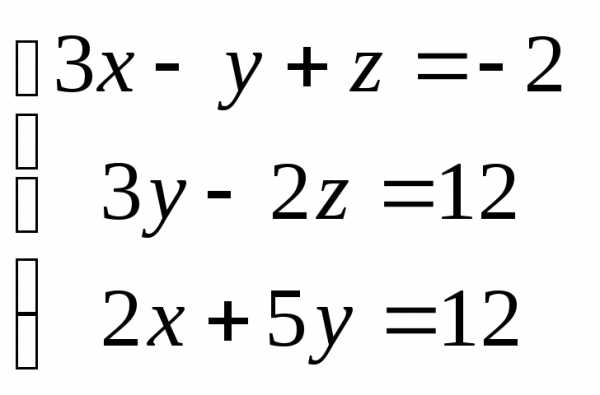
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 23
Задача 1. Вычислить определитель:
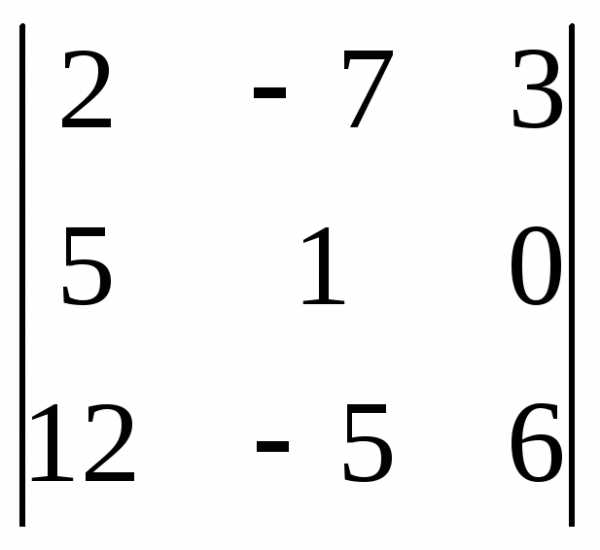
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
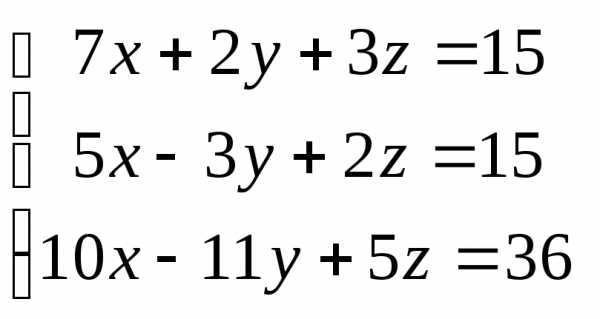
Задача 3. Выполнить действия:
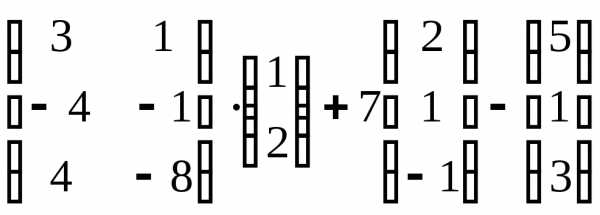
Контрольная работа №1.
Вариант 24
Задача 1. Вычислить определитель:
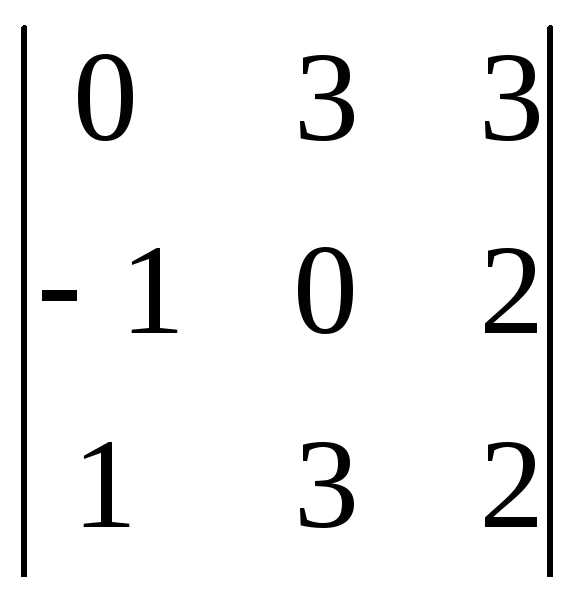
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
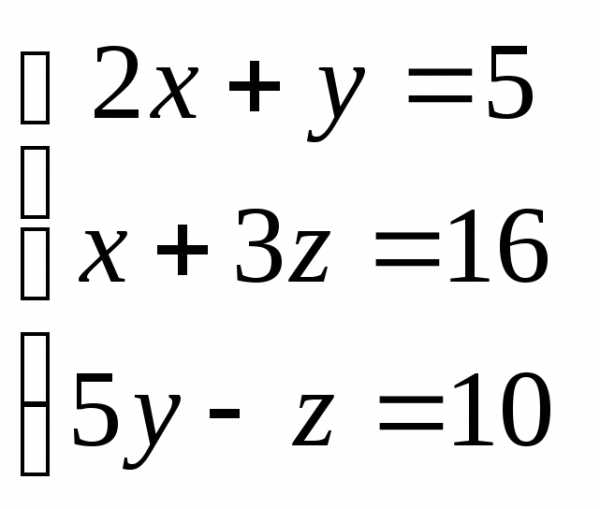
Задача 3. Выполнить действия:
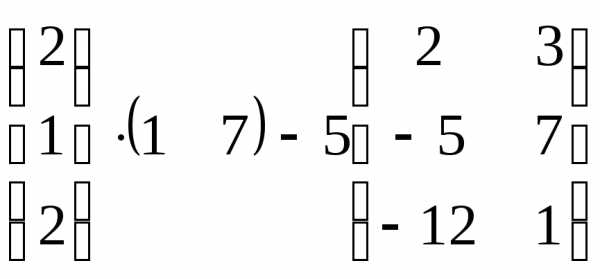
Контрольная работа №1.
Вариант 25
Задача 1. Вычислить определитель:
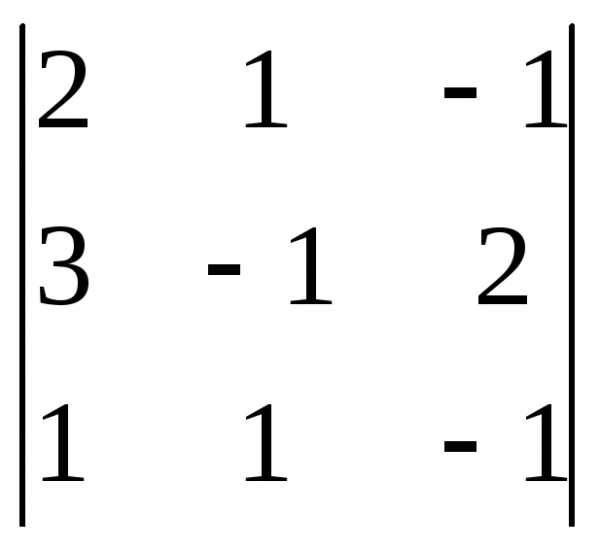
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
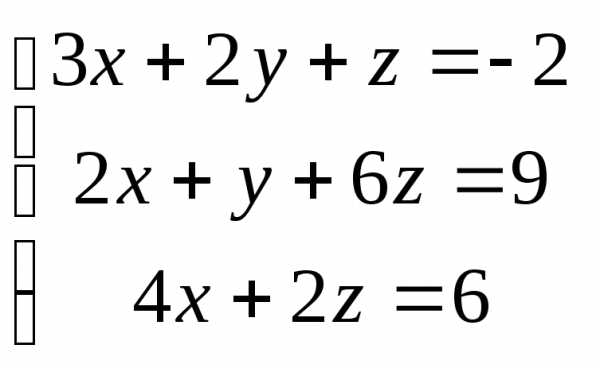
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 26
Задача 1. Вычислить определитель:
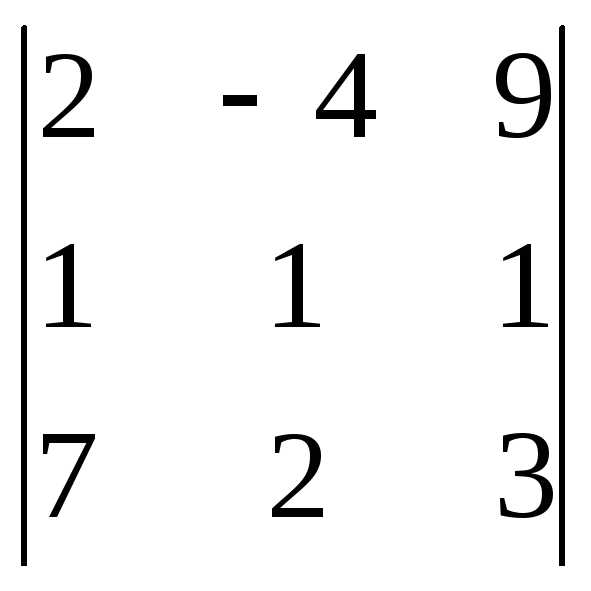
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
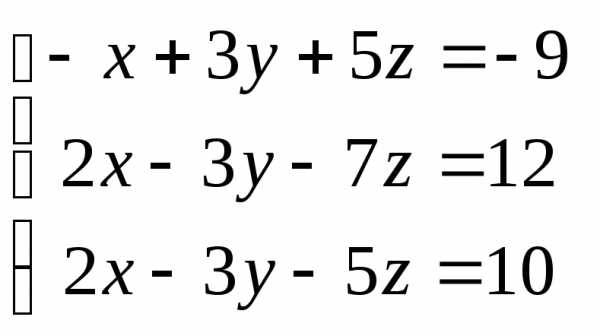
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 27
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера
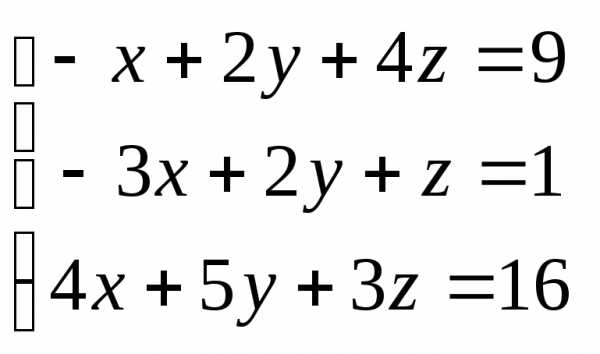
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 28
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера
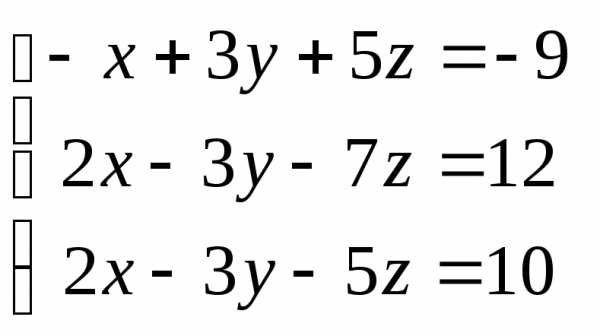
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 29
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера
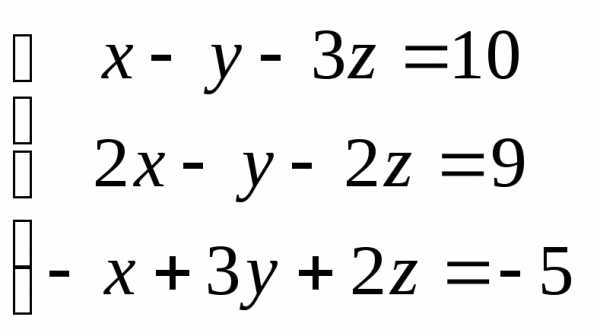
Задача 3. Выполнить действия:
Контрольная работа №1.
Вариант 30
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера
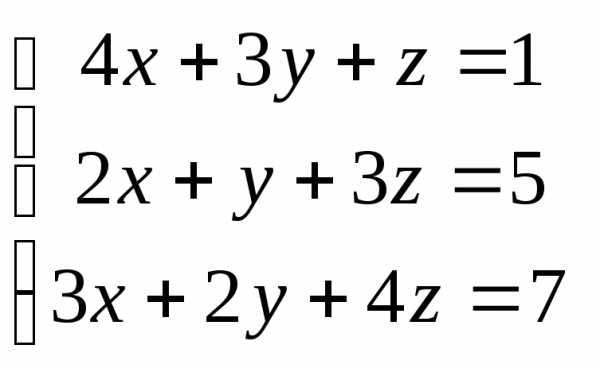
Задача 3. Выполнить действия:
studfiles.net
Контрольная работа « Матрицы и определители» для студентов 1 курса
Контрольная работа
«Матрицы и определители»
1). Дано: A,B. Найти:
1
а) 3A+B
б) AB
в)A -1
г)A -1A
2).Найти def A: а) методом треугольников;
б) приведением к каноническому виду
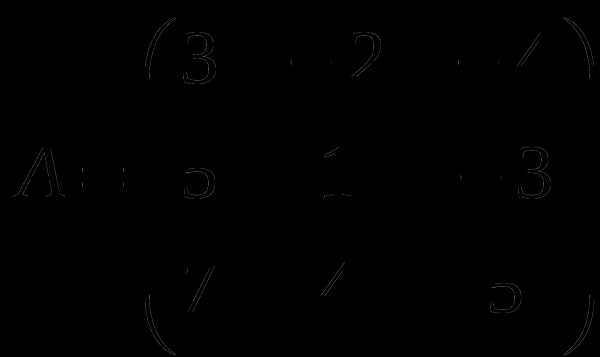
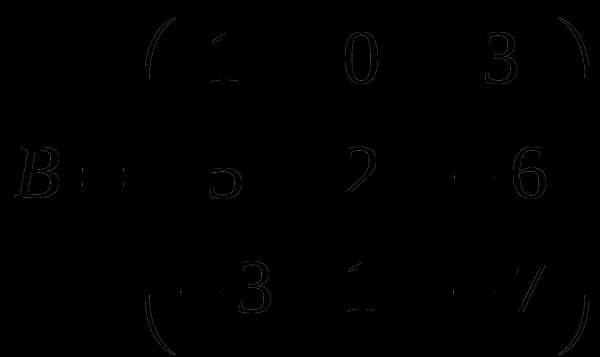
1). Дано: A,B. Найти:
2
а) -2A-B
б) BA
в)B -1
г) B -1B
2).Найти def A: а) приведением к каноническому виду;
б) методом треугольников;
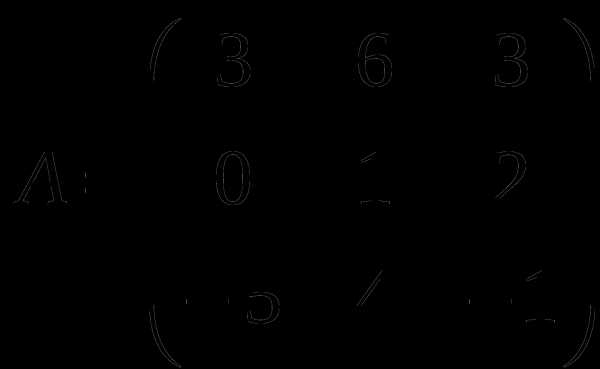
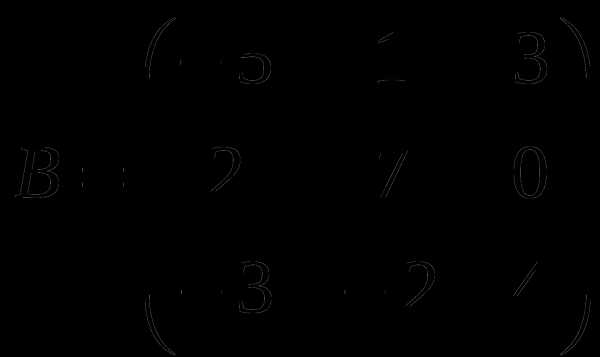
1). Дано: A,B. Найти:
3
а) 3B+A
б) BA
в)B -1
г)BB -1
2).Найти∆B: а) методом треугольников;
б) приведением к треугольному виду
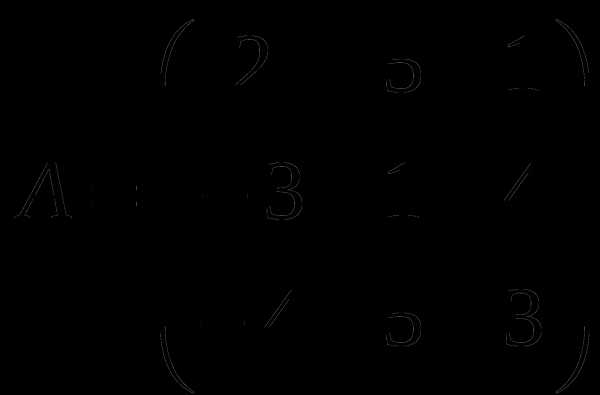
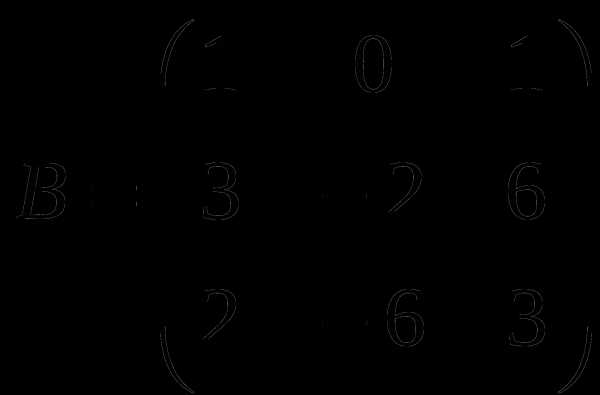
1). Дано: A,B. Найти:
4
а) 3A+B
б) AB
в)A -1
г)A -1A
2).Найти def B: а) методом треугольников;
б) приведением к каноническому виду
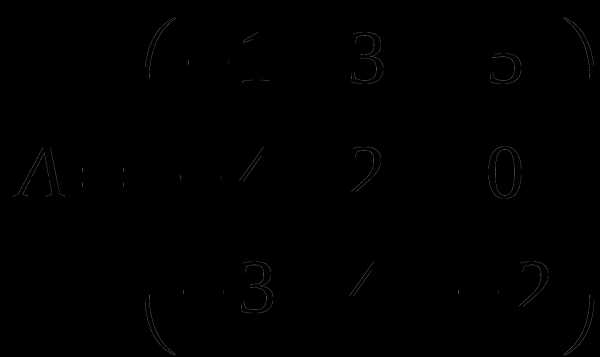
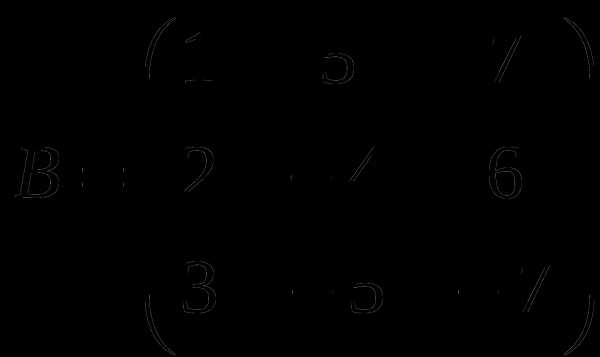
1). Дано: A,B. Найти:
5
а) 2A+B
б) AB
в)B -1
г) BB -1
2).Найти def A: а) методом треугольников;
б) приведением к треугольному виду;
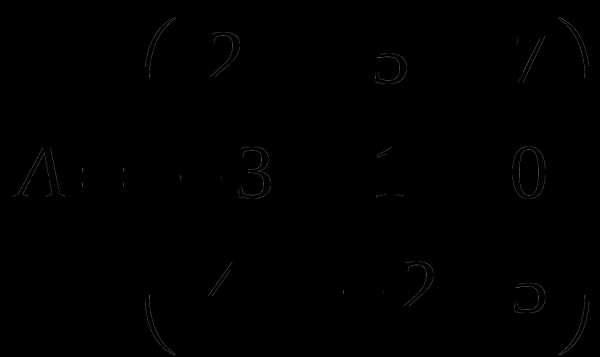
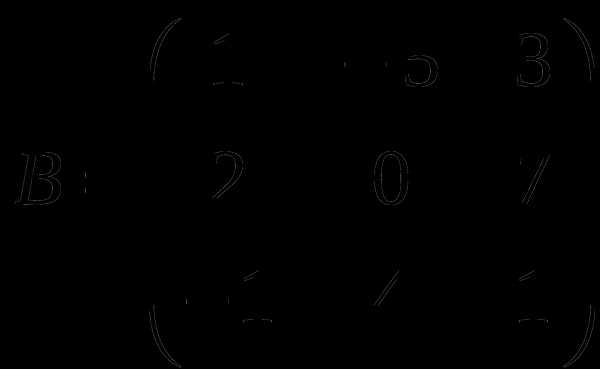
Контрольная работа № 1
1). Дано: A,B. Найти:
6
а) 3B-A
б) AB
в)A -1
г) AA -1
2).Найти ∆B: а) методом треугольников;
б) приведением к треугольному виду
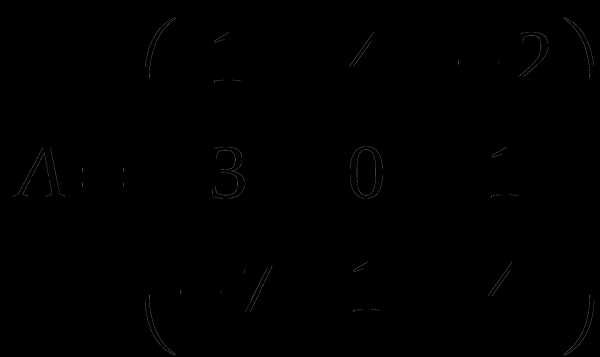
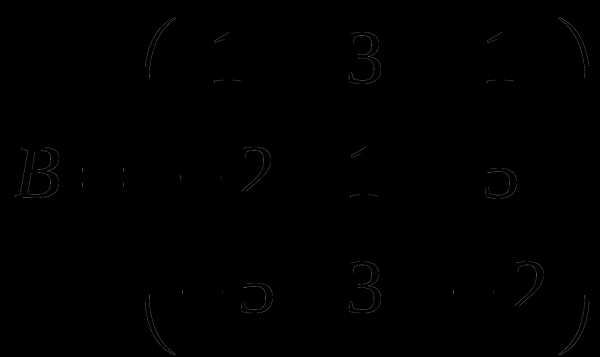
1). Дано: A,B. Найти:
7
а) 2B+3A
б) BA
в)A -1
г)A -1A
2).Найти∆B: а) методом треугольников;
б) приведением к треугольному виду
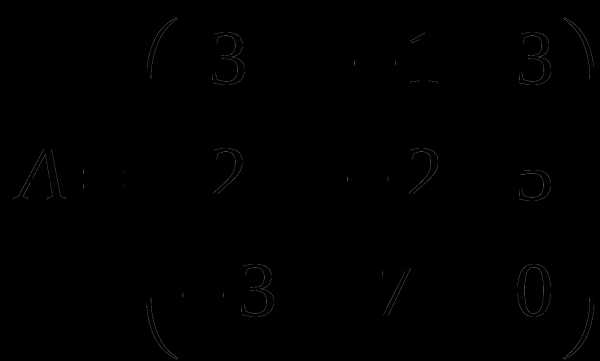
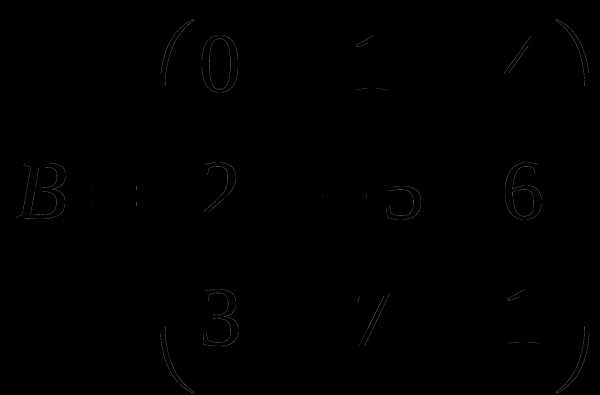
1). Дано: A,B. Найти:
8
а) 3B-A
б) AB
в)A -1
г)A -1A
2).Найти def B: а) методом треугольников;
б) приведением к треугольному виду
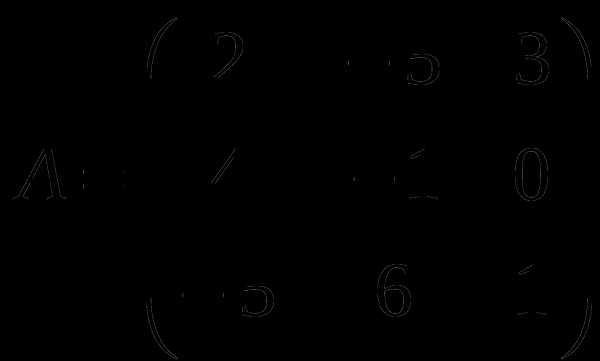
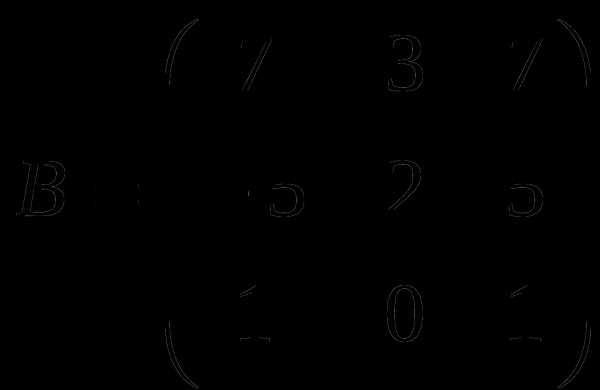
1). Дано: A,B. Найти:
9
а) 3B-A
б) AB
в)B -1
г) B -1B
2).Найти ∆ A: а) методом треугольников;
б) приведением к треугольному виду;
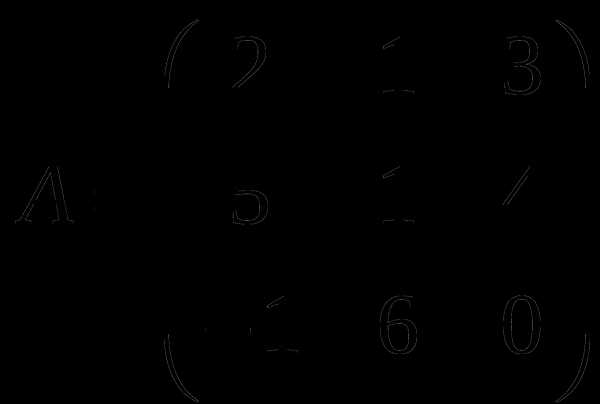
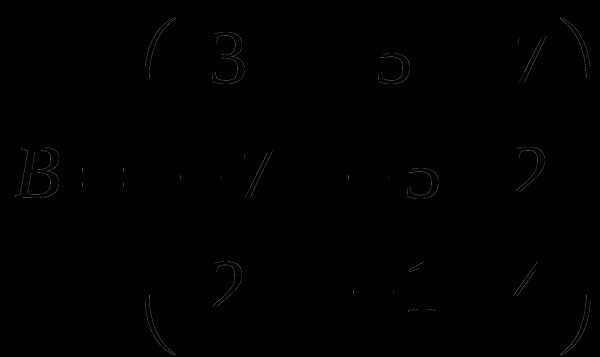
1). Дано: A,B. Найти:
10
а) 2B+2A
б) BA
в)A -1
г) AA -1
2).Найти ∆A: а) методом треугольников;
б) приведением к треугольному виду
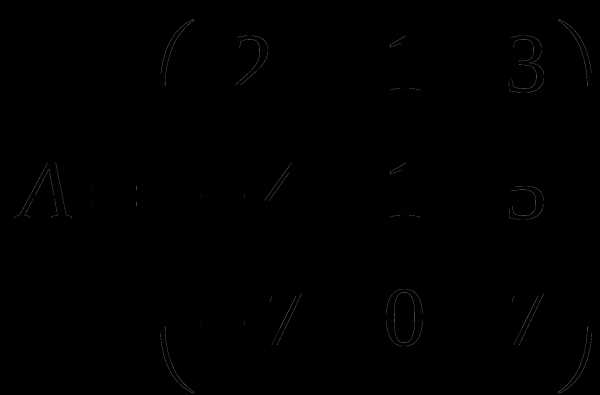
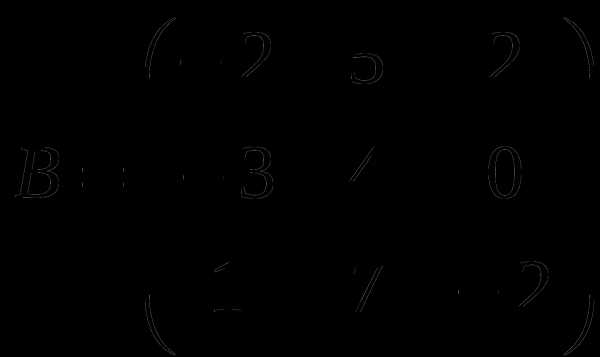
Контрольная работа № 1
1). Дано: A,B. Найти:
11
а) 2B-A
б) BA
в)B -1
г)B -1B
2).Найти def B: а) методом треугольников;
б) приведением к каноническому виду
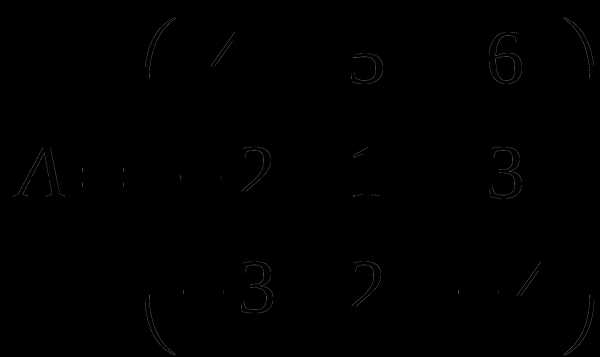
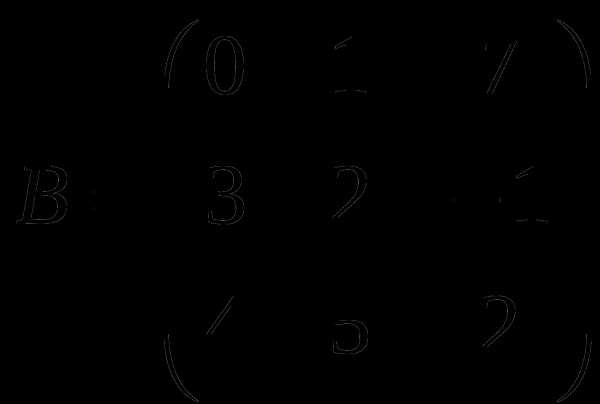
1). Дано: A,B. Найти:
12
а) 2B+A
б) AB
в)A -1
г)A -1A
2).Найти ∆ B: а) приведением к треугольному виду;
б) методом треугольников;
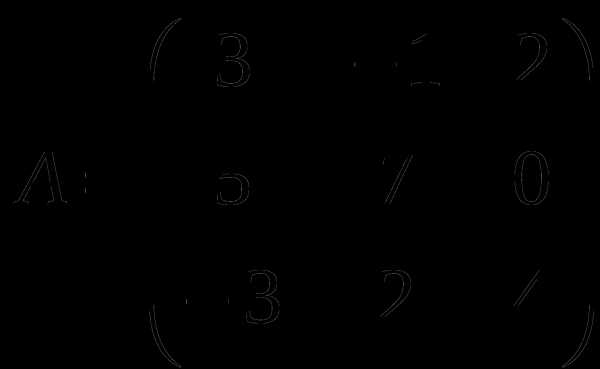
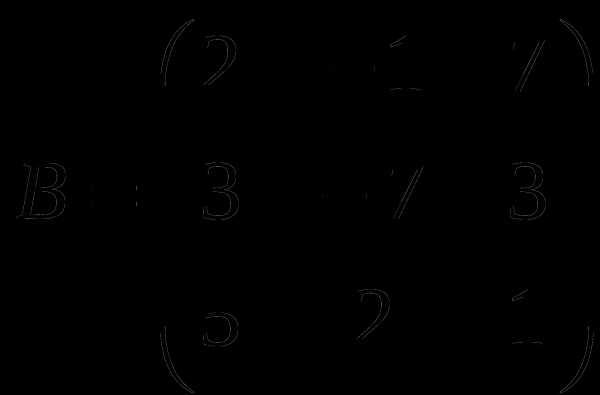
1). Дано: A,B. Найти:
13
а) 3A+B
б) AB
в)A -1
г) A -1A
2).Найти def B: а) методом треугольников;
б) приведением к треугольному виду
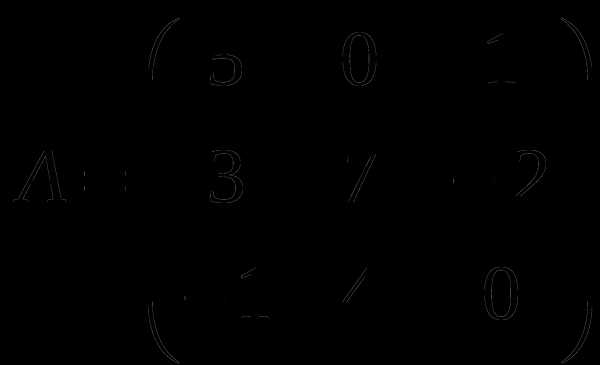
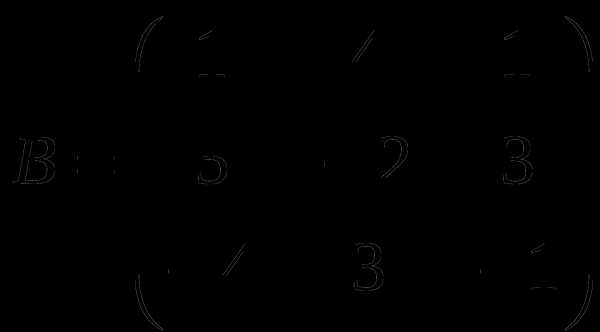
1). Дано: A,B. Найти:
14
а) 2B+3A
б) BA
в)B -1
г)B -1B
2).Найти ∆A: а) методом треугольников;
б) приведением к треугольному виду
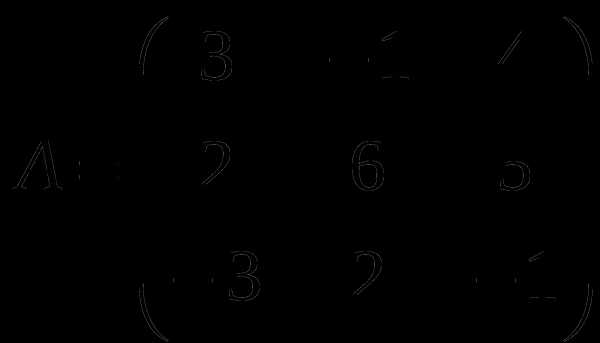
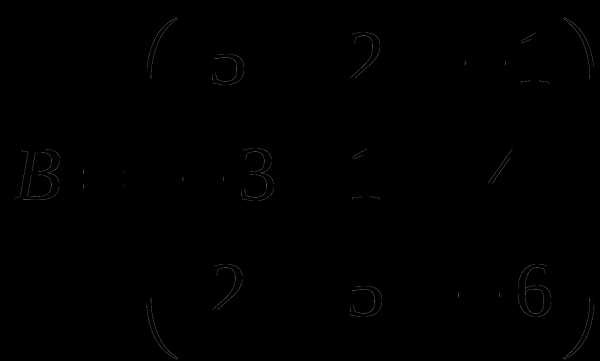
1). Дано: A,B. Найти:
15
а) 3A+B
б) BA
в)B -1
г)B -1B
2).Найти │A│: а) методом треугольников;
б) приведением к каноническому виду
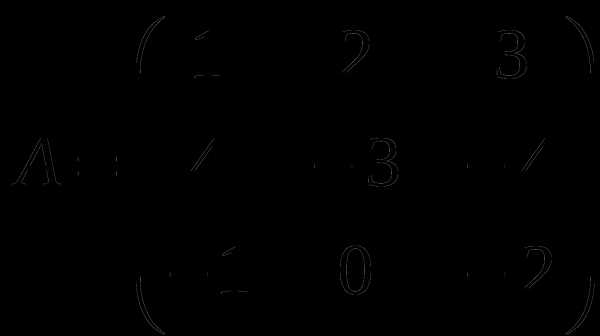
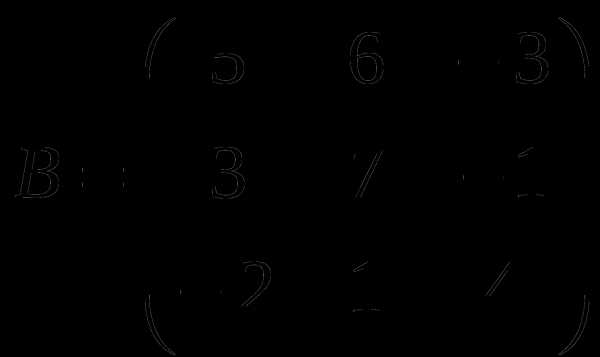
Контрольная работа № 1
1). Дано: A,B. Найти:
16
а) 2A+B
б) AB
в)A -1
г) AA -1
2).Найти def A: а) методом треугольников;
б) приведением к треугольному виду;
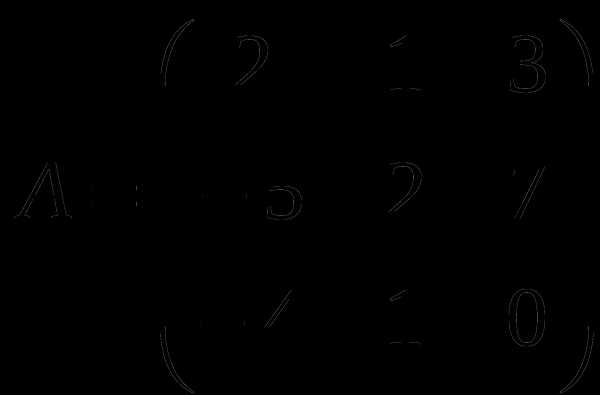
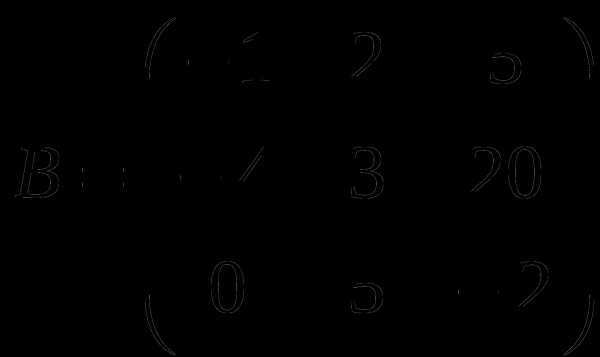
1). Дано: A,B. Найти:
17
а) 3A-B
б) AB
в)B -1
г) BB -1
2).Найти ∆A: а) методом треугольников;
б) приведением к треугольному виду
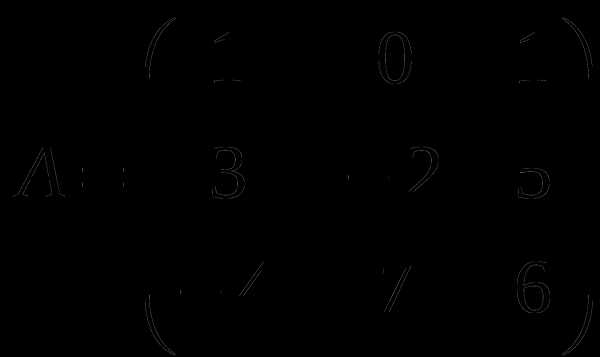
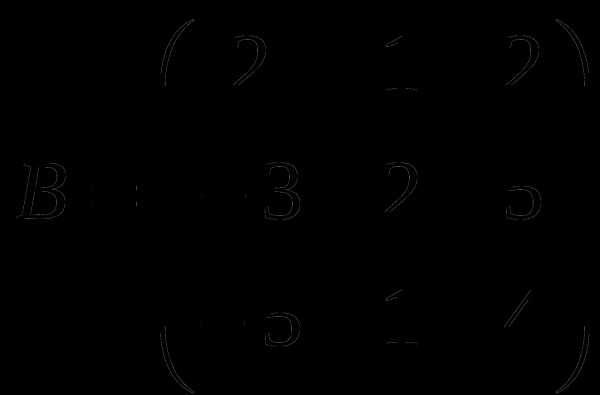
1). Дано: A,B. Найти:
18
а) A+2B
б) AB
в)B -1
г) B -1B
2).Найти def A: а) методом треугольников;
б) приведением к треугольному виду;
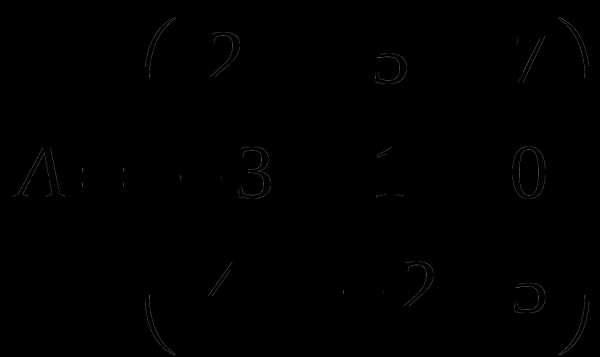
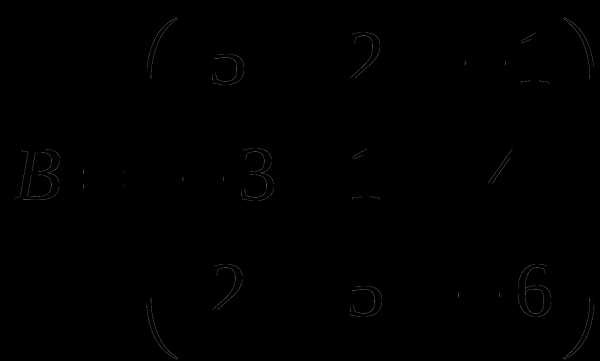
1). Дано: A,B. Найти:
19
а) B+3A
б) AB
в)B -1
г) BB -1
2).Найти def B: а) методом треугольников;
б) приведением к каноническому виду
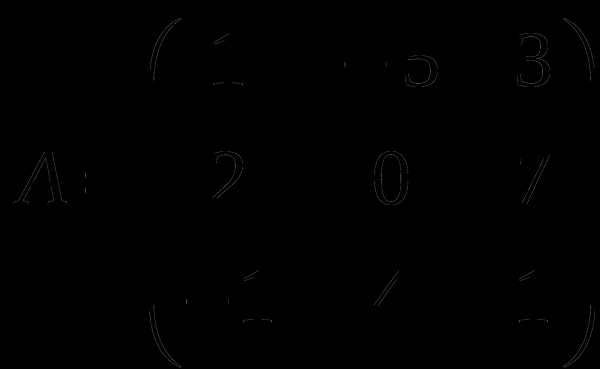
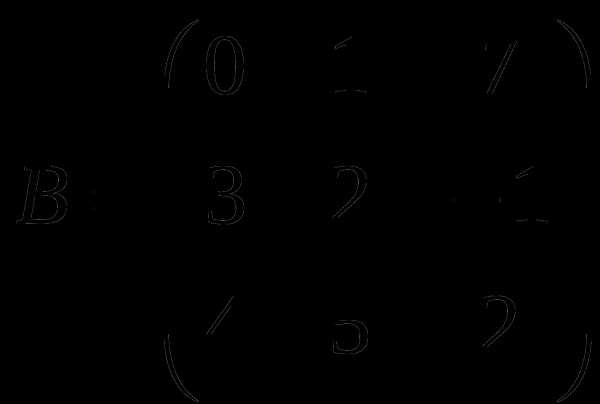
1). Дано: A,B. Найти:
20
а) 2A-B
б) AB
в)A -1
г) A -1A
2).Найти def A: а) методом треугольников;
б) приведением к треугольному виду;
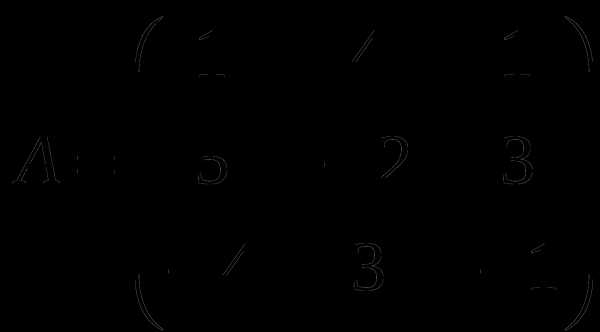
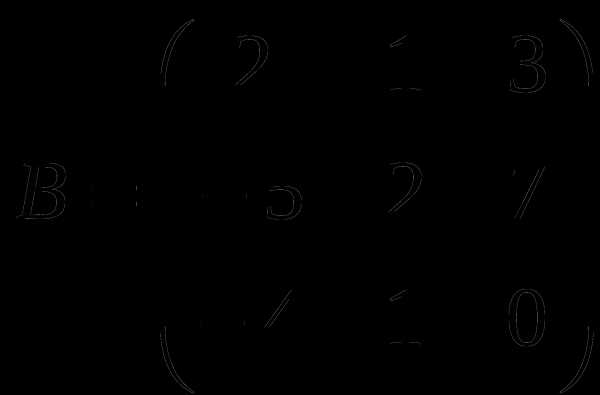
Контрольная работа № 1
infourok.ru
Тест по теме: «Матрицы. Определители. Системы линейных алгебраических уравнений».
Тест по теме: «Матрицы. Определители. Системы линейных алгебраических уравнений».
По дисциплине «Математика» (2 семестр).
Специальности: «Экономика и бух.учет»
Вариант 1.
Задания уровня А:
1. Выберите единичную матрицу из числа предложенных:
1)
2)
3)
4)
2. Укажите матрицу , если матрица A=
1)
2)
3)
4)
3. Выберите вектор – столбец из числа предложенных матриц
1)
2)
3) ;
4)
4. Найдите сумму матриц , если
1)
2)
3);
4) .
5. Найдите сумму матриц , если
- ;
6. Найдите , если
7. Найдите произведение матриц , если
- произведение не определено;
8. Найдите произведение матриц , если
1) ;
2)
3) произведение не определено;
4)
9. Как изменится определитель при транспонировании матрицы?
1) определитель не изменится;
2) знак определителя поменяется на противоположный;
3) значение определителя удвоится;
4) определитель примет значение, обратное исходному.
10. Вычислите определитель 2-го порядка
1) -7;
2) -5;
3) 1;
4) 5.
11. Вычислите определитель 3-го порядка
1) 98;
2) -30;
3) 90;
4) 104.
12. Выберите невырожденную матрицу из числа предложенных
13. Найдите минор m12 соответствующего элемента определителя
1) -2;
2) 13;
3) -5;
4) 5.
14. Найдите алгебраическое дополнение соответствующего элемента матрицы
- -18;
- -19;
- 18;
- 19.
15. Найдите значение , решив уравнение =0
1)
2) 0;
3)
4)
Задания уровня В:
1. Найдите матрицу, обратную данной
2. Решите систему линейных алгебраических уравнений
3. Вычислите определитель 4-го порядка
Тест по теме: «Матрицы. Определители. Системы линейных алгебраических уравнений».
По дисциплине «Математика» (2 семестр).
Специальности: «Экономика и бух.учет»
Вариант 2.
Задания уровня А:
1. Выберите треугольную матрицу из числа предложенных:
1)
2)
3)
4)
2. Укажите матрицу , если матрица
1)
2)
3)
4)
3. Выберите вектор – строку из числа предложенных матриц
4. Найдите разность матриц , если
1) ;
2) ;
3);
4)
5. Найдите сумму матриц , если
2)
3) ;
4)
6. Найдите , если
- ;
7. Найдите произведение матриц , если
1)
- .
- произведение не определено;
8. Найдите произведение матриц , если
1) произведение не определено;
2)
3)
4)
9. Как изменится определитель при перестановке двух его параллельных рядов?
1) определитель не изменится;
2) знак определителя поменяется на противоположный;
3) значение определителя удвоится;
4) определитель примет значение, обратное исходному.
10. Вычислите определитель 2-го порядка
1) -17;
2) 13;
3) 3;
4) -13.
11. Вычислите определитель 3-го порядка
1) 92;
2) 72;
3) 56;
4) 54.
12. Выберите вырожденную матрицу из числа предложенных.
13. Найдите минор m21 соответствующего элемента определителя
1) -10;
2) 3;
3) 4;
4) -4.
14. Найдите алгебраическое дополнение А32 соответствующего элемента матрицы .
- 50;
- 9;
- -50;
- -9.
15. Найдите значение х, решив уравнение =0
1) 6;
2) 9;
3) 18;
4) -18.
Задания уровень В:
1. Найдите матрицу, обратную данной
2. Решите систему линейных алгебраических уравнений
3. Вычислите определитель 4-го порядка
Ключи | |
Вариант 1 | Вариант 2 |
А1 2 | А1 1 |
А2 4 | А2 2 |
А3 4 | А3 3 |
А4 2 | А4 1 |
А5 1 | А5 2 |
А6 4 | А6 2 |
А7 3 | А7 4 |
А8 1 | А8 2 |
А9 1 | А9 2 |
А10 4 | А10 4 |
А11 1 | А11 3 |
А12 3 | А12 1 |
А13 4 | А13 3 |
А14 3 | А14 3 |
А15 1 | А15 4 |
В1 . | В1 . |
В2 (1;1;1). | В2 (1; 0; 2). |
В3 – 26 | В3 -20. |
nsportal.ru
Контрольная работа по теме ” Матрицы. Действия с матрицами. Решение систем уравнений методом Гаусса, Крамера, матричным методом.”
Просмотр содержимого документа
«Контрольная работа по теме ” Матрицы. Действия с матрицами. Решение систем уравнений методом Гаусса, Крамера, матричным методом.”»
Контрольная работа
По теме: «Матрица. Определители. Решение систем уравнений»
1. Даны матрицы:
A B
С D
E K
Вычислить:
(2A – 4B) * C 16) B * (-4A +2C)
(4B – 2A) * K 17) C * (2B – 3D)
(2C – 3D) * E 18) C * (2K – 3E)
(2D – 3C) * K 19) C * (-4D – 2B)
A * (2C + 3D) 20) D * (-3C + 3B)
B * (3A – 2E) 21) D * (-2E – 2A)
(4D – 2C) * E 22) D * (5B – 4C)
(-2E + 3D) * C 23) E * (-4B + 2A)
(-2K + B) * D 24) E * (-4K – 2C)
10) (-2A – K) * B 25) E * (2K – 4C)
11)A * (3B + 2C) 26) E * (5A + 3B)
12) A * (2C – 4K) 27) K * (5B – 3A)
13)A * (-2C + 3K) 28) K * (2D + 3C)
14) B * (2E – 3D) 29) K * (2E + 2D)
15) B * (2D + 3E) 30) K * (-3A + 2D)
2. Решить систему уравнений:
1) Матричным способом
2) Методом Гаусса
3) Методом Крамера
Вариант:
1) 11) 21)
2x + y +z =7 5x – 3y – z = -6 -x – y + z = -4
x + 2y + 7z = 8 3x + y + 2z = 7 -2x + y – 3z = 3
x + y + 2z = 9 y + z = 4 4x – y – 3z = 5
2) x + 2y + 3z = 3 12) 3x + 4y – 3z = 11 22) 5x + y – z = -2
3x + y + 2z = 7 2x + y – 3z = 3 3x – y + 2z = 5
2x + 3y + z = 3 -3x – y + 5z = -3 2x + 2y – z = -1
3) 6x + 2y – z = 2 13) x – y – z = 0 23) 7x – 3y – 2z = 6
4x – y + 3 = -3 -x + 3y + 2z = 3 x + 3y + z = 9
3x + 2y -2z = 3 4x – y + 3z = -1 2x – y – 2z = 0
4) 14) 24)
2x + y + 3z = 13 -x – y + 2z = -2 x + y = 3
x + y + z = 6 -3x + у +5z = 1 -x – y – 4z = 1
3x + y + z = 8 2x + y + z = 7 5x – 2y + z = 0
5) 2x + y – z = 6 15) 4x – y + 3z = 8 25) 4x + 4y + z = 7
3x – y + 2z = 5 -x + 3y + 2z = 9 3x – y + z = 2
4x + 2y – 5z = 9 x – y – z = -4 -2x – y + 2z = 5
6) x – 2y + 3z = 6 16) 5x – 4y + z = -4 26) 2x + 2y + z = 9
2x + 3y – 4z = 7 2x – y – z = 1 2x + y – 3z = 3
3x – 2y – 5z = 6 3x – y + 2z = -1 -x – 2y + 2z = -4
7) 5x + y – 3z = -2 17) 3x – y + 2z = 5 27) 3x – 4y + z = -6
4x + 3y + 2z = 16 2x – y + z = 2 x + 3y + 4z = 4
2x – 3y + z = 17 5x – 4y + 2z = 2 2x – 3y – 2z = -2
8) 18) 28)
3x – 2y + z = 10 x – y + 2z = 2 11x + 2y – z = -1
x + 5y – 2z = -15 2x – 3y + z = –1 10x + z = 3
2x – 2y – z = 3 -3x + y – z = -5 x – y + z = 2
9) 5x – 3y + 4z = 11 19) 2x + y – 2z = 4 29) 4x + y – 5z = 5
2x – y – 2z = -6 -2x + y + z = -1 x – 5y + 5z = -3
3x – 2y + z = 2 -3x – y + 3z = -5 -x + y – z = -1
10) 5x – 3y + 4z = 6 20) -x + y + 2z = 2 30) 2x + 2y – z = -1
2x + y + z = 0 3x – 2y – z = 1 2x – y = -1
x – 2y + z = 0 5x + y – z = 10 2x + 3y +5z = 18
multiurok.ru
Примеры решения заданий контрольной работы № 1 Матрицы и определители
Сумма (разность) определяется только для матриц одинаковой размерности. Пусть
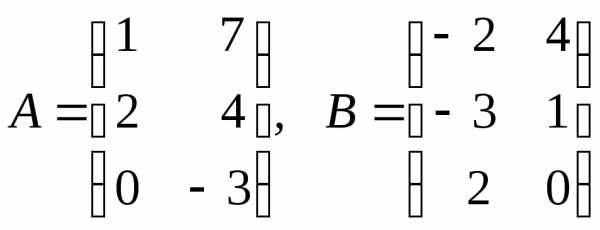 .
Тогда
.
.
Тогда
.
При умножении матрицы А на число 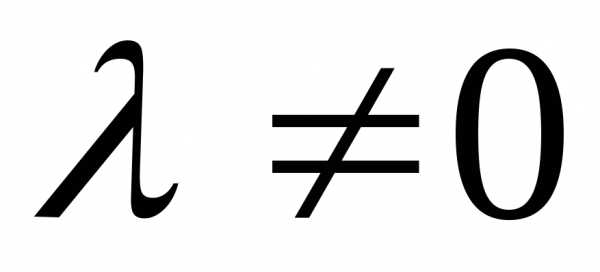 нужно все элементы матрицыА умножить на это число.
нужно все элементы матрицыА умножить на это число.
Если 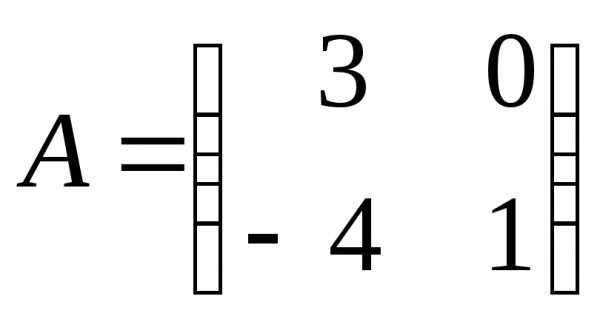 ,
то.
,
то.
Произведением матрицы 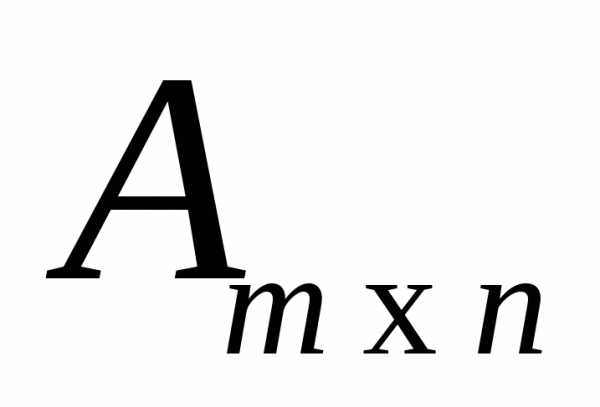 на матрицу
на матрицу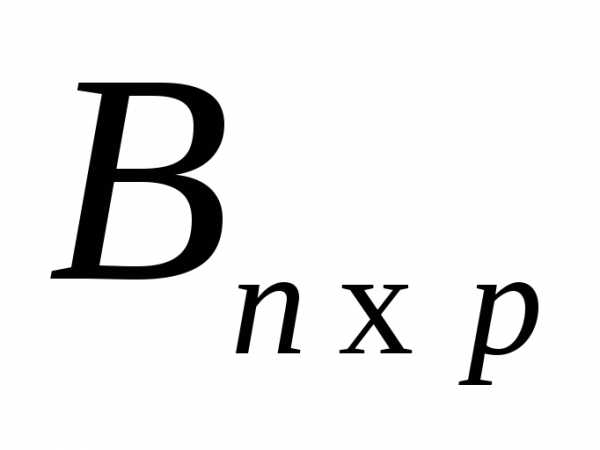 называется матрица
называется матрица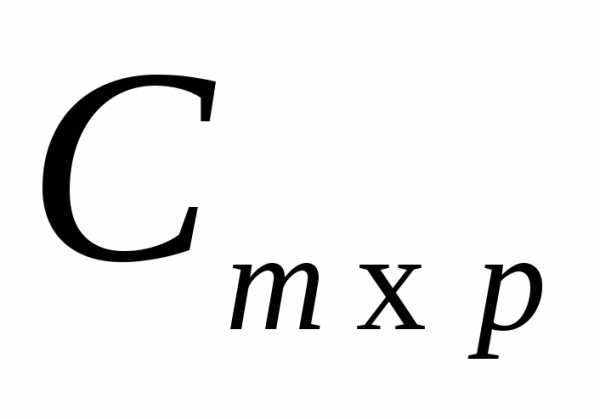 ,
элементы которой находятся по формуле
,
элементы которой находятся по формуле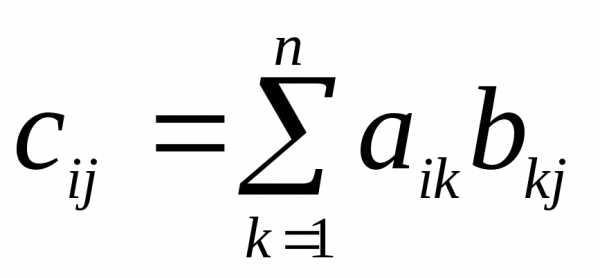 .
В общем случае
.
В общем случае
Пусть 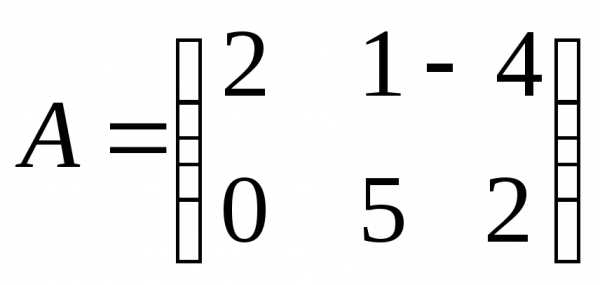 ,
,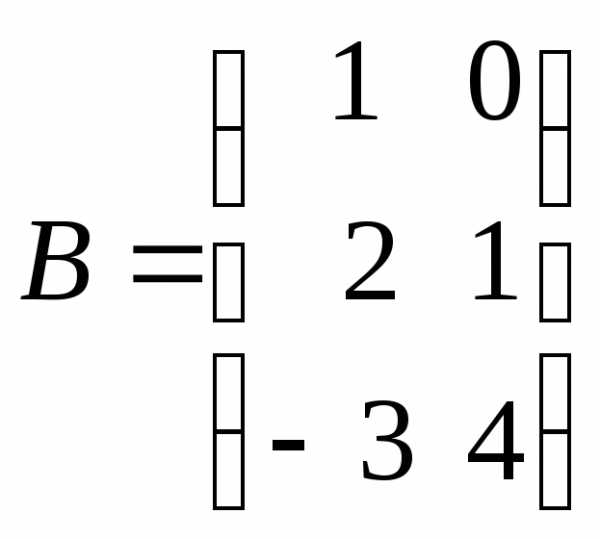 .
.
Имеем:, где
следовательно
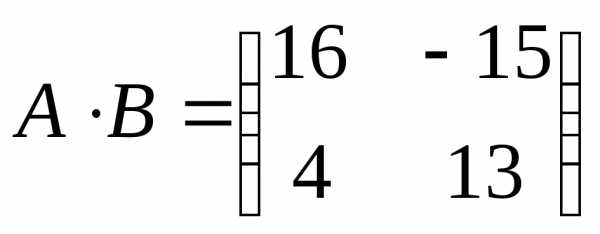 .
.
Определителем второго порядка называется число, равное . (1.1)
Примеры.
1) ; 2).
Определителем третьего порядка называется число, равное сумме произведений элементов его первой строки на их алгебраические дополнения.
. (1.2)
Аналогично определяются определители более высоких порядков.

Вычислим определитель, разложив его по элементам первой строки:
.
Определители третьего порядка можно вычислить и по правилу треугольников (правилу Саррюса) по схеме:
. (1.3)
Пример.
Системы линейных уравнений
Метод Крамера
Пример. Решить систему линейных уравнений по формулам Крамера
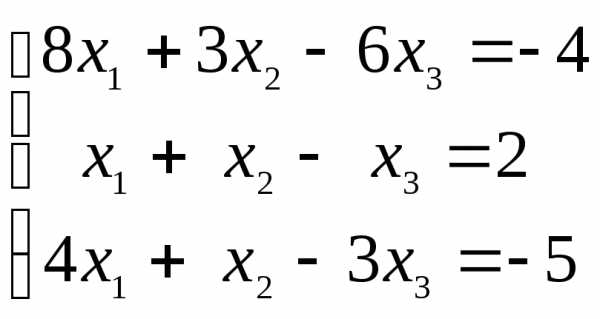 .
.
Вычислим определитель
системы 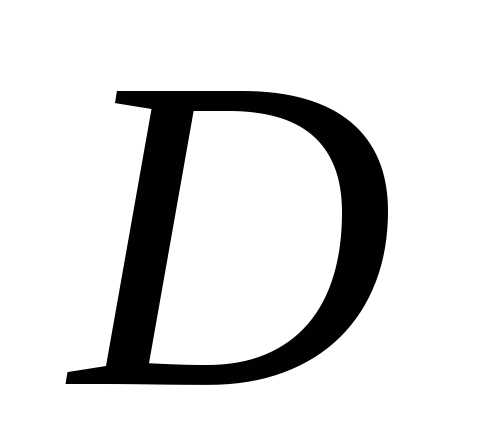
Вычислим определители D1, D2, D3, заменяя в определителе D элементы первого, второго и третьего столбцов соответственно элементами столбца из свободных членов.
.
Таким образом,
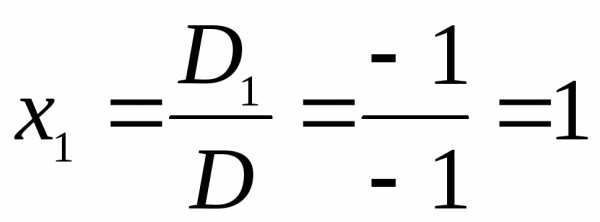 , х2=
, х2=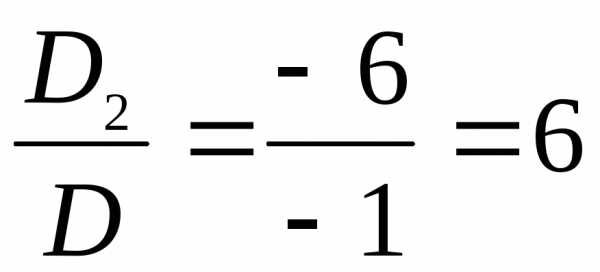 ,
,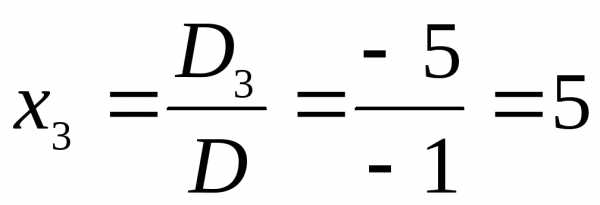 .
.
Итак,
х1=1, х2=6, х3=5.
Метод обратной матрицы
Определение. Матрица А называется невырожденной, если D=det А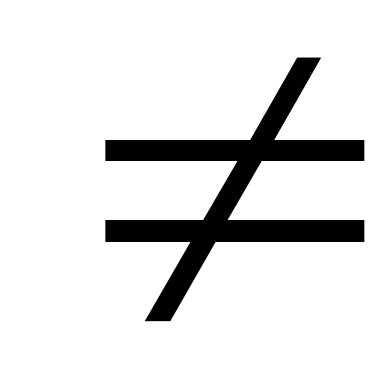 0.
0.
Каждая невырожденная
матрица А имеет обратную 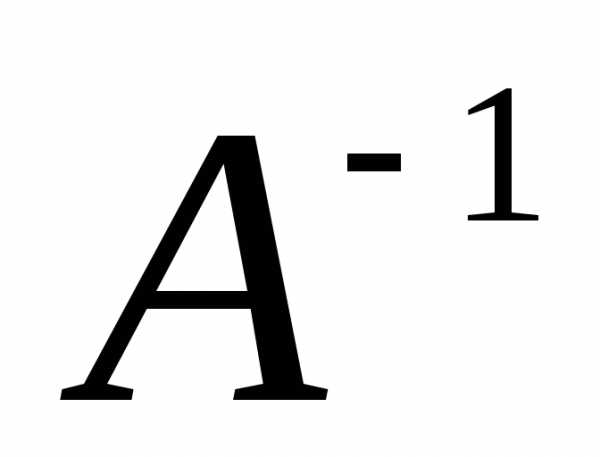 ,
причем для матрицы
,
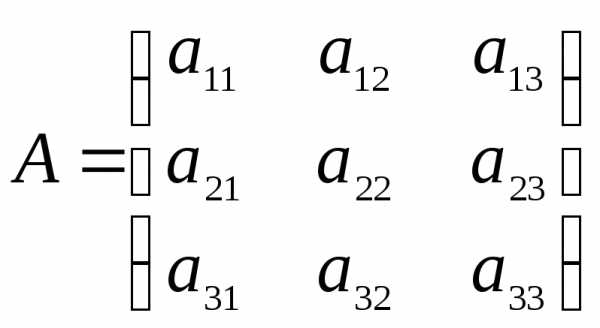
причем для матрицы третьего порядка с элементами
третьего порядка с элементами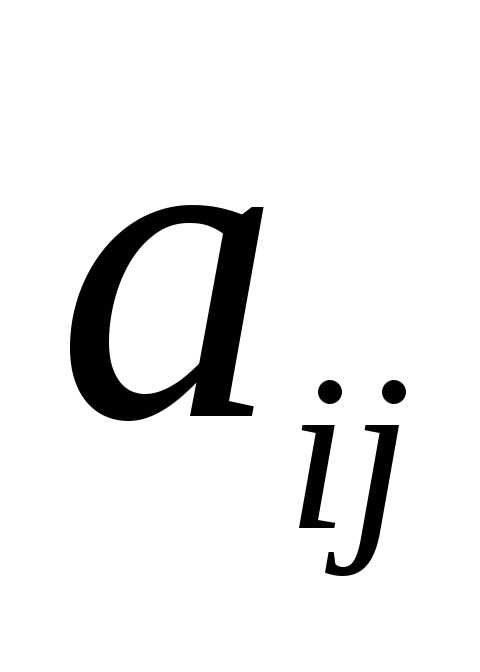 :
: обратная матрица
обратная матрица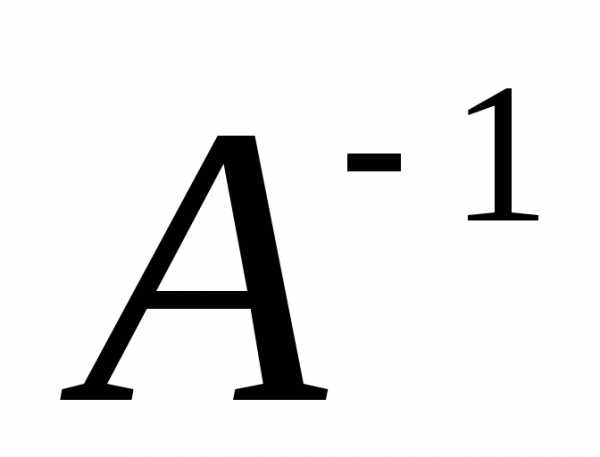 имеет вид:
имеет вид:
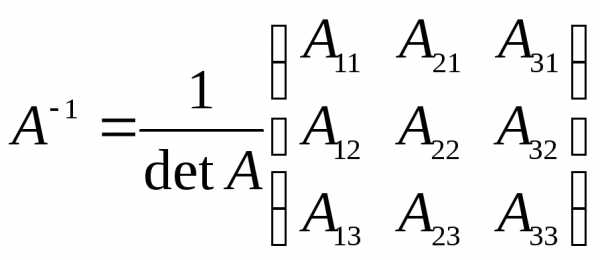 , (1.4)
, (1.4)
где А11, А12 ,…, А33 –
алгебраические
дополнения соответствующих элементов 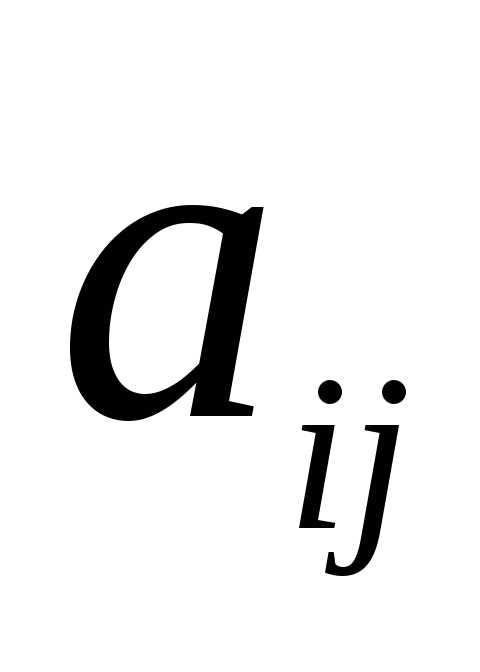 матрицы
матрицы ,
располагаемые по столбцам в новой
матрице.
,
располагаемые по столбцам в новой
матрице.
Пример. Решить систему уравнений матричным методом:
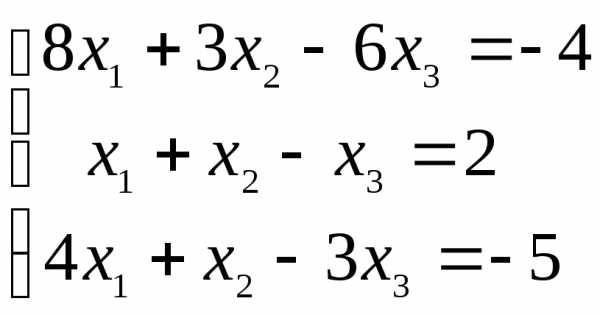 .
Имеем: А=
.
Имеем: А=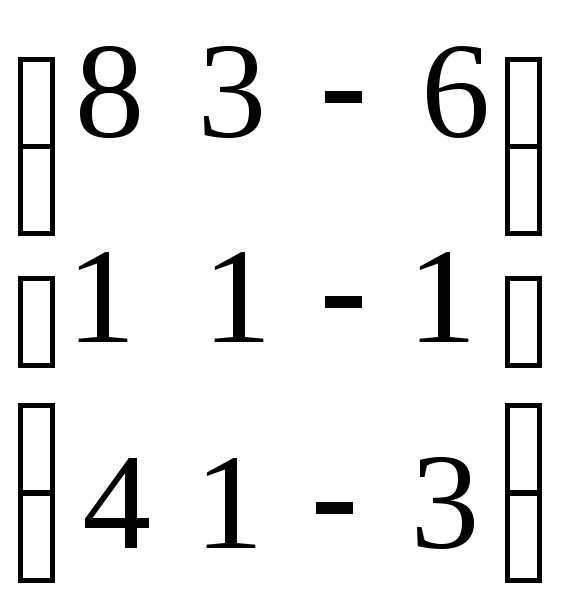 ,Х=
,Х=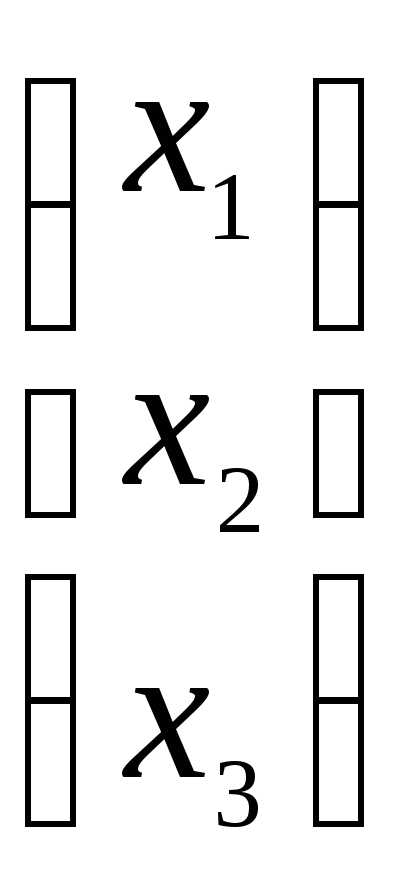 ,Н=
,Н=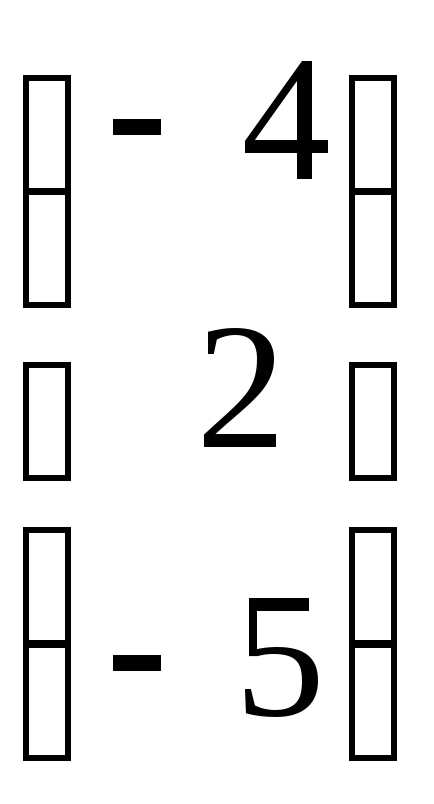 .
.
, .
Для нахождения обратной матрицы А-1 вычисляем все алгебраические дополнения элементов матрицы А:
, ,,
, ,,
, ,.
Составляем обратную матрицу (1.4):
.
Тогда
.
Таким образом, х1=1, х2=6, х3=5.
Метод Жордана-Гаусса последовательного исключения переменных
Пример. Решить систему методом Жордана-Гаусса. Найти общее, частное и базисное решение системы.
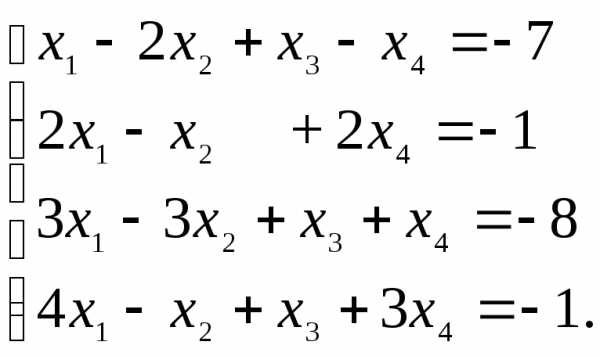
Составляем расширенную матрицу системы и проводя элементарные преобразования над строками матрицы исключаем переменные в соответствующих этой матрице системах линейных уравнений. В результате преобразований исходная матрица сводится к трапецеидальному виду. Преобразуем расширенную матрицу системы:
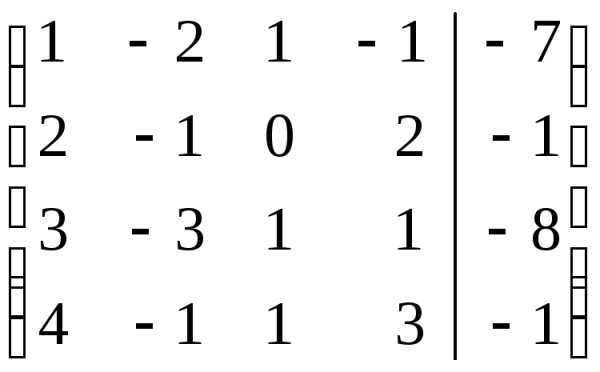
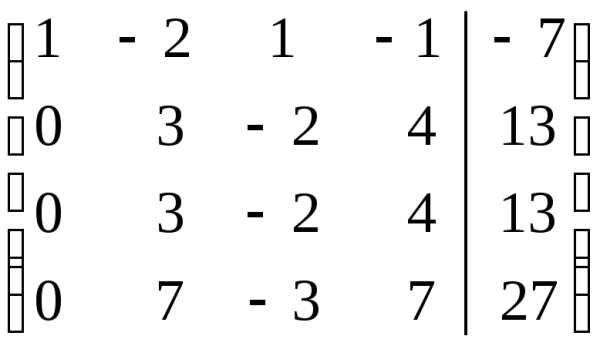
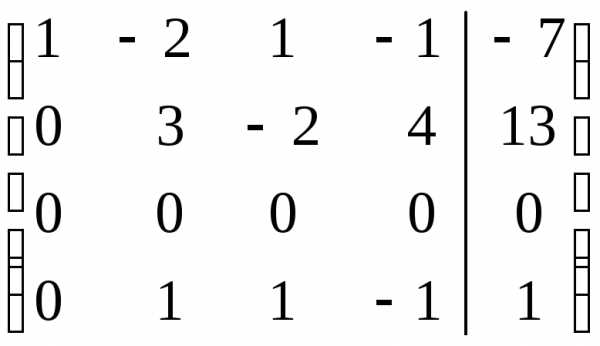

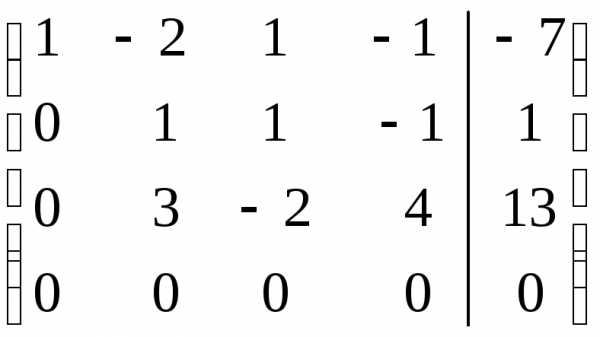


Поясним сделанные преобразования:
Первую строку умножим последовательно на (- 2), (-3), (-4) и прибавим ко второй, третьей и четвертой строкам соттветственно.
Вторую строку умножаем на (-1), (-2) и прибавим к третьей и четвертой строке соответственно.
Поменяем местами вторую и четвертую строчку.
Вторую строку умножаем на 2 и на (-3) и прибавим к первой и третьей строке соответственно. Удаляем четвертую – нулевую строку.
Третью строку умножаем на на (-1) и на (-3) и прибавляем ко второй и первой строке соответственно.
Используя последнюю матрицу, эквивалентную исходной, получаем равносильную систему уравнений следующего вида:
 х1+
х1+ +1,2х4 = 1
+1,2х4 = 1
х2+ +0,4х4 = 3
х3+ −1,4х4 =− 2.
Переменные х1,
х2,
х3
х1,
х2,
х3 назовём
базисными, переменную х4 − свободной. Полагая х4=0,
непосредственно находим базисное
решение: х1=1, х2=3, х3=−2.При х4=5,
получим частное решение: х3=5, х2=1, х1=−5.
При х4= t, где t
R,
получим общее решение системы:
назовём
базисными, переменную х4 − свободной. Полагая х4=0,
непосредственно находим базисное
решение: х1=1, х2=3, х3=−2.При х4=5,
получим частное решение: х3=5, х2=1, х1=−5.
При х4= t, где t
R,
получим общее решение системы:
х1=1-1,2 t
х2=3-0,4 t
х3=-2+1,4 t.
studfiles.net
тест Матрицы и определители
Линейная алгебраАнастасия
Тест по теме «Матрицы и определители»
1. Упорядоченная совокупность элементов, у которых номер строки и номер столбца совпадают называется:
– побочной диагональю матрицы
– ненулевой матрицей
+ главной диагональю матрицы
– диагональной матрицей
2. При перестановке дух строк определитель
– не изменится
+ меняет свой знак
– станет отрицательным
– увеличится
3. Если к элементам любой строки прибавить соответствующие элементы другой строки, умноженные на любое число, то определитель
+ не изменится
– умножится на это число
– поменяет знак
– увеличится
4. Когда существует обратная матрица ?
– когда исходная матрица А квадратная
+ когда исходная матрица А невырожденная
– когда исходная матрица А вырожденная
– когда определитель исходной матрицы А равен 0
5. Рангом матрицы называется
– наибольший порядок нулевых миноров
– произведение числа строк на число столбцов матрицы
– число строк матрицы
+ наибольший порядок отличных от нуля миноров
6. Такое свойство операций над матрицами как ассоциативность относительно сложения, можно записать в виде:
+ (А+В)+С=А+(В+С)
– А+В=В+А
– α(А+В)=αА+αА
– (α+β)А=αА+βА
7. Сколько обратных матриц может существовать для данной?
– только одна
+ ни одной или одна
– любое количество
– только две
8. Если матрица имеет две одинаковые строки, то её определитель
– равен сумме элементов, стоящих на главной диагонали
– равен сумме элементов, стоящих на побочной диагонали
+ равен нулю
– все ответы неверны
9. При умножении матрицы А на матрицу В должно соблюдаться условие
+ число столбцов матрицы А должно равняться числу строк матрицы В
– число столбцов матрицы А равно числу столбцов матрицы В
– число строк матрицы А равно числу строк матрицы В
– число строк матрицы А равно числу столбцов матрицы В
10. Что не относится к элементарным преобразованиям матрицы?
– перестановка любых двух строк матрицы
– умножение любой строки на производное, отличное от 0 число
– сложение любой строки с другой строкой, умноженной на произвольное число, отличное от нуля
+ замена элементов строки (столбца) произвольными числами
11. Произведение матрицы А размерностью на матрицу В существует, если размерность матрицы В равна
–
+
–
–
12. Даны матрицы А=и В=. Тогда матрица С=А×В имеет вид
+ – (11 8 24)
– (11 9 27) –
13. Определитель равен
– (-17)
– (-23)
– 23
+ 17
14. Для матрицы существует обратная, если она равна
– +
– –
15. Чему будет равен определитель третьего порядка матрицы
+ 1
– 0
– (-1)
– 2
16. Найти результат умножения матрицы А= на число 5.
+
17. Если протранспонировать матрицу А=, то будет равняться:
+
18. Для матрица А=указать сумму элементов, расположенных на побочной диагонали.
+ 2
0
айти определитель четвертого порядка матрицы А=.
(-4)
10
(-7)
8
20. Для матриц А=и В=найти элемент произведения С=В×А.
+ 4
7
10
21
studfiles.net
| Почему учителям и воспитателям следует проходить курсы повышения квалификации и профессиональной переподготовки в учебном центре «Инфоурок» ?• Огромный каталог: 677 курсов профессиональной переподготовки и повышения квалификации;• Очень низкая цена, при этом доступна оплата обучения в рассрочку – первый взнос всего 10%, оставшуюся часть необходимо оплатить до конца обучения; • Курсы проходят полностью в дистанционном режиме (форма обучения в документах не указывается); • Возможность оплаты курса за счёт Вашей организации. • Дипломы и Удостоверения от проекта «Инфоурок» соответствуют всем установленным законодательству РФ требованиям. (Согласно ФЗ «Об образовании в Российской Федерации» от 2012 года). |
infourok.ru

 Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда: 4 слайд
Описание слайда: 4 слайд  Описание слайда: 5 слайд
Описание слайда: 5 слайд 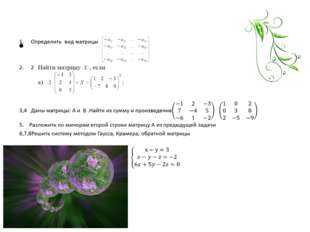 Описание слайда: 6 слайд
Описание слайда: 6 слайд  Описание слайда: 7 слайд
Описание слайда: 7 слайд  Описание слайда: 8 слайд
Описание слайда: 8 слайд 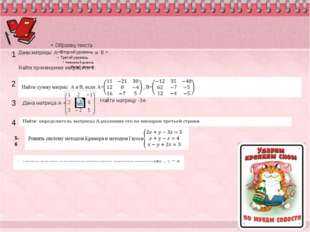 Описание слайда:
Описание слайда: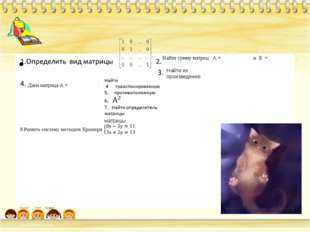 Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: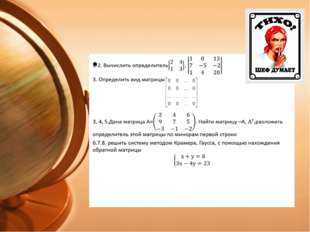 Описание слайда:
Описание слайда: