В физике работа и энергия – Почему работа и энергия считаются разными в физике, когда единицы одинаковы?

Глава 3 Работа и энергия

§11. Энергия, работа, мощность

Энергия — универсальная мера различ­ных форм движения и взаимодействия. С различными формами движения мате­рии связывают различные формы энергии: механическую, тепловую, электромагнит­ную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холод­ное), в других — переходит в иную фор­му (например, в результате трения меха­ническое движение превращается в тепло­вое). Однако существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной последним телом.

Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы

количественно характеризовать процесс обмена энергией между взаимодействую­щими телами, в механике вводится по­нятие

работы силы.

Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол а с на­правлением перемещения, то работа этой силы равна произведению проекции силы F_s на направление перемещения (F_s =Fcos), умноженной на перемещение точки приложения силы:

A = F_ss = F_scos. (11.1)

В общем случае сила может изменять­ся как по модулю, так и по направлению, поэтому формулой (11.1) пользоваться не­льзя. Если, однако, рассмотреть элемен­тарное перемещение dr, то силу F можно считать постоянной, а движение точки ее

22

приложения — прямолинейным. Элемен­тарной работой силы F на перемещении dr называется скалярная величина

dА =Fdr = Fcos•ds=F_sds,

где а — угол между векторами F и dr; ds = |dr| — элементарный путь; F_s — про­екция вектора F на вектор dr (рис. 13).

Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сум­ма приводится к интегралу

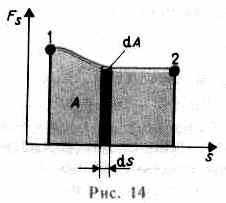
Для вычисления этого интеграла надо знать зависимость силы F_s от пути s вдоль траектории 1—2. Пусть эта зависимость представлена графически (рис. 14), тогда искомая работа А определяется на графи­ке площадью закрашенной фигуры. Если, например, тело движется прямолинейно, сила F=const и =const, то получим

где s — пройденный телом путь (см. также формулу (11.1)).

Из формулы (11.1) следует, что при </2 работа силы положительна, в этом случае составляющая

F_s совпадает

по направлению с вектором скорости дви­жения v (см. рис. 13). Если >/2, то работа силы отрицательна. При =/2 (сила направлена перпендикулярно пере­мещению) работа силы равна нулю.

Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой в 1 Н на пути в 1 м (1 Дж = 1 Н•м).

Чтобы охарактеризовать скорость со­вершения работы, вводят понятие мощ­ности:

N=da/dt. (11.3)

За время dt сила F совершает работу Fd

r, и мощность, развиваемая этой силой, в данный момент времени

N=Fdr/dt=Fv

т. е. равна скалярному произведению век­тора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная.

Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа в 1 Дж (1 Вт = 1 Дж/с).

studfiles.net

Как связаны работа и энергия? — Науколандия

Энергия — это физическая величина, которая определяет способность тела (или системы тел) совершить работу. То есть, чем большей энергией обладает тело, тем большую работу оно может совершить.

Единицей измерения энергии в системе СИ, также как и работы, является джоуль (Дж).

Как известно, работа есть произведение силы, действующей на тело, и пути, пройденного телом под действием этой силы (A = Fs). Таким образом, можно сказать, что энергия определяет способность тела двигаться.

Однако тело может обладать способностью совершать движение, но не реализовывать его в настоящий момент или реализовать еще не полностью. В таком случае говорят, что тело обладает потенциальной энергией. Потенциальная энергия определяет способность системы тел (или частей одного тела) совершить работу путем изменения их взаимного положения.

Например, поднятый вверх мяч в момент его отпускания обладает потенциальной энергией пока не упадет на поверхность. Потенциальная энергия здесь максимальна в самой верхней точке положения мяча. В момент, когда мяч касается земли, потенциальная энергия от взаимодействия мяча и силы тяжести Земли равна нулю.

Обратите внимание на фразу «потенциальная энергия от взаимодействия мяча и силы тяжести Земли». Потенциальная энергия существует как следствие взаимодействия тел. Например, на все тела близ Земли действует ее сила тяжести. Поэтому все поднятые над поверхностью тела обладают потенциальной энергией, которая «заставляет» их совершать движение, падая на поверхность Земли.

В качестве другого примера можно привести пружину. В сжатом или растянутом состоянии в ней возникает сила упругости. Эта сила приводит к тому, что пружина возвращается в исходное состояние. Однако в момент, когда она еще в него не вернулась, пружина обладает потенциальной энергией, то есть возможностью совершать движение. Здесь взаимодействуют между собой разные части пружины, перемещенные относительно друг друга.

Когда мяч, упав, касается поверхности, то в результате силы удара сжимаются сам мяч и поверхность. Возникают силы упругости, которые снова заставляют мяч подняться вверх.

Когда тело движется, то оно способно переместить другое тело. Например, сжатая пружина, распрямляясь, может толкнуть шарик, т. е. непосредственно совершить работу.

Кинетическая энергия определяется работой, которую совершает тело, двигаясь до полной своей остановки.

Чем больше скорость тела в данный момент и его масса, тем большей кинетической энергией оно обладает, потому что более массивное и быстро движущееся тело сильнее может толкать другое тело.

Мяч, падая, достигает максимальной своей скорости приближаясь к поверхности. Здесь его потенциальная энергия уменьшается, а кинетическая возрастает. Когда мяч непосредственно касается поверхности, его кинетическая энергия равна нулю, а потенциальная (из-за сжатия тел) на возможном максимуме. Оторвавшись от земли, мяч обладает максимальной кинетической энергией и минимальной потенциальной. Поднимаясь, его кинетическая энергия падает, но растет потенциальная. В процессе полета мяч обладает и потенциальной и кинетической энергией. Однако обе они не на максимуме.

Таким образом, кинетическая и потенциальная энергии тела могут превращаться одна в другую. Их сумма представляет собой полную механическую энергию тела. Обладая потенциальной энергией тело обладает способностью совершить работу, а обладая кинетической энергией, тело совершает работу.

Потенциальная энергия поднятого над землей груза равна работе, которую совершает этот груз, падая с высоты:

E_п = A = F_тh = mgh

Кинетическая энергия тела определяется по формуле:

E_к = mv²/2

scienceland.info

Работа, энергия и мощность – вспоминаем физику

Дата публикации: 1 февраля 2015

В текстах, публикуемых на этом сайте, часто встречаются различные термины, которые являются названиями физических величин. Многое мы изучали еще в школьном курсе физике, но знания имеют свойство забываться без постоянного употребления. В серии заметок, объединенных под общим заголовком «Вспоминаем физику» (можно было бы назвать «Снова в школу») мы постараемся напомнить вам, что означают основные термины, какие физические величины за этими терминами скрываются, как они связаны между собой, в каких величинах они измеряются. В общем, дать те основы, которые нужны для понимания публикуемых материалов.

Сайт нас в целом посвящен методам и технологиям получения энергии (конкретно, из возобновляемых источников). Энергия нужна людям для отопления и освещения собственных жилищ, для того, чтобы приводить в движение различные механизмы, которые совершают полезную для людей работу. То есть нам нужно получить в конечном итоге один из трех видов энергии — тепловую, механическую и энергию света. Как будет сказано ниже, в физике различают еще несколько видов энергии, но для нас важны в первую очередь эти три вида. Закончу с предисловиями и приведу те определения энергии, которые приняты в физике.

Работа и энергия

Еще из школьного курса физики (а школу я окончил 50 лет назад) я помню утверждение «Энергия является мерой способности физической системы совершить работу». Википедия дает менее понятное определение, утверждая, что

«Эне́ргия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется в этой системе на протяжении времени, в течение которого система будет являться замкнутой. Это утверждение носит название закона сохранения энергии.»

Энергия является скалярной величиной, для измерения которой применяются несколько разных единиц. Нам наиболее интересны джоуль и киловатт-час.

Джо́уль (русское обозначение: Дж; международное: J) — единица измерения работы, энергии и количества теплоты в Международной системе единиц (СИ). Джоуль равен работе, совершаемой при перемещении точки приложения силы, равной одному ньютону, на расстояние одного метра в направлении действия силы. В электричестве джоуль означает работу, которую совершают силы электрического поля за 1 секунду при напряжении в 1 вольт для поддержания силы тока в 1 ампер.

Впрочем, мы не будем углубляться в основы физики, выясняя, что такое сила и что такое один ньютон, просто примем понятие «энергия» за основу и запомним, что некое количество джоулей характеризует энергию, работу и количество теплоты. Еще одной величиной, с помощью которой измеряют количество энергии, является киловатт-час.

Килова́тт-час (кВт⋅ч) — внесистемная единица измерения количества произведенной или потреблённой энергии, а также выполненной работы. Используется преимущественно для измерения потребления электроэнергии в быту, народном хозяйстве и для измерения выработки электроэнергии в электроэнергетике.

Следует заметить, что правильно писать именно «кВт⋅ч» (мощность, умноженная на время). Написание «кВт/ч» (киловатт в час), часто употребляемое во многих СМИ и даже иногда в официальных документах, неправильно. Такое обозначение соответствует изменению мощности в единицу времени (что обычно никого не интересует), но никак не количеству энергии. Столь же распространённая ошибка — использовать «киловатт» (единицу мощности) вместо «киловатт-час».

В последующих статьях мы будем использовать джоуль и киловатт-час как единицы для оценки количества энергии или работы, имея в виду, что один киловатт-час равен 3,6·10⁶ джоулей.

С точки зрения интересующих нас тем именно свойство энергии совершать работу является основополагающим. Мы не будем выяснять, как физика трактует понятие «работа», будем считать, что это понятие является первоначальным и не определяемым. Только еще раз подчеркнем, что количественно энергия и работа выражаются в одних единицах.

В зависимости от вида энергии или работы величина энергии рассчитывается разными способами:

В механике: сила, умноженная на длину	E ~ F·l
В термодинамике: давление, умноженное на объём	E ~ P·V
Импульс, умноженный на скорость	E ~ p·v
Масса, умноженная на квадрат скорости	E ~ m·v²
В электростатике: заряд, умноженный на напряжение	E ~ q·U
Мощность, умноженная на время	E ~ N·t

Формы и виды энергии

Поскольку энергия, как сказано выше, является только мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие, различные формы энергии выделяются в соответствии с различными формами движения материи. Таким образом, в зависимости от уровня проявления, мож­но выделить следующие формы энергии:

• энергия макромира — гравитационная или энергия притяжения тел,
• энергия взаимодействия тел — механическая,
• энергия молекулярных взаимодействий — тепловая,
• энергия атомных взаимодей­ствий — химическая,
• энергия излучения — электромагнит­ная,
• энергия, заключенную в ядрах атомов, — ядерная.

Гравитационная энергия — энергия системы тел (частиц), обусловленная их взаимным гравитационным тяготением. В земных условиях, это, например, энергия, «запасенная» телом, поднятым на опреде­ленную высоту над поверхностью Земли — энергия силы тя­жести. Таким образом, энергию, запасенную в водохранилищах гидроэлектростанций, можно отнести к гравитационной энергии.

Механическая энергия — проявляется при взаимодей­ствии, движении отдельных тел или частиц. К ней относят энергию движения или вращения тела, энер­гию деформации при сгибании, растяжении, закручивании, сжатии упругих тел (пружин). Эта энергия наиболее широко используется в различных машинах — транспортных и техно­логических.

Тепловая энергия — энергия неупорядоченного (хаотичес­кого) движения и взаимодействия молекул веществ. Тепловая энергия, получаемая чаще всего при сжигании различных видов топлива, широко применяется для отопле­ния, проведения многочисленных технологических процес­сов (нагревания, плавления, сушки, выпаривания, перегон­ки и т. д.).

Химическая энергия — это энергия, «запасенная» в атомах веществ, которая высвобождается или поглощается при хими­ческих реакциях между веществами. Химическая энергия либо выделяется в виде тепловой при проведении экзотермических реакций (например, горении топлива), либо преобразуется в электрическую в гальваничес­ких элементах и аккумуляторах. Эти источники энергии ха­рактеризуются высоким КПД (до 98 %), но низкой емкостью.

Электромагнитная энергия — это энергия, порождаемая взаимодействием электрического и магнитного по­лей. Ее подразделяют на электрическую и магнитную энергии. Электрическая энергия — энергия движущихся по элек­трической цепи электронов (электрического тока).

Электромагнитная энергия проявляется также в виде электромагнит­ных волн, то есть в виде излучения, включающего видимый свет, инфракрасные, ультрафио­летовые, рентгеновские лучи и радиоволны. Таким образом, один из видов электромагнитной энергии — это энергия излучения. Излучение переносит энергию в форме энергии электромагнитной волны. Когда излучение поглощается, его энергия преобразуется в другие формы, чаще всего в теплоту.

Ядерная энергия — энергия, локализованная в ядрах ато­мов так называемых радиоактивных веществ. Она высвобож­дается при делении тяжелых ядер (ядерная реакция) или син­тезе легких ядер (термоядерная реакция).

В эту классификацию несколько не укладываются известные нам со школы понятия потенциальной и кинетической энергии. Современная физика считает, что понятия кинетической и потенциальной энергий (а также энергии диссипации) это не формы, а виды энергии:

Кинетическая энергия — энергия, которой обладают тела вследствие своего движения. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением. Когда тело не движется, кинетическая энергия равна нулю.

Потенциальная энергия — энергия, обусловленная взаимодействием различных тел или частей одного и того же тела. Потенциальная энергия всегда определяется положением тела относительно некоторого источника силы (силового поля).

Энергия диссипации (то есть рассеяния) — переход части энергии упорядоченных процессов в энергию неупорядоченных процессов, в конечном счёте — в теплоту.

Дело в том, что каждая из перечисленных выше форм энергии может проявляться в виде потенциальной и кинетической энергии. То есть виды энергии должны трактоваться в обобщенном смысле, ибо они относятся к любой форме движения и, следовательно, к любой форме энергии. Например, имеется кинетическая электрическая энергия, и это не то же самое, что кинетическая механическая энергия. Это кинетическая энергия движения электронов, а не кинетическая энергия механического движения тела. Точно так же потенциальная электрическая энергия это не то же самое, что потенциальная механическая энергия. А химическая энергия складывается из кинетической энергии движения электронов и электрической энергии их взаимодействия друг с другом и с атомными ядрами.

Вообще, насколько я понял при подготовке этого материала, пока не существует общепринятой классификации форм и видов энергии. Впрочем, возможно нам и не нужно до конца разбираться в этих физических понятиях. Важно только помнить, что энергия — это не какая-то реальная материальная субстанция, а только мера, предназначенная для оценки перемещения некоторых форм материи или преобразования одной формы материи в другую.

С понятием энергии и работы неразрывно связано понятие мощности.

Мощность

Мо́щность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

В Международной системе единиц (СИ) единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.

Мощность характеризует способность того или иного устройства совершать работу или производить энергию в течение определенного промежутка времени. Связь между мощностью, энергией и временем выражается следующим соотношением:

Киловатт-час (напомним, что это единица измерения энергии) равен количеству энергии, потребляемой (производимой) устройством мощностью один киловатт (единица мощности) в течение одного часа (единица времени).

Отсюда и уже упомянутое выше равенство 1 кВт⋅ч = 1000 Вт ⋅ 3600 с = 3,6·10⁶ Дж = 3,6 МДж.

Из трех рассмотренных на этой странице единиц именно мощность представляет для нас наибольший интерес, поскольку эта величина будет нам встречаться при рассмотрении и сравнении различных ветро- или гидро-генераторов и солнечных панелей. В этих случаях мощность характеризует способность этих устройств производить энергию. И наоборот, указание мощности на многих бытовых электроприборах характеризует потребление энергии этими приборами. Если мы хотим обеспечить некоторую совокупность бытовых приборов энергией, мы должны сопоставить суммарную потребляемую этими приборами мощность с суммарной мощностью, которую можем получить от производителей энергии.

Но подробнее о мощности мы поговорим в следующих статьях, посвященных конкретным видам энергии.  И начнем с электрической энергии, рассмотрим, какими величинами характеризуется электричество и в каких единицах оно измеряется.

altenergiya.ru

Работа, мощность, энергия – Физика – Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Механическая работа

К оглавлению…

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Работой, совершаемой постоянной силой F, называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы F и перемещения S:

Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.

Если же сила изменяется с течением времени, то для нахождения работы строят график зависимости силы от перемещения и находят площадь фигуры под графиком – это и есть работа:

Примером силы, модуль которой зависит от координаты (перемещения), может служить сила упругости пружины, подчиняющаяся закону Гука (F_упр = kx).

 

Мощность

К оглавлению…

Работа силы, совершаемая в единицу времени, называется мощностью. Мощность P (иногда обозначают буквой N) – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

По этой формуле рассчитывается средняя мощность, т.е. мощность обобщенно характеризующая процесс. Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:

По этой формуле мы можем рассчитать мгновенную мощность (мощность в данный момент времени), если вместо скорости подставим в формулу значение мгновенной скорости. Как узнать, какую мощность считать? Если в задаче спрашивают мощность в момент времени или в какой-то точке пространства, то считается мгновенная. Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.

КПД – коэффициент полезного действия, равен отношению полезной работы к затраченной, либо же полезной мощности к затраченной:

Какая работа полезная, а какая затраченная определяется из условия конкретной задачи путем логического рассуждения. К примеру, если подъемный кран совершает работу по подъему груза на некоторую высоту, то полезной будет работа по поднятию груза (так как именно ради нее создан кран), а затраченной – работа, совершенная электродвигателем крана.

Итак, полезная и затраченная мощность не имеют строгого определения, и находятся логическим рассуждением. В каждой задаче мы сами должны определить, что в этой задаче было целью совершения работы (полезная работа или мощность), а что было механизмом или способом совершения всей работы (затраченная мощность или работа).

В общем случае КПД показывает, как эффективно механизм преобразует один вид энергии в другой. Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:

 

Кинетическая энергия

К оглавлению…

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела (энергией движения):

То есть если автомобиль массой 2000 кг движется со скоростью 10 м/с, то он обладает кинетической энергией равной Е_к = 100 кДж и способен совершить работу в 100 кДж. Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.

Тело обладает энергией, если способно совершить работу. Например, движущееся тело обладает кинетической энергией, т.е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.

Физический смысл кинетической энергии: для того чтобы покоящееся тело массой m стало двигаться со скоростью v необходимо совершить работу равную полученному значению кинетической энергии. Если тело массой m движется со скоростью v, то для его остановки необходимо совершить работу равную его первоначальной кинетической энергии. При торможении кинетическая энергия в основном (кроме случаев соударения, когда энергия идет на деформации) «забирается» силой трения.

Теорема о кинетической энергии: работа равнодействующей силы равна изменению кинетической энергии тела:

Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Применять данную теорему удобно в задачах на разгон и торможение тела.

 

Потенциальная энергия

К оглавлению…

Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.

Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.

Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:

Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня). Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:

Часто в задачах на энергию приходится находить работу по поднятию (переворачиванию, доставанию из ямы) тела. Во всех этих случаях нужно рассматривать перемещение не самого тела, а только его центра тяжести.

Потенциальная энергия Ep зависит от выбора нулевого уровня, то есть от выбора начала координат оси OY. В каждой задаче нулевой уровень выбирается из соображения удобства. Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.

Потенциальная энергия растянутой пружины рассчитывается по формуле:

где: k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.

Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x₁, тогда при переходе в новое состояние с удлинением x₂ сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком (так как сила упругости всегда направлена против деформации тела):

Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Работа силы трения зависит от пройденного пути (такой вид сил, чья работа зависит от траектории и пройденного пути называется: диссипативные силы). Понятие потенциальной энергии для силы трения вводить нельзя.

 

Коэффициент полезного действия

К оглавлению…

Коэффициент полезного действия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой (формула уже приведена выше).

КПД можно рассчитывать как через работу, так и через мощность. Полезная и затраченная работа (мощность) всегда определяются путем простых логических рассуждений.

В электрических двигателях КПД – отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника. В тепловых двигателях – отношение полезной механической работы к затрачиваемому количеству теплоты. В электрических трансформаторах – отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.

В силу своей общности понятие КПД позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т.д.

Из–за неизбежных потерь энергии на трение, на нагревание окружающих тел и т.п. КПД всегда меньше единицы. Соответственно этому КПД выражается в долях затрачиваемой энергии, то есть в виде правильной дроби или в процентах, и является безразмерной величиной. КПД характеризует как эффективно работает машина или механизм. КПД тепловых электростанций достигает 35–40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением – 40–50%, динамомашин и генераторов большой мощности – 95%, трансформаторов – 98%.

Задачу, в которой нужно найти КПД или он известен, надо начать с логического рассуждения – какая работа является полезной, а какая затраченной.

 

Закон сохранения механической энергии

К оглавлению…

Полной механической энергией называется сумма кинетической энергии (т.е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):

Если механическая энергия не переходит в другие формы, например, во внутреннюю (тепловую) энергию, то сумма кинетической и потенциальной энергии остаётся неизменной. Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему (т.е. такую в которой не действует внешних сил, и их работа соответственно равна нолю) и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной:

Это утверждение выражает закон сохранения энергии (ЗСЭ) в механических процессах. Он является следствием законов Ньютона. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой силами упругости и тяготения. Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.

Алгоритм решения задач на закон сохранения энергии:

1. Найти точки начального и конечного положения тела.
2. Записать какой или какими энергиями обладает тело в данных точках.
3. Приравнять начальную и конечную энергию тела.
4. Добавить другие необходимые уравнения из предыдущих тем по физике.
5. Решить полученное уравнение или систему уравнений математическими методами.

Важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.

В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими силами действуют силы трения или силы сопротивления среды. Работа силы трения зависит от длины пути.

Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). Таким образом энергия в целом (т.е. не только механическая) в любом случае сохраняется.

При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.

Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.

 

Разные задачи на работу

К оглавлению…

Если в задаче требуется найти механическую работу, то сначала выберите способ её нахождения:

1. Работу можно найти по формуле: A = FS∙cosα. Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
2. Работу внешней силы можно найти, как разность механической энергии в конечной и начальной ситуациях. Механическая энергия равна сумме кинетической и потенциальной энергий тела.
3. Работу по подъёму тела с постоянной скоростью можно найти по формуле: A = mgh, где h – высота, на которую поднимается центр тяжести тела.
4. Работу можно найти как произведение мощности на время, т.е. по формуле: A = Pt.
5. Работу можно найти, как площадь фигуры под графиком зависимости силы от перемещения или мощности от времени.

 

Закон сохранения энергии и динамика вращательного движения

К оглавлению…

Задачи этой темы являются достаточно сложными математически, но при знании подхода решаются по совершенно стандартному алгоритму. Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:

1. Надо определить интересующую Вас точку (ту точку, в которой необходимо определить скорость тела, силу натяжения нити, вес и так далее).
2. Записать в этой точке второй закон Ньютона, учитывая, что тело вращается, то есть у него есть центростремительное ускорение.
3. Записать закон сохранения механической энергии так, чтобы в нем присутствовала скорость тела в той самой интересной точке, а также характеристики состояния тела в каком-нибудь состоянии про которое что-то известно.
4. В зависимости от условия выразить скорость в квадрате из одного уравнения и подставить в другое.
5. Провести остальные необходимые математические операции для получения окончательного результата.

При решении задач надо помнить, что:

• Условие прохождения верхней точки при вращении на нити с минимальной скоростью – сила реакции опоры N в верхней точке равна 0. Такое же условие выполняется при прохождении верхней точки мертвой петли.
• При вращении на стержне условие прохождения всей окружности: минимальная скорость в верхней точке равна 0.
• Условие отрыва тела от поверхности сферы – сила реакции опоры в точке отрыва равна нулю.

 

Неупругие соударения

К оглавлению…

Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.

Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.

С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц). В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Для описания любых ударов Вам нужно записать и закон сохранения импульса, и закон сохранения механической энергии с учетом выделяющейся теплоты (предварительно крайне желательно сделать рисунок).

 

Абсолютно упругий удар

К оглавлению…

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения. Центральный удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.

Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.

 

Законы сохранения. Сложные задачи

К оглавлению…

Несколько тел

В некоторых задачах на закон сохранения энергии тросы с помощью которых перемещаются некие объекты могут иметь массу (т.е. не быть невесомыми, как Вы могли уже привыкнуть). В этом случае работу по перемещению таких тросов (а именно их центров тяжести) также нужно учитывать.

Если два тела, соединённые невесомым стержнем, вращаются в вертикальной плоскости, то:

1. выбирают нулевой уровень для расчёта потенциальной энергии, например на уровне оси вращения или на уровне самой нижней точки нахождения одного из грузов и обязательно делают чертёж;
2. записывают закон сохранения механической энергии, в котором в левой части записывают сумму кинетической и потенциальной энергии обоих тел в начальной ситуации, а в правой части записывают сумму кинетической и потенциальной энергии обоих тел в конечной ситуации;
3. учитывают, что угловые скорости тел одинаковы, тогда линейные скорости тел пропорциональны радиусам вращения;
4. при необходимости записывают второй закон Ньютона для каждого из тел в отдельности.

Разрыв снаряда

В случае разрыва снаряда выделяется энергия взрывчатых веществ. Чтобы найти эту энергию надо от суммы механических энергий осколков после взрыва отнять механическую энергию снаряда до взрыва. Также будем использовать закон сохранения импульса, записанный, в виде теоремы косинусов (векторный метод) или в виде проекций на выбранные оси.

Столкновения с тяжёлой плитой

Пусть навстречу тяжёлой плите, которая движется со скоростью v, движется лёгкий шарик массой m со скоростью u_н. Так как импульс шарика много меньше импульса плиты, то после удара скорость плиты не изменится, и она будет продолжать движение с той же скоростью и в том же направлении. В результате упругого удара, шарик отлетит от плиты. Здесь важно понять, что не поменяется скорость шарика относительно плиты. В таком случае, для конечной скорости шарика получим:

Таким образом, скорость шарика после удара увеличивается на удвоенную скорость стены. Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:

Задачи о максимальных и минимальных значениях энергии сталкивающихся шаров

В задачах такого типа главное понять, что потенциальная энергия упругой деформации шаров максимальна, если кинетическая энергия их движения минимальна – это следует из закона сохранения механической энергии. Сумма кинетических энергий шаров минимальна в тот момент, когда скорости шаров будут одинаковы по величине и направлены в одном направлении. В этот момент относительная скорость шаров равна нулю, а деформация и связанная с ней потенциальная энергия максимальна.

educon.by

Работа и Энергия

Работа и Энергия

Термин “работа” в механике имеет два смысла: работа как процесс, при котором сила перемещает тело, действуя под углом, отличном от 90°; работа – физическая величина, равная произведению силы, перемещения и косинуса угла между направлением действия силы и перемещением:

А = Fs cos a.

Работа равна нулю, когда тело движется по инерции (F = 0), когда нет перемещения (s = 0) или когда угол между перемещением и силой равен 90° (cos а = 0). Единицей работы в СИ служит джоуль (Дж).

1 джоуль – это такая работа, которая совершается силой 1 Н при перемещении тела на 1 м по линии действия силы. Для определения быстроты совершения работы вводят величину “мощность”.

Мощность равняется отношению совершенной работы ко времени, за которое она выполнена:

Единицей мощности в СИ служит 1 ватт (Вт). 1 Вт – мощность, при которой совершается работа в 1 Дж за 1 секунду.

Рассмотрим действие на тело некоторой постоянной силы F. На участке пути s будет произведена работа А. В результате у тела изменится скорость:

Величину  для материальной точки называют кинетической энергией тела.

Кинетическая энергия – энергия движения, ею обладают все движущиеся тела. Эта величина является относительной, то есть она изменяется в зависимости от выбранной системы отсчета.

Кроме этого вида механической энергии, существует и другой ее вид – потенциальная энергия. Рассмотрим систему двух взаимодействующих тел. Например, тела, поднятого над Землей, и саму Землю.

Работа силы тяжести при перемещении тела на отрезке |h₁ – h₂| будет равна:

Величину mgh в соответствующей точке, которая расположена на высоте h, называют потенциальной энергией тела, находящегося в поле тяжести.

Из предыдущего уравнения вытекает, что работа не зависит от траектории движения в доле силы тяжести, а определяется лишь изменением высоты.

Потенциальная энергия характеризует и другие взаимодействующие тела. Так, потенциальной энергией обладает сжатая пружина:

где k – модуль упругости, х – смещение от положения равновесия.

Потенциальная энергия, как и кинетическая, является величиной относительной, поскольку и высота, и смещение зависят от выбора точки отсчета.

sfiz.ru

Физика (7 класс)/Работа и мощность. Энергия — Викиверситет

Механическая работа. Единицы работы.

В обыденной жизни под понятием “работа” мы понимаем всё.

В физике понятие работа несколько иное. Это определенная физическая величина, а значит, ее можно измерить. В физике изучается прежде всего механическая работа.

Рассмотрим примеры механической работы.

Поезд движется под действием силы тяги электровоза, при этом совершается механическая работа. При выстреле из ружья сила давления пороховых газов совершает работу – перемещает пулю вдоль ствола, скорость пули при этом увеличивается.

Из этих примеров видно, что механическая работа совершается, когда тело движется под действием силы. Механическая работа совершается и в том случае, когда сила, действуя на тело (например, сила трения), уменьшает скорость его движения.

Желая передвинуть шкаф, мы с силой на него надавливаем, но если он при этом в движение не приходит, то механической работы мы не совершаем. Можно представить себе случай, когда тело движется без участия сил (по инерции), в этом случае механическая работа также не совершается.

Итак, механическая работа совершается, только когда на тело действует сила, и оно движется.

Нетрудно понять, что чем большая сила действует на тело и чем длиннее путь, который проходит тело под действием этой силы, тем большая совершается работа.

Механическая работа прямо пропорциональна приложенной силе и прямо пропорциональна пройденному пути.

Поэтому, условились измерять механическую работу произведением силы на путь, пройденный по этому направлению этой силы:

работа = сила × путь

или

A = Fs,

где А – работа, F – сила и s – пройденный путь.

За единицу работы принимается работа, совершаемая силой в 1Н, на пути, равном 1 м.

Единица работы – джоуль (Дж) названа в честь английского ученого Джоуля. Таким образом,

1 Дж = 1Н · м.

Используется также килоджоули (кДж) .

1 кДж = 1000 Дж.

Формула А = Fs применима в том случае, когда сила F постоянна и совпадает с направлением движения тела.

Если направление силы совпадает с направлением движения тела, то данная сила совершает положительную работу.

Если же движение тела происходит в направлении, противоположном направлению приложенной силы, например, силы трения скольжения, то данная сила совершает отрицательную работу.

A = -Fs.

Если направление силы, действующей на тело, перпендикулярно направлению движения, то эта сила работы не совершает, работа равна нулю:

A = 0.

В

ru.wikiversity.org

Работа (физика) Википедия

Мeханическая работа — это физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел)^[1].

Используемые обозначения

Работа обычно обозначается буквой A (от нем. Arbeit — работа, труд) или буквой W (от англ. work — работа, труд).

Определение

Работа силы, приложенной к материальной точке

Суммарная работа по перемещению одной материальной точки, совершаемая несколькими силами, приложенными к этой точке, определяется как работа равнодействующей этих сил (их векторной суммой). Поэтому дальше будем говорить об одной силе, приложенной к материальной точке.

При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершённого точкой:

A=Fss=Fs cos(F,s)=F→⋅s→{\displaystyle A=F_{s}s=Fs\ \mathrm {cos} (F,s)={\vec {F}}\cdot {\vec {s}}}

Здесь точкой обозначено скалярное произведение, s→{\displaystyle {\vec {s}}} — вектор перемещения; подразумевается, что действующая сила F→{\displaystyle {\vec {F}}} постоянна в течение времени, за которое вычисляется работа.

В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки^[2]:

A=∫F→⋅ds→.{\displaystyle A=\int {\vec {F}}\cdot {\vec {ds}}.}

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений ds→,{\displaystyle {\vec {ds}},} если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат^[3], интеграл определяется^[4] следующим образом:

A=∫r→0r→1F→(r→)⋅dr→{\displaystyle A=\int \limits _{{\vec {r}}_{0}}^{{\vec {r}}_{1}}{\vec {F}}\left({\vec {r}}\right)\cdot {\vec {dr}}},

где r→0{\displaystyle {\vec {r}}_{0}} и r→1{\displaystyle {\vec {r}}_{1}} — радиус-векторы начального и конечного положения тела соответственно.

• Следствие. Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа (этой силы) равна нулю.

Работа сил, приложенных к системе материальных точек

Работа сил по перемещению системы материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершённые над каждой точкой системы, суммируются в работу этих сил над системой).

Даже если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.

• Эти определения могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Кинетическая энергия

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).

Если Atotal{\displaystyle A_{total}} — полная работа, совершённая над частицей, определяемая как сумма работ, совершенных приложенными к частице силами, то она выражается как:

Atotal=Δ(mv22)=ΔEk,{\displaystyle A_{total}=\Delta \left({\frac {mv^{2}}{2}}\right)=\Delta E_{k},}

где Ek{\displaystyle E_{k}} называется кинетической энергией. Для материальной точки кинетическая энергия определяется как половина произведения массы этой точки на квадрат её скорости и выражается как^[5]:

Ek=12mv2.{\displaystyle E_{k}={\frac {1}{2}}mv^{2}.}

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Потенциальная энергия

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая Ep{\displaystyle E_{p}}, такая, что

F→=−∇Ep.{\displaystyle {\vec {F}}=-\nabla E_{p}.}

Если все силы, действующие на частицу, консервативны, и Ep{\displaystyle E_{p}} является полной потенциальной энергией, полученной суммированием потенциальных энергий, соответствующих каждой силе, тогда:

F→⋅Δs→=−∇→Ep⋅Δs→=−ΔEp⇒−ΔEp=ΔEk⇒Δ(Ek+Ep)=0{\displaystyle {\vec {F}}\cdot \Delta {\vec {s}}=-{\vec {\nabla }}E_{p}\cdot \Delta {\vec {s}}=-\Delta E_{p}\Rightarrow -\Delta E_{p}=\Delta E_{k}\Rightarrow \Delta (E_{k}+E_{p})=0}.

Этот результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы,

∑E=Ek+Ep{\displaystyle \sum E=E_{k}+E_{p}}

является постоянной во времени. Этот закон широко используется при решении задач классической механики.

Работа в термодинамике

В термодинамике работа, совершённая газом при расширении^[6], рассчитывается как интеграл давления по объёму:

A1→2=∫V1V2PdV.{\displaystyle A_{1\rightarrow 2}=\int \limits _{V_{1}}^{V_{2}}PdV.}

Работа, совершённая над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.

• Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
• В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет

dA=PdSh.{\displaystyle dA=PdSh.}

Видно, что это и есть произведение давления на приращение объёма вблизи данной элементарной площадкой. А просуммировав по всем dS, получим конечный результат, где будет уже полное приращение объёма, как и в главной формуле раздела.

Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.

Пусть материальная точка M{\displaystyle M} движется по непрерывно дифференцируемой кривой G={r=r(s)}{\displaystyle G=\{r=r(s)\}}, где s — переменная длина дуги, 0≤s≤S{\displaystyle 0\leq s\leq S}, и на неё действует сила F(s){\displaystyle F(s)}, направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под F(s){\displaystyle F(s)} проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина F(ξi)△si,△si=si−si−1,i=1,2,…,iτ{\displaystyle F(\xi _{i})\triangle s_{i},\triangle s_{i}=s_{i}-s_{i-1},i=1,2,…,i_{\tau }}, называется элементарной работой силы F{\displaystyle F} на участке Gi{\displaystyle G_{i}} и принимается за приближённое значение работы, которую производит сила F{\displaystyle F}, воздействующая на материальную точку, когда последняя проходит кривую Gi{\displaystyle G_{i}}. Сумма всех элементарных работ ∑i=1iτF(ξi)△si{\displaystyle \sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} является интегральной суммой Римана функции F(s){\displaystyle F(s)}.

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма ∑i=1iτF(ξi)△si{\displaystyle \sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} всех элементарных работ, когда мелкость |τ|{\displaystyle |\tau |} разбиения τ{\displaystyle \tau } стремится к нулю, называется работой силы F{\displaystyle F} вдоль кривой G{\displaystyle G}.

Таким образом, если обозначить эту работу буквой W{\displaystyle W}, то, в силу данного определения,

W=lim|τ|→0∑i=1iτF(ξi)△si{\displaystyle W=\lim _{|\tau |\rightarrow 0}\sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}},

следовательно,

W=∫0sF(s)ds{\displaystyle W=\int \limits _{0}^{s}F(s)ds} (1).

Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра t{\displaystyle t} (например, времени) и если величина пройденного пути s=s(t){\displaystyle s=s(t)}, a≤t≤b{\displaystyle a\leq t\leq b} является непрерывно дифференцируемой функцией, то из формулы (1) получим

W=∫abF[s(t)]s′(t)dt.{\displaystyle W=\int \limits _{a}^{b}F[s(t)]s'(t)dt.}

Единицей измерения работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг

1 Дж = 1 кг·м²/с² = 1 Н·м

1 эрг = 1 г·см²/с² = 1 дин·см

1 эрг = 10⁻⁷Дж

См. также

Примечания

1. ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193-194. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
2. ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения ds→{\displaystyle {\vec {ds}}}, на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях ds→{\displaystyle {\vec {ds}}} суммируется, что и дает в результате интеграл.
3. ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
4. ↑ По сути через предыдущий, поскольку здесь F→(t)=F→(r→(t)){\displaystyle {\vec {F}}(t)={\vec {F}}({\vec {r}}(t))}; вектор же малого перемещения ds→{\displaystyle {\vec {ds}}} совпадает с dr→{\displaystyle d{\vec {r}}}.
5. ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
6. ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле ∫PdV{\displaystyle \int PdV} давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить её к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

Литература

• История механики с древнейших времен до конца XVIII в. В 2 т. М.: Наука, 1972.
• Кирпичёв В. Л. Беседы о механике. М.-Л.: Гостехиздат, 1950.
• Льоцци М. История физики. М.: Мир, 1970.
• Мах Э. Принцип сохранения работы: История и корень его. СПб., 1909.
• Мах Э. Механика. Историко-критический очерк её развития. Ижевск: РХД, 2000.
• Тюлина И. А. История и методология механики. М.: Изд-во МГУ, 1979.

wikiredia.ru