Ноль и бесконечность. С самого начала…
А.В.Никитин
Ноль и бесконечность. С самого начала…
Сначала хочу выразить благодарность Шенягину В.П. за статью [3], и руководству АТ за решение о публикации. От всех любителей математики. Хочу также поблагодарить В.Ю.Ипатова за участие в подготовке формул и обсуждении некоторых положений данной статьи.
Эта тема для дилетантов и любителей. Профессионалы тут и ухом не поведут…, у них есть вполне стройная теория множеств и теория пределов. Там все давно расписано.
Но, любопытство неистребимо.
Как мне кажется, почти любой начинающий математик
обязательно стукнется об эти бесконечно большие и бесконечно малые…,
попробует свои силы в действиях с бесконечностью. И придет к парадоксальному выводу:
бесконечность, это все равно – число, отношение или количество.
И, значит, мы вправе делать с ним те же действия, что и с остальными числами и множествами. Это вроде никто и не запрещал.
Правда, есть неопределенности, но, можно и их попробовать разрешить…
Почему эта тема постоянно интересна?
Потому, что книг, рассказывающих о действиях с бесконечностями простым и доступным для всех языком, или мало, или нет совсем, не знаю. Но мне такие пока не попадались. А в серьезных книгах и язык изложения соответствующий…, дилетанту не разобраться. Справочники, даже такие, как [4] и [5] помогают в этом мало.
Вот и пытаемся мы, дилетанты, дойти до понимания своим умом. Как умеем, так и доходим.
Надо подготовиться…
Введем несколько понятий для обоснования и вывода формул.
Данные ниже определения не претендуют на точность
формулировок. Для получения более полной информации можно обратиться к [1,2].
Счетным множеством называют множество чисел, например, натуральных или рациональных, которое имеет хоть и неизвестную, но счетную мощность. Любое число из счетного множества исчислимо и является счетной величиной.
Счетные величины:
– бесконечно малое рациональное число, .
М – бесконечно большое рациональное число,
а – конечное рациональное число.
Несчетным множеством называются множества, которые не могут быть вычислены. Это предел, к которому стремится то или иное счетное множество. Любое число несчетного множества потенциально неисчислимо и может назваться несчетной величиной. Примеры несчетных величин – константы π и е, например. Мы знаем их давно, но точное значение этих иррациональных чисел никогда не будет вычислено…
Нас интересуют такие несчетные величины:
0 – бесконечно малое вещественное число.
∞ – бесконечно большое вещественное число.
Если с понятием бесконечности и несчетности величины ∞ проблем почти не возникает, то с понятием несчетной величины 0 – одни проблемы.
Есть абсолютная величина 0 = НИЧЕГО. Пустое место. Это вроде понятно. Когда мы видим пример 1-1=0, то четко понимаем, в ответе - Ничего. Пустота.
Когда мы сталкиваемся с относительным пониманием, что 0, это предельная точность измерения или предел погрешности этих измерений, то тут начинаются сложности. Где «еще не 0», а где «уже точно - 0»?
Над этим можно бы и посмеяться, но посмотрите на электронные термометры, развешенные по улицам города для того, чтобы жители могли знать температуру воздуха. При температуре близкой к 0оС эти термометры начинают давать интересные показания: то +0, то -0…, и почти никогда без знака (+) или (-). Так 0 или не 0? Как это понимать?
А так и понимать, что в данном случае, 0 –
понятие относительное, связанное с точностью проводимых измерений.
И «0» становится неуловимым. К нему можно стремиться бесконечно.
Мы будем относиться к числу 0 в формулах несчетных величин, как относительной величине в пределе своего приближения к абсолютному значению. Да, это ноль, но все же … немножечко… не ноль. На самую малость. Она меньше чем даже бесконечно малая , но… абсолютной пустоты не дает. Вот эту малость мы и будем записывать как 0 в формулах с несчетными величинами. Вот примерно так…
Иначе переходить от счетных величин к несчетным будет трудно.
Теперь дадим основные соотношения и пояснения по введенным величинам.
Сначала дадим формулу для :
|
(1) |
Эта счетная бесконечно малая величина уже была введена автором статьи [3] формулой (35):
|
(2) |
И дополнением к формуле (38) там же [3]:
|
(3) |
Как мне кажется, совершенно справедливо и
обосновано.
Теперь дадим формулу получения М.
Например так:
|
(4) |
Бесконечно большое число М в своем пределе стремится к ∞.
Величины и М мы ввели как счетные эквиваленты несчетных величин 0 и ∞ соответственно.
Число а, это любое рациональное число в диапазоне . Как частные случаи, мы будем рассматривать и несколько числовых значений, например: а1=1.
Теперь можно составить шкалу размерностей:
|
0<; |
(5) |
Осталось одно замечание: Ниже, в
тексте статьи, в каждой нумерованной строке формул слева дается формула для
счетной величины, справа – для несчетной.
Все подготовительные действия сделаны. Можно переходить к изложению материала.
Основные математические действия с предельными величинами.
Начнем с самого простого.
Сложение.
Вычитание.
Эти действия сомнений не вызывают. Пока, во всяком случае.
Умножение.
Мы понимаем, что это только формальное допущение, а с другой стороны….
Вернемся к этому вопросу при рассмотрении действий
деления и действий со степенями.
А пока продолжим:
Эти выражения в комментариях вроде бы не нуждаются. Сомнения возникают разве что при рассмотрении формулы (16). Но примерно такое же мнение мы находим в [4] и [5] в параграфе о бесконечных…
Деление.
Деление величин одной размерности:
Здесь и делимое, и делитель, это величины одной размерности. И результат деления должен быть конечной счетной величиной.
Неопределенность результата деления несчетных величин, типа и , не устраняется, но формализуется введением деления их счетных эквивалентов. Формулы (18)…(20), прежде всего, отражают формальную счетность результата деления – частного, а не конкретную величина делимого и делителя.
Деление большего числа на меньшее:
Деление меньшего на большее:
Да, в формулах
(23) и (26) получилось вот так…, в соответствии с выводом автора [3] и
С. Алферова.
Алферова.
Действия со степенями.
Вот тут впервые появилось первое, но не последнее, конкретное значение счетной величины а в результате. В данном случае: а=1.
Следующие четыре формулы отражают скорее философский смысл, вкладываемый в понятие бесконечно большого числа – бесконечности. Естественно, бесконечность, как несчетное множество, при а≥1 и а→М, останется таковой в любой степени этого диапазона изменения а.
Точно также и бесконечно малое число, →0, при а≥1 и а→М, останется бесконечно малым.
Но формально формулы (23) и (26) справедливы. Мы обязаны учитывать и это. Тем более, когда речь идет о формально счетных множествах М и . Тем более что, чаще всего, при расчетах значения М и задаются.
В конце концов, у
равенств (29) …(31) , для 0 и ∞,
две стороны…, и их вполне возможно прочитать, как справа налево, так и
слева направо. Если мы говорим о
философских понятиях и категориях.
Если мы говорим о
философских понятиях и категориях.
Что выражает так любимое математиками выражение «…множество всех подмножеств…», как не максимально возможное из формулы (32)? Потому, что говорят они не о сумме каких-то множеств, а о предельно возможном количестве… в формально допустимой форме.
И это выражение сомнений у математиков не вызывает. А меньшая степень вызывает сомнения?
Мы переходим к другим диапазонам изменения счетной величины а и граничным точкам:
|
Граничная точка |
Диапазон изменения |
|
|
а=; |
а≥; |
(33) |
|
а=1; |
|
(34) |
|
а= |
а≤ |
(35) |
По сути дела мы рассматриваем окрестности точки: а=1;
Далее, для вывода формул нам необходимо
воспользоваться предельными выражениями. Посмотрим результат:
Посмотрим результат:
Теперь посмотрим, какой результат мы получим при возведении а, определенных выше диапазонов изменения, в любую исчислимую, а так же в бесконечно большую и бесконечно малую степень в граничных точках.
При а=1:
При а=:
При а=:
Формулы (43) и (45) являются модификацией формул (35) и дополнения к формуле (38) в статье[3].
Итог ожидаемый. Только целое число 1 в любой степени останется самим собой. Малейшее отклонение а от целой единицы, даже на бесконечно малую величину, ведет к изменению результата.
Вот на этом пока и остановимся.
Заключение.
Я не ставил себе целью полностью разобраться с бесконечными …
Мне кажется, что В.П. Шенягин
в своей работе [3] достаточно объективно оценил круг вопросов по этой
теме. Для меня интерес представляют
арифметические действия с нулем и бесконечностью. Вот на них я и
сосредоточился.
Для меня интерес представляют
арифметические действия с нулем и бесконечностью. Вот на них я и
сосредоточился.
И вопрос не в том, знаком ли я с трудами Кантора и Геделя, а в том, что действия с бесконечностями хотелось бы привести к виду, понимаемому всеми, а не только профессиональными математиками. К простым формулам, пусть и немного ограниченного применения, но без особых математических нагромождений.
Тема еще далека от своего исчерпания. Возможно, что последует продолжение разговора. Да и я еще немного подумаю…
Если возникнут вопросы – обращайтесь. На адрес: [email protected]
Или на сайт: http://andrejnikitin.narod.ru/
Поговорим…
Литература:
1. Счетное множество. Википедия. http://ru.wikipedia.org/?oldid=31487395
2. Теория множеств. Википедия.
http://ru.wikipedia. org/?oldid=33955155
org/?oldid=33955155
3. Шенягин В.П. Нуль (ноль): число, функция, образ, проявление и систематизация http://www.trinitas.ru/rus/doc/0016/001c/1828-shen.pdf
4. Выгодский М.Я. Справочник по элементарной математике. М, ФИЗМАТГИЗ, 1959г.
5. Выгодский М.Я. Справочник по высшей математике. М, ФИЗМАТГИЗ, 1961г.
0 бесконечность
Вы искали 0 бесконечность? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 0 в степени 0 неопределенность, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение.
Например, «0 бесконечность».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 0 бесконечность,0 в степени 0 неопределенность,0 в степени бесконечность,0 в степени бесконечность неопределенность,0 делить на 0 предел,0 делить на бесконечность,0 делить на бесконечность равно,0 на 0 бесконечность на бесконечность,0 на 0 предел,0 на 0 равно бесконечность,0 на бесконечность делить,0 на бесконечность делить на,0 на бесконечность умножить на бесконечность,0 разделить на бесконечность,0 умножить на бесконечность,1 умножить на бесконечность,бесконечность 0,бесконечность в 0 степени,бесконечность в нулевой степени,бесконечность в степени,бесконечность в степени 0,бесконечность в степени бесконечность пределы,бесконечность в степени бесконечность раскрытие неопределенности,бесконечность в степени минус бесконечность равно,бесконечность в степени ноль,бесконечность деленная на бесконечность равно,бесконечность делить на 0,бесконечность делить на 0 равно,бесконечность делить на бесконечность минус бесконечность,бесконечность делить на бесконечность предел,бесконечность делить на бесконечность равно,бесконечность делить на бесконечность равно бесконечность,бесконечность делить на минус бесконечность равно,бесконечность делить на ноль,бесконечность делить на ноль равно бесконечность,бесконечность минус бесконечность делить на бесконечность,бесконечность минус бесконечность неопределенность,бесконечность на бесконечность неопределенность,бесконечность на бесконечность предел,бесконечность на бесконечность равно,бесконечность на ноль,бесконечность на ноль неопределенность,бесконечность на ноль предел,бесконечность на ноль равно бесконечность,бесконечность равно 0,бесконечность разделить на 0,бесконечность разделить на бесконечность равно,бесконечность разделить на ноль,бесконечность умножить на 0,бесконечность умножить на 1,бесконечность умножить на бесконечность равно,бесконечность умножить на ноль,деление бесконечность на бесконечность,делить на 0 бесконечность,делить на 0 равно бесконечность,как раскрыть неопределенность бесконечность в степени бесконечность,минус бесконечность делить на бесконечность,минус бесконечность делить на бесконечность равно,неопределенность 0 в степени 0,неопределенность 0 в степени бесконечность,неопределенность 0 на 0,неопределенность 0 на бесконечность,неопределенность 1 в степени бесконечность как раскрыть,неопределенность бесконечность в степени 0,неопределенность бесконечность в степени бесконечность,неопределенность бесконечность на 0,неопределенность бесконечность на бесконечность,неопределенность бесконечность на ноль,неопределенность бесконечность умножить на бесконечность,неопределенность бесконечность умножить на ноль,неопределенность вида,неопределенность вида бесконечность в степени бесконечность,неопределенность вида бесконечность минус бесконечность,неопределенность вида бесконечность на бесконечность,неопределенность вида бесконечность умножить на бесконечность,неопределенность ноль на бесконечность,неопределенность ноль на ноль,неопределенность ноль умножить на бесконечность,неопределенность ноль умножить на ноль,ноль в степени бесконечность,ноль делить на бесконечность равно,ноль делить на ноль предел,ноль на бесконечность,ноль на бесконечность неопределенность,ноль на бесконечность предел,ноль на бесконечность умножить на бесконечность,ноль на ноль предел,ноль на ноль пределы,ноль на ноль равно бесконечность,ноль разделить на бесконечность,предел 0 делить на 0,предел 0 на 0,предел бесконечность в степени бесконечность,предел бесконечность делить на бесконечность,предел бесконечность на бесконечность,предел бесконечность на ноль,предел неопределенность бесконечность на бесконечность,предел ноль делить на ноль,предел ноль на бесконечность,предел ноль на ноль,пределы бесконечность в степени бесконечность,пределы бесконечность на бесконечность,пределы ноль на ноль,разделить бесконечность на ноль,раскрытие неопределенностей вида бесконечность на бесконечность,раскрытие неопределенности 1 в степени бесконечность,раскрытие неопределенности бесконечность в степени бесконечность,раскрытие неопределенности бесконечность на бесконечность,таблица неопределенностей,число в степени бесконечность равно,что будет если бесконечность разделить на бесконечность. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 0 бесконечность. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 0 в степени бесконечность).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 0 бесконечность. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 0 в степени бесконечность).
Где можно решить любую задачу по математике, а так же 0 бесконечность Онлайн?
Решить задачу 0 бесконечность вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
как понять самую красивую концепцию в истории
Концепция бесконечности, возможно, одна из самых изящных и смелых концепций, когда-либо созданных человечеством.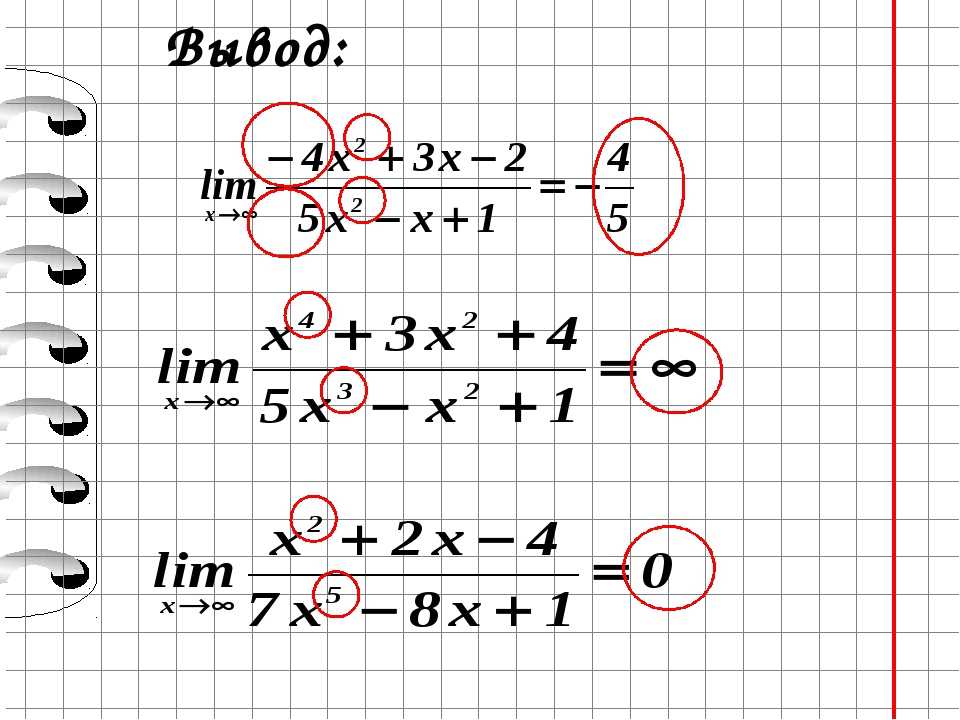 Однако еще со времен Древней Греции бесконечность не только завораживала, но и откровенно раздражала ученых и философов: она предполагала слишком много парадоксов, идущих вразрез со всякой логикой. Рассказывая о теории чисел и теории множеств, математик Хаим Шапира сосредоточил свое внимание на бесконечности, к которой каждая из этих теорий напрямую относится, и не без успеха попытался примирить многочисленные парадоксы с нашей картиной мира. Валерий Шлыков изучил его книгу в рамках совместного проекта «Горького» и премии «Просветитель» и выбрал из нее несколько наиболее важных и интересных эпизодов.
Однако еще со времен Древней Греции бесконечность не только завораживала, но и откровенно раздражала ученых и философов: она предполагала слишком много парадоксов, идущих вразрез со всякой логикой. Рассказывая о теории чисел и теории множеств, математик Хаим Шапира сосредоточил свое внимание на бесконечности, к которой каждая из этих теорий напрямую относится, и не без успеха попытался примирить многочисленные парадоксы с нашей картиной мира. Валерий Шлыков изучил его книгу в рамках совместного проекта «Горького» и премии «Просветитель» и выбрал из нее несколько наиболее важных и интересных эпизодов.
Хаим Шапира. Восемь этюдов о бесконечности. Математическое приключение. М.: КоЛибри, Азбука-Аттикус, 2021. Перевод с английского Дмитрия Прокофьева. Содержание
Бесконечность — это иррационально
Удивительно, но человечество далеко не сразу пришло к пониманию иррациональной сути бесконечности. Мы привыкли, что рациональность — это наивысшая степень ясности и логичности, нечто, присущее прежде всего строго разработанной науке, однако первобытные мифы обладали не менее четкой логикой.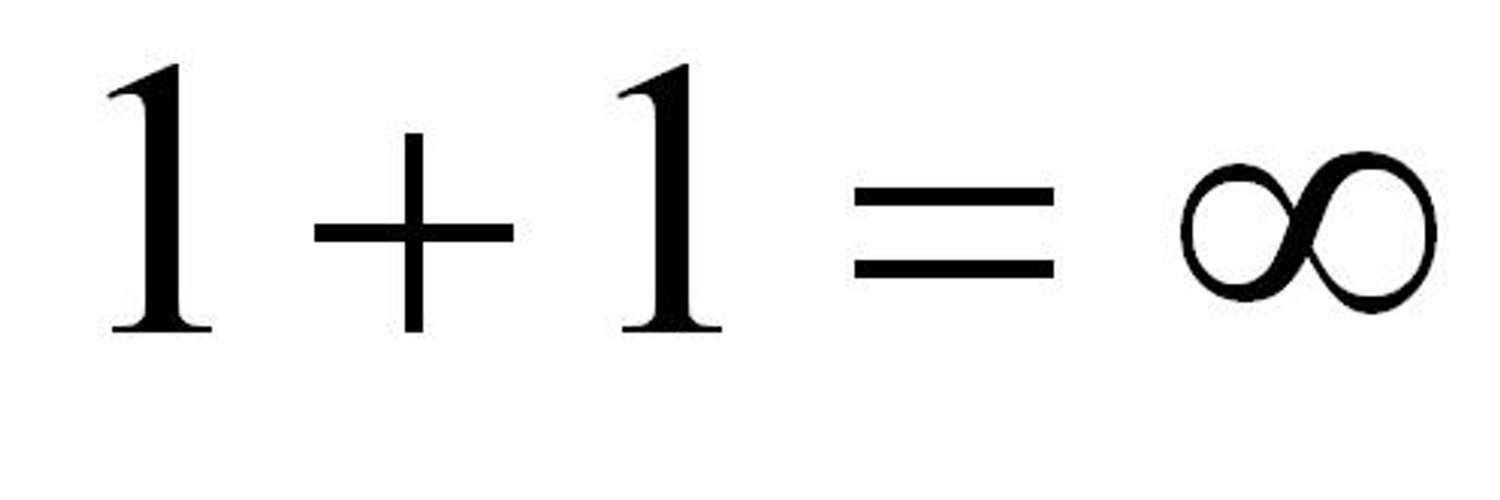 Понадобился гений древних греков, чтобы нехотя, со скандалом, но признать не укладывающуюся ни в какую логику бесконечность. Считается, что первым ее ввел в философский обиход Анаксимандр, автор концепции апейрона, хотя апейрон у него обозначал скорее неопределенность. Такая бесконечность особых возражений еще не вызвала. А вот Пифагору открылось нечто совершенно возмутительное. Пифагор-философ считал, что все состоит из натуральных (то есть положительных целых) чисел и ими может быть выражено. Числа были атомами его мира. А Пифагор-математик обнаружил, что соотношение между стороной квадрата и его диагональю невозможно выразить отношением натуральных чисел. Иными словами, √2 — иррациональное число (напомним: иррациональность числа подразумевает, что, во-первых, его десятичное представление бесконечно, а во-вторых, в нем никогда не возникают какие бы то ни было повторяющиеся структуры).
Понадобился гений древних греков, чтобы нехотя, со скандалом, но признать не укладывающуюся ни в какую логику бесконечность. Считается, что первым ее ввел в философский обиход Анаксимандр, автор концепции апейрона, хотя апейрон у него обозначал скорее неопределенность. Такая бесконечность особых возражений еще не вызвала. А вот Пифагору открылось нечто совершенно возмутительное. Пифагор-философ считал, что все состоит из натуральных (то есть положительных целых) чисел и ими может быть выражено. Числа были атомами его мира. А Пифагор-математик обнаружил, что соотношение между стороной квадрата и его диагональю невозможно выразить отношением натуральных чисел. Иными словами, √2 — иррациональное число (напомним: иррациональность числа подразумевает, что, во-первых, его десятичное представление бесконечно, а во-вторых, в нем никогда не возникают какие бы то ни было повторяющиеся структуры).
Джин из бутылки был выпущен. Две тысячи лет спустя Георг Кантор показал, что «почти» все вещественные (или действительные) числа иррациональны. Среди них и два самых важных числа в математике — число Эйлера и отношение длины окружности к ее диаметру, число п.
Среди них и два самых важных числа в математике — число Эйлера и отношение длины окружности к ее диаметру, число п.
Кстати, когда в 1593 году французский математик Франсуа Виет нашел замечательную формулу для вычисления π при помощи набора вложенных радикалов, он записал ее в следующем виде:
Стоящее в конце многоточие означает «продолжать ту же процедуру до бесконечности». Это первый случай, когда бесконечный процесс был явно обозначен в математической формуле. Ну а знаменитый знак бесконечности ∞ впервые использовал английский математик Джон Валлис в 1655 году.
Бесконечность — это парадоксально
Вернемся к грекам. По-настоящему скандал с бесконечностью раздул Зенон Элейский, ученик Парменида. С тех пор его знаменитые апории обсуждались бесчисленное количество раз. Рассел называл их «неизмеримо тонкими и глубокими», а Пуанкаре, напротив, эмоционально заявлял, что «Зенон был идиотом, и только идиоты могут заниматься его апориями».
До нас дошли девять апорий, но наиболее известны из них три. «Стрела» — о стреле, которая в каждый момент времени покоится, а значит, никуда не летит. «Дихотомия», в которой идущий из точки A в точку B никогда туда не доберется, так как ему сначала нужно пройти половину этого расстояния, а затем половину оставшегося расстояния и так далее, так что до точки B всегда будет оставаться еще какая-то крошечная половинка. И, конечно же, «Ахиллес и черепаха» — в которой Ахиллес никогда не догонит черепаху, если та пустилась в путь немного раньше, так как всякий раз, как Ахиллес прибывает на то место, где только что была черепаха, та успевает продвинуться хоть чуть-чуть, но дальше.
Рассуждения Зенона безупречны, однако допустить в реальности, чтобы бегун не перегнал какое-то пресмыкающееся, попросту нелепо. Так была найдена парадоксальная сторона бесконечности, которая противоречит всему нашему опыту. Изящным математическим выражением этой парадоксальности служит простое уравнение 1=0,999999… Здесь всякий поначалу заподозрит какой-то подвох. Нет, тут не может быть знака равенства: пусть на ничтожную величину, но правая часть формулы все-таки должна быть меньше единицы! Однако доказательство элементарно и безжалостно. Пусть a=0,9999999… В таком случае 10a=9,999999… Вычтя одно число из другого, получим 10a — a = 9,999999… — 0,999999… Что дает 9a=9, то есть a=1.
В бесконечности — значит нигде
Еще одна парадоксальная характеристика заключается в том, что, по формулировке Гегеля, «бесконечность нельзя найти ни в одной точке бесконечной прямой». Представим себе космический корабль, который движется по следующим правилам: первые полчаса он летит со скоростью 2 километра в час (или 2 тысячи, или 2 миллиона, что совершенно неважно). На следующую четверть часа его скорость несколько возрастает — до 4 километров в час. В течение следующей одной восьмой часа он летит со скоростью 8 километров в час — и так далее. Где этот космический корабль окажется через час? Цифры подобраны таким образом, чтобы получить несложный расчет: за первые полчаса он пролетит километр, за следующие четверть часа — еще километр, и так далее, то есть в итоге он преодолеет расстояние 1+1+1+1… Но поскольку это число бесконечно, мы не можем указать ни одну точку в космосе, где бы мог оказаться корабль, ведь до любой точки будет пусть сколько угодно большое, но конечное расстояние. Корабль попросту нигде, он исчез из нашего вычислимого мира. Словно бы перешел на иной уровень существования.
Бесконечность — это красиво
Греков бесконечность пугала. Она была чем-то вроде вторжения хаоса в их упорядоченный и размеренный космос. Однако вскоре обнаружилось, что бесконечность обладает своей завораживающей красотой, своей «рациональностью». Эта красота, например, очевидна в приведенной выше формуле Виета для вычисления π. А вот еще одна невероятная красота:
1/9801 = 0,0001020304050607080910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758…
Для наглядности напишем это число с пробелами:
1/9801 = 0,00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 99 00 01 02 03… 97 99 00 01 02 03 04 05 06…
Мы получили все двузначные числа, расположенные в правильном порядке и повторяющиеся до бесконечности, кроме числа 98! По сравнению с подобным меркнет вся красота конечного мира, ведь здесь мы прикасаемся к чему-то запредельному и как бы божественному — к той гармонии, которая, возможно, лежит в основе всего (а теперь попробуйте самостоятельно поделить 1 на 998 001).
Бесконечность — это божественно
В 1913 году профессор математики Кембриджского университета Годфри Харди получил письмо из Индии от никому не известного индийского юноши, закончившего только среднюю школу. В письме было несколько уравнений, потрясших Харди. Например:
Так мир узнал о Рамануджане. Он был гениальным самоучкой и поддерживал с числами какие-то мистические отношения. Иначе невозможно объяснить, как Рамануджан открывал свои формулы.
Многие сравнивали их с симфониями Моцарта или картинами эпохи Возрождения, но сам Рамануджан утверждал, что они внушались ему во время сна или медитации богиней Махалакшми. Как знать, не боги ли поспешили забрать к себе индийского гения (Рамануджан умер в 32 года), ведь он и так выдал немало их секретов. Подобных формул он успел записать более 3 900!
Брадобрей уделывает Кантора
Еще одним человеком, состоявшим с бесконечностью в чрезвычайно близких отношениях, был Георг Кантор, наш соотечественник (он родился в Санкт-Петербурге в 1845 году). Ему принадлежит разработка теории множеств, которая стала прорывом в математике. До него считалось, что «бесконечность распознаваема, но не познаваема» (Декарт). В лучшем случае бесконечность оценивали «на глазок», как, например, Эйлер, полагавший, что бесконечность 2/0 вдвое больше, чем 1/0. Кантор математически показал, что бесконечные множества (как и конечные) можно сравнивать, производить над ними операции, формулировать и доказывать теоремы с ними. Однако и здесь сразу же вмешались парадоксы — куда без них в бесконечности?
Когда Готлоб Фреге уже заканчивал фундаментальный двухтомный труд «Основные законы арифметики», в основу которого были положены выкладки Кантора, он получил письмо от Бертрана Рассела, заставившее его посыпать голову пеплом. В этом письме Рассел вывел свой знаменитый парадокс брадобрея, который бреет всех, кто не бреется сам. За софистическим с виду содержимым скрывалась серьезная проблема.
В теории Кантора множество — это совокупность каких-то объектов. Если среди этих объектов нет самого множества, такое множество считалось обычным. Например, множество всех кроликов само кроликом не является. Но множество не-кроликов уже «необычно» — ведь оно тоже «не-кролик», значит, входит в самого себя. Такое множество стали называть расселовским. Парадокс возникает, когда рассматривается множество всех обычных множеств, которое оказывается не обычным, не расселовским. Оно не обычное, так как, будучи обычным множеством, должно входить в самого себя, то есть на самом деле быть расселовским множеством. И оно не расселовское, так как, если оно входит в самого себя в качестве расселовского, это противоречит его определению как множеству только обычных множеств. Таким образом, оказалось, что разделение множеств на те, что не являются собственными элементами, и те, что являются таковыми, не исчерпывает всех множеств. Есть еще и «брадобреи».
Гранд-отель «Бесконечность» имени Гильберта: свободные номера есть всегда!
Немецкий математик Давид Гильберт придумал, пожалуй, самый изящный пример, связанный с парадоксами бесконечности. Представим себе отель с бесконечным количеством номеров, в котором живут постояльцы — все натуральные числа: 1, 2, 3, 4… Свободных номеров, естественно, нет, что вполне устраивает портье. Но вот в гостиницу пожаловал важный гость: 0. Можно ли его разместить? Сообразительный портье попросил каждого из жильцов переехать в следующий по порядку номер, освободив тем самым для ноля № 1. Лиха беда начало. Стало известно, что в отеле все-таки могут быть свободные номера, и первыми подсуетились все отрицательные числа, которых, понятно, тоже бесконечность. Прежний способ не работает: нельзя попросить постояльцев переехать на бесконечное число номеров. Однако можно переселить каждого жильца в номер с удвоенным значением: 2 в № 4, 3 в № 6 и так далее. Тогда все нечетные номера (3, 5, 7, 9…) освободятся и получится бесконечное количество незанятых комнат.
Слава о гостинице, в которой всегда есть свободные номера, растет, и теперь сюда желают пожаловать все положительные рациональные дроби. Портье с ужасом осознает, что прежний метод опять бесполезен: ведь одни только числа со знаменателем 2 могут полностью занять отель, если дробь ½ поселится в № 1, дробь 2/2 — в № 2, дробь 3/2 — в № 3 и так далее. А таких знаменателей бесконечность! То есть нужно разместить бесконечное количество бесконечных множеств. Тем не менее наш портье блестяще справился с этой задачей, оставив про запас еще одну бесконечность номеров. Как? Прочитайте в книге или посмотрите наглядный ролик.
Гранд-отель «Бесконечность» имени Гильберта: трест, который лопнул
Итак, в гостиницу постоянно и без проблем въезжают разные бесконечности и даже бесконечности бесконечностей. Поэтому портье и глазом не моргнул, когда к стойке регистрации подошло скромное множество всех чисел между 0 и 1. Конечно, в этом интервале тоже содержится бесконечное количество, но разве не в этом специализация нашего отеля? Однако все попытки перемножать, возводить в степень и прочие манипуляции с номерами ни к чему не привели: числа между 0 и 1 в отель не влезали. В отчаянье портье даже выселил всех постояльцев, но и пустая гостиница не могла вместить в себя не то что все числа между 0 и 1, но даже дроби, записанные с использованием только цифр 0 и 1, то есть 0,101 и так далее. Репутация отеля обвалилась, поползли слухи, что гранд-отель «Бесконечность» на самом деле маленький. Торжествующие конкуренты немедленно открыли рядом «Еще большую бесконечность». Но как такое возможно?
«Вижу, но не верю!»
Мы уже упоминали, что именно Кантор научился сравнивать бесконечные множества. Оказалось, что счетные множества (элементы которых можно пронумеровать натуральными числами) — это самые простые или «маленькие» множества. Их мощность (то есть количество элементов) обозначается буквой еврейского алфавита ℵ0 («алеф-нуль»). Мощность несчетных (состоящих из вещественных чисел) множеств больше и обозначается как ℵ. Равна ли она ℵ1, математики спорят до сих пор, однако несомненно, что есть множества с мощностью ℵ2, ℵ3 и так далее.
Мы видели, что даже простые счетные множества очень интересны, так как позволяют включать в себя разные бесконечности. Обладают ли таким свойством несчетные множества? Конечно! Их еще называют континуум-множествами, так как геометрически их можно представить в виде непрерывных отрезков или линий. При этом любые два отрезка равномощны, то есть имеют равное (хоть и несчетное) количество своих точек. Доказательство легко видно из рисунка:
С этим еще можно согласиться, но как вам равномощность любого конечного отрезка и бесконечного луча? Однако она становится очевидной, если провести те же линии соответствия на следующем рисунке:
И уж совсем невероятна равномощность бесконечной прямой и n-мерного пространства (для любого n!). Говорят, когда Кантор доказал это, он воскликнул: «Je le vois, mais je ne le crois pas!» («Вижу, но не верю!»)
Бесконечность — это трансцендентно
Теория счетных и несчетных множеств позволяет проникнуть в совсем уже запредельную тайну бесконечности. Как мы писали, все действительные числа можно разделить на рациональные и иррациональные. Однако в математике куда важнее другое разделение: на алгебраические и трансцендентные. Число называется алгебраическим, если оно является корнем какого-либо многочлена с целыми коэффициентами (простейший пример: bx — a). Любое рациональное число будет решением подобного многочлена, как и некоторые иррациональные числа: например, √2 является корнем уравнения x2 — 2 = 0. Характеристика алгебраичности очень важна, так как все алгебраические числа образуют счетное множество, внутри которого возможны четыре основных алгебраических действия: сложение, вычитание, умножение, деление (разумеется, кроме деления на 0).
А что же с неалгебраическими числами, то есть теми, которые невозможно представить в виде корней многочленов и которые образуют несчетное множество? Долгое время их попросту не могли найти! И только в 1844 году французский математик Жозеф Лиувилль открыл первое трансцендентное число. Вот оно:
Строится оно следующим образом. Сначала вычисляем все факториалы: 1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120… Затем составляем число, в котором после запятой встречаются только нули и единицы, причем 1 стоит на 1, 2, 6, 24, 120-м — и так далее — местах, а на всех остальных местах стоит 0. Лиувилль доказал, что это число не является корнем какого бы то ни было алгебраического уравнения с целыми коэффициентами.
Можно подумать, такое число — редкий зверь в числовом зверинце, но ничего подобного! Кантор обнаружил, что трансцендентные числа составляют большинство всех чисел. Другими словами, практически все числа не только не рациональны, по большей части они даже не относятся к алгебраическим!
Но где же тогда все эти трансцендентные числа? Видимо, где и должны быть: в трансцендентной бесконечности. Лишь некоторые нам удается изловить оттуда, изощренно доказывая, что они не являются алгебраическими. Так, трансцендентность числа π была доказана лишь в 1882 году, трансцендентность постоянной Гельфонда eπ — в 1934-м, а десятичный логарифм ln π до сих пор ждет решения своей судьбы. Бесконечность неохотно раскрывает свои тайны, коих у нее, без сомнения, бесконечное множество.
7.Правила лопиталя для раскрытия неопределённостей вида 0/0 и бесконечность/бесконечность. Раскрытие неопределённостей вида 0*бесконечность, бесконечность-бесконечность, 1бесконечность, 00
Правило Лопиталя-пусть функция f(x) и g(x) имеют производные в окрестности точки хо тогда: 1)если lim f(x)= lim g(x)=бесконечность, то limf(x)/g(x)=(бесконечность/бесконечность)= lim f’(x)/g’(x), при условии что последний предел существует. 2)если lim f(x)=lim g(x)=0, то lim f(x)/g(x)= (0/0)= lim f’(x)/g’(x), при условии что последний существует.
Следовательно если мы имеем неопределённости бесконечность/бесконечность, 0/0, воспользоваться правилом Лопиталя означает найти производные числителя и знаменателя, а затем вычислить новый предел.
Пример lim sin4x/x=(0/0)=lim(sin4x)’/x= lim4cos4x/1=4*cos0=4*1=4
3)0*бесконечность, пусть f стремиться к 0, g стремиться к бесконечности, тогда fg=f/ (1/g)= (0/0)=g/(1/f)= (бесконечность/бесконечность), т.е. мы свели данную неопределённость к 0/0 или бесконечность/бесконечность, после чего можно применять правило Лопиталя
4)бесконечность-бесконечность . Пусть f стремиться к бесконечности, g стремиться к бесконечности, тогда f-g=1/(1/f)- 1/(1/g)=(1/g)-(1/f)/(1/f)*(1/g)=(0/0)
5)1бесконечность,00, бесконечность0. Данные неопределённости также сводятся к неопределённостям бесконечность/бесконечность или 0/0 . для этого можно воспользоваться формулой fg=einfg=eglnf, f>0. Так, если f стремиться к 1, g стремиться к бесконечности, то получаем неопределённость 0*бесконечность (так как ln1=0), после чего можно получить бесконечность/бесконечность или 0/0
8.Дифференциал функции.Связь дифференциала и производной.Использование дифференциала в приближенных вычислениях.
Функция f(x) называется дифференцируемой в точке х0, если ее приращение в этой точке можно представить в виде дельта y=f(x0+дельтаx)-f(x0)=A*дельтаx+a(дельтаx)
Для того чтобы функция f(x) была дифференцируемой в точке х0, необходимо и достаточно, чтобы в точке х0 существовала произвлдная f’(x)=A.
F(x0+дельтаx)-f(х0)=f’(x0)*дельтаx+a(дельтах)
Функция f’(x0)*дельтаx есть главная линейная часть приращения функции f(x) в точке х0.Эту главную линейную часть приращения функции f(x) и называется дифференциалом функции f(x) в точке х0 и обозначают df(x0)=f’(x0)*дельтаХ, в частности для f(x)=x имеем df=dx=1*дельтаХ=дельтаХ, следовательно df(x0)=f’(x0)dx
Для дифференциалов функций f и g справедливы формулы, подобные формулам для производных функций:
1)d(f+g)=df+dg
2)d(f*g)=g*df+f*dg
3)d(f/g)=(gdf-fdg)/g2
Данные формулы будут широко применяться при вычислении интегралов функций. С помощью дифференциала можно также приближенно вычислить значения функции f для ч, близких к x0, Так как отбросив бесконечно малую функцию в формуле 2, получаем: f(x0+дельтаХ)=f(x0)+f’(x0)дельтаХ
9.Исследование на монотонность функции одной переменной. Точки экстремума. Необходимые и достаточные условия существования экстремума.
Пусть задана функция y=f(x) на множестве Х и х0-внутренняя точка множества Х.
Обозначим через U(x0) окрестность точки х0.В точке х0 функция f(x) имеет локальный максимум, если существует такая окрестность U(x0) точки х0, что для всех х из этой окрестности выполнено условие f(x)<=f(x0).
Точки локальных максимума и минимума называются точки локальных экстремумов, а значения функции в них-локальными экстремумами функции.Пусть функция f(x) определена на отрезке[a,b] и имеет локальный экстремум на каком0то из концов этого отрезка.Тогда такой экстремум называется локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для точки а и левой для точки b полуокрестностью.
Критическими точками , т.е. точки подозрительные на экстремум функции на интервале [a,b] , являются точки,в которых производная существует и равна 0 либо она не существует или равна бесконечности.
Первое достаточное условие экстремума-пусть непрерывная функция диффиринцируема в некоторой проколотой окрестности U(x0) точки х0, тогда: 1)если f’(x)>0 при х<x0, х принадлежит U(х0) и f’(x)<0 при х>x0, x принадлежит U(x0), то в точке х0-локальный максимум
2)если f’(x)<0 при x<x0 х принадлежит U(x0) и f’(x)>0при x>x0 x принадлежит U(x0), то в точке х0 локальный минимум.
Функция называется n раз непрерывно-дифференцируемой на некотором промежутке, если на этом промежутке она имеет непрерывные производные до порядка n включительно (n=0,1,2,….)
Второе достаточное условие экстремума- пусть функция f(x) дважды непрерывно-дифференцируема. Если х0-стационарная точка (f’(x0)=0) в которой f’’(x0)>0, то в точке х0 функция имеет локальный минимум. Если же f’’(x0)< 0 то в точке х0 функция имеет локальный максимум.
Раскрытие неопределенностей при вычислении пределов
С данной статьи начинаем цепочку публикаций, которые научат Вас находить особенности в границах, классифицировать неопределенности и применять правильную методику раскрытия. Дело заключается в том, что разработано много правил и приемов, которые позволяют по виду заданной функции или последовательности быстро сориентироваться как находить предел. Однако при изучении теоретического материала или на практических занятиях Вам или на этом не отмечают, или Ваши мысли гуляют за пределами аудитории.
Для охвата всего материала мы собрали много примеров из студенческой практики, модулей, контрольных, заказов и попытаемся здесь разъяснить, как и в каких случаях применять приведенные алгоритмы.
Пример 1. Вычислить предел последовательности:
Решение: При подстановке бесконечности получим неопределенность вида бесконечность разделить на бесконечность (∞/∞). Разделим числитель и знаменатель на переменную в наибольшей степени и сократим на нее. В результате избавимся от неопределенности, а слагаемые что останутся, будут стремиться к нулю при больших номерах последовательности
Все числа, что останутся и укажут куда стремится предел.
Пример 2. Вычислить предел последовательности:
Решение: При прямой подстановке бесконечно большого номера получим неопределенность бесконечность минус бесконечность (∞-∞).
Правило раскрытия такого типа неопределенности хорошо расписано в литературе и заключается в умножении и разделении неопределенности на множитель, сопряженный к ней.
Как правило, такие примеры содержат корни и чтобы их лишиться используем умножение на сопряженный множитель, что приводит к разности квадратов или кубов, в то время в знаменателе (или числителе) получим выражение с корнем, которое не содержит неопределенности.
Далее из числителя и знаменателя выделяем доминирующий множитель и упрощаем на него.
Все числа, что останутся и составят предел последовательности.
На языке формул этому отвечает запись
Пример 3. Найти предел функции:
Решение: При подстановке x=3 получим неопределенность 0/0.
Это означает, что и числитель и знаменатель содержат особенность.
Для раскрытия неопределенности выделим в числителе (x-3), а знаменатель умножим и разделим на сопряженное выражение .
В результате получим множитель (x-3), на который упрощаем дробь. Далее предел вычисляется методом подстановки переменной
Пример 4. Найти предел функции:
Решение: Задание для большинства студентов чрезвычайно сложное, а все потому что необходимо свести неопределенность типа 0/0 до известных случаев.
В результате преобразования функций получим выражения вида ln(1+x)/x, tan(x)/x, sin(x)/x при переменной стремящейся к нулю.
Далее выделяем первую замечательный предел и ее следствие, затем расписываем через произведение известных пределов.
Все остальное сводится к произведению единиц и отдельного множителя, который и является пределом заданной функции.
Внимательно разберите приведенный пример, он Вас многому научит.
На практике довольно трудно найти условие, которое бы объединяла несколько формул, поэтому учитесь на сложных примерах.
Тогда точно не будет сложностей в исчислении простых примеров.
Пример 5. Вычислить предел функции:
Решение: Подстановка 3 в функцию дает особенность вида единица в степени бесконечность (1^∞). Для ее раскрытия и в функции в скобках, и в дроби, что является показателем выделяем часть, что вносит особенность (х-3).
Далее, для упрощения манипуляций с выражениями делаем замену переменных x-3=t, новая переменная при этом стремится к нулю.
После этого выделяем второй замечательный предел и ищем лимит показателя, что остался.
На этом разбор распространенных примеров, которые распространены в учебной практике не завершается.
В соседней публикации будут проанализированы новые алгоритмы вычислений, и примеры пределов функций та последовательностей, которые помогут Вам быстрее освоить теоретический материал и подготовиться к контрольной, модулю, экзамене.
Бесконечность онлайн · Как пользоваться Контрольная Работа РУ
Этот сайт предоставляет возможность использовать символ бесконечности как для вычисления пределов и интегралов, но как и результат нахождения решений уравнений, пределов, исследования функций и др.
Данная статья описывает не совсем научное определение бесконечности, а просто “какие результаты приносит использование символа бесконечности в данной сервисе”.
Как вводить бесконечность в калькулятор?
- Можно вводить как две английские буквы “o”: oo
- Есть также отдельный символ для бесконечности: ∞
Посмотреть все примеры вы можете в калькуляторе упрощения выражений.
Деление бесконечности на бесконечность
“oo/oo” или “∞/∞”:
Деление бесконечности на ноль
“oo/0” или “∞/0”:
в результате Вы получите неопределённость (NaN)
(что такое nan – смотрите ниже)
Деление неопределённости на бесконечность
nan/oo (что такое неопределённость – смотрите ниже)
Результатом будет:
NaN
Умножение бесконечности на нуль
Тоже самое, что и умножение нуля на бесконечность.
“oo*0” или “∞*0”, “0*oo”:
Сложение бесконечностей
“∞ + ∞”
Вычитание бесконечностей
“∞ – ∞”
Результатом будет опять же NaN (неопределённость)
Виды бесконечностейПлюс бесконечность
“+oo” или “+∞”
Минус бесконечность
“-oo” или “-∞”
Бесконечность с неопределённым знаком
“±oo” или “±∞”
Комплексная бесконечность
Обозначается как “zoo”
Где используется бесконечностьПределы функций
При вычислении пределов требуется указать предел, к которому стремится функция, иногда требуется, чтобы это была бесконечность.2) при x от -oo до +oo:
Но бесконечность может быть и результатом вычисления несобственного интеграла, для этой функции:
1/(x – 1) при x от -1 до 1
Что такое неопределённость?
Неопределенность обозначается выражением nan или NaN.
Она означает, что при каких-то операциях не понятно, какой будет результат – к примеру, при делении бесконечности на бесконечность – не понятно: каждая из бесконечностей насколько большая, точно также при делении нуля на ноль – какой из нулей насколько мал. Поэтому возникает неопределённость.
С неопределённостью тоже интересно поиграться, вводить её в калькулятор:
nan/nan
nan/0
nan – oo
nan*0
Психология бесконечности, или Почему нельзя делить на ноль
Научпоп
Психология бесконечности, или Почему нельзя делить на ноль23 июня 1 576 просмотров
Антон Бахарев
Во всем мире школьников учат, что делить на ноль нельзя. Корень проблемы — в бесконечности. Деление на ноль вызывает бесконечность примерно так же, как доска для спиритических сеансов — духов из другого мира. Это рискованно. Не ходите туда. Философско-математические подробности вышеизложенного — в этой статье, подготовленной по книге «Бесконечная сила».
Бесконечность
Когда-то в далекие доисторические времена кто-то понял, что числа никогда не заканчиваются. Вместе с этой мыслью родилась бесконечность. Это числовой аналог глубин, скрытых в нашей психике, в наших ночных кошмарах о бездонных ямах и в наших надеждах на вечную жизнь.
Именно бесконечность лежит в основе множества наших мечтаний, страхов и безответных вопросов.
Насколько велика Вселенная? Сколько длится вечность? Насколько могуществен Бог? Тысячи лет бесконечность сбивает с толку лучшие умы человечества во всех областях мысли — от религии и философии до науки и математики. Ее запрещали, объявляли вне закона и отвергали. Во времена инквизиции монах Джордано Бруно был сожжен заживо на костре за предположение, что Бог в своей бесконечной силе создал бесчисленные миры.
Деление на ноль
Тем, кто не в силах сопротивляться искушению и желает понять, почему в тенях скрывается бесконечность, советуем поделить 6 на какое-нибудь маленькое число, близкое к нулю, но не равное ему, например 0,1. В этом ничего запретного нет. Если разделить 6 на 0,1, получится 60, довольно прилично.
Поделим 6 на еще меньшее число, скажем 0,01; ответ будет больше — 600. Если мы отважимся разделить 6 на число, которое гораздо ближе к 0, допустим, на 0,0000001, то ответ будет еще больше и составит 60 000 000.
Тенденция ясна. Чем меньше знаменатель, тем больше частное. В пределе, когда знаменатель приближается к нулю, частное стремится к бесконечности.
Вот настоящая причина, почему нельзя делить на 0.
Малодушные говорят, что ответ неопределенный. Но на самом деле он бесконечный.
По книге «Бесконечная сила».
неопределенных форм – я узнал, что 1/0 – это бесконечность, почему не минус бесконечность?
Поскольку у вас возникла эта путаница, я думаю, что полезно рассмотреть концепции нуля, бесконечности и «неопределенности».
В самом общем смысле деление противоположно умножению. Таким образом, тот факт, что 2 x 3 = 6, означает, что 6/3 = 2.
1 x 0 = 0. Применяя вышеуказанную логику, 0/0 = 1. Однако 2 x 0 = 0, поэтому 0/0 также должно быть 2. Фактически, похоже, что 0/0 может быть любым числом! Очевидно, что в этом нет никакого смысла – мы говорим, что 0/0 – это «undefined», потому что на самом деле ответа нет.
Точно так же 1/0 на самом деле не бесконечность. Бесконечность на самом деле не число, это скорее концепция. Если вы подумаете о том, как в школах часто описывается разделение, например, количество сладостей, распределяемых между несколькими людьми, вы увидите путаницу. Если я обойду некоторых людей, дав им по 0 конфет, сколько людей мне нужно будет обойти, пока я не раздаю свою 1 конфету? Бесконечное число? Отчасти потому, что я могу продолжать бесконечно. Однако я никогда не отдавал этот сладкий .Вот почему люди говорят, что 1/0 «стремится» к бесконечности – мы не можем использовать бесконечность как число, мы можем только представить, к чему мы приближаемся, когда мы движемся в направлении бесконечности. Однако в этом случае количество сладостей, которые у меня есть, никогда не меняется, так что я никуда не приближаюсь. Даже эта логика не работает.
Короче говоря, 1/0 не имеет смысла для вычисления. Когда мы действительно используем понятие бесконечности, мы склонны использовать положительную бесконечность там, где это не имеет значения чисто по соглашению.Однако, если вы думаете об этом слишком сильно, вы начинаете вникать в философию и тому подобное, например, “что на самом деле есть бесконечность?” и “подождите, что такое номер “?
Люди говорят о разных способах использования чисел, поэтому на самом деле они не считаются. Например, в тривиальном кольце есть только одно число, которое работает как 0 (добавьте его ко всему, и вы получите это) и 1 (умножьте его на что угодно, и вы снова получите то же самое) и имеет смысл, потому что вы можете только добавить его или умножить на себя, чтобы получить себя.На самом деле это довольно скучно, но в этом случае это одно число – назовем его x – равно 0 и 1, поэтому 1/0 = x / x = x, потому что все, что равно x. Как видите, это немного обман, потому что у нас даже недостаточно чисел, чтобы иметь представление о 1/0 в том смысле, в котором вы его думаете.
мягкий вопрос – Почему $ \ infty \ cdot 0 $ явно не равно $ 0 $?
Как отмечали некоторые другие, $ \ infty $ не является числом. Так что с этим нужно обращаться с некоторой осторожностью.
Чтобы прояснить ваши сомнения, вы написали, чтобы посмотреть на $ n \ times 0 $, а затем позволить $ n \ rightarrow \ infty $. Верно, что $$ \ displaystyle \ lim_ {n \ rightarrow \ infty} \ left (n \ times 0 \ right) = 0 $$
Однако, когда люди пишут $ \ infty \ times 0 $, обычно это сокращение для обозначения неопределенной формы, когда некоторая величина стремится к бесконечности, а какая-то другая величина стремится к нулю в ограничительном смысле, то есть выражения вида $$ \ lim_ { x \ rightarrow 0} \ left (е (x) \ times g (x) \ right) $$, где $ \ displaystyle \ lim_ {x \ rightarrow 0} f (x) = \ infty $ и $ \ displaystyle \ lim_ { x \ rightarrow 0} g (x) = 0 $.
(Обратите внимание, что $ \ infty $ не является числом в общепринятом смысле. Это просто сокращение для обозначения того, что что-то неограниченно растет, т.е. при любом числе ваша функция может принимать значение, превышающее это число.)
Например, пусть $ f (x) = \ frac {1} {x} $ как $ g (x) = x $, тогда $ f (x) \ times g (x) = 1 $, $ \ forall x \ neq 0 $ и, следовательно, $$ \ displaystyle \ lim_ {x \ rightarrow 0} \ left (f (x) \ times g (x) \ right) = \ lim_ {x \ rightarrow 0} 1 = 1 $$ Однако $ \ displaystyle \ lim_ {x \ rightarrow 0} f (x) = \ infty $ и $ \ displaystyle \ lim_ {x \ rightarrow 0} g (x) = 0 $ и, следовательно, в этом случае неопределенная форма оценивается как $ 1 $.
Случай, который напоминает то, что вы записали, – это когда $ f (x) = \ frac {1} {x} $ и $ g (x) = 0 $. Это снова неопределенная форма, поскольку $ \ displaystyle \ lim_ {x \ rightarrow 0} f (x) = \ infty $ и $ \ displaystyle \ lim_ {x \ rightarrow 0} g (x) = 0 $. Однако в этом случае $ f (x) \ times g (x) = 0 $, $ \ forall x \ neq 0 $ и, следовательно, $$ \ displaystyle \ lim_ {x \ rightarrow 0} \ left (f (x) \ умножить на g (x) \ right) = 0 $$
Еще один пример – посмотреть на $ f (x) = \ frac {1} {x} $ и $ g (x) = \ sqrt {x} $.+} \ frac {1} {\ sqrt {x}} = \ infty $$
Следовательно, вы не можете связать уникальное значение с $ \ infty \ times 0 $. Это зависит от решаемой проблемы. Подробнее о неопределенной форме можно прочитать здесь. (Как всегда с Википедией, прочтите ее, чтобы получить общее представление.)
Пределы– бесконечность над бесконечностью и бесконечность, умноженная на ноль, в вычислении, которое дает (правильно) 1
Надеюсь, вы не дублируете мой вопрос, поскольку он предназначен для конкретного случая, который я вам сейчас покажу, а именно о расчетах.2-1) $, я бы поступил следующим образом (просто для согласованности, потому что в предыдущем упражнении с той же функцией, но с пределом, приближающимся к 1, я проделал те же алгебраические шаги):
lim x, приближающийся к бесконечности, $ (x-2) (x + 1) / (x-1) (x + 1) $, применяя свойства пределов и алгебраическое свойство: lim x, которое приближается к бесконечности $ (x- 2) $ * lim x, который приближается к бесконечности $ (1 / x-1) $, засорение: (бесконечность – 2 = бесконечность) * (1 / бесконечность – 1 = бесконечность; 1 / бесконечность = 0).
Таким образом: бесконечность * 0 = undef .
Первый вопрос: это соглашение, что бесконечность * ноль и ноль * бесконечность не определены? Можно ли применить в этом случае свойство коммутативности? Не можем ли мы каким-либо образом интерпретировать эту операцию с 1 в результате? .
Также, если я сделаю то же самое вычисление другим способом (хотя, возможно, неверным с алгебраической точки зрения … Я не уверен, на самом деле, насчет этого … поскольку я не разрешаю процесс ограничения внутри скобка) Я получаю бесконечность * (1 / бесконечность) = бесконечность / бесконечность , и результат следует интерпретировать как неопределенный.То же самое с ограничением на минус бесконечность, я получаю -infinity * (1 / – inifnity) = -infinity / – infinity = undefined .
Однако Я знаю из графика, что бесконечно удаленный предел этой функции дает ровно 1! Означает ли это, что заявление о том, что операции не определены, является произвольным фактом или я делаю ошибки в своих алгебраических шагах? .
Если я поместил функцию в калькулятор, он выбрал бы разные алгебраические шаги – применяя более одного алгебраического свойства – чтобы избежать ситуации, которую я показал, а именно: бесконечность над бесконечностью, минус бесконечность над минус бесконечностью, 0 * бесконечность , как и в калькуляторе, мы вычисляем окончательно: $ (1-2 / x) / (1-1 / x) $, что дает $ 1-0 / 1-0 = 1 $.
Однако, поскольку я не вижу явных алгебраических ошибок в своих отрывках, я задаю вам этот вопрос. Из прочтения, которое у меня есть, я понимаю, что есть споры о бесконечности над бесконечностью, и это не так очевидно, учитывая операции, показанные выше как неопределенные, и, возможно, выбор зависит от отрасли математики и операции, которую мы выполняем или я совершенно не прав?
С практической точки зрения, вы предлагаете мне использовать отрывки из калькулятора для моих упражнений?
PS.Это результат работы калькулятора, но, пожалуйста, посмотрите и мои отрывки https://www.symbolab.com/solver/limit-calculator/%5Clim_%7Bx%5Cto%20%5Cinfty%7D%20%5Cfrac % 7B% 5Cleft% 28x% 5E% 7B2% 7D-x-2% 5Cright% 29% 7D% 7Bx% 5E% 7B2% 7D-1% 7D /? Origin = button
Имя: Джейсон Кто спрашивает: Студент Вопрос: Хай Джейсон, Мне нравится твой пример с картошкой. Меня несколько беспокоит то, что мы говорим о бесконечности, как если бы это было число, с которым мы можем обращаться так же, как и с другими числами.Мы все делаем это, но, сталкиваясь с подобным вопросом, важно спросить, откуда берется бесконечность (и ноль). Я собираюсь использовать обозначение функций, так как это упрощает выражение того, что я хочу. Я предполагаю, что у вас есть дробная часть формы f (x) / g (x) , и что когда x приближается к a, f (x) приближается к нулю, а g (x) приближается к бесконечности. Тогда возникает вопрос, каков предел f (x) / g (x) , когда x приближается к a? Чтобы немного облегчить себе жизнь, я предполагаю, что f (x) и g (x) никогда не бывают отрицательными.Таким образом, мне не нужно иметь дело с отрицательными знаками или абсолютными значениями. Если f (x) = 0 для каждого x, то f (x) / g (x) = 0 для каждого x, и, следовательно, предел равен нулю. (Это ваш пример картофеля.) Поскольку g (x) приближается к бесконечности, когда x приближается к a, когда x приближается к a, g (x)> 1. Таким образом, когда x приближается к a, 0 < f (x) / g (x)Если это то, что вы подразумеваете под «делением нуля на бесконечность», то это не неопределенно, это ноль. Пенни |
Является ли бесконечность, умноженная на ноль, = ноль?
Это часть серии статей, посвященных распространенным заблуждениям.
Это правда или ложь?
0 × ∞ = 00 \ раз \ infty = 00 × ∞ = 0
Почему некоторые говорят, что это правда: Ноль раз все равно нулю.
Почему некоторые люди говорят, что это ложь: Мы не можем выполнять арифметические действия с бесконечностью.
Подскажите правильный ответ
Утверждение ложно \ color {# D61F06} {\ textbf {false}} ложно.
Проба: Мы знаем, что не можем выполнять арифметику с бесконечностью. Но давайте возьмем предел и посмотрим, правда ли это:
limx → ∞f (x) = ∞, limx → ∞g (x) = 0, limx → ∞f (x) g (x) =? \ Lim_ {x \ to \ infty} f (x) = \ infty, \ quad \ lim_ {x \ to \ infty} g (x) = 0, \ quad \ lim_ {x \ to \ infty} f (x) g (x) = \ ,? x → ∞lim f (x) = ∞, x → ∞lim g (x) = 0, x → ∞lim f (x) g (x) =?
Нам известны две такие функции: f (x) = xf (x) = xf (x) = x и g (x) = 1xg (x) = \ frac {1} {x} g (x) = x1.Но тогда предел равен 111, а не 0, и, следовательно, это не обязательно 0. Мы можем сделать это ограничение любым значением, которое пожелаем, поэтому ∞ × 0 \ infty \ times 0∞ × 0 не определено. □ _ \ квадрат □
Ознакомьтесь с распространенными ложными опровержениями
Опровержение : Но любое число , умноженное на ноль, равно нулю, почему здесь этого не происходит?
Ответ : Вы правы, но бесконечность – это не число. 3} \\\\\\ \ lim_ {x \ to \ infty} f (x) g (x) & = \,? \ end {align} f (x) = x, g (x) x → ∞lim f (x) g (x) = x32 =?
. См. ТакжеДелится ли 1 на 0 неопределенным, бесконечным или и тем, и другим? | Тасним Мунира Проттяша | NSU ACM-W Student Глава
ОбложкаПрежде всего, попробуйте решить их и объяснить, не видя ответа.
Эти термины часто сбивают нас с толку, потому что большинство из нас не понимают их должным образом. А теперь посмотрите ответы.
ответов something / 0 :У вас может возникнуть вопрос, увидев эти ответы. Если нет – хорошо. Дело в том, что что-то деленное на 0 всегда не определено, потому что значение еще не определено. Итак, когда мы говорим, что это что-то, деленное на 0, есть бесконечность? Конечно, мы видели это много раз, но почему мы так говорим?
Ну, что-то деленное на 0 – бесконечность – единственный случай, когда мы используем лимит.Бесконечность – это не число, это длина числа. Когда мы используем limit, мы всегда думаем, что x к чему-то стремится, а не x к чему-то. Следовательно, мы не можем угадать это число. Поскольку мы не можем угадать точное число, мы рассматриваем его как длину числа или бесконечность. В обычных случаях значение чего-либо, деленного на 0, еще не установлено, поэтому оно не определено.
Неопределенная форма:
0/0 и деленная на бесконечность бесконечность неопределенна. Почему? В этом случае математические выражения верны.Должно быть значение, но мы не определили точное значение. Иногда он может иметь значение или быть неопределенным. Мы не знаем. Поэтому мы говорим, что эти термины имеют неопределенную форму.
По этой же причине бесконечность минус бесконечность и (минус бесконечность минус бесконечность) оба находятся в неопределенной форме, а не в нуле или минус бесконечности, потому что бесконечность может быть любым положительным или отрицательным числом. Итак, минус бесконечность минус бесконечность не всегда будет двигаться в отрицательном направлении.
Другое похожее выражение – бесконечность, умноженная на 0, следует этому правилу.Следовательно, он также находится в неопределенной форме.
1 делится на бесконечность:
В этом случае, если мы разделим небольшое число на большое число, результат будет очень близок к нулю. Поэтому мы считаем его нулевым.
Пример:
1/10 = 0,1
1/100 = 0,01
…
1/100000 = 0,00001Чем больше знаменатель, тем ближе частное к 0.
Итак, мы считаем результат равным 0.Ссылка:
1. Исчисление: ранние трансцендентальные, одинарная переменная, 9-е издание
John Wiley & Sons (2009)
Антон, Бивенс, Дэвис
Библиотека Microsoft ZeRO-Infinity содержит 32 триллиона параметров AI-модель
Microsoft недавно анонсировала ZeRO-Infinity, дополнение к своей обучающей библиотеке DeepSpeed AI с открытым исходным кодом, которая оптимизирует использование памяти для обучения очень больших моделей глубокого обучения.Используя ZeRO-Infinity, Microsoft обучила модель с 32 триллионами параметров на кластере из 32 графических процессоров и продемонстрировала тонкую настройку модели с 1 триллионом параметров на одном графическом процессоре.
Команда DeepSpeed описала новые функции в недавнем сообщении в блоге. ZeRO-Infinity – это последняя версия семейства методов оптимизации памяти Zero Redundancy Optimizer (ZeRO). ZeRO-Infinity представляет несколько новых стратегий для решения проблем с памятью и пропускной способностью при обучении больших моделей глубокого обучения, в том числе: новый механизм разгрузки для использования памяти ЦП и энергонезависимой памяти Express (NVMe), мозаика, ориентированная на память, для обработки больших операторов без параллелизм моделей, секционирование, ориентированное на полосу пропускания, для снижения затрат на полосу пропускания и дизайн, ориентированный на перекрытие, для планирования передачи данных.По данным команды DeepSpeed:
Усовершенствованный ZeRO-Infinity предлагает возможность системы выйти за пределы стены памяти графического процессора и обучать модели с десятками триллионов параметров, что на порядок больше, чем могут поддерживать современные системы. Он также предлагает многообещающий путь к обучению моделей со 100 триллионами параметров.
Недавняя тенденция в исследованиях глубокого обучения заключается в обучении более крупных моделей на большем количестве данных, при этом некоторые из крупнейших моделей достигают сверхчеловеческой производительности при выполнении определенных задач.Однако для обучения этих моделей требуются большие и дорогие кластеры графических процессоров. Во многих случаях разработчики моделей могут использовать трансферное обучение для точной настройки большой предварительно обученной модели, используя только часть вычислительных ресурсов, которые требовались для предварительного обучения; тем не менее, очень большие модели, такие как GPT-3, слишком велики для точной настройки на одной машине. Оба сценария часто требуют рефакторинга кода для использования распределенных платформ обучения.
Для решения этих проблем Microsoft впервые выпустила библиотеку DeepSpeed и оптимизатор с нулевым резервированием (ZeRO) в начале 2020 года в рамках своей программы AI at Scale.ZeRO был улучшен в три этапа, на каждом этапе добавлялось дополнительное разбиение состояния модели, а также возможность «выгружать» данные и выполнять вычисления с графического процессора на центральный процессор обучающей машины. Этап 3 был выпущен в начале этого года, с возможностью обучения моделей до 40 миллиардов параметров на одной машине и более 2 триллионов параметров в кластере из 512 графических процессоров.
Последняя итерация ZeRO, ZeRO-Infinity, предлагает новые схемы для устранения двух узких мест при обучении больших моделей: размер памяти и пропускная способность памяти.Механизм бесконечной разгрузки увеличивает объем памяти, доступной для хранения параметров модели и активаций, за счет использования памяти ЦП и NVMe; В отличие от предыдущих поколений ZeRO, движок бесконечности может выгружать всю модель в эти места. Ориентация на память – еще один новый метод, который сокращает объем памяти, занимаемый большими слоями модели, за счет их разбиения на более мелкие «плитки», которые могут выполняться последовательно; это позволяет обучать большие модели, не требуя параллелизма моделей.Для решения проблем с пропускной способностью ZeRO-Infinity вводит секционирование, ориентированное на полосу пропускания, которое разделяет параметры модели по нескольким параллельным процессам данных, и механизм перекрытия, который одновременно выполняет обмен данными между NVMe-CPU, CPU-to-GPU и GPU-GPU. .
Команда провела несколько экспериментов, чтобы проверить способность ZeRO-Infinity к масштабированию, обучая “GPT-подобные” модели трансформаторов разных размеров. По сравнению с современной средой 3D-параллелизма ZeRO-Infinity обрабатывала модели в 40 раз больше, используя то же вычислительное оборудование.По сравнению с предыдущей версией ZeRO, новая версия достигла двукратного ускорения на кластере с 64 GPU. При обучении модели с 1T-параметрами ZeRO-Infinity суперлинейно масштабировалась на кластерах различного размера от 64 до 512 графических процессоров.
Библиотека DeepSpeed, которая включает семейство оптимизаторов памяти ZeRO, написана для среды глубокого обучения PyTorch и была принята в нескольких других проектах на основе PyTorch.
