Законы Кеплера
Законы Кеплера§7. Законы Кеплера
Рис.62.
Первый закон. Планеты движутся по эллипсам, в общем фокусе которых находится Солнце.
Уравнение эллипса в полярной системе координат с полюсом в Солнце и с полярной осью, проходящей через перигелий, имеет вид:
где e=c/a – эксцентриситет. Отсюда следуют выражения для минимального и максимального расстояния планеты от Солнца: q=a(1-e) и Q=a(1+e). Например, для орбиты Земли a=149,6×106 км, e=1/60, q=147,1×106 км и Q=152,1×106 км.
Второй закон (закон площадей): за одинаковые промежутки времени радиус-вектор планеты ометает равные площади. На рис.63 точки К1, К2, К3 и К4 – положения планеты в моменты t1, t2, t3 и t4 соответственно.
Рис.63.
Второй закон можно записать в виде:
где и угол q выражен в радианах; Р – период обращения планеты вокруг Солнца.
Из второго закона Кеплера следует, например, что в перигелии скорость Земли в 1,0339 раз больше, чем в афелии (разность скоростей составляет примерно 1 км/с).
Третий закон: квадраты периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их орбит. Его можно записать так:
Если время выражать в периодах обращения Земли вокруг Солнца, а расстояния – в астрономических, единицах (1 а.е.= 149,6×106), то третий закон примет особенно простой вид: P=a3/2
Ньютон обобщил (и уточнил) все эти законы на случай двух произвольных материальных точек с массами m1 и m2, притягивающихся друг к другу по закону всемирного тяготения (других сил нет).
Точки находятся по разные стороны от центра масс их системы, который делит отрезок, соединяющий точки, на части, длины которых обратно пропорциональны массам соответствующих точек. При этом каждая из них движется по эллипсу, в фокусе которого находится указанный
центр масс, рис,64.
Рис.64.
Однако при достаточно больших скоростях точек орбитами могут быть также парабола или гипербола.
Случаи, рассмотренные Кеплером соответствуют ситуации, когда начало системы отсчёта помещено в Солнце (например, в массу m1 рис.64). Планета же (масса её – m2) движется по эллипсу с фокусом в первой точке. Притяжения других планет не учитываются. Математическая запись уточнённого третьего закона Кеплера такова:
В таком виде закон применяют при определении масс двойных звёзд, а также масс планет, у которых имеется спутник. Пусть, например, P и a – период обращения и большая полуось относительной орбиты спутника данной планеты (или звезды).
Тогда сумма масс планеты и спутника (или первой и второй звезды) может быть найдена по формуле:
Как правило, массой спутника планеты можно пренебречь. Чтобы определить отношение масс звёзд, необходимо исследовать их орбиты относительно центра масс системы этих звёзд. Если a
Книга, с которой начинается наука физика. К 325-летию “Математических начал натуральной философии» И. Ньютона
325 лет назад, летом 1687 года, вышел в свет фундаментальный труд Исаака Ньютона “Математические начала натуральной философии”. При жизни автора труд издавался еще дважды – в 1713 и 1725 годах.
“Начала натуральной философии» Ньютона составляют незыблемую основу теоретической механики, астрономии и физики. Лагранж назвал это произведение “величайшим из произведений человеческого ума”, поэтому понятна та польза, которую каждый может получить с изучения этого произведения “, – так начинает “Предисловие переводчика” к изданию труда Ньютона на русском языке академик А.
В истории науки “Начала” Ньютона сыграли исключительную роль. По этой книги не только начинается история физики как науки. Эта книга оказала огромное влияние и на основоположника классической политэкономии Адама Смита, и на молодого Иммануила Канта, и на французских философов-просветителей …
К сожалению, в наше время мало кто открывает “Начала” Ньютона и знакомится, хотя бы, с предисловиями к книге. Более того, в последние десятилетия вышло множество работ, где принципы механики Ньютона провозглашаются устаревшими, а ему приписываются взгляды, которых он не только не имел, но и против которых решительно выступал, в частности введения в физику действия на расстоянии.
Следует заметить, что фальсификация взглядов Ньютона началась еще при его жизни – во время подготовки второго издания «Начал», проводимого кембриджским профессором астрономии и экспериментальной физики Роджером Котсом под руководством инициатора издания директора Тринити-колледжа Кембриджа епископа Ричарда Бентли.
Поэтому, по случаю юбилея великой книги Ньютона, думаю, лучше будет не повторять еще раз известные слова о ее исторической роли, которые можно найти в энциклопедиях, а коротко рассказать о некоторых изложенных в ней идеях – тех, благодаря которым эта книга стала началом новой эры в науке. Но сначала несколько слов об обстоятельствах появления этой книги.
Над своим большим произведением Ньютон начал работать летом 1684 года. К тому времени он уже 15 лет был профессором математики Тринити-колледжа и 12 – членом Лондонского королевского общества, куда был избран за изобретение зеркального телескопа. Ньютон также изобрел метод бесконечно малых и выполнил известные исследования по оптике. Следует заметить, что полемика по поводу этих исследований надолго отбила у него желание публиковать новые результаты и втягиваться в дискуссии. Неизвестно, когда и в какой форме увидели бы мир результаты исследований Ньютона по механике, если бы не его друг астроном Эдмунд Галлей.
Летом 1684 года Е.
Галлей, Роберт Гук – секретарь Королевского общества, Кристофер Рен – член Общества и знаменитый архитектор во время встречи в одной из лондонских кафе обсуждали вопрос о траектории движения небесных тел, что притягиваются с силой, обратно пропорциональной квадрату расстояния между ними. Р.Гук утверждал, что знает решение этой задачи и пообещал представить его, однако обещание не выполнил. Тогда Галлей, находясь в августе 1684 г. в Кембридже, обратился с этим вопросом к Ньютону, который, не раздумывая, ответил: “Эллипс” и добавил, что знает это с 1679 года. В ноябре 1684 г. он передал рукопись Галлею, о чем тот доложил Королевскому обществу 10 декабря. Рукопись с решением задачи Общество получило в феврале 1685 г., но, по желанию Ньютона, его не отдали в печать, а только зарегистрировали на случай защиты приоритета.
Через год в протоколах заседаний Общества появилась исторический запись: “28 апреля 1686 г. д-р Винсент передал манускрипт Ньютона под названием” Principia mathematica philosophiae naturalis “, где дается математическое доказательство гипотезы Коперника в том виде, как она была предложена Кеплером, и все небесные движения объясняются на основании единого предположения о тяготении к центру Солнца, обратно пропорционального квадрату расстояния “.
19 мая 1686 г. было принято решение напечатать труд Ньютона на средства Общества, но денег не было, поскольку перед тем Общество издало книгу “История рыб» (авторы Willughly и Ray), которая не имела спроса, и исчерпало свой бюджет . Тогда Галлей решил выдать “Начала” за свой счет. Печать труда (в трех книгах) тиражом 300 экземпляров завершился в июле 1687 года.
“Начала” Ньютона произвели огромное впечатление на ученый мир. Это была первая работа, где рассматривались не те или иные проблемы механики, а механика вообще. В первой книге Ньютон дал определения основных понятий механики, а также сформулировал основные законы. Во второй книге он рассмотрел движение тел в среде. Третья книга содержала теорию движения небесных тел. Книга вызвала горячую полемику, в частности потому, что его идеи противоречили взглядам тогдашних основных школ философии.
В предисловии к первому изданию Ньютон ясно изложил замысел своего труда и сформулировал важнейшую программу исследования природы, которую затем реализовывало не одно поколение ученых.
“Поскольку древние ученые, по словам Паппуса (Паппус, Папп – греческий математик, III в. – В.И.) придавали большое значение механике при изучении природы, то новейшие авторы, отбросив субстанции и скрытые свойства, стараются подчинить явления природы законам математики …
Древние авторы рассматривали механику двояко: как рациональную (умозрительную),что развивается точными доказательствами, и как практическую. К практической механике относятся все ремесла и производства, именуемые механическими, от которых получила свое название и сама механика.
Поскольку ремесленники удовлетворяются в работе только малой степенью точности, то сложилось мнение, что механика тем отличается от геометрии,что все вполне точное относится к геометрии, менее точное относится к механике …
Однако само проведение прямых линий и кругов, что служит основой геометрии, по сути относится к механике. Геометрия не учит тому, как проводить эти линии, но предполагает (постулирует) осуществление этих построений .
..
Итак, геометрия основывается на механической практике и является не чем иным, как частью общей механики, в которой излагается и доказывается искусство точного измерения. Но поскольку в искусствах и производствах приходится в основном иметь дело с движением тел, то обычно все, что касается только величины, относят к геометрии, а все, что касается движения, к механике.
В этом смысле рациональная механика есть учение о движениях, вызванных любыми силами, и о силах, которые необходимы для порождения каких-либо движений, точно изложенным и доказанным.
В древности эта часть механики была разработана только в виде учения о пяти машинах (рычаг, коловорот, блок, винт, клин – В.И.) при этом даже вес (поскольку это не усилие, развиваемое руками) рассматривалась ими не как сила, а лишь как груз что движется указанными машинами. Мы же, рассуждая не об ремеслах, а об учении о природе, и, следовательно … о силах природы, будем, главным образом, заниматься тем, что относится к тяжести, легкости, силе упругости, сопротивления жидкостей и подобным силам – притягательным или напорным.
Поэтому и произведение это нами предлагается как математические начала натуральной философии (физики).
Вся сложность физики, как будет видно, состоит в том, чтобы за явлениями движения распознать силы природы, а затем этими силами объяснить другие явления. Для этой цели предназначены общие предположения, изложенные в первой и второй книгах. В третьей же книге мы даем пример вышеупомянутой программы, объясняя систему мира, потому что здесь из небесных явлений, с помощью предположений, доказанных в предыдущих книгах, математически выводятся силы притяжения тел к Солнцу и отдельных планет. Затем из этих сил, а также с помощью математических предположений выводится движение планет, комет, Луны и моря.
Желательно было бы вывести из начал механики другие явления природы, рассуждая подобным же образом, потому что многое заставляет меня думать, что все эти явления обусловливаются некоторыми силами, с которыми частицы тел, вследствие причин пока неизвестных, или стремятся друг к другу и объединяются в правильные фигуры, или же взаимно отталкиваются и удаляются друг от друга.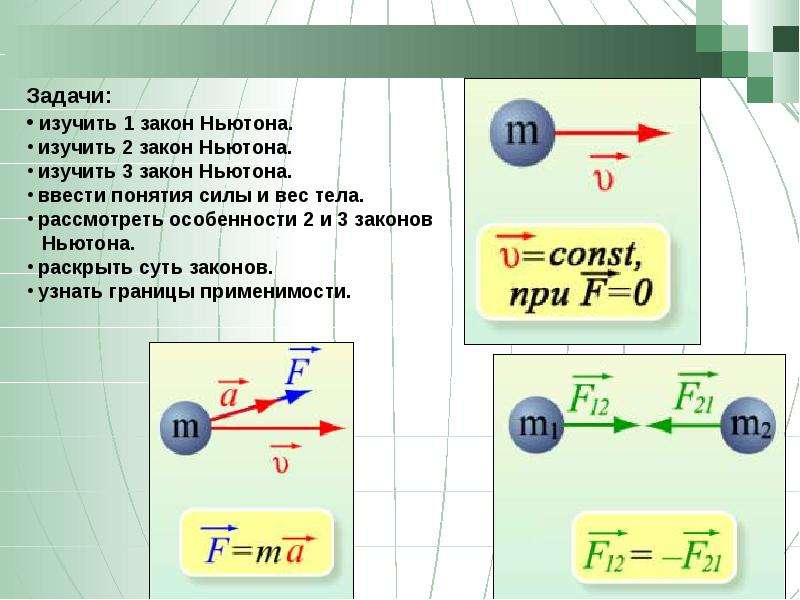
Поскольку эти силы неизвестны, то до сих пор попытки философов объяснить явления природы оставались бесплодными …
При издании этого произведения поспособствовал острый умом и во всех отраслях науки ученый муж Галлей, который не только исправил печатные корректуры и заботился об изготовлении рисунков, но даже только по его настоянию я приступил и к самому изданию … “.
Еще раз повторю слова с этого предисловия, которыми кратко выражено метод исследования Ньютона: “за явлениями движения распознать силы природы, а затем с этими силами объяснить другие явления”.
Более подробно метод Ньютона описал Роджер Котс в предисловии ко второму изданию «Начал».
“Тех, что пытаются преподавать физику вообще можно отнести к трем категориям. Прежде всего выделяются те, что приписывают разного рода предметам специальные скрытые качества, от которых неизвестно каким образом и должно происходить, по их мнению, взаимодействие отдельных тел. В этом заключалась суть схоластических учений, берущих свое начало от Аристотеля и перипатетиков.
они утверждали, что отдельные действия тел происходят вследствие особенностей самой их природы, в чем же эти особенности заключаются, они не учили, значит, по сути, они ничего не учили. Таким образом все сводилось к наименованиям отдельных предметов, а не к самой сути дела, и можно сказать, что ими создано философский язык, а не саму философию.
Другие … утверждали, что вся материя во вселенной однородная и все различия видов, которые заметны в телах, обусловленные некоторыми простыми и доступными пониманию свойствами частиц, составляющих тела … Но они предоставляют себе право предполагать которые им заблагорассудится неизвестные виды и величины частиц, неопределенные их расположения и движения, а также придумывать различные неощутимые жидкости что свободно проникают через поры тел и имеют всемогущую тонкость и скрытые движения.
.. Они, позаимствовав основу своих рассуждений из гипотез, даже если бы все дальнейшее развивали очень точно на основе законов механики, создали бы весьма изящную и красивую байку, но только байку.
Остается третья категория – последователи экспериментальной философии (т.е. экспериментального метода при исследовании явлений природы). Они также стремятся вывести причины всего сущего с возможно простых начал, но они ничего не принимают за начало, кроме того, что подтверждается явлениями, которые происходят. Они не придумывают гипотез и не вводят их в физику иначе, как в виде предположений, справедливость которых необходимо исследовать. Таким образом, они пользуются двумя методами – аналитическим и синтетическим. Силы природы и простейшие законы их действия они выводят аналитически из определенных явлений, а затем синтетически получают законы других явлений. Вот это лучший способ исследования природы и принят нашим знаменитым автором … “.
Стоит заметить, что метод исследований Ньютона – это не индукция, как говорили многие философы, а сочетание анализа и синтеза, когда на основе изучения явлений высказываются предположения об их причинах (начала), которые используются для объяснения других явлений, и только успех этих объяснений дает основание для вывода об истинности предположений.
Философ, который написал, что “Спиноза исходит из явственопродуманных предпосылок, а Ньютон, делая вид, будто у него вообще никаких предпосылок нет,выходит с непонятных для себя самого предпосылок, аксиом и постулатов”, похоже, никогда не читал работ Ньютона. Кстати, Ньютон не только проводил исследования действительно научным методом (сочетая анализ и синтез, используя наблюдение, эксперимент и теоретические исследования), но и в начале первой книги «Начал» четко сформулировал основные определения и принципы, а в начале третьей подал “Правила философствования “, первое из которых гласит:” Не следует принимать в природе иных причин сверх тех, которые истинны и достаточны для объяснения явлений … “.
Непонимание сути метода Ньютона дало основания некоторым философам, начиная с Гегеля, заявить, что закон всемирного тяготения, по сути, открытый Кеплером, поскольку его можно математически вывести из третьего закона Кеплера.
Ньютон опроверг это обвинение еще тогда, когда Гегеля не было на свете (отвечая на претензию Гука на открытие закона всемирного тяготения).
Поскольку существуют погрешности измерений, никто никогда не докажет на основании наблюдений, что в законе всемирного тяготения расстояние между небесными телами стоит в степени 2, а не, например, в степени 2,0000006. Более того, поскольку планеты притягиваются не только к Солнцу, но и друг к другу, точные наблюдения показывают, что движение планет противоречит законам Кеплера.
Ньютон же, проанализировав движение Луны, планет, тел на поверхности Земли, путем индукции получил предположение о том, что все тела притягиваются с силой, обратно пропорциональной квадрату расстояния. Положив это предположение в основу теории движения различных небесных тел и получив согласованность расчетов с данными наблюдений, Ньютон сделал вывод об истинности этого предположения.
В предисловии ко второму изданию «Начал» Р.Котс вспоминает “отбросов того безбожного стада, которые думают, что мир управляется роком, а не провидением, и материя, в силу своей собственной необходимости, всегда и везде существовала, что она бесконечна и вечна “, а дальше делает выводы:” надо быть слепым, чтобы с прекрасного и мудрого строения мира не увидеть величайшей доброты всемогущего творца, надо быть сумасшедшим, чтобы этого не признавать.
Поэтому замечательное произведение Ньютона является верной защитой против нападений безбожников, и нигде не найти лучшего оружия против нечестивой шайки, как в этом колчане “.
Чтобы книга Ньютона смогла стать таким оружием, Р.Котс внес в ее текст ряд изменений, не всегда согласованных с автором (см .: Цейтлин З.А. “Наука и гипотеза”. М.-Л., Госиздат. 1926).
С тех пор Ньютону приписывают представление о том, что тяготение является таким существенным свойством тел, которое объяснять не надо, что тела могут действовать на расстоянии через абсолютную пустоту (дальнодействия) и наука должна ограничиться описанием явлений. Действительные взгляды Ньютона можно понять со следующих высказываний.
Ньютон, в частности, писал: “Название притяжение (центром), напор или “стремление” (в центр) я применяю все равно одно вместо другого, рассматривая эти силы не физически, а математически”; “Рассматривая центростремительную силу как притяжение, стоило бы, если выражаться физически, называть ее более правильно напором”.
В письме к Бентли от 25 февраля 1693 г., Ньютон писал: “Предполагать, что тяготение является существенным, неразрывным и врожденным свойством материи, так что тело может действовать на другое на любом расстоянии в пустом пространстве, без посредства чего-то, что передает действие и силу, это, по моему мнению, такой абсурд, который немыслим ни для кого, кто умеет достаточно разбираться в философских предметах. Тяготение должно быть обусловлено агентом, что постоянно действует по определенным законам ».
По поводу действия на расстоянии: “Теперь следовало бы кое-что добавить об очень тонком эфире (spiritus), силой и действием которого частицы тел при очень малых расстояниях взаимно притягиваются, а при касании сцепляются; наэлектризованные тела действуют на большие расстояния, как отталкивая, так и привлекая близкие малые тела, свет излучается, отражается, преломляется … Но это нельзя изложить кратко, к тому же нет и достаточного запаса опытов, которыми законы действия этого эфира были бы точно определены и показаны ».
“Я не придумываю гипотез (hypotheses non fingo). Все, что не выводится из явлений, должно называться гипотезой; гипотезам же метафизическим, физическим, механическим, скрытым свойствам не место в экспериментальной философии”.
Ошибочным является утверждение, что Ньютон ввел методологию “чистого описания” природы, введя понятие силы. На самом деле он подчеркивал, что сила – это временный шаг, математическая фикция, которая упрощает движение вперед в познании природы.
Не могу не заметить, что многие не критически повторяют слова Эрнста Маха по поводу ньютоновского абсолютного пространства и времени: их надо отбросить, как чисто абстрактные вещи, которые опытами не выявляются. По такой логике следует отказаться от всех абстракций – чисел, геометрических фигур, общих понятий, которые тоже подлежат экспериментальным исследованиям. А еще Мах назвал неправильным Ньютоновское определения массы как произведения плотности на объем, не разобравшись, что под плотностью Ньютон понимал количество атомов в единице объема.
… Сегодня все больше авторов пишет о кризисе физики в ХХ – начале XXI века. На нескольких языках переведены книги Джона Хоргана “Конец науки” (1996.) и Ли Смолина “Неприятности с физикой” (2006 г.), в которых имеется констатация кризиса, но нет даже намеков на пути выхода из нее. И, кажется, я знаю почему. Потому что авторы этих книг не имеют никакого представления о методах исследования основоположника физики. Итак, читайте труды И. Ньютона, и прежде всего – “Математические начала натуральной философии»!
Октябрьская математическая образовательная программа: Преподаватели
Положение об октябрьской математической образовательной программе Центра «Сириус» по направлению «Наука»
1. Общие положения
1.1. Настоящее Положение определяет порядок организации и проведения октябрьской математической образовательной программы Центра «Сириус» (далее – образовательная программа), методическое и финансовое обеспечение образовательной программы.
1.2. Образовательная программа по математике проводится в Центре «Сириус» (Образовательный Фонд «Талант и Успех) со 2 по 25 октября 2019 года.
1.3. Для участия в образовательной программе приглашаются школьники 6-10 классов (по состоянию на февраль 2019 года) из образовательных организаций следующих регионов: Оренбургская область, Иркутская область, Калининградская область, Кировская область, Курганская область, Нижегородская область, Пермский край, Республика Башкортостан, Республика Мордовия, Республика Татарстан (Татарстан), Самарская область, Саратовская область, Свердловская область, Томская область, Тюменская область, Удмуртская Республика, Ульяновская область, Челябинская область, Чувашская Республика – Чувашия.
Участник образовательной программы должен обучаться в одном из указанных регионов как на момент подачи заявки, так и по состоянию на октябрь 2019 года.
1.4. К участию в образовательной программе допускаются школьники, являющиеся гражданами Российской Федерации.
1.5. Общее количество участников образовательной программы: до 300 школьников.
1.6. Регионами-организаторами, обеспечивающими научно-методическое и кадровое сопровождение образовательной программы, являются: Республика Татарстан, Удмуртская республика, Ульяновская область.
1.7. Персональный состав участников образовательной программы утверждается Экспертным советом Образовательного Фонда «Талант и успех» по направлению «Наука».
1.8. В связи с целостностью и содержательной логикой образовательной программы, интенсивным режимом занятий и объемом академической нагрузки, рассчитанной на весь период пребывания обучающихся в Образовательном центре «Сириус», не допускается участие школьников в отдельных мероприятиях или части образовательной программы: исключены заезды и выезды школьников вне сроков, установленных Экспертным советом Фонда.
1.9. В случае нарушений правил пребывания в Образовательном центре «Сириус» или требований настоящего Положения решением Координационного совета участник Образовательной программы может быть отчислен с образовательной программы.
2. Цели и задачи образовательной программы
2.1. Октябрьская математическая образовательная программа ориентирована на выявление математически одаренных школьников в регионах, указанных в п.1.3, максимальное развитие их математического потенциала, повышение общекультурного уровня участников образовательной программы.
2.2. Задачи образовательной программы:
• развитие математических способностей учащихся и расширение их математического кругозора путем интенсивных занятий по углубленной программе у ведущих педагогов России;
• развитие у школьников свойственного математике стиля мышления, повышение их общей и математической культуры, воспитание научной честности и умения вести научную дискуссию;
• подготовка учащихся к математическим олимпиадам;
• популяризация математики как науки.
3. Порядок отбора участников образовательной программы
3.1. Отбор участников Образовательной программы осуществляется координационным советом, формируемым руководителем Образовательного Фонда «Талант и успех», на основании требований, изложенных в настоящем Положении, а также общего порядка отбора в Центр «Сириус».
К участию в конкурсном отборе приглашаются учащиеся образовательных организаций, реализующих программы общего образования, из регионов, указанных в п.1.3.
3.2. Порядок отбора учащихся 6-х и 7-х классов (по состоянию на февраль 2019 г.).
3.2.1. К участию в конкурсном отборе приглашаются учащиеся 6-х и 7-х классов. К участию в конкурсном отборе в виде исключения могут быть допущены учащиеся 5 классов, прошедшие отбор по программе 6 класса. От таких учащихся требуется опережающее полное владение школьным курсом математики соответствующего уровня.
3.2.2. Для участия в конкурсном отборе необходимо пройти регистрацию на сайте Центра «Сириус» .
Регистрация будет открыта с 19 февраля по 12 марта 2019 года.
3.2.3. По итогам оценки академических достижений на образовательную программу без прохождения отборочных испытаний приглашаются:
– участники заключительного этапа всероссийской олимпиады по математике им.
Л.Эйлера 2018-2019 учебного года, набравшие пороговое количество баллов;
– участники регионального этапа всероссийской олимпиады по математике им. Л.Эйлера 2018-2019 учебного года, набравшие пороговое количество баллов.
Пороговые количества баллов будут определены и опубликованы на сайте Центра «Сириус» https://sochisirius.ru и в дистанционной системе Сириус.Онлайн 2 апреля 2019 г., после завершения заключительного этапа всероссийской олимпиады по математике им. Л.Эйлера.
3.2.4. С 25 февраля по 24 апреля 2019 г. состоится обучение зарегистрировавшихся школьников в дистанционном учебно-отборочном курсе на платформе Сириус.Онлайн.
3.2.5. По итогам обучения в дистанционном учебно-отборочном курсе формируются отдельно по классам списки школьников, на основе которого координационный совет программы утверждает список участников заочного отборочного тура. Этот список публикуется в дистанционной системе до 25 апреля 2019 г.
3.2.6. Заочный отборочный тур состоится 27 апреля 2019 г. Регламент проведения заочного отборочного тура публикуется в дистанционной системе до 15 апреля 2019 г. Школьники, нарушившие регламент проведения заочного отборочного тура, к заключительному очному отборочному туру не допускаются.
3.2.7. По совокупности результатов обучения в дистанционном учебно-отборочном курсе и результатов заочного отборочного тура будет сформирован список участников заключительного отборочного тура, который будет опубликован на сайте Центра «Сириус» https://sochisirius.ru и в системе Сириус.Онлайн до 29 апреля 2019 г.
3.2.8. Заключительный очный отборочный тур проводится 18 мая 2019 г. в регионах Российской Федерации, указанных в п.1.3. В одном регионе может быть несколько пунктов проведения. Регламент проведения заключительного очного отборочного тура будет опубликован на сайте Центра «Сириус» и в системе Сириус.Онлайн не позднее 29 апреля 2019 г. Работы школьников, нарушивших регламент проведения заключительного очного отборочного тура, не рассматриваются. Заключительный очный отборочный тур проводится с использованием средств видеофиксации. Работы участников заключительного очного отборочного тура проверяются централизованно. Порядок отправки отсканированных работ на централизованную проверку определяется координационным советом программы. Процедуры показа работ и апелляции детализируются в регламенте проведения очного отборочного тура.
3.2.9. На заключительный очный отборочный тур, вне зависимости от результатов обучения в дистанционном учебно-отборочном курсе и в заочном отборочном туре, приглашаются следующие учащиеся, прошедшие регистрацию на программу в соответствие с п.3.2.2 настоящего Положения:
– участники регионального этапа олимпиады им. Л.Эйлера 2018-2019 учебного года, набравшие не менее 32 баллов; баллы на региональном этапе олимпиады им. Л. Эйлера засчитываются по результатам проверки работ центральным жюри олимпиады;
– участники октябрьской образовательной математической программы по математике 2018 г., являющиеся учениками не выше 7 класса по состоянию на февраль 2019 г., успешно сдавшие до 15 апреля зачет в системе дистанционного постсопровождения. Список таких школьников публикуется в дистанционной системе в срок до 25 апреля 2019 г.
3.2.10. Отбор участников образовательной программы по итогам очного заключительного отборочного тура производится следующим образом. По итогам очного заключительного отборочного тура формируется ранжированный список школьников отдельно по каждой параллели и по каждому региону.
3.2.10.1. На образовательную программу приглашаются от каждого региона три ученика 7 класса с наивысшим рейтингом при условии, что они набрали необходимое пороговое количество баллов, определяемое координационным советом программы. На оставшиеся места приглашаются ученики 7 класса в соответствие с общим рейтингом.
3.2.10.2. На образовательную программу приглашаются от каждого региона три ученика 6 класса с наивысшим рейтингом при условии, что они набрали необходимое пороговое количество баллов, определяемое координационным советом программы. На оставшиеся места приглашаются ученики 6 класса в соответствие с общим рейтингом.
3.3. Порядок отбора учащихся 8-х классов (по состоянию на февраль 2019 г.).
Учащиеся 8-х классов (по состоянию на февраль 2019 г.) участвуют в конкурсном отборе на образовательную программу только при наличии достижений на математических мероприятиях высокого уровня.
3.3.1. По итогам оценки академических достижений на образовательную программу без прохождения отборочных испытаний приглашаются:
– участники заключительного этапа всероссийской олимпиады по математике им. Л.Эйлера 2018-2019 учебного года, набравшие пороговое количество баллов;
– участники регионального этапа всероссийской олимпиады по математике им. Л.Эйлера 2018-2019 учебного года, набравшие пороговое количество баллов;
– участники заключительного этапа всероссийской олимпиады школьников по математике 2018-2019 учебного года, набравшие пороговое количество баллов;
– участники регионального этапа всероссийской олимпиады школьников по математике 2018-2019 учебного года, набравшие пороговое количество баллов.
3.3.2. К участию в конкурсном отборе приглашаются учащиеся 8-х классов:
– набравшие на региональном этапе всероссийской олимпиады по математике им. Л.Эйлера 2018-2019 учебного года или на региональном этапе всероссийской олимпиады школьников по математике за 9 класс баллы в диапазоне, устанавливаемом координационным советом образовательной программы;
– участники октябрьской образовательной математической программы по математике 2018 г., являющиеся учениками 8 класса по состоянию на февраль 2019 г., успешно сдавшие зачет в системе дистанционного постсопровождения. Список таких школьников публикуется в дистанционной системе в срок до 20 апреля 2019 г.
Конкурсный отбор будет проходить в форме очного отборочного тура в сроки и по регламенту заключительного очного отборочного тура для 6-х и 7-х классов (см. п. 3.2.8). По его итогам участники приглашаются на образовательную программу в соответствие с общим для всех регионов рейтингом.
3.3.3. Пороговые количества баллов в п.3.3.1. и диапазон баллов в 3.3.2. будут определены и опубликованы на сайте Центра «Сириус» https://sochisirius.ru 2 апреля 2019 г., после завершения заключительного этапа всероссийской олимпиады по математике им. Л.Эйлера. Регистрация учащихся 8-х классов на образовательную программу и для участия в конкурсном отборе будет проходить с 2 по 25 апреля 2019 г. После завершения заключительного этапа всероссийской олимпиады школьников по математике списки участников, приглашаемых на образовательную программу по ее итогам, будут дополнены.
3.3.4. Если на основании п 3.3.1-3.3.3. на образовательную программу от региона не будет приглашено ни одного участника 8 класса,то от региона приглашается участник, набравший наибольшее количество баллов на очном отборочном туре, при условии, что он набрал необходимое пороговое количество баллов, определяемое координационным советом программы.
3.4. Порядок отбора учащихся 9-х и 10-х классов (по состоянию на февраль 2019 г.).
Учащиеся 9-х и 10-х классов (по состоянию на февраль 2019 г.) отбираются на образовательную программу только на основе своих достижений на математических олимпиадах высокого уровня.
3.4.1. По итогам оценки академических достижений на образовательную программу без прохождения отборочных испытаний приглашаются:
– участники заключительного этапа всероссийской олимпиады школьников по математике 2018-2019 учебного года, набравшие пороговое количество баллов;
– участники регионального этапа всероссийской олимпиады школьников по математике 2018-2019 учебного года, набравшие пороговое количество баллов.
3.4.2. Пороговые количества баллов по каждому классу будут определены и опубликованы на сайте Центра «Сириус» https://sochisirius.ru 1 мая 2019 г., после завершения заключительного этапа всероссийской олимпиады школьников по математике. Регистрация учащихся 9-х и 10-х классов на образовательную программу будет проходить с 1 по 20 мая 2019 г.
3.5. При отборе на образовательную программу учитываются академические достижения, загруженные в государственный информационный ресурс о детях, проявивших выдающиеся способности.
3.6. Список школьников, приглашенных к участию в октябрьской образовательной программе, публикуется на официальном сайте Центра «Сириус» не позднее 20 июня 2019 года.
3.7. Учащиеся, отказавшиеся от участия в октябрьской образовательной программе, могут быть заменены на следующих за ними по рейтингу школьников.
3.8. Предельная численность участников октябрьской образовательной программы от каждого региона Российской Федерации составляет 40 человек. В случае приглашения на основании п.3.2.3., 3.3.1. и 3.4.1. суммарно более 25 участников от одного региона координационный совет программы может изменить для этого региона критерии приглашения, перечисленные в этих пунктах. В случае прохождения на образовательную программу более 40 участников от одного региона по решению координационного совета программы в этом регионе могут изменены критерии приглашения в п 3.2.10.1 и 3.2.10.2. и/или проведен дополнительный очный отборочный тур. Дата и регламент проведения дополнительного отборочного тура утверждаются координационным советом программы.
3.9. Координационный совет программы может устанавливать для регионов-организаторов более высокие проходные баллы по итогам заключительного очного отборочного тура. В регионах-организаторах по решению координационного совета программы может быть проведен дополнительный очный отборочный тур среди учащихся 6-10 классов. Дата и регламент проведения дополнительного отборочного тура утверждаются координационным советом программы.
3.10. В сентябре 2019 г. все участники октябрьской образовательной программы из 7-х и 8-х классов (по состоянию на сентябрь 2019 г.) могут продолжить обучение в дистанционной системе. Темы занятий на октябрьской образовательной программе будут являться логическим продолжением тем дистанционного обучения, поэтому от участников предполагается, что они овладеют материалом, изучаемым в дистанционной системе.
4. Аннотация образовательной программы
Образовательная программа ориентирована на развитие математических и творческих способностей учащихся. Программа включает в себя углубленные занятия математикой, различные математические соревнования, лекции ведущих ученых и педагогов страны, общеобразовательную, обширную культурно-досуговую, развивающую и спортивно-оздоровительную программы.
Программа ориентирована на обучение школьников с разным уровнем подготовленности. Учащиеся будут разбиты на учебные группы с учетом их возраста и уровня подготовки. Изучаемые темы предполагают у участников хорошее знание всех разделов школьного курса математики.
5. Финансирование образовательной программы
Оплата проезда, пребывания и питания участников образовательной программы осуществляется за счет средств Образовательного Фонда «Талант и успех».
Второй закон Ньютона. 9-й класс
Цель: сформировать понятие “сила” как количественную характеристику действия одного тела на другое; сформулировать закон Ньютона и указать границы применимости закона.
Задачи:
- Активизировать знания учащихся по теме “Сила” (домашнее задание: повторить материал 7-м класса по теме “Сила”) и углубить понятие на конкретных примерах;
- Решить проблемную ситуацию: выяснить от чего зависит действие силы на тело и к чему это приводит;
- Закрепить полученный закон на примерах и уточнить границы применимости закона.
Ход урока:
I Организационный момент. Проверка отсутствующих, запись числа и темы урока в тетрадях.
На доске: Второй закон Ньютона.
II Подготовка к изучению нового материала.
Вопросы для повторения:
1. Что изучает динамика?
2. Инерция. Примеры проявления.
3. Объяснения первого закона Ньютона на примере.
4. Может ли тело сохранять скорость в одной системе отсчета, но изменить её в другой. Поясните.
III Изучение нового материала:
а) Понятие “Сила”.
Вопросы для определения понятия:
1. Что такое “сила”? Причиной чего является сила?
2. Почему тело совершает движение, что этому способствует?
3. Что при этом изменяется (указать какие характеристики движения изменяются и почему)?
4. Что такое равнодействующая и какой смысл она несет при взаимодействии тел?
б) Доказать, что ускорение прямо пропорциональна силе.
Рассмотрим рисунок (учащиеся переносят рисунок в тетрадь):
I случай: а) m1=m2, V1 =V2;
б) m1=m2, V1 V2 ( V1V2 ).
Вопросы для рассмотрения:
- Какое ускорение имеют тележки до столкновения?
- Какое ускорение у тележек после столкновения?
- Что изменилось. Почему?
- Какой вывод можно сделать?
Вывод: ускорение прямо пропорционально действующей силе. (можно сделать буквенную запись, тогда хорошо будет видна зависимость)
в) Доказать, что ускорение обратно пропорционально массе тела.
Вернемся к рисунку, но рассмотрим другой случай:
II случай: а) m1m2( m1m2), V1=V2;
б) m1m2 ( m1m2), V1V2 ( V1V2).
Вопросы для рассмотрения:
1. Как произойдет взаимодействие?
2. Что изменить и почему?
3. Что произойдет, если изменить скорости тел?
4. Что называют инертностью?
5. Какой вывод можно сделать?
Вывод: тело приобретает большее ускорение, если его масса мала, следовательно, ускорение обратно пропорционально массе тела. (можно сделать буквенную запись, тогда будет видно хорошо зависимость)
IV Обобщение полученных выводов и формулировка закона Ньютона.
Следовательно, второй закон Ньютона: ускорение тела прямо пропорционально взаимодействующей силе и обратно пропорционально массе этого тела.
Математическая запись закона: а=
V Границы применимости закона:
- Закону подчиняются небесные тела, мельчайшие частицы, гонимые ветром.
- Если отталкивать от себя пустую тележку и груженую, то пустой тележке сообщается большая скорость, а следовательно она приобретает большее ускорение.
VI Решение примера:
Поезд массой 500 т трогается с места,
через 25 с скорость 18 км/ч. Определите силу тяги.
Дано:
M= 500 т (СИ: 500000 кг)
t= 25 с
F= ?
Решение:
а= а=
V0=0 F= M ; F= 10 Н
Ответ: 100000 Н.
VII Домашнее задание
* Все, что выделено полужирным шрифтом, учитель пишет на доске, а учащиеся в тетради.
Законы движения Ньютона – Математика A-Level Revision
Законы движения Ньютона покрывают три закона Ньютона.
Силы
Сила – это «влияние, вызывающее движение тела» (Оксфордский словарь английского языка).
Силы обычно схематически изображаются в виде стрелки, указывающей в направлении силы. Например:
Сила измеряется в ньютонах (символ N).
Первый закон Ньютона
- Первый закон Ньютона гласит, что тело останется в покое или продолжит движение с постоянной скоростью, если не будет приложена внешняя сила.
Это означает, что для изменения ускорения тела к телу должна быть приложена результирующая сила. Другими словами, если силы на объекте уравновешиваются, ускорения не будет (объект продолжит движение с той же скоростью).
Итак, если нам говорят, что тело не ускоряется (т.е. если оно движется с постоянной скоростью), мы знаем, что результирующая (общая) сила в любом одном направлении будет равна нулю.
Пример
На тело действуют следующие силы.Тело движется с постоянной скоростью 5 м / с. Найдите силу X.
Должно быть ясно, что X = 5. Таким образом, сила равна 5Н.
Второй закон Ньютона
- Второй закон движения Ньютона гласит, что скорость изменения количества движения тела прямо пропорциональна приложенной чистой силе.
Другими словами, когда к объекту приложена общая сила, ускорение изменится. Насколько изменится ускорение, зависит от величины приложенной силы.
Фактически, из Второго закона Ньютона мы можем вывести следующее уравнение:
Иногда это записывается как F = ma, хотя вы должны убедиться, что понимаете, что это означает (в частности, обратите внимание, что F – это результирующая сила ).
Масса и масса
Студенты часто не понимают разницу между весом и массой. Вес равен силе из-за силы тяжести и измеряется в ньютонах. Масса – это количество вещества, содержащегося в теле, которое измеряется в килограммах (кг).Вес и масса связаны уравнением:
Это следствие Второго закона Ньютона.
Третий закон Ньютона
- Этот закон гласит, что каждое действие имеет равную и противоположную реакцию.
Например, если мяч помещен на стол, он будет воздействовать на стол с силой. Однако в то же время стол оказывает на мяч силу (именно эта сила препятствует втягиванию мяча в стол!).
Эта «равная и противоположная сила реакции» известна как нормальная сила реакции , и для ее обозначения обычно используются буквы N или R.
Что такое второй закон движения Ньютона? | Исаак Ньютон
Законы движения Исаака Ньютона были впервые изложены в его Principia Mathematica Philosophiae Naturalis в 1687 году. Первый закон гласит, что объект будет оставаться в покое или двигаться с постоянной скоростью, если на него не действуют внешние сила.Третий – это хорошо известная (хотя и не совсем понятная) идея о том, что каждое действие (сила) имеет равную, но противоположную реакцию – если вы толкнете дверь, дверь оттолкнется от вас.
Второй закон говорит вам, как рассчитать значение силы. Сила (измеряемая в Ньютонах) – одно из фундаментальных физических свойств системы и может принимать разные формы. Вы можете почувствовать это как толчок или притяжение (механическую силу), в то время как это величина вашего веса (гравитационная сила Земли, притягивающая вас), и ее можно увидеть в отталкивании или притяжении магнитов или электрических зарядов (электромагнитных сила).Сила может быть результатом любого количества фундаментальных физических взаимодействий между частицами материи, но второй закон Ньютона позволяет вам выяснить, как сила, когда она присутствует, повлияет на движение объекта.
В форме, изображенной выше, говорится, что сила (F) равна скорости изменения количества движения (p) во времени (t). Маленькие буквы «d» – это дифференциальная система обозначений, еще одно изобретение Ньютона, которое появляется в бесчисленных физических уравнениях и позволяет математически предсказать, как что-то изменится по мере постепенного изменения другого связанного параметра – в данном случае времени.
Импульс – это масса (в килограммах) объекта, умноженная на его скорость (в метрах в секунду). В большинстве ситуаций масса чего-либо не изменяется при движении, поэтому уравнение можно упростить до массы (m), умноженной на скорость изменения скорости, которую мы знаем как ускорение (a). Это дает нам более знакомую версию второго закона из школьных учебников: F = ma.
Как и остальная часть физики Ньютона, второй закон движения применим в огромном количестве повседневных ситуаций и является рабочей лошадкой в современной науке и технике.Используя его законы движения, можно определить способ движения почти всего: сколько силы потребуется, чтобы разогнать поезд, достигнет ли пушечное ядро своей цели, как движутся воздушные и океанские течения или будет ли летать самолет – все это приложения. второго закона Ньютона. Он даже использовал законы движения в сочетании со своим универсальным законом тяготения, чтобы объяснить, почему планеты движутся именно так.
Вес – это сила, равная массе объекта, умноженной на гравитационное ускорение, вызываемое Землей (равное 10 метрам в секунду в секунду), в направлении центра планеты.Причина, по которой вы не падаете сквозь землю, конечно, объясняется третьим законом движения Ньютона, который гласит, что поверхность Земли толкается к вашим ногам с силой, равной, но противоположной вашему весу.
Модифицированная версия второго закона применяется, когда масса объекта изменяется, например ракеты, которая сжигает топливо и становится легче при прохождении через атмосферу.
Все мы знаем второй закон на практике, если не в математике. Чтобы передвинуть тяжелый рояль, нужно приложить больше силы (и, следовательно, больше энергии), чем передвигать по полу небольшой табурет.Когда вы ловите быстро движущийся мяч для крикета, вы знаете, что вам будет меньше больно, если вы отодвинете руку назад, когда поймаете его – если дать движущемуся мячу больше времени, чтобы замедлить ход, ваша рука должна оказывать меньшее противодействующее усилие на мяч.
Пример мяча для крикета демонстрирует, что силы не только имеют размер, но и действуют в определенном направлении. Силы относятся к категории физических свойств, в которую входят импульс и скорость, известные как векторы. Они контрастируют со скалярами, которые имеют размер, но не имеют направления, например температуру или массу.
Буква F во втором законе Ньютона относится к чистой силе, действующей на объект. Таким образом, выяснение того, что происходит с объектом, на который действует несколько сил, требует учета как направления, так и размера каждой силы. Две силы могут иметь одинаковые размеры, но, если они направлены прямо напротив друг друга, они уменьшатся до нуля.
Игра в перетягивание каната – хороший способ подумать об этом. Когда две команды тянут в противоположных направлениях, движение веревки (рассчитанное по второму закону Ньютона) будет определяться чистой силой, действующей на веревку.Размер этой чистой силы – это разница в размерах сил, прилагаемых двумя командами. Направление чистой силы будет в направлении той команды, которая работает сильнее.
Для описания атомов и даже более мелких объектов физики используют версии силы и импульса в уравнениях, которые включают квантово-механические описания времени, а также пространства. В этом масштабе силы – это математические побочные продукты, возникающие, когда фундаментальные частицы материи, такие как электроны и кварки, обмениваются частицами, такими как фотоны, глюоны или частицы W или Z, которые «переносят» силы и в совокупности известны как калибровочные бозоны.
Второй закон Ньютона работает как способ описания движения всего в квантово-механической системе до тех пор, пока частицы не движутся со скоростью, близкой к скорости света.
Когда объект движется со скоростью, близкой к скорости света, мы попадаем в область специальной теории относительности, которая говорит нам, что масса объекта будет увеличиваться по мере того, как он движется быстрее. Это необходимо учитывать при расчете сил на этих скоростях.
Действительно, большая часть классической физики Ньютона нуждается в модификации в экстремальных ситуациях – второй закон не точен, когда присутствуют огромные гравитационные силы, например, вокруг черной дыры или в контексте огромных масс целых галактик, где обычно Относительность становится лучшим способом описания движения в системе.
Кем он был, почему падают яблоки Google
Сегодня на главной странице Google анимированное яблоко падает, снова и снова, с приятным ударом – дань уважения 367-летию сэра Исаака Ньютона.
Английский ученый родился особенно крошечным, но вырос в массивный интеллект и до сих пор остается огромным благодаря своим открытиям в области гравитации, света, движения, математики и многого другого.
Легенда гласит, что Исаак Ньютон сформулировал теорию гравитации в 1665 или 1666 году, увидев падение яблока и спросив, почему яблоко упало прямо вниз, а не боком или даже вверх.
«Он показал, что сила, заставляющая яблоко падать и удерживающая нас на земле, такая же, как сила, удерживающая Луну и планеты на их орбитах», – сказал Мартин Рис, президент Британского Королевского общества, Великобритания. Национальная академия наук, которую когда-то возглавлял сам Ньютон.
«Его теория гравитации не дала бы нам спутников для глобального позиционирования», – сказал Джереми Грей, историк математики из Открытого университета в Милтон-Кейнсе, Великобритания. «Но этого было достаточно для освоения космических путешествий.«
Исаак Ньютон, младший? Кружка кварты. Практичный ребенок, он любил конструировать модели, в том числе крошечную мельницу, которая фактически перемалывала муку, приводимая в движение мышью, вращающейся в колесе.
Поступивший в Кембриджский университет в 1661 году, Ньютон сначала не смог проявить себя как студент. .
В 1665 году школа временно закрылась из-за эпидемии бубонной чумы, и Ньютон вернулся домой в Линкольншир на два года. Именно тогда произошел мозговой штурм, связанный с падением яблока, и он описал свои годы в перерыве как «расцвет моего возраста для изобретений».
Несмотря на свою очевидную склонность к частным исследованиям, Ньютон вернулся в Кембридж в 1667 году и работал профессором математики и другими должностями до 1696 года.
Исаак Ньютон: больше, чем мастер гравитации вклад в математику и науку.Другой его основной математической подготовкой было вычисление, и вместе с немецким математиком Готфридом Лейбницем Ньютон разработал методы дифференцирования и интегрирования – методы, которые остаются фундаментальными для математиков и ученых.
Между тем, его интерес к оптике привел его к правильному предположению, что белый свет на самом деле представляет собой комбинацию света всех цветов радуги. Это, в свою очередь, прояснило причину хроматической аберрации – неточной цветопередачи – в телескопах сегодняшнего дня.(Связано: «Телескоп Галилея на 400: от подзорной трубы до Хаббла».)
Чтобы решить эту проблему, Ньютон сконструировал телескоп, в котором использовались зеркала, а не только стеклянные линзы, что позволило новому аппарату фокусировать все цвета в одной точке. – в результате получается более четкое и точное изображение. По сей день отражающие телескопы, в том числе космический телескоп Хаббла, являются опорой астрономии (изображение отражающего телескопа, разработанного Исааком Ньютоном).
Следуя своему яблочному пониманию, Ньютон разработал три закона движения, которые, по его собственным словам:
• Закон инерции Ньютона: Каждый объект остается в состоянии покоя или равномерного движения по прямой, если только он не вынужден изменить это состояние под воздействием воздействующих на него сил.
• Закон ускорения Ньютона: Сила равна изменению количества движения (мВ) за изменение во времени. Для постоянной массы сила равна массе, умноженной на ускорение [выраженное в знаменитом уравнении F = ma].
• Закон действия и противодействия Ньютона: Для каждого действия существует равное и противоположное противодействие.
Ньютон опубликовал свои открытия в 1687 году в книге под названием Philosophiae Naturalis Principia Mathematica (Математические принципы естественной философии) , широко известной как Principia.
«Принципы Ньютона сделали его знаменитым – немногие люди прочитали его и еще меньше поняли, но все знали, что это был великий труд, похожий на Теорию относительности Эйнштейна более двухсот лет спустя», – пишет математик Роберт Уилсон. Открытого университета в статье на университетском веб-сайте.
«Непривлекательная личность» Исаака Ньютона
Несмотря на богатство открытий, Исаака Ньютона не очень любили, особенно в старости, когда он был главой Королевского монетного двора Великобритании, служил в парламенте и писал о религии. среди прочего.
«Как личность, Ньютон был непривлекательным – одиноким и замкнутым в молодости, тщеславным и мстительным в последние годы, когда он тиранировал Королевское общество и энергично саботировал своих соперников», – сказал Риз из Королевского общества.
Сэр Дэвид Уоллес, директор Института математических наук Исаака Ньютона в Кембридже, Великобритания, добавил: «Он был сложным персонажем, который также занимался алхимией» – поиском метода превращения неблагородных металлов в золото »и, как магистр монетного двора, не проявил милосердия к фальшивомонетчикам [фальсификаторам], приговоренным к смертной казни.”
В 1727 году в возрасте 84 лет сэр Исаак Ньютон умер во сне и был с помпой и церемонией похоронен в Вестминстерском аббатстве в Лондоне.
СВЯЗАННЫЕ С
ИСТОЧНИКИ
Аналитическое доказательство законов силы Ньютона
Аналитическое доказательство законов силы НьютонаАналитическое доказательство законов силы Ньютона
Автор Джордж Дж. Спикс
1 Введение
Многие студенты интуитивно предполагают что законы инерции и силы тяготения Ньютона верны, поскольку они ясны и просты леОднако есть анализ, который связывает два уравнения вместе и демонстрирует, что они должны быть верными. Анализ дает ответы на такие вопросы, как: «Инертная масса в точности такая же, как и гравитационная масса? Почему показатель степени di позиция, 2, а не 1,99, 2,01 или 1? Почему в одном законе требуется постоянная, а в другом – нет? »
Идеальный способ доказать новые теоретические законы – это спрогнозировать результат эксперимента, используя законы, провести эксперимент и обнаружить, что результат соответствует прогнозу.Но природа уже провела эксперимент с планетами Солнечной системы, И Кеплер определил результаты. Итак, Ньютон в своей статье 1669 года «Математические принципы философии» (ныне часть Большой серии книг в местных библиотеках) применил свои законы силы к солнечной системе и получил те же результаты, что и Кеплер. заявил. Это подтвердило идеи Ньютона, поставило физику на прочную математическую основу и ответило на поставленные вопросы.
2 Резюме аналитического доказательства законов силы Ньютона
В следующей 8-шаговой процедуре законы силы Ньютона применяются к планете
– солнечной системе, и путь планеты (земли) вокруг Солнца показан в виде эллипса.Эта процедура ниже использует математику, найденную в текстах колледжа первого года обучения, и объясняет математику в пределах производных по мере их развития.- Наблюдения показывают, что планеты движутся по плавной кривой вокруг Солнца. Нарисуйте планету в позиции P , используя полярные координаты, r. и
2.1 Положение планеты в полярных координатах, r и
qЭто аналитическое доказательство законов силы Ньютона начинается с планеты P , движущейся по плавной кривой в полярной системе координат, как показано на рисунке 1. Планета движется относительно неподвижного Солнца.
Радиус-вектор r прикреплен к планете P и изменяется по длине при перемещении P
.Кроме того, угол q и скорость его изменения меняются при перемещении P . Следовательно, скорость и ускорение P постоянно меняются. поскольку планета движется по своему пути. Вспомните, что ускорение, скорость и сила имеют величину и направление.Ньютон ранее доказал, что с точки зрения силы тяжести вся масса планеты и Солнца может считаться центром их сфер. Радиус-вектор начинается в центре солнца и заканчивается в центре t он планета.
Определите положения x и y P в зависимости от r и
q , используя тригонометрические функции, указанные на рисунке 1.Расстояние по оси x P
от исходной точки; P x = r cos q .Расстояние y
P от исходной точки; P y ONT> = r sin q .По прошествии времени
P движется по своей кривой, делая r и q зависимыми от времени, t .Положения P как функции времени обозначены как;Это завершает шаг 1.
2.2 Скорость планеты в направлениях x и y
Рисунок 2 показывает, что изменение расстояний x и y является функцией как r
, так и q, поскольку P движется во времени по своему пути.Скорость планеты P – это изменение расстояния вдоль кривой за изменение во времени.Или
Расчетное выражение для скорости в направлении x, так как изменение времени очень мало:
Скорость по оси y равна;
Следовательно, скорость
P в направлении x равна;А скорость P в направлении y равна;
Правило исчисления для получения производной произведения двух переменных состоит в том, чтобы умножить первый член на производную второго члена плюс второй на производную первого.
Кроме того, производная синуса угла – это косинус угла, умноженный на его производную, а производная косинуса угла – это минус синус угла, умноженный на его производную.
Использование этих правил дифференциации;
Выражение для скорости P в направлении x:
Выражение для скорости P
в направлении y, следуя тем же правилам, выглядит следующим образом:На этом шаг 2 завершен.
2.3 Ускорение планет в направлениях x и y
Следующим шагом является получение выражений для ускорений планет в направлениях x и y, указанных на рисунке 3.
Напомним, что ускорение – это скорость изменения скорости.
Пусть ускорение планеты в направлении x будет a x .
Пусть ускорение планеты в направлении y будет a y .
Тогда;
и
Нахождение ускорения заставляет нас брать производную скорости по времени. Скорость, в свою очередь, является производной расстояния по времени. Следовательно, ускорение – это вторая производная расстояния по времени. Дери Альтернативная производная называется второй производной. Символ для вторая производная, в данном случае;
Замените v x и v y их производными выражениями, перечисленными в разделе 2.2. Следуйте тем же правилам дифференциации, как указано выше, и получите:
Это завершает шаг 3.
Ускорения a x и a y должны использоваться для получения выражений для радиального и поперечного ускорений планеты на шаге 5.
2.4 Приравнять гравитационную силу к силе инерции планеты
Закон силы тяжести Ньютона применительно к массе Земли m и солнечной массе M равен;
Где
r – радиус-вектор, изменяющееся расстояние от Земли до Солнца, а G – гравитационный минус. тант.F Гравитационный – это сила, действующая по прямой линии между планетой и солнцем. Эта сила заставила бы планету свободно падать к Солнцу, если бы не противодействующая сила инерции планеты.
Что такое сила инерции на планете?
Закон силы инерции Ньютона гласит, что сила инерции равна ускорению планеты, умноженному на массу планеты.
Силы инерции и гравитации должны быть равны друг другу по величине, но противоположны по направлению, иначе планета покинула бы свою орбиту.При неравных силах планета упала бы на солнце или перешла бы на другую орбиту в новом равновесии. м, или улететь в космос. Поскольку планета сохраняет свою орбиту, сумма двух сил должна быть равна нулю.
Разделим на m и получим;
Тогда;
Это важное место в доказательстве, где предполагается, что инерционная масса идентична массе силы тяжести, а радиальное ускорение показано противоположно притяжению силы тяжести.Мы должны по-прежнему скептически относиться к этим предположениям, в том числе к расст. до второй степени, пока мы не получим эллиптический путь планеты вокруг Солнца.
Это уравнение радиального ускорения показывает, что a Radial пропорционально обратному квадрату расстояния.
Применяя некоторые математические методы, мы изменим уравнение, чтобы получить a Radial как функцию r
и q .Это уравнение радиального ускорения является основным уравнением, которое превратится в уравнение, показывающее, что земная орбита является эллипсом.Заметьте также, что закон инерционной силы Ньютона можно рассматривать просто как определение единицы силы. После согласования стандартов килограмма, метра и секунды устанавливается единица инерционной силы. Нам нужна константа (G), чтобы сделать гравитационные единицы силы имеют те же размеры и ту же величину, что и единицы силы инерции.Но у нас нет оснований (пока) полагать, что сила инерции, основанная на случайных, но согласованных стандартах, прямо пропорциональна гравитации. национальная сила. Мы просто предположили эквивалентность, когда исключили «m» в приведенном выше выводе. Если путь Земли вокруг Солнца аналитически определен как эллипс, то предположение верно.
Это завершает шаг 4.
Следующая часть этого доказательства, чтобы найти выражения для радиального и поперечного ускорения планет на шаге 5 процедуры.
5.3 Второй закон Ньютона – University Physics Volume 1
Второй закон Ньютона тесно связан с его первым законом. Он математически показывает причинно-следственную связь между силой и изменениями в движении. Второй закон Ньютона является количественным и широко используется для расчета того, что происходит в ситуациях с применением силы. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, которое дает точное соотношение силы, массы и ускорения, нам нужно отточить некоторые идеи, о которых мы упоминали ранее.
Сила и ускорение
Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости. Изменение скорости по определению означает ускорение. Первый закон Ньютона гласит, что чистая внешняя сила вызывает изменение движения; таким образом, мы видим, что чистая внешняя сила вызывает ненулевое ускорение .
В разделе «Силы» мы определили внешнюю силу как силу, действующую на объект или систему, которая возникает вне объекта или системы.Давайте рассмотрим эту концепцию дальше. Интуитивное представление о внешнем верно – это вне интересующей системы. Например, на (Рисунок) (а) интересующая система – это автомобиль плюс человек в нем. Две силы, проявленные двумя учениками, – это внешние силы. Напротив, между элементами системы действует внутренняя сила. Таким образом, сила, с которой человек в автомобиле держится за рулевое колесо, представляет собой внутреннюю силу между элементами интересующей системы. Согласно первому закону Ньютона, только внешние силы влияют на движение системы.(Внутренние силы нейтрализуют друг друга, как объясняется в следующем разделе.) Следовательно, мы должны определить границы системы, прежде чем мы сможем определить, какие силы являются внешними. Иногда система очевидна, тогда как в других случаях определение границ системы более тонкое. Концепция системы является фундаментальной для многих областей физики, как и правильное применение законов Ньютона. Эта концепция многократно пересматривается при изучении физики.
Рисунок 5.10 Различные силы, действующие на одну и ту же массу, вызывают разное ускорение.(а) Два студента толкают заглохшую машину. Показаны все внешние силы, действующие на автомобиль. (b) Силы, действующие на автомобиль, переносятся на координатную плоскость (диаграмма свободного тела) для упрощения анализа. (c) Эвакуатор может создавать большую внешнюю силу при той же массе и, следовательно, большее ускорение.Из этого примера вы можете видеть, что разные силы, действующие на одну и ту же массу, вызывают разное ускорение. На (Рис.) (А) двое учеников толкают машину с водителем. Показаны стрелки, представляющие все внешние силы.Интересующая система – это автомобиль и его водитель. Вес
системы и опоры земли
также показаны для полноты и, как предполагается, отменяются (поскольку не было вертикального движения и дисбаланса сил в вертикальном направлении, чтобы создать изменение в движении). Вектор
представляет трение, действующее на автомобиль, и действует влево, противодействуя движению автомобиля.(Мы обсудим трение более подробно в следующей главе.) На (Рисунок) (b) все внешние силы, действующие на систему, складываются вместе, образуя результирующую силу
.Диаграмма свободного тела показывает все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, векторы показаны коллинеарно. Наконец, на (Рисунок) (c), большая чистая внешняя сила вызывает большее ускорение
когда эвакуатор тянет машину.
Кажется разумным, что ускорение будет прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении. Это предположение было проверено экспериментально и проиллюстрировано на (Рисунок). Чтобы получить уравнение для второго закона Ньютона, сначала запишем соотношение ускорения
и чистая внешняя сила
как пропорциональность
где символ
означает «пропорционально.»(Напомним из книги« Силы », что чистая внешняя сила представляет собой векторную сумму всех внешних сил и иногда обозначается как
) Эта пропорциональность показывает то, что мы сказали словами: ускорение прямо пропорционально чистой внешней силе. После выбора интересующей системы определите внешние силы и игнорируйте внутренние. Было бы огромным упрощением игнорировать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в телах учеников, не говоря уже о бесчисленных силах между атомами в объектах.Тем не менее, это упрощение помогает нам решать некоторые сложные проблемы.
Также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой. Как показано на (Рисунок), та же самая чистая внешняя сила, приложенная к баскетбольному мячу, вызывает гораздо меньшее ускорение, когда она применяется к кроссоверу. Пропорциональность записывается как
., где м, – масса системы, а – – величина ускорения.Эксперименты показали, что ускорение прямо обратно пропорционально массе, так же как оно прямо пропорционально чистой внешней силе.
Рисунок 5.11 Одна и та же сила, действующая на системы разной массы, вызывает разное ускорение. (a) Баскетболист толкает баскетбольный мяч, чтобы сделать передачу. (Игнорируйте влияние силы тяжести на мяч.) (B) Тот же игрок оказывает идентичную силу на остановившийся внедорожник и производит гораздо меньшее ускорение. (c) Диаграммы свободного тела идентичны, что позволяет напрямую сравнить две ситуации.По мере того, как вы решите больше задач и научитесь рисовать их в Рисование диаграмм свободного тела, появится серия шаблонов для диаграмм свободного тела.Было обнаружено, что ускорение объекта зависит только от чистой внешней силы и массы объекта. Комбинирование двух только что приведенных пропорциональностей дает второй закон Ньютона .
Второй закон движения Ньютона
Ускорение системы прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении, и обратно пропорционально ее массе.В форме уравнения второй закон Ньютона равен
.где
– ускорение,
– это чистая сила, а м – масса. Это часто записывается в более привычной форме
., но первое уравнение дает больше понимания того, что означает второй закон Ньютона. Если рассматривать только величину силы и ускорения, это уравнение можно записать в более простой скалярной форме:
Закон – это причинно-следственная связь между тремя величинами, которая не просто основана на их определениях.Справедливость второго закона основана на экспериментальной проверке. Диаграмма свободного тела, которую вы научитесь рисовать в «Рисование диаграмм свободного тела», является основой для написания второго закона Ньютона.
Пример
Какое ускорение может дать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н (около 11 фунтов) параллельно земле ((Рисунок)). Масса косилки 24 кг. Какое у него ускорение?
Рисунок 5.12 (a) Чистое усилие на газонокосилке составляет 51 Н. вправо. С какой скоростью газонокосилка ускоряется вправо? (б) Показана диаграмма свободного тела для этой задачи.Стратегия
Эта проблема связана только с движением в горизонтальном направлении; нам также дана чистая сила, обозначенная одним вектором, но мы можем подавить векторную природу и сосредоточиться на применении второго закона Ньютона. С
и м. , ускорение можно рассчитать непосредственно из второго закона Ньютона как
Решение
Величина ускорения a составляет
.Ввод известных значений дает
Если заменить ньютон на килограммы, умноженные на метры в секунду в квадрате, получим
.Значение
Направление ускорения совпадает с направлением результирующей силы, параллельной земле. Это результат векторной связи, выраженной во втором законе Ньютона, то есть вектор, представляющий чистую силу, является скалярным кратным вектору ускорения.В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, прикладываемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны нейтрализоваться, потому что в вертикальном направлении не происходит ускорение (косилка движется только по горизонтали). Обнаруженное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку.Такое усилие не продлится слишком долго, потому что человек скоро наберет максимальную скорость.
Проверьте свое понимание
На момент запуска HMS Titanic был самым массивным мобильным объектом из когда-либо построенных, с массой
единиц.. Если усилие 6 МН
был применен к кораблю, какое ускорение он испытает?
[показывать-ответ q = ”fs-id116503
66 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id116503
66 ″]
[/ hidden-answer]
В предыдущем примере мы имели дело с чистой силой только для простоты.Однако на газонокосилку действует несколько сил. Вес
(подробно обсуждается в разделе «Масса и вес») тянет косилку вниз к центру Земли; это создает контактное усилие на земле. Земля должна оказывать на газонокосилку восходящую силу, известную как нормальная сила
., который мы определяем в Common Forces. Эти силы уравновешены и поэтому не вызывают вертикального ускорения. В следующем примере мы показываем обе эти силы.Продолжая решать проблемы, используя второй закон Ньютона, не забудьте показать множественные силы.
Пример
Какая сила больше?
(a) Автомобиль, показанный на (Рисунок), движется с постоянной скоростью. Какая сила больше,
или
? Объяснять.
(b) Эта же машина сейчас ускоряется вправо. Какая сила больше,
или
Объясните.
Рис. 5.13 Автомобиль показан (а) движущимся с постоянной скоростью и (б) ускоряющимся. Как соотносятся силы, действующие на автомобиль в каждом конкретном случае? а) Что знание того, что автомобиль движется с постоянной скоростью, говорит нам о чистой горизонтальной силе, действующей на автомобиль, по сравнению с силой трения? б) Что знание того, что автомобиль ускоряется, говорит нам о горизонтальной силе, действующей на автомобиль, по сравнению с силой трения?Стратегия
Мы должны рассмотреть первый и второй законы Ньютона, чтобы проанализировать ситуацию.Нам нужно решить, какой закон применяется; это, в свою очередь, расскажет нам о соотношении сил.
Решение
- Силы равны. Согласно первому закону Ньютона, если результирующая сила равна нулю, скорость постоянна.
- В этом случае
должно быть больше
Согласно второму закону Ньютона, для ускорения требуется чистая сила.
Значение
Эти вопросы могут показаться тривиальными, но обычно на них отвечают неверно.Чтобы автомобиль или любой другой объект двинулся с места, его нужно разогнать до желаемой скорости; для этого требуется, чтобы сила двигателя была больше силы трения. Когда автомобиль движется с постоянной скоростью, результирующая сила должна быть равна нулю; в противном случае автомобиль будет ускоряться (набирать скорость). Чтобы решить проблемы, связанные с законами Ньютона, мы должны понять, применять ли первый закон Ньютона (где
) или второй закон Ньютона (где
не равно нулю).Это станет очевидным, когда вы увидите больше примеров и попытаетесь решить проблемы самостоятельно.
Пример
Какая ракетная тяга ускоряет этот снегоход?
До пилотируемых космических полетов ракетные сани использовались для испытания самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, которая была установлена на одной или двух направляющих и приводилась в движение несколькими ракетами.
Рассчитайте величину силы, прилагаемой каждой ракетой, которая называется ее тягой T , для четырехракетной двигательной установки, показанной на (Рисунок).Начальное ускорение салазок
, масса системы 2100 кг, сила трения, противодействующая движению, 650 Н.
Рис. 5.14 Салазки испытывают ракетную тягу, которая ускоряет их вправо. Каждая ракета создает одинаковую тягу T. Система здесь представляет собой салазки, их ракеты и их всадник, поэтому никакие силы между этими объектами не учитываются. Стрелка, обозначающая трениенарисован в крупном масштабе.
Стратегия
Хотя силы действуют как вертикально, так и горизонтально, мы предполагаем, что вертикальные силы компенсируются, потому что нет вертикального ускорения. Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления указываются знаками плюс или минус, при этом вправо принимается за положительное направление. См. Диаграмму свободного тела на (Рисунок).
Решение
Поскольку ускорение, масса и сила трения даны, мы начнем со второго закона Ньютона и ищем способы найти тягу двигателей.Мы определили направление силы и ускорения как действующее «вправо», поэтому в расчетах нам нужно учитывать только величины этих величин. Следовательно, мы начинаем с
где
– чистая сила в горизонтальном направлении. Из рисунка видно, что тяга двигателя увеличивается, а трение противодействует. В форме уравнения чистая внешняя сила равна
.Подставляя это во второй закон Ньютона, получаем
Используя небольшую алгебру, мы решаем общую тягу 4 T :
Подстановка известных значений дает
Следовательно, общая тяга
и индивидуальные тяги
Значение
Цифры довольно большие, поэтому результат может вас удивить.Подобные эксперименты проводились в начале 1960-х годов, чтобы проверить пределы человеческой выносливости, и установка была разработана для защиты людей при аварийных выбросах реактивных истребителей. Была получена скорость 1000 км / ч с ускорением 45 g ’s. (Напомним, что g , ускорение свободного падения, равно
. Когда мы говорим, что ускорение составляет 45 g с, это
., что составляет примерно
.) Хотя живые предметы больше не используются, наземная скорость 10 000 км / ч была получена с помощью ракетных саней.
В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Второй закон Ньютона – это больше, чем определение; это соотношение между ускорением, силой и массой. Это может помочь нам делать прогнозы. Каждую из этих физических величин можно определить независимо, поэтому второй закон говорит нам что-то основное и универсальное о природе.
Проверьте свое понимание
Спортивный автомобиль массой 550 кг сталкивается с грузовиком массой 2200 кг, и во время столкновения результирующая сила, действующая на каждое транспортное средство, равна силе, прилагаемой другим. Если величина ускорения грузовика
какова величина ускорения спортивного автомобиля?
[показывать-ответ q = ”fs-id1165039454293 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165039454293 ″]
[/ hidden-answer]
Составная форма второго закона Ньютона
Мы разработали второй закон Ньютона и представили его в виде векторного уравнения (рисунок).Это векторное уравнение можно записать в виде трехкомпонентных уравнений:
Второй закон – это описание того, как тело механически реагирует на окружающую среду. Влияние окружающей среды – чистая сила
.реакция тела – ускорение
, а сила отклика обратно пропорциональна массе м . Чем больше масса объекта, тем меньше его реакция (его ускорение) на влияние окружающей среды (заданная результирующая сила).Следовательно, масса тела является мерой его инерции, как мы объясняли в Первом законе Ньютона.
Пример
Сила на футбольном мяче
Игрок перебрасывает футбольный мяч весом 0,400 кг через поле; он подвергается ускорению, заданному
Найдите (а) результирующую силу, действующую на мяч, и (б) величину и направление результирующей силы.
Стратегия
Векторов в
и
, которые указывают направление силы вдоль оси x и оси y соответственно, поэтому мы применяем второй закон Ньютона в векторной форме.
Решение
- Применяем второй закон Ньютона:
- Величина и направление находятся с использованием компонентов
:
Значение
Мы должны помнить, что второй закон Ньютона является векторным уравнением. В (а) мы умножаем вектор на скаляр, чтобы определить результирующую силу в векторной форме. Хотя векторная форма дает компактное представление вектора силы, она не говорит нам, насколько он «большой» или куда он идет, в интуитивно понятных терминах.В (b) мы определяем действительный размер (величину) этой силы и направление, в котором она движется.
Пример
Масса автомобиля
Найдите массу автомобиля, если чистая сила равна
.дает ускорение
.
Стратегия
Векторное деление не определено, поэтому
не может быть выполнено. Однако масса м является скаляром, поэтому мы можем использовать скалярную форму второго закона Ньютона,
..
Решение
Мы используем
и подставляем величины двух векторов:
и
Следовательно,
Значение
Сила и ускорение были даны в
и
, но ответ, масса м , является скаляром и поэтому не дается в
и
форма.
Пример
Несколько сил на частицу
Частица массой
Надействуют четыре силы величин.
, с направлениями, показанными на схеме свободного тела на (Рисунок). Что такое ускорение частицы?
Рис. 5.15 Четыре силы в плоскости xy действуют на частицу массой 4,0 кг.Стратегия
Поскольку это двумерная задача, мы должны использовать диаграмму свободного тела.Первая,
необходимо разделить на компоненты x и y . Затем мы можем применить второй закон в каждом направлении.
Решение
Рисуем диаграмму свободного тела, как показано на (Рисунок). Теперь применим второй закон Ньютона. Мы рассматриваем все векторы, разделенные на компоненты x и y :
Таким образом, чистое ускорение равно
., который является вектором величины
.направлено на
к положительной оси x .
Значение
В повседневной жизни можно найти множество примеров, когда три или более сил действуют на один объект, например, кабели, идущие от моста Золотые Ворота, или футболиста, которого атакуют три защитника. Мы видим, что решение этого примера является просто продолжением того, что мы уже сделали.
Проверьте свое понимание
На автомобиль действуют силы, как показано ниже. Масса автомобиля 1000,0 кг. Дорога скользкая, поэтому трение можно не учитывать.а) Какова чистая сила, действующая на машину? б) Какое ускорение у машины?
[показать-ответ q = ”153079 ″] Показать ответ [/ показать-ответ] [скрытый-ответ a =” 153079 ″] a.; б.
[/ hidden-answer]
Второй закон и импульс Ньютона
Ньютон фактически сформулировал свой второй закон в терминах количества движения: «Мгновенная скорость изменения количества движения тела равна чистой силе, действующей на тело.»(« Мгновенная скорость »подразумевает, что задействована производная.) Это может быть задано векторным уравнением
Это означает, что второй закон Ньютона обращается к центральному вопросу движения: что вызывает изменение движения объекта? Импульс был описан Ньютоном как «количество движения», способ объединения скорости объекта и его массы. Мы посвящаем линейный импульс и столкновения изучению импульса .
Пока достаточно определить импульс
как произведение массы объекта м и его скорости
:
Поскольку скорость – вектор, импульс тоже.
Импульс легко визуализировать. Поезд, движущийся со скоростью 10 м / с, имеет больше импульса, чем поезд, движущийся со скоростью 2 м / с. В повседневной жизни мы говорим об одной спортивной команде как о «имеющей импульс», когда она набирает очки против команды соперника.
Если подставить (рисунок) в (рисунок), то получим
Когда м постоянна, мы имеем
Таким образом, мы видим, что импульсная форма второго закона Ньютона сводится к форме, приведенной ранее в этом разделе.
Исчисление I – Метод Ньютона
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с “узкой” шириной экрана (, то есть , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-13: Метод Ньютона
Следующее приложение, которое мы рассмотрим в этой главе, – это важное приложение, которое используется во многих областях. Если вы до сих пор следили за главой, вполне возможно, что у вас сложилось впечатление, что многие из рассмотренных нами приложений созданы нами для того, чтобы вы работали.Это прискорбно, потому что все приложения, которые мы рассмотрели до этого момента, являются реальными приложениями, которые действительно используются в реальных ситуациях. Проблема часто заключается в том, что для работы с более значимыми примерами приложений нам потребуется больше знаний о науке и / или физике, лежащих в основе проблемы, чем мы обычно имеем. Без этих знаний мы вынуждены приводить довольно упрощенные примеры, которые часто не кажутся очень реалистично, и поэтому трудно понять, что приложение, которое мы рассматриваем, является настоящим приложением.
Это изменится в этом разделе. Это приложение, которое мы все можем понять, и все мы можем понять, что иногда нужно делать это, даже если мы не понимаем физику / науку, лежащую в основе реального приложения.
В этом разделе мы рассмотрим метод приближения решений уравнений. Все мы знаем, что уравнения нужно решать время от времени, и на самом деле мы сами решили довольно много уравнений к этому моменту. Во всех примерах, которые мы рассмотрели к этому моменту, мы действительно смогли найти решения, но не всегда возможно сделать это точно и / или выполнить работу вручную.Вот тут-то и пригодится это приложение. Итак, давайте посмотрим, что это за приложение.
Предположим, что мы хотим приблизить решение к \ (f \ left (x \ right) = 0 \), а также предположим, что мы каким-то образом нашли начальное приближение к этому решению, скажем, \ ({x_0} \). Это начальное приближение, вероятно, не так уж и хорошо, на самом деле это может быть не более чем быстрое предположение, которое мы сделали, и поэтому мы хотели бы найти лучшее приближение. Сделать это достаточно просто.Сначала мы получим касательную к \ (f \ left (x \ right) \) в точке \ ({x_0} \).
\ [y = f \ left ({{x_0}} \ right) + f ‘\ left ({{x_0}} \ right) \ left ({x – {x_0}} \ right) \]Теперь взгляните на график ниже.
Синяя линия (если вы все равно читаете это в цвете…) – это касательная линия в точке \ ({x_0} \). Мы видим, что эта линия пересекает ось \ (x \) гораздо ближе к фактическому решению уравнения, чем \ ({x_0} \). Назовем эту точку, где касательная в \ ({x_0} \) пересекает \ (x \) – ось \ ({x_1} \), и мы будем использовать эту точку в качестве нашего нового приближения к решению.
Итак, как нам найти эту точку? Мы знаем его координаты, \ (\ left ({{x_1}, 0} \ right) \), и мы знаем, что он находится на касательной, поэтому подключите эту точку к касательной и решите для \ ({x_1} \ ) следующим образом:
\ [\ begin {align *} 0 & = f \ left ({{x_0}} \ right) + f ‘\ left ({{x_0}} \ right) \ left ({{x_1} – {x_0}} \ справа) \\ {x_1} – {x_0} & = – \ frac {{f \ left ({{x_0}} \ right)}} {{f ‘\ left ({{x_0}} \ right)}} \ \ {x_1} & = {x_0} – \ frac {{f \ left ({{x_0}} \ right)}} {{f ‘\ left ({{x_0}} \ right)}} \ end {align * } \]Итак, мы можем найти новое приближение при условии, что производная не равна нулю в исходном приближении.
Теперь мы повторяем весь процесс, чтобы найти еще лучшее приближение. Мы формируем касательную линию к \ (f \ left (x \ right) \) в \ ({x_1} \) и используем ее корень, который мы назовем \ ({x_2} \), как новое приближение к фактическое решение. Если мы сделаем это, мы придем к следующей формуле.
\ [{x_2} = {x_1} – \ frac {{f \ left ({{x_1}} \ right)}} {{f ‘\ left ({{x_1}} \ right)}} \]Эта точка также показана на графике выше, и мы можем видеть из этого графика, что если мы продолжим следовать этому процессу, мы получим последовательность чисел, которая очень приближается к фактическому решению.Этот процесс называется методом Ньютона.
Вот общий метод Ньютона
Метод Ньютона
Если \ ({x_n} \) является приближением решения \ (f \ left (x \ right) = 0 \) и если \ (f ‘\ left ({{x_n}} \ right) \ ne 0 \ ) следующее приближение дается выражением,
\ [{x_ {n + 1}} = {x_n} – \ frac {{f \ left ({{x_n}} \ right)}} {{f ‘\ left ({{x_n}} \ right)}} \]Это должно привести к вопросу, когда нам остановиться? Сколько раз мы проходим этот процесс? Одна из наиболее распространенных точек остановки в процессе – это продолжение до тех пор, пока два последовательных приближения не согласятся с заданным количеством десятичных знаков.
Перед тем, как приступить к работе с какими-либо примерами, мы должны решить две проблемы. Во-первых, нам действительно нужно решить \ (f \ left (x \ right) = 0 \), чтобы применить метод Ньютона. На самом деле это не такая уж большая проблема, но мы должны убедиться, что уравнение находится в этой форме, прежде чем использовать метод.
Во-вторых, нам нужно каким-то образом получить начальное приближение к решению (, то есть , нам нужно как-то \ ({x_0} \)). Один из наиболее распространенных способов получить \ ({x_0} \) – нарисовать график функции и использовать его для получения оценки решения, которое мы затем используем как \ ({x_0} \).Другой распространенный метод: если мы знаем, что есть решение функции в интервале, мы можем использовать середину интервала как \ ({x_0} \).
Давайте рассмотрим пример метода Ньютона.
Пример 1 Используйте метод Ньютона, чтобы определить приближение к решению \ (\ cos x = x \), которое лежит в интервале \ (\ left [{0,2} \ right] \). Найдите приближение к шести десятичным знакам. Показать решениеВо-первых, обратите внимание, что нам не давали первоначального предположения.Однако нам дали время посмотреть. Мы будем использовать это, чтобы получить наше первоначальное предположение. Как отмечалось выше, общее практическое правило в этих случаях состоит в том, чтобы принять начальное приближение за середину интервала. Итак, мы будем использовать \ ({x_0} = 1 \) в качестве нашего первоначального предположения.
Затем напомним, что должно иметь функцию в виде \ (f \ left (x \ right) = 0 \). Поэтому сначала перепишем уравнение как,
\ [\ cos x – x = 0 \]Теперь мы можем записать общую формулу для метода Ньютона.Это часто немного упрощает работу, поэтому, как правило, это неплохая идея.
\ [{x_ {n + 1}} = {x_n} – \ frac {{\ cos x_ {n} – x_ {n}}} {{- \ sin x_ {n} – 1}} \]Давайте теперь получим первое приближение.
\ [{x_1} = 1 – \ frac {{\ cos \ left (1 \ right) – 1}} {{- \ sin \ left (1 \ right) – 1}} = 0,7503638679 \]Здесь мы должны указать, что фраза «шесть знаков после запятой» не означает, что нужно просто получить \ ({x_1} \) до шести знаков после запятой, а затем остановиться.Вместо этого это означает, что мы продолжаем, пока два последовательных приближения не согласятся с шестью десятичными знаками.
Учитывая это условие остановки, нам явно нужно сделать хотя бы один шаг дальше.
\ [{x_2} = 0,7503638679 – \ frac {{\ cos \ left (0,7503638679 \ right) – 0,7503638679}} {{- \ sin \ left ({0,7503638679} \ right) – 1}} = 0,73909 \]
Хорошо, мы делаем успехи. Мы получили приближение к 1 десятичному знаку. Давайте сделаем еще один, оставив детали вычислений вам.
\ [{x_3} = 0,73334 \]Мы разделили до трех десятичных знаков. Нам понадобится еще один.
\ [{x_4} = 0,73332 \]И теперь у нас есть два приближения, которые согласуются с 9 десятичными знаками, и мы можем остановиться. Предположим, что решение приблизительно равно \ ({x_4} = 0,73
332 \).В этом последнем примере мы увидели, что нам не нужно делать слишком много вычислений, чтобы метод Ньютона дал нам приближение в желаемом диапазоне точности.Так будет не всегда. Иногда для достижения желаемой точности требуется много итераций процесса, а иногда он может полностью выйти из строя.
Следующий пример немного глупый, но он указывает на сбой метода.
Пример 2 Используйте \ ({x_0} = 1 \), чтобы найти приближение к решению \ (\ sqrt [3] {x} = 0 \). Показать решениеДа, глупый пример. Ясно, что решение – \ (x = 0 \), но это действительно очень важный момент.{- \ frac {2} {3}}}} = {x_n} – 3 {x_n} = – 2 {x_n} \]
На самом деле, здесь нам не нужно делать никаких вычислений. Эти вычисления удаляются все дальше и дальше от решения \ (x = 0 \) с каждой итерацией. Вот пара вычислений, чтобы понять суть дела.
\ [\ begin {align *} {x_1} & = – 2 \\ {x_2} & = 4 \\ {x_3} & = – 8 \\ {x_4} & = 16 \\ & т. д. \ end {align * } \]Итак, в этом случае метод терпит неудачу и дает очень эффектную ошибку.
Итак, нам нужно быть немного осторожнее с методом Ньютона. Обычно он быстро находит приближение к уравнению. Однако бывают случаи, когда это требует много работы или когда это вообще не работает.
Что Ньютон первоначально сказал об интеграции?
Большинство из нас узнают о математике из современных учебников, с современными обозначениями и часто оторванными от исторического оригинала. Неудивительно, что люди думают, что математика – это современное изобретение, предназначенное только для того, чтобы мучить студентов!
Исаак Ньютон изложил свои идеи об исчислении в книге под названием The Principia (или, точнее, Philosophiae Naturalis Principia Mathematica , что означает «Математические принципы естественной философии»).Это была удивительная книга для того времени (впервые опубликованная в 1687 году), в которую вошли его «Законы движения».
Обложка Principia . [Источник]
Ньютон написал свои Principia на латыни. Вплоть до XIX века математики писали на латыни, хотя другие ученые писали (возможно, более разумно) на своих родных языках (или на обычно используемых языках, таких как французский, немецкий и английский).
Давайте посмотрим на одну небольшую часть (которую он назвал «Леммой II») работы Ньютона из первого английского перевода, сделанного в 1729 году.Вы можете увидеть весь этот перевод здесь, благодаря Google Книгам (см. Лемму II на стр. 42):
1729 Английский перевод Principia
Приведенная ниже проблема была очень важной для ученых в конце 17 века, поскольку в навигации, астрономии и механических системах существовали насущные проблемы, которые нельзя было решить с помощью существующих неэффективных математических методов.
Некоторые пояснения перед тем, как мы начнем:
- A Лемма – это доказанное утверждение, которое приводит к более обширному результату.
- В староанглийском языке знак ∫ – это буква «S». Первое слово, где это встречается ниже, – «вписанный», который мы бы записали как «вписанный». (Обратите внимание, что «s», используемое для существительных во множественном числе, совпадает с нашим.) Удлиненный символ S ∫ стал использоваться как символ «интегрирования», поскольку он тесно связан с «суммой».
- «Dimini∫hed» означает «уменьшаться» и означает «уменьшаться».
- – это «& c», которое в наши дни мы бы записали как «и т. Д.» ( et cetera )
- «Расширенный» означает «стать больше».
- « Ad infinitum » на латыни означает «продолжать делать это, пока не приблизишься к бесконечности».
Это диаграмма, на которую имеется ссылка в тексте выше.
Пояснение
Давайте рассмотрим это по одной концепции за раз, с соответствующими настройками диаграммы. Мы пытаемся найти область между кривой abcdE и двумя линиями Aa и AE.
Другими словами, если мы будем рисовать все больше и больше более тонких прямоугольников таким же образом, площадь нижних прямоугольников и площадь верхних прямоугольников сойдутся в области под кривой.Это та область, которую нам нужно найти.
Ниже представлен случай, когда у нас есть 25 прямоугольников. Мы видим, что общая площадь прямоугольников приближается к площади под кривой. Конечно, следующее соотношение приближается к 1, как говорит Ньютон.
нижние прямоугольники: верхние прямоугольники: площадь под кривой
| Нижние прямоугольники | Верхние прямоугольники |
Это фундаментальная идея исчисления – найти область (или наклон) для небольшого количества наблюдений, увеличить число наблюдений « до бесконечности » и сделать вывод, что мы приближаемся к желаемому ответу.
Вы можете подробнее изучить эту концепцию (используя интерактивный график) в статье о суммах Римана.
Вклад Архимеда
Эта концепция поиска областей искривленных поверхностей с использованием бесконечных сумм не была такой уж новой, поскольку Архимед знал об этом 2000 лет назад.