Слободянюк А.И. Второй закон Ньютона
Слободянюк А.И. Второй закон Ньютона: или ? // Фiзiка: праблемы выкладання. – 1998. – № 2. – С. 61-70.
Любой учебник физики, как для средних школ, так и для вузов, не обходился без изложения законов динамики – трех законов Ньютона. По-видимому, ни в одном из разделов курса физики нельзя найти столько различных подходов, методик изложения, определений, как в разделе «Динамика материальной точки». Возможно, эта тема кажется слишком известной и простой, поэтому каждый автор привносил нечто свое и оригинальное.
Однако любая попытка изложить вопросы динамики достаточно строго и последовательно упирается в ряд трудноопределимых препятствий. На мой взгляд, основная проблема в изложении данной темы – дать строгое определение таких физических величин, как масса и сила. Говоря об определении той или иной физической величины, прежде всего необходимо указать принципиальный метод ее измерения (операциональное определение). С этой точки зрения, все физические величины могут быть определены только на основании какого-либо физического закона. Поэтому прежде чем говорить, что «ускорение тела прямо пропорционально приложенной силе и обратно пропорционально массе тела», необходимо определить понятия массы и силы.
С этой точки зрения, все физические величины могут быть определены только на основании какого-либо физического закона. Поэтому прежде чем говорить, что «ускорение тела прямо пропорционально приложенной силе и обратно пропорционально массе тела», необходимо определить понятия массы и силы.
Проанализируем некоторые подходы авторов учебных пособий к этим вопросам. Начнем обзор с высказывания, которое не вызывает сомнений [1]. «Понятие силы весьма трудно, но им можно овладеть, потому, что силы проявляют себя повсюду…». И далее идет перечисление и описание различных сил (гравитации, силы трения и др.)· Такой подход, конечно, необходим на начальном этапе изучения, он призван сформировать интуитивное представление о силе, как о мере взаимодействия. Однако при дедуктивном построении науки (подобном «Началам» Эвклида) следует все же дать определения, а уж затем оперировать с конкретными величинами.
Можно обойтись без строгого определения на более высоком уровне изучения (как, например, в курсе теоретической механики), когда используемые понятия стали настолько привычными, что не требуют пояснений. Так, например, в [2] первый раз понятие «масса» встречается в такой «аранжировке»: «Функция Лагранжа в рассматриваемом случае пропорциональна квадрату скорости
Так, например, в [2] первый раз понятие «масса» встречается в такой «аранжировке»: «Функция Лагранжа в рассматриваемом случае пропорциональна квадрату скорости
где m – постоянная. Величина m называется массой материальной точки».
Еще один пример на эту же тему [3]: «Частицы системы характеризуются определенными константами m1, m2, …, такими, что
Каждая из констант mi называется массой частицы».
К сожалению, и в некоторых учебных пособиях, предназначенных для учащихся средних школ (например, [4-5]), практически отсутствуют даже описательные определения, хотя их без труда можно найти в справочниках. Так в [6] дано: «Масса – одна из основных характеристик любого материального объекта, являющаяся мерой его инертности и гравитации. Сила – векторная величина, являющаяся мерой механического действия одного материального тела на другое».
Как уже отмечалось ранее, физическое определение должно быть (или, по крайней мере, содержать в себе) операциональным. Понятно, что на основании одного закона дать два независимых способа измерения двух физических величин невозможно – неизбежно возникнет замкнутый «порочный круг». Поэтому необходимо искать способ определения одной из двух величин – массы или силы (мы считаем, что ускорение определяется кинематически – на основе эталонов длины и времени).
Ряд авторов пытаются дать определение силы исходя из других законов. Иными словами, выбирают некий эталон силы и указывают способ ее измерения. В качестве такого эталона выбирается чаще всего либо вес эталонной гири [8-10], либо сила упругости деформированной пружины. Затем масса тела определяется, как отношение действующей силы к приобретаемому ускорению (иначе говоря, второй закон Ньютона формулируется как ).
На мой взгляд, такой подход не является логически безупречным, так как неявно постулирует иные законы: закон Гука – для деформаций, закон тяготения – для веса. Более того, эти законы являются приближенными: деформация не всегда пропорциональна действующей силе, вес тела зависит от того, в какой точке Земли он измеряется.
Более того, эти законы являются приближенными: деформация не всегда пропорциональна действующей силе, вес тела зависит от того, в какой точке Земли он измеряется.
{mosimage}Наиболее последовательно позиция о необходимости введения независимого определения силы защищается в книге [11], поэтому остановимся на ней подробнее. Автор [11] прямо заявляет: «Второй закон Ньютона может рассматриваться как закон, а не как определение силы, только в том случае, если имеется независимое от этого закона определение силы». Далее на основании ряда экспериментов и логических рассуждений доказывается, что сила является вектором, и устанавливается процедура измерения сил, независимая от измерения ускорений. За единицу силы принимается сила упругости пружины, растянутой в строго определенной степени (чем избегается использование закона Гука). Шкала сил строится на основании векторного закона сложения сил. Только после этого дается определение массы, как отношения силы к ускорению.
При таком подходе второй закон Ньютона выступает в качестве определения массы, что ничуть не лучше, чем простое определение силы. Однако далее автор приводит достаточно убедительные аргументы в защиту значимости закона, вкладывая в него дополнительное физическое содержание (аддитивность масс, векторный закон сложения сил, независимость их действия, обобщение на релятивистский случай и др.).
Второй диаметрально противоположный подход (дать независимое определение массы) используется в книгах [12-16]. В качестве примера рассмотрим изложение этих вопросов в [16], где проблемам определений уделяется серьезное внимание.
На основании ряда экспериментов обобщается тот факт, что при взаимодействии двух тел отношение ускорений (или, что равносильно, изменение скоростей), приобретаемых телами, постоянно для данных тел и не зависит от вида взаимодействия, его интенсивности. Это отношение есть характеристика тел, а не взаимодействия, иными словами это – отношение масс тел. Поэтому, если некоторое тело выбрать в качестве эталона (его массу считать постулированной), то тем самым однозначно определяется масса любого другого тела. Отметим, что такой подход используется и в наиболее популярном школьном учебнике [17]. После того, как дано определение массы, рассматривается определение силы на основании второго закона Ньютона . Далее автор [16] приводит свидетельства того, что этот закон является фундаментальным законом природы, а не простым определением, причем эта аргументация во многом схожа с [11], упомянутой ранее. Таким образом, второй закон Ньютона логически следует за третьим, как утверждение о том, что отношение ускорений взаимодействующих тел обратно отношению их масс, фактически является законом «равенства действия и противодействия».
Поэтому, если некоторое тело выбрать в качестве эталона (его массу считать постулированной), то тем самым однозначно определяется масса любого другого тела. Отметим, что такой подход используется и в наиболее популярном школьном учебнике [17]. После того, как дано определение массы, рассматривается определение силы на основании второго закона Ньютона . Далее автор [16] приводит свидетельства того, что этот закон является фундаментальным законом природы, а не простым определением, причем эта аргументация во многом схожа с [11], упомянутой ранее. Таким образом, второй закон Ньютона логически следует за третьим, как утверждение о том, что отношение ускорений взаимодействующих тел обратно отношению их масс, фактически является законом «равенства действия и противодействия».
Как видим из проведенного обзора, в учебной литературе отсутствует единый взгляд на методику изложения основных законов динамики. Вполне возможно, что это и естественно, важно только, чтобы содержание материала было физически корректным и логически стройным.
Не претендуя на абсолютную истину и оптимальность, представлю кратко собственную последовательность изучения данной темы, которая используется в физических классах Лицея Белгосуниверситета.
Лейтмотивом моего построения этого раздела является исторический подход (например, с использованием [18]): после небольшого рассказа об античной механике (главным образом об Аристотеле) необходимо показать, какой революционный переворот совершил Г.Галилей введением закона инерции. Действительно, этот закон противоречит повседневному опыту, постоянно убеждающему нас, что, для того чтобы тело двигалось, необходимо прикладывать некоторые (иногда весьма значительные) усилия. Отметим, что в изложении Галилея закон инерции тесно переплетен с принципом относительности. Значение этого закона настолько велико, что И.Ньютон включил его в свою систему законов под первым номером. Исторически неверно утверждать, что Ньютон использовал этот закон как постулат существования инерциальных систем отсчета (как это вполне логично делается сейчас), так как он не сомневался в существовании абсолютного пространства и абсолютного времени, а принцип относительности выступал в качестве достаточно интересного, но не обязательного факта. В настоящее время, однако, первый закон Ньютона трактуется именно как определение тех систем отсчета, в которых будет вестись дальнейшее описание.
В настоящее время, однако, первый закон Ньютона трактуется именно как определение тех систем отсчета, в которых будет вестись дальнейшее описание.
Следующий этап – описание взаимодействия тел. Основной показатель наличия взаимодействия – изменение скорости тел, появление ускорения. Причем необходимо отметить, что ускорение тел зависит как от свойств самих тел, так и от свойств, характеристик взаимодействия. Поэтому возникает необходимость разделения этих свойств. Основываясь на многочисленных экспериментальных фактах (некоторые из них можно продемонстрировать [19]), доказываем, что при любом взаимодействии двух тел отношение ускорений есть величина постоянная, зависящая только от самих тел, но не от вида и интенсивности взаимодействия (третий закон Ньютона). Следовательно, это отношение может послужить основой введения характеристики инерционных свойств тел – их массы. Здесь уместно опять обратиться к истории и здравому смыслу: в обыденном бытовом понимании (и в определении Ньютона) масса есть мера количества материи, вещества, а в данном определении масса – просто количественная мера одного из свойств тела. Далее можно поговорить о таком классическом свойстве массы, как ее аддитивность. Заметим, что это свойство есть приближенный экспериментальный факт, в дальнейшем упоминается о том, что масса взаимодействующих тел отличается от суммы масс каждого из этих тел. Однако если масса есть только характеристика инерционных свойств, то в изменении массы нет ничего таинственного, если же масса воспринимается как мера количества материи, то в изменении массы появляется нечто таинственное – «исчезновение материи»(?!).
Далее можно поговорить о таком классическом свойстве массы, как ее аддитивность. Заметим, что это свойство есть приближенный экспериментальный факт, в дальнейшем упоминается о том, что масса взаимодействующих тел отличается от суммы масс каждого из этих тел. Однако если масса есть только характеристика инерционных свойств, то в изменении массы нет ничего таинственного, если же масса воспринимается как мера количества материи, то в изменении массы появляется нечто таинственное – «исчезновение материи»(?!).
Определив количественную характеристику инерционных свойств тел, можно продолжить изучение взаимодействий – пытаясь найти характеристику этих взаимодействий. Как уже было отмечено, проявлением взаимодействия является ускорение, следовательно, характеристика взаимодействия должна быть связана с ускорением, приобретаемым телом. Опять же, основываясь на экспериментальных фактах, показываем, что для одного и того же взаимодействия (например, посредством одной и той же пружины, пары магнитов и т.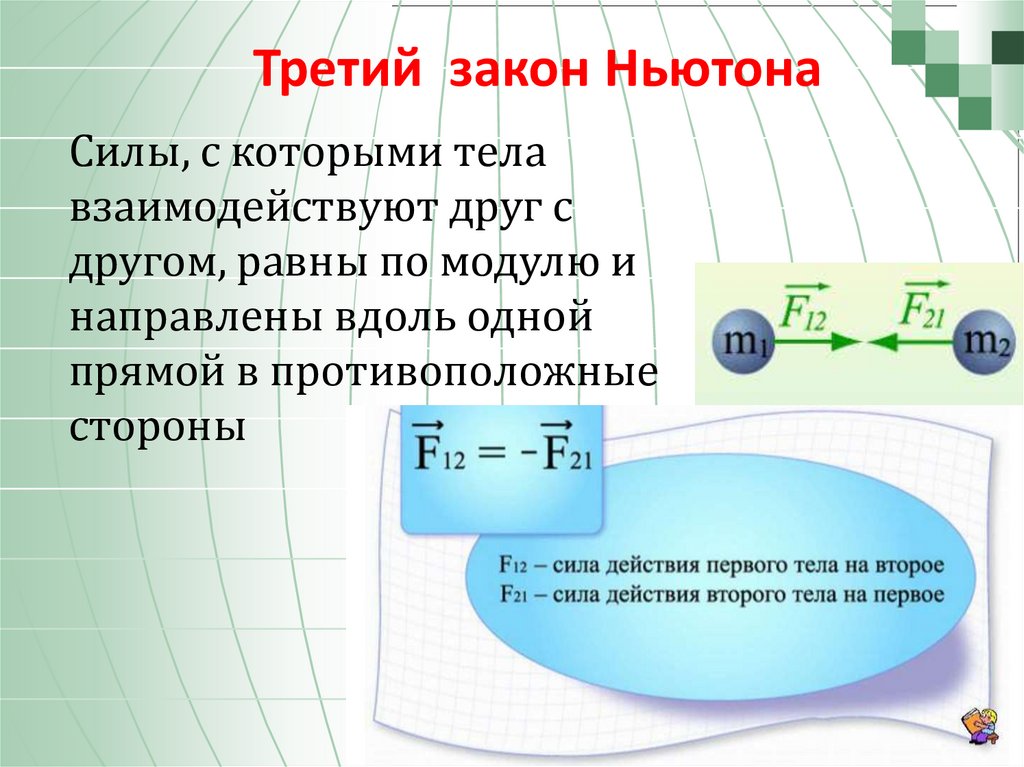 д.) произведение ускорения на массу тела (или что то же самое – ускорение обратно пропорционально массе) есть величина постоянная, не зависящая от взаимодействующих тел, следовательно, она может служить характеристикой самого взаимодействия. Эта характеристика называется силой (иначе говоря, ). Само слово, конечно, знакомо учащимся, в обыденном понимании оно ассоциируется, как правило, с мышечным усилием, тягой различных движителей. Однако в физике оно имеет строго определенный и однозначный смысл, кроме того, следует показать, что сила является векторной величиной. Заметим, что, помимо простого определения силы, этот второй закон Ньютона в такой формулировке имеет другое важнейшее значение – он выступает в роли метода изучения взаимодействий различной природы, метода экспериментального получения законов взаимодействий (всемирного тяготения Ньютона, Гука, Кулона, Ампера и многих других).
д.) произведение ускорения на массу тела (или что то же самое – ускорение обратно пропорционально массе) есть величина постоянная, не зависящая от взаимодействующих тел, следовательно, она может служить характеристикой самого взаимодействия. Эта характеристика называется силой (иначе говоря, ). Само слово, конечно, знакомо учащимся, в обыденном понимании оно ассоциируется, как правило, с мышечным усилием, тягой различных движителей. Однако в физике оно имеет строго определенный и однозначный смысл, кроме того, следует показать, что сила является векторной величиной. Заметим, что, помимо простого определения силы, этот второй закон Ньютона в такой формулировке имеет другое важнейшее значение – он выступает в роли метода изучения взаимодействий различной природы, метода экспериментального получения законов взаимодействий (всемирного тяготения Ньютона, Гука, Кулона, Ампера и многих других).
На основании полученных законов появляется возможность конструировать приборы для более простых экспериментальных способов измерения как масс тел (на основании измерения силы тяжести – весы), так и сил (на основании закона Гука для упругих деформаций) – динамометры. В том, что реально измерения физических величин проводятся не на основании их определений, нет ничего удивительного – можно вспомнить об электроизмерительных приборах, не всегда функционирующих строго на основании определений соответствующих физических величин.
В том, что реально измерения физических величин проводятся не на основании их определений, нет ничего удивительного – можно вспомнить об электроизмерительных приборах, не всегда функционирующих строго на основании определений соответствующих физических величин.
{mosimage}Если известны законы, позволяющие вычислить силы, то появляется прекрасная возможность использовать второй закон Ньютона как метод вычисления ускорения и затем нахождения законов движения (т.е. закон принимает вид ). Однако для того чтобы им можно было пользоваться, необходимо сформулировать и обосновать (опять же экспериментально) принцип суперпозиции – показать, что силы, действующие на одно тело, можно складывать (естественно, векторно). Сам Ньютон рассматривал свои три закона вместе с законом всемирного тяготения – только в такой связке, вместе с законом, позволяющим независимо определять силу, система уравнений становится полной и достаточной для вычисления характеристик движения. Отметим, что в формулировках Ньютона первый закон является следствием второго, однако такова историческая традиция, например, у Архимеда можно найти порядка десяти законов плавания тел (при плотностях тела, больших и меньших плотности жидкости, и т. д.), но сейчас мы пользуемся одним законом Архимеда.
д.), но сейчас мы пользуемся одним законом Архимеда.
На мой взгляд, принципиально важно при изучении рассматриваемой здесь темы подчеркнуть единство трех законов – каждый из них, взятый в отрыве от других, имеет малую ценность, кроме того, они взаимосвязаны хотя бы тем, что оперируют с одним набором физических величин – ускорение, масса, сила (даже в числе законов есть своя логика: три величины – три закона). Первый закон определяет системы отсчета, в которых проводятся измерения ускорений, но сам закон предполагает использование понятия взаимодействия. Третий закон дает возможность определить понятие массы; но, помимо того, также использует понятие взаимодействия и предполагает умение измерять ускорения. Хотя это не совсем относится к основной теме изложения, отметим, что если говорить о взаимодействии (а не о действии силы на объект), то этот закон полностью очевиден – есть взаимодействие, есть его характеристика – сила, естественно, она должна быть одинакова для обоих взаимодействующих тел. Второй закон – определение силы, но и с добавлением принципа суперпозиции, мощнейший метод решения основной задачи механики.
Второй закон – определение силы, но и с добавлением принципа суперпозиции, мощнейший метод решения основной задачи механики.
Прежде чем далее переходить к изучению конкретных видов взаимодействий (сил), требуется рассказать, что развитие механики не закончилось на установлении законов Ньютона, законов взаимодействия и развития математических методов решения уравнений, следующих из этих законов. С одной стороны, сами законы послужили основой более глубоких обобщений (таких, как законы сохранения), а с другой стороны – выявились ограниченные рамки их применимости (установленные теорией относительности и квантовой механикой).
Меня можно упрекнуть в том, что я фактически ухожу от ответа на вопрос, вынесенный в заголовок статьи. Однако если мы признаем двоякую роль второго закона Ньютона, то следует признать и необходимость двух его формулировок, пользоваться же следует той, которая соответствует стоящей перед исследователем проблеме – для изучения новых видов взаимодействия – первая, для нахождения закона движения – вторая.
Хочу заметить, что не только обсуждаемый здесь закон носит такую двойственность. Достаточно вспомнить закон Кулона (особенно в системе единиц СГСЭ): с одной стороны – позволяет вычислять силу взаимодействия двух известных зарядов, с другой – определять единицу заряда. Аналогичная ситуация с законом взаимодействия токов (законом Ампера).
1. Роуэл Г., Герберт С. Физика. – М.: Просвещение, 1993.
2. Ландау Л.Д., Лившиц Е.М. Теоретическая физика. – Т. 1. Механика. – М.: Наука, 1988.
3. Астахов А.В. Курс физики. – Т. 1. – М.: Гл. ред. физ.-мат. литературы, 1977.
4. Павленко Д.Г. Начала физики. – М.: Изд-во МГУ, 1988.
5. Кузмичев В.Е. Законы и формулы физики. – Киев: Навукова думка, 1989.
6. Чертов А.Г. Физические величины. – М.: Высшая школа, 1990.
7. Детлаф А.А., Яворский Б.М., Милковская Л.Б. Курс физики. – Т. 1. – М. : Высшая школа, 1973.
: Высшая школа, 1973.
8. Элементарный учебник физики/Под ред. Г.С.Ландсберга. -Т. 1. – М.: Наука, 1975.
9. Яворский Б.М., Пинский А.А. Основы физики. – Т. 1. -М.: Наука, 1969.
10. Стрелков С.П. Механика. – М.: Наука, 1975.
11. Матвеев А.Н. Механика и теория относительности. – М.: Высшая школа, 1986.
12. Яворский Б.М., Селезнев Ю.А. Справочное пособие по физике для поступающих в ВУЗы и самообразования. – М.: Наука, 1984.
13. Кабардин О.Ф. Физика. Справочные материалы. – М.: Просвещение, 1988.
14. Сивухин Д.В. Общий курс физики. – Т. I, – М.: Наука, 1974.
15. Савельев И.В. Курс физики. – Т. 1. – М.: Наука, 1989.
16. Орир Дж. Физика. – Т. 1. – М.: Мир, 1981.
17. Кикоин И.К., Кикоин А.К. Физика. 9 класс. – М.: Просвещение, 1990.
18. Кудрявцев П.С. Курс истории физики. – М.: Просвещение, 1974.
– М.: Просвещение, 1974.
19. Демонстрационный эксперимент по физике в средней школе / Под ред. А.А.Покровского. – М.: Просвещение, 1978.
Конспекты уроков по физике
Конспектирование — удобная и эффективная, с точки зрения организации и проверки процесса освоения знаний, форма работы. Она позволяет существенно упростить и ускорить процесс систематизации и запоминания даже больших объемов информации. Именно на конспектировании, как основе, строится послешкольный образовательный процесс — в колледжах, ВУЗах и техникумах. Поэтому эта технология, освоенная еще в школьный период, позволит быстрее адаптироваться к особенностям преподавания, с которыми подросток столкнется впоследствии. Удобные и понятные конспекты уроков по всем предметам позволят в кратчайшие сроки повторить всю необходимую информацию перед проверочной, контрольной, коллоквиумом, экзаменом и пр. Если повторение по учебникам и практикумам заняло бы дни, недели, то законспектированный материал позволит сделать это за считанные часы. Но только в том случае, если оно выполнено грамотно и профессионально. Научиться составлять собственные материалы-конспекты возможно, а в качестве образца многие эксперты и педагоги рекомендуют готовые, представленные на платформе Еуроки.
Но только в том случае, если оно выполнено грамотно и профессионально. Научиться составлять собственные материалы-конспекты возможно, а в качестве образца многие эксперты и педагоги рекомендуют готовые, представленные на платформе Еуроки.
Кому пригодятся конспекты уроков по различным предметам?
Актуальные и практичные в применении конспекты для классных записей, приведенные на указанной выше площадке, будут полезны:
- школьникам, активно интересующимся той или иной наукой. С их помощью они смогут ознакомиться с учебным материалом, изложенным в разных программах, УМК по выбранной ими дисциплине. Тем самым, расширится их кругозор, знания станут более полными и глубокими;
- подросткам, испытывающим те или иные трудности с освоением курса определенных школьных программ. Законспектированные понятия, законы, термины, их взаимосвязи помогут быстрее запомнить базовые, ключевые моменты из учебного материала школьных предметов. Спустя непродолжительное время учащиеся смогут заметить улучшение результатов — более высокие оценки, глубокие знания, интерес к познанию в целом;
- тем учащимся, которые часто по тем или иным причинам пропускают уроки в школе.
 Например, ездят на соревнования, спортивные сборы, творческие конкурсы, часто болеют или проходят долгую и сложную реабилитацию. С помощью законспектированных данных они смогут, не тратя много времени на подготовку, быть в курсе того, что в данный момент изучается в школе их одноклассниками.
Например, ездят на соревнования, спортивные сборы, творческие конкурсы, часто болеют или проходят долгую и сложную реабилитацию. С помощью законспектированных данных они смогут, не тратя много времени на подготовку, быть в курсе того, что в данный момент изучается в школе их одноклассниками.
Есть ли толк от готовых конспектов по различным предметам?
Полезные материалы площадки оценили многие, но не все. Например, некоторые родители и школьные педагоги с предубеждением относятся к различным платформам. Возможно, их точка зрения изменится, если они оценят все те преимущества, которыми располагает краткая запись параграфов учебника по школьным дисциплинам:
- наглядность. Вся информация представлена в сжатой форме, а значит можно, бегло изучив ее, быстро найти все необходимое для ответа, выполнения задания учителя;
- удобство применения. Заниматься по этому источнику можно в любое время и в любом месте, удобном пользователю. Можно составить свой собственный план работы, учитывающий все индивидуальные задачи и особенности обучения;
- быстрота запоминания.
 Краткие тезисы, основные мысли запомнить намного проще, чем обширный материал учебников, особенно по ряду дисциплин.
Краткие тезисы, основные мысли запомнить намного проще, чем обширный материал учебников, особенно по ряду дисциплин.
Еще одно важное преимущество, которое отмечают практически все пользователи, в том числе — педагоги и эксперты. Занимаясь по готовым законспектированным материалам, школьники постепенно обретают и закрепляют навыки самостоятельного грамотного конспектирования. Главное, чтобы эта работа велась системно и регулярно. И тогда уже в школе столь ценное умение, которое обязательно пригодится впоследствии, будет приобретено и отработано. Это актуально, полезно и выгодно для семейного бюджета.
5.2 Первый закон Ньютона – University Physics Volume 1
5 Законы движения Ньютона
Цели обучения
К концу раздела вы сможете:
- Описывать первый закон движения Ньютона
- Распознать трение как внешнюю силу
- Определить инерцию
- Определить инерциальные системы отсчета
- Рассчитать равновесие для системы
Опыт показывает, что покоящийся объект остается в покое, если его оставить в покое, и что движущийся объект имеет тенденцию замедляться и останавливаться, если не предпринимать никаких усилий для поддержания его движения. Однако Первый закон Ньютона дает более глубокое объяснение этому наблюдению.
Однако Первый закон Ньютона дает более глубокое объяснение этому наблюдению.
Первый закон движения Ньютона
Тело в состоянии покоя остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует результирующая внешняя сила.
Обратите внимание на повторное использование глагола «остается». Мы можем думать об этом законе как о сохранении статус-кво движения. Также обратите внимание на выражение «постоянная скорость». это означает, что объект сохраняет путь по прямой линии, поскольку ни величина, ни направление вектора скорости не меняются. Мы можем использовать рисунок, чтобы рассмотреть две части первого закона Ньютона.
Рис. 5.7 (а) Хоккейная шайба показана в состоянии покоя; он остается в покое до тех пор, пока внешняя сила, такая как хоккейная клюшка, не изменит его состояние покоя; б) изображена хоккейная шайба в движении; он продолжает движение по прямой линии до тех пор, пока внешняя сила не заставит его изменить свое состояние движения.
Вместо того, чтобы противоречить нашему опыту, первый закон Ньютона говорит, что должна быть причина для любого изменения скорости (изменение либо величины, либо направления). Эта причина является чистой внешней силой, которую мы определили ранее в этой главе. Объект, скользящий по столу или полу, замедляется из-за суммарной силы трения, действующей на объект. Если трение исчезнет, будет ли объект по-прежнему замедляться?
Представление о причине и следствии имеет решающее значение для точного описания того, что происходит в различных ситуациях. Например, рассмотрим, что происходит с объектом, скользящим по шероховатой горизонтальной поверхности. Объект быстро останавливается. Если мы посыпаем поверхность тальком, чтобы сделать поверхность более гладкой, объект будет скользить дальше. Если мы сделаем поверхность еще более гладкой, нанеся на нее смазочное масло, объект будет скользить еще дальше.
Рассмотрим стол для аэрохоккея (рисунок). Когда воздух отключен, шайба скользит только на короткое расстояние, прежде чем трение замедляет ее до остановки. Однако, когда воздух включен, создается поверхность, практически лишенная трения, и шайба скользит на большие расстояния, не замедляясь. Кроме того, если мы достаточно знаем о трении, мы можем точно предсказать, насколько быстро объект замедляется.
Рисунок 5.8 Таблица аэрохоккея полезна для иллюстрации законов Ньютона. Когда воздух выключен, трение быстро замедляет шайбу; но когда воздух включен, он сводит к минимуму контакт между шайбой и хоккейным столом, и шайба скользит далеко по столу. Эксперименты подтвердили, что любое изменение скорости (скорости или направления) должно быть вызвано внешней силой. Идея общеприменимых или универсальных законов важна — это основная черта всех законов физики. Выявление этих законов похоже на распознавание закономерностей в природе, из которых можно обнаружить дальнейшие закономерности. Гениальность Галилея, впервые разработавшего идею первого закона движения, и Ньютона, разъяснившего его, заключалась в том, чтобы задать фундаментальный вопрос: «Что есть причина?» Мышление в терминах причины и следствия в корне отличается от типичного древнегреческого подхода, когда такие вопросы, как «Почему у тигра полосы?» ответили бы в аристотелевской манере, например: «Такова природа зверя». Способность мыслить в категориях причины и следствия — это способность установить связь между наблюдаемым поведением и окружающим миром.
Эксперименты подтвердили, что любое изменение скорости (скорости или направления) должно быть вызвано внешней силой. Идея общеприменимых или универсальных законов важна — это основная черта всех законов физики. Выявление этих законов похоже на распознавание закономерностей в природе, из которых можно обнаружить дальнейшие закономерности. Гениальность Галилея, впервые разработавшего идею первого закона движения, и Ньютона, разъяснившего его, заключалась в том, чтобы задать фундаментальный вопрос: «Что есть причина?» Мышление в терминах причины и следствия в корне отличается от типичного древнегреческого подхода, когда такие вопросы, как «Почему у тигра полосы?» ответили бы в аристотелевской манере, например: «Такова природа зверя». Способность мыслить в категориях причины и следствия — это способность установить связь между наблюдаемым поведением и окружающим миром.Гравитация и инерция
Независимо от масштаба объекта, будь то молекула или субатомная частица, два свойства остаются действительными и поэтому представляют интерес для физики: гравитация и инерция.
Масса также связана с инерцией , способностью объекта сопротивляться изменениям в его движении, другими словами, сопротивляться ускорению. Первый закон Ньютона часто называют законом инерции . Как мы знаем из опыта, одни объекты обладают большей инерцией, чем другие. Изменить движение большого валуна сложнее, чем, например, баскетбольного мяча, потому что валун имеет большую массу, чем баскетбольный мяч. Другими словами, инерция объекта измеряется его массой. Отношения между массой и весом исследуются далее в этой главе.
Инерциальные системы отсчета
Ранее мы сформулировали первый закон Ньютона следующим образом: «Тело в состоянии покоя остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует результирующая внешняя сила». Его также можно сформулировать так: «Каждое тело остается в состоянии равномерного прямолинейного движения, если оно не вынуждено изменить это состояние под действием действующих на него сил». Для Ньютона «равномерное прямолинейное движение» означало постоянную скорость, включая случай нулевой скорости или покоя. Следовательно, первый закон гласит, что скорость объекта остается постоянной, если результирующая сила, действующая на него, равна нулю.
Его также можно сформулировать так: «Каждое тело остается в состоянии равномерного прямолинейного движения, если оно не вынуждено изменить это состояние под действием действующих на него сил». Для Ньютона «равномерное прямолинейное движение» означало постоянную скорость, включая случай нулевой скорости или покоя. Следовательно, первый закон гласит, что скорость объекта остается постоянной, если результирующая сила, действующая на него, равна нулю.
Первый закон Ньютона обычно считается утверждением о системах отсчета. Он предоставляет метод для идентификации специального типа системы отсчета: инерциальной системы отсчета . В принципе, мы можем сделать результирующую силу, действующую на тело, равной нулю. Если его скорость относительно данной системы отсчета постоянна, то эта система называется инерциальной. Итак, по определению, инерциальная система отсчета — это система отсчета, в которой действует первый закон Ньютона. Первый закон Ньютона применим к объектам с постоянной скоростью.
Наконец, ни одна инерциальная система отсчета не является более особенной, чем любая другая. Что касается законов природы, то все инерциальные системы эквивалентны. При анализе проблемы мы предпочитаем одну инерциальную систему отсчета просто из соображений удобства.
Первый закон Ньютона и равновесие
Первый закон Ньютона говорит нам о равновесии системы, то есть о состоянии, в котором силы, действующие на систему, уравновешены. Возвращаясь к силам и фигуристам на рисунке, мы знаем, что силы [латекс]{\mathbf{\overset{\to }{F}}}_{1}[/латекс] и [латекс]{\mathbf{\ overset{\to}{F}}}_{2}[/latex] объединяются, чтобы сформировать результирующую силу или результирующую внешнюю силу: [latex]{\mathbf{\overset{\to}}{F}}}_ {\ text {R}} = {\ mathbf {\ overset {\ to} {F}}} _ {\ text {net}} = {\ mathbf {\ overset {\ to} {F}}} _ {1 }+{\mathbf{\overset{\to }{F}}}_{2}. [/latex] Чтобы создать равновесие, нам нужна уравновешивающая сила, которая будет производить чистую силу, равную нулю. Эта сила должна быть равна по величине, но противоположна по направлению [латекс] {\ mathbf {\ overset {\ to {F}}} _ {\ текст {R}}, [/ латекс], что означает, что вектор должен быть [ латекс]\текст{−}{\mathbf{\overset{\to }{F}}}_{\text{R}}.[/latex] Имеются в виду фигуристы, для которых мы нашли [латекс]{\ mathbf{\overset{\to}}{F}}}_{\text{R}}[/latex] равно [латекс]30,0\mathbf{\шляпа{i}}+40,0\mathbf{\шляпа{j} }\,\text{N}[/latex], мы можем определить уравновешивающую силу, просто найдя [латекс]\text{−}{\mathbf{\overset{\to }{F}}}_{\text{ R}}=-30,0\mathbf{\hat{i}}-40,0\mathbf{\hat{j}}\,\text{N}.[/latex] См. диаграмму свободного тела на рисунке (b).
[/latex] Чтобы создать равновесие, нам нужна уравновешивающая сила, которая будет производить чистую силу, равную нулю. Эта сила должна быть равна по величине, но противоположна по направлению [латекс] {\ mathbf {\ overset {\ to {F}}} _ {\ текст {R}}, [/ латекс], что означает, что вектор должен быть [ латекс]\текст{−}{\mathbf{\overset{\to }{F}}}_{\text{R}}.[/latex] Имеются в виду фигуристы, для которых мы нашли [латекс]{\ mathbf{\overset{\to}}{F}}}_{\text{R}}[/latex] равно [латекс]30,0\mathbf{\шляпа{i}}+40,0\mathbf{\шляпа{j} }\,\text{N}[/latex], мы можем определить уравновешивающую силу, просто найдя [латекс]\text{−}{\mathbf{\overset{\to }{F}}}_{\text{ R}}=-30,0\mathbf{\hat{i}}-40,0\mathbf{\hat{j}}\,\text{N}.[/latex] См. диаграмму свободного тела на рисунке (b).
Мы можем представить первый закон Ньютона в векторной форме: F}}}_{\text{net}}=\mathbf{\overset{\to }{0}}\,\text{N}.[/latex]
Это уравнение говорит, что чистая сила, равная нулю, подразумевает что скорость [латекс]\mathbf{\overset{\to}}{v}}[/латекс] объекта постоянна.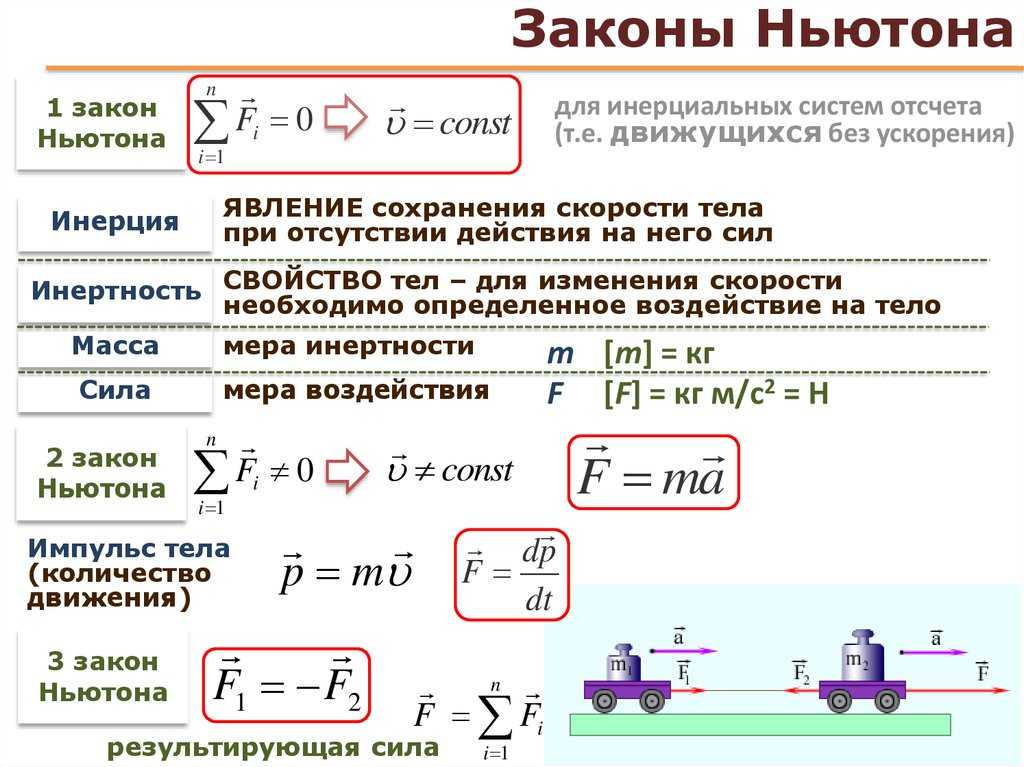 (Слово «постоянная» может означать нулевую скорость.)
(Слово «постоянная» может означать нулевую скорость.)
Первый закон Ньютона обманчиво прост. Если автомобиль находится в состоянии покоя, то единственными силами, действующими на автомобиль, являются вес и контактная сила дорожного покрытия, воздействующая на автомобиль (рисунок). Легко понять, что для изменения состояния движения автомобиля требуется ненулевая результирующая сила. Однако, если автомобиль движется с постоянной скоростью, распространенное заблуждение состоит в том, что сила двигателя, толкающая автомобиль вперед, больше по величине, чем сила трения, препятствующая движению вперед. На самом деле обе силы имеют одинаковую величину.
Рисунок 5.9 Автомобиль показан (а) припаркованным и (б) движущимся с постоянной скоростью. Как законы Ньютона применимы к припаркованному автомобилю? Что знание того, что автомобиль движется с постоянной скоростью, говорит нам о чистой горизонтальной силе, действующей на автомобиль?Пример
Когда первый закон Ньютона применим к вашему автомобилю?
Законы Ньютона применимы ко всем физическим процессам, связанным с силой и движением, включая такие обыденные вещи, как вождение автомобиля.
(a) Ваш автомобиль припаркован возле вашего дома. Применим ли в данном случае первый закон Ньютона? Почему или почему нет?
(b) Ваша машина движется с постоянной скоростью по улице. Применим ли в данном случае первый закон Ньютона? Почему или почему нет?
Стратегия
В (а) мы рассматриваем первую часть первого закона Ньютона, касающуюся покоящегося тела; в (b) мы рассматриваем вторую часть первого закона Ньютона для движущегося тела.
Решение
- Когда ваш автомобиль припаркован, все силы, действующие на автомобиль, должны быть уравновешены; сумма векторов равна 0 Н. Таким образом, результирующая сила равна нулю, и действует первый закон Ньютона. Ускорение автомобиля равно нулю, и в этом случае скорость также равна нулю.
- Когда ваш автомобиль движется с постоянной скоростью по улице, результирующая сила также должна быть равна нулю в соответствии с первым законом Ньютона. Двигатель автомобиля создает поступательное усилие; трение, сила между дорогой и шинами автомобиля, противодействующая движению вперед, имеет точно такую же величину, что и сила двигателя, поэтому результирующая сила равна нулю.

Значение
Как показывает этот пример, существует два вида равновесия. В (а) автомобиль находится в состоянии покоя; мы говорим, что он находится в статическом равновесии . В (b) силы, действующие на автомобиль, уравновешены, но автомобиль движется; мы говорим, что он находится в динамическом равновесии . (Мы рассматриваем эту идею более подробно в разделе «Статическое равновесие и эластичность».) Опять же, две (или более) силы могут воздействовать на объект, но при этом объект будет двигаться. Кроме того, чистая сила, равная нулю, не может создавать ускорение.
Проверьте свое понимание
Парашютист раскрывает парашют и вскоре после этого движется с постоянной скоростью.
а. Его вес действует вниз, а сила сопротивления воздуха с парашютом действует вверх. б. ни один; силы равны по модулю
Используйте эту симуляцию, чтобы качественно предсказать, как внешняя сила повлияет на скорость и направление движения объекта. Объясните эффекты с помощью диаграммы свободного тела. Используйте диаграммы свободного тела для построения графиков положения, скорости, ускорения и силы и наоборот. Объясните, как графики соотносятся друг с другом. Учитывая сценарий или график, нарисуйте все четыре графика.
Резюме
- Согласно первому закону Ньютона, для любого изменения скорости (изменения величины или направления) должна существовать причина. Этот закон также известен как закон инерции.
- Трение — это внешняя сила, которая заставляет объект замедляться.
- Инерция — это тенденция объекта оставаться в покое или оставаться в движении. Инерция связана с массой объекта.

- Если скорость объекта относительно данной системы отсчета постоянна, то система инерциальна. Это означает, что для инерциальной системы отсчета справедлив первый закон Ньютона.
- Равновесие достигается, когда силы в системе уравновешены.
- Нулевая результирующая сила означает, что объект либо покоится, либо движется с постоянной скоростью; то есть не ускоряется.
Концептуальные вопросы
Принимая систему отсчета, связанную с Землей, как инерциальную, к каким из следующих объектов не может быть присоединена инерциальная система отсчета, и какие из них являются инерциальными системами отсчета?
(a) Автомобиль, движущийся с постоянной скоростью
(b) Автомобиль, ускоряющийся
(c) Лифт в свободном падении
(d) Космическая капсула на орбите Земли
(e) Лифт, спускающийся равномерно
Женщина везла открытую коробку с кексами на школьную вечеринку. Машина перед ней внезапно остановилась; она немедленно затормозила. Она была пристегнута ремнем безопасности и не получила никакого физического вреда (просто сильное смущение), но кексы полетели в приборную панель и превратились в «смушкейки». Объясните, что произошло.
Она была пристегнута ремнем безопасности и не получила никакого физического вреда (просто сильное смущение), но кексы полетели в приборную панель и превратились в «смушкейки». Объясните, что произошло.
Скорость кекса перед торможением была такой же, как и у автомобиля. Таким образом, кексы были неограниченными телами в движении, и когда машина внезапно останавливалась, кексы продолжали двигаться вперед в соответствии с первым законом Ньютона.
Задачи
Две силы [латекса] {\ mathbf {\ overset {\ to} {F}}} _ {1} = \ frac {75.0} {\ sqrt {2}} (\ mathbf {\ hat {i }}-\mathbf{\шляпа{j}})\,\text{N}[/латекс] и [латекс]{\mathbf{\overset{\to}}{F}}}_{2}=\frac {150.0}{\sqrt{2}}(\mathbf{\hat{i}}-\mathbf{\hat{j}})\,\text{N}[/latex] действуют на объект. Найдите третью силу [латекс]{\mathbf{\overset{\to}}{F}}}_{3}[/латекс], которая необходима для уравновешивания первых двух сил. 9\circ[/latex] к востоку от севера с магнитудой 180,0 Н. (a) Найдите результирующую силу в компонентной форме.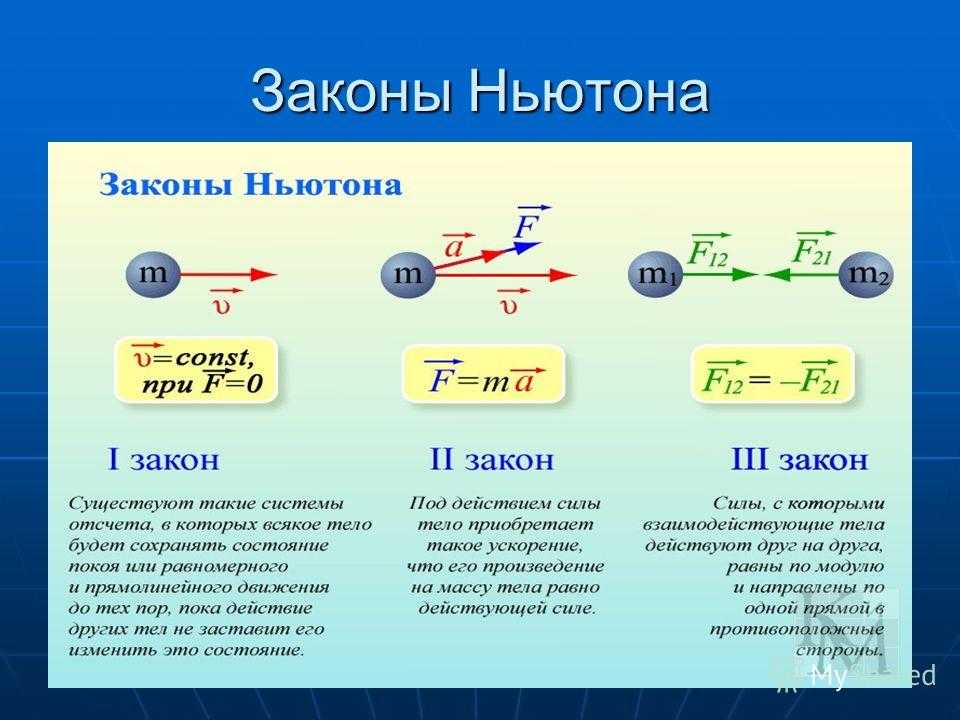 б) Найдите модуль и направление равнодействующей силы. (c) Если соседи по дому Андреа и Дженнифер, Дэвид и Стефани, не согласны с переездом и хотят предотвратить его перемещение, с помощью какой совместной силы [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {DS}}[/latex] должны ли они толкать, чтобы диван не двигался?
б) Найдите модуль и направление равнодействующей силы. (c) Если соседи по дому Андреа и Дженнифер, Дэвид и Стефани, не согласны с переездом и хотят предотвратить его перемещение, с помощью какой совместной силы [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {DS}}[/latex] должны ли они толкать, чтобы диван не двигался?
а. [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {net}} = 95,0 \ mathbf {\ hat {i}} + 283 \ mathbf {\ hat {j}} \ text {N}[/латекс]; б. 29\circ[/latex] к северу от востока; в. [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {DS}} = \ text {−} (95,0 \ mathbf {\ hat {i}} + 283 \ mathbf {\ hat {j}})\,\text{N}[/латекс]
Глоссарий
- инерция
- способность объекта сопротивляться изменениям в его движении
- инерциальная система отсчета
- система отсчета, движущаяся с постоянной скоростью относительно инерциальной системы отсчета, также является инерциальной; система отсчета, ускоряющаяся относительно инерциальной системы отсчета, не является инерциальной
- закон инерции
- см.
 первый закон движения Ньютона
первый закон движения Ньютона
- Первый закон Ньютона
- тело в состоянии покоя остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует результирующая внешняя сила; также известный как закон инерции
Mr Wnuk PE – Законы Ньютона
Чтобы произвести спортивное движение, наши тела должны иметь дело и использовать ряд сил, которые работают по-разному и часто противоречат друг другу. Элитные спортсмены способны манипулировать этими силами в своих интересах, и понимание физики движения представляет первостепенный интерес для спортивных ученых и спортивных тренеров. Три закона Ньютона используются спортивными учеными для объяснения того, как спортсмен может точно и не очень точно контролировать свои движения.
Закон инерции
«Тело останется в покое или в постоянном равномерном движении, если на него не действует сила»
Первый закон Ньютона состоит из двух компонентов. Во-первых, неподвижный объект не будет двигаться, если к нему не приложена сила. Во-вторых, движущийся объект будет двигаться в том же направлении и с той же скоростью, если на него не действует сила.
Во-первых, неподвижный объект не будет двигаться, если к нему не приложена сила. Во-вторых, движущийся объект будет двигаться в том же направлении и с той же скоростью, если на него не действует сила.
Есть несколько соображений, которые необходимо учитывать при применении этого закона к спорту. Мы можем видеть это, глядя на некоторые удары, которые делает игрок в гольф. Когда игрок в гольф помещает свой мяч на площадку-ти на первой лунке, мяч остается (в состоянии покоя) на площадке-ти до тех пор, пока игрок в гольф не ударит клюшкой по мячу (применив силу). Если бы по мячу ударили в космосе (где нет гравитации), он бы продолжал двигаться с той же скоростью и в том же направлении вечно… конечно, до тех пор, пока на его пути не встанет метеор, спутник или планета! На земле мяч будет двигаться, но сопротивление воздуха и гравитация (сила!) будут действовать на мяч, препятствуя его равномерному движению. Действительно, если вы плохой игрок в гольф, то дерево, куст, забор или другая опасность могут помешать мячу лететь в постоянном равномерном движении! Если мяч попал высоко над деревом, он замедлится в верхней части полета, но ускорится, когда вернется к лужайке.
Еще одно соображение для первого закона Ньютона касается силы, необходимой для перемещения объекта. Инерция определяется как «нежелание объекта изменить свое состояние движения». Чем больше масса объекта, тем больше его инерция, поскольку они имеют большую тенденцию сопротивляться изменениям в движении. Очевидно, что вы двигаете футбольный мяч, прикладывая небольшое усилие, когда толкаете его или пинаете, однако, если вы попытаетесь толкнуть или потянуть грузовик, как это делают на World’s Strongest Man , вы не сможете приложить достаточную силу для перемещения. это. Это одна из причин, по которой борцы сумо очень эндоморфны; у них много жира, поэтому их труднее вытолкнуть с ринга. Термин «импульс» применяется к движущимся объектам и относится к силе, необходимой для остановки или изменения направления движения. Объекты с большей массой или те, которые движутся быстрее, труднее изменить направление или остановиться. Вот почему игроки в регби пытаются увеличить свою мышечную массу, если их считают «легковесными», так как это затруднит их остановку. Представьте, что вы пытаетесь остановить футбольный мяч или грузовик, если они оба катятся с холма со скоростью 30 км/ч -1 .
Представьте, что вы пытаетесь остановить футбольный мяч или грузовик, если они оба катятся с холма со скоростью 30 км/ч -1 .
Импульс – относится к массе объекта, умноженной на его скорость. Если 5-килограммовый набивной мяч катится по полу с той же скоростью, что и 2-килограммовый, то более тяжелый из двух будет иметь больший импульс из-за большей массы. Однако более легкий мяч мог бы иметь такой же импульс (и для его остановки потребовалась бы такая же сила), если бы его бросили сильнее, поэтому он имел бы большую скорость.
Закон ускорения
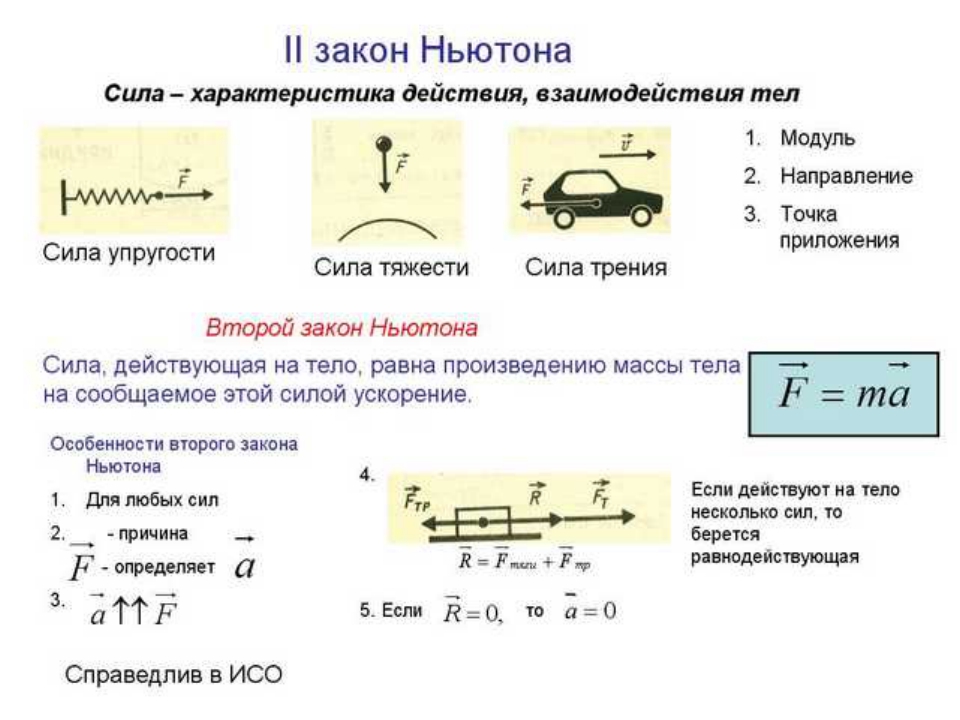
«Скорость изменения импульса (или ускорения) объекта прямо пропорциональна приложенной к нему силе и в том же направлении, что и ее приложение».
Второй закон Ньютона (закон ускорения) гласит, что скорость изменения ускорения тела или объекта зависит от величины приложенной силы. Эта сила также задает направление движения объекта. Чем больше приложенная сила, тем больше достигается ускорение, а это означает, что больший вес может поднять спортсмен или большее вертикальное ускорение достигается при отталкивании для прыжка в высоту.
Если мы посмотрим на теннисиста, выполнившего несколько успешных размашистых и залповых бросков в сетку, мы сможем увидеть второй закон Ньютона в действии. Сомнительно, чтобы какой-либо из этих кадров был идентичным. Когда элитные игроки наносят решающий удар, они могут ударить по мячу с такой силой, что он отскакивает от поля соперника, а затем отскакивает над его головой. Тем не менее, залп будет деликатно направлен в угол площадки противника, двигаясь с меньшей скоростью, поэтому они не смогут достичь его, пока он не отскочит дважды. Ускорение мяча будет зависеть от силы, с которой игрок ударит по мячу, поэтому, чтобы ударить по мячу с большим ускорением, игрок будет быстрее раскачивать ракетку. Чтобы изменить направление мяча, игрок вступает с ним в контакт, чтобы он двигался в нужном направлении; удар по мячу ближе к его вершине означает, что он отскочит близко к сетке.
Чтобы изменить направление мяча, игрок вступает с ним в контакт, чтобы он двигался в нужном направлении; удар по мячу ближе к его вершине означает, что он отскочит близко к сетке.
Закон противодействия
«На каждое действие есть равное и противоположное противодействие».
3-й закон Ньютона (реакции) гласит, что на каждую силу существует равная и противоположно направленная сила противодействия, а это означает, что, когда дайвер вдавливается в платформу для прыжков в воду, доска будет оказывать равную и противоположную силу обратно на дайвера.
Когда мы смотрим на результаты вертикального прыжка или сержантского прыжкового теста, мы видим, что элитные спринтеры и прыгуны в высоту могут прыгать в воздух более чем на 80 см, в то время как среднему студенту физкультуры уровня А повезет достичь более 40 см.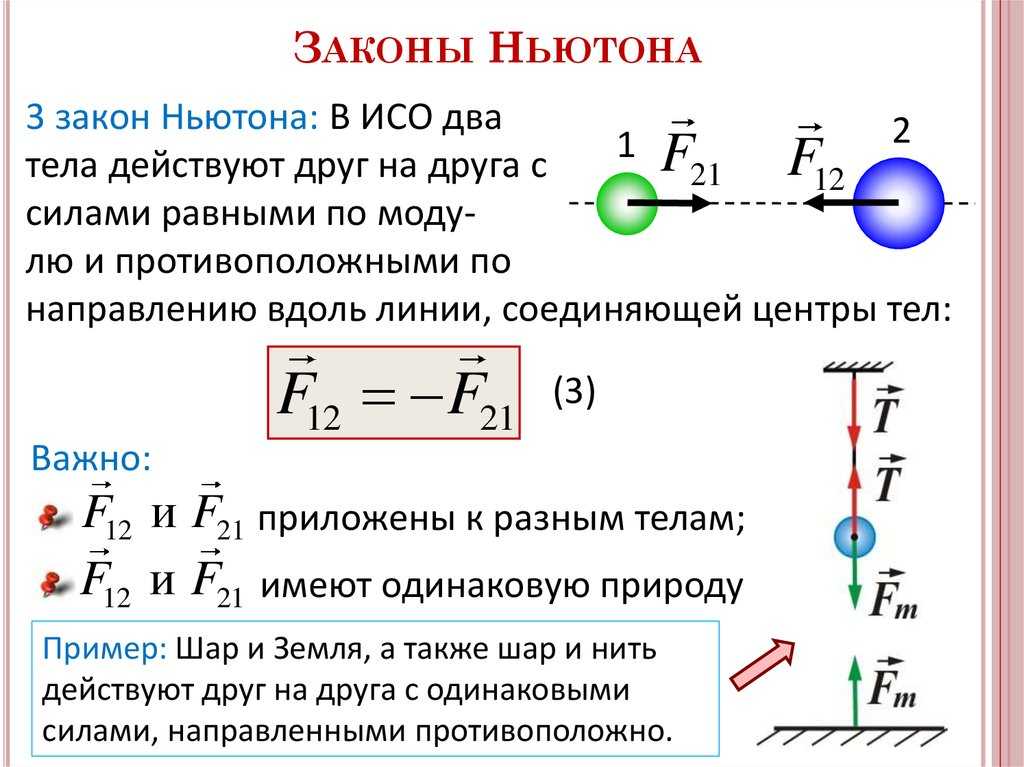 Чтобы объяснить различия в результатах, нам нужно применить второй и третий законы Ньютона. Мы видели, как ускорение объекта связано с величиной силы, прилагаемой мышцами ног (второй закон Ньютона). Третий закон Ньютона также является фактором, потому что, когда мышцы сокращаются, они передают силу на землю (известную как силы реакции земли [GRF]). Поскольку земля имеет большую инерцию, чем перемычка, она не двигается. Однако от земли к человеку прикладывается равная и противоположная сила, так что он поднимается в воздух (вертикальная составляющая). Чем больше приложенная сила, тем больше сила, приложенная землей (третий закон Ньютона), а это означает, что чем быстрее будет ускоряться прыгун, тем дальше он пролетит (второй закон Ньютона). При выполнении прыжка в длину с места применяются те же принципы, но на этот раз сила, которую прикладывает прыгун, направлена в другом направлении, поэтому он движется вперед, а также вверх. Человек оторвется от земли, если сила, приложенная к земле, больше силы гравитации.
Чтобы объяснить различия в результатах, нам нужно применить второй и третий законы Ньютона. Мы видели, как ускорение объекта связано с величиной силы, прилагаемой мышцами ног (второй закон Ньютона). Третий закон Ньютона также является фактором, потому что, когда мышцы сокращаются, они передают силу на землю (известную как силы реакции земли [GRF]). Поскольку земля имеет большую инерцию, чем перемычка, она не двигается. Однако от земли к человеку прикладывается равная и противоположная сила, так что он поднимается в воздух (вертикальная составляющая). Чем больше приложенная сила, тем больше сила, приложенная землей (третий закон Ньютона), а это означает, что чем быстрее будет ускоряться прыгун, тем дальше он пролетит (второй закон Ньютона). При выполнении прыжка в длину с места применяются те же принципы, но на этот раз сила, которую прикладывает прыгун, направлена в другом направлении, поэтому он движется вперед, а также вверх. Человек оторвется от земли, если сила, приложенная к земле, больше силы гравитации.

 Например, ездят на соревнования, спортивные сборы, творческие конкурсы, часто болеют или проходят долгую и сложную реабилитацию. С помощью законспектированных данных они смогут, не тратя много времени на подготовку, быть в курсе того, что в данный момент изучается в школе их одноклассниками.
Например, ездят на соревнования, спортивные сборы, творческие конкурсы, часто болеют или проходят долгую и сложную реабилитацию. С помощью законспектированных данных они смогут, не тратя много времени на подготовку, быть в курсе того, что в данный момент изучается в школе их одноклассниками.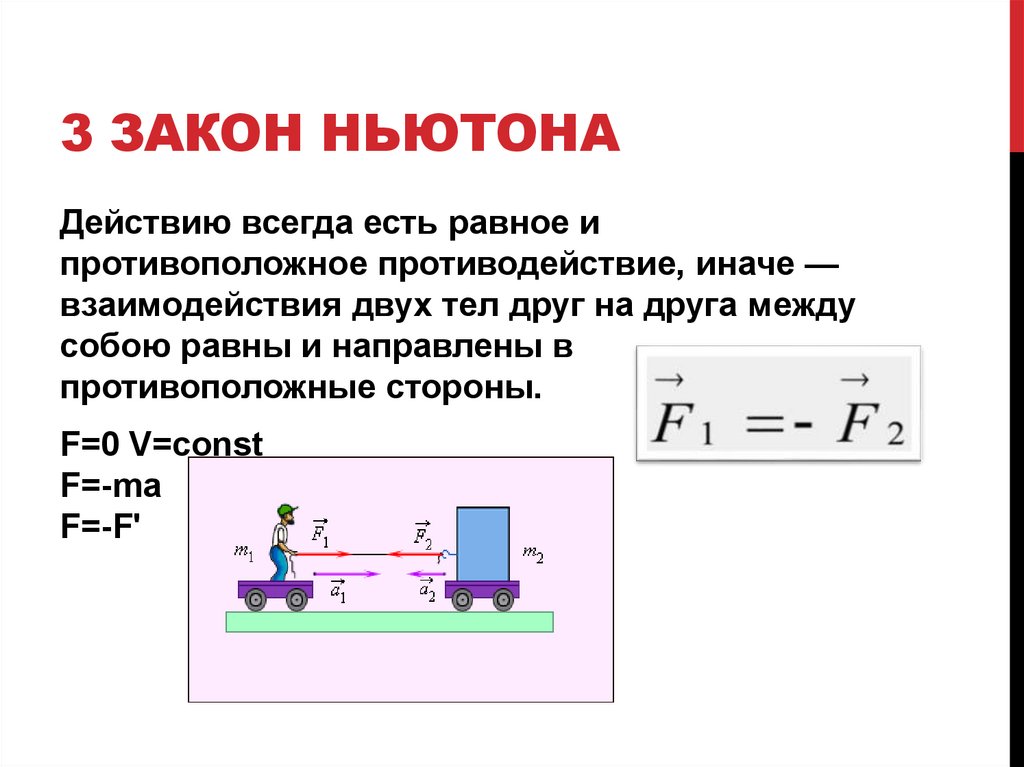 Краткие тезисы, основные мысли запомнить намного проще, чем обширный материал учебников, особенно по ряду дисциплин.
Краткие тезисы, основные мысли запомнить намного проще, чем обширный материал учебников, особенно по ряду дисциплин.

 первый закон движения Ньютона
первый закон движения Ньютона