1 закона ньютона определение: Что такое первый закон Ньютона? (статья)

формулы и определения простыми словами первого, второго и третьего законов

Три закона Ньютона лежат в основе классической физики, хотя за прошедшие годы стало понятно, что они — лишь частный случай теории относительности. В нашей статье разбираем формулы и определения законов Ньютона простыми словами

Законы Ньютона. Фото: pixabay.com

Андрей Найденов Преподаватель математики и физики онлайн-школы TutorOnline Борис Михеев Автор КП

Содержание

1. История открытия законов
2. Первый закон
3. Второй закон
4. Третий закон
5. Вопросы и ответы

Вплоть до XVII века мировая наука жила в условиях почти религиозной веры в постулаты, заданные великим философом Аристотелем. Покушение на них воспринималось как ересь и безжалостно наказывалось. Доходило даже до инквизиции. В этих условиях деятельность Галилея, Декарта, Ньютона была не только научным, но и человеческим подвигом. Их открытия сегодня могут быть даже переформулированы, не теряя своего смысла и значения.

История открытия законов Ньютона

Про то, как Ньютон открыл закон всемирного тяготения, знают практически все. Это та самая история про яблоко, которое упало ему на голову. На самом деле, яблоко на голову Ньютона не падало, но все это происходило в осеннем яблоневом саду, где яблоки действительно падали.

А вот как были сформулированы три знаменитых закона Ньютона, ставшие фундаментом классической механики, знают далеко не все. Впервые формулировки этих законов появились в книге Ньютона «Математические начала натуральной философии» (1687 год). Название этого труда достаточно известно именно потому, что в них впервые Ньютон дал определения всех трех законов.

Но перед тем, как формулировки этих законов были напечатаны, много чего произошло. Начиная с Древней Греции, многие мыслители пытались облечь в слова фундаментальные законы движения. Потребовалось несколько веков, чтобы сложились предпосылки для этого. Ближе всего к этому подошел Галилей. Но и ему помешали господствующие в научном сообществе иллюзии. Все были безоговорочно уверены, что небесные тела движутся строго по круговым орбитам, потому что это творение Бога, и это творение должно быть совершенно и безупречно. Пошатнуть эти иллюзии удалось Кеплеру. Но и он в своих размышлениях пошел не туда.

Гениальность Ньютона заключается в том, что, изучая труды своих великих предшественников, он смог разглядеть неочевидные вещи, которые даже нам кажутся парадоксальными. Именно Ньютон выдвинул революционную идею, что если на тело не действуют никакие силы, то тело может двигаться прямолинейно и равномерно. В условиях Земли это невозможно, так как действует сила земного тяготения. А вот вне Земли — это обычное дело.

Долгие годы размышлений, черновых набросков, сомнений, которые он выражал в письмах своим коллегам, завершились блестящими формулировками всех трех законов. И эти законы по праву носят имя Ньютона. О каждом из этих законов можно написать отдельную статью — настолько велико и многогранно их значение.

Первый закон Ньютона

Первый закон Ньютона еще называют закон инерции. Фактически он был открыт Галилеем, но именно Исаак Ньютон дал точную его формулировку и включил в число основных законов механики.

Определение

Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго. Формулы первый закон Ньютона не имеет.

Второй закон Ньютона

Действие второго закона Ньютона мы можем часто наблюдать в жизни. Возьмём теннисную ракетку и мяч. Если ударить ракеткой по мячу, то мяч приобретёт ускорение равное отношению равнодействующей всех сил к массе.

Определение

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

Формула

это интересно

Сила трения

Единицы измерения силы трения, от чего она зависит и какие виды существуют

подробнее

Третий закон Ньютона

Третий закон Ньютона объясняет, как, например, двигаются утки. Они находятся во взаимодействии с водой, отталкивая ее назад лапками, а сами благодаря ответному действию двигаются вперед.

Определение

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению.

Формула

Популярные вопросы и ответы

Отвечает Андрей Найденов, преподаватель физики и математики в онлайн-школе TutorOnline.

Сколько законов Ньютона изучают в школе?

В школе изучают четыре закона Ньютона. Первые три являются фундаментом классической динамики. С их помощью можно описать любое движение тела, которое движется со скоростью, значительно меньшей скорости света.

Особняком стоит закон всемирного тяготения. Он лежит в основе классической теории гравитации. Этот закон перекликается со вторым законом, касающемся соотношения между ускорением тела, его массой и действующей на него силой. Но все же это разные законы. Так как второй закон Ньютона более универсален, чем закон всемирного тяготения.

Как и где выполняются законы Ньютона в жизни?

Эти законы настолько фундаментальны, что увидеть их можно практически всюду. Пуля из ружья летит туда, куда толкают ее пороховые газы. Ракета летит туда, куда толкают ее продукты горения ракетного топлива. Мяч летит туда, куда пинает его футболист. Это примеры действия первого закона Ньютона.

Второй закон связан с ускорением, которое приобретает тело под действием силы, действующей на это тело. Например, болид «Формулы 1» разгоняется намного быстрее, чем простой серийный легковой автомобиль. На них действуют разные по величине силы тяги их двигателей. Мощность двигателя в спортивной машине на порядок выше, чем у обыкновенной.

Третий закон Ньютона устанавливает закон взаимодействия тел. Сила действия равна силе противодействия. Например, если чашка кофе стоит на столе и не проваливается сквозь него на пол, значит, стол оказывает достаточное противодействие силе тяжести, действующей на чашку. В результате эти две силы уравновешивают друг друга, и чашка стоит на столе без какого-либо движения.

Как Ньютон изменил третий закон Кеплера?

Законы Кеплера — это три соотношения, которые выведены Кеплером на основе астрономических наблюдений. Эти законы описывают идеализированную планету, движущуюся по круговой орбите. Опираясь на третий закон Кеплера, Ньютон сформулировал закон всемирного тяготения. При этом третий закон Кеплера в рамках теории всемирного тяготения Ньютона является решением частной задачи, которая касается двух тел. Другими словами, третий закон Кеплера стал частью более общей теории Ньютона.

Об извращённом толковании Первого закона Ньютона в современной физике / Хабр

В начале ХХ века в физике появились умники-недоучки, не признающие саму методологию научного творчества и объявившие о неких «ограничениях», сужающих область применимости механики Ньютона (I. Newton).

Начнём с того, как трактуются законы Ньютона в современных учебниках по физике. Например, в книге А.В. Перышкина и Е.М. Гутника [1] на стр.42 написано следующее:

<…> с точки зрения современных представлений первый закон Ньютона формулируется так:

существуют такие системы отсчёта, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел компенсируются.

Сравним это убожество с формулировкой самого Ньютона [2], кстати, приведённого в той же книжке страницей ранее:

Всякое тело продолжает удерживаться в состоянии покоя или равномерного прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

Как видим, ни о какой системе отсчёта нет и речи. И что? Ньютон был «глупее» современных «умников», «улучшающих» его законы? Да нет же! Ньютон подробно рассматривает вопрос о…: «кажущихся» и «истинных» движениях! Вот что он пишет в «Поучении» в разделе «Определения» (см. книгу[2]):

Причины происхождения, которыми различаются истинные и кажущиеся движения, суть те силы, которые надо к телам приложить, чтобы произвести эти движения. Истинное абсолютное движение не может ни произойти, ни измениться иначе, как от действия сил, приложенных непосредственно к самому движущемуся телу, тогда как относительное движение тела может быть и произведено, и изменено без приложения сил к этому телу; достаточно, чтобы силы были приложены к телам, по отношению к которым это движение определяется.

Т.е., Ньютон рассматривал вопрос о системах отсчёта очень скрупулёзно и сумел абстрагироваться от кажущихся (относительных) движений, мешающих понять первопричину всех движений и изменения движений – действие силы.

В этом умении абстрагироваться от, искажающих суть, факторов и заключается гениальность Ньютона и его предшественников – коперниканцев, отвергнувших теорию движения планет Птолемея (Πτολεμαΐος), основанную только на описании относительных, кажущихся движений, и, именно поэтому, бессильной в определении причин, приводящих к таким движениям. Получается, что «поправляющие» Ньютона пытаются отбросить нас в эпоху Птолемея и Аристотеля (Αριστοτέλης)…

Кстати, вся теория относительности Эйнштейна рассматривает именно относительные, кажущиеся движения и неудивительно, что следствиями этой теории являются неразрешимые парадоксы.

Также следует отметить, что в теории Эйнштейна абсолютизируется состояние покоя, что, опять же, является возвратом к временам Аристотеля и Птолемея. А Ньютон, своим Первым законом, специально подчёркивает, что v = 0 = const не имеет никаких преимуществ по сравнению с v = const > 0.

Включение в формулировку Первого закона инерциальной системы отсчёта неприемлемо и в том смысле, что физический закон реализуется независимо от того – наблюдаем мы за процессом или нет, измеряем что-либо или нет… Тем более, что определение инерциальной системы отсчёта дают через Первый закон Ньютона (см., например, на стр.13 в [3]), а потом переформулируют этот же закон, используя понятие «инерциальной системы отсчёта»… Очень «научный» подход…

Итак, одна из главных идей Первого закона Ньютона заключается в том, что «состояние покоя» не является особым случаем, а как раз наоборот, это – частный случай «состояния прямолинейного равномерного движения», когда скорость равна нулю, т.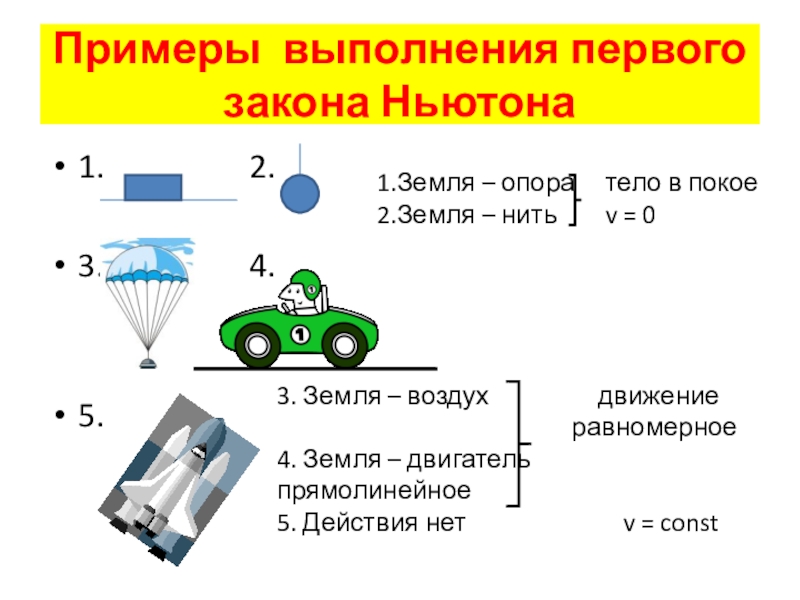 е. любое другое число, равноправно во всех отношениях с нулём!

Именно эта мысль – главный удар по теории Аристотеля, которая недалеко ушла (точнее: никуда не ушла) от обыденного представления о движении, когда считается, что для того, чтобы привести в движение физическое тело и поддерживать это движение в дальнейшем, требуется всё время прикладывать усилие (силу). Разумеется, те примеры движения, такие как «полёт брошенного камня», «полёт стрелы после прекращения действия тетивы», где не видно, «поддерживающей движение», силы, ставят в тупик эти представления о движении.

Второй важный момент. Утверждают, что Ньютон «искал» какую-то абсолютную точку отсчёта и, в конце концов, «закончил» эти поиски в центре Солнца. Как бы то ни было, но Первый закон, как раз, отрицает абсолютность нулевой скорости, а, следовательно, и абсолютность какой-либо точки отсчёта… Вполне возможно, что эти «поиски» (если они, на самом деле, были…) – другое проявление самого Ньютона, не как физика, а как теолога. Ведь, само утверждение «существуют такие системы отсчёта» в корне неверно! При точных измерениях мы всегда обнаружим ускорения. Даже корабль, двигающийся с постоянной скоростью при полном штиле не является инерциальной системой отсчёта, потому что Земля шарообразная и корабль движется по кривой поверхности моря, не говоря уже о том, что сама Земля вращается…

И ещё. Что бы ни говорили «квантомеханики»: нет ни одного эксперимента, показывающего, что в микромире этот закон не выполняется!.. Наоборот, то же Броуновское движение доказывает «дословное» (т.е. без дополнительных пояснений) выполнение закона: микрочастица движется от одного столкновения до другого по прямой и с постоянной скоростью.

Т.е., утверждая выше об отсутствии инерциальных систем отсчёта я немного погорячился? В микромире они существуют? Похоже на то!

Но, в то же время в микромире отсутствуют… ускорения (!), потому что там нет «полей» как в макромире и все взаимодействия происходят только посредством «столкновений» в очень малой области пространства за очень короткое время… Для подтверждения этого тезиса сошлюсь на авторитет Ричарда Фейнмана (Richard Feynman), утверждавшего в [4]:

Хочу особенно подчеркнуть, что свет существует именно в виде частиц – это очень важно знать. Это особенно важно знать тем из вас, кто ходил в школу, где, возможно, что-то говорили о волновой природе света. Я говорю вам, как он на самом деле ведёт себя – как частицы

Кстати, сами фейнмановские диаграммы изначально строились как «траектории» частиц до и после взаимодействия в одной пространственной и одной временной осях координат, но потом «увлеклись» математикой и об этом «забыли», опять же, потому что решили «ограничить» применимость Законов Ньютона…

Литература

1. Перышкин А.В. Физика. 9 кл.: учебник / А.В. Перышкин, Е.М. Гутник. – М.: Дрофа, 2014. – 319,[1] с.: ил.
2. Ньютон Исаак. Математические начала натуральной философии. – М.: Наука, 1989. (перевод с латинского и комментарии А.Н. Крылова).
3. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб.пособ.: Для вузов. В 10т. Т. II. Теория поля.— 8-е изд., стереот.-М.: ФИЗМАТЛИТ, 2003.-536 с
4. Фейнман Ричард. КЭД – странная теория света и вещества: Пер. с англ.—М.: Наука. Гл. ред. физ.-мат. лит., 1988.—144с.—(Б-чка «Квант». Вып.66.)

Первый закон движения Ньютона — Easy Peasy All-in-One High School

Закон Ньютона 1 ^st    часто называют Законом Инерции . Инерция — это свойство материи, противодействующее любому изменению движения.

Закон Ньютона 1 ^st

 можно сформулировать так: объект в состоянии покоя будет оставаться в состоянии покоя, а объект в движении будет продолжать двигаться с постоянной скоростью по прямой линии [если на него не воздействует какая-либо неуравновешенная (сеть) сила]. Ньютона 1 ^st Закон движения описывает, что происходит, когда на объект не действует неуравновешенная сила.

Если объект изначально покоится, он останется в статическом равновесии. Изучение тел в состоянии покоя называется статикой . Это подразделение более крупной категории динамики , которая является подкатегорией механики .

Чтобы объект оставался в покое или продолжал свое движение без возмущений, сумма действующих на него сил должна равняться нулю. Заметьте, это не требование, чтобы на него не действовали никакие силы, просто чтобы их сумма была = 0,9.0009

Σ F = 0

[ПРИМЕЧАНИЕ: = греческая буква сигма представляет собой сумму]

Вот пример статической задачи.

Для приведенной ниже диаграммы постройте диаграмму свободного тела, состоящую из W, T ₁  и T ₂ . Назначьте угол для T ₁  относительно оси x и угол для T ₂  относительно оси x

Изображение с http://mypages.iit.edu/~smart/acadyear /statics.htm

 

Например, предположим, что W = 500.N и угол 1 равен 30 ^o  и угол 2 равен 50 ^o . Найдите значения T ₁  и T ₂ .

Поскольку система покоится (или движется с постоянной скоростью), она находится в равновесии.

Следовательно, F _netx  = 0 и правые силы = левые силы

T ₁  cos 30 = T ₂  cos 50; 0,866 Т ₁ = 0,643 Т ₂ ; T ₁  = 0,742 T

2

 

Это лучшее, что получается для оси X, так как есть два неизвестных. К счастью, у нас есть ось Y для нашего второго уравнения.

F _net = 0 и верхние силы = нижние силы

T ₁ SIN 30 + T ₂ SIN 50 = W SIN 90

0,500 T ₁ + 0,766 T ₂ = 500. N (Eq 1)

Substitution of T ₁  = 0.742 T ₂  into the equation yields…

0.500 (0.742 T ₂ ) + 0.766 T ₂  = 500. N

0.371 T ₂ + 0,766 T ₂  = 500. N

1,137 T

2  = 500. N

T ₂ = 440. N

Замена на (уравнение 1) Выходные он поддерживает большую часть веса. Х-компонента силы натяжения тратится впустую при поддержании вертикального веса!

 

(источник)

Искать:

Семейная реклама EP, EP Swag и многое другое в магазине!

Задать вопрос

Прежде чем задавать вопрос, проверьте страницу часто задаваемых вопросов! Группа поддержки Или найдите определенное место или группу уровня Список групп facebook

Подпишитесь на EP на facebook

Следите за блогом по электронной почте

Введите свой адрес электронной почты, чтобы следить за этим блогом и получать уведомления о новых сообщениях по электронной почте.

Адрес электронной почты:

Чудесные истории Ли – не будем бояться

Отказ от ответственности

Задания, набор ссылок, структура учебного плана и файлы, созданные на этом сайте, принадлежат этому владельцу блога и не могут быть скопированы и опубликованы на другом сайте или использованы для какой-либо коммерческой выгоды.

Copyright 2023 Lee Giles

Все права защищены

Статика: законы движения Ньютона

Ключевые вопросы

• Какие существуют два типа движения?

• Какие три соотношения определяют законы движения Ньютона?

• Каковы физические примеры каждого из трех законов движения Ньютона?

Английский ученый сэр Исаак Ньютон заложил основы механики в 1687 году своими тремя законами движения, которые описывают отношения между силами, объектами и движением. Движение можно разделить на два типа:

• Трансляция — когда тело меняет положение без изменения ориентации в пространстве, и

• Вращение — когда тело вращается вокруг неподвижной в пространстве оси, не изменяя своего среднего положения.

Некоторые движущиеся тела просто движутся, другие просто вращаются, а многие делают и то, и другое. Обычно мы можем разделить перенос и вращение и проанализировать их по отдельности с помощью независимых уравнений.

Ниже описаны три закона Ньютона и их применение в отношении перемещения и вращения.

Подраздел 1.1.1. Первый закон Ньютона.

Первый закон Ньютона гласит, что

объект будет оставаться в состоянии покоя или в равномерном прямолинейном движении, если на него не воздействует внешняя сила .

Этот закон, также иногда называемый «законом инерции», говорит нам, что тела сохраняют свою текущую скорость, если для ее изменения не применяется результирующая сила. Другими словами, объект в состоянии покоя останется в покое, а движущийся объект сохранит свою текущую скорость и направление, если только неуравновешенная сила не вызовет изменение скорости. Помните, что скорость — это векторная величина, которая включает в себя как скорость, так и направление, поэтому неуравновешенная сила может заставить объект ускоряться, замедляться или изменять направление.

Рисунок 1.1.1. Этот камень покоится с нулевой скоростью и будет оставаться в покое до тех пор, пока неуравновешенная сила не заставит его двигаться. Рисунок 1.1.2. В глубоком космосе, где силы трения и гравитации пренебрежимо малы, объект движется с постоянной скоростью; вблизи небесного тела гравитационное притяжение непрерывно меняет свою скорость.

Первый закон Ньютона также применяется к угловым скоростям, однако вместо силы соответствующая величина, которая заставляет объект вращаться, называется крутящим моментом физиками, но инженеры обычно называют моментом . Момент, как вы узнаете из главы 4, — это тенденция силы к вращению. Точно так же, как сила вызывает изменение линейной скорости, момент вызывает изменение угловой скорости. Это можно увидеть в таких вещах, как волчки, маховики, велотренажеры и другие объекты, которые вращаются вокруг оси под действием момента, но в конечном итоге останавливаются из-за противоположного момента, создаваемого трением.

Рисунок 1.1.3. Волчок демонстрирует вращательное движение.

В отсутствие трения этот волчок будет вращаться вечно, но небольшой момент трения, возникающий в точке контакта со столом, в конце концов остановит его.

Подраздел 1.1.2 Второй закон Ньютона

Второй закон Ньютона обычно лаконично выражается знакомым уравнением

\begin{уравнение} \vec{F} = м \vec{a} \tag{1.1.1} \end{уравнение}

, где \(\vec{F}\) – результирующая сила, \(m\) – масса, а \(\vec{a}\) – ускорение.

Вы заметите, что сила и ускорение выделены жирным шрифтом. Это означает, что это векторные величины, имеющие как величину, так и направление. С другой стороны, масса — это скалярная величина, которая имеет только величину. Это уравнение указывает, что сила заставит объект ускоряться в направлении результирующей силы, и величина ускорения будет пропорциональна результирующей силе, но обратно пропорциональна массе объекта.

В этом курсе «Статика» нас интересуют только тела, которые не ускоряются, что значительно упрощает дело. Когда объект не ускоряется \(a = 0\text{,}\), это означает, что он либо покоится, либо движется с постоянной скоростью. С этим ограничением второй закон Ньютона для перевода упрощается до

.

\begin{уравнение} \сумма \vec{F}=0\тег{1.1.2} \end{уравнение}

, где \(\sum \vec{F}\) используется для обозначения чистой силы, действующей на объект.

Второй закон Ньютона для вращательного движения аналогичен

\begin{уравнение} \vec{M} =I \boldsymbol{\alpha}\text{.}\tag{1.1.3} \end{уравнение}

Это уравнение утверждает, что суммарный момент \(\vec{M}\), действующий на объект, вызывает угловое ускорение \(\boldsymbol{\alpha}\), пропорциональное суммарному моменту и обратно пропорциональное \(I\text {,}\) величина, известная как момент инерции массы . Момент инерции массы для вращательного ускорения аналогичен обычной массе для линейного ускорения. Мы еще поговорим о моменте инерции в главе 10.

Опять же, мы видим, что чистый момент и угловое ускорение являются векторами, величинами с величиной и направлением. С другой стороны, момент инерции массы является скалярной величиной и имеет только величину. Кроме того, поскольку Статика имеет дело только с объектами, которые имеют 90 209, а не 90 210 ускорений \(\boldsymbol{\alpha} = 0\text{,}\), они всегда будут находиться в состоянии покоя или вращаться с постоянной угловой скоростью. С этим ограничением второй закон Ньютона подразумевает, что чистый момент всех статических объектов равен нулю.

\begin{уравнение} \сумма \vec{M}=0\тег{1.1.4} \end{уравнение}

Подраздел 1.1.3 3-й закон Ньютона

Третий закон Ньютона гласит

На каждое действие есть равное противодействие.

Действия и реакции, о которых говорит Ньютон, составляют сил . Силы возникают всякий раз, когда один объект взаимодействует с другим, либо напрямую, как толчок или притяжение, либо косвенно, как магнитное или гравитационное притяжение. Любая сила, действующая на одно тело, всегда сопряжена с другой равной и противоположной силой, действующей на какое-либо другое тело.

Рисунок 1.1.4. Земля оказывает гравитационное воздействие на Луну, а Луна оказывает на Землю равную и противоположную силу.

Эти пары равных и противоположных могут сбивать с толку, особенно когда есть несколько взаимодействующих тел.