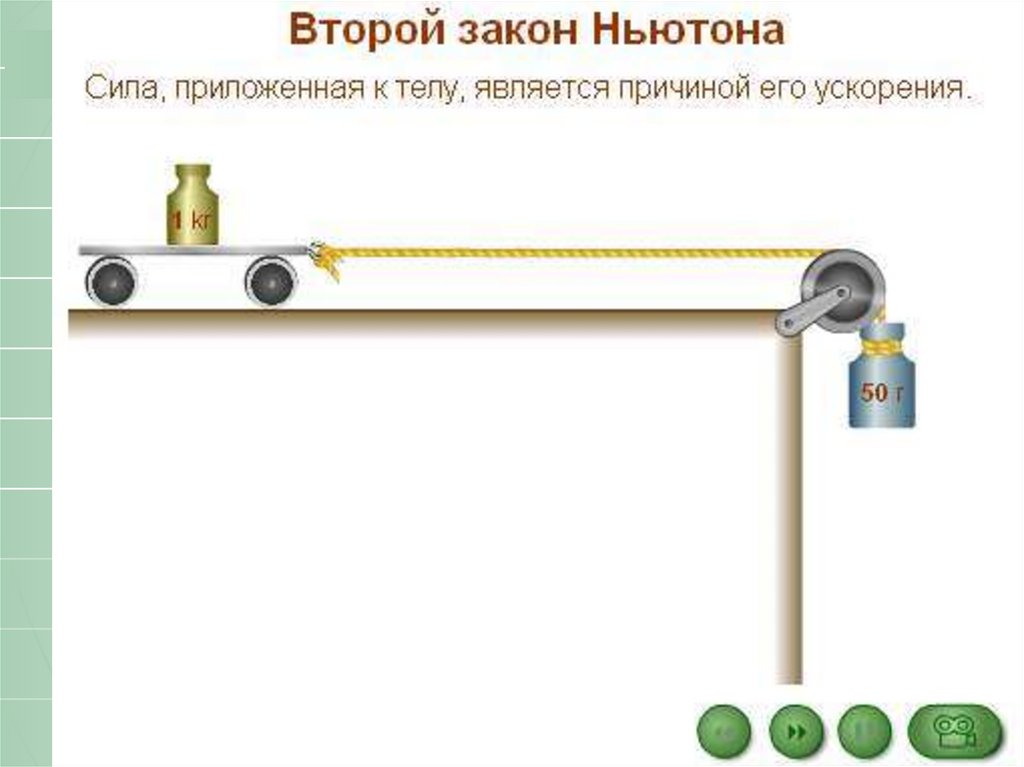
Примеры решения задач по теме «Второй закон Ньютона»
- Подробности
- Просмотров: 1775
«Физика – 10 класс»
Познакомимся с задачами, для решения которых не нужно знать, как зависят силы от расстояний между взаимодействующими телами (или частями одного тела) и от их скоростей. Единственное, что нам потребуется, — это выражение для силы тяжести вблизи поверхности Земли: τ = m.
Задача 1.
К центру однородного шарика массой m = 0,2 кг приложена сила F = 1,5 Н. Определите модуль и направление силы 1, которую необходимо приложить к центру шарика помимо силы , чтобы шарик двигался с ускорением а = 5 м/с2, направленным так же, как и сила (рис. 2.17).
Р е ш е н и е.
На шарик действуют две силы: сила и искомая сила 1.
Поскольку модуль и направление силы неизвестны, можно изобразить на рисунке сначала только силу (см. рис. 2.17).
Согласно второму закону Ньютона m = +
Отсюда 1 = m – .
Так как векторы m и в любой момент времени должны быть расположены на одной прямой, то и сила 1, являясь их разностью, расположена на той же прямой.
Таким образом, искомая сила может быть направлена либо так же, как сила , либо противоположно ей.
Чтобы определить модуль и направление силы 1, найдём её проекцию на ось X, направление которой совпадает с силой .
Учитывая, что Fx = F и аx = а, выражение для силы 1 в проекциях на ось X можно записать в виде F1x = mа – F.
Проанализируем последнее выражение.
Если mа > F, то F
Если же mа < F, то F1x < 0, т. е. сила F1 направлена противоположно направлению оси X. Для рассматриваемого случая
F1x – 0,2 • 5Н – 1,5 Н = -0,5 Н.
Следовательно, сила F1 направлена противоположно оси X (рис. 2.18).
Задача 2.
В результате полученного толчка брусок начал скользить вверх по наклонной плоскости из точки О с начальной скоростью υ0 = 4,4 м/с. Определите положение бруска относительно точки О через промежуток времени t
Р е ш е н и е.
Поскольку требуется найти положение бруска относительно точки О, начало координат возьмём в этой точке. Ось X направим вдоль наклонной плоскости вниз, а ось Y — перпендикулярно этой плоскости вверх (рис. 2.19). При движении бруска на него действуют две силы: сила тяжести m и сила реакции опоры наклонной плоскости, перпендикулярная последней. Эту силу иногда называют силой нормальной реакции. Она всегда перпендикулярна поверхности, на которой находится тело.
Согласно второму закону Ньютона m = m + .
При сделанном выборе направления оси X и начала координат имеем х0 = 0 и υ0x = -υ0. Проекцию ускорения ах на ось X найдём по второму закону Ньютона. Для рассматриваемого случая mах = mgx + Nx. Учитывая, что gx = g sinα и Nx = 0, получим ах = g sinα. Таким образом,
Задача 3.
Два тела массами m1 = 10 г и m2 = 15 г связаны нерастяжимой и невесомой нитью, перекинутой через невесомый блок, установленный на наклонной плоскости (рис. 2.20). Плоскость образует с горизонтом угол α = 30°. Определите ускорение, с которым будут двигаться эти тела. Трение не учитывайте.
Р е ш е н и е.
Предположим, что тело массой m1 перетягивает.
Выберем оси координат так, как показано на рисунке 2.21.
В проекциях на оси Х1 и X уравнения движения тел запишем в виде:
m2ах = Т2 — m2g sinα,
|ах| =|ax1|, так как нить нерастяжима.
Силы натяжения нити равны, так как нить и блок невесомы.
Сложив левые и правые части уравнении, получим
Так как ах > 0, то движение тел происходит в выбранном направлении.
Задача 4.
Автомобиль массой т = 1000 кг движется со скоростью v = 36 км/ч по выпуклому мосту, имеющему радиус кривизны R = 50 м. С какой силой F давит автомобиль на мост в его середине? С какой минимальной скоростью umin должен двигаться автомобиль для того, чтобы в верхней точке он перестал оказывать давление на мост?
Р е ш е н и е.
Силы, действующие на автомобиль вдоль радиуса моста, изображены на рисунке 2.
22:
m — сила тяжести;
— сила нормальной реакции моста.
По третьему закону Ньютона искомая сила давления равна по модулю силе реакции моста .
При движении тела по окружности всегда направляем одну из осей координат от тела к центру окружности.
Согласно второму закону Ньютона центростремительное ускорение автомобиля определяется суммой сил, действующих на него вдоль радиуса окружности, по которой он движется:
mυ2/R = mg – N.
Отсюда
F = N = m(g – υ2/R) = 7,8 кН.
Сила давления на мост станет равной нулю при mυ2min/R = mg, так что υmin = 80 км/ч.
При скорости, превышающей υmin, автомобиль оторвётся от поверхности моста.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Следующая страница «Третий закон Ньютона»
Назад в раздел «Физика – 10 класс, учебник Мякишев, Буховцев, Сотский»
Динамика – Физика, учебник для 10 класса – Класс!ная физика
Основное утверждение механики —
Сила —
Инертность тела.
Второй закон Ньютона
Дата добавления: 2014-10-03 | Просмотров: 1355
Сила тяжести и вес. Невесомость.Утверждает, что
.
Зная значение импульса материальной точки, получим
,
Т.е. мы получили новую формулировку второго закона Ньютона: произведение массы частицы на ее ускорение равно силе, действующей на частицу.
При F=0 т.е. (в отсутствии воздействий на данное тело других тел) ускорение равно нулю, т.е. тело движется прямолинейно и равномерно. Таким образом, первый закон Ньютона, казалось бы, входит во второй как его частный случай. Несмотря на это первый закон формулируется независимо от второго, поскольку в нем утверждается существование ИСО.
Третий закон Ньютона
Силы, с которыми действуют друг на друга тела, равны по величине, противоположны по направлению и никогда не уравновешивают друг друга, т.к. приложены к разным телам.
F12 = – F21,
Т.
е всякому движению есть противодействие.
|Р|=|N|, где Р – вес тела, приложенного к опоре, N – сила реакции опоры, приложенная к телу Рисунок 1.
Всовременной физике различают 4-е вида взаимодействий:1) сильное или ядерное, 2) электромагнитное, 3) слабое, 4) гравитационное.В классической физике используют фундаментальные силы.
Закон Всемирного тяготения.
Гравитационная сила, с которой притягиваются друг к другу две материальные точки (или тела) прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
,
где т1, т2 – массы материальных точек, r – расстояние между ними и G=6,67·10-11 Н·м2/кг2 – гравитационная постоянная.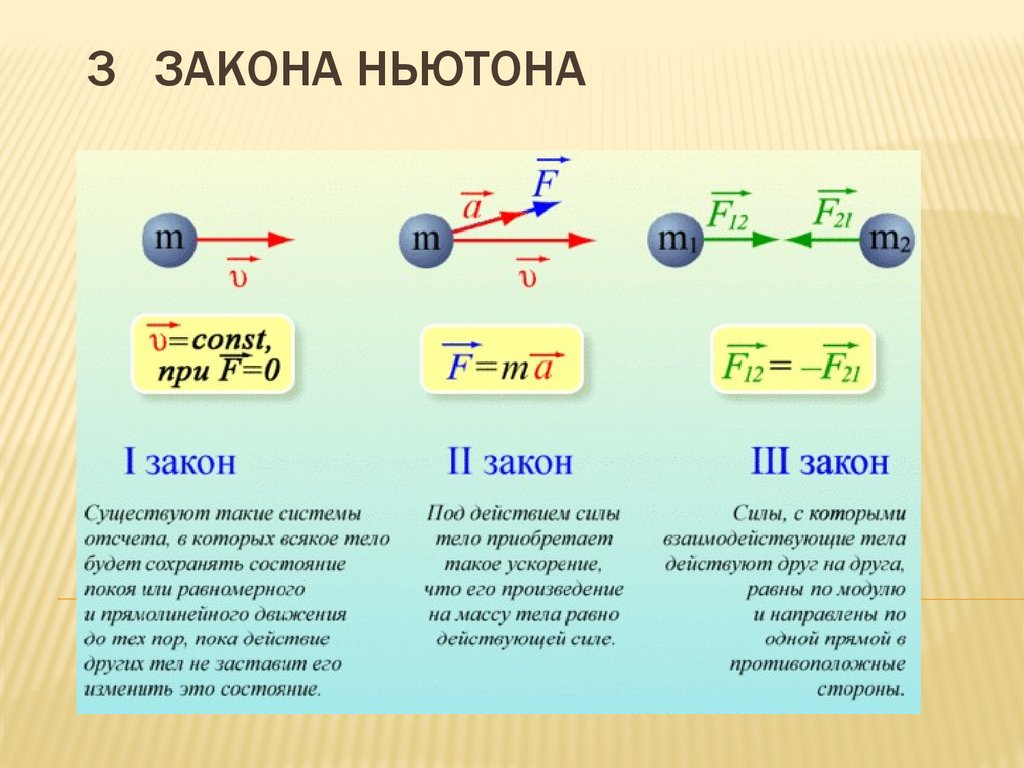
Рисунок 2.
Рисунок 2.
Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела. Закон Всемирного тяготения установлен для тел принимаемых за материальные точки, т.е. для таких тел, размеры которых малы по сравнению с расстоянием между ними.
Сила тяготения к Земле тела массы т направлена к центру Земли, а её модуль равен
,
где Мз = масса Земли, а Rз= радиус Земли. Гравитационные силы являются определяющими в движении космических кораблей, планет, звезд и др. макрообъектов. Обычные объекты на Земле имеют малую силу гравитационного взаимодействия. Поэтому для расчета сил, действующих вблизи поверхности Земли, используют силу тяжести или вес.
Второй закон Ньютона – новый взгляд
Второй закон Ньютона гласит, что ускорение объекта прямо пропорционально суммарной силе, действующей на объект, и обратно пропорционально массе объекта.
Закон часто выражается в виде следующих двух уравнений.
Второй закон Ньютона использовался для анализа различных физических ситуаций. Идея заключалась в том, что если любую данную физическую ситуацию анализировать с точки зрения отдельных сил, действующих на объект, то эти отдельные силы должны складываться в виде векторов результирующей силы. Кроме того, результирующая сила должна быть равна произведению массы на ускорение. Впоследствии можно найти ускорение объекта, если известны масса объекта, а также величины и направления каждой отдельной силы. А величину любой отдельной силы можно определить, если известны масса объекта, ускорение объекта и величина других отдельных сил. Процесс анализа таких физических ситуаций с целью определения неизвестной информации зависит от способности представить физическую ситуацию с помощью диаграммы свободного тела. Диаграмма свободного тела — это векторная диаграмма, отображающая относительную величину и направление всех отдельных сил, действующих на объект.
В этом уроке мы будем использовать принципы Модуля 2 (диаграммы свободного тела, уравнение второго закона Ньютона и т. д.) и концепции кругового движения для анализа различных физических ситуаций, связанных с движением объектов по кругу или по криволинейным траекториям. . Математические уравнения, обсуждавшиеся в уроке 1, и концепция требования центростремительной силы будут применяться для анализа американских горок и других аттракционов в парке развлечений, а также различных спортивных движений.
Круговое движение в горизонтальной плоскости
Чтобы проиллюстрировать, как принципы кругового движения можно объединить со вторым законом Ньютона для анализа физической ситуации, рассмотрим автомобиль, движущийся по горизонтальному кругу на ровной поверхности. На приведенной ниже диаграмме автомобиль изображен с левой стороны круга.
Применяя концепцию требования центростремительной силы, мы знаем, что результирующая сила, действующая на объект, направлена внутрь.
Поскольку автомобиль расположен на левой стороне круга, результирующая сила направлена вправо. Анализ ситуации показал бы, что на объект действуют три силы: сила тяжести (действующая вниз), нормальная сила дорожного покрытия (действующая вверх) и сила трения (действующая внутрь или вправо). Именно сила трения обеспечивает центростремительную силу, необходимую для движения автомобиля по горизонтальному кругу. Без трения автомобиль вращал бы колеса, но не двигался бы по кругу (как это бывает на обледенелой поверхности). Этот анализ приводит к диаграмме свободного тела, показанной справа. Обратите внимание, что каждая сила представлена векторной стрелкой, указывающей конкретное направление, в котором действует сила; также обратите внимание, что каждая сила помечена в соответствии с типом (F frict , F norm и F grav ). Такой анализ является первым шагом любой задачи, связанной со вторым законом Ньютона и круговым движением.
Теперь рассмотрим следующие две задачи, относящиеся к этому физическому сценарию поворота автомобиля на горизонтальной поверхности.
Пример задачи №1 Максимальная скорость, с которой автомобиль массой 945 кг совершает поворот на 180 градусов, составляет 10,0 м/с. Радиус окружности, по которой поворачивает автомобиль, равен 25,0 м. Определить силу трения и коэффициент трения, действующие на автомобиль. Коэффициент трения, действующий на автомобиль массой 945 кг, равен 0,850. Автомобиль совершает разворот на 180 градусов по кривой радиусом 35,0 м. Определить максимальную скорость, с которой автомобиль может совершить поворот. |
Пример задачи №1 предоставляет информацию о кинематике (v и R) и запрашивает значение отдельной силы. Таким образом, решение проблемы потребует сначала определить ускорение и результирующую силу; тогда индивидуальное значение силы можно найти с помощью диаграммы свободного тела.
Пример задачи #2 предоставляет информацию об отдельных значениях силы (или, по крайней мере, информацию, позволяющую определить отдельные значения силы) и запрашивает значение максимальной скорости автомобиля. Таким образом, его решение потребует использования отдельных значений силы для определения чистой силы и ускорения; то ускорение можно использовать для определения максимальной скорости автомобиля. Обе проблемы будут решаться с использованием одних и тех же общих принципов. Тем не менее, поскольку предоставленная и запрошенная информация в каждом из них различна, метод решения будет немного отличаться.
Известная и запрашиваемая информация в примере задачи №1:
Известная информация: м = 945 кг | Запрашиваемая информация: F трение = ??? |
Массу объекта можно использовать для определения силы тяжести, действующей в направлении вниз.
Используйте уравнение
, где г равно 9,8 м/с/с. Зная, что вертикального ускорения автомобиля нет, можно сделать вывод, что вертикальные силы уравновешивают друг друга. Таким образом, F грав = F норма = 9261 N . Это позволяет нам определить две из трех сил, указанных на диаграмме свободного тела. Только сила трения остается неизвестной.
Поскольку сила трения является единственной горизонтальной силой, она должна быть равна суммарной силе, действующей на объект. Таким образом, если результирующую силу можно определить, то известна и сила трения. Чтобы определить результирующую силу, массу и кинематические данные (скорость и радиус) необходимо подставить в следующее уравнение:
Замена данных значений дает чистую силу 3780 ньютонов. Таким образом, сила трения равна 3780 Н .
Наконец, коэффициент трения (μ) можно определить с помощью уравнения, связывающего коэффициент трения с силой трения и нормальной силой.
Замена 3780 Н на F трение и 9261 Н на F норма дает коэффициент трения 0,408 .
И снова задача начинается с определения известной и запрашиваемой информации. Известная информация и запрошенная информация в примере задачи № 2:
Известная информация: м = 945 кг | Запрашиваемая информация: v = ??? |
Массу автомобиля можно использовать для определения силы тяжести, действующей в направлении вниз.
Используйте уравнение
, где g составляет 9,8 м/с/с. Зная, что вертикального ускорения автомобиля нет, можно сделать вывод, что вертикальные силы уравновешивают друг друга. Таким образом, Ф грав = Ф норма = 9261 Н . Поскольку задан коэффициент трения (μ), силу трения можно определить с помощью следующего уравнения:
Это позволяет нам определить все три силы, указанные на диаграмме свободного тела.
Суммарная сила, действующая на любой объект, представляет собой векторную сумму всех отдельных сил, действующих на этот объект. Таким образом, если известны все значения отдельных сил (как в данном случае), можно рассчитать результирующую силу. Сумма вертикальных сил равна 0 Н. Поскольку сила трения является единственной горизонтальной силой, она должна быть равна суммарной силе, действующей на объект.
Таким образом, F нетто = 7872 N .
После определения результирующей силы можно быстро рассчитать ускорение с помощью следующего уравнения.
Подстановка данных значений дает ускорение 8,33 м/с/с . Наконец, скорость, с которой автомобиль мог двигаться по повороту, можно рассчитать, используя уравнение для центростремительного ускорения:
Подставив известные значения для a и R в это уравнение и алгебраическое решение дает максимальную скорость 17,1 м/с .
Разработка правильного подхода к решению проблем
Каждая из двух приведенных выше примеров задач была решена с использованием одного и того же базового подхода к решению проблем. Подход можно резюмировать следующим образом.
|
Представьте каждую силу векторной стрелкой и пометьте силы в соответствии с типом.
И в качестве другого примера, если известны период и радиус, то можно определить ускорение.) Метод, описанный выше, хорошо послужит вам при решении задач кругового движения. Однако следует сделать одно предостережение. Каждая задача по физике отличается от предыдущей. Как такового нет волшебная формула для решения каждой. Использование соответствующего подхода к решению таких проблем (который включает в себя построение FBD, определение известной информации, определение запрашиваемой информации и использование доступных уравнений) никогда не избавит от необходимости думать, анализировать и решать проблемы .
По этой причине приложите усилия, чтобы разработать соответствующий подход к каждой проблеме; но всегда используйте свои навыки критического анализа в процессе решения. Если бы физические проблемы сводились к простому следованию надежной формуле из 5 шагов или использованию какого-то заученного алгоритма, то мы бы не называли их «задачами».
Мы хотели бы предложить…
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного равномерного кругового движения, интерактивной модели американских горок или нашего моделирования горизонтального круга. Вы можете найти эти интерактивы в разделе Physics Interactives на нашем веб-сайте. Эти интерактивы позволяют учащемуся в интерактивном режиме исследовать отношения между скоростью, ускорением и силой для объекта, движущегося по кругу или по криволинейной траектории.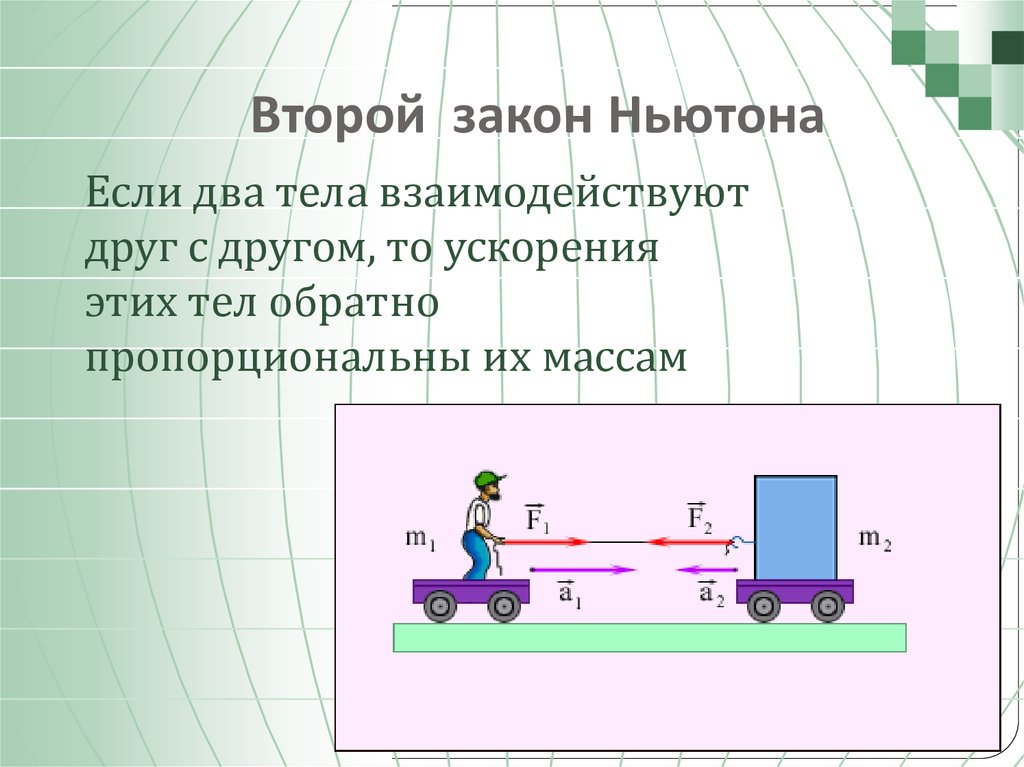
Посетите: Равномерное круговое движение | Модель американских горок || Моделирование горизонтального круга
Используйте свое понимание второго закона Ньютона и принципов кругового движения, чтобы определить неизвестные значения в следующих практических задачах. Нажмите кнопку, чтобы проверить свои ответы.
1. Ведро с водой массой 1,50 кг связано веревкой и вращается по кругу радиусом 1,00 м. В верхней части круговой петли скорость ковша составляет 4,00 м/с. Определите ускорение, результирующую силу и отдельные значения силы, когда ковш находится в верхней части кругового контура.
м = 1,5 кг
а = ________ м/с/с
F нетто = _________ N
2.
Ведро с водой массой 1,50 кг связано веревкой и вращается по кругу радиусом 1,00 м. В нижней части круговой петли скорость ковша составляет 6,00 м/с. Определите ускорение, результирующую силу и отдельные значения силы, когда ковш находится в нижней части круговой петли.
м = 1,5 кг
а = ________ м/с/с
F нетто = _________ N
Следующий раздел:
Перейти к следующему уроку:
14A: Законы Ньютона № 1: Использование диаграмм свободного тела
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2494
- Джеффри В.
Шник - Колледж Святого Ансельма
ШникЕсли вы подбросите камень вверх в присутствии другого человека и спросите этого другого человека, что заставляет камень двигаться вверх после того, как он выскользнет из вашей руки, но до того, как достигнет наибольшей высоты, этот человек может неправильно сказать вам, что сила рука человека держит его в движении. Это иллюстрирует распространенное заблуждение, что сила — это что-то, что дается камню рукой и что камень «имеет», пока он находится в воздухе. Нет, это не так. Сила — это что-то, что делается с объектом. Мы определили силу как постоянный толчок или притяжение. Это то, жертвой чего может быть объект, но никогда не то, что объект имеет. Пока сила действует на объект, движение объекта согласуется с тем фактом, что сила действует на объект. Раз сила больше не действует на объект, такой силы нет, и движение объекта согласуется с тем фактом, что сила отсутствует. (Как показано в этой главе, правильный ответ на вопрос о том, что заставляет камень двигаться вверх, — «Ничего».
Продолжать двигаться вверх — это то, что он делает сам по себе, если он уже движется вверх. Вам не нужно что-нибудь, чтобы заставить его продолжать делать это. Фактически, единственная причина, по которой камень не продолжает двигаться вверх вечно, заключается в том, что на него действует нисходящая сила. Когда на объект действует нисходящая сила и только нисходящая сила, этот объект испытывает нисходящее ускорение. Это означает, что движущаяся вверх порода замедляется, затем меняет направление движения на противоположное и движется вниз еще быстрее.) Представьте себе, что звезды неподвижны в пространстве, так что расстояние между одной звездой и другой никогда не меняется. (Они не фиксированы. Звезды движутся относительно друг друга.) Теперь представьте, что вы создаете декартову систему координат; набор из трех взаимно ортогональных осей, которые вы обозначили как \(x\), \(y\) и \(z\). Ваша декартова система координат является системой отсчета. Теперь, пока ваша система отсчета не вращается и либо фиксирована, либо движется с постоянной скоростью относительно (фиктивных) неподвижных звезд, тогда ваша система отсчета является инерциальной системой отсчета.
Обратите внимание, что скорость имеет как величину, так и направление, и когда мы утверждаем, что скорость вашей системы отсчета должна быть постоянной, чтобы она была инерциальной системой отсчета, мы не просто говорим, что величина должна быть постоянной, но что направление также должен быть постоянным. Величина скорости есть скорость. Итак, чтобы величина скорости была постоянной, скорость должна быть постоянной. Чтобы направление было постоянным, система отсчета должна двигаться по прямолинейному пути. Таким образом, инерциальная система отсчета – это система, которая либо фиксирована, либо движется с постоянной скоростью по прямолинейному пути относительно (фиктивных) неподвижных звезд.
Концепция инерциальной системы отсчета важна при изучении физики, поскольку именно в инерциальных системах отсчета применяются законы движения, известные как законы движения Ньютона. Вот три закона движения Ньютона, которых, по наблюдениям, придерживается любая частица материи в инерциальной системе отсчета:
- Если на частицу не действует результирующая сила, то скорость этой частицы не меняется.
- Если на частицу действует результирующая сила, то эта частица испытывает ускорение, прямо пропорциональное силе, причем константа пропорциональности является величиной, обратной массе частицы.
- Каждый раз, когда один объект воздействует на второй объект, второй объект оказывает равную, но противоположную силу обратно на первый объект.
Обсуждение закона Ньютона 1
st Несмотря на название, на самом деле именно Галилей придумал первый закон. Он позволил мячу скатиться по пандусу, а другой пандус был обращен в другую сторону перед ним, так что после того, как он скатился по одному пандусу, мяч катился по другому. Он заметил, что мяч катился вверх по второму склону, постоянно замедляясь, пока не достиг той же высоты, с которой мяч был первоначально выпущен из состояния покоя. Затем он многократно уменьшал угол, который вторая рампа составляла с горизонталью, и отпускал мяч из состояния покоя из исходного положения для каждого нового наклона второй рампы.
Чем меньше угол, тем медленнее снижалась скорость мяча на пути вверх по второму пандусу и тем большее расстояние он должен был пройти по поверхности второго пандуса, прежде чем достиг своей исходной высоты. Когда он, наконец, установил угол на ноль, казалось, что мяч вообще не замедляется на второй рампе. У него не было бесконечно длинной рампы, но он предположил, что если бы она была, со второй горизонтальной рампой, мяч продолжал бы катиться вечно, никогда не замедляясь, потому что независимо от того, как далеко он катился, он никогда не поднимался бы вверх. так что он никогда не доберется до начальной высоты. Его вывод заключался в том, что если объект двигался, то, если ничто не мешало его движению, он продолжал бы двигаться с той же скоростью в том же направлении. Так что же поддерживает его? Ответ «ничего». В этом весь смысл. Объекту ничего не нужно для поддержания своего существования. Если он уже движется, он движется с постоянной скоростью, пока на него не действует результирующая сила.
На самом деле, для изменения скорости объекта требуется сила.
Нетрудно понять, почему потребовался огромный отрезок человеческой истории, чтобы кто-то понял, что если на движущийся объект не действует результирующая сила, он будет продолжать двигаться с постоянной скоростью, потому что дело в том, что там, где мы живем, на поверхности Земли неизбежно действует результирующая сила на движущийся объект. Вы подбрасываете что-то вверх, и Земля притягивает это все время, пока объект находится в полете. Он не будет продолжать двигаться вверх по прямой линии, пока его не притянет Земля. Даже если вы попытаетесь скользить чем-то по гладкой поверхности замерзшего пруда, где нисходящее притяжение гравитационного поля Земли нейтрализуется льдом, давит на объект, вы обнаружите, что объект замедляется из-за силы трения, давит на объект. в направлении, противоположном скорости объекта, и сила сопротивления воздуха делает то же самое. При наличии этих вездесущих сил человечеству потребовалось много времени, чтобы осознать, что если бы не было сил, то движущийся объект оставался бы в движении по прямолинейному пути с постоянной скоростью, а объект в состоянии покоя оставался бы с постоянной скоростью.
отдыхать.
Обсуждение закона Ньютона 2
nd Галилей привлек еще кое-что интересное из своих экспериментов с мячом на рампе, сосредоточив свое внимание на первом рампе, о котором говорилось выше. Наблюдение за мячом, выпущенным из состояния покоя, показало ему, что мяч неуклонно ускорялся по пути вниз по рампе. Попытайся. Пока вы не делаете пандус слишком крутым, вы можете видеть, что мяч не просто катится по пандусу с некоторой фиксированной скоростью, он ускоряется на всем пути вниз. Далее Галилей заметил, что чем круче будет пандус, тем быстрее будет двигаться мяч по пути вниз. Он делал пробу за пробой, начиная со слегка наклонной плоскости и постепенно делая ее все круче и круче. Каждый раз, когда он делал его круче, мяч на пути вниз по пандусу ускорялся быстрее, чем раньше, пока пандус не становился настолько крутым, что он больше не мог видеть, как он ускоряется по пути вниз по пандусу… это просто происходило слишком быстро, чтобы его можно было заметить.
Но Галилей предположил, что по мере того, как он продолжал делать уклон круче, происходило то же самое. То есть скорость мяча все еще увеличивалась по пути вниз по пандусу, и чем больше угол, тем быстрее мяч будет ускоряться. Фактически, он вывел, что если он увеличит крутизну до конечного угла, 90°, что мяч будет двигаться вниз по пандусу быстрее, чем под любым меньшим углом, но все равно будет ускоряться на пути вниз. Теперь, когда пандус наклонен на 90°, мяч на самом деле падает, а не катится по пандусу, поэтому Галилей пришел к выводу, что когда вы роняете объект (для которого сопротивление воздуха незначительно), происходит следующее: объект ускоряется весь путь вниз, пока не упадет на Землю.
Таким образом, Галилей сделал немало, чтобы подготовить почву для сэра Исаака Ньютона, родившегося в тот же год, когда умер Галилей. Именно Ньютон открыл взаимосвязь между силой и движением. Он тот, кто понял, что существует связь между силой и ускорением, а точнее, что всякий раз, когда объект испытывает результирующую силу, этот объект испытывает ускорение в том же направлении, что и сила.
Теперь некоторые объекты более чувствительны к силе, чем другие объекты — мы можем сказать, что каждый объект имеет свой собственный фактор чувствительности, так что чем больше фактор чувствительности, тем больше ускорение объекта при заданной силе. Коэффициент чувствительности обратно пропорционален массе объекта, поэтому мы можем написать, что
\[\vec{a}=\dfrac{1}{m} \sum \vec{F} \label{14-1}\]
где \(\vec{a}\) – ускорение объект, \(m\) — масса объекта, а \(\Sigma\vec{F}\) — векторная сумма всех сил, действующих на объект, то есть \(\sum \ vec{F}\) — результирующая сила, действующая на объект. Обсуждение третьего закона Ньютона было признание аспекта природы, который на первый взгляд кажется довольно простым и прямолинейным, но быстро приводит к выводам, которые, какими бы правильными они ни были, и они действительно правильны, совершенно противоречат интуиции. Ньютона 3 9Закон 0431 rd является констатацией того факта, что любая сила является лишь половиной взаимодействия, где взаимодействие в этом смысле есть взаимное отталкивание или притяжение, которое довольно часто происходит, когда один объект находится вблизи другого.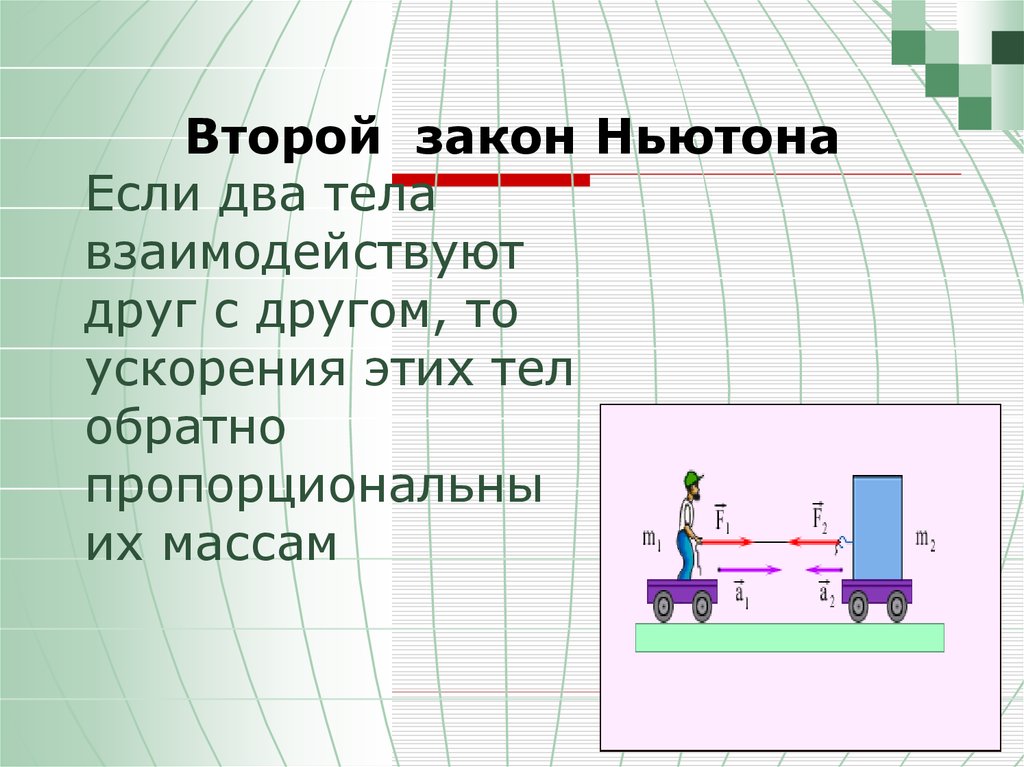
В некоторых случаях, когда эффект очевиден, справедливость третьего закона Ньютона совершенно очевидна. Например, если два человека с одинаковой массой катаются на роликовых коньках и стоят лицом друг к другу, и один толкает другого, мы видим, что оба ролика катятся назад, в разные стороны. Поначалу может быть трудно принять тот факт, что второй фигурист отталкивает руки первого фигуриста, но мы можем сказать, что фигурист, которого мы считаем толкающим, также должен быть «толкателем», потому что мы можно увидеть, что она испытывает обратное ускорение. На самом деле, когда происходит толкание, сила, действующая на нее, должна быть такой же большой, как сила, которую она оказывает на другого фигуриста, потому что мы видим, что ее конечная скорость назад такая же, как у другого (той же массы) фигуриста. .
А как насчет тех случаев, когда действие хотя бы одной из сил в паре взаимодействия совсем не очевидно? Предположим, например, что у вас есть метла, прислоненная к скользкой стене.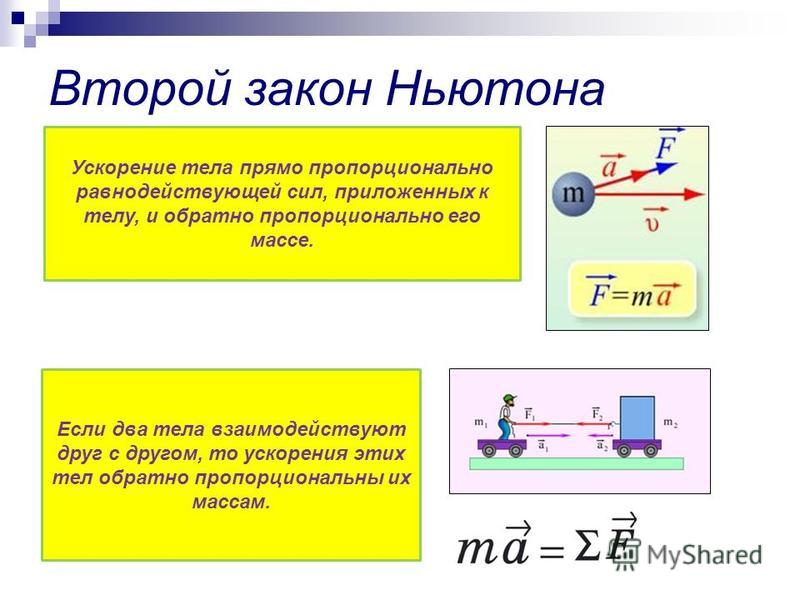
Помимо нашего знания законов Ньютона, как мы можем убедить себя, что метла давит на стену, то есть что метла постоянно воздействует на стену; а также; как мы можем убедить себя, что стена оказывает обратное воздействие на метлу? Один из способов убедить себя — позволить своей руке играть роль стены. Переместите метлу и положите руку на место стены так, чтобы метла была прислонена к вашей ладони под тем же углом, что и к стене, а ладонь была обращена прямо к кончику ручки. Вы можете почувствовать, как кончик ручки прижимается к ладони. На самом деле, вы можете увидеть углубление, которое кончик ручки метлы делает в вашей руке. Вы можете почувствовать силу рукоятки метлы на своей руке и можете предположить, что, когда стена находится там, где находится ваша рука относительно метлы, ручка метлы должна давить на стену с такой же силой.
Как насчет того, что стена давит на кончик ручки метлы? Опять же, когда ваша рука играет роль стены, быстро уберите руку с дороги. Метла, конечно, падает.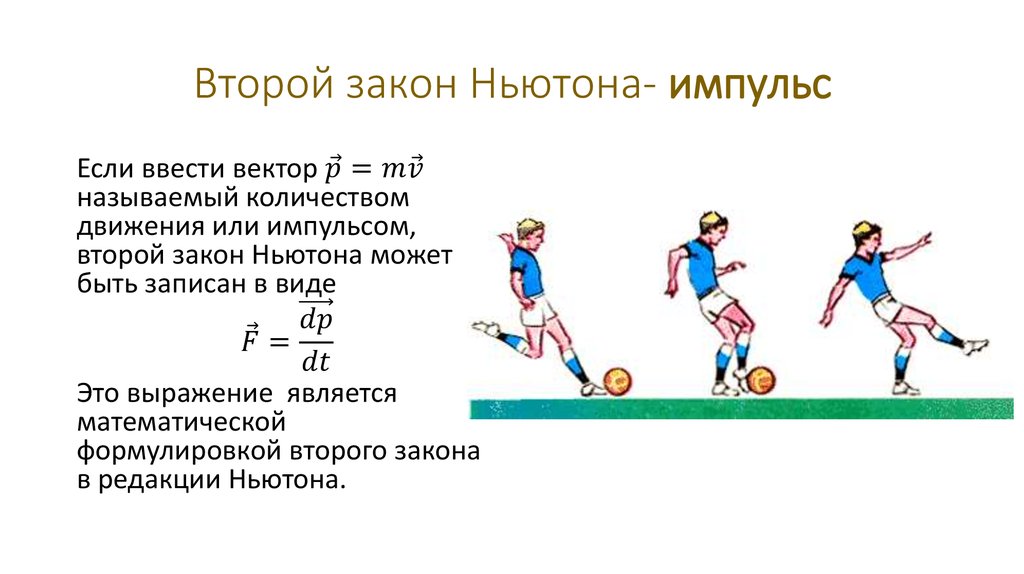
Прежде чем двигать рукой, вы, должно быть, приложили силу к метле, иначе метла тогда бы упала. Вы можете возразить, что ваша рука не обязательно прикладывала силу, а просто «мешала». Что ж, я здесь, чтобы сказать вам, что «быть на пути» — это применение силы. Когда метла прислонена к стене, тот факт, что метла не падает, означает, что стена воздействует на метлу силой, которая уравновешивает другие силы, так что метла не опрокидывается. На самом деле, если бы стена не была достаточно прочной, чтобы приложить такую силу, она бы сломалась. Тем не менее, было бы неплохо получить интуитивное представление о силе, действующей на метлу у стены. Пусть ваша рука играет роль стены, но на этот раз пусть метла прислонится к вашему мизинцу, возле кончика пальца. Чтобы удерживать метлу в том же положении, в каком она была прислонена к стене, вы можете почувствовать, что вам нужно приложить усилие к кончику ручки метлы. На самом деле, если вы немного увеличите эту силу, ручка метлы больше наклонится вверх, а если вы уменьшите ее, она наклонится больше вниз.
Опять же, вы можете почувствовать, что вы нажимаете на кончик ручки метлы, когда вы заставляете ручку метлы оставаться неподвижной в той же ориентации, в которой она была, когда она была прислонена к стене, и вы можете вызвать это, когда стена находится в том месте, где она находится. ваша рука относительно метлы, стена должна давить на ручку метлы с такой же силой. Обратите внимание, что направление, в котором стена давит на метлу, находится от стены под прямым углом к стене. Такая сила действует на любой предмет, находящийся в контакте с твердой поверхностью. Эта контактная сила, оказываемая твердой поверхностью на объект, находящийся в контакте с этой поверхностью, называется «нормальной силой», потому что сила перпендикулярна поверхности, а слово «нормальный» означает «перпендикулярный».
Использование диаграмм свободного тела
Ключ к успешному решению задачи закона Ньютона 2 и состоит в том, чтобы нарисовать хорошую диаграмму свободного тела объекта, движение которого изучается, а затем использовать эту диаграмму свободного тела для расширения задачи Ньютона.
2 nd Закон, то есть заменить \(\Sigma\vec{F}\) фактической почленной суммой сил. Обратите внимание, что закон Ньютона 2 nd
\[\vec{a}=\dfrac{1}{m}\sum \vec{F}\]
является векторным уравнением и, следовательно, в наиболее общем случае ( \(3\) измерения) на самом деле представляет собой три скалярных уравнения в одном, по одному для каждого из трех возможных взаимно ортогональных направлений в пространстве. (Скаляр — это число. Что-то, что имеет только величину, в отличие от вектора, который имеет величину и направление.) В курсе физики вы, как правило, будете иметь дело с силами, лежащими в одной плоскости, и, следовательно, вы будете обычно получают два уравнения из
\[\vec{a}=\dfrac{1}{m}\Sigma\vec{F}.\]
Относительно диаграмм свободного тела: сложная часть состоит в том, чтобы создать их из описания физического процесса в рассмотрение; легкая часть использует их. В том немногом, что осталось от этой главы, мы сосредоточимся на простой части: используя диаграмму свободного тела, используйте ее, чтобы найти неизвестную силу или неизвестные силы, и/или используйте ее, чтобы найти ускорение объекта.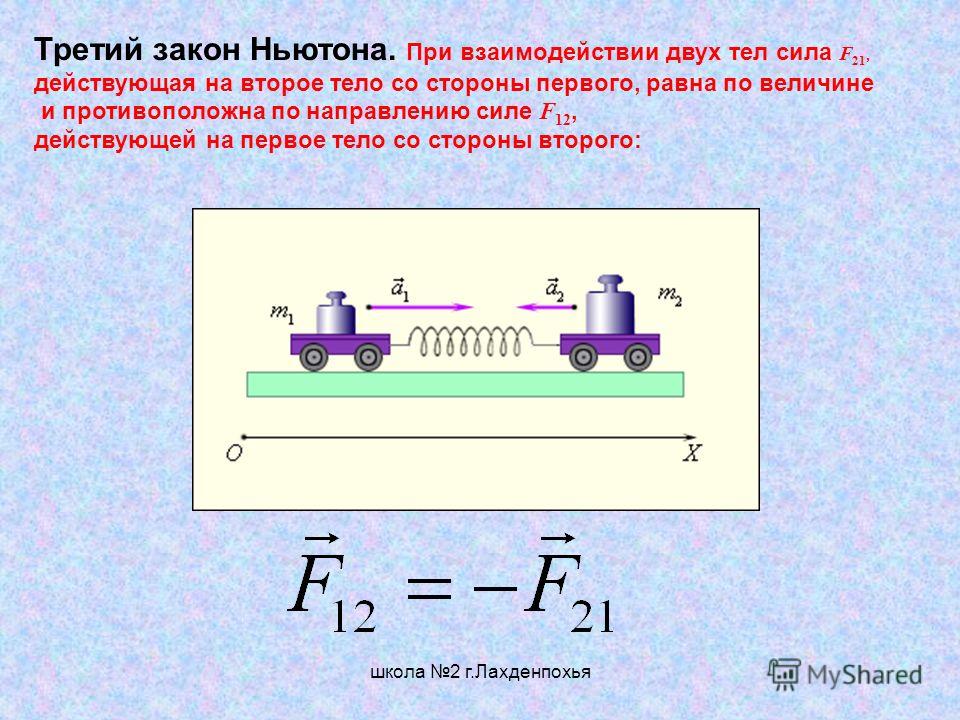
Например, для схемы свободного тела
для объекта массой \(2,00 кг\), найти величину нормальной силы \(F_N\) и найти величину ускорения a. (Обратите внимание, что мы определяем символы, которые мы используем для представления компонентов сил и компонента ускорения на диаграмме свободного тела. Мы делаем это, рисуя стрелку, стержень которой представляет собой линию, вдоль которой лежит сила, и чей наконечник мы определяем положительное направление для этой составляющей силы, а затем помечаем стрелку выбранным нами символом.Отрицательное значение для определенного таким образом символа просто означает, что соответствующая сила или ускорение направлены в направлении, противоположном направлению, в котором стрелка указывает
Решение
Обратите внимание, что ускорение и все силы лежат вдоль одной или другой из двух воображаемых линий (одна из которых горизонтальна, а другая вертикальна), которые перпендикулярны друг другу. Ускорение вдоль одной линии не зависит от каких-либо сил, перпендикулярных этой линии, поэтому мы можем рассматривать одну линию за раз.
Сначала разберемся с горизонтальной линией. Запишем закон Ньютона 2 и для горизонтальной линии как
\[a_{\rightarrow}=\dfrac{1}{m} \Sigma F_{\rightarrow} \label{14-2}\]
, в котором стержни стрелок указывают линию, вдоль которой мы суммируем силы (оси в уравнении 14-2 горизонтальны, поэтому мы должны суммировать силы по горизонтали), а наконечник стрелки указывает, какое направление мы считаем положительным направлении (любая сила противоположного направления входит в сумму со знаком минус).
Следующим шагом является замена \(a_{\rightarrow}\) на символ, который мы использовали на диаграмме для обозначения ускорения вправо, а \(\Sigma F_{\rightarrow}\) на фактический термин- условная сумма сил, которая включает только горизонтальные силы и в которую силы, направленные вправо, входят через «\(+\)», а силы, направленные влево, входят через «\(-\)». Это дает: 92}\]
Теперь обратим внимание на вертикальное направление. Для вашего удобства диаграмма свободного тела воспроизведена здесь:
Снова мы начнем с закона Ньютона 2 и , на этот раз записанного для вертикального направления:
\[a_{\downarrow}=\dfrac{1} {m} \Sigma F_{\downarrow}\]
Мы заменяем \(a_{\downarrow}\) на то, что есть, и мы заменяем \(\Sigma F_{\downarrow}\) на почленно сумма сил с «\(+\)» для направленных вниз сил и «\(-\)» для направленных вверх сил.
Обратите внимание, что единственная буква a на диаграмме свободного тела горизонтальна. Тот, кто придумал эту диаграмму свободного тела, говорит нам, что ускорение в вертикальном направлении отсутствует, то есть \(a_{\downarrow}=0\). Таким образом:
\[0=\dfrac{1}{m}(F_g-F_N)\]
Решение для \(F_N\) дает:
\[F_N=F_g\]
Замена значений единицами приводит к окончательный ответ:
\[F_N=19.6\; Н\]
Эта страница под названием 14A: Законы Ньютона № 1: Использование бесплатных диаграмм тела распространяется в соответствии с лицензией CC BY-SA 2.5 и была создана, изменена и/или курирована Джеффри В. Шником через исходный контент, который был отредактирован в соответствии со стилем. и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Джеффри В.
