Уравнения Максвелла — что это, их обе формы и физический смысл
Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.
Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):
- Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
- В дальнейшем он вызывает появление магнитного поля.
Уравнения Максвелла в дифференциальной форме
Уравнение 1: Закон Гаусса или Теорема Гаусса
Первое уравнение Максвелла (в дифференциальной форме): div D = ρДивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.
Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.
Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.
Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.
Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).
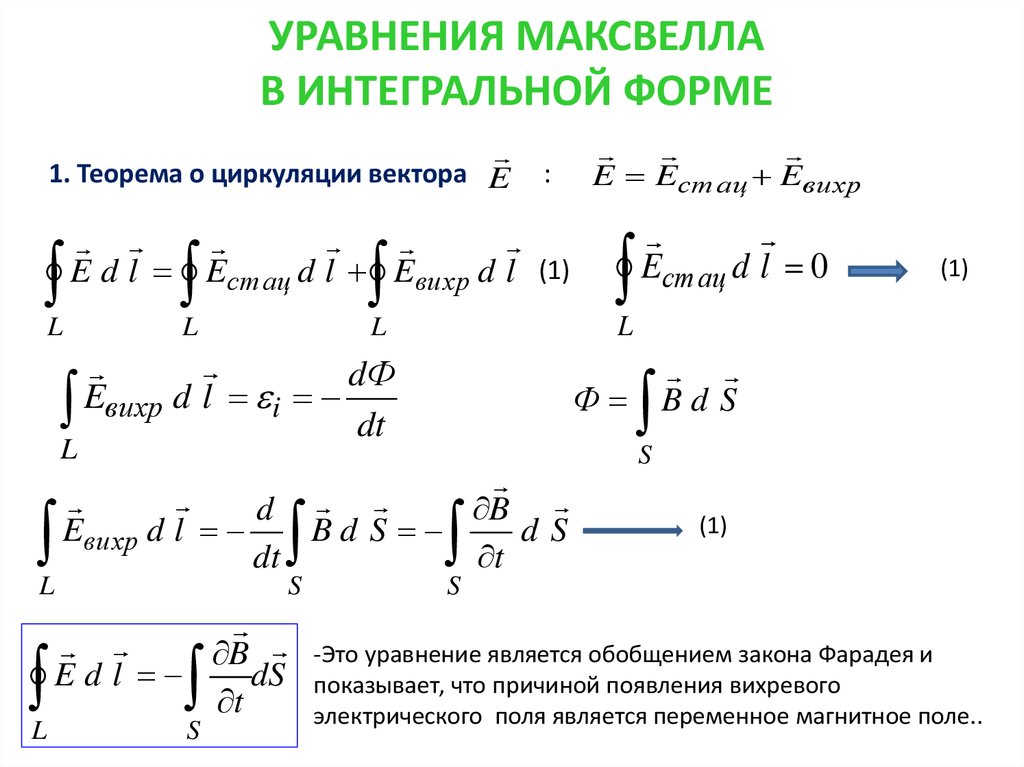
Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
Второе уравнение Максвелла (в дифференциальной форме): rot E = — ∂B/∂tМожно создать электрическое поле, изменив магнитное поле.
Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:
- Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
- Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
- Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.
Уравнение 3: Закон Гаусса для магнетизма
Третье уравнение Максвелла (в дифференциальной форме): div B = 0Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.
Закон Гаусса для магнетизма утверждает (очень кратко):
- Магнитных монополей не существует.
- Расхождение полей B или H всегда равно нулю в любом объёме.
- На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.
Уравнение 4: Закон Ампера
Четвёртое уравнение Максвелла (в дифференциальной форме): rot H = j + ∂D/∂tМагнитное поле создаётся с помощью тока или изменяющегося электрического поля.
Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.
Уравнения Максвелла в интегральной и дифференциальной форме
Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.
Уравнение 1: Закон Гаусса (Теорема Гаусса)
Первое уравнение Максвелла (в дифференциальной форме): div D = ρЭто же уравнение в интегральной форме:
Первое уравнение в интегральной форме: ∮DdS = ∫ρdVПоток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).
Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
Второе уравнение Максвелла (в дифференциальной форме): rot E = — ∂B/∂tИ это же уравнение в интегральной форме:
Второе уравнение Максвелла (в интегральной форме) ∮Edl = – ∫ ∂B/∂t dSЦиркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.
Уравнение 3: Закон Гаусса для магнетизма
Третье уравнение Максвелла (в дифференциальной форме): div B = 0И это же уравнение в интегральной форме:
Третье уравнение Максвелла в интегральной форме: ∮BdS = 0Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.
Уравнение 4: Закон Ампера
Четвёртое уравнение Максвелла (в дифференциальной форме): rot H = j + ∂D/∂tИ это же уравнение в интегральной форме:
Четвёртое уравнение Максвелла в интегральной форме: ∮Hdl = ∫ (j +∂D/∂t)dSЦиркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур.
Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.
Узнайте также про Напряжённость электрического поля, Резонанс и Магнитную индукцию.
Дата обновления 07/04/2021.
Другие значения и понятия, которые могут вас заинтересовать
- Закон сохранения энергии
- Модуль Юнга
- Магнитная индукция
- Источники права
- Теорема Виета
- Сансара
- Напряженность электрического поля
- Карма
- Сила Архимеда
- Колесо сансары
2.
4. Четвертое уравнение МаксвеллаЧетвертое уравнение Максвелла базируется на законе Гаусса для магнитного поля, который можно сформулировать следующим образом: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
(2.16) |
Это уравнение означает, что не существует линий вектора магнитной индукции, которые только входят в замкнутую поверхность S или только выходят из нее. Они всегда пронизывают замкнутую поверхность насквозь.
Уравнение (2.16) называют четвертым уравнением Максвелла в интегральной форме.
К дифференциальной форме уравнения можно перейти с помощью теоремы Остроградского-Гаусса так же, как это было сделанов случае третьего уравнения Максвелла. В результате получим:
(2. |
17)Уравнение (2.17) называется четвертым уравнением Максвелла. Оно утверждает факт отсутствия в природе магнитных зарядов. Из этого уравнения следует также, что силовые линии магнитного поля являются непрерывными.
2.5. Уравнение непрерывности
Уравнение непрерывности является математической формулировкой закона сохранения заряда, которыйутверждает, чтони при каких условиях электрические заряды не могут самопроизвольно зарождаться или бесследно исчезать
Рассмотрим произвольный замкнутый объем V, ограниченный поверхностьюS. Пусть внутри этого объема содержится некоторый заряд Q. Величина этого заряда может быть найдена интегрированиемобъемной плотности заряда по всему объему:
(2. |
18)Предположим, что величина заряда в объеме изменяется. В соответствии с законом сохранения заряда следует считать, что часть зарядов пересекает поверхность
Проинтегрируем плотность тока проводимости по поверхности, ограничивающей наш объем. Получим:
(2.19) |
По определению ток проводимости – это скорость изменения заряда:
(2.20) |
Знак минус говорит о том, что ток считается
положительным, если величина заряда
внутри объема уменьшается. С помощью
формул (2.19) и (2.
(2.21) |
Для получения дифференциальной формы закона сохранения заряда преобразуем уравнение аналогично тому, что было сделано в предыдущем параграфе:
(2.22) |
Соотношение (2.22) называется уравнением непрерывности.
2.6. Полная система уравнений Максвелла
Каждое из рассмотренных выше уравнений описывает некоторые свойства электромагнитного поля. Однако анализ электромагнитных процессов возможен только на основе решения системы уравнений Максвелла. Большинство задач электродинамики решается с помощью системы уравнений в дифференциальной форме:
(2. | ||
23)Систему (2.23) необходимо решать совместно с материальными уравнениями, связывающими между собой векторы электромагнитного поля. В случае линейных изотропных сред эти уравнения имеют вид:
(2.24) |
Уравнения Максвелла позволяют выделить следующие основные свойства электромагнитного поля:
электрическое и магнитное поля тесно связаны между собой: любое изменение одного из них вызывает изменение другого;
источниками электромагнитного поля являются заряды и токи;
магнитное поле всегда вихревое, электрическое поле может быть вихревым и потенциальным;
силовые линии электрического поля могут иметь истоки и стоки, силовые линии магнитного поля всегда непрерывны.
Из первого уравнения Максвелла следует, что линии магнитного поля охватывают линии полного тока, образуя с ними правовинтовую систему (рис. 2.3, а). Из второго уравнения Максвелла вытекает, что линии вихревого электрического поля охватывают линии вектора дВ/дt, образуя с ними левовинтовую систему (рис. 2.3, б).
Рис. 2.1. Взаимосвязи электрической и магнитной составляющих переменного электромагнитного поля |
Уравнения Максвелла и
материальные уравнения являются
линейными дифференциальными уравнениями.
Поэтому электромагнитные поля
удовлетворяют принципу
суперпозиции: поле, созданное
несколькими источниками, можно
рассматривать как сумму полей созданных
каждым источником.
В дополнение к уравнениям Максвелла в дифференциальной форме в ряде случаев необходимо использовать уравнения Максвелла в интегральной форме:
(2.25) | ||
уравнений Максвелла
уравнение МаксвеллаУравнения Максвелла представляют собой один из самых элегантных и лаконичных способов изложения основ электричества и магнетизма. Из них можно развить большинство рабочих отношений в этой области. Из-за их сжатого изложения они воплощают высокий уровень математической сложности и поэтому обычно не вводятся во вводное рассмотрение предмета, за исключением, возможно, сводных соотношений. Эти основные уравнения электричества и магнетизма можно использовать в качестве отправной точки для продвинутых курсов, но обычно они впервые встречаются как объединяющие уравнения после изучения электрических и магнитных явлений.
| Index Концепции уравнений Максвелла | |||||||||||||||||||
| Назад | |||||||||||||||||||
Интегральная форма в отсутствие магнитных или поляризуемых сред:
| Индекс Концепции уравнений Максвелла | |||||||||||||||||||||||||||||||||||||||||
Уравнения Максвелла с их законамиУравнения Максвелла Эта статья посвящена уравнениям Максвелла. Наука — это предмет, основанный на приложениях, и он помогает нам по-новому познавать окружающую среду. В нем есть три дисциплины: физика, изучающая поведение Вселенной; химия, которая занимается изучением веществ, их свойств и химических реакций; и биология, которая включает изучение живых организмов в окружающей среде и их функционирования. Как обсуждалось ранее, физика занимается изучением различных процессов, объясняющих поведение природы. Его приложения широко используются в повседневной жизни, и его законы управляют Вселенной. Мобильные телефоны, автомобильные ремни безопасности, объективы фотоаппаратов, наушники, паровой утюг и шариковые ручки — вот лишь некоторые из бесчисленных примеров применения физики в повседневной жизни людей. Максвелл первым рассчитал скорость распространения электромагнитных волн. Максвелл объяснил, что скорость оказалась такой же, как у света, из чего он сделал вывод, что электромагнитные волны и видимый свет на самом деле очень похожи. Уравнения Максвелла являются основой электромагнетизма, которая включает в себя закон электромагнитной индукции, данный Фарадеем, закон электричества, данный Гауссом, и закон тока, данный Ампером в проводнике. Эти уравнения Максвелла уступают место математической модели для электричества, статического электричества, радиотехнологий, оптики, производства энергии, радара, электродвигателя, линз и т. д. Эти уравнения описывают рабочий характер электрических и магнитных полей и то, как они создаются. зарядами, токами и из-за изменений в электрических или магнитных полях. Эти уравнения Максвелла названы в честь шотландского физика-математика Джеймса Клерка Максвелла, сформулировавшего классическую теорию электромагнитного излучения. Он опубликовал эти вопросы, включив закон силы Лоренца между 1861 и 1862 годами. Первое уравнение Максвелла обсуждает электромагнитную природу света. Первое уравнение Максвелла Основой первого уравнения Максвелла является электростатический закон Гаусса, согласно которому «полный электрический поток замкнутой поверхности равен заряду внутри нее, деленному на диэлектрическую проницаемость». Закон электричества Гаусса устанавливает связь между статическим электрическим полем и производимым им электрическим зарядом. Направление, в котором точка статического электрического поля всегда направлена от положительного заряда к отрицательному заряду. Закон также объясняет, что общий отток электрического поля от замкнутой поверхности прямо пропорционален общему количеству заряда внутри этой поверхности. Линии электрического поля начинаются с положительного заряда и заканчиваются с отрицательным зарядом. Чистое количество линий электрического поля, пересекающих замкнутую поверхность, деленное на диэлектрическую проницаемость в свободном пространстве, дает чистое количество заряда на этой поверхности. Интегральная форма первого уравнения Максвелла: e = q/e0 ——– (i) Кроме того, e = ∫E⃗ . Сравнение уравнений (i) и (ii) , имеем: ∫E⃗ .dA⃗ = q/∈₀ —- (iii) Дифференциальная форма первого уравнения Максвелла:Сумма полной плотности заряда через плотность объемного заряда равна q = ∫pdv Таким образом, уравнение (iii) принимает вид: ∫E⃗ .dA⃗ =1e0∫Pdv Если мы применим теорему о расходимости к левой части уравнения, мы получим, ∫ (▿⃗ .e⃗) d.v = 1ϵ0∫pdv ∫ (▿⃗ .e⃗) d.v -1ϵ0∫pdv = 0 ∫ [(▿⃗ .e⃗) −pϵ0] d.v = 0 (▿. ⃗ .E⃗ )−Pϵ0 Второе уравнение МаксвеллаВторое дифференциальное уравнение Максвелла основано на законе магнетизма Гаусса, который гласит, что полный магнитный поток магнитного поля, пересекающего замкнутую поверхность, равен нулю. Это связано с тем, что магниты всегда существуют в диполях. Магнитных монополей нет. Магнитное поле создается из-за дипольной природы магнитного поля. Суммарный отток из магнитного поля через замкнутую систему равен нулю. Закон магнетизма Гаусса гласит, что петли создаются силовыми линиями магнитного поля, которые исходят от магнита и уходят в бесконечность, и наоборот. Другими словами, если силовые линии магнитного поля входят в тело, они также будут выходить из него. На гауссовой поверхности полное магнитное поле равно нулю. Кроме того, это соленоидальное векторное поле. Выше показаны линии магнитного поля, которые не начинаются и не заканчиваются; скорее, они образуют петли. Третье уравнение Максвелла Третье уравнение Максвелла основано на законе электромагнитной индукции Фарадея. Закон индукции Фарадея был изменен Максвеллом, и он описывает электрическое поле, создаваемое магнитным полем, которое изменяется во времени. Согласно этому закону работа, необходимая для перемещения единичного заряда по замкнутой структуре, такой как петля, равна магнитному полю, преобразующемуся вокруг этой петли. Индуцированные линии электрического поля подобны линиям магнитного поля, если на них не накладывается статическое электрическое поле. Эта концепция электромагнитной индукции является основой принципа работы нескольких электрических устройств, таких как вращающиеся стержневые магниты, используемые для создания переменных магнитных полей. Это дополнительно приводит к возникновению электрических полей в проводящем проводе, расположенном поблизости. Магнитное поле Земли изменяется во время геомагнитной бури из-за увеличения потока заряженных частиц. Это в дальнейшем приводит к индукции электрического поля в атмосфере Земли. Интегральная формула для третьего уравнения Максвелла: ∈ = -Ndm/dt- ————– (1) Поскольку электродвижущая сила связана с электрическим полем соотношением ∈ =∫E .dA, если мы подставим эти значения в уравнение 1, получим: ∫E.dA=−N∫E .d A∫B⃗ .d A Если N = 1, получаем ∫E .dA=−ddt∫B .d A Дифференциальная формула для третьего уравнения Максвелла:Применяя теорему Стокса, получаем: . ∫(▿⃗ .E )dA +ddt∫B .dA =0 (▿⃗ .E )+dB dt=0 (▿⃗ .E )= −dB dt Дополнение Максвелла к закону АмпераСогласно этому закону, магнитное поле может создаваться либо изменением электрического поля, либо электрическим током. Вторая часть утверждения соответствует закону Ампера, а первая часть — дополнению Максвелла. Магнитное поле, индуцируемое вокруг замкнутого контура, связано с током, вытесняемым через этот замкнутый контур, или непосредственно с электрическим током в нем. Этот закон устанавливает взаимосвязь для формирования набора уравнений, математически выровненного с нестатическими полями, без изменения закона Гаусса для статических полей и закона Ампера. Однако магнитное поле создается изменяющимся электрическим полем и наоборот. Следовательно, эти уравнения создают возможность для электромагнитных волн, которые могут поддерживать себя, так что они могут проходить через вакуум. Согласно наблюдениям и расчетам, скорость электромагнитной волны равна скорости света. Эти уравнения, данные Максвеллом, наряду с законом силы Лоренца являются фундаментальными для классической оптики, электрических цепей и классической электродинамики. Интегральная форма уравнения Максвелла лучше всего объясняет, как электрические токи и электрические заряды формируют электрические и магнитные поля. Он описывает, как магнитное поле создается электрическим полем и наоборот. Надеюсь, что эта статья смогла развеять все ваши сомнения относительно уравнений Максвелла. Часто задаваемые вопросы1. Каково значение уравнений Максвелла? Уравнение Максвелла лучше всего объясняет, как электрические и магнитные поля создаются переменными токами и зарядами. Переходу термодинамических переменных от одного набора к другому способствуют уравнения Максвелла. Предположим, вам нужно рассчитать изменение энтропии системы при постоянной энтальпии и заданном давлении. Хотя температуру, объем и давление в системе можно очень легко измерить, не существует устройства для измерения энтропии системы. 3.Что изменил Максвелл в законе Ампера? Максвелл внес некоторые изменения в закон Ампера, так как обнаружил в нем некоторые недостатки. Чтобы закон Ампера был точным, он предположил, что между пластинами конденсатора должен существовать некоторый ток. Ток вне конденсатора был обусловлен потоком электронов. |
Закон Гаусса для электричества
Закон индукции Фарадея
Закон Гаусса для электричества
Давайте начнем.
В математических терминах закон Гаусса выражается как «произведение поверхностного интеграла и вектора плотности электрического потока по замкнутой поверхности, равному заряду, заключенному в поверхности».
dA⃗ ——- (ii)
Магнитные диполи действуют как токовые петли с отрицательными и положительными магнитными зарядами, которые нельзя отделить друг от друга.
E )dA =−ddt∫B .dA
Подобно радиоволнам и рентгеновским лучам, свет также является формой электромагнитного излучения. Максвелл установил связь между светом и электромагнитными волнами в 1861 году. С этого момента теории электромагнетизма и оптики были объединены.
Навигация в переменных магнитных и электрических полях со скоростью света описывается этими уравнениями. Они имеют основополагающее значение для функционирования большинства современных устройств и приборов, таких как компьютеры, мобильные телефоны и электричество.