5 закон ньютона: Знаменитые законы Ньютона

Знаменитые законы Ньютона

4 января – это особая дата в научном обществе, ведь именно в этот день появился на свет Исаак Ньютон. О том, как его законы действуют в “Артеке”, читайте в статье медиаотряда д/л “Янтарный”

4 января весь мир отмечает День Ньютона. 
Не слышали о таком празднике? Сейчас мы вам расскажем!

Кто такой Исаак Ньютон? Это выдающийся английский ученый, разработавший и открывший ряд важнейших для мировой науки законов и теорий в физике, математике и астрономии. Многие из его открытий входят в школьную программу для старших классов.

Самый знаменитый закон Ньютона — это закон всемирного тяготения: Два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними. 
 

                 Каждую смену артековцы обязательно притягиваются к вкусной анимации.

Второй закон Ньютона: Ускорение тела прямо пропорционально равнодействующей всех сил, приложенных к телу, и обратно пропорционально его массе.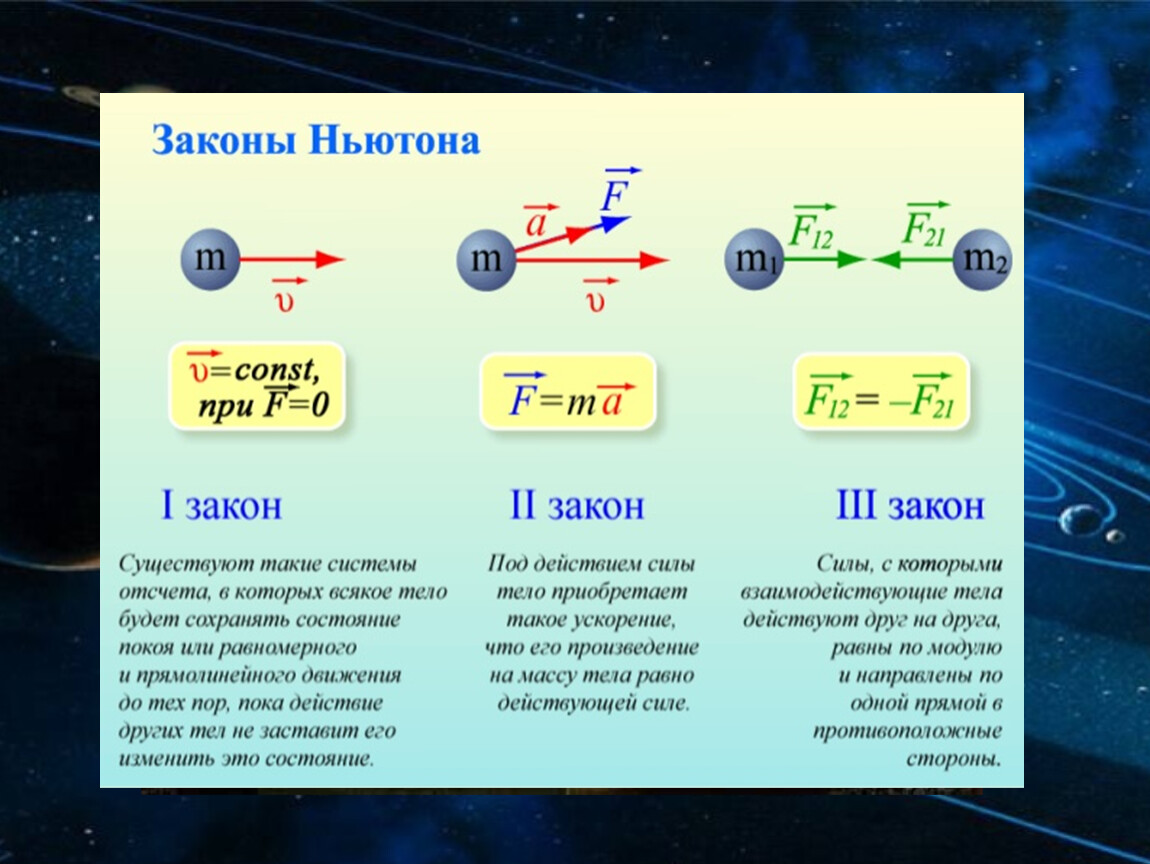

Приходя к Дереву Желаний, каждый артековец хочет, чтобы его мечта сбылась намного скорее.

Третий закон Ньютона гласит: Взаимодействия двух тел друг на друга равны между собой и направлены в противоположные стороны.

Интересный факты:

– Хотя многоцветный спектр радуги непрерывен, по традиции в нём выделяют семь цветов. Считается, что первым выбрал число семь Исаак Ньютон. Причём первоначально, он различал только пять цветов – красный, жёлтый, зелёный, голубой и фиолетовый, о чём и написал в своей книге ”Оптика”.

– Благодаря Ньютону сократилось создание фальшивых монет, так как он сообразил по бокам делать линии, которые предотвращали срезание металла.

– На первом логотипе Apple был изображён Исаак, который сидел под яблоней.

Авторы: медиаотряд д/л «Янтарный», 15 смена 2019 года

первый, второй, третий закон кратко с объяснением, формулами

Мы уже говорили об основах классической механики.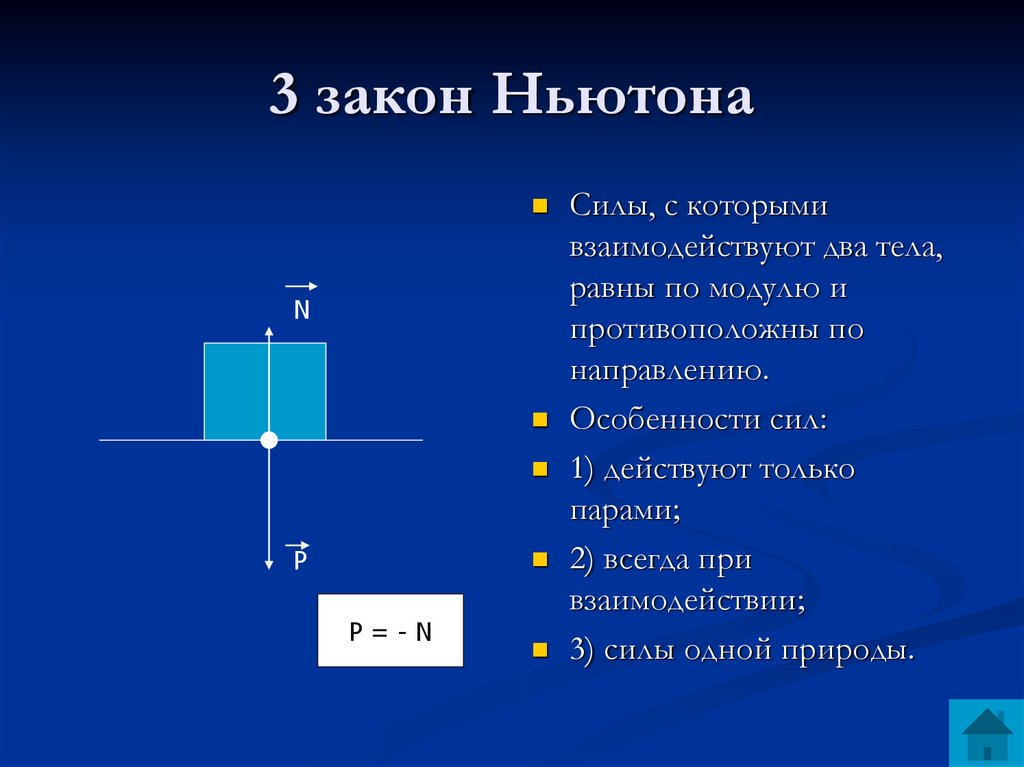 Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о

законах Ньютона.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».

Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.

(Эпиграмма 18-го века)

Но сатана недолго ждал реванша –

Пришел Эйнштейн, и стало все как раньше.

(Эпиграмма 20-го века)

Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.

Первый закон Ньютона

Первый закон Ньютона гласит:

Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.

Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.

Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.

До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих “Математических началах натуральной философии”.

Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.

Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.

 

Второй закон Ньютона

Помните пример про тележку? В этот момент мы приложили к ней

силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.

В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением.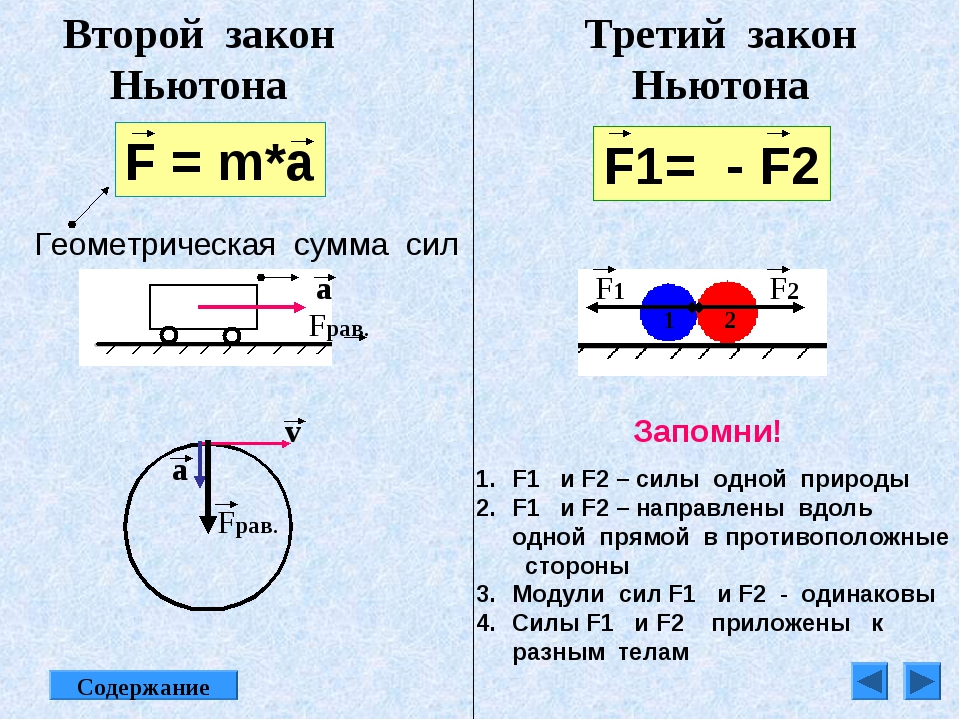 Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.

Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.

Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:

Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.

 

Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.

В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.

Существует более универсальная формулировка данного закона,  так называемый дифференциальный вид.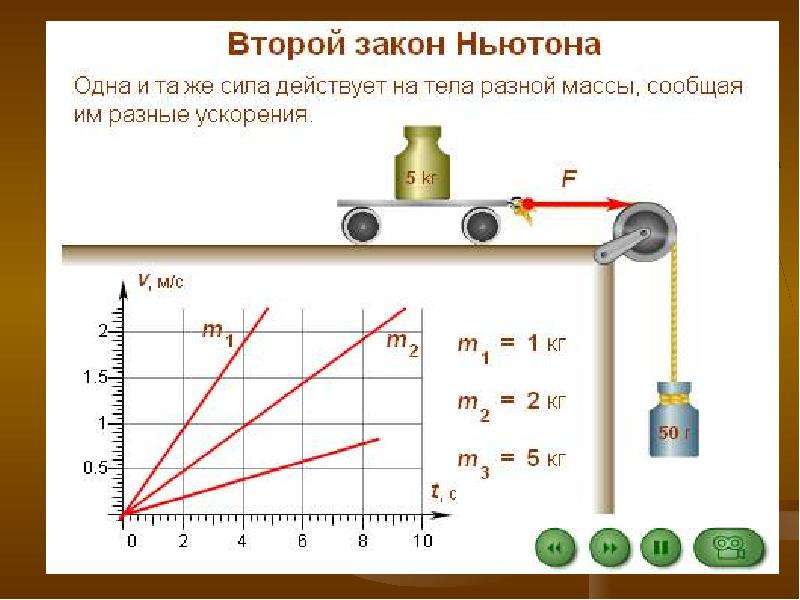

В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.

Третий закон Ньютона

В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.

3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:

Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.

Формула, выражающая третий закон Ньютона:

Другими словами, третий закон Ньютона – это закон действия и противодействия.

 

Пример задачи на законы Ньютона

Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.

Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.

Решение:  

Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.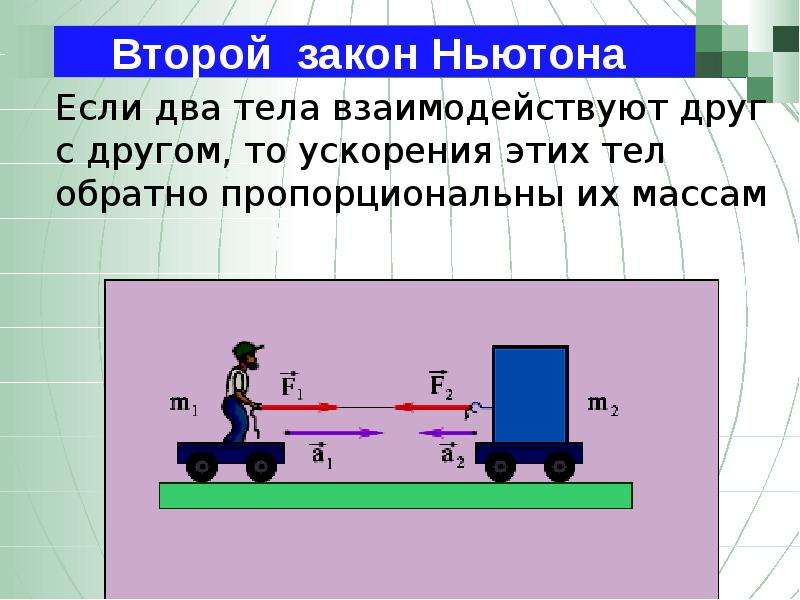

На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.

По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.

Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.

Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.

Решение:

По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.

Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.

Исаак Ньютон: мифы и факты из жизни

На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.

Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.

Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.

• Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
• Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
• Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
• Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
• Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.

Дорогие друзья, помните – любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы. Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!

В самом конце предлагаем посмотреть видеоурок на тему “Законы Ньютона”.

Сила, второй закон Ньютона — ЗФТШ, МФТИ

Сила является мерой взаимодействия (взаимного действия). 2}\quad \mathrm{(ньютон)}.

5) Если на тело одновременно действуют несколько сил, то каждая сила действует независимо от других. (Принцип суперпозиции сил). Тогда все силы необходимо сложить векторно и получить результирующую силу (рис. 4).

Рис. 4

Из приведённых свойств силы следует, как обобщение опытных фактов, второй закон Ньютона:

Второй закон Ньютона: Сумма всех сил, действующих на тело, равна произведению массы тела на ускорение, сообщаемое этой суммой сил:

∑F→=ma→.\boxed{\sum \vec{F} = m\vec{a}}.

Данное выражение можно представить и в другой форме: так как a→=v→к-v→0t\vec a = \frac{\vec v_\mathrm{к} – \vec v_0}{t}, то второй закон Ньютона примет вид: ∑F→=mv→к-v→0t\sum \vec F = m\frac{\vec v_\mathrm{к} – \vec v_0}{t}.

Произведение массы тела и его скорости называют импульсом тела:

p→=mv→\vec p = m\vec v,

тогда получим новое выражение для второго закона Ньютона:

∑F→=mv→к-mv→0t=p→к-p→0t=Δp→t\boxed{\sum \vec F = \frac{m\vec v_\mathrm{к} – m\vec v_0}{t}} = \frac{\vec p_\mathrm{к} – \vec p_0}{t} = \frac{\Delta \vec p}{t}.

∑F→=p→к-p→0t\boxed{\sum \vec F = \frac{\vec p_\mathrm{к} – \vec p_0}{t}} — второй закон Ньютона в импульсной форме для среднего значения силы. Здесь p→к-p→0=Δp→\vec p_\mathrm{к} – \vec p_0 = \Delta \vec p — изменение импульса тела, t -t\ – время изменения импульса тела.

∑F→=dp→dt -\boxed{\sum \vec F = \frac{d\vec p}{dt}}\ – второй закон Ньютона в импульсной форме для мгновенного значения силы.

Из второго закона в частности следует, что ускорение тела, подвергающегося действию нескольких сил, равно сумме ускорений, сообщаемых каждой силой:

a→=∑a→i=a→1+a→2+…+a→i=∑F→m=F→1+F→2+…+F→im=F→1m+F→2m+…+F→im\boxed{\vec a = \sum \vec a_i = \vec a_1 + \vec a_2 + \dots + \vec a_i = \frac{\sum \vec F}{m} = \frac{\vec F_1 + \vec F_2 + \dots + \vec F_i}{m} = \frac{\vec F_1}{m} + \frac{\vec F_2}{m} + \dots + \frac{\vec F_i}{m}}.

Первая форма записи второго закона (∑F→=ma→)(\sum \vec F = m\vec a) справедлива только при малых скоростях по сравнению со скоростью света. И, разумеется, выполняется второй закон Ньютона только в инерциальных системах отсчёта. Так же следует отметить, что второй закон Ньютона справедлив для тел неизменной массы, конечных размеров и движущихся поступательно.

Второе (импульсное) выражение имеет более общий характер и справедливо при любых скоростях.

Как правило, в школьном курсе физики сила со временем не меняется. Однако последняя импульсная форма записи позволяет учесть зависимость силы от времени, и тогда изменение импульса тела будет найдено с помощью определённого интеграла на исследуемом интервале времени. В более простых случаях (сила изменяется со временем по линейному закону) можно брать среднее значение силы.


Рис. 5

Иногда очень полезно знать, что произведение F→·t\vec F \cdot t называют импульсом силы, и его значение F→·t=Δp→\vec F \cdot t = \Delta \vec p равно изменению импульса тела.

Для постоянной силы на графике зависимости силы от времени можем получить, что площадь фигуры под графиком равна изменению импульса (рис. 5).

Но даже если сила будет изменяться со временем, то и в этом случае, разбивая время на малые интервалы Δt\Delta t такие, что величина силы на этом интервале остаётся неизменной (рис. 6), а потом, суммируя полученные «столбики», получим:

Площадь фигуры под графиком F(t)F(t) численно равна изменению импульса.

В наблюдаемых природных явлениях сила, как правило, меняется со временем. Мы же часто, применяя простые модели процессов, считаем силы постоянными. Сама же возможность использования простых моделей появляется из возможности подсчёта средней силы, т. е. такой постоянной силы, у которой площадь под графиком от времени будет равна площади под графиком реальной силы.

Рис. 6

Следует добавить ещё одно очень важное следствие второго закона Ньютона, связанное с равенством инертной и гравитационной масс. 









Неразличимость гравитационной и инертной масс означает, что и ускорения, вызванные гравитационным взаимодействием (законом всемирного тяготения) и любым другим тоже неразличимы.

Пример 2. Мяч массой 0,5 кг0,5\ \mathrm{кг} после удара, длящегося 0,02 с0,02\ \mathrm{с}, приобретает скорость 10 м/с10\ \mathrm{м}/\mathrm{с}. Найти среднюю силу удара.

Решение. В данном случае рациональнее выбрать второй закон Ньютона в импульсной форме, т. к. известны начальная и конечная скорости, а не ускорение, и известно время действия силы. Также следует отметить, что сила, действующая на мяч, не остаётся постоянной. По какому закону меняется сила со временем, неизвестно. Для простоты мы будем пользоваться предположением, что сила постоянная, и её мы будем называть средней.

Тогда ∑F→=Δp→t\sum \vec F = \frac{\Delta \vec p}{t}, т. е. F→ср·t=Δp→\vec F_\mathrm{ср}\cdot t = \Delta \vec p. В проекции на ось, направленной вдоль линии действия силы, получим: Fср·t=pк-p0=mvкF_\mathrm{ср}\cdot t = p_\mathrm{к}-p_0 = mv_\mathrm{к}. Окончательно для искомой силы получим:

\[F_\mathrm{ср} = \frac{mv_\mathrm{к}}{t}.\]

Количественно ответ будет таким: Fср=0,5 кг·10 мс0,02 с=250 НF_\mathrm{ср} = \frac{0,5\ \mathrm{кг}\cdot 10\ \frac{\mathrm{м}}{\mathrm{с}}}{0,02\ \mathrm{с}} = 250\ \mathrm{Н}.

§5. Второй и третий законы Ньютона.

Второй закон сформулирован И. Ньютоном следующим образом [6, с.233]: “Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует”.
Чтобы представить этот закон в математическом виде, Ньютону пришлось ввести понятие массы, характеризующей количество материи, содержащейся в теле.
Если следовать приведенному определению, то второй закон Ньютона должен иметь следующее математическое выражение:
,                                                                                    (1)
где – изменение количества движения mV, k – коэффициент пропорциональности, F– приложенная к телу сила. Вполне очевидно, что данная формулировка не соответствует общепринятой формулировке второго закона, устанавливающего связь между силой и ускорением:
,                                                    (2)
так как время нельзя считать коэффициентом пропорциональности, поскольку оно изменяется и, следовательно, не является постоянной величиной.
Предполагается, что форму (2) второму закону Ньютона впервые придал Д. Бернулли [10, с.89].
В таком же виде выше нами было получено соотношение между мгновенным воздействием и изменением скорости при взаимодействии материальных объектов (см. главу I):
,                                                                                        (3)
где – фактор мгновенного воздействия, представляющий силу F, действующую на рассматриваемый материальный объект, – мгновенное изменение скорости в функции времени (ускорение).
Следует отметить, что соотношение (3) нельзя считать строгим доказательством второго закона Ньютона, это скорее результат, вытекающий из здравого смысла, поэтому его можно рассматривать просто в качестве гипотезы.
Ньютон нигде не дает доказательства второго закона, он его просто постулирует. Можно даже сказать, что он просто угадан Ньютоном и то неточно. И после Ньютона никто не смог вывести этот закон из каких-то более общих предпосылок. Таким образом, второй закон Ньютона следует считать одной из аксиом или гипотез, лежащих в основе механики. И тем не менее открытие этого закона является величайшим достижением человеческого ума, позволившим механике стать настоящей наукой и давшим ей основу для дальнейшего развития.
Мы показали, что второй закон Ньютона характеризует мгновенное локальное взаимодействие тел и устанавливает связь между силой и ускорением, возникающим при взаимодействии в данной точке пространства. Понятие мгновенного взаимодействия не устанавливает физической сущности силы, то есть не является ее определением. Поэтому нельзя говорить, что сила это произведение массы тела на его ускорение. Это соотношение определяет величину силы, но не ее физическую сущность. Физическая сущность силы может быть понята из соотношений, полученных нами в первой главе:
,                                                                                             (4)
,                                                                                   (5)
где первое выражение может трактоваться как силовая характеристика поля кинетической энергии для сплошной среды, а второе – выражение силы для дискретного тела, энергия которого изменяется при движении в пространстве. Именно изменение энергии в пространстве, а точнее скорость ее изменения по пространственной координате, и характеризует физическую сущность силы. Чем быстрее будет изменяться энергия, тем больше будет сила, и наоборот. Это объясняется тем, что именно кинетическая энергия является тем свойством движущейся материи, которым обмениваются при взаимодействии материальные объекты.
Выражения (4) и (5) имеют более широкую область применения, чем второй закон Ньютона в форме (2). Это объясняется тем, что мгновенное взаимодействие материальных объектов можно рассматривать не только в виде дискретных тел, но и в виде сплошных сред, что приводит к полевой форме взаимодействия. Поэтому второй закон Ньютона можно считать частным случаем выражений (4) и (5).
Однако, следует обратить внимание на следующее важное обстоятельство. При выводе соотношения (3) мы считали, что изменение скорости от внешнего воздействия будет одинаково и происходит одновременно для всех точек тела. Такое предположение для реальных тел не всегда будет точно выполняться, так как все материальные объекты деформируются из-за конечной скорости распространения воздействия. Исключение могут составлять только воздействия, осуществляющиеся одновременно по всему объему тела, как, например, при действии сил тяготения. Поэтому второй закон Ньютона будет в определенной степени приближенным при использовании его для исследования движения реальных тел. Ниже будет показано, как можно учесть влияние деформации тел на характер их движения.
Следует иметь в виду также и то, что выражение силы через кинетическую энергию будет справедливо только для энергии, связанной с упругой деформацией тел. Энергия же, затраченная на структурные преобразования и нагрев тел, учитываться не должна. Это будут так называемые потери энергии, изменяющие энергию составляющих тело частиц, но не механическую энергию движения тела в целом.
Переходим теперь к рассмотрению третьего закона Ньютона, который гласит [6, с.233]: “Действию всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга равны и направлены в противоположные стороны”.
Этот закон находится как бы в стороне от двух первых законов Ньютона и не связан с ними. Если закон инерции можно вывести из второго закона Ньютона, устранив внешнее воздействие на тело, то есть приняв силу равной нулю, то третий закон существует как бы сам по себе. Ньютон пришел к необходимости этого закона по следующим причинам (цитируем [6, с.234]): “Третий закон динамики был подтвержден опытами Рена и Мариотта над ударами шаров. Сам Ньютон повторил эти опыты с большей точностью, введя поправку на сопротивление воздуха. Он нашел, что “третий закон по отношению к удару и отражению подтверждается теорией, вполне согласующейся с опытом”.
Подтверждается третий закон и для взаимодействий на расстоянии. Если бы эти взаимодействия не были бы равны, то поместив между взаимно притягивающимися телами препятствие, мешающее их сближению, можно было бы обнаружить, как это препятствие уступает действию большей силы. “Я производил подобный опыт с магнитом и железом; если их поместить каждый в отдельный сосуд и пустить плавать на спокойной воде так, чтобы сосуды взаимно касались, то ни тот, ни другой не приходят в движение, но вследствие равенства взаимного притяжения сосуды испытывают равные давления и остаются в равновесии”. Точно так же, если бы взаимные притяжения частей Земли не уравновешивались, то Земля ушла бы ускоренным движением в бесконечность”.
И, тем не менее, этот закон Ньютона можно считать только полуэмпирическим, так как он не имеет строгого теоретического доказательства, и поэтому его следует рассматривать только в качестве гипотезы или аксиомы.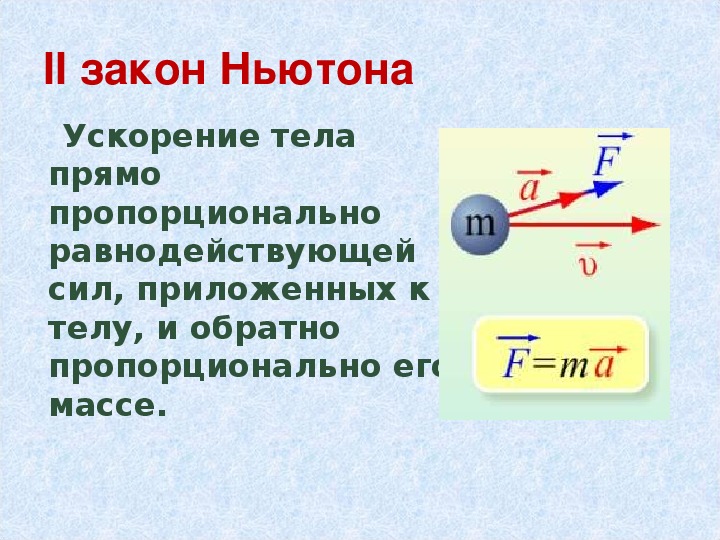
Однако между двумя гипотезами, лежащими в основе второго и третьего закона Ньютона, существует достаточно тесная связь, которую мы сейчас и попытаемся установить. Для этого сперва используем второй закон в форме (3):

Так как характеризует величину мгновенного воздействия на тело, то есть воздействия на тело при данном его положении в пространстве, то, суммируя все мгновенные воздействия при перемещении тела в пространстве, получим следующее соотношение (см. формулу (1.5.8)):
,                                              (6)
где – проекция силы F на направление движения тела, V и – скорости движения тела в конце и в начале движения, – изменение кинетической энергии тела на перемещении s.
Выражение (6) говорит о том, что работа внешних сил затрачивается на изменение кинетической энергии движущегося тела. Из выражения (6) вытекает также необходимость понятия самой кинетической энергии.
Теперь рассмотрим сам факт мгновенного взаимодействия с другой стороны. Если на данный материальный объект со стороны других дискретных материальных объектов или материальной среды существует какое-то воздействие в данном месте пространства, то будет вполне логичным предположить, что такое же воздействие будет и со стороны данного тела на контактирующие с ним материальные объекты, так как при взаимодействии материальных объектов обязательно должен быть непосредственный контакт между ними. Это утверждение, кстати, будет относиться ко всем видам взаимодействий, существующим в природе. И если даже тела взаимодействуют друг с другом на каком-то расстоянии, то это значит, что взаимодействие происходит с помощью промежуточной среды, когда воздействие передается от частицы к частице. Правомерность такого утверждения будет нами доказана в последующих главах.
Следует отметить, что, когда мы говорим о равенстве мгновенных взаимодействий, то имеем в виду полные мгновенные взаимодействия F, отнесенные к взаимодействующим объектам в целом, а не к единице их массы.
Если считать такое предположение верным, то для внешних по отношению к данному телу материальных объектов будет справедливо выражение (6), представленное в следующем виде:
,                                         (7)
где изменение скоростей и энергий будет иметь противоположное значение по сравнению с данным объектом, что и характеризуется знаком минус.
Так как силы , характеризующие мгновенное воздействие, для обоих объектов будут по величине одинаковыми, то их работы на одном и том же перемещении, определяемые интегралами в левой части выражения (7), также будут одинаковыми, а это значит, что будут равны и правые части, то есть:
(8)
Отсюда следует, что какую энергию приобретет тело при внешнем воздействии на него, точно такую же энергию потеряют действующие на него материальные объекты, а это и есть не что иное, как закон сохранения энергии.
Таким образом, закон сохранения энергии получается как следствие закона равенства действия и противодействия, то есть третьего закона Ньютона, рассматриваемого совместно со вторым его законом. И если учесть то обстоятельство, что все взаимодействия, как мы покажем это ниже, имеют механическую природу, то можно считать, что второй и третий законы Ньютона являются основными законами природы.
Хотя эти законы и не имеют строгого обоснования, то с точки зрения здравого смысла и их практического использования они вполне достоверны. Действительно, если вдуматься в процесс взаимодействия материальных объектов, то сам факт взаимодействия за счет непосредственного контакта между материальными объектами в одном и том же месте пространства не должен вызывать сомнения. Взаимное действие материальных объектов при их непосредственном контакте вряд ли может быть различным, поскольку оно осуществляется в одном и том же месте пространства в одно и то же время. Несомненно также, что мгновенные взаимодействия будут являться причиной всех материальных процессов и явлений, происходящих в природе. Этот факт лежит в основе принципа причинности и детерминизма. На наш взгляд, такое объяснение будет вполне естественным и логичным.
Ниже будет показано, что закон сохранения энергии лежит в основе многих законов механики. Поскольку мы его получили из двух законов Ньютона, то тем самым мы исключили одну гипотезу, каковой до настоящего времени являлся закон сохранения энергии, то есть число недоказанных гипотез стало меньше. Тем самым мы привели основания механики к более строгому виду.
Однако, на рассматриваемую ситуацию можно взглянуть и с другой точки зрения. Мы предполагали, что при взаимодействии материальных объектов должны выполняться две гипотезы в форме второго и третьего законов Ньютона, из которых вытекает закон сохранения кинетической энергии, причем в гипотезе о втором законе Ньютона, характеризуемой выражением (3), использование массы является чисто эмпирическим фактом и, кроме того, эта характеристика взаимодействия не может быть отнесена к тем случаям, когда отсутствует движение в направлении взаимодействия материальных объектов. Для таких случаев следует использовать условие взаимодействия в форме выражений (4) или (5), по отношению к которым условие (3) можно считать частным случаем. Выражения (4) и (5) представляют собой скорость изменения кинетической энергии по пространственной координате, они могут быть получены, как будет показано в следующем параграфе, из закона сохранения кинетической энергии при взаимодействии материальных объектов. Тогда в качестве основной характеристики взаимодействия в качестве гипотезы можно использовать закон сохранения кинетической энергии, при этом исключается гипотеза о равенстве действия и противодействия, а второй закон Ньютона будет являться просто математической формулой, устанавливающей связь между силой и скоростью изменения кинетической энергии. В итоге, вместо двух гипотез, положенных нами в основу законов механики, останется всего одна, причем масса тел органично входит в выражение кинетической энергии. Такое использование закона сохранения кинетической энергии в качестве основной и единственной гипотезы представляется нам целесообразным. Это свойство закона сохранения кинетической энергии отображено в таблице иерархии основных понятий, законов и принципов механики.
При рассмотрении третьего закона Ньютона следует обратить внимание на одно важное обстоятельство, связанное с наличием сил инерции. До сих пор под равенством действия и противодействия понималось равенство сил, с которыми взаимодействующие тела действуют друг на друга. Но ведь при взаимодействии возникают и силы инерции, которые, как мы показали, тоже являются реальными силами. Сила инерции является реакцией со стороны тела на внешнее воздействие. Она в точности равна действующей на тело внешней силе и направлена ей навстречу. Отсюда следует, что сила инерции будет уравновешивать движущую силу, то есть система действующих на тело сил с учетом силы инерции будет уравновешена. Таким образом, мы получили доказательство принципа Даламбера в его современной формулировке, сущность которого будет подробно рассмотрена в §7.
Третий закон Ньютона имеет и еще одно важное следствие, на которое до сих пор не обращали внимания. Так, если тело движется, преодолевая какое-либо сопротивление среды или силы трения, то на него будет действовать, уравновешиваясь попарно, уже четыре силы: движущая сила и сила инерции (упругая сила деформации) с одной стороны и сила инерции и сила сопротивления с другой стороны, причем силы инерции в обоих случаях будут направлены в разные стороны (рис.1), навстречу действующим на тело внешним силам. То же самое будет происходить и в случае неподвижного тела, когда действие внешней силы уравновешивается реакцией опоры (рис.2). Таким образом, в этих случаях движущая сила и сила сопротивления будут уравновешиваться не непосредственно друг другом, а через посредство силы инерции, являющейся упругой силой деформации. И вообще, следует обратить внимание на то, что силы, действующие на тело, включая и силы инерции, должны существовать попарно, образуя уравновешенную систему, независимо от состояния тела или характера его движения. Поэтому утверждение о том, что центростремительная сила может существовать без центробежной силы инерции, которое некоторые ученые используют для объяснения фиктивности сил инерции, и с этой точки зрения неверно. Сила может уравновешиваться только силой, и ничем больше.

 

Закон всемирного тяготения Ньютона • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Между всеми телами во Вселенной действует сила взаимного притяжения.

На склоне своих дней Исаак Ньютон рассказал, как это произошло: он гулял по яблоневому саду в поместье своих родителей и вдруг увидел луну в дневном небе. И тут же на его глазах с ветки оторвалось и упало на землю яблоко. Поскольку Ньютон в это самое время работал над законами движения (см. Законы механики Ньютона), он уже знал, что яблоко упало под воздействием гравитационного поля Земли. Знал он и о том, что Луна не просто висит в небе, а вращается по орбите вокруг Земли, и, следовательно, на нее воздействует какая-то сила, которая удерживает ее от того, чтобы сорваться с орбиты и улететь по прямой прочь, в открытый космос. Тут ему и пришло в голову, что, возможно, это одна и та же сила заставляет и яблоко падать на землю, и Луну оставаться на околоземной орбите.

Чтобы в полной мере оценить весь блеск этого прозрения, давайте ненадолго вернемся к его предыстории. Когда великие предшественники Ньютона, в частности Галилей, изучали равноускоренное движение тел, падающих на поверхность Земли, они были уверены, что наблюдают явление чисто земной природы — существующее только недалеко от поверхности нашей планеты. Когда другие ученые, например Иоганн Кеплер (см. Законы Кеплера), изучали движение небесных тел, они полагали что в небесных сферах действуют совсем иные законы движения, нежели законы, управляющие движением здесь, на Земле. История науки свидетельствует, что практически все аргументы, касающиеся движения небесных тел, до Ньютона сводились в основном к тому, что небесные тела, будучи совершенными, движутся по круговым орбитам в силу своего совершенства, поскольку окружность — суть идеальная геометрическая фигура. Таким образом, выражаясь современным языком, считалось, что имеются два типа гравитации, и это представление устойчиво закрепилось в сознании людей того времени. Все считали, что есть земная гравитация, действующая на несовершенной Земле, и есть гравитация небесная, действующая на совершенных небесах.

Прозрение же Ньютона как раз и заключалось в том, что он объединил эти два типа гравитации в своем сознании. С этого исторического момента искусственное и ложное разделение Земли и остальной Вселенной прекратило свое существование.

Результаты ньютоновских расчетов теперь называют законом всемирного тяготения Ньютона. Согласно этому закону между любой парой тел во Вселенной действует сила взаимного притяжения. Как и все физические законы, он облечен в форму математического уравнения. Если M и m — массы двух тел, а D — расстояние между ними, тогда сила F взаимного гравитационного притяжения между ними равна:

F = GMm/D²

где G — гравитационная константа, определяемая экспериментально. В единицах СИ ее значение составляет приблизительно 6,67 × 10^–11.

Относительно этого закона нужно сделать несколько важных замечаний. Во-первых, его действие в явной форме распространяется на все без исключения физические материальные тела во Вселенной. В частности, сейчас вы и эта книга испытываете равные по величине и противоположные по направлению силы взаимного гравитационного притяжения. Конечно же, эти силы настолько малы, что их не зафиксируют даже самые точные из современных приборов, — но они реально существуют, и их можно рассчитать. Точно так же вы испытываете взаимное притяжение и с далеким квазаром, удаленным от вас на десятки миллиардов световых лет. Опять же, силы этого притяжения слишком малы, чтобы их инструментально зарегистрировать и измерить.

Второй момент заключается в том, что сила притяжения Земли у ее поверхности в равной мере воздействует на все материальные тела, находящиеся в любой точке земного шара. Прямо сейчас на вас действует сила земного притяжения, рассчитываемая по вышеприведенной формуле, и вы ее реально ощущаете как свой вес. Если вы что-нибудь уроните, оно под действием всё той же силы равноускоренно устремится к земле. Галилею первому удалось экспериментально измерить приблизительную величину ускорения свободного падения (см. Уравнения равноускоренного движения) вблизи поверхности Земли. Это ускорение обозначают буквой g.

Для Галилея g было просто экспериментально измеряемой константой. По Ньютону же ускорение свободного падения можно вычислить, подставив в формулу закона всемирного тяготения массу Земли M и радиус Земли D, помня при этом, что, согласно второму закону механики Ньютона, сила, действующая на тело, равняется его массе, умноженной на ускорение. Тем самым то, что для Галилея было просто предметом измерения, для Ньютона становится предметом математических расчетов или прогнозов.

Наконец, закон всемирного тяготения объясняет механическое устройство Солнечной системы, и законы Кеплера, описывающие траектории движения планет, могут быть выведены из него. Для Кеплера его законы носили чисто описательный характер — ученый просто обобщил свои наблюдения в математической форме, не подведя под формулы никаких теоретических оснований. В великой же системе мироустройства по Ньютону законы Кеплера становятся прямым следствием универсальных законов механики и закона всемирного тяготения. То есть мы опять наблюдаем, как эмпирические заключения, полученные на одном уровне, превращаются в строго обоснованные логические выводы при переходе на следующую ступень углубления наших знаний о мире.

Картину устройства солнечной системы, вытекающую из этих уравнений и объединяющую земную и небесную гравитацию, можно понять на простом примере. Предположим, вы стоите у края отвесной скалы, рядом с вами пушка и горка пушечных ядер. Если просто сбросить ядро с края обрыва по вертикали, оно начнет падать вниз отвесно и равноускоренно. Его движение будет описываться законами Ньютона для равноускоренного движения тела с ускорением g. Если теперь выпустить ядро из пушки в направлении горизонта, оно полетит — и будет падать по дуге. И в этом случае его движение будет описываться законами Ньютона, только теперь они применяются к телу, движущемуся под воздействием силы тяжести и обладающему некой начальной скоростью в горизонтальной плоскости. Теперь, раз за разом заряжая в пушку всё более тяжелое ядро и стреляя, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра падают всё дальше и дальше от подножия скалы.

Теперь представьте, что вы забили в пушку столько пороха, что скорости ядра хватает, чтобы облететь вокруг земного шара. Если пренебречь сопротивлением воздуха, ядро, облетев вокруг Земли, вернется в исходную точку точно с той же скоростью, с какой оно изначально вылетело из пушки. Что будет дальше, понятно: ядро на этом не остановится и будет и продолжать наматывать круг за кругом вокруг планеты. Иными словами, мы получим искусственный спутник, обращающийся вокруг Земли по орбите, подобно естественному спутнику — Луне. Так мы поэтапно перешли от описания движения тела, падающего исключительно под воздействием «земной» гравитации (ньютоновского яблока), к описанию движения спутника (Луны) по орбите, не изменяя при этом природы гравитационного воздействия с «земной» на «небесную». Вот это-то прозрение и позволило Ньютону связать воедино считавшиеся до него различными по своей природе две силы гравитационного притяжения.

Остается последний вопрос: правду ли рассказывал на склоне своих дней Ньютон? Действительно ли всё произошло именно так? Никаких документальных свидетельств того, что Ньютон действительно занимался проблемой гравитации в тот период, к которому он сам относит свое открытие, сегодня нет, но документам свойственно теряться. С другой стороны, общеизвестно, что Ньютон был человеком малоприятным и крайне дотошным во всем, что касалось закрепления за ним приоритетов в науке, и это было бы очень в его характере — затемнить истину, если он вдруг почувствовал, что его научному приоритету хоть что-то угрожает. Датируя это открытие 1666-м годом, в то время как реально ученый сформулировал, записал и опубликовал этот закон лишь в 1687 году, Ньютон, с точки зрения приоритета, выгадал для себя преимущество больше чем в два десятка лет.

Я допускаю, что кого-то из историков от моей версии хватит удар, но на самом деле меня этот вопрос мало беспокоит. Как бы то ни было, яблоко Ньютона остается красивой притчей и блестящей метафорой, описывающей непредсказуемость и таинство творческого познания природы человеком. А является ли этот рассказ исторически достоверным — это уже вопрос вторичный.

См. также:

Как решать 2 задание ЕГЭ по физике, примеры решения (Ростов-на-Дону)

Из последних КИМов ЕГЭ по физике следует, что задание 2 относится к разделу «Динамика» и может содержать расчетные задачи по следующим темам: «Законы Ньютона, закон всемирного тяготения, закон Гука, сила трения».

Основные формулы, которые необходимо знать для успешного решения задания 2.

Сила тяжести		m – масса тела g=10 м/с2 – ускорение свободного падения
Сила упругости		Δx – удлинение пружины k – коэффициент жесткости пружины
Сила трения		µ – коэффициент трения N – сила реакции опоры
Сила Архимеда (выталкивающая сила)		V – объём погруженной части тела g=10 м/с2 – ускорение свободного падения
Сила притяжения между телами (закон Всемирного тяготения)		G = 6,67*10-11 Н*м2/кг2 – гравитационная постоянная m1 и m2 - массы взаимодействующих тел r – расстояние между телами
Второй закон Ньютона		m – масса тела R – равнодействующая всех сил, действующих на тело a – ускорение, с которым движется тело под действием этих сил

При решении задач из раздела «Динамика» желательно придерживаться следующего алгоритма решения:

1. Сделать рисунок, на котором указать вектора всех сил, действующих на тело.

2. Если тело двигается с ускорением, указать направление этого ускорения. Если тело покоится или двигается равномерно, его ускорение a=0.

3. Составить уравнение движения (второй закон Ньютона) для рассматриваемого тела в его векторном виде.

3. Выбрать систему координат и спроецировать полученное уравнение на выбранные оси координат.

4. Расшифровать неизвестные величины, вошедшие в уравнение движения.

5. Решить полученную систему уравнений.

Задание 2 – это расчётные задачи базового уровня сложности, и для решения некоторых из них этот алгоритм будет чересчур подробным и перегруженным, так как их можно решить и без вспомогательного рисунка или даже без записи второго закона Ньютона. Это касается, например, заданий, в которых на тело действует только одна сила. Но привычка решать задания по приведенному выше алгоритму поможет ученикам успешно справиться с расчетными задачами по разделу «Динамика» повышенного и высокого уровней сложности – такие задания могут стоять в ЕГЭ под номерами 25 и 29.

Ответом на задание 2 является число, именно его нужно вписать в бланк ответов 1, не указывая единицы измерения.

Примеры решения

1. (ЕГЭ-2019)

Пружина жёсткостью 2*10⁴ Н/м одним концом закреплена в штативе. На какую величину она растянется под действием силы 400 Н?

Ответ: ___________________________ см.

Решение:

Сделаем чертёж

Пружина под действием силы F привели в растянутое состояние. Кроме растягивающей силы F и силы упругости , стремящейся вернуть пружину в нерастянутое состояние, больше никакие силы на нее не действуют.

Запишем проекции сил на вертикальную ось Oy

F=F_упр

По закону Гука, сила упругости F_упр = k *Δx, следовательно,

k – коэффициент жёсткости пружины, Δx – её удлинение.

Выразим величину растяжения пружины

Ответ: 2

2. (ЕГЭ – 2020. Вариант 1 досрочного ЕГЭ)

Тело движется по горизонтальной плоскости. Нормальная составляющая силы воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н. Определите коэффициент трения скольжения.

Ответ: _______ .

Решение:

Силу трения можно найти по формуле

F_тр= µN,

где N – сила реакции опоры, или по-другому нормальная составляющая силы воздействия тела на плоскость.

Ответ: 0,25.

2. (ЕГЭ – 2020. Демонстрационный вариант)

Два одинаковых маленьких шарика массой m каждый, расстояние между центрами которых равно r, притягиваются друг к другу с силами, равными по модулю 0,2 пН. Каков модуль сил гравитационного притяжения двух других шариков, если масса каждого из них равна 2m, а расстояние между их центрами равно 2r?

Ответ: _______ пН.

Решение:

По закону Всемирного тяготения шары массами m₁и m₂, находящиеся друг от друга на расстоянии r, притягиваются друг к другу с силой

.

В первом случае

Во втором случае

Ответ: 0,2

2. (ЕГЭ – 2019. Демонстрационный вариант)

По горизонтальному полу по прямой равномерно тянут ящик, приложив к нему горизонтальную силу 35 Н. Коэффициент трения скольжения между полом и ящиком равен 0,25. Чему равна масса ящика?

Ответ _______ кг.

Решение:

Сделаем чертёж, на котором обозначим все силы, действующие на тело.

По второму закону Ньютона, равнодействующая всех сил, действующих на тело, будет равна нулю, так как по условию задачи тело движется равномерно, то есть ускорение тела a=0.

Запишем это в проекциях на оси Ox и Oy

Ox: F_тр – F = 0,

Oy: N – m g=0.

Откуда N = mg, следовательно,

F_тр = µ N = µ mg.

Масса тела

Ответ: 14

2. (ЕГЭ – 2018)

К пружине подвесили груз массой 150 г, вследствие чего пружина удлинилась на 1 см. Чему будет равно удлинение этой пружины, если к ней подвесить груз 450 г?

Ответ: __________ см.

Решение:

Переведём единицы измерения физических величин в систему СИ

m₁ = 150 г = 0,15 кг, m₂ = 450 г = 0,45 кг, Δx=1 см = 0,01 м.

Сделаем чертёж, на котором обозначим все силы, действующие на тело.

На тело действует сила тяжести (F_т = mg), направленная вертикально вниз, и сила упругости со стороны пружины (F_упр = k Δx), направленная вертикально вверх.

В проекции на вертикальную ось Oy.

F_т =F_упр

mg = kΔx (1)

k – коэффициент жёсткости пружины, Δx – её удлинение.

Найдём, чему равен коэффициент жёсткости пружины

Выразим из выражения (1) удлинение пружины во втором случае

Ответ: 3

РЕКОМЕНДУЕМЫЕ ТОВАРЫ

Три закона Ньютона | Физика

Раздел механики, в котором изучают, как взаимодействие тел влияет на их движение, называют динамикой.

Основные законы динамики открыли итальянский ученый Галилео Галилей и английский ученый Исаак Ньютон. Вы изучали эти законы в курсе физики основной школы. Напомним их.

1. Первый закон ньютона (закон инерции)

Повторим один из опытов, которые поставил итальянский ученый Галилео Галилей.

Поставим опыт
Будем скатывать шар по наклонной плоскости и наблюдать за его дальнейшим движением по горизонтальной поверхности.
Если она посыпана песком, шар остановится очень скоро (рис. 13.1, а).
Если она покрыта тканью, шар катится значительно дольше (рис. 13.1, б).
А вот по стеклу шар катится очень долго (рис. 13.1, в).

На основании этого и подобных опытов Галилей открыл закон инерции: если на тело не действуют другие тела или действия других тел скомпенсированы, то тлело движется равномерно и прямолинейно или покоится.

Сохранение скорости тела, когда на него не действуют другие тела или действия других тел скомпенсированы, называют явлением инерции.

? 1. Почему при встряхивании мокрого зонта с него слетают капли воды?

Особенно красиво смотрится явление инерции в фигурном катании (рис. 13.2).

Закон инерции называют также первым законом Ньютона, потому что Ньютон включил его в качестве первого закона в систему трех законов динамики, которые называют «тремя законами Ньютона».

Инерциальные системы отсчета

Закон инерции выполняется с хорошей точностью в системе отсчета, связанной с Землей. Но он не выполняется, например, в системе отсчета, связанной с тормозящим автобусом: при резком торможении пассажиры отклоняются вперед, хотя на них не действуют направленные вперед силы.
Системы отсчета, в которых выполняется закон инерции, называют инерциальными.

Инерциальных систем отсчета бесконечно много. Ведь если некоторая система отсчета является инерциальной, то инерциальной будет любая другая система отсчета, движущаяся относительно нее прямолинейно и равномерно.

Сформулируем теперь первый закон Ньютона с указанием систем отсчета, в которых он выполняется.

Существуют системы отсчета (называемые инерциальными), относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел скомпенсированы.

Изучать влияние взаимодействия тел на их движение удобнее всего именно в инерциальных системах отсчета, потому что в этих системах отсчета изменение скорости тела обусловлено только действием других тел на это тело.

Принцип относительности Галилея

Как показывает опыт, во всех инерциальных системах отсчета все механические явления протекают одинаково при одинаковых начальных условиях.

Это утверждение называют принципом относительности Галилея.

В справедливости принципа относительности Галилея легко убедиться, сидя в поезде, который плавно движется с постоянной скоростью. В таком случае все опыты с механическими явлениями, поставленные в вагоне, дадут одинаковые результаты независимо от того, едет поезд или стоит: например, лежащее на столе яблоко будет покоиться, а свободно падающие предметы будут падать вертикально вниз (относительно вагона!).

Поэтому пассажир может определить, едет поезд или стоит на станции, только посмотрев в окно (рис. 13.3).

2. Второй закон ньютона

Равнодействующая

Как вы уже знаете из курса физики основной школы, силы – векторные величины: каждая сила характеризуется числовым значением (модулем) и направлением. Силы измеряют с помощью динамометров. Единицей силы в СИ является 1 ньютон (Н). Определение ньютона мы дадим позже.

Если на тело, которое можно считать материальной точкой, действуют несколько сил, то их можно заменить одной силой, которая является векторной суммой этих сил. Ее называют равнодействующей.

На рисунке 13.4 показано, как найти равнодействующую двух сил: а

? 2. К телу приложены две силы, равные по модулю 1 Н и 2 Н. Отвечая на следующие вопросы, сделайте пояснительные чертежи.
а) Какое наименьшее значение может принимать равнодействующая этих сил? Как направлены силы в этом случае?
б) Какое наибольшее значение может быть у равнодействующей этих сил? Как направлены силы в атом случае?
в) Может ли равнодействующая этих сил быть равной 2 Н?

? 3. К телу приложены две силы, равные по модулю 3 Н и 4 Н. Может ли их равнодействующая быть равной 5 Н? Если да, то чему в этом случае равен угол между приложенными силами?

? 4. К телу приложены три равные по модулю силы по 1 Н каждая. Как они должны быть направлены, чтобы:
а) равнодействующая была равна 1 Н?
б) равнодействующая была равна нулю?
в) равнодействующая была равна 2 Н?

Масса тела

В курсе физики основной школы рассказывалось также об опытах, которые доказывают, что под действием постоянной силы тело движется с постоянным ускорением.

Коэффициент пропорциональности между силой и ускорением характеризует инертные свойства тела и называется массой тела. Чем больше масса тела, тем большую силу надо приложить к телу, чтобы сообщить ему то же ускорение.

Единицей массы в СИ является 1 килограмм (кг). Это масса эталона, хранящегося в Международном бюро мер и весов (Франция). Приближенно можно считать, что одному килограмму равна масса 1 л воды.

Обозначают массу буквой m.

Второй закон Ньютона

Соотношение между равнодействующей всех сил, приложенных к телу, массой тела и его ускорением Ньютон сформулировал как второй из трех основных законов механики.

Равнодействующая всех сил, приложенных к телу, равна произведению массы тела на его ускорение:

В инерциальной системе отсчета сила является причиной ускорения, поэтому второй закон Ньютона часто записывают так:

Итак, приобретаемое телом ускорение прямо пропорционально равнодействующей приложенных к телу сил, одинаково с ней направлено и обратно пропорционально массе тела.

Заметим, что второй закон Ньютона справедлив только в инерциальных системах отсчета. Напомним: в этих системах отсчета ускорение тела обусловлено только действием на него других тел.

Единицу силы в СИ определяют на основе второго закона Ньютона: сила в 1 ньютон сообщает телу массой 1 кг ускорение 1 м/с². Поэтому 1 Н = 1 кг * м/с².

Сила тяжести

Как вы уже знаете, под действием притяжения Земли все тела падают с одинаковым ускорением – ускорением свободного падения . Силу притяжения, действующую на тело со стороны Земли, называют силой тяжести и обозначают _т.

Когда тело свободно падает, на него действует только сила тяжести, поэтому она и является равнодействующей всех приложенных к телу сил. При атом тело движется с ускорением , поэтому из второго закона Ньютона получаем:

? 5. С какой силой Земля притягивает:
а) килограммовую гирю?
б) человека массой 60 кг?

Сила, скорость и ускорение – кто «третий лишний»?

Неочевидное следствие второго закона Ньютона состоит в том, что он утверждает: направление ускорения тела совпадает с направлением равнодействующей приложенных телу сил. Скорость же вела может быть при этом направлена как угодно!

Поставим опыт

Бросим шарик вниз, затем – вверх, а потом – под углом к горизонту (рис. 13.5)

На шарик во время всего движения действует только направленная вниз сила тяжести. Однако в первом случае (а) скорость шарика совпадает по направлению с этой силой, во втором случае (б) – скорость вначале противоположна силе тяжести, а в третьем (в) – скорость направлена под углом к силе тяжести (например, в верхней точке траектории скорость перпендикулярна силе тяжести).

? 6. Тело равномерно движется по окружности. Чему равен угол между скоростью тела и равнодействующей?

? 7. Чему равен угол между скоростью автомобиля и равнодействующей приложенных к нему сил, когда автомобиль:
а) разгоняется на прямой дороге?
б) тормозит на прямой дороге?
в) движется равномерно по дуге окружности?

3. Третий закон ньютона

Поставим опыт

Предложим первокласснику и десятикласснику посоревноваться в перетягивании каната, стоя на скейтбордах: тогда трением между колесами и полом можно пренебречь (схема опыта показана на рисунке 13.6).

Мы увидим, что оба соперника движутся с ускорением. Значит, на каждого из них действу другого. Ускорения соперников направлено противоположно, причем ускорение первоклассника намного больше ускорения десятиклассника.

Точные опыты, подобные описанном выше, показывают, что модули ускорений обратно пропорциональны массам тел:

a₁/a₂ = m₂/m₁.

Поскольку ускорения направлены противоположно,

Согласно второму закону Ньютона m₁₁ = ₁ и m₂₂ = ₂, где ₁ – сила, действующая на первое тело со стороны второго, а ₂ – сила, действующая на второе тело со стороны первого.

Из соотношения (5) следует, что ₁ = –₂. Это и есть третий закон Ньютона.

Тела взаимодействуют друг с другом с силами, равными по модулю и противоположными по направлению.

Свойстве сил, с которыми тела взаимодействуют друг с другом:
– эти силы обусловлены одним и тем же взаимодействием и поэтому имеют одну и ту же физическую природу;
– эти силы направлены вдоль одной прямой;
– эти силы приложены к разным телам и поэтому не могут уравновешивать друг друга.

Примеры проявления третьего закона Ньютона

Когда камень падает на Землю, на него действует сила тяжести ₁ со стороны Земли, а на Землю – сила ₂ притяжения со стороны камня (рис. 13.7, для наглядности масштаб не соблюден). Обе эти силы относятся к силам всемирного тяготения.

? 8. Согласно третьему закону Ньютона F₁ = F₂. Почему же ускорение камня заметно, а ускорение Земли – нет?

Когда камень лежит на Земле, на него кроме силы тяжести, которую будем обозначать теперь _т, действует еще направленная вверх сила давления со стороны опоры (рис. 13.8, а). Она направлена перпендикулярно поверхности опоры, поэтому ее называют силой нормальной реакции (перпендикуляр называют часто нормалью). (Когда тело можно считать материальной точкой, все действующие на него силы желательно изображать на чертежах приложенными в одной точке.)

Когда камень покоится, его ускорение равно нулю. Значит, согласно второму закону Ньютона равнодействующая приложенных к камню сил и _т, равна нулю (будем говорить, что в таком случае силы уравновешивают друг друга):

Отсюда следует:

Опора давит на камень силой , направленной вверх, а камень, по третьему закону Ньютона, давит на опору силан , направленной вниз (рис. 13.8, 6). Обе эти силы – силы упругости.

Силу, с которой тело вследствие действия на него силы тяжести давит на горизонтальную опору или растягивает вертикальный поднес, называют весом тела.

Итак, – это вес камня. По третьему закону Ньютона

Из формул (8) и (9) следует:

Итак, вес покоящегося тела равен действующей на это тело силе тяжести. Однако несмотря на это вес и сила тяжести существенно отличаются друг от друга:
– эти силы приложены к разным телам: вес действует на опору или поднес, а сила тяжести – на само тело;
– эти силы имеют разную физическую природу: вес – это сила упругости, а сила тяжести – проявление сил всемирного тяготения.

Кроме того, как мы увидим несколько позже (§ 16), вес может быть не равен силе тяжести и даже быть равным нулю.

Дополнительные вопросы и задания

9. Ускорение тела в некоторой инерциальной системе отсчета равно 3 м/с2 и направлено вдоль оси x. Чему равно ускорение этого тела в инерциальной системе отсчета, движущейся относительно заданной со скоростью 4 м/с, направленной вдоль оси y? Есть ли здесь лишние данные?

10. Брусок массой 0,5 кг соскальзывает с наклонной плоскости с углом наклона 30º. Скорость бруска увеличивается. Ускорение бруска равно 2 м/с₂. Изобразите на чертеже равнодействующую приложенных к бруску сил. Чему она равна? Есть ли в задаче лишние данные?

11. Зависимость координаты x автомобиля от времени выражается в единицах СИ формулой x = 20 – 10t + t². Ось x направлена вдоль дороги, масса автомобиля 1 т.
а) Чему равна равнодействующая приложенных к автомобилю сил?
б) Как она направлена в начальный момент – в направлении скорости автомобиля или противоположно ей?

12. Автомобиль массой 1 т едет со скоростью 72 км/ч по выпуклому мосту, имеющему форму дуги окружности радиусом 50 м. Сделайте чертеж и ответьте на вопросы.
а) Чему равна и как направлена равнодействующая сил, приложенных к автомобилю в верхней точке моста?
б) Какие силы действуют на автомобиль в этой точке? Как они направлены и чему они равны?
в) Во сколько раз вес автомобиля в верхней точке моста меньше действующей на автомобиль силы тяжести?

законов движения Ньютона | Исследовательский центр Гленна

Каковы законы движения Ньютона?

1. Покоящийся объект остается неподвижным, а объект в движении остается в движении с постоянной скоростью и по прямой, если на него не действует неуравновешенная сила.
2. Ускорение объекта зависит от массы объекта и количества приложенной силы.
3. Каждый раз, когда один объект оказывает силу на другой объект, второй объект оказывает равное и противоположное воздействие на первый.

Сэр Исаак Ньютон работал во многих областях математики и физики. Он разработал теории гравитации в 1666 году, когда ему было всего 23 года. В 1686 году он представил свои три закона движения в «Principia Mathematica Philosophiae Naturalis».

Разработав три закона движения, Ньютон произвел революцию в науке. Законы Ньютона вместе с законами Кеплера объяснили, почему планеты движутся по эллиптическим орбитам, а не по кругу.

Ниже представлен короткий фильм с участием Орвилла и Уилбура Райтов и обсуждение того, как законы движения Ньютона применимы к полету их самолета.

Первый закон Ньютона: инерция

Покоящийся объект остается неподвижным, а объект в движении остается в движении с постоянной скоростью и по прямой, если на него не действует неуравновешенная сила.

Первый закон Ньютона гласит, что каждый объект будет оставаться в покое или в равномерном движении по прямой линии, если он не будет вынужден изменить свое состояние под действием внешней силы. Эта тенденция сопротивляться изменениям в состоянии движения составляет инерции .На объект не действует чистая сила (если все внешние силы нейтрализуют друг друга). Тогда объект будет поддерживать постоянную скорость . Если эта скорость равна нулю, объект остается в покое. Если на объект действует внешняя сила, скорость изменится из-за силы.

Примеры инерции, связанные с аэродинамикой:

• Движение самолета, когда пилот меняет положение дроссельной заслонки двигателя.
• Движение шара, падающего в атмосфере.
• Модель ракеты, запускаемой в атмосферу.
• Движение воздушного змея при перемене ветра.

Второй закон Ньютона: сила

Ускорение объекта зависит от массы объекта и величины приложенной силы.

Его второй закон определяет, что сила равна изменению импульса (масса, умноженная на скорость) за изменение во времени. Импульс определяется как масса объекта м , умноженная на его скорость V .

Предположим, что у нас есть самолет в точке «0», определяемой его местоположением X0 и временем t0 . Самолет имеет массу m0 и движется со скоростью V0 . Внешняя сила F на самолет, показанный выше, перемещает его в точку «1». Новое местоположение самолета – X1 , время – t1 .

Масса и скорость самолета изменяются во время полета до значений m1 и V1 .Второй закон Ньютона может помочь нам определить новые значения V1 и m1 , если мы знаем, насколько велика сила F . Давайте просто возьмем разницу между условиями в точке «1» и условиями в точке «0».

F = (m1 * V1 – m0 * V0) / (t1 – t0)

Второй закон Ньютона говорит об изменениях количества движения (м * В), поэтому на данный момент мы не можем отделить, насколько изменилась масса и насколько изменилась скорость. Мы знаем только, сколько продукта (m * V) изменилось.

Предположим, что масса остается постоянной величиной, равной м . Это предположение довольно хорошо для самолета, единственное изменение массы будет для топлива, сожженного между точкой «1» и точкой «0». Вес топлива, вероятно, невелик по сравнению с весом остальной части самолета, особенно если мы будем смотреть только на небольшие изменения во времени. Если бы мы обсуждали полет бейсбольного мяча, то, конечно, масса остается постоянной. Но если бы мы обсуждали полет баллонной ракеты, то масса не остается постоянной, и мы можем смотреть только на изменение количества движения.Для постоянной массы м второй закон Ньютона выглядит так:

F = м * (V1 – V0) / (t1 – t0)

Изменение скорости, деленное на изменение во времени, и есть определение ускорения a . Затем второй закон сводится к более знакомому произведению массы и ускорения:

F = м * а

Помните, что это соотношение подходит только для объектов с постоянной массой. Это уравнение говорит нам, что объект, на который действует внешняя сила, будет ускоряться и что величина ускорения пропорциональна величине силы.Величина ускорения также обратно пропорциональна массе объекта; при равных силах более тяжелый объект будет испытывать меньшее ускорение, чем более легкий объект. Рассматривая уравнение количества движения, сила вызывает изменение скорости; и аналогично изменение скорости порождает силу. Уравнение работает в обоих направлениях.

Скорость, сила, ускорение и импульс имеют как величину величин , так и направление , связанное с ними. Ученые и математики называют это векторной величиной.Показанные здесь уравнения на самом деле являются векторными уравнениями и могут применяться в каждом из направлений компонентов. Мы рассмотрели только одно направление, и, как правило, объект движется во всех трех направлениях (вверх-вниз, влево-вправо, вперед-назад).

Пример силы, связанной с аэродинамикой:

Третий закон Ньютона: действие и противодействие

Каждый раз, когда один объект воздействует на второй объект, второй объект оказывает на первый равную и противоположную силу.

Его третий закон гласит, что для каждого действия (силы) в природе существует равное и противоположное противодействие .Если объект A оказывает силу на объект B, объект B также оказывает равную и противоположную силу на объект A. Другими словами, силы возникают в результате взаимодействий.

Примеры действий и противодействий, связанных с аэродинамикой:

• Движение подъемной силы от профиля, воздух отклоняется вниз под действием профиля, и в ответ крыло толкается вверх.
• Движение вращающегося шара, воздух отклоняется в одну сторону, а мяч реагирует движением в противоположную сторону
• Движение реактивного двигателя создает тягу, и горячие выхлопные газы выходят из задней части двигателя, а сила тяги создается в противоположном направлении.

Обзор законов движения Ньютона

1. Первый закон движения Ньютона (инерция)	Покоящийся объект остается неподвижным, а объект в движении остается в движении с постоянной скоростью и по прямой, если на него не действует неуравновешенная сила.
2. Второй закон движения Ньютона (Сила)	Ускорение объекта зависит от массы объекта и количества приложенной силы.
3. Третий закон движения Ньютона (действие и противодействие)	Каждый раз, когда один объект оказывает силу на другой объект, второй объект оказывает равное и противоположное воздействие на первый.

Законы движения Ньютона | Определение, примеры и история

Законы движения Ньютона , отношения между силами, действующими на тело, и движением тела, впервые сформулированные английским физиком и математиком сэром Исааком Ньютоном.

Ньютон, Исаак; Законы движения

Титульный лист книги Исаака Ньютона Philosophiae Naturalis Principia Mathematica (1687; Mathematical Principles of Natural Philosophy ), работы, в которой физик представил свои три закона движения.

Photos.com/Thinkstock

Популярные вопросы

Каковы законы движения Ньютона?

Законы движения Ньютона связывают движение объекта с действующими на него силами. В первом законе объект не изменит своего движения, если на него не действует сила.Во втором законе сила, действующая на объект, равна его массе, умноженной на его ускорение. В третьем законе, когда два объекта взаимодействуют, они прикладывают друг к другу силы равной величины и противоположного направления.

Почему законы движения Ньютона важны?

Законы движения Ньютона важны, потому что они лежат в основе классической механики, одного из основных разделов физики. Механика – это изучение того, как объекты движутся или не двигаются, когда на них действуют силы.

Первый закон Ньютона гласит, что если тело находится в состоянии покоя или движется с постоянной скоростью по прямой линии, оно будет оставаться в покое или продолжать движение по прямой с постоянной скоростью, если на него не действует сила.Этот постулат известен как закон инерции. Закон инерции был впервые сформулирован Галилео Галилеем для горизонтального движения на Земле, а затем был обобщен Рене Декартом. До Галилея считалось, что любое горизонтальное движение требует прямой причины, но Галилей вывел из своих экспериментов, что движущееся тело будет оставаться в движении, если сила (например, трение) не заставит его остановиться.

баскетбол; Законы движения Ньютона

Когда баскетболист делает бросок в прыжке, мяч всегда следует по дуге.Мяч следует по этому пути, потому что его движение подчиняется законам движения сэра Исаака Ньютона.

© Mark Herreid / Shutterstock.com

Второй закон Ньютона – это количественное описание изменений, которые сила может вызвать при движении тела. Он утверждает, что скорость изменения количества движения тела по величине и направлению равна силе, приложенной к нему. Импульс тела равен произведению его массы на скорость. Импульс, как и скорость, является векторной величиной, имеющей как величину, так и направление.Сила, приложенная к телу, может изменить величину импульса или его направление, или и то, и другое. Второй закон Ньютона – один из самых важных во всей физике. Для тела, масса которого m постоянна, это можно записать в виде F = m a , где F (сила) и a (ускорение) являются векторными величинами. Если на тело действует чистая сила, оно ускоряется в соответствии с уравнением. И наоборот, если тело не ускоряется, на него не действует действующая сила.

Третий закон Ньютона гласит, что при взаимодействии двух тел они прикладывают друг к другу силы, равные по величине и противоположные по направлению. Третий закон также известен как закон действия и противодействия. Этот закон важен при анализе задач статического равновесия, в которых все силы уравновешены, но он также применим к телам, находящимся в равномерном или ускоренном движении. Силы, которые он описывает, являются реальными, а не просто бухгалтерскими приборами. Например, книга, лежащая на столе, прикладывает направленную вниз силу, равную ее весу на столе.Согласно третьему закону, стол прилагает к книге равную и противоположную силу. Эта сила возникает из-за того, что вес книги заставляет стол слегка деформироваться, так что он толкает книгу назад, как спиральная пружина.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас Законы

Ньютона впервые появились в его шедевре, Philosophiae Naturalis Principia Mathematica (1687), широко известном как Principia . В 1543 году Николай Коперник предположил, что в центре Вселенной может находиться Солнце, а не Земля.За прошедшие годы Галилей, Иоганн Кеплер и Декарт заложили основы новой науки, которая заменит аристотелевское мировоззрение, унаследованное от древних греков, и объяснит работу гелиоцентрической вселенной. В «Началах » Ньютон создал эту новую науку. Он разработал свои три закона, чтобы объяснить, почему орбиты планет представляют собой эллипсы, а не круги, что ему удалось, но оказалось, что он объяснил гораздо больше. Серия событий от Коперника до Ньютона известна под общим названием Научная революция.

В 20 веке законы Ньютона были заменены квантовой механикой и теорией относительности как наиболее фундаментальными законами физики. Тем не менее, законы Ньютона продолжают давать точное описание природы, за исключением очень маленьких тел, таких как электроны, или тел, движущихся со скоростью, близкой к скорости света. Квантовая механика и теория относительности сводятся к законам Ньютона для более крупных тел или для тел, движущихся медленнее.

Первый закон движения Ньютона

В предыдущей главе исследования было описано различных способов, с помощью которых движение может быть выполнено (слова, графики, диаграммы, числа и т. Д.) обсуждалось. В этом модуле (Законы движения Ньютона) будут обсуждаться способы объяснения движения . Исаак Ньютон (ученый 17 века) выдвинул множество законов, объясняющих, почему объекты движутся (или не двигаются) именно так. Эти три закона стали известны как три закона движения Ньютона. В центре внимания Урока 1 находится первый закон движения Ньютона, который иногда называют законом инерции .

Первый закон движения Ньютона часто обозначается как

Покоящийся объект остается неподвижным, а объект в движении остается в движении с той же скоростью и в том же направлении, если на него не действует неуравновешенная сила.

Два пункта и условие

В этом утверждении есть два пункта или части – один, который предсказывает поведение неподвижных объектов, а другой, который предсказывает поведение движущихся объектов. Эти две части представлены на следующей диаграмме.

Поведение всех объектов можно описать, сказав, что объекты имеют тенденцию «продолжать делать то, что они делают» (если на них не действует несбалансированная сила).Если они находятся в состоянии покоя, они будут продолжать в том же состоянии покоя. Если они движутся со скоростью 5 м / с на восток, они продолжат движение в том же состоянии (5 м / с, восток). Если они будут двигаться со скоростью 2 м / с влево, они продолжат движение в том же состоянии (2 м / с, слева). Состояние движения объекта сохраняется до тех пор, пока на объект , а не действует неуравновешенная сила. Все объекты сопротивляются изменениям в своем состоянии движения – они склонны «продолжать делать то, что делают».«

Есть важное условие, которое должно быть выполнено, чтобы первый закон был применим к любому данному ходатайству. Состояние описывается фразой «… если на него не действует неуравновешенная сила». Пока силы не разбалансированы, то есть пока силы уравновешены, применяется первый закон движения. Эта концепция сбалансированной и неуравновешенной силы будет обсуждаться более подробно позже в Уроке 1.

Предположим, вы наполнили форму для запекания водой до края и прошли по овальной дорожке, пытаясь пройти круг за наименьшее количество времени.Вода имеет тенденцию выливаться из контейнера в определенных местах на трассе. В общем вода пролилась когда:

• контейнер был неподвижен, и вы попытались его переместить
• контейнер находился в движении, и вы пытались его остановить
• : контейнер двигался в одном направлении, и вы попытались изменить его направление.

Вода разливается при изменении состояния движения контейнера.Вода сопротивлялась этому изменению в своем собственном состоянии движения. Вода имела тенденцию «продолжать делать то, что делала». Контейнер был переведен из состояния покоя на высокую скорость на старте; вода осталась в покое и пролилась на стол. Контейнер был остановлен около финиша; вода продолжала двигаться и пролилась через переднюю кромку контейнера. Контейнер был вынужден двигаться в другом направлении, чтобы сделать изгиб; вода продолжала двигаться в том же направлении и пролилась через край.Поведение воды во время круга по трассе можно объяснить первым законом движения Ньютона.

Повседневное применение Первого закона Ньютона

Есть много применений первого закона движения Ньютона. Рассмотрим некоторые из ваших опытов в автомобиле. Вы когда-нибудь наблюдали поведение кофе в чашке, наполненной до краев, при запуске автомобиля из состояния покоя или при переводе автомобиля в состояние покоя из состояния движения? Кофе “продолжает делать то, что делает.«Когда вы разгоняете машину из состояния покоя, дорога создает неуравновешенную силу на вращающиеся колеса, толкая машину вперед; однако кофе (который был в состоянии покоя) хочет оставаться в состоянии покоя. Пока машина ускоряется вперед, кофе остается в в том же положении; впоследствии машина ускоряется из-под кофе, и кофе разливается вам на колени. С другой стороны, при торможении из состояния движения кофе продолжает движение вперед с той же скоростью и в том же направлении , в конечном итоге ударил лобовое стекло или приборную панель.Кофе в движении остается в движении.

Испытывали ли вы когда-нибудь инерцию (сопротивление изменениям в вашем состоянии движения) в автомобиле, когда он тормозит до полной остановки? Сила дороги на заблокированные колеса обеспечивает неуравновешенную силу, чтобы изменить состояние движения автомобиля, но нет неуравновешенной силы, чтобы изменить ваше собственное состояние движения. Таким образом, вы продолжаете движение, скользя по сиденью в поступательном движении. Человек в движении остается в движении с той же скоростью и в том же направлении… если на него не действует неуравновешенная сила ремня безопасности. Да! Ремни безопасности используются для обеспечения безопасности пассажиров, движение которых регулируется законами Ньютона. Ремень безопасности обеспечивает неуравновешенное усилие, которое переводит вас из состояния движения в состояние покоя. Возможно, вы могли бы предположить, что произойдет, если ремень безопасности не используется.

Есть еще много приложений первого закона движения Ньютона.Ниже перечислены несколько приложений. Возможно, вы могли бы подумать о законе инерции и дать объяснения для каждого приложения.

• Кровь приливает к ногам, быстро останавливаясь при езде на спускающемся лифте.
• Головку молотка можно закрепить на деревянной ручке, ударив нижней частью ручки о твердую поверхность.
• Кирпич безболезненно разбивают о руку учителя физики, ударив по нему молотком.(ВНИМАНИЕ: не пытайтесь сделать это дома!)
• Чтобы вытолкнуть кетчуп со дна бутылки с кетчупом, его часто переворачивают вверх дном и толкают вниз на высокой скорости, а затем резко останавливают.
• Подголовники устанавливаются в автомобилях для предотвращения хлыстовых травм при наезде сзади.
• Во время езды на скейтборде (тележке или велосипеде) вы летите вперед от доски при ударе о бордюр, камень или другой объект, который резко останавливает движение скейтборда.

Попробуйте дома

Приобретите металлическую вешалку для одежды, на которую у вас есть разрешение на и уничтожение . Раздвиньте плечики. Прикрепите изолентой два теннисных мяча к противоположным концам плечиков, как показано на рисунке справа.Согните вешалку так, чтобы на голове человека была плоская деталь. Концы вешалки с теннисными мячами должны свисать низко (ниже точки балансировки). Наденьте вешалку на голову и уравновесите ее. Затем быстро крутите по кругу. Что делают теннисные мячи?

5.2 Первый закон Ньютона | Университетская физика, том 1,

Цели обучения

По окончании раздела вы сможете:

• Опишите первый закон движения Ньютона
• Распознавать трение как внешнюю силу
• Определить инерцию
• Определить инерциальные системы отсчета
• Расчет равновесия для системы

Опыт подсказывает, что покоящийся объект остается неподвижным, если его оставить в покое, и что движущийся объект имеет тенденцию замедляться и останавливаться, если не прилагать каких-либо усилий для его движения.Однако первый закон Ньютона дает более глубокое объяснение этому наблюдению.

Первый закон движения Ньютона

Тело в состоянии покоя остается в состоянии покоя или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует чистая внешняя сила.

Обратите внимание на неоднократное использование глагола «остается». Мы можем думать об этом законе как о сохранении статус-кво движения. Также обратите внимание на выражение «постоянная скорость»; это означает, что объект сохраняет путь вдоль прямой линии, поскольку ни величина, ни направление вектора скорости не меняются.Мы можем использовать (рисунок), чтобы рассмотреть две части первого закона Ньютона.

Рис. 5.7 (a) Хоккейная шайба изображена в покое; он остается в состоянии покоя до тех пор, пока внешняя сила, такая как хоккейная клюшка, не изменит его состояние покоя; (b) хоккейная шайба движется; он продолжает движение по прямой линии, пока внешняя сила не заставит его изменить свое состояние движения. Хотя ледяная поверхность гладкая, она обеспечивает некоторое трение, которое замедляет шайбу.

Первый закон Ньютона не противоречит нашему опыту, а утверждает, что должна быть причина для любого изменения скорости (изменения величины или направления).Эта причина – чистая внешняя сила, которую мы определили ранее в этой главе. Предмет, скользящий по столу или полу, замедляется из-за действующей на объект чистой силы трения. Если трение исчезнет, ​​будет ли объект по-прежнему замедляться?

Идея причины и следствия имеет решающее значение для точного описания того, что происходит в различных ситуациях. Например, рассмотрим, что происходит с объектом, скользящим по шероховатой горизонтальной поверхности. Объект быстро останавливается. Если мы распыляем на поверхность тальк, чтобы сделать поверхность более гладкой, объект скользит дальше.Если мы сделаем поверхность еще более гладкой, нанеся на нее смазочное масло, объект будет скользить еще дальше. Экстраполируя на поверхность без трения и игнорируя сопротивление воздуха, мы можем представить объект, скользящий по прямой бесконечно долго. Таким образом, трение является причиной замедления (в соответствии с первым законом Ньютона). Объект не замедлился бы, если бы трение было устранено.

Рассмотрим стол для аэрохоккея ((рисунок)). Когда подача воздуха отключена, шайба скользит лишь на небольшое расстояние, прежде чем трение замедляет ее до полной остановки.Однако, когда воздух включен, он создает поверхность, почти не имеющую трения, и шайба скользит на большие расстояния, не замедляясь. Кроме того, если мы достаточно знаем о трении, мы можем точно предсказать, насколько быстро объект замедляется.

Рисунок 5.8 Стол для аэрохоккея полезен для иллюстрации законов Ньютона. Когда воздух отсутствует, трение быстро замедляет движение шайбы; но когда есть воздух, это сводит к минимуму контакт между шайбой и хоккейным столом, и шайба скользит далеко вниз по столу.

Первый закон Ньютона является общим и может применяться ко всему: от объекта, скользящего по столу, до спутника на орбите и крови, перекачиваемой из сердца. Эксперименты подтвердили, что любое изменение скорости (скорости или направления) должно быть вызвано внешней силой. Идея общеприменимых или универсальных законов важна – это основная черта всех законов физики. Выявление этих законов похоже на распознавание закономерностей в природе, из которых можно обнаружить дальнейшие закономерности.Гений Галилея, который первым разработал идею первого закона движения, и Ньютона, разъяснившего ее, заключался в том, чтобы задать фундаментальный вопрос: «В чем причина?» Причинно-следственное мышление в корне отличается от типичного древнегреческого подхода, когда возникают такие вопросы, как «Почему у тигра полосы?» можно было бы ответить по-аристотелевски, например: «Такова природа зверя». Способность мыслить в терминах причины и следствия – это способность устанавливать связь между наблюдаемым поведением и окружающим миром.

Гравитация и инерция

Независимо от масштаба объекта, будь то молекула или субатомная частица, два свойства остаются действительными и поэтому представляют интерес для физики: гравитация и инерция. Оба связаны с массой. Грубо говоря, масса – это мера количества материи в чем-то. Гравитация – это притяжение одной массы к другой, например, притяжение между вами и Землей, прижимающее ваши ноги к полу. Величина этого притяжения – это ваш вес и сила.

Масса также связана с инерцией , , способностью объекта сопротивляться изменениям в его движении – другими словами, сопротивляться ускорению. Первый закон Ньютона часто называют законом инерции , . Как мы знаем из опыта, некоторые объекты обладают большей инерцией, чем другие. Изменить движение большого валуна сложнее, чем, например, баскетбольного мяча, потому что валун имеет большую массу, чем баскетбольный мяч. Другими словами, инерция объекта измеряется его массой.Взаимосвязь между массой и весом исследуется далее в этой главе.

Инерциальная система отсчета

Ранее мы сформулировали первый закон Ньютона: «Покоящееся тело остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует чистая внешняя сила». Его также можно сформулировать так: «Каждое тело остается в состоянии равномерного движения по прямой, если только оно не вынуждено изменить это состояние под действием сил, действующих на него». Для Ньютона «равномерное движение по прямой» означало постоянную скорость, включая случай нулевой скорости или покоя.Следовательно, первый закон гласит, что скорость объекта остается постоянной, если результирующая сила, действующая на него, равна нулю.

Первый закон Ньютона обычно считается утверждением о системе отсчета. Он предоставляет метод для идентификации особого типа опорного кадра: инерциального опорного кадра . В принципе, мы можем сделать результирующую силу, действующую на тело, равной нулю. Если его скорость относительно данной системы отсчета постоянна, то эта система отсчета называется инерциальной. Итак, по определению, инерциальная система отсчета – это система отсчета, в которой действует первый закон Ньютона.Первый закон Ньютона применим к объектам с постоянной скоростью. Из этого факта можно вывести следующее утверждение.

Инерциальная система отсчета

Система отсчета, движущаяся с постоянной скоростью относительно инерциальной системы, также является инерциальной. Опорный кадр, ускоряющийся относительно инерциального кадра, не является инерционным.

Распространены ли в природе инерционные системы отсчета? Оказывается, что с точностью до ошибки эксперимента система отсчета в состоянии покоя относительно самых далеких или «неподвижных» звезд является инерциальной.{2} [/ латекс]). Таким образом, если не указано иное, мы считаем фиксированные на Земле системы отсчета инерциальными.

Наконец, ни одна инерциальная система отсчета не является более особенной, чем любая другая. Что касается законов природы, все инерциальные системы отсчета эквивалентны. При анализе проблемы мы выбираем одну инерциальную систему отсчета над другой просто из соображений удобства.

Первый закон и равновесие Ньютона

Первый закон Ньютона говорит нам о равновесии системы, то есть о состоянии, в котором силы в системе уравновешены.Возвращаясь к силам и фигуристам на (рис.), Мы знаем, что силы [латекс] {\ overset {\ to} {F}} _ {1} [/ latex] и [латекс] {\ overset {\ to} {F}} _ {2} [/ latex] объединяются, чтобы сформировать результирующую силу или чистую внешнюю силу: [latex] {\ overset {\ to} {F}} _ {\ text {R}} = {\ overset {\ to} {F}} _ {\ text {net}} = {\ overset {\ to} {F}} _ {1} + {\ overset {\ to} {F}} _ {2}. [/ latex] Чтобы создать равновесие, нам нужна уравновешивающая сила, которая произведет нулевую чистую силу. Эта сила должна быть равной по величине, но противоположной по направлению [latex] {\ overset {\ to} {F}} _ {\ text {R}}, [/ latex], что означает, что вектор должен быть [latex] \ text {-} {\ overset {\ to} {F}} _ {\ text {R}}.[/ latex] Ссылаясь на фигуристов, для которых мы обнаружили [latex] {\ overset {\ to} {F}} _ {\ text {R}} [/ latex] как [latex] 30.0 \ hat {i } +40.0 \ hat {j} \, \ text {N} [/ latex], мы можем определить балансирующую силу, просто найдя [latex] \ text {-} {\ overset {\ to} {F}} _ { \ text {R}} = – 30,0 \ hat {i} -40,0 \ hat {j} \, \ text {N}. [/ latex] См. диаграмму свободного тела на (Рисунок) (b).

Мы можем представить первый закон Ньютона в векторной форме:

[латекс] \ overset {\ to} {v} = \ text {constant when} \, {\ overset {\ to} {F}} _ {\ text {net}} = \ overset {\ to} {0 } \, \ text {N}.[/ латекс]

Это уравнение говорит, что чистая сила, равная нулю, означает, что скорость [latex] \ overset {\ to} {v} [/ latex] объекта постоянна. (Слово «постоянная» может указывать на нулевую скорость.)

Первый закон Ньютона обманчиво прост. Если автомобиль находится в состоянии покоя, единственными силами, действующими на автомобиль, являются вес и сила контакта дорожного покрытия, толкающего автомобиль вверх ((Рисунок)). Легко понять, что для изменения состояния движения автомобиля требуется ненулевая результирующая сила.Однако, если автомобиль движется с постоянной скоростью, распространено заблуждение, что сила двигателя, толкающая автомобиль вперед, больше по величине, чем сила трения, которая препятствует движению вперед. Фактически, эти две силы имеют одинаковую величину.

Рисунок 5.9 Автомобиль показан (а) припаркованным и (б) движущимся с постоянной скоростью. Как законы Ньютона применяются к припаркованной машине? Что знание того, что автомобиль движется с постоянной скоростью, говорит нам о чистой горизонтальной силе, действующей на автомобиль?

Пример

Когда к вашей машине применим Первый закон Ньютона?

Законы Ньютона могут применяться ко всем физическим процессам, связанным с силой и движением, включая такие повседневные вещи, как вождение автомобиля.

(a) Ваш автомобиль припаркован возле вашего дома. Применяется ли в этой ситуации первый закон Ньютона? Почему или почему нет?

(b) Ваш автомобиль движется по улице с постоянной скоростью. Применяется ли в этой ситуации первый закон Ньютона? Почему или почему нет?

Стратегия

В (а) мы рассматриваем первую часть первого закона Ньютона, касающуюся покоящегося тела; в (b) мы рассматриваем вторую часть первого закона Ньютона для движущегося тела.

Решение

1. Когда ваша машина припаркована, все силы, действующие на нее, должны быть уравновешены; векторная сумма равна 0 Н.Таким образом, результирующая сила равна нулю, и применяется первый закон Ньютона. Ускорение автомобиля равно нулю, и в этом случае скорость тоже равна нулю.
2. Когда ваша машина движется по улице с постоянной скоростью, результирующая сила также должна быть равна нулю в соответствии с первым законом Ньютона. Двигатель автомобиля производит поступательную силу; трение, сила между дорогой и шинами автомобиля, которая препятствует движению вперед, имеет точно такую ​​же величину, что и сила двигателя, создавая результирующую силу, равную нулю.Тело остается в состоянии постоянной скорости, пока результирующая сила не станет отличной от нуля. Поймите, что чистая сила, равная нулю, означает, что объект либо находится в состоянии покоя, либо движется с постоянной скоростью, то есть не ускоряется. Как вы думаете, что происходит, когда машина разгоняется? Мы исследуем эту идею в следующем разделе.

Значение

Как показывает этот пример, существует два вида равновесия. В (а) автомобиль неподвижен; мы говорим, что он находится в состоянии статического равновесия .В (b) силы, действующие на автомобиль, уравновешены, но автомобиль движется; мы говорим, что находится в динамическом равновесии . (Мы исследуем эту идею более подробно в статье «Статическое равновесие и эластичность».) Опять же, две (или более) силы могут воздействовать на объект, но при этом объект перемещается. Кроме того, чистая сила, равная нулю, не может вызвать ускорение.

Проверьте свое понимание

Парашютист раскрывает свой парашют, и вскоре после этого он движется с постоянной скоростью.а) Какие силы действуют на него? б) Какая сила больше?

Показать решение

а. Его вес действует вниз, а сила сопротивления воздуха с парашютом действует вверх. б. ни один; силы равны по величине

Сводка

• Согласно первому закону Ньютона, для любого изменения скорости (изменения величины или направления) должна быть причина. Этот закон также известен как закон инерции.
• Трение – это внешняя сила, которая заставляет объект замедляться.
• Инерция – это тенденция объекта оставаться в покое или оставаться в движении. Инерция связана с массой объекта.
• Если скорость объекта относительно данного кадра постоянна, то кадр инерционный. Это означает, что для инерциальной системы отсчета действует первый закон Ньютона.
• Равновесие достигается, когда силы в системе уравновешены.
• Чистая сила, равная нулю, означает, что объект либо находится в состоянии покоя, либо движется с постоянной скоростью; то есть не ускоряется.

Концептуальные вопросы

Принимая рамку, прикрепленную к Земле, как инерциальную, к каким из следующих объектов нельзя прикрепить инерциальные системы отсчета, а какие являются инерциальными системами отсчета?

(a) Автомобиль движется с постоянной скоростью

(б) Автомобиль, разгоняющийся

(в) Лифт в свободном падении

(d) Космическая капсула на орбите Земли

(e) Равномерно спускающийся лифт

Женщина несла открытую коробку кексов на школьную вечеринку.Автомобиль перед ней внезапно остановился; она немедленно притормозила. Она была пристегнута ремнем безопасности и не пострадала от физического вреда (просто большое смущение), но кексы влетели в приборную панель и превратились в «сладкие пирожные». Объясните, что произошло.

Показать решение

Скорость кекса до торможения была такой же, как у автомобиля. Таким образом, кексы были телами, движущимися без ограничений, и когда машина внезапно останавливалась, кексы продолжали двигаться вперед согласно первому закону Ньютона.

Проблемы

Две силы [латекса] {\ overset {\ to} {F}} _ {1} = \ frac {75.0} {\ sqrt {2}} (\ hat {i} – \ hat {j}) \, \ text {N} [/ latex] и [latex] {\ overset {\ to} {F}} _ {2} = \ frac {150.0} {\ sqrt {2}} (\ hat {i} – \ hat {j}) \, \ text {N} [/ latex] воздействуют на объект. Найдите третью силу [латекс] {\ overset {\ to} {F}} _ {3} [/ latex], которая необходима для уравновешивания первых двух сил.

Скользя кушеткой по полу, Андреа и Дженнифер прилагают усилия [латекс] {\ overset {\ to} {F}} _ {\ text {A}} [/ latex] и [латекс] {\ overset {\ to } {F}} _ {\ text {J}} [/ latex] на диване.Сила Андреа направлена ​​на север с магнитудой 130,0 Н, а сила Дженнифер – [латекс] 32 \ text {°} [/ latex] к востоку от севера с величиной 180,0 Н. (a) Найдите чистую силу в форме компонентов. (b) Найдите величину и направление результирующей силы. (c) Если соседи Андреа и Дженнифер, Дэвид и Стефани, не согласны с переездом и хотят предотвратить его переезд, с какой комбинированной силой [латекс] {\ overset {\ to} {F}} _ {\ text {DS}} [/ latex] они должны толкать, чтобы диван не шевелился?

Показать решение

а.[латекс] {\ overset {\ to} {F}} _ {\ text {net}} = 95,0 \ hat {i} +283 \ hat {j} \ text {N} [/ latex]; б. 299 с.ш. в [латексе] 71 \ text {°} [/ latex] к северу от востока; c. [латекс] {\ overset {\ to} {F}} _ {\ text {DS}} = \ text {-} (95,0 \ hat {i} +283 \ hat {j}) \, \ text {N} [/ латекс]

Глоссарий

инерция

Способность объекта сопротивляться изменениям в его движении

инерциальная система отсчета

Система отсчета

, движущаяся с постоянной скоростью относительно инерциальной системы, также является инерциальной; опорный кадр, ускоряющийся относительно инерциального кадра, не является инерционным

Закон инерции

см. Первый закон движения Ньютона

Первый закон движения Ньютона

тело в состоянии покоя остается в покое или, если оно находится в движении, остается в движении с постоянной скоростью, если на него не действует чистая внешняя сила; также известный как закон инерции

ФИЗ 124

ФИЗ 124

НАУЧНЫЙ ФАКУЛЬТЕТ, ОСЕНЬ 2007

PHYS 124 LEC A1: Частицы и волны (Инструктор: Марк де Монтиньи)

Уокер, Физика, Глава 5: Законы движения Ньютона

• Раздел 5-1: Сила и масса
  • Этот небольшой раздел можно прочитать на стр.108.
  • Сила – вектор (единица: Н = кг м / с ² ). Масса – скаляр (единица измерения: кг).
  • Масса – это мера инерции данного объекта. Инерция , в свою очередь, есть тенденция объекта противодействовать любому изменение скорости.
  • В этой главе рассматриваются различные типы сил. Много примеров будет обсуждаться в главе 6.
• Раздел 5-2: Первый закон движения Ньютона
  • Вы можете просмотреть стр.108-110.
  • «Нет чистой силы» не означает, что не нет силы; это означает, что сумма всех присутствующих сил равна нулю.
  • Обратите внимание, что этот закон (как и Второй закон Ньютона) действует в без ускорения только системы отсчета. Использование ускоренного системы отсчета обычно подразумевают введение так называемого фиктивного силы (например, центростремительная сила, ускоряющая или замедляющая автобус), которые необходимы ускоренному наблюдателю для учета для кажущихся сил, вызванных ускорением.
• Раздел 5-3: Второй закон движения Ньютона
  • Второй закон Ньютона дается формулой. 5-1 на стр. 111.
  • Практический интерес представляет диаграмма свободного тела , секция , С. 113, рисунок 5-5.
  • P. 117, Пример 5-2, обсуждается в классе.
  • С. 140, Задача 57, решена в классе
  • Хотя мы не обсуждаем больше примеров в этом пункте, мы используйте Второй Закон снова и снова в следующей главе.
• Раздел 5-4: Третий закон движения Ньютона
  • Обозначение: F _AB обозначает приложенное усилие на объект A силой B
  • Используя это обозначение, Третий закон Ньютона (см. Стр. 118) читается как
    F _BA = – F _AB
    
  • Краткое описание стр. 120, Пример 5-4 (а) и Пример 5-4 (б).
  • Вот вам загадка:
    Представьте лошадь, пытающуюся вытащить телегу с места на неровной поверхности. Студент, неверно истолковавший Третий закон Ньютона, делает следующее утверждение: “Если лошадь тянет повозку вперед, то закон действия-противодействия Ньютона считает, что повозка одинаково сильно тянет лошадь назад. Таким образом, силы отменить, и система не может быть запущена ».
    Кратко объясните, что неверно в утверждении этого студента. [из моя весна 2006 г., среднесрочная перспектива]
    Ответ
    
• Раздел 5-5: Векторная природа сил: силы в двух измерениях
  • Ур. 5-1 из п. 111 прямо читается следующим образом:
    ∑ F _x = ma _x , ∑ F _y = ma _y
    Если мы будем работать в трех измерениях, нам нужно будет добавить третье уравнение: ∑ F _z = ma _z .
  • С. 138, Задача 28, решена в классе.
• Раздел 5-6: Вес
  • С. 124, Ур. 5-5: W = мг
  • Вес – это не то же самое, что масса: вес – это сила.
  • Обозначается W .
  • Раздел Кажущийся вес на стр. 126–128 временно опущен. Мы вернется к нему после Раздела 5-7.
• Раздел 5-7: Нормальные силы
  • Здесь и далее нормальный означает «перпендикулярный».
  • Обозначается N .
  • Предупреждение: как указано в пункте 3 Раздела 5-7, как правило, нормальная сила может быть или не быть равна по величине весу объекта. Это проиллюстрировано на стр. 129, Рисунок 5-13.
  • Обсудим составляющие веса объекта на наклонная поверхность, п. 131, рисунок 5-15.
  • В задачах, где требуется, чтобы объект покинул некоторую поверхность, Дело в том, чтобы установить нормальную силу равной нулю.Другими словами, «покинуть поверхность» или «не касаться» означает N = 0.
  • Когда объекты сложены друг на друга, удобно использовать снова обозначение N _AB для представления «нормальная сила, действующая на поверхность A со стороны B».
  • Вернуться к разделу Кажущийся вес , стр. 126–128. В Короче говоря, «кажущийся вес» объекта – это просто нормальный сила, действующая от пола (или шкалы и т. д.)) на этом объекте. См. Стр. 126, Рисунок 5-11. Кажущийся вес часто включает ускорение. Например, вы чувствуете себя тяжелее в лифте, который ускоряется вверх, потому что пол действует на вас с нормальной силой больше вашего веса.
  • P. 127, Пример 5-7, будет обсуждаться в классе.

Вернуться к PHYS 124, Веб-страница LEC A1

Физлет физики: Глава 5: Законы Ньютона 2

До сих пор мы изучили простые проблемы с законами Ньютона и теперь рассмотрим дополнительные приложения, такие как трение (включая трение воздуха), круговое движение и пружины.

Иллюстрации

• Рисунок 5.1: Статическое и кинетическое трение.
• Иллюстрация 5.2: Равномерное круговое движение.
• Иллюстрация 5.3: Колесо обозрения.
• Иллюстрация 5.4: Закон Спрингса и Гука.
• Иллюстрация 5.5: Воздушное трение.

Исследования

• Исследование 5.1: Круговое движение.
• Исследование 5.2: Обвести объект вокруг круга.
• Разведка 5.3: Сила пружины.
• Исследование 5.4: Круговое движение и сила пружины.
• Исследование 5.5: Введите формулу силы.
• Исследование 5.6: Воздушное трение.
• Исследование 5.7: введите формулу F _x и F _y для Силы.

Проблемы

• Задача 5.1: Учебник физики весом 2 кг, прижатый к стене, не двигается.
• Задача 5.2: Учебник физики весом 2 кг, прижатый к стене, движется.
• Задача 5.3: Учебник физики весом 2 кг, прижатый к стене, движется.
• Задача 5.4: Блок толкается разной силой.
• Задача 5.5: 4-килограммовый блок стоит на 8-килограммовом блоке, проталкиваемом по полу.
• Задача 5.6: Блок массой 10 кг стоит на блоке массой 20 кг.
• Задача 5.7: Ящик весом 12 кг скользит по наклонному пандусу 26,56 °.
• Задача 5.8: Прокатиться на колесе обозрения.
• Задача 5.9: На поворотной платформе стоит груз.
• Задача 5.10: Шайба, лежащая на столе для аэрохоккея, привязана к веревке.
• Задача 5.11: 5-граммовая монета находится на вращающемся подносе.
• Задача 5.12: Пружину можно растянуть, перетащив синий шарик.
• Задача 5.13: 200-граммовый кирпич падает на платформу.
• Задача 5.14: Мяч стреляет по блоку, связанному с пружиной.

Механика TOC

Обзор TOC

Второй закон Ньютона (Закон движения)

Вы можете быть удивлены, узнав, что Ньютон не был гением, стоящим за законом инерции.Но сам Ньютон писал, что он мог видеть до сих пор только потому, что стоял «на плечах гигантов». И посмотреть, куда он сделал. Хотя закон инерции определяет силы как действия, необходимые для остановки или начала движения, он не дает количественной оценки этих сил. Второй закон Ньютона восполнял недостающее звено, связывая силу с ускорением. Вот что он сказал:

Когда сила действует на объект, объект ускоряется в направлении силы. Если масса объекта остается постоянной, увеличение силы увеличит ускорение.Если сила, действующая на объект, остается постоянной, увеличение массы уменьшит ускорение. Другими словами, сила и ускорение прямо пропорциональны, а масса и ускорение обратно пропорциональны.

Технически Ньютон приравнивал силу к дифференциальному изменению количества движения в единицу времени. Импульс – характеристика движущегося тела, определяемая произведением массы тела и скорости. Чтобы определить дифференциальное изменение количества движения в единицу времени, Ньютон разработал новый тип математики – дифференциальное исчисление.Его исходное уравнение выглядело примерно так:

F = (m) (Δv / Δt)

, где символы дельты означают изменение. Поскольку ускорение определяется как мгновенное изменение скорости в момент времени (Δv / Δt), уравнение часто переписывается как:

F = ma

Форма уравнения второго закона Ньютона позволяет нам указать единицу измерения. измерения силы. Поскольку стандартной единицей массы является килограмм (кг), а стандартной единицей ускорения является метр в секунду в квадрате (м / с2), единица измерения силы должна быть произведением двух – (кг) (м / с2). .Это немного неудобно, поэтому ученые решили использовать Ньютон в качестве официальной единицы силы. Один ньютон, или N, эквивалентен 1 килограмм-метру на секунду в квадрате. В 1 фунте 4,448 Н.

Итак, что вы можете сделать со вторым законом Ньютона? Как оказалось, F = ma позволяет количественно оценить движение каждого вида. Скажем, например, вы хотите рассчитать ускорение собачьей упряжки, показанной ниже.

Теперь предположим, что масса саней осталась на уровне 50 килограммов и что в команду добавлена ​​еще одна собака.Если предположить, что вторая собака тянет с той же силой, что и первая (100 Н), общая сила будет 200 Н, а ускорение – 4 м / с2.

Наконец, давайте представим, что к саням прикреплена вторая упряжка с собаками, которая может тянуть в обратном направлении.