| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | 2 1/2÷22000000 | |
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | окружность (4) | | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | 5 | ||
| 54 | Перевести в процентное соотношение | 3/9 | |
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
правила, примеры, решения, как умножать десятичные дроби
В этой статье мы рассмотрим такое действие, как умножение десятичных дробей.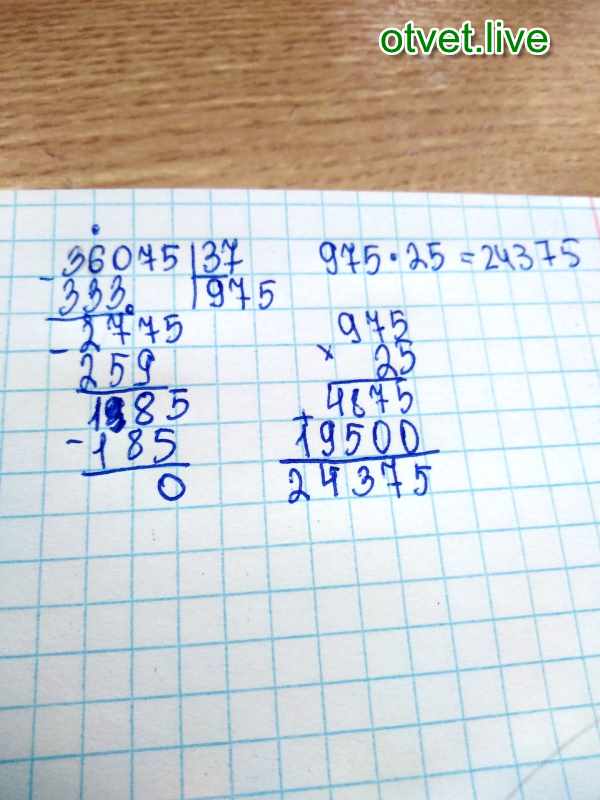
Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100, 10 и др.)
В рамках этого материала мы коснемся только правил умножения положительных дробей. Случаи с отрицательными разобраны отдельно в статьях об умножении рациональных и действительных чисел.
Умножение десятичных дробей: общие принципы
Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.
Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.
Посмотрим, как решаются такие задачи.
Пример 1Вычислите произведение 1,5 и 0,75.
Решение: для начала заменим десятичные дроби на обыкновенные. Мы знаем, что 0,75 – это 75/100, а 1,5 – это 1510. Мы можем сократить дробь и произвести выделение целой части. Полученный результат 1251000 мы запишем как 1,125.
Ответ: 1,125.
Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.
Пример 2Умножьте одну периодическую дробь 0,(3) на другую 2,(36).
Решение
Для начала приведем исходные дроби к обыкновенным. У нас получится:
0,(3)=0,3+0,03+0,003+0,003+…=0,31-0,1=0,39=39=132,(36)=2+0,36+0,0036+…=2+0,361-0,01=2+3699=2+411=2411=2611
Следовательно, 0,(3)·2,(36)=13·2611=2633.
Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:
Ответ: 0,(3)·2,(36)=0,(78).
Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см.
статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.
Вычислите произведение 5,382… и 0,2.
Решение
У нас в задаче есть бесконечная дробь, которую нужно предварительно округлить до сотых. Получится, что 5,382…≈5,38. Второй множитель округлять до сотых смысла не имеет. Теперь можно подсчитать нужное произведение и записать ответ: 5,38·0,2=538100·210=1 0761000=1,076.
Ответ: 5,382…·0,2≈1,076.
Как умножать десятичные дроби столбиком
Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:
Определение 1Умножение десятичных дробей столбиком выполняется в 2 шага:
1. Выполняем умножение столбиком, не обращая внимание на запятые.
2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе.
Если в результате не хватает для этого цифр, дописываем слева нули.
Разберем примеры таких расчетов на практике.
Пример 4Умножьте десятичные дроби 63,37 и 0,12 столбиком.
Решение
Первым делом выполним умножение чисел, игнорируя десятичные запятые.
Теперь нам надо поставить запятую на нужное место. Она будет отделять четыре цифры с правой стороны, поскольку сумма десятичных знаков в обоих множителях равна 4. Дописывать нули не придется, т.к. знаков достаточно:
Ответ: 3,37·0,12=7,6044.
Пример 5Подсчитайте, сколько будет 3,2601 умножить на 0,0254.
Решение
Считаем без учета запятых. Получаем следующее число:
Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:
Ответ: 3,2601·0,0254=0,08280654.
Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д
Умножать десятичные дроби на такие числа приходится часто, поэтому важно уметь делать это быстро и точно. Запишем особое правило, которым мы будем пользоваться при таком умножении:
Определение 2Если мы умножим десятичную дробь на 0,1, 0,01 и т.д., в итоге получится число, похожее на исходную дробь, запятая которого перенесена влево на нужное количество знаков. При нехватке цифр для переноса нужно дописывать нули слева.
Так, для умножения 45,34 на 0,1 надо перенести в исходной десятичной дроби запятую на один знак. У нас получится в итоге 4,534.
Пример 6Умножьте 9,4 на 0,0001.
Решение
Нам придется переносить запятую на четыре знака по количеству нулей во втором множителе, но цифр в первом для этого не хватит. Приписываем необходимые нули и получаем, что 9,4·0,0001=0,00094.
Ответ: 0,00094.
Для бесконечных десятичных дробей мы пользуемся тем же правилом.
Так, к примеру, 0,(18)·0,01=0,00(18) или 94,938…·0,1=9,4938…. и др.
Как перемножить десятичную дробь с натуральным числом
Процесс такого умножения ничем не отличается то действия умножения двух десятичных дробей. Удобно пользоваться методом умножения в столбик, если в условии задачи стоит конечная десятичная дробь. При этом надо учитывать все те правила, о которых мы рассказывали в предыдущем пункте.
Подсчитайте, сколько будет 15·2,27.
Решение
Умножим столбиком исходные числа и отделим два знака запятой.
Ответ: 15·2,27=34,05.
Если мы выполняем умножение периодической десятичной дроби на натуральное число, надо сначала поменять десятичную дробь на обыкновенную.
Пример 8Вычислите произведение 0,(42) и 22.
Решение
Приведем периодическую дробь к виду обыкновенной.
Далее умножаем:
0,42·22=1433·22=14·223=283=913
Итоговый результат можем записать в виде периодической десятичной дроби как 9,(3).
Ответ: 0,(42)·22=9,(3).
Бесконечные дроби перед подсчетами надо предварительно округлить.
Пример 9Вычислите, сколько будет 4·2,145….
Решение
Округлим до сотых исходную бесконечную десятичную дробь. После этого мы придем к умножению натурального числа и конечной десятичной дроби:
4·2,145…≈4·2,15=8,60.
Как умножить десятичную дробь на 1000, 100, 10 и др
Умножение десятичной дроби на 10, 100 и др. часто встречается в задачах, поэтому мы разберем этот случай отдельно. Основное правило умножения звучит так:
Определение 3Чтобы умножить десятичную дробь на 1000, 100, 10 и др., нужно перенести ее запятую на 3, 2,1 цифры в зависимости от множителя и отбросить слева лишние нули. Если цифр для переноса запятой недостаточно, дописываем справа столько нулей, сколько нам нужно.
Покажем на примере, как именно это делать.
Пример 10Выполните умножение 100 и 0,0783.
Решение
Для этого нам надо перенести в десятичной дроби запятую на 2 цифры в правую сторону. Мы получим в итоге 007,83Нули, стоящие слева, можно отбросить и записать результат как 7,38.
Ответ: 0,0783·100=7,83.
Пример 11Умножьте 0,02 на 10 тысяч.
Решение: мы будем переносить запятую на четыре цифры вправо. В исходной десятичной дроби нам не хватит для этого знаков, поэтому придется дописывать нули. В этом случае будет достаточно трех 0. В итоге получилось 0,02000,перенесем запятую и получим 00200,0. Игнорируя нули слева, можем записать ответ как 200.
Ответ: 0,02·10 000=200.
Приведенное нами правило будет работать так же и в случае с бесконечными десятичными дробями, но здесь следует быть очень внимательным к периоду итоговой дроби, так как в нем легко допустить ошибку.
Вычислите произведение 5,32(672) на 1 000.
Решение: первым делом мы запишем периодическую дробь как 5,32672672672…, так вероятность ошибиться будет меньше.
После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326,726726… Заключим период в скобки и запишем ответ как 5 326,(726).
Ответ: 5,32(672)·1 000=5 326,(726).
Если в условиях задачи стоят бесконечные непериодические дроби, которые надо умножать на десять, сто, тысячу и др., не забываем округлить их перед умножением.
Как перемножить десятичную дробь с обыкновенной или со смешанным числом
Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.
Пример 13Умножьте 0,4 на 356
Решение
Cначала переведем десятичную дробь в обыкновенную. Имеем: 0,4=410=25.
Далее считаем: 0,4·356=25·236=2315=1815.
Мы получили ответ в виде смешанного числа. Можно записать его как периодическую дробь 1,5(3).
Ответ: 1,5(3).
Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.
Вычислите произведение 3,5678…·23
Решение
Второй множитель мы можем представить как 23=0,6666…. Далее округлим до тысячного разряда оба множителя. После этого нам будет нужно вычислить произведение двух конечных десятичных дробей 3,568 и 0,667. Посчитаем столбиком и получим ответ:
Итоговый результат нужно округлить до тысячных долей, так как именно до этого разряда мы округляли исходные числа. У нас получается, что 2,379856≈2,380.
Ответ: 3,5678…·23≈2,380
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Калькулятор умножения
Создано Maciej Kowalski, кандидатом наук
Отзыв Стивена Вудинга
Последнее обновление: 3 сентября 2022 г.
Содержание:- Как умножать числа?
- Умножение десятичных дробей
- Пример: использование калькулятора умножения
- Часто задаваемые вопросы
Добро пожаловать в Omni калькулятор умножения , где мы изучим одну из четырех основных арифметических операций: умножение .
Короче говоря, мы используем его всякий раз, когда хотим добавить одно и то же число несколько раз. Например, 16 умножить на 7 (записано как 16 * 7 ) — это то же самое, что добавить 16 семь раз или, что то же самое, добавить 7 шестнадцать раз. Удобно, что наш инструмент работает также как калькулятор умножения десятичных дробей . Более того, даже если вам нужно умножить более двух чисел, вы все равно можете найти их произведение с помощью этого калькулятора.
Примечание : Если вы хотите увидеть пошаговые решения умножения больших чисел, воспользуйтесь калькулятором умножения длинных чисел Omni или калькулятором частичных произведений.
Давайте не будем терять ни секунды и посмотрим как умножать числа !
Как умножать числа?
Продукт и умножение — это одно и то же: они получаются в результате умножения чисел (или других объектов, если уж на то пошло).
К счастью, процесс очень прост: он сводится к добавлению значения подходящее количество раз. Например, 24 умножить на 5 означает, что мы прибавляем 24 пять раз, т. е.
24 * 5 = 24 + 24 + 24 + 24 + 24 = 120 .
Аналогично, 12 умножить на 20 переводится как сложение 12 двадцать раз:
12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 1 + 12 + 122 + 12 + 12 + 12 + 12 + 12 + 12 + 12 = 240 .
Однако обратите внимание, что мы всегда можем обратить процесс нахождения произведения с умножением. Другими словами, 24 раза 5 может также означать добавление 5 двадцать четыре раза:
5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 120 ,
и мы можем получить 12 умножить на 20 , прибавив 20 двенадцать раз:
2 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 = 240 .
Мы всегда выбираем, как умножать числа, так как результат будет одинаковым в любом случае . В математических терминах это означает, что произведение или умножение является коммутативной операцией . Обратите внимание, что то же самое верно и для сложения. С другой стороны, оно не выполняется, скажем, для вычитания.
🔎 Знаете ли вы, что существует больше способов записи арифметических операций, чем “классический” оператор в среднем ? Попробуйте их с нашим конвертером польской нотации!
Кроме того, наш калькулятор умножения работает только с числами , но математики придумали, как умножать другие объекты. Ниже мы перечисляем несколько других калькуляторов умножения от Omni.
- Калькулятор умножения матриц;
- Калькулятор умножения дробей; и
- Калькулятор умножения радикалов.
Однако не всегда мы имеем дело с целыми числами , такими как 2 , 18 или 2020 .
Мы научились умножать их и что, скажем, 16 умножить на 7 , но как найти произведение десятичных дробей? Например, сколько будет 0,2 умножить на 1,25 ? Наш калькулятор умножения тоже калькулятор умножения десятичных дробей ?
О, еще бы!
🙋 Хотите научиться обрабатывать сложные математические выражения, включающие более одной арифметической операции? Проверьте наш калькулятор распределительной собственности.
Умножение десятичных дробей
По сути, десятичных дробей — это дроби . Таким образом, один из способов умножения десятичных дробей состоит в том, чтобы преобразовать их в правильные дроби, а затем использовать основное правило : числитель умножить на числитель на знаменатель, умножить на знаменатель 9.0155 . Например,
0,2 * 1,25 = (2/10) * (125/100) = (2 * 125) / (10 * 100) = 250/1000 = 0,25 .
Конечно, мы могли бы также найти более простые дроби, эквивалентные двум данным до умножения.
В этом случае мы могли бы сказать, что 0,2 = 1/5 и 1,25 = 5/4 , поэтому
0,2 * 1,25 = (1/5) * (5/4) = (1 * 5) / (5 * 4) = 5/20 = 1/4 .
Оба ответа верны ; это всегда ваш выбор, как умножать десятичные дроби. Однако, кроме двух упомянутых, есть еще .
При умножении десятичных дробей, скажем, 0,2 и 1,25 , мы можем начать с , забыв о точках . Это означает, что для нахождения 0,2 * 1,25 мы начнем с нахождения 2 * 125 , что равно 250 . Затем подсчитываем, сколько цифр справа от точек у нас было всего в числах, с которых мы начали (в данном случае их три: одна в 0,2 и две в 1,25 ). Затем мы пишем точку, столько цифр справа в том, что мы получили. Для нас это означает поставить точку слева от 2 , что дает 0,250 = 0,25 (мы пишем 0 , если перед точкой нет числа).
В общем, мы видели как умножать десятичные дроби тремя способами . Честно говоря, первые два были почти одинаковыми; просто промежуточные шаги были в другом порядке. Тем не менее, на этом часть о том, как умножать без калькулятора, заканчивается. Теперь опишем подробно, как это сделать с одним, а если быть точным, то с с калькулятором умножения Omni .
Пример: с помощью калькулятора умножения
Найдем 2020 умножить на 12 с помощью калькулятора умножения. В верхней части нашего инструмента мы видим формулу:
результат = а₁ * а₂ .
Это означает, что для расчета 2020 * 12 нам нужно ввести:
a₁ = 2020 и a₂ = 12 .
В тот момент, когда мы даем второе число, калькулятор умножения выдает ответ в поле Результат .
результат = 2020 * 12 = 24240
Однако, скажем, вы хотите умножить результат еще на на 1,3 (помните, что наш инструмент также работает как калькулятор умножения десятичных дробей).
Мы могли бы просто очистить поля и записать ответ сверху в один из множителей, т.е. ввести a₁ = 24240 и a₂ = 1,3 . В качестве альтернативы, мы можем просто выбрать много чисел под Умножить… , что позволяет нам найти произведение умножения для большего количества чисел . Если мы это сделаем, мы получим возможность ввести a₁ , a₂ , a₃ и так далее до a₁₀ (обратите внимание, что изначально только a₁ и a₂4, переменные появляются, как только вы начинаете заполнять поля). Тогда достаточно ввести:
а₁ = 2020 , а₂ = 12 , а₃ = 1,3 ,
и читаем ответ снизу:
результат = 2020 * 12 * 1.3 = 31512 .
Ну, этот калькулятор умножения действительно экономит много времени. Можете ли вы представить, что пишет две тысячи двадцать раз число 12 , как мы это делали в первом разделе? Мы, например, нет.
Часто задаваемые вопросы
Произведение совпадает с умножением?
Умножение — одно из четырех основных арифметических действий (три других — сложение, вычитание и деление).
Произведение является результатом выполнения умножения: когда мы умножаем два числа (множимое и множитель), мы получаем их произведение.
Какие части умножения?
Два числа, которые мы перемножаем, называются множимым и множителем или просто множителями. Результат умножения называется произведением. Например, в задаче на умножение 3 × 5 = 15 число 3 является множимым, 5 — это множитель, 3 и 5 — множители, а 15 — произведение.
Каковы свойства умножения?
Арифметическая операция умножения двух чисел:
- Ассоциативный;
- Распределительный; и
- Коммутативный.
Что такое нейтральный элемент умножения?
Нейтральный элемент (также известный как элемент идентичности) умножения — это число 9.
0023 1 . Это означает, что 1 — это (уникальное) число, такое, что при умножении любого числа на 1 мы получаем то же число, с которого начали.
Как умножить на 100?
Чтобы умножить любое число на 100 , выполните следующие действия:
- Если у вас целое число, напишите два дополнительных нуля в правом конце вашего числа.
- Если в вашем числе есть десятичная точка, вам нужно переместить десятичную точку на два знака вправо. Добавьте один или два нуля в конце, если десятичных цифр меньше двух.
Maciej Kowalski, кандидат PhD
Умножение …
Факторы
РЕЗУЛЬТАТ
Проверьте 61 АРИТМЕТИКА. – Find Prime Factorization/Factors of 500
Коэффициенты 500 — это целые числа, которые при умножении парами дают произведение, равное 500. Всего множители 500 имеют 12 множителей, а также 6 пар положительных и отрицательных множителей.
. На этом уроке мы вычислим множители 500, простые множители 500 и множители 500 попарно. Мы также решим задачи, связанные с множителями 500.
- Коэффициенты 500: 1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250 и 500.
- Факторизация числа 500: 500 = 2 2 × 5 3
| 1. | Какие множители числа 500? |
| 2. | Как рассчитать коэффициенты 500? |
| 3. | Коэффициенты 500 с помощью простой факторизации |
| 4. | Коэффициенты 500 в парах |
| 5. | Важные примечания |
| 6. | Сложные вопросы |
| 7. | Часто задаваемые вопросы о коэффициентах 500 |
Каковы множители 500?
Прежде чем мы узнаем о множителях 500, давайте узнаем о множителях.
Коэффициенты 500 — это числа, которые при умножении дают значение 500. Множители 500 — это числа, которые делят его без остатка. Итак, когда любые два целых числа умножаются друг на друга и получается 500 в качестве ответа, говорят, что оба эти числа являются делителями 500.
Как рассчитать коэффициенты числа 500?
Давайте научимся рассчитывать коэффициенты числа 500.
- Шаг 1: Запишите число, которое нужно разложить на множители. Число, которое нужно разложить, равно 500.
- Шаг 2: Найдите два числа, произведение которых дает 500.
Произведение чисел, которое дает 500, равно 2 и 250, 100 и 5 и так далее. Таким образом, коэффициенты 500 равны 1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250 и 500.
Изучите коэффициенты с помощью иллюстраций и интерактивных примеров
- Множители 25 – Множители 25 равны 1, 5 и 25.
- Множители 125 – множители 125 равны 1, 5, 25 и 125.
- Коэффициенты 250 – множители 250 равны 1, 2, 5, 10, 25, 50, 125 и 250.
- Коэффициенты 54 – множители 54 равны 1, 2, 3, 6, 9, 18, 27, 54
- Коэффициенты 150 – множители 150 – это 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75 и 150
- Факторы 450 – Множители 450 равны 1, 2, 3, 5, 6, 9, 10, 15, 18, 25, 30, 45, 50, 75, 9.0, 150, 225
и 450
Факторизация числа 500 с помощью простой факторизации
Факторизация числа представляет собой выражение числа через произведение его простых делителей. Для этого мы можем использовать метод деления вверх или дерево факторов.
1. Факторизация простых чисел по методу деления вверх продолжается до тех пор, пока частное не станет неделимым.
Поскольку 500 — четное число, оно будет делиться на 2 и на его кратное число.
Разделим 500 на простое число 2
- 500 ÷ 2 = 250
250 опять четно, опять делим на 2
- 250 ÷ 2 = 125
Этот процесс повторяется до тех пор, пока мы не получим частное 1.
Простая факторизация числа 500 показана ниже:
Простая факторизация числа 500 = 2 × 2 × 5 × 5 × 5 = 2 2 × 5 3
2.
Факторизация простых чисел с помощью дерева факторов Другой способ факторизации простых чисел, когда 500 используется в качестве корня, мы создаем ветви, деля его на простые числа. Этот метод аналогичен описанному выше методу деления. Разница заключается в представлении факторизации.
На рисунке ниже показано дерево множителей 500. Составные числа будут иметь ветви, поскольку они делятся дальше. Мы продолжаем делать ответвления, пока у нас не останутся только простые числа.
Числа внутри кружков являются простыми делителями числа 500. Следовательно, простые делители числа 500 равны 2 и 5 .
Коэффициенты 500 в парах
Коэффициенты пар 500 можно задать следующим образом:
- 1 × 500 = 500
- 2 × 250 = 500
- 4 × 125 = 500
- 5 × 100 = 500
- 10 × 50 = 500
- 20 × 25 = 500
Положительные парные множители числа 500: (1, 500), (2, 250), (4, 125), (5, 100), (10, 50), (20, 25).
Возможны и отрицательные парные множители, потому что произведение двух отрицательных чисел дает положительное число. Давайте посмотрим на отрицательные парные множители 500.
- -1 × -500 = 500
- -2 × -250 = 500
- -4 × -125 = 500
- -5 × -100 = 500
- -10 × -50 = 500
- -20 × -25 = 500
Отрицательные парные коэффициенты 500: (-1, -500), (-2, -250), (-4, -125), (-5, -100), (-10, -50), ( -20, -25).
Важные примечания:
- 1 — наименьший делитель каждого числа. Следовательно, 1 является коэффициентом 500.
- 500 не является идеальным квадратным числом. Таким образом, он имеет четное число факторов.
- 500 — четное число; следовательно, 2 является одним из их множителей.
Задающие вопросы:
- У Кристофера есть 2 книги по 500 страниц в каждой. Если ему требуется 1 час, чтобы написать 1 страницу в любой книге, сколько времени потребуется ему, чтобы заполнить 10 таких книг?
- Как Джулия разделит 500 долларов поровну между четырьмя своими друзьями?
Часто задаваемые вопросы о множителях 500
Что такое множители 500?
Коэффициенты 500 равны 1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250 и 500.