| \meta | |
| \title Производные и градиенты | |
| \author Илья Щуров | |
| \affiliation НИУ ВШЭ | |
| \project | |
| Машинное обучение для факультета экономики, 2017-18 учебный год | |
| \url http://wiki.cs.hse.ru/Машинное_обучение_(факультет_экономических_наук) | |
| \lang ru | |
| В машинном обучении часто приходится находить производные и градиенты от | |
функций, заданных в виде каких-то операций над матрицами. n$. Если в | |
| этом пространстве введён базис и в этом базисе $h=(h_1, \ldots, h_n)$, то любой такой | |
| функционал имеет вид $Ah=a_1 h_1+\ldots a_n h_n$. В этом случае $a_k$, | |
| $k=1,\ldots, n$ — это частная производная функции $f$ по $x_k$: | |
| \equation \label eq:differential | |
| Ah = \frac{\partial f}{\partial x_1}(x)h_1+\ldots+\frac{\partial f}{\partial x_n}(x)h_n | |
Эта штука более известна как \emph{дифференциал} функции нескольких переменных. Мы будем обозначать его через $df_{x}$, то есть $df_{x}(h)=Ah$. 1$, $k=1, | |
| \ldots, m$. Тогда матрица отображения $A$ — это матрица частных производных: | |
| \eq | |
| A_{ij}=\frac{\partial f_i}{\partial x_j}(x). | |
| Эта матрица также известна как матрица Якоби. Мы будем обозначать | |
| соответствующее отображение через $D_{x}f$. | |
| \remark | |
| Само понятие производной не требует введения какого-либо базиса и каких-либо | |
координат. 1$. Его | |
| \emph{градиентом} в точке $x$ называется такой вектор $u$, что | |
| \eq | |
| df_{x}(h)=\langle u, h\rangle, | |
| где $df_{x}$ — дифференциал функции $f$ в точке $x$. | |
| Это определение замечательно своей бескоординатностью: оно не требует введения | |
| частных производных, а требует только наличия скалярного произведения. Тем не | |
| менее, если скалярное произведение задаётся стандартным образом ($\langle u, v | |
| \rangle = u_1 v_1 + \ldots + u_n v_n$), то градиент оказывается вектором, | |
составленным из частных производных, как мы и привыкли. | |
| части формулы \ref{eq:differential} написано скалярное произведение вектора | |
| $\frac{\partial f}{\partial x_1}(x), \ldots, \frac{\partial f}{\partial | |
| x_n}(x)$ и вектора $h$. | |
| Мы будем обозначать градиент через $\nabla_{x} f$. | |
| \section Некоторые стандартные производные | |
| Здесь мы используем данные выше определения для вычисления некоторых производных | |
| и градиентов. В дальнейшем мы будем использовать матричную нотацию, вектор $u\in | |
| \mathbb R^n$ будет отождествляться с вектор-столбцом (матрицей с одним столбцом | |
и $n$ строками), транспонирование будет обозначаться верхним индексом $T$. T)x. | |
| \subsection След | |
| Рассмотрим функцию «след» $\newcommand{\Tr}{\mathop{\mathrm{Tr}}}\Tr$ из пространства матриц в числа. Для матрицы $A=(a_{ij})$ след определяется как сумма диагональных элементов: | |
| \eq | |
| \Tr A = a_{11} + \ldots + a_{nn} | |
| След играет важную роль в дальнейшем, поскольку с его помощью можно легко | |
| записать скалярное произведение между матрицами. Действительно, давайте введём в | |
| пространстве матриц базис, состоящий из матриц, у которых на $ij$-ом месте стоит | |
1, а на всех остальных местах — нули. 2}$, записывая, например, | |
| все компоненты матрицы по строкам в качестве компонент этого вектора. Так | |
| матрица | |
| \eq | |
| \begin{pmatrix} a_{11} & a_{12} \\\\ | |
| a_{21} & a_{22} | |
| \end{pmatrix} | |
| превращается в вектор $(a_{11}, a_{12}, a_{21}, a_{22})$. | |
| Если ввести теперь на матрицах скалярное произведение так же, как на векторах, | |
| то оно будет записываться в виде | |
| \equation \label eq:ABTR | |
\langle A, B \rangle = \Tr (A^TB). | |
| Проверка этого факта проводится непосредственым вычислением, которое мы | |
| предлагаем сделать читателю самостоятельно. | |
| \subsection Производная и градиент следа | |
| Найдём теперь производную следа в точке $X$. Аргументом следа является | |
| матрица, поэтому мы получим «производную по матрице» и $X$ тоже является | |
| матрицей. | |
| \eq | |
| \Tr(X+H)=\Tr(X)+\Tr(H). | |
Это равенство следует из определения следа. Таким образом, производная следа | |
| — это тоже след, $D_{X} \Tr(H)=\Tr(H)$. | |
| Чему равен градиент следа? Иными словами, какую матрицу $W$ нужно взять, чтобы | |
| скалярное произведение $H$ с этой матрицей равнялось $\Tr(H)$. Из формулы | |
| \ref{eq:ABTR} видим, что $W=E$, тождественная матрица. | |
| Конечно, аналогичный результат можно было бы получить (вероятно, даже проще) | |
| исходя из координатного определения следа. | |
| \subsection Производная и градиент определителя | |
Рассмотрим отображение $f(A)=\det A$. {-1}H$ через $Y$. Пусть собственные значения $Y$ равны | |
| $\lambda_1, \ldots, \lambda_n$. Поскольку $H$ маленькая, то $Y$ тоже маленькая и | |
| её собственные значения маленькие. Определитель не меняется при заменах базиса, | |
| поэтому перейдём к жорданову базису для $H$. Матрица $E$ при этом переходе не | |
| изменится (она вообще в любом базисе выглядит как тождественная). Получающаяся | |
| при этом матрица верхнетреугольная и на её диагонали стоят числа $1+\lambda_1, | |
| \ldots, 1+\lambda_n$. Определитель верхнетреугольной матрицы равен произведению | |
| чисел на диагонали и значит | |
| \eq | |
| \det (E+Y)=(1+\lambda_1)\cdot(1+\lambda_n)=1+(\lambda_1 + \ldots + | |
| \lambda_n)+o(\|Y\|) | |
| Здесь мы воспользовались тем, что собственные значения маленкие и их | |
произведения имеют ещё больший порядок малости. T$. |
Новые дикатионные производные хлорина е6
1. Mironov A.F. The Current State of Chemistry of Porphyrin-Based Photosensitizers and Related Compounds. In: Advances in Porphyrin Chemistry, Vol. 4. St.-Petersburg, 2004. pp. 271–292 (in Russ.)
2. Reshetnikov A.V., Shvets V.I., Ponomarev G.V. Water-Soluble Tetrapyrrole Photosensitizers for Photodynamic Therapy of Cancer. In: Advances in Porphyrin Chemistry, Vol. 2. St.-Petersburg, 1999. pp. 70–114 (in Russ.)
3. Feofanov A., Sharonov G., Grichine A., Refregier M., Maurizot J.-C., Vigny P., Karmakova T., Pljutinskaya A., Yakubovskaya R., Lebedeva V., Ruziyev R., Mironov A. Photochem. Photobiol. 2004, 79, 172–188.
http://dx.doi.org/10.1562/0031-8655(2004)079<0172:CSOPPO>2.0.CO;2
4. Zamilatskov I.A., Savinkina E.V., Volov A.N., Grigoriev M.S., Lonin I.S., Obolenskaya L.N., Ponomarev G.V., Koifman O.I., Kuzovlev A.S., Kuzmicheva G.M., Tsivadze A.Yu.
Macroheterocycles 2012, 5, 308–314.
http://dx.doi.org/10.6060/mhc2012.121100z
5. Nyman E.S., Hynninen P.H. J. Photochem. Photobiol. B: Biol. 2004, 73, 1–28.
http://dx.doi.org/10.1016/j.jphotobiol.2003.10.002
6. Rubin A.B. Nanobiotechnologies, Moscow: Binom, 2011. 384 p. (in Russ.)
7. Likhacheva E.V., Alekseev Yu.V., Mazur E.M., Ponomarev G.V. Lazernaya Meditsina 2011, 15(2), 66–67 (in Russ.).
8. Likhacheva P.D., Likhacheva E.V., Ponomarev G.V. Ross. Bioterapevt. Zh. 2013, 12(2), 54 (in Russ.).
9. Takhchidi Kh.P., Beliy Yu.A., Tereshchenko A.V., et al. Oftalmokhirurgiya 2005, N. 1, 45–51 (in Russ.).
10. Fedorov S.N., Kopaeva V.G., Andreev Yu.V., Ponomarev G.V., Ronkina T.I. Oftalmokhirurgiya 1996, N. 1, 17–23 (in Russ.).
11. Lyapina E.A., Larkina E.A., Tkachevskaya E.P., Mironov A.F., Machneva T.V., Osipov A.N. Biophysics 2010, 55, 296–300.
http://dx.doi.org/10.
1134/S0006350910020223
12. Strakhovskaya M.G., Zhukhovitskiy V.G., Mironov A.F. Dokl. Akad. Nauk 2002, 384, 155–158 (in Russ.).
13. Konan Y.N., Gurny R., Allemann E. J. Photochem. Photobiol. B: Biol. 2002, 66, 89–106.
http://dx.doi.org/10.1016/S1011-1344(01)00267-6
14. Nazarova A.I., Feofanov A.V., Sharonov G.V., Karmakova T.A., Plyutinskaya A.D., Yakubovskaya R.I., Lebedeva V.S., Mironov A.F., Maurizot J.-C., Vigny P. Russ. J. Bioorg. Chem. 2005, 31, 482–494.
http://dx.doi.org/10.1007/s11171-005-0066-9
15. Nechaev A.V., Mironov A.F. Russ. J. Bioorg. Chem. 2008, 34, 245–251.
http://dx.doi.org/10.1134/S1068162008020167
16. Zenkevich E., Sagun E., Knyukshto V., Shulga A., Mironov A., Efremova O., Bonnett R., Phinda Songca S., Kassem M. J. Photochem. Pholobiol. B: Biol. 1996, 33, 171–180.
http://dx.doi.org/10.1016/1011-1344(95)07241-1
17. Fomichev Yu.A., Zorin V.P., Zorina T.
E., Cherenkevich S.N. Mikrobiologiya 1991, 60, 507–511 (in Russ.).
18. Pashkovskaya A.A., Sokolenko E.A., Sokolov V.S., Kotova E.A., Antonenko Y.N. Biochimica et Biophysica Acta 2007, 1768, 2459–2465.
http://dx.doi.org/10.1016/j.bbamem.2007.05.018
19. Zhilina Z.I., Vozdinskiy S.V., Ishkov Yu.V. In: Advances in Porphyrin Chemistry, Vol. 3, St.-Petersburg, 2001. pp. 7–21 (in Russ.).
20. Novikov N.V., Starkov V.V., Formirovskiy K.A., Bragina N.A., Ushakova I.P., Mironov A.F. Vestnik MITHT 2009, 4(4), 26–30 (in Russ.).
21. Batinic-Haberle I., Spasojevic I., Stevens R.D., Hambright P., Fridovich I. J. Chem. Soc. Dalton Trans 2002, 2689–2696.
http://dx.doi.org/10.1039/b201057g
22. Kos I., Benov L., Spasojevic I., Reboucas J.S., Batinic-Haberle I. J. Med. Chem. 2009, 52, 7868–7872.
http://dx.doi.org/10.1021/jm900576g
23. Ko Y.-J., Yun K.-J., Kang M.-S., Park J., Lee K.-T., Park S.B., Shin J.
-H. Bioorg. Med. Chem. Lett. 2007, 17, 2789–2794.
http://dx.doi.org/10.1016/j.bmcl.2007.02.083
24. Evstigneeva R.P. In: Advances in Porphyrin Chemistry, Vol. 3, St.-Petersburg, 2001. pp. 150–159 (in Russ.).
25. Olshevskaya V.A., Korotkova N.S., Makarenkov A.V., Luzgina V.N., Kalinin V.N. Vestnik Nizhegorodskogo Universiteta im. Lobachevskogo 2013, N.1, 118–123 (in Russ.).
26. Mironov A.F., Grin M.A., Tsiprovskiy A.G. J. Porphyrins Phthalocyanines 2003, 7, 725–730.
http://dx.doi.org/10.1142/S1088424603000902
27. Mironov A.F., Grin M.A., Tsiprovskiy A.G., Titeev R., Nizhnik E., Lonin I. Mendeleev Commun. 2004, 5, 204–207.
http://dx.doi.org/10.1070/MC2004v014n05ABEH001941
28. Pandey R.K., Shiau F.U., Smith N.N., Dougherty D.J., Smith K.M. Tetrahedron 1992, 48, 7591–7600.
http://dx.doi.org/10.1016/S0040-4020(01)90371-0
29. Gushchina O.I., Larkina E.A., Mironov A.F. Macroheterocycles 2014, 7, 414–416.
http://dx.doi.org/10.6060/mhc140931g
30. Belykh D.V., Tarabukina I.S., Gruzdev I.V., Kodess M.I., Kutchin A.V. J. Porphyrins Phthalocyanines 2009, 13, 949–956.
http://dx.doi.org/10.1142/S1088424609001133
31. Belykh D.V., Karmanova L.P., Spirikhin L.V., Kutchin A.V. Russ. J. Org. Chem. 2007, 43, 126–134.
http://dx.doi.org/10.1134/S1070428007010174
32. Belykh D.V., Kopylov E.A., Gruzdev I.V., Kutchin A.V. Russ. J. Org. Chem. 2010, 46, 577–585.
http://dx.doi.org/10.1134/S1070428010040238
33. Belykh D.V., Startseva O.M., Patov S.A. Macroheterocycles 2014, 7, 401–413.
http://dx.doi.org/10.6060/mhc140500b
34. Belykh D.V., Tarabukina I.S., Gruzdev I.V., Kuchin A.V. Macroheterocycles 2010, 3, 145–149.
http://dx.doi.org/10.6060/mhc2010.2-3.145
35. Belykh D.V., Karmanova L.P., Spirikhin L.V., Kutchin A.V. Mendeleev Commun. 2002, 12, 77–78.
http://dx.doi.org/10.
1070/MC2002v012n02ABEH001536
Производные – AP Calculus AB
Все ресурсы AP Calculus AB
3 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 … 72 73 Следующая →
AP Calculus AB Помощь » Производные
Дифференцировать,
Возможные ответы:
Правильный ответ:
Объяснение:
Дифференцировать,
Стратегия
На первый взгляд это кажется сложным, даже если мы признаем, что цепное правило необходимо; у нас есть функция внутри функции внутри функции внутри функции. Чтобы избежать ошибок, лучше всего начать с определения переменных, чтобы упростить вычисления.
Начнем с самой внешней функции, которую мы напишем как функцию от настройки,
______________________________________________________
_______________________________________________________
Similarly, define to write as a function of
_______________________________________________________
Write as a function of
_______________________________________________________
Finally, определите самую внутреннюю функцию, , как функцию
________________________________________________________
Так как мы просто подставим это и перейдем вперед.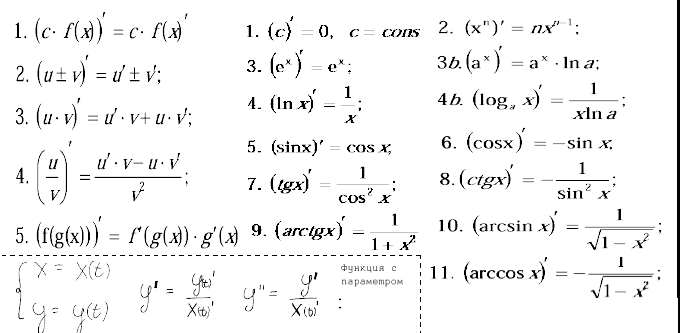
Это было достаточно просто, теперь просто запишите все в терминах , вернувшись к определениям и .
Сообщить об ошибке
Найти касательную. Учитывая точку (1,2)
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти касательную в заданной точке, нужно сначала взять производную от заданной функции.
Степенное правило:
Степенное правило говорит, что мы берем показатель степени значения «x» и выносим его вперед. Затем мы вычитаем единицу из показателя степени.
Следовательно, становится
Отсюда мы подставляем “1” из точки, чтобы получить значение m уравнения. Когда мы подставляем «1» к y’, мы получаем m=-1. Затем оттуда мы подключим нашу точку теперь, когда мы нашли m, чтобы найти наше значение b.
Итак,
Therefore, the tangent line is equal to
Report an Error
Find the line tangent at the point (0,1)
Possible Answers:
Correct answer:
Объяснение:
Чтобы найти касательную в заданной точке, нужно сначала взять производную от заданной функции. Правило для функций с буквой “е” говорит, что это производная от Однако с этой функцией также есть 3 в показателе степени, поэтому мы также будем использовать цепное правило. Цепные правила гласят, что мы работаем снаружи внутрь. Это означает, что мы возьмем производную внешней части уравнения и умножим ее на производную внутренней части уравнения.
Чтобы поместить это в уравнение, оно будет выглядеть как
Отсюда мы подставим “0” из точки, чтобы получить значение m уравнения.
Когда мы подставляем «0» к y’, мы получаем m=3. Затем оттуда мы подключим нашу точку к теперь, когда мы нашли m, чтобы найти наше значение m. Итак,
, затем снова подставьте все это в уравнение, и у нас останется
Сообщить об ошибке
Найдите касательную по точке (2,4) и уравнению
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти касательную в заданной точке, нам нужно сначала взять производную данной функции, используя правило мощности
Правило мощности говорит, что мы берем показатель степени значения «x» и выносим его вперед . Затем мы вычитаем единицу из показателя степени.
Оттуда мы подставляем «2» от точки, чтобы получить значение m уравнения. Когда мы подставляем «2» к y’, мы получаем m=8. Затем оттуда мы подключим нашу точку теперь, когда мы нашли m, чтобы найти наше значение b.
Подключите это обратно в
Отчет о ошибке
Найдите уравнение линии, касающейся кривой в точке, где
Ответы:
:
:
:
9000
9000
Правильный ответ:Объяснение:
Найти уравнение касательной к кривой в данной точке
Наклон касательной в данной точке будет равен производной от в этой точке. Вычислите производную и найдите наклон для нашей линии:
Оцените секундный термин:
Поэтому наклон таховой линии просто:
наклон касательной и может написать уравнение, а затем решить его для
Чтобы найти , нам нужна одна точка на прямой. Используйте точку, где касательная пересекает кривую. Используйте исходную функцию, чтобы найти координату «y» на этой точке:
Теперь мы имеем нашу точку:
Используйте точку, чтобы найти
Сообщить об ошибке
Найдите наклон линии, касательной к кривой d(g), когда g=6.
Правильный ответ:
Пояснение:
Найдите наклон линии, касательной к кривой d(g), когда g=6.
Все, что нам нужно здесь, это силовое правило. В нем говорится, что для нахождения производной многочлена просто вычтите 1 из каждого показателя степени, а затем умножьте каждый член на их исходный показатель степени.
Постоянные члены исчезнут, когда мы это сделаем, а линейные члены станут постоянными.
Отсюда подставьте g=6.
Сообщить об ошибке
Приведите уравнение касательной к графику уравнения
в точке.
Возможные ответы:
Правильный ответ:
Объяснение:
Касательная к графику в точке – это линия с наклоном , проходящая через эту точку. Найдите производную :
Применить правило суммы:
Следовательно, линия тангенса-это линия с наклоном с 5 до.
Сообщить об ошибке
Приведите уравнение касательной к графику уравнения
в точке .
Возможные ответы:
Ни один из других вариантов не дает правильного ответа.
Правильный ответ:
Ни один из других вариантов не дает правильного ответа.
Объяснение:
Касательная к графику в точке – это линия с наклоном , проходящая через эту точку. Найдите производную :
Примените постоянное кратное и правила сумм:
Установите и примените цепное правило.
Заменить обратно:
Оценка с использованием замены:
. Следовательно, линейка тангенса является линейной линией со Slope. является -перехватом, поэтому примените формулу наклона-перехвата, чтобы получить уравнение
.
Этого нет среди предложенных вариантов.
Сообщить об ошибке
Найти уравнение прямой, параллельной функции at и проходящей через точку
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала мы начнем с нахождения наклона рассматриваемой линии, что мы делаем, взяв производную и оценив ее в .
,
Затем мы используем форму наклона точки, чтобы получить уравнение линии в точке
Сообщить об ошибке
Найдите уравнение прямой, касательной к в точке .
Возможные ответы:
Правильный ответ:
Объяснение:
Первый шаг — найти производную заданной функции, которая равна . Затем найдите наклон в (1,4), подставив x=1 и найдя , который является наклоном. Вы должны получить . Это означает, что наклон новой линии также равен -1, потому что в точке, где наклон и линия касаются, они имеют одинаковый наклон. Используйте уравнение, чтобы выразить свою линию. Y и x — переменные, а m — наклон, поэтому вам нужно найти только b. Подставьте точку и наклонитесь, чтобы получить . Теперь вы можете выразить общее уравнение линии как .
Сообщить об ошибке
← Назад 1 2 3 4 5 6 7 8 9 … 72 73 Далее →
Уведомление об авторских правах
Все ресурсы AP Calculus AB
3 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
Концепция производной — AP Calculus AB
Все ресурсы AP Calculus AB
3 Диагностические тесты 164 практических теста Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 4 5 6 7 8 9 Следующая →
AP Исчисление AB Справка » Производные » Понятие производной
Функция дифференцируема в точке . Перечислите, какие из следующих утверждений должны быть истинными относительно :
1) Ограничение существует.
_________________________________________________________
2)
________________________________________________________________
3)
_________________________________________________________
4)
_________________________________________________________
5)
Possible Answers:
1, 3, and 5
1,3 ,4 и 5
1 и 5
Все должно быть верно.
1, 2 и 4
Правильный ответ:
1, 2 и 4
Объяснение:
1) Если функция дифференцируема, то по определению дифференцируемости существует предел, определяемый выражением
. Поэтому (1) требуется по определению дифференцируемости. _______________________________________________________________
2) Если функция дифференцируема в какой-то точке, то она должна быть и непрерывной в этой точке. (Это неверно, наоборот).
Чтобы функция была непрерывной в точке, мы должны иметь:
Следовательно, (2) и (4) необходимы.
————————————————————– ———————————————————
3)
Это не требуется, левая часть уравнения является определением производной в точке для функции . Производная в точке не обязательно должна равняться значению функции в этой точке, она равна уклон в этой точке. Поэтому 3 не обязательно должно быть правдой.
Однако мы можем отметить, что функция и ее производная могут быть равны для данной точки. Синус и косинус, например, будут периодически пересекаться. Другим примером может служить экспоненциальная функция, которая имеет себя в качестве производной.
______________________________________________________________
4) См. 2
____________________________________________________________
5)
Опять же, функция не должна приближаться к тому же пределу, что и ее производная. Функция может вести себя таким образом, например, в случае синуса и его производного косинуса, которые будут иметь одинаковый предел в точках пересечения.
Сообщить об ошибке
Когда предел не существует,
Возможные ответы:
Ничего из вышеперечисленного обязательно
Функция не дифференцируема в .
Функция не определена в .
Функция не является непрерывной в .
Правильный ответ:
Функция не дифференцируема в .
Объяснение:
По определению дифференцируемости, когда существует предел. Когда существует, мы говорим, что функция “дифференцируема в “.
Сообщить об ошибке
Какая из следующих функций дифференцируема в , но не непрерывна в ней?
Возможные ответы:
Все они дифференцируемы и непрерывны на
Правильный ответ:
Они все дифференцируемы и непрерывны на
. Объяснение:
Все функции дифференцируемы в . Если вы посмотрите на график каждой из функций, то увидите, что все они определены в точке и не имеют там угла, излома или скачка; все они гладкие и связные (не обязательно везде, только в ). Кроме того, невозможно иметь функцию, дифференцируемую в точке, но не непрерывную в этой же точке; дифференцируемость влечет непрерывность.
Сообщить об ошибке
Для какой из следующих функций существует предел в , но не значение y?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы ответить на вопрос, мы должны найти уравнение, удовлетворяющее двум критериям:
(1) оно должно иметь пределы по обе стороны от , приближающиеся к одному и тому же значению и (2) оно должно иметь дырку в точке .
Каждый из возможных ответов дает ситуации, демонстрирующие каждую комбинацию (1) и (2). Другими словами, некоторые уравнения включают и как предел и значение y в точке, ни то, ни другое, или, в случае кусочной функции, значение y и несуществующий предел.
В функции числитель умножает на
, а знаменатель умножает на . В результате график этой функции
похож на график для , но с дырой в точке . Поэтому предел
в существует, хотя значение y не определено в .
Сообщить об ошибке
Что является производным от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту проблему, мы можем использовать правило мощности. Это означает, что мы уменьшаем показатель степени переменной на единицу и умножаем переменную на исходный показатель степени.
Помните, что все в нулевой степени равно единице.
Сообщить об ошибке
Что является производным от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту проблему, мы можем использовать правило мощности. Это означает, что мы уменьшаем показатель степени переменной на единицу и умножаем переменную на исходный показатель степени.
Мы будем рассматривать как , так как все в нулевой степени равно единице.
Это означает, что эта задача будет выглядеть следующим образом:
Обратите внимание, что любое произведение на ноль равно нулю.
Помните, что все в нулевой степени равно единице.
Сообщить об ошибке
Что является производным от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы получить , мы можем использовать правило мощности.
Поскольку показатель степени равен as, мы уменьшаем показатель степени на единицу, а затем умножаем коэффициент на исходный показатель степени:
Все, что в степени равно.
Сообщить об ошибке Объяснение:
Чтобы решить это уравнение, мы можем использовать правило степени. Чтобы использовать правило степени, мы уменьшаем показатель степени переменной и умножаем на этот показатель.
Мы будем рассматривать как , так как все в нулевой степени равно единице.
Обратите внимание, что, поскольку любое произведение, умноженное на ноль, равно нулю.
Сообщить об ошибке
Что является производным от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить это уравнение, мы можем использовать правило степени. Чтобы использовать правило степени, мы уменьшаем показатель степени переменной и умножаем на этот показатель.
Мы будем рассматривать как , так как все в нулевой степени равно единице.
Обратите внимание, что, поскольку любое произведение, умноженное на ноль, равно нулю.
Остается .
Упрощение.
Как было сказано ранее, все, что в нулевой степени равно единице, остается:
Сообщить об ошибке
Что такое производная от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить это уравнение, мы можем использовать правило степени. Чтобы использовать правило степени, мы уменьшаем показатель степени переменной и умножаем на этот показатель.
Мы будем считать, что все в нулевой степени равно единице.
Обратите внимание, что, поскольку любое произведение, умноженное на ноль, равно нулю.
Как уже упоминалось ранее, все в нулевой степени равно единице.