Что такое центростремительное ускорение? Формула
2 мин. на чтение
Может ли тело ускоряться, если оно движется с постоянной скоростью? Ага! Многие люди сначала находят это нелогичным, потому что забывают, что изменение направления движения объекта — даже если объект сохраняет постоянную скорость — по-прежнему считается ускорением.
Ускорение — это изменение скорости либо по величине , т. е. по скорости, либо по направлению , либо по тому и другому . При равномерном круговом движении направление скорости постоянно меняется, поэтому всегда есть соответствующее ускорение, даже если скорость может быть постоянной. Вы сами испытываете это ускорение, когда поворачиваете в своей машине — если вы держите руль неподвижно во время поворота и двигаетесь с постоянной скоростью, вы находитесь в равномерном круговом движении.
На следующей диаграмме показано тело, движущееся по круговой траектории с постоянной скоростью.
Здесь направление центростремительного ускорения направлено к центру кривизны. Кроме того, вы должны отметить, что треугольники, созданные радиусами r, Δs и векторами скорости, одинаковы. Кроме того, треугольники PQR и ABC имеют две одинаковые стороны, что означает, что они равнобедренные треугольники. Более того, эти две одинаковые стороны треугольников вектора скорости являются скоростями v1 = v2 = v. Тогда, используя признаки двух равных треугольников, находится:
- Δv/v = Δs/r
Ускорение равно Δv / Δt, а решение для Δv:
- Δv = ( v / r )Δs
Далее, разделив на Δt,
- Δv / Δt = v / r × Δs / Δt
Итак, наконец, обратите внимание, что
Δv / Δt = a c , а Δs / Δt = v, тангенциальная или линейная скорость, величина центростремительного ускорения a c = v 2 / r
Итак, с помощью этого уравнения вы можете определить, что центростремительное ускорение более значимо на высоких скоростях и на кривых меньшего радиуса.
Примечание: единицей СИ для центростремительного ускорения является м/с2 .
Решенные числа
1. Камень, привязанный к веревке, движется с фиксированной скоростью 10,0 м/с по окружности радиусом 8,0 м. Оцените примерную величину центростремительного ускорения породы.
Решение. По формуле a c = v 2 / r
Следовательно, а с = (10) 2 / 8
а с = 12,5 м/с 2
2. В случае набора игровых автоматов его максимальное центростремительное ускорение без выброса с гусеницы составляет 3,8 метра в секунду в квадрате. Замечено, что эти игровые автоматы слетают с трассы, когда их скорость превышает 1,1 метра в секунду. Каков радиус кривой на треке? Ответ в метрах.
Решение. Максимально возможное центростремительное ускорение равно а = 3,8 м/с 2 , а максимальная скорость, которую могут развивать эти игровые автомобили, не слетая с пути, составляет 1,1 м/с.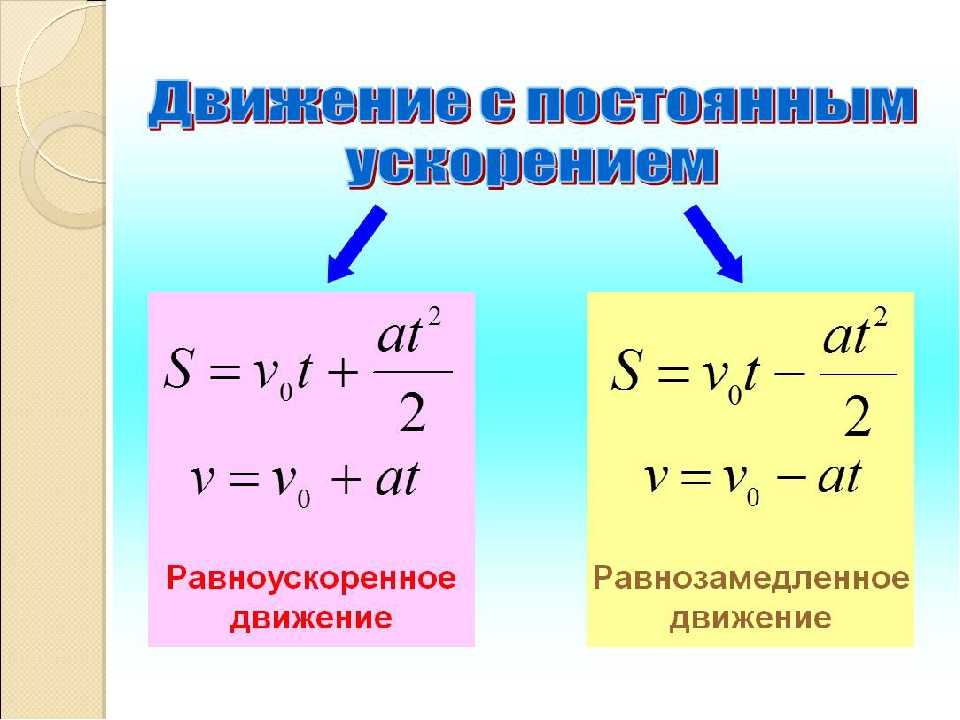
Применяя эту формулу центростремительного ускорения, получаем ответ:
а с = v 2 / г
Следовательно, r = v
= (1,1 м/с) 2 / 3,8 м/с 2
= 0,32 м
Криволинейное движение
Физика / ФИЗИКА / shpory / физика / Физика / Физика(Глеба) / архив лекций(1 семестр) / Глава-1-2
Понятие
скорости и ускорения естественным
образом обобщаются на случай движения
материальной точки по криволинейной
траектории. Положение движущейся точки на траектории
мы будем задавать радиус-вектором r
Положение движущейся точки на траектории
мы будем задавать радиус-вектором r
риальная точка находится в положении М с радиус-вектором r = r(t). Спустя короткое время t , она переместится в положение М1 с радиусом – вектором r1 = r(t + t). Радиус – вектор материальной точки получит приращение, определяемое геометрической разностью |
(1. 11)
11)
называется средней скоростью движения за время t или, точнее, за время между t и t + t . Она является величиной векторной, так как получается делением вектора r
Предел средней скорости при t 0, т.е. производная радиуса – вектора r по времени
(1.12)
называется истинной или мгновенной скоростью материальной точки. Истинная скорость есть вектор, направленный по касательной к траектории движущейся точки.
Совершенно аналогично определяется ускорение при криволинейном движении. Ускорением а называется вектор, равный первой производной вектора скорости
(1. 13)
13)
(1.14)
Отметим следующую формальную аналогию между скоростью и ускорением. Из произвольной неподвижной точки О1 будем откладывать вектор скорости V движущейся точки во всевозможные моменты времени (рис.1.6.).
Конец вектора V называется скоростной точкой. Геометрическое место скоростных точек есть кривая, называемая годографом скорости. Когда материальная точка описывает траекторию, соответствующая ей скоростная точка движется по годографу. |
Рис.
1.5. отличается от рис.1.6.
только обозначениями. Радиус – вектор r заменен на вектор
скорости V,
материальная точка – на скоростную
точку, траектория – на годограф. Математические операции над вектором
Математические операции над вектором
Скорость V направлена по касательной траектории. Поэтому ускорение a будет направлено по касательной к годографу скорости. Можно сказать, что ускорение есть скорость движения скоростной точки по годографу. Следовательно, все соотношения и теоремы, полученные для скорости, остаются справедливыми и для ускорения, если в них произвести замену величин и терменов согласно следующей таблице:
Материальная точка
Радиус – вектор
Траектория
Скорость
Скоростная точка
Вектор скорости
Годограф
Ускорение
В качестве простейшего примера
найдем ускорения точки, равномерно
вращающейся по окружности
радиуса r (Рис. 1.7.а).
Скорость V направлена по касательной к окружности,
ее величина определяется выражением
1.7.а).
Скорость V направлена по касательной к окружности,
ее величина определяется выражением
. (1.15)
Годоргафом будет окружность радиуса V (Рис.1.7.б). Когда материальная точка М вращается по окружности радиуса r, соответствующая ей скоростная точка А вращается в том же направлении по окружности радиуса V, описывая эту окружность за то же время Т. Положениям материальной точки на траектории М1, М2, М3, М4 соответствуют на годографе положения скоростной точки А1, А2, А3, А4 . Ускорение а направлено по касательной к окружности – годографу и притом, как видно из рисунка, к центру О траектории вращающейся точки М. По аналогии с формулой (1.15) для величины ускорения можно написать
. (1.16)
(1.16)
Это – известная формула для центростремительного ускорения. Ее можно записать в векторной форме
. (1.17)
Знак минус указывает на то, что направления векторов а и r взаимно противоположны, т.е. ускорение а направлено к центру круговой траектории, по которой вращается материальная точка. Можно также написать для любого положения движущейся точки
, (1.18)
где n – единичный вектор нормали к круговой траектории движущейся точки, направленный к центру О (см. рис.1.7а).
Имея в виду дальнейшие обобщения,
представим вектор скорости в виде V = V , где единичный
вектор касательной к окружности. Первый
множитель V дает численную величину скорости,
второй множитель указывает ее направление. При равномерном
вращении абсолютное значение скорости V остается неизменным,
меняется только направление скорости,
т.е. единичный вектор . Дифференцированию подлежит только
этот вектор, а потому
.
Сравнивая это выражение с (1.18) получим
Первый
множитель V дает численную величину скорости,
второй множитель указывает ее направление. При равномерном
вращении абсолютное значение скорости V остается неизменным,
меняется только направление скорости,
т.е. единичный вектор . Дифференцированию подлежит только
этот вектор, а потому
.
Сравнивая это выражение с (1.18) получим
. (1.19)
Формула (1.19) допускает обобщение на
случай произвольной гладкой кривой.
Здесь необходимо определить два новых
понятия: величина 1/r и единичный вектор n.
Величина 1/r называется кривизной
кривой, r – радиусом кривизны, а n – единичным вектором главной
нормали к кривой. При этом кривизна
1/r считается существенно положительной.
А потому единичный вектор n всегда направлен сторону вогнутости
кривой. Оправданием такой терминологии
служит интуитивное представление, что
при рассмотрении кривизны малый элемент
кривой приближенно можно рассматривать
как дугу окружности. Это приближение
тем точнее, чем меньше длина дуги S . В случае окружности кривизна 1/r постоянна на протяжении
всей кривой. В общем случае произвольно
гладкой кривой кривизна непрерывно
меняется от точки к точке.
Это приближение
тем точнее, чем меньше длина дуги S . В случае окружности кривизна 1/r постоянна на протяжении
всей кривой. В общем случае произвольно
гладкой кривой кривизна непрерывно
меняется от точки к точке.
Рассмотрим общий случай движения материальной точки по криво – линейной траектории. Для этого представим вектор скорости в виде V = V . Применяя к этому выражению правило дифференцирования произведения, получим
, (1.20)
или ввиду формулы (1.19)
. (1.21)
Отсюда следует, что вектор ускорения а лежит в плоскости векторов и n. В общем случае ускорение а направлено под углом к траектории. Первое слагаемое в формуле (1.21)
(1.22)
есть
вектор, направленный по касательной к
траектории. Этот вектор называется касательным или тангенциальным
ускорением.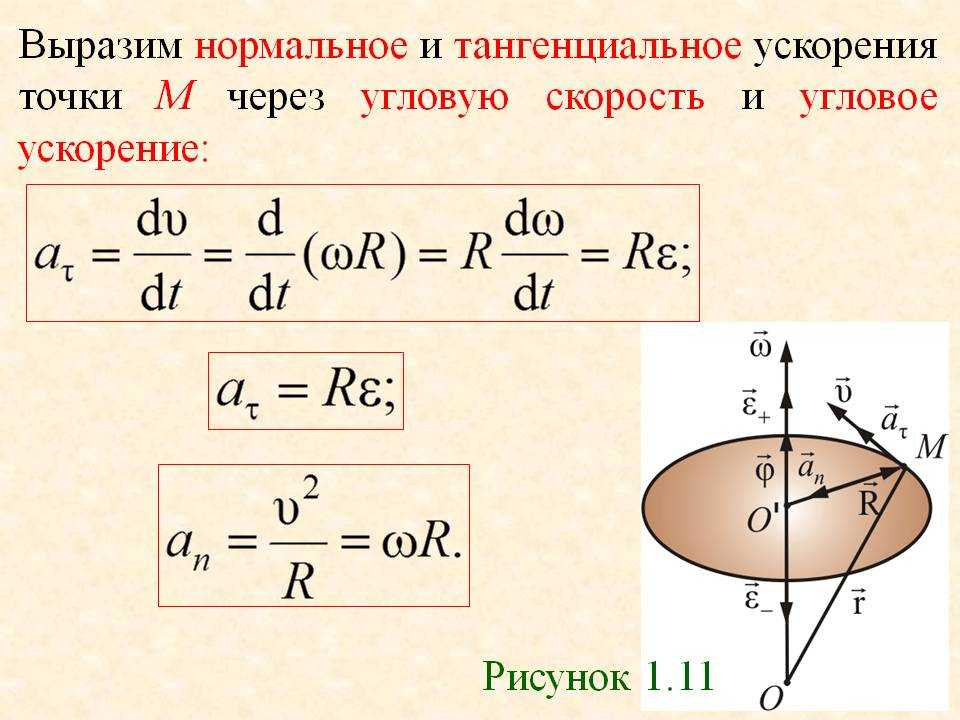 Второе слагаемое
Второе слагаемое
(1.23)
есть вектор, направленный вдоль главной нормали в сторону вогнутости траектории. Он называется нормальным ускорением. Таким образом, в общем случае ускорение а можно представить в виде геометрической суммы тангенциального и нормального ускорения:
. (1.24)
Тангенциальное ускорение меняет скорость только по величине, нормальное ускорение меняет ее только по направлению.
Модуль полного ускорения точки
. (1.25)
Направления полного ускорения и его составляющих ( а , аn ) для случая ускоренного движения приведены на рис. 1.8. При замедленном движении вектор а имеет противоположное направление. |
Поступательное движение. Это такое движение тела, при котором любая прямая, связанная с телом, все время остается параллельной своему начальному положению. Например, вагон, движущийся по прямому участку пути; кабина колеса обозрения и др.
При поступательном движении все точки тела совершают за один и тот же промежуток времени равные перемещения. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Это обстоятельство позволяет свести изучение поступательного движения тела к изучению движения отдельной точки тела, т.е. к задаче кинематики точки.
Таким образом, поступательное движение тела может быть полностью описано, если известны зависимость от времени радиуса – вектора r (t) любой точки этого тела и положение последнего в начальный момент.
Контрольные вопросы
Может ли криволинейное движение быть равномерным?
Чему равно скалярное произведение скорости и ускорения в случае равномерного движения по окружности?
Что характерно для скоростей и ускорений точек тела, движущегося поступательно?
В каких случаях модуль перемещения точки равен длине пути, пройденного точкой за тот же промежуток времени?
Как движется точка, если скорость этой точки все время ортогональна ее ускорению?
Какова траектория плоского движения точки, если ее радиальная скорость равна нулю?
Задачи
Можно ли утверждать, что точка движется без ускорения в случаях:
=const; б) =const?
Является ли движение точки обязательно прямолинейным в случаях:
=const; б) a=const?
Какой знак связывает выражения и при произвольном движении точки? 1)>; 2); 3)<; 4); 5)=.

Какие из перечисленных выражений совпадают в случае свободного падения тела; a) ; б) ; в) г) ; д) , где единичный вектор, касательный к траектории и направленный по движению?
1) а и д, б, в, г; 2) а и д, в и г; 3) б и в; 4) а и д, б и г; 5) нет таких.
Точка движется равномерно по окружности. Начало ее радиус-вектора r совпадает с центром окружности. Отличны ли от нуля выражения и ?
При каком движении материальной точки выполняются соотношения a=0, an= const 0: а) при равномерном движении по окружности; б) при равномерном движении по винтовой линии; в) при равномерном прямолинейном движении; г) при равнопеременном движении по окружности?
1)а, б, в; 2) а, б; 3) г; 4) а; 5) а, б, г.
Применима ли для вычисления тангенциального ускорения формула a=/t в случаях: а) =2t+6; б) =3t2; в) =5t ( – в м/с; t – в с)?
Математический маятник совершает гармонические колебания.
 Отличны ли от нуля в крайней
точке траектории маятника: а) нормальное
ускорение; б) тангенциальное ускорение?
Отличны ли от нуля в крайней
точке траектории маятника: а) нормальное
ускорение; б) тангенциальное ускорение?Тело бросили вертикально с некоторой высоты: а) вверх; б) вниз. Начальные скорости в обоих случаях одинаковы. Сравнить скорости в момент падения тела на землю. Сопротивлением воздуха пренебречь.
Какой график скорости соответствует графику пути на рисунке?
Применима ли для вычисления углового ускорения формула =/t в случаях: а) =2t+8; б) =9t2; в) =6 ( – в рад/с, t – в с)?
Движение тела с неподвижной осью задано уравнением =2(6t-3t2) ( – в рад, t – в с). Начало движения при t=0. Сколько оборотов сделает тело до момента изменения направления вращения?
14. |
1 5. У подножия горы санкам сообщена некоторая скорость, в результате чего санки въезжают на гору и, достигнув точки А начинают скользить обратно. Как направлены нормальное и тангенциальное ускорения в точке А.
16.Тело скользит без трения по вогнутой поверхности. Как в наинизшей точке направлены нормальное и тангенциальное ускорения.
16
кинематика – Скорость из уравнения ускорения
$\begingroup$
Я работал с акселерометром, и мне поручили найти скорость по акселерометру, я беру данные об ускорении каждые 10 мс (частота дискретизации 100 кГц) и использую уравнение: Vf = V0 + a* t, где t равно 10 мс
V0 сначала равно 0, а затем принимает старое значение Vf
Я пробовал перемещать акселерометр в направлении Y+, а затем Y-, используя только ось y.
И это работает нормально, см. рисунок ниже:
но недавно я увидел, что это уравнение предназначено для использования в приложении с постоянным ускорением, почему оно работает для меня? Или я ошибаюсь здесь?
- кинематика
- ускорение
- скорость
- обработка сигналов
$\endgroup$
$\begingroup$
Давайте посмотрим, откуда появилось это уравнение: $$ a_\mathrm{ave} = \frac{\Delta v}{\Delta t} $$
Среднее ускорение за интервал времени равно тому, насколько изменилась скорость, $\Delta v = v_f – v_i$, деленная на длину интервала времени $\Delta t$. Если $a$ константа, то $a_\mathrm{ave}$ — это просто $a$.
Мы можем решить это уравнение относительно $v_f$ и получить ваше уравнение: $$ a_\mathrm{ave} = \frac{v_f – v_i}{\Delta t} \ подразумевает v_f = v_i + a_\mathrm{ave} \Delta t$$
Суть в том, что для $a$ равен $a_\mathrm{ave}$, он не обязательно должен быть постоянным на протяжении всего эксперимента. Он должен быть постоянным только на каждом интервале $10$ мс. Если временной интервал достаточно короткий, то $a$ будет примерно постоянным, и уравнение является хорошей моделью того, что происходит.
Он должен быть постоянным только на каждом интервале $10$ мс. Если временной интервал достаточно короткий, то $a$ будет примерно постоянным, и уравнение является хорошей моделью того, что происходит.
На практике ваш акселерометр, скорее всего, определяет $a$ путем усреднения временного интервала $10$ мс между выходными данными. Так что, вероятно, в любом случае он сообщает вам среднее ускорение в каждом интервале.
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Ускорение: определение, формула, типы, задачи и примеры
HelpYouBetter » Физика » Одномерное движение » Ускорение: определение, формула, типы, задачи и примеры
Неравномерное движение — это движение, при котором скорость частицы изменения. Скорость может измениться из-за изменения величины (скорости), изменения направления движения или того и другого. При одномерном движении движение происходит в заданном направлении, а изменение скорости происходит только за счет изменения величины скорости.
Содержание
Ускорение – определение
Когда скорость объекта изменяется со временем, говорят, что он имеет ускорение. Таким образом, ускорение определяется как скорость изменения скорости тела.
Единицей ускорения в системе СИ является мс -2 , а формула измерения – [M 0 L 1 T -2 ].
Ускорение является векторной величиной, так как скорость является векторной величиной. Однако направление движения тела определяется направлением скорости, а не направлением ускорения. Например, если тело движется вверх, его скорость направлена вверх, а ускорение направлено вниз.
Однако направление движения тела определяется направлением скорости, а не направлением ускорения. Например, если тело движется вверх, его скорость направлена вверх, а ускорение направлено вниз.
Ускорение может быть положительным, отрицательным или нулевым. Когда скорость тела увеличивается со временем, ускорение имеет положительное значение, и говорят, что тело движется с ускорением. С другой стороны, если скорость тела со временем уменьшается, ускорение отрицательно, и говорят, что тело движется с замедлением или замедлением. Отрицательное ускорение называется замедлением или запаздыванием. Если тело движется равномерно, его ускорение равно нулю.
Пример: Скорость падающего тела не меняет своего направления, но ее величина изменяется со временем равномерно. Следовательно, тело имеет ускорение.
Ускорение – формула
Если ускорение в каждый момент движения одинаково, говорят, что объект движется с равномерным или постоянным ускорением.
Рассмотрим объект, движущийся с равномерным ускорением «а».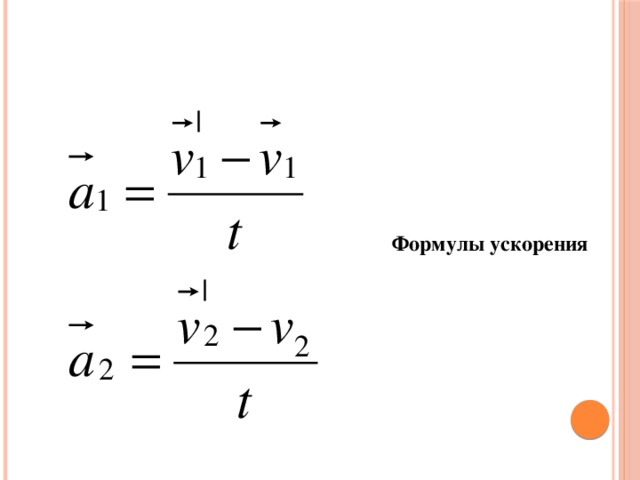 Если v 1 и v 2 являются его скоростями в моменты времени t 1 и t 2 соответственно (где t 2 > t 1 ), то ускорение объекта определяется выражением
Если v 1 и v 2 являются его скоростями в моменты времени t 1 и t 2 соответственно (где t 2 > t 1 ), то ускорение объекта определяется выражением
то есть скорость увеличивается в течение интервала, говорят, что ускорение положительно.
Если скорость v 2 < v 1 , то есть скорость уменьшается со временем, то ускорение отрицательно и называется замедлением или замедлением.
То есть в общих чертах можно сказать, что ускорение означает ускорение, а замедление означает замедление.
Аналогично, для частицы, имеющей скорость v 0 при t = 0 и скорость v t через время t, ускорение определяется формулой равномерное ускорение, среднее ускорение и мгновенное ускорение.
Равномерное ускорение:
Как было сказано ранее, говорят, что тело движется с равномерным ускорением, если за равные промежутки времени происходят одинаковые изменения скорости, какими бы малыми ни были эти промежутки времени.
Пример: движение свободно падающего тела
Среднее ускорение:
Если ускорение частицы неравномерно в течение интервала времени, говорят, что частица движется с неравномерным ускорением. Отношение изменения скорости ко времени называется средним ускорением.
Пусть (v 2 – v 1 ) изменение скорости на интервале времени (t 2 – t 1 ). Тогда среднее ускорение равно
Мгновенное ускорение:
Ускорение объекта в любой момент называется мгновенным ускорением.
Пусть Δv — изменение скорости за бесконечно малый интервал времени Δt вокруг t, тогда мгновенное ускорение a t в момент t определяется выражением
То есть мгновенное ускорение равно секунде производная положения по времени.
Ускорение свободного падения
Земля притягивает все тела к своему центру. Следовательно, если предмет падает с высоты, он свободно падает вниз с равномерным ускорением.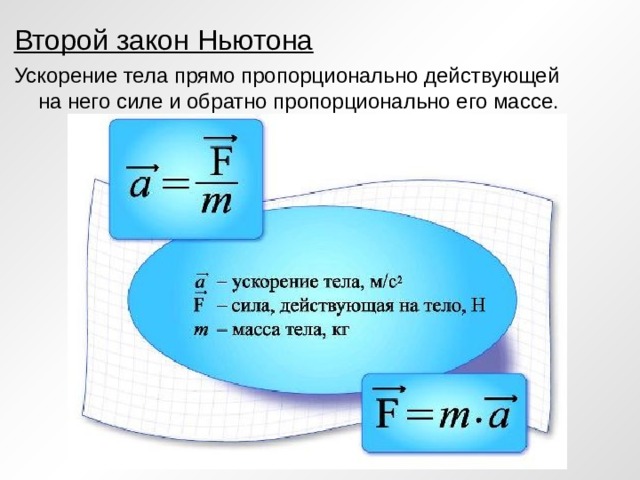 Это равномерное ускорение называется ускорением свободного падения и обозначается буквой «g». Значение «g» составляет почти 9,8 мс -2 для всех свободно падающих тел у поверхности земли.
Это равномерное ускорение называется ускорением свободного падения и обозначается буквой «g». Значение «g» составляет почти 9,8 мс -2 для всех свободно падающих тел у поверхности земли.
Значение «g» варьируется от места к месту на поверхности земли. Его значение максимально на полюсах и минимально на экваторе. Над и под поверхностью земли его значение меньше, чем на поверхности земли. Значение g равно нулю в центре Земли.
Общие соотношения, связывающие положение, скорость и ускорение
Общие соотношения, связывающие координату положения и скорость при одномерном движении, задаются формулой,
Таким образом, скорость объекта является производной положения по времени.
Аналогично, отношение, связывающее скорость объекта в момент t и ускорение объекта, определяется как
Таким образом, ускорение объекта является второй производной положения по времени.
Применение дифференцирования и интегрирования к равномерно ускоренному движению
Зависимость скорости от времени
Мгновенное ускорение объекта при равномерно ускоренном движении определяется выражением,
Пусть u – скорость объекта в момент времени t = 0 v — скорость в момент времени t.
Интегрируя обе части уравнения (1) в пределах начальной скорости u и конечной скорости v и времени t = 0 и t = t,
Зависимость перемещение – время
Мгновенная скорость объекта при его смещении на ds определяется выражением
Как получено в предыдущем разделе {уравнение (2)}, если начальная скорость объекта в момент времени t = 0 равна u, и скорость в момент времени t = t равна v, тогда
Интегрируя обе части приведенного выше уравнения между пределами s = 0 до s и временем t = 0 до t, мы получаем,
Проблемы ускорения и решения
Задача 1:
Смещение частицы, движущейся по прямой, равно x = k 0 + k 1 t + k 2 t 2 где k 0 , k 1 и k 2 — константы. Найдите ускорение.
Ответ:
Задача 2:
Положение объекта в любой момент времени t определяется соотношением x = mt + nt 2 + pt 3 , где m, n и p — константы. Найдите мгновенное ускорение тела в момент времени t = 8 с.
Найдите мгновенное ускорение тела в момент времени t = 8 с.
Ответ:
Задача 3:
Расстояние x частицы, движущейся в одном измерении под действием постоянной силы, связано со временем t уравнением
где x в метрах и оловянных секундах. Найдите перемещение частицы, когда: а) ее скорость равна нулю, б) ее скорость равна 4 м/с.
Решение:
Задача 4:
Ускорение объекта определяется выражением a = α + βt, где α и β — константы. В момент времени t = 0 пусть x 0 и v 0 – положение и скорость объекта. Найдите выражение для положения и скорости тела в любой момент времени t.
Решение:
Задача 5:
Положение объекта, движущегося вдоль оси x, определяется выражением x = a + bt 2 , где a = 8,5 м, b = 2,5 мс -2 , а t измеряется в секундах. Какова его скорость в моменты времени t = 0 с и t = 2 с? Какова средняя скорость между t = 2 с и t = 4 с?
Ответ:
Задача 6:
Перемещение частицы по оси x определяется выражением x = 3 + 8t + 7t 2 .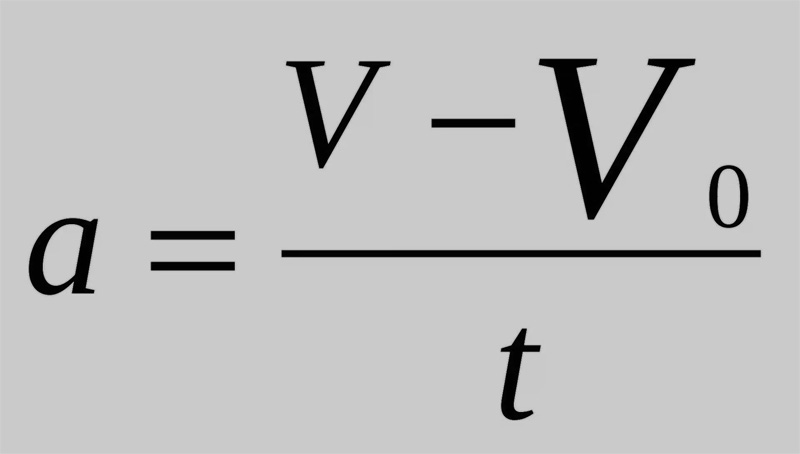



 Отличны ли от нуля в крайней
точке траектории маятника: а) нормальное
ускорение; б) тангенциальное ускорение?
Отличны ли от нуля в крайней
точке траектории маятника: а) нормальное
ускорение; б) тангенциальное ускорение? Стержень длинной l упирается
верхним концом в стену, а нижним – в
пол. Конец, упирающийся в стену,
равномерно опускается вниз. Будет ли
движение другого конца равномерным?
Стержень длинной l упирается
верхним концом в стену, а нижним – в
пол. Конец, упирающийся в стену,
равномерно опускается вниз. Будет ли
движение другого конца равномерным?