Главная
Айти интеграл: Неопределенный интеграл

Айти интеграл: Неопределенный интеграл

Интеграл тангенса и котангенса

Среди простых формул интегрирования отсутствуют готовые зависимости, позволяющих найти интеграл от тангенса (tg (x)) и котангенса (ctg (x)). Но такие примеры в задачах встречаются и нужно знать: “Как вычислить интеграл от тангенса и котангенса?“.
Начнем с тангенса, распишем его в виде частки синуса на косинус
tg(x)=sin(x)/cos(x)
и подставим в интеграл.
Сейчас Вам понятно. Далее нужно внести синус под дифференциал, чтобы свести интеграции в логарифма
В результате получимТаким образом вывели простую и нужную на практике формулу – интеграл от тангенса равен логарифму косинуса со знаком минус.
Int(tan(x),x)=-log(cos(x)).
По приведенной схеме выведем формулу для интеграла от котангенса. Записываем частку косинуса на синус в интеграл и после внесения косинуса под дифференциал сводим интеграл к логарифму
Интеграл от котангенса равный логарифму от синуса.
Int(cot(x),x)=log(sin(x)).
Простые на вид формулы интегралов от тангенса и котангенса позволяют решить немало сложных примеров, например интегрирования тангенса двойного угла или котангенса половины угла.

Пример 1. Найти интеграл от тангенса tan(4*x).
Вычисления: Применяем приведенную выше методику для интегрирования тангенса

Здесь в скобках мы сначала вычисляем дифференциал от косинуса, а дальше выделяем значение, которое нам нужно достать. Далее интегрирования сводим к логарифму.
Таким образом можем записать обобщенную формулу для интегралаtan(k*x)
Int(tan(k*x),x)=-1/k*(log(cos(x)).
По этой формуле интеграл от тангенса двойного угла равен логарифму косинуса двойного угла умноженному на -0,5.
Для тангенса половины угла tan (phi / 2) интеграл равен -2 умножить на логарифм косинуса половины угла
По индукции получим формулу интеграла для тангенса одной третьей угла tan(phi/3)

Пример 2. Проинтегрировать котангенс двойного угла
Вычисления: По аналогии с формулами для тангенса мы могли бы выписать готовую формулу, но лучше выполнить промежуточные переходы чтобы Вы лучше поняли и заучили методику внесения под дифференциал

Таким образом, если имеем котангенс тройного угла то перед интегралом получим множителем 1/3
Интегралы от котангенса половины и трети угла будут иметь множителями перед логарифмом соответственно двойку и тройку
При нахождении первоначальной от тангенса и котангенса следует справа добавить постоянную
Зная данную методику, Вы знаете как найти интеграл от тангенса, аргумент которого содержит множителем произвольное число.
Вычисления определенных интегралов от тангенса и котангенса в данной статье рассматривать не будем. Если Вы вычисляли такие интегралы от простых функций то, зная синусы и косинусы углов найти определенный интеграл от тангенса или котангенса сможете без проблем.
С методикой интегрирования обратных тригонометрических функций, иррациональных и показательных Вы можете ознакомиться на страницах категории “Интегрирование функции” в левом меню сайта.

  • Назад
  • Вперёд

1352. Найти интеграл

Решение.

Произведем подстановку t= , т. е. x = t3. Эта подстановка приведет к тому, что под знаком синуса окажется переменная интегрирования, а не корень из нее. Найдем дифференциал dx=3t2dt, Отсюда получаем

Ответ должен быть выражен через старую переменную х. Подставляя в резуль­тат интегрирования t= , получим

▲

1353.

Найти интеграл .

Решение.

Этот интеграл можно найти и не производя замены переменной. Здесь достаточно развернуть выражение (2x+1)20 по формуле бинома Ньютона и применить почленное интегрирование. Однако этот прием связан с большим коли­чеством вычислений. При помощи замены переменной можно сразу свести данный интеграл к табличному,

Полагая 2x+1=t, имеем 2dx = dt, т. е, dx = (1/2)dt. Отсюда получаем

▲

Вообще, если интеграл является табличным, то интеграл может быть легко найден при помощи подстановки ax+b = t.

Например, применим эту подстановку к интегралу, Имеем ax+b = t, adx = dt и dx = (1/a)dt. Следовательно,

Возвратившись к старой переменной, получаем

Аналогично можно показать, что

, и т.д.

При нахождении интеграла записи самой подстановки ax+b = t можно фактически и не производить. Здесь достаточно принять во внимание, что

. Таким образом,

где F— первообразная для f.

1354. Найти интеграл

Решение.

Положим ; тогда х3+5 = t.

Дифференцируем обе части равенства: 3x2dx = 2tdt. Отсюда х2 dx = (2/3) t dt и, следовательно,

Данный интеграл можно найти и при помощи подстановки x2+5=t

Эта подстановка сразу приводит интеграл к табличному вследствие того, что первый множитель подынтегрального выражения x2 отличается от производной подкоренного выражения x3+5 только постоянным множителем 1/3, т.

е. x2 =(1/3)( x2 +5)’ ▲

___________

Вообще, если подынтегральная функция является произведением двух мно­жителей, один из которых зависит от некоторой функции ψ(x), а другой явля­ется производной ψ(x) (с точностью до постоянного множителя), то целесообразно сделать замену переменной по формуле ψ(x)= t.

1355. Найти интеграл .

Решение.

Перепишем данный интеграл в виде

. Так

как производная выражения 2lnx+3 равна 2/х, а второй множитель 1/х отли­чается от этой производной только постоянным коэффициентом 2, то нужно применить подстановку 2lnx+3=t. Тогда , . Следовательно,

▲

1356. Найти интеграл

Решение.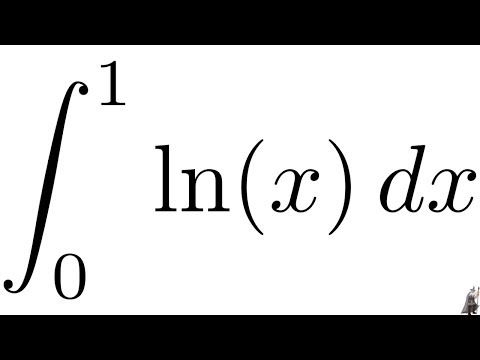

Произведем подстановку f(x) = t . Тогда f’(x)dx=dt и

Например,

Здесь мы не пишем знака модуля, так как x2 +1>0 ▲

1357. Найти интеграл

Решение.

Положим f(x) = t. Тогда f’(x)dx=dt и

Заметим, что данный интеграл можно было найти при помощи подстановки

. ▲

1358. Найти интеграл , если а≠0

Решение.

Для того чтобы свести интеграл к табличному (см. формулу IV), разделим числитель и знаменатель подынтегрального выражения на

а2:

Мы подвели постоянный множитель 1/а под знак дифференциала. Рассматривая х/а как новую переменную, получим

К этому же результату мы пришли бы и с помощью подстановки x=at. ▲

1359. Найти интеграл , если а>0.

Решение.

Разделив числитель и знаменатель на а, получаем

Принимая х/а за новую переменную, получим

. ▲

Дополним теперь таблицу основных интегралов следующими формулами:

XVI.

XVII.

XVIII.

XIX.

XX.

XXI.

XXII.

XXIII.

XXV.

Формулы I — XXV нужно знать наизусть, так как большинство интегралов, используемых на практике, сводится к интегралам, берущимся по этим формулам.

1360. Найти интеграл

Решение.

Произведем подстановку ; тогда 2х — 9 = t2, х =( t2 +9)/2 и dx = tdt. Итак,

Применив формулу XVIII, получим

▲

1361. Найти интеграл .

Решение.

Произведем подстановку cos2x = t, тогда -2 cosx sinx dx = dt, т.е. sin2xdx=dt. Теперь находим

(мы использовали формулу XX). ▲

1362. Найти интеграл .

Решение.

Применим подстановку 2 sin (x/2) + 3 =t; тогда cos (x/2)dx= dt и

▲

1363. Найти интеграл

Решение.

Применим подстановку x 5 = t; тогда 5x 4dx = dt, x 4dx = (1/5) dt и

(см, формулу XXI). Итак,

▲

1364. Найти интеграл

Решение.

Преобразуя знаменатель дроби, получим x4+2x2+5=(x2+1)2+4 Произведем подстановку x2

+1=t, тогда xdx=(1/2)dt. Отсюда

(см, формулу XVIII). Таким образом,

▲

1343. Найти интеграл

Решение.

Положим e2x = t, тогда e2x dx = (1/2) dt и

(мы применили формулу XIX). Итак,

▲

1366. Найти интеграл

Решение.

Произведя ту же подстановку, что и в предыдущем примере, получим

▲

1367. Найти интеграл .

Решение.

Полагая , x =t2, dx = 2tdt, получим

(см. формулы XXII и XXIII). Возвращаясь к старой переменной, получим

▲

Найти интегралы:

1368. 1369.

1370. 1371.

1372. 1373.

1374. 1375.

1376. 1377.

1378. 1379.

Указание: представить интеграл в виде суммы интегралов.

1380. 1381.

1382. 1383. 1384.

3. Интегрирование по частям. Интегрирозанием по частям называется нахож­дение интеграла по формуле

,

где u=φ(x), v=ψ(x) — непргрывно дифференцируемые функции от x. С помощью этой формулы нахождение интеграла сводится к отысканию другого интег­рала ; ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.

При этом за u берется такая функция, которая при дифференцировании упрощается, а за dv—та часть подынтегрального выражения, интеграл от кото­рой известен или может быть найден.

Так, например, для интегралов вида , , , где Р (х)—многочлен, за и следует принять Р (х), а за dv — соответственно выра­жения еах dx, sin axdx, cosaxdx; для интегралов вида , , за и принимаются соответственно функции ln x, arcsin x, агссоs x; а за dv—выражение Р (х) dx.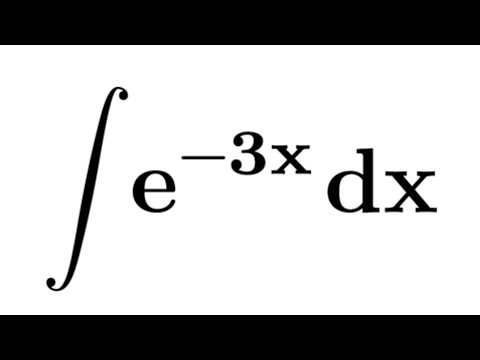

1385. Найти интеграл .

Решение.

Положим и=lпх, dv=dx; тогда v=x, . Используя формулу интегрирования по частям, получаем

▲

1386. Найти интеграл

Решение.

Пусть u=arctgx, dv=dx; тогда , v=x. По формуле интегрирования по частям находим

▲

1387. Найти интеграл

Решение.

Положим и=х, dv=sinxdx; тогда du = dx, x=-cosx. Отсюда

Если бы выражения и и dv мы выбрали иначе, например u = sinx, dv =xdx, то получили бы du = cosxdx, v = (1/2)x2, откуда

,

и пришли бы к интегралу более сложному, чем исходный, так как степень сомно­жителя при тригонометрической функции повысилась на единицу. ▲

1388. Найти интеграл .

Решение.

Положим u = x2, dv = exdx; тогда du = 2xdx, v=ex. Применяем формулу интегрирования по частям:

.

Мы добились понижения степени х на единицу. Чтобы найти , приме­ним еще раз интегрирование по частям. Полагаем и=х, dv=exdx; тогда du=dx, и=ех и

. ▲

1389. Найти интеграл .

Решение.

Пусть и = ех, dv = sinxdx; тогда du=exdx, v=-cosx. Следо­вательно,

.

Создается впечатление, что интегрирование по частям не привело к цели, так как интеграл не упростился. Попробуем, однако, еще раз проинтегрировать по частям. Приняв и = ех; dv = cosxdx, откуда du = exdx, v = sinx, получаем

, т.е.

Применив дважды операцию интегрирования по частям, мы в правой части снова получили исходный интеграл. Таким образом, приходим к уравнению с неизвестным интегралом I. Из этого уравнения находим

, т. е. .

В окончательном результате мы прибавили к найденной первообразной функ­ции произвольную постоянную.

1390. Найти интеграл , если а>0.

Решение.

Положим , dv = dx, откуда , v =x. Следовательно,

или

.

Отсюда получаем

т. е.

▲

1391. Вывести рекуррентную формулу для интеграла .

Решение.

Заданный интеграл можно преобразовать так:

Положим u=х, ; тогда du = dx,

откуда

или

т. е.

Полагая n=2, получаем выражение интеграла I2 через элементарные функ­ции. Полагая теперь n=3, находим интеграл I3 (ведь интеграл I2 уже найден). Таким образом, можно найти In при любом целом положительном n. ▲

Найти интегралы:

1392. . 1393.

1394. . 1395.

1396. . 1397. 1398.

Указание: положить x2=t.

1399. 1400.

1401. 1402.

Указание: положить .

Интегральные ИТ-предложения Ведущие ИТ-услуги в секторе

Знаете ли вы о БОЛЬШОЙ проблеме Microsoft 365?

Большинство компаний массово недоиспользуют Microsoft 365, что приводит к….