Лекция 19. Алгебра матриц
Лекции по алгебре и геометрии. Семестр 2.
Лекция 19. Алгебра матриц.
Краткое содержание: Основные определения, действия с матрицами и их свойства, нулевая и единичная матрицы, обратная матрица и ее свойства, обратимые матрицы.
Глава 1. Алгебра матриц.
п.1. Основные определения.
Пусть К – поле. Элементы поля К мы будем называть скалярами. Под полем К можно понимать или поле действительных чисел или поле комплексных чисел.
Определение. Матрицей размера над полем К называется таблица элементов поля К, имеющую строк и столбцов.
Обозначение:
.
Определение. Элементы называются элементами матрицы, где i – номер строки, в которой находится элемент , j – номер столбца.
Определение. Матрица размеров :
называется строкой длины .
Определение. Матрица размеров :
называется столбцом высоты .
Определение. Матрица размеров называется квадратной матрицей – го порядка.
Определение. Матрица, все элементы которой равны нулю, называется нулевой.
В квадратной матрице выделяют две диагонали, как диагонали квадрата: главную диагональ и побочную диагональ.
Главную диагональ образуют элементы , т.е. элементы с одинаковыми нижними индексами.
Побочную диагональ образуют элементы .
Определение. Квадратная матрица, в которой все элементы вне главной диагонали равны 0, называется диагональной:
.
Определение. Матрица В размера называется транспонированной по отношению к матрице А размера , если к – й столбец матрицы В состоит из элементов к – й строки матрицы А, для всех .
Обозначение: .
Определение.
Процесс (процедура) получения
транспонированной матрицы из данной
называется транспонированием матрицы.
Пример:
, .
Определение. Две матрицы и называются равными, если они имеют одинаковые размеры и для всех значений индексов выполняется равенство .
п.2. Сложение матриц.
Определение. Суммой матриц и одинаковой размерности называется третья матрица такой же размерности , где ее элементы определяются равенством для всех значений индексов.
Другими словами, для того, чтобы найти сумму двух матриц одинаковой размерности, нужно сложить соответствующие элементы (т.е. элементы, имеющие одинаковые нижние индексы) этих матриц.
Замечание. Сложение матриц различных размеров не определено. (Их нельзя складывать!)
Пример: , ,
.
Определение. Матрица В называется противоположной матрице А, если она удовлетворяет равенству , где 0 – нулевая матрица.
Обозначение: .
Множество всех матриц размера над полем K обозначим через
Теорема. (Свойства сложения матриц.)
Множество относительно сложения является абелевой группой.
Другими словами, сложение матриц подчиняется следующим законам:
1) ассоциативность: справедливо равенство ;
2) существование нулевой матрицы:
– нулевая матрица, такая, что верны равенства ;
3) существование противоположной матрицы:
, : ;
4) коммутативность:
.
п.3. Умножение матрицы на скаляр.
Определение. Произведением скаляра на матрицу называется матрица тех же размеров, что и матрица А, где элементы определяются равенством , для всех значений индексов.
Обозначение: .
Другими словами, для того, чтобы умножить матрицу на скаляр, нужно каждый элемент матрицы умножить на данный скаляр.
Пример:
,
.
Замечание. Легко видеть, что умножив матрицу на (–1) мы получаем противоположную матрицу: .
Теорема. (Свойства
умножения матрицы на скаляр.)
(Свойства
умножения матрицы на скаляр.)
Умножение матрицы на скаляр подчиняется законам:
5) ассоциативность: и
;
6) если 1 – единица поля K, тогда
;
7) дистрибутивность умножения относительно сложения скаляров: и
;
8) Дистрибутивность умножения относительно сложения матриц: и
.
Следствие. Множество относительно сложения матриц и умножения матриц на скаляр является векторным пространством над полем К.
Обозначим через множество всех столбцов высоты n с элементами из поля K.
Следствие. Множество является векторным пространством над полем K.
Определение. Векторное пространство называется арифметическим векторным пространством столбцов высоты n.
п.4. Умножение матриц.
Определение. Произведением строки длины n на столбец высоты n называется скаляр, вычисляемый по правилу:
.
Замечание. Из определения следует, что для умножения строки на столбец необходимо, чтобы длина строки была равна высоте столбца. В противном случае произведение строки на столбец не определено.
Пример.
Определение. Произведением матрицы размера на матрицу размера называют матрицу размера , где элемент является результатом произведения – й строки матрицы А на – й столбец матрицы В для всех значений индексов , , т.е.
или
.
Обозначение: .
Другими словами, чтобы умножить две матрицы, нужно каждую строку первой матрицы умножить на каждый столбец второй матрицы. Умножая первую строку первой матрицы на каждый столбец второй матрицы мы получим все элементы первой строки матрицы произведения, затем делаем то же самое для второй строки первой матрицы и т.д.
Замечание. Из
определения следует, что умножение
матриц возможно только тогда, когда
ширина первой матрицы (т.е. число ее
столбцов) равна высоте второй (т.е. числу
ее строк)
Из
определения следует, что умножение
матриц возможно только тогда, когда
ширина первой матрицы (т.е. число ее
столбцов) равна высоте второй (т.е. числу
ее строк)
Пример.
.
Определение. Квадратную матрицу – го порядка называют единичной матрицей n-го порядка и обозначают буквой Е, если для любой квадратной матрицы А – го порядка справедливо равенство: .
Множество всех квадратных матриц n-го порядка будем обозначать через .
Теорема. Множество содержит единичную матрицу n-го порядка, которой является матрица
.
Доказательство этой теоремы предоставляется читателю.
Теорема. Единичная матрица Е является единственной в множестве .
Доказательство. Пусть еще одна единичная матрица. Тогда, по определению, . Положим , тогда . Далее, по определению, . Положим здесь . Получаем равенство, отсюда имеем , ч.т.д.
Заметим, что точно также доказывается единственность нейтрального элемента (при условии его существования) в любой алгебраической структуре.
Теорема доказана.
Из теоремы следует, что никакая другая матрица, кроме матрицы не является единичной.
Теорема. (Свойства умножения матриц.)
Умножение матриц подчиняется следующим законам:
9) ассоциативность:
;
10) существование единичной матрицы:
: ;
дистрибутивность умножения относительно сложения матриц:
11) дистрибутивность умножения относительно сложения матриц:
и
12) умножение матриц связано с умножением матрицы на число естественным законом: и верно равенство:
.
Замечание. Для квадратных матриц одного порядка выполняются все 12 свойств. Это говорит о том, что множество всех квадратных матриц одного и того же порядка образует алгебру матриц над полем К.
Замечание. Умножение матриц не обладает свойством
коммутативности. Для доказательства
достаточно привести один контрпример.
Умножение матриц не обладает свойством
коммутативности. Для доказательства
достаточно привести один контрпример.
Пусть , . Тогда , .
Аналогичный пример можно привести для квадратных матриц любого порядка.
Последнее равенство говорит о том, что квадратные матрицы имеют делители нуля.
Следствие. Множество всех квадратных матриц n-го порядка над полем K является некоммутативным кольцом с единицей и с делителями нуля.
Доказательство. На множестве всех квадратных матриц n-го порядка над полем K определены две операции: сложение матриц и их умножение, которые подчиняются законам 1) – 4) и 9) – 11), откуда и следует, по определению, что является кольцом с единицей (см. лекцию 1, п.14 и п.15). Пример, приведенный перед формулировкой данного следствия, показывает, что кольцо имеет делители нуля.
Следствие доказано.
Определение. Натуральной степенью квадратной матрицы А называется матрица .
Нулевую степень квадратной матрицы А – го порядка по определению полагают равной единичной матрице того же порядка: .
п.5. Обратная матрица.
Определение. Матрица В называется обратной по отношению к матрице А, если
.
Из определения следует, что если матрица А имеет обратную, то обе они должны быть квадратными матрицами одного порядка.
Из определения следует, что если матрица В является обратной по отношению к матрице А, то и матрица А является обратной по отношению к матрице А.
Определение. Матрица имеющая обратную матрицу называется обратимой.
Теорема. Если квадратная матрица А имеет обратную, то она единственная.
Доказательство. Пусть В и С – две матрицы обратные к матрице А. Тогда и . Имеем,
, ч.т.д.
Теорема доказана.
Заметим, что точно также доказывается единственность симметричного элемента в любой полугруппе при условии его существования.
Обозначение: если
матрица А обратимая, то обратная к ней
обозначается (мы можем это сделать в
силу ее единственности) через
.
Заметим, что если матрица А обратимая, то обратная к ней матрица также является обратимой.
Обозначение. Множество всех обратимых матриц n-го порядка над полем K обозначается через
.
Теорема. (Свойства обратных матриц.)
1. Произведение обратимых матриц одного и того же порядка является обратимой матрицей:
, и .
2. Единичная матрица является обратимой, т.е. если Е – единичная матрица n-го порядка, то
и .
3. Если А обратимая, то и также является обратимой, т.е. если , то и .
Доказательство. 1) Пусть А и В – обратимые матрицы и , – обратные к ним. Покажем, что произведение является матрицей обратной к произведению :
.
Аналогично получаем . Следовательно, матрица АВ имеет обратную и . Отсюда следует, что матрица АВ является обратимой, т.е. , ч.т.д.
2) Так как , то по определению, , т.е. единичная матрица имеет обратную и, следовательно, единичная матрица является обратимой и .
3) Действительно, из определения следует, что матрица А является обратной по отношению к матрице , следовательно, матрица обратимая и . Более того, в силу единственности обратной матрицы следует, что
.
Теорема доказана.
Следствие. Множество является некоммутативной группой относительно умножения.
Доказательство. На множестве умножение матриц является внутренней бинарной алгебраической операцией, поэтому осталось лишь проверить аксиомы группы.
1) Ассоциативность умножения в множестве выполняется потому что умножение квадратных матриц ассоциативно (см теорему о свойствах умножения матриц).
Далее, в предыдущей теореме доказано, что:
2) единичная матрица ;
3) существует обратная ей .
Следствие доказано.
Определение.
Обратимая квадратная матрица называется
также неособой или невырожденной. Если
квадратная матрица не имеет обратной,
то она называется особой или вырожденной.
Если
квадратная матрица не имеет обратной,
то она называется особой или вырожденной.
Замечание. Легко доказать существование особых матриц. Например, матрица
является особой (вырожденной, необратимой). Действительно, если бы она была обратимой, то существовала бы обратная к ней и . Пусть далее, . Тогда и отсюда получаем
или , т.е. получаем противоречие.
Аналогично, легко показать существование особых матриц любого порядка. Отсюда следует вывод, что не все квадратные матрицы являются обратимыми.
В дальнейшем, мы найдем необходимое и достаточное условие обратимости квадратной матрицы любого порядка и не только докажем существование обратимых матриц, отличных от единичной матрицы, но и выведем формулу для ее вычисления.
Матрицы примеры решения задач, формулы и онлайн калькуляторы
Задание. Вычислить $A B$ и $B A$, если $A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right), B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)$
Решение. Так как $A=A_{3 \times 2}$ , а $B=B_{2 \times 2}$ , то произведение возможно и результатом операции умножения будет матрица $C=C_{3 \times 2}$ , а это матрица вида $C=\left( \begin{array}{cc}{c_{11}} & {c_{12}} \\ {c_{21}} & {c_{22}} \\ {c_{31}} & {c_{32}}\end{array}\right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}=1 \cdot 1+(-1) \cdot 2=-1 $
$ c_{12}=a_{11} \cdot b_{12}+a_{12} \cdot b_{22}=1 \cdot 1+(-1) \cdot 0=1 $
$ c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}=2 \cdot 1+0 \cdot 2=2 $
$ c_{22}=a_{21} \cdot b_{12}+a_{22} \cdot b_{22}=2 \cdot 1+0 \cdot 0=2 $
$ c_{31}=a_{31} \cdot b_{11}+a_{32} \cdot b_{21}=3 \cdot 1+0 \cdot 2=3 $
$ c_{31}=a_{31} \cdot b_{12}+a_{32} \cdot b_{22}=3 \cdot 1+0 \cdot 0=3 $
Итак, $C=A B=\left( \begin{array}{rl}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ .
Выполним произведения в более компактном виде:
$=\left( \begin{array}{rrr}{1 \cdot 1+(-1) \cdot 2} & {1 \cdot 1+(-1) \cdot 0} \\ {2 \cdot 1+0 \cdot 2} & {2 \cdot 1+0 \cdot 0} \\ {3 \cdot 1+0 \cdot 2} & {3 \cdot 1+0 \cdot 0}\end{array}\right)=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$
Найдем теперь произведение $D=B A=B_{2 \times 2} \cdot A_{3 \times 2}$. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы $B$ не совпадает с количеством строк матрицы $A$ .
Matrices & Linear Algebra | Mathematica & Wolfram Language for Math Students—Fast Intro
В Языке Wolfram матрицы представляются как списки списков:
| In[1]:= | ⨯{{1, 2}, {3, 4}} |
Их можно вводить в табличном виде, используя CTRL+ ENTER для добавления строк и CTRL+ , для добавления столбцов:
| In[2]:= | ⨯{
{a, b},
{c, d}
} |
| Out[2]= |
Функция MatrixForm позволяет отобразить матрицу в классическом виде:
| In[3]:= | ⨯MatrixForm[{{a, b}, {c, d}}] |
| Out[3]= |
Матрицы можно создавать с помощью итерационных функций:
| In[1]:= | ⨯Table[x + y, {x, 1, 3}, {y, 0, 2}] |
| Out[1]= |
Или импортировать данные, которые представляют собой матрицу:
| In[2]:= | ⨯Import["data. |
| Out[2]= |
IdentityMatrix, DiagonalMatrix и другие встроенные функции используются для создания матриц специального вида.
Стандартные матричные операции работают поэлементно:
| In[1]:= | ⨯{1, 2, 3} {a, b, c} |
| Out[1]= |
Вычисление произведения двух матриц:
| In[2]:= | ⨯{{1, 2}, {3, 4}}.{{a, b}, {c, d}} |
| Out[2]= |
Вычисление детерминанта:
| In[3]:= | ⨯Det[{{a, b}, {c, d}}] |
| Out[3]= |
Поиск обратной матрицы:
| In[4]:= | ⨯Inverse[{{1, 1}, {0, 1}}] |
| Out[4]= |
Функция LinearSolve используется для решения систем линейных уравнений:
| In[1]:= | ⨯LinearSolve[{{1, 1}, {0, 1}}, {x, y}] |
| Out[1]= |
Реализованы также функции для минимизации и декомпозиции матриц.
Справочная информация: Матрицы и линейная алгебра »
Hands–on Start to
Wolfram Mathematica »
Полная документация »
Demonstrations Project »
От действий над матрицами к пониманию их сути… / Хабр
Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья “Математика на пальцах”, и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.
Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья “Математика на пальцах”, и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше…
Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.
Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что “площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма”. Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.
Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.
Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.
Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…
Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.
Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?
Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…
Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…
Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.
В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1). Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.
Любая статья заканчивается в тот момент, когда автору надоедает её писать. Поскольку я не ставил перед собой цели объять необъятное, а исключительно хотел понять суть описанных операций над матрицами и то, как именно матрицы связаны с решаемыми мной системами уравнений, я не полез в дальнейшие дебри линейной алгебры, а вернулся к эконометрике и множественной регрессии, но сделал это уже более осознанно. Понимая, что и зачем я делаю и почему только так, а не иначе. То, что у меня получилось в этом материале, можно озаглавить как «глава о сути основных операций линейной алгебры, которую почему-то забыли напечатать в учебниках». Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».
Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».
Алгебра матриц и линейные пространства
Главная / Математика / Алгебра матриц и линейные пространства / Тест 5 Упражнение 1:Номер 1
Возведение матрицы в нулевую степень дает в результате
Ответ:
 (1) единицу 
 (2) единичную матрицу 
 (3) нулевую матрицу 
Номер 2
Что получится в результате возведения матрицы в нулевую степень?
Ответ:
 (1) нуль 
 (2) нулевая матрица 
 (3) единичная матрица 
Номер 3
Получится ли нулевая матрица в результате возведения другой матрицы в нулевую степень?
Ответ:
 (1) нет, не получится 
 (2) да, получится 
 (3) не во всех случаях 
Упражнение 2:
Номер 1
Матрица считается обратной исходной в том случае, если
Ответ:
 (1) произведение двух этих матриц равно 0 
 (2) произведение двух этих матриц равно 1 
 (3) произведение двух этих матриц равно единичной матрице 
Номер 2
Если умножение матрицы на другую дает в результате единичную матрицу, то
Ответ:
 (1) эта матрица нулевая 
 (2) эта матрица обратная данной 
 (3) эта матрица треугольная 
Номер 3
Как называется матрица, которая при умножении на другую матрицу дает единичную матрицу?
Ответ:
 (1) обратимая 
 (2) обратная 
 (3) транспонированная 
Упражнение 3:
Номер 1
Если обратная матрица B к матрице A существует, то
Ответ:
 (1) ее определитель равен нулю 
 (2) она однозначно определена 
 (3) она неопределена 
Номер 2
Обратная к другой матрице матрица определяется
Ответ:
 (1) множественным образом 
 (2) однозначно 
 (3) порядком матрицы 
Номер 3
Верно ли утверждение, что обратная матрица определяется множественным образом?
Ответ:
 (1) да, это верно 
 (2) нет, это неверно 
 (3) это верно только в некоторых частных случаях 
Упражнение 4:
Номер 1
Для любого элемента моноида обратный элемент является
Ответ:
 (1) неоднозначным 
 (2) единственным 
 (3) неопределенным 
Номер 2
Для любого элемента моноида обратный элемент является единственным.Верно ли это?
Ответ:
 (1) да, утверждение верно 
 (2) нет, это не так, но только в некоторых случаях 
 (3) нет, обратных элементов существует бесконечное множество 
Номер 3
Можно ли считать верным утверждение о том, что для любого элемента моноида существует не менее двух обратных элементов?
Ответ:
 (1) да, так и есть 
 (2) утверждение верно только в некоторых частных случаях 
 (3) нет, это неверно 
Упражнение 5:
Номер 1
Если определитель матрицы равен нулю, то
Ответ:
 (1) обратная матрица будет единичной 
 (2) обратная матрица будет нулевой 
 (3) обратная матрица не существует 
Номер 2
Может ли существовать обратная матрица, если определитель исходной равен нулю?
Ответ:
 (1) нет, не может 
 (2) может, но такие случаи встречаются редко 
 (3) да, может всегда 
Номер 3
Определитель матрицы равен нулю.Верно ли, что матрица, обратная данной тоже будет нулевой?
Ответ:
 (1) нет, это неверно 
 (2) да, так и есть, согласно определению 
 (3) это верно только в частных случаях 
Упражнение 6:
Номер 1
Элемент обратной матрицы получается в результате
Ответ:
 (1) перемножения элементов исходной матрицы на величину определителя 
 (2) сложения определителя с элементами главной диагонали 
 (3) деления соответствующих элементов присоединенной матрицы на определитель 
Упражнение 7:
Номер 1
Верно ли, что определитель обратной матрицы обратно пропорционален определителю исходной матрицы?
Ответ:
 (1) нет, утверждение противоречит определению обратной матрицы 
 (2) да, это верно 
 (3) это верно только в частных случаях 
Номер 2
Произведение определителя обратной матрицы на определитель исходной дает в результате
Ответ:
 (1) 1 
 (2) 0 
 (3) -1 
Номер 3
Что является результатом произведения определителя обратной матрицы на определитель исходной?
Ответ:
 (1) нулевая матрица 
 (2) единица 
 (3) двойка в степени размерности матрицы по строкам 
Упражнение 8:
Номер 1
Матрица, имеющая правую обратную
Ответ:
 (1) необратима 
 (2) обратима 
 (3) неопределена 
Номер 2
Если матрица обратима, то она имеет
Ответ:
 (1) левую обратную 
 (2) правую обратную 
 (3) как левую обратную, так и правую 
Номер 3
Верно ли утверждение, что матрица, имеющая правую обратную, обратима?
Ответ:
 (1) нет, это противоречит определению 
 (2) да, это верно 
 (3) это может быть верно только в очень редких случаях 
Упражнение 9:
Номер 1
Для существования матрицы, обратной произведению двух матриц необходимо, чтобы
Ответ:
 (1) существовала матрица, обратная левой матрице 
 (2) существовала матрица, обратная правой матрице 
 (3) существовали обе обратные матрицы 
Номер 2
Верно ли то, что матрица, обратная к произведению двух матриц, равна произведению матриц, обратных к данным?
Ответ:
 (1) да, это верно 
 (2) нет, это неверно 
 (3) это может быть очень редко, а в основном утверждение неверно 
Упражнение 10:
Номер 1
Дает ли матрица, обратная обратной в результате исходную?
Ответ:
 (1) да, это верно 
 (2) нет, утверждение неверно 
 (3) это может быть правильно только в очень редких случаях, а в остальном неверно 
Номер 2
От обратной матрицы взяли обратную, и в результате получили
Ответ:
 (1) нулевую матрицу 
 (2) единичную матрицу 
 (3) исходную матрицу 
Номер 3
Множество обратимых матриц с операцией умножения является
Ответ:
 (1) детерминированной группой 
 (2) линейной группой 
 (3) интерпретационной группой 
Упражнение 11:
Номер 1
Множество матриц с единичным определителем с операцией умножения является
Ответ:
 (1) линейной группой 
 (2) специальной линейной группой 
 (3) обратимой линейной группой 
Номер 2
Специальная линейная группа - это
Ответ:
 (1) множество обратимых матриц с операцией умножения 
 (2) множество необратимых матриц с операцией конъюнкции 
 (3) множество матриц с единичным определителем с операцией умножения 
Упражнение 12:
Номер 1
Если обратная матрица равна транспонированной, то исходная матрица называется
Ответ:
 (1) ортогональной 
 (2) деструктивной 
 (3) интерпретационной 
Номер 2
Матрица называется ортогональной тогда, когда
Ответ:
 (1) все элементы ниже побочной диагонали равны нулю 
 (2) транспонированная матрица равна обратной 
 (3) элементы побочной диагонали противоположны по знаку элементам главной 
Номер 3
Верно ли то, что матрица является ортогональной тогда, когда ее транспонированная матрица равна обратной?
Ответ:
 (1) да, это верно 
 (2) нет, это неверно 
 (3) это может быть верно только в частных случаях 
Матрицы.
 Действия над матрицами. Свойства операций над матрицами. Виды матриц.
Действия над матрицами. Свойства операций над матрицами. Виды матриц.Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.
Матрицы (и соответственно математический раздел – матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин “матрица” появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.
Матрицей A=Amn порядка m*n называется прямоугольная таблица чисел, содержащая m – строк и n – столбцов.
Элементы матрицы aij, у которых i=j, называются диагональными и образуют главную диагональ.
Для квадратной матрицы (m=n) главную диагональ образуют элементы a11, a22,…, ann .
Равенство матриц.
A=B, если порядки матриц A и B одинаковы и aij=bij (i=1,2,…,m; j=1,2,…,n)
Действия над матрицами.
1. Сложение матриц – поэлементная операция
2. Вычитание матриц – поэлементная операция
3. Произведение матрицы на число – поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)
Amk*Bkn=Cmn причем каждый элемент сijматрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.
Покажем операцию умножения матриц на примере
5. Возведение в степень
m>1 целое положительное число. А – квадратная матрица (m=n) т.е. актуально только для квадратных матриц
А – квадратная матрица (m=n) т.е. актуально только для квадратных матриц
6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A’
Строки и столбцы поменялись местами
Пример
Свойства опрераций над матрицами
A+B=B+A
(A+B)+C=A+(B+C)
λ(A+B)=λA+λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ(AB)=(λA)B=A(λB)
A(BC)=(AB)C
(A’)’=A
(λA)’=λ(A)’
(A+B)’=A’+B’
(AB)’=B’A’
Виды матриц
1. Прямоугольные: m и n – произвольные положительные целые числа
2. Квадратные: m=n
3. Матрица строка: m=1. Например, (1 3 5 7 ) – во многих практических задачах такая матрица называется вектором
4. Матрица столбец: n=1. Например
5. Диагональная матрица: m=n и aij=0, если i≠j. Например
6. Единичная матрица: m=n и
7. Нулевая матрица: aij=0, i=1,2,…,m
j=1,2,…,n
8. Треугольная матрица: все элементы ниже главной диагонали равны 0.
Пример.
9. Симметрическая матрица: m=n и aij=aji(т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A’=A
Например,
10. Кососимметрическая матрица: m=n и aij=-aji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т. к. при i=j имеем aii=-aii)
к. при i=j имеем aii=-aii)
Пример.
Ясно, A’=-A
11. Эрмитова матрица: m=n и aii=-ãii (ãji– комплексно – сопряженное к aji, т.е. если A=3+2i, то комплексно – сопряженное Ã=3-2i)
Пример
Как линейная алгебра используется в машинном обучении?
В предыдущей статье речь шла о математическом анализе. Продолжая серию публикаций к запуску авторского «Онлайн-курса по математике в Data Science Lite», поговорим о применении линейной алгебры в машинном обучении (завершит цикл статья о теории вероятностей и статистике – прим. ред.). За примерами далеко ходить не нужно: напротив, очень трудно найти такую сферу машинного обучения, в которой не используется линейная алгебра. Причем не только ее основные методы, вроде операций с векторами и матрицами, но и продвинутые вроде сингулярного разложения матрицы (Singular Value Decomposition, SVD), метода главных компонент (Principal Component Analysis, PCA) и метода опорных векторов (Support Vector Machines, SVM). Последний – один из основных алгоритмов машинного обучения.
Далеко не каждый курс линейной алгебры, даже на математических факультетах, рассматривает все ее приложения в машинном обучении. (То же самое можно сказать и о статистике, которая также является одной из основ Data Science и машинного обучения). Это обусловливает необходимость специальных курсов математики для Data Science.
Основы
Линейная алгебра работает с векторами и матрицами – а точнее, с их линейными комбинациями, также являющимися векторами и матрицами. Математически вектор можно представить набором действительных чисел:
Математически вектор можно представить набором действительных чисел:
Такой набор может представлять очень разные сущности: например, геометрический вектор в некоторой системе координат (при этом числа ai умножаются на векторы базиса), полином (числа ai умножаются на xi) и вообще любую линейную комбинацию каких-либо элементов. Матрица – это такой же набор действительных чисел, но организованный в виде прямоугольника. Матрицу тоже можно представить в виде длинного вектора, если поставить ее столбцы друг на друга.
Что в машинном обучении можно представить в виде векторов и матриц? Практически всё! Например, одна строка из набора данных – это вектор, каждый элемент которого представляет значение некоторого признака. Весь тренировочный набор данных (или, в случае нейронной сети, один batch из этого набора) – это матрица. Изображение, которое будет распознавать сверточная нейронная сеть – тоже матрица чисел, соответствующих отдельным пикселям. Градиент функции потерь – это вектор, и так далее.
Произведение векторов, умножение матрицы на вектор и произведение матриц – все это используется в машинном обучении. Например, модель линейной регрессии с вектором весов w и вектором признаков x можно записать в виде произведения векторов, если добавить в вектор признаков x[0] = 1:
Поскольку результат линейной регрессии – произведение векторов, произведение матрицы тренировочного набора данных на вектор весов дает вектор предсказаний модели. Если вычесть из него вектор истинных значений, получится вектор ошибок, который можно передать в функцию потерь.
Если вычесть из него вектор истинных значений, получится вектор ошибок, который можно передать в функцию потерь.
В качестве примера перемножения матриц представим, что у нас есть набор изображений для обучения сверточной нейронной сети, и мы хотим дополнить этот набор поворотами этих изображений, чтобы сеть могла распознавать изображения независимо от их наклона. Поворот изображения – это частный случай умножения матрицы векторов координат на матрицу трансформации, которую также изучает линейная алгебра. Матрица трансформации для поворота координат на угол theta выглядит так:
Измерения
Норма вектора – это термин линейной алгебры, определяющий длину вектора и расстояние между векторами (как длину разности между ними). Существуют нормы различных порядков, но обычно используются только первые два:
Геометрическое место точек, у которых норма равна единице: L1 (слева) и L2 (справа)Норма L2(x-y) – это расстояние между векторами x и y. Обе нормы используются в машинном обучении для регуляризации функции потерь: лассо-регуляризация использует L1, регуляризация Тихонова – L2, а эластичная сеть – и ту, и другую.
Косинус угла между двумя векторами x и y линейная алгебра определяет так:
Эта формула – самый популярный метод оценки сходства двух векторов. Если косинус угла близок к единице, то угол между векторами минимален, то есть векторы направлены почти одинаково. Если он близок к минус единице, векторы направлены почти противоположно. Наконец, если косинус близок к нулю, то векторы перпендикулярны (ортогональны), то есть, совершенно не зависят друг от друга.
Измерение меры сходства используется в машинном обучении очень широко – например, рекомендательные системы часто измеряют сходство векторов пользователей по их предпочтениям, и на основании этого сходства принимается решение, что похожим пользователям можно рекомендовать продукты, которые уже понравились одному из них.
Разумеется, оценка сходства широко применяется и в моделях кластеризации – например, метод k-Nearest Neighbors размечает кластеры именно по степени сходства элементов друг с другом.
Сингулярное разложение матриц (SVD)
Квадратная матрица называется ортогональной, если все ее столбцы ортонормальны – норма каждого из них равна единице, и все они попарно ортогональны, то есть образуют ортонормальный базис. Ортогональные матрицы обладают следующими свойствами:
Сингулярное разложение матрицы вводится следующей теоремой линейной алгебры: любую невырожденную прямоугольную матрицу Am*n можно представить в виде произведения трех матриц Um*m, Em*n и Vn*n, где U и V – ортогональные матрицы, а E – прямоугольная матрица, в которой все элементы, кроме диагональных, равны нулю.
Сингулярное разложение широко используется в рекомендательных системах. Оно позволяет найти базисы пространства строк и пространства столбцов, то есть элементарные признаки обоих пространств. Например, если строки матрицы соответствуют читателям, столбцы – книгам, а сама матрица содержит оценки, которые пользователи поставили книгам, то сингулярное разложение матрицы выделит “типичных читателей” и “типичные книги”. Каждого реального читателя и каждую реальную книгу можно представить линейной комбинацией “типичных”, после чего будет достаточно легко рассчитать ожидаемую оценку любой книги любым читателем.
Методов, позволяющих современным компьютерам обрабатывать огромные разреженные матрицы пользовательских оценок за приемлемое время, очень мало, так что сингулярное разложение матриц применяется очень широко.
Метод главных компонент (PCA)
Метод главных компонент – один из основных методов сокращения размерности данных, используемых в машинном обучении. Сокращение размерности применяется как при анализе данных, чтобы найти наиболее важные переменные и сконструировать новые признаки на их основе, так и при моделировании, если количество признаков очень велико, и большинство из них слабо влияют на результат. Метод главных компонент находит такую проекцию данных на пространство меньшей размерности, которая максимально сохраняет дисперсию данных.
Продемонстрируем работу метода главных компонент на примере двухмерного набора данных, который мы будем проецировать на одномерное подпространство (линию). Метод состоит из нескольких шагов:
Метод состоит из нескольких шагов:
- Вычитаем среднее значение, чтобы набор данных имел среднее значение 0. Это сокращает риск возникновения числовых проблем.
- Стандартизируем. Делим элементы данных на стандартное отклонение sigmad по каждому измерению d. Теперь данные не имеют единиц измерения, а их дисперсия по каждой оси равна 1, что отмечено на рис. в) голубыми стрелками.
- Выполняем спектральное разложение матрицы ковариации. Вычисляем матрицу ковариации данных, ее собственные векторы и собственные значения. На рис. г) собственные векторы масштабированы соответствующими собственными значениями (голубые стрелки), и более длинный вектор соответствует подпространству главных компонент. Матрица ковариации данных изображена в виде эллипса.
- Проецируем данные в подпространство. Рисунок е) показывает итоговую проекцию, перенесенную в исходное пространство данных.
Из описания метода главных компонент видно, что в нем используются понятия не только линейной алгебры, но и статистики (среднее значение, дисперсия, отклонение, матрица ковариации). Тем не менее, основные операции выполняются методами линейной алгебры, ведь именно она описывает проекции из одного пространства в другое, собственные векторы и собственные значения, а также спектральное разложение матриц.
Метод опорных векторов (SVM)
Один из основных методов построения моделей машинного обучения – это метод опорных векторов (Support Vector Machine). Этот метод основан на построении гиперплоскости, максимально разделяющей объекты разных классов – то есть, обеспечивающей максимальное расстояние между граничными точками. Мы не будем вдаваться в детали его реализации, поскольку они достаточно сложны и выходят за рамки нашей статьи. Метод очень подробно, с примерами кода и анимацией, описан в статье на Хабре, откуда взята следующая иллюстрация:
Мы не будем вдаваться в детали его реализации, поскольку они достаточно сложны и выходят за рамки нашей статьи. Метод очень подробно, с примерами кода и анимацией, описан в статье на Хабре, откуда взята следующая иллюстрация:
Метод опорных векторов широко используется для задач бинарной классификации, а также сегментации изображений и многих других задач. Существует множество различных вариаций этого метода, причем он позволяет задать спрямляющее ядро, при правильном выборе которого результирующая модель зачастую оказывается более точной, чем модели на основе нейронных сетей – однако это ядро невозможно подобрать автоматически, так что его выбор представляет собой искусство Data Scientist’а. Метод хорошо работает с данными небольшого объема и с данными, имеющими большое количество признаков.
Для нас главное – то, что векторы и гиперплоскости относятся к линейной алгебре, как и весь метод в целом, и для его успешного применения, а также для правильной интерпретации его результатов, хорошее знание линейной алгебры просто необходимо.
Заключение
Мы рассмотрели только самые важные и очевидные приложения линейной алгебры в машинном обучении, но из приведенных примеров понятно, насколько широко она применяется, и насколько глубоко требуется ее знать для уверенного понимания хотя бы основных методов. Разумеется, для реальной работы в области машинного обучения придется изучить намного больше, чем описано в этой статье (предыдущая публикация была посвящена приложениям математического анализа, а в следующей речь пойдет о теории вероятностей и статистике – прим. ред.).
ред.).
Надеюсь, что вы по-настоящему любите математику, или, по крайней мере, она вас не пугает.
***
Если вы хотите наработать необходимую для изучения Data Science математическую базу и подготовиться к углубленным занятиям в «Школе обработки данных» или Computer Science Center, обратите внимание на онлайн-курс «Библиотеки программиста». С помощью опытных преподавателей из ведущих вузов страны сделать это будет намного проще, чем самостоятельно по книгам.
Матрицыи матричная алгебра – Статистика Как к
Матрицы и содержание матричной алгебры (щелкните, чтобы перейти к этому разделу):
- Матричная алгебра: введение
- Добавление матрицы: другие примеры
- Умножение матриц
- Определение сингулярной матрицы
- Матрица идентичности
- Что такое обратная матрица?
- Собственные значения и собственные векторы
- Расширенные матрицы
- Определитель матрицы
- Диагональная матрица
- Что такое симметричная и кососимметричная матрицы?
- Что такое матрица транспонирования?
- Что такое матрица дисперсии-ковариации?
- Корреляционные матрицы
- Идемпотентная матрица.
Матрица – это прямоугольный массив чисел, упорядоченный по столбцам и строкам (как в электронной таблице). Матричная алгебра используется в статистике для выражения наборов данных. Например, ниже представлен рабочий лист Excel со списком оценок за экзамены:
Преобразование в матричную алгебру в основном включает удаление идентификаторов столбцов и строк. Добавляется идентификатор функции (в данном случае «G» для оценок):
Добавляется идентификатор функции (в данном случае «G» для оценок):
Числа, которые появляются в матрице, называются элементами матрицы .
: Обозначение
Почему странная нотация?
Мы используем другую нотацию (в отличие от хранения данных в формате электронной таблицы) по простой причине: соглашение. Соблюдение соглашений упрощает соблюдение правил матричной математики (таких как сложение и вычитание). Например, в элементарной алгебре, если у вас есть список, подобный этому: 2 яблока, 3 банана, 5 виноградин, вы должны изменить его на 2a + 3b + 5g, чтобы придерживаться соглашения.
Некоторые из наиболее распространенных терминов, с которыми вы столкнетесь при работе с матрицами:
- Размер (также называемый порядком): сколько строк и столбцов имеет матрица.Сначала перечислены строки, за ними следуют столбцы. Например, матрица 2 x 3 означает 2 строки и 3 столбца.
- Элементы : числа, которые появляются внутри матрицы.
- Матрица идентичности (I): Диагональная матрица с нулями в качестве элементов, за исключением диагонали, у которой есть единицы.
- Скаляр : любое действительное число.
- Матрица Функция: скаляр, умноженный на матрицу, чтобы получить другую матрицу.
Матрицы идентичности. Изображение: Википедия.com.
Матричная алгебра: сложение и вычитание
Размер матрицы (т.е. 2 x 2) также называется размером матрицы или порядком матрицы. Если вы хотите сложить (или вычесть) две матрицы, их размерность должна быть точно так же, как . Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не матрицу 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одинаковые числа в одно и то же место (например, складываете все числа в столбце 1, строке 1 и все числа в столбце 2, строке 2).
Примечание к обозначениям: рабочий лист (например, в Excel) использует буквы столбцов (ABCD) и номера строк (123), чтобы указать местоположение ячейки, например A1 или D2. Для матриц типично использование обозначений типа g ij , что означает i-ю строку и j-й столбец матрицы G.
Матричное вычитание работает точно так же.
В начало
Матричное дополнение – это всего лишь серия дополнений. Для матрицы 2 × 2:
- Сложите верхние левые числа вместе и запишите сумму в новую матрицу в верхнем левом углу.
- Сложите верхние правые числа и запишите сумму в правом верхнем углу.
- Сложите нижние левые числа вместе и запишите сумму в нижнем левом углу.
- Сложите числа справа внизу и запишите сумму справа внизу:
Используйте ту же процедуру для матрицы 2 × 3:
Фактически, вы можете использовать этот базовый метод для добавления любых матриц, если ваши матрицы имеют одинаковые размеры (одинаковое количество столбцов и строк).Другими словами, , если матрицы одинакового размера, вы можете их добавить. Если они разного размера, вы не можете их добавить.
- Матрица с 4 строками и 2 столбцами может быть добавлена к матрице с 4 строками и 2 столбцами.
- Матрица с 4 строками и 2 столбцами не может быть добавлена к матрице с 5 строками и 2 столбцами.
Вышеупомянутый метод иногда называют «начальным суммированием», поскольку вы просто складываете элементы и фиксируете результат.
Другой способ подумать об этом…
Подумайте, что представляет собой матрица. Эта очень простая матрица [5 2 5] может представлять 5x + 2y + 5z. И эта матрица [2 1 6] могла бы равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
5x + 2y + 5z + 2x + y + 6z = 7x + 3y + 11z.
Это тот же результат, что и при сложении записей в матрицах.
Дополнение матрицы для неравных размеров
Если у вас неравные размеры, вы все равно можете сложить матрицы вместе, но вам придется использовать другой (гораздо более продвинутый) метод. Один из таких приемов – прямая сумма. Прямая сумма (⊕) любой пары матриц A размера m × n и B размера p × q является матрицей размера (m + p) × (n + q):
Один из таких приемов – прямая сумма. Прямая сумма (⊕) любой пары матриц A размера m × n и B размера p × q является матрицей размера (m + p) × (n + q):
Например:
В начало
Относительно легко умножить на одно число (так называемое «скалярное умножение»), например 2:
Просто умножьте каждое число в матрице на 2, и вы получите новую матрицу. На изображении выше:
2 * 9 = 18
2 * 3 = 6
2 * 5 = 10
2 * 7 = 14
Результат четырех умножений дает числа в новой матрице справа.
Умножение матриц: две матрицы
Когда вы хотите перемножить две матрицы, процесс становится немного сложнее. Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и по столбцам второй матрицы. После того, как вы умножили, сложите продукты и запишите ответы в виде новой матрицы.
Если все это звучит немного сложно, это (очень короткое) видео показывает, как это делается:
Вы можете выполнить матричное умножение двух матриц, только если количество столбцов в первой матрице равно количеству строк во второй матрице.Например, вы можете умножить матрицу 2 x 3 (две строки и три столбца) на матрицу 3 x 4 (три строки и четыре столбца).
Очевидно, что это может стать очень сложным (и утомительным) процессом. Тем не менее, вы можете найти множество достойных инструментов для умножения матриц в Интернете. Мне нравится этот от Матрицы Решиш. После расчета вы можете умножить результат на другую матрицу и другую, что означает, что вы можете умножить несколько матриц вместе.
Microsoft Excel также может выполнять матричное умножение с использованием функций «массива».Вы можете найти инструкции здесь, на сайте Стэнфорда. Прокрутите вниз до места, где написано Матричные операции в Excel.
В начало
Быстрый взгляд на матрицу может сказать вам, является ли она сингулярной матрицей. Если матрица квадратная и имеет одну строку или столбец с нулями или , два равных столбца или две равные строки, то это особая матрица. Например, следующие десять матриц являются единственными (изображение: Wolfram):
Существуют и другие типы сингулярных матриц, некоторые из которых не так-то легко обнаружить.Следовательно, необходимо более формальное определение.
Следующие три свойства определяют сингулярную матрицу:
- Матрица квадратная и
- Не имеет инверсии.
- Имеет определитель 0.
1. Квадратная матрица
Квадратная матрица имеет (как следует из названия) равное количество строк и столбцов. Говоря более формально, вы бы сказали, что матрица из m столбцов и n строк является квадратной, если m = n.Матрицы, которые не являются квадратными, являются прямоугольными.
Сингулярная матрица – это квадратная матрица, но не все квадратные матрицы сингулярны.
Необратимые матрицы
Если квадратная матрица не имеет обратной, то это особая матрица.
Обратная матрица – это то же самое, что и обратная величина числа. Если умножить матрицу на обратную, получится единичная матрица , , матричный эквивалент 1. Идентификационная матрица в основном представляет собой последовательность единиц и нулей.Идентификационная матрица различается в зависимости от размера матрицы.
Матрицы идентичности. Изображение: Wikipedia.com.
Если вы не знакомы с поиском инверсий, вы можете посмотреть это короткое видео:
Определитель нуля
Определитель – это просто специальное число, которое используется для описания матриц и поиска решений систем линейных уравнений. Формула для вычисления определителя различается в зависимости от размера матрицы.Например, матрица 2 × 2, формула ad-bc.
Формула для вычисления определителя различается в зависимости от размера матрицы.Например, матрица 2 × 2, формула ad-bc.
Эта простая матрица 2 × 2 сингулярна, потому что ее определитель равен нулю:
К началу
Единичная матрица – это квадратная матрица с единицами в качестве элементов на главной диагонали сверху слева направо снизу и нулями в остальных местах. Когда вы умножаете квадратную матрицу на единичную матрицу, исходная квадратная матрица остается неизменной. Например:
По идее аналогичен айдентике. В базовой математике элемент идентичности оставляет число неизменным.Например, кроме того, тождественный элемент равен 0, потому что 1 + 0 = 1, 2 + 0 = 2 и т. Д., А при умножении тождественный элемент равен 1, потому что любое число, умноженное на 1, равно этому числу (т. Е. 10 * 1 = 10 ). В более формальных терминах, если x – действительное число, то число 1 называется мультипликативным тождеством , потому что 1 * x = x и x * 1 = x. По той же логике единичная матрица I получила свое название, потому что для всех матриц A , I * A = A и A * I = A .
В матричной алгебре единичный элемент различается в зависимости от размера матрицы, с которой вы работаете; в отличие от сингулярной единицы для мультипликативной идентичности и 0 для аддитивной идентичности, не существует единой единичной матрицы для всех матриц. Для любой матрицы n * n существует единичная матрица I n * n . На главной диагонали всегда будут единицы, а оставшиеся пробелы – нули. На следующем изображении показаны матрицы идентичности для матрицы 2 x 2 и матрицы 5 x 5:
Аддитивная идентификационная матрица
Когда люди говорят о «матрице идентичности», они обычно имеют в виду мультипликативную матрицу идентичности.Однако есть и другой тип: аддитивная единичная матрица. Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах – нули. Поэтому их иногда называют нулевой матрицей .
Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах – нули. Поэтому их иногда называют нулевой матрицей .
Аддитивная единичная матрица для матрицы 3 * 3.
Вернуться к началу
Обратные матрицы – это то же самое, что и обратные. В элементарной алгебре (а может быть, и раньше) вы столкнулись с идеей обратного: одно число, умноженное на другое, может равняться 1.
Изображение предоставлено LTU
Если вы умножите одну матрицу на ее обратную, вы получите матричный эквивалент 1: Identity Matrix , которая по сути представляет собой матрицу с единицами и нулями.
Поиск обратной матрицы состоит из нескольких шагов. Посмотрите это короткое видео о том, как найти обратную матрицу, или выполните следующие действия:
Шаг 1: Найдите адъюгат матрицы. Сопряжение матрицы можно найти, переставив одну диагональ и взяв негативы другой:
Чтобы найти сопряжение матрицы 2 × 2, поменяйте местами диагонали a и d, а затем поменяйте местами знаки c и d.
Шаг 2: Найдите определитель матрицы. Для матрицы
A B C D (см. Изображение выше) определитель равен (a * d) – (b * c).
Шаг 3: Умножить 1 / определитель * адъюгат. .
Проверка ответа
Вы можете проверить свой ответ умножением матриц. Умножьте свою матрицу ответов на исходную матрицу, и вы получите единичную матрицу. Вы также можете воспользоваться онлайн-калькулятором здесь.
В начало
Собственное значение (λ) – это специальный скаляр, используемый при матричном умножении и имеющий особое значение в нескольких областях физики, включая анализ устойчивости и небольшие колебания колеблющихся систем.Когда вы умножаете матрицу на вектор и получаете тот же вектор в качестве ответа вместе с новым скаляром, скаляр называется собственным значением . Основное уравнение:
Основное уравнение:
A x = λ x ; мы говорим, что λ является собственным значением A.
Все приведенное выше уравнение говорит о том, что , если вы возьмете матрицу A и умножите ее на вектор x , вы получите то же самое, как если бы вы взяли собственное значение и умножили его на вектор x .
Пример собственного значения
В следующем примере 5 – собственное значение A, а (1,2) – собственный вектор:
Давайте рассмотрим это по шагам, чтобы наглядно продемонстрировать, что такое собственное значение.В обычном умножении, если вы умножаете матрицу размера n x n на вектор n x 1, в результате вы получаете новый вектор n x 1. На следующем изображении показан этот принцип для матрицы 2 x 2, умноженной на (1,2):
Что если бы вместо новой матрицы nx 1 можно было получить ответ с тем же вектором, который вы умножили на вместе с новым скаляром?
Когда это возможно, вектор умножения (то есть тот, который также есть в ответе) называется собственным вектором, а соответствующий скаляр – собственным значением.Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение для λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (их можно иметь несколько значений для одной и той же матрицы) известно в разложении на собственные значения . Разложение на собственные числа всегда возможно, если матрица, состоящая из собственных векторов матрицы A, является квадратной.
Расчет
Найдите собственные значения для следующей матрицы:
Шаг 1: Умножьте единичную матрицу на λ.Единичная матрица для любой матрицы 2 × 2 равна [1 0; 0 1], поэтому:
Шаг 2: Вычтите ответ из шага 1 из матрицы A, используя вычитание матрицы:
Шаг 3: Найдите определитель матрицы, вычисленной на шаге 2:
det = (5- λ) (- 1-λ) – (3) (3)
Упрощая, получаем:
-5 – 5λ + λ + λ 2 – 9
= λ 2 – 4λ – 14
Шаг 4: Установите уравнение, которое вы нашли на шаге 3, равным нулю и решите для λ:
0 = λ 2 – 4λ – 14 = 2
Мне нравится использовать свой TI-83, чтобы найти корни, но вы можете также воспользуйтесь алгеброй или этим онлайн-калькулятором. Находя корни (нули), получаем x = 2 + 3√2, 2 – 3√2
Находя корни (нули), получаем x = 2 + 3√2, 2 – 3√2
Ответ : 2 + 3√2 и 2-3√2
Математика для больших матриц такая же, но вычисления могут быть очень сложными. Для матриц 3 × 3 используйте калькулятор внизу этого раздела; для больших матриц попробуйте этот онлайн-калькулятор.
В начало
На изображении выше показана расширенная матрица (A | B) внизу. Расширенные матрицы обычно используются для решения систем линейных уравнений, и именно поэтому они были впервые разработаны.Три столбца слева от полосы представляют коэффициенты (по одному столбцу для каждой переменной). Эта область называется матрицей коэффициентов . Последний столбец справа от полосы представляет собой набор констант (т. Е. Значений справа от знака равенства в наборе уравнений). Она называется расширенной матрицей , потому что матрица коэффициентов была «дополнена» значениями после знака равенства.
Например, следующая система линейных уравнений:
x + 2y + 3z = 0
3x + 4y + 7z = 2
6x + 5y + 9z = 11
Может быть помещено в следующую расширенную матрицу:
После того, как вы поместили свою систему в расширенную матрицу, вы можете выполнять операции со строками для решения системы.
У вас нет , у вас нет , чтобы использовать вертикальную черту в расширенной матрице. Обычно матрицы вообще не содержат линий. Полоса просто упрощает отслеживание ваших коэффициентов и ваших констант справа от знака равенства. Если вы вообще используете вертикальную полосу, зависит от учебника, который вы используете, и от предпочтений вашего преподавателя.
Написание системы уравнений
Вы также можете работать в обратном направлении, чтобы написать систему линейных уравнений, заданную расширенной матрицей.
Пример вопроса: Напишите систему линейных уравнений для следующей матрицы.
Шаг 1: Запишите коэффициенты для первого столбца, за которым следует «x». Обязательно запишите положительные или отрицательные числа:
Обязательно запишите положительные или отрицательные числа:
-1x
2x
6x
Шаг 2: Напишите коэффициенты для второго столбца, а затем укажите «y». Сложите, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y
2x + 4y
6x + 2y
Шаг 3: Напишите коэффициенты для второго столбца, после чего укажите «z.«Сложите, если это положительное число, и вычтите, если оно отрицательное:
-1x + 7y + 3
2x + 4y – 7
6x + 2y + 9
Шаг 3. Запишите константы в третьем столбце, поставив перед знаком равенства.
-1x + 7y + 3 = 0
2x + 4y – 7 = 2
6x + 2y + 9 = 7
Примечание : если на этом этапе у вас стоит отрицательный знак, просто сделайте константу отрицательным числом.
В начало
Определитель матрицы – это просто специальное число, которое используется для описания матриц для нахождения решений систем линейных уравнений, нахождения обратных матриц и для различных приложений в исчислении.Определить на простом английском языке невозможно; обычно его определяют в математических терминах или в терминах того, что он может вам помочь. Определитель матрицы имеет несколько свойств:
- Это реальный номер. Сюда входят отрицательные числа.
- Определители существуют только для квадратных матриц.
- Обратная матрица существует только для матриц с ненулевыми определителями.
Символ для определителя матрицы A – это | A |, который также является тем же самым символом, который используется для абсолютного значения, хотя эти два символа не имеют ничего общего друг с другом.
Формула для вычисления определителя матрицы различается в зависимости от размера матрицы.
Определитель матрицы 2 × 2
Формула определителя матрицы 2 × 2 – ad-bc. Другими словами, умножьте верхний левый элемент на нижний правый, затем вычтите произведение верхнего правого и нижнего левого.
Определитель матрицы 3 × 3
Определитель матрицы 3 × 3 находится по следующей формуле:
| A | = a (ei – fh) – b (di – fg) + c (dh – eg)
Это может показаться сложным, но если вы пометили элементы с помощью a, b, c в верхнем ряду, d, e, f во второй строке и g, h, i в последней, становится основной арифметикой.
Пример :
Найдите определитель следующей матрицы 3 × 3:
= 3 (6 × 2-7 × 3) –5 (2 × 2-7 × 4) +4 (2 × 3-6 × 4)
= -219
По сути, здесь происходит умножение a, b и d на детерминанты меньших 2×2 в матрице 3×3. Этот шаблон продолжается для поиска определителей матриц более высокого порядка.
Определитель матрицы 4 × 4
Чтобы найти определитель матрицы 4 × 4, вам сначала нужно найти определители четырех матриц 3 × 3, которые находятся в матрице 4 × 4.В виде формулы:
Вернуться к началу
Диагональная матрица – это симметричная матрица со всеми нулями, кроме ведущей диагонали, которая проходит от верхнего левого угла до нижнего правого.
Записи на самой диагонали также могут быть нулями; любую квадратную матрицу со всеми нулями еще можно назвать диагональной матрицей.
Единичная матрица, которая имеет все 1 по диагонали, также является диагональной матрицей. Любая матрица с равными элементами по диагонали (т. Е.2,2,2 или 9,9,9), является скалярным кратным единичной матрицы и также может быть классифицировано как диагональное.
Диагональная матрица имеет максимум n чисел, которые не равны нулю, где n – порядок матрицы. Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.
Обозначение
Обозначение, обычно используемое для описания диагональной матрицы: diag (a, b, c) , где abc представляет числа в первой диагонали.Для приведенной выше матрицы это обозначение будет diag (3,2,4). .
Верхняя и нижняя треугольные матрицы
Диагональ матрицы всегда относится к ведущей диагонали. Ведущая диагональ в матрице помогает определить два других типа матриц: нижнетреугольные матрицы и верхние треугольные матрицы. В нижнетреугольной матрице числа под диагональю; верхнетреугольная матрица имеет числа над диагональю.
Диагональная матрица – это матрица с нижней диагональю и с нижней диагональю.
Прямоугольные диагональные матрицы
Для наиболее распространенного использования диагональная матрица представляет собой квадратную матрицу с порядком (размером) n . Существуют и другие формы, которые обычно не используются, например прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы – нули. Ведущая диагональ берется из наибольшего квадрата неквадратной матрицы.
В начало
Транспонирование матрицы (или транспонирование матрицы) – это как раз то место, где вы переключаете все строки матрицы в столбцы.Матрицы транспонирования полезны при комплексном умножении.
Альтернативный способ описания транспонированной матрицы состоит в том, что элемент в строке «r» и столбце «c» транспонируется в строку «c» и столбец «r». Например, элемент в строке 2, столбце 3 будет транспонирован в столбец 2, строку 3. Размер матрицы также изменится. Например, если у вас есть матрица 4 x 5, вы бы транспонировали ее в матрицу 5 x 4.
Симметричная матрица – это частный случай транспонированной матрицы; он равен своей транспонированной матрице.
Говоря более формальным языком, A = A T .
Символы для транспонированной матрицы
Обычный символ для транспонированной матрицы – A T Однако Wolfram Mathworld утверждает, что также используются два других символа: A ‘ и.
Свойства матриц транспонирования
Свойства транспонированных матриц аналогичны основным числовым свойствам, с которыми вы столкнулись в базовой алгебре (например, ассоциативным и коммутативным). Основные свойства матриц:
- (A T ) T = A: транспонированная матрица транспонирования является исходной матрицей.
- (A + B) T = A T + B T : Транспонирование двух сложенных вместе матриц такое же, как транспонирование каждой отдельной матрицы, сложенной вместе.

- (rA) T = rA T : когда матрица умножается на скалярный элемент, не имеет значения, в каком порядке вы транспонируете (примечание: скалярный элемент – это величина, которая может умножать матрицу).
- (AB) T = B T A T : транспонирование двух матриц, умноженных вместе, совпадает с произведением их матриц транспонирования в обратном порядке.
- (A -1 ) T = (A T ) -1 : транспонирование и инверсия матрицы могут выполняться в любом порядке.
В начало
Симметричная матрица – это квадратная матрица, имеющая симметрию относительно ведущей диагонали, сверху слева направо. Представьте себе складку в матрице по диагонали (не включайте числа в действительную диагональ). Верхняя правая половина матрицы и нижняя левая половина являются зеркальными отображениями относительно диагонали:
Если вы можете сопоставить числа друг с другом вдоль линии симметрии ( всегда ведущая диагональ), как в примере справа , у вас симметричная матрица.
Альтернативное определение
Другой способ определить симметричную матрицу состоит в том, что симметричная матрица равна ее транспонированной. транспонирование матрицы – это когда первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы.
Если вы возьмете симметричную матрицу и транспонируете ее, матрица будет выглядеть точно так же, отсюда и альтернативное определение, что симметричная матрица равна ее транспонированию.С математической точки зрения, M = M T , где M T – матрица транспонирования.
Максимальное количество номеров
Поскольку большинство чисел в симметричной матрице дублируются, существует ограничение на количество различных чисел, которые она может содержать. Уравнение для максимального количества чисел в матрице порядка n: n (n + 1) / 2. Например, в симметричной матрице 4-го порядка, подобной приведенной выше, имеется максимум 4 (4 + 1) / 2 = 10 различных чисел. Это имеет смысл, если подумать: диагональ – это четыре числа, и если вы сложите числа в нижней левой половине (исключая диагональ), вы получите 6.
Уравнение для максимального количества чисел в матрице порядка n: n (n + 1) / 2. Например, в симметричной матрице 4-го порядка, подобной приведенной выше, имеется максимум 4 (4 + 1) / 2 = 10 различных чисел. Это имеет смысл, если подумать: диагональ – это четыре числа, и если вы сложите числа в нижней левой половине (исключая диагональ), вы получите 6.
Диагональные матрицы
Диагональная матрица – это частный случай симметричной матрицы. Диагональная матрица имеет все нули, кроме ведущей диагонали.
Что такое асимметричная матрица?
Кососимметричная матрица, иногда называемая антисимметричной матрицей , представляет собой квадратную матрицу, симметричную относительно обеих диагоналей. Например, следующая матрица является асимметричной:
Математически асимметричная матрица удовлетворяет условию a ij = -a ji .Например, возьмите запись в строке 3, столбец 2, которая равна 4. Его симметричный аналог – -4 в строке 2, столбце 3. Это условие также можно записать в терминах его транспонированной матрицы: A T = – А. Другими словами, матрица является кососимметричной, только если A T = -A, где A T – это транспонированная матрица.
Все старшие диагональные элементы в кососимметричной матрице должны быть нулевыми. Это потому, что из i, i = −a i, i следует i, i = 0.
Еще одним интересным свойством этого типа матрицы является то, что если у вас есть две кососимметричные матрицы A и B одинакового размера, вы также получите кососимметричную матрицу, если сложите их вместе:
Добавление двух кососимметричных матриц все вместе.
Этот факт может помочь вам доказать, что две матрицы кососимметричны. Первый шаг – убедиться, что все элементы на главной диагонали равны нулю (что невозможно «доказать» математически!).Второй шаг – сложение матриц. Если результатом является третья матрица, которая является кососимметричной, то вы доказали, что a ij = – a ji .
Косоэрмитский
Косоэрмитова матрица по существу такая же, как кососимметричная матрица, за исключением того, что косоэрмитова матрица может содержать комплексные числа.
Косоэрмитова матрица, показывающая комплексные числа.
Фактически, кососимметричный и кососимметричный эквивалентны для вещественных матриц (матрицы, которая почти полностью состоит из действительных чисел).Старшая диагональ косоэрмитовой матрицы должна содержать чисто мнимые числа; в мнимой сфере ноль считается мнимым числом.
Вернуться к началу
Матрица ковариации и дисперсии (также называемая матрицей ковариации или матрицей дисперсии) – это квадратная матрица, которая отображает дисперсию и ковариацию двух наборов двумерных данных вместе. Разница – это мера того, насколько разбросаны данные. Ковариация – это мера того, насколько две случайные величины перемещаются вместе в одном направлении.
Дисперсии отображаются в диагональных элементах, а ковариации между парами переменных отображаются в недиагональных элементах. Дисперсии находятся в диагоналях ковариантной матрицы, потому что, по сути, эти дисперсии являются ковариатами каждой отдельной переменной с самой собой.
Следующая матрица показывает дисперсию для A (2,00), B (3,20) и C (0,21) в диагональных элементах.
Ковариации для каждой пары показаны в других ячейках.Например, ковариация для A и B равна -0,21, а ковариация для A и C равна -0,10. Вы можете посмотреть столбец и строку или строку и столбец (например, AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, ковариация дисперсии матрица также является симметричной матрицей.
Создание матрицы дисперсии-ковариации
Многие статистические пакеты, включая Microsoft Excel и SPSS, могут создавать ковариативно-вариативные матрицы. Обратите внимание, что Excel вычисляет ковариацию для генеральной совокупности (знаменатель n), а не для выборки (n-1). Это может привести к немного неправильным вычислениям для матрицы дисперсии-ковариации. Чтобы исправить это, вам нужно умножить каждую ячейку на n / n-1.
Это может привести к немного неправильным вычислениям для матрицы дисперсии-ковариации. Чтобы исправить это, вам нужно умножить каждую ячейку на n / n-1.
Если вы хотите сделать один вручную:
Шаг 1: Вставьте отклонения для ваших данных в диагонали матрицы.
Шаг 2: Рассчитайте ковариацию для каждой пары и введите их в соответствующую ячейку. Например, ковариация для A / B в приведенном выше примере появляется в двух местах (A B и B A). На следующей диаграмме показано, где каждая ковариация и дисперсия появляются для каждого варианта.
В начало
См. Также:
Что такое матрица неточностей?
Следующий : Форма Row Echelon Form / Форма Row Echelon Form
————————————————– —————————-Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Матрицы
Матрица – это массив чисел:
Матрица
(в ней 2 строки и 3 столбца)
Речь идет об одной матрице , или нескольких матрицах .
Мы можем многое с ними сделать …
Добавление
Чтобы сложить две матрицы: сложите числа в соответствующих позициях:
Это расчеты:
| 3 + 4 = 7 | 8 + 0 = 8 |
| 4 + 1 = 5 | 6−9 = −3 |
Две матрицы должны быть одинакового размера, т.е.е. строки должны совпадать по размеру, а столбцы должны совпадать по размеру.
Пример: матрица с 3 строками и 5 столбцами может быть добавлена к другой матрице из 3 строки и 5 столбцов .
Но его нельзя было добавить в матрицу с 3 строками и 4 столбцами (столбцы не совпадают по размеру)
отрицательный
Негатив матрицы тоже прост:
Это расчеты:
| – (2) = – 2 | – (- 4) = + 4 |
| – (7) = – 7 | – (10) = – 10 |
Вычитание
Чтобы вычесть две матрицы: вычтите числа в совпадающих позициях:
Это расчеты:
| 3-4 = -1 | 8−0 = 8 |
| 4−1 = 3 | 6 – (- 9) = 15 |
Примечание: вычитание фактически определяется как сложение отрицательной матрицы: A + (-B)
Умножить на константу
Мы можем умножить матрицу на константу (в данном случае значение 2) :
Это расчеты:
| 2 × 4 = 8 | 2 × 0 = 0 |
| 2 × 1 = 2 | 2 × −9 = −18 |
Мы называем константу скаляром , поэтому официально это называется «скалярное умножение».
Умножение на другую матрицу
Чтобы умножить две матрицы вместе, немного сложнее … прочтите Умножение матриц, чтобы узнать, как.
Разделение
А что с делением? Ну, мы не делим матрицы на , мы делаем это так:
A / B = A × (1 / B) = A × B -1
, где B -1 означает «инверсию» B.
Итак, мы не делим, вместо этого мы умножаем на обратное .
И есть особые способы найти обратное, подробнее см. Обратный к матрице.
Обратный к матрице.
Транспонирование
Чтобы «транспонировать» матрицу, поменяйте местами строки и столбцы.
Мы ставим букву “Т” в верхнем правом углу, чтобы обозначить транспонирование:
Обозначение
Матрица обычно обозначается заглавной буквой (например, A или B)
Каждая запись (или «элемент») обозначается строчной буквой с «нижним индексом» строки , столбец :
Строки и столбцыИтак, какая строка, а какая колонка?
Чтобы помнить, что строки идут перед столбцами, используйте слово «дуга» : а р, в |
Пример:
| B = |
Вот несколько примеров записей:
b 1,1 = 6 (запись в строке 1, столбце 1 – 6)
b 1,3 = 24 (запись в строке 1, столбце 3 – 24)
b 2,3 = 8 (запись в строке 2, столбце 3 – 8)
Учебник по матричной алгебре
Это руководство представляет собой краткое, легкое для понимания введение в матричную алгебру, акцентируя внимание на матричных методах, широко используемых в статистике и математика.> Начать урок 1
Об учебнике
После прохождения этого руководства вы познакомитесь с номенклатурой и обозначения, используемые матричной алгеброй. И вы сможете:
- Выполнять стандартные операции с матрицами (сложение, вычитание, умножение,
так далее.
 ).
). - Определить ранг матрицы (т.е. отличить сингулярное от несингулярного матрицы).
- Найдите определитель и обратную величину для любой квадратной матрицы.
- Используйте матричную алгебру для решения одновременных линейных уравнений.
- Компактно выражайте вычисления и системы уравнений в матричном формате.
- И многое другое …
Темы представлены в виде коротких, простых для понимания модулей. Каждый урок охватывает одну тему, и большинство уроков включают один или несколько контрольных вопросов для закрепления знаний.
Это руководство предназначено для студентов и исследователей, знакомых с вводной статистикой (например,g., курс статистики средней школы или Расширенная статистика размещения).
Как использовать этот учебник
Индивидуальные уроки доступны через оглавление, которое можно находится в вертикальном столбце в левой части страницы. Если вы уже знакомы с матричной алгеброй, вы можете выбрать любое занятие наугад и работать эффективно.
Индивидуальные уроки доступны через оглавление, которое можно доступ к нему можно получить, нажав кнопку «Матричная алгебра: оглавление» вверху страницы.Если вы уже знакомы с матричной алгеброй, вы можете выбрать любое занятие наугад и работать эффективно.
Однако, если вы новичок в этой теме, вы должны проработать уроки в том порядке, в котором они появляются; потому что каждый урок основан на предыдущие уроки.
Как работать с матрицами (алгебра 2, матрицы) – Mathplanet
Матрицы считаются равными, если они имеют одинаковые размеры и если каждый элемент одной матрицы равен соответствующему элементу другой матрицы.Вы можете умножить матрицу на любую константу, это называется скалярным умножением.
Пример
$$ 2 \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} = \ begin {bmatrix} {\ color {green} 2} \ cdot 1 & {\ color {green} 2} \ cdot2 \ \ {\ color {green} 2} \ cdot3 & {\ color {green} 2} \ cdot4 \ end {bmatrix} = \ begin {bmatrix} 2 & 4 \\ 6 & 8 \ end {bmatrix} $$
Матрицы одинакового размера могут быть добавлены и вычтены, а матрицы совместимых размеров могут быть умножены.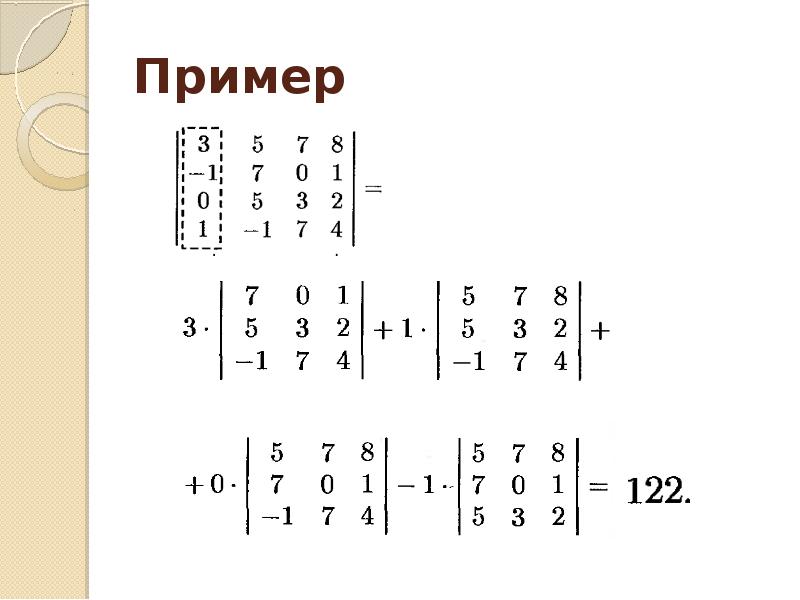
Пример
Сложите две матрицы A и B:
$$ A = \ begin {bmatrix} {\ color {green} 2} & {\ color {green} -1} \\ {\ color {green} 1} & {\ color {green} 0} \ end { bmatrix} B = \ begin {bmatrix} {\ color {blue} 1} & {\ color {blue} 4} \\ {\ color {blue} 2} & \, {\ color {blue} 3} \ end { bmatrix} $$
Это возможно, поскольку A и B, поскольку обе матрицы имеют две строки и два столбца. Мы добавляем каждый элемент в матрицу A к соответствующему элементу в матрице B:
$$ A + B = \ begin {bmatrix} {\ color {green} 2} + {\ color {blue} 1} & {\ color {green} -1} + {\ color {blue} 4} \\ {\ color {green} 1} + {\ color {blue} 2} & {\ color {green} 0} + \, {\ color {blue} 3} \ end {bmatrix} = \ begin {bmatrix} 3 & 3 \\ 3 & 3 \ end {bmatrix} $$
Матрицы вычитаются таким же образом.
Если умножить матрицу A p * q и матрицу B m * n , то произведение будет
$$ A_ {p \ times q} + B_ {m \ times n} = (AB) _ {p \ times n} $$
Элемент в g-й строке и h-м столбце AB является суммой произведения соответствующих элементов в g-й строке A и h-м столбце B. Вы можете перемножить только две матрицы. если количество столбцов в первой матрице и количество строк во второй равны.
Пример
Умножаем матрицы A и B:
$$ A = \ begin {bmatrix} {\ color {green} 1} & {\ color {green} 3} \\ {\ color {green} -1} & {\ color {green} 0} \ end { bmatrix} B = \ begin {bmatrix} {\ color {blue} 2} & {\ color {blue} 1} & {\ color {blue} 1} \\ {\ color {blue} -1} & {\ color {blue} 2} & {\ color {blue} 4} \ end {bmatrix} $$
Это возможно, поскольку первая матрица содержит 2 столбца, а вторая – 2 строки.
$$ \\ AB = \ begin {bmatrix} {\ color {green} 1} \ cdot {\ color {blue} 2} + {\ color {green} 3} \ cdot {\ color {blue} -1} & {\ color {green} 1} \ cdot {\ color {blue} 1} + {\ color {green} 3} \ cdot {\ color {blue} 2} & {\ color {green} 1} \ cdot { \ color {blue} 1} + {\ color {green} 3} \ cdot {\ color {blue} 4} \\ {\ color {green} -1} \ cdot {\ color {blue} 2} + {\ color {зеленый} 0} \ cdot {\ color {blue} -1} & {\ color {green} -1} \ cdot {\ color {blue} 1} + {\ color {green} 0} \ cdot {\ color {blue} 2} & {\ color {green} -1} \ cdot {\ color {blue} 1} + {\ color {green} 0} \ cdot {\ color {blue} 4} \ end {bmatrix} = \\ \\ = \ begin {bmatrix} -1 & 7 & 13 \\ -2 & -1 & -1 \ end {bmatrix} $$
Видеоурок
Если возможно, выполните указанную операцию:
$$ \ begin {bmatrix} 2 & 0 \\ 1 & 3 \\ -4 & 1 \ end {bmatrix} \ cdot \ begin {bmatrix} 6 & 2 & 3 \\ 0 & -2 & 4 \ end {bmatrix} $$
youtube.com/embed/T8IxPm8Yals?fs=1&hl=sv_SE&rel=0″ allowfullscreen=””/>
Операции с матрицами
Что касается линейной алгебры, две наиболее важные операции с векторами – это сложение векторов [сложение двух (или более) векторов] и скалярное умножение (умножение вектора на скаляр).Аналогичные операции определены для матриц.
Сложение матрицы . Если A и B являются матрицами одного размера , то они могут быть добавлены. (Это похоже на ограничение на добавление векторов, а именно, можно добавить только векторы из того же пространства R n ; например, вы не можете добавить 2-вектор к 3-вектору.) Если A = [ a ij ] и B = [ b ij ] – обе матрицы m x n , затем их сумма, C = A + B , также является матрицей m x n , и ее элементы задаются формулой
Таким образом, чтобы найти записи A + B , просто добавьте соответствующие записи A и B .
Пример 1 : Рассмотрим следующие матрицы:
Какие два можно добавить? Какова их сумма?
Поскольку можно складывать только матрицы одного размера, определяется только сумма F + H ( G не может быть добавлен ни к F , ни к H ). Сумма F и H составляет
.Поскольку сложение действительных чисел коммутативно, отсюда следует, что сложение матриц (если оно определено) также коммутативно; то есть для любых матриц A и B одинакового размера, A + B всегда будет равно B + A .
Пример 2 : Если какая-либо матрица A добавляется к нулевой матрице того же размера, результат явно будет равен A :
Это матричный аналог утверждения a + 0 = 0 + a = a , который выражает тот факт, что число 0 является аддитивной единицей в наборе действительных чисел.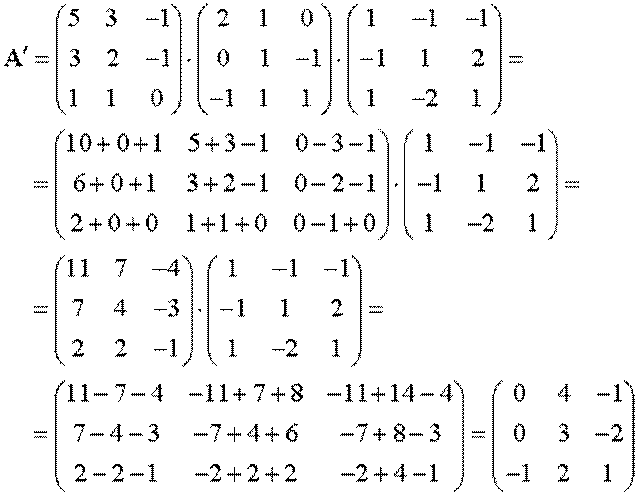
Пример 3 : Найдите матрицу B такую, что A + B = C , где
Если
, тогда матричное уравнение A + B = C становится
Поскольку две матрицы равны тогда и только тогда, когда они имеют одинаковый размер и их соответствующие элементы равны, из этого последнего уравнения следует
Следовательно,
Этот пример мотивирует определение вычитания матрицы : Если A и B являются матрицами одинакового размера, то элементы A – B находятся простым вычитанием элементов B из соответствующие записи A .Поскольку уравнение A + B = C эквивалентно B = C – A , использование вычитания матрицы выше даст тот же результат:
Скалярное умножение . Матрицу можно умножить на скаляр следующим образом. Если A = [ a ij ] – матрица, а k – скаляр, то
То есть матрица kA получается путем умножения каждой записи A на k .
Пример 4 : Если
, то скалярное кратное 2 A получается путем умножения каждой записи A на 2:
Пример 5 : Если A и B – матрицы одинакового размера, то A – B = A + (- B ), где – B – скалярное кратное (-1) В . Если
, затем
Это определение вычитания матрицы согласуется с определением, проиллюстрированным в Примере 8.
Пример 6 : Если
, затем
Умножение матриц . Безусловно, наиболее важной операцией, связанной с матрицами, является умножение матриц , процесс умножения одной матрицы на другую. Первый шаг в определении умножения матриц – вспомнить определение скалярного произведения двух векторов. Пусть r и c будут двумя векторами n ‐. Записывая r как матрицу-строку 1 x n и c как матрицу столбца n x 1, скалярное произведение r и c равно
Первый шаг в определении умножения матриц – вспомнить определение скалярного произведения двух векторов. Пусть r и c будут двумя векторами n ‐. Записывая r как матрицу-строку 1 x n и c как матрицу столбца n x 1, скалярное произведение r и c равно
Обратите внимание, что для определения скалярного произведения r и c оба должны содержать одинаковое количество записей.Кроме того, здесь важен порядок, в котором эти матрицы записаны в этом продукте: вектор-строка идет первым, вектор-столбец – вторым.
Теперь последний шаг: как умножаются две общие матрицы? Во-первых, чтобы сформировать продукт AB, количество столбцов A должно соответствовать количеству строк B ; если это условие не выполняется, то продукт AB не определен. Этот критерий следует из указанного выше ограничения на умножение матрицы строк r на матрицу столбцов c , а именно, что количество записей в r должно соответствовать количеству записей в c .Если A составляет м x n и B составляет n x p , то продукт AB определен, и размер матрицы продукта AB будет м x с. . Следующая диаграмма помогает определить, определен ли матричный продукт, и если да, то размеры продукта:
Представление матрицы m x n A как составной из векторов-строк r 1 , r 2 ,…, r m из R n и n x p матрица B , составленная из векторов-столбцов c 1 , c 2 ,…, c p от R № ,
и
правило вычисления элементов матричного произведения AB : r i · c j = ( AB ) ij , то есть
Пример 7 : Учитывая две матрицы
определяет, какой матричный продукт, AB или BA , определен, и оценивает его.
Поскольку A – 2 x 3, а B – 3 x 4, произведение AB в таком порядке определяется, а размер матрицы произведения AB будет 2 x 4. Произведение BA – это , а не , поскольку первый фактор ( B ) имеет 4 столбца, а второй коэффициент ( A ) имеет только 2 строки. Количество столбцов первой матрицы должно соответствовать количеству строк второй матрицы, чтобы их произведение было определено.
Взяв скалярное произведение строки 1 в строке A и столбца 1 в строке B , получаем запись (1, 1) в строке AB . С
запись (1, 1) в AB – это 1:
Скалярное произведение строки 1 в A и столбца 2 в B дает запись (1, 2) в AB ,
и скалярное произведение строки 1 в A и столбце 3 в B дает запись (1, 3) в AB :
Первая строка произведения завершается скалярным произведением строки 1 в A и столбца 4 в B , что дает запись (1, 4) в AB :
Теперь для второй строки AB : скалярное произведение строки 2 в A и столбца 1 в B дает запись (2, 1) в AB ,
и скалярное произведение строки 2 в A и столбце 2 в B дает запись (2, 2) в AB :
Наконец, взяв скалярное произведение строки 2 в A со столбцами 3 и 4 в B , получаем (соответственно) записи (2, 3) и (2, 4) в AB :
Следовательно,
Пример 8 : Если
и
вычисляет (3, 5) запись продукта CD .
Во-первых, обратите внимание, что, поскольку C составляет 4 x 5, а D составляет 5 x 6, произведение CD действительно определено, и его размер равен 4 x 6. Однако нет необходимости вычислять все двадцать‐ четыре записи CD , если требуется только одна конкретная запись. Запись (3, 5) в CD является скалярным произведением строки 3 в C и столбца 5 в D :
Запись (3, 5) в CD является скалярным произведением строки 3 в C и столбца 5 в D :
Пример 9 : Если
убедитесь, что
но
В частности, обратите внимание, что хотя оба продукта AB и BA определены, AB не равно BA ; действительно, они даже не одного размера!
Предыдущий пример иллюстрирует, возможно, самое важное различие между умножением скаляров и умножением матриц.Для действительных чисел a и b всегда выполняется уравнение ab = ba , то есть умножение действительных чисел коммутативно; порядок, в котором написаны коэффициенты, не имеет значения. Однако категорически неверно, что умножение матриц коммутативно. Для матриц A и B , приведенных в примере 9, были определены оба произведения AB и BA , но они определенно не были идентичными. Фактически, матрица AB была 2 x 2, а матрица BA была 3 x 3.Вот еще одна иллюстрация некоммутативности умножения матриц: Рассмотрим матрицы
Поскольку C составляет 3 x 2, а D – 2 x 2, продукт CD определен, его размер составляет 3 x 2, и
Продукт DC , однако, не определен, так как количество столбцов D (которое равно 2) не равно количеству строк C (которое равно 3). Следовательно, CD ≠ DC , поскольку DC даже не существует.
Из-за чувствительности к порядку записи коэффициентов обычно не говорят просто: «Умножьте матрицы A, и B, ». Обычно важно указать, какая матрица идет первой, а какая – второй в продукте. По этой причине выражение «Умножить A справа на B » означает образовать произведение AB , а «Умножить A слева на B » означает образовать произведение BA .
Пример 10 : Если
и x – это вектор (−2, 3), покажите, как A можно умножить справа на x и вычислить произведение.
Поскольку A равно 2 x 2, чтобы умножить A справа на матрицу, эта матрица должна иметь 2 строки. Следовательно, если x записано как 2 x 1 столбец матрица
, то можно вычислить произведение A x , и в результате получится еще одна матрица столбца 2 x 1:
Пример 11 : Рассмотрим матрицы
Если A умножить справа на B , получится
, но если A умножить слева на B , то получится
Обратите внимание, что оба продукта определены и имеют одинаковый размер, но не равны.
Пример 12 : Если A и B – квадратные матрицы, такие, что AB = BA , то A и B говорят, что коммутируют . Покажите, что любые две квадратные диагональные матрицы порядка 2 коммутируют.
Пусть
– две произвольные диагональные матрицы 2 x 2. Тогда
и
Начиная с a 11 b 11 = b 11 a 11 и a 22 b 22 = b 2212 a 22 , AB действительно равно BA , как и нужно.
Хотя матричное умножение обычно не коммутативно, оно иногда коммутативно; например, если
, затем
Несмотря на такие примеры, как эти, необходимо указать, что в целом умножение матриц не является коммутативным .
Есть еще одно различие между умножением скаляров и умножением матриц. Если a и b – действительные числа, тогда уравнение ab = 0 означает, что a = 0 или b = 0. То есть, единственный способ, при котором произведение действительных чисел может быть равным 0, – это если хотя бы один из множителей сам равен 0. Аналогичное утверждение для матриц, однако, неверно. Например, если
То есть, единственный способ, при котором произведение действительных чисел может быть равным 0, – это если хотя бы один из множителей сам равен 0. Аналогичное утверждение для матриц, однако, неверно. Например, если
, затем
Обратите внимание, что даже несмотря на то, что ни G , ни H не являются нулевой матрицей, произведение GH является.
Еще одно различие между умножением скаляров и умножением матриц – это отсутствие общего закона сокращения для умножения матриц.Если a, b и c являются действительными числами с a ≠ 0, то, отбрасывая множитель a , уравнение ab = ac подразумевает b = c . Для умножения матриц такого закона не существует; то есть утверждение AB = AC не означает , а не , подразумевает B = C , даже если A не равно нулю. Например, если
, затем оба
и
Таким образом, даже если AB = AC и A не является нулевой матрицей, B не равно C .
Пример 13 : Хотя умножение матриц не всегда коммутативно, оно всегда ассоциативно . То есть, если A, B и C являются любыми тремя матрицами, так что продукт (AB) C определен, то продукт A (BC) также определен, и
То есть, пока порядок факторов не меняется, то, как они сгруппированы , не имеет значения.
Проверить ассоциативный закон для матриц
Первый, с
продукт (AB) C –
Сейчас, с
продукт A (BC) равен
Следовательно, (AB) C = A (BC) , как и ожидалось.Обратите внимание, что ассоциативный закон подразумевает, что произведение A, B и C (в таком порядке) может быть записано просто как ABC ; круглые скобки не нужны, чтобы разрешить двусмысленность, потому что нет двусмысленности.
Пример 14 : Для матриц
проверьте уравнение ( AB ) T = B T A T .
Первая,
означает
Сейчас, с
B T A T действительно равно ( AB ) T .Фактически, уравнение
верно для любых двух матриц, для которых определено произведение AB . Это говорит о том, что если продукт AB определен, то транспонирование продукта равно произведению перемещений в обратном порядке .
Матрицы идентичности . Нулевая матрица 0 m x n играет роль аддитивной идентичности в наборе матриц m x n точно так же, как число 0 в наборе действительных чисел (вспомните пример 7).То есть, если A является матрицей m x n и 0 = 0 m x n , то
Это матричный аналог утверждения, что для любого действительного числа a ,
Имея в руках аддитивную идентичность, вы можете спросить: «А как насчет мультипликативной идентичности ?» В наборе действительных чисел мультипликативным тождеством является число 1, так как
Есть ли матрица, которая играет эту роль ? Рассмотрим матрицы
и убедитесь, что
и
Таким образом, AI = IA = A .Фактически, можно легко показать, что для этой матрицы I оба продукта AI и IA будут равны A для любой матрицы 2 x 2 A . Следовательно,
– мультипликативная единица в наборе матриц 2 x 2. Аналогично матрица
– мультипликативная единица в наборе матриц 3 x 3 и так далее. (Обратите внимание, что I 3 – это матрица [δ ij ] 3 x 3 .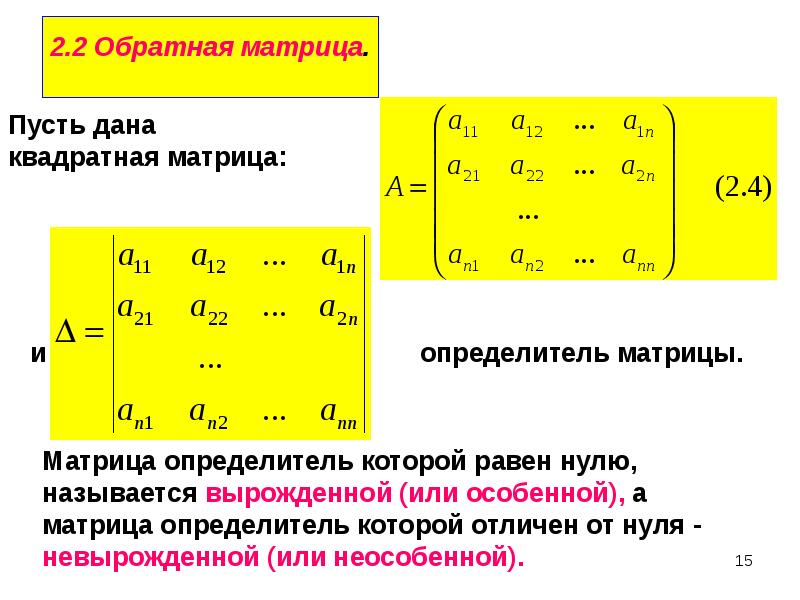 В общем случае матрица I n – диагональная матрица nxn с каждым диагональным элементом, равным 1 – называется единичной матрицей порядка n и служит мультипликативной единицей в наборе всех nxn матриц.
В общем случае матрица I n – диагональная матрица nxn с каждым диагональным элементом, равным 1 – называется единичной матрицей порядка n и служит мультипликативной единицей в наборе всех nxn матриц.
Есть ли мультипликативная идентичность в наборе всех матриц m x n , если m ≠ n ? Для любой матрицы A в M mxn ( R ) матрица I m является левой единицей ( I m A = A ) и I n – это правый идентификатор ( AI n = A ).Таким образом, в отличие от набора матриц n x n , набор неквадратных матриц m x n не обладает двухсторонней идентичностью qunique , потому что I m ≠ I n , если m ≠ n .
Пример 15 : Если A – квадратная матрица, то A 2 обозначает продукт AA, A 3 обозначает продукт AAA и т. Д. Если A – это матрица
показывают, что A 3 = – A .
Расчет
показывает, что A 2 = – I . Умножение обеих частей этого уравнения на A дает A 3 = – A , если требуется. [Техническое примечание: можно показать, что в определенном точном смысле набор матриц вида
, где a и b – действительные числа, структурно идентичен набору из комплексных чисел a + bi .Поскольку матрица A в этом примере имеет такую форму (с a = 0 и b = 1), A соответствует комплексному числу 0 + 1 i = i и аналогу матричное уравнение A 2 = – I , полученное выше, равно i 2 = -1, уравнение, которое определяет мнимую единицу, i . ]
]
Пример 16 : Найдите недиагональную матрицу, которая коммутирует с
Проблема состоит в том, чтобы получить недиагональную матрицу B , такую что AB = BA .Как и A , матрица B должна быть 2 x 2. Один из способов создать такую матрицу B – сформировать A 2 , поскольку, если B = A 2 , ассоциативность подразумевает
(Это уравнение доказывает, что A 2 будет коммутировать с A для любой квадратной матрицы A ; кроме того, оно предлагает, как можно доказать, что каждая интегральная степень квадратной матрицы A будет добираться до A .)
В данном случае
, который недиагонален. Эта матрица B действительно коммутирует с A , что подтверждается расчетами
.и
Пример 17 : Если
доказывают, что
для каждого натурального числа n .
Несколько предварительных расчетов показывают, что данная формула действительно верна:
Однако, чтобы установить, что формула выполняется для всех натуральных чисел n , необходимо дать общее доказательство.Здесь это будет сделано с использованием принципа математической индукции , который читается следующим образом. Пусть P (n) обозначает предложение относительно натурального числа n . Если можно показать, что
и
, то утверждение P (n) действительно для всех натуральных чисел n . В данном случае утверждение P (n) является утверждением
Поскольку A 1 = A , утверждение P (1) определенно верно, поскольку
Теперь, предполагая, что P (n) истинно, то есть предполагая, что
теперь необходимо установить действительность выписки П ( n + 1), что составляет
Но это утверждение действительно верно, потому что
По принципу математической индукции доказательство завершено.
Обратная матрица . Пусть a будет заданным действительным числом. Поскольку 1 является мультипликативным тождеством в наборе действительных чисел, если существует число b такое, что
, затем b называется , обратным или мультипликативным обратным для a и обозначается a -1 (или 1/ a ). Аналог этого утверждения для квадратных матриц выглядит следующим образом. Пусть A будет заданной матрицей n x n .Поскольку I = I n является мультипликативным тождеством в наборе матриц n x n , если существует матрица B , такая что
, затем B называется (мультипликативным) , обратным из A и обозначается A -1 (читается « A inverse»).
Пример 18 : Если
, затем
с
и
Еще одно различие между умножением скаляров и умножением матриц заключается в существовании инверсий.Хотя каждое ненулевое действительное число имеет обратное, существуют ненулевые матрицы, у которых нет обратного .
Пример 19 : Показать, что ненулевая матрица
не имеет обратного.
Если бы эта матрица имела инверсию, то
для некоторых значений a, b, c и d . Однако, поскольку вторая строка A является нулевой строкой, вы можете видеть, что вторая строка продукта также должна быть нулевой строкой:
(Когда звездочка, * появляется как запись в матрице, это означает, что фактическое значение этой записи не имеет отношения к настоящему обсуждению.) Поскольку (2, 2) элемент произведения не может равняться 1, произведение не может быть равным единичной матрице. Следовательно, невозможно построить матрицу, которая могла бы служить обратной для A .
Если матрица имеет инверсию, она называется обратимой . Матрица в примере 23 обратима, а матрица в примере 24 – нет. Позже вы узнаете различные критерии для определения обратимости данной квадратной матрицы.
Пример 20 : Пример 18 показал, что
Учитывая, что
проверьте уравнение ( AB ) −1 = B −1 A −1 .
Сначала вычислим AB :
Затем вычисляем B −1 A −1 :
Теперь, поскольку произведение AB и B −1 A −1 равно I ,
B −1 A −1 действительно является инверсией AB . Фактически, уравнение
справедливо для любых обратимых квадратных матриц того же размера.Это говорит о том, что если A и B являются обратимыми матрицами одинакового размера, то их произведение AB также обратимо, и обратное произведение равно произведению обратных чисел в обратном порядке . (Сравните это уравнение с уравнением с транспонированием в примере 14 выше.) Этот результат можно в общем доказать, применяя ассоциативный закон для матричного умножения. С
и
следует, что ( AB ) -1 = B -1 A -1 , как требуется.
Пример 21 : Обратная матрица
это
Покажите, что обратное значение B T равно ( B −1 ) T .
Форма B T и ( B -1 ) T и умножьте:
Этот расчет показывает, что ( B -1 ) T является обратным к B T . [Строго говоря, это показывает только то, что ( B -1 ) T – это правый обратный B T , то есть когда он умножает B T справа, продукт – это личность. Также верно, что ( B −1 ) T B T = I , что означает ( B −1 ) T – левый обратный из В Т .Однако нет необходимости явно проверять оба уравнения: если квадратная матрица имеет обратное, нет различия между левым обратным и правым обратным.] Таким образом,
[Строго говоря, это показывает только то, что ( B -1 ) T – это правый обратный B T , то есть когда он умножает B T справа, продукт – это личность. Также верно, что ( B −1 ) T B T = I , что означает ( B −1 ) T – левый обратный из В Т .Однако нет необходимости явно проверять оба уравнения: если квадратная матрица имеет обратное, нет различия между левым обратным и правым обратным.] Таким образом,
уравнение, которое фактически выполняется для любой обратимой квадратной матрицы B . Это уравнение говорит, что если матрица обратима, то ее транспонирование также является обратимым, а обратное транспонирование – это транспонирование обратного.
Пример 22 : Используйте свойство распределения для матричного умножения, A ( B ± C ) = AB ± AC , чтобы ответить на этот вопрос: если матрица 2 x 2 D удовлетворяет уравнение D 2 – D -6 I = 0 , каково выражение для D −1 ?
По указанному выше распределительному свойству D 2 – D = D 2 – DI = D (D – I) .Следовательно, из уравнения D 2 – D -6 I = 0 следует D (D – I) = 6 I . Умножение обеих частей этого уравнения на 1/6 дает
, что означает
В качестве иллюстрации этого результата матрица
удовлетворяет уравнению D 2 – D -6 I = 0 , как вы можете убедиться.С
и
матрица 1/6 ( D-I ) действительно равна D -1 , как заявлено.
Пример 23 : Уравнение ( a + b ) 2 = a 2 + 2 ab + b 2 является тождеством, если a и b настоящие числа. Однако покажите, что ( A + B ) 2 = A 2 + 2 AB + B 2 – это , а не , если A и B – это матрицы 2 x 2.[Примечание: законы распределения для матричного умножения: A ( B ± C ) = AB ± AC , данные в Примере 22, и сопутствующий закон ( A ± B ) C = AC ± BC .]
Из законов распределения для умножения матриц следует
Поскольку матричное умножение не коммутативно, BA обычно не равно AB , поэтому сумма BA + AB не может быть записана как 2 AB .В общем, тогда ( A + B ) 2 ≠ A 2 + 2 AB + B 2 . [Любые матрицы A и B , которые не коммутируются (например, матрицы в примере 16 выше), предоставят конкретный контрпример к утверждению ( A + B ) 2 = A 2 + 2 AB + B 2 , что также установило бы, что это не личность.]
Пример 24 : Предположим, что B обратимый. Если A коммутирует с B , покажите, что A также коммутирует с B -1 .
Доказательство . Сказать « A коммутирует с B » означает AB = BA . Умножьте это уравнение на B −1 слева и справа и используйте ассоциативность:
Пример 25 : Число 0 имеет только один квадратный корень: 0.Покажите, однако, что нулевая матрица (2 на 2) имеет бесконечно много квадратных корней, найдя все матрицы 2 x 2 A такие, что A 2 = 0 .
Точно так же, как число a называется квадратным корнем из b , если a 2 = b , матрица A называется квадратным корнем из B , если A 2 = B . Пусть
– произвольная матрица 2 x 2.Возводя его в квадрат и устанавливая результат равным 0 , получаем
Записи (1, 2) в последнем уравнении подразумевают b ( a + d ) = 0, что выполняется, если (Случай 1) b = 0 или (Случай 2) d = – а .
Случай 1. Если b = 0, то диагональные записи подразумевают, что a = 0 и d = 0, а записи (2, 1) означают, что c произвольно. Таким образом, для любого значения c каждая матрица вида
– это квадратный корень из 0 2×2 .
Случай 2. Если d = – a , то оба недиагональных входа будут равны 0, а диагональные записи будут равны a 2 + bc . Таким образом, пока b и c выбраны так, что bc = – a 2 , A 2 будет равно 0 .
Аналогичная цепочка рассуждений, начинающаяся с записей (2, 1), приводит либо к a = c = d = 0 (и b произвольно), либо к такому же выводу, что и раньше: до тех пор, пока b и c выбираются так, что bc = – a 2 , матрица A 2 будет равна 0 .
Все эти случаи можно резюмировать следующим образом. Любая матрица следующей формы будет иметь свойство, состоящее в том, что ее квадрат представляет собой нулевую матрицу 2 на 2:
Поскольку существует бесконечно много значений a, b и c , таких что bc = – a 2 , нулевая матрица 0 2×2 имеет бесконечно много квадратных корней. Например, выбор a = 4, b = 2 и c = −8 дает ненулевую матрицу
площадью
Основы матричной алгебры – открытая библиотека учебников
Отзыв Тима Брауха, доцента Манчестерского университета, 15.06.19
Полнота рейтинг: 4 видеть меньше
В предисловии автор поясняет, что этот текст не является текстом линейной алгебры.Он избегает большей части теории, связанной с линейной алгеброй; впрочем, автор по мере необходимости затрагивает теоремы. Избегание теории, но использование термина «теорема» может потребовать некоторого обсуждения в классе, которого избегают в учебнике. Имея в виду, что эта книга посвящена вычислениям, а не теории, она охватывает основные вычислительные аспекты матричной алгебры. В разделе умножения матриц большое внимание уделяется квадратным матрицам в примерах, хотя в домашнем задании используются неквадратные матрицы.Возможно, это потребуется дополнить неквадратными примерами, чтобы учащиеся могли ссылаться на них при выполнении домашнего задания.
Точность содержания рейтинг: 4
По содержанию книга кажется безошибочной. Я не проверял решения всех примеров и проблем, но те, которые я проверял, были правильными.
Актуальность / долголетие рейтинг: 5
Линейная алгебра и матричная алгебра не устаревают. Примеры достаточно безобидны, чтобы не устареть. Примеры довольно неинтересные.Иногда автор пытается сказать, что идеи в этой книге полезны в реальной жизни, но примеры искусственны.
Ясность рейтинг: 4
Форма сокращенного эшелона рядов проходит быстро. После одного раздела автор предполагает, что читатель является экспертом в данной теме. Я обнаружил, что некоторым студентам на освоение этой темы могут потребоваться недели и даже месяцы. Отсутствие подробностей при отображении шагов в последующих разделах экономит место в тексте, но может запутать учащихся.Раздел об умножении матриц немного неуклюжий. Автор старается избегать теоретических аспектов традиционного курса линейной алгебры. Это приводит к сомнительным обозначениям при введении матричного умножения. По сути, автор определяет скалярное произведение без использования этой нотации. В том же разделе автор умножает векторы путем конкатенации (xy означает x, умноженное на y). Поскольку существует несколько способов умножения векторов, отсутствие знака неоднозначно. Однако, если рассматривать векторы как матрицы и есть стандартное умножение матриц для матриц, это имело бы смысл.Автор также утверждает, что покомпонентное умножение матриц неверно. Хотя это не стандартный способ умножения матриц, возникают ситуации, когда это требуется. Векторные операции обсуждаются в главе, посвященной матричным операциям. В этом сложность природы векторов в линейной алгебре. Это матрицы. Это геометрические объекты. Обсуждение одного аспекта почти требует обсуждения другого аспекта. Однако «чистого» способа сделать это не существует.Акцент делается на геометрии, без усиления алгебраических идей из разделов матричных операций, а затем он переключается на сосредоточение внимания на алгебре и игнорирование геометрии (до следующей главы).
Последовательность рейтинг: 4
Обозначения, словарный запас и тому подобное кажется последовательным повсюду. В общем, теоремы представлены без доказательства, хотя в нескольких разделах даются попытки доказательства (возможно, даже формальные доказательства без использования этого языка).
Модульность рейтинг: 4
Главы кажутся довольно модульными, даже если они идут последовательно.Однако большинство разделов заканчиваются «наводящими вопросами» для следующего раздела (например, раздел об умножении матриц заканчивается вопросами, которые предполагают, что обратная матрица будет существовать, что объясняется в следующем разделе). Это может вызвать проблемы, если некоторые разделы будут пропущены, поскольку учащиеся подготовлены к следующему разделу. Это не представляет проблемы, если используются полные главы. Каждый раздел подходит, но требует следующего раздела.
Организация / структура / поток рейтинг: 4
Общая проблема с текстами по линейной алгебре, с которой сталкивается эта книга, заключается в том, рассматривать ли векторы или матрицы, или и то, и другое.Эта книга переключается взад и вперед. Хотя кажется, что нет хорошего способа справиться с этим, и в этой книге используется стандартный (традиционный) подход, переключение на этот способ может сбить с толку студентов.
Интерфейс рейтинг: 5
Книга представляет собой PDF-файл с закладками для глав и разделов. Все изображения четкие и очень качественные.
Грамматические ошибки рейтинг: 3
Есть несколько мелких опечаток, ни одна из которых не отвлекает от текста (например, «получить» вместо «получить»).В других местах интервалы нечетные.
Культурная значимость рейтинг: 3
В сноске есть комментарий об именах для девочек и мальчиков, в котором говорится, что у мальчика есть имя для девочки. Это не обязательно оскорбительно, но ничего не добавляет к тексту. В остальном книга в порядке. Примеры могут быть более многокультурными, но они, как правило, не зависят от культуры.
КомментарииВ целом книга делает то, что намеревается делать. Он обучает матричной алгебре с минимальной теорией и упором на вычисления.Он не лишен теории полностью и мягко входит в мир доказательства.
Quick-R: Матричная алгебра
Большинство методов на этом веб-сайте фактически описывают программирование матриц. Он глубоко встроен в язык R. В этом разделе просто рассматриваются операторы и функции, специально предназначенные для линейной алгебры. Перед тем, как продолжить, многие захотят просмотреть разделы, посвященные типам данных и операторам.
Матрица
В следующих примерах A и B – это матрицы, а x и b – векторы.
| Оператор или функция | Описание |
| А * В | Поэлементное умножение |
| A% *% B | Умножение матриц |
| A% o% B | Внешний продукт. AB ‘ |
| крестовина (A, B) крестовина (A) | A’B и A’A соответственно. |
| т (A) | Транспонировать |
| диаг (x) | Создает диагональную матрицу с элементами x по главной диагонали |
| диаг (A) | Возвращает вектор, содержащий элементы главной диагонали |
| диаг (к) | Если k – скаляр, это создает единичную матрицу k x k.Иди разбери. |
| решить (A, b) | Возвращает вектор x в уравнении b = Ax (т.е. A -1 b ) |
| решить (A) | Инверсия A , где A – квадратная матрица. |
| гинв (А) | Обобщенная инверсия Мура-Пенроуза A . ginv (A) требует загрузки пакета MASS . |
| y <-eigen (A) | y $ val – собственные значения A y $ vec – собственные векторы A |
| y <-svd (A) | Разложение на одно значение A . y $ d = вектор, содержащий сингулярные значения A y $ u = матрица со столбцами, содержащая левые сингулярные векторы A y $ v = матрица со столбцами содержит правые сингулярные векторы А |
| R <- хол (A) | Факторизация Холецкого A .Возвращает множитель верхнего треугольника, так что R’R = A . |
| y <- qr (A) | QR-разложение A . y $ qr имеет верхний треугольник, содержащий разложение, и нижний треугольник, содержащий информацию о разложении Q. y $ rank – это ранг A. y $ qraux вектор, который содержит дополнительную информацию о Q. y $ pivot содержит информацию об используемой стратегии поворота. |
| cbind (A, B, …) | Объедините матрицы (векторы) по горизонтали. Возвращает матрицу. |
| rbind (A, B, …) | Объедините матрицы (векторы) по вертикали. Возвращает матрицу. |
| Ряд Средств (A) | Возвращает вектор средних значений строки. |
| строка Сумма (A) | Возвращает вектор сумм строк. |
| СРЕДСТВА (A) | Возвращает вектор средних значений столбца. |
| Столбцы (A) | Возвращает вектор сумм столбцов. |
Эмуляция Matlab
Пакет matlab содержит функции-оболочки и переменные, используемые для наилучшей репликации вызовов функций MATLAB.

 csv"]
csv"] Верно ли это?
Верно ли это? Верно ли, что матрица, обратная данной тоже будет нулевой?
Верно ли, что матрица, обратная данной тоже будет нулевой?
 ).
).