Урок алгебры по теме “Производная”
- Сальникова Оксана Викторовна
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (788 кБ)
Тип урока: обобщающий.
Цели: Слайд 2
- Обобщить, систематизировать и углубить знания о производной. Выявить уровень усвоения вопросов теории по теме, а так же уровень сформированности умений по решению задач на применение знаний о производной.
- Развитие умений в применении знаний в конкретной ситуации; развитие логического мышления, умений сравнивать, обобщать, правильно излагать мысли; развитие самостоятельной деятельности учащихся.
- Воспитывать культуру труда общения, навыки самоконтроля, взаимоконтроля
и взаимопомощи; формировать познавательный интерес.

Оборудование: компьютер, проектор, экран, таблица с формулами и правилами нахождения производных.
Ход урока
I. Организационный момент.
Сегодня на уроке нам предстоит обобщить, систематизировать и углубить знания о производной. Мне бы хотелось взять эпиграфом к нашему уроку высказывания Конфуция:
Три пути ведут к знанию:
- путь размышления – это путь самый благородный,
- путь подражания – это путь самый легкий и
- путь опыта – это путь самый горький.
Таким образом, на уроке мы будем размышлять, подражать и набираться опыта.
II. Актуализация знаний. Слайд 3–9
а) Теоретический опрос:
- Сформулировать определение производной функции.
- Как называется математическая операция нахождения производной функции?
- В чем состоит геометрический смысл производной?
- В чем состоит механический смысл производной?
- Какие точки называются стационарными?
- Назвать достаточные условия существования экстремума.

- Как монотонность функции связана с производной?
б) Вспомнить формулы и правила нахождения производных (таблица на доске).
III. Решение тренировочных упражнений:
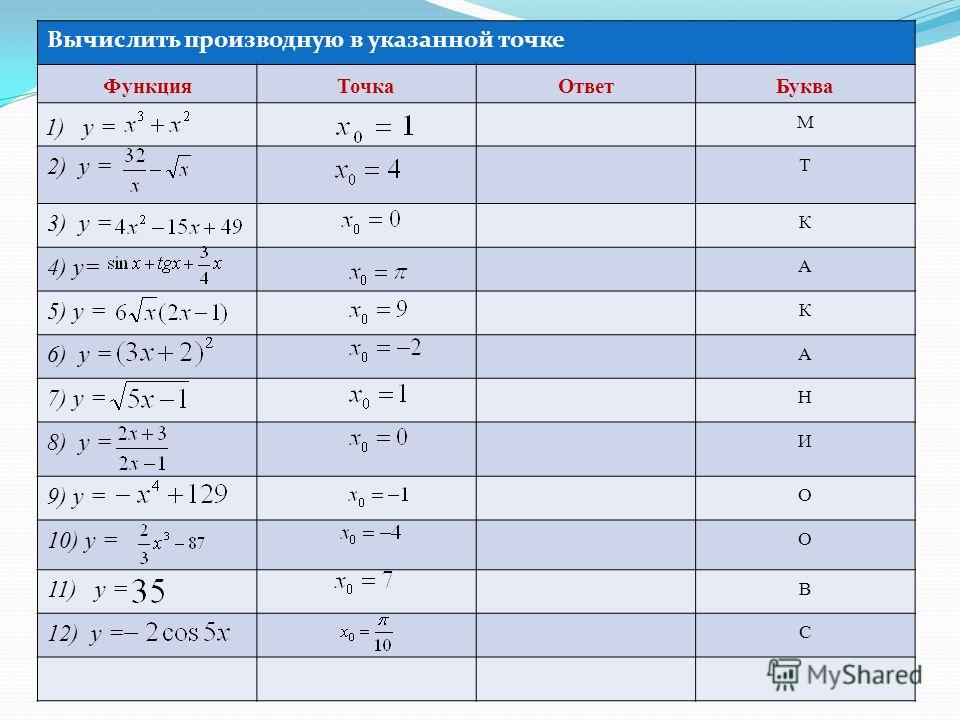
1) Найдите производную функции. Слайд 10.
2) По характеру изменения графика функции укажите на каких промежутках производная положительна, на каких – отрицательна (каждая из функций определена на R) Слайд 11.
3) С помощью графика производной найдите промежутки возрастания и убывания функции: Слайд 12.
4) На рисунке изображен график функции y=f(x) и отмечены девять точек на оси абсцисс: x1,x2,x3,…,x9
Физкультминутка для глаз.
5) Работа с тестами (в парах).
а) Даны графики функции и графики производных. Для каждой из функций, графики
которых изображены в верхнем ряду, найдите график ее производной. Слайд 13.
Для каждой из функций, графики
которых изображены в верхнем ряду, найдите график ее производной. Слайд 13.
б) Дифференцирование. Найдите пары “функция – график производной этой функции”. Слайд 14.
в) Связь свойств функции и производной. Завершите фразы: “Если на отрезке [1; 3] производная ……., то на этом отрезке функция у…….
Подведение итогов работы с тестами.
6) Решение задач (у доски) подобных тем, что даны в текстах ЕГЭ. Слайд 16.
а) Точка движется прямолинейно по закону x(t) = 2t3 + t – 3. Найти скорость в момент времени t. В какой момент времени скорость будет равна 7 м/с (х – координата точки в метрах, t – время в секундах).
б) Тело движется по прямой так, что расстояние S (в метрах) от него до точки
М этой прямой изменяется по закону S(t) = t2 + t + 2 (t – время
движения в секундах).
в) Тело движется прямолинейно по закону x(t) = 2t3 + t – 3. Найти ускорение в момент времени t. В какой момент времени ускорение равно 0,6 м/с2 (х – координата точки в метрах, t – время в секундах).
IV. Экскурс в историю. Слайд 17.
Математический анализ, ядро которого составляют дифференциальное и интегральное исчисление – самая тонкая область всей математики. Раздел математики, в котором изучаются производные и их применение к исследованию функций, называется дифференциальным исчислением.
Дифференциальное исчисление создано Исааком Ньютоном и Готфридом Вильгельмом Лейбницом. И.Ньютон в основном опирался на физическое представление о мгновенной скорости движения, а Г.Лейбниц использовал понятие бесконечно малой.
Основные понятия дифференциального исчисления долгое время не были должными
образом обоснованы. Однако в начале XIX в. французский математик О.Коши дал
строгое построение дифференциального исчисление на основе понятия предела.
Однако в начале XIX в. французский математик О.Коши дал
строгое построение дифференциального исчисление на основе понятия предела.
Применяемая сейчас система обозначений для производной была введена Ж.Лагранжем.
В настоящее время понятие производной находит большое применение в различных областях науки и техники.
V. Заключительная часть: Слайд 18
– подведение итогов;
– объявление оценок;
– задание на дом (подготовить презентацию по теме “Применение производной”).
Литература:
- Алгебра и начало математического анализа. 10–11 классы. В 2 ч. (базовый уровень). /А.Г. Мордкович – М.: Мнемозина, 2009.
- Задачи по алгебре и началам анализа: Пособия для уч-ся 10–11кл. /С.М. Саакян, А.М. Гольдман. – Просвещение, 2008.
- Зачеты в системе дифференцированного обучения математики: Библиотека
учителя математика /
 – М.,
Просвещение, 1993.
– М.,
Просвещение, 1993. - Математика. 5–11 классы: игровые технологии на уроках /Н.В.Барышникова. – Волгоград: Учитель, 2007.
- Уроки математики с применением информационных технологий.5–10классы. Л.И.Горохова и др.-М. Глобус, 2010.
Презентация по алгебре и начала анализа Производная (10 класс) доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация по алгебре и начала анализа Производная (10 класс), предмет презентации: Алгебра. Этот материал в формате pptx (PowerPoint) содержит 19 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 19 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Производная
Содержание
Понятие производной.
Алгоритм нахождения производной.
Примеры.
Таблица производных.
Физический смысл производной.
Правила нахождения производных.
Непрерывность функции.
Геометрический смысл производной.
Понятие производной
Производной функции у = f(x), заданной на некотором интервале (a; b), в некоторой точке х этого интервала называют предел отношения приращения функции в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.
Нахождение производной называют дифференцированием
Понятие производной
х0
х0+ ∆х
f(x0)
f(x0 + ∆х)
∆х
х
у
0
∆f
у = f(x)
Зафиксировать значение х0, найти f(x0).
Дать аргументу х0 приращение ∆х, перейти в новую точку х0 + ∆х, найти f(x0 + ∆х).
Найти приращение функции: ∆f = f(x0 + ∆х) – f(x0).
Составить отношение .
Вычислить lim .
Этот предел и есть f ′(x0).
Алгоритм нахождения производной
Примеры
1. Найти производную функции y = kx + b в точке хo
Примеры
2. Найти производную функции y = C (C – const) в точке хo
Примеры
3. Найти производную функции y = x2 в точке хo
Найти производную функции y = x2 в точке хo
Примеры
Примеры
Примеры
5. Найти производную функции y = 1/x в точке хo
Примеры
5. Найти производную функции y = 1/x в точке хo
Таблица производных
Физический ( механический ) смысл производной
Если при прямолинейном движении путь s, пройденный точкой, есть функция от времени t, т.е. s = s(t), то скорость точки есть производная от пути по времени, т.е. v(t) = s′(t).
Производная выражает мгновенную скорость в момент времени t.
Правила нахождения производной
1. Если функции u(x) и v(x) имеют в точке х производные, то их сумма u(x) + v(x) также имеет в этой точке производную, причем
Если функции u(x) и v(x) имеют в точке х производные, то их сумма u(x) + v(x) также имеет в этой точке производную, причем
(u + v)′ = u′ + v′
2. Если функция u(x) имеет в точке х производную и С – данное число, то функция С∙u(x) также имеет в этой точке производную, причем
(Сu)′ = С∙u′
Правила нахождения производной
3. Если функции u(x) и v(x) имеют в точке х производные, то их произведение u(x) ∙ v(x) также имеет в этой точке производную, причем
(u ∙ v)′ = u′∙v + u∙v′
4. Если функция v(x) имеет в точке х производную и v(x) ≠ 0, то функция также имеет в этой точке производную, причем
Правила нахождения производной
5. Если функции u(x) и v(x) имеют в точке х производные и v(x) ≠ 0, то функция также имеет в этой точке производную, причем
Производная сложной функции
(f(g(x)))′ = f′(g(x))∙g′(x)
Примеры:
1. ((5x – 3)3)′ = 3(5x – 3)2∙(5x – 3)′ =
((5x – 3)3)′ = 3(5x – 3)2∙(5x – 3)′ =
= 3(5x – 3)2 ∙ 5 = 15(5x – 3)2
2. (sin(4x + 8))′ = cos(4x + 8)∙(4x + 8)′ =
= cos(4x + 8)∙4 = 4 cos(4x + 8)
Если функция имеет производную (дифференцируема) в точке х, то она непрерывна в этой точке.
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
10 класс. Алгебра. Производная. Примеры вычисления основных производных. Таблица производных. Типовые задачи. – Примеры вычисления основных производных. Таблица производных. Типовые задачи.
Комментарии преподавателя Примеры вычисления производных. Пример 1 Дано: Найти . Зафиксируем точку и найдем значение производной от конкретной функции в конкретной точке. Действуем по алгоритму. 1)Вычисляем значение . Иллюстрируем все это графиком. Рис. 1. Кубическая парабола. Зафиксировав точку , вычислим значение функции в этой точке. Получим . 2) Даем аргументу приращение ,получаем – новое значение аргумента. Примечание. В данном случае приращение положительное. Можно дать приращение отрицательное, тогда функция будет либо увеличиваться, либо уменьшаться. Важно, что –любое. 3) Вычислить значение функции в новой точке , подставив эту точку в функцию. . 4) Найдем , то есть разность между значением функции в новой точке минус значение функции в старой точке. . Имеем две точки: значение аргумента и значение функции в точке , новое значение аргумента и значение функции при новом значении аргумента. Разность этих значений функции дает . 5) Найдем разностное отношение . Знаменатель для всех функций один и тот же, – приращение аргумента, а числитель – свой для каждой функции. Получили разностное отношение. Далее надо упростить его, сократить на и сделать дальнейший анализ. Упрощать в данном случае можно по-разному. Можно применить формулу или куб суммы, или разность кубов. Напомним, что . В данном случае – это , – это . Имеем Раскрывая скобки, получили многочлен. Приведем подобные члены. Дальше надо преобразовать так, чтобы сократить. Вынесем за скобки, получим Теперь можно сократить на , ведь , оно не равно нулю. Имеем соотношение следующего вида . Осталось узнать, что происходит, когда . В данном случае второй член выражения пропадет, и третий член пропадет. Останется , то есть . Результат , то есть смысл такой: 3 выносим как сомножитель и показатель уменьшили на единицу. Итак, зафиксировали точку , нашли производную от конкретной функции в конкретной точке . Точка может быть любая. Ответ: . Итак, мы зафиксировали функцию – кубическую параболу. Была задача: найти производную этой функции в конкретной точке . Мы зафиксировали точку и действовали по алгоритму, который был изложен в общем виде, и применен к данной функции. Этот алгоритм можно применять к любой функции, а именно: вычислить значение функции в точке , подставив значение в закон соответствия, то есть в функцию, дать приращение аргумента, найти значение функции при новом значении аргумента и получить приращение функции, то есть разность между значениями функции в новой точке и старой. Далее, надо найти разностное отношение , упростить его так, чтобы вынести за скобку и сократить на . В результате получится выражение, члены которого зависят от и не зависят от него. Если члены, которые зависят от прямо пропорциональны ему, то они при стремятся к нулю, то есть пропадают. Остаются только члены, которые не зависят от . Таким образом получим значение производной. Для знакомых с пределами . Важно понять, что есть члены с члены и члены без . При этом члены с пропадают, остается то, что называется производной. Итак, производная от кубической функции в любой точке – это . Возьмем конкретный пример. Дано: Найти: , то есть конкретное значение функции в точке . Решение. 1) Найти производную в любой точке . . 2) Найти . . Физический и геометрический смысл решения задачи. В момент , если двигаться (уезжать от дома) по закону , скорость равна 12. Если к этой кривой мы проведем касательную в точке , то эта касательная имеет угол наклона (см.рис.2). Так вот . Это говорит о том, что угол довольно большой, так как растет быстро (от дома мы уезжаем довольно быстро). Более того, чем дальше, тем быстрее скорость. Рис. 2. Физический и геометрический смысл решения задачи. Итак, рассмотрено подробное применение общего алгоритма нахождения производной для конкретной функции. Дифференцирование функций «с нуля», т. е. исходя из определения производной и теории пределов – вещи достаточно трудоёмкая. Поэтому математики вычислили производные элементарных функций. Получилась таблица производных, где всё уже готово. Производные некоторых элементарных функций: 1. 2. 3. 4. 5. 6. 7. 8. Дано: Доказать: Доказательство Изобразим график функции: (см. Рис. 1). Зафиксируем точку и приращение аргумента . Получаем новое значение аргумента и, соответственно, новое значение функции . То есть при переходе от значения аргумента к значения функции изменяются соответственно от до . Получили прямоугольный треугольник (выделен красным цветом), катетами которого являются два приращения – приращение аргумента () и приращение функции (– разность между значением функции в новой точке и значением функции в старой точке). Рис. 1. Иллюстрация к доказательству Найдём отношение : Умножим числитель и знаменатель на выражение : В числителе получили выражение разности квадратов: Следовательно: Проанализируем данное выражение при : – произвольное допустимое число, поэтому: Что и требовалось доказать. Дано: Найти: Решение 1. Найдём производную в любой точке : 2. Найдём производную в заданной точке: Как известно, это значение является тангенсом угла наклона касательной к кривой , проведённой в точке с абсциссой 4 (см. Рис. 2. Иллюстрация к задаче Ответ: Дано: Доказать: Доказательство На рисунке 3 показано, каким образом ведёт себя функция . Зафиксируем точку и приращение аргумента . Получаем новое значение аргумента (новую точку) . При переходе от значения аргумента к значения функции изменяются соответственно от до . Рис. 3. Иллюстрация к доказательству Найдём отношение : Для упрощения этого выражения используем формулу разности синусов: При : Объясним это, рассмотрев тригонометрический круг с радиусом 1 и угол, равный (см. Рис. 4). Нам необходимо найти длину дуги и длину хорды . Рис. 4. Иллюстрация к доказательству Длина дуги равна произведению радиуса на центральный угол: Радиус равен 1, поэтому длина дуги численно равна центральному углу, который равен . Хорда состоит из двух катетов треугольников и , которые равны произведению гипотенузы (единица, так как это радиус) на синус противолежащего угла. Следовательно: При длина дуги стремится к длине хорды: То есть при маленьком угле дуга и хорда по длине неразличимы. Таким образом, домножив выражение на 2, получаем выражение , которое есть отношение длины хорды к длине дуги: Но так как , то: Следовательно, при : Поэтому: Что и требовалось доказать. Дано: Найти: Решение 1. Найдём производную в любой точке : 2. Найдём производную в заданной точке: Ответ: . Дано: Найти: тангенс угла наклона касательной к кривой в точках: а) ; б) ; в) Решение На рисунке 5 показана иллюстрация к задаче. Рис. 5. Иллюстрация к задаче Так как , то: а) Для точки тангенс угла наклона касательной будет равен: б) Для точки тангенс угла наклона касательной будет равен: Следовательно, прямая , изображённая на рисунке 5, является касательной к синусоиде в точке 0. в) Для точки , тангенс угла наклона касательной будет равен: Следовательно, в этом случае касательная параллельна оси . Ответ: а) ; б) ; в) . ИСТОЧНИК http://x-uni.com/algebra/10-klass/video/primery-vychisleniya-proizvodnyh-funktsiya-f-x-x-sup-3-sup-tipovye-zadachi http://interneturok. http://www.youtube.com/watch?v=fuCBw8gdRH8 http://11book.ru/images/shcoolbook_ru/10/10_a_mord_baz.pdf http://www.absolom.ru/mathprofi/tipovye_zadachi_s_proizvodnoi.html Сегодня на уроке мы поговорим о мгновенной скорости. Введём
понятие производной функции. Сформулируем определение предела функции. Скажем,
какие функции называют непрерывными на некотором промежутке. Сформулируем
строгое определение непрерывности функции. Давайте с вами решим задачу. Поезд, двигаясь равнозамедленно с
ускорением м/c², проходит м и
останавливается. Определите скорость поезда в момент начала торможения. Итак, нам надо найти скорость в момент начала торможения, то есть
мгновенную скорость в этот момент времени. Воспользуемся формулами из курса физики: . Теперь учтём, что проекция ускорения на ось x отрицательная (так как поезд
двигается равнозамедленно), а конечная скорость поезда равна нулю. Подставим в систему уравнений известные из условия значения пути и
ускорения. Решим её. Отметим, что от мгновенной скорости зависит решение многих
практических задач. При нахождении мгновенной скорости используется средняя скорость
движения за малый промежуток времени. Давайте рассмотрим, как связаны между собой средняя и мгновенная
скорости движения. Итак, пусть материальная точка движется вдоль
оси , где О – положение этой точки в момент времени t = 0. Если в момент времени t координата материальной точки
равна , где , то функцию называют законом
движения точки . При неравномерном движении материальная точка за равные по
длительности промежутки времени может совершать перемещения, разные как по
величине, так и по направлению. За промежуток времени от до средняя
скорость движения материальной точки определяется как , . Если рассматриваемое движение не является равномерным, то средняя
скорость при фиксированном будет
меняться при изменении . Скоростью точки в момент времени (мгновенной
скоростью) называют предел, к которому стремится средняя скорость, когда , то есть
скорость в момент времени определяется
равенством . Таким образом, получается, что скорость в момент времени – это предел
отношения приращения координаты за промежуток времени от до к приращению
времени при , если этот
предел существует. Так, например, пусть материальная точка движется по закону
свободного падения . Тогда . Откуда , то есть . Отношение называют разностным
отношением, а его предел – производной функции и обозначают
. Итак, пусть функция определена
на некотором промежутке. – точка
этого промежутка и число , такое, что также
принадлежит данному промежутку. Тогда предел разностного отношения при (если такой
предел существует) называется производной функции в точке и
обозначается . Отметим, что в этой формуле число может быть и
положительным, и отрицательным, при этом число должно
принадлежать промежутку, на котором определена функция . Если функция имеет
производную в точке , то она
называется дифференцируемой в точке . Если функция имеет
производную в каждой точке некоторого промежутка, то говорят, что она дифференцируема
на этом промежутке. Давайте найдём производную функции . Давайте найдём производную функции , где – заданное
число. Составим разностное отношение. Получается, что оно равно 0 при любом , то есть его
значение не меняется . Таким образом, производная постоянной равна нулю. Давайте выясним, чему равна производная линейной функции . Составим разностное отношение. Разностное отношение равно при любом , тогда
предел этого отношения при равен . Следовательно, . Например, , , . Так как изучение теории пределов не входит в программу средней
школы, то в школьном курсе математики некоторые формулы производных строго не
доказываются или вообще принимаются без доказательства. При нахождении производных простейших функций мы пользуемся
наглядными представлениями. Например, считаем наглядно понятным, что если , то , , . Но несмотря на это, мы всё же приведём строгое определение предела
функции в точке. Число А называется пределом функции в точке и
обозначается , если для
любого числа существует
такое число , что для
всех ,
удовлетворяющих условию , где , выполняется
неравенство . Давайте поясним это определение. Число А является пределом
функции в точке , если
значения при , достаточно
близких к , становятся
как угодно близкими к числу А, то есть значения становятся как угодно малыми. Это означает, что можно взять сколь угодно малое положительное
число и убедиться
в том, что для всех ,
отличающихся от меньше, чем
на некоторое число , . Например, если , то . Поэтому для всех , таких, что , где , справедливо
неравенство . Так, например, если , то . Понятие предела функции тесно связано с понятием непрерывности. Если график функции представляет собой непрерывную линию на
некотором промежутке, то эту функцию называют непрерывной на этом промежутке. Все элементарные функции (линейная, квадратичная, тригонометрические
и другие), которые мы изучаем в школьном курсе математики, являются
непрерывными на каждом промежутке, на котором они определены. На следующем рисунке изображён график функции , которая не
является непрерывной. Она непрерывна на промежутках и . Но она разрывна в точке . Поэтому она
не является непрерывной на отрезке . Сформулируем строгое определение непрерывности функции.
Функция называется непрерывной
в точке , если . Если функция непрерывна в каждой точке некоторого интервала, то её
называют непрерывной на этом интервале. Например, функция , график
которой мы рассмотрели, непрерывна на интервале , а вот на
интервале она не
является непрерывной. Отметим, что если функция имеет производную на некотором
интервале, то на этом интервале она непрерывна. А сейчас давайте выполним задание. Используя определение
производной, найдите , если: а) ; б) . Решение. КАК ПРОХОДЯТ Ученик и учитель видят и слышат
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно ИЛИ Позвонить и Вам поможет специалист 8 (800) 333 58 91 * Звонок является бесплатным на территории РФ ПОДАТЬ ЗАЯВКУ Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41 Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям. Отправляя форму, Вы принимаете
Условия использования
и даёте
Согласие на обработку персональных данных
Вы также можете воспользоваться
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от за 60 мин. и зависит ОТ ОПЫТА и ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже) Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР ОПТИМАЛЬНОЕ ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ
ОБРАЗОВАНИИ У ВСЕХ
РЕПЕТИТОРОВ НАДЕЖНОСТЬ И ОПЫТ. ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ
ЭТО НЕОБХОДИМО
375572 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
И вот, что УЧЕНИКИ ГОВОРЯТ Чулпан Равилевна Насырова “ Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!! “ Алина Крякина Надежда Васильевна Токарева “ Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. “ Эльмира Есеноманова Ольга Александровна Мухаметзянова “ Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо. “ Оксана Александровна Наталья Борисовна Карасева “ Мы восторге от репетитора. Наталья Борисовна грамотный педагог, она любит свою профессию, любит учеников. Занятия с сыном (2 класс), он находится на домашнем обучении, проходят по скайпу в комфортной обстановке. Репетитор умеет заинтересовать ребенка и выстраивает занятие с учетом его способностей, доступно объясняя предметы русский язык и математику. “ Елена Васильевна Клиентам Репетиторам Партнеры 1.Производная функции. Производной
функции f в точке хº
называется число, к которому стремится
разностное отношение при ∆х, стремящимся к нулю. Функцию,
имеющую производную
в точке хº,
называют дифференцируемой
в этой
точке. Пусть
D1 —
множество точек,
в которых
функция дифференцируема.
Сопоставляя каждомух
€ D1 число
f ‘(x)1получим новую
функцию с
областью определения
D1. Эта функция
называется производной
функции y=f
(х) и
обозначается f
‘ или у’.
Нахождение производной
данной функции
f называется
дифференцированием. В
этом пункте
мы получили
следующие формулы
дифференцирования:
(х2)’=2х, (х3)’=Зх2,
(kx+b)’=k.
Полагая в
формуле (kx+b)’=k,
что k=0,
b=C,
где С—произвольная
постоянная, получаем,
что С’=0, т.
е. производная
постоянной равна нулю. 2.Производная суммы. Производная
суммы равна сумме производных.
(Пример) 3.Производная произведения Производные
перемножаются по формуле.
.(Пример.) 4.Производная частного. Производные
делятся по формуле.
.(Пример.) 5.Производная сложной функции. Для
того, что бы взять производную сложной
функции необходимо выразить производную
внешней функции, а затем производную
внутренней. f(g(x))=f(u)
где, u=g(x) 6.Производная логарифмической функции. Графики функций y=log(x)a
и y=x(a)симметричны
относительно прямой y=x
. Т.к. показательная функция дифференцируема,
а ее производная не обращается в нуль,
то логарифмическая функция дифференцируема
на всей области определения. Докажем,
что производная логарифмической функции
для любого x из области
определения находится по формуле
ln’x=1\x.
По основному логарифмическому тождеству при всех положительных x,
то . 7.Производная степенной функции. f(x)=x(a)
– степенная функция. Если a>0,
то степенная функция определена и при x=0, т.к. 0(a)=0.
Исследование степенной функции достаточно
провести только на промежутке (0;∞).
Докажем, что для любого x из области определения производная
степенной функции равна .
Т.к. то, .
Отсюда, 8. Производная показательной функции. Функция f(e(x))
– показательная. Теорема 1: Функция e(x)
дифференцируема в каждой точке области
определения, и (e)’=e(x).
Теорема 2: Показательная функция d(x)
дифференцируема в каждой точке области
определения и (a(x))’=a(x)lna.
Следствие: Показательная функция
непрерывна в каждой точке своей области
определения, т. 9.Производная функции y=sin x. Функция
синус имеет производную в любой точке
и .(Пример.) 10.Производная функции y=cos x. Функция
косинус имеет производную в каждой
точке своей области определения и .(Пример.) 11.Производная функции y=tg x. Функция
тангенс имеет производную в каждой
точке своей области определения и .(Пример.) 12.Производная функции y=ctg x. Функция
котангенс имеет производную в каждой
точке своей области определения и .
(Пример.) 13.Производная
функции y=arcsin x. 14.Производная функции y=arccos x. Функция арккосинус
имеет производную в каждой точке своей
области определения и .
(Пример.) 15.Производная
функции y=arctg x. Функция
арктангенс имеет производную в каждой
точке своей области определения и .
(Пример.) 16.Производная
функции y=arcctg x. Функция
арккотангенс имеет производную в каждой
точке своей области определения и .
(Пример.) 17.Вторая производная. Производная
функции f в точке xº
называется число, к которому стремиться
разностное отношение .
Вторая производная – это производная,
полученная из первой производной. 18.Возрастание и убывание функции. Если
f'(x)>0
в каждой точке интервала I,
то функция f возрастает
на интервале I. Если f'(x)<0
в каждой точке интервала I,
то функция f убывает на
интервале I. 19.Выпуклость и вогнутость. Точки
перегиба. Кривая y=f(x)
называется выпуклой в точке xº
(вогнутой в точке xº), если
она расположена под касательной (над
касательной). y”>0, то
вогн. y”<0, то выпукл.
Теорема: (признак выпуклости, вогнутости).
Если вторая производная положительна
(отрицательна) на интервале a.b,
то она вогнута (выпукла), в каждой точке
этого интервала. Точка xº
называется точкой перегиба графика
функции y=f(x),
если она отделяет интервалы выпуклости
и вогнутости. Теорема: (Признак перегиба).
Если вторая производная непрерывна, на
интервале a.b,
и меняет знак при переходе через точкуxº,
на интервале a.b,
то, xº- точка перегиба. 20.Экстремумы функции. Точки максимума и минимума называются
точками экстремума. Теорема: Если точка xº
является точкой экстремума, то производная
в этой точке равна нулю, т.е. f'(xº)=0.
Теорема 2: Если производная функции
y=f(x)
при переходе, через точку xº
меняет свой знак, то xº –
точка экстремума. 21.Дифференциалфункции. . – главная часть приращение функции..
Дифференциалом функции (d
y) называется главная
часть приращения функции (y’)
∆x. dy=y’dx.
dy=y’dx.
Дифференциал функции равен произведению
производной функции на дифференциал
функции. y=x². dy=(x²)’*dx=2xdx. 22.Схема исследования функции. Область
определения функции Д (y). 23.Таблица производных. 1.(lnx)’=1\x. 2.(log(a)x)’=1\x
ln a. 3. (x(n))’=nx(n-1). 4. (√x)’=1\2√x. 5. (a(x))’=a(x)*ln
a. 6. (e(x))’=e(x). 7. (sinx)’=cosx. 8. (cosx)’=-sinx. 9. (tgx)’=1\cos²x. 10. (ctgx)’=-1\sin²x. 24. Первообразная. Функция
F называется
первообразной для функции f
на заданном промежутке, если для всех x из
этого промежутка справедливо равенство
F'(x)=f(x).
Теорема: Любая первообразная для функции
f на промежутке
I может быть
записана в виде F(x)+C,
где F(x)
– одна из первообразных для функции
f(x)
на промежутке I,
а C –
произвольная постоянная. 25. Неопределенный интеграл. Множество всех
первоообразных F(x)+C,
функции y=f(x’)
на некотором интервале называется
неопределенным интервалом функции
y=f(x).
интег f(x)dx=F(x)+C,
где: f(x)dx – подинтегральное выражение, f(x)
– подинтегральная функция, dx – дифференциал аргумента. 26. Свойства неопределенного
интеграла. 1.) (ин
f(x)dx)’=f(x). 1). Постоянный множитель можно
вынести за знак еопределенного интеграла.
Ин kf(x)dx=k
ин f(x)dx.
2). Неопределенный интеграл суммы равен
сумме неопределенных интегралов. ин
(f(x)+g(x))dx=ин
f(x)+fg(x)dx.
3). d ин
f(x)dx=f(x)dx.
4). ин dF(x)=F(x)+C
ин dx=x+C. 27. Основные формулы
интегрирования. 1). ин
x(n)dx=x(n-1)\n+1+C,
при x не =
-1. 2). ин dx\x=ln
IxI+C.
3). ин e(x)dx=e(x)+C.
4). ин a(x)dx=a(x)\ln
a+C.
5). ин sin
xdx=-cos+C.
6). ин cosxdx=sinx+C.
7). ин dx\cos²x=tgx+C.
8). ин dx\sin²x=-ctgx+C.
9). ин dx\√1-x²=arcsinx+C. 28. Интегрирование способом
подстановки. Надо
заменить часть подинтегральной функции
новой переменной, таким образом, чтобы
оставшаяся часть подинтегрального
выражения была ее дифференциалом, с
точностью до коэфицента. Пример: 29. Способ интегрирования
по частям. В качестве
U выбираем часть подинтегральной функции
так, что бы du было проще, чем U, а по du
легко находилось V. Пример: 30. Площадь криволинейной трапеции. Пусть
на отрезке
[a; b]
оси ox
задана непрерывная
функция f,
не меняющая
на нем
знака. Фигуру,
ограниченную графиком
этой функции, отрезком
[а; b]
и прямыми
x=a
и x=b;
называют криволинейной
трапецией. Для
вычисления площадей
криволинейных трапеций
применяется следующая
теорема. Теорема: Если
f —
непрерывная и
неотрицательная на
отрезке [a;
b] функция,
а F
— ее
первообразная на
этом отрезке,
равна приращению
первообразиой на отрезке
[а; b] , т. Алгебра производных функций : Теория понятия производных немного абстрактна. Производная является фундаментальной и очень важной темой исчисления, тогда как производная функций следует концепции пределов. Он имеет множество применений в реальных сценариях, включая расчет скорости изменения. Например, скорость изменения смещения космического корабля — это его скорость, а скорость изменения его скорости — это его ускорение, необходимое для достижения определенной точки в данное время. Обладая базовыми знаниями алгебры функций, а также тремя основными производными и четырьмя правилами алгебраических операций с производными, можно хорошо усвоить тему. Основные правила, изложенные в этой статье, могут стать основой для углубленных исследований, связанных с деривативами. Производная функции с действительным знаком измеряет тенденцию функции к изменению значений по отношению к изменению ее независимой переменной. Наклон касательной в точке функции равен производной функции в этой точке. Давайте разберемся с основными алгебраическими операциями и правилами, связанными с производными функций. Производная суммы двух функций может быть вычислена как сумма их производных. То есть, если \(f\left( x \right)\) и \(g\left( x \right)\) две действительнозначные дифференцируемые функции в интервале \(I,\), то Доказательство: Правило сумм можно доказать, используя свойства пределов и определение производных как \(f’\left( x \right) = \underset{{h \to 0}}{\mathop {\lim }} \frac{{f\left({x + h} \right) – f\left( x \right)}}{h}\) Подобно правилу сумм, производная разности двух функций также может быть вычислена как разность их производных. То есть, если \(f\left( x \right)\) и \(g\left( x \right)\) две действительнозначные дифференцируемые функции в интервале \(I,\), то \( \frac{d}{{dx}}\left[{f\left( x \right).g\left( x \right)} \right] = \frac{d}{{dx}}\left[ { е \ влево ( х \ вправо)} \ вправо]. г \ влево ( х \ вправо) + е \ влево ( х \ вправо). \ влево [{\ гидроразрыва {d} {{dx}} г \ влево ( х \справа)} \справа]\) Доказательство: Доказательство: Цепное правило используется для нахождения производной сложной функции. Если функция \(h\) является составной функцией \(f\) и \(g,\), то составная функция \(\left({f \circ g} \right)\left( x \right)\ ) вычисляется для значения \(x\), сначала оценивая \(g\left( x \right)\), а затем вычисляя значение функции \(f\) в \(g\left( x \right ).\) Теперь цепное правило объясняет метод вычисления производной \(\left({f \circ g} \right)\left( x \right)\) как произведения производной функции \ (f\) в \(g\left( x \right)\), умноженном на производную от \(g\left( x \right).\) 92}} \right) + 3\frac{d}{{dx}}\left( x \right) – 0\) Q.2. Докажите, что производная от \(g\left( x \right) = x\,\cos \,x\) равна \(\cos x – x\,\sin \,x. В статье говорится о том, как важно знать, как обращаться с производными функций, которые имеют множество практических применений. Затем он разрабатывает основное определение производной функции. Кроме того, статья переходит к алгебре производных, которая объясняет производные вещественных дифференцируемых функций с помощью основных операций — сложения, вычитания, умножения и деления. Он разрабатывает вывод четырех правил — правила сумм, правила разности, правила произведения и правила частного. Далее также перечислены несколько других важных правил, таких как постоянное правило, правило мощности, общее правило мощности и правило цепочки. Затем он завершается несколькими примерами, чтобы понять вычисления, связанные с алгеброй производных функций. Узнайте о применении исчисления в нашей повседневной жизни Q. Q.2. Что такое алгебра дифференцирования? Q. Вопрос 4. Каковы правила дифференцирования 7 ? Q.5. Как работает правило продукта? Практические вопросы о производных функциях с советами и решениями Производные являются неотъемлемой частью исчисления. Они измеряют скорость изменения любого количества. Предположим, есть резервуар для воды, из которого вытекает вода. Местного инженера просят измерить время, за которое резервуар для воды опустеет. Производные инструменты основаны на концепции пределов. Они измеряют разницу между значениями функции в интервале, ширина которого приближается к нулевому значению. Например, пусть задана функция f(x), и цель состоит в том, чтобы вычислить производную этой функции в точке x = a с использованием пределов. Обозначается через или f'(x). При x = a, Обратите внимание на рисунок: интервал «h» приближается к нулю. Производные некоторых основных функций В таблице ниже показаны производные некоторых стандартных основных функций. В приведенной выше таблице представлены производные некоторых стандартных функций, но в реальной жизни функции не всегда бывают простыми. Рассмотрим две функции f(x) и g(x). Допустим, есть третья функция h(x), которая объединяет эти две функции. Правило суммирования и разности: Случай 1: h(x) = f(x) + g(x) Эта функция представляет собой сумму производной f(x) и g(x) таких функций определяется выражением ⇒ или h'(x) = f'(x) + g'(x) Случай 2: h(x) = f(x) – g(x) Эта функция представляет собой разность f(x) и g(x), производная таких функций определяется выражением ⇒ или h'(x) = f'(x) – g'(x) Правила произведения и деления: Случай (i): h(x) = f( x) x g(x) Эта функция является произведением функций f(x) и g(x), производная таких функций определяется выражением ⇒ или h'(x) = f'(x)g(x) + g'(x) f(x) Случай (i): h(x) = Эта функция представляет собой деление f(x) и g(x), производная таких функций определяется выражением ⇒ или h'(x) = Правила деления и произведения также называются правилами Лейбница. Давайте рассмотрим несколько примеров задач с этими правилами. Вопрос 1. Найдите производную для заданной функции f(x). f(x) = x 2 + 3x Решение: Эта функция является суммой двух различных функций. Здесь будет использоваться правило суммы. f(x) = x 2 + 3x Здесь h(x) = x 2 и g(x) = 3x. f(x) = h(x) + g(x) ⇒f'(x) = h'(x) + g'(x) ⇒ f'(x) = ⇒f’ (x) = ⇒f'(x) = 2x + 3 Вопрос 2: Найдите производную для заданной функции f(x). f(x) = e x + sin(x) Решение: Эта функция является суммой двух различных функций. Здесь будет использоваться правило суммы. f(x) =e x + sin(x) Здесь h(x) =e x и g(x) = sin(x) f(x) = h(x) + g(x) ⇒f'(x) = h'(x) + g'(x) ⇒ f'(x) = ⇒f'(x) = ⇒f'(x ) = e x + cos(x) Вопрос 3. f(x) = 5x 4 – 3x 2 Решение: Эта функция представляет собой разность двух разных функций. Здесь будет использоваться правило разности. f(x) = 5x 4 – 3x 2 Здесь h(x) = 5x 4 и g(x) = 3x 2 fx(x) = fx(x) – g(x) ⇒f'(x) = h'(x) – g'(x) ⇒ f'(x) = ⇒f'(x) = ⇒f'(x ) = 20x 3 + 6x Вопрос 4. Найдите производную для заданной функции f(x), f(x) = 5log(x) – 3x 6 Решение: 6 функция есть разность двух разных функций. Здесь будет использоваться правило разности. f(x) = 5log(x) – 3x Здесь h(x) = 5log(x) и g(x) = 3x f(x) = h(x) – g (x) ⇒f'(x) = h'(x) – g'(x) ⇒ f'(x) = ⇒f'(x) = ⇒f'(x) = Вопрос 5: Найдите производную для заданной функции f(x), f (x) = 5x 4 . Решение: Эта функция является произведением двух разных функций. Здесь будет использоваться правило произведения. f(x) =5x 4 .sin(x) Здесь h(x) =5x 4 и g(x) = sin(x) f(x) = h(x) .g(x) ⇒ f'(x) = h'(x) g(x) + h(x)g'(x) ⇒ f'(x) = ⇒f'(x) = ⇒f’ (x) = 20x 3 sin(x) + 5x 4 cos(x) x .log(x) Решение: Эта функция является произведением двух разных функций. Здесь будет использоваться правило произведения. f(x) =5e x .log(x) Здесь h(x) = 5e x и g(x) = log(x) f(x) = h(x).g(x) ⇒f'(x) = h’ (x) g(x) + h(x)g'(x) ⇒ f'(x) = ⇒f'(x) = ⇒f'(x) = Вопрос 7 : Найдите производную для заданной функции f(x), f(x) = Решение: Эта функция представляет собой деление двух разных функций. f(x) = Здесь h(x) =x + 1 и g(x) = 2x f(x) = ⇒f'(x) = ⇒ f'(x) = ⇒f'( x) = ⇒f'(x) = ⇒f'(x) = Решение: Эта функция представляет собой разделение двух разных функций. Здесь будет использоваться правило деления. f(x) = Здесь h(x) = log(x) и g(x) = 2x 9по чистым производным алгебра Пусть R — любая коммутативная уникальная область факторизации (UFD) и неопределенные значения x и h. Например, пусть R=ℝ обычных действительных чисел или любого другого поля. Мы рассматриваем R[x] как подкольцо R[x,h]. Мы выводим определение производных полиномиальных и рациональных функций над R вместе с обычными правилами: правилом произведения и правилом степени. Несмотря на абстрактный характер определений, механика отражает общее понимание вводного исчисления без какой-либо апелляции к ε-δ пределам анализа в стиле Коши. Определить где f(x+h)-f(x)=ha1(x,h)⋯am(x,h) в УФО R[x,h].
Кроме того, учитывая g(x,h)∈R[x,h], определите (это просто гомоморфизм вычислений при h=0.)
Наконец определите Мы также обозначаем dfdx через f′(x). 3
3


 Детализировано подробно каждое действие, решили одну из типовых задач, а именно, как находить значение производной функции в конкретной точке. Для этого нужно найти значение функции в произвольной точке, а потом найти значение производной в конкретной точке.
Детализировано подробно каждое действие, решили одну из типовых задач, а именно, как находить значение производной функции в конкретной точке. Для этого нужно найти значение функции в произвольной точке, а потом найти значение производной в конкретной точке. Значение функции в новой точке равно .
Значение функции в новой точке равно . Рис. 2):
Рис. 2): Следовательно:
Следовательно: Изображена синусоида, к точке кривой с абсциссой проведена касательная, которая образует угол с осью . Тангенс данного угла необходимо найти. Также необходимо найти тангенс угла, который образовывается при пересечении оси абсцисс с касательной, проведённой к точке кривой с абсциссой 0 и .
Изображена синусоида, к точке кривой с абсциссой проведена касательная, которая образует угол с осью . Тангенс данного угла необходимо найти. Также необходимо найти тангенс угла, который образовывается при пересечении оси абсцисс с касательной, проведённой к точке кривой с абсциссой 0 и . ru/ru/school/algebra/10-klass/proizvodnaya/tablitsa-proizvodnyh-proizvodnye-trigonometricheskih-funktsiy-tipovye-zadachi
ru/ru/school/algebra/10-klass/proizvodnaya/tablitsa-proizvodnyh-proizvodnye-trigonometricheskih-funktsiy-tipovye-zadachiПроизводная
 Нам надо
найти (скорость в
момент начала торможения).
Нам надо
найти (скорость в
момент начала торможения). При этом
чем меньше будет , тем точнее
средняя скорость будет характеризовать движение точки в момент времени .
При этом
чем меньше будет , тем точнее
средняя скорость будет характеризовать движение точки в момент времени .


 А вот обратное утверждение
неверно. То есть непрерывная на промежутке функция может не иметь производную в
некоторых точках этого промежутка.
А вот обратное утверждение
неверно. То есть непрерывная на промежутке функция может не иметь производную в
некоторых точках этого промежутка.Дистанционный репетитор – онлайн-репетиторы России и зарубежья
ОНЛАЙН-ЗАНЯТИЯ?
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
** Время приема звонков с 10 до 22 по МСК
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
расширенной формой подачи заявки
800 до 5000 ₽
квалификации
репетитора
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
DisTTutor на рынке с 2008 года.
уже сделали свой выбор
о наших репетиторах
 Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью. По результатам занятий можно сразу заметить повышение уровня успеваемости ученика. Наталья Борисовна хороший педагог, умеет быстро найти общий язык с ребенком, внимательная, легко передающая знания ученику. С большим удовольствием будем продолжать наши занятия, т.к. мы всем довольны.
По результатам занятий можно сразу заметить повышение уровня успеваемости ученика. Наталья Борисовна хороший педагог, умеет быстро найти общий язык с ребенком, внимательная, легко передающая знания ученику. С большим удовольствием будем продолжать наши занятия, т.к. мы всем довольны. RU
RU
Алгебра

 Зная, что х’=1 находим 1=xln’x,
откуда ln’x=1\x.
Эта формула показывает, что для функции
1\x на промежутке (0;∞)
любая первообразная может быть записана
в виде ln x+C.
На любом промежутке, не содержащим точку
0 первообразной для функции 1\x
является функция ln IxI.
Зная, что х’=1 находим 1=xln’x,
откуда ln’x=1\x.
Эта формула показывает, что для функции
1\x на промежутке (0;∞)
любая первообразная может быть записана
в виде ln x+C.
На любом промежутке, не содержащим точку
0 первообразной для функции 1\x
является функция ln IxI. е. при .
Теорема 3:Первообразная для функции
a(x) на R
является функция a(x)\lna.
е. при .
Теорема 3:Первообразная для функции
a(x) на R
является функция a(x)\lna. Функция
арксинус имеет производную в каждой
точке своей области определения и
Функция
арксинус имеет производную в каждой
точке своей области определения и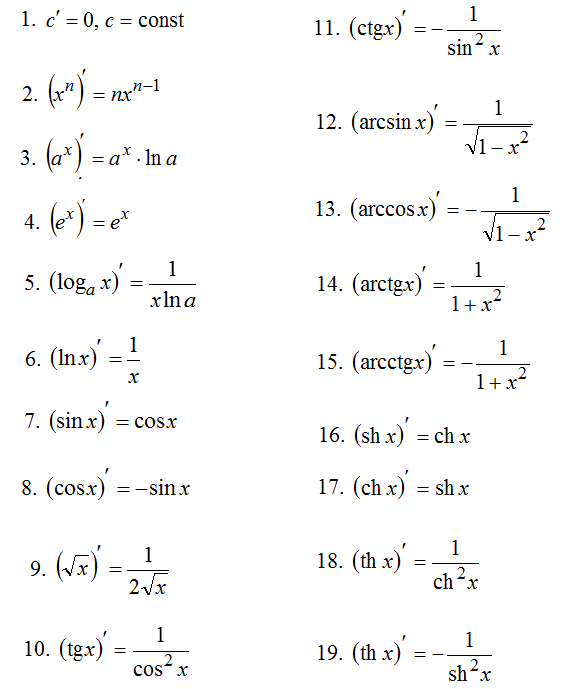
 Точка x1
называется точкой максимума, если для
всех X из интервала a
b, содержащего точку x1
выполняется неравенство f(x1)>f(x).
Точка x2 называется точкой
минимума функции y=f(x),
если для всех X из интервала
c.d, содержащего
точку x2 выполняется
неравенство f(x2)
> f(X).
Точка x1
называется точкой максимума, если для
всех X из интервала a
b, содержащего точку x1
выполняется неравенство f(x1)>f(x).
Точка x2 называется точкой
минимума функции y=f(x),
если для всех X из интервала
c.d, содержащего
точку x2 выполняется
неравенство f(x2)
> f(X). 1.Производная функции у'(x).
2.Критические точки функции у’=0.
3.Возростание, убывание, точки экстремумов.
4.Экстремальные точки (max
min). 5.Вторая
производная y”=(f'(x))’.
6.Критические точки второго рода y”=0.
7.Выпуклость, вогнутость. 8.Точки перегиба.
9.Дополнительные точки x=0,
y=f(0),
y=0, f(x)=0.
10.Строим график функции.
1.Производная функции у'(x).
2.Критические точки функции у’=0.
3.Возростание, убывание, точки экстремумов.
4.Экстремальные точки (max
min). 5.Вторая
производная y”=(f'(x))’.
6.Критические точки второго рода y”=0.
7.Выпуклость, вогнутость. 8.Точки перегиба.
9.Дополнительные точки x=0,
y=f(0),
y=0, f(x)=0.
10.Строим график функции.
 10). ин dx\1+x²=arctgx+C.
10). ин dx\1+x²=arctgx+C. е.
S=F(b)
– F(a)
е.
S=F(b)
– F(a) Алгебра производных функций: определение, виды, правила, примеры

Определение производных финансовых инструментов
Функция \(f\left( x \right)\ ) называется дифференцируемой в интервале \(I,\), если она дифференцируема в каждой точке \(I.\). Производная функции \(f\left( x \right)\) обозначается как:
\(\frac{d}{{dx}}\left[{f\left( x \right)} \right]\) или \(f’\left( x \right).\) Производные как Наклон касательной линии
 \) Аналогично, производные в точках \({x_2}\) и \({x_3}\) являются наклонами касательных в соответствующих точках, как показано на рисунке.
\) Аналогично, производные в точках \({x_2}\) и \({x_3}\) являются наклонами касательных в соответствующих точках, как показано на рисунке. Алгебра производных функций: важные правила
1. Правило суммы
\( \frac{d}{{dx}}\left[{f\left( x \right) + g\left(x \right)} \right] = \frac{d}{{dx}}\left[{ f\left( x \right)} \right] + \frac{d}{{dx}}\left[{g\left(x \right)} \right]\)
\(\следовательно \frac{d}{{dx}} \ left[{f\left(x\right) + g\left(x\right)} \right]=\underset{{h \to 0}}{\mathop {\lim}} \frac{{f\left ({x + h} \right) + g\left({x + h} \right) – \left[{f\left( x \right) + g\left( x \right)} \right]}} {h}\)
\( = \underset{{h \to 0}}{\mathop {\lim }} \frac{{f\left({x + h}\right) – f\left( x \ вправо) + g\влево({x + h} \вправо) – g\влево( x \вправо)}}{h}\)
\( = \underset{{h \to 0}}{\mathop {\lim }} \frac{{f\left({x + h}\right) – f\left(x \right)}}{ h} + \ underset{{h \to 0}}{\mathop {\lim}} \frac{{g\left({x + h} \right) – g\left(x \right)}}{h }\)
\( = \frac{d}{{dx}}\left[{f\left( x \right)} \right] + \frac{d}{{dx}}\left[{g\ left( x \right)} \right]\)
Таким образом, мы имеем \(\frac{d}{{dx}}\left[{f\left( x \right) + g\left( x \right )} \right] = \frac{d}{{dx}}\left[{f\left( x \right)} \right] + \frac{d}{{dx}}\left[{g\left ( х \справа)} \справа]\) 2.
 Правило отличия
Правило отличия
\( \frac{d}{{dx}}\left[{f\left( x \right) – g\left(x \right)} \right] = \frac{d}{{dx}}\left[{ f\left( x \right)} \right] – \frac{d}{{dx}}\left[{g\left(x \right)} \right]\)
Доказательство: Правило разности можно доказать, используя свойства пределов и определение производных как \(f’\left( x \right) = \underset{{h \to 0}}{\mathop {\lim } } \frac{{f\left({x + h} \right) – f\left( x \right)}}{h}\)
\(\следовательно \frac{d}{{dx}} \left [{f\left( x \right)} \right] – \frac{d}{{dx}}\left[{g\left( x \right)} \right]=\underset{{h \to 0 }}{\ mathop {\lim }} \frac{{f\left({x + h} \right) – f\left(x \right)}}{h}\underset{{h \to 0}} {\ mathop {\ lim }} \ frac {{g \ left ({x + h} \ right) – g \ left (x \ right)}} {h} \)
\( = \underset{{h \to 0}}{\mathop {\lim }} \frac{{f\left({x + h}\right) – f\left( x \right) – g\ влево ({x + h} \ right) + g \ left ( x \ right)}} {h} \)
\ ( = \ underset {{h \ to 0}} {\ mathop {\ lim }} \ frac {{f\left( {x + h} \right) – g\left( {x + h} \right) – \left[ {f\left( x \right) – g\left( x \right)} \right]}}{h}\)
\(=\frac{d}{{dx}}\left[ {f\left( x \right) – g\left( x \right)} \right]\ )
Следовательно, имеем \(\frac{d}{{dx}}\left[{f\left( x \right) – g\left( x \right)} \right] = \frac{d} {{dx}}\left[{f\left( x \right)} \right] – \frac{d}{{dx}}\left[{g\left( x \right)} \right]\) 3.
 Правило продукта Правило произведения гласит, что производная произведения двух функций равна сумме производной первой функции, умноженной на вторую функцию, и первой функции, умноженной на производную второй функции.
Правило продукта Правило произведения гласит, что производная произведения двух функций равна сумме производной первой функции, умноженной на вторую функцию, и первой функции, умноженной на производную второй функции.
То есть, если \(f\left( x \right)\) и \(g\left( x \right)\) две действительнозначные дифференцируемые функции в интервале \(I\), то
Правило произведения также можно доказать, используя свойства пределов и определение производных как \(f’\left(x \right) = \underset{{h \to 0}}{\mathop { \lim }} \frac{{f\left({x + h} \right) – f\left( x \right)}}{h}.\)
\(\следовательно\frac{d}{{dx }}\left[{f\left(x \right).g\left( x \right)}\right] = \ underset{{h \to 0}}{\mathop {\lim }} \frac{{ f\left({x + h} \right)g\left({x + h} \right) – f\left( x \right)g\left( x \right)}}{h}\)
Добавление и вычитая \(f\left({x + h} \right)g\left( x\right)\) в числителе, мы получаем,
\( = \underset{{h \to 0}}{\mathop {\lim }} \frac{{f\left({x + h} \right)g\left({x + h} \right) – f\left({x + h} \right)g\left( x \right) + f\left({x + h} \right)g\left( x \right) – f\left( x \right) )g\left( x \right)}}{h}\)
\( = \underset{{h \to 0}}{\mathop {\lim }} \frac{{f\left({x + h } \right)\left[{g\left({x + h} \right) – g\left( x \right)} \right] + g\left(x \right)\left[{f\left( {x + h}\right) – f\left( x \right)} \right]}}{h}\)
\( = \underset{{h \to 0}}{\mathop {\lim }} f\left({x + h} \right)\frac{{\left[{g\left({x + h} \right) – g\left(x \right)} \right]}}{h} + \ underset {{h \ to 0}} {\ mathop {\ lim}} г \ влево ( х \ вправо) \ гидроразрыва {{\ влево [{f \ влево ({x + h} \ вправо) – f \ влево( х \вправо)} \вправо]}}{ч}\)
\( = \ underset {{h \ to 0}} {\ mathop {\ lim }} f \ left ({x + h} \ right) \ underset {{h \ to 0}} {\ mathop {\ lim }} \frac{{\left[{g\left({x + h}\right) – g\left(x \right)} \right]}}{h} + \ underset{{h \to 0} {\ mathop {\ lim}} г \ влево ( х \ вправо) \ underset {{ч \ до 0}} {\ mathop {\ lim }} \ frac {{\ влево [{f \ влево ({х + h} \right) – f\left( x \right)} \right]}}{h}…. .\left({\text{i}} \right)\)
.\left({\text{i}} \right)\)
Здесь, используя определение, мы можем скажем, что
\(\ underset{{h \to 0}}{\mathop {\lim }} f\left({x + h} \right) = f\left( x \right),\,\, \,\underset{{h \to 0}}{\mathop {\lim}}\frac{{\left[{g\left({x + h} \right) – g\left(x \right)} \right]}}{h} = \frac{d}{{dx}}g\left( x \right)\)
\(\ underset{{h \to 0}}{\mathop {\lim }}g\left(x\right)\,=\,g\left(x\right),\,\,\,\ подмножество {{h \ to 0}} {\ mathop {\ lim}} \ frac {{\ left [{f \ left ({x + h} \ right) – f \ left ( x \ right)} \ right] }}{h} = \frac{d}{{dx}}f\left( x\right)\)
Применение их в \(\left({\text{i}} \right),\)
\ ( = f\left( x \right) \cdot \left[ {\frac{d}{{dx}}g\left(x\right)} \right] + \frac{d}{{dx}}\ left[ {f\left( x \right)} \right] \cdot g\left( x \right)\)
Следовательно, имеем \( \frac{d}{{dx}}\left[{f \left( x \right).g\left( x \right)}\right] = \frac{d}{{dx}}\left[{f\left( x \right)} \right].g\ влево ( х \ вправо) + f \ влево ( х \ вправо). \ влево [{\ гидроразрыва {d} {{dx}} г \ влево ( х \ вправо)} \ вправо] \)
Это правило также известно как правило дифференцирования Лейбница. 2}}}\)
2}}}\)
Факторное правило также можно вывести, используя свойства пределов и определение производных как \(f’\left( x \right) = \underset{{h \to 0}}{\mathop { \lim }} \frac{{f\left({x + h} \right) – f\left( x \right)}}{h}.\)
\(\следовательно \frac{d}{{dx }}\left[{\frac{{f\left( x \right)}}{{g\left(x \right)}}} \right] = \underset{{h \to 0}}{\ mathop {\ lim }} \ frac {{\ frac {{f \ left ({x + h} \ right)}} {{g \ left ({x + h} \ right)}} – \ frac {{f \ влево(х\вправо)}}{{г\влево(х\вправо)}}}}{ч}\)
\( = \underset{{h \to 0}}{\mathop {\lim}} \frac{1}{h}\,\frac{{f\left({x + h} \right)g\ влево( x \вправо) – f\влево( x \вправо)g\влево({x + h} \вправо)}}{{g\влево( x \вправо)g\влево({x + h} \вправо )}}\)
Вычитание и добавление \(f\left( x \right)g\left( x \right)\) в числителе,
\( = \underset{{h \to 0}}{\mathop {\ lim}} \ frac {1} {h} \, \ frac {{f \ left ({x + h} \ right) g \ left ( x \ right) + f \ left ( x \ right) g \ влево( x \вправо) – f\влево( x \вправо)g\влево({x + h} \вправо)}}{{g\влево( x \вправо)g\влево({x + h} \вправо )}}\)
\( = \underset{{h \to 0}}{\mathop {\lim }} \frac{1}{{g\left( x \right)g\left({x + h} \right)} }\frac{{f\left({x + h} \right)g\left( x \right) – f\left( x \right)g\left( x \right) + f\left( x \right )g\left( x \right) – f\left( x \right)g\left({x + h}\right)}}{h}\)
\( = \underset{{h \to 0} {\ mathop {\ lim }} \ frac {1} {{g \ left ( x \ right) g \ left ({x + h} \ right)}} \ left [{\ frac {{f \ left ( {x + h} \right)g\left( x\right) – f\left( x \right)g\left(x \right)}}{h} + \frac{{f\left(x \right) )g\left( x\right) – f\left( x \right)g\left({x + h} \right)}}{h}} \right]\)
\( = \underset{{h \to 0}}{\mathop {\lim }} \frac{1}{{g\left( x \right)g\left({x + h} \right)} }\left[{g\left( x \right)\frac{{f\left({x + h} \right) – f\left( x \right)}}{h} – f\left( x \ right)\frac{{g\left({x + h} \right) – g\left( x \right)}}{h}} \right]\)
По основным свойствам пределов имеем,
\( = \ frac {1} {\ underset {{h \ to 0}} {\ mathop {\ lim}} g \ left ({x + h} \ right) \ underset {{h \ to 0}} {\ mathop {\ lim}} г \ влево (х \ вправо)}} \ влево [{\ underset {{h \ to 0}}} {\ mathop {\ lim}} г \ влево (x \ вправо) \ underset {{h \to 0}}{\mathop{\lim }} \frac{{f\left({x + h} \right) – f\left( x \right)}}{h} – \underset{ {h \ to 0}} {\ mathop {\ lim}} f \ left ( x \ right) \ underset {{h \ to 0}} {\ mathop {\ lim }} \ frac {{g \ left ({ x + h} \right) – g\left( x \right)}}{h}} \right]…\left({{\text{ii}}}\right)\)
Следовательно,
\( \underset{{h \to 0}}{\mathop {\lim }} f\left({x + h} \right) = f\left( x \right),\,\, \, \ underset {{h \ to 0}} {\ mathop {\ lim}} \ frac {{\ left [{f \ left ({x + h} \ right) – f \ left (x \ right)} \right]}}{h} = \frac{d}{{dx}}f\left( x \right)\)
\(\underset{{h \to 0}}{\mathop {\lim }} g\left({x + h} \right) = g\left(x \right),\,\,\,\underset{{h \to 0}}{\mathop {\lim}} \frac{{ \left[{g\left({x + h} \right) – g\left( x \right)} \right]}}{h} = \frac{d}{{dx}}g\left( x \right)\)
\( \underset{{h \to 0}}{\mathop {\lim }} f\left( x \right) = f\left( x \right),\,\,\, \ underset {{h \ to 0}} {\ mathop {\ lim}} г \ влево ( х \ вправо) = г \ влево ( х \ вправо) \) 9{n – 1}}. f’\left( x \right)\)
f’\left( x \right)\) 7.
Цепная линейка
Применяя степенное правило производных,
\( = 4\left({2x} \right ) + 3\left( 1 \right)\)
\( = 8x + 3\)
Следовательно, \(f’\left( x \right) = 8x + 3.\) 2}\,x\)? 92}}}\)
2}\,x\)? 92}}}\) 1.Как найти производную функции от функции?
1.Как найти производную функции от функции?
Ответ: Производную функции можно вычислить с помощью цепного правила дифференцирования, которое гласит:
\(\frac{d}{{dx}}\left[{f \circ g\left ( x \right)} \right] = \frac{d}{{dx}}\left[{f\left({g\left( x \right)} \right)} \right].\frac{d }{{dx}}g\left( x \right)\) 92}} \right).2x\)
\( = 5\left({2x} \right)\)
\( = 10\,x\)
Ответ: Основные операции над производными также известны как алгебра дифференцирования.
1. Правило суммы: \(\frac{d}{{dx}}\left[{f\left( x \right) + g\left(x \right)} \right] = \frac{d}{ {dx}}\left[{f\left( x\right)} \right] + \frac{d}{{dx}}\left[{g\left( x\right)} \right]\)
2. Правило разности: \(\frac{d}{{dx}}\left[{f\left( x \right) – g\left(x \right)} \right] = \frac{d}{{ dx}}\left[{f\left( x\right)} \right] – \frac{d}{{dx}}\left[{g\left( x\right)} \right]\) 92}} \справа)}}\) 3. Что такое производная функции в исчислении?
3. Что такое производная функции в исчислении?
Ответ: Если \(f\left( x \right)\) – функция с действительным знаком, дифференцируемая в точке a, и если область содержит открытый интервал \(I\), содержащий a и предел \ (L = \ underset{{h \to 0}}{\mathop {\lim}} \frac{{f\left({a + h}\right) – f\left(a \right)}}{h }\) существует, этот предел называется производной функции \(f\left( x \right)\) в точке \(a.\)
Ответ: Основные семь правил дифференцирования таковы:
i. Правило суммы:
\(\frac{d}{{dx}}\left[{f\left( x \right) + g\left( x \right)} \right] = \frac{d}{{dx }}\left[{f\left( x \right)}\right] + \frac{d}{{dx}}\left[{g\left( x \right)} \right]\)
ii. Правило разности:
\(\frac{d}{{dx}}\left[{f\left( x \right) – g\left( x \right)} \right] = \frac{d}{{dx }}\left[{f\left( x \right)}\right] – \frac{d}{{dx}}\left[{g\left( x \right)} \right]\)
III. 2}}}\) 9{n – 1}}\)
2}}}\) 9{n – 1}}\)
vii. Цепное правило: \(\frac{d}{{dx}}\left[{f \circ g\left( x \right)}\right] = \frac{d}{{dx}}\left[{f \left({g\left( x \right)} \right)} \right].\frac{d}{{dx}}g\left( x \right)\)
Ответ: Когда есть произведение двух функций, производная которых должна быть вычислена, следует использовать правило произведения производных. Согласно правилу произведения производная произведения двух функций равна сумме производной первой функции, умноженной на вторую, и первой функции, умноженной на производную второй функции. 92} + 82х + 3\) Алгебра производных функций
 В таком сценарии инженеру необходимо знать две вещи — размер резервуара для воды и скорость, с которой вода вытекает из него. Размер резервуара можно легко узнать, но для измерения скорости утечки воды ему придется использовать производные. Таким образом, производные переплетаются в нашей жизни. Легко вычислить производные для простых функций, но когда функции становятся сложными, правильный подход к этой проблеме состоит в том, чтобы разбить проблему на подзадачи, которые легче решить. Давайте посмотрим на некоторые правила и подходы, чтобы сделать это в случае деривативов.
В таком сценарии инженеру необходимо знать две вещи — размер резервуара для воды и скорость, с которой вода вытекает из него. Размер резервуара можно легко узнать, но для измерения скорости утечки воды ему придется использовать производные. Таким образом, производные переплетаются в нашей жизни. Легко вычислить производные для простых функций, но когда функции становятся сложными, правильный подход к этой проблеме состоит в том, чтобы разбить проблему на подзадачи, которые легче решить. Давайте посмотрим на некоторые правила и подходы, чтобы сделать это в случае деривативов. Производные инструменты
 Линия приближается к касательной от хорды. Это означает, что теперь производная, когда h приближается к нулю, дает нам наклон касательной в этой конкретной точке.
Линия приближается к касательной от хорды. Это означает, что теперь производная, когда h приближается к нулю, дает нам наклон касательной в этой конкретной точке. Common Function Function Derivative Constant Function c f'(x) = 0 Line Ax + b f ‘(x) = A Квадрат x 2 f'(x) = 2x Square Root √x f'(x) = Exponential e x e x Exponential a x ln(a)a x Logarithms log e x Logarithms log a x Trigonometry sin(x) cos(x) Trigonometry cos(x) -sin(x) Trigonometry tan(x) sec 2 ( x) Правила дифференцирования
 Обычно встречающиеся функции включают более одной функции, связанной друг с другом операторами, такими как сложение, вычитание, умножение и деление. В таких случаях очень громоздко решать производные через определение их пределов. Для облегчения таких расчетов были даны определенные правила:
Обычно встречающиеся функции включают более одной функции, связанной друг с другом операторами, такими как сложение, вычитание, умножение и деление. В таких случаях очень громоздко решать производные через определение их пределов. Для облегчения таких расчетов были даны определенные правила:  .
. Примеры задач
 Найдите производную для заданной функции f(x),
Найдите производную для заданной функции f(x),  sin(x)
sin(x)  Здесь будет использоваться правило деления.
Здесь будет использоваться правило деления.
Определение 1.
f(x+h)-f(x)h=a1(x,h)⋯am(x,h) limh→0g(x,h)=g(x,0) dfdx:=limh→0f(x+h)-f(x)h=a1(x,0)⋯am(x,0). Пример 1.
ддx(5x2-7x+9)=10x-7.
Доказательство.
Сначала мы уменьшаем дробь способом, идентичным обычным методам исчисление:
| ддх(5х2-7х+9) | = | limh→0(5(x+h)2-7(x+h)+9)-(5x2-7x+9)h | ||
| = | limh→05x2+10xh+5h3-7x-7h+9-5x2+7x-9h | |||
| = | limh→010xh+5h3-7hh | |||
| = | limh→010x+5h-7. |
На этом этапе мы должны интерпретировать limh→0. Поскольку предельное обозначение просто означает, что для оценки этого многочлена при h = 0 мы находим:
| ддx(5x2-7x+9)=10x+5(0)-7=10x-7. |
Это отличается от типичного подхода, когда говорят, что h «приближается» 0. Однако в решении нет разницы и почти нет разницы находится в методе, только в интерпретации метода. ∎
Предложение 2.
Формула производной корректно определена. Особенно, h делит f(x+h)-f(x)∈R[x,h] для каждого f(x)∈R[x], и a1(x,h)⋯am(x,h) уникальны для f(x).
Доказательство.
Для всех f(x),g(x)∈R[x] следует
| (f+g)(x+h)-(f+g)(x)=f(x+h)+g(x+h)-f(x)-g(x) (f(x+h)-f(x))+(g(x+h)-g(x)). |
Кроме того, для всех a∈R
| (af)(x+h)-(af)(x)=af(x+h)-af(x)=a(f(x+h) )-f(x)). |
Итак, теперь, если мы возьмем f(x)=a0+a1x+⋯+anxn,
тогда h|(f(x+h)-f(x)) если h|((x+h)i-xi) для каждого i∈ℕ. Когда i=0, (x+h)0-x0=0, поэтому h|((x+h)0-x0). Теперь возьмем i>0
и используя биномиальную теорему, чтобы найти:
Когда i=0, (x+h)0-x0=0, поэтому h|((x+h)0-x0). Теперь возьмем i>0
и используя биномиальную теорему, чтобы найти:
| (х+ч)i-xi | = | ∑j=0i(ij)xi-jhj-xi | ||
| = | ∑j=1i(ij)xi-jhj | |||
| = | ч∑j=1i(ij)xi-jhj-1. |
Следовательно, h|(f(x+h)-f(x)).
Поскольку R является UFD, то и R[x,h]. Также h неприводим в R[x,h] и h|(f(x+h)-f(x)), поэтому f(x+h)-f(x)=ha1(x,h)⋯am(x,h) для некоторых ai(x,h)∈R[x,h], 1≤i≤m, причем каждое ai(x,h) уникально для f(x+h)-f(x) с точностью до умножения на единица R[x,h], то есть единица R. В частности, a1(x,h)⋯am(x,h) уникален для f(x+h)- f(x), и поэтому уникален для f(x). ∎
Теорема 4.
Производные удовлетворяют следующим правилам:
- Линейность
Для f(x),g(x)∈R[x] и a∈R
ddx(f(x)+g(x))=dfdx+dgdx,ddx(af(x))=adfd х, - Силовое правило
ддx(xn)=nxn-1. 
- Правило продукта
ddx(f(x)g(x))=dfdxg(x)+f(x)dgdx.
Эта форма формальной производной применима к любому UFD, а значит, и к ℝ. Таким образом, можно выразить полиномиальное исчисление в терминах алгебраической теории без какого-либо надлежащего использования пределов. Это скрывает многие геометрические свойства, такие как наклон касательной к графику. Однако с вычислительной точки зрения этот метод показывает, что ε, δ-пределы не требуются для вычисления производных.
Хотя для правильного понимания R[x,h]/(h) требуется абстрактная алгебра, такая как частное колец, этот подход по-прежнему обеспечивает элементарные доказательства производных правил, таких как правило произведения. Хотя в этом нет необходимости, проводить различие между R[x] и R[x,h]/(h) можно использовать ≡, когда мы рассматриваем выражения в R[x,h]/(h), если различие уточняется.
Можно также обобщить производную для применения к общей рациональной функции f(x)∈R(x) соблюдая 1=xnx-n. Поэтому
| ддx(1)=ддx(xnx-n) | ||
| 0=ддx(xn)x-n+xnddx(x-n) | ||
| 0=nxn-1x-n+xnddx(x-n)=nx+xnddx(x-n). |
Теперь найдите ddx(x-n).
| ддx(xn)=-nx1xn=(-n)x(-n)-1. |
Таким образом, мы также получаем обычное правило частных:
| ддx(fg)=f′(x)g(x)-f(x)g′(x)g(x)2. |
Производные Бернштейна–Зелевского: подход на основе алгебры Гекке | Уведомления о международных математических исследованиях
Журнальная статья
Кей Юэн Чан,
Кей Юэн Чан
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Гордан Савин
Гордан Савин
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
International Mathematics Research Notices , Volume 2019, Issue 3, February 2019, Pages 731–760, https://doi. org/10.1093/imrn/rnx138
org/10.1093/imrn/rnx138
Опубликовано:
06 июля 2017
История статьиПолучен:
28 февраля 2017 г.
Полученная ревизия:
18 мая 2017
Принято:
30 мая 2017
Опубликовано:
06 июль 2017
- Содержание статьи
- Рисунки и таблицы
- видео
- Аудио
- Дополнительные данные
Цитировать
Cite
Kei Yuen Chan, Gordan Savin, Bernstein – Zelevinsky Derivatives: a Hecke Algebra Approach, International Mathematics Research Notices , Volume 2019, Issue 3, February 2019, Pages 731–760, https://doi. org /10.1093/имрн/rnx138
org /10.1093/имрн/rnx138
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Разрешения
- Электронная почта
- Твиттер
- Фейсбук
- Подробнее
Фильтр поиска панели навигации Уведомления о международных исследованиях в области математикиЭтот выпускPure MathematicsКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Уведомления о международных исследованиях в области математикиЭтот выпускPure MathematicsКнигиЖурналыOxford Academic Термин поиска на микросайте
Advanced Search
Abstract
Пусть G — общая линейная группа над p-адическим полем. Хорошо известно, что бернштейновы компоненты категории гладких представлений группы G описываются алгебрами Гекке, возникающими из типов Бушнелла–Куцко. Мы описываем компоненты Бернштейна представления Гельфанда–Граева группы G явными модулями алгебры Гекке. Этот результат используется для перевода теории производных Бернштейна–Зелевинского на язык представлений алгебр Гекке, где мы развиваем исчерпывающую теорию.
Хорошо известно, что бернштейновы компоненты категории гладких представлений группы G описываются алгебрами Гекке, возникающими из типов Бушнелла–Куцко. Мы описываем компоненты Бернштейна представления Гельфанда–Граева группы G явными модулями алгебры Гекке. Этот результат используется для перевода теории производных Бернштейна–Зелевинского на язык представлений алгебр Гекке, где мы развиваем исчерпывающую теорию.
1 Введение
Производные Бернштейна–Зелевинского были впервые введены и изучены в [5] и [23] и являются важным инструментом в теории представлений общих линейных групп над p-адическими полями. Одна из целей этой статьи — сформулировать функторы для алгебр Гекке, соответствующие производным Бернштейна–Зелевинского, и показать, что производные Бернштейна–Зелевинского могут быть определены из соответствующих функторов алгебры Гекке. Преимущество нашего подхода состоит в том, что некоторые представления, такие как обобщенные модули Шпеха, имеют явное описание в терминах соответствующих модулей алгебры Гекке, а не просто определяются как факторы Ленглендса. Таким образом, в качестве приложения нашего исследования мы вычисляем производные Бернштейна–Зелевинского обобщенных модулей Шпе методом, который не использует детерминантную формулу Тадича [20] и Лапида–Мингеса [13] или полиномы Каждана–Люстига [10]. , 24].
Таким образом, в качестве приложения нашего исследования мы вычисляем производные Бернштейна–Зелевинского обобщенных модулей Шпе методом, который не использует детерминантную формулу Тадича [20] и Лапида–Мингеса [13] или полиномы Каждана–Люстига [10]. , 24].
1.1 Основные результаты
Пусть F — p-адическое поле. Пусть G — общая линейная группа над F. Категория ℜ(G) гладких представлений группы G может быть описана алгебрами Гекке, возникающими из типов Бушнелла–Куцко [7]. Чтобы упростить обозначения, мы будем обсуждать только простые типы. Это ограничение не приведет к потере общности в том, что касается теории производных Бернштейна–Зелевинского. Итак, пусть G (или Gn, если нам нужно различать общие линейные группы разного ранга) будет группой GLnr(F), где r — фиксированное целое число. Группа G содержит группу Леви L=GLr(F)n. Пусть δ — суперкаспидальное представление группы GLr(F). Тогда τ=δ⊠…⊠δ является суперкаспидальным представлением L. Пара s=[L,τ] (или sn) определяет бернштейновскую компоненту ℜs(G) ℜ(G).
Пара s=[L,τ] (или sn) определяет бернштейновскую компоненту ℜs(G) ℜ(G).
Тип — это представление ρ открытой компактной подгруппы K группы G. Если π является гладким представлением G, то πρ=(π⊗ρ∨)K, естественно, является модулем для H(G,ρ), алгебры Гекке End(ρ∨)-значных функций на G. Тип ρ называется типом Бушнелла–Куцко, если π↦πρ является эквивалентностью ℜs(G) и категории H(G,ρ)-модулей. Для описанного выше sn такой тип ρn построен в [7] и в [22] в ручном случае. Кроме того, доказано, что H(G,ρn) изоморфна Hn, алгебре Ивахори–Гекке группы GLn(F′), где F′ является расширением F, зависящим от ρn. Группа Вейля GLn(F′) изоморфна группе матриц перестановок Sn, а Hn имеет конечномерную подалгебру HSn с базисом Tw характеристических функций двойных смежных классов по w∈Sn. Алгебра HSn имеет одномерное представление sign, Tw↦(−1)l(w), где l — функция длины на Sn.
Пусть U — унипотентная подгруппа всех строго верхних треугольных матриц в G. Пусть ψ — характер Уиттекера U. Одним из основных результатов данной статьи является описание бернштейновских компонент представления Гельфанда–Граева indUGψ в терминах действия алгебры Гекке:
Одним из основных результатов данной статьи является описание бернштейновских компонент представления Гельфанда–Граева indUGψ в терминах действия алгебры Гекке:
Эта теорема доказана в [9] для компоненты, состоящей из представлений, порожденных их -фиксированные векторы явным вычислением. Здесь мы даем более абстрактное доказательство, использующее проективность indUGψ и то, что компоненты Бернштейна indUGψ конечно порождены, результат Бушнелла и Хенниарта [6]. Таким образом, наш результат является уточнением их результатов для общей линейной группы. Проективность indUGψ была доказана Прасадом в [16] с помощью аргумента, весьма специфичного для общих линейных групп. В Приложении мы доказываем проективность представления Гельфанда–Граева в очень общем случае.
Теорема 1.1 играет важную роль в формулировке производных Бернштейна–Зелевинского на языке алгебр Гекке. Для этого пусть
Sn=(∑w∈Sn(1/q)l(w))−1∑w∈Sn(−1/q)l(w)Tw∈Hn.
Если σ — Hn-модуль, то Sn(σ) — sign-изотипное подпространство σ. Для каждого i=1,…,n−1 имеем вложение алгебры Гекке Hn−i⊗Hi в Hn. В частности, отображение h↦h⊗1 реализует Hn−i как подалгебру в Hn. Пусть Sin — образ 1⊗Si в Hn, где Si — проектор знака в Hi. Для каждого Hn-модуля σ
Для каждого i=1,…,n−1 имеем вложение алгебры Гекке Hn−i⊗Hi в Hn. В частности, отображение h↦h⊗1 реализует Hn−i как подалгебру в Hn. Пусть Sin — образ 1⊗Si в Hn, где Si — проектор знака в Hi. Для каждого Hn-модуля σ
BZi(σ):=Sin(σ)
(1.1)
естественно является Hn−i-модулем. Это i-я производная от σ. Пусть π — гладкое представление Gn, а π(l) — его l-я производная Бернштейна–Зелевинского. Если π принадлежит ℜsn(Gn), то π(l)=0, если только l не кратно r, и тогда π(ir) является объектом в ℜsn−i(Gn−i).
Аналогично можно сформулировать производные Бернштейна–Зелевинского для градуированных алгебр Гекке. В разделах 5 и 6 мы проверяем, что производные Бернштейна–Зелевинского аффинных алгебр Гекке и градуированных алгебр Гекке согласуются при редукциях Люстига. Причина формулировки производных Бернштейна–Зелевинского для градуированных алгебр Гекке заключается в том, что можно применить теорию представлений симметрических групп, в частности правило Литтлвуда-Ричардсона, для вычисления производных Бернштейна–Зелевинского обобщенных представлений Шпе, подробности см. в разделе 7. .
в разделе 7. .
2 Аффинная алгебра Гекке
2.1 Проективные модули
Пусть Hn — алгебра Ивахори–Гекке группы GL(n) над p-адическим полем F′. Как абстрактная алгебра, Hn порождается элементами T1,…,Tn−1 и алгеброй An=ℂ[x1±1,…,xn±1] многочленов Лорана. Алгебра An изоморфна групповой алгебре решетки ℤn следующим образом. Групповая алгебра состоит из элементов θx, где x∈ℤn с умножением θx⋅θy=θx+y. Мы можем идентифицировать две алгебры как θx=x1m1⋯xnmn, где x=(m1,…,mn)∈ℤn. Мы будем использовать оба обозначения для элементов из An по своему усмотрению. Элементы Tj удовлетворяют квадратичному соотношению (Tj+1)(Tj−q)=0 (и соотношению кос), а отношение между Tj и f∈An определяется соотношением
Tjf−fsjTj=(q−1)xjf−fsjxj−xj+1,
(2.2)
где sj — перестановка (j,j+1), а fsj получается из f перестановкой xj и xj+ 1. Группа Вейля GL(n) изоморфна группе перестановок Sn, а центр Zn группы Hn равен подалгебре Sn-инвариантных полиномов Лорана в An. Воспользуемся тем, что An — свободный Zn-модуль ранга |Sn|. Пусть HSn — подалгебра в Hn, порожденная элементами Tj, j=1,…,n−1. Это конечная алгебра, натянутая на элементы Tw, w∈Sn, где Tw — произведение Tj, заданное кратчайшим выражением w как произведения простых отражений. В частности, размерность HSn равна |Sn|. Мы также воспользуемся тем, что умножение в Hn элементов из An и HSn дает изоморфизмы
Группа Вейля GL(n) изоморфна группе перестановок Sn, а центр Zn группы Hn равен подалгебре Sn-инвариантных полиномов Лорана в An. Воспользуемся тем, что An — свободный Zn-модуль ранга |Sn|. Пусть HSn — подалгебра в Hn, порожденная элементами Tj, j=1,…,n−1. Это конечная алгебра, натянутая на элементы Tw, w∈Sn, где Tw — произведение Tj, заданное кратчайшим выражением w как произведения простых отражений. В частности, размерность HSn равна |Sn|. Мы также воспользуемся тем, что умножение в Hn элементов из An и HSn дает изоморфизмы
Hn≅An⊗ℂHSn≅HSn⊗ℂAn.
Алгебра HSn имеет два одномерных представления: тривиальное, где Tj=q для всех j, и знаковое представление, где Tj=−1 для всех j. Скрученное представление Стейнберга — это одномерное представление Hn такое, что его ограничение на HSn является представлением со знаком. Этот параграф посвящен доказательству следующей теоремы.
Из леммы вместе с первым предположением о Π следует, что Π≅Anr как An-модуль.
Пусть J и π такие, как в лемме. Тогда Π/JΠ имеет композиционный ряд такой, что любой неприводимый подфактор изоморфен π. Поскольку Π/JΠ аннулируется J, по простому применению леммы 2.3 это прямая сумма r копий π. Отсюда r=1 по второму предположению относительно Π.
Доказательство этой леммы находится в следующем разделе. Из леммы в сочетании с третьим предположением о Π следует, что Π изоморфен Hn⊗HSnsgn. Это завершает доказательство теоремы 2.1.
Примечание 2.5.
Авторы благодарят рецензента за указание на то, что структуру конечно порожденных проективных модулей можно понять из K-теории аффинных алгебр Гекке [18, раздел 5.1]. Некоторые явные K-теоретические вычисления можно найти в [17, гл. 6]. □
2.2 Hn-модульная структура на An
Основная цель этого параграфа — доказать лемму 2. 4. Это будет достигнуто явным вычислением h3, из которого мы выведем общий случай. Мы работаем в более общем контексте и заменяем A2 на A[x1±1,x2±1], где A — ℂ-алгебра. Итак, предположим, что у нас есть h3-структура на A[x1±1,x2±1]. В частности, если g(x1,x2)∈A[x1±1,x2±1] обратима, то
4. Это будет достигнуто явным вычислением h3, из которого мы выведем общий случай. Мы работаем в более общем контексте и заменяем A2 на A[x1±1,x2±1], где A — ℂ-алгебра. Итак, предположим, что у нас есть h3-структура на A[x1±1,x2±1]. В частности, если g(x1,x2)∈A[x1±1,x2±1] обратима, то
T1(g(x1,x2))=f(x1,x2)g(x1,x2)
для некоторого f(x1,x2)∈A[x1±1,x2±1], в зависимости от g (x1,x2). Используя соотношение (2.2), из соотношения T12=(q−1)T1+q следует, что f(x1,x2) удовлетворяет следующему полиномиальному уравнению:
f(x1,x2)f(x2,x1)=(q −1)(x1f(x2,x1)−x2f(x1,x2)x1−x2)+q.
Итак, наша задача — решить это полиномиальное уравнение. С этой целью мы сокращаем
f˜(x1,x2)=x1f(x2,x1)−x2f(x1,x2)x1−x2,
и выводим некоторые явные формулы для f˜. Предположим, что f(x1,x2)=x1nx2m. Если m≥n, то
f˜(x1,x2)=x1mx2n+x1m−1x2n+1+…+x1nx2m.
Если m f˜(x1,x2)=−x1n−1x2m+1−…−x1m+1x2n−1. Напишите f(x1,x2)=∑an,mx1nx2m и определите maxdeg(f(x1,x2))=max{n+m∈ℤ:an,m≠0},mindeg(f(x1,x2 ))=мин{n+m∈ℤ:an,m≠0}. Из леммы следует, что решением полиномиального уравнения является полином Лорана f(x), где x=x2/x1. Мы сокращаем f˜(x)=x−1/2f(x−1)−x1/2f(x)x−1/2−x1/2. С учетом разложения тензорного продукта hn≅an⊗ℂhsn следующее следствие завершает доказательство Lemma 2.4:
3 Gelfand – Graev. р-адическая редуктивная группа. Пусть K — открытая компактная подгруппа группы G, а (ρ, E) — гладкое конечномерное представление группы K. Пусть H(G,ρ) — алгебра End(E∨)-значных функций на G с компактным носителем, таких что f(kgk′)=ρ∨(k)f(g)ρ∨(k′) для k,k ′∈К.
 Пусть S(G) — пространство локально постоянных функций с компактным носителем на G, и пусть eρ∈S(G) определяется равенством
Пусть S(G) — пространство локально постоянных функций с компактным носителем на G, и пусть eρ∈S(G) определяется равенством
eρ(x)=dim(ρ)vol(K)trE(x−1)
, если x∈K, и 0 в противном случае. Тогда eρ∗eρ=eρ. Пусть Hρ=eρ∗S(G)∗eρ. Две алгебры связаны каноническим изоморфизмом Hρ≅H(G,ρ)⊗End(E), см. [8]. Если (π, V) — гладкое представление G, пусть
Vρ=HomK(E,V)≅(E∨⊗V)K.
Заметим, что f∈H(G,ρ) естественным образом действует на e∨⊗v∈E∨⊗V по формуле
πρ(f)(e∨⊗v)=∫Gf(g)(e∨)⊗ π(g)(v) dg.
Это действие сохраняет подпространство (E∨⊗V)K и определяет структуру H(G,ρ)-модуля на Vρ. С другой стороны,
π(eρ)⋅V≅Vρ⊗E
, естественно, является Hρ-модулем. Эти две структуры совместимы относительно изоморфизма Hρ≅H(G,ρ)⊗End(E).
Пусть f∈H(G,ρ).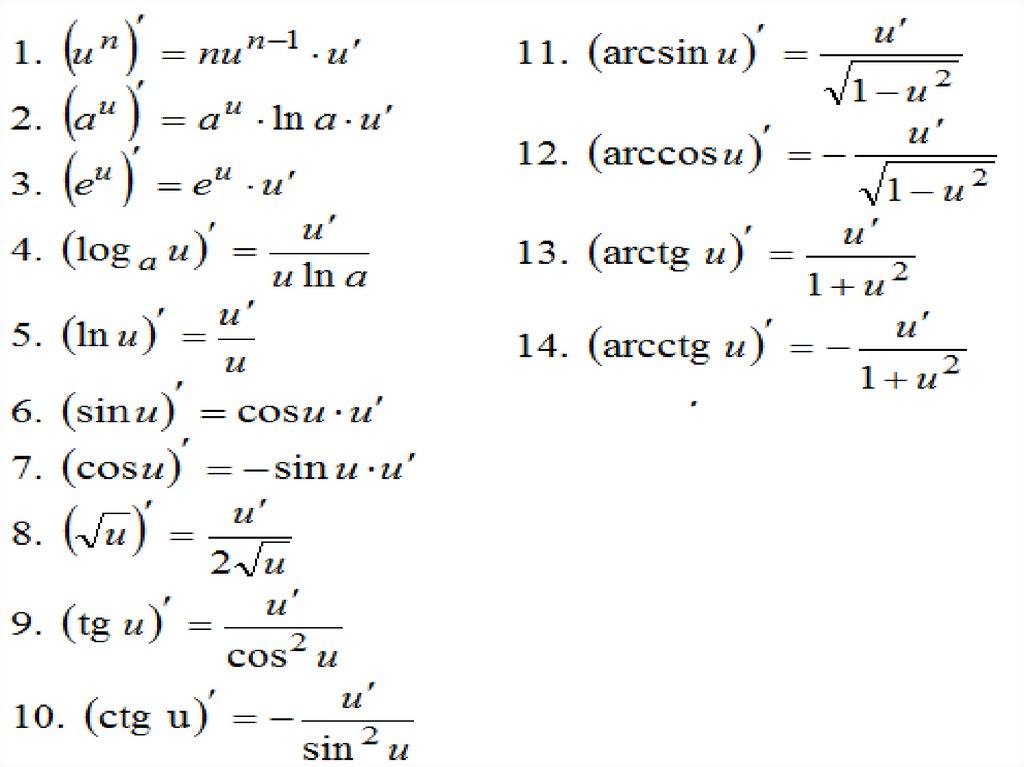 Тогда f(g)∈End(E). Пусть f¯(g) — образ f(g) при композиции следующих изоморфизмов:
Тогда f(g)∈End(E). Пусть f¯(g) — образ f(g) при композиции следующих изоморфизмов:
End(E)≅E⊗E∨≅End(E∨).
Пусть f*(g)=f¯(g−1). Тогда отображение f↦f* является антиизоморфизмом H(G,ρ) и H(G,ρ∨). Пусть (π∨,V∨) — гладкий дуал к (π,V). Тогда Vρ∨∨ — H(G,ρ∨)-модуль. Имеем естественный изоморфизм
(Vρ)*=((E∨⊗V)K)*≅(E⊗V∨)K=Vρ∨∨
векторных пространств, где (Vρ)* — линейная двойственность к Vρ. На (Vρ)* у нас есть антидействие πρ* группы H(G,ρ). Через изоморфизм (Vρ)*≅Vρ∨∨ два действия связаны формулой
πρ*(f)=πρ∨(f*).
3.2 Разложение Бернштейна
Пусть ℜ(G) — категория гладких представлений группы G. Напомним некоторые понятия и свойства разложения Бернштейна и теории типов Бушнелла–Куцко [7, 8], в основном для случая общих линейных групп.
Пусть B(G) — множество классов G-инерциальной эквивалентности. Для каждого s∈B(G) пусть ℜs(G) будет компонентой Бернштейна, ассоциированной с s. Точнее, класс инерционной эквивалентности s состоит из пар (L,τ), где L — подгруппа Леви группы G, τ — суперкуспидальное представление, а ℜs(G) — полная подкатегория ℜ(G), объекты которой имеют свойство, состоящее в том, что каждый неприводимый подфактор появляется как композиционный фактор группы IndPG(τ⊗χ) для некоторого неразветвленного характера χ группы L, а P является параболической подгруппой с частью Леви L. Две пары (L1,τ1) и (L2,τ2) принадлежат одному и тому же классу эквивалентности тогда и только тогда, когда они определяют одни и те же подкатегории в ℜ(G). Разложение Бернштейна утверждает, что существует эквивалентность категорий:
Для каждого s∈B(G) пусть ℜs(G) будет компонентой Бернштейна, ассоциированной с s. Точнее, класс инерционной эквивалентности s состоит из пар (L,τ), где L — подгруппа Леви группы G, τ — суперкуспидальное представление, а ℜs(G) — полная подкатегория ℜ(G), объекты которой имеют свойство, состоящее в том, что каждый неприводимый подфактор появляется как композиционный фактор группы IndPG(τ⊗χ) для некоторого неразветвленного характера χ группы L, а P является параболической подгруппой с частью Леви L. Две пары (L1,τ1) и (L2,τ2) принадлежат одному и тому же классу эквивалентности тогда и только тогда, когда они определяют одни и те же подкатегории в ℜ(G). Разложение Бернштейна утверждает, что существует эквивалентность категорий:
ℜ(G)≅∏s∈B(G)ℜs(G).
Рассмотрим теперь частный случай, когда G=GLnr(F) и класс инерционной эквивалентности sn задается как
τ=δ⊠…⊠δ,
(3. 4)
4)
, где δ — суперкуспидальное представление GLr(F), а число факторов равно n. Пусть P — параболическая подгруппа группы GLnr(F) с L Леви, состоящая из блочных верхнетреугольных матриц. Пусть Stn(δ) — единственный неприводимый фактор
IndPG(ν1−n2δ⊠ν3−n2δ⊠…⊠νn−12δ)
как в [5, раздел 9.1]. Тогда Stn(δ) является представлением, существенно интегрируемым с квадратом, также известным как обобщенное представление Стейнберга. Мы имеем следующий результат, принадлежащий Бушнеллу и Куцко (и Вальдспургеру [22] в ручном случае):
Пусть U — унипотентная группа верхнетреугольных матриц в G. Пусть ψ:U→ℂ× — функционал Уиттекера. Представление Гельфанда–Граева — это индуцированное представление indUG(ψ), состоящее из функций на G с компактным носителем по модулю U.
Помимо изоморфизма ϵ:Hn→H(G,ρn) существует также изоморфизм ϵ∨:Hn→H(G,ρn∨). Поскольку (ϵ(Tj))* поддерживается тем же двойным смежным классом, что и ϵ∨(Tj), и удовлетворяет тому же квадратному уравнению, эти два элемента должны быть одинаковыми. Следовательно, следующая диаграмма коммутирует, здесь левая вертикальная стрелка — это антиинволюция HSn, определяемая Tj*=Tj для всех j=1,…,n−1.
Следовательно, следующая диаграмма коммутирует, здесь левая вертикальная стрелка — это антиинволюция HSn, определяемая Tj*=Tj для всех j=1,…,n−1.
Если (π, V) — гладкое представление G, пусть VU,ψ — максимальное частное V, такое, что U действует на него посредством ψ. Напомним, что
Sn=(∑w∈Sn(1/q)l(w))−1∑w∈Sn(−1/q)l(w)Tw,
, где l — функция длины на Sn, равна проектор знаков.
Теперь предположим, что V допустимо. Тогда VU,ψ¯ и Sn(Vρn) конечномерны. По лемме Йонеды из леммы 3.6 следует теорема 3.5. ▪
Пусть I подгруппа Ивахори группы G. В случае, когда (π,V) принадлежит бернштейновской компоненте представлений, порожденных их I-неподвижными векторами, теорема 3.5 верна для всех гладких представлений, т.е. без предположения о допустимости. Это следствие 4.5 в [9], что доказывается с помощью явной версии теоремы 3. 4, доступной для случая Ивахори. В этом случае Sn(Vρn) — это просто Sn(VI). Включение Sn(VI) в V с последующим проецированием на VU,ψ¯ дает отображение ϕV.
4, доступной для случая Ивахори. В этом случае Sn(Vρn) — это просто Sn(VI). Включение Sn(VI) в V с последующим проецированием на VU,ψ¯ дает отображение ϕV.
4 Производные Бернштейна–Зелевинского
В этом разделе мы немного изменим обозначения и напишем Gn=GLnr(F). Мы также будем использовать π для обозначения пространства гладкого представления группы Gn. Как и ранее, ρn является sn-типом.
4.1 Функтор Жаке
Пусть P=MN — минимальная параболическая подгруппа группы Gn блочно-верхних треугольных матриц с матрицей Леви M=Gn−i×Gi и унипотентным радикалом N. Ограничение K-типа ρn на KM=K∩M неприводимо и изоморфно ρn−i⊠ρi. Имеем следующую коммутативную диаграмму, являющуюся следствием теоремы (7.6.20) из [7]:
, где вертикальные отображения — инъекции. Левое вертикальное отображение m явно описывается следующим образом: m(Tj⊗1)↦Tj и m(xj⊗1)↦xj, для j=1,…n−i−1; m(1⊗Tj)↦Tj+n−i и m(1⊗xj)↦xj+n−i для j=1,…i−1.
Пусть π — гладкое представление группы Gn. Тогда πρn является H(M,ρn−i⊠ρi)-модулем по ограничению из H(Gn,ρn). Пусть πN — нормированный функтор Жаке, т. е. максимальное частное числа π, при котором N действует тривиально. Тогда у нас есть естественное отображение πρn→(πN)ρn−i⊠ρi.
4.2 Производные Бернштейна–Зелевинского
Пусть Ui — подгруппа M, состоящая из матриц вида
(Ir(n−i)00u),
, где u — строго верхняя треугольная матрица в Gi. Характер ψ¯ проводника p определяет характер Уиттекера ψ многообразия Ui
ψ(u)=∑j=r(n−i)+1rn−1ψ¯(uj,j+1),
, где uj,j+1 относится к элементам матрицы. Пусть ω — гладкий M-модуль. Пусть ωUi,ψ — пространство ψ-скрученных Ui-коинвариантов. Это, естественно, Gn−i-модуль. i-я производная Бернштейна–Зелевинского гладкого Gn-модуля π определяется формулой
π(ri)=(πN)Ui,ψ.
(4.5)
Таким образом, ri-я производная Бернштейна–Зелевинского является функтором из категории гладких Gn-модулей в категорию гладких Gn−i-модулей. Отметим, что l-я производная π(l) определена для любого неотрицательного целого числа l, однако, если π является объектом в ℜs(Gn), то π(l)=0, если только l не делится на r.
4.3 Производная Бернштейна–Зелевинского для Hn
Злоупотребляя обозначениями, отождествим Hn−i и m(Hn−i⊗1). Пусть Si∈Hi — проектор знаков. Пусть Sin=m(1⊗Si). Пусть σ — Hn-модуль. i-я производная Бернштейна–Зелевинского от σ есть натуральный Hn−i-модуль
BZi(σ):=Sin(σ).
Как и в случае теоремы 3.5, в случае бернштейновской компоненты представлений, порожденных их неподвижными по Ивахори векторами, теорема 4. 2 верна без предположения о допустимости π.
2 верна без предположения о допустимости π.
5 Правило Лейбница
5.1 Аффинные алгебры Гекке
Мы сформулируем определение аффинной алгебры Гекке в большей общности, которая потребуется в следующих подразделах.
Пусть (X,R,X∨,R∨) — корневое данное, где R — приведенная система корней, а X — ℤ-решетка, содержащая R. Пусть W — группа Вейля группы R. Зафиксируйте набор простых корней Δ. Выбор ∆ определяет множество S простых отражений в W. Пусть l:W→ℤ — функция длины такая, что l(s)=1 для всех s∈S. Пусть A≅ℂ[X] — групповая алгебра X. Другими словами, A имеет базис из элементов θx, x∈X, таких что θxθy=θx+y для всех x,y∈X.
Обозначим через HW конечномерную подалгебру в H, порожденную Tw (w∈W). Имеем изоморфизм векторных пространств H≅A⊗ℂHW. Пусть T=Hom(X,ℂ×). Центр Z группы H изоморфен ℂ[X]W. Следовательно, центральные характеры H параметризуются W-орбитами в T. Обозначим через Wt W-орбиту точки t∈T. Пусть JWt — соответствующий максимальный идеал в Z. Для конечномерного H-модуля χ пусть χ[Wt] будет подпространством χ, аннулируемым степенью JWt. Тогда
Следовательно, центральные характеры H параметризуются W-орбитами в T. Обозначим через Wt W-орбиту точки t∈T. Пусть JWt — соответствующий максимальный идеал в Z. Для конечномерного H-модуля χ пусть χ[Wt] будет подпространством χ, аннулируемым степенью JWt. Тогда
χ≅⊕Wt∈T/Wχ[Wt].
Пусть Xn=Xn∨=⊕k=1nℤϵk — ℤ-решетка. Положим αkl=ϵk−ϵl (k≠l), а также положим αk=αk,k+1 (k=1,…,n). Пусть Rn=Rn∨={ϵk−ϵl:l≠k} — система корней типа An−1. Пусть Δn={ϵi−ϵi+1:i=1,…,n−1}. Алгебра Ивахори–Гекке Hn группы GL(n) (из раздела 2) изоморфна H(Xn,Rn,∆n,q).
5.2. Первая теорема редукции Люстига
Нам понадобится вариант [15, § 2] теоремы редукции Люстига для аффинной алгебры Гекке Hn [14, § 8]. Пусть Tn=Hom(Xn,ℂ×). Любой t∈Tn отождествляется с набором из n (z1,…,zn) ненулевых комплексных чисел, где zi — значение t в точке ϵi. Пусть Tr=Hom(Xn,ℝ>0) и Tun=Hom(Xn,S1). Любой t∈Tn имеет полярное разложение t=vu, где v∈Tr и u∈Tun. Напишите x(u) для значения u в точке x∈Xn. Следовательно, u=(z1,…,zm), где zk=ϵk(u). Мы можем переставить элементы u так, что для разбиения n=(n1,…,nm) числа n z1=…=zn1≠zn1+1=… и т. д. Пусть
Напишите x(u) для значения u в точке x∈Xn. Следовательно, u=(z1,…,zm), где zk=ϵk(u). Мы можем переставить элементы u так, что для разбиения n=(n1,…,nm) числа n z1=…=zn1≠zn1+1=… и т. д. Пусть
Rn={α∈Rn:α(u)=1}.
Это корневая подсистема Rn, которая, как видно из обозначений, зависит от раздела n. Оно изоморфно произведению Rn1×…×Rnm. Пусть Sn≅Sn1×…×Snm — его группа Вейля. Пусть ∆n — множество простых корней в Rn, определяемое соотношением Rn+=Rn+∩Rn. Пусть
Hn:=H(Xn,Rn,∆n,q)≅Hn1⊗…⊗Hnm
— ассоциированная аффинная алгебра Гекке (определение 5.1). Пусть Zn=AnSn — центр Hn. Пусть JSnt идеал в Zn, соответствующий центральному характеру Snt. Пусть σ — конечномерный Hn-модуль, аннулируемый степенью JSnt. Тогда ι(σ)=Hn⊗Hnσ аннулируется степенью JSnt.
Следующий результат и доказательство являются разновидностью [14, разделы 8.16 и 10.9].
3″> 5.3 Первая редукция для производных Бернштейна–ЗелевинскогоПродолжаем использовать обозначения из предыдущего пункта. В частности, мы зафиксировали t=vu∈Tn и имеем канонический изоморфизм Hn≅Hn1⊗…⊗Hnm, где n=(n1,…,nm) — разбиение n, возникающее из u.
Исправьте целое число i≤n. Для каждого m-набора i=(i1,…,im) целых чисел, такого что i1+…+im=i и 0≤ik≤nk (k=1,…,m), определите другой m-набор n− i=(n1−i1,…,nm−im). Каждая пара (nk−ik,ik) порождает вложение Hnk−ik⊗Hik⊆Hnk, как в разделе 4.1, а их комбинация дает вложение
Hn−i⊗Hi⊆Hn
, где Hi≅Hi1⊗…⊗Him и т. д. (Заметим, что если ik=0, то соответствующий множитель есть тривиальная алгебра ℂ.) Злоупотребляя обозначениями, отождествим Hn−i со своим образом в Hn через отображение h↦h⊗1. Пусть Si∈Hi — проектор знаков в Hi, а Sin — образ 1⊗Si в Hn. Пусть σ — Hn-модуль. Тогда Sin(σ) естественно является Hn−i-модулем. Таким образом, мы имеем функтор
BZin(σ):=Sin(σ)
из категории Hn-модулей в категорию Hn−i-модулей.
Заметим, что Hn−i — подалгебра Леви в Hn−i, а Hi — подалгебра Леви в Hi. Теперь мы готовы сформулировать первый результат редукции.
6. Сведение к градуированным алгебрам Гекке
6.1. Пусть V=X⊗Zℂ.
В частности, ℍ≅S(V)⊗ℂ[W] как векторные пространства. Мы также устанавливаем A=S(V), градуированный алгебраический аналог A. Пусть ℤ=AW — центр ℍ [14, § 4]. Пусть V*=Hom(X,ℂ). Центральные характеры неприводимых представлений параметризуются W-орбитами в V*. Если ζ∈V*, пусть Wζ обозначает соответствующую орбиту и центральный характер. Пусть JWζ⊂ℤ — соответствующий максимальный идеал.
6.2 Вторая редукция Люстига
Пусть H=H(X,R,∆,q) — аффинная алгебра Гекке, определенная в разделе 5. 1, A≅ℂ[X] — коммутативная подалгебра и Z≅ℂ[X]W быть центром H. Пусть F будет частным полем A. Пусть HF≅HW⊗ℂF со структурой алгебры, естественным образом продолжающейся с H.
1, A≅ℂ[X] — коммутативная подалгебра и Z≅ℂ[X]W быть центром H. Пусть F будет частным полем A. Пусть HF≅HW⊗ℂF со структурой алгебры, естественным образом продолжающейся с H.
Следуя Люстигу [14, раздел 5], для α∈Δ определим τsα∈HF как θαq−1θα−1∈F.
В [14, § 5] показано, что отображение из W в единицы HF, определяемые формулой sα↦τsα, является инъективным групповым гомоморфизмом.
Со стороны градуированной алгебры Гекке пусть ℍ=ℍ(V,R,∆,logq) такое же, как в определении 6.1. Пусть F будет частным полем A, а ℤ будет центром ℍ. Пусть ℍF≅ℍW⊗ℂF со структурой алгебры, естественным образом продолжающейся с ℍ. Для α∈Δ определим τ¯sα∈ℍF как
τ¯sα+1=(tsα+1)g(α)−1,
, где
g(α)=α+logqα∈F.
Как и в аффинном случае, отображение из W в единицы ℍF, определяемые формулой sα↦τ¯sα, является инъективным групповым гомоморфизмом.
Любое ζ∈V* определяет t∈T=Hom(X,ℂ×) как x(t)=ex(ζ) для всех x∈X. Мы выразим эту связь через t=exp(ζ). Будем говорить, что ζ равно 9x,
, где h∈H и x∈π. Обратите внимание, что функтор распространяется на категорию конечномерных ℍ-модулей, являющихся суммами ℍ-модулей, где каждое слагаемое аннулируется степенью JWζ для некоторого вещественного ζ.
Имеем следующее следствие из предложения 6.4:
6.3 Производные Бернштейна–Зелевинского для градуированных алгебр
Для каждого i=0,…,n у нас есть подалгебра Леви ℍn−i⊗ℍi. Пусть si∈ℍi — проектор знаков, а sin∈ℍn — образ 1⊗si при включении ℍn−i⊗ℍi⊆ℍn.
Пусть π — конечномерное представление ℍn. i-я производная Бернштейна–Зелевинского от π — это натуральный ℍn−i-модуль
gBZi(π):=sin(π).
Запишите любое ζ∈Vn*=Hom(Xn,ℂ) в виде n-кортежа (ζ1,…,ζn), где ζi — значение ζ на стандартном базисном элементе ϵi∈Xn. В этом случае ζ действительно для Rn тогда и только тогда, когда ζk−ζl∈ℝ для всех 1≤k,l≤n.
В этом случае ζ действительно для Rn тогда и только тогда, когда ζk−ζl∈ℝ для всех 1≤k,l≤n.
6.4 Вторая редукция для производных Бернштейна–Зелевинского
В этом разделе мы переносим задачу вычисления производных Бернштейна–Зелевинского BZin в теореме 5.3 к соответствующей задаче для градуированных алгебр Гекке. Мы сохранили обозначения из разделов 5.2 и 5.3. В частности, n=(n1,…,nm) является разбиением n, и мы зафиксировали t∈Tn так, что α(t)>0 для всех α∈Rn. Тогда существует ζ∈Vn*, вещественное для системы корней Rn, такое, что t=exp(ζ). Пусть
ℍn:=ℍ(Vn,Rn,Δn,logq)≅ℍn1⊗…⊗ℍnm.
Пусть i=(i1,…,im) — набор из m целых чисел, такой что 0≤ik≤nk для всех k и n−i=(n1−i1,…,nm−im). Каждая пара (nk−ik,ik) порождает вложение ℍnk−ik⊗ℍik⊆ℍnk, а их комбинация дает вложение
ℍn−i⊗ℍi⊆ℍn
, где ℍi≅ℍi1⊗…⊗ℍim и т. д. Злоупотребляя обозначениями, мы будем отождествлять ℍn−i с его образом в ℍn через отображение h↦h⊗1. Пусть si∈ℍi — проектор знаков в ℍi, а sin — образ 1⊗si в ℍn. Пусть σ — ℍn-модуль. Тогда sin(σ) естественно является ℍn−i-модулем. Таким образом, у нас есть функтор
д. Злоупотребляя обозначениями, мы будем отождествлять ℍn−i с его образом в ℍn через отображение h↦h⊗1. Пусть si∈ℍi — проектор знаков в ℍi, а sin — образ 1⊗si в ℍn. Пусть σ — ℍn-модуль. Тогда sin(σ) естественно является ℍn−i-модулем. Таким образом, у нас есть функтор
gBZin(σ):=sin(σ)
из категории ℍn-модулей в категорию ℍn−i-модулей. Следующее утверждение доказывается так же, как теорема 6.6.
7 Производные Бернштейна–Зелевинского от представлений Speh
7.1 Модули Speh
Представления Speh p-адических групп были тщательно изучены Тадичем как часть изучения унитарного двойственного. Напомним определение (обобщенных) представлений Шпеха. Пусть n¯ будет разбиением n, запишите n¯t=(e1,…,ef), e1≥…≥ef, где t — транспонирование. Пусть Stek будет представлением Стейнберга группы GL(ek,F), и пусть Stek′=νek−12Stek будет поворотом Stek, где ν(g)=|det(g)|F. Пусть Pn¯ — стандартная параболическая подгруппа, ассоциированная с разбиением n¯t. Пусть ρ(g)=|det(g)|Fr для некоторого комплексного числа r. Единственный фактор индуцированного представления
Пусть Pn¯ — стандартная параболическая подгруппа, ассоциированная с разбиением n¯t. Пусть ρ(g)=|det(g)|Fr для некоторого комплексного числа r. Единственный фактор индуцированного представления
π(n¯,ρ)=IndPn¯GL(n,F)(ρSte1′⊠ρν−1Ste2′⋯⊠ρν−f+1Stef′)
— обобщенное представление Шпеха, связанное с (n¯,ρ ). Если e1=e2=…=ef, то πn¯ является представлением Шпеха.
В условиях эквивалентности Бореля–Кассельмана обобщенные представления Шпеа соответствуют Hn-модулям с одним HSn-типом (см. [2, 3, 11]). Поскольку эти Hn-модули имеют вещественный инфинитезимальный характер, мы можем рассмотреть соответствующие модули для градуированной алгебры ℍn. Следуя [2], внутренне модули будем строить следующим образом. Для κ=−rlogq имеем следующие элементы Джусиса–Мерфи: для k=2,…,n,
JMk:=−p(ts1,k+…+tsk−1,k)+κ
(7.9)
и JM1=κ, где p=logq. Несложно проверить, что отображения ϵk↦JMk и tw↦tw определяют гомоморфизм алгебр из ℍn в ℂ[Sn]. Пусть σn¯ — неприводимый ℂ[Sn]-модуль, соответствующий n¯. Например, разбиение (n) определяет тривиальное представление, а (1,…,1) определяет представление знака. Пусть σ(n¯,κ) — ℍ-модуль, извлеченный из σn¯ с помощью определенного выше отображения, где JMk зависит от κ. это обобщенный модуль Speh , связанный с (n¯,κ). Модуль σ(n¯,κ) соответствует π(n¯,ρ) при эквивалентности Бореля–Кассельмана и эквивалентности Люстига в теореме 6.3.
Несложно проверить, что отображения ϵk↦JMk и tw↦tw определяют гомоморфизм алгебр из ℍn в ℂ[Sn]. Пусть σn¯ — неприводимый ℂ[Sn]-модуль, соответствующий n¯. Например, разбиение (n) определяет тривиальное представление, а (1,…,1) определяет представление знака. Пусть σ(n¯,κ) — ℍ-модуль, извлеченный из σn¯ с помощью определенного выше отображения, где JMk зависит от κ. это обобщенный модуль Speh , связанный с (n¯,κ). Модуль σ(n¯,κ) соответствует π(n¯,ρ) при эквивалентности Бореля–Кассельмана и эквивалентности Люстига в теореме 6.3.
Напомним, что gBZi(π) — i-я производная Бернштейна–Зелевинского ℍn-модуля π.
Восстановим теперь результат Лапида–Мингеса (для случая обобщенных модулей Шпеха).
Следствие 7.2.
Пусть π – обобщенное представление Шпеха группы GL(n,F), ассоциированное с (n¯,ρ). Тогда π(i) есть прямая сумма обобщенных модулей Шпеха, связанных с (n¯′,ρ), где n¯′ проходит через все разбиения, полученные удалением i ящиков из n¯ не более чем по одному в каждой строке, так что полученная диаграмма по-прежнему является диаграммой Юнга. □
□
Доказательство.
Поскольку Λ(σn¯,κ)=πIn, достаточно вычислить gBZi(σn¯,κ) по теореме 6.6. Из наблюдения леммы 7.1 достаточно определить ℂ[Sn−i]-модульную структуру gBZi(σn¯,κ), что следует из частного случая правила Литтлвуда–Ричардсона (или формулы Пьери) . ▪
Обобщенные модули Speh образуют подкласс лестничных представлений, определенных Лапидом и Мингесом [13]. Производные Бернштейна–Зелевинского лестничных представлений вычисляются там с помощью детерминантной формулы Тадича.
Финансирование
Эта работа была поддержана Coucher Postdoctoral Fellowship KYC; и NSF [DMS-1359774 для GS].
Благодарности
Эта работа была начата во время конференции Sphericity 2016 в Германии. Авторы благодарят организаторов за создание прекрасных условий для дискуссий. Авторы хотели бы поблагодарить рецензента за информативный отчет.
Приложение
Проективность представления Гельфанда–Граева
В этом приложении мы докажем, что представление Гельфанда–Граева квазирасщепляемой редуктивной группы проективно. Грубо говоря, это следует из двух фактов: его бернштейновы компоненты конечно порождены, а двойственное к нему инъективно.
A.1 Некоторая алгебра
Пусть H — ℂ-алгебра с 1, центр Z — нётерова алгебра, а H — Z-модуль с конечным числом порождений. В частности, каждый конечно порожденный H-модуль π также является конечно порожденным Z-модулем. Следовательно, любая восходящая цепочка подмодулей π стабилизируется. Отсюда следует, что любой конечно порожденный H-модуль имеет неприводимые факторы. Предположим также, что H счетномерно как векторное пространство над ℂ. Тогда любой конечно порожденный H-модуль π счетномерен. В этой ситуации верна лемма Шура, то есть, если π неприводимо, то π аннулируется максимальным идеалом J в Z. Отсюда следует, что любой неприводимый H-модуль конечномерен. 9* является сюръективным для каждого завершения. Но это верно по лемме A.2. Это завершает доказательство теоремы. ▪
Отсюда следует, что любой неприводимый H-модуль конечномерен. 9* является сюръективным для каждого завершения. Но это верно по лемме A.2. Это завершает доказательство теоремы. ▪
А.2. Представление Гельфанда–Граева
Пусть G — квазирасщепляемая редуктивная группа над p-адическим полем. Пусть K — хорошая открытая компактная подгруппа группы G, как в следствии 3.9 в [4]. Пусть H — алгебра Гекке K-биинвариантных функций с компактным носителем на G. Тогда по [4], в частности следствию 3.4 там, алгебра H удовлетворяет условиям, сформулированным в начале этого параграфа. Пусть π — гладкий G-модуль. Чтобы доказать проективность π по теореме A.1, достаточно показать следующие две пули:
Для каждого K слагаемое π, порожденное K-фиксированными векторами, конечно порождено.
Функтор HomG(π,⋅) точен на категории модулей конечной длины.
Пусть π* обозначает гладкую двойственную группу G. Поскольку HomG(π,σ*)≅HomG(σ,π*), второй пункт верен, если π* — инъективный G-модуль. Это верно, если π является представлением Гельфанда–Грива, в силу точности функтора Жаке. Первый пункт также верен для представления Гельфанда–Грива согласно [6]. Таким образом, мы получили следующее следствие:
Поскольку HomG(π,σ*)≅HomG(σ,π*), второй пункт верен, если π* — инъективный G-модуль. Это верно, если π является представлением Гельфанда–Грива, в силу точности функтора Жаке. Первый пункт также верен для представления Гельфанда–Грива согласно [6]. Таким образом, мы получили следующее следствие:
Сообщение проф. Фрейдуна Шахиди
Ссылки
[1]
Atiyah
M.
,
MacDonald
7
I.
Введение в коммутативную алгебру
.
Массачусетс
:
Addison-Wesley Publishing
,
1969
.
[2]
Барбаш
Д.
,
Чуботару
Д.
. «
«
Унитарные модули алгебры Гекке с ненулевыми когомологиями Дирака
». В
Симметрия в теории представлений и ее приложениях: в честь Нолана Уоллаха
,
1
–
20
.
.
Нью-Йорк
:
Биркхойзер
,
2014
.
[3]
Барбаш
Д.
,
Мой
А.
. «
Классификация одного представления K-типа
».
Пер. амер. Мат. соц.
351
, №
10
(
1999
):
4252
–
61
.
[4]
Bernstein
J. N.
Deligne
P.
“
Le center de Bernstein
.” В
Представления редуктивных групп над локальным полем
,
.
Париж
:
Герман
,
1984
.
[5]
Бернштейн
И. Н.
,
Зелевинский
А. В.
. «
Индуцированные представления редуктивных p-адических групп
».
Я, Энн. науч. Эк. Норма. Супер
.
10
(
1977
):
441
–
72
.
[6]
Bushnell
C.
,
Henniart
G.
. «
Обобщенные модели Уиттакера и центр Бернштейна
».
Амер. Дж. Математика
.
125
, №
3
(
2003
):
513
–
47
.
[7]
Бушнелл
CJ
,
Куцко
PC
.
Допустимый двойник GL(N) через компактные открытые подгруппы
.
.
Принстон
:
Принстонский ун-т. Нажмите
Нажмите
,
1993
.
[8]
Bushnell
C.J.
,
Kutzko
P.C.
, “
40017
».
Проц. Лонд. Мат. Соц
.
77
, №
3
(
1998
):
582
–
634
.
[9]
Чан
К.Ю.
,
Савин
Г.
. «Компонент Ивахори представления Гельфанда-Граева». Матем. Z. (
2017
), doi:10. 1007/s00209-017-1882-3.
1007/s00209-017-1882-3.
[10]
Крисс
Н.
,
Гинзбург
В.
.
Теория представлений и комплексная геометрия
.
Бостон, Массачусетс
:
Биркхойзер
,
1997
.
[11]
Чуботару
D.
,
Мой
A.
, “
Дираковские когомологии5 ».
Проц. амер. Мат. Соц
.
143
(
2015
):
1001
–
13
.
[12]
Клещев
А.
Линейные и проективные представления симметричных групп
.
, том.
163
.
Кембридж
:
Издательство Кембриджского университета
,
2005
.
[13]
Лапид
E.
,
Мингес
A.
. «
По детерминантной формуле Тадича
».
Амер. Дж. Математика
.
136
(
2014
):
111
–
42
.
[14]
Люстиг
G.
“
Аффинные алгебры Гекке и их градуированные версии
».
Дж. Амер. Мат. Соц
.
2
(
1989
):
599
–
635
.
[15]
Опдам
Э. М.
,
Соллевелд
М.
. «
Характеры дискретных рядов для аффинных алгебр Гекке и их формальные степени
».
Acta Math
.
205
(
2010
):
105
–
87
.
[16]
Прасад
Д.
.
[17]
Solleveld
М.
,
2007
.
[18]
Solleveld
M.
«
О классификации неприводимых представлений аффинных алгебр Гекке с неравными параметрами
».
Представитель. Теория
16
(
2012
):
1
–
87
.
[19]
Лебедь
R. G.
“
Проективные модули над кольцами многочленов Лорана
. ”
”
Пер. амер. Мат. соц.
,
237
(
1978
):
111
–
20
7
.
[20]
Тадич
М.
«
О характерах неприводимых унитарных представлений общих линейных групп
».
Абх. Мат. Семин. ун-т Хэмб
.
65
(
1995
):
341
–
63
.
[21]
Мийец
V.
«
О представлениях аффинных алгебр Гекке типа B
».
Алгебр. Представлять. Теория
11
, №
4
(
2008
):
369
–
405
.
[22]
Waldspurger
J.-L.
«
Алгебры Гекке и прочее представление cuspidales, pour GL ( N )
».
Дж. Рейн Ангью. Математика
.
370
(
1986
):
127
–
91
.
[23]
Зелевинский
А.
«
Индуцированные представления редуктивных p-адических групп II
».
Энн. науч. Эк. Норма. Супер
.
13
(
1980
):
154
–
210
.
[24]
Zelevinski
A.
”
Два замечания о градуированных нильпотентных классах
».
Успехи мат. Наук
40
, нет.
1
(
1985
):
199
–
200
.
© Автор, 2017 г. Опубликовано Oxford University Press. Все права защищены. Для разрешений, пожалуйста, по электронной почте: [email protected].
© Автор, 2017 г. Опубликовано Oxford University Press. Все права защищены. Для разрешений, пожалуйста, по электронной почте: [email protected].
Опубликовано Oxford University Press. Все права защищены. Для разрешений, пожалуйста, по электронной почте: [email protected].
Раздел выдачи:
Артикул
Скачать все слайды
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Ссылки на статьи по номеру
Последний
Самые читаемые
Самые цитируемые
Нильпотентные группы и билипшицевы вложения в L 1
Деформации F-чистоты в кольцах ℚ-Горенштейна
О неравенстве Богомолова–Гизекера в положительной характеристике
Многоуровневые деревья и тета-операторы
О присоединенных гомологических модулях Зельмера для SL 2 -представления групп узлов
Реклама
линейная алгебра.
 k$$ для всех $q_k \in R,$, мы называем приведенное выше полиномиальное уравнение $ Q(\alpha) = 0$, и тогда к этому числу можно присоединить полиномы степени $n – 1$ с коэффициентами из $R$ и вычисляемые в $\alpha$: кольцо формально обозначается $R[\alpha ]/Q(\alpha),$ “фактор-группа полиномов с коэффициентами в $R$ некоторого параметра $\alpha$ при их эквивалентности по модулю полиномиального деления на $Q(\alpha)$” 9n$, соответствующий такому многочлену в этом кольце, она будет иметь вид матрицы
$$\alpha \leftrightarrow A = \begin{bmatrix}0 & 0 & 0 & \dots & 0 & q_0\\
1 & 0 & 0 & \ точки & 0 & q_1 \\
0 & 1 & 0 & \ точки & 0 & q_2 \\
\точки & \точки & \точки & \точки & \точки & \точки \\
0 & 0 & 0 & \dots & 0 & q_{n-2} \\
0 & 0 & 0 & \dots & 1 & q_{n-1} \\
\end{bmatrix},$$
и представить такую матрицу в виде эшелона, сокращенного по строкам, на самом деле настолько просто, что мы можем сразу же усилить наше утверждение о том, что указанное выше кольцо $R[\alpha]/Q(\alpha)$ является полем, когда $R$ является поле и $q_0 \ne 0.
k$$ для всех $q_k \in R,$, мы называем приведенное выше полиномиальное уравнение $ Q(\alpha) = 0$, и тогда к этому числу можно присоединить полиномы степени $n – 1$ с коэффициентами из $R$ и вычисляемые в $\alpha$: кольцо формально обозначается $R[\alpha ]/Q(\alpha),$ “фактор-группа полиномов с коэффициентами в $R$ некоторого параметра $\alpha$ при их эквивалентности по модулю полиномиального деления на $Q(\alpha)$” 9n$, соответствующий такому многочлену в этом кольце, она будет иметь вид матрицы
$$\alpha \leftrightarrow A = \begin{bmatrix}0 & 0 & 0 & \dots & 0 & q_0\\
1 & 0 & 0 & \ точки & 0 & q_1 \\
0 & 1 & 0 & \ точки & 0 & q_2 \\
\точки & \точки & \точки & \точки & \точки & \точки \\
0 & 0 & 0 & \dots & 0 & q_{n-2} \\
0 & 0 & 0 & \dots & 1 & q_{n-1} \\
\end{bmatrix},$$
и представить такую матрицу в виде эшелона, сокращенного по строкам, на самом деле настолько просто, что мы можем сразу же усилить наше утверждение о том, что указанное выше кольцо $R[\alpha]/Q(\alpha)$ является полем, когда $R$ является поле и $q_0 \ne 0. k$, который реализует все необходимые операции как матричные операции. 9n$$ подчиняется закону Фибоначчи, и мы можем просто выбрать $A = \sqrt{1/5},\; B = -\sqrt{1/5}$, чтобы получить стандартные начальные точки $F_{0,1} = 0,1$: это последовательность Фибоначчи, определяемая исключительно в терминах возведения в степень.
k$, который реализует все необходимые операции как матричные операции. 9n$$ подчиняется закону Фибоначчи, и мы можем просто выбрать $A = \sqrt{1/5},\; B = -\sqrt{1/5}$, чтобы получить стандартные начальные точки $F_{0,1} = 0,1$: это последовательность Фибоначчи, определяемая исключительно в терминах возведения в степень. Но есть проблема с использованием этого на компьютере: тип Double , к которому компьютер имеет доступ, имеет только конечную точность, и приведенные выше выражения будут сильно округляться. Чего мы действительно хотим, так это использовать нашу произвольную точность 92 = 5.$ Тогда наше кольцо состоит из чисел $a + b \sqrt{5}$, которые являются матрицами: $$\begin{bmatrix}a & 5b\\b & a\end{bmatrix}.$$ И это легко-легко программировать. Однако ваши «единичные векторы» могут быть аналогичным образом выбраны как $1$ и $\varphi$, что приводит к «серьезной» матрице $$a + b \varphi = \begin{bmatrix}a & b\\ b & a + b\end{bmatrix}$$, что я называю “серьезным”, потому что для $a = 0, b = 1$ это на самом деле рекуррентное соотношение Фибоначчи для векторов $[F_{n-1}, F_ {n}],$, который является способом получить этот результат, не проходя через описанные выше обручи. Существует также интересная «симметричная» версия, где $\varphi$ и $\bar\varphi$ являются нашими «единичными векторами», а матрица (я думаю) $a \varphi + b \bar\varphi \leftrightarrow [2a- б,\; -а+б;\;а – б,\; -а + 2b].$ 92 = -1,$, поэтому вышеизложенное предписывает расширить наше поле до поля $$
a + b \sqrt{-1} \leftrightarrow \begin{bmatrix}a & -b\\b & a\end{bmatrix}.$$Когда мы заменяем $a$ на $r\cos\theta$ и $b $ с $r\sin\theta$ мы обнаруживаем, что на самом деле все эти «комплексные числа» являются просто масштабированными матрицами вращения: $$ r (\cos\theta + i~\sin\theta) = r \begin{bmatrix} \cos\theta & -\sin\theta\\\sin\theta & \cos\theta\end{bmatrix} = r~R_\theta,$$, что дает нам непосредственное геометрическое понимание комплексного числа как масштабированного вращения ( и тогда аналитические функции — это как раз те, которые локально выглядят как масштабированное вращение.) 92/2$ напрямую.
Существует также интересная «симметричная» версия, где $\varphi$ и $\bar\varphi$ являются нашими «единичными векторами», а матрица (я думаю) $a \varphi + b \bar\varphi \leftrightarrow [2a- б,\; -а+б;\;а – б,\; -а + 2b].$ 92 = -1,$, поэтому вышеизложенное предписывает расширить наше поле до поля $$
a + b \sqrt{-1} \leftrightarrow \begin{bmatrix}a & -b\\b & a\end{bmatrix}.$$Когда мы заменяем $a$ на $r\cos\theta$ и $b $ с $r\sin\theta$ мы обнаруживаем, что на самом деле все эти «комплексные числа» являются просто масштабированными матрицами вращения: $$ r (\cos\theta + i~\sin\theta) = r \begin{bmatrix} \cos\theta & -\sin\theta\\\sin\theta & \cos\theta\end{bmatrix} = r~R_\theta,$$, что дает нам непосредственное геометрическое понимание комплексного числа как масштабированного вращения ( и тогда аналитические функции — это как раз те, которые локально выглядят как масштабированное вращение.) 92/2$ напрямую.
Степенное правило для производных
Обычно первым быстрым правилом, которое вы изучаете для поиска производных, является степенное правило. Причина в том, что это простое правило, которое нужно запомнить, и оно применимо ко всем видам функций. Для числа n правило степени гласит:
Причина в том, что это простое правило, которое нужно запомнить, и оно применимо ко всем видам функций. Для числа n правило степени гласит:
Давайте начнем с нескольких действительно простых примеров, чтобы увидеть его в действии.
реклама
Пример
Найдите производную каждой функции. 9{545}\)
Как видите, все дело в запоминании шаблона. Теперь мы увидим, как этот шаблон можно применить к более сложным примерам.
Производные полиномиальных функций
Напомним, что производная константы всегда равна нулю. Таким образом, производная от 5 равна 0, а производная от 2000 также равна 0. Кроме того, вы можете разбить производную на сложение/вычитание и умножение на константы. Сочетание этих идей со степенным правилом позволяет нам использовать его для нахождения производной любого многочлена. 92 – 6х + 10}\)
Вы можете подумать, что это все, что вы можете сделать с правилом силы. Однако пара старых фактов из алгебры может помочь нам применить это к более широкому кругу функций. Ниже мы рассмотрим два таких случая.
Ниже мы рассмотрим два таких случая.
Производные функций с отрицательными показателями
Правило степени применяется независимо от того, положительный или отрицательный показатель. Но иногда функцию, не имеющую показателей степени, можно переписать, используя отрицательные показатели степени. Если это так, то мы можем применить правило степени, чтобы найти производную. Основное свойство, которое мы будем использовать: 9{3}}}\конец{выравнивание}\)
Обратите внимание, что на последнем шаге в нижнюю часть дроби были перемещены только члены с отрицательным показателем степени. У восьмерки не было отрицательного показателя, поэтому она осталась.
Производные функций с радикалами (квадратный корень и другие корни)
Другое полезное свойство из алгебры заключается в следующем.
Используя это правило, мы можем взять функцию, записанную с корнем, и найти ее производную, используя степенное правило.
Пример
Найдите производную функции.



 – М.,
Просвещение, 1993.
– М.,
Просвещение, 1993.