Алгоритм метод гаусса: Решение систем линейных уравнений методом Гаусса

НОУ ИНТУИТ | Лекция | Решение систем линейных уравнений

Аннотация: В лекции рассматривается задача решения систем линейных уравнений. Приводятся необходимые определения и постановка задачи. Описывается последовательный и параллельный варианты одного из прямых методов решения линейных систем общего вида – метода Гаусса. Далее дается описание последовательного и параллельного алгоритмов, реализующих итерационный метод сопряженных градиентов

Ключевые слова: система линейных уравнений, Трансцендентное уравнение, линейное уравнение, решение системы линейных уравнений, алгоритм Гаусса, балансировка вычислений, операции передачи данных, топология сети передачи данных, MPI, вычислительный эксперимент, EM64T, computer cluster, итерационные методы решения систем линейных уравнений, итерационный алгоритм, метод сопряженных градиентов, горизонтальное разделение, программная реализация

Системы линейных уравнений возникают при решении ряда прикладных задач, описываемых дифференциальными, интегральными или системами нелинейных (трансцендентных) уравнений.

Они могут появляться также в задачах математического программирования, статистической обработки данных, аппроксимации функций, при дискретизации краевых дифференциальных задач методом конечных разностей или методом конечных элементов и др.

Матрицы коэффициентов систем линейных уравнений могут иметь различные структуру и свойства. Матрицы решаемых систем могут быть плотными, и их порядок может достигать несколько тысяч строк и столбцов. При решении многих задач могут появляться системы, обладающие симметричными положительно определенными ленточными матрицами с порядком в десятки тысяч и шириной ленты в несколько тысяч элементов. И, наконец, при рассмотрении большого ряда задач могут возникать системы линейных уравнений с разреженными матрицами с порядком в миллионы строк и столбцов.

8.1. Постановка задачи

Линейное уравнение с n неизвестными x0, x1, ѕ, xn-1 может быть определено при помощи выражения

( 8. 1)

где величины a₀,a₁,…,a_n-1 и b представляют собой постоянные значения.

Множество из n линейных уравнений

( 8.2)

называется системой линейных уравнений или линейной системой. В более кратком ( матричном ) виде система может представлена как

Ax = b,

где A=(a_i,j) есть вещественная матрица размера nxn, а векторы b и x состоят из n элементов.

Под задачей решения системы линейных уравнений для заданных матрицы А и вектора b обычно понимается нахождение значения вектора неизвестных x, при котором выполняются все уравнения системы.

8.2. Алгоритм Гаусса

Метод Гаусса – широко известный прямой алгоритм решения систем линейных уравнений, для которых матрицы коэффициентов являются плотными. Если система линейных уравнений

невырожденна, то метод Гаусса гарантирует нахождение решения с погрешностью, определяемой точностью машинных вычислений. Основная идея метода состоит в приведении матрицы А посредством эквивалентных преобразований (не меняющих решение системы (8.2)) к треугольному виду, после чего значения искомых неизвестных могут быть получены непосредственно в явном виде.

В подразделе дается общая характеристика метода Гаусса, достаточная для начального понимания алгоритма и позволяющая рассмотреть возможные способы параллельных вычислений при решении систем линейных уравнений. Более полное изложение алгоритма со строгим обсуждением вопросов точности получаемых решений может быть получено, например, в работах [ [ 6 ] , [ 22 ] , [ 47 ] ] и др.

8.2.1. Последовательный алгоритм

Метод Гаусса основывается на возможности выполнения преобразований линейных уравнений, которые не меняют при этом решения рассматриваемой системы (такие преобразования носят наименование эквивалентных ). К числу таких преобразований относятся:

• умножение любого из уравнений на ненулевую константу;
• перестановка уравнений;
• прибавление к уравнению любого другого уравнения системы.

Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе – прямой ход метода Гаусса – исходная система линейных уравнений при помощи последовательного исключения неизвестных приводится к верхнему треугольному виду

где матрица коэффициентов получаемой системы имеет вид

intuit.ru/2010/edi”>На обратном ходе метода Гаусса (второй этап алгоритма) осуществляется определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной x_n-1, после этого из предпоследнего уравнения становится возможным определение переменной x_n-2 и т.д.

8.2.1.1. Прямой ход алгоритма Гаусса

Прямой ход метода Гаусса состоит в последовательном исключении неизвестных в уравнениях решаемой системы линейных уравнений. На итерации i, 0<=i<n-1, метода производится исключение неизвестной i для всех уравнений с номерами k, большими i (т.е. i<k<=n-1 ). Для этого из этих уравнений осуществляется вычитание строки i, умноженной на константу ( a

ki/a_ii ), с тем чтобы результирующий коэффициент при неизвестной x_i в строках оказался нулевым – все необходимые вычисления могут быть определены при помощи соотношений:

(следует отметить, что аналогичные вычисления выполняются и над вектором b ).

Поясним выполнение прямого хода метода Гаусса на примере системы линейных уравнений вида:

На первой итерации производится исключение неизвестной x0 из второй и третьей строки. Для этого из этих строк нужно вычесть первую строку, умноженную соответственно на 2 и 1. После этих преобразований система уравнений принимает вид:

В результате остается выполнить последнюю итерацию и исключить неизвестную x₁ из третьего уравнения. Для этого необходимо вычесть вторую строку, и в окончательной форме система имеет следующий вид:

На рис. 8.1 представлена общая схема состояния данных на i -й итерации прямого хода алгоритма Гаусса. Все коэффициенты при неизвестных, расположенные ниже главной диагонали и левее столбца i, уже являются нулевыми. На i -й итерации прямого хода метода Гаусса осуществляется обнуление коэффициентов столбца i, расположенных ниже главной диагонали, путем вычитания строки i, умноженной на нужную ненулевую константу.

После проведения (n-1) подобной итерации матрица, определяющая систему линейных уравнений, становится приведенной к верхнему треугольному виду.

Рис. 8.1. Итерация прямого хода алгоритма Гаусса

При выполнении прямого хода метода Гаусса строка, которая используется для исключения неизвестных, носит наименование

ведущей, а диагональный элемент ведущей строки называется ведущим элементом. Как можно заметить, выполнение вычислений является возможным только, если ведущий элемент имеет ненулевое значение. Более того, если ведущий элемент a_i,i имеет малое значение, то деление и умножение строк на этот элемент может приводить к накоплению вычислительной погрешности и вычислительной неустойчивости алгоритма.

Возможный способ избежать подобной проблемы может состоять в следующем: при выполнении каждой очередной итерации прямого хода метода Гаусса следует определить коэффициент с максимальным значением по абсолютной величине в столбце, соответствующем исключаемой неизвестной, т.

е.

и выбрать в качестве ведущей строку, в которой этот коэффициент располагается (данная схема выбора ведущего значения носит наименование метода главных элементов).

Вычислительная сложность прямого хода алгоритма Гаусса с выбором ведущей строки имеет порядок O(n³).

8.2.1.2. Обратный ход алгоритма Гаусса

После приведения матрицы коэффициентов к верхнему треугольному виду становится возможным определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной x_n-1, после этого из предпоследнего уравнения становится возможным определение переменной x_n-2 и т.д. В общем виде выполняемые вычисления при обратном ходе метода Гаусса могут быть представлены при помощи соотношений:

Поясним, как и ранее, выполнение обратного хода метода Гаусса на примере рассмотренной в п. 8.2.1.1 системы линейных уравнений

Из последнего уравнения системы можно определить, что неизвестная x₂ имеет значение 3. В результате становится возможным разрешение второго уравнения и определение значение неизвестной x₁=13, т.е.

На последней итерации обратного хода метода Гаусса определяется значение неизвестной x₀, равное -44.

С учетом последующего параллельного выполнения можно отметить, что вычисление получаемых значений неизвестных может выполняться сразу во всех уравнениях системы (и эти действия могут выполняться в уравнениях одновременно и независимо друг от друга). Так, в рассматриваемом примере после определения значения неизвестной x₂ система уравнений может быть приведена к виду

Вычислительная сложность обратного хода алгоритма Гаусса составляет O(n²).

Алгоритм метода исключения Гаусса

Перейти к содержимому

Ищи:

авг 1, 2015

Манас Шарма

• Старт
• Объявите переменные и прочитайте порядок матрицы n.
• Возьмите коэффициенты линейных уравнений как:
  Do для k=1 до n
  Do для j=1 до n+1
  Чтение a[k][j]
  Конец для j
  Конец для k
• Do для k=1 до n-1
  Do для i=k+1 до nDo для j=k+1 до n+1
  a[i][j]=a[i][j]-a[i ][k]/a[k][k]*a[k][j]
  Конец для j
  Конец для i
  Конец для k
• Вычислить x[n]=a[n][n+1]/a[n][n]
• Do для k=n-1 до 1
  sum=0
  Do для j=k+1 до nsum=sum+a[k][j]*x[j]
  End for j
  x[k]=1 /a[k][k]*(a[k][n+1]-sum)
  Конец для k
• Показать результат x[k]
• Стоп

Блок-схема:

Манас Шарма

Кандидат наук. научный сотрудник Йенского университета им. Фридриха-Шиллера, Германия. Я физик, специализирующийся на вычислительном материаловедении. Я пишу эффективные коды для моделирования взаимодействия света и материи в атомарных масштабах. Мне нравится время от времени разрабатывать приложения и программное обеспечение, связанные с физикой, DFT и машинным обучением. Может программировать на большинстве популярных языков. Мне нравится делиться своими знаниями по физике и приложениям с помощью этого блога и канала YouTube.

manas.bragitoff.com/

Нравится:

Нравится Загрузка…

[wpedon align=”center”]

Опубликовано в Программирование на C++, Программирование

Следите за нами на FB

• Список свободно доступных программ для визуализации молекулярной или кристаллической структуры

  9 декабря 2022 г.

• Каковы приближения в ДПФ Кона-Шама?

  3 декабря 2022 г.

• Как установить PySCF на UBUNTU или MacOSX?

  2 декабря 2022 г.

• Краткое введение в теорию функционала плотности

  2 декабря 2022 г.

• В чем разница между ТПФ и методом Хартри-Фока?

  2 декабря 2022 г.

• Стихотворение/песня о High Harmonic Generation

  2 декабря 2022 г.

Конфиденциальность и файлы cookie: этот сайт использует файлы cookie. Продолжая использовать этот веб-сайт, вы соглашаетесь на их использование.
Чтобы узнать больше, в том числе о том, как управлять файлами cookie, см. здесь: Политика в отношении файлов cookie

Алгоритм исключения Гаусса

Оглавление

1. АИ=А
2. Я=А А-1
3. Пример метода исключения Гаусса!
4. (Решить систему линейных уравнений)
5. ;
6. ;
7. Пример метода Гаусса-Жордана!
8. (Чтобы просто найти обратную матрицу)

Предварительный просмотр текста

В линейной алгебре исключение Гаусса — это алгоритм решения систем линейных уравнений, нахождения ранга матрицы и вычисления обратной обратимой квадратной матрицы.

Исключение Гаусса названо в честь немецкого математика и ученого Карла Фридриха Гаусса. ГАУСС / ЖОРДАНА (G / J) – это метод нахождения обратной матрицы с использованием элементарных операций над матрицами. Чтобы найти ранг матрицы, мы используем метод исключения Гаусса Жордана, но мы используем метод Гаусса Жордана в случае, если нам нужно найти только обратная обратимая матрица.

Обзор алгоритма Алгоритм метода Гаусса Жордана прост. Мы должны сделать матрицу единичной, используя элементарную операцию над ней. Сначала он записывается в виде

AI=A

Сначала мы напишем верхнее уравнение, а затем выполним элементарную операцию с правой частью матрицы матрицы и одновременно с единичной матрицей, чтобы получить следующую матрицу.

I=A A-1

Процесс исключения Гаусса состоит из двух частей. Первая часть (прямое исключение) сводит данную систему к треугольной или ступенчатой ​​форме или приводит к вырожденному уравнению без решения, что указывает на то, что система не имеет решения. Это достигается за счет использования элементарных операций над строками. На втором этапе используется обратная замена, чтобы найти решение приведенной выше системы.

Эквивалентно для матриц: первая часть сводит матрицу к форме эшелонирования строк с помощью элементарных операций со строками, а вторая сводит ее к форме редуцированного эшелонирования строк или канонической форме строк. Другая точка зрения, которая оказывается очень полезной для анализа алгоритма, заключается в том, что метод исключения Гаусса вычисляет разложение матрицы. Три элементарные операции со строками, используемые в исключении Гаусса (умножение строк, перестановка строк и добавление кратных строк к другим строкам), сводятся к умножению исходной матрицы на обратимые матрицы слева.

Первая часть алгоритма вычисляет LU-разложение, а вторая часть записывает исходную матрицу как произведение однозначно определенной обратимой матрицы и однозначно определенной редуцированной ступенчато-строковой матрицы. Исключение Гаусса В линейной алгебре исключение Гаусса — это алгоритм решения систем линейных уравнений, нахождения ранга матрицы и вычисления обратной обратимой квадратной матрицы. Исключение Гаусса названо в честь немецкого математика и ученого Карла Фридриха Гаусса, что делает его примером закона Стиглера. Элементарные операции со строками используются для приведения матрицы к эшелонированной форме строк.

Исключение Гаусса-Жордана, расширение этого алгоритма, еще больше сводит матрицу к сокращенной ступенчатой ​​форме строк. Одного исключения Гаусса достаточно для многих приложений, и оно дешевле, чем версия -Жордана. История Метод исключения Гаусса появляется в восьмой главе «Прямоугольные массивы» важного китайского математического текста «Цзючжан суаньшу» или «Девять глав по математическому искусству».

Его использование проиллюстрировано в восемнадцати задачах с двумя-пятью уравнениями. Первое упоминание о книге под этим названием датируется 179 г.н.э., но некоторые его части были написаны примерно в 150 г.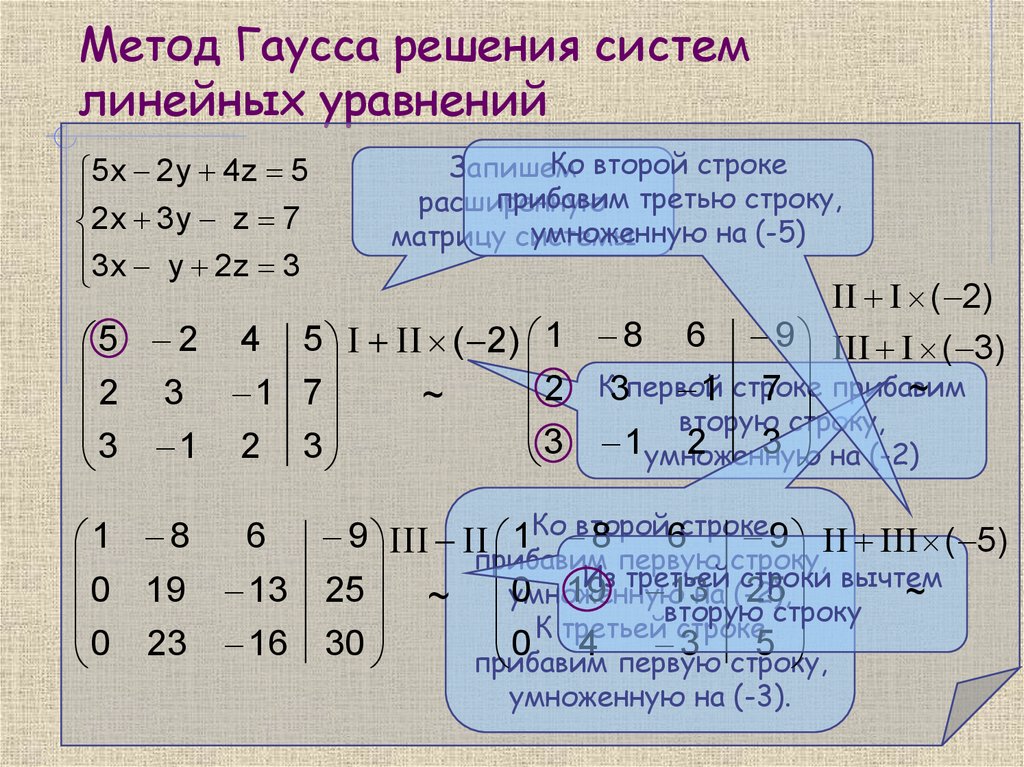 до н.э. Это прокомментировал Лю Хуэй в 3 веке. Метод в Европе стеблей

См. Весь документ Присоединяйтесь к FreeBookSummary, чтобы продолжить чтение

См. Весь документ Присоединяйтесь к FreeBookSummary, чтобы продолжить чтение

из заметок Исаака Ньютона.

В 1670 году он писал, что во всех известных ему книгах по алгебре отсутствует урок решения одновременных уравнений, который затем снабдил Ньютон. Кембриджский университет в конце концов опубликовал эти заметки под названием Arithmetica Universalis в 1707 году, спустя много времени после того, как Ньютон оставил академическую жизнь. Заметки широко имитировались, что сделало (то, что сейчас называется) исключением Гаусса стандартным уроком в учебниках алгебры к концу 18 века. Карл Фридрих Гаусс в 1810 году разработал нотацию для симметричного исключения, которая была принята в XIX веке. века с помощью профессиональных ручных компьютеров для решения нормальных уравнений задач наименьших квадратов. Алгоритм, который преподается в средней школе, был назван в честь Гаусса только в 1950-х годах из-за путаницы в истории предмета. Обзор алгоритма Процесс исключения Гаусса состоит из двух частей.

Первая часть (прямое исключение) приводит заданную систему к треугольной или ступенчатой ​​форме или приводит к вырожденному уравнению без решения, что указывает на то, что система не имеет решения. Это достигается за счет использования элементарных операций над строками. На втором этапе используется обратная замена, чтобы найти решение приведенной выше системы. Эквивалентно для матриц, первая часть сводит матрицу к форме эшелона строк, используя элементарные операции со строками, а вторая сводит ее к форме редуцированного эшелона строк или канонической форме строк. Другая точка зрения, которая оказывается очень полезной для анализа алгоритма, заключается в том, что метод исключения Гаусса вычисляет разложение матрицы. Три элементарные операции со строками, используемые в исключении Гаусса (умножение строк, перестановка строк и добавление кратных строк к другим строкам), сводятся к умножению исходной матрицы на обратимые матрицы слева.

Первая часть алгоритма вычисляет LU-разложение, а вторая часть записывает исходную матрицу как произведение однозначно определенной обратимой матрицы и однозначно определенной редуцированной ступенчато-строковой матрицы. Пример Предположим, что цель состоит в том, чтобы найти и описать решение (решения), если таковые имеются, следующей системы линейных уравнений: Алгоритм следующий: исключить x из всех уравнений ниже L1, а затем исключить y из всех уравнений ниже L2. Это придаст системе треугольную форму. Затем, используя обратную подстановку, можно решить каждое неизвестное.

В этом примере x удаляется из L2 путем добавления к L2. x затем исключается из L3 путем добавления L1 к L3. Формально: Результат таков: теперь y исключается из L3 путем добавления 4L2 к L3: Результат таков: Этот результат представляет собой систему линейных уравнений в треугольной форме, и поэтому первая часть алгоритма завершена. Последняя часть, обратная замена, состоит из решения известных в обратном порядке. Таким образом, можно видеть, что Затем z можно подставить в L2, что затем можно решить, чтобы получить Далее, z и y можно подставить в L1, что можно решить, чтобы получить Система решена.

Некоторые системы не могут быть приведены к треугольной форме, но все же имеют по крайней мере одно правильное решение: например, если y не встречается в L2 и L3 после первого шага выше,

См. Весь документ Присоединяйтесь к FreeBookSummary, чтобы продолжить чтение

Алгоритм

не смог бы привести систему к треугольной форме. Однако это все равно привело бы к ступенчатой ​​форме системы. В этом случае система не имеет единственного решения, так как содержит хотя бы одну свободную переменную. Затем набор решений может быть выражен параметрически (то есть в терминах свободных переменных, так что, если выбраны значения для свободных переменных, будет сгенерировано решение).

На практике системы обычно не рассматриваются в терминах уравнений, а вместо этого используется расширенная матрица (которая также подходит для компьютерных манипуляций). Например: Таким образом, алгоритм исключения Гаусса, примененный к расширенной матрице, начинается с: который в конце первой части (исключение Гаусса, нули только под ведущей 1) алгоритма выглядит так: То есть это в виде эшелонированного ряда. В конце алгоритма, если применяется исключение Гаусса-Жордана (нули под и над ведущей 1): то есть он находится в сокращенной эшелонированной форме строки или канонической форме строки.

Пример метода исключения Гаусса!

(для решения системы линейных уравнений)

Один простой пример операций со строками G/J предлагается непосредственно над поворотной ссылкой; пример ниже: Ниже приведена система уравнений, которую мы будем решать, используя шаг 1 G/J. Ниже представлена ​​1-я расширенная матрица: поворот на «1», обведенный красным. Операции со строками для 1-го поворота названы ниже. цифра «5» в позиции 2-2, обведенная ниже

Ниже результат выполнения П1 на элементе в позиции 2-2. Далее мы должны выполнить P2 Ряд операций P2 ниже. Результат 2-го поворота ниже.

Теперь повернитесь на «-7», обведенное красным. Используя P1 ниже, мы меняем «-7» на «1».

Ниже приведен результат выполнения P1 на «-7» в позиции 3-3. Затем мы должны выполнить P2. Операции со строками P2 приведены ниже. Результат третьего (и последнего) поворота приведен ниже с ISM-матрицей 3 × 3, выделенной синим цветом. Шаг [3] G/J. Переписывая окончательную матрицу, поскольку уравнения дают решение. к исходной системе Другие приложения Нахождение обратной матрицы Предположим, что A — матрица, и вам нужно вычислить ее обратную. Единичная матрица увеличивается справа от A, образуя матрицу (блочная матрица B = [A,I]). Путем применения элементарных операций со строками и алгоритма исключения Гаусса левый блок B может быть приведен к единичной матрице I, что оставляет A 1 в правом блоке B. Если алгоритм не может привести A к треугольной форме, то А не обратим.

Общий алгоритм вычисления рангов и оснований Алгоритм исключения Гаусса можно применить к любой матрице A. Если мы «застреваем» в данном столбце, мы переходим к следующему столбцу. Таким образом, например, некоторые матрицы могут быть преобразованы в матрицу, имеющую сокращенную ступенчатую форму строк, например (* — произвольные элементы). Эта ступенчатая матрица T содержит много информации об A: ранг A равен 5

.

См. Весь документ Присоединяйтесь к FreeBookSummary, чтобы продолжить чтение

, так как в T 5 ненулевых строк; векторное пространство, натянутое на столбцы A, имеет основу, состоящую из первого, третьего, четвертого, седьмого и девятого столбцов A (столбцы тех, что в T), а * говорят вам, как другие столбцы A можно записать в виде линейных комбинаций базовых столбцов.

Анализ Исключение Гаусса для решения системы n уравнений с n неизвестными требует n(n+1)/2 делений, (2n3 + 3n2 5n)/6 умножений и (2n3 + 3n2 5n)/6 вычитаний,[3] всего примерно 2n3/3 операций. Так что у него есть сложность. Этот алгоритм можно использовать на компьютере для систем с тысячами уравнений и неизвестных. Однако стоимость становится непомерно высокой для систем с миллионами уравнений. Эти большие системы обычно решаются с использованием итерационных методов.

Существуют специальные методы для систем, коэффициенты которых соответствуют регулярному шаблону (см. систему линейных уравнений). Исключение Гаусса можно выполнять над любым полем. Исключение Гаусса численно стабильно для диагонально доминирующих или положительно определенных матриц. Для общих матриц исключение Гаусса обычно считается устойчивым на практике, если вы используете частичное вращение, как описано ниже, даже если есть примеры, для которых оно нестабильно. Исключение Гаусса-Жордана В линейной алгебре исключение Гаусса-Жордана представляет собой алгоритм получения матриц в сокращенной эшелонированной форме строк с помощью элементарных операций над строками. Это вариант исключения Гаусса. Исключение Гаусса помещает нули под каждым опорным пунктом в матрице, начиная с верхней строки и двигаясь вниз.

Матрицы, содержащие нули под каждой опорной точкой, называются эшелонированными строками. Исключение Гаусса-Джордана идет еще дальше, помещая нули выше и ниже каждой опорной точки; о таких матрицах говорят, что они имеют уменьшенную эшелонированную форму строк. Каждая матрица имеет редуцированную ступенчатую форму строк, и метод Гаусса-Жордана гарантированно ее найдет. Он назван в честь Карла Фридриха Гаусса и Вильгельма Джордана, потому что это вариант исключения Гаусса, описанный Джорданом в 1887 году. Однако этот метод также появляется в статье Клазена, опубликованной в том же году. Джордан и Класен, вероятно, независимо друг от друга открыли метод исключения Гаусса-Жордана.

[1] Теория сложности компьютерных наук показывает, что исключение Гаусса-Жордана имеет временную сложность O(n3) для матрицы n на n (с использованием нотации Big O). Этот результат означает, что он эффективно разрешим для большинства практических целей. В результате он часто используется в компьютерном программном обеспечении для различных приложений. Тем не менее, это часто является ненужным шагом после исключения Гаусса. Исключение Гаусса разделяет временную сложность Гаусса-Джордона O (n3), но обычно быстрее.

Следовательно, в случаях, когда нет необходимости в уменьшении эшелонированной формы строки по сравнению с формой эшелона строки, обычно предпочтительнее использовать метод исключения Гаусса. Это можно сделать, дополнив квадратную матрицу единичной матрицей той же размерности и применив следующие операции с матрицами: Если исходная квадратная матрица A задается следующим выражение: Тогда, после увеличения на тождество, получается следующее: Выполняя элементарные операции со строками над

См. Весь документ Присоединяйтесь к FreeBookSummary, чтобы продолжить чтение

[AI] до тех пор, пока она не достигнет формы сокращенного эшелона строк, конечным результатом является следующее: Увеличение матрицы теперь можно отменить, что дает следующее: Матрица является неособой (это означает, что она имеет обратную матрицу), если и только если единичную матрицу можно получить, используя только элементарные операции со строками.