Архимеда закон кратко: Закон Архимеда — урок. Физика, 7 класс.

в теории и на практике

Рассказываем историю открытия и объясняем, почему он важен.

Кто такой Архимед?

Древнегреческий ученый и изобретатель из Сиракуз. Жил в 3-м веке до нашей эры и сделал много открытий в геометрии, заложил основы механики и гидро- и аэростатики. К последним двум относится закон Архимеда. 

Источник: pinterest.com

Как был открыт закон Архимеда?

По распространенной версии, Архимед получил задание от царя Гиерона определить, из чистого ли золота сделана корона. Ученые того времени уже понимали связь между объемом и удельным весом вещества, но корона была неправильной формы. Архимед размышлял над тем, как измерить ее объем.

Решение пришло, когда он принимал ванну (точнее, тазик с водой). Ученый заметил, что когда тело погружается в воду, ее уровень становится выше. Это навело на мысль, что тело вытесняет объем воды, равный собственному объему

.

Кстати, корона оказалась с примесями серебра. Архимед понял это, когда равный ей по массе слиток золота вытеснил меньшее количество воды, чем само изделие.

Впоследствии оказалось, что этот закон применим и для предметов, помещенных в газовую среду. 

Почему так происходит?

На погружаемое тело действует выталкивающая или подъемная сила (сила Архимеда), равная весу объема вытесненного вещества — жидкости или газа. Это и есть закон Архимеда.

Источник: pinterest.com

Сама формула силы Архимеда выглядит так:

 

Чтобы понять, погрузится тело или нет, нужно высчитать его силу тяжести:

• Если сила тяжести больше, чем сила Архимеда, то тело утонет. 
• Если обе силы равны, то тело не сможет утонуть или самостоятельно погрузиться. В жидкости оно будет плавать.
• Если сила тяжести меньше, то объект будет плавать на поверхности или подниматься, пока не всплывет.  

Но можно обойтись знанием плотности вещества, из которого состоит объект, и вещества среды, в которое он может погрузиться. Тогда получаем:

• Если плотность тела больше, чем плотность среды, то оно утонет. 
• Если обе плотности равны, то тело «зависнет» в среде и не сможет самостоятельно погрузиться или подняться.
• Если плотность тела ниже, чем плотность среды, то объект будет плавать на поверхности или подниматься, пока не всплывет. 

Как это работает в жизни?

С явлением, описанным законом Архимеда, мы сталкиваемся постоянно. Благодаря этому знанию можете рассчитать конструкцию огромного корабля, который не утонет, и воздушного шара, который поднимется вверх.

Источник: mawdoo3.com

Хотя для таких расчетов, конечно, знания основного закона статики недостаточно. Помочь разобраться в теме и сделать точные вычисления могут специалисты ФениксХелп.

Закон Архимеда – это.

.. Что такое Закон Архимеда?

Зако́н Архиме́да — один из главных законов гидростатики и статики газов.

Формулировка и пояснения

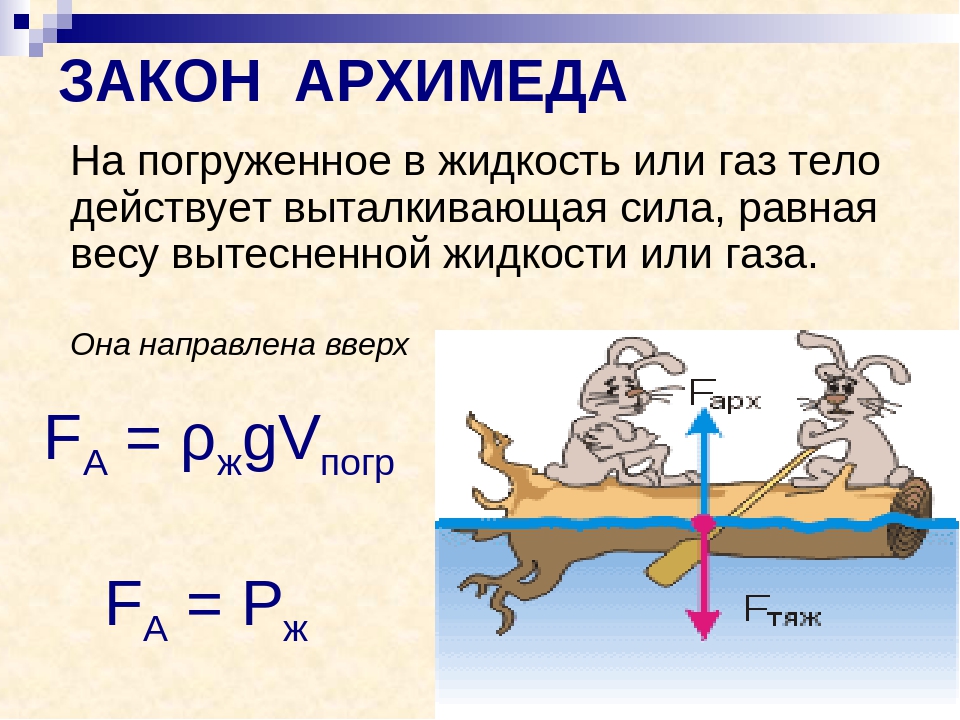
Закон Архимеда формулируется следующим образом^[1]: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа). Сила называется силой Архимеда:

где  — плотность жидкости (газа),  — ускорение свободного падения, а  — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.

Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.

Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.

Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.

Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.

где P_A, P_B — давления в точках A и B, ρ — плотность жидкости, h — разница уровней между точками A и B, S — площадь горизонтального поперечного сечения тела, V — объём погружённой части тела.

В теоретической физике также применяют закон Архимеда в интегральной форме:

,

где  — площадь поверхности,  — давление в произвольной точке, интегрирование производится по всей поверхности тела.

В отсутствие гравитационного поля, то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.

Обобщения

Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: проводящее тело вытесняется из области магнитного поля большей интенсивности в область с меньшей.

Вывод закона Архимеда для тела произвольной формы

Гидростатическое давление жидкости на глубине есть . При этом считаем давление жидкости и напряжённость гравитационного поля постоянными величинами, а  — параметром. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат , причём выберем направление оси z совпадающим с направлением вектора . Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку . На неё будет действовать сила давления жидкости направленная внутрь тела, . Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:

При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.

Получаем, что модуль силы Архимеда равен , а направлена она в сторону, противоположную направлению вектора напряжённости гравитационного поля.

Условие плавания тел

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести и силы Архимеда , которые действуют на это тело. Возможны следующие три случая:

•  — тело тонет;
•  — тело плавает в жидкости или газе;
•  — тело всплывает до тех пор, пока не начнет плавать.

Другая формулировка (где  — плотность тела,  — плотность среды, в которую оно погружено):

•  — тело тонет;
•  — тело плавает в жидкости или газе;
•  — тело всплывает до тех пор, пока не начнет плавать.

См. также

Примечания

1. ↑ Всё написанное ниже, если не оговорено иное, относится к однородному полю силы тяжести (например, вблизи поверхности планеты).

Ссылки

коротко о теме ЗАКОН АРХИМЕДА

ПОМОГИТЕ С ТЕСТОМ ПО ФИЗИКЕ! 90 баллов1. Определи абсолютную влажность в помещении объёмом 11 м³, если в нём содержится водяной пар массой 116 г.Ответ … (округли до десятых):2. Как вы думаете, появится ли туман при температуре воздуха 3 °С и относительной влажности 80 %? Определите точку росы, используя данные таблицы.Ответ: точка росы равна? °С, поэтому туман появиться или нет?t, °С p, кПа ρ0, гм30 0,61 4,81 0,65 5,22 0,71 5,63 0,76 64 0,81 6,45 0,88 6,86 0,93 7,37 1 7,88 1,06 8,33.Используя данные таблицы, укажи температуру, при которой водяной пар станет насыщенным, если его давление равно 1,81 кПа.

Ответ: температура насыщенного водяного ? парабудет равна?t, °С p,кПа ρ0, гм310 1,23 9,411 1,33 1012 1,4 10,713 1,49 11,414 1,6 12,115 1,71 12,816 1,81 13,617 1,93 14,518 2,07 15,419 2,2 16,320 2,33 17,34. Используя данные таблицы, укажи точку росы водяного пара, если пар становится насыщенным при давлении 10 мм рт.ст.Ответ:? °C.t, °С p,кПа ρ0, гм310 1,23 9,411 1,33 1012 1,4 10,713 1,49 11,414 1,6 12,115 1,71 12,816 1,81 13,617 1,93 14,518 2,07 15,419 2,2 16,320 2,33 17,35. Сухой термометр показывает 17 °С, а смоченный — 12 °С. Определи относительную влажность, используя данные таблицы.Ответ: при разности температур Δt=?°С относительная влажность равна ? %.(Психометрическая таблица)6. Определи массу паров воды в воздухе актового зала объёмом 69 м³ при температуре воздуха 24 °С и относительной влажности 63 %. Плотность насыщенного пара равна 17,3 гм3.Ответ (округли до десятых): ? г.7. При температуре 13 °С относительная влажность воздуха была равна 77 %. Используя данные таблицы, определи, на сколько уменьшилась или увеличилась относительная влажность воздуха, если температуру повысили до 18 °С.

Ответ (округли до десятых): относительная влажность воздуха увеличилась или уменьшилась? на ? %.t, °С p,кПа ρ0, гм310 1,23 9,411 1,33 1012 1,4 10,713 1,49 11,414 1,6 12,115 1,71 12,816 1,81 13,617 1,93 14,518 2,07 15,419 2,2 16,320 2,33 17,3

СРОООООООЧНО ДАМ 30 баллов Найдите плотность молока, если 200 г молока занимают объем 2•10 м3?

фізика 7 клас пж даю 90 балів пж срочно​

фізика пж даю 100 балів​

Вместимость цистерны 45м³. Сколько килограмм нефти можно в ней хранить(Плотность нефти 800 кг/м³). Срочно пожалуйста.​

ДАЮ СТО БАЛЛОВ Пожалуйста помогите. Если можно вместе с графиком(как на фото, только заполненным)Заранее Большое спасибо.если не знаете не пишите​

ПОЖАЛУЙСТА СРОЧНО ПОМОГИТЕ!!!!!!!

напрямку вантажний потяг довжиною 600м зі швидкістю 36км/год, та електропотяг зі швидкістю 72км/год і довжиною 100м. а) З якою швидкістю рухається еле … ктропотят вiдносно вантажного? б) Побудуйте графіки швидкості обох поïiв у ній системi вiдлiку; в) За який час електропотяг обгонить вантажний потяг?​

«Определение плотности жидкостей и твердых тел» Цель работы: научиться определять плотность твёрдого тела с помощью весов и мензурки с водой. 3 а масса 100 кг?

Закон Архимеда первый – Энциклопедия по машиностроению XXL

Решения отдельных частных вопросов гидростатики, т. е. разделы гидравлики, рассматривающие вопросы равновесия жидкостей, были даны еще Архимедом в 250 г. до н. э. в его трактате О плавающих телах , который считается первым научным трудом в области гидравлики. Известный закон Архимеда, определяющий силы давления жидкости на поверхность погруженного в нее тела, дошел в полной неприкосновенности до наших дней.  [c.6]

Изменение скорости газа от первой до второй критической, сопровождаемое сильным расширением слоя, увеличит долю пустот, что в свою очередь катастрофически отразится на плотности кипящего слоя, которая упадет практически до нуля или, вернее, до величины, близкой к плотности газа. Другими словами, если, например, в стадии однородного псевдоожижения плотность слоя, состоящего из применяемой в топках кипящего слоя смеси угля и доломита, существенно превышает плотность воды знаменитого Мертвого моря в Палестине, в котором, не нарушая закона Архимеда, нельзя утонуть, то при псевдоожижении, когда доля пустот начнет приближаться к 70 %, даже профессиональному пловцу вряд ли удастся удержаться на поверхности. В таком море судам пришлось бы постоянно менять ватерлинию в зависимости от скорости фильтрации газа.  [c.75]

Так как далее будут рассматриваться только несжимаемые жидкости, то нет необходимости принимать во внимание в явном виде силы тяжести, действующие на жидкость. Таким образом,, более правильно интерпретировать р как гидродинамическое, а не как полное давление. Первое не включает в себя гидростатическое давление. В соответствии с принятым определением давления р силу F, представленную уравнением (2.3.1), удобно определить как гидродинамическую силу, действующую на тело со стороны жидкости. Она равна нулю для жидкости, находящейся в покое. Так как на самом деле гравитация всегда действует на жидкость, то для того, чтобы получить полную силу, действующую со стороны жидкости на тело, необходимо добавить к уравнению (2.3.1) выталкивающую силу, действующую на тело. Согласно закону Архимеда, эта дополнительная сила равна весу жидкости, вытесненной телом. Если g — вектор ускорения свободного падения, направленный вертикально вниз (предполагается, что он постоянен), и т/ — масса вытесненной жидкости, то выталкивающая сила равна  [c.46]

Механика—одна из самых древних наук. Более 2000 лет тому назад А р X и медом (287—212 гг. до нашей эры) были даны первые строго научные основы учения о равновесии твердых и жидких тел. В своем сочинении о равновесии плоских фигур и центрах тяжести Архимед изложил разработанную им теорию равновесия рычага и определил положение центра тяжести плоских фигур параллелограмма, треугольника, трапеции, сегмента, параболы. Архимед заложил основы гидростатики — науки о равновесии жидкостей он открыл один из основных законов этой науки, носящий его имя (закон Архимеда). Наряду с теоретическими открытиями Архимед сделал множество значительных изобретений в инженерной области.  [c.5]

Первым законом гидравлики, устанавливающим количественную связь между отдельными элементами явлений, считают общеизвестный закон Архимеда. Этот закон был установлен великим математиком и механиком древности Архимедом за 250 лет до нашей эры.  [c.8]

Приведем некоторые сведения из истории механики. Подобно всем другим наукам механика возникла и развивалась под влиянием практических нужд человеческого общества. Она является одной нз древнейших наук и ее история насчитывает приблизительно 25 веков напряженных исканий. В примитивном виде первичные понятия механики, в частности, понятия силы и скорости, появились еще в античный период. Чисто практическое применение катков, наклонной плоскости, рычага, блоков при постройке грандиозных сооружении древности (пирамиды, дворцы и т. п.) накапливало определенный опыт и, очевидно, должно было привести к обобщению этого опыта, к установлению некоторых законов механики (статики). Так, в трактате Механические проблемы Аристотель (384 — 322 до н. э.) рассматривает конкретные практические задачи при помощи метода, основанного на законе рычага. Однако первые попытки установления динамических законов оказались неудачными.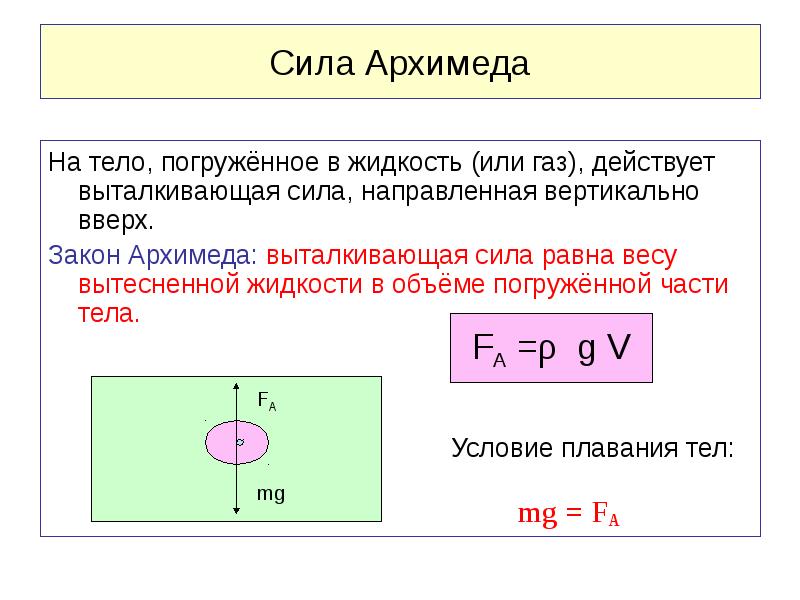 Аристотель ошибочно полагал, что скорости падающих тел пропорциональны их весам и что равномерное и прямолинейное движение является результатом действия постоянной силы. Потребовалось почти два тысячелетия, чтобы преодолеть эти ошибочные представления и заложить научные основы динамики. К числу бесспорных достижений античной механики следует отнести работы Архимеда (287—212 до и. э.), который был не только выдающимся инженером своего времени, но и дал ряд научных обобщений, относящихся к гидростатике (закон Архимеда), учению о равновесии и центре тяжести.  [c.9]

Два следующих перпетуум мобиле, описания которых мы приводим ниже, должны были работать в соответствии с законом Архимеда о подъемной силе в жидкостях. Главной частью первого из них, как ясно из рис. 43, является вращающийся вокруг горизонтальной оси барабан с наглухо закрытыми торцами, внутри которого располагались две взаимно перпендикулярные перекрещивающиеся тяги с насаженными на них большими пробковыми шарами. На внешних концах этих тяг, пропущенных сквозь боковую поверхность барабана через водонепроницаемые вводы, укреплялись металлические грузы. При этом пробковые поплавки должны были отклонять тяги в соответствующем направлении, что обеспечивало бы необходимое неравновесие сил, приводившее барабан в непрерьшное и равномерное вращение.  [c.71]

Первые существенные научные результаты в области механики мы находим в работах Архимеда (287—212 гг. до. н. э.). Ему принадлежит один из основных законов гидростатики и теория рычага.  [c.20]

Механика— одна нз первых наук о природе — возникла примерно в IV веке до н. э. в древней Греции. Ее зарождение связывают обычно с именем великого ученого древности Аристотеля (384—322 до н. э.). Им и был впервые введен термин механика , означающий в переводе с греческого изобретение, машина, сооружение . Дальнейшее развитие механика получила в трудах Архимеда (287—212 до н. э.). Ему, в частности, принадлежат закон равновесия рычага и учение о центре тяжести тел.  [c.13]

Первые указания о научном подходе к решению гидравлических вопросов относятся к 250 году до нашей эры, когда Архимедом был открыт закон о равновесии тела, погруженного в жидкость. В дальнейшем, однако, на протяжении последующих более чем полутора тысячелетий гидравлика не получила сколько-нибудь заметного развития. В эту эпоху, характеризовавшуюся общим застоем в науке и культуре, были не только утеряны первые элементы знания, но и в значительной степени забыты практические навыки инженерного искусства. И только в XVI— XVn вв., в эпоху Возрождения, когда появились работы Сте-вина, Леонардо да Винчи, Галилея, Паскаля, Ньютона, исследо-  [c.5]

Таковы вопросы, рассматриваемые в первой книге Архимеда. Во второй книге Архимед, на основе тех н е принципов, дает законы равновесия различных тел, получающихся от вращения конических сечений и погруженных в жидкости, обладающие большим весом, чем эти тела он рассматривает случаи, когда эти коноиды могут оставаться в наклонном положении, случаи, когда они должны сохранять свое отвесное положение, а также случаи, когда они должны опрокинуться или же выпрямиться.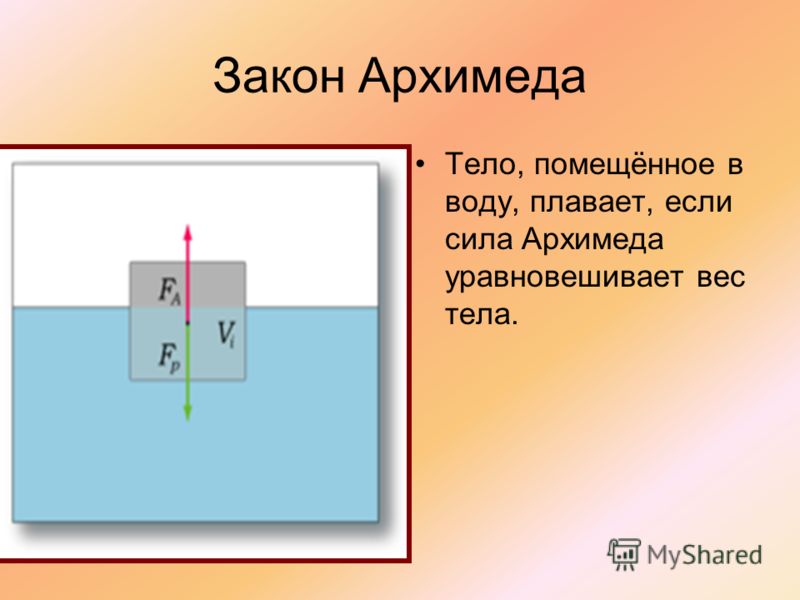 Эта книга является одним из прекраснейших памятников гения Архимеда, она содержит теорию устойчивости плавающих тел, к которой современные ученые прибавили очень немного.  [c.236]

Первый шаг в этом направлении сделал, по-видимому, великий Леонардо да Винчи (1452—1519 гг.). В рукописи 1515 г. он ввел понятие, которое теперь называется в механике статическим моментом силы . Со времен Архимеда был известен закон, который определял условия равновесия прямого рычага. Он составлял содержание VI теоремы Архимеда из сочинения по механике Два соизмеримых груза находятся в равновесии, если они обратно пропорциональны плечам, на которые эти грузы подвешены . Другими словами (рис. 1.9, а), если вес (т. е. силу, с которой грузы притягиваются к земле) изобразить в виде отрезков А и В соответствующих направлений и длины, то условие равновесия будет таким А B = Qb Qa, или, что то же самое (следует из свойств пропорции), А-Оа = В-ОЬ.  [c.27]

Обычно в технических вузах на вводную лекцию в курсе теоретической механики планируется всего один академический час (45 или 50 шн). Поэтому реализация материала исторического очерка должна предусматриваться в наиболее подходящих местах в течение всего времени, отводимого курсу механики в учебном плане. Так, например, об Архимеде целесообразно рассказать в статике (когда формулируется закон рычага или определяются центры тяжести однородных тел), а о Даламбере — в динамике (когда формулируется принцип Даламбера) и т. д. По нашему опыту, первая лекция должна быть посвящена главным образом рассказу о могуществе механики и ее значении для современного научно-технического прогресса. Нам удавалось во вводной лекции кратко охарактеризовать влияние исследований Аристотеля, Галилея, Ньютона, Эйлера, Жуковского, Мещерского, Циолковского и Эйнштейна на ход исторического развития знаний о механической форме движения.  [c.52]

К таким известным ученым относится в первую очередь древнегреческий физик и математик Архимед (287— 212 гг. до н. э.), который вывел и обосновал законы рычага, условия равновесия твердых тел в жидкостях, построил многие оригинальные машины.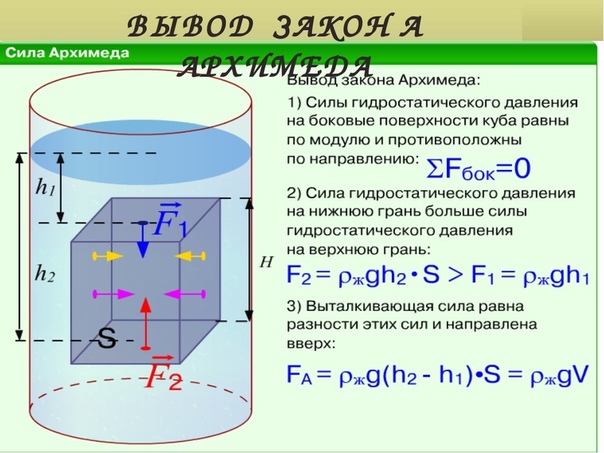 В средние века крупные работы сделали Леонардо-да-Винчи (1452—1519), Галилей (1564—1642), Ньютон (1643—1727) и другие. Обобщая накопленные к тому времени знания, эти ученые подготовили почву для последующего развития механики. Особое значение имели труды Галилея и Ньютона. Они стали основой не только механики, но и ряда других наук.  [c.6]

Первым научным трудом в области гидравлики считается трактат Архимеда (287—212 гг. до и. э.) О плавающих телах , хотя сведения о некоторых законах гидравлики были, видимо, известны и ранее, так как задолго до Архимеда строились оросительные каналы и водопроводы.  [c.5]

Первым ученым, чьи труды в области гидравлики дошли до нас, был Архимед (ок. 287—212 гг. до н.э.), открывший, в частности, закон плавания тел. В сочинениях Герона (ок. 1 в.) приведены описания различных гидравлических устройств, в том числе насосов. В античные времена закладывался фундамент гидравлики как прикладной науки. В эпоху Средневековья развитие научной мысли было приостановлено, и лишь спустя тысячелетие, в эпоху Возрождения, начался новый период расцвета науки и искусства. В это время трудами Леонардо Да Винчи (1452—1519 гг.), Г. Галилея (1564—1642 гг.), Б. Паскаля (1623—1662 гг.) были заложены основы экспериментальной гидравлики.  [c.5]

Первые свидетельства о научном подходе к решению гидравлических задач относятся к 250 году до нашей эры, когда Архимедом был открыт закон о равновесии тела, погруженного в жидкость.  [c.4]

Первые, очень важные результаты исследований в области гидравлики связаны с именем древнегреческого ученого Архимеда (287—212 гг. до н. э.), открывшего закон о равновесии тела, погруженного в жидкость. Однако после Архимеда на протяжении почти 1700 лет гидравлика не получила заметного развития.  [c.3]

Естественно, что в ходе развития науки о природе в первую очередь соответствующая количественная мера была установлена для наиболее простой формы движения — для движения механического (перемещения в пространстве). Было выяснено, что в случае всяких механических явлений при любых превращениях механического движения остается неизменной некоторая вполне определенная физическая величина, получившая название работы (в простейшей зачаточной форме понятие работы содержится, как было показано, уже в законе рычага Архимеда). Именно эта величина, очевидно, и должна быть принята в качестве меры механической формы движения материи.  [c.20]

Первые фактические знания по гидравлике и опыт практического применения их были еще у древних народов Египта, Китая, Ассирии, Греции и др. Об этом свидетельствует строительство водоподъемных колес, кораблей, каналов, плотин, акведуков для водоснабжения и т. п. Остатки древних гидротехнических сооружений в ряде стран сохранились до наших дней. Все это способствовало накоплению практических представлений о движении и равновесии жидких тел. Одним из первых трудов (250 г. до н. э.), относящихся к гидравлике, является трактат О плавающих телах (закон Архимеда).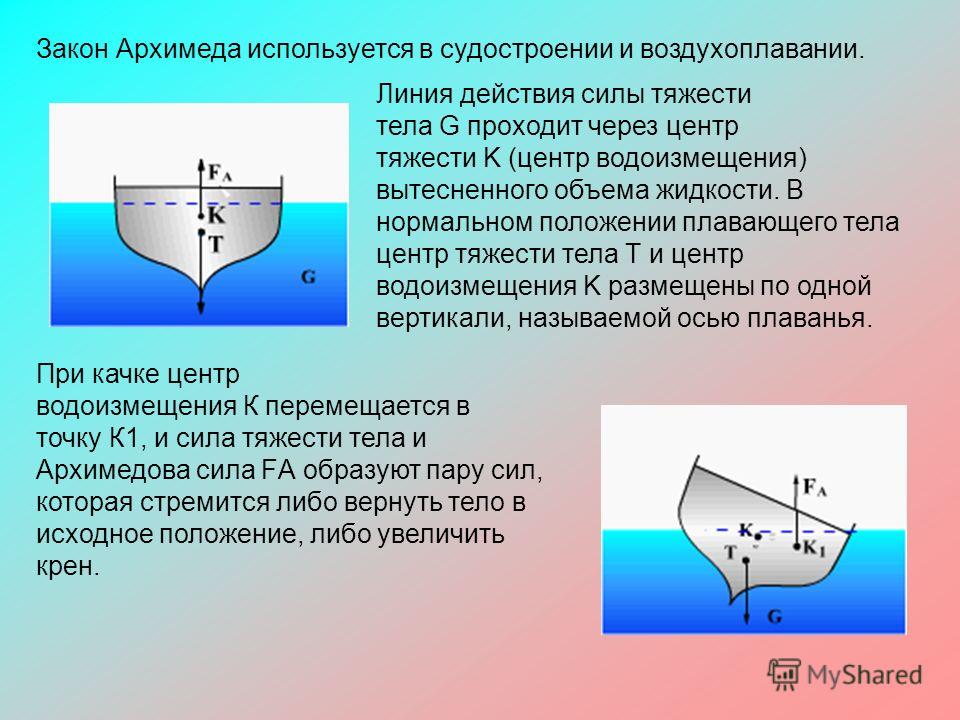  [c.4]

Гидравлика — наука древняя. За несколько тысяч лет до наилей эры древними народами, населявшими Египет, Вавилон, Месопотамию, Индию и Китай, были построены плотины, оросительные каналы, водяные колеса. Первым теоретическим обобщением в области гидравлики считается трактат О плавающих телах , написанный за 250 лет до н. э. выдающимся греческим математиком и механиком Архимедом. Им был открыт закон о равновесии тела, погруженного в жидкость, — общеизвестный закон Архимеда. Только через многие столетия после Архимеда, в эпоху Возрождения, наступает новый этап в развитии гидравлики. В XV в. в Италии Леонардо Да Винчи (14Й— 1519) проводит экспериментальные и теоретические исследования в самых различных областях. Он изучает работу гидравлического пресса, истечение жидкости через отверстие и водосливы. В 1586 г. нидерландский математик-инженер Симон Стёвин (1548— 1620) опубликовывает работу Начала гидростатики , в которой решает вопрос о величине гидростатического давления на плоскую фигуру и объясняет гидростатический парадокс . В этот же период итальянский физик, математик и астроном Г а л и л е о Галилей (1564— 1642) устанавливает зависимость величины  [c.258]

Первые представления о гидравлике появились еще у древних народов Египта, Китая, Вавилонии, Ассирии, Греции, Рима, а также у народов, живших на территориях, входящих в состав СССР. Строительство кораблей, каналов для орошения полей, водопроводов и других гидротехнических сооружений способствовало накоплению З1 ий о равновесии и движении жидкостей. Еще в третьем еке до нашего летосчисления появился трактат Архимеда (287—212 гг. до н. л.) О плавающих телах , содержащий его известный закон (закон Архимеда).  [c.3]

Идеи Архимеда были возрождены и продолжены Стевином (1548—1620), Галилеем (1564—1642) и Паскалем (1623—1662). Сте-вйн первый строго проформулировал известный в механике принцип затвердевания, позволяющий в гвдростатике применять обычные приемы статики твердого тела. При пользовании этим принципом закон Архимеда доказывается крайне просто. Галилей и Паскаль использовали для решения задач гидростатики принцип возможных пере-легцений.  [c.19]

В состоянии равновесия вес понтона О уравновешивается архимедовой силой Р. Если это состояние по какой-либо причине нарушается и понтон дополнительно погрузится в воду, то согласно закону Архимеда выталкивающая сила возрастет, т. е. получит приращение, направленное вверх. Понятно, что при любых отклонениях понтона от положения равновесия приращение силы Р будет направлено против отклонения. Если понтон прямостенный (в первом приближении это можно принять), то приращение архимедовой силы пропорционально отклонению х и определяется соотношением  [c.41]

Так как за единицу массы в G -системе (абсолютной системе физич. величин) выбрана масса 1 см чистой воды, равная 1 г при ее наибольшей плотности (3,99°), то П. воды при 4° равна 1, и уд. в. любого тела по отношению к воде при 4°, как к стандарту, численно равен плотности этого тала при1)о= 1, -P D.U. газа по отношению к водороду или к воздуху часто называют (не вполне правильно) уд. в. этого газа относительно водорода или воздуха, взятых при тех же условиях. П. твердых тел и жидкостей обычно измеряют или по методу гидростатич. взвешивания (пользуясь законом Архимеда) или же пикнометром (см.). К первому же способу относится и наиболее употребительное в технике измерение П. с помощью ареометра.  [c.371]

Архимеда, т. е. до времени Стевина (1548—1620), который в 1586 г. впервые занялся механикой наклонной плоскости, и Галилея (1564 — 1642), который сделал первое важное открытие в области кинематики. Таким образом механические принципы, относящиеся к движению тел, не были известны почти до нового времени. Основной ошибкой в рассуждениях большинства исследователей было их предположение о необходимости непрерывно действующей силы для поддержания движения тела. Они думали, что для тела более свойственно состояние покоя, чем движения, что противоречит закону инерции (первый закон Ньютона). Этот закон был открыт Галилеем совершенно случайно при изучении движения тел, скатывающихся по наклонной плоскости на горизонтальную поверхность. Галилей принял следующее основное положение изменение скорости или ускорение определяется силами, которые действуют на тело. Это положение содержит почти целиком два первые положения Ньютона. Галилей применил свои принципы с полным успехом при открытии законов падающих тел и законов движения снарядов. Благодаря своим открытиям он справедливо считается основателем динамики. Он первый применил маятник для измерения времени.  [c.43]

Первым научным трудом в области гидравлики счита ется написанный примерно за 250 лет до нашей эры трактат Архимеда О плавающих телах , в котором величайший ученый древности сформулировал закон о давлении жидкости на погруженное в нее тело.  [c.6]

Первой из дошедших до нас научных работ в области гидравлики был трактат Архимеда О плавающих телах (250 г. до н. э.). Последующие научные открытия появились лишь в XVI — XVII веках н. э. К их числу следует отнести работы Леонардо-да-Винчи в области плавания тел, движения жидкости по трубам и открытым руслам и др. законы давления жидкости на дно и стенки сосуда С. Стевина  [c.6]

Как видно из некоторых мест Механических проблем Аристотеля, сложение движений было уже известно древним. Его применяли главным образом геометры для описания кривых, например, Архимед — для спирали, Никомед — для конхоиды и т. д. Среди ученых нового времени Роберваль вывел из него остроумный метод проведения касательных к кривым, которые можно описать с помощью двух движений, закон которых известен. Однако Галилей является первым, применившим в механике исследование сложного движения для определения кривой, описываемой тяжелым телом под действием силы тяжести и силы бросания [ ].  [c.31]

Для инженера того времени, когда понятия об энергии и законе ее сохранения еще не было, в такой идее не было ничего странного. Множество изобретателей работало, пытаясь воплотить ее в жизнь. Только некоторые великие умы понимали, что это невозможно и одним из первых среди них был универсальный гений.— Леонардо да Винчи. В его тетрадях был найден эскиз гидравлического ppm (рис. 1.20), Горизонтальная линия внизу рисунка показывает уровень в резервуаре, из которого машина берет воду. Машина состоит из двух связанных между собой вращающихся устройств А и В, между которыми установлена чаша, заполняемая водой. Устройство А представляет собой архимедов винт, подающи воду из нижнего резервуара в чашу. Устройство В вращается, приводимое в движение водой, сливающейся из чаши, и крутит насос А — архимедов винт отработавшая вода сливается снова в резервуар.  [c.43]

Первым законом гндоавликл, устанавливающим количественную связь между отдельными элел ентами явлений, считают общеизвестный ааксн Архимеда.  [c.250]

Одним из первых трудов, относящихся к гидравлике, является трактат Архимеда О плавающих телах , содержащий его знаменитый закон. Согласно этому закону, на всякое тело, погруженное в жидкость, действует со стороны этой жидкости подъемная сила , направленная вверх и равная весу вытесненной тело1М жидкости.  [c.6]

Архимед из Сиракуз (278—212 до н. э.) был автором первых правильных идей, касаюп1ихся механических законов. Он правильно определил принципы рычага и значение центра тяжести тел. Его учение было развито и обобщено Леонардо д а-В и н ч и (1452—1519) в его исследованиях статического момента. Вся статика твердого тела заключает лиш1. приложение математики к этим принципам.  [c.42]

---

Легенда об Архимеде – Технарь

Существует легенда о том, как Архимед пришел к открытию, что выталкивающая сила равна весу жидкости в объеме тела. Он размышлял над задачей, заданной ему сиракузским царем Гиероном (250 лет до н. э.).

Царь Гиерон поручил ему проверить честность мастера, изготовившего золотую корону. Хотя корона весила столько, сколько было отпущено на нее золота, царь заподозрил, что она изготовлена из сплава золота с другими, более дешевыми металлами. Архимеду было поручено узнать, не ломая короны, есть ли в ней примесь или нет.

Достоверно неизвестно, каким методом пользовался Архимед, но можно предположить следующее, Сначала он нашел, что кусок чистого золота в 19,3 раза тяжелее такого же объема воды. Иначе говоря, плотность золота в 19,3 раза больше плотности воды.

Архимеду надо было найти плотность вещества короны. Если эта плотность оказалась бы больше плотности воды не в 19,3 раза, а в меньшее число раз, значит, корона была изготовлена не из чистого золота.

Взвесить корону было легко, но как найти ее объем? Вот что затрудняло Архимеда, ведь корона была очень сложной формы. Много дней мучила Архимеда эта задача. И вот однажды, когда он, находясь в бане, погрузился в наполненную водой ванну, его внезапно осенила мысль, давшая решение задачи. Ликующий и возбужденный своим открытием, Архимед воскликнул; «Эврика! Эврика!», что значит; «Нашел! Нашел!».

Архимед взвесил корону сначала в воздухе, затем в воде. По разнице в весе он рассчитал выталкивающую силу, равную весу воды в объеме короны. Определив затем объем короны, он смог уже вычислить ее плотность. А зная плотность, ответить на вопрос царя: нет ли примесей дешевых металлов в золотой короне?

Легенда говорит, что плотность вещества короны оказалась меньше плотности чистого золота. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием. Историки рассказывают, что задача о золотой короне побудила Архимеда заняться вопросом о плавании тел. Результатом этого было появление замечательного сочинения «О плавающих телах», которое дошло до нас.

Седьмое предложение (теорема) этого сочинения сформулировано Архимедом следующим образом:

Тела, которые тяжелее жидкости, будучи опущены в нее, погружаются все глубже, пока не достигают дна, и, пребывая в жидкости, теряют в своем весе столько, сколько весит жидкость, взятая в объеме тел.

Упр. Предположив, что золотая корона царя Гиерона в воздухе весит 20Н, а в воде 18,75Н, вычислите плотность вещества короны. Полагая, что к золоту было подмешено только серебро, определите, сколько в короне было золота и сколько серебра. При решении задачи плотность золота считайте равной округленно 20 000 кг/м3, плотность серебра — 10 000 кг/м3.

Определение принципа Архимеда: урок для детей

Принцип Архимеда

Джейми и ее отец обнаружили, что Архимед был математиком и изобретателем из Древней Греции. Однажды ночью, садясь в ванну, он заметил, что чем дальше он опускался, тем выше поднималась вода и тем больше выливалось воды из ванны. Это привело его к разработке научного закона, названного принципом Архимеда , который гласит, что подъемная сила на погруженном объекте равна весу жидкости, вытесняемой объектом .

Архимед

Папа объяснил, что «погруженный» означает «под водой», а «смещенный» – «оттесненный». Когда объект падает в воду, часть этой воды вытесняется. В то же время плавучесть толкает объект вверх, что изменяет его вес. Если вес объекта больше, чем количество воды, которое он вытесняет, объект утонет. Если количество вытесненной воды равно весу объекта, он будет плавать.

Объект утонет, если он весит больше, чем вытесняемая им вода.

Важность принципа

Джейми хотел знать, почему принцип Архимеда так важен. Она выяснила, что его используют в судостроении для обеспечения плавучести кораблей. Корабли обычно изготавливаются из металла и имеют полый корпус, позволяющий равномерно перемещать воду. Корабль будет погружаться в воду только до тех пор, пока вес вытесняемой им воды не сравняется с весом корабля.

Металлический корпус корабля

Папа объяснил, что это также идея спасательного жилета, который Джейми должен носить на своей лодке. Спасательные жилеты и другие плавсредства позволяют людям плавать на поверхности воды, а не тонуть. Теория также используется для измерения удельного веса жидкостей, помощи в полетах воздушных шаров и управления устройствами, которые регулируют или полагаются на точный уровень воды.

Краткое содержание урока

Принцип Архимеда , названный в честь изобретателя и математика, жившего в Древней Греции, утверждает, что подъемная сила на погруженном объекте равна весу жидкости, вытесняемой этим объектом. Плавучесть – это способность объекта плавать в воде или воздухе. Если вес объекта больше, чем количество воды, которое он вытесняет, объект утонет; если количество вытесненной воды равно весу объекта, он будет плавать.

Принцип Архимеда – Заявление, вывод и применение

Заявление о принципе Архимеда

Любая жидкость оказывает одинаковое давление во всех направлениях. Это давление является результатом веса жидкости. Когда объект частично или полностью погружен в жидкость, он оказывает на объект направленную вверх силу. Эта восходящая сила называется подъемной силой. Из-за подъемной силы наблюдается явное уменьшение веса объекта.Уменьшенный вес равен весу жидкости, вытесняемой объектом. Это отношение было изобретено Архимедом. От больших кораблей до небольших лодок, самолетов и подводных лодок – все они работают по принципу плавучести.

Кажущийся вес

Исходный вес объекта воздействует вниз через его центр тяжести. Когда объект погружается в жидкость, к объекту прилагается восходящая тяга, а именно выталкивающая сила. Из-за этой направленной вверх силы результирующая направленная вниз сила уменьшается, и объект становится легче.Если объект плавает на поверхности, он фактически невесомый. Кажущееся уменьшение веса равно величине восходящей выталкивающей силы.

[Изображение будет загружено в ближайшее время]

Кажущийся вес объекта определяется разницей между фактическим весом и выталкивающей силой.

Выведение принципа Архимеда

Принцип основан на принципе плавучести, который гласит, что газ или жидкость могут оказывать восходящую силу на любой объект, полностью или частично погруженный в него.Тяга вверх называется подъемной силой.

[Изображение будет загружено в ближайшее время]

На приведенной выше диаграмме цилиндр высотой h и радиусом r вертикально погружен в жидкость так, что его плоские поверхности находятся на глубинах h₁ и h₂ с h₁

F₁ = (P \ [_ {atm} \] + h₁ρg) πr²

Сила, направленная вверх на нижней поверхности. равно,

F₂ = (P \ [_ {atm} \] + h₂ρg) πr²

Поскольку, h₁

F \ [_ {b} \ ] = F₂ – F₁

F \ [_ {b} \] = (h₂ – h₁) ρgπr²

Поскольку h = h₂ – h₁ – высота цилиндра, а V = πr²h – его объем, тяга вверх может быть выражается как,

F \ [_ {b} \] = ρVg

Правая часть этой формулы восходящего надвига представляет собой не что иное, как вес жидкости того же объема V, что и погруженный объект.Однако величина подъемной силы равна кажущемуся уменьшению веса объекта. Следовательно,

Кажущееся уменьшение веса объекта = вес жидкости, вытесненной объектом

Закон плавания

Будет ли погруженный объект плавать или тонуть, зависит от величин фактического веса W₁ объекта и плавучести. сила W₂, действующая со стороны жидкости.

• W₁> W₂: Результирующая сила на объект направлена ​​вниз, заставляя его тонуть.Это состояние возникает, когда плотность объекта больше, чем у жидкости.

• W₁ = W₂: когда плотности объекта и жидкости равны, фактический вес и выталкивающая сила становятся равными. Объект может плавать на любой глубине в полностью погруженном состоянии.

• W₁

Применение принципа Архимеда

• Используя закон Архимеда, можно вычислить объем или плотность любого твердого тела. Пропорции металлов, составляющих сплав, могут быть легко рассчитаны с использованием этого принципа.

• Подводные лодки работают по теории Архимеда. Он имеет большой балластный резервуар, который контролирует глубину морской пехоты. Регулируя количество воды в балластной цистерне, можно изменять фактический вес подводной лодки и, таким образом, достичь желаемой глубины.

• Корабли сделаны полыми, так что эффективная плотность меньше плотности воды. Из-за того, что подъемная сила имеет большую величину, чем вес корабля, корабль может плавать в частично погруженном состоянии. Самолеты созданы по той же концепции.

• Плотность жидкостей вычисляется с использованием ареометров, которые работают в соответствии с принципом плавучести Архимеда.

• Воздушные шары могут парить в воздухе, поскольку плотность горячего воздуха меньше плотности окружающего холодного воздуха.

Знаете ли вы?

• Архимед Сиракузский представил теорию плавучести в своей книге «Плавающие тела» (написанной на греческом языке) около 250 г. до н. Э. Эта теория считается краеугольным камнем в изучении гидростатики.

• Сообщается, что Архимед крикнул «Эврика», что означает «Я нашел (это)», когда он наконец понял, как определить, сделана ли корона из нечистого золота, используя теорию плавучести.

• Плавающее тело не имеет видимого веса.

• Эффект поверхностного натяжения или капиллярности не учитывается в принципе Архимеда.

• Большой лунный ударный кратер назван в честь Архимеда.

• Портрет Архимеда выгравирован на престижной «Филдсовской медали».

Что такое короткий ответ на принцип Архимеда? – Реабилитацияrobotics.net

Что такое краткий ответ на принцип Архимеда?

Принцип

Архимеда гласит, что восходящая выталкивающая сила, которая действует на тело, погруженное в жидкость, полностью или частично, равна весу жидкости, которую тело вытесняет.

Кто крикнул Эврика и выпрыгнул из ванны?

Архимед

Кто первым сказал Эврика и почему?

приписывается древнегреческому ученому Архимеду. Сообщается, что он провозгласил «Эврика! Эврика! » после того, как он вошел в ванну и заметил, что уровень воды поднялся, он внезапно понял, что объем вытесненной воды должен быть равен объему той части его тела, которую он погрузил.

Почему царь вызвал Архимеда?

Однажды, в 3 веке до нашей эры, король Сиракуз Иеро II, Сицилия, вызвал Архимеда – молодого греческого физика и математика с длинной распущенной белой бородой – чтобы убедиться, что его новая корона сделана из чистого золота. или что золото было обманным путем подменено серебром.

Корона Архимеда из золота?

Он заметил, что корона ювелира вытеснила в два раза больше воды, чем золото, и пришел к выводу, что корона ювелира не была сделана из золота. Таким образом, Архимед показал, что вытеснение воды было хорошим методом для измерения объема неправильных объектов (как, безусловно, Архимед!).

Корона из золота?

Как я уже упоминал, коронка может быть изготовлена ​​из металла, металла и керамики или из керамики.В большинстве удаляемых в наши дни коронок есть металл. Обычно в качестве металла используется золото или платина / палладий. Вы можете признать эти металлы дорогими металлами.

Какой вывод сделал Архимед из своего наблюдения?

Архимед пришел к выводу, что корона не была полностью сделана из золота, подтверждая подозрения царя, и поэтому он смог точно сказать, сколько золота пропало.

Как Архимед решил проблему короны?

«Архимед обнаружил метод измерения объема объекта неправильной формы.Таким образом, он мог измерить объем короны, измерив объем воды, вытекшей из контейнера, наполненного водой до краев, когда корона была полностью погружена в него.

Как Архимед нашел число Пи?

Метод Архимеда находит аппроксимацию числа пи путем определения длины периметра многоугольника, вписанного в круг (который меньше длины окружности), и периметра многоугольника, описанного вне круга (который больше, чем длина окружности). длина окружности).

Откуда взялось выражение «момент эврики»?

Архимед вошел в историю как парень, который голым бегал по улицам Сиракуз с криком «Эврика!» – или “У меня есть!” на греческом. История этого события заключалась в том, что Архимеду было поручено доказать, что новая корона, сделанная для Гиерона, царя Сиракуз, не была чистым золотом, как утверждал ювелир.

Что было для Эбрайт моментом эврики?

Ответ. Полтора года спустя, на первом курсе, Эбрайту пришла в голову идея своей новой теории о клеточной жизни.Это произошло, когда он рассматривал рентгеновские снимки химической структуры гормона. Когда он увидел эти фотографии, Эбрайт не крикнул: «Эврика! …

Что такое момент?

: момент внезапного осознания, вдохновения, озарения, признания или понимания. Момент, который вы испытываете, когда пытаетесь вспомнить название песни, а через три часа оно поражает вас… – Джеффри Клюгер.

Что означает «Эврика» по-испански?

Английский язык. Español. eureka interj.(волнение от открытия) eureka interj.

Почему Эврика называется Эврика?

Калифорнийская золотая лихорадка привела поселенцев в залив Гумбольдта в 1850-х годах, и городу было присвоено название «Эврика» от греческого слова, означающего «Я нашел его». К 1853 году количество белых поселенцев в конце концов превысило численность людей вийотов, и армия США построила форт Гумбольдт для оказания помощи в разрешении конфликта между…

Что вы называете моментом лампочки?

Синонимы: Поворотные моменты и важные этапы.поворотный момент. пик. кульминация.

Был ли момент у лампочки?

момент, когда вы внезапно что-то понимаете или у вас появляется хорошая идея: для меня это был момент, когда я понял, что больше не могу жить без посторонней помощи.

Почему лампочки олицетворяют идеи?

Лампа олицетворяет все изобретательское мастерство Эдисона. Но именно мультфильм начала двадцатого века «Кот Феликс» закрепил идею лампочки как новой идеи. Именно на этих символических изображениях мы впервые видим лампочку, которая символизирует новую идею.

Что символизирует идею?

Символизм – это практика или искусство использования объекта или слова для представления абстрактной идеи. Действие, человек, место, слово или предмет могут иметь символическое значение. Когда автор хочет предложить определенное настроение или эмоцию, он также может использовать символизм, чтобы намекнуть на это, а не просто открыто сказать.

Что символизируют лампочки?

Лампочка – символ изобретения, а иногда и интеллекта. Лампочка также является символом света и соединений.

Что символизирует свет?

Свет – один из самых универсальных и фундаментальных символов. Это духовное и божественное, это озарение и разум. Свет – это источник добра и высшая реальность, он сопровождает трансцендентность в Нирвану буддийской доктрины.

Что символизирует свет в христианстве?

Помимо физического элемента, свет в Библии означает духовное озарение и истину. Он включает в себя все чистое, доброе и святое, в отличие от тьмы зла.Слово Божье – это «светильник ноге моей и свет стезе моей» (Пс. 118: 105).

Почему в христианстве важен свет?

Христиане – дети Света в непрекращающейся войне с силами тьмы. Свет представляет очищающее присутствие бога. Нет никаких свидетельств какого-либо церемониального использования огней в христианском богослужении в течение первых двух веков его существования.

(PDF) Новый взгляд на принцип Архимеда

P. Mohazzabi

842

Наконец, мы отмечаем, что принцип Архимеда не учитывает поверхностное

натяжение.Фактически наличие поверхностного натяжения приводит к нарушению принципа

[21]. Более того, принцип Архимеда не работает в сложных жидкостях [22].

Благодарности

Я хотел бы поблагодарить Ричарда В. Карватка за внимательное рассмотрение сценария мануала

и за полезные предложения.

Ссылки

[1] Loverude, M.E., Kautz, C.H. и Heron, P.R.L. (2003) Помощь студентам в развитии

понимания принципа Архимеда.I. Исследование понимания студентами.

Американский журнал физики

, 71, 1178-1187. https://doi.org/10.1119/1.1607335

[2] Heron, P.R.L., Loverude, M.E., Shaffer, P.S. и McDermott, L.C. (2003) Помогая

студентам развить понимание принципа Архимеда. II. Разработка

научно-методических материалов.

Американский журнал физики

, 71, 1188-

1195. https://doi.org/10.1119 / 1.1607337

[3] Бирман, Дж. И Кинканон, Э. (2003) Пересмотр принципа Архимеда.

Учитель физики

, 41, 340-344. https://doi.org/10.1119/1.1607804

[4] Граф, Э. (2004) Что сказал Архимед о плавучести?

The Physics Tea-

cher

, 42, 296-299. https://doi.org/10.1119/1.1737965

[5] Викандер, Р. и Монро, Дж. С. (2006) Основы геологии. 4-е издание, Thomson

Brooks / Cole, Belmont, 239.

[6] Monroe, J.S. и Викандер Р. (2012) Изменяющаяся Земля, Изучение геологии и

Evolution. 6-е издание, Brooks / Cole CENGAGE Learning, Belmont, 253.

[7] Mohazzabi, P. and James, M.C. (2012) Простой прибор для демонстрации сил жидкости

и третьего закона Ньютона.

Учитель физики

, 50, 537-539.

https://doi.org/10.1119/1.4767486

[8] Vermillion, R.E. (1991) Выводы принципа Архимеда.

Американский журнал

Physics

, 59, 761-762. https://doi.org/10.1119/1.16763

[9] Лерой Б. (1985) Принцип Архимеда: простой вывод.

Европейский журнал

Physics

, 6, 56-57. https://doi.org/10.1088/0143-0807/6/1/107

[10] Холлидей Д., Резник Р. и Уокер Дж. (2005) Основы физики. 7-е изд.

, Вили, Нью-Йорк, 367-368.

[11] Сирс Ф.В. и Земанский М.W. (1960) Физический колледж. 3-е издание, Addison-

Wesley, Reading, 244.

[12] Duncan, W.J., Thom, A.S. и Янг, А.Д. (1970) Механика жидкостей. 2-е издание

, American Elsevier Publishing Company, Нью-Йорк, 24-25.

[13] Уолшоу, А.С., Джобсон, Д.А. (1972) Механика жидкостей. 2-е издание, Long –

человек, Лондон, 2.

[14] Мюррей, Р.Л. и Кобб, Г.К. (1970) Физика, концепции и следствия. Prentice-

Hall, Englewood Cliffs, 371.

[15] Грейнджер, Р.А. (1995) Механика жидкости. Довер, Нью-Йорк, 127–128.

[16] Ланц, М.А., О’Ши, С.Дж. and Welland, M.E. (1997) Atomic-Force-Microscope Stu-

dy площади контакта и трения на NbSe2.

Physical Review B

, 55, 10776-10785.

https://doi.org/10.1103/PhysRevB.55.10776

[17] Ланц, М.А., О’Ши, С.Дж. и Велланд, M.E. (1997) Одновременные измерения силы и проводимости в атомно-силовой микроскопии.

Physical Review B

, 56, 15345-

Объяснение плавучести: принцип Архимеда

Греческий математик, физик и инженер Архимед Сиракузский в своей работе 250 г. до н. Э. «О плавающих телах» предположил, что любой объект, полностью или частично погруженный в жидкость, поддерживается силой, равной весу вытесненной жидкости. по объекту.

Печально известное утверждение, сделанное древнегреческим эрудитом, теперь известно как принцип Архимеда или физический закон плавучести.По сути, это объясняет, почему определенные объекты плавают в жидкости, а точнее, почему массивные объекты, такие как корабли, плавают, несмотря на свой вес.

Основы принципа Архимеда: объяснение плавучести

Помните, что Принцип Архимеда объясняет плавучесть или, более конкретно, восходящую силу, создаваемую жидкостью, называемую выталкивающей силой. Принцип гласит, что подъемная сила, действующая на погруженный объект, равна весу жидкости, вытесняемой этим объектом.

Это можно резюмировать следующим образом: объект тонет, если вес вытесняемой им воды меньше веса этого конкретного объекта. С другой стороны, этот объект не будет ни тонуть, ни подниматься, если его вес равен весу воды, которую он вытесняет.

Корабли являются яркими примерами. При запуске в водоем конкретный корабль, естественно, тонет до тех пор, пока вес вытесняемой им воды не станет равным его собственному весу. Однако по мере того, как корабль загружен, он все больше тонет и вытесняет больше воды.Величина подъемной силы постоянно соответствует весу корабля.

Обратите внимание, что этот принцип также объясняет, что объект будет подниматься, если его вес меньше веса вытесняемой жидкости. Примеры этого явления включают бумажные кораблики, деревянный блок и пластмассу, помещенную на водоем.

Недостатки и ограничения принципа

Одна из основных проблем с принципом, сформулированным Архимедом, заключается в том, что он не принимает во внимание другие факторы, которые могут влиять на динамику между объектом и жидкостью.Рассмотрим в качестве примера поверхностное натяжение.

Поверхностное натяжение относится к тенденции жидких поверхностей сжиматься до минимально возможной площади поверхности. По сути, это сила притяжения, действующая на молекулы жидкости на поверхности со стороны других молекул жидкости под ней. Это явление позволяет некоторым насекомым плавать и скользить по поверхности воды.

Принцип также не работает в определенных условиях, особенно в сложных жидкостях. Эти сложности присутствуют как в естественной, так и в преднамеренной обстановке.Например, в промышленных применениях тяжелые соли или коллоидные наночастицы добавляют к жидкостям для создания градиента плотности в растворителе, необходимого для разделения различных компонентов в суспензии.

ДОПОЛНИТЕЛЬНАЯ ЧТЕНИЕ И ССЫЛКИ

• Mohazzab, P. 2017. «Возвращение к принципу Архимеда». Журнал прикладной математики и физики . 5 (4): 836-843. DOI: 10.4236 / jamp.2017.54073
• Уилсон, Р. М. 2019. «Принцип Архимеда получает обновления.» Физика сегодня . 65 (9): 15-17. DOI: 10.1063 / PT.3.1701

Законы науки и великие умы, стоящие за ними

“Я не согласен с представление о том, что Вселенная – это загадка …. Я чувствую, что эта точка зрения не соответствует действительности к научной революции, начатой ​​почти четыреста лет назад Галилей и продолжил Ньютон . Они показали, что по крайней мере некоторые области Вселенная… подчиняются точным математическим законам. За прошедшие с тех пор годы мы расширили работа Галилея и Ньютон …. Теперь у нас есть математические законы, которые управляют всем, что мы обычно испытываем ».

– Стивен Хокинг , Черные дыры и детские вселенные и другие очерки

Введение и фон

В котором мы обсуждаем определение одноименных законов, жизни и невзгод законодателей, наука и религиозность, различие между законами и теориями, и географическое и временное распределение законодателей.

Законы природы

Законодатели

Справедливо ли называть Закон после человека?

Теории и законы

Мы открываем или изобретаем Законы?

Простая математика и реальность

Что такое на самом деле реальность?

Организация и назначение книги

Распространение юридических открытий через Время

Где проживали Законодатели

Когда будет открыт последний закон?

Часть I: 250 Б.К. 1700

Принцип Архимеда Плавучесть, c. 250 г. до н.э.

г.

Законы планетарной системы Кеплера Движение, 1609, 1618

Закон преломления Снеллиуса, 1621

Закон упругости Гука, 1660

Закон Бойля о газе, 1662

Ньютона Законы движения, гравитации,

и Охлаждение, 1687 и 1701

Часть II: 1700 1800

Закон жидкости Бернулли Динамика, 1738

Закон излучения Ламберта, 1760

Планетарный закон Боде Расстояния, 1766

Закон электростатики Кулона, 1785

Газовый закон Чарльза, 1787

Часть III: 1800 1900

Далтона Закон частичных давлений, 1801

Закон Генри о газе, 1802 г.

Закон Гей-Люссака объединения газов Объемы, 1808

Закон Авогадро о газе, 1811

Закон света Брюстера Поляризация, 1815

Закон Дюлонга-Пети Заплывы, 1819

Закон магнитного поля Био-Савара Force, 1820

Закон тепла Фурье Кондукция, 1822

Циркулярный закон Ампера Электромагнетизм, 1825

Закон электричества Ома, 1827

Закон излияния Грэма, 1829

Законы индукции Фарадея и Электролиз, 1831 и 1833

Закон электричества Гаусса и Магнетизм, 1835

Закон Пуазейля потока жидкости, 1840

Закон Джоуля электрического нагрева, 1840

Кирхгофа и Законы о радиации 1845 и 1859 гг.

Закон Клаузиуса Термодинамика, 1850

Закон вязкости Стокса, 1851

Закон поглощения Пива, 1852 г.

Закон Видемана-Франца Электропроводность, 1853

Закон диффузии Фика, 1855

Ветер и давление бюллетеней покупок Закон, 1857

Закон капиллярности Этвса, 1866

Законы Кольрауша Электропроводность, 1874, 1875

Закон магнетизма Кюри и Закон Кюри-Вейсса 1895,

Обобщено в 1907 г.

Часть IV: 1900 и позднее

Закон излучения Планка, 1900

Закон кристалла Брэгга Дифракция, 1913 г.

Неопределенность Гейзенберга Принцип, 1927

Закон Хаббла о космосе Расширение, 1929 г.

Заключительные комментарии о красоте математики в физике

В котором мы кратко обсуждаем красота математики и человеческих достижений, физики и религии, а также дополнительные важные физики и уравнения, в том числе: принцип Эйнштейна сохранение массы-энергии, уравнения Максвелла, уравнение Шредингера, уравнение Де Бройля, уравнение поля Эйнштейна для общих Относительность, уравнение Дирака, ряд Бальмера Уравнение, уравнение Планка, уравнение Янга-Миллса, уравнение Дрейка, уравнения Шеннона и логистическая карта.

Красота математики Великие уравнения науки Listmania и человеческие достижения «Величайшие уравнения всех времен» Никарагуа Список почтовых марок Физика и религия

Великие соперники

В котором мы прощаемся к законам и законодателям, каталогизируя далеко идущий второй набор одноименных законы.

1600-1700

Закон Мерсенна (1626 г.), Закон Торричелли (1643)

1700-1800

Правило Мопертюи (1746 г.), Закон Рихтера (1791 г.)

1800-1900

Закон Малуса (1809), Bell-Magendie Закон (1811 г.) Закон фон Гумбольдта (1817 г.), Законы Френеля-Араго (1819 г.), Закон Митчерлиха (1821 г.), Принцип Гамильтона (1835 г.), Принцип Бабине (1838 г.), Закон Гесса (1840 г.), Правило Бергмана (1847 г.), Закон Гладстона-Дейла (1858 г.), Закон Коппа (1864 г.), Закон Маттиссена правило (1864 г.), закон Максвелла (1866 г.), принцип Бертело-Томсена (1867 г.), Закон Менделеева (1869 г.), Лоренц-Лоренц Закон (1870 г.), Закон Коппета (1871 г.), Распределение Больцмана Закон (1871 г.), Закон Абни (1877 г.), Правило Аллена (1877 г.), Закон Нернста Закон (1880 г.), Закон Рауля (1882 г.), Вант Закон Хоффа (1885 г.), Закон Рамзи-Янга (1885 г.), Кайлетет и Закон Матиаса (1886 г.), Закон Долло (1890 г.), Закон Сазерленда (1893 г.), Закон силы Лоренца (1895 г.)

1900-2000

Закон Грнайзена (1908 г.), Закон Сабины (1910 г.), Закон о детях (1911), Правило Гейгера-Наттолла (1911), Эйнштейн-Старк Закон (1912 г.), Закон Ливитта (1912 г.), Закон Фриделя (1913), Закон Мозли (1913), Закон Штейнмеца (1916), Бозе-Эйнштейн Закон о распределении (1924 г.), Принцип Франка-Кондона (1925 г.), Паули. Принцип исключения (1925), Закон о распределении Ферми-Дирака (1926), Правило Московица-Ломбарди (1973), Законы Хокинга (1970-е)

Список литературы

Закон светимости Абни, 468

Абсолютный ноль, 327, 328, 332

Поглощение.См. Закон поглощения Бера; Био Закон абсорбции

Акустика, 5, 172, 224, 227, 234, 247, 252, 289, 462, 473

Адамс, Джон Коуч, 101

Аэрозоли, 344, 345, 347

Крылья самолета, 1, 126, 133-134, 350

Правило формы тела Аллена, 468

Закон трения Амонтона, 168

Ампер (единица), 152, 244, 246, 248, 253, 269, 278, 303

Ампре, Андр-Мари, 6, 8, 161, 180, 215, 239-245, 275

Circuital Ампре Закон электромагнетизма, 223, 239-245, 275, 278, 487

Араго, Франуа, 161, 214, 217, 218, 244, 275, 461

Архимед 41-51, 277, 286, 295, 490, 497

Формула рычага Архимеда, 497

Принцип плавучести Архимеда, 41-51

Закон диссоциации Аррениуса, 387

Астрология, 55, 57, 61, 100, 101, 109, 128

Астрономия, 5, 7, 10, 11, 15, 70, 71, 77-78, 101, 142, 290, 292, 317, 318, 391, 453, 458, 475, 480-483.См. Также Закон Боде о планетных расстояниях; Галактики; Закон Хаббла о космосе Расширение; Законы черной дыры Хокинга; Законы движения планет Кеплера; Закон светимости Ливитта

Атомная бомба, 2, 262, 441

Атомная теория, 175-181, 186, 200, 245

Авогадро, Амедео, 197-202

Закон Авогадро о газе, 85-86, 190, 197-202, 256

номер Авогадро, 197–198, 201, 213, 229, 268

Принцип дифракции Бабине, 462

Воздушные шары, 166-169, 225

Уравнение серии Бальмера, 492-493

Барометр, 80, 192, 456

Красота математика, 485-486

Беккерель, Антуан, 161, 401

Пиво, август, 355-358

Закон поглощения Бера, 140, 355-358

Закон Белла-Мажанди о нервной функции, 460

Правило размера видов Бергмана, 463

Бернулли, Даниэль, 9, 11, 125–136

Бернулли, Иоганн, 115, 127, 129, 225

Закон Бернулли гидродинамики, 1, 125-136, 491

Закон Бернулли-Эйлера, 133

Принцип химии Бертло-Томсена Реакция, 465

Бетатрон, 267

Большой взрыв, 84, 318, 408, 445, 449, 450, 482

Поглощение Био Юриспруденция, 226

Биот, Жан-Батист, 5, 9, 193, 222-228

Закон магнитной силы Био-Савара, 222-228, 240-241

Закон Био Вращающаяся дисперсия, 226

Черные дыры, 68, 304, 480-483

Чернотела, 28, 315, 318, 320, 409, 478.Смотрите также Закон излучения Планка

Кровоток, 298, 300, 370

Боде, Иоганн, 10, 144-151

Закон планетных расстояний Боде, 19, 144-151, 287

Бом, Давид, 452

постоянная Больцмана, 213, 219, 334, 336, 346, 359, 410-414, 419, 479, 492

Закон распределения Больцмана, 467

Больцманн, Людвиг 9, 121, 213, 219, 324-325, 334, 336, 378, 384, 411-412, 467, 492. См. Также Закон Стефана-Больцмана о радиации

Бойяи, Джнос, 13, 290, 292

Родился, Макс, 33, 438, 495

Закон о распределении Бозе-Эйнштейна, 477

Бугер, Пьер, 140, 156, 356

Закон Бугера-Пива, 140, 357

Бойль, Роберт, 6, 31, 74, 76-77, 85-92, 354

Газ Бойля Юриспруденция, 19, 85-92, 465

Брэгг, Уильям Генри, 6, 11, 425-433

Брэгг, Уильям Лоуренса, 11, 206, 425-433

Закон дифракции кристаллов Брэгга, 425-433

Браге, Тихо, 52, 60-63, 70, 208

Брюстер, Дэвид, 10, 203-211

Закон Брюстера о поляризации света, 203-211

Броуновский движение, 346, 362, 472

Бунзен, Роберт, 319-320, 382

Плавучесть, 41-42, 51, 86, 344-345

Buys-Ballot, Кристоф, 373-378

Закон Байса о ветре и давлении, 373-378, 445

Закон плотности Кайлетэ-Матиаса, 471

Исчисление, 13, 44, 47, 102, 104, 106, 107, 110, 113, 115-117, 127, 240, 347, 352, 420, 437, 458

Канниццаро, Станислао, 198

Капиллярность, 217, 289, 356, 379-384

Карно, Сади, 161, 325, 330-333

Кассини, Джованни Доменико, 77

Кавендиш, Генри, 99, 159, 160, 259, 381, 467, 490

Кавитация, 185

переменные Cephid, 446

Церера, 145, 290

Чарльз, Жак, 19, 165–172

Газовый закон Чарльза, 19, 86, 165-172, 178, 192-193

Детский закон диодного тока, 474

Христианство, 6-8, 31, 32, 48, 56, 63, 89, 90, 106, 107, 208, 224, 271, 281, 305, 306, 309, 353, 437, 464

Кристал, Джордж, 247

Клаузиус, Рудольфа, 6, 323-341, 376, 418

Закон термодинамики Клаузиуса, 306, 323-341, 491

Кофе, 260

Гроб, Джеймс, 376

Коэн, Леон, 336

Коллоиды, 257, 258, 260, 261

Дальтонизм, 10, 175-177, 180-181

Кондорсе, Николя де Карита, 233

Электропроводность.Видеть Закон теплопроводности Фурье; Законы проводимости Кольрауша; Закон проводимости Видемана-Франца

Копенгаген устный перевод, 435

Коперник, 28, 31, 37, 120, 142, 282, 358, 450, 491

Закон Коппета о понижении точки замерзания, 467

Космологический постоянная, 449

Кулон (шт.), 152, 269

Кулон, Шарль-Огюстен, 8-9, 152-164, 169

Закон электростатики Кулона, 8, 152-164, 275, 381, 419, 487-488

Закон Кулона трения, 158, 169

Креационизм, 325 г.

Крик, Фрэнсис, 431

Кристаллография, 399.См. Также Закон Брэгга о дифракции кристаллов

.

Кристаллоидов, 260

Температура Кюри, 392-396, 403

Кюри, Ирн, 11, 402

Кюри, Мари, 5, 11, 398-404, 490

Кюри, Пьер, 5, 11, 392-408, 490

Закон магнетизма Кюри и закон Кюри-Вейсса, 276, 392-408

Да Винчи, Леонардо, 457

Дальтон, Джон, 10, 173–183, 186, 191–192, 194, 200, 259, 305

Закон Частности Дальтона Давления, 13, 86, 173-183

Дамур, Тибо, 304

Дэви, Хамфри, 9, 11, 12, 215, 252, 259, 270, 272, 273

Де Бройля Уравнение, 434, 487, 492, 497

Дебай, Петра, 219

Дебая Т ³ Лоу, 219

Декарт, Рен, 15, 71, 100, 120, 233, 354

Диамагнетизм, 276, 395, 397, 400

Алмазный, 66, 67, 212, 219, 230, 231, 232, 427, 430

Дихроичные кристаллы, 203

Дифракция, 114, 349, 425-433, 462-463, 476

Диффузионная, 1, 233, 237, 256-262, 346, 365-371, 376, 472.См. Также Законы диффузии Фика; Закон Грэма излияния

Дирак. Видеть Закон о распределении Ферми-Дирака

Дельта Дирака функция, 202

Дирак, Поль, 33, 202, 284, 441, 479, 486, 490-491, 494-495

Уравнение Дирака, 33, 487, 493-495

Закон эволюции Долло, 471

Эффект Доплера, 375, 445, 475

Дрейка Уравнение, 493

Дюлонг, Пьер, 10, 162, 212-221

Закон о степени пяти четвертых Дюлонга-Пети, 214

Закон о теплоемкости Дюлонга-Пети, 212-221, 272

Дайсон, Фриман, 51, 228, 238, 255, 281, 302, 495

E = mc ² , vii, 27, 135, 212, 454, 482, 488, 491-493, 495-497

Эддингтон, Артур, 328

Выпот, 256–264

Эйфелева башня ученые, 161-163

Эйнштейн, Альберт, vii, viii, 1, 2, 4, 14, 16, 17, 22, 27, 40, 55, 72, 73, 98, 100, 102, 103, 121, 142, 149, 151, 153, 163, 170, 183, 188, 212, 218-220, 263, 264, 277, 293, 302, 346, 358, 382, ​​415, 416, 420, 421, 438, 443, 449, 466, 472, 475, 477-478, 479, 482, 486, 488, 490, 491, 493-495, 500.

диффузия уравнение, 472

Распределение Бозе-Эйнштейна, 477-478, 479

Броуновское движение, 346, 472

космологическая постоянная, 449

тепловая мощность 218-219

Закон космического расширения Хаббла, 449

фотоэффект, 420

Планка и, 415, 416, 420

квант и, 415, 416, 420

относительность. См. Относительность

.

специфический тепло, 219

отношение Стокса, 346

Эйнштейна Уравнение поля для общей теории относительности, 486, 493, 495.См. Также «Относительность».

Принцип сохранения энергии и массы Эйнштейна. См. E = mc ²

Закон поглощения фотона Эйнштейна-Штарка, 475

Эластичность, 33, 133, 159, 179, 349. См. Также Гука. Закон упругости

Электричество, vii, 8, 12, 24, 51, 66, 67, 172, 194, 199, 203, 206, 230, 236, 326, 332, 395, 399, 40, 422, 442, 465, 466, 469, 472-475, 477, 487, 488, 491, 497. См. Также Окружной закон Ампера. Электромагнетизм; Закон электростатики Кулона; Законы индукции Фарадея и электролиз; Законы электричества и магнетизма Гаусса; Закон Джоуля Электрическое отопление; Закон Кирхгофа об электрических цепях и тепловом излучении; Законы проводимости Кольрауша; Закон Нернста электродных потенциалов, Ома Закон Электричества; Закон проводимости Видемана-Франца

Электролиз.Видеть Законы индукции и электролиза Фарадея

Электролиты, 194. См. Также законы Фарадея. Индукция и электролиз; Законы проводимости Кольрауша

Электрохирургия, 303-304

ЭМФ, 266, 267, 274, 314

Энтропия, 29, 323, 340. См. Также Закон Клаузиуса Термодинамика

Etvs, Лорнд, 379-384, 495

Закон капиллярности Этвса, 379-384

Эпонимия. Видеть Законы, наименования

Уравнения наука, 487-488

Эрдс, Пол 289

Евклид, 65, 58, 77, 243, 288, 291, 292

Эйлер, Леонхард, 43, 129, 130, 133, 134, 243, 286, 288, 492, 497, 498

Фарад (шт.), 270

Фарадея (единица), 270

Фарадей постоянная, 268, 469

Фарадей, Михаил, vii, 5, 6, 8, 9, 11–12, 51, 215, 240, 261, 265–281, 306, 490, 491

Законы Фарадея индукции и электролиза, vii, 240, 265-282, 306, 486-487, 489, 491

Последняя теорема Ферма, 498

Закон о распределении Ферми-Дирака, 479

Энергия Ферми, 219

Феррел, Уильям, 376

Фейнман, Ричард, 22, 28, 29, 69, 91, 106, 121, 135, 150, 220, 238, 245, 264, 279, 296, 334, 441, 443, 490

Волоконная оптика, 67

Фик, Адольф, 11, 365-372

Законы диффузии Фика, 1, 365-372

Фика Принцип (физиология сердца), 370

Первый закон термодинамики, 310, 331

Флемстид, Джон, 148

Жидкости, 112-113, 310, 368, 437, 456-457.Смотрите также Принцип плавучести Архимеда; Закон Бернулли гидродинамики; Etvs’s Закон капиллярности; Законы диффузии Фика; Закон Пуазейля о потоке жидкости; Закон вязкости Стокса; Закон Торричелли оттока

Флуоресценция, 48, 346, 351, 355

ряд ​​Фурье, 234-236, 497

Закон теплопроводности Фурье, 229-238, 251, 308, 360, 369, 486

Фурье, Джозеф, 10, 162, 229-238, 497

Фракталов, 33, 141

Принцип электроники Франка-Кондона Распространение, 478

Франц, Рудольф, 359-364

Линии Фраунгофера, 317

Fraunhofer, Joseph von, 317

Френель, Огюстен, 208

Законы оптики Френеля-Араго, 461

Трение, 94, 95, 97, 125, 157, 158, 168, 169, 307, 310, 312, 342-346, 349, 350

Закон отражения рентгеновских лучей Фриделя, 476

Галактики, 2, 36, 98, 100, 103, 140, 141, 149, 302, 444-451, 493

Галилео, xi, 4, 7, 32, 37, 49, 52, 53, 57, 60, 64, 88, 94-96, 99, 108, 109, 112, 208, 255, 277, 358, 371, 443, 450, 451, 458, 490, 491

Гамов, Георгий, 415, 449

Гарднер, Мартин, vi, viii, 2, 20, 210

Закон о газе, идеальный, 86, 470

Газы, связанные с законом, 13, 19, 77, 216-218, 267, 308-309, 317, 319, 332-337, 369, 376, 464, 465, 467, 469, 470, 472, 493, 497.См. Также Закон Авогадро о газе; Газовый закон Бойля; Газовый закон Чарльза; Далтона Закон частичных давлений; Закон Гей-Люссака объединения объемов газа; Грэхема Закон излияния; Закон Генри о газе

Гаусс

постоянная, 287, 294

шт.284, 477

ошибка функция, 293

Гаусс, Карла, 5, 6, 9, 13, 43, 282-296, 388, 498

мозг оф, 293

Законы электричества и магнетизма Гаусса, 278, 282-296, 487, 488

Gaussia, 293

по Гауссу

раздача, 294

Функция

, 294

гравитационный постоянная, 294

Гей-Люссак, Джозеф, 13, 162, 165, 179, 190–196, 225

Закон Гей-Люссака объединения объемов газа, 13, 19, 165, 168, 190-196, 200

Правило Гейгера-Наттолла энергии частиц, 474

Гелл-Манн, Мюррей, 486

Свободная энергия Гиббса, 337

Гиббс, Джозия, 121, 337-339

Закон преломления Гладстона-Дейла, 464

Бог.См. Религия и Бог

Гоф, Джон, 176

Грэм, Томас, 9-10, 256-264

Закон излияния Грэма, 2, 86, 256-264

Гравитация, 8, 17-19, 22, 81, 121, 122, 125, 146, 153–154, 156, 150, 160, 161, 183, 220, 294, 343, 344, 348, 350, 357, 364, 380-382, 406, 433, 445, 481-482, 486, 488, 493, 495. См. Также Newton, Исаак; Планеты, положения и движения; Теория относительности, общая теория

Закон теплового расширения Грнайзена, 473

Герике, Отто фон, 275

Хаген, Готхильф, 297, 301

Закон Хагена-Пуазейля, 297

Hagenbach, Jacob, 301

Галлей, Эдмонд, 15

Принцип динамических систем Гамильтона, 461

Харриот, Томас, 15, 71

Хокинг, Стивен, xi, 1, 7, 23, 33, 103, 113, 143, 163, 348, 423, 480-483

Хокинга Законы о черной дыре, 480-483

Тепло, 9, 33, 253, 312, 315-316, 320, 409, 463, 464, 468, 473, 486, 501.См. Также Закон термодинамики Клаузиуса; Закон Дюлонга-Пети удельной плавки; Закон теплопроводности Фурье; Закон Джоуля электрического Обогрев; Законы движения, гравитации и охлаждения Ньютона; Закон Планка Радиация; Закон проводимости Видемана-Франца

Хевисайд, Оливер, 202, 236, 487

Гейзенберг, Вернера, 20, 358, 434-443, 475, 479, 490, 491, 494

Принцип неопределенности Гейзенберга, 2, 33, 255, 421, 434-443

Гельмгольц, Герман фон, 275, 382

Генри, Джозеф, 240, 252, 281

Генри, Уильям 184–189

Закон Генри о газе, 184-189

Heptadecagon, 288

Гершель, Уильям, 148, 165, 184

Герц, Генрих, 274, 493

Закон Гесса постоянного суммирования тепла, 338, 463

Гитлер, Адольф, 416, 421, 440

Гук, Роберт, 9-10, 74-84, 88, 96, 114, 490

Закон Гука Эластичность, 19, 74-84

Хойл, Фред, 449

Хаббл, Эдвин, 444-453

Закон космического расширения Хаббла, 444-453, 493

Космический телескоп Хаббла, 446, 450

Человек достижение, 489-490

Хьюмасон, Милтон, 446

Гумбольдт, Александр фон.См. Фон Гумбольдт, Александр

Харрикейнз, 133, 376

Гюйгенс, Кристиан, 15, 66, 71, 77, 96, 490

Гистерезис, 477

Инерция, 94-95

Инерциальная система отсчета, 99

Принцип обратных квадратов, 26, 53, 81, 103, 110, 111, 114, 222

Ислам, 31, 32, 37, 61

Джинс, Джеймс, 40, 235, 263, 294, 354, 413, 455

евреев, 32, 84, 416, 421, 440, 475

Джоуль (единица), 172, 212, 303, 310, 380, 413, 477

Джоуль, Джеймс, 6, 7, 35, 181-182, 303-312, 331, 333, 490

Закон электрического нагрева Джоуля, 253, 303-312, 331, 333

Эффект Джоуля-Томсона, 309

Каку, Мичио, vii, 22, 83, 328

Калейдоскоп, 205, 207, 208

Кельвина (Уильям Томсон) 6, 231, 244, 308-310, 333, 338, 347, 352

Кеплер, Йоханнес, 6-7, 10-11, 19, 22, 28, 31, 49, 52-64, 70-71, 73, 98, 100-101, 110–111, 142, 202, 208, 237, 358, 406, 450, 488, 491, 498

Законы Кеплера планетарного движения, 52-64

Керст, Дональд, 267

Кинетическая теория газов, 19, 29, 50, 334, 336, 369, 465, 467

Кирхгоф, Густав, 6, 10, 313-222, 382, ​​418, 490

Цепи Кирхгофа и законы излучения, 254, 289, 313-222, 409, 411

Кирхгофа Законы спектрального образования, 316-317

Уравнение Клейна-Гордона,

Кольрауш, Фридриха, 11, 385-391

Законы проводимости Кольрауша, 385-391

Закон теплоемкости Коппа, 464

Кун, Томас, 23, 264

Ламберт, Иоганна, 5, 10, 137-143, 148, 356-357

Закон косинусов Ламберта, 137

Закон излучения Ламберта, 137-143, 356-357

Land, Эдвин, 207

Ландауэр, Рольф, 325

Лауэ, Макс фон, 428, 429

Лавуазье, Антуан, 233, 277, 491

Закон множественных пропорций, 178

Закон квадратичной взаимности, 288

Законодатели

отсутствие женщин, 27

бедствия, 9-10

детство гении, 5

ранний смерть жен, 6

эффект случайности, 11-12

гений семьи, 11

процента в чужой жизни, 10-11

нетрадиционных образования, 5

религиозность, 6-8, 32.См. Также Религия и Бог

.

сопротивление родителей, 9-10

сопротивление идей, 8-9

одновременно открытий, 12-13, 37

Законы

страна или страна происхождения, 29-30, 456

Распределение по времени

, 27-28, 455

эмпирический, 19

одноименного, 4-5, 12-16, 25-28, 35

изобретать против открывать, 2, 20

наименование. См. Законы, одноименный

реал а, 21-24

простота, 2, 14, 16, 17, 20-23, 25, 40, 55, 60, 89, 91, 105, 124, 145, 150, 163, 189, 199, 211, 221, 245, 278, 280, 296, 334, 340, 364, 384, 424, 428, 436, 442, 454, 489, 501

против уравнений, 487-489

против теорий, 16-20

Принцип Ле Штельера, 489

Закон светимости Ливитта, 475

Лейбниц, Готфрид, 13, 110, 116, 128, 196, 420

Леметр, Жорж, 449, 450

Закон Ленца, 266, 489

Leverrier, Urbain, 101

Лайт, 15, 17, 26, 44, 56, 81, 98, 102-104, 106, 113-114, 153, 218, 226, 270, 274, 276, 349-351, 362, 369, 375, 382, ​​388, 438, 444, 445, 458, 459, 461, 463, 466, 468, 475, 481, 486, 491.См. Также Закон поглощения Бера; Брэгга Закон дифракции кристаллов; Закон Брюстера о поляризации света; Закон Ламберта эмиссии; Оптика; Закон излучения Планка; Закон преломления Снеллиуса

Лобачевский, Николая, 13, 292, 486

Формула логарифма, 497

Логистика картография, 493

Закон силы Лоренца, 472

Закон показателей преломления Лоренца-Лоренца, 466

Число Лоренца, 359

Лоренц, Людвиг, 359, 466

Лошмидт, Иоганн, 198, 201

Мах, Эрнст, 9, 336

Магнетизм, vii, 2, 5, 8, 11, 24, 51, 61, 66, 70, 76, 100, 172, 192, 193, 203, 242, 246–247, 251, 361, 388, 390, 414, 441, 442, 472, 477, 480, 487-489, 494, 497.Также круговой закон Ампера. Электромагнетизм; Закон магнитной силы Био-Савара; Закон Кулона Электростатика; Закон магнетизма Кюри и закон Кюри-Вейсса; Законы Фарадея индукции и электролиза; Законы электричества и магнетизма Гаусса

Закон поляризации Малуса, 459

Мандельштам, Леонида, 435

Маркони, Гульельмо, 274, 392

Математика и красавица, 485-486

Матрица механики, 438

Правило удельного электрического сопротивления Маттиссена, 465

Правило наименьшего действия Мопертюи, 458

Максвелл, Джеймс Клерк, 6, 8, 51, 121, 240, 242, 247, 265, 266, 272, 274, 277, 334, 338, 352, 373, 465, 467, 488, 490.Смотрите также Уравнения Максвелла

Максвелла Уравнения, 27, 66, 240, 278-279, 328, 473, 486, 487, 492, 493, 497

Закон вязкости газа Максвелла, 465

Майер, Юлиус фон, 304

Майер, Тобиас, 148

Среднее арифметико-геометрическое, 287-288

Мейтнер, Лиза, 336

МЭМС, 169

Периодический закон элементов Менделеева, 466

Закон вибрации Мерсенна, 455

Мертон, Роберт, 4, 15

Метеорология.См. Закон о ветре и давлении

Buys-Ballot.

Мичелл, Джон, 159–160, 381

Закон изоморфизма Митчерлиха, 461

Импульс, 19, 53, 54, 95-98, 434-435, 439, 440, 494

МОНД, 103

Монополи, магнитные, 278, 284, 487, 494

Закон рентгеновского излучения Мозли, 476

Правило Московица-Ломбарди Магнитное распределение, 480

Формула логарифма Напьера, 497

Навье, Клод, 349, 350

Навье-Стокса Уравнения, 350

Нернст, Вальтер, 327, 469

Закон электродных потенциалов Нернста, 469

Neumann, Franz, 301

Ньютон, Исаак, vii, ix, 1-3, 7-9, 13-14, 17-18, 31, 43, 75-76, 81-82, 93-124, 208, 224, 252, 277, 286, 295, 408, 424, 442, 443, 454, 490-492, 498, 501

Законы Ньютона движения, гравитации и охлаждения, 1, 7, 19, 22, 26, 28, 31, 51, 53-55, 61, 81, 93-124, 153-154, 382, ​​391, 443, 488, 492, 497

Ньютоновские жидкости, 113

Никарагуа почтовые марки, 496-497

Нобелевская премия, 5, 11, 33, 236, 248, 318, 379, 390, 396, 401, 402, 411, 415, 417, 420, 421, 426, 427, 429, 430, 439, 444, 466, 469, 471, 475, 476

Ом (ед.), 172, 246, 248, 250, 253, 303, 361

Ом, Георга, 5, 8-9, 246-255

Закон электричества Ома, 8, 19, 246-255, 319, 385, 391

Ольберс, Генрих, 202, 285, 446

Оннес, Хайке, 248

Оптика, 9, 17, 56, 57, 66-67, 113, 114, 117, 118, 226, 350, 380, 429, 459, 461, 462.См. Также Закон поглощения Бера; Закон света Брюстера Поляризация; Законы оптики Френеля-Араго; Закон излучения Ламберта; Свет; Закон преломления Снеллиуса

рстед, Ганс Кристиан, 8, 225, 239-242, 275, 277

Осмос, 363, 470

Оствальд, Вильгельм, 9, 336, 387, 389, 390

Закон Оствальда о разбавлении, 387

Параллельные вселенные, 103, 451

Парамагнетизм. См. Закон магнетизма Кюри и Закон Кюри-Вейсса

Паскаль (единицы), 85, 174, 342

Паули Вольфганг, 436-439, 478-479, 491

Принцип исключения Паули, 478-479

Пенроуз, Роджер, 21, 23-24, 188, 311, 482

Разрешающая способность, 152, 154, 155, 287, 419

Война в Персидском заливе, 345

Perutz, Макс, 426, 428, 431

Пети, Алексис, 5, 6, 9, 212-221

Фотоэлектрический эффект, 420

Фотонный решетка, 422

Пи (π), 5, 46, 47, 49, 54, 70,111, 138, 141, 152, 154, 219, 222, 223, 234, 293, 294, 297, 301, 342, 359, 412, 419, 434, 480, 492, 493, 496

Piazzi, Джузеппе, 290

Пьезоэлектричество, 398, 399

единиц Планка, 418-419, 481

Планка, Макс, 6, 263, 320, 409-424

Планка константа, 219, 410, 414, 415, 419, 434, 493, 494, 497

Закон излучения Планка, 28, 316, 409-424

Планеты, положения и движения.См. Закон Боде Планетарные расстояния; Законы движения планет Кеплера; Ньютона Законы движения, гравитации и охлаждения

Платоновы тела, 58-59, 60

Пуаз (единица), 301

Пуазейля, 297-302

Закон потока жидкости Пуазейля, 250, 297-302

Пуассон, Симеон, 162, 349

Поляризация, 226, 276, 350, 351, 362, 459, 461. См. Также Закон Брюстера о поляризации света

Polaroid, 204

Поппер, Карл, 17, 150, 263, 264, 321, 354, 391, 483

Давления, 10, 42, 43, 46, 50, 80, 113, 134, 217, 250, 261, 306-309, 325, 331, 337, 350, 363, 369, 370, 465, 469, 470, 489, 491.См. Также Закон Бернулли гидродинамики; Ветер и давление Buys-Ballot Закон; Газы, законы, относящиеся к; Закон Пуазейля потока жидкости

Священник, Иосиф, 160, 259

Теорема о простых числах, 288-289

Принцип наименьшего действия, 458, 492

Птолемей, 71, 120, 210

Теорема Пифагора, 497

Квантовая механика, 18, 28, 29, 32-33, 98, 102, 164, 212, 218, 221, 248, 255, 281, 328, 341, 361, 364, 406, 409-424, 435, 438-441, 461, 466, 474, 475, 478-479, 481, 487, 494, 499.См. Также принцип неопределенности Гейзенберга; Исключение Паули Принцип; Закон Планка о радиации

квантовые нанопроволоки, 361

Капли дождя, 69, 96, 112, 344, 345, 350

Закон о давлении пара Рамзи-Юнга, 470

Закон давления пара Рауля, 469

Закон Рэлея-Джинса, 413, 416

Реальность и законов, 21-24

Красные смещения, 444, 445, 450

Преломление. См. Закон преломления Снеллиуса; Лоренц-Лоренц Закон показателей преломления

Теория относительности, 28, 341, 440, 475

отличия между специальным и общим, 102

общая теория, 17, 22, 29, 55, 73, 102, 103, 124, 163, 221, 382, ​​449, 481, 482, 488, 490, 493, 495

специальной теории, 16, 29, 98, 102, 153, 188, 189, 381, 416, 466, 488, 490, 491, 494

терминология, viii-ix

Религия и Бог, v, vi, 1, 3, 4, 6-8, 10, 22, 31, 32, 37, 48, 55, 56, 57, 58, 61, 62, 63, 77, 83, 87, 89, 90, 92, 105-108, 112, 113, 120, 121, 128, 135, 140, 141, 146, 148, 149, 150, 164, 170, 182–183, 188, 196, 201, 205, 206, 228, 241, 243, 244, 254, 269-271, 281, 286, 293, 295, 302, 305, 306, 310, 311, 347-349, 352-354, 358, 362, 374, 378, 384, 391, 404, 406, 408, 416, 418, 419, 421, 423, 427, 437, 441, 442, 447, 454, 456, 464, 483, 485, 489, 498-500

Сопротивление электрическое.См. Закон электричества Ома; Правило удельного электрического сопротивления Маттиссена

Закон химических реакций Рихтера, 459

Правосторонняя линейка, 223-224

Робертсон, Х. П., 449

Закон Роуленда, 247

Резерфорд, Эрнест, 23, 153, 402, 490-491

Закон акустики Сабины, 473

Сен-Венан, Адмар де, 349

Sandage, Аллан, 446

Сандеманиан, 269-271, 273, 275

Savart (шт.), 227

Саварт, Фликс, 5, 222-228

Шредингер, Эрвин, 436, 479, 490, 491

Уравнение Шредингера, 27, 436, 487, 489, 492, 493-495

Шварцшильд, Карл, 481

Аквалангистов, 174, 185

Второй закон термодинамики, 245, 323-339, 391, 491.См. Также Закон Клаузиуса Термодинамика; Нагревать; Закон Джоуля электрического нагрева

Седиментация, 342, 343, 345

Шеннон, Клод, 325

Шеннон Уравнения, 493

Простота. См. Законы, простота

Одновременность. Смотрите Законодатели, одновременные открытия

Снелл, Виллеброрд, 15, 65-73, 203

Закон Снеллиуса Преломление, 19, 65-73, 203, 391

Зоммерфельд, Арнольд, 436, 437, 440

Спектроскопия, 260, 315-320, 351, 355, 357, 362, 429, 430, 438, 439, 445, 446, 450, 468, 475, 476, 478, 479, 480, 492.См. Также закон излучения Планка

.

Санкт-Петербург Парадокс, 129

Закон Стефана-Больцмана о радиации, 411-412

Закон магнетизма Штейнмеца, 477

Стенгер, Виктор, 24

Стереоскоп, 208

Закон Стиглера эпонимии, 14-15

Закон флуоресценции Стокса, 351

Стоукс, Джордж, 3, 342-354

Закон вязкости Стокса, 342-354

Стокса-Эйнштейна Отношение, 346

Теория струн, 16, 22, 210, 302

Поверхностное натяжение, 379-381

Закон вязкости газа Сазерленда, 472

Симметрия, 2, 58, 72, 83, 101, 188-189, 208, 283, 284, 399, 424, 436, 442, 448, 476, 486

Тамма, Игоря, 435

Тегмарк, Макс, 23

Тенар, Жак, 162, 194, 195, 216

Теории против законов, 16-20

Термодинамика 9, 11, 29, 245, 304, 323-339, 403, 411, 418, 481, 491, 501.Смотрите также Закон термодинамики Клаузиуса; Нагревать; Закон Джоуля электрического нагрева

Третий закон термодинамики, 327

Томсон, Уильям (лорд Кельвин) 6, 231, 244, 308-310, 333, 338, 347, 352

Тиций, Даниил, 144-147

Закон Тициуса-Боде 144–147. См. Также Закон Боде

.

Торричелли Закон оттока, 456

Весы торсионные, 99, 157-160, 362, 381, 382, ​​399

Уравнение ракеты Циолковского

Ультрафиолетовая катастрофа, 413

Закон осмотического давления Вант-Гоффа, 470

Эффект Вентури, 126

Вязкость, 113, 125, 158, 297-301, 310, 342-350, 388, 457, 465, 472

фон Гумбольдт, Александр, 190, 193, 460

Закон фон Гумбольдта о линиях деревьев, 460

Уотсон, Джеймс, 431

Вебер, Вильгельм, 289, 388, 390

Веберс (отряд), 240, 266, 278

Вайс, Пьер, 392-408

Видеманн, Густава, 11, 359-364

Закон проводимости Видемана-Франца, 11, 359-364

Закон Видеманна-Франца-Лоренца, 359

Закон о перемещении Вена, 410-411, 416

Закон о радиации Вена, 416

Вигнер, Юджин, 452

Wilberforce, Лайонел, 298

Рентген, 48, 267, 351, 392, 476.Также Закон Брэгга. дифракции кристаллов

Уравнение Янга-Миллса, 493

Модуль Юнга, 75, 133

Зак, Франц Ксавер фон, 290

Движение нулевой точки, 328

.

.

.

.

.

.

Закон Бойля и принцип Архимеда упрощены.

Иногда, когда вы занимаетесь фридайвингом, физика может быть немного сложной – особенно для тех, кто считает физику немного сложной.Ниже приводится простое объяснение того, что происходит с несколькими диаграммами для иллюстрации. Если у вас есть какие-либо вопросы, свяжитесь со мной, заполнив форму на главной странице.

Эта статья будет охватывать несколько тем из физики; что происходит с нашим телом во время фридайвинга при спуске / подъеме и как это влияет на наши погружения.

Когда вы начинаете опускаться всего на несколько метров, давление сразу начинает действовать на наше тело. Фактически, это первые 10 метров, которые имеют наибольшее изменение давления – взгляните на таблицу ниже.Это давление намного больше, чем то, которое действует на наши тела в повседневной жизни, потому что вода намного плотнее воздуха.

Очень важно, чтобы во фридайвинге мы научились медленно справляться с этим давлением, имели представление о том, что происходит с физиологией нашего тела, и имели адаптивный менталитет к глубине.

и так далее….

Как видно из таблицы, на уровне поверхности у нас есть 1 бар – обычно это называется атмосферным давлением. На каждые 10 метров, которые мы спускаемся, давление увеличивается на 1 бар, тем самым оказывая давление на воздушные пространства тела еще на 1 бар – и именно здесь вступает в силу закон Бойля .

Закон Бойля

«Пока температура остается постоянной, объем газа обратно пропорционален абсолютному давлению» .

По сути, это означает, что увеличение или уменьшение давления будет иметь прямое и противоположное влияние на объем. По мере увеличения давления объем уменьшается и наоборот. Взгляните на таблицу.

Что означает обратно пропорциональная величина?

Это просто. Все это означает, что произведение двух переменных (в данном случае давления и объема) всегда должно быть равно одному и тому же числу – в данном случае 1.Взгляните на схему ниже.

При фридайвинге необходимо уравнять 4 воздушных пространства: маска, уши, носовые пазухи и легкие.

Первое место, где мы чувствуем изменение давления, – это наши уши и носовые пазухи. Это дает почти мгновенный эффект, и первое, что нам нужно сделать, это уравновесить давление. Как мы уже отмечали ранее, наибольшее изменение давления происходит в первые десять метров (на 50%), поэтому очень важно постоянно выравнивать эти воздушные пространства, поскольку это может привести к травмам!

Это уменьшение объема наших легких влияет на нашу плавучесть; и приходит Принцип Архимеда

Принцип Архимеда

‘Тело, полностью или частично погруженное в жидкость, по-видимому, теряет вес, равный весу вытесненной жидкости’

Объем воды, вытесненный плавающее тело также известно как аптраст, действующий на тело.Мы можем сделать вывод, что «плавающее тело» вытесняет воду под собственным весом.

Именно изменение объема наших легких определяет, положительно, отрицательно или естественно плавучесть мы. Многие люди ошибочно полагают, что это «воздух в наших легких», который поддерживает нас в плавучести. Основным источником воздуха является количество, на которое наши легкие заполнены, что определяет объем наших легких на поверхности.

Давайте посмотрим на пример.

Возьмите цельный блок; , его объем составляет 1 м (в кубе) (1 м x 1 м x 1 м), а вес – 8 тонн.

Если бы он был помещен в пресную воду (плотность 1 т / м в кубе), он вытеснил бы 1 м (куб) воды, который весил бы 1 тонну. Теперь казалось, что вес блока составляет всего 7 тонн, когда он был погружен в воду.

Вот как:

Смещение – это объем воды, который вытесняет блок. Как было сказано выше, вытеснение воды также известно как подъем вверх – сила, толкающая блок вверх.

Итак, здесь у нас есть сила толчка вниз 8Т и сила толчка вверх 1Т (смещение или плавучесть).Результирующая сила между ними составляет 7Т в нисходящем направлении (принимает большее из двух). Поэтому блок утонет!

Если мы возьмем тот же блок и превратим его в полую коробку, его вес останется прежним (8 тонн), однако его объем теперь будет увеличен.

Если бы ящик был увеличен до 3 м (куб) в объеме, он теперь вытеснил бы 3 м (куб) воды, обеспечивая подъем плавучести 3 тонны; его кажущийся вес в пресной воде теперь составляет 5 тонн.

При дальнейшем увеличении объема ящика он вытеснил бы еще больше воды и приобрел бы большую плавучесть, а его видимый вес под водой еще больше уменьшился бы.

Если объем ящика сделать равным 8 м (в кубе), вытеснив 8 м (куб) воды, кажущийся вес ящика в воде теперь будет 0, то есть 8 тонн в воздухе – 8 тонн плавучести в воде.

При дальнейшем увеличении объема ящика до более чем 8 м (в кубе) эквивалентный объем вытесненной воды будет весить больше, чем ящик. Если бы его теперь поместили в воду, он был бы вытеснен вверх!

Зачем нам это знать?

Утяжелители для фридайвинга очень важны для нашей безопасности.Обычно мы хотим сохранять положительную плавучесть на поверхности; особенно первые 10 метров. Это связано с тем, что, когда мы выходим из погружения, у нас будет мало кислорода, поэтому мы не хотим бороться в последней части.

Затемнение на мелководье также очень распространено с глубин от 0 до 10 метров при выходе из погружения. Если на такой глубине происходит отключение электричества, вашему напарнику будет намного легче пройти необходимые меры безопасности, поскольку вы действительно сохраняете плавучесть.

Другая причина – свободное падение; По мере того, как вы начнете совершенствоваться в своем фридайвинге, вы изучите новые техники.По мере того, как мы спускаемся, и объем наших легких начинает уменьшаться, мы вытесняем все меньше и меньше воды, становясь все менее плавучей (как показано в примере выше).