Предел x ln x : Анализ-I
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| Aaron |
| ||
15/07/14 |
| ||
| |||
| Xaositect |
| |||
06/10/08 |
| |||
| ||||
| Aaron |
| ||
15/07/14 |
| ||
| |||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| Aaron |
| ||
15/07/14 |
| ||
| |||
| AV_77 |
| |||
11/11/07 |
| |||
| ||||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| Otta |
| |||
09/05/13 |
| |||
| ||||
| Aaron |
| ||
15/07/14 |
| ||
| |||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| ИСН |
| |||
18/05/06 |
| |||
| ||||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
7 Предел функции на бесконечности
Организационная часть:
Приветствие учителя, отметить отсутствующих, проверить подготовку к уроку. Сообщить тему и цель урока. В дальнейшем все задания выводятся на интерактивную доску.
Сообщить тему и цель урока. В дальнейшем все задания выводятся на интерактивную доску.
Актуализация опорных знаний учащихся:
1. Что такое предел функции .
2.Часто при вычислении пределов появляются выражения, значение которых не определено, как они называются (неопределенностями) 3. С какими основными видами неопределенностей вы познакомились? . 4.В каком случае функция называется непрерывной (в данной точке).5.Как можно раскрыть неопределенности
Изложение нового материала:
Пример с бесконечностью:
Разбираемся, что такое ? Это тот случай, когда неограниченно возрастает, то есть: сначала , потом , потом , затем и так далее до бесконечности.
А что в это время происходит с функцией ?
, , , …
Итак: если , то функция стремится к минус бесконечности:
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию бесконечность и получаем ответ.
Еще один пример с бесконечностью:
Опять начинаем увеличивать до бесконечности и смотрим на поведение функции:
Вывод: при функция неограниченно возрастает:
И еще серия примеров:
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:
, , , , , , , , ,
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если , попробуйте построить последовательность , , . Если , то , , .
! Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: , то все равно , так как рано или поздно «икс» начнёт принимать такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.
Что нужно запомнить и понять из вышесказанного?
1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
2) Вы должны понимать и сразу решать простейшие пределы, такие как , , и т.д.
Пределы с неопределенностью вида и метод их решения
Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
Пример:
Вычислить предел
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что , и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим в старшей степени:
Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим в старшей степени:
Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.
Разделим числитель и знаменатель на
Вот оно как, ответ , а вовсе не бесконечность.
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:
Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Пример 2
Найти предел
Снова в числителе и знаменателе находим в старшей степени:
Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности делим числитель и знаменатель на .
Полное оформление задания может выглядеть так:
Разделим числитель и знаменатель на
Пределы с неопределенностью вида и метод их решения
Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с четвёртым уроком о бесконечно малых функциях. А пока всем начинающим изучать математический анализ предлагаю читать далее.
А пока всем начинающим изучать математический анализ предлагаю читать далее.
Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.
Пример 3.
Найти предел функции y=f(x), при x стремящимся к бесконечности.
Разделим числитель и знаменатель дроби на x в третьей степени.
Воспользуемся свойствами предела на бесконечности
исчисление – Пределы и бесконечность минус бесконечность
Бесконечность не является числом.
Таким образом, нет никакого общего смысла ни в одном выражении “бесконечная арифметика”.
Иногда , тем не менее, существует предельная теорема, которую можно интерпретировать как бесконечное арифметическое выражение.
Вот один пример такой теоремы:
Теорема: Даны последовательности $(x_n)$ и $(y_n)$ в $\mathbb R$, если $\lim_{n \to \infty} x_n = \infty$, и если $\lim_{n \ в \infty} y_n = \infty$, тогда $\lim_{n \to \infty} (x_n + y_n) = \infty$.
Из-за этой теоремы можно утверждать, что справедливо «расщепить пределы», как вы говорите, что приводит к выражению «бесконечная арифметика». $$\infty + \infty = \infty $$ Ладно пока.
Но то, что можно написать выражение «бесконечной арифметики», не означает, что существует теорема, поддерживающая это выражение.
Так, например, НЕТ такой теоремы:
Неверная теорема: Даны последовательности $(x_n)$ и $(y_n)$ в $\mathbb R$, если $\lim_{n\to\infty} x_n = \infty$ и $\lim_{n \to \infty} y_n = \infty$, тогда $\lim_{n \to \infty} (x_n – y_n) = $BLAH.
Неважно, что вы подставите вместо BLAH, результирующее утверждение будет ложным. Независимо от того, подставите ли вы BLAH $=0$, или BLAH $= 1$, или BLAH $=42$, или BLAH $=$что-нибудь еще, результирующее утверждение будет ложным.
Чтобы доказать это, позвольте мне привести два контрпримера:
- Контрпример 1: Если $x_n = n$ и $y_n = n$, то $\lim_{n\to\infty} x_n = \infty$, и $ \lim_{n \to \infty} y_n = \infty$ и $$\lim_{n \to \infty} (x_n – y_n)= \lim_{n \to \infty} (n – n) = \lim_{n \to \infty} 0 = 0 $$
- Контрпример 2: Если $x_n = n$ и $y_n = n-1$, то $\lim_{n \to \infty} x_n = \infty$ и $\lim_{n \to \infty} y_n$ и $$\lim_{n \to \infty}(x_n-y_n) = \lim_{n \to \infty} (n – (n-1)) = \lim_{n \to \infty} 1 = 1 $$
Итак, если бы вы попытались убедить меня в истинности “Ложной теоремы” с помощью замены BLAH $=0$, я бы показал вам контрпример 2. А если бы вы попытались убедить меня в истинности “Ложной теоремы” с помощью любую замену, не равную $0$, такую как BLAH $=1$ или BLAH $=42$ или BLAH $=\infty$ или BLAH $=$любое другое, не равное нулю, то я покажу вам контрпример 1.
А если бы вы попытались убедить меня в истинности “Ложной теоремы” с помощью любую замену, не равную $0$, такую как BLAH $=1$ или BLAH $=42$ или BLAH $=\infty$ или BLAH $=$любое другое, не равное нулю, то я покажу вам контрпример 1.
В Исчислении 1 мы учим, что выражение “$\infty-\infty$” является неопределенной формой. На самом деле это означает то, о чем я сказал выше: не существует предельной теоремы, оправдывающей любое вычисление $\infty-\infty$. Когда вы сталкиваетесь с чем-то, похожим на выражение $\infty-\infty$, вашей лучшей математической стратегией будет СДЕЛАТЬ ЧТО-НИБУДЬ ЕЩЕ , т. е. повторно вычислить выражение, переписать его, изменить каким-либо образом (соблюдая законы алгебры). ), чтобы он больше не имел форму $\infty-\infty$.
Итак, для первого примера в вашем посте математическая стратегия, как вы говорите, заключается в рационализации радикалов. И вы, вероятно, узнали другие $\infty-\infty$ примеры с различными математическими стратегиями.
Принцип неопределенности Гейзенберга — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1693
Принцип неопределенности Гейзенберга является одним из самых знаменитых результатов квантовой механики и утверждает, что нельзя (часто, но не всегда) знать все о частице (как это определяется ее волновой функцией) в одно и то же время. Этот принцип математически проявляется в виде некоммутирующих операторов.
Введение
Принцип неопределенности Гейзенберга утверждает, что акту измерения переменной частицы присуща неопределенность. Обычно применяемый к положению и импульсу частицы, принцип гласит, что чем точнее известно положение, тем более неопределенным является импульс, и наоборот.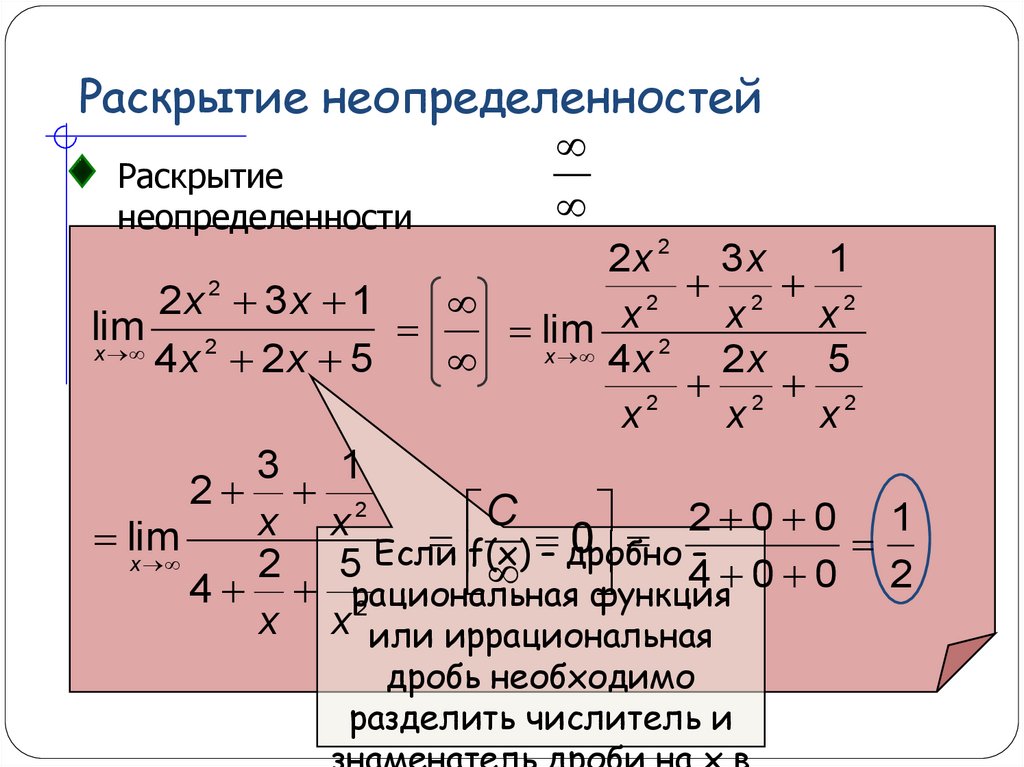 Это противоречит классической ньютоновской физике, которая считает, что все переменные частиц могут быть измерены с произвольной неопределенностью при наличии достаточно хорошего оборудования. Принцип неопределенности Гейзенберга — это фундаментальная теория квантовой механики, которая объясняет, почему ученый не может одновременно измерять несколько квантовых переменных. До появления квантовой механики считалось, что все переменные объекта могут быть известны с точной точностью одновременно для данного момента. Ньютоновская физика не накладывала ограничений на то, как более совершенные процедуры и методы могут уменьшить неопределенность измерений, так что можно было предположить, что при надлежащей тщательности и точности вся информация может быть определена. Гейзенберг сделал смелое предположение, что существует нижний предел этой точности, что делает наше знание о частице изначально неопределенным.
Это противоречит классической ньютоновской физике, которая считает, что все переменные частиц могут быть измерены с произвольной неопределенностью при наличии достаточно хорошего оборудования. Принцип неопределенности Гейзенберга — это фундаментальная теория квантовой механики, которая объясняет, почему ученый не может одновременно измерять несколько квантовых переменных. До появления квантовой механики считалось, что все переменные объекта могут быть известны с точной точностью одновременно для данного момента. Ньютоновская физика не накладывала ограничений на то, как более совершенные процедуры и методы могут уменьшить неопределенность измерений, так что можно было предположить, что при надлежащей тщательности и точности вся информация может быть определена. Гейзенберг сделал смелое предположение, что существует нижний предел этой точности, что делает наше знание о частице изначально неопределенным.
Точнее, если известен точный импульс частицы, невозможно узнать точное положение, и наоборот. Это соотношение также применимо к энергии и времени, поскольку невозможно измерить точную энергию системы за конечное время. Неопределенности в произведениях «сопряженных пар» (импульс/позиция) и (энергия/время) были определены Гейзенбергом как имеющие минимальное значение, соответствующее постоянной Планка, деленной на \(4\pi\). Нагляднее:
Это соотношение также применимо к энергии и времени, поскольку невозможно измерить точную энергию системы за конечное время. Неопределенности в произведениях «сопряженных пар» (импульс/позиция) и (энергия/время) были определены Гейзенбергом как имеющие минимальное значение, соответствующее постоянной Планка, деленной на \(4\pi\). Нагляднее:
\[\Delta{p}\Delta{x} \ge \dfrac{h}{4\pi}\]
\[\Delta{t}\Delta{E} \ge \dfrac{h}{4 \pi}\]
Где \(\Delta\) относится к неопределенности этой переменной, а h – постоянная Планка.
Помимо математических определений, можно понять это, представив себе, что чем тщательнее мы пытаемся измерить положение, тем больше нарушений в системе, что приводит к изменениям импульса. Например, сравните влияние измерения положения на импульс электрона и теннисного мяча. Скажем, для измерения этих объектов требуется свет в виде фотонных частиц. Эти фотонные частицы обладают измеримой массой и скоростью и вступают в контакт с электроном и теннисным мячом, чтобы достичь значения своего положения. Когда два объекта сталкиваются с их соответствующими импульсами (p=m*v), они передают эти импульсы друг другу. Когда фотон контактирует с электроном, часть его импульса передается, и теперь электрон будет двигаться относительно этого значения в зависимости от соотношения их масс. Более крупный теннисный мяч при измерении также будет передавать импульс от фотонов, но эффект будет меньше, поскольку его масса на несколько порядков больше массы фотона. Чтобы дать более практическое описание, представьте себе танк и велосипед, сталкивающиеся друг с другом, причем танк изображает теннисный мяч, а велосипед — фотон. Сама масса танка, хотя он может двигаться с гораздо меньшей скоростью, увеличит его импульс намного выше, чем у велосипеда, фактически заставляя велосипед двигаться в противоположном направлении. Конечный результат измерения положения объекта приводит к изменению его импульса и наоборот.
Когда два объекта сталкиваются с их соответствующими импульсами (p=m*v), они передают эти импульсы друг другу. Когда фотон контактирует с электроном, часть его импульса передается, и теперь электрон будет двигаться относительно этого значения в зависимости от соотношения их масс. Более крупный теннисный мяч при измерении также будет передавать импульс от фотонов, но эффект будет меньше, поскольку его масса на несколько порядков больше массы фотона. Чтобы дать более практическое описание, представьте себе танк и велосипед, сталкивающиеся друг с другом, причем танк изображает теннисный мяч, а велосипед — фотон. Сама масса танка, хотя он может двигаться с гораздо меньшей скоростью, увеличит его импульс намного выше, чем у велосипеда, фактически заставляя велосипед двигаться в противоположном направлении. Конечный результат измерения положения объекта приводит к изменению его импульса и наоборот.
Все квантовое поведение следует этому принципу, и это важно при определении ширины спектральной линии, поскольку неопределенность в энергии системы соответствует ширине линии, наблюдаемой в областях светового спектра, изучаемых в спектроскопии.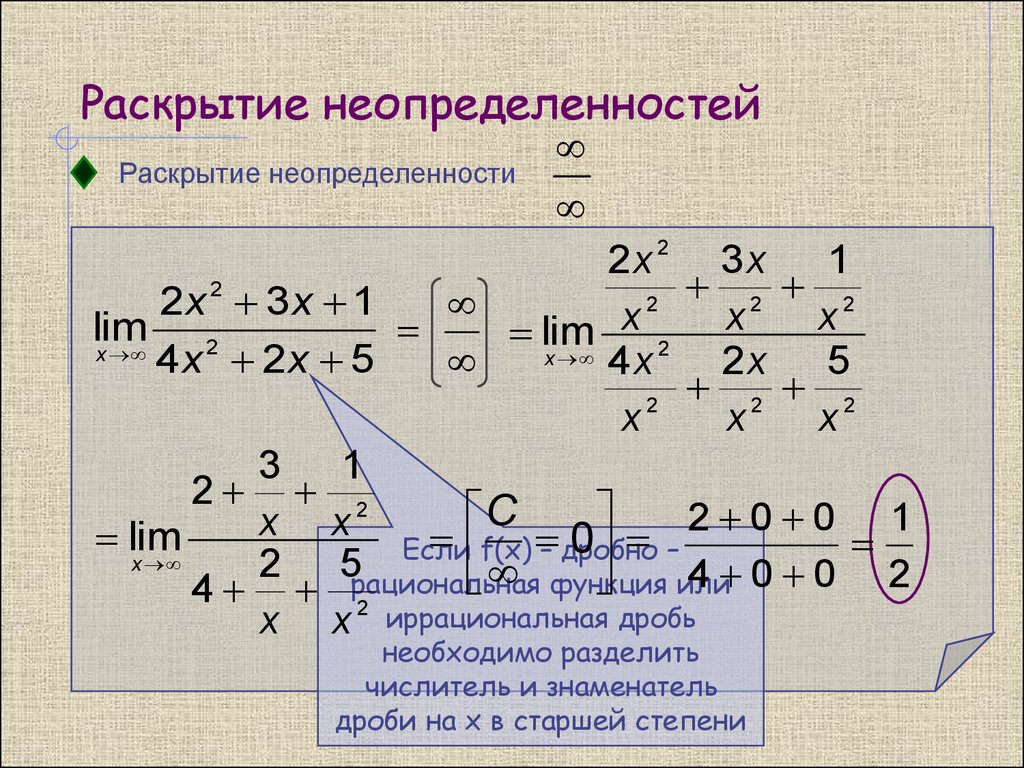
Что это значит?
Трудно представить себе, что нельзя точно знать, где находится частица в данный момент. Интуитивно кажется, что если частица существует в пространстве, то мы можем указать, где она находится; однако принцип неопределенности Гейзенберга ясно показывает обратное. Это связано с волновой природой частицы. Частица рассредоточена по пространству, так что у нее просто нет точного местоположения, которое она занимает, а вместо этого она занимает ряд позиций. Точно так же нельзя точно знать импульс, поскольку частица состоит из пакета волн, каждая из которых имеет свой собственный импульс, так что в лучшем случае можно сказать, что частица имеет диапазон импульсов.
Рисунок \(\PageIndex{1}\): Волновой пакет в пространстве Рассмотрим, можно ли точно измерить квантовые переменные. Волна, положение которой можно точно измерить, схлопывается в одну точку с неопределенной длиной волны и, следовательно, неопределенным импульсом согласно уравнению де Бройля.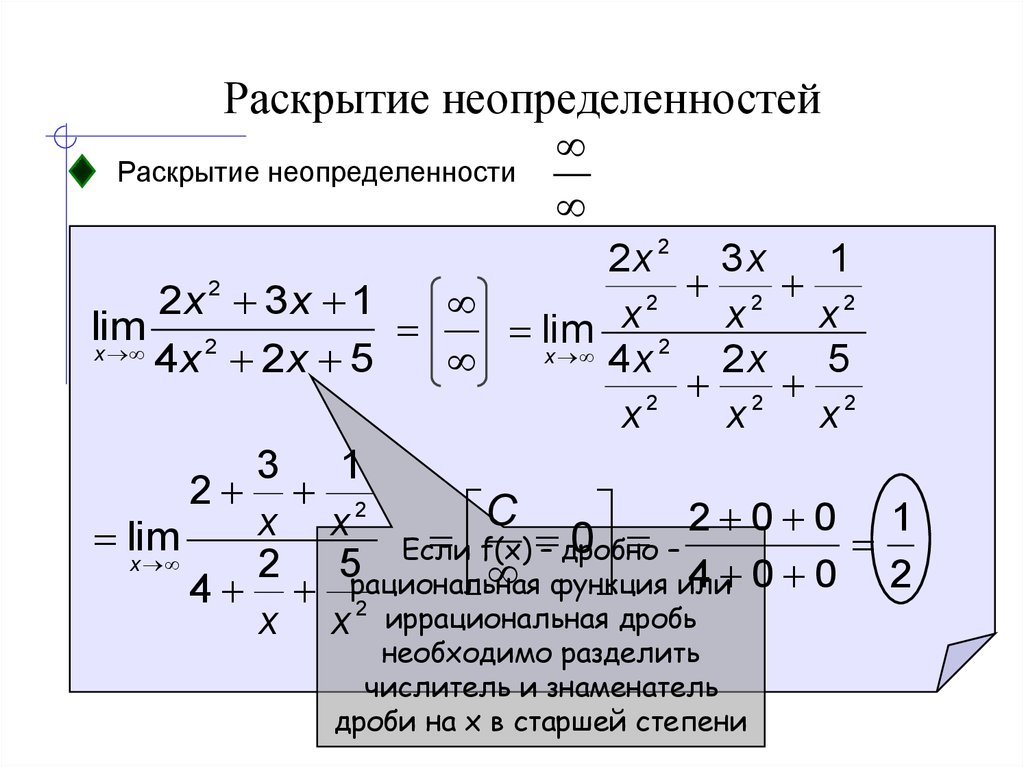 Точно так же волна с совершенно измеримым импульсом имеет длину волны, которая бесконечно колеблется во всем пространстве и, следовательно, имеет неопределенное положение.
Точно так же волна с совершенно измеримым импульсом имеет длину волны, которая бесконечно колеблется во всем пространстве и, следовательно, имеет неопределенное положение.
Вы можете провести такой же мысленный эксперимент с энергией и временем. Чтобы точно измерить энергию волны, потребовалось бы бесконечное количество времени, в то время как измерение точного экземпляра волны в пространстве потребовало бы схлопывания в один момент, который имел бы неограниченную энергию.
Последствия
Принцип Гейзенберга имеет большое значение для практической науки и планирования экспериментов. Рассмотрим измерение импульса или положения частицы. Чтобы создать измерение, должно произойти взаимодействие с частицей, которое изменит другие ее переменные. Например, чтобы измерить положение электрона, должно произойти столкновение между электроном и другой частицей, такой как фотон. Это передаст часть импульса второй частицы измеряемому электрону и тем самым изменит его. Для более точного измерения положения электрона потребуется частица с меньшей длиной волны и, следовательно, более энергичная, но тогда это еще больше изменит импульс во время столкновения. Эксперимент, предназначенный для определения импульса, окажет такое же влияние на положение. Следовательно, эксперименты могут собирать информацию только об одной переменной за раз с любой степенью точности. 9{-31} кг\).
Эксперимент, предназначенный для определения импульса, окажет такое же влияние на положение. Следовательно, эксперименты могут собирать информацию только об одной переменной за раз с любой степенью точности. 9{-31} кг\).
Ответы
9{-31} кг\). Масса воды на 2 порядка меньше массы футбольного мяча, а результирующая неопределенность положения на 2 порядка больше. Между электроном и водой существует разница в 28 порядков как по массе, так и по \(\Delta{x}\). Существует прямая корреляция обратной пропорциональности между \(\Delta{x}\) и \(\Delta{p}\), как описано в принципе неопределенности Гейзенберга, и гораздо меньший электрон имеет большую позицию неопределенности 1,5 м по сравнению с более крупными футбольными мячами \(\ 3,3 \times 10^{-30} м\)5
Одним из примеров, который можно использовать, является стакан воды в подстаканнике в движущемся автомобиле.

 11.2014, 19:40
11.2014, 19:40 
 11.2014, 20:04
11.2014, 20:04  11.2014, 20:05
11.2014, 20:05  11.2014, 20:06
11.2014, 20:06  11.2014, 20:09
11.2014, 20:09 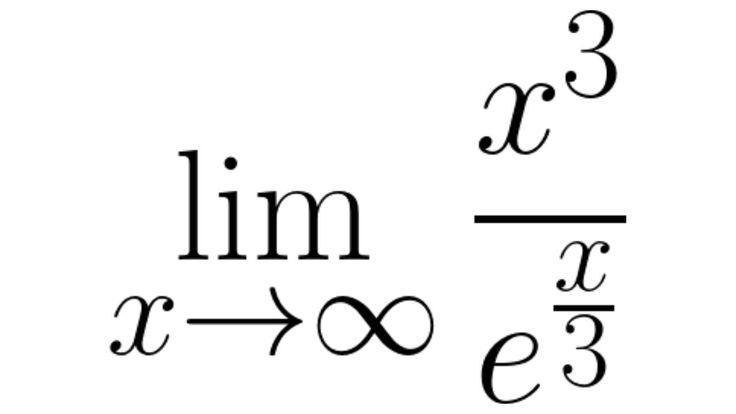 11.2014, 20:11
11.2014, 20:11  11.2014, 20:14
11.2014, 20:14  11.2014, 20:23
11.2014, 20:23  11.2014, 20:37
11.2014, 20:37  11.2014, 08:05
11.2014, 08:05 