Блок и система блоков | 7 класс Онлайн
Конспект по физике для 7 класса «Блок и система блоков». ВЫ УЗНАЕТЕ: Что такое блок. Какой блок называют неподвижным, а какой – подвижным. Что представляют собой системы блоков.
Конспекты по физике Учебник физики Тесты по физике
Если перекинуть верёвку через прочную ветку дерева, за один конец привязать груз, а за другой конец верёвки потянуть, то можно поднять груз на нужную высоту и закрепить его там. Такая система лежит в основе ещё одного простого механизма – блока.
НЕПОДВИЖНЫЙ БЛОК
Блок представляет собой колесо с жёлобом, через который пропущена верёвка, трос или цепь.
Блоки бывают двух видов — неподвижные и подвижные. Неподвижным называют такой блок, ось которого закреплена и при подъёме грузов не поднимается и не опускается.
Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи сил равны радиусу колеса: ОА = ОВ.
Согласно правилу моментов F1l1 = F2l1, где F1 — сила, с которой действует на точку подвеса груз, F2 — сила, которую прикладывают для того, чтобы груз поднять, а l1 – радиус блока. Получается, что F1 = F2.
Такой блок не даёт выигрыша в силе, но позволяет менять направление действия силы.
ПОДВИЖНЫЙ БЛОК
Подвижный блок — это блок, ось которого поднимается и опускается вместе с грузом. Для того чтобы поднять груз, необходимо приложить силу F1, которая стремится повернуть блок вокруг его оси вращения, проходящей через точку О, расположенную не в центре. Плечо силы F1 — отрезок ОВ — является диаметром блока.
Момент этой силы таким образом равен М1 = F1l1.
Груз, прикреплённый к центру блока, своим весом создаёт момент М2 = F2l2, где сила F2 равна весу груза, а плечо силы l2 = l1/2, так как l2 — это радиус блока ОА.
Согласно правилу моментов M1 = М2, т. е. F1l1 = F2l1/2.
Получается, что F1/F2 = 2. Это значит, что подвижный блок дает выигрыш в силе в 2 раза.
КОМБИНАЦИЯ НЕПОДВИЖНОГО БЛОКА С ПОДВИЖНЫМ
На практике удобно применять комбинацию неподвижного блока с подвижным.
Неподвижный блок применяют только для удобства. Он не даст выигрыша в силе, по изменяет направление действия силы, например, позволяет поднимать груз, стоя на земле.
Если же выигрыша в силе в 2 раза недостаточно, можно сконструировать систему из подвижных и неподвижных блоков таким образом, чтобы она давала выигрыш в силе, например, в 4 раза и более.
На практике широко используют устройство, называемое полиспастом (от др.греч. potyspastos — натягиваемый многими веревками или канатами). Это устройство, состоящее из собранных в подвижную и неподвижную обоймы блоков, последовательно огибаемых канатом, и предназначенное для выигрыша в силе.
Полиспаст часто применяют для подъёма небольших грузов (шлюпок на судне). Также он является частью механизма подъемного крана. В альпинизме полиспаст используют для организации переправ через пропасти.
ИСПОЛЬЗОВАНИЕ ПРОСТЫХ МЕХАНИЗМОВ
Рычажные весы — простейший рычаг, где силы — это веса грузов. Рычаги имеются у многих машин.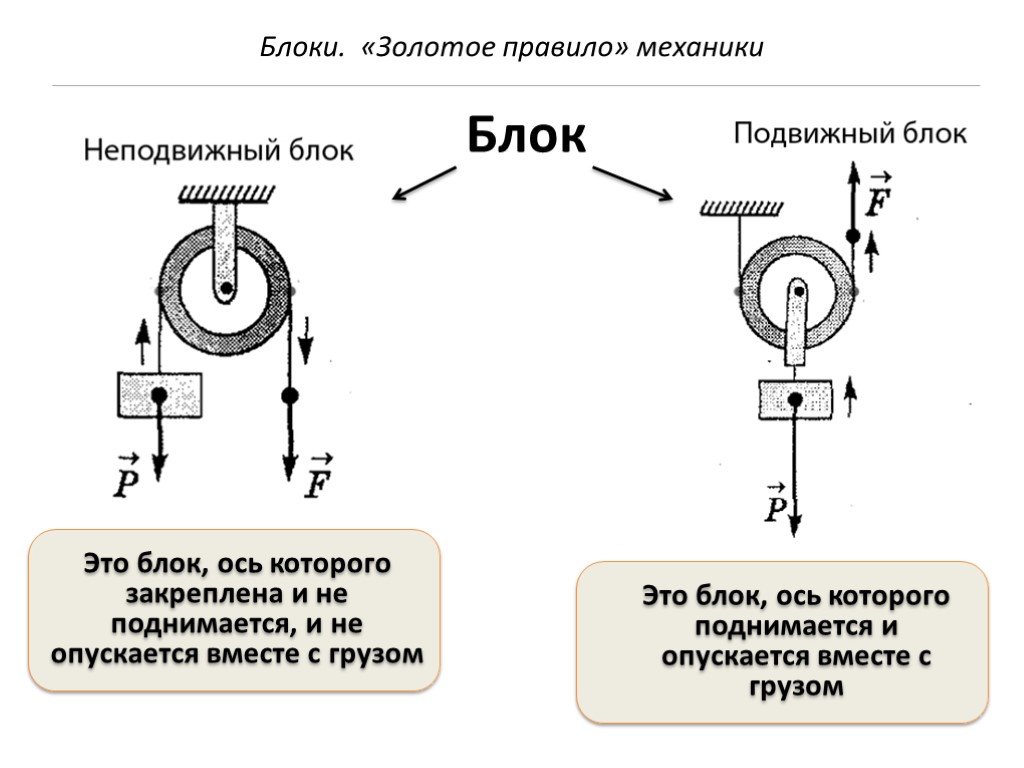
Педали и ручной тормоз велосипеда, педали автомобиля, клавиши пианино — всё это примеры рычагов, используемых в машинах и инструментах.
Для подъёма воды из колодцев чаще используют устройство, называемое воротом. Ворот состоит из барабана в форме цилиндра и прикреплённой к нему рукоятки. Выигрыш в силе, даваемый воротом, тем больше, чем больше отношение радиуса окружности, описываемой рукояткой ворота к радиусу барабана, на который намотана верёвка.
Издревле при строительстве хозяйственных построек сооружалась бревенчатая наклонная плоскость, которая потом использовалась для поднятия тяжёлых грузов.
Вы смотрели Конспект по физике для 7 класса «Блок и система блоков»: Что такое блок. Какой блок называют неподвижным, а какой – подвижным. Что представляют собой системы блоков.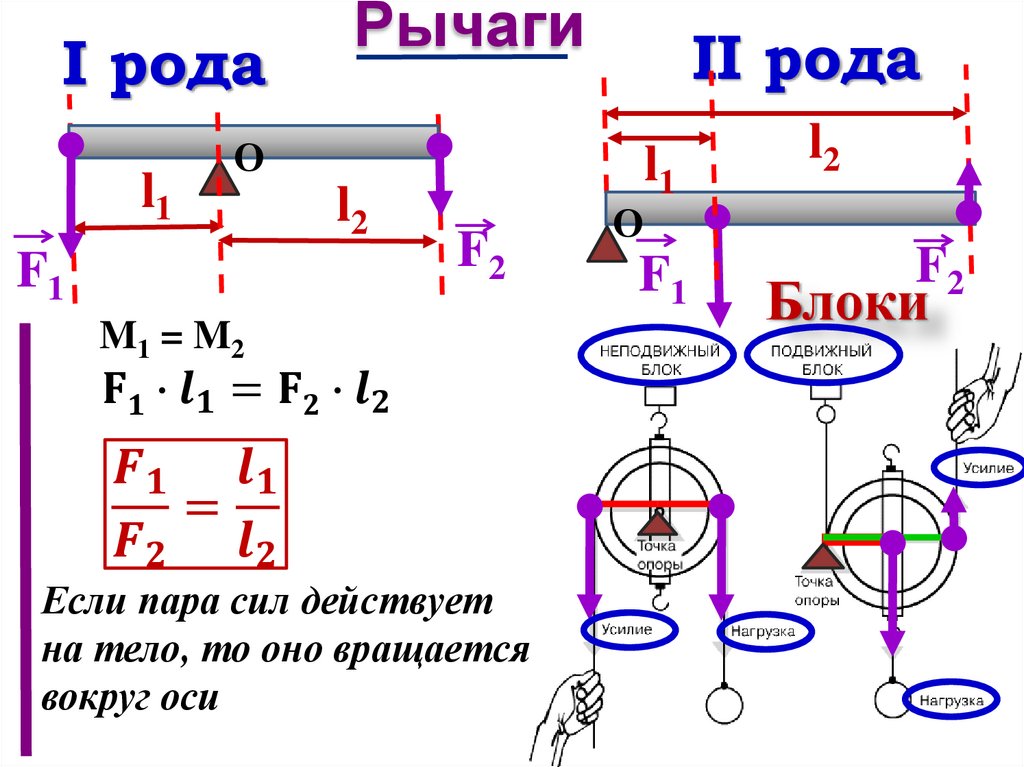
Вернуться к Списку конспектов по физике (В оглавление).
Пройти онлайн-тест «»
что это в физике, как выглядит, формула, где применяется
Содержание:
- Преимущество подвижного блока
- Расчет силы
- Где применяется
- Примеры расчета
Содержание
- Преимущество подвижного блока
- Расчет силы
- Где применяется
- Примеры расчета
В физике механическое приспособление в виде колеса с желобом называется блоком.
Этот простой механизм вращается вокруг своей оси, а углубление в нем предназначено для троса, который подцепляется к грузу. Основное назначение устройства — облегчение подъема и экономия силы.
Различают два вида блоков: подвижный и неподвижный. Первый перемещается вместе с грузом. Второй остается на месте, но позволяет менять направление движения.
Блоки использовали еще в Древней Греции. Архимед видел сходство между блоком и рычагом. Неподвижный блок он соотносил с равноплечим рычагом, а подвижный с неравноплечим.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Примечание
По легенде, Архимед использовал подвижный блок для спуска огромного корабля на воду.
Преимущество подвижного блока
При использовании этого блока происходит двукратный выигрыш в силе.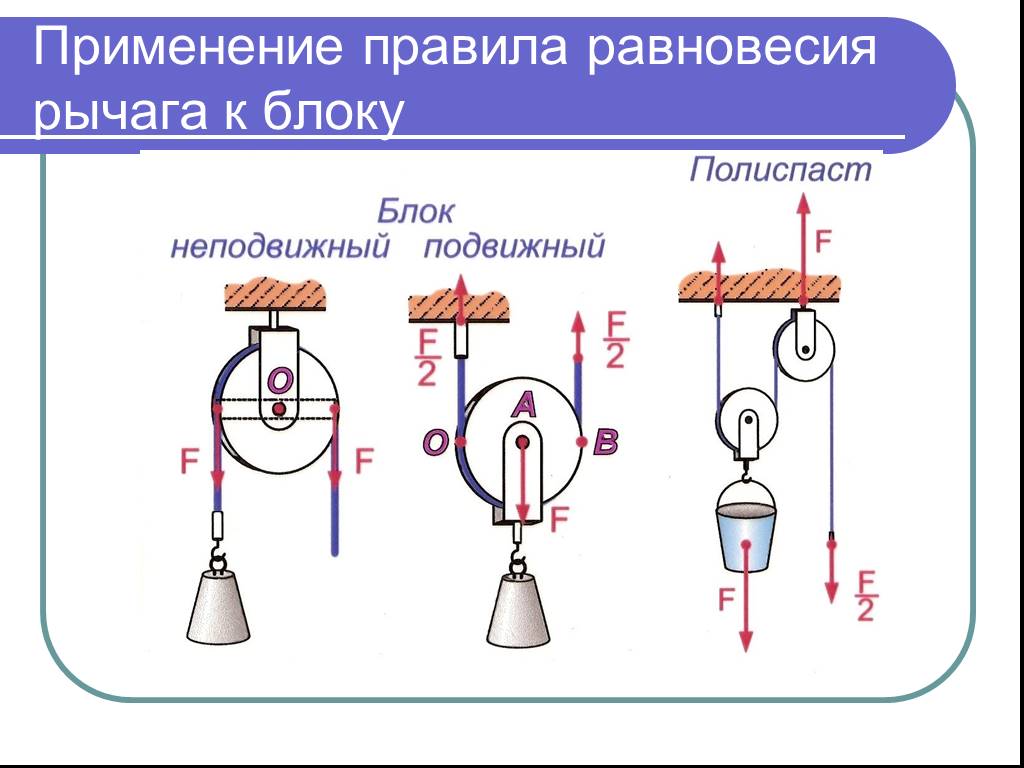
Ось его не зафиксирована, а движется вместе с грузом, который прикрепляется к центру устройства. Согласно правилу, момент силы — это произведение силы и плеча веса:
M=F × l
Экономия происходит вследствие того, что плечо веса (F1) и плечо силы тяги (F2) неравнозначны. Первое равно радиусу блока, а второе — его диаметру.
Расчет силы
Сила, с которой нужно воздействовать на подвижный блок, рассчитывается по формуле:
\(F = \frac{P}{2} \)
Но в этой формулировке не учитывается такая величина, как сила трения, затрудняющая движение груза. Поэтому уравнение соответствует идеальному блоку.
Для определения работы блока в реальных условиях в выражение добавляют коэффициент трения.
Где применяется
Подвижный блок облегчает подъем груза, поэтому прежде всего этот механизм стали применять в работе с тяжелыми грузами: в строительстве, разгрузочных работах, спуске на воду тяжелых судов.
Устройство помогает работать канатным дорогам, лодочным лебедкам и буровым установкам. Французские шторы — жалюзи — работают по схеме подвижного блока.
В некоторых машинах задействуют системы сочетания блоков, например, в грузоподъемной технике используют полиспаст — обойму из подвижных и неподвижных блоков.
Примеры расчета
Определите вес груза, который поднимают с помощью подвижного блока, если известно, что веревку тянут с силой 150Н.
Решение
Так как подвижный блок дает выигрыш в силе в 2 раза, то рассчитать вес нужно по формуле:
\(P=F×2=150×2=300Н\)
Задача 2
С какой силой нужно тянуть груз весом 50Н с помощью подвижного блока?
Решение
\(F=P/2=50/2=25H\)
Насколько полезной была для вас статья?
Рейтинг: 3.75 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Формула натяжения.
Веревка тянет блоки горизонтально с кинетическим трениемКогда мы тянем блок с помощью веревки, в веревке создается натяжение в противоположном направлении. Для простоты расчетов мы обычно предполагаем, что веревка невесома, а поверхность лишена трения. В нашем предыдущем сообщении в блоге мы рассчитали формулу натяжения для аналогичного случая, но без учета силы трения. Но в идеальном случае всегда будет небольшая сила кинетическое трение, противодействующее движению блоков. Если сила, приложенная к блоку, меньше предельного трения , то на блоки будет действовать трение покоя , и блоки будут находиться в состоянии покоя.
Формула для натяжения одного блока Формула для натяжения блока, тянущегося горизонтально с учетом кинетического трения Блок массой m1 тянут с ускорением a. В канате возникает натяжение Т. Между поверхностью и блоком будет кинетическое трение, поскольку он находится в движении.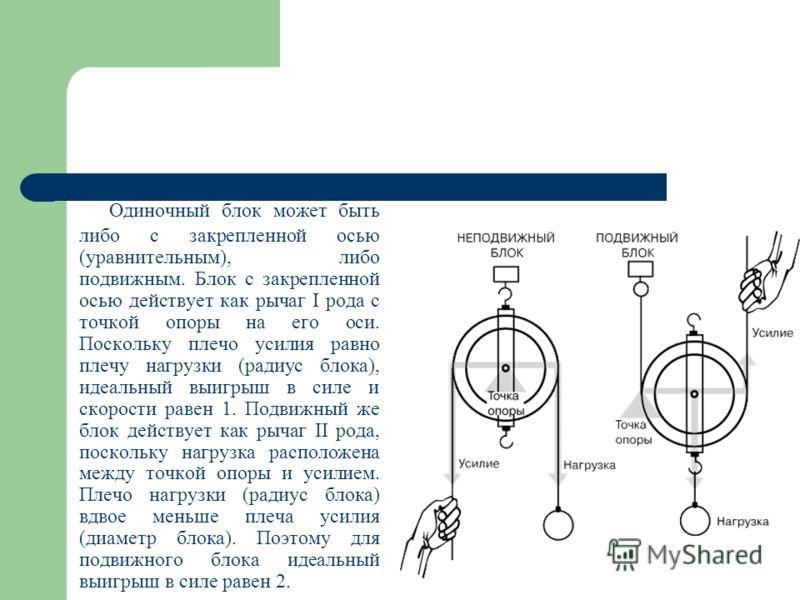
Кинетическое трение будет равно μ k * m1 * g
Таким образом, уравнение для натяжения будет таким:
T = m1*a + μ k * m1 * g
T = m1(a + μ k g)
Эта формула для натяжения согласуется с общим наблюдением, так как натяжение должно быть равна приложенной силе, которая здесь равна приложенной силе плюс сила трения.
Формула натяжения в случае сдвоенных блоков, соединенных веревкой Формула натяжения в случае сдвоенных блоков, соединенных веревкойВ приведенной ниже задаче имеется сила, тянущая два блока, соединенных отрезком веревки. . Теперь нам нужно найти формулу натяжения веревки. Также дано, что коэффициент трения между поверхностью и блоком равен μ k .
Прежде чем продолжить, вы можете прочитать следующие записи в блоге, чтобы получить более глубокое представление о напряженности и трении:
- Что такое сила трения?
- Что такое кинетическое трение?
- Что такое напряжение?
- Формула для натяжения
Сначала рассчитаем значение трения, действующего на систему:
N = μ k *(m всего г)
f k = μ k (m 1 +m 2 )g
Теперь это трение – это трение всей системы (с учетом обоих блоков вместе) для силы F с массой М1+М2.
Теперь рассчитаем ускорение системы:
Fnet = F – трение
ускорение(a) = F/общая масса
1 +m 2 )g]/(m 1 +m 2 )
Теперь, поскольку мы вычислили формулу ускорения системы, мы можем посмотреть на диаграмму свободного тела обоих блоков.
Уравнение растяжения для блока 1 Диаграмма свободного тела блока 1Силы, действующие на блок 1, представляют собой силы растяжения и силы трения. Сумма этих сил должна быть равна чистой силе.
Fnet = T – трение
T= Fnet + трение
T = μ k *m 1 *g + m 1 *a ——–(1)
Уравнение растяжения для блока 2 Диаграмма свободного тела для блока 2 Силы, действующие на блок 2 приложенная сила F, сила трения и сила натяжения. Сумма этих сил должна быть равна чистой силе.
Fnet = F – T – трение
T = F- трение – Fnet
T = F – μ k *m 2 *g – m 2 *a –——- (2)
Формула для натяженияВ случае одиночного блока:
T = M1 (A + µ K G) 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 T = M1.
Для двойных блоков:
Использование диаграммы свободного тела блока 1:
T = μ k *m 1 *g + m 1 *a 9000 Использование диаграммы свободного тела блок 2:
T = F – μ k *m 2 *g – m 2 *a
Используя два приведенных выше уравнения, мы можем найти значения натяжения в аналогичном случае.
Для случаев, когда есть три блока или, выполните те же шаги:
- Сначала рассчитайте ускорение системы.
- Рассчитайте трение в системе
- Используйте диаграмму свободного тела каждого блока для расчета натяжения каждой веревки.
1) Брусок массой 1 кг тянут горизонтально с силой 40 Н. Коэффициент трения равен 0,25. Найдите натяжение веревки.
Числовое значение растяженияСначала найдем ускорение системы:
F = m*a
40 = 1* a
Ускорение(a) = 40 м/с2
Воспользуемся формулой для полученное нами напряжение.
T = m1(a + μ k g)
T = 1(40 + 0,25*9.8)
T = 42,45 Н
2) Два бруска массами 3 кг и 2 кг тянут горизонтально по поверхности с коэффициентом кинетического трения 1. Найти натяжение проволоки, соединяющей брусок 1 и брусок 2.
Здесь в этой задаче коэффициент трения равен 1. Это очень большое трение, поэтому вы видите очень маленькое ускорение. Мы применим формулу для натяжения, как указано выше, и рассчитаем значение натяжения веревки. Мы проверим, используя оба блока.
Сначала вычисляется трение системы, равное 49 Н. Так как это значение меньше силы 50 Н, система будет двигаться. Если значение трения больше приложенной силы, то система не будет двигаться. Это будет случай статического трения.
Теперь рассчитывается чистое ускорение системы с учетом силы трения, действующей на систему. Ускорение получается 0,2 м/с2.
Применить формулу натяжения для блока 1:
Fnet = T – трение
0,4 = T – 19,6
T = 20 Н
Примените формулу натяжения для блока 2:
Fnet = 50 – T – 0 0 0 4 – 29,4 T = 20 Н Из обеих формул получаем, что величина силы натяжения одинакова. Колесницы — хороший пример того, как веревки тянут предметы по горизонтали. Хотя блоков здесь нет. Колесницы используют колеса для уменьшения трения. Трение скольжения преобразуется в трение качения, чтобы уменьшить необходимое тяговое усилие.
Следовательно, наша формула натяжения проверена на правильность.
- Формула натяжения-Туг войны
- Натяжение натяжного натяжного натяжения в веревке 9004
- Formula для напряжения
977 - Formula для напряжения 977
- .
Формула натяжения: Натяжение в вертикально подвешенном проводе с грузом - Натяжение элеватора
- Формула натяжения при круговом движении
- Система шкивов 92}только $. Давайте узнаем, как.
Сначала я воспользуюсь второй диаграммой
Для этой системы уравнение для обеих масс будет таким:-
Для блока массой $m_1$ (в данном случае 4 кг)
$m_1 g-T = m_1 a_1$ $—-eq 1$
{взяла положительное направление вниз}
И Для блока массой $m_2$ (в данном случае 2 кг)
$T=m_2 a_2$ $- —-eq 2$
{Принял направление RHS положительным}
Следовательно, мы можем сказать, что это движение в связи, поэтому для этого полная работа, выполненная напряжением в системе, будет равна нулю.
Работа, выполненная натяжением 4-килограммового блока, равного $m_1$, будет равна
$W_1 = \vec{T} . \vec{x_1}$
Таким образом, смещение и натяжение точно в одном и том же направлении, поэтому угол между ними будет 180 градусов
И проделанная работа будет равна
$W_1 = T x_1$
Аналогично для Блок $m_2$ массой 2 кг работа натяжения будет:-
$W_1 = \vec{T} .
\vec{x_2}$$W_1 = -T x_2$
Таким образом, из вывода о том, что полная работа, совершаемая натяжением всей системы, будет равна нулю, тогда:-
$T x_1 – T x_2 = 0$
Сократив напряжение с обеих сторон, мы получим
$x_1 = x_2$
Таким образом, продифференцировав обе стороны два раза по времени, мы получим ускорение.
$a_1 = a_2$
Это означает, что оба блока ускоряются с одинаковой скоростью.
Таким образом, положив $a_1 = a_2 = a$
Решив все приведенные выше уравнения, мы получим
$m_1 g – T=m_1 a$
И для m_2
$T = m_2 a$
92}$Теперь, как мы знаем, согласно второму закону движения результирующая сила, действующая на объект, будет равна его массе, умноженной на ускорение. Таким образом, из этого уравнения результирующая сила, действующая на брусок массой $m_1$ (в данном случае 4 кг), будет равна $m_1 g-T$. T будет отрицательным только потому, что он действует в противоположном направлении, а мы зафиксировали нисходящее направление как положительное, и все, что произойдет в его противоположном направлении, будет считаться отрицательным.
Формула натяжения: Натяжение в вертикально подвешенном проводе с грузом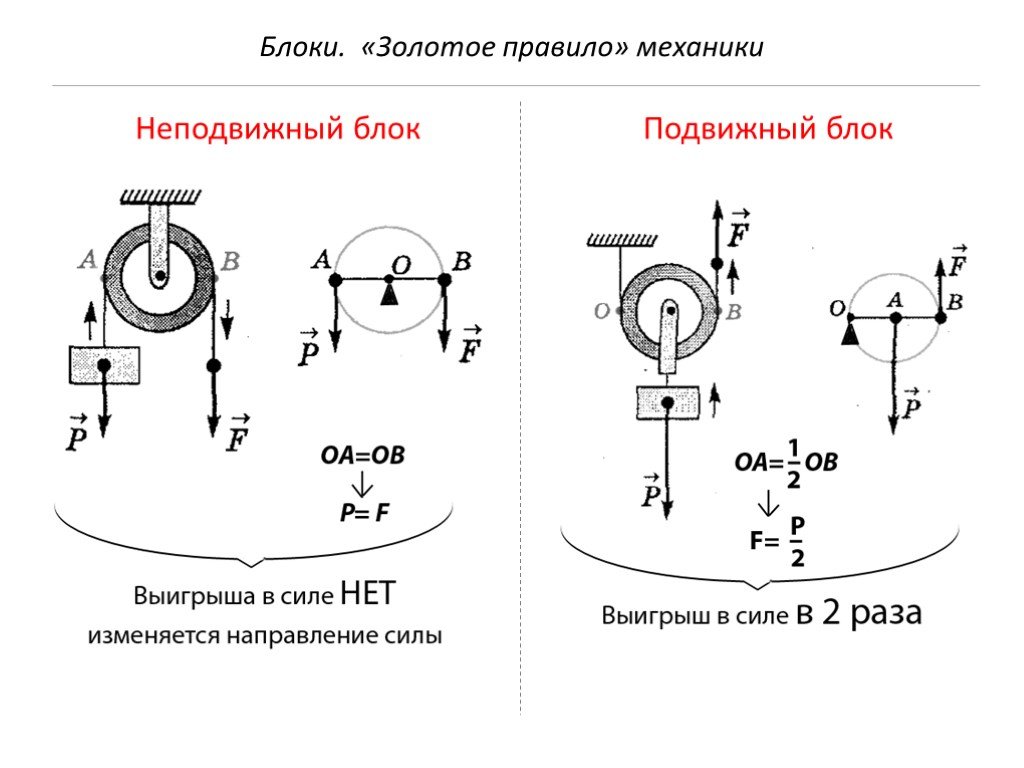 
\vec{x_2}$