| · = | ||||||||||||||||||||
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как умножать числа столбиком (видео по математике)
Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.
Те, кто в школе относился к урокам математики с пренебрежением, наверняка хотя бы несколько раз в жизни бывали в неловкой ситуации. Как посчитать, сколько оставить на чай или сумму коммунального платежа? Если знать пару простых приёмов, это займёт у вас буквально секунду. А уж во время экзамена знание правил умножения больших чисел может помочь сэкономить критически недостающее время. «Мел» совместно с Creu делится простыми секретами вычислений.
Для тех, кто готовится к главному школьному экзамену
1. Умножение на 11
Все мы знаем, что при умножении на десять к числу добавляется ноль, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он:
Возьмите исходное число и представьте промежуток между двумя знаками (в этом примере мы используем число 52): 5_2
Теперь сложите два числа и запишите их посередине: 5_(5+2)_2.
Таким образом, ваш ответ: 572.Если при сложении чисел в скобках получается двузначное число, просто запомните вторую цифру, а единицу прибавьте к первому числу: 9_(9+9)_9 (9+1)_8_9 10_8_9 1089.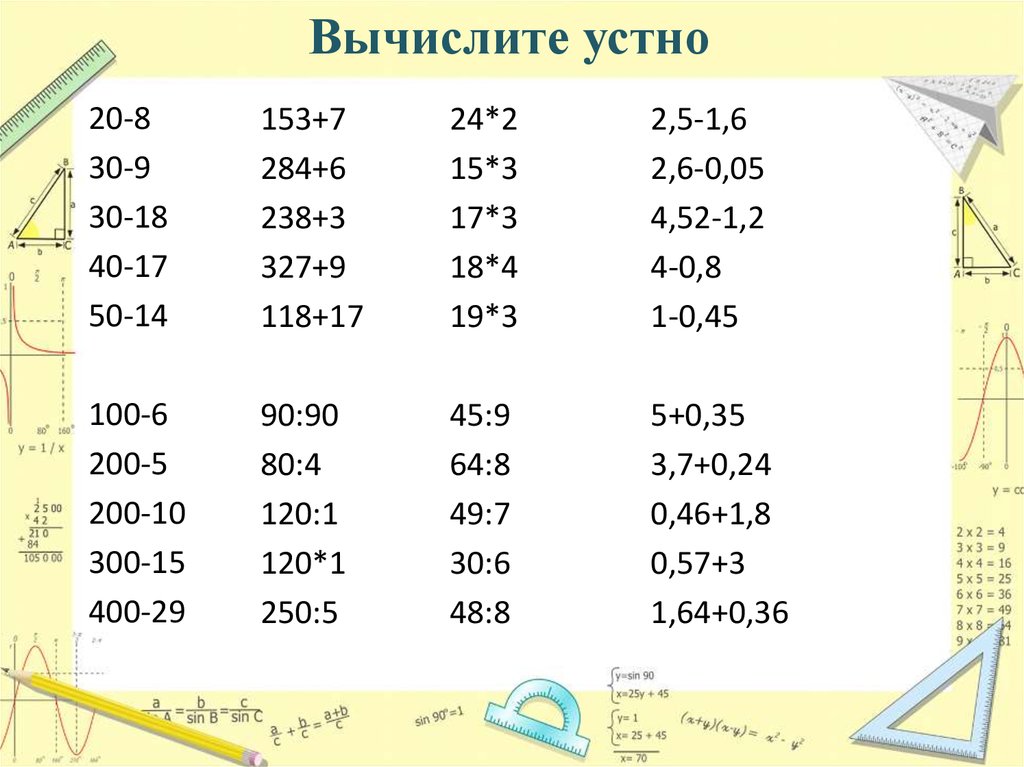 Это срабатывает всегда.
Это срабатывает всегда.
2. Быстрое возведение в квадрат
Этот приём поможет быстро возвести в квадрат двузначное число, которое заканчивается на пять. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и всё! 252 = (2x(2+1)) & 25
3. Умножение на пять
Большинству очень просто даётся таблица умножения на пять, но когда приходится иметь дело с большими числами, сделать это становится сложнее.
Этот приём невероятно прост. Возьмите любое число и поделите пополам. Если в результате получилось целое число, припишите ноль в конце. Если нет, не обращайте внимание на запятую и в конце добавьте пять. Это срабатывает всегда:
2682×5 = (2682 / 2) & 5 или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
Давайте попробуем другой пример:
2943,5 (дробное число, пропустите запятую, добавьте 5)
4. Умножение на девять
Это просто. Чтобы умножить любое число от одного до девяти на девять, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например, 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это два), затем посчитайте после загнутого пальца (в нашем случае – семь). Ответ – 27.
Загните палец, который соответствует умножаемому числу (например, 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это два), затем посчитайте после загнутого пальца (в нашем случае – семь). Ответ – 27.
5. Умножение на четыре
Это очень простой приём, хотя очевидный лишь для некоторых. Хитрость в том, что нужно просто умножить на два, а затем опять умножить на два: 58×4 = (58×2) + (58×2) = (116) + (116) = 232.
6. Подсчёт чаевых
Если вам нужно оставить 15% чаевых, есть простой способ сделать это. Высчитайте 10% (разделите число на десять), а потом добавьте получившееся число к его половине и получите ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75
7. Сложное умножение
Если вам нужно умножать большие числа, причём одно из них – чётное, вы можете просто перегруппировать их, чтобы получить ответ:
32×125 всё равно что:
16×250 всё равно что:
8×500 всё равно что:
8.
 Деление на пять
Деление на пятьНа самом деле делить большие числа на пять очень просто. Нужно просто умножить на два и перенести запятую:
1 . 195 * 2 = 390
2 . Переносим запятую: 39,0 или просто 39.
1 . 2978 * 2 = 5956
2 . 595,6
9. Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом. Отнимите от девяти все цифры, кроме последней. А последнюю цифру отнимите от десяти:
1 . От 9 отнимите 6 = 3
2 . От 9 отнимите 4 = 5
3 . От 10 отнимите 8 = 2
10. Систематизированные правила умножения
Умножение на 5 : Умножьте на 10 и разделите на 2.
Умножение на 6 : Иногда проще умножить на 3, а потом на 2.
Умножение на 9 : Умножьте на 10 и отнимите исходное число.
Умножение на 12 : Умножьте на 10 и дважды прибавьте исходное число.
Умножение на 13 : Умножьте на 3 и 10 раз прибавьте исходное число.
Умножение на 14 : Умножьте на 7, а затем на 2.
Умножение на 15 : Умножьте на 10 и 5 раз прибавьте исходное число, как в предыдущем примере.
Умножение на 16 : Если хотите, 4 раза умножьте на 2. Или умножить на 8, а потом на 2.
Умножение на 17 : Умножьте на 7 и 10 раз прибавьте исходное число.
Умножение на 18 : Умножьте на 20 и дважды отнимите исходное число.
Умножение на 19 : Умножьте на 20 и отнимите исходное число.
Умножение на 24 : Умножьте на 8, а потом на 3.
Умножение на 27 : Умножьте на 30 и 3 раза отнимите исходное число.
Умножение на 45 : Умножьте на 50 и 5 раз отнимите исходное число.
Умножение на 90 : Умножьте на 9 и припишите 0.
Умножение на 98 : Умножьте на 100 и дважды отнимите исходное число.
Умножение на 99 : Умножьте на 100 и отнимите исходное число.
БОНУС: проценты
Вычислить 7% от 300.
Сперва нужно понять значение слова «процент» (percent). Первая часть слова – про (per). Per = для каждого. Вторая часть – цент (cent), это как 100. Например, столетие = 100 лет. 100 центов в одном долларе и так далее. Итак, процент = для каждой сотни.
Первая часть слова – про (per). Per = для каждого. Вторая часть – цент (cent), это как 100. Например, столетие = 100 лет. 100 центов в одном долларе и так далее. Итак, процент = для каждой сотни.
Итак, получается, что 7% от 100 будет семь. (Семь для каждой сотни, только одной сотни).
8% от 100 = 8.
35,73% от 100 = 35,73
Но как это может быть полезным? Вернёмся к задачке 7% от 300.
7% от первой сотни равно 7. 7% от второй сотни – то же 7, и 7% от третьей сотни – все те же 7. Итак, 7 + 7 + 7 = 21. Если 8% от 100 = 8, то 8% от 50 = 4 (половина от 8).
Дробите каждое число, если нужно вычислить проценты из 100, если же число меньше 100, просто перенесите запятую влево.
Примеры:
8%200 =? 8 + 8 = 16.
8%250 =? 8 + 8 + 4 = 20,
8%25 = 2,0 (Передвигаем запятую влево).
15%300 = 15+15+15 =45
15%350 = 15+15+15+7,5 = 52,5
Также полезно знать, что вы всегда можете поменять числа местами: 3% от 100 – то же самое, что 100% от 3. А 35% от 8 – то же самое, что и 8% от 35.
А 35% от 8 – то же самое, что и 8% от 35.
Способы умножения чисел в уме
Содержание
- 1 Первый способ – раскладка на десятки и единицы
- 2 Второй способ – арифметические подгонки
- 3 Третий способ — мысленная визуализация умножения в столбик
- 4 Разложение чисел
Умение мгновенно считать в уме может стать бесценным подспорьем в работе и в условиях скоростных темпов жизни современного человека.
Как быстро умножать большие числа, как овладеть такими полезными навыками? У большинства вызывает затруднения устное перемножение двузначных чисел на однозначные. А о сложных арифметических расчетах и говорить нечего. Но при желании способности, заложенные в каждом человеке, можно развить. Регулярные тренировки, немного усилий и применение, разработанных учеными, эффективных методик позволят достичь потрясающих результатов.
Выбираем традиционные методы
Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.
Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.
Умножение с помощью разложения чисел
Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются. Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме.
Например, для умножения 38 на 57 необходимо:
- разложить число на (30+8)*(50+7);
- 30*50 = 1500 – запомнить результат;
- 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
- (1500 + 610) + 8*7 = 2110 + 56 = 2166
Естественно, необходимо отлично знать таблицу умножения, так как быстро умножать в уме этим способом не удастся без соответствующих умений.
Умножение в столбик в уме
Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:
Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:
- 47*1 = 47 – запомнить;
- 47*8 = 376 – запоминаем;
- 376*10 + 47 = 3807.
Запоминать промежуточные результаты поможет проговаривание их вслух с одновременным суммированием в уме. Несмотря на сложность мысленных вычислений, после непродолжительных тренировок этот метод станет вашим любимым.
Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.
Умножение на 11
Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.
Достаточно между цифрами множителя вставить их сумму:
13*11 = 1(1+3)3 = 143
Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.
28*11 = 2 (2+8) 8 = 308
Умножение больших чисел
Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.
- Каждое число необходимо представить как разницу 100 и еще одного числа:
(100 — 13)*(100 — 9)
Ответ будет состоять из четырех цифр, две первые из которых – разница первого множителя и вычитаемого из второй скобки или наоборот – разница второго множителя и вычитаемого из первой скобки.
87 – 9 = 78
91 – 13 = 78 - Вторые две цифры ответа — результат перемножения вычитаемых из двух скобок.13*9 = 144
- В результате получаются числа 78 и 144. Если при записывании окончательного результата получается число из 5 цифр вторую и третью цифру суммируем. Результат: 87*91 = 7944.
Это самые простые способы перемножения. После многократного их применения, доведения вычислений до автоматизма можно осваивать более сложные техники. И через некоторое время проблема, как быстро умножить двузначные числа перестанет вас волновать, а память и логика существенно улучшатся.
И через некоторое время проблема, как быстро умножить двузначные числа перестанет вас волновать, а память и логика существенно улучшатся.
Поделитесь этим постом с друзьями
Давайте рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе. Некоторые из этих методов, могут позволить вам быстро перемножать в уме двузначные числа при достаточной тренировке. Знать эти методы полезно. Однако важно понимать, что это лишь вершина айсберга. В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.
Первый способ – раскладка на десятки и единицы
Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.
Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
- Первое действие: 60*80 = 4800 — запоминаем
- Второе действие: 60*5+3*80 = 540 – запоминаем
- Третье действие: (4800+540)+3*5= 5355 – ответ
Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.
Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат. Следует принять во внимание другие способы.
Второй способ – арифметические подгонки
Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:
Пример 49*49 может решаться так: (49*100)/2-49. Сначала считается 49 на сто – 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.
Произведение 56*92 решается так: 56*100-56*2*2*2. Получается: 56*2= 112*2=224*2=448. Из 5600 вычитаем 448, получаем 5152.
Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.
К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.
Вывод. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.
Третий способ — мысленная визуализация умножения в столбик
56*67 – посчитаем в столбик.
Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков
Первое действие: 56*7 = 350+42=392 – запомните и не забывайте до третьего действия.
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752 – тут посложнее, но вы можете начинать называть первое число, в котором уверены – «три тысячи…», а пока говорите, складывайте 360 и 392.
Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Что лучше – вопрос на любителя.
Как можно заметить, ни один из описанных выше способов не позволяет считать в уме достаточно быстро и точно все примеры умножения двузначных чисел. Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.
В эпоху калькуляторов мы стали все реже производить вычислительные операции в уме. Между тем, такие упражнения отлично развивают мышление и тренируют память. Как правильно начать умножать в уме многозначные числа, чтобы эту методику понял и взрослый и ребенок? Попробуем разобраться вместе!
Способы умножения чисел в уме существуют не один десяток лет. Выберите тот, который подходит вам наиболее всего!
Выберите тот, который подходит вам наиболее всего!
Разложение чисел
Считается наиболее простым способом. Большие числа нужно разложить на тысячи, сотни, десятки и единицы и перемножить разряды между собой. Попробуем перемножить 38 и 57.
- Сначала разложим числа на десятки и единицы. В первом случае это будет 30+8
- Во втором 50+7
- Умножаем десятки: 30х50=1500. Полученный результат необходимо запомнить.
- Дальше умножаем десятки на единицы того же числа. Вот так: 30х7+8=210+400=610
- Полученный результат снова запоминаем.
- Дальше вспоминаем первый полученный результат: 1500. Плюсуем к нему второй полученный результат 1500 + 610 = 2110
- Мы почти закончили! Теперь нам остается перемножить единицы (8х7=56) И полученный результат прибавляем к полученной ранее, сумме
- 2110 + 56 = 2166
Как запомнить промежуточные результаты? Первое время, возможно, придется записывать их. Но уже через пару дней вам будет достаточно простого проговаривания вслух. После нескольких недель тренировок ваш мозг будет отлично справляться с такими задачами, и умножение не только двузначных, но и более сложных чисел, будет даваться вам легко.
После нескольких недель тренировок ваш мозг будет отлично справляться с такими задачами, и умножение не только двузначных, но и более сложных чисел, будет даваться вам легко.
Выбрасывай калькулятор: 17 полезных математических трюков
Собрали подборку классных математических трюков в помощь. С ними ты сможешь быстро считать в уме, не прибегая к калькулятору!
Привет!
Здесь 17 крутых математических трюков, которые полезны не только школьникам, но и взрослым. Они помогают производить сложные вычисления в голове. Освой эти техники, и будешь решать даже те задачи, которые когда-то казались непосильными.
А после можешь пройти наш быстрый математический тест 😉
Сложение крупных чисел в голове − намного более лёгкий процесс, чем кажется. А этот метод показывает, как упростить процесс, округлив все числа до десятка. Вот пример:
644 + 238
Чтобы было проще работать, округляем каждое из чисел. Итак, 644 превращаем в 650, а 238 становится 240.
Затем складываем 650 и 240. Получается 890. Чтобы найти ответ на исходное уравнение, нужно определить, сколько мы добавили к числам, чтобы их округлить.
650 – 644 = 6 и 240 – 238 = 2
Получается, что к первому числу (644) мы добавили 6, а ко второму (238) − 2. Складываем 6 и 2 вместе, получаем 8.
Остаётся вычесть из суммы округлённых чисел (890) лишнее (8):
890 – 8 = 882
Получаем, что 644 + 238 = 882. Это один из основных математических трюков, которые стоит знать.
Вот основное правило вычитания большого числа из 1000: раздели своё трёхзначное число на первую, вторую, третью цифру. Теперь вычти первую из 9, вторую из 9, а третью из 10. Например:
1000 – 556
Шаг 1: вычитаем 5 из 9 = 4
Шаг 2: вычитаем 5 из 9 = 4
Шаг 3: вычитаем 6 из 10 = 4
Ответ 444.
Умножая число 5 на четное число, можно быстро найти ответ. Например, 5 х 4:
Шаг 1: Берём число, которое хотим умножить на 5 и делим его пополам. В нашем случае, 4 превращаем в 2.
В нашем случае, 4 превращаем в 2.
Шаг 2: Добавляем ноль к получившемуся числу, чтобы найти ответ. К числу 2 ставим рядом 0, получаем 20.
5 х 4 = 20
При умножении нечетного числа на 5 формула немного отличается. Например, рассмотрим 5 х 3:
Шаг 1: Вычитаем единицу из числа, которое хотим умножить на 5. В нашем случае, 3 превращаем в 2.
Шаг 2: Теперь делим получившееся число (2) пополам, получаем 1. Ставим последнее получившееся число на первое место, а число 5, на которое мы хотели умножать изначально, приставляем рядом. Получается, рядом с 1 ставим 5, становится 15.
5 х 3 = 15
Вот быстрый способ узнать, когда число может быть равномерно разделено на эти же числа:
- 10, если число заканчивается на 0.
- 9, когда цифры складываются вместе, а сумма делится поровну на 9.
- 8, если последние три цифры делятся на 8, или число оканчивается на 000.
- 6, если при сложении чётных чисел сумма делится на 3.

- 5, если число заканчивается на 0 или 5.
- 4, если число оканчивается на 00 или двузначное число, которое делится на 4.
- 3, если при сложении цифр числа результат делится на 3.
- 2, если оно заканчивается на 0, 2, 4, 6 или 8.
Это ещё один из математических трюков, который полезен в жизни. Нужен он для умножения любого числа на 9. Вот как это работает:
Покажем на примере умножения 9 на 3.
Шаг 1: Вычитаем 1 из числа, которое умножается на 9.
3 – 1 = 2
Число 2 является первым числом в ответе на уравнение.
Шаг 2: Вычитаем получившееся число из 9.
9 – 2 = 7
Число 7 является вторым числом в ответе на уравнение.
Итого, 9 х 3 = 27.
Хитрость в умножении любого числа на 10 состоит в добавлении нуля к концу числа. Например, 62 х 10 = 620.
Существует также простой способ умножения любого двузначного числа на 11. Вот оно:
11 х 25
Возьмём двузначное число и отделим первую часть числа от второй − из 25 сделаем 2 и 5.
Теперь складываем эти два числа вместе и помещаем результат в центр, между 2 и 5:
2 (2 + 5) 5
2 7 5
Ответ: 11 х 25 = 275.
Если число в центре содержит две цифры, добавь первое число из суммы к первой цифре итогового числа, а второе оставь на месте. Вот пример для уравнения 11 х 88:
8 (8 + 8) 8
8 (16) 8
(8 + 1) 6 8
9 6 8
Получаем ответ: 11 х 88 = 968.
Найти процент от числа может быть несколько сложно, если не подумать о способе решения, а просто считать. С этим методом всё проще. Чтобы узнать, сколько составляет 5% от 235, нужно:
Шаг 1: Переместить десятичную точку на одно значение вправо, 235 (235.0): становится 23.5.
Шаг 2: Разделить 23.5 на число 2, ответ − 11.75. Это ответ на исходное уравнение.
Используем число 35 в качестве примера:
Шаг 1: Умножим первую цифру на сумму единицы и первой цифры.
Шаг 2: В окончание поставим 25.
35 в квадрате = 3 x (3 + 1) & 25
3 x (3 + 1) = 12
12 и 25 = 1225
35 в квадрате = 1225.
Если при умножении больших чисел одно из них является четным, раздели первое число пополам, а второе умножь на 2. Например 20 х 120:
Шаг 1: Делим 20 на 2, получаем 10. Умножаем 120 на 2, получаем 240.
Затем умножаем два ответа вместе:
10 х 240 = 2400
Ответ: 20 х 120 = 2400.
Суть метода в том, чтобы умножить числа без 0, а потом добавить нули. Рассмотрим умножение 200 на 400:
Шаг 1: Умножаем первые числа − 2 на 4:
2 х 4 = 8
Шаг 2: Ставим рядом убранные нули:
80000
200 х 400 = 80000
Это похоже на метод со сложением − здесь тоже нужно округлять. Рассмотрим его на примере выражения 97 x 96:
Округлим каждое из чисел до 100. Получим 100 и 100.
Получим 100 и 100.
Теперь из первых 100 вычитаем первое число (97) и получаем 3, из вторых 100 вычитаем второе число (96) и получаем 4. Складываем получившиеся числа:
3 + 4 = 7
Теперь из 100 вычитаем 7: получается 93. Это будут первые две цифры итогового результата. Чтобы получить оставшиеся две цифры, нужно не сложить, а умножить 3 и 4. Приписываем результат 12 к 93, получается 9312.
Посмотри на свои руки (в идеальном случае, должно быть 10 пальцев). Представим, что ты хочешь умножить 7 на 8.
Из 10 (как и пальцев на руках) вычти первое число (7), осталось 3. Запомни это число. Теперь вычти из 10 второе число (8), получается 2.
Теперь сложи получившиеся числа, результат (5) поставь на первое место. Затем, перемножь 3 и 2. Получится 6, цифру ставим на второе место, получается 56.
Казалось бы, как подборка математических трюков может помочь в таком серьёзном деле, как инвестирование? Может!
Если ты хочешь утроить свои инвестиции, запомни число 115. К примеру, инвестиции, которые дают 5% в год, утроятся через 23 года − 115 : 5 = 23.
К примеру, инвестиции, которые дают 5% в год, утроятся через 23 года − 115 : 5 = 23.
Хотим посчитать 51 х 51. Возьмём одну из цифр, например, 1, к ней прибавим 25. Получается 26.
Теперь перемножим ту же цифру (1), получим 1 (01).
Соединим получившееся, 26 ставим первым числом, 01 вторым. Получается 2601.
Найти корень из таких чисел, как 49 или 81 достаточно просто, потому что корни являются целыми числами. Но как можно найти корень с остатком? Покажем на примере числа 420.
Шаг 1: Находим ближайшее число, которое можно получить возведением в квадрат. В данном случае, это число 400, которое получают возведением в квадрат числа 20.
Шаг 2: Делим наше число (420) на корень того, ближайшего числа (20). Получаем 21.
Шаг 3: Теперь находим среднее между результатом и корнем первого числа − среднее между 21 и 20 равно 20,5.
А корень числа 420 равен 20,494. Получается, что наш ответ максимально близок.
Допустим, мы хотим узнать, чему равно 81 в квадрате.
81 х 81 = ?
Округляем число до меньшего − 80, возводим его в квадрат. Получается 6400.
Теперь к сумме дважды прибавляем округленное число − 6400 + 80 + 80, а в конце добавляем ещё один.
Получается 6560 + 1 = 6561.
Как бы ты посчитал значение выражения 32 х 125? Лучше упростить его:
32 х 125 = ?
16 х 250 = ?
8 х 500 = ?
4 х 1000 = 4000
На этом наша подборка математических трюков заканчивается. Практика этих быстрых математических приемов может помочь как в жизни, так и в работе. А ещё, может быть, пробудит интерес к математике.
Понравилась подборка математических трюков? Тебя точно заинтересует следующее:
- 12 простых советов тем, кто самостоятельно учит математику
- Математика для программистов: 7 крутых YouTube-каналов
- Математика для программиста: советы, разделы, литература
Источник: 10 математических трюков в блоге Concorida University-Portland
Расскажи, какими математическими трюками пользуешься ты?
6 традиционных МЕТОДОВ УМНОЖЕНИЯ В УМЕ – выбери лучший!
Нам предстоит изучить только лучшие способы перемножения двухзначных чисел. Статья содержит наиболее распространенные и потому эффективные приёмы. В результате они позволят вам научиться умножать двухзначные числа в уме в разы быстрее.
Статья содержит наиболее распространенные и потому эффективные приёмы. В результате они позволят вам научиться умножать двухзначные числа в уме в разы быстрее.
Способ №1 – разложение числа на десятки и единицы
Наиболее легким и понятным является методика перемножения двухзначных чисел из школьной программы. Суть этого способа заключается в разбиении множителей на десятки и единицы. Далее получившиеся четыре числа перемножаются между собой. Метод простой, но для его использования необходимо умение запоминать одновременно несколько числовых значений и производить с ними арифметические расчеты.
Например: 54*73 = (50+4)*(70+3) = 50*70 + 50*3 + 4*70 + 4*3 = 3500+150+280+12 = 3942
Проще всего подобные примеры решать в три действия. В первом действии перемножаются десятки, во втором – единицы с десятками и суммируются между собой, а в третьем действии к полученной сумме прибавляется произведение единиц.
Это выглядит так:
1. 50*70 = 3500 – запомнить в уме
50*70 = 3500 – запомнить в уме
2. 50*3+4*70 = 430 – запомнить в уме
3. (3500+430)+3*4 = 3942 – итоговый результат
Для того чтобы за максимально короткое время решать такие примеры, необходимо обладать достаточно прочными знаниями таблицы умножения и уметь суммировать однозначные и двузначные числа, а также обладать способностью быстрого переключения внимания между производимыми расчетами, запоминая их в уме. Этот навык можно натренировать с помощью визуального представления совершаемых арифметических вычислений. Как он осуществляется? При помощи представления картинки вашего решения и получившихся промежуточных результатов.
Как видно из примера, эту методику умножения нельзя назвать самой простой и эффективной, поэтому следует иметь в виду и другие, альтернативные ей способы.
Способ №2 – арифметические подгонки
Среди вариантов вычислений в уме этот способ можно считать одним из наиболее распространенных. Подгонка примера применяется в случае, если необходимо быстро вычислить примерный или точный результат. Этот способ наиболее широко применяется в школах и высших учебных заведениях с математическим уклоном. Школьников и студентов обучают искать наиболее простые алгоритмы вычислений. Далее представлено несколько примеров таких подгонок:
Этот способ наиболее широко применяется в школах и высших учебных заведениях с математическим уклоном. Школьников и студентов обучают искать наиболее простые алгоритмы вычислений. Далее представлено несколько примеров таких подгонок:
Подгонка примеров к соответствующему виду считается очень популярным способом подсчетов в уме. Она применяется, когда вам требуется в короткие сроки определить приблизительный или правильный ответ. Школьников и студентов обучают искать наиболее удобные алгоритмы вычислений для разнообразных задач. Варианты подгонок представлены ниже:
Пример 49*49 решается следующим образом: (49х100) / 2 – 49. В первую очередь 49 умножается на сто – 4900. Потом 5900 делится на два – 2450. Из полученного результата вычитается 49. В итоге получается 2401.
Произведение чисел 56х92 вычисляется следующим образом: 56х100-56х2х2х2. Из этого следует: 56х2 = 112х2 = 224х2 = 448. Далее из 5600 вычитается 448, получается 5152.
Подобный вариант решения может быть применим только тогда, когда вы способны в уме умножать двузначные и однозначные числа и запоминать все полученные результаты. Помимо этого, приходится постоянно подбирать правильный алгоритм решения каждого примера и следить за его соблюдением.
Помимо этого, приходится постоянно подбирать правильный алгоритм решения каждого примера и следить за его соблюдением.
Вывод. Этот способ отлично подходит для тренировки умственных способностей и памяти, но вероятность получить неверный результат из-за неправильно выбранного алгоритма решения значительно выше, чем при применении способа №1.
Способ №3 – визуальное представление в уме перемножения в столбик
56х67 – произведем расчеты в столбик.
Сложность такого умножения заключается в необходимости постоянно держать в памяти несколько вспомогательных чисел, а количество арифметических действий значительно больше, чем у других методов. Но произведение расчетов можно сделать значительно проще. В ЭТОЙ статье мы говорили о важности умения быстро перемножать однозначные числа с двузначными. Если вы уже научились это делать, то вычислить в столбик в уме для вас не составит труда. Порядок действий следующий:
1. 56х7=350 + 42 = 392 – запоминаем.
2. 56х6 = 300 + 36 = 336 – запоминаем.
3. 336х10 + 392 = 3360 + 392 = 3752 – это уравнение сложнее, но вычисление можно сделать проще путем проговаривания числа, которое не вызывает у вас трудностей. Пока вы проговариваете, суммируйте 360 и 392.
В итоге мысленные вычисления в столбик напрямую сложны, но можно значительно упростить этот процесс, если натренировать способность быстрого перемножения двузначных и однозначных чисел. Проще говоря, умножение в столбик является более сложной вариацией способа №1. Что лучше – выбирать вам.
Главным плюсом 3-х способов перемножения двухзначных чисел для устного счета в уме, приведенных выше, является их универсальность – они могут применяться для различных вычислений. Имея достаточно навыка устных вычислений, и зная эти способы, вы сможете найти правильное решение соответствующей задачи. Но при использовании правильных алгоритмов решения, можно значительно сократить количество выполняемых при решении в уме действий.
Способ 4. При умножении на 11
Наиболее простым является умножение любого двухзначного числа на 11. Для вычисления между первыми двумя цифрами множителя, отличного от 11, ставится сумма этих чисел.
Например, при умножении 14 на 11,между 1 и 4 вставляем сумму этих чисел (1+4). В итоге получается: 14*11 = 1 (1+4) 4 = 154.
Если центральные цифры в сумме дают результат больше десяти, то к первой цифре следует добавить единицу, а вторую цифру надо заменить суммой цифр умножаемого числа с вычетом 10.
Например: 56*11 = 5 (5+6) 6 = 5 (11) 6 = 616.
Этот способ можно использовать для умножения на 11 любых двухзначных чисел. Можно привести дополнительные примеры:
73 * 11 = 7 (7+3)3 = 803
45 * 11 = 4 (4+5) 5 = 495
Быстро производить умножение двухзначных и любых других чисел на одиннадцать в уме легко.
Формулы сокращенного умножения: квадраты суммы и разности
Для возведения в квадрат двухзначных чисел хорошо подходят формулы квадратов суммы и разницы.
К примеру:
142= (10+4)2 = 102 + 4*2*10 + 42 = 100+80+16 = 196
782 = (80-2)2 = 802 – 80*2*2 + 22 = 6400-320+4 = 6084
Способ 5. Возведение в квадрат чисел, которые заканчиваются на 5
Числа, заканчивающиеся на пять, возводятся в квадрат по очень простому алгоритму. Числа до конечной 5-ки умножаются на это же число, и добавляется единица. К оставшемуся числу прибавляется число 25.
352 = (3*(3+1)) 25 = 1225
452 = (4*(4+1)) 25 = 2025
752 = (7*(7+1)) 25 = 5625
Такой же алгоритм применяется для более сложных примеров:
3552 = (35*(35+1)) 25 = (35*36)25 = 126025
Способ 6. Умножение чисел до 20
Этап № 1. В качестве примера будем использовать числа 15 и 19. К одному из чисел добавляем количество единиц другого. Получаем: 15+9=24
Этап № 2. Полученное число нужно умножить на 10. Получаем: 24*10=240
Получаем: 24*10=240
Этап № 3. Далее получившееся число складываем с произведением единиц 15 и 19 – 240+5*9=285
Данный пример можно «сократить» в записи:
15*19 = (15+9)*10+5*9 = 285
Доказать верность этого метода можно следующим образом: 15*19 = (10+5)*(10+9) = 10*10+10*5+10*9+5*9 = 10*(10+5+9) +5*9.
Фактически этот метод представляет собой способ применения для расчетов опорных чисел. В конкретном примере опорным числом является десятка. Последнее выражение наглядно показывает, что именно на это число мы и умножали расположенное внутри скобки. Вместо десяти опорным числом может выступать и любое другое число. Наиболее удобными принято считать числа 100, 50, 25 и 20. В ЭТОЙ статье более подробно рассматривается использование опорных чисел. Здесь же приведем только ознакомительное описание этой темы.
Применим методику опорного числа для перемножения чисел 14 и 16. Тут, так же как и в прошлом примере, удобнее будет использовать 10-ку как опорное число. 14 больше десяти на 4, а 16 – на 6. Для определения произведения этих чисел нужно произвести следующие действия:
14 больше десяти на 4, а 16 – на 6. Для определения произведения этих чисел нужно произвести следующие действия:
К одному из множителей прибавляется число, на которое второй множитель больше опорного. А именно, 6 – к 14, или 4 – к 16 (не делайте этого одновременно!). В обоих случаях получается одно и то же: 20. Затем 20 умножаем на опорное число, то есть на 10. Результат: 200.
К 200 прибавляем произведение 4*6. Ответ: 224.
Похожие статьи
Please enable JavaScript to view the comments powered by Disqus.
Умножать цифры в уме. Как быстро умножать двузначные числа в уме? Говорить о том, что ошибки
Здравствуйте, уважаемые родственники и близкие учеников начальной школы! Первый класс уже позади, и сложность школьных заданий неуклонно растёт, не так ли? Вот и пришло время узнать, как выучить таблицу умножения с ребёнком без долгой и скучной зубрёжки. «Эврика» знает несколько способов!
Игра с карточками
В игровой форме ребёнок учится гораздо быстрее. Ещё бы, ведь так он чувствует себя спокойно и расслабленно, а также увлечён процессом. Особенно здорово играть, если победителя ждёт небольшой приз.
Ещё бы, ведь так он чувствует себя спокойно и расслабленно, а также увлечён процессом. Особенно здорово играть, если победителя ждёт небольшой приз.
Чтобы изучение таблицы умножения превратить в весёлую игру, нужно купить или сделать самому картонные карточки с примерами на умножение однозначных чисел. В начале игры их нужно разложить перед ребёнком лицевой стороной вниз.
Все игроки по очереди тянут карточки и называют ответ. За каждый правильный ответ игроку присваивается 1 балл. У всех участников должно быть равное число попыток. Выиграл тот, кто набрал самое большое количество баллов. Думать долго – например, дольше 15 секунд – нельзя, иначе балл не засчитывается.
В этой игре можно пойти на маленькую хитрость и позволить ребёнку выиграть. Для этого нужно договориться с ним, что за исправление ошибки другого игрока ему будет засчитан дополнительный балл. В ходе игры время от времени стоит давать неправильные ответы, которые малыш должен заметить и исправить.
В эту игру нужно играть регулярно – тогда таблицу умножения ученик выучит быстро и будет давать правильные ответы не задумываясь.
Таблица умножения через сложение
При изучении таблицы умножения важно, чтобы ребёнок понимал логику этого действия. Поэтому каждый пример таблицы умножения стоит расписать через сложение одинаковых цифр.
2 × 2 = 2 + 2 + 4;
2 × 3 = 2 + 2 + 2 = 6;
2 × 4 = 2 + 2 + 2 + 2 = 8;
Расширенный вариант таблицы умножения можно повесить на видном месте перед столом, за которым ребёнок учит уроки. В таком случае большинство примеров ему не придётся запоминать, он будет просто вычислять их в уме, пока ответ не отложится в памяти окончательно.
Умножение на пальцах
Стоит познакомить ребёнка с умножением при помощи пальчиков. Это хорошо работает на первых этапах знакомства с таблицей умножения. Рассмотрим пример: 4 × 5. Представим, что каждый пальчик равен 5. Оставляем прямыми 4 пальчика, а остальные загибаем. Теперь просто пересчитываем прямые пальчики, суммируя пятёрки: 5, 10, 15, 20.
Таблица умножения в музыкальных клипах и мультфильмах
Мультфильмы любят все дети, поэтому возьмите парочку «математических» мультиков себе на вооружение и время от времени показывайте ребёнку. Этот способ хорош тем, что вы в это время будете свободны.
Этот способ хорош тем, что вы в это время будете свободны.
Также эффективны клипы, в которых вместо обычных слов звучат примеры на умножение с правильными ответами. Такие клипы – просто находка для музыкальных детей. Пусть ребёнок спокойно занимается своим любимым делом: рисует или складывает конструктор, а вы тем временем просто включите ему «математическую» песенку для фона.
Вскоре вы с удивлением заметите, что малыш напевает слова из песни, без труда вспоминая примеры на умножение.
Увлекательные способы умножения с цифрой 9
Цифра 9 – особенная, даже магическая. Расскажите об этом ребёнку и легко умножайте на 9 любое другое число.
Умножаем на 9 с пальчиками
Пусть малыш положит ладони на стол и выпрямит все пальцы. Теперь нужно каждому пальчику присвоить порядковый номер слева направо. Демонстрируем чудеса математики: например, найдём ответ для примера «9 × 3»:
- находим палец номер 3;
- считаем, сколько пальцев слева от третьего.
 Это десятки нашего ответа;
Это десятки нашего ответа; - считаем, сколько пальцев справа от третьего. Это единицы ответа.
Ставим 2 цифры рядом и получаем правильный ответ – 27.
Смотрим на второй множитель при умножении на 9
Есть ещё один интересный способ умножить любое однозначное число на 9. Рассмотрим пример «9 × 3». Проделаем с цифрой 3 следующие метаморфозы:
- возьмём 3 десятка;
- отнимем от них 3 единицы;
- получим 30 − 3;
- ответ: 27.
Таблица умножения в стихах
Многие учителя используют стихи для запоминания таблицы умножения. Когда нужно дать правильный ответ, то строки стихотворения сами всплывают в памяти. Помните песенку «Дважды два – четыре»? Вот по такому же принципу и происходит запоминание примеров на умножение.
Что такое «умножение»?
Это умное сложение.
Ведь умней умножить раз,
Чем слагать всё целый час.
1 × 1 = 1
Один пингвин гулял средь льдин.
Одиножды один – один.
1 × 2 = 2
Один в поле не воин.
Одиножды два – двое.
2 × 2 = 4
Два атлета взяли гири.
Это: дважды два – четыре.
2 × 3 = 6
Сел петух до зари
На высокий шест:
– Кукареку!.. Дважды три,
Дважды три – шесть!
2 × 4 = 8
В пирог вонзилась пара вилок:
Два на четыре – восемь дырок.
2 × 5 = 10
Двух слонов решили взвесить:
Дважды пять – получим десять.
То есть весит каждый слон
Приблизительно пять тонн.
2 × 6 = 12
Повстречался с раком краб:
Дважды шесть – двенадцать лап.
2 × 7 = 14
Дважды семь мышей –
Четырнадцать ушей!
2 × 8 = 16
Осьминоги шли купаться:
Дважды восемь ног – шестнадцать.
2 × 9 = 18
Вы видали подобное чудо?
Два горба на спине у верблюда!
Стали девять верблюдов считаться:
Дважды девять горбов – восемнадцать.
2 × 10 = 20
Дважды десять – два десятка!
Двадцать, если скажем кратко.
3 × 3 = 9
Кофе пили три букашки
И разбили по три чашки.
Что разбито, то не склеить…
Трижды три – выходит девять.
3 × 4 = 12
Целый день твердит в квартире
Говорящий какаду:
– Тррри умножить на четыррре,
Тррри умножить на четыррре –
Двенадцать месяцев в году.
3 × 5 = 15
Школьник стал писать в тетрадь:
Сколько будет «трижды пять»?
Был он страшно аккуратен:
Трижды пять – пятнадцать пятен!
3 × 6 = 18
Стал Фома оладьи есть:
Восемнадцать – трижды шесть.
3 × 7 = 21
Трижды семь – двадцать один:
На носу горячий блин.
3 × 8 = 24
Прогрызли мыши дыры в сыре:
Трижды восемь – двадцать четыре.
3 × 9 = 27
Трижды девять – двадцать семь.
Это нужно помнить всем.
3 × 10 = 30
Три девицы под окном
Наряжались вечерком.
Перстни мерили девицы:
Трижды десять будет тридцать.
4 × 4 = 16
Четыре милых свинки
Плясали без сапог:
Четырежды четыре – шестнадцать голых ног.
4 × 5 = 20
Четыре учёных мартышки
Ногами листали книжки.
На каждой ноге – пять пальцев:
Четырежды пять – двадцать.
4 × 6 = 24
Шла на парад
Картошка-в-мундире:
Четырежды шесть – двадцать четыре!
4 × 7 = 28
Цыплят считают под осень:
Четырежды семь – двадцать восемь!
4 × 9 = 36
У Бабы-яги сломалась ступа.
Четырежды восемь – тридцать два зуба!
Беж жубов ей нечем есть:
Четырежды девять – «тридцать шешть»!
4 × 10 = 40
Гуляли сорок сорок,
Нашли творожный сырок.
И делят на части творог:
Четырежды десять – сорок.
5 × 5 = 25
Вышли зайцы погулять:
Пятью пять – двадцать пять.
5 × 6 = 30
Забежала в лес лисица:
Пятью шесть – выходит тридцать.
5 × 7 = 35
Пять медведей из берлоги
Шли по лесу без дороги –
За семь вёрст кисель хлебать:
Пятью семь – тридцать пять!
5 × 8 = 40
Влезть сороконожке
Трудно на пригорок:
Утомились ножки –
Пятью восемь – сорок.
Встали пушки на пригорок:
Пятью восемь – вышло сорок.
5 × 9 = 45
Пушки начали стрелять:
Пятью девять – сорок пять.
Если лаптем щи хлебать:
Пятью девять – сорок пять.
Будет этот лапоть
Всем на брюки капать!
5 × 10 = 50
Рыли грядку кабачков
Пять десятков пятачков.
И хвостов у поросят:
Пятью десять – пятьдесят!
6 × 6 = 36
Шесть старушек пряли шерсть:
Шестью шесть – тридцать шесть.
6 × 7 = 42
Шесть сетей по шесть ершей –
Это тоже тридцать шесть.
А попалась в сеть плотва:
Шестью семь – сорок два.
6 × 8 = 48
Бегемоты булок просят:
Шестью восемь – сорок восемь.
6 × 9 = 54
Нам не жалко булок –
Рот откройте шире:
Шестью девять будет
Пятьдесят четыре.
6 × 10 = 60
Шесть гусей ведут гусят:
Шестью десять – шестьдесят.
7 × 7 = 49
Дураков не жнут, не сеют,
Сами нарождаются:
Семью семь – сорок девять…
Пусть не обижаются!
7 × 8 = 56
Раз олень спросил у лося:
«Сколько будет семью восемь?»
Лось не стал в учебник лезть:
«Пятьдесят, конечно, шесть!»
7 × 9 = 63
У семи матрёшек
Вся семья внутри:
Семью девять крошек –
Шестьдесят три.
7 × 10 = 70
Учат в школе семь лисят:
Семью десять – семьдесят!
8 × 8 = 64
Пылесосит носом
Слон ковры в квартире:
Восемь на восемь –
Шестьдесят четыре.
8 × 9 = 72
Восемь медведей рубили дрова:
Восемью девять – семьдесят два.
8 × 10 = 80
Самый лучший в мире счёт:
Наступает Новый год!
В восемь рядов игрушки висят:
Восемью десять – восемьдесят!
9 × 9 = 81
Свинка свинёнка решила проверить:
– Сколько получится «девять на девять»?
– Восемьдесят – хрю – один! –
Так ответил юный свин.
9 × 10 = 90
Невелик кулик, а нос-то!
Девятью десять – девяносто.
10 × 10 = 100
На лугу кротов десяток –
Каждый роет десять грядок.
А на десять десять – сто:
Вся земля как решето!
Вовсе не обязательно заучивать все куплеты. Можно выбрать только те примеры, которые ребёнку сложно запомнить.
Только без фанатизма: компьютерные игры
Даже дети, которые не любят математику, с удовольствием поиграют в компьютерную игру. Если ваши педагогические способности не на высоте, то пускай за дело возьмётся Баба-яга или какой-нибудь другой персонаж.
Если ваши педагогические способности не на высоте, то пускай за дело возьмётся Баба-яга или какой-нибудь другой персонаж.
Выполняя нехитрые задания и постепенно повышая сложность игры, ребёнок и сам не заметит, как быстро выучит таблицу умножения назубок.
Подойдите к учебному процессу креативно – тогда он принесёт только положительные эмоции вам и вашему ребёнку. Эти простые советы от «Эврики» упростят изучение таблицы умножения:
- Повесьте примеры на видном месте.
- Учите умножать и делить сразу.
- Когда выучите умножение на 2, переходите к умножению на 4, а затем на 8.
- После умножения на 3 переходите к умножению на 6 и 9.
- Одновременно с умножением на 5 удобно изучать циферблат часов.
- Хвалите и будьте терпеливы.
- Ваши помощники – мультфильмы, музыкальные клипы, обучающие видео и игры с математическим уклоном.
Ну что, теперь таблица умножения не кажется вам наказанием? Мы верим, что ваш положительный настрой передастся и ребёнку. «Эврика» желает вам лёгкой учёбы! До новых встреч в широком кругу наших читателей!
«Эврика» желает вам лёгкой учёбы! До новых встреч в широком кругу наших читателей!
Умножение двузначных чисел – навык, крайне необходимый для нашей повседневной жизни. Люди постоянно сталкиваются с потребностью перемножить что-либо в уме: ценник в магазине, массу продуктов или размер скидки. Но как умножать двузначные числа быстро и без проблем? Давайте разберемся.
Как умножить двузначное число на однозначное?
Начнем с простой задачи – как умножать двузначные числа на однозначные.
Для начала, двузначное число – это такое число, которое состоит из определенного количества десятков и единиц.
Для того чтобы умножить двузначное число на однозначное в столбец, нужно написать нужное двузначное число, а под ним соответствующее однозначное. Далее следует поочередно умножить на заданное число сначала единицы, а потом – десятки. Если при умножении единиц получилось число больше 10, то количество десятков нужно просто перенести в следующий разряд, прибавив их.
Умножение двузначных чисел на десятки
Умножение двузначных чисел на десятки – задача ненамного сложнее, чем умножение на однозначные числа. Основной порядок действий остается тем же:
Основной порядок действий остается тем же:
- Выписать числа друг под другом в столбец, при этом нуль должен находиться как бы «сбоку», чтобы не мешать при арифметических действиях.
- Умножить двузначное число на количество десятков, не забыть про перенос некоторых цифр в следующие разряды.
- Единственное, что отличает этот пример от предыдущего – в конце получившегося ответа нужно добавить нуль, так что десятки, которые были опущены в начале, становятся учтенными.
Как перемножить два двузначных числа?
После того как вы полностью разобрались с умножением двузначных и однозначных чисел, можно начинать думать, как умножать столбиком двузначные числа друг на друга. На самом деле это действие тоже не должно потребовать от вас больших усилий, так как принцип все еще остается тем же.
- Выписываем данные числа в столбец – единицы под единицами, десятки под десятками.
- Начинаем умножение с единицы точно так же, как в примерах с однозначными числами.

- После того как вы получили первое число, умножив единицы на данную цифру, нужно таким же образом умножить десятки на эту же цифру. Внимание: ответ нужно записывать строго под десятками. Пустое место под единицами – это неучтенный нуль. Вы можете записывать его, если вам так удобнее.
- Перемножив и десятки, и единицы и получив два числа, записанных одно под одним, их нужно сложить в столбец. Получившееся значение и является ответом.
Как правильно умножать двузначные числа? Для этого недостаточно просто прочитать или выучить приведенную инструкцию. Помните, для того чтобы освоить принцип, как умножать двузначные числа, в первую очередь нужно постоянно практиковаться – решать как можно больше примеров, как можно реже пользоваться калькулятором.
Как умножать в уме
Научившись блестяще умножать на бумаге, можно задаться вопросом, как быстро умножить двузначные числа в уме.
Конечно, это не самая простая задача. Она требует некоторой концентрации, хорошей памяти, а также способности удерживать в голове некоторое количество информации.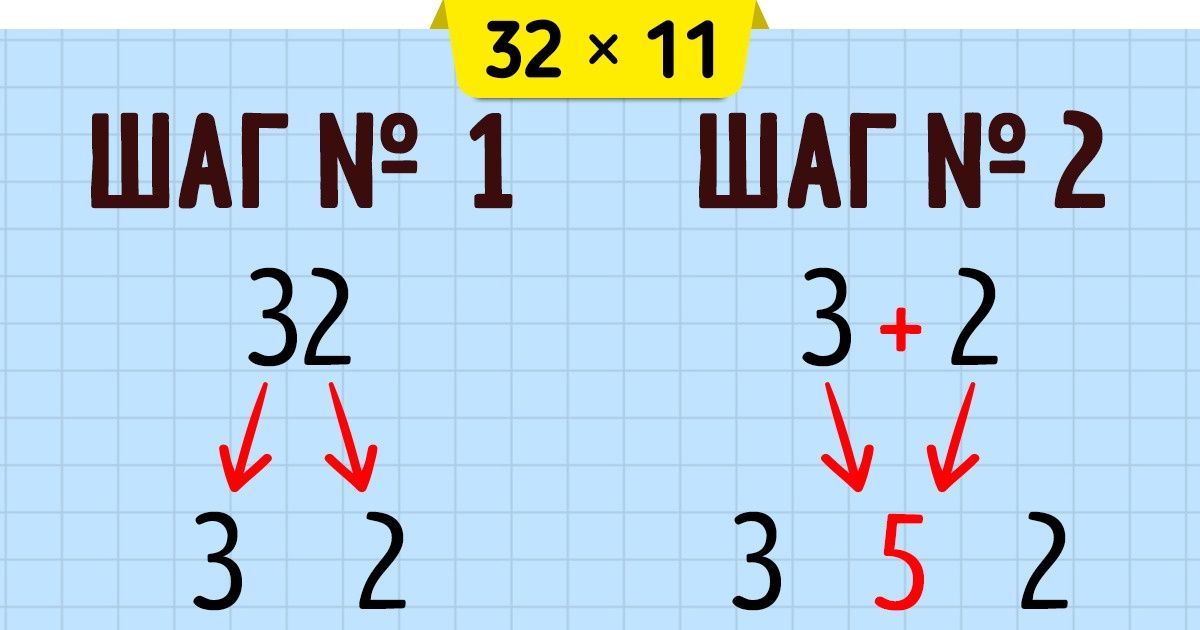 Однако и этому можно научиться, приложив достаточно усилий, тем более если подобрать правильный алгоритм. Очевидно, что легче всего умножать на круглые числа, поэтому самым простым способом является разложение чисел на множители.
Однако и этому можно научиться, приложив достаточно усилий, тем более если подобрать правильный алгоритм. Очевидно, что легче всего умножать на круглые числа, поэтому самым простым способом является разложение чисел на множители.
- Для начала следует разбить одно из данных двузначных чисел на десятки. Например, 48 = 4 × 10 + 8.
- Далее нужно последовательно перемножить сначала единицы, а потом десятки со вторым числом. Это достаточно сложные для выполнения в уме операции, так как нужно одновременно умножать числа друг на друга и держать в уме уже получившийся результат. Вероятнее всего, вам будет трудно справиться с этой задачей с первого раза, но, если быть достаточно усердным, этот навык можно развить, ведь понять, как правильно умножать двузначные числа в уме, можно только на практике.
Некоторые хитрости при умножении двузначных чисел
Но существует ли более легкий способ в уме умножать двузначные числа, и как это сделать?
Есть несколько хитростей. Они помогут вам легко и быстро умножать двузначные числа.
Они помогут вам легко и быстро умножать двузначные числа.
- При умножении на одиннадцать нужно просто поставить сумму десятков и единиц в середину данного двузначного числа. К примеру, нам понадобилось умножить 34 на 11.
Ставим 7 в середину, 374. Это и есть ответ.
Если при сложении получается число больше 10, то следует просто добавить единицу к первому числу. Например, 79 × 11.
- Иногда легче разложить число на множители и последовательно умножить их. Например, 16 = 2 × 2 × 2 × 2, поэтому можно просто 4 раза умножить исходное число на 2.
14 = 2 × 7, поэтому при выполнении математических операций можно умножить сначала на 7, а потом на 2.
- Для того чтобы умножить число на числа, кратные 100, например, 50 или 25, можно умножить это число на 100, а потом разделить на 2 или 4 соответственно.
- Еще нужно помнить, что иногда при умножении легче не складывать, а отнимать числа друг от друга.
Например, чтобы умножить число на 29, можно сначала умножить его на 30, а потом отнять от полученного числа данное число один раз. Это правило справедливо для любых десятков.
Это правило справедливо для любых десятков.
Как научить ребенка умножению быстро и легко, чтобы уже с начальных классов он хорошо решал разные математические задачи? Если вы хотите, чтобы ваш ребенок получал всестороннее развитие, без помощи ему не обойтись.
В наш век изобилия информации можно найти множество вспомогательных материалов – карточки, курсы в игровой форме, аудио- и видеопрограммы и многое другое, однако ни один из способов не является универсальным. Все дети по-своему уникальны, поэтому и подход к каждому нужен индивидуальный. В нашей статье мы предлагаем вам несколько способов освоения таблицы умножения. Изучив их, вы сможете подобрать наиболее эффективный для вашего ребенка.
Методов изучения таблички сейчас достаточно – нужно лишь подобрать самый подходящий для ребенка
Важный подготовительный момент
Когда дети начинают изучать таблицу умножения, они уже имеют представление о более простых арифметических действиях – сложении и вычитании. Теперь нужно объяснить им, в чем суть действия умножения. Ранее освоенные навыки помогут вам в этом.
Теперь нужно объяснить им, в чем суть действия умножения. Ранее освоенные навыки помогут вам в этом.
В чем заключается принцип умножения? Это многократное сложение. Например, чтобы умножить 4 на 3, нужно 3 раза сложить 4 (4+4+4). Освоив это, ребенок будет допускать меньше ошибок в дальнейшем процессе обучения.
Кроме того, дети должны понимать и то, как ориентироваться в устройстве таблицы. Нужно объяснить, что произведением является число на пересечении строки и столбца.
Начало
Большая таблица с множеством чисел может привести ребенка в уныние, если не совсем отбить желание учиться. По этой причине начинать лучше с самых простых примеров. Чтобы справиться с ними, не нужно прилагать больших усилий. К тому же ребенок сможет выполнить их самостоятельно, тогда часть работы будет уже проделана:
- Умножаем на 1. Любое число при этом остается тем же самым числом.
- Что нужно сделать, чтобы умножить на 10? Достаточно всего лишь в конце числа поставить 0.

- Умножение на 2 – это сложение двух одинаковых чисел. По крайней мере, с простыми числами дети уже умеют совершать такие действия, когда приступают к изучению умножения.
- Перемена множителей. Это так называемый переместительный (коммутативный) закон умножения. То есть, если переставить местами множители, произведение не изменится. Таким образом, получается, что нужно выучить лишь половину таблицы.
Как видите, картина становится более оптимистичной. Ребенок это тоже заметит и дальше будет работать с большим энтузиазмом, чем в начале.
Ребенок должен прежде всего понять, что умножение – это знакомое ему сложение, только многократное
Целенаправленное запоминание
После освоения самых простых значений можно продвигаться дальше. Чтобы справиться с более сложными множителями, понадобится подключить другие приемы – повторять, дробить на части, выстраивать ассоциации, применять знания на практике. Теперь уже для запоминания понадобится многократное повторение действий и значений.
Мнения педагогов расходятся в вопросе последовательности действий. Некоторые придерживаются методики, когда сначала осваиваются самые сложные примеры, а затем более простые. Практика же показывает, что такой способ годится далеко не для всех и часто может даже вызывать определенный стресс у учеников. Оптимальным вариантом считается научить их сначала более простым действиям и в конце – самым сложным. Чем это объясняется? При умножении небольших чисел (например, 3 на 3) ребенок может проверить себя на пальцах – в начале обучения это прием полезен. Если же сразу обязать детей запомнить произведение 8 на 9, то это будет просто механическое запоминание без применения на практике. Такая методика может запросто демотивировать.
Квадраты чисел
Новый этап в освоении таблицы умножения начинаем с квадратов чисел. Вывести квадрат числа – это значит умножить его на самое себя. Квадратов в таблице всего 10, запомнить их не так сложно (во многом это благодаря тому, что какие-то из них зарифмованы – например, «пятью пять – двадцать пять»). Квадрат 10 на 10 запомнить вообще ничего не стоит.
Квадрат 10 на 10 запомнить вообще ничего не стоит.
Чтобы ребенок действительно понял, а не только запомнил табличку, начинать изучение каждого ряда нужно с квадрата
Умножение на 3
Здесь уже дело обстоит немного сложнее. Если вы заметили, что ребенку не дается запоминание каких-то действий, проанализируйте его наклонности и подключайте те вспомогательные материалы, которые подойдут в вашем конкретном случае. Для многих детей идеально подходят карточки. В случае же с гуманитарным складом ума хорошо использовать уроки в стихотворной форме (об использовании специальных стихов для запоминания мы подробно расскажем в разделе ниже).
Умножение на 4
Здесь будет немного проще. Предложите ребенку попробовать самому логически выстроить то действие, и он наверняка догадается, что умножить на 4 – это то же самое, что 2 раза умножить на 2. Если же он будет затрудняться, вы легко объясните ему это. Карточки и стихи также будут полезны на данном этапе освоения материала.
Умножать на 5 также несложно, детям обычно нравится эта часть обучающего процесса. Во-первых, все значения этого умножения расположены друг от друга через 5 чисел. Во-вторых, заканчиваются они на 5 или на 0. В конце четных чисел, умноженных на 5, будет стоять 0, а нечетных – 5. Как видите, все просто.
Если рассмотреть произведения умноженных на 5 чисел, можно увидеть – все они заканчиваются на 5 или 0
Умножение на 6, 7, 8 и 9
Последний этап в освоении таблицы умножения – самый сложный, но состоит он из запоминания всего шести произведений. Чтобы хорошо их запомнить, придется потрудиться, ведь даже многие взрослые путаются с ответами.
Чтобы ребенку было проще, используйте карточки, причем не 6, а 12. С таким набором карточек вы сможете практиковаться с переменой мест множителей, а это значительно облегчит запоминание.
Игра с карточками
Обучение в виде игры для детей просто необходимо. Оно выполняет главную функцию – способствует возникновению интереса. Если ребенок заинтересуется процессом, это уже будет практически гарантией того, что он успешно его освоит.
Если ребенок заинтересуется процессом, это уже будет практически гарантией того, что он успешно его освоит.
Несмотря на то, что сейчас существует много более современных вспомогательных приспособлений и материалов (программы, онлайн-игры, звуковые плакаты и другие), обыкновенные карточки не теряют своей популярности. Они доступны всем и просты в применении. Если даже вы используете разные методики изучения таблицы умножения, карточки помогут вам на любом этапе.
Первым делом вам нужно распечатать карточки или нарезать и заполнить вручную. Желательно наклеить их на картон для лучшей сохранности в ходе эксплуатации. На каждой карточке нужно написать пример из таблицы умножения. Ответ писать не нужно.
В чем заключается сама игра? Поскольку подключать карточки вы будете с любого, даже самого раннего этапа обучения, то на каждое занятие нужно отбирать те примеры, которые соответствуют сегодняшнему плану. Затем карточки перемешиваются, и ребенок наугад вытаскивает любую из стопки. Ему нужно прочитать пример и назвать правильный ответ. После этого карточка откладывается в сторону и вытаскивается другая. Если ребенок ответил неправильно, карточка возвращается в стопку. При этом обязательно озвучивайте правильный ответ, чтобы ребенок его запомнил и ответил правильно, когда повторно вытащит эту карточку.
Ему нужно прочитать пример и назвать правильный ответ. После этого карточка откладывается в сторону и вытаскивается другая. Если ребенок ответил неправильно, карточка возвращается в стопку. При этом обязательно озвучивайте правильный ответ, чтобы ребенок его запомнил и ответил правильно, когда повторно вытащит эту карточку.
Для заблаговременного обучения малыша достаточно распечатать набор карточек
Преимущества такого простого процесса:
- Подключается зрительная память. Детям, особенно визуалам, будет гораздо легче выучить даже самые сложные примеры.
- Запоминание при таком подходе дается намного лучше. Осуществляется многократное повторение в диалоговой форме, а не простая зубрежка.
- Результат от проделанной работы ребенок видит сразу. У него появляется стимул быстрее закончить игру и выйти победителем, не оставив ни одной карточки в стопке. В таком игровом подходе можно устроить соревнование, подключив еще одного ребенка.

Другие приемы изучения
Чем больше приемов вы будете иметь в запасе, тем успешнее будет продвигаться процесс изучения вашим ребенком таблицы умножения. Разные способы можно применять не только в зависимости от склада ума детей, но и от уровня сложности конкретно взятого урока. Вам просто нужно постоянно анализировать ситуацию и ориентироваться в ней, тогда вы сможете доступно объяснить даже самый сложный пример, а ваш ребенок – быстро выучить его. Предлагаем вашему вниманию некоторые из таких приемов. Они ничуть не сложнее игры с карточками.
Примеры из практики
Чтобы найти наглядные примеры для обучения, не нужно далеко ходить – множество них находится рядом с вами в обычной повседневной обстановке. Проявите наблюдательность и немного пофантазируйте, тогда ваш ребенок сможет выучить таблицу умножения не только с легкостью, но и с большим интересом.
Сколько понадобится колесиков для 3 машинок? Сколько нужно посадить цветов на 3 клумбы, если на каждой их помещается 8? Сколько всего лапок у 4 плюшевых медведей? Как видите, вариантов множество. Можно предложить ребенку самостоятельно найти их или задавать задачи на умножение другу, беря примеры из домашней обстановки.
Можно предложить ребенку самостоятельно найти их или задавать задачи на умножение другу, беря примеры из домашней обстановки.
Отличная идея – обучать ребенка при помощи его же игрушек, бытовых предметов, сладостей и так далее
Примеры повышенной сложности
Более сложным примерам и тем, которые ребенку трудно даются, уделяйте максимум внимания. При этом не перегружайте детскую память – чередуйте простые и сложные. Когда увидите, что материал освоен, переходите к другому. Не старайтесь выложить сразу всю информацию для запоминания, разделите ее на несколько подходов.
Умножение на пальцах
Пользуясь этим приемом, можно освоить всю таблицу умножения, но наиболее популярным в этом случае является умножение на 6, 7, 8 и 9. Использовать его можно дополнительно на любых уроках, но имейте в виду, что прежде чем показывать такую игру ребенку, вам нужно самому хорошо разобраться и выучить ее принцип.
На стол кладем бумагу, сверху – руки пальцами горизонтально друг к другу. Обводим контуры рук и нумеруем пальцы таким образом: большой – 5, указательный – 6, средний – 7, безымянный – 8, мизинец – 9. Эти контуры пригодятся, когда мы будем смещать руки в ходе процесса. Теперь выбираем пример, который нужно решить: пусть это будет умножение 7 на 8. Средний палец левой руки будет обозначать 7, а безымянный правой – 8. Их нужно соединить и сдвинуть руки к краю стола. Пальцы перед соединенными, которые при этом свесятся вниз, будут обозначать десятки, а все остальные пальцы, которые останутся лежать на столе – единицы. Теперь считаем. Пальцев внизу 5 – значит, десятков 5. Пальцы же, которые лежат на столе, нужно перемножить. На левой руке их 3, а на правой – 2. Теперь 3 умножаем на 2 – получаем 6 единиц. Ответ – 56.
Обводим контуры рук и нумеруем пальцы таким образом: большой – 5, указательный – 6, средний – 7, безымянный – 8, мизинец – 9. Эти контуры пригодятся, когда мы будем смещать руки в ходе процесса. Теперь выбираем пример, который нужно решить: пусть это будет умножение 7 на 8. Средний палец левой руки будет обозначать 7, а безымянный правой – 8. Их нужно соединить и сдвинуть руки к краю стола. Пальцы перед соединенными, которые при этом свесятся вниз, будут обозначать десятки, а все остальные пальцы, которые останутся лежать на столе – единицы. Теперь считаем. Пальцев внизу 5 – значит, десятков 5. Пальцы же, которые лежат на столе, нужно перемножить. На левой руке их 3, а на правой – 2. Теперь 3 умножаем на 2 – получаем 6 единиц. Ответ – 56.
Теперь умножение на 9. Положите руки рядом на стол, чтобы пальцы располагались вертикально. Каждый палец нужно пронумеровать от 1 до 10 слева направо. Можно сделать это на бумаге, чтобы не запутаться. Мизинец левой руки – это 1, а мизинец правой – 10. Теперь загибаем палец с числом, которое хотим умножить на 9. Например, это будет 5. Пальцы слева от него будут десятками, а справа – единицами. Ответ – 45.
Теперь загибаем палец с числом, которое хотим умножить на 9. Например, это будет 5. Пальцы слева от него будут десятками, а справа – единицами. Ответ – 45.
Изучение таблицы умножения при помощи рифмы (стихотворений)
Этот прием запоминания относится к мнемотехническим. В приемах мнемотехники абстрактные понятия заменяются представлениями, основанными на каком-либо чувственном восприятии (в данном случае – аудиальном). То есть такой прием является по большей часть психологическим.
Этот способ запоминания информации любят все дети, независимо от склада ума и характера. Почему? Рифма хорошо и быстро запоминается, стихотворения живописно иллюстрируют содержание и учить короткие веселые стишки куда более интересно, чем механически зубрить пусть даже несложные примеры.
Однако основывать на этом приеме весь процесс не стоит, иначе вы рискуете перегрузить память ребенка излишним заучиванием. Мы бы порекомендовали использовать его в наиболее сложных случаях, чтобы снять напряжение и добавить в процесс элемент игры. При желании можно даже подключить картинки, иллюстрирующие какой-либо пример в стихах.
При желании можно даже подключить картинки, иллюстрирующие какой-либо пример в стихах.
Найти стихотворную таблицу умножения несложно, существует несколько вариантов разных авторов. Мы приведем примеры задач, которые обычно вызывают затруднения у всех. Некоторые примеры из книги Александра Усачева «Таблица умножения в стихах»:
- 6 х 9: Нам не жалко булок. Рот откройте шире: Шестью девять будет – Пятьдесят четыре.
- 7 х 8: Раз олень спросил у лося: – Сколько будет семью восемь? – Лось не стал
в учебник лезть: – Пятьдесят, конечно, шесть! - 8 х 9: Восемь медведей рубили дрова. Восемью девять – семьдесят два.
Красиво два на семь умножить
Февральский праздник нам поможет,
День всех влюбленных, помню я,
ЧЕТЫРНАДЦАТОГО, друзья!
Сколько будет дважды восемь,
Десятиклассников мы спросим.
Они подскажут нам ответ,
Ведь им уже ШЕСТНАДЦАТЬ лет!
Также возможны музыкальные распевки, которые особенно помогут ребенку с хорошим аудиальным восприятием.
Прежде чем отправлять материал для публикации, убедитесь, что он соответствует правилам
- Материал должен быть авторским и уникальным. Материал должен иметь текстовое наполнение. Это значит, что автором материала должны являться именно Вы, и он нигде не должен быть опубликован ранее на других сайтах. Публикация чужих материалов (в том числе переработка чужих произведений) без предварительного согласия их авторов запрещается и администрация сайта, не несет ответственности за публикацию таких материалов. Также запрещается публикация фотокопий (фото/скан версия своих произведений, PrintScreen изображений своих произведений).
- В случае обнаружения нарушения авторских прав (плагиата) опубликованный материал удаляется с сайта до выяснения обстоятельств.
- После добавления материала на наш сайт, Вы не имеете права добавлять этот же материал на другие сайты. В противном случае этот материал будет удалён с нашего сайта.
- Отправляя материал на сайт, Вы безвозмездно, без требования авторского вознаграждения, передаете администрации сайта права на использование материалов в коммерческих или некоммерческих целях, в частности, право на воспроизведение, публичный показ, перевод и переработку произведения, доведение до всеобщего сведения – в соотв.
 с ГК РФ (ст. 1270 и др.). Ни при каких обстоятельствах администрация сайта не несет обязательств по выплате в чью-либо пользу какого-либо вознаграждения за опубликованные материалы. Ни при каких обстоятельствах и условиях администрация сайта не несет ответственности за косвенные или побочные убытки либо за упущенную выгоду и неполученные доходы, связанные с публикацией авторских материалов.
с ГК РФ (ст. 1270 и др.). Ни при каких обстоятельствах администрация сайта не несет обязательств по выплате в чью-либо пользу какого-либо вознаграждения за опубликованные материалы. Ни при каких обстоятельствах и условиях администрация сайта не несет ответственности за косвенные или побочные убытки либо за упущенную выгоду и неполученные доходы, связанные с публикацией авторских материалов. - Копирование материалов, опубликованных на сайте, не допускается.
- Всю ответственность за опубликованные материалы и содержащиеся в них сведения несут их авторы. Администрация сайта не несет ответственности за содержание опубликованных работ и нарушение авторских прав. Администрация сайта не несет ответственности за дальнейшую судьбу материалов после их опубликования.
- Авторы публикуемых материалов дают согласие и заявляют о том, что администрация сайта не обязана изучать или оценивать предоставленные к обнародованию авторские материалы, или безошибочность указанных материалов.

- Администрация сайта вправе удалить тот или иной материал в любой момент по своему усмотрению или требованию пользователей сайта. Администрация сайта не обязана вступать в переписку или комментировать свои действия.
- Отправка материала на публикацию означает полное принятие настоящих правил.
С детства знакомая песенка «2х2=4» вызывает улыбку у взрослых. Сразу вспоминаются школьные годы и таблица умножения, которая многим давалась с большим трудом. Сейчас ничего не изменилось и детям тоже приходится учить таблицу. Существует много методик изучения таблицы умножения, некоторые даже обещают выучить табличку за несколько минут.
Как выучить таблицу умножения за 5 минут – грамотный подход
С чего начинаем изучать таблицу? С основ и сначала придется объяснять ребенку, как умножать число на число. То есть перед тем, как приступить к зубрежке таблицы, необходимо понимать принцип умножения.
Объясняем ребенку, что простой пример 2 умножить на 3 это значит, цифру 2 нужно сложить 3 раза. И показываем понятный ему пример, записываем так: 2+2+2=6. Объясняя суть умножения. Если ребенку трудно понять, почему этот пример записывается как 2х3=6, тогда берем счетные палочки, семечки, конфеты, вишенки и т.д. и при помощи этих предметов показываем пример на умножение.
И показываем понятный ему пример, записываем так: 2+2+2=6. Объясняя суть умножения. Если ребенку трудно понять, почему этот пример записывается как 2х3=6, тогда берем счетные палочки, семечки, конфеты, вишенки и т.д. и при помощи этих предметов показываем пример на умножение.
Если ребенок это усвоил, тогда можно переходить к следующему этапу, собственно, изучению таблицы.
Какую таблицу умножения проще выучить?
Учителя старой закалки утверждают, что таблица, которая сейчас представлена на обратной стороне тетрадки в виде столбиков, не подходит для первого знакомства. Ее можно просто выучить, но не понимать, как пользоваться. А настоящая таблица, которая открывает все возможности умножения, это таблица Пифагора. Она и была размещена на каждой тетрадке в советские годы. Такой таблицей пользовались наши мамы и бабушки.
Числа в табличке расположены симметрично и ребенок, даже не задумываясь, будет искать симметрию и быстро найдет нужный ответ.
И еще, если ребенок увидел и понял принцип, как пользоваться табличкой-подсказкой, то ему нужно будет выучить только половину таблицы. Потому что оставшаяся часть – это повторение выученного материала. И еще, столбики и примеры обычной таблицы иногда отвлекают и школьник может запутаться, зачем нужна лишняя информация. Он может выучить таблицу по порядку, но пользоваться выученным материалом вразброс – задача не из легких.
Потому что оставшаяся часть – это повторение выученного материала. И еще, столбики и примеры обычной таблицы иногда отвлекают и школьник может запутаться, зачем нужна лишняя информация. Он может выучить таблицу по порядку, но пользоваться выученным материалом вразброс – задача не из легких.
Как выучить таблицу умножения за 5 минут
Таблицу на 2 и на 10 легко выучить даже за 5 минут! Тут важно показать ребенку, чтобы он понял принцип умножения, а дальше простая математика. Например, чтобы умножить число на 10, нужно сложить его столько же раз, то есть, 10 раз. И так далее. А чтобы получить ответ, необходимо просто добавить к полученной цифре 0 и сказать полученный ответ. Дети, закончившие первый класс, уже прекрасно считают в пределах 100 и смогут перевести единицу в десятки.
Как легко выучить таблицу на 2? Сделать это можно буквально за 5 минут. Ребенок уже знает, как складывать одинаковые числа, нужно только объяснить ему принцип и отработать усвоенный материал.
Выучили табличку на 2? Смело переходим к цифре 4, а таблицу на 3 отложим на потом. Ребенок запомнит быстрее таблицу на 4, если ему объяснить, что это такая же табличка, как на 2, только все ответы нужно удваивать. Если 2х2=4, то 2х4=8 и т.д. Умножили на 2, получили ответ, потом результат умножили еще раз на 2.
Умножение на 3 иногда дается тяжелее, чем вся таблица, поэтому поможет простая считалочка:
Как выучить таблицу умножения. Легкий способ
Таблица умножения на 5 учится также легко, как на 2 и на 10. Простые ответы, счет в пределах 5. Маленькая подсказка: если умножается четное на нечетное, ответ – всегда нечетное на 0. Например, 5 умножить на 2 будет 10, на 4 будет 20, на 6 будет 30. И наоборот, если четное умножили на 5, получили в ответе число, заканчивающееся на эту цифру: 5 на 3 = 15 и т.д.
После таблицы на 5 сразу перескочите на изучение таблички на 9. А учить таблицу легко при помощи пальчиков. Когда освоите эту цифру, легко дадутся все остальные: таблица на 6,7 и 8. Ребенку нужно просто объяснить, что он уже знает ответы на эти примеры, только они записаны наоборот. Если 2 на 8 будет 16, то и 8 на 2 тоже будет 16.
Ребенку нужно просто объяснить, что он уже знает ответы на эти примеры, только они записаны наоборот. Если 2 на 8 будет 16, то и 8 на 2 тоже будет 16.
Теперь вы знаете, как быстро выучить таблицу умножения, а мы советуем не спешить, не заставлять ребенка делать то, чего он не хочет, заниматься в удовольствие всегда и везде, даже на отдыхе и транспорте, превратив уроки в игру. Удачи!
Быстрый устный счет. Часть 1. Сложение и вычитание «в уме» двузначных чисел.
Репетиторы ❯ Математика ❯ Быстрый устный счет. Часть 1. Сложение и вычитание «в уме» двузначных чисел.
Автор: Лидия В., онлайн репетитор по математике
●
30.03.2012
●
Раздел: Математика
Поражали ли тебя когда-нибудь люди, которые с легкостью складывают и умножают в уме трехзначные числа или мгновенно называют корень из 729?
На самом деле это не так сложно как кажется, просто здесь как и в любом мастерстве нужны знание техники и регулярные тренировки. Ну что же, тренировки зависят только от тебя, а технику мы сейчас разберем.
Ну что же, тренировки зависят только от тебя, а технику мы сейчас разберем.
Начнем со сложения двузначных чисел.
Пусть нам необходимо вычислить 37 + 85 + 29 + 42. Для этого сначала сложим все десятки: 3 + 8 + 2 + 4. Заметим, что 8 + 2 = 10, 3 + 4 = 7, вместе 17. Запомнили. Теперь складываем единицы: 7 + 5 + 9 + 2 = 23.
17 десятков – это 170. 170 + 23 = 193. Как видим, это быстрее, чем складывать 37 и 85, потом добавлять 29 и т.д.
Кстати, точно так же можно делать, если мы складываем трехзначные числа.
Например: 228 + 39 + 485 + 91.
Складываем десятки:
22 + 3 + 48 + 9 = (22 + 48) + (3 + 9) = 70 + 12 = 82.
Теперь складываем единицы:
8 + 9 + 5 + 1 = (8 + 5) + (9 + 1) = 13 + 10 = 23.
(Если два числа в сумме дают десять, их всегда удобно сложить первыми).
Ну и теперь 82 десятка, т.е. 820 плюс 23 будет 843.
Теперь перейдем к более интересной теме – умножению двухзначных чисел. Тут мы тоже будем поступать необычно. Прием который мы сейчас рассмотрим называется умножение «крестиком» или индусский способ умножения.
Прием который мы сейчас рассмотрим называется умножение «крестиком» или индусский способ умножения.
Мы хотим умножить 76 на 28. Поступаем следующим образом:
Сначала перемножим единицы: 6 · 8 = 48,
теперь умножаем «крестиком» 7 · 8 + 2 · 6 = 56 + 12 = 68 десятков, и с учетом 4 десятков из числа 48, имеем 72 десятка и 8 единиц или 720 и 8. Теперь перемножим сотни: 7 · 2 = 14 сотен или с учетом 7 сотен из числа 720 имеем 21 сотню, 2 десятка и 8 единиц. Ответ: 2128.
Мы рассмотрели способ, который подходит для любых двузначных чисел, но часто вычисления можно упростить, заметив определенные особенности наших множителей.
Например, в нашем случае 76 это ни что иное как 75 + 1.
Тогда: 28 · 76 = 28 · (75 + 1) = 28 · 75 + 28 = 28 · (50 + 25) + 28 = 28 · 50 + 28 · 25 + 28 = 2800/2 + 1400/2 + 28 =
= 1400 + 700 + 28 = 2128
Конечно, мы не расписываем все эти вычисления, а производим их в уме. Они, как и рисунок с крестиком приведены для того, чтобы показать алгоритм умножения.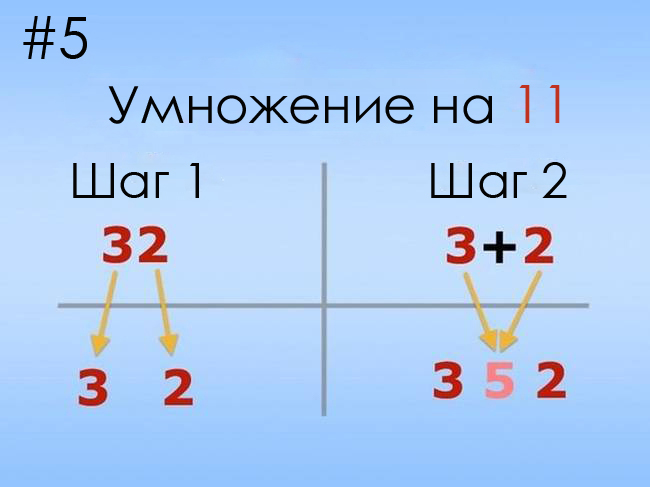 На самом деле все вычисления проводятся «в уме». Да, вначале вычисления по этому методу могут показаться сложными, но мы не забываем о второй составляющей успеха – практике. Немного тренировки и все получится!
На самом деле все вычисления проводятся «в уме». Да, вначале вычисления по этому методу могут показаться сложными, но мы не забываем о второй составляющей успеха – практике. Немного тренировки и все получится!
Ну а для любознательных «теоретиков» мы покажем каким образом был изобретен данный метод.
Рассмотрим умножение двух двузначных чисел в общем виде: умножим ab на cd.
Мы всегда можем записать ab как a · 10 + b, а cd как c · 10 + d. Тогда:
(a · 10 + b)(c · 10 + d) =
= 100 · a · c + 10 · a · d + 10 · b · c + b · d =
= a · c · 100 + (a · d + b · c) · 10 + b · d
Из результата умножения видно, что для того, чтобы получить сотни необходимо перемножить первые цифры наших числе, чтобы получить десятки – перемножаем их крестиком и складываем, ну и наконец умножение последних цифр даем нам число единиц.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
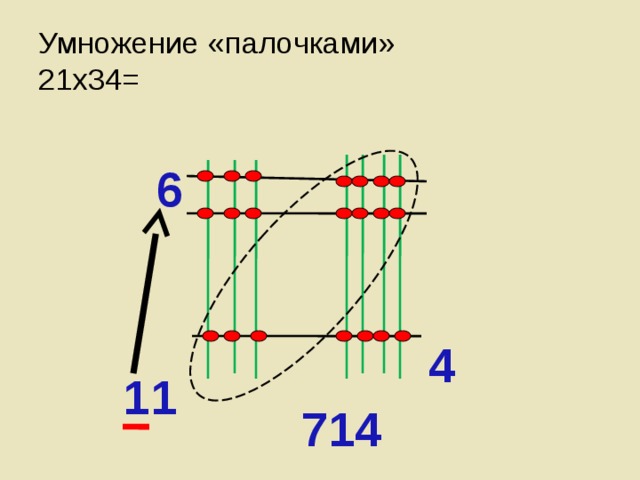
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
Умножение на двузначные числа — Подход к ментальной математике
Уловки с ментальной арифметикой, чтобы стать человеком-калькулятором
Техника умножения на двузначные числа, описанная в этом разделе, вдохновлена ведической математикой. Этот трюк поможет вам умножить любое двузначное число в уме. Это обобщенный подход, вы можете получить решение еще до того, как узнаете его. То есть, применяя метод умножения на двузначное число, описанный в этом посте, вы можете вычислить результат слева направо.
Этот трюк поможет вам умножить любое двузначное число в уме. Это обобщенный подход, вы можете получить решение еще до того, как узнаете его. То есть, применяя метод умножения на двузначное число, описанный в этом посте, вы можете вычислить результат слева направо.
Эта техника отличается от того, чему мы научились в детстве. В этом вам нужно умножать двузначное число справа налево, что включает в себя запоминание или запись переноса. Это значительные накладные расходы в подходе к ментальной математике. Умножение на 2-значное число с использованием подхода слева направо, вы можете вычислить произведение в уме, не беспокоясь о переносе.
К концу этого поста вы научитесь следующим трюкам
- Умножение 2 цифр на 1 цифру
- Умножение 2 цифр на 2 цифры
В следующем уроке по умножению трех цифр мы расширили прием умножения двух цифр из этого урока и использовали его для умножения 3 цифр на 2 цифры.
Умножение на двузначные числа – Видео
Подход к умножению трехзначных чисел объясняется в видеороликах ниже с помощью двух примеров. В первом примере основное внимание уделяется умножению двузначных чисел без переноса, а во втором — с переносом.
В первом примере основное внимание уделяется умножению двузначных чисел без переноса, а во втором — с переносом.
Пример 1
Пример 2
Умножение на 2 цифровых числа – подход
Как объясняется в видео выше, мы собираемся использовать версии и перекрестный умножать двузначные числа. Этот метод помогает нам легко умножать двузначные числа в уме. Мы рассмотрим этот трюк с умножением, разделив подход к умножению на двузначные числа на следующие разделы:
Этот метод помогает нам легко умножать двузначные числа в уме. Мы рассмотрим этот трюк с умножением, разделив подход к умножению на двузначные числа на следующие разделы:
- Как умножать два двузначных числа
- Как умножать двузначные числа на однозначные числа
Умножение двухзначных чисел на двузначные
Давайте изучим метод умножения двузначных чисел слева направо. Обратите внимание, что описанный здесь метод двузначного умножения также может быть рассчитан справа налево. Но мы рекомендуем делать это слева направо, так как идея изучения этих трюков состоит в том, чтобы помочь улучшить наши навыки счета в уме. Прежде всего, умственный расчет — это расчет слева направо.
Итак, ниже приведен метод умножения двух цифр, объясненный с помощью двух примеров. Подход, показанный в этих примерах, можно использовать для умножения любого двузначного числа.
Пример 1: Умножение 21 и 32
- Чтобы выполнить умножение на 2 цифры, разделим решение на 3 части.
 Количество частей здесь получается как 2x$n$-1, где $n$ представляет значение в n-разрядном умножении. В случае двузначного умножения n равно 2. Следовательно,
Количество частей здесь получается как 2x$n$-1, где $n$ представляет значение в n-разрядном умножении. В случае двузначного умножения n равно 2. Следовательно,
21
x 32
————————
? | ? | ?
- Самая левая часть получается путем умножения крайних левых цифр 2 из 21 и 3 из 32 => 2×3 = 6
21
x 32
————————
6 | ? | ?
- Средняя часть получается путем перекрестного умножения первых двух цифр 2 и 2 и 1 и 3 с последующим сложением соответствующих произведений => 2×2 + 1×3 = 7
21
x 32
—— ——————
6 | 7 | ?
- Самая правая часть получается путем умножения самых правых цифр в обоих числах => 1×2 = 2
21
x 32
————————
6 | 7 | 2
- Таким образом, результат умножения двузначных чисел 21 и 32 равен 672.
Пример 2: Произведение 76 и 53 53, предварительно разделив раствор на три части.
76
x 53
————————
? | ? | ?
- Большая левая часть получается путем умножения цифр десятков 7 в 76 и 5 в 53=>7×5=35
76
x 53
————————
35 | ? | ?
- Средняя часть получается путем перекрестного умножения 7 и 3, 6 и 5 и сложения соответствующих значений => 7×3+6×5=21+30=51
76
x 53
——— —————
35 | 51 | ?
Примечание. За исключением левой части, все остальные части должны содержать только одну цифру, лишняя цифра, если таковая имеется, будет перенесена влево. Следовательно, избыток 1 из 51 будет перенесен в левую часть. Таким образом:
За исключением левой части, все остальные части должны содержать только одну цифру, лишняя цифра, если таковая имеется, будет перенесена влево. Следовательно, избыток 1 из 51 будет перенесен в левую часть. Таким образом:
76
x 53
————————
35 | 51 | ?
=> 40 | 1 | ?
- Правая часть получается путем умножения самых правых цифр в обоих числах => 6×3 = 18
76
x 53
————————
40 | 1 | 18
=> 40 | 2 | 8
- Итак, мы вычислили результат умножения двузначных чисел 76 и 53 без использования калькулятора.
Как умножать двузначные числа на однозначные числа
Теперь давайте изучим подход слева направо к умножению двузначного числа на однозначное число.
Если AB является двузначным числом, которое нужно умножить на однозначное число, скажем, C. Затем подход слева направо к двузначному умножению на однозначное выполняется путем умножения A на C, а затем B на C.
A B
x C
————
=====>
Во время этого процесса умножения, если произведение B и C дает более 1 цифры, лишняя цифра будет перенесена влево.
Пример: произведение 46 и 7
В 46 x 7 сначала умножьте крайнюю левую цифру 4 в 46 на 7 => 4×7 = 28
4 6
x 7
————–
28 | ?
Теперь умножьте цифру единиц 6 на 7: 6×7 = 42, а затем перенесите лишние 4 влево. Таким образом, 28 становится 32. Следовательно, мы имеем 46 x 7 = 322
4 6
x 7
————–
28 | 42
=> 32 | 2
Проверьте свое понимание
арифметика – Какой самый быстрый способ умножить двузначные числа?
Спросил
Изменено 6 лет назад
Просмотрено 51k раз
$\begingroup$
В последнее время я играл в различные математические игры на своем Android (например, в Math Cruncher).
Я заметил, что не могу быстро (менее 7-8 секунд) умножить двузначные числа (т.е. 18$ * 17$). Итак, мой вопрос: как быстрее всего умножать двузначные числа?
- арифметика
- ментальная арифметика
$\endgroup$
11
$\begingroup$
Как я это выучил:
$$\begin{array}{rrl} & 18 & \\ \раз & 17 & \\ \hline & 156 & (10\умножить на 10 + 8\умножить на 7) \\ + & 70 & (10\умножить на 7) \\ + & 80 & (10\умножить на 8) \\ \hline = & 306 &\\ \hline \end{array}$$
Всего:
$$\begin{массив}{rrl} & {\гм АВ} & \\ \times & {\rm CD} & \\ \hline & {\rm ACBD} & \text{(добавить 0, если необходимо)} \\ + & {\ гм до н.э.} 0 & \\ + & {\ rm AD} 0 & \\ \hline \end{array}$$
Это просто деление на многочлен: $(10+7)\times (10+8)$. И это позволяет мне визуализировать легче, чем традиционный метод.
$\endgroup$
1
$\begingroup$
Самый быстрый способ умножать двузначные числа — это уже знать результат, выучив таблицу умножения двузначных чисел точно так же, как вы выучили таблицу умножения однозначных чисел. Конечно, это означает много работы впереди.
$\endgroup$
$\begingroup$
Мой метод умножения некоторых двузначных чисел не будет работать хорошо во всех случаях, и его недостатком является то, что вы должны запомнить все квадраты. Но я представляю это просто как еще один трюк, которому вы можете научиться. Я добавил +1 к ответу FiniteA, так как это кажется хорошим способом, который хорошо работает практически в любом случае и требует очень небольшого запоминания или навыков, т. Е. Он сводит его к простейшим частям. 92=2500$ и, следовательно, 50*42=2500-400$.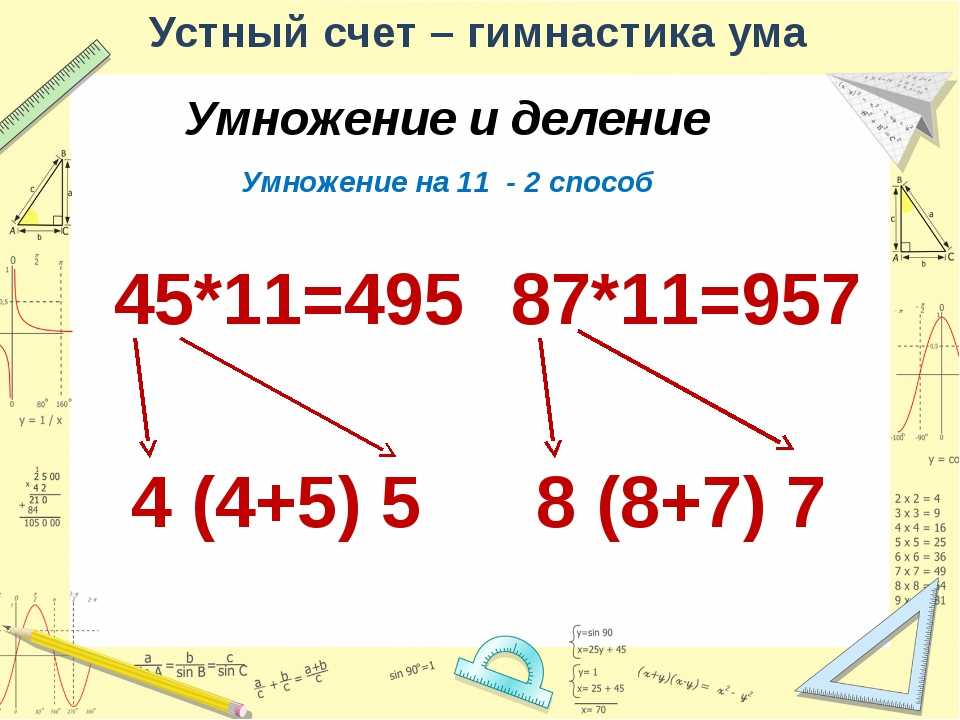
(2) Как правило, округляйте в большую или меньшую сторону до ближайшего числа, кратного 10$, а затем исправьте: например, вычислите 93*42=100*42-7*42$. Это особенно полезно, если вам не нужно точное значение — тогда вы очень быстро получите хорошее приближение. Единственный выбор, который вам нужно сделать здесь, — это округлить одно из двух чисел, и вы должны сделать это, чтобы максимизировать результирующее упрощение. В выбранном мной примере лучше округлить 93$ до 100$, так как умножить на 100$ немного проще, чем умножить на 40$.
(3) Когда вы начнете считать в уме с большими числами, вы поймете, что главное препятствие — не скорость, а пространство: вы столкнетесь с проблемой, что не можете надежно хранить в голове больше нескольких цифр за раз . Чтобы преодолеть это, вам понадобится мнемоника. Один относительно безболезненный способ описан в книге Арта Бенджамина «Секреты ментальной математики: руководство математика по молниеносным вычислениям и удивительным математическим трюкам»: превращайте числа в фразы, стихи, рассказы или песни!
$\endgroup$
1
$\begingroup$
Уловка калькулятора в уме состоит в том, чтобы начать слева:
$$
\начать{массив}{г}
17\\
\ раз 18
\конец{массив}
$$
$$
\begin{массив}{с л}
\text{‘перекрестное’ вычисление} &\text{ частичный результат}\\
1\cdot 1=1 и 1\\
1\cdot 8+7\cdot 1=15 и 25\\
7\cdot 8=56 &306
\конец{массив}
$$
Другой пример
$$
\начать{массив}{г}
237\\
\ раз 543
\конец{массив}
$$
$$
\begin{массив}{с л}
\text{‘перекрестное’ вычисление} &\text{ частичный результат}\\
2\cdot 5=10 и 10\\
2\cdot 4+3\cdot 5=23 и 123\\
2\cdot 3+3\cdot 4 +7\cdot5=53 &1283\\
3\cdot 3+7\cdot 4=37 и 12867\\
7\cdot 3=21 и 128691\\
\конец{массив}
$$
Тот же трюк (работа слева направо) используется для других операций. Аккуратно и быстро!
Аккуратно и быстро!
$\endgroup$
$\begingroup$
На You Tube есть очень хорошие видео на эту тему. Вот один из них:
Быстрые математические трюки – Как быстро умножить двузначные числа до 100!
$\endgroup$
$\begingroup$
Я разбиваю одно из чисел на 10, так что это разбивается на 3 простых умножения.
$$\begin{выравнивание} &18 \умножить на 17 = 18 \умножить на 10 + 18 \умножить на 7\\ &18 х 7 = 7 х 10 + 7 х 8. \end{align}$$
По этой логике $$ 18 х 17 = 18 х 10 + 7 х 10 + 8 х 7. $$
Потребуется несколько попыток, чтобы уложить в голове схему, но у меня работает!
$\endgroup$
$\begingroup$
Ребята, вы слишком усердствуете. Просто выучите один раз две цифры внутри и снаружи, а затем сделайте это. 69 * 89. Получаем 6*89 = 534. Прибавляем это к первым двум цифрам 9*89 = 801. Делаем так: 534 + 80 = 614. Приклеиваем 1 к концу. Получаем 6141. Это должен быть лучший способ, так как я химик с низким уровнем жизни, но могу сделать это за секунды (без карандаша или ручки). Присоединяйтесь к клубу сейчас, мое последнее предложение. 92 + N(a’+b’) + a’\times b’ = N\times(a +b’)+a’\times b’$$
69 * 89. Получаем 6*89 = 534. Прибавляем это к первым двум цифрам 9*89 = 801. Делаем так: 534 + 80 = 614. Приклеиваем 1 к концу. Получаем 6141. Это должен быть лучший способ, так как я химик с низким уровнем жизни, но могу сделать это за секунды (без карандаша или ручки). Присоединяйтесь к клубу сейчас, мое последнее предложение. 92 + N(a’+b’) + a’\times b’ = N\times(a +b’)+a’\times b’$$
В этом случае, принимая $N = 20$, получаем:
$18\times 17 = 20\times(18-3) + 6 = 306$$
Другие примеры:
$$984\times 993 = 1000\times(984-7) + 16\times 7 = 977112 $$
$$\begin{split}9876\times 9913 &= 10,000\times(9876-87)+ 124\times 87 \\&=97,890,000+100\times(124 – 13) – 24\times 13\ \ &=97,901,100 – 20\х(24-7)+4\х7\\ &=97 901 100 – 340 +28\\ & = 97 900 788 \end{split}$$
$\endgroup$
Предварительное исчисление по алгебре. Какой метод мысленного вычисления двузначных задач на умножение сводит к минимуму количество мысленных шагов?
Спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 717 раз
$\begingroup$
В последнее время я много практиковался в ментальной арифметике и, конечно же, как часть этого, умножая двузначное число на другое двузначное число. Я провел некоторое исследование того, какой самый быстрый способ вычислить результат такого умножения, но я все еще обнаруживаю, что мне приходится выполнять слишком много шагов в голове для каждого упражнения. Цель состоит в том, чтобы кто-то рассказал вам задачу, а затем, не заставляя повторять задачу, вычислить ответ.
Я провел некоторое исследование того, какой самый быстрый способ вычислить результат такого умножения, но я все еще обнаруживаю, что мне приходится выполнять слишком много шагов в голове для каждого упражнения. Цель состоит в том, чтобы кто-то рассказал вам задачу, а затем, не заставляя повторять задачу, вычислить ответ.
Возьмем в качестве примера: $63*88$
Я пройдусь по нескольким известным мне методам мысленного вычисления и объясню свои проблемы с каждым из них.
1) Элементарный метод. Я думаю, что это первый метод умножения, который все усваивают. Он находит ответ путем умножения и сложения грубой силы. Использование этого метода в нашем примере упражнения означало бы, что мы предпримем следующие шаги:
- Сначала упростим левый множитель и умножим его на полный правый множитель, получив:
60*88=60*80+60*8=4800+480=5280$
- Затем умножьте оставшиеся 3$ на наш правильный множитель и прибавьте его к результату выше, получив:
$3*88=264 \rightarrow 5280+264=5544$
Сразу становится понятно, что этот способ слишком долгий и может превратиться в довольно сложную кашу, ведь приходится быстро совмещать нетривиальное умножение и сложение. С помощью этого метода вы должны запомнить задачу, затем результат первого умножения, затем выполнить второе умножение и запомнить все результаты, чтобы сложить их вместе. Мы могли бы думать о каждом знаке «$=$» как об умственном шаге.
С помощью этого метода вы должны запомнить задачу, затем результат первого умножения, затем выполнить второе умножение и запомнить все результаты, чтобы сложить их вместе. Мы могли бы думать о каждом знаке «$=$» как об умственном шаге.
2) Второй метод исходит из ветви, называемой ведической математикой. На бумаге этот способ умножения выглядит более сложным, но после небольшой практики становится очевидным, что он намного быстрее. Это работает так:
- Сначала умножьте два самых правых числа друг на друга, получив:
$3*8=24$
- У нас есть $2$, а $4$ — это последняя цифра нашего окончательного ответа. Затем мы выполняем перекрестное умножение, при котором мы умножаем правую цифру второго множителя на левую цифру первого множителя и наоборот, и складываем результаты вместе (не забывая о переносимых $2$), что дает:
$8*6+8*3+2=48+24+2=74$
- Из этого мы видим, что наша предпоследняя цифра также равна $4$, и мы снова будем нести $7$.
 На последнем шаге мы умножаем левую цифру первого множителя на левую цифру правого множителя (не забывая о наших переносимых $7$). Это дает:
На последнем шаге мы умножаем левую цифру первого множителя на левую цифру правого множителя (не забывая о наших переносимых $7$). Это дает:
$6*8+7=48+7=55$
- Теперь мы знаем, что наши первые две цифры равны $5$ и $5$, что дает общий ответ $5544$
Опять же, на бумаге это выглядит как гораздо больше шагов, чем метод грубой силы, но гораздо проще отслеживать вещи, которые вы должны помнить для окончательного ответа.
3) Необязательный третий метод может быть похож на описанный выше метод, но вместо перекрестного умножения в качестве второго шага мы делаем его в качестве первого шага, а затем выполняем исходный первый шаг. Я бы предположил, что мнения о том, действительно ли это быстрее, разделились, но это помогает ограничить количество вычислений, которые нужно запомнить.
4) Наконец, стандартный метод может состоять в том, чтобы округлить один из множителей до ближайшего десятикратного, а затем вычесть любое добавленное вами превышение. В этом случае это даст:
В этом случае это даст:
$63*90=5670 \rightarrow 5670-2*63=5544$
Однако этот метод становится намного сложнее, когда мы пытаемся вычислить что-то вроде $44*86$, потому что округление до ближайших десяти оставляет нам гораздо больше лишнего.
Возможно, ответ на мой довольно общий вопрос прост: «быстрое умножение приходит с опытом». Тем не менее, мне очень любопытно услышать о любых других методах, которые существуют. Извиняюсь за длинный пост, но я надеюсь, что достаточно прояснил свой мыслительный процесс.
- алгебра-предварительное исчисление
- мягкий вопрос
- арифметика
- ментальная арифметика
$\endgroup$
1
$\begingroup$
Может быть, ответ на мой относительно общий вопрос прост: «быстрое умножение приходит с опытом».
Я действительно так думаю.
Все ваши методы работают, и по опыту вы узнаете, когда использовать простоту этих методов.
93$.$63 \times 11 = 693$
Следовательно,
$63 \times 88 = 693 \times 2\times 2 \times 2 = 1386 \times 2 \times 2 = 2772 \times 2 = 5544$
Я за это каждый раз, когда мне приходится умножать на степени 2 (2,4,8,16,…), потому что «$\times 2$» — это операция, которую ваш мозг использует с самого раннего возраста. Выполнение этого несколько раз иногда может быть быстрее, чем выполнение одного выстрела “$\times 16$” или “$\times 32$”.
Более того, здесь, когда вы закончите со степенями двойки, у вас останется 11, а «$\times 11$» также оказывается очень простой операцией над двузначными числами.
$\endgroup$
2
$\begingroup$
Для меня это зависит от того, почему я решаю задачу и требуемой точности. Если мне нужен точный ответ, я работаю слева направо, сначала выполняя наиболее значимое умножение. Я изменю ваш пример на $63*87$, чтобы мы могли различать все цифры. Я бы сначала сделал $6 * 8 = 48 $, затем $ 3 * 8 = 24 $ и добавил это к одной цифре, чтобы получить $ 480 + 24 = 504 $, затем $ 6 * 7 = 42 $ и добавил это к $ 504 + 42 = 546. $ и, наконец, $3 * 7 = 21 $ и добавьте это в один справа, получив $ 5460 + 21 = 5481 $. Если более низкая точность приемлема, вы можете остановиться на полпути (что более важно, если цифр больше — я могу отслеживать таким образом $4 \times 3$ на практике).
Если мне нужен точный ответ, я работаю слева направо, сначала выполняя наиболее значимое умножение. Я изменю ваш пример на $63*87$, чтобы мы могли различать все цифры. Я бы сначала сделал $6 * 8 = 48 $, затем $ 3 * 8 = 24 $ и добавил это к одной цифре, чтобы получить $ 480 + 24 = 504 $, затем $ 6 * 7 = 42 $ и добавил это к $ 504 + 42 = 546. $ и, наконец, $3 * 7 = 21 $ и добавьте это в один справа, получив $ 5460 + 21 = 5481 $. Если более низкая точность приемлема, вы можете остановиться на полпути (что более важно, если цифр больше — я могу отслеживать таким образом $4 \times 3$ на практике).
Для приблизительных значений я часто буду округлять и исправлять, поэтому я бы сделал $63*88\приблизительно 60*(1+0,05)*90*(1-0,02)\приблизительно 5400*(1+0,03)\приблизительно 5550$
Знание большего количества фактов помогает. Если вы знаете, что $3*37=111$, вы можете умножить $63*37=21*111=2331$. Если вы знаете, что $7 * 11 * 13 = 1001 $, это очень поможет, когда он появится. Говорят, что некоторые сценические калькуляторы просто знают таблицу умножения до $99*99$
$\endgroup$
3
$\begingroup$
Я надеюсь, что примера будет достаточно, чтобы показать общую картину. С практикой это очень выполнимо.
С практикой это очень выполнимо.
Если у вас хорошая память, вы можете умножить двузначное число на двузначное в уме. например, сделать
$$\begin{array}{r} 56 \\\times 78 \\\hline \end{array}$$
в уме.
$6 \х8$ равно $48$. Поместите $8$ и запомните $4$.
$$\begin{массив}{r} \цвет{красный} 4 \фантом{0} \\ 56\\ \times 78 \\\hline 8 \конец{массив} $$
$5\умножить на 8 + 7\умножить на 6 + 4 = 40 + 42 + 4 = 86$ Поместите $6$ и запомните $8$.
$$\begin{массив}{r} \цвет{красный}{84} \фантом{0} \\ 56\\ \times 78 \\\hline 68 \конец{массив} $$
Наконец, $5 \ умножить на 7 + 8 = 35 + 8 = 43$. Поместите $43$.
$$\begin{массив}{r} \цвет{красный}{84} \фантом{0} \\ 56\\ \times 78 \\\hline 4368 \конец{массив} $$
Если две цифры в строке или столбце совпадают, вы можете сократить путь. Например, чтобы умножить $63\times 88$.
$$\begin{массив}{r} 63 \\ \раз 88\\ \hline \end{массив} $$
$3\8 = 24$. Поместите $4$ и запомните $2$.
$$\begin{array}{r} \color{red}2 \phantom 0 \\ 63\\ \раз 88\\ \hline 4 \конец{массив} $$
$(6 + 3) \times 8 + \color{red} 2 = 74$. Поместите $4$ и запомните $7$.
$$\begin{array}{r} \color{red}{72} \phantom 0 \\ 63\\ \раз 88\\ \hline 44 \конец{массив} $$
$6 \times 8 + \color{red} 7 = 55$. Поместите $ 55 $.
$$\begin{array}{r} \color{red}{72} \phantom 0 \\ 63\\ \раз 88\\ \hline 5544 \конец{массив} $$
$\endgroup$
1
$\begingroup$
Чтобы ответить на этот вопрос, вы должны сделать очень большое количество предположений, лишь немногие из которых можно проверить. Например, вполне возможно, что мнемонисты могут запомнить всю таблицу умножения. В качестве альтернативы, часто первым шагом является какая-то классификация проблемы (9).0434 даже умножить на даже или сумма цифр, делящихся на 3 и т. д.), и очень трудно узнать, сколько шагов используется. Более того, некоторые задачи “тривиальны” ($20\times 20$ или $10\times x$ для любых $x$) и одним из предложенных хитрых приемов их не решить. Таким образом, будете ли вы количественно определять «ожидаемое» количество операций?
Например, вполне возможно, что мнемонисты могут запомнить всю таблицу умножения. В качестве альтернативы, часто первым шагом является какая-то классификация проблемы (9).0434 даже умножить на даже или сумма цифр, делящихся на 3 и т. д.), и очень трудно узнать, сколько шагов используется. Более того, некоторые задачи “тривиальны” ($20\times 20$ или $10\times x$ для любых $x$) и одним из предложенных хитрых приемов их не решить. Таким образом, будете ли вы количественно определять «ожидаемое» количество операций?
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. Ментальная арифметика
Ментальная арифметика. Есть ли простой способ умножить два двузначных числа, в которых цифры перевернуты?
Спросил
Изменено 3 года, 2 месяца назад
Просмотрено 1к раз
$\begingroup$
В настоящее время я учусь на втором курсе средней школы, участвующей в академических соревнованиях UIL в Техасе. Я участвую в тесте на чувство числа. Среди вопросов есть необходимость быстро умножить 2 двузначных числа, но, как и во всех вопросах, присутствующих в тесте, всегда есть более быстрый способ сделать что-то. Один тип вопросов, который повторяется в каждом тесте на каждом соревновании (я дошел до 3 до сих пор (:), — это необходимость умножить два двузначных числа вместе, цифры которых перевернуты по сравнению с другим числом (43 * 34). и 56*65). Мне было интересно, есть ли более быстрый способ сделать это, чем мысленно перемножить их. Спасибо за помощь!
и 56*65). Мне было интересно, есть ли более быстрый способ сделать это, чем мысленно перемножить их. Спасибо за помощь!
P.S. Если есть способ улучшить форматирование вопроса, было бы очень признательно, если бы вы сказали мне!
- ментальная арифметика
$\endgroup$
2
$\begingroup$
Предлагаю следующую наглядную схему.
Редактировать: прочитав другие ответы, я заметил, что у $\color{darkblue}{Arby}$ та же идея.
Чтобы умножить числа $\overline{ab}\times\overline{ba}$ 92$, но я думаю, что так проще сделать мысленно.
Добавление переноса может показаться пугающим, но на самом деле это происходит только для $73,77,85,88,94,95,96,98,99$ и их зеркал, во всех остальных случаях это простое добавление.
$\endgroup$
$\begingroup$
Пусть два числа равны $xy$ и $yx$, и мы хотим вычислить их произведение. Есть очень простая процедура.
Есть очень простая процедура.
$1.$ Умножьте обе цифры. 9{2}$$
101 несложно умножить, особенно если учесть, что в этом сценарии $a \times b$ никогда не будет более чем двузначным числом.
Если вы можете возвести в квадрат и поставить 0 на конце, вы справитесь с первой и последней частями.
Попробуем из вашего примера $56\times 65$. Это 250 + 360 + 3030 = 610 + 3030 = 3640 долларов.
Понял?
Существует всего 41 различная задача на двузначные числа, так что можно подумать и о запоминании. 9 из этих 41 на самом деле просто мысленно возводят в квадрат числа, кратные 11, до 9.2=9+49=58$, что на самом деле будет 580 (почему?). Вы добавили бы 21, получив 601. Затем снова используйте $3\times7=21$, но на этот раз вы получите 2100 (опять же, почему?). Прибавив 601, вы получите окончательный ответ 2701.
Этот метод хорошо обобщает. $ab\times cd=ac/(ad+cb)/bd$ Вы также можете вычислить формулы для большего количества цифр.
Редактировать: между прочим, еще один легко запоминающийся прием из ведической математики — умножение двух двузначных чисел с одинаковыми первыми цифрами и суммой последних цифр 10. В этом случае $ab\times ac$ — это просто первое число, умноженное на единицу больше, чем первое число, за которым следует произведение последних чисел (при необходимости с использованием нуля в разряде десятков). Легче показать, чем объяснить. $79\times 71=(7\times 8)+09=5609$, $24\times 26=(2\times 3)+24=624$, $65\times 65=(6\times 7)+25=4225$
В этом случае $ab\times ac$ — это просто первое число, умноженное на единицу больше, чем первое число, за которым следует произведение последних чисел (при необходимости с использованием нуля в разряде десятков). Легче показать, чем объяснить. $79\times 71=(7\times 8)+09=5609$, $24\times 26=(2\times 3)+24=624$, $65\times 65=(6\times 7)+25=4225$
$\endgroup$
2
$\begingroup$
Если вы, как и я, знаете все квадраты двузначных чисел, то вы можете сделать это так: $$36\times 63=36\times(100-36-1) = 3600-1296-36 = 2268 .$$
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Советы по умножению двузначных чисел в уме
Здесь я перечислил все известные мне методы умножения двузначных чисел, многие из которых можно использовать для этого в уме. Некоторые из них проще, чем другие, но для освоения всех требуется хотя бы некоторая практика.
Во-первых, большинство ответов состоят из четырех цифр, и расчеты часто включают сложение или вычитание из них. Один из способов сделать это — представить четырехзначное число как два двузначных числа. Например, я произношу число 8723 как «восемьдесят семь двадцать три». Затем, если я хочу добавить к этому, скажем, 315, я добавляю 3 к 87 и 15 к 23. Если кому-то удобно складывать или вычитать двузначные числа, это упрощает задачу.
При вычитании полезно знать «дополнение» числа , то есть где количество цифр числа . (Хотя это и не формальный термин, здесь он используется для удобства.) Например, дополнение 34 равно 66, а дополнение 330 равно 670. Это просто 9.минус каждая цифра или 10 минус последняя ненулевая цифра и все последующие нулевые цифры. Тогда эквивалентно добавлению и дополнению . Это полезно, если есть перенос. Например, чтобы сделать , найдите дополнение 56 как 44, затем выполните 12 – 4 – 1 (единица представляет собой перенос) для цифры сотен и 34 + 44 = 78 для остатка, чтобы получить 778.
Это просто 9.минус каждая цифра или 10 минус последняя ненулевая цифра и все последующие нулевые цифры. Тогда эквивалентно добавлению и дополнению . Это полезно, если есть перенос. Например, чтобы сделать , найдите дополнение 56 как 44, затем выполните 12 – 4 – 1 (единица представляет собой перенос) для цифры сотен и 34 + 44 = 78 для остатка, чтобы получить 778.
Если удвоить трех- или четырехзначное число помогает рассматривать число как удобную группу цифр. Например, чтобы удвоить 4567, я бы удвоил 67 (134), затем добавил перенос 1 к удвоенному 45, чтобы получить 9.134.
Наконец, если я использую обозначение a | b, это означает либо 100a + b, либо 10a + b в зависимости от контекста (надеюсь понятно). Например, квадрат числа 50 + a имеет форму , а число, кратное 11, имеет форму .
Возведение двузначных чисел в квадрат
- Числа, оканчивающиеся на 0:
напр. - Номера, оканчивающиеся на 5:
напр. - Числа близкие к 50:
напр.
- Числа близкие к 25:
напр. - Числа близкие к 75:
напр. - Числа, оканчивающиеся на 1 или 9:
напр. - Любое число, которое выглядит сложным: используйте для того, чтобы с ним было легко работать (обычно число округляется до кратного 5).
напр. - Альтернатива: использовать там, где мало и легко найти (кратно 5).
напр.
Метод средней школы (распределительное право)
-
напр. 34 х 87 = 2400 + 240 + 210 + 28 = 2958
Это более или менее то, чему учат во многих школах, но произведения 34 x 7 и 34 x 80 обычно пишутся одно над другим, а их сумма пишется ниже.
Трудность этого метода вычисления в уме заключается в том, чтобы удерживать в голове такое количество продуктов. Это можно упростить, используя следующие варианты.
Метод «бабочка» или «крест-накрест»
Здесь мне кажется, что проще всего рассчитать (перекрестная часть) сначала умножить на 10, добавить это к , а затем добавить к в конце. Это помогает интерпретировать два числа как четыре цифры в этом методе.
Это помогает интерпретировать два числа как четыре цифры в этом методе.
напр. чтобы найти 86 х 67, я получаю 6 х 6 = 36 и 8 х 7 = 56. Складывая их, я получаю 92. Затем добавьте 10 раз это (920) к 6 x 7, чтобы получить 962. Наконец, добавьте это к 8 x 6 x 100 = 4800, чтобы получить 5762.
- Особый случай: если a = c и b + d = 10 , это становится a(a + 1) | бд
напр. 47 х 43 = 2021
Следующие три метода я использую чаще всего.
Разработайте аналогичный, более простой продукт, затем скорректируйте разницу
- Используйте там, где и легче найти, чем .
напр. 35 х 33 = 35 х 35 – 35 х 2 = 1225 – 70 = 1155
Часто можно выбрать круглое число и малую величину.
Этот метод особенно хорошо работает, когда одно из чисел близко к кратному 10 (особенно 20 или 50).
Анкерный метод
Этот термин взят из [1] и использует следующее тождество.
Здесь мы выбираем быть привязкой (хорошее число), уменьшаем одно число на , увеличиваем другое на , затем добавляем , где разница между числом, которое нужно увеличить, и привязкой.
Это прекрасно работает, когда два числа близки друг к другу. Например, 54 x 52 = 50 x 56 + 2 x 4 = 2808. Если якорь находится между двумя числами, член отрицательный.
напр. 82 x 77 = 80 x 79 – 2 x 3 = 6400 – 80 – 6 = 6314.
Используя разность полных квадратов
Это особенно хорошо, если вы умеете вычислять квадраты (см. выше) и два числа различаются на четное число, еще лучше, если разница невелика или если их сумма кратна 10.
напр. 33 x 47 = 40 x 40 – 7 x 7 = 1600 – 49 = 1551.
32 x 38 = 35 x 35 – 3 x 3 = 1225 – 9 = 1216.
Обратите внимание, что это частный случай якоря метод, где
Если два числа отличаются на нечетное число, мы можем внести небольшую корректировку в приведенное выше тождество.
напр. 34 x 47 = 40 x 41 – 6 x 7 = 1640 – 42 = 1598
Кратность 5
- Чтобы умножить на 5, разделите его пополам, а затем умножьте на 10.
- Чтобы умножить на 10, добавьте 0.

- Чтобы умножить на 15, сначала умножьте на 10, а затем прибавьте половину результата.
- Чтобы умножить на 20, удвойте его, а затем добавьте 0.
- Чтобы умножить на 50, разделите его пополам, а затем умножьте на 100.
- Чтобы умножить на 25, возьмите четверть и умножьте на 100.
- Чтобы умножить на 75, вычтите из него четверть, а затем умножьте на 100.
- Также потенциально полезно тождество (10x+5)(10y+5) = 100xy + 50(x+y) + 25 = 100(xy + (x+y)/2) + 25, но часто легче использовать разность квадратов 92 = 3600 – 225 = 3375.
Удобные продукты
Большинство следующих продуктов близки к кратным 100 и, следовательно, могут оказаться полезными ступеньками при умножении.
12 х 9 = 108
13 х 8 = 104
15 х 7 = 105
17 х 6 = 102, 17 х 47 = 899, 17 х 53 = 901
21 х 19 = 399 90 706 23, 23 23 х 13 = 299
29 х 7 = 203
31 х 13 = 403
33 х 3 = 99
34 х 3 = 102
37 х 3 = 111, 37 х 19 = 703, 37 х 27 = 06 37 х 27 х 06 907 907 8 = 304
39 x 23 = 897
41 x 17 = 697, 41 x 22 = 902
43 x 7 = 301, 43 x 31 = 1333
45 x 9 = 405 х 13 = 702
56 х 9 = 504
59 х 17 = 1003
63 х 8 = 504
64 х 11 = 704
67 х 3 = 201
68 х 3 = 204 7
69 х 0 29 = 504
73 х 11 = 803
76 х 4 = 304
77 х 13 = 1001
78 х 9 = 702
84 х 6 = 504
87 х 23 = 2001
6 9 х 8 8 0 = 7
91 х 11 = 1001
93 x 43 = 3999
Использование множителей
Часто полезно разбить числа на множители и перегруппировать их или выполнить умножение однозначных чисел.
Например, умножить четное число на число, кратное 5, легко, потому что .
напр. 15 x 16 = 3 x 5 x 2 x 8 = 3 x 10 x 8 = 240
Вот несколько других примеров:
42 x 63 = 2 x 21 x 21 x 3 = 6 x 441 = 6 x 450 – 6 х 9 = 2700 – 54 = 2646
38 х 21 = 2 х 19 х 21 = 2 х 392 = 3600 – 529 = 3071
Еще несколько специальных приемов:
- 13x: используйте 13 x 8 = 104
например. 13 х 28 = 13 х 8 х 3,5 = 104 х 3,5 = 312 + 52 = 364 - 17x: используйте 17 x 6 = 102
напр. 17 х 43 = 17 х 42 + 17 = 17 х 6 х 7 + 17 = 102 х 7 + 17 = 714 + 17 = 731 - 23x: умножьте на 25, затем вычтите двойное число
, например. 23 х 38 = 25 х 38 – 2 х 38 = 950 – 76 = 874 - 37x: используйте 37 x 3 = 111
напр. 37 х 59 = 37 х 60 – 37 = 37 х 3 х 20 – 37 = 111 х 20 – 37 = 2220 – 37 = 2183 - 43x: используйте 43 x 7 = 301
напр. 43 х 66 = 43 х 7 х 9 + 43 х 3 = 301 х 9 + 129 = 2709 + 129 = 2838 - 47x, 53x: изменить от 50x
напр. 53 х 64 = 50 х 64 + 3 х 64 = 3200 + 192 = 3392
53 х 64 = 50 х 64 + 3 х 64 = 3200 + 192 = 3392 - 67x: используйте 67 x 3 = 201
например. 67 х 78 = 67 х 3 х 26 = 201 х 26 = 5226 - 73x: используйте 73 x 7 = 511
напр. 73 х 43 = 73 х 42 + 73 = 73 х 7 х 6 + 73 = 511 х 6 + 73 = 3066 + 73 = 3139 - 83x: используйте 83 x 6 = 498
напр. 83 х 18 = 83 х 6 х 3 = 498 х 3 = 1500 – 6 = 1494 - 97x: используйте (100 – 3)x
напр. 97 х 28 = 100 х 28 – 3 х 28 = 2800 – 84 = 2716
Прочие продукты
- Чтобы умножить на любое число, кратное 9, сначала умножьте его на ближайшее кратное 10, затем вычтите 10% из этого числа, т. е. 9x = 10x – x
, например. 27 х 53 = 30 х 53 – 3 х 53 = 1590 – 159 = 1431 - Чтобы умножить на 11, сложите соседние цифры с учетом переноса (ab x 11 = a | a+b | b)
напр. 45 х 11 = 495, так как 9 = 4 + 5, 46 х 11 = 506, так как 10 = 4 + 6 - Чтобы умножить на 24 или 26, сначала умножьте на 25, затем скорректируйте
, например. 26 x 64 = 25 x 64 + 64 = 1664
26 x 64 = 25 x 64 + 64 = 1664
Умножение 26 на кратное 4 оказывается очень простым делом, поскольку последние две цифры всегда являются самим числом! - Чтобы умножить на 33, возьмите треть числа, умножьте на 100 (игнорируя все после запятой), затем вычтите первые две цифры.
напр. 33 х 59 = 1966 – 19 = 1947, 33 х 87 = 2900 – 29 = 2871 - Чтобы умножить на 49 или 51, сначала умножьте на 50, а затем умножьте на 9.0706 напр. 51 x 66 = 50 x 66 + 66 = 3366
Умножить 51 на кратное 2 очень просто, так как последние две цифры — это само число, а первые две цифры — половина этого числа! - Если оба числа близки к 100, используйте (100 – a)(100 – b) = (100 – a – b) | аб
напр. 98 х 97 = 9556 - Если оба числа близки к 50, используйте (50 + a)(50 + b) = (25 + (a + b)/2) | аб
напр. 53 х 54 = 2850 + 12 = 2862 - Если одно число близко к 50, а другое близко к 100, используйте (50 + a)(100 – b) = (50 + a – b/2) | -аб 92, когда a + c = 10
, например. 36 х 76 = (21 + 6) | 36 = 2736
36 х 76 = (21 + 6) | 36 = 2736
Умножение на маленькие числа
- Оба числа, имеющие разряд десятков 1: (10 + b)(10 + d) = 10(10 + b + d) + bd
например. 14 х 13 = 10 (14 + 3) + 4 х 3 = 182 - Одно из чисел с цифрой десятков 1: (10 + b)(10c + d) = 10(bc + 10c + d) + bd
например. 13 х 64 = 10 (3 х 6 + 64) + 3 х 4 = 832 - Одно из чисел с цифрой десятков 2: (20 + b)(10c + d) = 10(bc + 2(10c + d)) + bd (т.е. удвоить большее число) 92).
Легко умножить одно- или двузначное число, сделав этот метод привлекательным.
напр. чтобы найти 47 х 74 мы сначала находим . Умножьте это на 10, чтобы получить 650. Затем мы прибавляем это к 2828 (101 x 4 x 7), чтобы получить 3478.
Другой пример: 68 x 86 = 4848 + 100 x 10 = 5848. Легко!
Этот метод усложняется только там, где есть возможность переноса между десятками и сотнями. Например,
98 х 89 = 7272 + 1450 = 8722.
Этот перенос происходит в следующих случаях: 25 x 52, 58 x 85, 88 x 88, 49 x 94, 69 x 96, 59 x 95, 89 x 98, 99 x 99. В большинстве случаев одна из цифр равна 8. или 9.
В большинстве случаев одна из цифр равна 8. или 9.
В этих случаях может быть проще прибегнуть к другим методам, описанным выше.
напр. 98 х 89 = (89 – 2)100 + 2 х 11 = 8922, 58 х 85 = 29 х 170 = (510 – 17)10 = 4930
Можно было бы попытаться расширить , но это сложнее распознать ( например, 37 x 67 имеет такую форму).
Наконец, существуют методы, для которых может потребоваться сочетание вышеперечисленного.
напр.
Прелесть двузначного умножения в том, что есть много способов решить каждую задачу, что дает один способ проверить ответ. Не забудьте быстро проверить свой ответ на правильность, используя округленные оценки и проверив правильность последней цифры.
Ссылки
[1] Ron Doerfler, Dead Reckonings » Lightning Calculators II: The Methods
[2] Bill Handley ” Speed Mathematics: Secret Skills for Quick Calculation », John Wiley & Sons, 2012.
[3] А. Бенджамин и М. Шермер, « Секреты ментальной математики: руководство математика по молниеносным вычислениям и удивительным математическим трюкам », Three Rivers Press, 2006.
Нравится:
Нравится Загрузка…
Игры для детей на умножение двухзначных чисел на двузначные Онлайн
КЛАСС
ТИП СОДЕРЖИМОГО
- Чувство числа (387)
- Дополнение (341)
- Вычитание (238)
- Умножение (199)
- Введение в умножение (44)
- Многозначное умножение (39)
- Умножение двузначных чисел на однозначные (9)
- Умножение двузначных чисел на двузначные (12)
- Умножение трехзначных чисел на однозначные (7)
- Умножение трехзначных чисел на двузначные (4)
- Умножение 4-значных чисел на 1-значное (7)
- Свойства умножения (12)
- Предварительное умножение (19)
- Таблицы умножения (85)
- Дивизия (109)
- Фракции (173)
- Десятичные дроби (150)
- Геометрия (128)
- Измерение (175)
- Время (35)
- Деньги (57)
- Алгебра (35)
- Словесные задачи (57)
- Чтение (2209)
- Письмо (184)
Определите недостающую цифру в продукте
Раскройте мудрость математики, научившись определять недостающую цифру в продукте.
5 5.НБТ.5
ПОСМОТРЕТЬ ДЕТАЛИ
Произведение двузначных чисел
Используйте свои навыки умножения, чтобы найти произведение двузначных чисел.
5 5.НБТ.5
ПОСМОТРЕТЬ ДЕТАЛИ
Умножение двузначных чисел с использованием модели площадей
Используйте свои навыки умножения, чтобы умножать двузначные числа с использованием моделей площадей.
4 4.НБТ.5
ПОСМОТРЕТЬ ДЕТАЛИ
Умножение двузначных чисел
Добавьте больше стрелок в математический колчан вашего ребенка, умножая двузначные числа.
4 4.НБТ.5
ПОСМОТРЕТЬ ДЕТАЛИ
Выберите недостающую цифру в продукте
Наслаждайтесь чудом математической мультивселенной, изучая, как выбрать недостающую цифру в произведении.
4 4.НБТ.5
ПОСМОТРЕТЬ ДЕТАЛИ
Введите ответ и завершите умножение
Дети должны ввести ответ, чтобы выполнить умножение.
4 4.НБТ.5
ПОСМОТРЕТЬ ДЕТАЛИ
Сопоставьте произведение с его выражением умножения
Проявите себя в мире математики, сопоставив произведение с его выражением умножения.
4 4.НБТ.5
ПОСМОТРЕТЬ ДЕТАЛИ
Найдите произведение путем умножения двузначных чисел
Используйте свои математические способности, чтобы найти произведение путем умножения двузначных чисел.
4 4.НБТ.5
ПОСМОТРЕТЬ ДЕТАЛИ
Завершите умножение двух двузначных чисел
Помогите своему ребенку взлететь, научившись выполнять умножение двух двузначных чисел.
5 5.НБТ.5
ПОСМОТРЕТЬ ДЕТАЛИ
Умножьте двузначные числа и заполните произведение
Дети должны умножить двузначные числа и составить произведение.
4 4.НБТ.5
ПОСМОТРЕТЬ ДЕТАЛИ
Выберите произведение двузначных чисел
Окунитесь в безумие математической мультивселенной, исследуя, как выбрать произведение двузначных чисел.
4 4.НБТ.5
ПОСМОТРЕТЬ ДЕТАЛИ
Умножение двух двузначных чисел с использованием разрядных значений
Проявите себя в мире математики, научившись умножать два двузначных числа с помощью разрядных значений.
5 5.НБТ.5
ПОСМОТРЕТЬ ДЕТАЛИ
Обучение двузначному умножению в увлекательной игровой форме После того, как ваш ребенок освоил умножение однозначных чисел, стратегическое обучение двузначному умножению является следующим строительным блоком в расширении его знаний.
Дети получают пользу от изучения фундаментального двузначного умножения, которое является важным навыком, используемым почти каждый день, от домашних дел до сложных вычислений на работе. Дети начинают с разбора процесса умножения, используя интригующее распределительное свойство умножения, а затем работают с моделями площадей, чтобы лучше понять, как работает типичный алгоритм умножения.
Вот некоторые из игр SplashLearn «Умножение двухзначных чисел на двузначные числа»:
- Завершите умножение двух двузначных чисел: понятие умножения в процессе. В этой игре нужно найти произведение любых случайных двузначных чисел. Студенты знакомятся с различными способами решения вопросов на умножение и обретают уверенность.
- Умножьте два двузначных числа, используя разрядное значение: В этой игре учащиеся умножат два двузначных числа, используя разрядное значение, с перегруппировкой и без нее.
 Это хороший способ попрактиковаться в принципах умножения и повысить эффективность.
Это хороший способ попрактиковаться в принципах умножения и повысить эффективность.
- Определите недостающую цифру в произведении: Эта игра побуждает учащихся применить свои математические знания, чтобы найти недостающую цифру в произведении. Студенты должны заполнить свои ответы, а затем нажать кнопку, чтобы отправить их. За правильный ответ учащийся получает балл. Если ответ неверный, учащиеся получают предупреждающее сообщение и должны повторить попытку.
- Произведение двух двузначных чисел: Учащиеся улучшат свои навыки умножения, решая набор задач, поставленных в игре. Уровень сложности задач увеличивается по мере прохождения игроком уровней. Эта игра помогает учащимся развивать скорость и точность выполнения арифметических действий.
Зарегистрируйтесь на сайте SplashLearn, чтобы получить доступ к увлекательным обучающим играм по умножению двузначных чисел на двузначные, благодаря которым каждый ребенок станет опытным и уверенным в умножении.

 Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:





 Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола). До самой смерти большую часть вычислений Гаусс производил в уме.
До самой смерти большую часть вычислений Гаусс производил в уме.

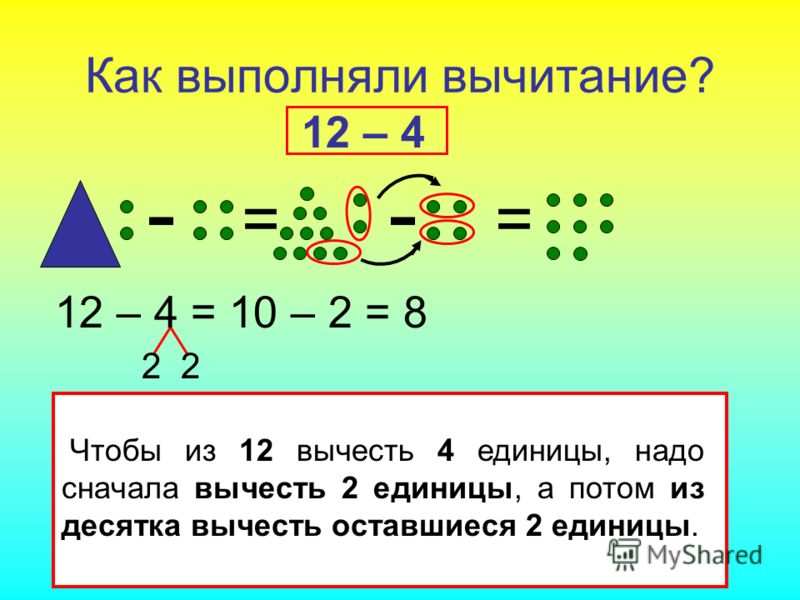
 Получившееся в итоге трехзначное число – результат умножения исходного числа на 11 .
Получившееся в итоге трехзначное число – результат умножения исходного числа на 11 . По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
 Согласно таблице умножения, нам подходят результаты 4 и 9 . Логично предположить, что результатом деления может быть либо число 74 , либо 79 . Проверяем:
Согласно таблице умножения, нам подходят результаты 4 и 9 . Логично предположить, что результатом деления может быть либо число 74 , либо 79 . Проверяем: А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

 Это десятки нашего ответа;
Это десятки нашего ответа;


 с ГК РФ (ст. 1270 и др.). Ни при каких обстоятельствах администрация сайта не несет обязательств по выплате в чью-либо пользу какого-либо вознаграждения за опубликованные материалы. Ни при каких обстоятельствах и условиях администрация сайта не несет ответственности за косвенные или побочные убытки либо за упущенную выгоду и неполученные доходы, связанные с публикацией авторских материалов.
с ГК РФ (ст. 1270 и др.). Ни при каких обстоятельствах администрация сайта не несет обязательств по выплате в чью-либо пользу какого-либо вознаграждения за опубликованные материалы. Ни при каких обстоятельствах и условиях администрация сайта не несет ответственности за косвенные или побочные убытки либо за упущенную выгоду и неполученные доходы, связанные с публикацией авторских материалов.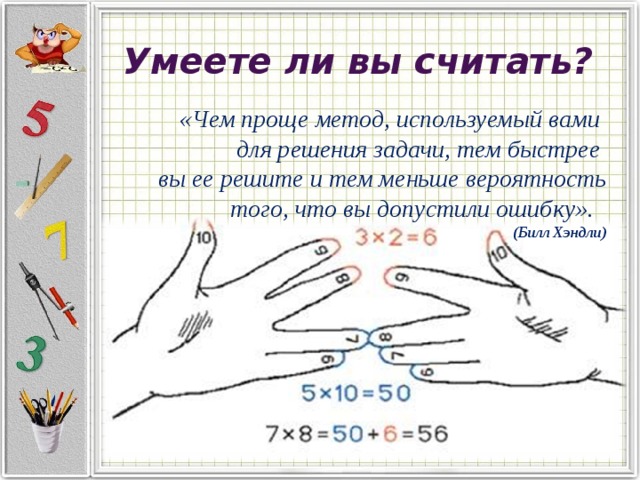
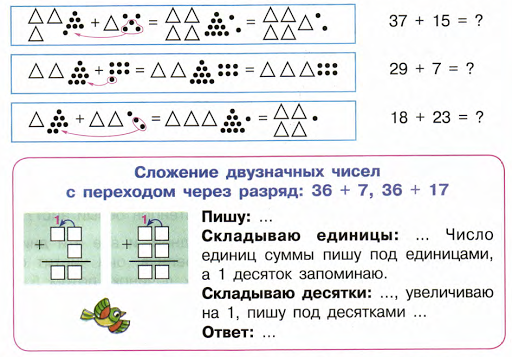 Количество частей здесь получается как 2x$n$-1, где $n$ представляет значение в n-разрядном умножении. В случае двузначного умножения n равно 2. Следовательно,
Количество частей здесь получается как 2x$n$-1, где $n$ представляет значение в n-разрядном умножении. В случае двузначного умножения n равно 2. Следовательно, На последнем шаге мы умножаем левую цифру первого множителя на левую цифру правого множителя (не забывая о наших переносимых $7$). Это дает:
На последнем шаге мы умножаем левую цифру первого множителя на левую цифру правого множителя (не забывая о наших переносимых $7$). Это дает:

 53 х 64 = 50 х 64 + 3 х 64 = 3200 + 192 = 3392
53 х 64 = 50 х 64 + 3 х 64 = 3200 + 192 = 3392 26 x 64 = 25 x 64 + 64 = 1664
26 x 64 = 25 x 64 + 64 = 1664  36 х 76 = (21 + 6) | 36 = 2736
36 х 76 = (21 + 6) | 36 = 2736 Это хороший способ попрактиковаться в принципах умножения и повысить эффективность.
Это хороший способ попрактиковаться в принципах умножения и повысить эффективность.