C в физике формула: Как найти c из формулы Q=c*m*(t2-t1)

Что означает C в физике? – Обзоры Вики

Латинские буквы

Смысл	Единица измерения СИ
элементарный заряд	кулон (C)
сила	Ньютон (N)
Постоянная Фарадея	кулонов на моль (Cmol – 1 )
частота	герц (Гц)

Что такое значение C? Скорость света в вакууме, обычно обозначаемая c, является универсальной физической константой, важной во многих областях физики. Его точное значение определяется как 299792458 метров в секунду (приблизительно 300000 186000 км / с или XNUMX XNUMX миль / ч).

Что означает C в E mc2?

E = Энергия. m = Масса. c = Скорость света. от латинского слова celeritas, что означает «скорость» ² = В квадрате.

Что означает C в теории Эйнштейна? Уравнение, выведенное физиком двадцатого века Альбертом Эйнштейном, в котором E представляет единицы энергии, m представляет единицы массы, а c2 –

скорость света в квадрате, или умноженный на себя. 2. Эта формула позволит найти недостающее C-значение в уравнении стандартной формы.

Почему C-значение называется парадоксом?

Так называемый парадокс C-ценности относится к наблюдение, что размер генома не увеличивается равномерно в зависимости от воспринимаемой сложности организмов, например, позвоночные по отношению к беспозвоночным животным или «низшие» по сравнению с «высшими» позвоночными животными (красный прямоугольник).

Что означает маленький c в физике?

«Что касается c, это скорость света в вакууме, и если вы спросите, почему c, ответ будет, что это начальная буква слова Celeritas, латинское слово, означающее скорость ».

Почему E mc2 неправильный?

Вторая ошибка Эйнштейна с его уравнением заключалась в том, что он не понял, что основной смысл E = MC²том, что он определяет массу фотона как точную меру массы. … В этом случае материя все еще содержит кинетическую энергию, имеющую массу, за исключением того, что кинетическая энергия фотона не имеет массы.

Что такое расчет энергии c?

Пояснение: h – постоянная Планка, f – частота, c – скорость света, λ – длина волны излучения. Вычислите энергию фотона излучения с частотой 5.00 × 1014 Гц.

Что означает c в теории относительности?

Его версия основного уравнения Ньютона F = ma была dc = p dt, где c означает «celeritas », что означает скорость, а p означает «потенциал», что означает силу. Помимо теории относительности, наиболее распространенное использование c для обозначения скорости сегодня – в волновом уравнении.

Что на самом деле означает E mc2?

E = MC². Это самое известное уравнение в мире, но что оно на самом деле означает? «Энергия равна массе, умноженной на квадрат скорости света.. » На самом базовом уровне уравнение гласит, что энергия и масса (материя) взаимозаменяемы; это разные формы одного и того же.

Что означает C в стандартной форме?

Алан П. 1 июня 2015 г. Ax + By + C – это обобщенная форма (фактически стандартная обобщенная форма) для линейного уравнения. где A, B и C – заполнители для констант (x и y – переменные).

Что такое C в стандартной форме?

Определения: Стандартная форма: стандартная форма строки находится в форме Топор + В = С где A – натуральное число, а B и C – целые числа. Обсуждение. Стандартная форма линии – это просто еще один способ написать уравнение линии.

C – перехват Y?

Одна форма уравнения прямой линии называется формой пересечения наклона, поскольку она содержит информацию об этих двух свойствах. … Значение c называется вертикальным пересечением линии. это значение y при x = 0. При рисовании линии c указывает положение, в котором линия пересекает вертикальную ось.

Что такое C-генетика?

C-значение количество ДНК в гаплоидном геноме организма. … Количество геномной ДНК в сложных эукариотах намного больше, чем количество, необходимое для кодирования белков. Например: у млекопитающих от 30,000 50,000 до 3 10 генов, но размер их генома (или C-значение) составляет XNUMX x XNUMX.⁹ б.п.

Что такое C в составе ДНК?

Содержание ДНК составляет 2C, где C определяется как масса ДНК, присутствующая в наборе гаплоидных хромосом. … На этом этапе количество хромосом равно количеству хроматид, и они одинаковы у мужчин и женщин.

Какое значение C у кишечной палочки?

Общее количество ДНК в гаплоидном геноме называется его значением C.

…

Размеры генома.

	E. coli O157: H7
Пар оснований	5.44 х 10 6
Гены	5,416
Заметки	патогенный для человека штамм; имеет 1,346 генов, не обнаруженных в E. coli K-12

Существуют ли червоточины?

Червоточины – это ярлыки в пространстве-времени, популярные среди авторов научной фантастики и кинорежиссеров. Их никогда не видели, но согласно общей теории относительности Эйнштейна они могут существовать. … Они тоже являются возможным результатом теории Эйнштейна.

Возможно ли путешествие во времени?

Вкратце: Да, путешествие во времени действительно реально. Но это не совсем то, что вы, вероятно, видели в фильмах. При определенных условиях можно наблюдать, как время течет с другой скоростью, чем 1 секунда в секунду.

Сколько джоулей в герцах?

Преобразование из Гц в Дж
Преобразование уравнения:	(1 Гц) в = х Дж х = {ч }
Значение коэффициента преобразования:	х = 6.626 070 х 15 – 34
Ваше входное значение:	1.000 000… Гц
Ваша преобразованная ценность:	6.626 070 150 000 00 10… x XNUMX – 34 J

Что означает E mc2?

E = MC².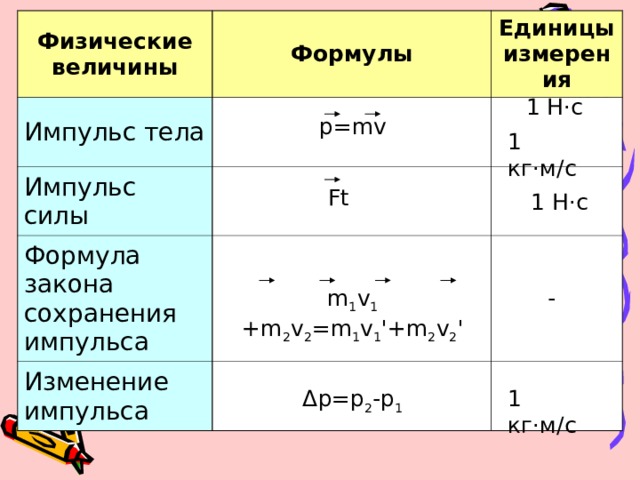 Это самое известное уравнение в мире, но что оно на самом деле означает? «Энергия равна массе, умноженной на квадрат скорости света.. » На самом базовом уровне уравнение гласит, что энергия и масса (материя) взаимозаменяемы; это разные формы одного и того же.

Как вы рассчитываете джоули?

В форме уравнения: работа (джоули) = сила (ньютоны) x расстояние (метры), где джоуль – это единица работы, как определено в следующем абзаце. На практике даже небольшая сила может сделать много работы, если приложить ее на большом расстоянии.

Что такое c в уравнении скорости света?

Как и все другие электромагнитные волны, он подчиняется уравнению с = fλ, где c = 3 × 10⁸ м / с – скорость света в вакууме, f – частота электромагнитных волн, а λ – их длина волны.

Что символ c обозначает в науке?

Иногда легко определить, какой элемент обозначает символ. Например, C означает углерод и Li обозначает литий.

Сколько лет было Эйнштейну на момент публикации?

Также в 1905 году, который был назван annus mirabilis Эйнштейна (удивительный год), он опубликовал четыре новаторских статьи о фотоэлектрическом эффекте, броуновском движении, специальной теории относительности и эквивалентности массы и энергии, которые должны были привлечь его внимание. академический мир, в возрасте 26.

Теги: СмыслСоциальные сетиUrban DictionaryЧто означает C?Вики

Удельная теплоемкость вещества – формулы и таблица

4.1

Средняя оценка: 4.1

Всего получено оценок: 190.

4.1

Средняя оценка: 4.1

Всего получено оценок: 190.

Удельная теплоемкость вещества – параметр материалов, характеризующий их способность к нагреванию. Ее величину учитывают при проектировании электрических цепей, обогревателей и других приборов.

Общие сведения

При изменении температуры тела определенной массы расходуется тепло. Коэффициент пропорциональности между этими величинами называют удельной теплоёмкостью. Она рассчитывается следующим образом:

$C = \frac {dQ}{m \cdot dT}$, где dQ – количество полученной (отданной в случае охлаждения) теплоты, m – масса нагреваемого вещества, dT – изменение температуры. Из формулы удельной теплоемкости вещества следует и ее определение – это количества тепла, необходимое для изменение 1 кг вещества на 1 К.

Знак дифференциала берется по той причине, что теплоемкость зависит от температуры, поэтому для ее расчета надо рассматривать малые величины.

Единица измерения удельной теплоемкости в системе СИ – $\frac {Дж}{кг \cdot К}$. Для различных материалов, взятых при разных диапазонах нагревания, составлены таблицы удельной теплоемкости веществ.

Теплоемкость в разных процессах

Из определения ясно, что теплоемкость – это не только характеристика вещества, но еще и конкретного процесса, в котором телу передается тепло. Рассмотри, например, нагревание газа в условиях постоянного давления. Так происходит в сосуде с поршнем – при повышении температуры происходит расширение газа, из-за чего поршень выталкивается, а давление внутри остается прежним.

В таком процессе для изменения температуры необходимо затратить больше тепла, чем для аналогичного нагревания того же газа в условиях постоянного объема.

Для жидкостей и твердых тел термическое расширение не столь значительно, поэтому для них значения теплоемкости в разных процессах примерно одинаково. Объясняется это различиями в молекулярной структуре.

Рис. 1. Молекулярные структуру твердых тел, жидкостей и газов.

Процесс, в котором остается постоянным объем, называется изохорическим. Для него теплоемкость обозначается $C_V$ и рассчитывается по формуле:

$C_V = (\frac {dQ}{dT})_V$

Рис. 2. Изохорический нагрев газа.

Но поскольку при постоянном объеме газ не совершает работы, то dQ = dU, где dU – внутренняя энергия. Тогда для одного моля газа запишем:

$C_V \cdot dT = dU$

Или, учитывая выражение для внутренней энергии:

$C_V \cdot dT = \frac {i}{2} \cdot R \cdot dT$,

где i – степень свободы атомов газа, а R – универсальная газовая постоянная.

Отсюда следует, что при малых изменениях температуры для одного моля одноатомного газа удельная теплоемкость при постоянном объеме есть величина постоянная:

$C_V = \frac {3}{2} \cdot R$

Она соответственно будет увеличиваться при увеличении количества вещества.

Аналогично для теплоемкости одного моля вещества при постоянном давлении формула удельной теплоёмкости будет выглядеть так:

$ C_P = (\frac {dQ}{dT})_P$

Рис. 3. Изобарический нагрев газа.

Но в данном случае газ совершает работу. Она вычисляется по формуле:

$dA = p \cdot dV$ или $dA = R \cdot dT$.

Внутренняя энергия же от объема не зависит, поэтому запишем:

$C_P = \frac {5}{2} \cdot R$

Получается, что при постоянном давлении теплоемкость также зависит только от температуры и количества вещества, но для малых изменений температуры остается постоянной.

Связь между теплоемкостями в изохорическом и изобарном процессах выражается формулой Майера:

$C_P = C_V + R$

Задачи

На провод массой 0,1 кг подали напряжение, после чего началось выделение мощности. Через пятнадцать минут напряжение выключили. Если провод от комнатной температуры нагрелся до 340 К, а выделяемая мощность равнялась 2000 Вт, чему равна теплоёмкость провода? Потерями тепла пренебречь.

Решение

$Q = P \cdot t$ – тепло, полученное проводником.

Тогда теплоемкость найдем по формуле:

$C = \frac {P \cdot t}{m \cdot \delta T} = \frac {2000 \cdot 0,25}{0,1 \cdot (340-293)} = \frac {500}{4,7} = 106 \: \frac {Дж}{кг \cdot К}$

Что мы узнали?

В ходе урока дали определение удельной теплоёмкости вещества, узнали, от чего она зависит и чем отличают теплоемкости при разных процессах (изохорическом, изобарном). После чего решили задачу для закрепления пройденного материала.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

• Диана Гаврилова

  8/10

• Марина Ковтун

  9/10

Оценка доклада

4.

1

Средняя оценка: 4.1

Всего получено оценок: 190.

---

А какая ваша оценка?

AP Physics C Equations Sheet Explanation

AP Physics (C) Equation Sheet

Оба теста AP Physics (C) включают удобную информационную страницу с экзаменационным пакетом в день экзамена. Лист уравнений AP Physics C — это информационный лист, который битком набит физическими формулами и уравнениями, что делает его очень ценным для изучения и сдачи экзаменов AP Physics (C). Этот информационный листок переполнен физическими формулами и уравнениями, что делает его очень ценным для изучения и сдачи экзаменов AP по физике (C).

Трехстраничный лист уравнений, представленный на тестах AP по физике (C), содержит много информации. Крайне важно знать материал на листе и знать, как использовать его в своих интересах во время экзаменов AP.

В этом учебном пособии мы также выполним следующие действия, чтобы помочь вам в изучении деталей справочных таблиц по физике AP (C):

• Приведите три показателя использования листа уравнений для подготовки к экзаменам по физике AP (C).
• Назовите три показателя использования листа уравнений во время тестов AP.
• По частям объясните, как использовать таблицу уравнений AP Physics (C).

Из-за пандемии коронавируса COVID-19 экзамены AP теперь будут проводиться в три сессии в период с мая по июнь. Даты ваших экзаменов и то, будут ли они онлайн или оффлайн, будут определяться вашей школой.

В этой статье мы также сделаем следующие вещи, чтобы помочь вам в изучении тонкостей справочных таблиц AP Physics C:  

• Предоставьте пошаговые инструкции по использованию листа уравнений AP Physics C.
• Дайте три балла за использование листа уравнений, чтобы подготовиться к тестам AP Physics C.
• Пожалуйста, предложите три совета по использованию таблицы уравнений в тестах AP.

Экзамен AP по физике (C)

Существует два экзамена AP по физике (C):
● Один посвящен механике
● Другой посвящен магнетизму и электричеству.

Оба теста AP по физике (C) исследуют применение учащимися научных процессов, связанных с великими понятиями изменения, полей, силовых взаимодействий и сохранения. The courses of AP physics (C) put students to the exam on the following topics:

Magnetism and Electricity	Mechanics
Electric Circuits	Kinematics
Conductors, Dielectrics, Конденсаторы,	Gravitation
Electrostatics	Energy, Work, and Power
Magnetic Fields	Systems of Linear Momentum and Particles
Electromagnetism	Rotation
	Oscillations
	Newton’s Законы движения

Оба теста по физике AP (C) длятся 1 час 30 минут. Он включает в себя один раздел бесплатных ответов и один вопрос с несколькими вариантами ответов. Часть MCQ состоит из 35 вопросов по обоим тестам и длится 45 минут. Часть со свободным ответом состоит из трех вопросов по обоим тестам AP по физике (C). Он длится 45 минут. Бесплатные ответы и части с несколькими вариантами ответов составляют половину общего балла. Хорошая новость заключается в том, что таблица уравнений магнетизма и электричества AP-физики (C) и таблица уравнений механики AP-физики (C) идентичны. Поэтому вам не придется учиться по двум разным документам.

Лист уравнений AP Physics

Лист формул AP Physics (C) включен в экзаменационный буклет для всех участников экзамена AP Physics (C). Лист уравнений для каждого экзамена одинаков. Лист уравнений, предоставленный во время экзамена, не является полной таблицей физических уравнений. Он содержит уравнения, в основном используемые в константах, физике, коэффициенты преобразования, значения наиболее часто используемых функций, символы и префиксы.

Как использовать формулы таблицы уравнений

Таблица формул AP Physics (C) состоит из пяти разделов:

• Префиксы
• Уравнения
• Символы единиц измерения
• Константы и коэффициенты пересчета
• Значения тригонометрических функций для типичных углов

Часть уравнений таблицы формул самая длинная. Он разделен на подразделы на основе формулы. Подразделы уравнений информационного листа включают электричество и магнетизм, механику, геометрию и тригонометрию, а также исчисление. Каждая область листа с формулами также может использоваться для различных целей в тесте.

Коэффициенты пересчета и константы

Коэффициенты пересчета и постоянные коэффициенты на листе формул физики AP (C) пригодятся при выполнении различных расчетов теста AP. Эти значения, часто называемые «универсальными константами» или «физическими константами», отличаются постоянным значением в природе независимо от ситуации.
Константы, включенные в таблицу формул, следующие:

• Масса протона
• Вакуумная диэлектрическая проницаемость
• Постоянная закона Кулона
• Номер Авогадро
• Универсальная газовая постоянная
• Масса нейтрона
• Масса электрона
• постоянная Больцмана
• Величина заряда электрона
• Универсальная гравитационная постоянная
• Ускорение силы тяжести у поверхности Земли
• Один электрон-вольт
• Скорость света
• Одна унифицированная атомная единица массы
• постоянная Планка
• Вакуумная проницаемость
• Магнитная постоянная
• Давление в одну атмосферу

Некоторые константы не имеют единиц измерения, но те, у которых они есть, могут нуждаться в преобразовании и представлении в других единицах измерения теста. В тесте будут использоваться коэффициенты преобразования. Коэффициенты преобразования на листе могут изменять константы из одной части в другую путем их деления или умножения.

Тригонометрические функции, символы единиц измерения и префиксы для общих углов При сдаче экзамена AP Physics C вам будет полезно использовать как таблицу символов единиц измерения, так и таблицу префиксов. Когда вы отвечаете на вопросы экзамена, вы должны сочетать префикс со словом для определенной единицы, чтобы описать число или измерение, например, килограмм с граммами или гига с ваттами (единица измерения). Таблица префиксов на листе формул может помочь вам вспомнить значение (в десятках тысяч!) определенного префикса, если вы не можете этого сделать.

 

Символы для каждого префикса также представлены в таблице префиксов, которую можно использовать вместе с соответствующим знаком единицы при ответе на экзаменационные вопросы. Допустимо использовать либо миллисекунды, либо мс, либо гигагерцы, либо ГГц, например, при указании значения.

Таблица префиксов также содержит коэффициент каждого префикса или научное обозначение. Они отображаются как 10 с показателем степени, например 109 или 1012. На экзамене AP Physics C вы можете ожидать использования экспоненциальной записи для передачи наибольших и наименьших измерений.

Тригонометрические функции для обычных углов приведены в последней части на первой странице листа уравнений. Они будут полезны для экзаменационных задач AP по геометрии, тригонометрии и исчислению. Вы можете использовать таблицу, чтобы быстро найти значения sin, cos и tan под разными углами, когда будете решать задачи на экзамене AP Physics C.

Уравнения 

 Большая часть таблицы формул, которую вы получите на экзаменах AP Physics C, содержит стандартные физические уравнения. Три категории, на которые делятся эти уравнения, — это механика, электричество и магнетизм, геометрия и тригонометрия.

Чтобы помочь запомнить значение каждого символа в конкретном уравнении, в каждый раздел уравнений включена клавиша с символами.

Уравнения электричества и магнетизма

Следующая таблица таблицы формул содержит 29 типичных уравнений электричества и магнетизма. Во время испытаний эти уравнения можно использовать для определения, определения, описания и расчета следующего:

• Емкость и конденсаторы
• Сопротивление, эквивалентное сопротивление и определение мощности или скорости тепловых потерь через резистор
• Электрические поля и свойства электрических полей
• Разность потенциалов, потенциал за счет множественных точечных зарядов и электростатическая потенциальная энергия
• Величина электростатической силы
• Токи и плотность тока
• Магнитные поля, магнитная сила и магнитный поток

Уравнения в механике

Таблица уравнений AP Physics (C) содержит 31 широко используемое уравнение механики. На тесте эти уравнения можно использовать для определения, описания, расчета и определения следующего:

• Кинематические соотношения и угловые кинематические соотношения
• Потенциальная энергия, потенциальная энергия пружинящего объекта и гравитационная потенциальная энергия
• Мощность
• Импульс, угловой момент для вращающегося объекта, общая скорость и импульс для одного объекта, движущегося с некоторой скоростью
• Импульс
• Работа, совершаемая над объектом силой, силой трения и силой тяжести
• Кинетическая энергия и кинетическая энергия вращающегося объекта,
• Крутящий момент
• Момент инерции
• Простое гармоническое движение

Уравнения электричества и магнетизма  

В следующей таблице на листе формул приведено 29 общих уравнений для электричества и магнетизма.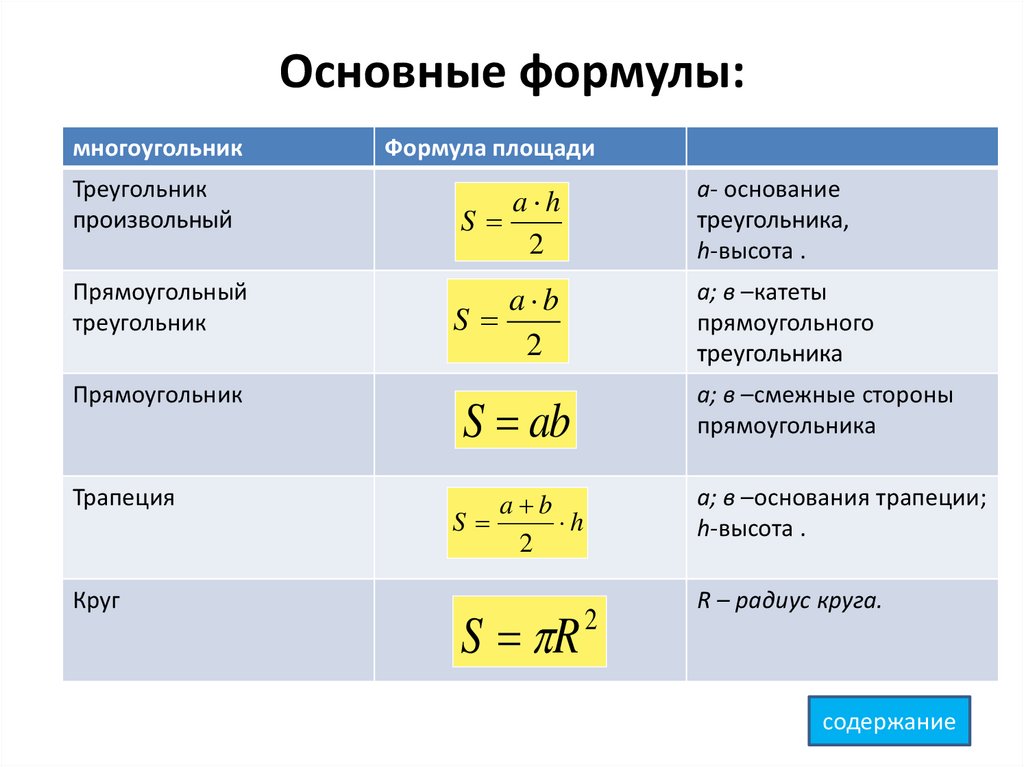 Во время экзамена с помощью этих уравнений можно рассчитать, идентифицировать, определить и определить следующее:

• Напряженность электростатического поля
• Электрические поля и их характеристики
• Электростатическая потенциальная энергия, разность потенциалов и потенциал, возникающий в результате многочисленных точечных зарядов 
• Батареи и емкость
•  Определение мощности или скорости тепловых потерь через резистор, эквивалентное сопротивление и сопротивление 
• Потоки тока и их плотность
•  магнитные поля, магнитный поток и магнитная сила 

Тригонометрические и геометрические функции

Наконец, таблицу уравнений, содержащую 14 тригонометрических и геометрических функций, можно использовать для вычисления следующего для экзамена по физике AP (C):

• Площадь треугольника
• Площадь, окружность и длина дуги окружности
• Площадь прямоугольника
• Объем и площадь поверхности шара
• Объем прямоугольного твердого тела
• Объем и площадь поверхности цилиндра
• Формулы для определения величины углов прямоугольного треугольника

Формулы, связанные с законами

Раздел по электричеству и магнетизму также включает формулы для следующих законов:

• Закон Ома
• Закон Ампера
• Закон Кулона
• Закон Гаусса
• Закон Био-Савара
• Закон Фарадея

Общие обозначения угловых единиц, префиксы и тригонометрические функции

Таблица обозначений и префиксов единиц поможет вам подготовиться к экзамену AP по физике (C). При ответе на вопросы теста префикс сочетается с термином для определенной единицы измерения, чтобы описать число или измерение, например, гига (префикс) и ватты (единицы) или кило (префикс) и граммы (единицы). Если вы не можете вспомнить значение определенного префикса, страница формул может помочь вам с приведенной таблицей.

Таблица префиксов также включает символ для каждого префикса, который может сочетаться с правильным знаком единицы для ответов на вопросы теста. Например, допустимо указывать значение в гигагерцах (ГГц) или миллисекундах (мс). Наконец, таблица префиксов включает коэффициент или научное обозначение для каждого префикса. Они представлены числом 10 плюс показатель степени, 1012 или 109. Вы можете ожидать использования экспоненциальной записи для представления наименьшего и наибольшего измерений в тесте AP-физики (C).

Тригонометрические функции для обычных углов приведены в последнем разделе на первой странице листа уравнений. Они будут полезны для задач AP-тригонометрии, геометрии и исчисления. В таблице представлены значения cos, sin и tan в различных степенях, которые вы можете использовать в качестве быстрой справки при решении задач на экзамене AP по физике (C).

3 Стратегии изучения с помощью листа формул AP Physics C 

Перед экзаменом Совет колледжей размещает лист уравнений AP Physics C в Интернете, поэтому, возможно, стоит его просмотреть. Вот три предложения, как эффективно учиться с листом уравнений!

Совет 1: Преобразование упражнений На экзамене AP у вас будет больше времени, чтобы проверить свою работу и убедиться, что ваши ответы точны, чем быстрее вы сможете правильно выполнять задания. Выполнение преобразований, даже не обращаясь к листу формул во время экзамена, возможно, если вы используете страницу уравнений, чтобы попрактиковаться в выполнении частых преобразований во время подготовки к тесту. Кроме того, каждая сэкономленная секунда имеет значение, поскольку время теста AP Physics C ограничено.

Совет 2: Выбор конкретных практических вопросов — Как правило, перед тестом рекомендуется потренироваться с конкретными уравнениями, которые появляются в справочных таблицах AP Physics C, если вы понимаете, что у вас возникают проблемы с их запоминанием или правильным применением. Уравнения, перечисленные на листе формул, будут использоваться на протяжении всего экзамена, поэтому просмотр тех, которые кажутся вам сложными, поможет вам лучше использовать свое время.

Совет 3: Символы отзыва – Несмотря на то, что в справочных таблицах AP Physics C содержится более 90 уравнений, у вас, вероятно, не возникнет проблем с запоминанием того, что обозначает каждый символ. В каждой таблице уравнений на листе уравнений есть ключ с символами, который объясняет, что означает каждый символ в уравнении. Вы можете сэкономить время на тесте, интерпретируя формулы, переменные и константы, указанные в экзаменационных вопросах, без необходимости сверяться со страницей уравнений, запоминая значения всех символов.

AP Physics C Таблица уравнений

Опубликовано вТеоретическая астрофизика

от astrophys_owipuk 30 июня 2022 г. 27 июня 2022 г.

Содержание

С AP Физика C: Обширная и углубленная учебная программа по курсу «Электричество и магнетизм». Важно иметь универсальный ресурс, который может помочь по любой теме. Если вы ищете лист уравнений AP Physics C, вы попали в нужное место. В этой статье мы объясним, что входит в каждый из разделов таблицы физических уравнений.

Мы также дадим вам несколько советов, как использовать его наиболее эффективно. Кроме того, мы покажем вам несколько примеров на листах, созданных учащимися. Мы начнем со всех подразделов скорости, которые проходят через всю страницу вашего листа уравнений AP Physics C.

Что такое AP Physics C Equation Sheet? Источник: Flipping Physics

AP Physics C — это курс уровня колледжа, предназначенный для подготовки к экзамену AP. Хотя курс фокусируется на физических принципах, он также включает в себя некоторые экспериментальные методы. А также математические навыки, необходимые для успеха этого теста.

Следующий лист уравнений AP Physics C содержит все уравнения, которые вам необходимо знать для теста. Если вам нужна дополнительная информация об использовании этого листа, ознакомьтесь с нашим руководством о том, как готовиться к тестам AP с листом уравнений.

AP Physics C Лист уравнений

1. Сила = масса x ускорение (закон движения Ньютона)

2. F = ma (теорема работы-энергии)

Теорема энергии)

4. Мощность = выполненная работа / время (теорема работа-энергия)

5. Энергия – это способность совершать работу (уравнение энергии)

6. Полная энергия сохраняется в изолированной системе (уравнение энергии)

7. Кинетическая энергия пропорциональна квадрату скорости (кинематика)

Методы на листе уравнений AP Physics C и способы их применения

Префиксы, константы и коэффициенты преобразования; значения тригонометрических функций для обычных углов; символы единиц и уравнения. Все они описаны в листе формул AP Physics C, который состоит из пяти разделов.

Далее рассмотрим каждую из основных частей более подробно.

Префиксы, символы единиц и тригонометрические функции для общих углов

Таблицы префиксов и символов единиц помогут вам сдать экзамен AP Physics C. При ответе на экзаменационные вопросы префикс сочетается со словом, обозначающим определенную единицу, для описания значения или количества; например, килограмм (префикс) и грамм (единица измерения) или гига (префикс) и ватт (единица измерения). Таблица префиксов на листе уравнений может помочь освежить вашу память. Если вы не можете вспомнить цифру определенной приставки.

Константы и коэффициенты преобразования

Константы и коэффициенты преобразования из таблицы формул AP Physics C пригодятся при выполнении различных вычислений на экзамене AP. Эти величины, часто называемые «физическими константами» или «универсальными константами», отличаются тем, что имеют постоянное значение независимо от ситуации в природе.

Уравнения Источник: CSheet

Большая часть листа решений во время экзаменов AP Physics C содержит основные формулы физики. Механика, электричество и магнетизм, геометрия и тригонометрия — вот три области, в которых подразделяются эти уравнения.

Каждая часть вычислений включала символьный ключ. Чтобы вы поняли, что означает каждая цифра в данном выпуске. Хотя фактические методические листы для экзамена AP Physics C не используют это, наш вариант методического листа дает краткое обсуждение каждой формулы. А также, как вы можете использовать его для экзамена.

Уравнения в механике

Ниже приводится список уравнений, которые будут полезны при решении задач по физике. Имейте в виду, что вы можете решить любое уравнение путем замены, исключения, сложения или вычитания. Если уравнение кажется сложным для решения, попробуйте использовать один из этих методов, чтобы упростить его.

Второй закон Ньютона.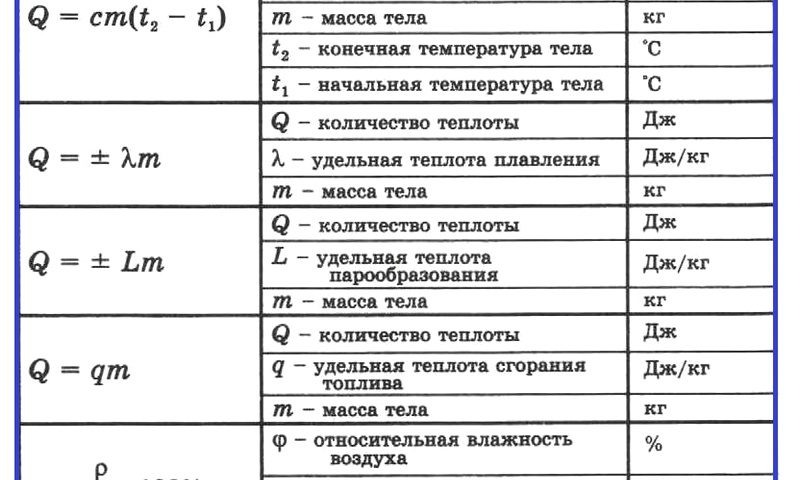 Теорема о работе и энергии

Теорема о работе и энергии утверждает, что изменение кинетической энергии равно работе, совершаемой системой. Оно выглядит следующим образом:

• Где W — работа постоянной силы F над массой m при перемещении s вдоль направления ее движения; его также называют импульсным (J).
• Импульс представляет собой интеграл силы по времени; F = ∫Fdt, где F — сила (Н), t — время (с).

Третий закон Ньютона: силы и ускорения

• Сила F, действующая на объект, создает ускорение в соответствии с третьим законом Ньютона: на каждое действие есть равное и противоположное противодействие.

Уравнения электричества и магнетизма

1) Закон Гаусса: поверхностный интеграл от B, умноженный на вектор электрического поля, равен нулю.

2) Закон Фарадея: Линейный интеграл магнитного потока через замкнутый путь пропорционален общему заряду, заключенному в пути, и обратно пропорционален его длине.