Частные производные вычислить: Найти частные производные | Онлайн калькулятор - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

3.4.1. Частные производные MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

1465 0

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 – 11

Главная
База знаний
CAD / CAM
org/Breadcrumb”>MathCAD 12

Дифференцирование
3.1. Аналитическое дифференцирование
- 3.1.1. Аналитическое дифференцирование функции
- 3.1.2. Вычисление производной функции в точке
- 3.1.3. Определение функций пользователя через оператор дифференцирования
- 3.1.4. Дифференцирование при помощи меню
3.2. Численное дифференцирование
- 3.2.1. Дифференцирование в точке
- 3.2.2. Об алгоритме дифференцирования
3.3. Производные высших порядков
3.4. Частные производные
- 3.4.1. Частные производные
- 3.4.2. Примеры: градиент, дивергенция и ротор
- 3.4.3. Пример: якобиан
3.5. Разложение функции в ряд Тейлора
- 3.5.1. Разложение в ряд при помощи меню
- 3.5.2. Оператор разложения в ряд

Примеры отыскания частных производных функции двух переменных приведены в листингах 3. 11 и 3.12. В первой строке обоих листингов определяется сама функция, а в последующих (символьным или численным образом) рассчитываются ее производные по обеим переменным — х и k. Чтобы определить частную производную в точке, необходимо предварительно задать значения всех аргументов, что и сделано в следующих строках листинга 3.12. Обратите внимание, что для символьного поиска производной функции нет необходимости задавать значения всех ее аргументов (третья строка листинга 3.12), а вот для численного дифференцирования (последняя строка листинга) должны быть предварительно определены все аргументы функции, иначе вместо результата появится сообщение об ошибке.

Листинг 3.11. Аналитическое вычисление частных производных

Листинг 3.12. Символьное и численное вычисления частных производных в точке

Частные производные высших порядков рассчитываются точно так же, как и обычные производные высших порядков (см. разд. 3.3). Листинг 3.13 иллюстрирует расчет вторых производных функции по переменным х и у, а также смешанной производной.

Листинг 3.13. Вычисление второй частной производной

Возможно, вы обратили внимание, что во всех трех листингах 3.11—3.13 оператор дифференцирования записан в традиционной форме частной производной (с округлыми символами дифференциала). Запись оператора не влияет на вычисления, а служит лишь более привычной формой представления расчетов.

Рис. 3.8. Изменение вида оператора дифференцирования

Для того чтобы изменить вид оператора дифференцирования на представление частной производной, следует:

1. Вызвать контекстное меню из области оператора дифференцирования нажатием правой кнопки мыши.

2. Выбрать в контекстном меню верхний пункт View Derivative As (Показывать производную как).

3. В появившемся подменю (рис. 3.8) выбрать пункт Partial Derivative (Частная производная).

Чтобы вернуть вид производной, принятый по умолчанию, выберите в подменю пункт Default (По умолчанию) либо, для представления ее в обычном виде, — Derivative (Производная).

Нравится

Твитнуть

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

10042 0

Глава 10 Работа с информационными ресурсами Mathcad 11

7032 0

Глава 2 Работа с файлами Mathcad 11

12733 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2141 s

Калькулятор Частичных Производных – Mathcracker.Com

Инструкции:

Используйте этот калькулятор частичных производных для нахождения производной функции более чем одной переменной, которую вы задаете относительно конкретной переменной, показывая все этапы процесса.

2 без полного определения, будет считаться, что предоставлена функция двух переменных x и y.

Как только вы зададите действительную дифференцируемую функцию и действительную переменную, следующим шагом будет нажатие на кнопку “Вычислить”, после чего будут показаны все этапы процесса, со всеми используемые производные правила , прямо указано.

Деривативы и их естественное расширение до частных производных по нескольким переменным являются одними из самых важных предметов изучения в математике. Это связано с тем, что они имеют дело со скоростью изменения и течением многих моделей, которые часто появляются в приложениях.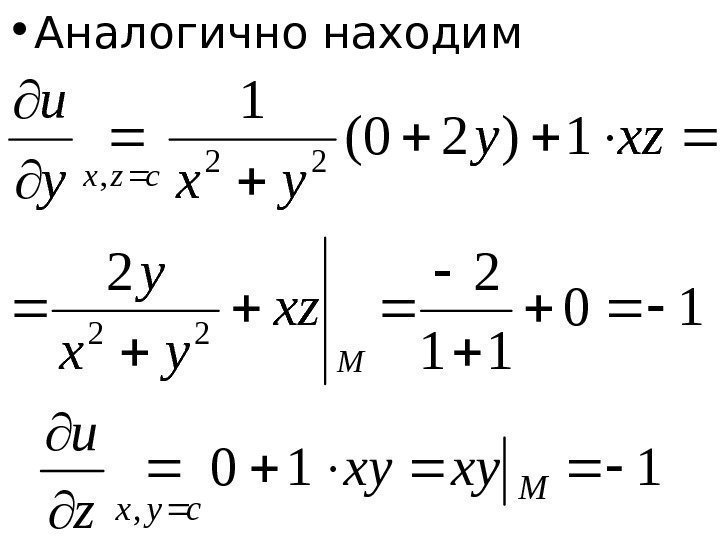

Что такое частичная производная?

Проще говоря, частичная производная состоит в том, чтобы провести то же самое, что и обычное дифференцирование относительно одной переменной, предполагая, что остальные переменные постоянны.

Если бы мы хотели формально определить частичную производную, давайте упростим задачу и сделаем это для функции двух переменных, $x$ и $y$. Частная производная по отношению к $x$ в точке $(x_0, y_0)$ имеет вид

\[\frac{\partial f}{\partial x}(x_0, y_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h, y_0) – f(x_0, y_0)}{h} \]

Итак, как мы видим, по сути это то же самое, что и определение обычной производной, только здесь есть еще одна переменная, но она остается постоянной в процессе вычисления.

Аналогично, частная производная по отношению к $y$ в точке $(x_0, y_0)$ равна

\[\frac{\partial f}{\partial y}(x_0, y_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0, y_0 + h) – f(x_0, y_0)}{h} \]

Вектор всех частных производных называется градиентом. Если вам нужно действительно получить все частные производные, вы можете использовать следующее градиентный калькулятор .

Шаги для вычисления частных производных

Шаг 1: Определите функцию, частную производную которой вы хотите вычислить. Не забудьте сначала упростить ее
Шаг 2: Обратите внимание, что не все функции дифференцируемы, поэтому вам нужно убедиться, что функция, о которой идет речь, действительно дифференцируема
Шаг 3: Используйте все соответствующие правила производной для функции и дифференцируйте функцию, как обычно, по дифференцируемой переменной, а любую другую переменную считайте постоянной

Таким образом, когда мы выполняем частичную производную по x для чего-то вроде ‘x^2+y^2’, в процессе частичного дифференцирования по x переменная y рассматривается как константа. 2)}{\partial x} = 0\), поскольку y предполагается постоянным относительно x.

Зачем использовать калькулятор частных производных

Вычисление частных производных может быть относительно простым упражнением, но это не значит, что оно обязательно будет легким. Важно быть очень систематичным во время применения соответствующего Правила производных .

Использование калькулятора частичных производных с шагами может помочь вам, по крайней мере, проверить результат и точно увидеть, какие шаги являются правильными и какие правила вычисления производных необходимо использовать.

Особенно в сложных задачах, с алгебраически сложными выражениями калькулятор действительно может пригодиться.

Каковы правила производных для частичных производных?

Они точно такие же, как и для обычных производных. Для частных производных у нас есть линейность, а также Правило Продукта , Правило цепи и Правило квоты . Как правило, для более сложных примеров производных вы в конечном итоге будете использовать комбинацию всех этих правил.

Что такое неявная дифференциация

Существует ситуация, когда задействовано более одной переменной, в которой мы не предполагаем, например, что y изменяется с x, как это делается в частных производных. В некоторых случаях, когда есть уравнение, связывающее переменные, мы предполагаем наличие неявной зависимости между y и x, и пишем y = y(x).

Это контекст неявное дифференцирование это своего рода гибрид между частичной и обычной дифференциацией.

И есть одна вещь, которую невозможно переоценить: Частичные производные действительно являются одним из основных инструментов, используемых в инженерии, физике и экономике.

Пример: вычисление частичной производной

Вычислите частную производную $\frac{\partial f}{\partial y}$ для: $f(x,y) = \sin(xy)$

Решение:

чем завершается расчет. 2}\)

Другие калькуляторы calculus

Понятие производной находится в центре Calculus, а использование производный калькулятор может значительно помочь вам во многих различных приложениях Calculus, включая оптимизацию, одну из самых “больших”.

Идея производной естественно распространяется на случай функции со многими переменными, где a Калькулятор частичных производных будет делать то же самое, что и обычная производная, но теперь предполагается, что изменяется только одна переменная, в то время как другие переменные принимаются фиксированными.

Часто бывает так, что известно, что $y$ зависит от $x$, но не явно, а скорее неявно, с помощью уравнения связи, в этом случае можно использовать неявное дифференцирование использовать правила производных, чтобы получить выражение, для которого затем можно решить производную $\frac{d f}{d x}$ .

Калькулятор производных с шагами | Калькулятор дифференцирования

Введение в калькулятор производных с шагами

В исчислении есть два основных понятия, т. е. интегрирование и дифференцирование. Дифференциация обратна интегрированию. Как и интеграция, расчет деривативов носит технический характер и требует надлежащего внимания и внимания.

Калькулятор производных представляет собой онлайн-инструмент, который обеспечивает полное решение дифференцирования. Калькулятор дифференцирования помогает кому-то вычислять производные во время выполнения с помощью нескольких щелчков мыши.

Калькулятор дифференциации предоставляет полезные результаты в виде шагов, которые помогают пользователям и особенно учащимся подробно изучить эту концепцию.

Для вычисления производных по x и y используйте калькулятор неявного дифференцирования с шагами.

Формулы, используемые калькулятором производных

Калькулятор производных обратных функций использует приведенную ниже формулу для нахождения производных функции. Формула производной:

$$ \frac{dy}{dx} = \lim\limits_{Δx \to 0} \frac{f(x+Δx) – f(x)}{Δx} $$ 92 x $$

Связанный: Нажмите на исчисление, если хотите изучить различные способы нахождения производной функции.

Производные правила, используемые Калькулятором дифференцирования

С помощью производной мы можем найти наклон функции в любой заданной точке. Правила дифференцирования используются для вычисления производной функции. Наиболее важные правила дифференцирования:

$$ \frac{d}{dx} (f(x) \pm g(x)) = \frac{d}{dx}f(x) \pm \frac{d }{dx}g(x) $$

9{n-1} $$

Постоянное множественное правило:

$$ \frac{d}{dx}[cf(x)] = c. \frac{d}{dx}f(x) $$

Здесь c = реальное число

Правило суммы и разности:

Правило продукта:

$$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x) \frac{d}{dx}[g(x)] + g(x) \frac{ d}{dx}[f(x)] $$

или

$$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x)g'(x) + g(x)f'(x) $$

Вы также можете использовать калькулятор производных правил произведения для обучения и практики. 92} $$

Также найдите калькулятор производной частного правила для более точных вычислений.

Этот веб-сайт предоставляет полное решение для дифференцирования и всех расчетов, связанных с деривативами. Найдите калькулятор частичной дифференцировки и калькулятор производной по направлению на этом веб-сайте, чтобы еще больше укрепить свои представления о дифференцировании.

Как работает калькулятор производных?

Калькулятор производных с шагами — это онлайн-инструмент, который использует формулы и правила производных для вычисления точных результатов. Калькулятор дифференциации позволяет пользователям вводить данные в виде уравнения.

Калькулятор дифференцирования затем решает это уравнение, используя другие правила производных или формулы. Если вы хотите продолжить расчет, используйте калькулятор второй производной с шагами.

Кроме того, если вы хотите рассчитать его выше, на этом сайте есть другое решение для вас. Вы можете использовать калькулятор третьей производной с шагами на этой платформе, чтобы получить точные результаты.

Как найти калькулятор производных?

Онлайн-калькулятор производных найти несложно. Вы можете либо ввести полный URL-адрес этого калькулятора дифференциации в своей поисковой системе, либо выполнить поиск в Google по его названию. Вы можете выполнить поиск в Google с помощью «калькулятора производной» или «калькулятора обратной производной», и вы найдете наш новейший и точный онлайн-инструмент.

Связанный: На этой платформе вы также можете найти аппроксимацию касательной с помощью калькулятора линеаризации. Вы также можете получить большую помощь от бесплатного онлайн-калькулятора производных цепного правила.

Как использовать калькулятор производных с шагами?

Наш дифференциальный калькулятор очень прост в использовании, так как вам необходимо следовать приведенной ниже процедуре:

Напишите свое уравнение в первом поле ввода или загрузите любое уравнение, нажав на кнопку.
Выберите переменную, которую вы хотите дифференцировать.
Выберите, сколько раз вы хотите различать.
Нажмите кнопку «РАССЧИТАТЬ».

Сразу после нажатия на кнопку расчета наш калькулятор дифференцирования решит ваше уравнение и предоставит подробные результаты. Эти результаты помогут вам понять и изучить концепцию, практикуясь во время выполнения.

Для закрепления расчетов относительно нормальной линии уравнения, вам нужно попробовать калькулятор уравнения нормальной линии, предлагаемый этим веб-сайтом.

Связанные калькуляторы

Существует множество других калькуляторов, связанных с дифференциальным калькулятором, которые вы можете использовать на этом веб-сайте бесплатно. Эти инструменты:

Калькулятор производной в точке
Калькулятор n-ой производной
Калькулятор крайних точек
Калькулятор уклона криволинейной линии
Калькулятор производных графиков
Калькулятор производной касательной линии
Калькулятор 4-й производной
Калькулятор производной обратной функции
Калькулятор второго неявного дифференцирования
Определение калькулятора производной
Калькулятор 5-й производной
Калькулятор 6-й производной

Часто задаваемые вопросы

Как дифференцировать функцию f(x)=5,4x+2,4?

Данная функция:

$$ f(x) \;=\; 5.4x+2.4 $$

Дифференцирование с обеих сторон по ‘x’

$$f'(x) \;=\; d/dx(5. 4x+2.4)$$

Имеем,

$$ f'(x) \;=\; d/dx(5.4x)+d/dx(2.4) $$ $$ f'(x) \;=\; 5.4(1)+0 \;=\; 5.4 $$

Таким образом, мы можем различать эту простую функцию вручную. Кроме того, мы также можем использовать дифференциальный калькулятор функций для онлайн-расчетов.

Как вычислить производную функции?

Чтобы вычислить производную функции, необходимо выполнить следующие шаги:

Помните, что производная — это вычисление скорости изменения функции.
Применить производную к функции по независимой переменной, входящей в функцию.
Упростите функцию, чтобы получить точное значение производной.

Та же процедура использовалась калькулятором производных для расчета скорости изменения функции в режиме онлайн.

Что такое производная x?

Производная x равна 1. Она относится к результату, полученному дифференцированием x различными способами. Нахождение скорости изменения функции включает в себя процесс дифференцирования. Таким образом, вы можете найти калькулятор производной для этого процесса. 9⁡2x $$

Производная от cos ² x является производной тригнометрической функции, которая несколько сложна для студентов, которые не могут запомнить тригнометрические тождества. Для таких студентов решатель производных является отличным инструментом для вычисления производной тригонометрической функции.

Как отличить e

^x?

Поскольку производная экспоненциальной функции с основанием “e” равна e ^x , дифференцирование e в степени x эквивалентно самому e в степени x. Математически это записывается как d/dx (e ^х) = е ^х.

Это может оцениваться в дифференцирующем решателе для перекрестной проверки ответа и его шагов онлайн.

Алан Уокер

Последнее обновление 28 февраля, 2023

Я математик, технарь и автор контента. Я люблю решать шаблоны различных математических запросов и писать так, чтобы все могли понять. Математика и технология сделали свое дело, и теперь пришло время извлечь из этого пользу.

Калькулятор производных с шагами | Дифференциальный калькулятор