Частота колебаний в контуре: Частота электромагнитных колебаний – формула

2={1\over LC}$$

Рис. 2. График электрических колебаний в контуре.

Формула Томсона

Из последнего соотношения можно получить значение периода электромагнитных колебаний:

$$T={2\pi\over \omega}={2\pi\sqrt{LC}}$$

Данная формула впервые была получена У. Томсоном и носит его имя.

Рис. 3. У. Томсон (Кельвин).

Из данной формулы можно видеть, что время одного колебания (период) тем дольше, тем больше индуктивность и емкость. Это происходит потому, что большая емкость требует больше времени для полной зарядки. А большая индуктивность при изменении тока порождает большую ЭДС самоиндукции, которая, согласно правилу Ленца, направлена так, чтобы сопротивляться причине, ее порождающей. Таким образом, ток через большую индуктивность меняется медленнее, что также увеличивает период колебаний.

Во многих случаях удобнее использовать формулу частоты электромагнитных колебаний, которая получается из формулы Томсона, если учесть, что период и частота – взаимно обратны:

$$\nu ={1\over 2\pi\sqrt{LC}}$$

Что мы узнали?

Простейшей системой, в которой возможны электромагнитные колебания, является колебательный контур, состоящий из катушки индуктивности и конденсатора. Частота электромагнитных колебаний в контуре может быть получена из значений емкости конденсатора и индуктивности катушки с использованием формулы Томсона.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.4

Средняя оценка: 4.4

Всего получено оценок: 97.

---

А какая ваша оценка?

Колебательный контур — что это такое? Формулы и схемы

Сегодня нас ждёт увлекательный эксперимент: мы перейдём от этапа «вообще не понимаю, что это» к «надо же, как всё просто и логично» всего за одну статью. Не верите? Мы вам обещаем! Мы поговорим о колебательных контурах, электромагнитных волнах и том, как мы встречаемся с этими понятиями в обычной жизни.

Колебания

Начнём обсуждение этой темы с колебаний.

В обычной жизни мы часто слышим это слово: «цветок колеблется на ветру», «я не могу принять решение, колеблюсь», «температура воздуха колеблется в диапазоне…». Но что такое колебания в физике?

Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.

Попробуйте привести несколько примеров такого движения. Верно, к колебаниям можно отнести движение стрелки, вращение качели, качание маятника часов.

Колебания бывают вынужденными и свободными.

• Вынужденные колебания — это колебания, происходящие под действием внешней периодически меняющейся силы.

  Посадите свою маленькую сестрёнку или братишку на качели: раскачивая их, вы станете той самой внешней силой, под действием которой качели движутся, совершая при этом вынужденные колебания.

• Свободные колебания — это колебания, происходящие под действием внутренних сил в колебательной системе.

  Груз колеблется на нити или пружине — вот самый распространённый пример свободных колебаний. Такие колебания всегда затухающие, потому что ни у одной системы нет бесконечного запаса энергии для такого движения: рано или поздно колебание прекратится.

Что может совершать свободные колебания? Математический (груз + нить) и пружинный (груз + пружина) маятники, а также электромагнитные волны.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Электромагнитные волны

В курсе школьной физики 8-го класса вы изучали отдельно главы про электричество и магнетизм, и только в 9–10-х классах узнали, что такое разделение не совсем верно. Дело в том, что электричество и магнетизм — две стороны одной монеты, они не могут существовать друг без друга. Движущееся электрическое поле порождает магнитное, а движущееся магнитное поле порождает электрическое. Эти поля распространяются в пространстве одновременно и, что удивительно, в разных плоскостях. Взгляните на рисунок!

Электромагнитные волны — это распространение в пространстве с течением времени переменных (вихревых) электрических и магнитных полей.

Вихревым электрическим полем называется поле, силовые линии которого представляют собой замкнутые линии.

В разрезе этой темы стоит запомнить две фамилии: Максвелл и Герц. Вот увидите, как сойдёт с ума от счастья учитель физики, когда вы их назовёте. 😅 Джеймс Максвелл описал основные положения электромагнитной теории, а Генрих Герц доказал существование электромагнитных волн опытным путём.

К электромагнитным волнам относятся радио, Wi-Fi и даже свет. Более подробно об этом можно прочесть в нашей статье.

Что такое колебательный контур?

Колебательный контур — это устройство, в котором могут происходить свободные электромагнитные колебания.

Также можно сказать, что колебательный контур — это электрическая цепь, работа которой порождает электромагнитное поле.

Но зачем кому-то создавать такие колебания?

Колебательные контуры — неотъемлемая часть многих производственных процессов. С их помощью изготавливают радиоприёмники, генераторы сигналов, блоки измерения частоты, контроллеры частоты напряжения на двигателях.

Возможно, вам может показаться, что это устройство давно устарело и используется в каких-то непонятных вещах, но стоит понимать, что без них не было бы возможно создание домофона, электромагнитов, различных датчиков, с которыми мы встречаемся ежедневно.

Колебательный контур состоит из двух компонентов: катушки и конденсатора, и выглядит вот так:

Катушка индуктивности (или соленоид) — это стержень с несколькими слоями обмотки медной проволокой.

Именно он создаёт колебания в колебательном контуре. Стержень, находящийся в середине катушки, называется дроссель, или сердечник.

Катушка способна создавать колебания, только если есть электрический заряд. Она обладает низким сопротивлением.

Конденсатор — это элемент, способный накопить в себе большое количество электрического заряда. Он состоит из двух обкладок, между которыми находится диэлектрик (вещество, не проводящее электрический ток).

В чём его отличие от обычного аккумулятора? В аккумуляторе происходит превращение механической, химической, световой и других энергий в электрическую, в конденсаторе же накапливается заряд, который он может отдать весь сразу.

Часто в электрическую цепь колебательного контура подключают ещё один элемент — резистор, который обладает сопротивлением и контролирует силу тока и напряжение в цепи.

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Виды колебательных контуров

По типу соединения колебательные контуры можно разделить на последовательный и параллельный.

Колебательный контур, схема последовательного соединенияКолебательный контур, схема параллельного соединения

Также физики выделяют особый тип контура — идеальный.

Идеальный колебательный контур — контур, сопротивление которого отсутствует, порождая при этом незатухающие свободные электромагнитные колебания.

Как вы думаете, можно ли создать такой контур и работать с ним на практике? К сожалению, такое маловероятно. Идеальный колебательный контур — всего лишь математическая модель, допущение, с помощью которого можно вывести формулы, ускорить расчёты и оценить характеристики контура в производстве.

Характеристики колебательного контура

Главные характеристики как параллельного, так и последовательного колебательного контура:

Индуктивность катушки — это показатель, который численно равен электродвижущей силе (в вольтах), возникающей в цепи при изменении силы тока на 1 А за 1 секунду. Измеряется в генри (Гн).

Когда катушка подключена к цепи постоянного тока, то её индуктивность описывает энергию магнитного поля, которое создается этим током по формуле:

, где W — энергия магнитного поля, L — индуктивность, I — сила тока в цепи.

Индуктивность зависит от геометрических размеров контура и магнитных свойств среды (сердечника).

Электроёмкость — характеристика конденсатора, равная отношению заряда конденсатора к напряжению, под которым он находится. Измеряется в фарадах (Ф).

Электроёмкость можно вычислить по следующим формулам:

• , где e₀ — диэлектрическая проницаемость материала диэлектрика (табличная величина), S — площадь обкладок конденсатора, d — расстояние между пластинами.
• , где q — заряд, U — напряжение в цепи.

Кстати, 1 фарад — весьма большая величина, поэтому электроёмкость конденсатора чаще всего выражается в пико- или нанофарадах.

Принцип действия колебательного контура

Итак, каким же образом работает колебательный контур? Разделим процесс на два этапа.

Первый этап

Второй этап (обратный)

Заряженная положительно пластина конденсатора начинает разряжаться. Ток поступает в электрическую цепь, протекая от положительного заряда к отрицательному через соленоид. В контуре возникают электромагнитные колебания. Ток разряда конденсатора, проходя по виткам катушки, порождает магнитное поле. В катушке возникает ЭДС самоиндукции, препятствующая мгновенной разрядке конденсатора, ток нарастает постепенно. С ростом тока разряда убывает электрическое поле в конденсаторе, но возрастает магнитное поле катушки. В момент, когда поле конденсатора исчезнет (конденсатор разрядится), магнитное поле катушки будет максимальным. Ток, пройдя через соленоид, переходит на вторую пластину и заряжает её положительно (в то время как первая обкладка, с которой шёл ток, получает отрицательный заряд).

Процесс происходит в обратном порядке: Разрядившись окончательно, конденсатор благодаря энергии ЭДС катушки, которая в этот момент будет максимальна, начнёт заряжаться вновь. По мере заряда ток ослабевает, а вместе с ним и магнитное поле. Ток проходит через катушку с положительно заряженной пластины (той, которая в начале первого этапа была заряжена отрицательно) на отрицательно заряженную. Все заряды встают на свои первоначальные места.

Цикл повторяется до тех пор, пока на конденсаторе будет заряд. В идеальном колебательном контуре этот процесс происходил бы бесконечно, а в реальном неизбежны потери энергии, и колебания затухают.

Формула Томпсона

Характеристики L и С колебательного контура связаны между собой с помощью формулы Томпсона, которая описывает период свободных колебаний в LC-контуре:

, где T — период электромагнитных колебаний, L — индуктивность катушки колебательного контура, C — ёмкость конденсатора, π — число пи.

Эта формула для колебательного контура является одной из основных, обратите на неё особенное внимание!

Закон сохранения энергии в колебательном контуре

В колебаниях, как и в любом другом движении, работают законы сохранения энергии. Как именно это выражается?

Принцип работы контура основан на трансформации энергии, превращении электрической энергии в магнитную и наоборот. Тогда энергию колебательного контура можно описать так:

W = WC(t) + WL(t) = const

Когда энергия электрического поля становится максимальной, энергия магнитного поля равна нулю, что работает и в обратном направлении.

Этап	Энергия электрического поля	Энергия магнитного поля
1	Максимальна при q max:	0
2	0	Максимальна при I max::

Так как энергии достигают своего максимума с равным числовым значением, сделаем вывод:

Резонанс в LC-контуре

Обещаем, последнее на сегодня!

Помимо вышеперечисленных характеристик, есть ещё одна величина, которая описывает колебания в контуре, и это резонансная частота.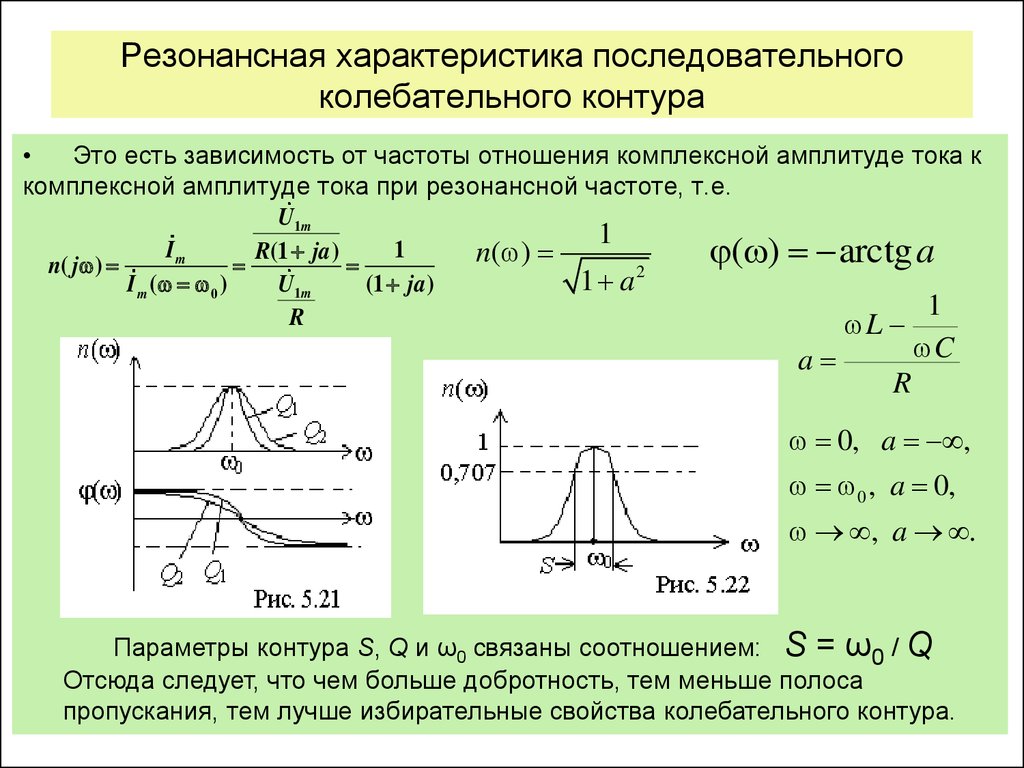

Ну, здесь всё просто. Помним, что частота колебаний и период — взаимно обратные величины, а значит:

«Ну хорошо», — скажете вы, «и в чём вообще суть?».

А вот в чём: в электрическом колебательном контуре резонанс (резкое увеличение амплитуды колебаний) происходит на определённой частоте, когда индуктивность L и ёмкость C уравновешены. Благодаря этому энергии могут свободно циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Наше сегодняшнее путешествие в мир физики было весьма увлекательным, хоть и непростым, согласны? На онлайн-курсе физики в школе Skysmart вы сможете ещё больше утвердиться в мысли, что физика — наука для жизни, а ещё подготовитесь к экзаменам и научитесь уверенно и без затруднений делать лабораторные работы.

Руководство по колебательным частотам в электронике

Ключевые выводы

• Узнайте, что такое частоты колебаний.

• Исследуйте применение колебательных частот в электронике.

• Понять, как компенсировать потери энергии в генераторах.

Когда я активно играл на пианино, у меня было почти идеальное чувство ритма. Даже без метронома у меня не возникнет проблем с сохранением ритма на протяжении всего музыкального произведения. Прошло несколько десятков лет с тех пор, как я в последний раз касался пианино. Мое чувство ритма, к сожалению, ухудшилось.

В последнее время я постоянно пропускаю ритм, когда напеваю любимую мелодию. Это прекрасный пример того, как отсутствие практики может притупить чувства. И я должен проглотить свою гордость, снова сделав метроном своим лучшим другом. Качающийся маятниковый стержень метронома напоминает мне о роли колебательных частот в электронике.

Что такое колебательные частоты?

Возможно, лучший способ визуализировать колебательные частоты — это подумать об океанских волнах. У волн есть свои взлеты и падения, когда они постоянно ударяются о берег. Когда вы обратите внимание на волны, вы будете загипнотизированы периодическим звуком грохота.

Есть три важных элемента для колеблющихся частот: период времени, амплитуда и длина волны. Период времени указывает интервал между полным циклом колебаний, тогда как амплитуда – это максимальная и минимальная точки колебания.

Как колебания выглядят в форме волны.

Из периода времени частоту колебательной волны можно рассчитать по следующей формуле:

Частота (f) = 1/ период времени

Будь то океанские волны или звук, для совершения одного цикла колебаний требуется минимальное физическое расстояние. Этот параметр называется длиной волны и представляет собой физическое измерение между одной и той же точкой на последовательных интервалах.

Частоты колебаний в электронике

При проектировании электроники вы обязательно столкнетесь с частотами колебаний и соответствующими цепями. Функционирование многих компонентов зависит от точных частот колебаний. В отличие от естественных океанских волн, осциллирующие волны в электронике часто неоднородны по периоду времени и амплитуде.

Постоянная и точная частота колебаний используется для питания часов реального времени в конструкциях. Часы зависят от кристалла, часто 32,768 кГц, чтобы обеспечить необходимые «такты» для увеличения регистров часов. Микроконтроллеры также зависят от постоянной частоты колебаний для выполнения своего кода с требуемой скоростью.

Цепи генератора также используются в телевизорах, радио и других типах радиопередатчиков. Они генерируют несущий сигнал с определенной частотой, который затем модулируется информацией. На приемной стороне резонатор настраивается на частоту колебаний, чтобы улавливать и демодулировать радиочастотный сигнал.

Существует несколько типов осцилляторов, но в основе их лежит схема LC. Он также известен как контур бака LC. Ток колеблется между полностью заряженным конденсатором и катушкой индуктивности по закону Ленца. Когда катушка индуктивности заряжается, создается обратная ЭДС, противодействующая изменениям тока, которая заряжает конденсатор в противоположном направлении.

Цепь бака LC, общая сердцевина цепей генератора.

Потери энергии на колебательных частотах

В идеале LC-цепь будет генерировать непрерывный колебательный сигнал с одинаковой амплитудой после начала цикла. Однако идеальная синусоидальная форма колебаний невозможна в реальной LC-схеме. Полное сопротивление компонентов и соединений приводит к потерям энергии с течением времени.

Затухающие колебания с постепенно уменьшающейся амплитудой.

В результате у вас будут затухающие колебания, амплитуда которых постепенно уменьшается. Чтобы LC-схема достигла непрерывных колебаний, на нее должен поступать сигнал обратной связи. Сигнал обратной связи используется для усиления существующего и для компенсации потерь.

Практическое применение схемы генератора часто включает такие варианты, как генератор с настроенным коллектором, генератор с настроенным генератором, генератор Хартли и генератор Колпитца. Эти схемы генератора используют либо транзистор, либо операционный усилитель для усиления колебательного сигнала.

При проектировании автономного колебательного контура важно убедиться, что он не имеет ни избыточного, ни недостаточного демпфирования. Это означает обеспечение того, чтобы коэффициент усиления с обратной связью Aβ был равен 1. A — коэффициент усиления схемы усилителя, а β — коэффициент усиления цепи обратной связи.

Расчет коэффициента усиления с обратной связью более сложен, чем определение частоты колебаний. Следовательно, использование правильного программного обеспечения для проектирования печатных плат помогает сократить время проектирования. Allegro PCB Editor позволит повысить эффективность процесса проектирования, а Allegro PSPICE Designer предоставляет полезные возможности моделирования.

Если вы хотите узнать больше о том, какое решение у Cadence есть для вас, обратитесь к нам и нашей команде экспертов.

Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.

Подпишитесь на LinkedIn Посетить сайт Больше контента от Cadence PCB Solutions

УЧИТЬ БОЛЬШЕ

14.5 Колебания в LC-цепи – University Physics Volume 2

Глава 14. Индуктивность

Цели обучения

К концу этого раздела вы сможете:

• Объяснять, почему заряд или ток колеблются между конденсатором и индуктивностью, соответственно, при последовательном соединении
• Опишите взаимосвязь между зарядом и током, колеблющимся между конденсатором и катушкой индуктивности, соединенными последовательно

Стоит отметить, что и конденсаторы, и катушки индуктивности накапливают энергию в своих электрических и магнитных полях соответственно. Цепь, содержащая катушку индуктивности ( L ) и конденсатор ( C ), может колебаться без источника ЭДС, перемещая энергию, хранящуюся в цепи, между электрическим и магнитным полями. Таким образом, концепции, которые мы развиваем в этом разделе, непосредственно применимы к обмену энергией между электрическим и магнитным полями в электромагнитных волнах или свете. Мы начнем с идеализированной цепи с нулевым сопротивлением, которая содержит катушку индуктивности и конденсатор, 9{2}}{С}.[/латекс]

Когда переключатель замкнут, конденсатор начинает разряжаться, создавая ток в цепи. Ток, в свою очередь, создает магнитное поле в индукторе. Конечным результатом этого процесса является передача энергии от конденсатора с его уменьшающимся электрическим полем к индуктору с его увеличивающимся магнитным полем.

Рисунок 14.16  (a–d) Колебания накопления заряда при изменении направления тока в LC-цепи. д) На графиках показано распределение заряда и тока между конденсатором и катушкой индуктивности. 9{2}.[/латекс]

После достижения своего максимума [латекс]{I}_{0},[/латекс] ток i(t) продолжает переносить заряд между обкладками конденсатора, тем самым перезаряжая конденсатор. Поскольку индуктор сопротивляется изменению тока, ток продолжает течь, даже если конденсатор разряжен. Этот непрерывный ток заставляет конденсатор заряжаться с противоположной полярностью. Электрическое поле конденсатора увеличивается, а магнитное поле индуктора уменьшается, и общий эффект заключается в передаче энергии от индуктора 9.0031 обратно на конденсатор. Согласно закону сохранения энергии, максимальный заряд, который вновь приобретает конденсатор, равен [латекс]{q}_{0}.[/латекс] Однако, как показано на рис. 14.16(в), пластины конденсатора заряжены против . к тому, чем они были изначально.

При полной зарядке конденсатор снова передает свою энергию катушке индуктивности, пока снова не разрядится полностью, как показано на рис. 14.16(d). Затем в последней части этого циклического процесса энергия возвращается к конденсатору, и восстанавливается исходное состояние цепи. 9{2}\text{/}2[/латекс]. При отсутствии трения в системе масса-пружина колебания продолжались бы бесконечно. Точно так же колебания цепи LC без сопротивления будут продолжаться вечно, если их не беспокоить; однако эта идеальная схема LC с нулевым сопротивлением непрактична, и любая схема LC будет иметь по крайней мере небольшое сопротивление, которое со временем будет излучать и терять энергию.

Частота колебаний в безрезистивном 9{2}.[/латекс]

Эквивалентность двух систем очевидна. Чтобы перейти от механической системы к электромагнитной, мы просто заменим m на L , v на i , k на 1/ C и x на2 q . Теперь x(t) равно

.

[латекс] х \ влево (т \ вправо) = А \ фантом {\ правило {0.2em} {0ex}} \ текст {cos} \ влево (\ омега т + \ varphi \ вправо) [/латекс]

, где [латекс]\омега =\sqrt{k\текст{/}м}.[/латекс] Следовательно, заряд конденсатора в Цепь LC задана

[латекс] q \ влево (т \ вправо) = {q} _ {0} \ фантом {\ правило {0.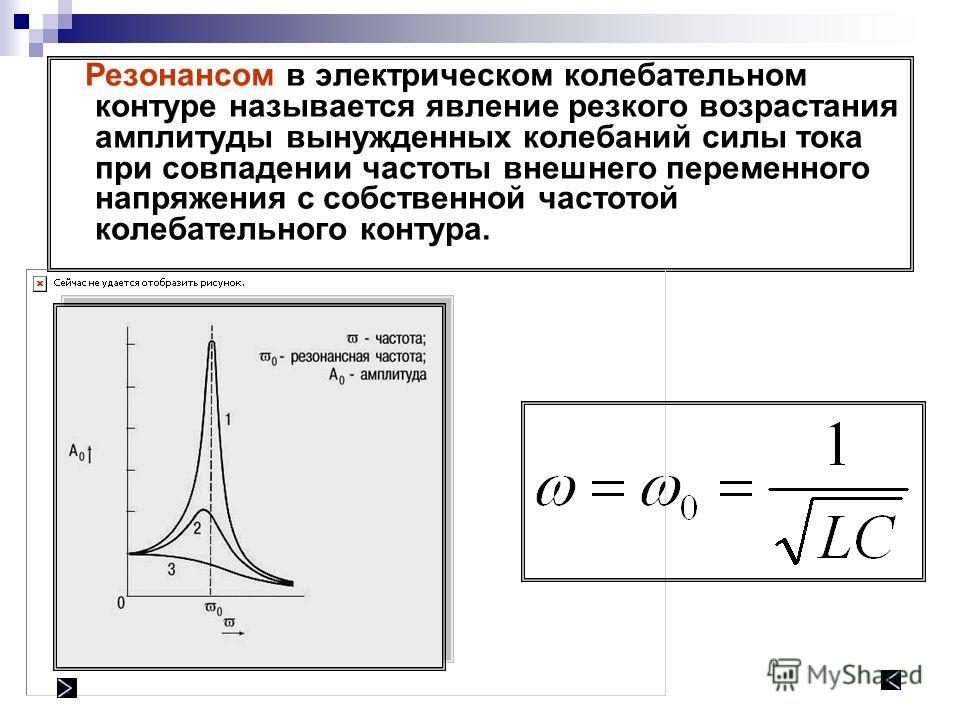 2em} {0ex}} \ текст {cos} \ влево (\ омега т + \ varphi \ вправо) [ /латекс]

где угловая частота колебаний в контуре

[латекс]\омега =\sqrt{\frac{1}{LC}}.[/латекс]

Наконец, ток в цепи LC находится путем взятия производной по времени от q(t) :

[латекс] я \ влево (т \ вправо) = \ гидроразрыва {dq \ влево (т \ вправо)} {дт} = \ текст {-} \ омега {q} _ {0} \ фантом {\ правило {0,2 em}{0ex}}\text{sin}\left(\omega t+\varphi \right).[/latex] 9{-5}[/latex] C. (a) Какова угловая частота колебаний в цепи? б) Каков максимальный ток, протекающий по цепи? в) Через какое время конденсатор полностью разрядится? (d) Найдите уравнение, которое представляет q(t) .

Стратегия

Угловая частота цепи LC определяется уравнением 14.41. Чтобы найти максимальный ток, максимальная энергия в конденсаторе устанавливается равной максимальной энергии в катушке индуктивности. Время, в течение которого конденсатор разрядится, если он изначально заряжен, составляет четверть периода цикла, поэтому, если мы вычислим период колебаний, мы сможем узнать, какую четверть этого времени нужно найти. {3}t\right).[/latex]

Значение

Соотношение энергий, установленное в части (b), — не единственный способ приравнивания энергий. В большинстве случаев некоторая энергия сохраняется в конденсаторе, а некоторая энергия хранится в катушке индуктивности. Мы можем поместить оба термина в каждую часть уравнения. Исследуя цепь только при отсутствии заряда на конденсаторе или отсутствии тока в катушке индуктивности, мы упрощаем уравнение энергии.

Проверьте свои знания

Угловая частота колебаний в 9{3}[/latex] рад/с. (a) Если [латекс]L=0,10\фантом{\правило{0,2em}{0ex}}\текст{H}[/латекс], чему равно C ? (b) Предположим, что при [latex]t=0,[/latex] вся энергия запасается в индукторе. Каково значение [latex]\varphi ?[/latex] (c) Второй идентичный конденсатор подключен параллельно исходному конденсатору. Какова угловая частота этого контура?

Показать раствор

а. [латекс] 2,5 мк\текст {F}[/латекс]; б. [латекс]\pi \text{/}2\phantom{\rule{0.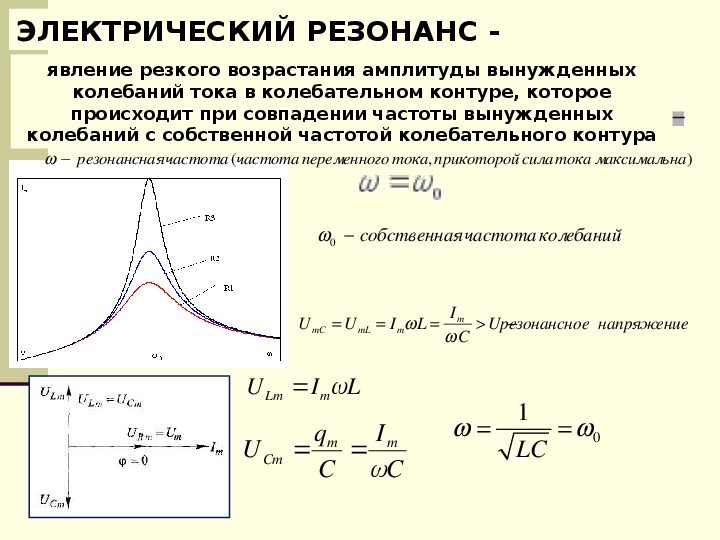 {3} \ фантом {\ правило {0.2em} {0ex} }\text{рад/с}[/латекс]

Резюме

• Энергия, передаваемая колебательным образом между конденсатором и катушкой индуктивности в цепи LC , происходит с угловой частотой [латекс]\омега =\sqrt{\frac{1}{LC}}[/latex] .
• Заряд и ток в цепи задаются как

  [латекс]\begin{array}{ccc}\hfill q\left(t\right)& =\hfill & {q}_{0}\phantom{\rule {0.2em}{0ex}}\text{cos}\left(\omega t+\varphi \right),\hfill \\ \hfill i\left(t\right)& =\hfill & \text{-}\ omega {q}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin}\left(\omega t+\varphi \right).\hfill \end{array}[/latex]

Концептуальные вопросы

Применяются ли правила Кирхгофа к цепям, содержащим катушки индуктивности и конденсаторы?

Показать решение

да

Может ли элемент схемы иметь как емкость, так и индуктивность?

Что в схеме LC определяет частоту и амплитуду колебаний энергии в катушке индуктивности или в конденсаторе?

Показать решение

Амплитуда колебаний энергии зависит от начальной энергии системы.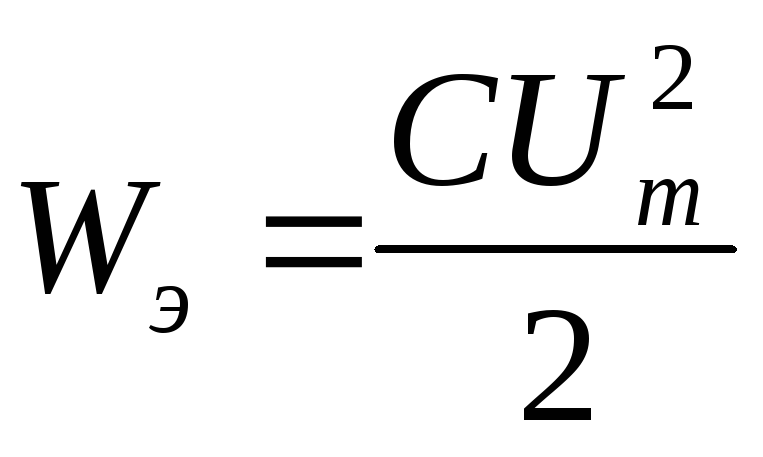 Частота в 9Схема 0031 LC зависит от значений индуктивности и емкости.

Проблемы

Конденсатор емкостью 5000 пФ заряжается до 100 В, а затем быстро подключается к катушке индуктивности 80 мГн. Определите (а) максимальную энергию, запасенную в магнитном поле индуктора, (б) пиковое значение тока и (в) частоту колебаний цепи.

Собственная индуктивность и емкость схемы LC составляют 0,20 мГн и 5,0 пФ. С какой угловой частотой колеблется контур? 9{-7}\phantom{\rule{0.2em}{0ex}}\text{s}[/latex]

Собственная индуктивность и емкость колебательного контура LC составляют [латекс]L=20\phantom{\rule{0.2em}{0ex}}\text{мГн и}\phantom{\rule{0.2em}{ 0ex}}C=1.0\phantom{\rule{0.2em}{0ex}}\mu \text{F},[/latex] соответственно. а) Какова частота колебаний? б) Если максимальная разность потенциалов между пластинами конденсатора равна 50 В, какова максимальная сила тока в цепи?

В качающемся LC , максимальный заряд конденсатора [латекс]{q}_{м}[/латекс].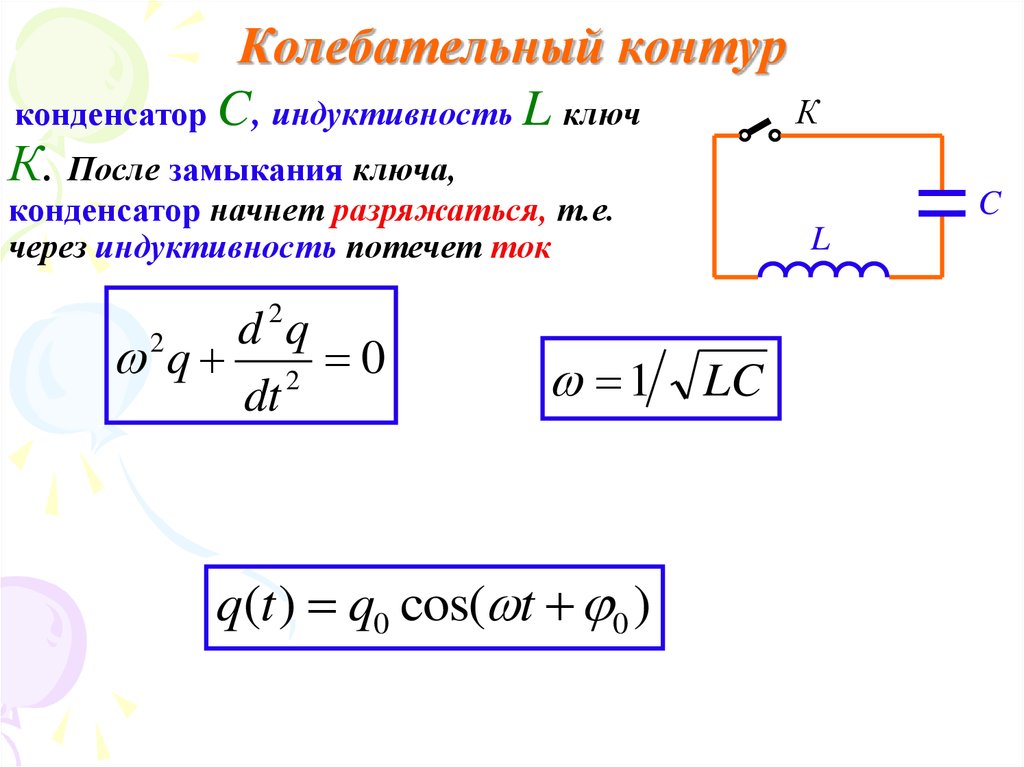 Определить заряд конденсатора и ток через катушку индуктивности, когда энергия распределяется поровну между электрическим и магнитным полями. Выразите ответ в терминах [латекс]{q}_{m}[/латекс], L и C .

Показать решение

[латекс]q=\frac{{q}_{m}}{\sqrt{2}},I=\frac{{q}_{m}}{\sqrt{2LC}} [/латекс]

В схеме, показанной ниже, [латекс]{\текст{S}}_{1}[/латекс] одновременно размыкается и [латекс]{\текст{S}}_{2}[/латекс] закрывается. Определить: а) частоту результирующих колебаний, б) максимальный заряд конденсатора, в) максимальный ток через катушку индуктивности, г) электромагнитную энергию колебательного контура. 9{-12}\phantom{\rule{0.2em}{0ex}}\text{F}\hfill \end{массив}[/latex]

Глоссарий

LC схема

Цепь

, состоящая из источника переменного тока, катушки индуктивности и конденсатора

.

Лицензии и атрибуты

Колебания в цепи LC. Автор: : Колледж OpenStax.