Чем скорость отличается от ускорения: Отличие скорости от ускорения

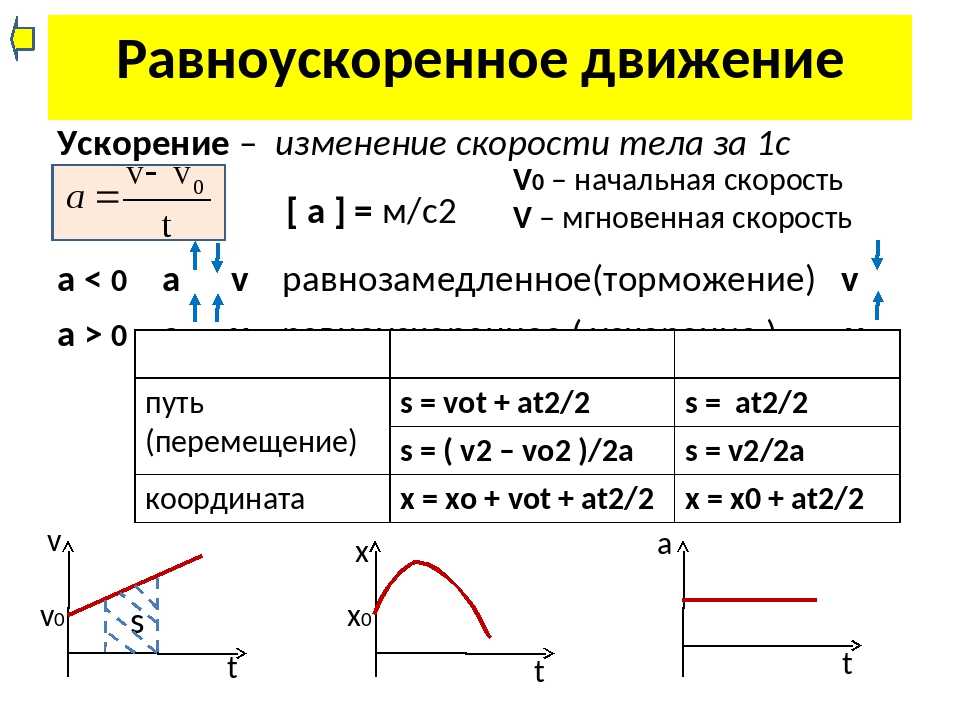
Разница между скоростью и ускорением

Скорость и ускорение — это разные понятия, используемые при обсуждении движения. Следовательно, они оба связаны с движением.

Содержание

1

Скорость используется для определения одного термина, а другой основан на изменении скорости. Оба имеют много общего и также используются для одной и той же цели.

Однако их значение существенно отличается, и они используются для определения в первую очередь разных вещей. 

Скорость против ускорения 

Основное различие между скоростью и ускорением заключается в том, что они имеют разные значения. Термин скорость используется для описания скорости объекта в заданном направлении. Метр в секунду (м/с) — это единица измерения. С другой стороны, когда объект меняет свою скорость относительно времени, это ускорение. Метр/секунда ² (РС²) — единица, используемая для его измерения.  

Объекты движутся с заданной скоростью, и их скорость описывает их направление. Это определяет скорость, с которой кто-то или что-то меняет положение относительно времени или скорость движущегося объекта из одного места в другое.

Метры в секунду (м/с), километры в час (км/ч), мили в час (миль/ч) — единицы, используемые для измерения скорости.  

Термин ускорение используется для описания изменения скорости во времени. В дополнение к своей величине, она также включает в себя направление в вектор выражение.

Скорость или направление движущегося объекта может увеличиваться или уменьшаться, когда объект ускоряется. Он показывает, как движение тела изменяется во времени. 

Таблица сравнения скорости и ускорения 

Параметры сравнения	Скорость	Ускорение
Ед. изм	Метр в секунду является единицей измерения.	Метр/секунда 2 (РС2) — единица измерения.
Расчет	Смещение используется для расчета.	Скорость используется для расчета.
констатирует	В каком направлении и с какой скоростью движется объект.	Изменение скорости движущегося объекта во времени.
Движение	Отрицательное, положительное или ноль.	Отрицательный или положительный. Не может быть нулем.
Смысл	Термин скорость используется для описания скорости объекта в заданном направлении.	Когда объект меняет свою скорость относительно времени, это Ускорение.

Что такое скорость? 

Объекты движутся с заданной скоростью, и их скорость описывает их направление. Это определяет скорость, с которой кто-то или что-то меняет положение относительно времени или скорость движущегося объекта из одного места в другое.

Следовательно, это перемещение объекта, деленное на время перемещения. Он может быть отрицательным, положительным или нулевым.  

Метры в секунду (м/с), километры в час (км/ч), мили в час (миль/ч) — единицы, используемые для измерения скорости.

Двумя возможными значениями скорости являются средняя скорость объекта (расчет его скорости за период) и его мгновенная скорость (его скорость в определенный момент времени).

В каком направлении и с какой скоростью движется предмет, это и определяется понятием. 

Отслеживание тканей эхокардиография (TTE) в первую очередь касается отслеживания точки или интересующей области. Как правило, скорость относится к скорости, с которой движется миокард.

Во время систолы миокард движется к верхушке с положительной скоростью. Диастолическая скорость сердца во время диастолы отрицательна. Смещение сегмента миокарда – это то, насколько далеко он смещается от своего исходного положения.

Единицей эхокардиографии плода являются миллиметры, и она указывается положительно.  

Что такое ускорение? 

Термин ускорение используется для описания изменения скорости во времени. В дополнение к своей величине, она также включает в себя направление в вектор выражение.

Его компоненты, такие как направление, указывают на изменение скорости и направления объекта. Он может быть отрицательным или положительным. Однако она никогда не может быть равна нулю, так как для нее всегда должно быть какое-то движение.  

Метр/секунда 2 (м/с2) — это единица измерения. Считается, что объект ускоряется или его скорость увеличивается, когда ускорение параллельно скорости.

И наоборот, когда ускорение антипараллельно скорости, объект замедляется или замедляется. Кроме того, составляющая ускорения, параллельная скорости, указывает, насколько изменилось направление объекта.  

Различают два типа ускорения, а именно: центростремительный и Тангенциальный. Равномерная скорость при круговом движении, таком как вращение Земли, называется центростремительным ускорением, поскольку направление объекта изменяется.

С другой стороны, тангенциальное ускорение возникает, когда меняется не направление, а скорость. Изменение во времени скорости движущегося объекта определяется понятием. 

Основные различия между скоростью и ускорением 

1. Термин «скорость» в значительной степени используется для описания скорости объекта в заданном направлении. С другой стороны, термин «ускорение» в основном используется для описания изменения скорости во времени.  
2. Первый определяется с помощью смещения. С другой стороны, последняя определяется с помощью скорости.  
3. Отрицательной, положительной или нулевой может быть скорость. С другой стороны, отрицательное или положительное значение может использоваться для обозначения ускорения. Однако он никогда не может быть равен нулю.  
4. Формула, используемая для расчета первого, представляет собой перемещение объекта, деленное на время перемещения. С другой стороны, формула, используемая для расчета последней, состоит в делении изменения скорости на время, в течение которого это изменение произошло.   
5. Скорость в основном используется для определения того, в каком направлении и с какой скоростью движется объект. С другой стороны, ускорение в основном используется для определения изменения скорости движущегося объекта во времени. 

Заключение 

Скорость и ускорение — это разные понятия, используемые при обсуждении движения. Следовательно, они оба связаны с движением. Скорость используется для определения одного термина, а другой основан на изменении скорости.

Оба имеют много общего и также используются для одной и той же цели. Однако их значение существенно отличается, и они используются для определения в первую очередь разных вещей.  

Двумя возможными значениями скорости являются средняя скорость объекта (расчет его скорости за период) и его мгновенная скорость (в определенный момент времени).

В каком направлении и с какой скоростью движется предмет, это и определяется понятием.   

Считается, что объект ускоряется или его скорость увеличивается, когда ускорение параллельно скорости.

И наоборот, когда ускорение антипараллельно скорости, объект замедляется или замедляется. Кроме того, компонент Ускорения, параллельный скорости, указывает, насколько изменилось направление объекта.

Концепция устанавливает изменение скорости движущегося объекта во времени. 

Рекомендации 

1. https://link.springer.com/article/10.1140/epjb/e2005-00304-3 
2. https://psycnet.apa.org/record/1976-06066-001 

Один запрос?

Я приложил столько усилий, чтобы написать этот пост в блоге, чтобы предоставить вам ценность. Это будет очень полезно для меня, если вы подумаете о том, чтобы поделиться им в социальных сетях или со своими друзьями/родными. ДЕЛИТЬСЯ ♥️

Пиюш Ядав

Пиюш Ядав занимается всеми темами, связанными с наукой. На сегодняшний день опубликовано более 3000 статей, и цель Пиюша – помочь студентам получить образование в области науки, будь то физика, химия или биология.

Piyush работает над тем, чтобы обеспечить наилучшие различия и сравнения. Он также имеет специализацию по физике.

Линейная скорость через угловую, теория и онлайн калькуляторы

Линейная скорость через угловую, теория и онлайн калькуляторы

Определение

Мгновенной (истинной) скоростью ($\overline{v}$) называют векторную физическую величину, равную производной от вектора перемещения по времени ($t$):

\[\overline{v}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta \overline{r}}{\Delta t}=\frac{d\overline{r}}{dt}\ }\left(1\right).\]

$\Delta \overline{r}$- вектор перемещения материальной точки, это перемещение точка совершает за отрезок времени $\Delta t$.

Выражение линейной скорости через угловую скорость

Скорость называют мгновенной, так как ее значение показывает величину скорости в определенный момент времени.

Так как вектор перемещения $\Delta \overline{r}$ направлен по хорде, которая соединяет две близкие точки криволинейной траектории движения частицы, при уменьшении расстояния между этими точками, вектор $\Delta \overline{r}$ занимает положение касательной к линии, по которой движется частица.

Из определения (1) следует, что мгновенная скорость направлена по касательной к траектории движения.

Скорость прохождения пути ($s$) определяют:

\[v={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta s}{\Delta t}=\frac{ds}{dt}\left(2\right).\ }\]

Мгновенную скорость называют линейной тогда, когда хотят подчеркнуть ее отличие от угловой скорости.

Если материальная точка движется по окружности, то ее положение характеризуют при помощи угла поворота ($\varphi $), который образует радиус-вектор ($\overline{r}$), определяющий положение рассматриваемой точки А с выделенным неизменным направлением от которого производят отсчет (рис.1).

Быстроту изменения угла поворота $\varphi $ характеризуют при помощи такой физической величины как угловая скорость. Обычно угловую скорость обозначают буквой $\omega $. Угловая скорость равна:

\[\omega =\frac{d\varphi }{dt}\left(3\right).\]

Вращение называют равномерным, если угловая скорость постоянна $\omega =const$. При равномерном вращении $\omega $ можно называть угловой частотой.

Линейная скорость движения точки по окружности связана с угловой скоростью. Пусть точка проходит путь равный длине дуги XA (рис.1). Этот путь обозначим $s$. Если радиус окружности равен$\ R=const$, то длину дуги найдем как:

\[s=R\varphi \ \left(4\right).\]

Продифференцируем обе части выражения (4) по времени, имеем:

\[\frac{ds}{dt}=\frac{d\left(R\varphi \right)}{dt}=R\frac{d\varphi }{dt}\left(5\right).\]

Мы видим, что в левой части получена величина линейной скорости, в правой части радиус окружности умножен на угловую скорость:

\[v=R\omega \left(6\right).\]

Формула (6) будет справедлива при движении точки по криволинейной траектории отличной от окружности, но в этом случае $R$ – радиус кривизны траектории в месте нахождения частицы.

В векторном виде выражение (6) записывают так:

\[\overline{v}=\overline{\omega }\times \overline{r}\left(7\right),\]

$\overline{r}$ – вектор, соединяющий ось вращения и движущуюся точку (рис. 2). Модуль скорости, используя формулу (7) найдем как:

\[v=\omega r{\sin \alpha \ \left(8\right),\ }\]

где $\alpha $ – угол между вектором угловой скорости и $\overline{r}.$

Угловая скорость через линейную

Исходя из приведенных выше формул угловую скорость можно выразить через линейную. При движении по окружности:

\[\omega =\frac{v}{R}\left(9\right).\]

Или используя формулу (8) угловую скорость выразим как:

\[\omega =\frac{v}{r{\sin \alpha \ }}\left(10\right).\]

Примеры задач с решением

Пример 1

Задание. Диск равномерно вращается вокруг оси (O), перпендикулярной его плоскости, проходящей через его центр (рис.3). Линейная скорость точки A равна $v_1$, Точка B находится на расстоянии $\Delta l$ ближе к оси и имеет лилейную скорость $v_2$. Какова угловая скорость вращения диска ($\omega $)?

Решение. Основой для решения задачи будет формула:

\[\omega =\frac{v}{R}\left(1.1\right).\]

Угловые скорости движения точки A и B одинаковы (${\omega }_A={\omega }_B$), запишем выражение для каждой из этих скоростей используя (1.1):

\[{\omega }_A=\frac{v_1}{R_1};;\ {\omega }_B=\frac{v_2}{R_2}\left(1.2\right).\]

$R_1$ – расстояние от точки O до точки A; $R_2=R_1-\Delta l$ – расстояние от точки B до точки O. Приравняем правые части выражений (1.2), выразим расстояние $R_1$:

\[\frac{v_1}{R_1}=\frac{v_2}{R_1-\Delta l}\to R_1=\frac{\Delta l\cdot v_1}{v_1-v_2}\left(1.3\right).\]

Найдем угловую скорость точки A:

\[{\omega }_A=v_1\cdot \frac{v_1-v_2}{\Delta l\cdot v_1}=\frac{v_1-v_2}{\Delta l}.\]

Ответ. Угловая скорость всех точек диска равна $\omega =\frac{v_1-v_2}{\Delta l}$

Пример 2

Задание.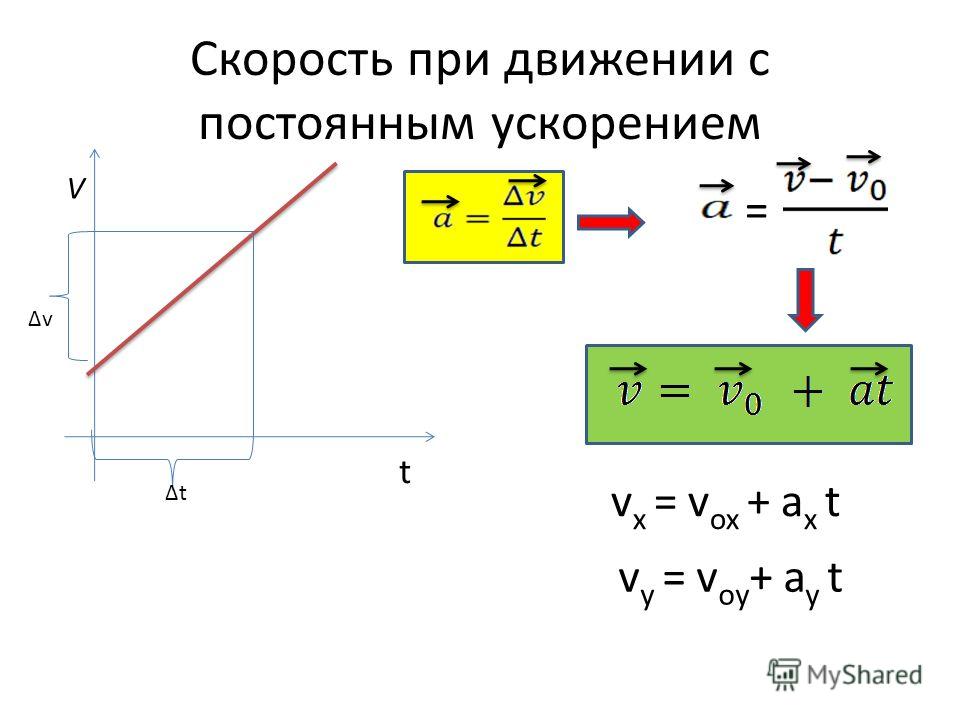 2=15\ \left(\frac{м}{с}\right).\]

Ответ. $v\left(t’\right)=15\frac{м}{с}$

Читать дальше: масса и плотность вещества.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Разница между скоростью и ускорением в табличной форме

Механика

Скорость против ускорения

Скорость и ускорение — два основных условия движения. Скорость — это расстояние, пройденное объектом в единицу времени, а ускорение — скорость изменения скорости. В этом посте мы объяснили разницу между скоростью и ускорением.

 Что такое скорость?

Скорость — это физическая величина, представляющая расстояние, пройденное объектом за определенный интервал времени. Например, если объект прошел 6 метров за 30 секунд, его скорость будет именно такой, 6 метров каждые 30 секунд.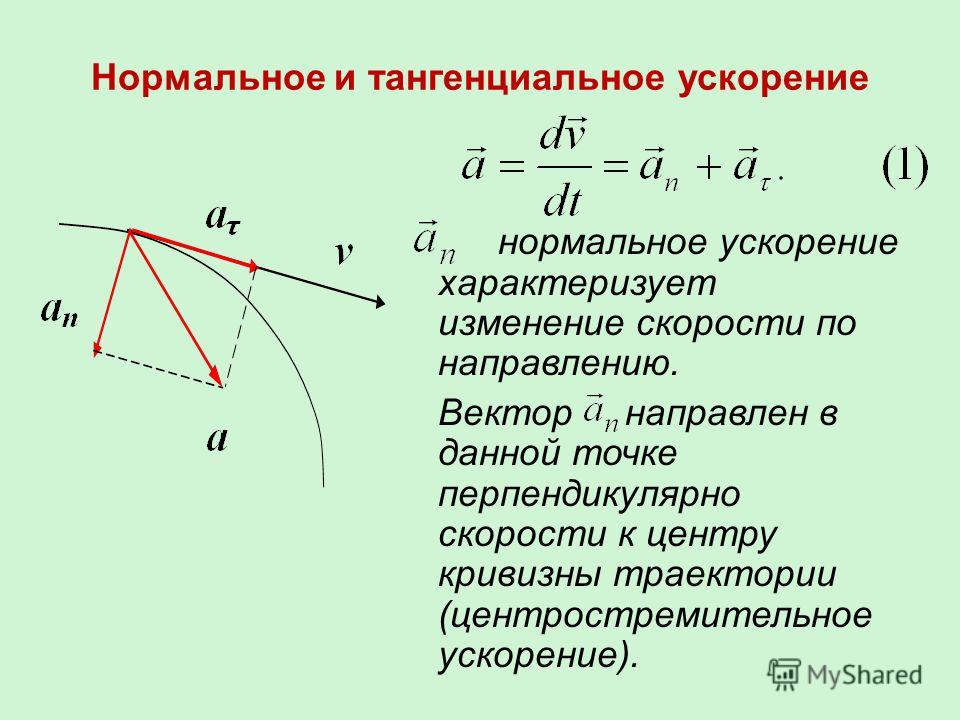 В Международной системе единиц скорость выражается в метрах в секунду (м/с), поэтому эта скорость будет равна 0,2 м/с.
Одним из математических свойств скорости является то, что она является векторной величиной, что означает, что она определяется векто r, и поэтому необходимо учитывать направление движения. Если направление не принимается во внимание, в физике говорят о скорости или скорости, скалярной величине с теми же размерностями пространства и времени, что и скорость, но которая не является вектором.
Чтобы вычислить скорость, просто разделите пройденное расстояние на затраченное время:
v = s/t
Скорость также используется в других областях, помимо физики движения, с аналогичной концепцией. Например, в химии скорость или скорость реакции используется для измерения скорости, с которой субстраты превращаются в продукты, что также подразумевает направление вектора.
См. также: Разница между скоростью и скоростью

Что такое ускорение?

Ускорение — это величина, связанная со скоростью, поскольку она измеряет скорость изменения скорости в заданный период. Продолжая предыдущий пример, если объект проходит 6 метров за 30 секунд, его средняя скорость будет 0,2 м/с, но это не означает, что объект постоянно двигался с этой скоростью в течение 30 секунд. В течение одной секунды он был в состоянии двигаться со скоростью 0,4 м/с, а в течение другой секунды он был способен развивать скорость 0,1 м/с, хотя результат также составляет 6 метров за 30 секунд.
Если объект меняет скорость, это изменение измеряется ускорением, которое рассчитывается как разность скоростей в единицу времени (скорость/время). Например, если объект переходит из состояния покоя (скорость 0 м/с) в скорость 0,2 м/с за 1 секунду, его ускорение составит 0,2 м/с ² , значит, скорость объекта увеличивается на 0,2 м/с каждую секунду. Если теперь объект перейдет от движения со скоростью 0,2 м/с к движению со скоростью 0,3 м/с и совершит этот переход за 2 с, то ускорение будет:
0,3 – 0,2 = 0,1 / 2 = 0,05 м/с ²
Это означает, что скорость увеличивается на 0,05 метра каждую секунду. Можно сказать, что ускорение измеряет скорость изменения скорости. Ускорение может быть отрицательным, если скорость в конце рассматриваемого периода меньше скорости в начале, что известно как замедление или отрицательное ускорение.
Ускорение, в отличие от скорости, не подразумевает направление, в котором движется объект, поэтому это не векторная величина . Если объект движется с постоянной скоростью, его ускорение равно нулю.

Ключевые отличия

1. Скорость измеряет скорость движения  объекта, то есть расстояние, пройденное за единицу времени.
2. Ускорение измеряет скорость изменения скорости , то есть изменение скорости между двумя разными моментами.

Связанные темы:

• Скорость 
• Разница между скоростью и скоростью
• Формула ускорения
• Разница между угловой и тангенциальной скоростью
• Мгновенная скорость
• Терминальная скорость
• Разница между ускорением и скоростью

Связанные артистики

Связанные артистики

.

Обогатите свои знания с помощью наших информативных блогов

• Забронировать демо-класс

Прежде чем понять различия между тремя терминами, необходимо понять всю концепцию и определения.

Итак, давайте разберемся с концепцией на примере.

Рассмотрим картинку, на которой люди бегут по полю. Итак, размышляя об этом, что приходит на ум?

Может быть, вы подумаете о скорости, чтобы объяснить, как быстро они бегают?

Или вы можете подумать об ускорении, чтобы объяснить, как бегуны на картинке набирают скорость?

А некоторые могут подумать о скорости, чтобы объяснить направление, в котором они бегут?

Но что означают эти термины? Поскольку все три термина связаны с движением, в чем между ними разница?

Говоря о терминах, связанных с движением, важно начать с обсуждения системы отсчета.

Движение обычно описывает изменение движения, местоположения или направления объекта, а термины скорость, ускорение и скорость описывают движение объекта.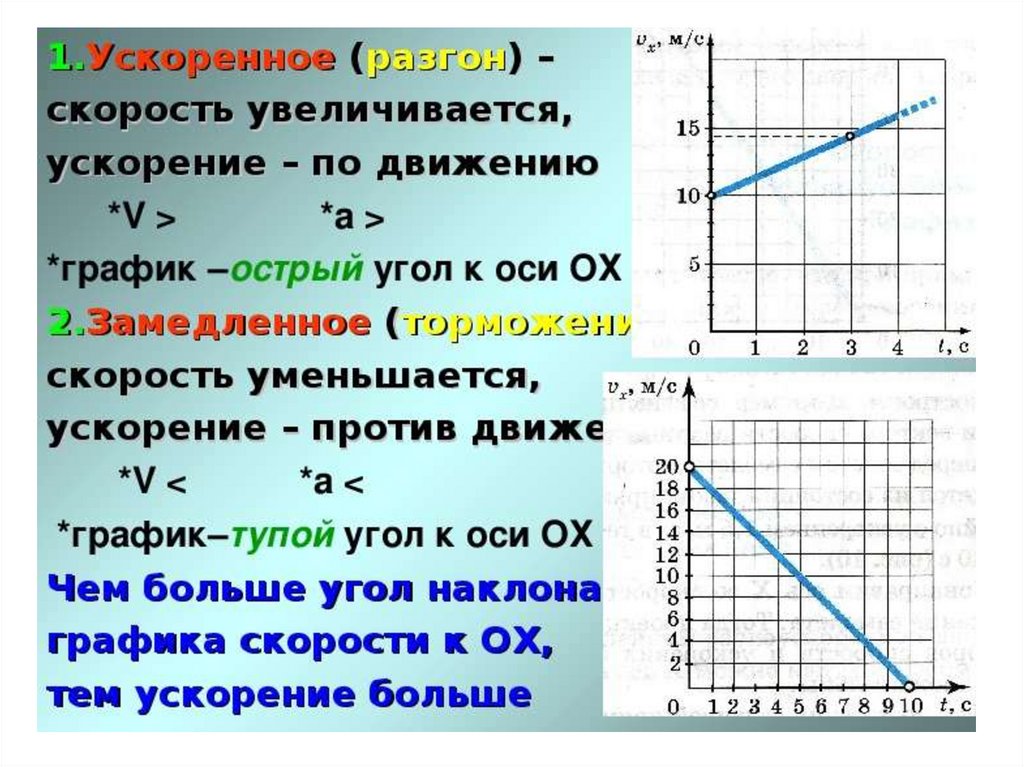

Забронируйте 60-минутный бесплатный пробный урок СЕЙЧАС!

Итак, это система отсчета. Познакомимся со всеми тремя терминами по отдельности.

Скорость

Скоростью называется расстояние, пройденное за единицу времени независимо от направления. Таким образом, здесь единственной величиной важности является скалярная величина.

Скорость обычно используется для измерения скорости движения объекта и рассчитывается путем деления его пути на время, необходимое для преодоления расстояния.

Скорость объекта может быть рассчитана как расстояние/время

Скорость

Скорость относится к расстоянию, пройденному за единицу времени в определенном направлении. Итак, здесь важны и направление, и величина, и они являются векторной величиной.

В нем указано, что «Как быстро объект движется и в каком направлении?» Скорость также измеряется в тех же единицах, что и скорость, но в этом случае также указывается направление движения.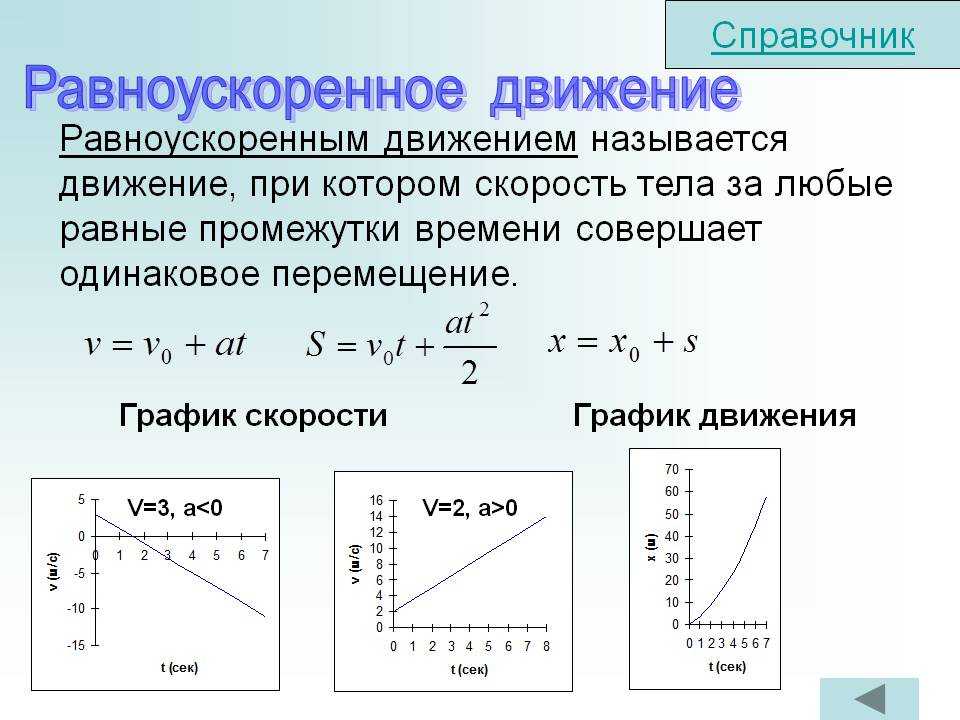

Скорость можно рассчитать как перемещение/время

Ускорение

Ускорение относится к скорости изменения скорости объекта. Здесь учитываются и направление, и величина, поэтому это векторная величина.

В нем говорится, что «Как быстро скорость объекта меняется со временем?» По сути, это скорость изменения скорости в течение определенного периода времени.

Ускорение можно рассчитать как a=v-u/t

Где «a» — ускорение, «v» — конечная скорость, «u» — начальная скорость, а «t» — время.

Давайте теперь сосредоточимся на ключевых различиях между всеми тремя терминами.

Забронируйте 60-минутный бесплатный пробный урок СЕЙЧАС!

Разница между скоростью, ускорением и временем

Параметры сравнения	Скорость	Ускорение	Скорость
Количество Тип	Скалярная величина	Вектор Количество	Вектор Количество
Определяющие факторы	Расстояние и время	Скорость и время	Перемещение и время
Связь с движением	Скорость движения	Направление и скорость движения	Скорость изменения скорости
Формула	Расстояние/Время	Скорость/Время	Смещение/Время
Единицы измерения	м/с, км/ч, миль/ч	м/с 2	м/с
Констатирует	С какой скоростью движется объект?	Как быстро скорость объекта меняется со временем?	С какой скоростью движется объект и в каком направлении?

 

Заключение

Все три термина могут быть определены как

Скорость — это скорость изменения расстояния, представляющая, какое расстояние пройдено за определенное время.